Interlaminar fracture toughness of ultra-high molecular weight polyethylene fiber reinforced composite laminates
-
摘要: 作为装甲解决方案的一组重要材料，超高分子量聚乙烯(UHMWPE)纤维增强复合材料在冲击作用下主要的破坏模式之一是分层脱粘。针对UHMWPE复合材料层合板提出一种改进的双悬臂梁(DCB)试件，研究了其I型层间断裂韧性(GIC)和失效特性，分析了DCB试件厚度及纤维铺层方向对GIC的影响，讨论了层间断裂破坏机制及结构塑性对裂纹扩展过程的影响，评估了现有试验标准中层间断裂韧性计算方法的适用性。结果表明：较小厚度的DCB试件呈现明显的塑性行为，由此测得的层间断裂韧性受结构塑性的影响显著，适当增加试件厚度可有效避免塑性的影响。本文结果为UHMWPE复合材料进一步的动态层间性能及其理论模型的研究提供实验参考和数据支撑，对复合材料防护结构设计具有重要的工程意义。Abstract: Ultra-high molecular weight polyethylene (UHMWPE) fiber reinforced composites are considered as state-of-the-art materials for armor solutions, and interlaminar delamination is one of the main failure mechanisms for the composites under impact loadings. For UHMWPE composite laminates, an improved double cantilever beam (DCB) specimen was proposed. The interlaminar fracture toughness (GIC) and failure characteristics were then studied. Analysis were conducted regarding the influence of the specimen thickness and fiber layups on the GIC. The failure mechanism of interlaminar fracture and the effect of structural plasticity on the crack propagation process were further discussed. Evaluation was also implemented on the applicability of the existing test standards for the calculation of the interlaminar fracture toughness. Results show that the DCB specimen with small thickness exhibits obvious plastic behavior, and the measured interlaminar fracture toughness is significantly affected by structural plasticity. Increasing the thickness of the specimen can effectively avoid the influence of plasticity. Conclusively, the results presented in this paper provide experimental reference and data support for the study of dynamic interlaminar properties and theoretical models of UHMWPE composites, that have important engineering significance for the design of composite protective structures.
-
工程用水泥基复合材料(Engineered cementitious composites，ECC)是一种通过微观力学和断裂力学原理对材料体系进行系统设计和优化的短纤维乱向水泥基复合材料[1-2]，国内外学者围绕ECC的受拉、受弯等基本力学性能开展了大量相关研究工作，并取得了众多优异成果[3-8]。然而ECC的抗拉强度仍然有限，用于结构加固时对构件的抗拉、抗弯承载力和抗裂性能的增强效果有限，仍需与性能优异的增强材料共同使用，为此，众多学者相继开展筋材、网材等用于增强ECC受力性能的研究。
Fischer等[9]、Mihashi等[10]进行了钢筋增强ECC单轴拉伸试验，结果表明，钢筋增强ECC试件裂缝分布更加均匀，减小了裂缝宽度，提高了变形能力。郑宇宙等[11]、朱忠锋等[12]对纤维增强ECC复合材料进行了单轴拉伸试验，结果表明，增强材料可以明显改善ECC的受拉性能，其轴向刚度、极限承载力也得到了显著提高。但是已研究的增强材料中，采用普通钢筋时，ECC的优越性能不能完全发挥，使用纤维编织网增强材料又降低了经济性。而高强不锈钢绞线抗拉强度高，具有良好的耐腐蚀性能和经济性。相关学者对高强不锈钢绞线加固混凝土结构的研究表明，其能有效提高加固构件的抗弯、抗剪承载力和刚度[13-17]。目前该加固技术已成功应用于实际工程，并取得了优异的效果[18-19]。
综上分析，高强不锈钢绞线网是由不锈钢绞线编制而成，本身具有很强的耐腐蚀、抗锈蚀能力；ECC具有良好的裂缝分散能力，正常使用状态裂缝宽度很小[1-10]，二者结合后，可以使ECC开裂后钢绞线不发生锈蚀，耐久性好。因此，朱俊涛等[20]提出了新型高性能复合材料“高强不锈钢绞线网增强ECC”。已对高强不锈钢绞线网与ECC的粘结锚固性能[21-22]进行了试验和理论研究，结果表明，在试验所得的粘结滑移曲线中，平均粘结应力达到峰值开始微下降至峰值的85%左右之后，即进入延性强化段，该阶段平均粘结应力不再降低，仅滑移量呈水平线增长，说明高强不锈钢绞线网与ECC具有良好的粘结锚固性能。为了尽快使该复合材料在实际工程中得到应用，本文对高强不锈钢绞线网增强ECC的受拉性能进行试验和理论研究。
1. 试验概况
1.1 试件设计及材性试验
为了研究ECC抗拉强度、高强不锈钢绞线网受拉方向配筋率及高强不锈钢绞线网增强ECC试件宽度三个影响因素对高强不锈钢绞线增强ECC抗拉性能的影响，共设计了9组试件，每组3个共27个试件，各组试件参数见表1。为了避免试件在加载过程中在变截面处应力集中破坏，本试验受拉试件均采用哑铃型试件，试件变截面处为弧形，试件示意图如图1所示。试验中ECC的两种配合比见刘伟康[5]研究成果，试件标准养护28天。对预留的ECC受拉薄板试件(280 mm×40 mm×15 mm)进行拉伸试验，得到两种ECC配合比的抗拉性能，各组试件的ECC抗拉性能见表2。高强不锈钢绞线直径均为2.4 mm，对其进行拉伸试验(3根)，得到高强不锈钢绞线应力-应变曲线如图2所示。
表 1 高强不锈钢绞线网增强工程水泥基复合材料(ECC)试件参数Table 1. Parameters of engineered cementitious composites(ECC) reinforced by high-strength stainless steel wire mesh specimensGroup number Test section width bc /mm Steel strand spacing/mm Reinforcement ratio of steel strand TC12 80 50 0.0028 TC22 70 40 0.0032 TC32 60 30 0.0037 TC42 50 20 0.0048 TC52 90 30 0.0037 TD12 80 50 0.0028 TD22 70 40 0.0032 TD32 60 30 0.0037 TD42 50 20 0.0048 ![]()
图 1 高强不锈钢绞线网增强ECC试件设计详图(虚线表示钢绞线)Figure 1. Design details of ECC reinforced by high-strength stainless steel wire mesh specimens (Dotted line indicates steel strand)表 2 ECC受拉试验结果Table 2. Tensile test results of ECCGroup number Tensile strength/MPa Ultimate tensile strain Cracking stress/MPa Cracking strain TC12 3.53 0.0179 2.45 0.000204 TC22 3.53 0.0179 2.45 0.000204 TC32 3.53 0.0179 2.45 0.000204 TC42 3.53 0.0179 2.45 0.000204 TC52 3.53 0.0179 2.45 0.000204 TD12 3.46 0.0297 2.39 0.000189 TD22 3.46 0.0297 2.39 0.000189 TD32 3.46 0.0297 2.39 0.000189 TD42 3.46 0.0297 2.39 0.000189 ![]()
图 2 高强不锈钢绞线应力-应变曲线Figure 2. Stress-strain curves of high-strength stainless steel strand1.2 加载及测试方法
单轴拉伸试验采用100 kN电液伺服万能试验机。试验加载采用位移控制，加载速率为0.2 mm/min。试件正反面分别粘贴应变片，测试区段两侧面分别布置量程为30 mm的位移计。
1.3 试验现象及机制分析
高强不锈钢绞线网增强ECC试件受拉试验的加载装置如图3(a)所示。当荷载达到极限荷载的25%~30%时，在试件接近中间位置表面出现一条细微裂缝(如图3(b)所示)，宽度仅为0.02 mm。随着荷载的增加，试件表面不断出现新的裂缝，已有的裂缝宽度缓慢增大；当荷载增加到极限荷载的85%~90%，裂缝数量达到饱和状态(如图3(c)所示)，试件表面布满相互平行的细微裂缝，此时各试件的最大裂缝宽度为0.2~0.28 mm，该状态的荷载远远超过了规范GB 50010—2010[23]规定的正常使用极限状态。继续加载，试件表面不再出现新裂缝，已有裂缝变宽。达到极限荷载时，试件表面的某条裂缝发展成主裂缝，同时伴随着明显的纤维拔出和断裂声，随后主裂缝处的纵向高强不锈钢绞线拉断。试件破坏形态如图3(d)所示。
![]()
图 3 高强不锈钢绞线网增强ECC试件受拉破坏过程Figure 3. Tensile failure process of ECC reinforced by high-strength stainless steel wire mesh specimens分析上述试验现象发现，高强不锈钢绞线的加入增加了ECC裂缝分散能力，其机制主要是钢绞线表面的螺旋进一步限制了ECC裂缝的开展，使受拉试件在达到极限承载力的85%~90%时，最大裂缝宽度依然满足规范GB 50010—2010[23]中正常使用极限状态裂缝要求。充分表明了本文研究的新型复合材料高强不锈钢绞线网增强ECC具有良好的抗裂性能；验证了高强不锈钢筋网和ECC具有很好的粘结性能。
2. 试验结果及分析
2.1 试验结果
各组高强不锈钢绞线网增强ECC试件拉伸试验结果见表3 (试验值均取同一组试件的平均值，应力为试验拉力除以受力面积)。
表 3 高强不锈钢绞线网增强ECC试件拉伸试验结果Table 3. Tensile test results of ECC reinforced by high-strength stainless steel wire mesh specimensGroup number Cracking stress/MPa Cracking strain Ultimate tensile stress/MPa Ultimate tensile strain Elastic modulus/MPa TC12 2.20 0.000156 7.09 0.030874 14 471 TC22 2.25 0.000162 7.94 0.034056 14 122 TC32 2.41 0.000171 8.77 0.030581 14 492 TC42 2.56 0.000182 10.65 0.034815 14 578 TC52 2.54 0.000181 8.82 0.033683 14 642 TD12 1.97 0.000145 6.41 0.031929 14 216 TD22 1.99 0.000149 7.81 0.043660 14 727 TD32 2.07 0.000139 8.62 0.041116 14 460 TD42 2.19 0.000159 10.30 0.035051 14 496 2.1.1 试件宽度对高强不锈钢绞线网增强ECC受拉性能的影响
对比表3中TC32组和TC52组试件，结果表明，增大截面宽度对受拉试件的开裂应力和极限应力几乎没有影响。
2.1.2 高强不锈钢绞线配筋率对高强不锈钢绞线网增强ECC受拉性能的影响
对比表3中TC12~TC42及TD12~TD42试件的试验结果可知，随着高强不锈钢绞线配筋率的增大，受拉试件的开裂应力略有增大，极限应力明显增大。
2.1.3 ECC抗拉强度对高强不锈钢绞线网增强ECC受拉性能的影响
对比表3中TC12组与TD12组、TC22组与TD22组、TC32组与TD32组及TC42组与TD42组试件结果可知，随着ECC抗拉强度的增大，受拉试件的开裂应力和极限应力均明显增大。
2.2 高强不锈钢绞线网增强ECC受拉应力-应变曲线
高强不锈钢绞线网增强ECC试件在单轴荷载作用下的受拉应力-应变曲线如图4所示。可知，高强不锈钢绞线网增强ECC试件受拉应力-应变曲线呈现出明显的两阶段特征，故可将其分为两个阶段：(1)可表征为弹性阶段，从试件开始加载到试件开裂为止，为峰值的25%~30%。在该阶段ECC和不锈钢绞线均处于弹性工作状态；应力-应变曲线接近为直线；(2)可表征为弹塑性阶段，对应于试件ECC开裂至完全破坏(纵向高强不锈钢绞线拉断)。该阶段应力-应变曲线为非线性关系，试件表现出明显的弹塑性性质。此阶段主要是ECC裂缝出现和发展，由于裂缝处的聚乙烯醇(PVA)纤维尚未从水泥基中拔出或拉断，而高强不锈钢绞线表面的螺旋增大了与ECC的粘结力。因此，该阶段ECC和高强不锈钢绞线依然共同承担拉力，亦是高强不锈钢绞线网增强ECC受拉的主要阶段。由图4还可以看出，极限应力是开裂应力的3~5倍，极限应变为开裂应变的200倍以上，达到3%~5%，超过了本文采用的ECC和高强不锈钢绞线本身的极限拉应变，显示了该新型高性能复合材料优越的变形能力。
![]()
图 4 高强不锈钢绞线网增强ECC试件受拉应力-应变曲线Figure 4. Tensile stress-strain curves of ECC reinforced by high-strength stainless steel wire mesh specimens3. 高强不锈钢绞线网增强ECC受拉本构模型
3.1 模型提出
由图4可知，高强不锈钢绞线网增强ECC受拉应力-应变曲线可分为弹性阶段(OA段)和应变硬化阶段(AB段)。弹性阶段即认为应力-应变为线性关系；弹塑性(应变硬化)阶段应力由ECC和钢绞线共同承担，其本构模型由二者应力-应变关系组合而成。同时考虑该阶段高强不锈钢绞线网和ECC可能产生相对滑移，用γ表示钢绞线的应力发挥系数。本文提出了高强不锈钢绞线网增强ECC受拉本构模型，如图5所示。其表达式如下：
![]()
图 5 高强不锈钢绞线网增强ECC受拉应力-应变曲线模型Figure 5. Tensile stress-strain curve model of ECC reinforced by high-strength stainless steel wire meshσse={Eseεse(εse⩽ (1) 式中：σse、σse,cr和σse,u分别为高强不锈钢绞线网增强ECC试件的受拉应力、开裂应力和极限拉应力；σe和σs分别为ECC和高强不锈钢绞线的应力；Ese为高强不锈钢绞线网增强ECC的弹性模量；εse、εse,cr和εse,u分别为高强不锈钢绞线网增强ECC试件的受拉应变、开裂应变和极限拉应变；γ为高强不锈钢绞线的应力发挥系数；ρs为高强不锈钢绞线的配筋率。
3.2 模型参数分析
3.2.1 弹性阶段
高强不锈钢绞线网增强ECC受拉试件开裂前，由高强不锈钢绞线和ECC共同承担外部荷载；该阶段高强不锈钢绞线网与ECC间无滑移。根据应变协调原理得出弹性阶段高强不锈钢绞线网增强ECC受拉试件的弹性模量Ese如下式：
{E_{\rm{se}}} = {E_{\rm{e}}} + {E_{\rm{s}}}\frac{{{A_{\rm{s}}}}}{{{A_{\rm{se}}}}} (2) 式中：Ee和Es分别为ECC和高强不锈钢绞线的弹性模量；Ase和As分别为高强不锈钢绞线网增强ECC和高强不锈钢绞线的截面面积。
3.2.2 弹塑性阶段
首先建立高强不锈钢绞线受拉本构模型。对本试验得到的高强不锈钢绞线应力-应变曲线(图2)采用三次多项式进行拟合，如下式：
\frac{{{\sigma _{\rm{s}}}}}{{{\sigma _{\rm{s,u}}}}} = a\frac{{{\varepsilon _{\rm{s}}}}}{{{\varepsilon _{\rm{s,u}}}}} + (3 - 2a){\left( {\frac{{{\varepsilon _{\rm{s}}}}}{{{\varepsilon _{\rm{s,u}}}}}} \right)^2} + (a - 2){\left( {\frac{{{\varepsilon _{\rm{s}}}}}{{{\varepsilon _{\rm{s,u}}}}}} \right)^3}\tag{3a} (3a) 式中：σs,u为高强不锈钢绞线的极限拉应力；εs和εs,u分别为高强不锈钢绞线应变和极限拉应变。
根据式(3a)，基于最小二乘法对试验数据进行回归分析，得到待定常数a的值。对三组数据进行拟合，其值分别为3.37、3.26和3.36。由拟合结果可知，各组值较接近，故可取其平均值a=3.33。将a代入式(3a)，则有：
\frac{{{\sigma _{\rm{s}}}}}{{{\sigma _{\rm{s,u}}}}} = 3.33\frac{{{\varepsilon _{\rm{s}}}}}{{{\varepsilon _{\rm{s,u}}}}} - 3.66{\left( {\frac{{{\varepsilon _{\rm{s}}}}}{{{\varepsilon _{\rm{s,u}}}}}} \right)^2} + 1.33{\left( {\frac{{{\varepsilon _{\rm{s}}}}}{{{\varepsilon _{\rm{s,u}}}}}} \right)^3}\tag{3b} (3b) ECC的受拉应力-应变关系采用刘伟康[5]的研究成果，如下式：
\!\!\!\!\!\!\quad{\sigma _{\rm{e}}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{\sigma _{\rm{e,cr}}}}}{{{\varepsilon _{\rm{e,cr}}}}}{\varepsilon _{\rm{e}}}}&{\;\;\left( {{\varepsilon _{\rm{e}}} \leqslant {\varepsilon _{\rm{e,cr}}}} \right)}\\ {\left( {0.31\dfrac{{{\varepsilon _{\rm{e}}}}}{{{\varepsilon _{\rm{e,u}}}}} + 0.69} \right){\sigma _{\rm{e,u}}}}&{\left( {{\varepsilon _{\rm{e,cr}}} \leqslant {\varepsilon _{\rm{e}}} \leqslant {\varepsilon _{\rm{e,u}}}} \right)} \end{array}} \right. (4) 式中：σe,cr和σe,u为ECC的开裂应力和极限拉应力；εe、εe,cr和εe,u为ECC的应变、开裂应变和极限拉应变。
3.2.3 高强不锈钢绞线应力发挥系数γ
将式(2)、式(3b)和式(4)代入式(1)，则高强不锈钢绞线网增强ECC受拉本构关系可表示为
{\sigma _{\rm{se}}}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {\left( {{E_{\rm{e}}} + {E_{\rm{s}}}\dfrac{{{A_{\rm{s}}}}}{{{A_{\rm{se}}}}}} \right){\varepsilon _{\rm{se}}}} \\ \begin{array}{l} \!\!\!\!\!\!\!\!\gamma \left[ {{\rm{3}}{\rm{.33}}\dfrac{{{\varepsilon _{\rm{se}}}}}{{{\varepsilon _{\rm{se,u}}}}}{\rm{ - 3}}{\rm{.66}}{{\left( {\dfrac{{{\varepsilon _{\rm{se}}}}}{{{\varepsilon _{\rm{se,u}}}}}} \right)}^2}{\rm{ + 1}}{\rm{.33}}{{\left( {\dfrac{{{\varepsilon _{\rm{se}}}}}{{{\varepsilon _{\rm{se,u}}}}}} \right)}^3}} \right]{\sigma _{\rm{s,u}}}\dfrac{{{A_{\rm{s}}}}}{{{A_{\rm{se}}}}} +\\ \!\! \left( {{\rm{0}}{\rm{.31}}\dfrac{{{\varepsilon _{\rm{se}}}}}{{{\varepsilon _{\rm{se,u}}}}} + 0.69} \right){\sigma _{\rm{e,u}}} \\ \end{array} \end{array}} \right. (5) 基于应变协调，高强不锈钢绞线网增强ECC的开裂应变与ECC相等，即εse,cr=εe,cr；同时高强不锈钢绞线网增强ECC受拉试件的破坏形态为纵向高强不锈钢绞线拉断破坏，其极限应变主要取决于高强不锈钢绞线的极限应变大小，即εse,u=εs,u。
分别将开裂状态和破坏状态的应变值代入式(5)，利用MATLAB软件进行分析，得到式(5)中高强不锈钢绞线应力发挥系数γ的值，如表4所示。可知，各组值较接近，故取其平均值(0.725)作为式(5)中γ的值。
表 4 高强不锈钢绞线应力发挥系数γ取值Table 4. Value of stress development coefficient γ of high-strength stainless steel strandGroup number γ R2 TC12 0.73 0.9267 TC22 0.72 0.9459 TC32 0.76 0.9607 TD12 0.71 0.9157 TD22 0.72 0.9755 TD32 0.71 0.9325 3.2.4 开裂应力和抗拉强度公式
基于高强不锈钢绞线网增强ECC受拉试件的本构关系模型(式(5))，推导出高强不锈钢绞线网增强ECC受拉试件的开裂应力和极限拉应力即抗拉强度的计算公式：
\left\{ {\begin{array}{*{20}{l}} {{\sigma _{\rm{se,cr}}} = \left( {{E_{\rm{e}}} + {E_{\rm{s}}}\dfrac{{{A_{\rm{s}}}}}{{{A_{\rm{se}}}}}} \right){\varepsilon _{\rm{se,cr}}}} \\ {{f_{\rm{se,u}}} = 0.725{\sigma _{\rm{s,u}}}\dfrac{{{A_{\rm{s}}}}}{{{A_{\rm{se}}}}} + {\sigma _{\rm{e,u}}}} \end{array}} \right. (6) 式中，fse,u为高强不锈钢绞线网增强ECC受拉试件的极限应力，即抗拉强度。
3.3 模型验证
为验证本文提出的高强不锈钢绞线网增强ECC受拉本构模型，将试验得出的应力-应变曲线与式(5)计算的应力-应变曲线进行对比，如图6所示。将试验得出的开裂应力和极限拉应力(抗拉强度)与式(6)计算的结果进行对比，如表5所示。
表 5 试验与式(6)计算得到的高强不锈钢绞线网增强ECC试件开裂应力和极限应力的对比Table 5. Comparison of cracking stress and ultimate tensile stress of ECC reinforced by high-strength stainless steel wire mesh specimens obtained by test and equation (6)Group number Cracking stress/MPa Ultimate tensile stress/MPa T C R T C R TC12 2.20 2.26 0.97 7.09 6.79 1.04 TC22 2.25 2.27 0.99 7.94 7.25 1.10 TC32 2.41 2.28 1.06 8.77 7.87 1.11 TC42 2.56 2.30 1.11 10.65 9.19 1.16 TC52 2.54 2.28 1.11 8.82 7.87 1.12 TD12 1.97 1.94 1.01 6.41 6.58 0.97 TD22 1.99 1.95 1.02 7.81 7.03 1.11 TD32 2.07 1.96 1.06 8.62 7.63 1.13 TD42 2.19 1.98 1.11 10.30 8.90 1.16 Notes: T—Test value; C—Calculated value; R—T/C. ![]()
图 6 高强不锈钢绞线网增强ECC受拉本构模型验证Figure 6. Verification of tensile constitutive model of ECC reinforced by high-strength stainless steel wire mesh从图6可看出，本文提出的本构模型与试验应力-应变曲线整体趋势完全一致。其中，本文所提的受拉本构关系曲线的弹性阶段与试验值基本重合，符合良好；其弹塑性阶段与试验曲线弯曲度均吻合较好(TD42稍有差别)，仅试验在ECC开裂后，荷载有微小波动，属于正常情况。因此，本文提出的高强不锈钢绞线网增强ECC受拉本构模型能较准确地预测受拉应力-应变关系全曲线。表5中的高强不锈钢绞线网增强ECC受拉试件的开裂应力试验值与计算值比值的平均值为1.05，标准差为0.05，变异系数为0.05；极限应力试验值与计算值比值的平均值为1.10，标准差为0.06，变异系数为0.05，说明本文提出的式(6)计算结果和试验值吻合良好。
综上所述，本文提出的高强不锈钢绞线网增强ECC受拉本构模型和开裂应力、抗拉强度计算公式可用于反映高强不锈钢绞线网增强ECC受拉状态的应力-应变关系和分析其受拉性能。
4. 结 论
对高强不锈钢绞线网增强工程水泥基复合材料(Engineered cementitious composites，EEC) 的受拉性能进行试验和理论研究，提出了其受拉本构关系模型。
(1)高强不锈钢绞线表面的螺旋进一步限制了ECC裂缝的开展，增加了ECC裂缝的分散能力，使受拉试件在达到极限承载力的85%时，最大裂缝宽度依然小于规范GB 50010—2010[23]中正常使用极限状态裂缝要求。充分显示了高强不锈钢绞线网增强ECC的良好抗裂性能。
(2)高强不锈钢绞线网增强ECC受拉应力-应变曲线分为弹性阶段和弹塑性阶段，弹塑性阶段是其主要受拉阶段，该阶段是ECC和钢绞线共同受拉至钢绞线拉断，极限应变可达到3%~5%，显示了该新型复合材料优越的变形能力。
(3)随着ECC抗拉强度提高和纵向钢绞线配筋率增大，高强不锈钢绞线网增强ECC的开裂应力和极限拉应力(抗拉强度)均增大。
(4)所建立的受拉本构模型及模型参数计算公式与试验结果吻合良好，能够较好地反映高强不锈钢绞线网增强ECC的受拉应力-应变关系，预测其受力状态；所提出的高强不锈钢绞线网增强ECC受拉开裂应力、抗拉强度的计算公式与试验结果吻合良好，可以用于分析该新型复合材料受拉性能。
-
![]()
图 1 弯曲载荷作用下板的互反弯曲变形[22]
Figure 1. Anticlastic bending deformation of plates under bending load[22]
L, W and t—Length, width and thickness of the rectangular plate, respectively; mx—Bending moment per unit width applied to the plate edges; Rx0 and Ry0—Radii of curvature of the corresponding deformation
![]()
图 2 双悬臂梁(DCB)试件的中间分层界面纤维铺层：(a) 0°/0°；(b) 0°/90°；(c) 90°/90°
Figure 2. Intermediate delamination interface fiber layup directions of double cantilever beam (DCB) specimen: (a) 0°/0°; (b) 0°/90°; (c) 90°/90°
![]()
图 3 超高分子量聚乙烯(UHMWPE)复合材料层压板的成型温度及压力设置
Figure 3. Forming temperature and pressure setting of ultra-high molecular weight polyethylene (UHMWPE) composite laminates
![]()
图 4 (a) 带层间预制裂纹的DCB试件；(b) 粘贴刻度和加载合页的DCB试件
P—Applied load
Figure 4. (a) DCB specimen with interlaminar pre-crack; (b) DCB specimen with pasted scale and loaded hinge
![]()
图 5 厚度为5.2 mm (H5) (a)、10.3 mm (H10) (b)和20.6 mm (H20) (c)的DCB试件
Figure 5. DCB specimens with thickness of 5.2 mm (H5) (a), 10.3 mm (H10) (b) and 20.6 mm (H20) (c)
![]()
图 6 UHMWPE复合材料I型层间断裂韧性试验
Figure 6. Mode I interlaminar fracture toughness test of UHMWPE composites
![]()
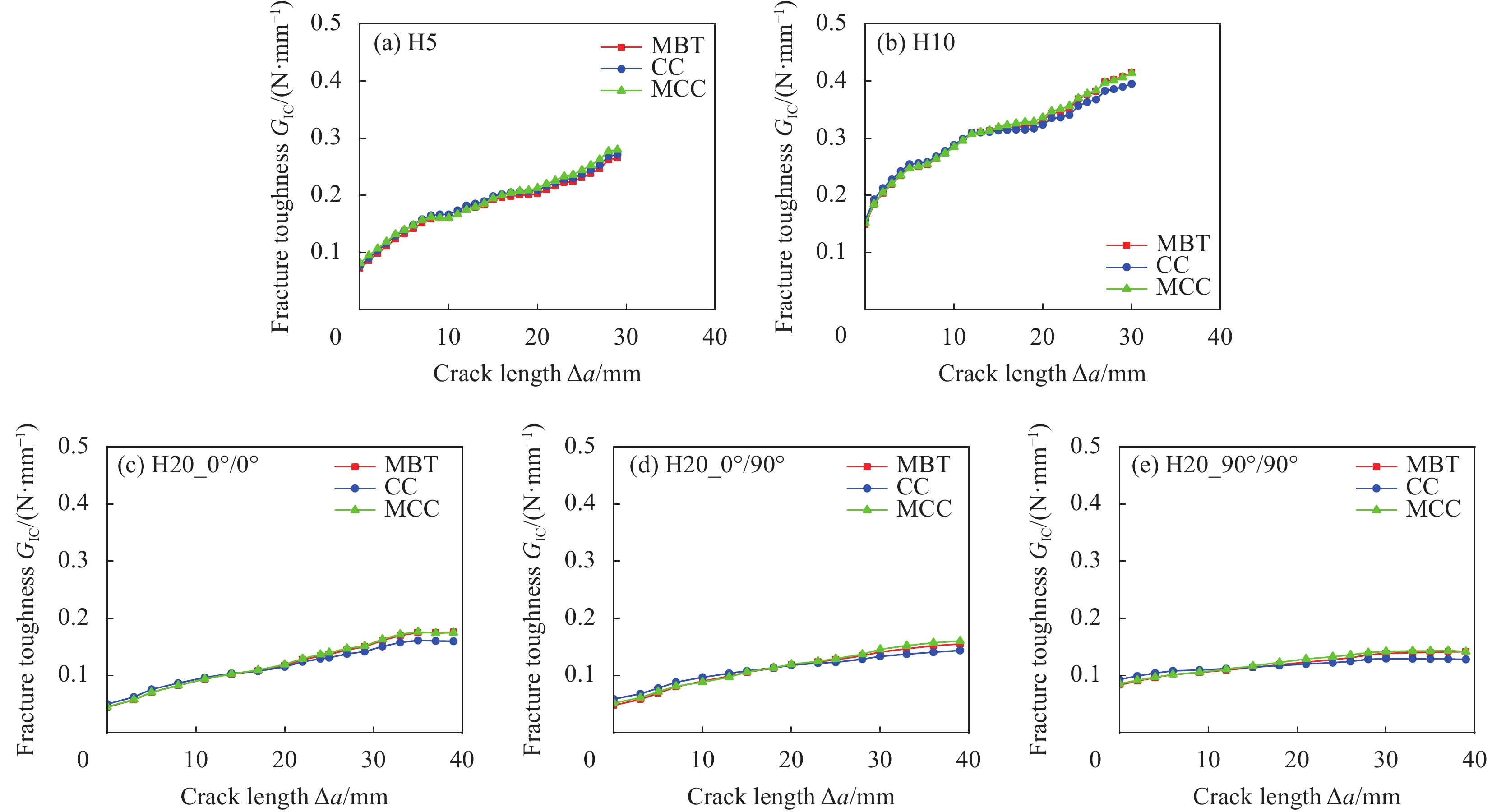
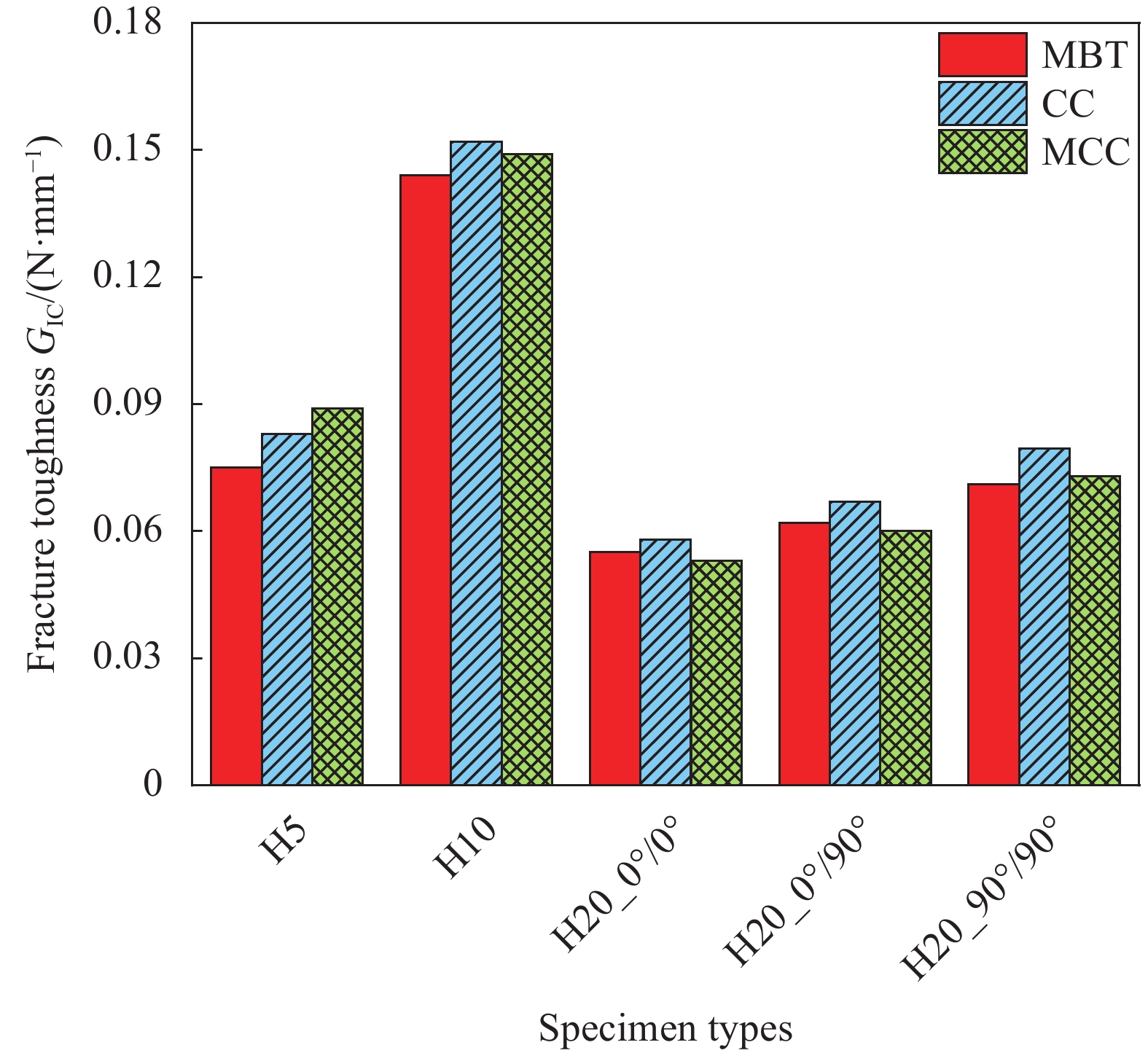
图 7 ASTM D5528-13标准[15]中3种I型层间断裂韧性(GIC)计算方法的拟合参数：(a) 修正梁理论(MBT)；(b) 柔度校正(CC)；(c) 修正柔度校正(MCC)
Figure 7. Fitting parameters of three mode I interlaminar fracture toughness (GIC) calculation methods in ASTM D5528-13[15]: (a) Modified beam theory (MBT); (b) Compliance correction (CC); (c) Modified compliance correction (MCC)
C = δ/P—Compliance of DCB specimen, where δ is the load point deflection and P is the applied load; a—Delamination of DCB specimen; Δ—Effective delamination extension to correct for rotation of DCB arms at delamination front for the MBT method; n = Δx/Δy—Curve fitting parameters required for the CC method, where Δx is the incremental change in lga and Δy is the incremental change in lgC; h—Thickness of DCB specimen; A1—Slope of plot of a/h versus C1/3
![]()
图 8 不同厚度DCB试件的载荷-张开位移曲线
Figure 8. Load-opening displacement curves of DCB specimens with different thicknesses
![]()
图 9 中间界面为0°/0° (a)、0°/90° (b)和90°/90° (c)纤维铺层方向的H20试件裂纹扩展模式比较
Figure 9. Comparison of crack growth modes of H20 specimens with intermediate interface fiber layup directions of 0°/0° (a), 0°/90° (b) and 90°/90° (c)
![]()
图 10 试验过程中DCB试件的变形对比：(a) H5；(b) H10；(c) H20
Figure 10. Deformation comparison of DCB specimens during the test: (a) H5; (b) H10; (c) H20
![]()
图 12 UHMWPE复合材料层合板层间界面破坏后的SEM图像
Figure 12. SEM images of the damaged interlaminar interface of UHMWPE composite laminates
![]()
图 13 不同类型DCB试件的R曲线：不同计算方法的对比
MBT—Modified beam theory; CC—Compliance calibration method; MCC—Modified compliance calibration method
Figure 13. R curves of DCB specimens with different types: Comparison of different calculation methods
-
[1] DAVID N V, GAO X L, ZHENG J Q. Ballistic resistant body armor: Contemporary and prospective materials and related protection mechanisms[J]. Applied Mechanics Reviews,2009,62(5):1201-1210.
[2] 叶卓然, 罗靓, 潘海燕, 等. 超高分子量聚乙烯纤维及其复合材料的研究现状与分析[J]. 复合材料学报, 2022, 39(9):4286-4309. DOI: 10.13801/j.cnki.fhclxb.20220803.002 YE Zhuoran, LUO Liang, PAN Haiyan, et al. Research status and analysis of ultra-high molecular weight polyethylene fiber and its composites[J]. Acta Materiae Compositae Sinica,2022,39(9):4286-4309(in Chinese). DOI: 10.13801/j.cnki.fhclxb.20220803.002
[3] LIU B. Micromechanics of ultra-high molecular weight polyethylene fibre composites [D]. Cambridge: University of Cambridge, 2018.
[4] GRUJICIC M, ARAKERE G, HE T, et al. A ballistic material model for cross-plied unidirectional ultra-high molecular-weight polyethylene fiber-reinforced armor-grade compo-sites[J]. Materials Science and Engineering: A,2008,498(1-2):231-241. DOI: 10.1016/j.msea.2008.07.056
[5] HERU UTOMO B D. High-speed impact modelling and testing of dyneema composite[D]. Delft: Delft University of Technology, 2011.
[6] KARTHIKEYAN K, KAZEMAHVAZI S, RUSSELL B P. Optimal fibre architecture of soft-matrix ballistic lami-nates[J]. International Journal of Impact Engineering,2016,88:227-237.
[7] KARTIKEYA S, CHOUHAN H, AHMED A, et al. Determination of tensile strength of UHMWPE fiber-reinforced polymer composites[J]. Polymer Testing,2020,82:106293. DOI: 10.1016/j.polymertesting.2019.106293
[8] KARTHIKEYAN K, RUSSELL B P, FLECK N A, et al. The effect of shear strength on the ballistic response of laminated composite plates[J]. European Journal of Mechanics-A/Solids,2013,42:35-53. DOI: 10.1016/j.euromechsol.2013.04.002
[9] NGUYEN L H, RYAN S, CIMPOERU S J, et al. The effect of target thickness on the ballistic performance of ultra high molecular weight polyethylene composite[J]. International Journal of Impact Engineering,2015,75:174-183.
[10] ZHANG R, QIANG L S, HAN B, et al. Ballistic performance of UHMWPE laminated plates and UHMWPE encapsulated aluminum structures: Numerical simulation[J]. Composite Structures, 2020, 252: 112686.
[11] ZHANG R, HAN B, ZHONG J Y, et al. Enhanced ballistic resistance of multilayered cross-ply UHMWPE laminated plates[J]. International Journal of Impact Engineering,2022,159:104035. DOI: 10.1016/j.ijimpeng.2021.104035
[12] GREENHALGH E S, BLOODWORTH V M, IANNUCCI L, et al. Fractographic observations on dyneema® composites under ballistic impact[J]. Composites Part A: Applied Science and Manufacturing,2013,44:51-62. DOI: 10.1016/j.compositesa.2012.08.012
[13] BENMEDAKHENE S, KENANE M, BENZEGGAGH M L. Initiation and growth of delamination in glass/epoxy composites subjected to static and dynamic loading by acoustic emission monitoring[J]. Composites Science and Technology,1999,59(2):201-208. DOI: 10.1016/S0266-3538(98)00063-3
[14] KARTIKEYA K, CHOUHAN H, RAM K, et al. Ballistic evaluation of steel/UHMWPE composite armor system against hardened steel core projectiles[J]. International Journal of Impact Engineering,2022,164:104211. DOI: 10.1016/j.ijimpeng.2022.104211
[15] ASTM International. Standard test method for mode I interlaminar fracture toughness of unidirectional fiber-reinforced polymer matrix composites: ASTM D5528—13[S]. West Conshohocken: ASTM International, 2013.
[16] WANG Y J, ZHAO D M. Characterization of interlaminar fracture behaviour of woven fabric reinforced polymeric composites[J]. Composites,1995,26(2):115-124. DOI: 10.1016/0010-4361(95)90411-R
[17] GASSAN J, BLEDZKI A K. Possibilities for improving the mechanical properties of jute/epoxy composites by alkali treatment of fibres[J]. Composites Science and Technology,1999,59(9):1303-1309. DOI: 10.1016/S0266-3538(98)00169-9
[18] HUANG B Z, HU X Z, LIU J. Modelling of interlaminar toughening from chopped Kevlar fibers[J]. Composites Science and Technology,2004,64(13):2165-2175.
[19] BRUNNER A J, BLACKMAN B R K, DAVIES P. A status report on delamination resistance testing of polymer-matrix composites[J]. Engineering Fracture Mechanics,2008,75(9):2779-2794. DOI: 10.1016/j.engfracmech.2007.03.012
[20] 贺启林. 基于J-积分和构型力理论的材料断裂行为研究[D]. 哈尔滨: 哈尔滨工业大学, 2010. HE Qilin. Study of material fracture behavior based on J-integral and configurational force theory[D]. Harbin: Harbin Institute of Technology, 2010(in Chinese).
[21] DING J C, XU W. Determination of mode I interlaminar fracture toughness of composite by a wedge-insert double cantilever beam and the nonlinear J integral[J]. Compo-sites Science and Technology,2021,206:108674. DOI: 10.1016/j.compscitech.2021.108674
[22] WANG J F, WAGONER R H, MATLOCK D K, et al. Anticlastic curvature in draw-bend springback[J]. International Journal of Solids and Structures,2005,42(5):1287-1307.
[23] SWANSON S R. Anticlastic effects and the transition from narrow to wide behavior in orthotropic beams[J]. Compo-site Structures,2001,53(4):449-455. DOI: 10.1016/S0263-8223(01)00055-1
[24] GONG Y, CHEN X J, ZOU L H, et al. Experimental and numerical investigations on the mode I delamination growth behavior of laminated composites with different Z-pin fiber reinforcements[J]. Composite Structures,2022,287:115370. DOI: 10.1016/j.compstruct.2022.115370
[25] JAIN L K, DRANSFIELD K A, MAI Y W. Effect of reinforcing tabs on the mode I delamination toughness of stitched CFRPs[J]. Journal of Composite Materials,1998,32(22):2016-2041. DOI: 10.1177/002199839803202202
[26] SHANMUGAM L, NAEBE M, KIM J, et al. Recovery of mode I self-healing interlaminar fracture toughness of fiber metal laminate by modified double cantilever beam test[J]. Composites Communications,2019,16:25-29. DOI: 10.1016/j.coco.2019.08.009
[27] 谢宗蕻, 蔡书杰, 郭奇, 等. 碳纤维增强复合材料层间断裂韧度[J]. 航空材料学报, 2018, 38(4):137-142. DOI: 10.11868/j.issn.1005-5053.2016.000189 XIE Zonghong, CAI Shujie, GUO Qi, et al. Interfacial fracture toughness of carbon fiber reinforced composites[J]. Journal of Aeronautical Materials,2018,38(4):137-142(in Chinese). DOI: 10.11868/j.issn.1005-5053.2016.000189
[28] 矫桂琼, 高健, 邓强. 复合材料的 Ⅰ 型层间断裂韧性[J]. 复合材料学报, 1994, 11(1):113-118. JIAO Guiqiong, GAO Jian, DENG Qiang. Mode I interlaminar fracture toughness of composite[J]. Acta Materiae Compositae Sinica,1994,11(1):113-118(in Chinese).
[29] 董雁瑾, 杨海升, 白以龙. 玻璃纤维增强复合材料的I型层间断裂韧性[J]. 材料研究学报, 1999, 13(2):147-152. DONG Yanjin, YANG Haisheng, BAI Yilong. Mode I interlaminar fracture toughness of glass woven fibric reinforced composites[J]. Chinese Journal of Materials Research,1999,13(2):147-152(in Chinese).
[30] RUSSELL B P, KARTHIKEYAN K, DESHPANDE V S, et al. The high strain rate response of ultra high molecular-weight polyethylene: From fibre to laminate[J]. International Journal of Impact Engineering,2013,60:1-9. DOI: 10.1016/j.ijimpeng.2013.03.010
-
期刊类型引用(16)
1. 王新玲，李世伟，金蕾蕾，范家俊. 高强不锈钢绞线网/ECC约束高强混凝土受压本构模型. 工程力学. 2023(09): 153-160 . 
百度学术
2. 王新玲，罗鹏程，钱文文，李可. 高强不锈钢绞线网增强工程水泥基复合材料薄板受弯承载力研究. 建筑结构学报. 2022(01): 164-172 . 百度学术
3. 姚淇耀，陆宸宇，彭林欣，滕晓丹，罗月静. 氯盐侵蚀作用下BFRP筋增强海砂ECC的拉伸及弯曲性能试验. 复合材料学报. 2022(03): 1215-1227 . 本站查看
4. 朱俊涛，张凯，邹旭岩，李可，张普. 钢绞线与水泥基复合材料局部黏结滑移模型. 哈尔滨工程大学学报. 2022(04): 541-548 . 百度学术
5. 王新玲，李赟璞，李苗浩夫，范家俊. 高强不锈钢绞线网增强ECC加固RC短柱轴心受压试验. 复合材料学报. 2022(05): 2308-2317 . 本站查看
6. 朱俊涛，张凯，王新玲，李可. 高强钢绞线网增强ECC与混凝土界面黏结-滑移关系研究. 工程力学. 2022(09): 204-214 . 百度学术
7. 李可，王宇，李志强，朱俊涛. 高强钢绞线网增强ECC加固无损RC梁受弯承载力研究. 建筑结构学报. 2022(12): 82-90 . 百度学术
8. 李可，李思辰，周擎威，王新玲. 高强钢绞线与工程水泥基复合材料黏结性能试验. 沈阳工业大学学报. 2022(06): 706-713 . 百度学术
9. 惠迎新，王文炜，朱忠锋. FRP-ECC复合约束混凝土圆柱反复受压力学性能. 复合材料学报. 2022(11): 5586-5598 . 本站查看
10. 王新玲，陈永杰，钱文文，李可，朱俊涛. 高强不锈钢绞线网增强工程水泥基复合材料弯曲性能试验. 复合材料学报. 2021(04): 1292-1301 . 本站查看
11. 王春红，左祺，支中祥，徐磊，SARANI Zakaria，SHERAZ Hussain Siddique Yousfani. 聚乙烯醇乳液改性对汉麻秸秆纤维/水泥基复合材料性能的影响. 复合材料学报. 2021(05): 1567-1575 . 本站查看
12. 朱俊涛，赵奎，邹旭岩，王新玲，李可，张哲. 高强不锈钢绞线网在ECC中的搭接性能. 土木与环境工程学报(中英文). 2021(03): 174-182 . 百度学术
13. 朱俊涛，侯晶强，王新玲，李可. 基于损伤演化的钢绞线网/ECC黏结滑移关系. 华中科技大学学报(自然科学版). 2021(06): 103-108 . 百度学术
14. 范建伟，李可，王新玲. 高性能复合材料“高强钢绞线/ECC”板受弯试验分析. 建筑科学. 2021(09): 130-136 . 百度学术
15. 王新玲，卫垚鑫，范建伟，朱俊涛. 新型复合材料“高强钢绞线网/ECC约束素混凝土”受压性能试验研究. 复合材料学报. 2021(11): 3904-3911 . 本站查看
16. 王新玲，赵要康，周擎威，朱俊涛. 高强不锈钢绞线与ECC黏结滑移性能研究. 华中科技大学学报(自然科学版). 2020(12): 108-113 . 百度学术
其他类型引用(2)
-
目的
作为装甲解决方案的一组重要材料，超高分子量聚乙烯(UHMWPE)纤维增强复合材料在冲击作用下主要的破坏模式之一是分层脱粘。UHMWPE复合材料层合板层间性能的准确表征意义重大，而目前已有的标准试验方法并不完全适用于此类塑性较强的复合材料，导致该材料层间断裂特性的研究较为缺乏。本文旨在为UHMWPE复合材料进一步的动态层间性能及其理论模型的研究提供实验参考和数据支撑，进而指导复合材料防护结构的设计。
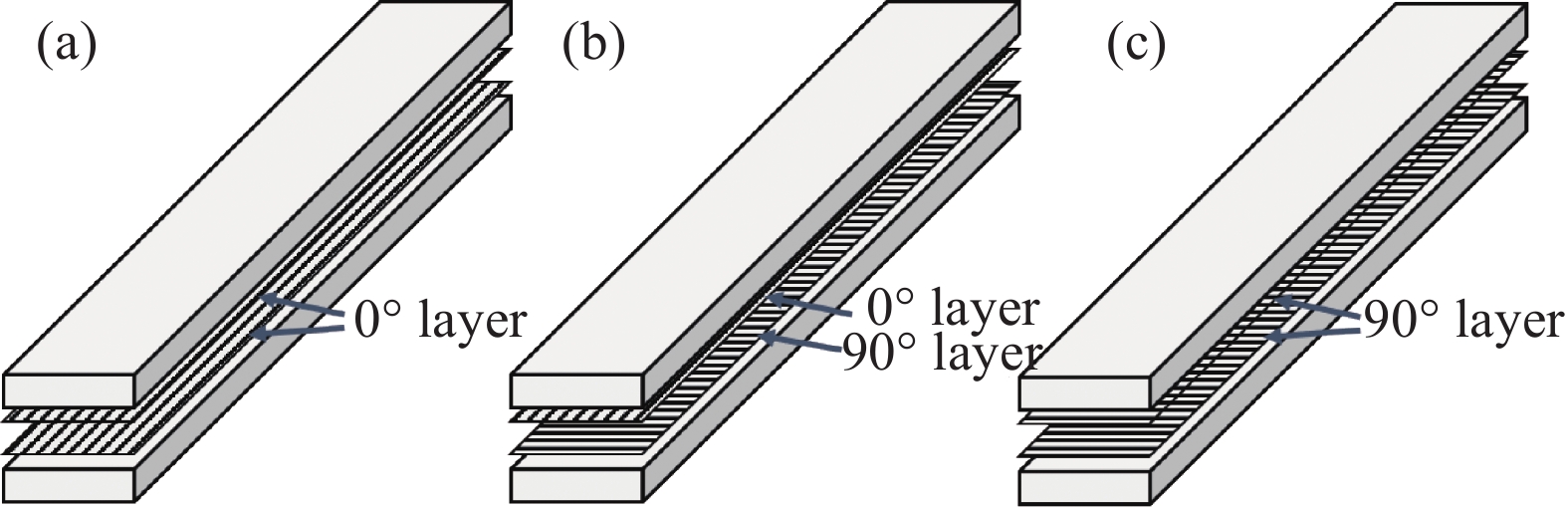
方法针对UHMWPE复合材料层合板在ASTM D5528标准的基础上提出一种改进的双悬臂梁(DCB)试件，对UHMWPE复合材料层合板进行有效的层间断裂实验。ASTM D5528标准为的测定提供了全面的测试方案和数据处理方法，一般适用于具有脆性聚合物基体的碳纤维和玻璃纤维增强层合板。基于改进型试件对厚度为5 mm，10 mm和20 mm以及中间分层界面纤维铺层方向为 0°/0° 、 0°/90° 和 90°/90° 的UHMWPE复合材料层合板DCB试件进行试验，系统分析了不同试件厚度及中间分层界面纤维铺层方向对层间断裂试验的影响。此外，本文采用修正梁理论方法，柔度校正法和修正柔度校正法分别测定不同类型DCB试件的层间断裂韧性，以分析数据处理方法对不同类型试件测定结果的影响。
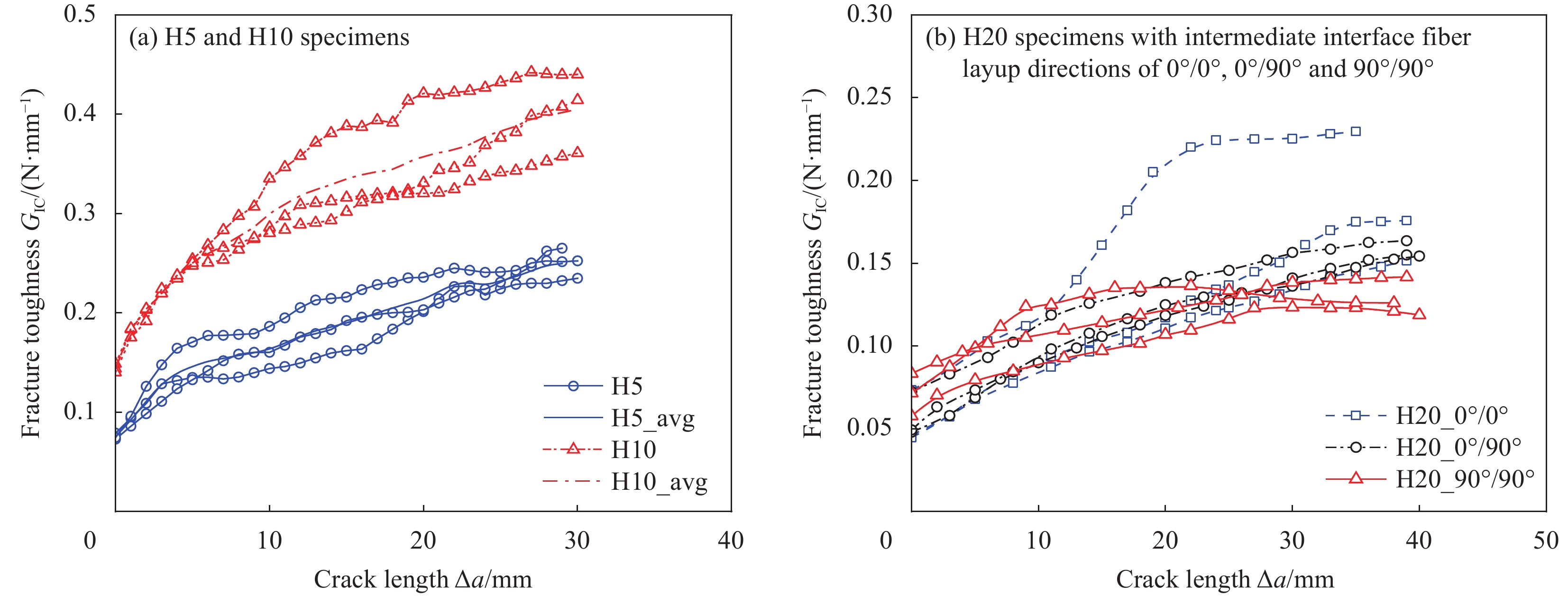
结果UHMWPE复合材料DCB试件的载荷-张开位移曲线在载荷达到最大值后存在明显的平台区，这主要归因于UHMWPE复合材料的强塑性行为及其较为复杂的层间裂纹扩展模式。比较不同厚度DCB试件在层间裂纹扩展过程的变形：在裂纹尚未开始扩展阶段，随着厚度的增加，试件的弯曲变形程度显著变化，尤其是塑性变形减少，表明加载过程中弹性变形的线性段在裂纹未扩展阶段占比相应增加。观察试件的变形过程发现，厚度为5 mm试件的裂纹扩展集中在中间层，未出现分层迁移和多裂纹等其他裂纹偏离行为，且无纤维桥联现象；10 mm厚度试件在中间层界面出现明显的纤维桥联；20 mm厚度试件的不同分层界面铺层导致其层间裂纹呈现复杂的扩展模式，但未出现明显的纤维桥联。对比3种纤维铺层的20 mm厚度试件得到的载荷-张开位移曲线，发现： 0°/0° 和 0°/90° 试件的峰值力相当，且随着裂纹的扩展载荷未明显下降，待试件完全张开后才迅速下降； 90°/90° 试件的峰值力相对较小，随裂纹的扩展呈现较明显的下降趋势。此外，比较3种不同中间界面纤维铺层20 mm厚度试件的裂纹扩展模式可知，改变界面纤维铺层方向会明显改变层间裂纹的扩展路径。三种不同厚度UHMWPE层合板的R曲线有很大差异。厚度为5 mm和10 mm试件的平均初始值分别为0.075 N/mm和0.144 N/mm，且随分层扩展长度的增加，这两种厚度试件的能量耗散率继续增大，彼此之间始终存在0.1 N/mm的差距。20 mm厚度试件的平均值约为0.06 N/mm，低于5 mm和10 mm厚度试件的平均值，其中分层界面 90°/90° 纤维铺层试件的能量耗散率会逐渐趋于稳定。就20 mm厚度试件而言，类似于其载荷-张开位移曲线，该厚度试件的中间分层界面纤维铺层方向对测定的值影响较小。厚度为20 mm试件的层间裂纹会迁移到相邻的 0°/90° 界面，或主要出现在试件中间的 0°/90° 和 90°/90° 界面，仅宽度方向的纤维出现桥联，不影响裂纹的进一步扩展。采用修正梁理论方法，柔度校正法和修正柔度校正法测定的结果呈现极强的一致性：3种计算方法得到的R曲线基本重合，平均初始层间断裂韧性之间的相对差异不超过7%。测得结果之间如此小的差异与ASTM D5528标准对该3种不同计算方法的描述相符。
结论针对UHMWPE纤维增强复合材料的 Ⅰ 型层间断裂力学行为，本文在预制层合板铺层及几何形状上对传统的双悬臂梁(DCB)试件进行了改进，基于改进方案对不同类型层合板DCB试件进行了试验，系统分析了不同试件厚度及中间分层界面纤维铺层方向对层间断裂试验的影响，主要结论如下：(1) 在裂纹扩展发生前后，UHMWPE层合板试件均出现非线性力学响应，且采用基于断裂力学的层间断裂韧性计算方法得到的R曲线与常规脆性复合材料的R曲线有明显差异。(2) 增加DCB试件的厚度能有效减少塑性变形的影响；20 mm试件的三种不同分层界面纤维铺层方向导致不同程度的纤维桥接，对试验过程、试验结果也有一定影响。(3) 采用中间界面纤维铺层为 90°/90° 且厚度为20 mm的DCB试件，可有效地开展UHMWPE复合材料的 Ⅰ 型层间断裂试验。(4) 基于改进的DCB试件，采用修正梁理论、柔度校正法和修正柔度校正法得到的层间断裂韧性高度一致，表明本文采用修正梁理论对UHMWPE复合材料层间断裂韧性进行分析的可靠性。
-
超高分子量聚乙烯(UHMWPE)纤维增强复合材料具备优越的抗冲击性能及低密度特性，近年来成为抗冲击及抗侵彻结构设计的优选材料，而层间分层是UHMWPE复合材料层合板在冲击载荷下的一种主要破坏模式。UHMWPE复合材料层合板层间性能的准确表征意义重大，而目前已有的标准试验方法并不完全适用于此类塑性较强的复合材料，导致该材料层间断裂特性的研究较为缺乏。
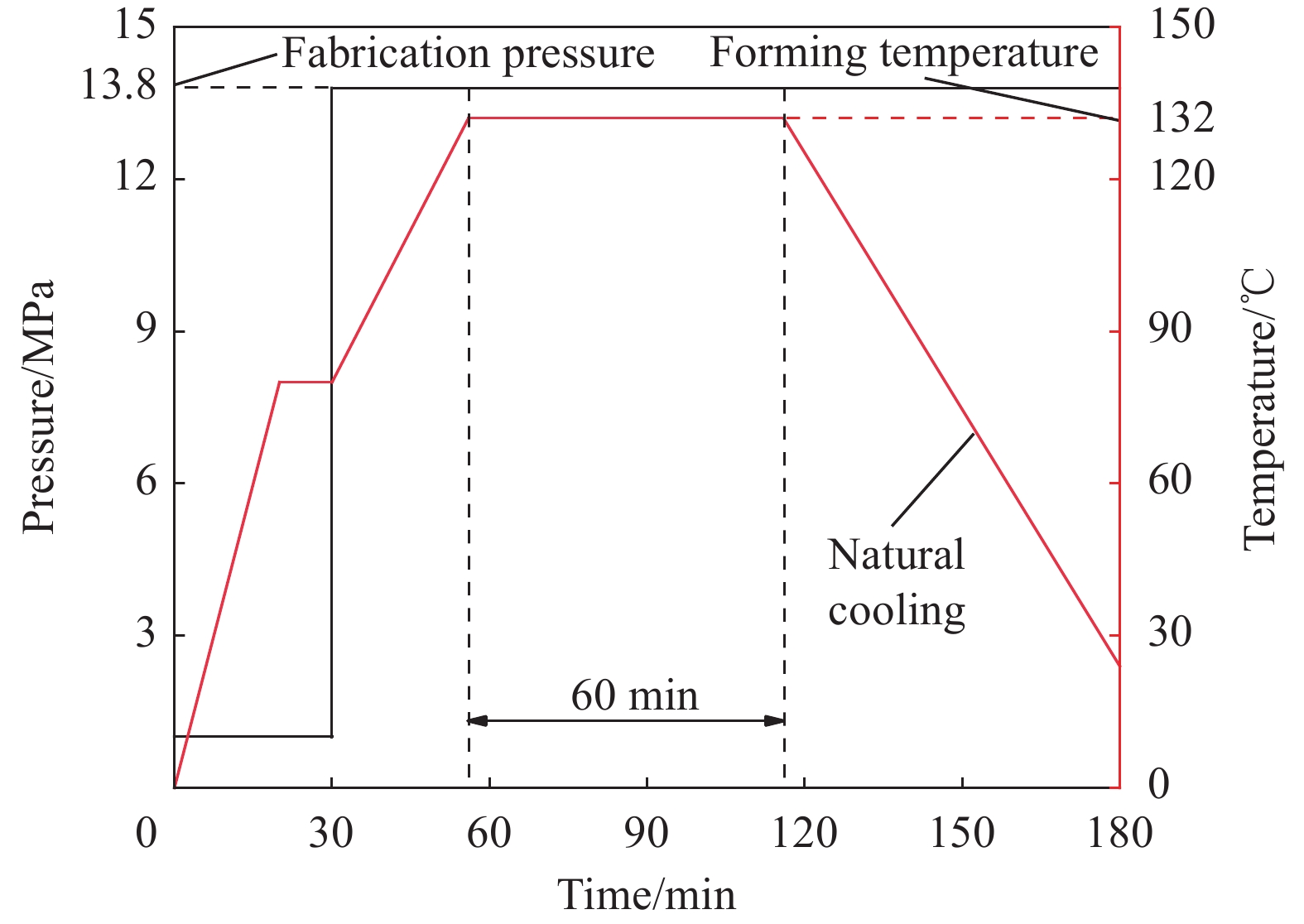
本文在ASTM D5528标准的基础上，考虑到UHMWPE层合板在变形过程中会表现出较强塑性，不完全适用于标准中基于线弹性断裂力学GIC计算方法，对传统的DCB试验方法做出相应改进。基于改进的试验方法，本文测得UHMWPE层合板DCB试件的载荷-张开位移曲线，结合试件变形过程获得R曲线，分析层间断裂破坏机理及塑性对裂纹扩展的影响，同时还研究了DCB试件厚度和中间分层界面的纤维铺层方向对GIC的影响规律。
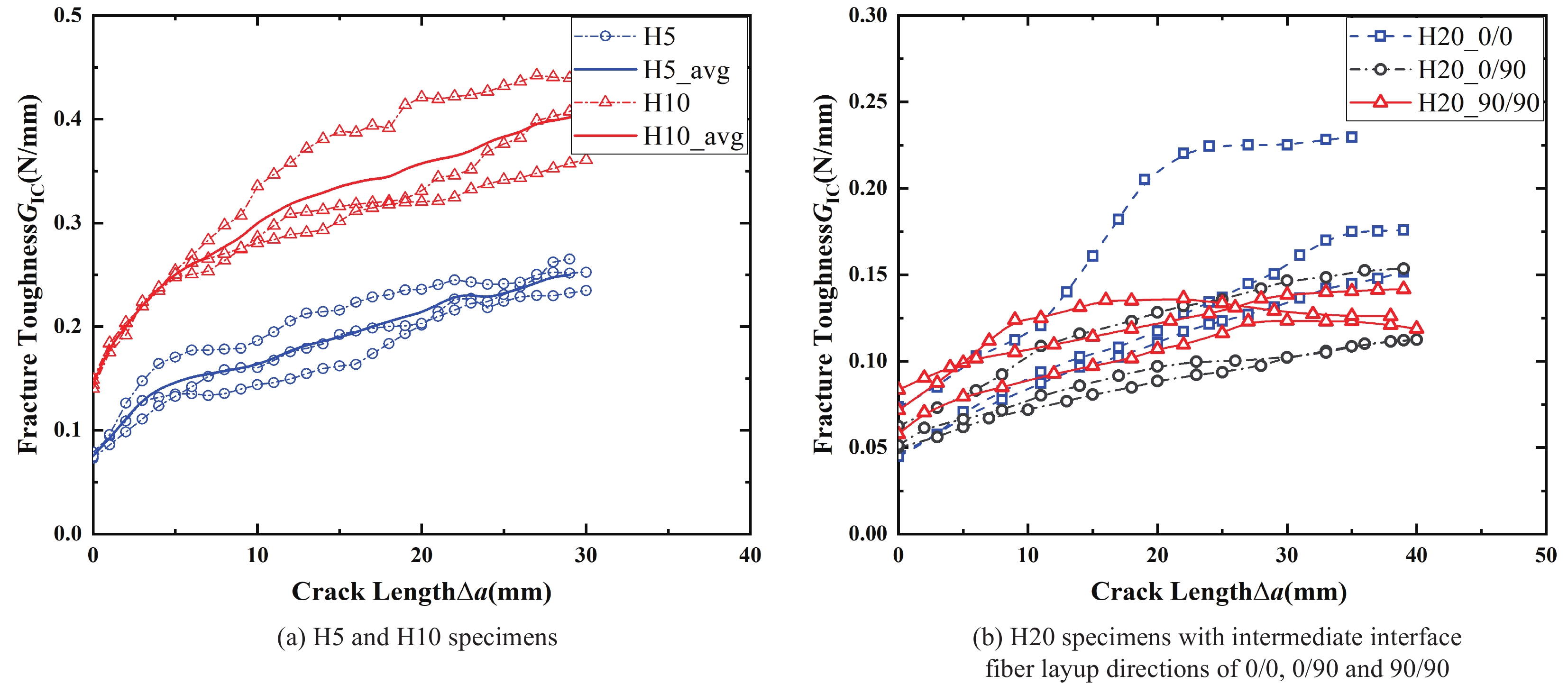
不同厚度UHMWPE层合板DCB试件的R曲线
下载:
计量
- 文章访问数: 1110
- HTML全文浏览量: 485
- PDF下载量: 115
- 被引次数: 18
