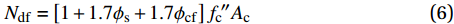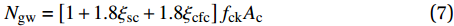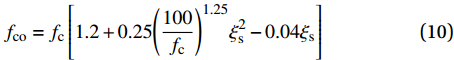CFRP约束钢管-活性粉末混凝土短柱轴压性能

焦楚杰; 李松; 崔力仕; 王志仁; 简超

doi:10.13801/j.cnki.fhclxb.20200608.003

CFRP约束钢管-活性粉末混凝土短柱轴压性能

广州大学　土木工程学院，广州 510006

基金项目: 国家自然科学基金(51478128；51778158)；广东省水利科技创新重点资助项目(2017-32)；广州大学研究生创新能力培养资助项目(2018GDJC-D08)

详细信息

通讯作者:
焦楚杰，博士，教授，研究方向为高性能混凝土　E-mail：jiaochujie@sina.com

中图分类号: TU398.9
计量
- 文章访问数: 1398
- HTML全文浏览量: 454
- PDF下载量: 70
出版历程
- 收稿日期: 2020-04-06
- 录用日期: 2020-05-23
- 网络出版日期: 2020-06-08
- 刊出日期: 2021-02-14

Axial compression behaviour of CFRP confined reactive power concrete filled steel tube stub columns

College of Civil Engineering, Guangzhou University, Guangzhou 510006, China

摘要

摘要: 为研究圆碳纤维增强树脂复合材料(CFRP)约束钢管-活性粉末混凝土(RPC)短柱的轴压性能，以CFRP粘贴层数和钢管壁厚为参数进行了12根CFRP约束钢管-RPC短柱、4根钢管-RPC短柱及4根钢管短柱的轴压力学性能试验。通过荷载-位移曲线分析了CFRP层数和钢管壁厚对试件极限荷载和变形能力的影响，探讨了提高系数、CFRP应变效率和延性系数等相关性能指标，最后通过提高系数关联套箍率提出了CFRP约束钢管-RPC短柱承载力模型。结果表明：CFRP约束能有效地增强钢管-RPC短柱的承载能力和变形能力。与CFRP约束钢管-混凝土相比，CFRP约束钢管-RPC表现出CFRP应变效率的下降，并且其延性不如CFRP约束钢管-混凝土。在钢管-RPC承载力的基础上提出了实用的CFRP约束钢管-RPC短柱轴压承载力计算模型。
- CFRP约束钢管-活性粉末混凝土 /
- 荷载-位移曲线 /
- 极限荷载 /
- CFRP应变效率 /
- 延性系数
Abstract: The axial compression behaviour of circular carbon fiber reinforced polymer (CFRP) confined reactive powder concrete (RPC) filled steel tube stub columns was investigated. The mechanical tests of 12 CFRP confined steel tube-RPC stub columns, 4 steel tube-RPC stub columns and 4 steel tube stub columns were performed with the number of the CFRP layers and the steel tube thickness as parameters. The load-displacement curves were used to analyze the effects of the CFRP layer number and the steel tube thickness on the ultimate load and deformation capacity of the specimens. Subsequently, the performance indicators such as improvement coefficient, CFRP strain efficiency and ductility coefficient were discussed. Finally, a model of CFRP confined steel tube-RPC stub columns was proposed by increasing the coefficient associated confinement ratio. The experimental results indicate that the bearing capacity and deformation capacity of the CFRP confined steel tube-RPC stub columns are significantly improved by CFRP. In contrast to the CFRP confined concrete filled steel tube (CFRP confined steel tube-C), the CFRP confined steel tube-RPC exhibites a decrease in CFRP strain efficiency, and its ductility is worse than the CFRP confined steel tube-C. Based on the bearing capacity of steel tube-RPC, a practical model for calculating the bearing capacity of CFRP confined steel tube-RPC stub columns is proposed.
- CFRP confined reactive power concrete filled steel tube stub columns /
- load-displacement curve /
- ultimate load /
- CFRP strain efficiency /
- ductility coefficient

HTML全文

活性粉末混凝土(Reactive powder concrete，RPC)是一类力学性能良好、具备高强与高耐久性能的水泥基复合材料^[1]，为推动RPC的持续发展，国内外学者对RPC的基本力学性能进行了广泛的研究^[2-4]，然而RPC是一类受压过峰值后脆性较大的混凝土材料，这会限制其在工程结构领域的发展^[5]，虽然钢纤维的添加可以提高RPC的抗拉强度，但是对于RPC的抗压延性的提高仍然有限^[6-7]。为弥补RPC抗压延性的不足，复合RPC的组合结构应运而生，特别是RPC复合钢管形成的钢管-RPC，在利用RPC高强度的同时，钢管的约束有效的增强了RPC的延性，很好的进行了材料的优势互补，另外钢管的约束不仅可以增强RPC的抗压延性，其抗拉延性也能得到有效的增强，因此无钢纤维的RPC复合钢管形成的钢管-RPC构件成为研究的热点之一，其在减少材料价格从而形成良好的经济效益方面更能满足工程的需求。

与传统的钢结构与混凝土结构相比，钢管-RPC组合结构因其高强特点可以减小构件截面面积，进而进一步带来材料上的经济优势，另外还能为大跨度、高层与高耸建筑、重载工程建设提供性能优越的竖向构件^[8]。目前多数学者对不掺钢纤维的钢管-RPC的基本力学性能与承载力模型进行了研究^[9-11]，研究表明，此类复合构件的结构性能优于传统钢结构或混凝土结构，因为钢管能从外部限制核心RPC膨胀，同时RPC能有效抑制钢管向内屈曲的发生。然而，从这些研究^[9-11]中可以看出，钢管-RPC的破坏模式共同特点是钢管向外局部屈曲，这类破坏导致了由于过度的非弹性变形而造成的强度和延性的下降。因此，为了使钢管-RPC构件能够进一步承受更高荷载而延缓或抑制这类破坏的发生，必须对钢管-RPC构件进行有效的加固。

碳纤维增强树脂复合材料(Carbon fibre reinforced polymer，CFRP)是一类质轻高强、抗腐蚀佳、耐久性好的高性能材料，且因易于施工被广泛地运用于混凝土结构与钢结构的加固^[12-13]。目前，CFRP约束混凝土构件与约束钢管-混凝土构件在国内外的研究与应用中取得了较大的成果。研究表明^[14-17]，CFRP的约束能有效的提高钢管-混凝土构件的承载力，并能迟缓钢管的向外局部屈曲，但是研究的混凝土主要是低强的混凝土，对于CFRP约束无钢纤维的钢管-高强RPC却鲜有公开报道。对于CFRP约束钢管-RPC这类新型复合构件，其CFRP提供的约束效果如何、钢管与RPC的相互作用如何等诸多问题值得探讨。为此本文以钢管壁厚(2 mm、3 mm、4 mm、5 mm)和CFRP粘贴层数(0、1、2、3层)为参数进行了12根CFRP约束钢管-RPC短柱、4根钢管-RPC短柱及4根钢管短柱的轴压性能对比试验，根据所得荷载-位移曲线，分析了CFRP约束钢管-RPC短柱的轴压承载力与变形能力，探讨了提高系数、CFRP应变效率和延性系数等相关性能指标，并依据提高系数与套箍率的线性关系建立了CFRP约束钢管-RPC短柱承载力计算模型，为这类新型组合构件的深入研究提供了基础性的参考。

1. 试验概况

1.1 试件设计与制作

试验设计了4根圆钢管、4根圆钢管-RPC短柱，12根圆CFRP约束钢管-RPC短柱，长径比(L/D)均为3。CFRP约束钢管-RPC短柱采用无缝钢管，钢管壁厚t_s分别为2 mm、3 mm、4 mm、5 mm，CFRP层数n_f以0、1、2、3层分别环向全包粘贴，钢管内填RPC的强度为120 MPa，每个试件的两端采用尺寸为120 mm×120 mm的方形钢板密封焊接。各个试件规格参数如表1所示，以试件C120t3CF2为例，其标号表示钢管内部填充RPC强度为120 MPa，钢管壁厚为3 mm，并以CFRP环向粘贴2层的复合柱。

表 1 试件编号及参数

Table 1. Parameters of specimens

Specimen	D×t_s×L/mm	f_y/MPa	E_s/GPa	f_cu/MPa	f_c/MPa	n_f	ξ_s	ξ_cf	k_ε	µ_d	r_cap/%	N_u/kN
t2CF0	103×2×303	356	208	−	−	−	−	−	−	−	−	328
C120t2CF0	103×2×303	356	208	127	108	0	0.272	0	−	3.75	0	1 081
C120t2CF1	103×2×303	356	208	127	108	1	0.272	0.221	0.666	2.49	14.5	1 238
C120t2CF2	103×2×303	356	208	127	108	2	0.272	0.442	0.727	2.08	20.8	1 306
C120t2CF3	103×2×303	356	208	127	108	3	0.272	0.663	0.776	1.46	32.0	1 428
t3CF0	102×3×303	310	204	−	−	−	−	−	−	−	−	379
C120t3CF0	102×3×303	310	204	127	108	0	0.37	0	−	3.96	0	1 132
C120t3CF1	102×3×303	310	204	127	108	1	0.37	0.233	0.679	2.92	13.7	1 288
C120t3CF2	102×3×303	310	204	127	108	2	0.37	0.466	0.753	2.13	21.8	1 379
C120t3CF3	102×3×303	310	204	127	108	3	0.37	0.699	0.792	1.86	31.2	1 485
t4CF0	101×4×304	291	202	−	−	−	−	−	−	−	−	443
C120t4CF0	101×4×304	291	202	127	108	0	0.484	0	−	4.03	0	1 221
C120t4CF1	101×4×304	291	202	127	108	1	0.484	0.246	0.738	3.11	9.7	1 340
C120t4CF2	101×4×304	291	202	127	108	2	0.484	0.492	0.781	2.56	20.7	1 474
C120t4CF3	101×4×304	291	202	127	108	3	0.484	0.738	0.805	2.19	32.8	1 621
t5CF0	102×5×306	318	207	−	−	−	−	−	−	−	−	501
C120t5CF0	102×5×306	318	207	127	108	0	0.675	0	−	4.21	0	1 370
C120t5CF1	102×5×306	318	207	127	108	1	0.675	0.253	0.764	3.66	2.2	1 400
C120t5CF2	102×5×306	318	207	127	108	2	0.675	0.506	0.801	2.91	10.1	1 508
C120t5CF3	102×5×306	318	207	127	108	3	0.675	0.759	0.808	2.63	21.1	1 659
Notes: D—Diameter of steel tube; t_s—Steel tube thickness; L—Length of a specimen; f_y—Yield strength of steel; E_s—Elastic modulus of steel; f_cu—Cubic compressive strength of reactive powder concrete (RPC); f_c—Axial compressive strength of RPC; n_f—Number of carbon fiber reinforced polymer (CFRP) layers; ξ_s—Steel tube confinement factor; ξ_cf—CFRP confinement factor; k_ε—Strain efficiency of CFRP; µ_d—Ductility factor; r_cap—Increase factor; N_u—Ultimate load. The letter C denotes the nominal RPC strength, the letter t is the steel tube thickness, and the letters CF denote the CFRP confined components. For example, the C120t2CF3 indicates that the strength of the specimen is 120 MPa, the thickness of the steel tube is 2 mm, and the specimen is wrapped in three CFRP layers.

下载: 导出CSV

| 显示表格

核心RPC采用P·O 52.5R硅酸盐水泥、硅灰、石英粉、三类不同粒径的硅砂(270~550 μm、150~270 μm、75~150 μm)、河砂、消泡剂、高效聚羧酸减水剂及水按一定比例制备，试验用配合比为水泥∶硅灰∶石英粉∶硅砂∶河砂∶消泡剂∶减水剂∶水 =977∶172∶150∶8∶747∶271∶12.2∶12.2∶220。将浇注好的钢管在常温下浸水养护90天，养护完取出后将试件表面除锈打磨，待粘贴CFRP后将钢管上端用打磨机修割整平并用牙科石膏产品进行找平，以便能在试验机中几何对中试验机上下盖板。

1.2 材料试验

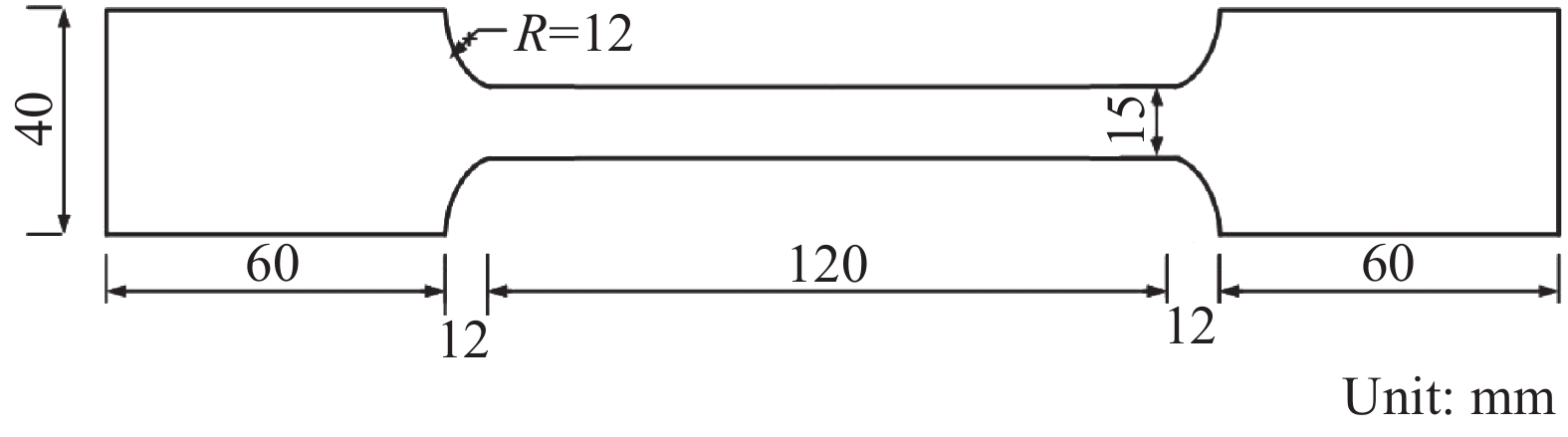
CFRP约束钢管-RPC材料性能试验采用金属波纹管万能试验机进行，其设计拉伸试样如图1所示，试验按标准GB/T 228.1—2010^[18]进行，四类钢管壁厚试样各准备3个，计算结果取三者平均值，试验所测屈服强度f_y与弹性模量E_s列于表1。

图 1 CFRP约束钢管-RPC拉伸试样尺寸

Figure 1. Size of CFPR confined steel tube-RPC tensile specimen

下载: 全尺寸图片幻灯片

本试验采用的CFRP为单向CFRP布，单层厚度为0.167 mm，抗拉强度f_cf为3400 MPa，CFRP的粘贴工艺按建规固[2002]006号规定^[19]进行。

RPC立方体抗压强度与轴心抗压强度采用的试件尺寸分别为100 mm×100 mm×100 mm和100 mm×100 mm× 300 mm，试验强度测定与计算按GB/T 31387—2015标准^[20]执行。RPC材料性能试验与钢管-RPC短柱浇注所用RPC为同一批次，试验测得RPC立方体抗压强度f_cu、轴心抗压强度f_c如表1所示。

1.3 试验装置与加载制度

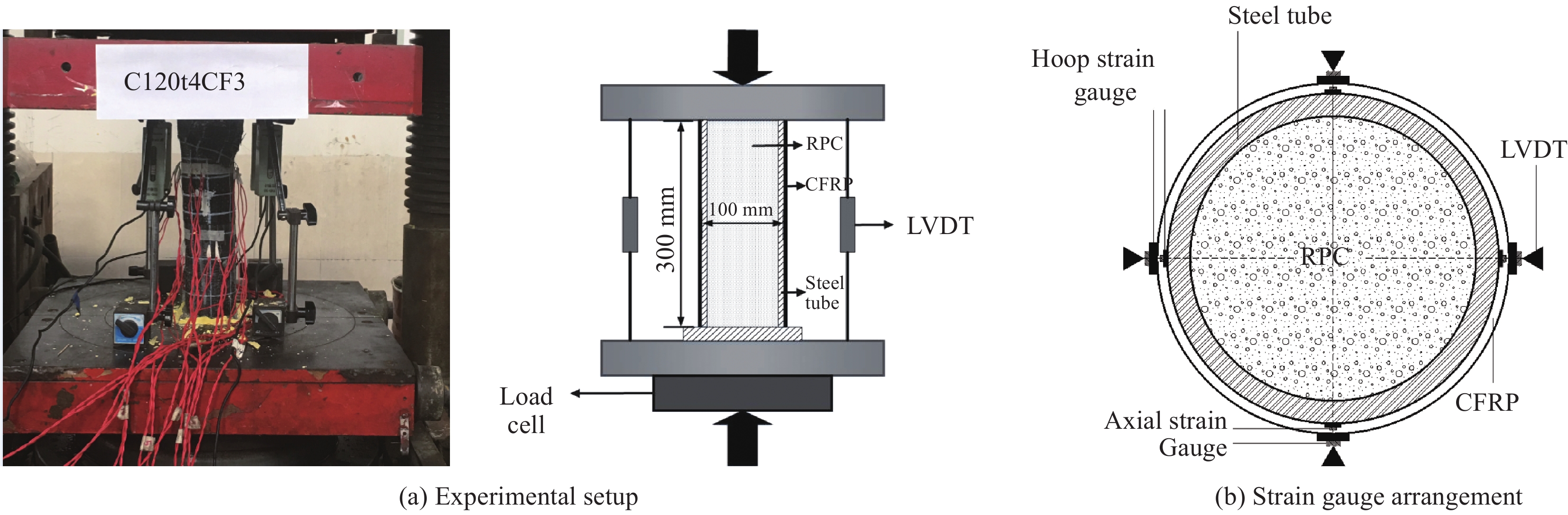
试验加载采用500 t电液伺服万能试验机，加载方式为试件全截面受压，并用YHD-50位移传感器与DH3816N应变测试系统进行数据采集。应变片粘贴于中部区域的CFRP表面与钢管表面，并每间隔90°均匀布置8对互相垂直的环向与纵向应变片，试验装置与应变片布置如图2所示。试验进行预加载，监测应变片读值是否均匀，并对试件进行几何与物理对中，待试件满足要求后进行轴压试验。试验采用分级加载，初期每级加载增量为预测极限荷载的10%左右，每级大约持续2~3 min，当荷载加载至预测极限荷载的80%~90%时，每级荷载增量为预测极限荷载的5%左右，每级加载大约持续3~5 min，加载过程中观察试验现象并连续采集数据直至试件半数以上应变片失效。

图 2 加载装置与应变片布置

Figure 2. Experimental setup and strain gauge arrangement

LVDT—Linear variable differential transformer

下载: 全尺寸图片幻灯片

2. 试验结果与讨论

2.1 试验现象与CFRP约束钢管-RPC破坏模式

图3为试件破坏模式。试验发现，钢管的轴压试验同其材料性能试验类似，表现出较大的塑性。CFRP约束钢管-RPC轴压试验，其加载初期达到预测极限荷载90%左右时，试件表面无明显变化，偶尔能听到“嗞嗞”的些许碳纤维胶嗞裂声，随着继续加载试件外观有少许应变片脱落，然后试件外观较快的呈现钢管外露鼓曲与上下错动的趋势，最后中上部CFRP绷裂直到试件完全破坏。整个试件中，钢管-RPC呈现出中部区域的剪切破坏，C120t3CF3、C120t4CF3、C120t5CF2、C120t5CF3四根短柱表现出中上部区域的鼓曲破坏，其余CFRP约束钢管-RPC为中上部的剪切破坏。

图 3 CFRP约束钢管-RPC试件破坏模式

Figure 3. Failure modes of CFPR confined steel tube-RPC specimens

下载: 全尺寸图片幻灯片

图3(a)中钢管主要发生顶部的鼓曲，随着钢管壁厚的增加，上端部向下鼓曲范围变小；图3(a)中的t3CF0和图3(b)中C120t3CF0分别对应的是3 mm壁厚钢管破坏形态和3 mm壁厚钢管-RPC的破坏形态与剥开面貌。可知，RPC灌注填充钢管使钢管由顶部的鼓曲破坏转变为剪切破坏。分析可知，钢管的变形表现出较大的塑性，因而破坏成形具备更明显的鼓曲延性，但随着壁厚的增加，钢管整体的刚度也会增大，因而鼓曲会向端部紧缩变小，而C120t3CF0因钢管灌注RPC，在强度大幅度提高的同时，RPC所带来的脆性性质也会让整个构件出现破坏形态的变化。

图3(c)为C120t3CF2的破坏形态。图3(d)为C120t3CF3鼓曲破坏的剥开形貌。观察图3(b)~图3(d)可知，随着CFRP粘贴层数的增加，试件由中部剪切破坏变成中上部剪切破坏，后转为中上部鼓曲破坏。分析图3(d)剥开形貌可知，RPC被挤碎，有细末RPC碎渣掉落。

2.2 CFRP约束钢管-RPC的荷载-位移曲线

图4为典型约束混凝土的轴向荷载-位移(N-∆)曲线^{[8, 21-25]}，其中CFRP约束钢管-RPC典型荷载-位移曲线通过试验采集的数据绘制而成。与CFRP约束钢管-混凝土短柱相比，CFRP约束钢管-RPC短柱荷的载-位移曲线弹性阶段有所加长，极限荷载得到了有效提高，两者破坏过程相似，可分为四个阶段：(1) 弹性阶段，初始加载状态下，RPC横向变形系数小于钢管的横向变形系数，钢管与RPC分别单独承受轴向荷载，钢管和RPC都处于线弹性状态；(2) 弹塑性阶段，与普通混凝土相比，因无约束的RPC荷载-位移曲线弹性阶段较长，因此RPC仍处于弹性阶段，而钢管进入了弹塑性状态，因而引起了两者之间的内力重分布，导致荷载-位移曲线呈现非线性变化，此阶段结束的标志是钢管屈服，加载达到峰值荷载N_p；(3) 硬化阶段，过峰值荷载对应的位移∆_p后，钢管的屈服促使轴向应力较大转变为恒定的环向应力而使CFRP产生较大的约束作用而不断的提供围压，进而延缓了钢管-RPC柱刚度的退化，此过程结束的标志为CFRP被绷断，加载达到极限荷载N_u；(4) 强化阶段，核心RPC处于钢管残余应力约束之下的同时仍然受到部分未完全破坏的CFRP的约束效应，其残余强度表现出回升幅度增大的趋势。

图 4 约束混凝土轴向荷载-位移曲线

Figure 4. Axial load-displacement curves of confined concretes

下载: 全尺寸图片幻灯片

2.2.1 CFRP层数的影响

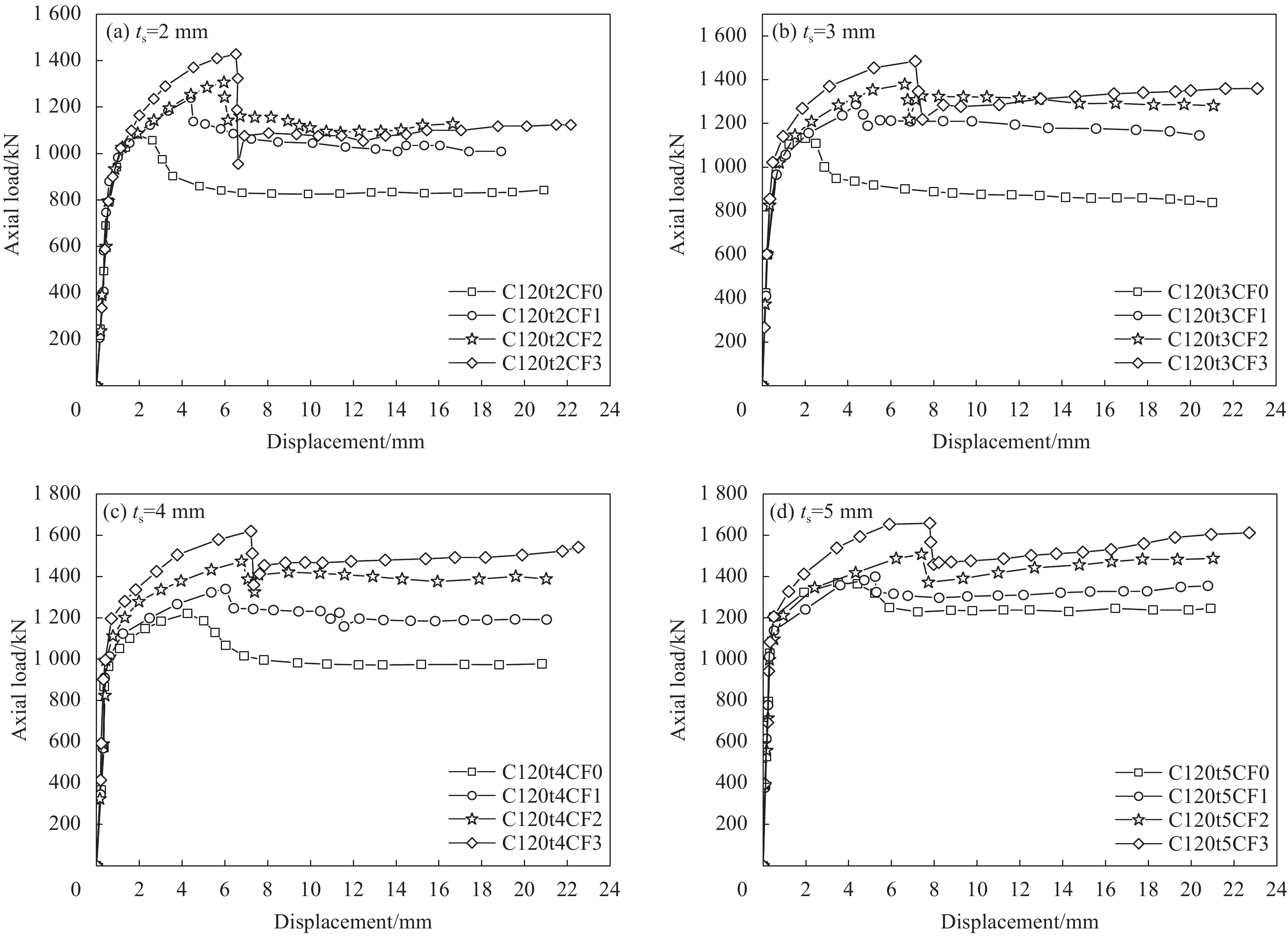
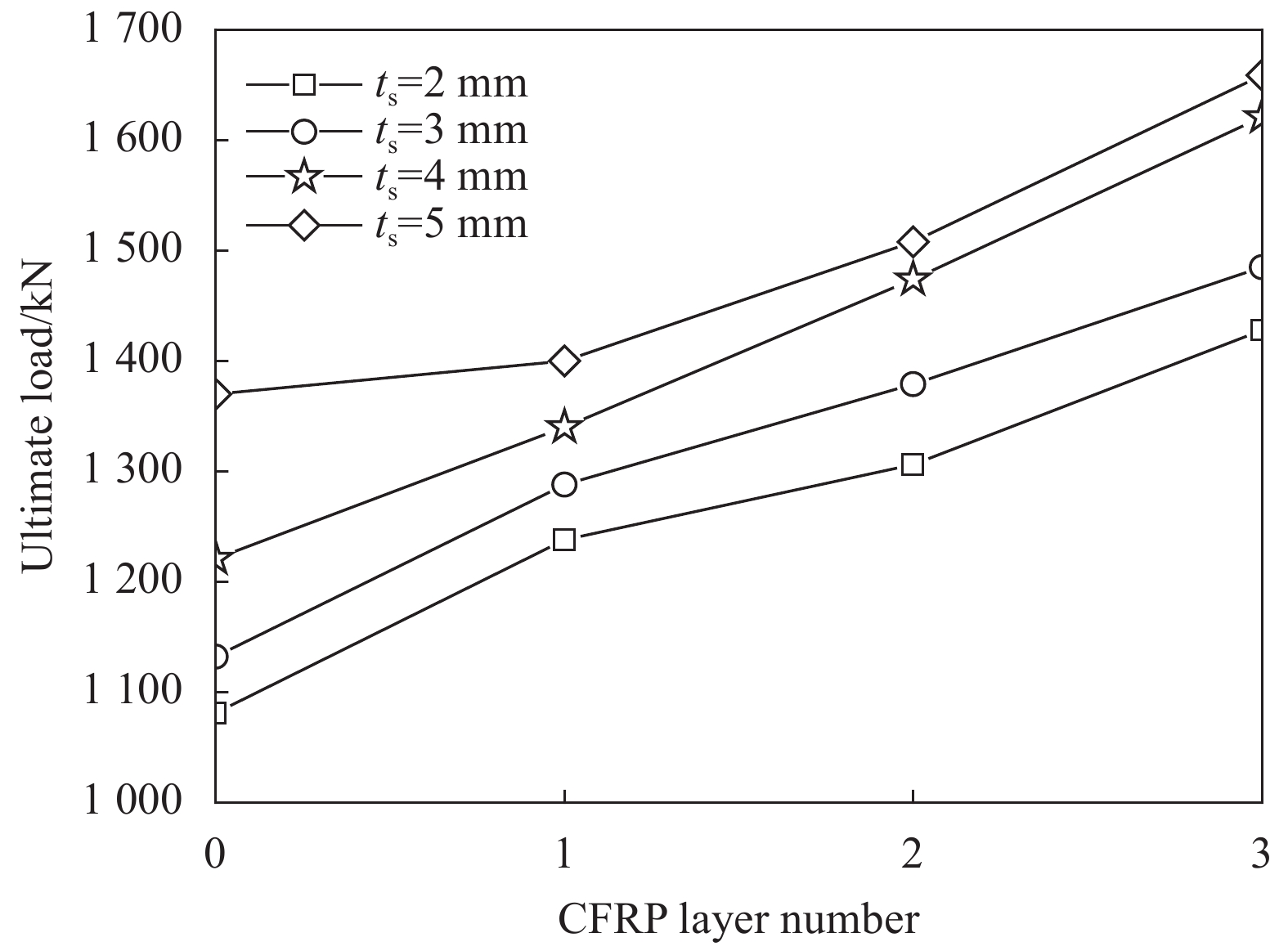
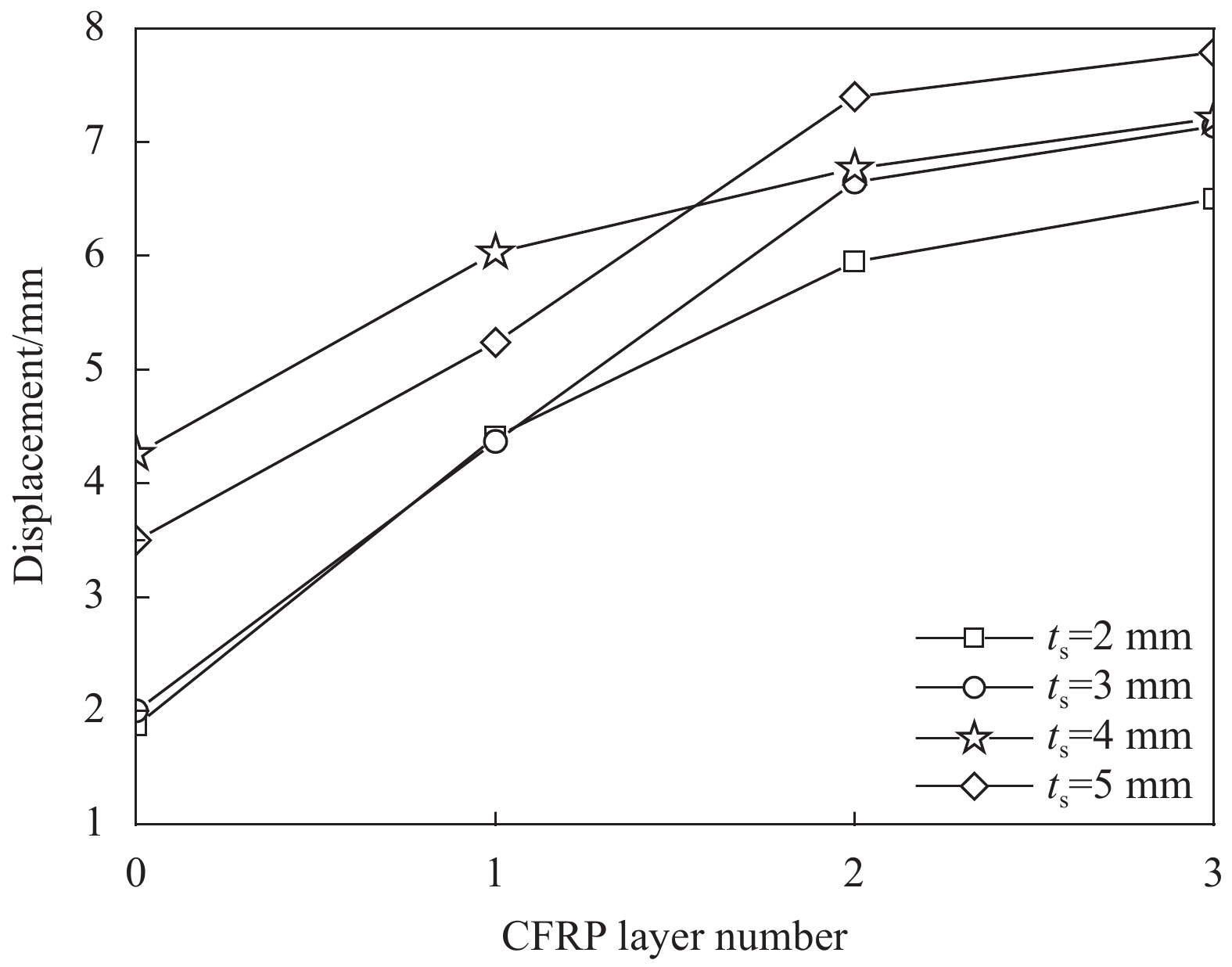
图5是不同CFRP层数的CFRP约束钢管-RPC短柱轴向的荷载-位移曲线。可知，在相同钢管壁厚下，CFRP约束钢管-RPC在钢管屈服前的荷载-位移曲线基本一致，钢管屈服后荷载-位移曲线进入线性硬化阶段，这主要是钢管的屈服激活了CFRP的约束效应，进而有效抑制了钢管-RPC试件刚度的退化，并且随着CFRP层数的增加，其硬化阶段的线性斜率呈增大趋势。CFRP被拉断达到极限荷载后，试件进入强化阶段，此阶段核心RPC在CFRP与钢管的残余应力作用约束之下，呈现出随着CFRP层数的增加，曲线从平台逐渐转变为上升的趋势。图6和图7分别为极限荷载N_u和极限荷载对应的位移∆_u随CFRP层数的变化。可知，试件极限荷载N_u与极限荷载对应的位移∆_u随CFRP层数增加而增大。在CFRP约束下的钢管-RPC短柱与同组的钢管-RPC短柱相比，极限荷载N_u增大范围在2.2%~32.8%之间，极限荷载对应的位移∆_u增大范围为42%~257%。

图 5 不同CFRP层数的CFRP约束钢管-RPC轴向荷载-位移曲线

Figure 5. Axial load-displacement curves of CFRP confined steel tube-RPC with different CFRP layer numbers

下载: 全尺寸图片幻灯片

图 6 不同CFRP层数的CFRP约束钢管-RPC极限荷载变化

Figure 6. Ultimate load change of CFRP confined steel tube-RPC with different CFRP layer numbers

下载: 全尺寸图片幻灯片

图 7 不同CFRP层数的CFRP约束钢管-RPC极限荷载对应位移变化

Figure 7. Displacement corresponding to ultimate load change of CFRP confined steel tube-RPC with different CFRP layer numbers

下载: 全尺寸图片幻灯片

2.2.2 钢管壁厚的影响

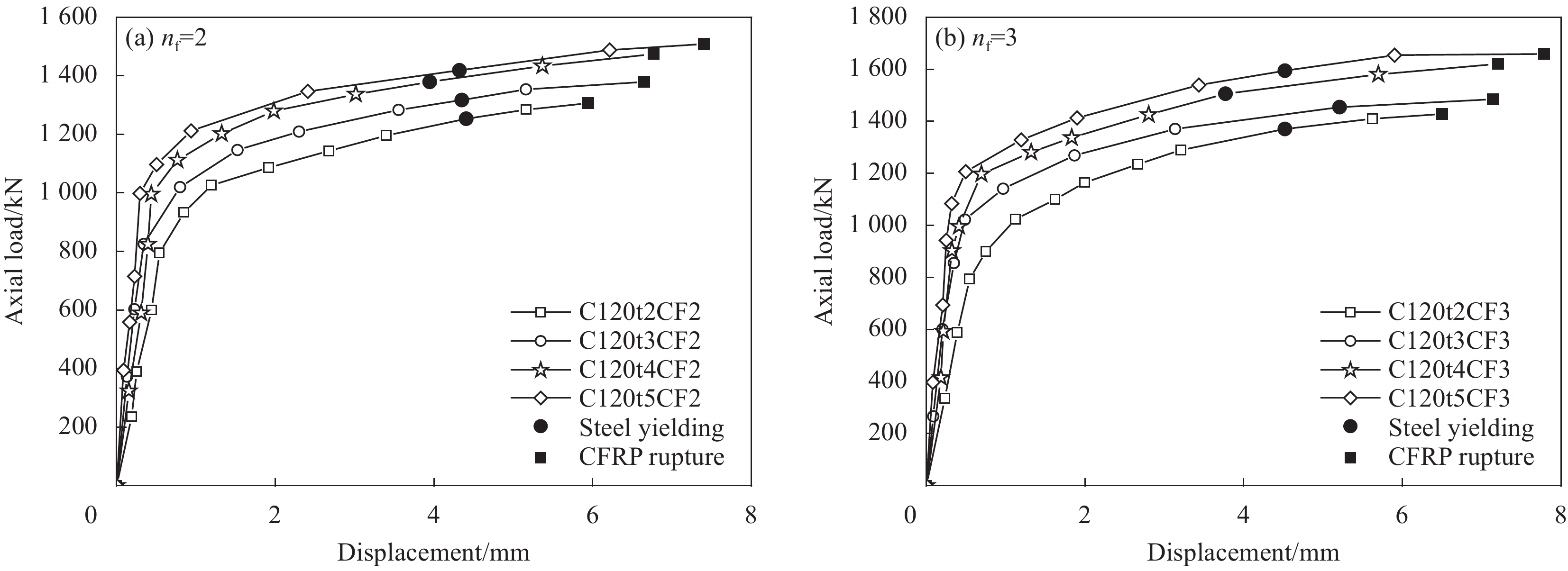
根据表1试件极限荷载数据可知，随着钢管壁厚的增加，试件极限荷载单调增大。图8为CFRP层数n_f=2和n_f=3两个系列的不同钢管壁厚的CFRP约束钢管-RPC荷载-位移曲线。根据荷载-位移曲线变化的四个阶段，取前三阶段进行说明。弹性阶段中，随着钢管壁厚的增加，其斜率单调增大；弹塑性阶段中，曲线表现为缓慢上升，钢管壁厚对其影响逐渐减小；硬化阶段中，随着钢管壁厚的增加，曲线互相之间近似平行。这是由于钢管屈服后，承载力的上升主要来源于CFRP对于RPC围压的增大，由于CFRP层数相同，故表现为曲线斜率近似相等的平行增大。从图8(a)和图8(b)可以看出，钢管的屈服点与CFRP的断裂点对应荷载相隔较近，因此钢管屈服点对于极限荷载的计算有很好的借鉴作用，这与文献[26]中两点荷载相近观点类似。文献[26]中对于CFRP约束钢管-混凝土承载力的计算以钢管屈服点与CFRP拉断位置点两种情况分别进行了讨论。

图 8 不同钢管壁厚CFRP约束钢管-RPC的轴向荷载-位移曲线

Figure 8. Axial load-displacement curves of CFRP confined steel tube-RPC with different steel tube thicknesses

下载: 全尺寸图片幻灯片

2.3 CFRP约束钢管-RPC提高系数

图6和图7反映出钢管-RPC短柱在CFRP约束之下承载力和变形能力得到了有效的提高，CFRP约束钢管-RPC柱的轴压承载能力的增强可以通过定义极限荷载增加百分比的提高系数r_cap来衡量^[24]：

${r_{{\rm{cap}}}} = \frac{{{N_{\rm{u}}} - N}}{N} \times 100\%$

(1)

式中：N_u为CFRP约束钢管-RPC短柱的极限荷载；N为无约束的钢管-RPC短柱的极限荷载。根据式(1)计算的提高系数r_cap列于表1。

CFRP约束钢管-RPC短柱为三类材料复合结构柱，其组合形式为RPC受钢管与CFRP双重约束而形成的复合结构。为便于分析提高系数r_cap与钢管和CFRP约束的关系，引入钢管套箍系数ξ_s^[27]与CFRP套箍系数ξ_cf^[13]：

${\xi _{\rm{s}}} = {A_{\rm{s}}}{f_{\rm{y}}}/({A_{\rm{c}}}{f_{\rm{c}}})$

(2)

${\xi _{{\rm{cf}}}} = {A_{{\rm{cf}}}}{f_{{\rm{cf}}}}/({A_{\rm{c}}}{f_{\rm{c}}})$

(3)

式中：A_c、A_s、A_cf分别为短柱中核心混凝土、钢管、FRP的横截面面积；f_c、f_y、f_cf分别为无约束混凝土轴心抗压强度、钢管屈服强度、CFRP抗拉强度。

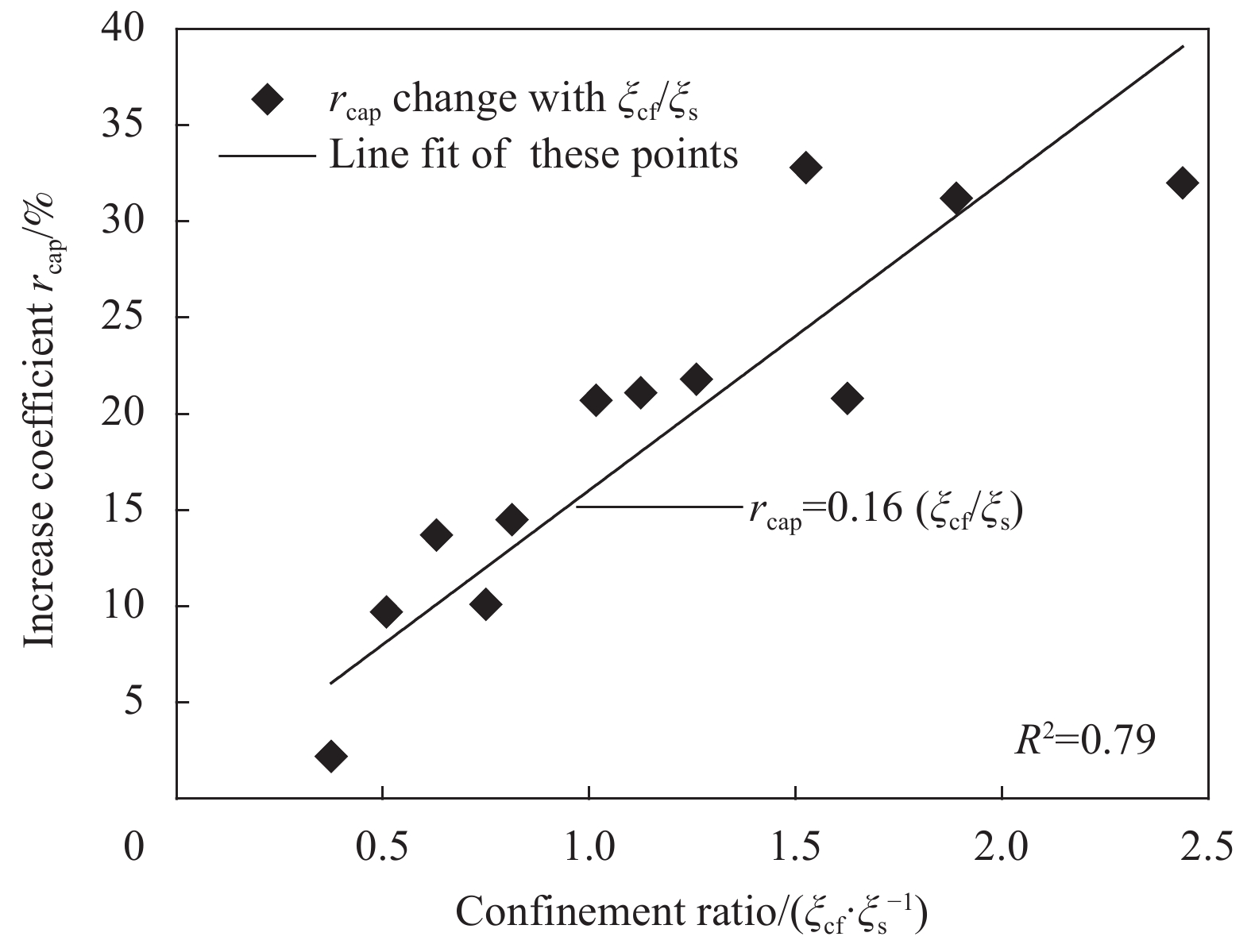
通过式(2)和式(3)所计算的套箍系数列于表1。可知：相同CFRP层数时，提高系数r_cap随着钢管套箍系数ξ_s的增大总体上减小；相同钢管壁厚时，提高系数r_cap随着CFRP套箍系数ξ_cf的增大而单调增大。因此提高系数r_cap随着套箍率ξ_cf/ξ_s增大而单调增大，图9将提高系数r_cap与套箍率ξ_cf/ξ_s进行线性拟合。可见，其拟合度为0.79，由此可知提高系数r_cap能与套箍率ξ_cf/ξ_s进行较好的关联。

图 9 CFRP约束钢管-RPC提高系数随套箍率的变化

Figure 9. Increase coefficient change with confinement ratio of CFRP confined steel tube-RPC

下载: 全尺寸图片幻灯片

2.4 CFRP应变效率

纤维增强树脂复合材料(FRP)的应变效率通常以FRP效率指标k_ε来表示。其定义为FRP约束钢管-混凝土试件中FRP环向断裂应变平均值与FRP材料性能试验测得的极限抗拉强度对应的应变值之比^[28-29]。一般由k_ε1和k_ε2两个指标计算得到：

${k_\varepsilon } = {k_{\varepsilon 1}}{k_{\varepsilon 2}}$

(4)

式中：k_ε1表示试件中FRP环向断裂应变平均值与FRP环向断裂应变最大值之比；k_ε2表示FRP环向断裂应变最大值与FRP材料性能试验测得的极限抗拉强度对应的应变值之比。CFRP应变效率k_ε能表征核心混凝土横向变形的变化，k_ε 越大其CFRP筒中应变越均匀，核心混凝土与钢管相互作用的内力重分布均匀性也就越好。

试验中通过计算所得k_ε值如表1所示，k_ε值变化范围在0.666~0.808之间，平均值为0.76。

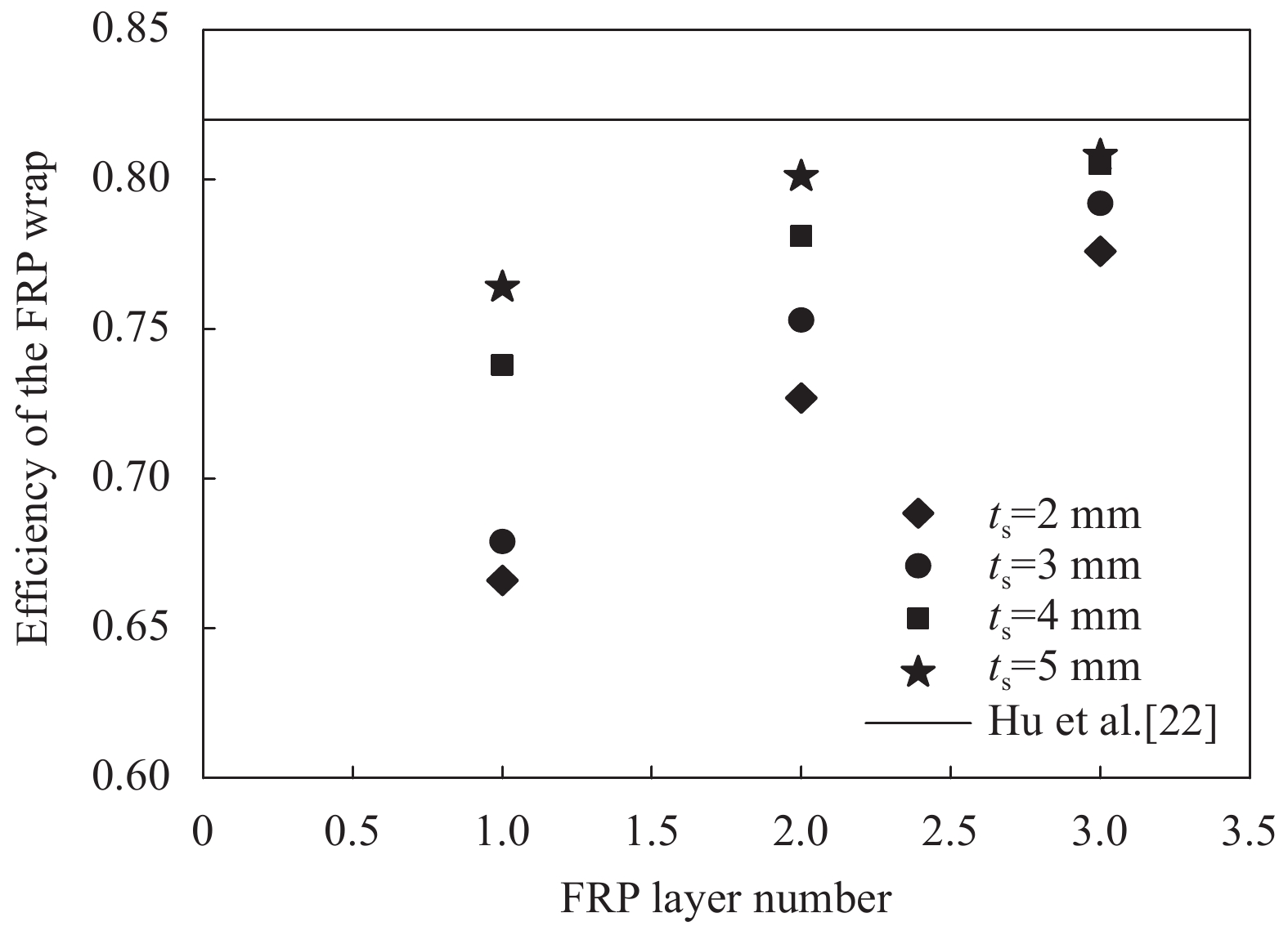
文献[22]中GFRP钢管混凝土k_ε1的均值为0.865，k_ε2均值为0.948，两者相乘得到k_ε的均值为0.82，将本文所得结果同文献[22]所得值绘于图10。可知，CFRP应变效率表现出随CFRP层数的增加而增大，玻璃纤维增强树脂复合材料(GFRP)约束钢管-混凝土的应变效率高于CFRP约束钢管-RPC，其原因在于GFRP套箍系数大于CFRP套箍系数^[12]，另外CFRP约束钢管-RPC短柱的核心RPC横向变形破坏比普通混凝土更急促，导致钢管与RPC相互作用的不均匀性更大。

图 10 纤维增强树脂复合材料(FRP)应变效率随FRP层数的变化

Figure 10. Fiber reinforced polymer(FRP) strain efficiency change with FRP layer number

下载: 全尺寸图片幻灯片

2.5 CFRP约束钢管-RPC延性系数

RPC具有较高的强度，但是其延性又比普通混凝土差，为了研究钢管-RPC短柱在CFRP约束作用下的延性性能，引入延性指标(µ_d)^[16]：

${\mu _{\rm{d}}} = \frac{{{\varepsilon _{0.85}}}}{{{\varepsilon _{\rm{u}}}}}$

(5)

其中：ε_0.85为荷载下降到极限荷载85%时对应的轴向应变；ε_u为ε_0.75/0.75，其中ε_0.75为峰值荷载之前荷载上升到极限荷载75%时对应的轴向应变。

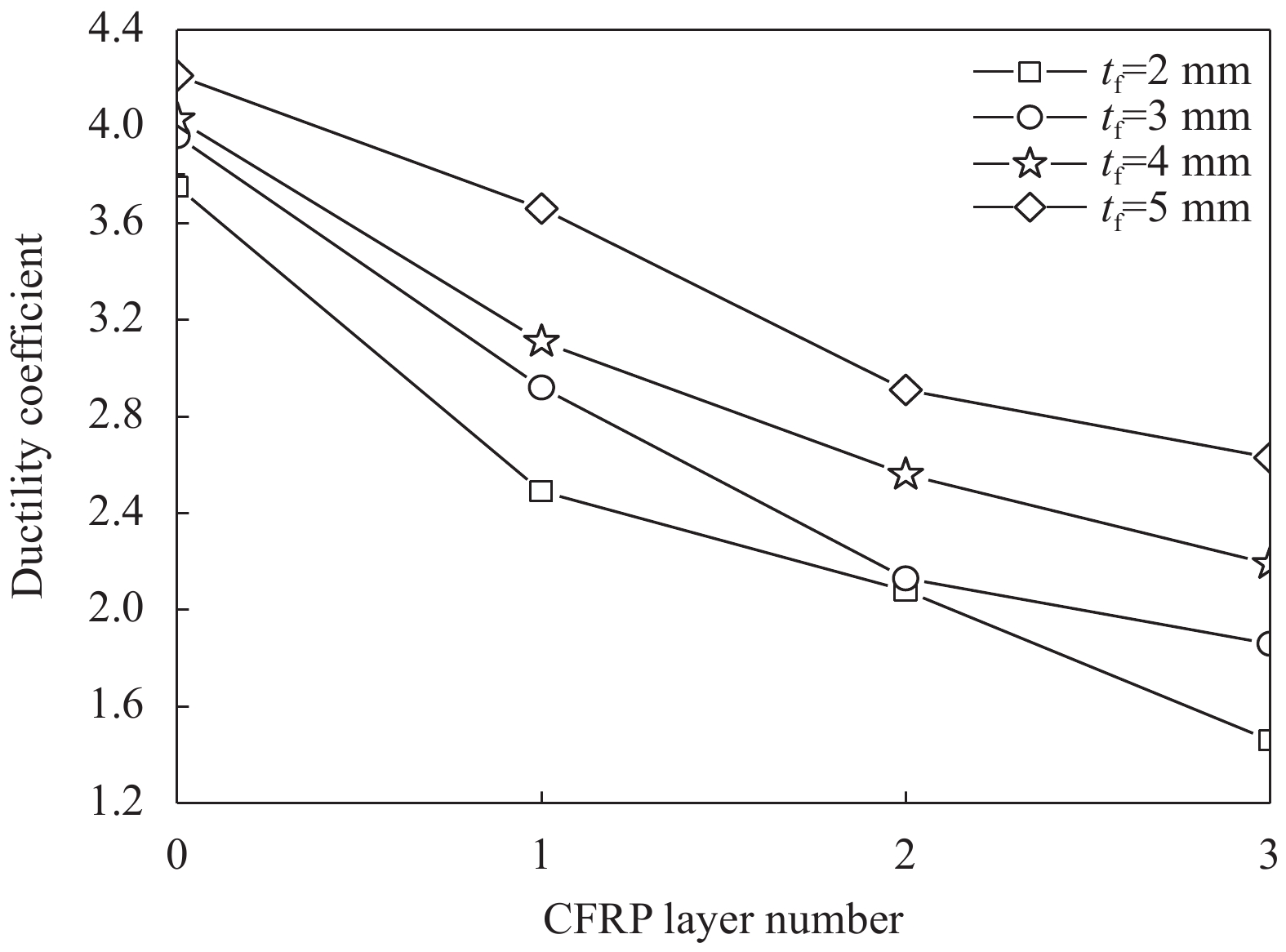
通过式(5)计算的延性系数列于表1，并绘制延性指标随CFRP层数的变化趋势如图11所示。可知，随着CFRP层数的增加延性系数减小，表1中延性指标值变化范围为1.46~4.21，而文献[30]中CFRP约束钢管-混凝土的延性指标变化范围为2.6~14.8，分析可知CFRP约束钢管-RPC短柱延性总体上不如CFRP约束钢管-混凝土。

图 11 CFRP约束钢管-RPC延性系数随CFRP层数的变化

Figure 11. Ductility coefficient change with CFRP layer number of CFRP confined steel tube-RPC

下载: 全尺寸图片幻灯片

3. CFRP约束钢管-RPC承载力的计算

3.1 现存CFRP钢管-高强混凝土承载力模型

CFRP约束钢管-高强混凝土短柱的预测模型的公开研究较少，丁发兴等^[16]基于极限平衡法与弹塑性方法提出了CFRP约束钢管-混凝土的承载力模型，并在此模型上拓展参数范围提出适合计算70 MPa、90 MPa、120 MPa的CFRP约束钢管-高强混凝土短柱的承载力模型；顾威等^[23]在CFRP约束钢管-混凝土的基础之上，对于钢管套箍系数与CFRP套箍系数进行折减提出了CFRP约束钢管-高强混凝土的承载力计算公式。两者分别为：

${N_{{\rm{df}}}} = \left[1 + 1.7{\phi _{\rm{s}}} + 1.7{\phi _{{\rm{cf}}}}\right]f_{\rm{c}}\!{'\!'}{A_{\rm{c}}}$

(6)

${N_{{\rm{gw}}}} = \left[1 + 1.8{\xi _{{\rm{sc}}}} + 1.8{\xi _{{\rm{cfc}}}}\right]{f_{{\rm{ck}}}}{A_{\rm{c}}}$

(7)

其中：N_df为式(6)承载力计算值；φ_s和φ_cf分别为式(6)的钢管套箍系数和CFRP套箍系数，φ_s=A_s f_y/(A_c f_c″)，φ_cf =A_cf f_cf/(A_c f_c″)；f_c″为对应式(6)的无约束混凝土抗压强度，f_c″=0.4f_cu^7/6；N_gw为式(7)承载力计算值；ξ_sc和ξ_cfc分别为式(7)的钢管套箍系数和CFRP套箍系数，ξ_sc=A_s f_y/(A_c f_ck)，ξ_cfc=A_cf f_cf/(A_c f_ck)；f_ck为对应式(7)的无约束混凝土抗压强度，f_ck=0.67f_cu。此次试验中f_cu=127.66，f_c″=114.58，f_ck=85.53。

用式(6)与式(7)预测计算CFRP约束钢管-RPC短柱承载力，并将预测计算结果与试验实测结果列于表2。可知：式(6)的N_df/N_u的平均值为1.34，标准差为0.134，变异系数为0.1；式(7)的N_gw/N_u的平均值为1.23，标准差为0.161，变异系数为0.131。由此可知模型(6)与模型(7)预测计算CFRP约束钢管-RPC短柱承载力都偏于安全，且计算离散性与波动性都偏大，因此模型(6)和模型(7)不适用于计算CFRP约束钢管-RPC短柱承载力。

表 2 CFRP约束钢管-高强混凝土预测结果与实测承载力结果比较

Table 2. Comparisons of experimental results and predicted results of CFRP confined high-strength concrete filled steel tube

Specimen	D×t_s×L/mm	φ_s	φ_cf	ξ_sc	ξ_cfc	N_u/kN	N_df/kN	N_gw/kN	N_up/kN	N_df/N_u	N_gw/N_u
C120t2CF0	103×2×303	0.256	0	0.343	0	1 081	1 265	1 064	1 228	1.17	0.98
C120t2CF1	103×2×303	0.256	0.208	0.343	0.279	1 238	1 577	1 395	1 387	1.27	1.13
C120t2CF2	103×2×303	0.256	0.417	0.343	0.558	1 306	1 890	1 725	1 547	1.45	1.32
C120t2CF3	103×2×303	0.256	0.625	0.343	0.837	1 428	2 202	2 056	1 707	1.54	1.44
C120t3CF0	102×3×303	0.349	0	0.467	0	1 132	1 320	1 139	1 179	1.17	1.01
C120t3CF1	102×3×303	0.349	0.219	0.467	0.294	1 288	1 629	1 466	1 298	1.26	1.14
C120t3CF2	102×3×303	0.349	0.439	0.467	0.588	1 379	1 939	1 794	1 417	1.41	1.3
C120t3CF3	102×3×303	0.349	0.658	0.467	0.882	1 485	2 248	2 121	1 536	1.51	1.43
C120t4CF0	101×4×304	0.456	0	0.611	0	1 221	1 381	1 219	1 259	1.13	1
C120t4CF1	101×4×304	0.456	0.232	0.611	0.31	1 340	1 687	1 544	1 362	1.26	1.15
C120t4CF2	101×4×304	0.456	0.463	0.611	0.621	1 474	1 994	1 868	1 464	1.35	1.27
C120t4CF3	101×4×304	0.456	0.695	0.611	0.931	1 621	2 300	2 192	1 567	1.42	1.35
C120t5CF0	102×5×306	0.636	0	0.852	0	1 370	1 585	1 440	1 400	1.16	1.05
C120t5CF1	102×5×306	0.636	0.239	0.852	0.32	1 400	1 894	1 767	1 484	1.35	1.26
C120t5CF2	102×5×306	0.636	0.478	0.852	0.64	1 508	2 203	2 095	1 568	1.46	1.39
C120t5CF3	102×5×306	0.636	0.717	0.852	0.96	1 659	2 512	2 422	1 652	1.51	1.46
Notes: φ_s—Steel tube confinement factor of equation (6); φ_cf—CFRP confinement factor of equation (6); ξ_sc—Steel tube confinement factor of equation (7); ξ_cfc—CFRP confinement factor of equation (7); N_df—Ultimate load of equation (6); N_gw—Ultimate load of equation (7).

下载: 导出CSV

| 显示表格

3.2 CFRP约束钢管-RPC承载力模型

图9中对提高系数r_cap与套箍率ξ_cf/ξ_s进行了线性拟合，其线性拟合结果良好，基于此可通过下式提出CFRP约束钢管-RPC承载力模型：

${N_{{\rm{up}}}} = (1 + {r_{{\rm{cap}}}}){N_{{\rm{RPCFST}}}}$

(8)

${N_{{\rm{RPCFST}}}} = {f_{\rm{y}}}{A_{\rm{s}}} + {f_{{\rm{co}}}}{A_{\rm{c}}}$

(9)

${f_{{\rm{co}}}} = {f_{\rm{c}}}\left[1.2 + 0.25{\left(\frac{{100}}{{{f_{\rm{c}}}}}\right)^{1.25}}\xi _{\rm{s}}^2 - 0.04{\xi _{\rm{s}}}\right]$

(10)

${r_{{\rm{cap}}}} = 0.16\frac{{{\xi _{{\rm{cf}}}}}}{{{\xi _{\rm{s}}}}}$

(11)

式中：N_up是CFRP约束钢管-RPC短柱承载力计算值；N_RPCFST为钢管-RPC短柱承载力计算值；式(9)和式(10)是钢管-RPC短柱在轴压下的承载力计算公式^[11]，式(11)是图9拟合结果的公式。需要指出的是式(8)~(11)计算模型提出的范围有较小的局限，如果使用可以进行更多变量范围的试验，并可结合多种理论与数值分析方面进行拓展，另外本文所做试验与引用公式针对的是无钢纤维的RPC，针对掺钢纤维的RPC所形成的CFRP约束钢管-RPC短柱，其模型适用性有待进一步的探讨与研究。

4. 结论

以钢管壁厚(2 mm、3 mm、4 mm、5 mm)与碳纤维增强树脂复合材料(CFRP)粘贴层数(0、1、2、3层)为变化参数进行了12根CFRP约束钢管-活性粉末混凝土(RPC)短柱、4根钢管-RPC短柱及4根钢管短柱的轴压试验，分析了钢管壁厚和CFRP层数对CFRP约束钢管-RPC承载力与变形能力的影响，研究了试件提高系数、CFRP应变效率和延性系数等相关性能指标，并将提高系数关联CFRP套箍系数与钢管套箍系数提出了CFRP约束钢管-RPC的承载力模型，通过分析表明所提模型计算结果与试验结果吻合较好。

(1)钢管的破坏为顶端的鼓曲破坏，并随着壁厚增加鼓曲范围变小；钢管-RPC短柱呈现出中部区域的剪切破坏；CFRP约束钢管-RPC短柱随着CFRP层数增加，其破坏模式逐渐由剪切破坏转变为鼓曲破坏，但其破坏都发生在中上部区域。

(2)相同钢管壁厚下，与钢管-RPC短柱相比，CFRP约束钢管-RPC短柱的极限荷载增大范围在2.2%~32.8%之间，极限荷载对应的位移增大范围在42%~257%之间；相同CFRP层数下，随着钢管壁厚的增加，试件荷载-位移曲线斜率增大，并在硬化阶段互相平行。

(3)与CFRP约束钢管-混凝土相比，CFRP约束钢管-RPC表现出CFRP应变效率的下降，且其延性不如CFRP约束钢管-混凝土。

(4) 通过提高系数关联CFRP套箍系数与钢管套箍系数提出了CFRP约束钢管-RPC短柱承载力的实用计算模型。

图 1 CFRP约束钢管-RPC拉伸试样尺寸

Figure 1. Size of CFPR confined steel tube-RPC tensile specimen

下载: 全尺寸图片幻灯片

图 2 加载装置与应变片布置

Figure 2. Experimental setup and strain gauge arrangement

LVDT—Linear variable differential transformer

下载: 全尺寸图片幻灯片

图 3 CFRP约束钢管-RPC试件破坏模式

Figure 3. Failure modes of CFPR confined steel tube-RPC specimens

下载: 全尺寸图片幻灯片

图 4 约束混凝土轴向荷载-位移曲线

Figure 4. Axial load-displacement curves of confined concretes

下载: 全尺寸图片幻灯片

图 5 不同CFRP层数的CFRP约束钢管-RPC轴向荷载-位移曲线

Figure 5. Axial load-displacement curves of CFRP confined steel tube-RPC with different CFRP layer numbers

下载: 全尺寸图片幻灯片

图 6 不同CFRP层数的CFRP约束钢管-RPC极限荷载变化

Figure 6. Ultimate load change of CFRP confined steel tube-RPC with different CFRP layer numbers

下载: 全尺寸图片幻灯片

图 7 不同CFRP层数的CFRP约束钢管-RPC极限荷载对应位移变化

Figure 7. Displacement corresponding to ultimate load change of CFRP confined steel tube-RPC with different CFRP layer numbers

下载: 全尺寸图片幻灯片

图 8 不同钢管壁厚CFRP约束钢管-RPC的轴向荷载-位移曲线

Figure 8. Axial load-displacement curves of CFRP confined steel tube-RPC with different steel tube thicknesses

下载: 全尺寸图片幻灯片

图 9 CFRP约束钢管-RPC提高系数随套箍率的变化

Figure 9. Increase coefficient change with confinement ratio of CFRP confined steel tube-RPC

下载: 全尺寸图片幻灯片

图 10 纤维增强树脂复合材料(FRP)应变效率随FRP层数的变化

Figure 10. Fiber reinforced polymer(FRP) strain efficiency change with FRP layer number

下载: 全尺寸图片幻灯片

图 11 CFRP约束钢管-RPC延性系数随CFRP层数的变化

Figure 11. Ductility coefficient change with CFRP layer number of CFRP confined steel tube-RPC

下载: 全尺寸图片幻灯片

表 1 试件编号及参数

Table 1 Parameters of specimens

Specimen	D×t_s×L/mm	f_y/MPa	E_s/GPa	f_cu/MPa	f_c/MPa	n_f	ξ_s	ξ_cf	k_ε	µ_d	r_cap/%	N_u/kN
t2CF0	103×2×303	356	208	−	−	−	−	−	−	−	−	328
C120t2CF0	103×2×303	356	208	127	108	0	0.272	0	−	3.75	0	1 081
C120t2CF1	103×2×303	356	208	127	108	1	0.272	0.221	0.666	2.49	14.5	1 238
C120t2CF2	103×2×303	356	208	127	108	2	0.272	0.442	0.727	2.08	20.8	1 306
C120t2CF3	103×2×303	356	208	127	108	3	0.272	0.663	0.776	1.46	32.0	1 428
t3CF0	102×3×303	310	204	−	−	−	−	−	−	−	−	379
C120t3CF0	102×3×303	310	204	127	108	0	0.37	0	−	3.96	0	1 132
C120t3CF1	102×3×303	310	204	127	108	1	0.37	0.233	0.679	2.92	13.7	1 288
C120t3CF2	102×3×303	310	204	127	108	2	0.37	0.466	0.753	2.13	21.8	1 379
C120t3CF3	102×3×303	310	204	127	108	3	0.37	0.699	0.792	1.86	31.2	1 485
t4CF0	101×4×304	291	202	−	−	−	−	−	−	−	−	443
C120t4CF0	101×4×304	291	202	127	108	0	0.484	0	−	4.03	0	1 221
C120t4CF1	101×4×304	291	202	127	108	1	0.484	0.246	0.738	3.11	9.7	1 340
C120t4CF2	101×4×304	291	202	127	108	2	0.484	0.492	0.781	2.56	20.7	1 474
C120t4CF3	101×4×304	291	202	127	108	3	0.484	0.738	0.805	2.19	32.8	1 621
t5CF0	102×5×306	318	207	−	−	−	−	−	−	−	−	501
C120t5CF0	102×5×306	318	207	127	108	0	0.675	0	−	4.21	0	1 370
C120t5CF1	102×5×306	318	207	127	108	1	0.675	0.253	0.764	3.66	2.2	1 400
C120t5CF2	102×5×306	318	207	127	108	2	0.675	0.506	0.801	2.91	10.1	1 508
C120t5CF3	102×5×306	318	207	127	108	3	0.675	0.759	0.808	2.63	21.1	1 659
Notes: D—Diameter of steel tube; t_s—Steel tube thickness; L—Length of a specimen; f_y—Yield strength of steel; E_s—Elastic modulus of steel; f_cu—Cubic compressive strength of reactive powder concrete (RPC); f_c—Axial compressive strength of RPC; n_f—Number of carbon fiber reinforced polymer (CFRP) layers; ξ_s—Steel tube confinement factor; ξ_cf—CFRP confinement factor; k_ε—Strain efficiency of CFRP; µ_d—Ductility factor; r_cap—Increase factor; N_u—Ultimate load. The letter C denotes the nominal RPC strength, the letter t is the steel tube thickness, and the letters CF denote the CFRP confined components. For example, the C120t2CF3 indicates that the strength of the specimen is 120 MPa, the thickness of the steel tube is 2 mm, and the specimen is wrapped in three CFRP layers.

下载: 导出CSV

表 2 CFRP约束钢管-高强混凝土预测结果与实测承载力结果比较

Table 2 Comparisons of experimental results and predicted results of CFRP confined high-strength concrete filled steel tube

Specimen	D×t_s×L/mm	φ_s	φ_cf	ξ_sc	ξ_cfc	N_u/kN	N_df/kN	N_gw/kN	N_up/kN	N_df/N_u	N_gw/N_u
C120t2CF0	103×2×303	0.256	0	0.343	0	1 081	1 265	1 064	1 228	1.17	0.98
C120t2CF1	103×2×303	0.256	0.208	0.343	0.279	1 238	1 577	1 395	1 387	1.27	1.13
C120t2CF2	103×2×303	0.256	0.417	0.343	0.558	1 306	1 890	1 725	1 547	1.45	1.32
C120t2CF3	103×2×303	0.256	0.625	0.343	0.837	1 428	2 202	2 056	1 707	1.54	1.44
C120t3CF0	102×3×303	0.349	0	0.467	0	1 132	1 320	1 139	1 179	1.17	1.01
C120t3CF1	102×3×303	0.349	0.219	0.467	0.294	1 288	1 629	1 466	1 298	1.26	1.14
C120t3CF2	102×3×303	0.349	0.439	0.467	0.588	1 379	1 939	1 794	1 417	1.41	1.3
C120t3CF3	102×3×303	0.349	0.658	0.467	0.882	1 485	2 248	2 121	1 536	1.51	1.43
C120t4CF0	101×4×304	0.456	0	0.611	0	1 221	1 381	1 219	1 259	1.13	1
C120t4CF1	101×4×304	0.456	0.232	0.611	0.31	1 340	1 687	1 544	1 362	1.26	1.15
C120t4CF2	101×4×304	0.456	0.463	0.611	0.621	1 474	1 994	1 868	1 464	1.35	1.27
C120t4CF3	101×4×304	0.456	0.695	0.611	0.931	1 621	2 300	2 192	1 567	1.42	1.35
C120t5CF0	102×5×306	0.636	0	0.852	0	1 370	1 585	1 440	1 400	1.16	1.05
C120t5CF1	102×5×306	0.636	0.239	0.852	0.32	1 400	1 894	1 767	1 484	1.35	1.26
C120t5CF2	102×5×306	0.636	0.478	0.852	0.64	1 508	2 203	2 095	1 568	1.46	1.39
C120t5CF3	102×5×306	0.636	0.717	0.852	0.96	1 659	2 512	2 422	1 652	1.51	1.46
Notes: φ_s—Steel tube confinement factor of equation (6); φ_cf—CFRP confinement factor of equation (6); ξ_sc—Steel tube confinement factor of equation (7); ξ_cfc—CFRP confinement factor of equation (7); N_df—Ultimate load of equation (6); N_gw—Ultimate load of equation (7).

下载: 导出CSV

参考文献(30)

[1]	郑文忠, 吕雪源. 活性粉末混凝土研究进展[J]. 建筑结构学报, 2015, 36(10):44-58. ZHENG Wenzhong, LV Xueyuan. Research development of reactive powder concrete[J]. Journal of Building Structures,2015,36(10):44-58(in Chinese).
[2]	TAI Y S. Uniaxial compression tests at various loading rates for reactive powder concrete[J]. Theoretical and Applied Fracture Mechanics,2009,52(1):14-21. DOI: 10.1016/j.tafmec.2009.06.001
[3]	YAZICI H, YARDIMCI M Y, AYDIN S, et al. Mechanical properties of reactive powder concrete containing mineral admixtures under different curing regimes[J]. Construction & Building Materials,2009,23(3):1223-1231.
[4]	HIREMATH P N, YARAGAL S C. Influence of mixing method speed and duration on the fresh and hardened properties of reactive powder concrete[J]. Construction & Building Materials,2017,141(Complete):271-288.
[5]	YI N H, KIM J J, CHO Y G, et al. Blast-resistant characteristics of ultra-high strength concrete and reactive powder concrete[J]. Construction & Building Materials,2012,28(1):694-707.
[6]	TAI Y S, PAN H H, KUNG Y N. Mechanical properties of steel fiber reinforced reactive powder concrete following exposure to high temperature reaching 800℃[J]. Nuclear. Engineering & Design,2011,241(7):2416-2424.
[7]	YAN K, XU C, ZHANG X. Compressive behavior of steel fiber-reinforced reactive powder concrete at elevated temperatures[J]. Science of Advanced Materials,2016,8(7):1454-1463. DOI: 10.1166/sam.2016.2758
[8]	戎芹, 曾宇声, 侯晓萌, 等. 圆钢管RPC轴压短柱有限元分析与承载力计算[J]. 哈尔滨工业大学学报, 2018, 50(12):61-66. DOI: 10.11918/j.issn.0367-6234.201807186 RONG Qin, ZENG Yusheng, HOU Xiaomeng, et al. Finite element analysis and bearing capacity calculation for RPC-filled circular steel tube columns under axial compression[J]. Journal of Harbin Institute of Technology,2018,50(12):61-66(in Chinese). DOI: 10.11918/j.issn.0367-6234.201807186
[9]	闫志刚, 张武奇, 安明喆. 圆钢管RPC短柱轴心受压极限承载力分析[J]. 北京工业大学报, 2011, 37(3):361-367. YAN Zhigang, ZHANG Wuqi, AN Mingzhe. Analysis of ultimate loading capacity for circular RPC filled steel tube stub columns under axial compression[J]. Journal of Beijing University of Technology,2011,37(3):361-367(in Chinese).
[10]	林震宇, 吴炎海, 沈祖炎. 圆钢管活性粉末混凝土轴压力学性能研究[J]. 建筑结构学报, 2005, 26(4):52-57. DOI: 10.3321/j.issn:1000-6869.2005.04.008 LIN Zhenyu, WU Yanhai, SHEN Zuyan. Research on behavior of RPC filled circular steel tube column subjected to axial compression[J]. Journal of Building Structures,2005, 26(4):52-57(in Chinese). DOI: 10.3321/j.issn:1000-6869.2005.04.008
[11]	吴炎海, 林震宇. 钢管活性粉末混凝土轴压短柱受力性能试验研究[J]. 中国公路学报, 2005, 18(1):61-66. WU Yanhai, LIN Zhenyu. Experimental study on the mechanical behavior of activated powder concrete filled steel tube axial compression short column[J]. China Journal of Highway and Transport,2005, 18(1):61-66(in Chinese).
[12]	LU Y, LI N, LI S. Behavior of FRP-confined concrete-filled steel tube columns[J]. Polymers,2014,6(5):1333-1349. DOI: 10.3390/polym6051333
[13]	王庆利. CFRP-钢管混凝土[M]. 北京: 科学出版社, 2017: 2-3. WANG Qingli. CFRP confined concrete filled steel tube[M]. Beijing: Science Press, 2017: 2-3(in Chinese).
[14]	PHAM T M, HADI M N S. Confinement model for FRP confined normal-and high-strength concrete circular columns[J]. Construction and Building Materials,2014,69(30):83-90.
[15]	欧阳利军, 许峰, 陆洲导. 玄武岩纤维布增强树脂基复合材料约束高温损伤混凝土轴压力学性能[J]. 复合材料学报, 2018, 35(8):2002-2013. OUYANG Lijun, XU Feng, LU Zhoudao. Axial compressive behavior of basalt fiber reinforced polymer-confined damaged concrete after exposed to elevated temperatures[J]. Acta Materiae Compositae Sinica,2018,35(8):2002-2013(in Chinese).
[16]	DING Faxing, LU Deren, BAI Yu, et al. Behaviour of CFRP-confined concrete-filled circular steel tube stub columns under axial loading[J]. Thin-Walled Structures,2018,125:107-118. DOI: 10.1016/j.tws.2018.01.015
[17]	翟存林, 魏洋, 李国芬, 曹兴. FRP—钢复合管混凝土桥墩设计与应用研究[J]. 公路, 2012(01):83-87. DOI: 10.3969/j.issn.0451-0712.2012.01.017 ZHAI Cunlin, WEI Yang, LI Guofen, et al. Research on design and application of FRP steel composite pipe concrete pier[J]. Highway,2012(01):83-87(in Chinese). DOI: 10.3969/j.issn.0451-0712.2012.01.017
[18]	中国国家标准化管理委员会. 金属材料-室温拉伸试验方法: GB/T 228—2010[S]. 北京: 中国标准出版社, 2010. Standardization Administration of China. Metallic materials-tensile testing at ambient temperatures: GB/T 228—2010[S]. Beijing: Standards Press of China, 2010(in Chinese).
[19]	建设部建筑物鉴定与加固规范管理委员会. 粘贴碳纤维复合材料加固混凝土工程施工与验收暂行规定: 建规固[2002]006[S]. 北京: 中国标准出版社, 2002. Building Appraisal and Reinforcement Specification Management Committee of the Ministry of Construction. Interim provisions on construction and acceptance of concrete engineering reinforced with carbon fiber composite materials: Construction regulations [2002] 006[S]. Beijing: Standards Press of China, 2002(in Chinese).
[20]	中国国家标准化管理委员会. 活性粉末混凝土技术标准: GB/T 31387—2015[S]. 北京: 中国标准出版社, 2015. Standardization Administration of China. Reactive powder concrete: GB/T 31387—2015[S]. Beijing: Standards Press of China, 2015(in Chinese).
[21]	谭彬. 活性粉末混凝土受压应力应变全曲线的研究[D]. 长沙: 湖南大学, 2007. TAN B. Research on stress-strain curves of reactive powder concrete under uniaxial compression[D]. Changsha: Hunan University, 2007(in Chinese).
[22]	HU Y M, YU T, TENG J G. FRP-confined circular concrete-filled thin steel tubes under axial compression[J]. Journal of Composites for Construction,2011,15(5):850-860. DOI: 10.1061/(ASCE)CC.1943-5614.0000217
[23]	CHEN M, HOU X. Comparative study on the axial compression and bearing capacity of reactive powder concrete-filled circular steel tube[J]. Advances in Materials Science & Engineering,2018,2018:1-11.
[24]	TANG H, CHEN J, FAN L, et al. Experimental investigation of FRP-confined concrete-filled stainless steel tube stub columns under axial compression[J]. Thin-Walled Structures,2020,146:106483. DOI: 10.1016/j.tws.2019.106483
[25]	张依睿, 魏洋, 柏佳文, 等. FRP-钢复合圆管约束混凝土轴压性能预测模型[J]. 复合材料学报, 2020(5):1-8. ZHANG Yirui, WEI Yang, BAI Jiawen, et al. Models for predicting axial compression behavior of FRP-steel compo-site circular tube confined concrete[J]. Acta Materiae Compositae Sinica,2020(5):1-8(in Chinese).
[26]	顾威, 赵颖华, 尚东伟. CFRP-钢管混凝土轴压短柱承载力分析[J]. 工程力学, 2006, 23(1):149-153. DOI: 10.3969/j.issn.1000-4750.2006.01.027 GU Wei, ZHAO Yinghua, SHANG Dongwei, et al. Analysis of the bearing capacity of CFRP concrete filled steel tubular short columns[J]. Engineering Mechanics,2006, 23(1):149-153(in Chinese). DOI: 10.3969/j.issn.1000-4750.2006.01.027
[27]	顾维平, 蔡绍怀, 冯文林. 钢管高强度混凝土的性能与极限强度[J]. 建筑科学, 1991(1):23-27. GU Weiping, CAI Shaohuai, FENG Wenlin. Performance and ultimate strength of high-strength concrete filled steel tube[J]. Building Science,1991(1):23-27(in Chinese).
[28]	LAM L, TENG J G. Design-oriented stress-strain model for FRP-confined concrete[J]. Construction and Building Materials,2003,17(6):471-489.
[29]	PESSIKI S, HARRIES K A, KESTNER J T, et al. Axial behavior of reinforced concrete columns confined with FRP jackets[J]. Journal of Composites for Construction,2001,5(4):237-245. DOI: 10.1061/(ASCE)1090-0268(2001)5:4(237)
[30]	CHE Y, WANG Q L, SHAO Y B. Compressive performances of the concrete filled circular CFRP-steel tube (C-CFRP-CFST)[J]. International Journal of Advanced Steel Construction,2012,8(4):311-338.

施引文献(12)

期刊类型引用(6)

1.	徐冬梅，刘华新，李艳. BFRP条带-PVC管材复合加固纤维再生混凝土短柱轴压性能. 复合材料科学与工程. 2024(06): 95-105 . 百度学术
2.	刘磊，何真，汪鹏，蔡新华，韩笛扬，罗滔. 新型CFRP-UHPC组合管混凝土圆柱轴压性能. 复合材料学报. 2023(04): 2390-2404 . 本站查看
3.	何修义，李松，焦楚杰，何松松. 轴压作用下CFRP约束钢管-活性粉末混凝土短柱承载力计算模型. 混凝土. 2023(06): 69-74+90 . 百度学术
4.	李松，焦楚杰，何松松，梁健，李宏宇. CFRP约束钢管高强混凝土轴压短柱承载力的极限分析. 工程科学与技术. 2022(02): 162-169 . 百度学术
5.	李庆文，胡露露，曹行，曾杏钢，高森林，祝青云，刘艺伟，禹萌萌，黄筱. CFRP布均匀约束煤圆柱轴压性能. 复合材料学报. 2022(11): 5611-5624 . 本站查看
6.	曹玉贵，赵国旭，尹亚运. 基于广义回归神经网络的纤维增强聚合物复合材料约束损伤混凝土强度预测. 复合材料学报. 2021(05): 1623-1628 . 本站查看