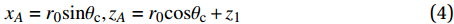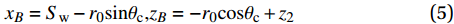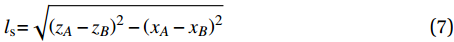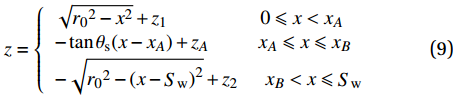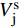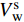An improved numerical prediction method of elastic properties based on two unit-cells models for 3D angle-interlock woven composites and experimental verification
-
摘要: 为准确预测三维角联锁机织复合材料的宏观弹性性能，对基于CT图像几何参数实测数据建立的内单胞和面单胞细观实体模型进行数值分析，其中面单胞模型采用组合面单胞形式，并开展了三维角联锁机织超高分子量聚乙烯(UHMWPE)纤维/聚氨酯复合材料的经向拉伸实验。结果表明：基于两单胞模型预测该复合材料的宏观弹性模量与实验结果吻合较好，组合面单胞的经向拉伸模量小于内单胞；经向拉伸时复合材料在经纱间接触面处、纬纱沿宽度方向的端部和经纱与基体的交界面处易出现应力集中现象；当纬纱层数小于30层时，应该考虑表面区域对复合材料整体力学性能的影响。Abstract: To accurately predict the macroscopic elastic properties of 3D angle-interlock woven composites, interior and surface unit-cells mesoscopic solid models were established for numerical analysis based on the geometric parameters measured in CT images, and surface unit-cells were modeled in the form of integrated surface unit-cells. Then a tensile test in warp direction was conducted for 3D angle-interlock woven ultra-high molecular weight polyethylene (UHMWPE) fiber/polyurethane composites. The results show that the predicted macroscopic elastic modulus values of the composites based on two unit-cells models are in good agreement with the experimental values. The tensile modulus in the warp direction of the integrated surface unit-cells is smaller than that of the interior unit-cells. During the tensile test in the warp direction, stress concentration tends to occur at the interface among warp yarns, the end of weft yarns along the width and the interface between warp yarns and matrix. When the number of weft layers is less than 30, the effect of surface region on the overall mechanical properties of the composites should be considered.
-
Keywords:
- 3D woven composites /
- unit cells /
- elastic modulus /
- finite element analysis /
- tensile test
-
三维角联锁机织复合材料由经纱、纬纱和基体组成，所有经纱组成经纱体系，所有纬纱组成纬纱体系，经纱和纬纱相互交织形成空间网状结构，经基体固化成为纤维增强复合材料，具有比强度、比模量高和抗冲击能力强等优点，在防护工程、航空航天等领域具有广泛的应用前景[1-3]。三维角联锁机织复合材料的宏观力学性能由组分材料的基本力学性能和复合材料的细观结构决定，可以对复合材料的细观实体模型采用数值分析的方法预测其宏观弹性性能[4-6]。
三维角联锁机织复合材料的弹性性能数值预测通常基于复合材料细观结构的周期性特征选取单胞模型进行分析，以便减小数值计算的工作量。Zhang等[7]根据CT图像的实测参数建立三维机织复合材料细观实体模型，提取内单胞为研究对象用数值仿真的方法预测了复合材料经向和纬向的弹性模量并与单轴拉伸实验结果进行比较。卢子兴等[8]建立了三维机织复合材料的内单胞模型，模型中考虑了纱线内纤维丝排布的随机性，通过渐进损伤分析模拟了经向和纬向的压缩应力-应变曲线。Zeng等[9]根据CT图像建立了考虑纱线路径变化和纱线横截面局部变形的三维机织复合材料全尺寸单胞模型，通过数值仿真预测其宏观力学性能并与实验结果进行比较。Green等[10]基于CT图像建立了具有真实细观几何结构的三维机织复合材料全尺寸单胞模型，通过数值仿真预测的经向和纬向拉伸模量比理想化的全尺寸单胞模型预测值更接近实验结果。仲苏洋[11]以内单胞和面单胞为研究对象，获得各单胞的经向拉伸应力-应变曲线，经体积加权平均后得到复合材料的宏观力学性能。然而，仅以内单胞模型作为研究对象[7-8]预测三维机织复合材料的模量忽略了表面细观结构对该材料整体弹性性能的影响；若以全尺寸单胞模型为研究对象[9-10]进行数值预测，计算规模和时间成本又会随纬纱层数的增加而增大；当以内单胞和面单胞为研究对象进行数值分析时[11]，面单胞的细观结构沿厚度方向上的非周期性特征和经纱不连续性会对复合材料整体力学性能的数值预测结果造成一定误差。
本文基于CT图像实测参数建立了三维角联锁机织超高分子量聚乙烯(UHMWPE)纤维/聚氨酯复合材料内单胞和组合面单胞的细观实体模型，通过数值仿真预测复合材料的宏观弹性性能，与实验结果进行了比较，并研究了经向拉伸模量和纤维体积含量随复合材料纬纱层数的变化规律。
1. 三维角联锁机织复合材料细观实体模型
1.1 三维角联锁机织复合材料细观几何模型
以三维角联锁机织UHMWPE纤维/聚氨酯复合材料为研究对象进行CT断层扫描，复合材料平板由武汉纺织大学提供，平均厚度为5.6 mm，纤维为湖南中泰特种装备公司生产的UHWMPE纤维ZTX99，基体为德国巴斯夫公司生产的聚氨酯。复合材料内纬纱层数为6层，纬纱密度为3根/cm，纬纱细度为4500D，经纱密度为9根/cm，经纱细度为3000D，UHMWPE纤维丝密度为0.97 g/cm3，复合材料内纤维体积分数为48.5vol%。
纱线细度的含义是在基体固化前公定回潮率下9000米长纱线的重量克数，单位为旦尼尔(Denier，D)。纱线细度T与纱线内纤维丝总横截面面积A(单位为mm2)的关系如下：
A=T9000ρ (1) 式中，ρ为纤维丝密度(g/cm3)。
在整体坐标系下，以经向为x方向，纬向为y方向，由CT扫描得到的复合材料经向断面和纬向断面图像分别如图1(a)和图1(b)所示，断面位置分别为经纱和纬纱的中线处。
![]()
图 1 三维角联锁机织超高分子量聚乙烯(UHMWPE)纤维/聚氨酯复合材料经向和纬向断面图Figure 1. Profiles in warp and weft directions of 3D angle-interlock woven ultrahigh molecular weight polyethylene (UHMWPE) fiber/polyurethane composites通过图1，可以对纱线路径和纱线横截面形状作出如下假设：
(1) 经纱的横截面形状为矩形，纬纱的横截面形状为两个半径相同的圆重叠取交集而得到的凸透镜形，圆半径r如下式[4]：
r=H2w+W2w4Hw (2) 式中：Hw为纬纱横截面高度；Ww为纬纱横截面宽度。
(2) 纬纱路径平直且相互平行排列，经纱路径由圆弧段和直线段组成。
(3) 经纱沿纬向排列紧密，经纱宽度与经纱间距相等。
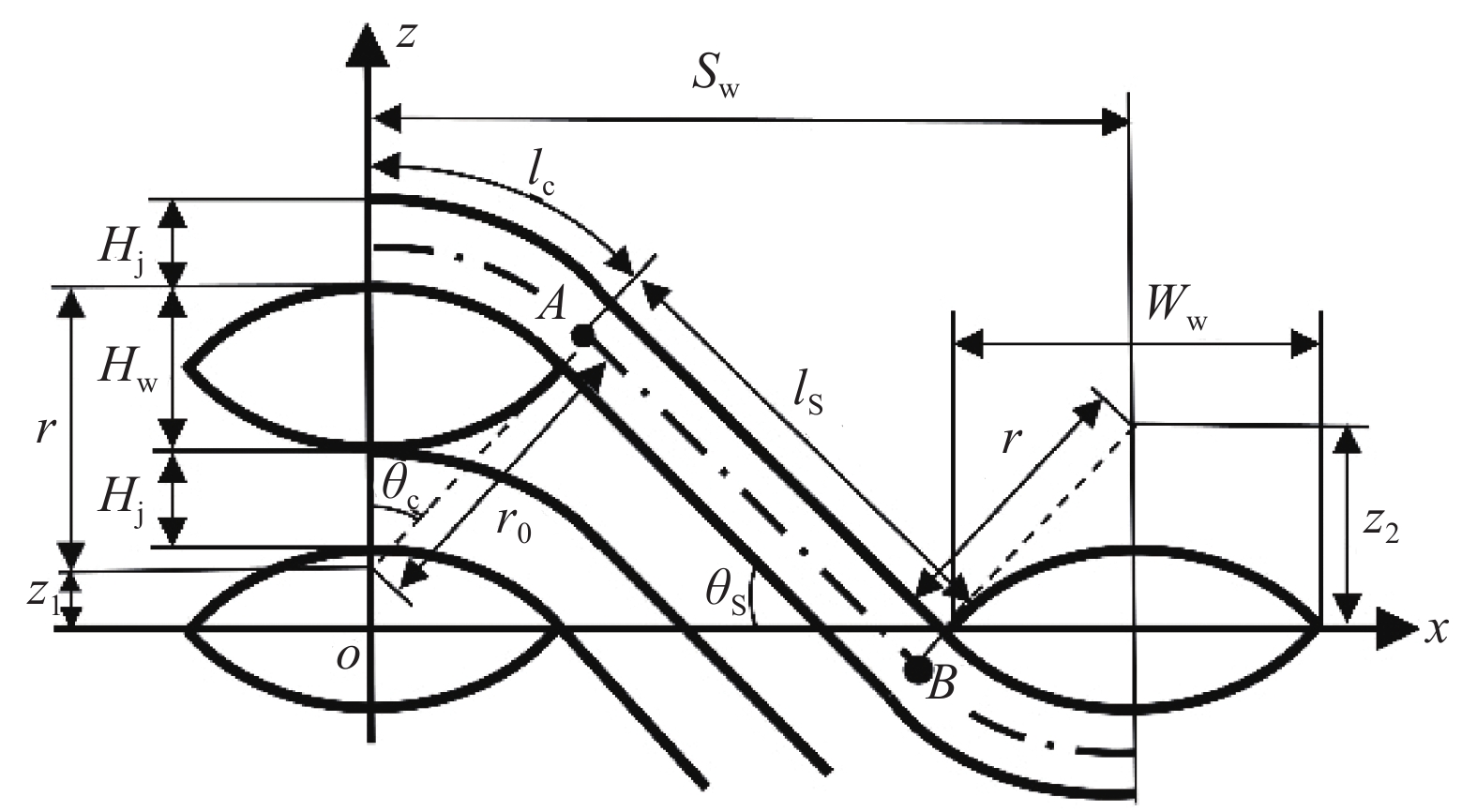
三维角联锁机织复合材料细观几何模型[6]如图2所示，其中纬纱朝向与y轴平行，经纱路径在图中用点划线表示。
![]()
经纱路径圆弧段lc对应的圆心角θc如下式[4]：
θc=arcsin2HwWwH2w+W2w (3) 令z1=1.5Hw+Hj−r，z2=r−0.5Hw，r0=r+0.5Hj，图2中经纱路径直线段与圆弧段交于A(xA，zA)、B(xB，zB)两点，则各点的坐标分量如下式：
xA=r0sinθc,zA=r0cosθc+z1 (4) xB=Sw−r0sinθc,zB=−r0cosθc+z2 (5) 式中，Sw为纬纱间距。
直线段的倾斜角θs如下式：
θs=arctan|zA−zBxA−xB| (6) 直线段长度ls和曲线段长度lc如下式：
ls=√(zA−zB)2−(xA−xB)2 (7) lc=(r+0.5Hj)θc (8) 经纱中心线路径函数如下式：
z={√r02−x2+z10⩽ (9) 该经纱路径通过轴对称变换和平移变换后可得到经纱系统内所有经纱完整的路径。
1.2 基于CT图像的细观结构几何参数测量
通过图像处理软件ImageJ，根据CT图像上一个像素代表20.0855 μm，可以对三维角联锁机织UHMWPE纤维/聚氨酯复合材料的细观几何参数进行准确测量，为建立完整的复合材料细观实体模型，需要测量的参数在图1中进行了标注，对测量结果进行统计，统计结果和复合材料建模时参数实际取值如表1所示。
表 1 三维角联锁机织UHMWPE纤维/聚氨酯复合材料细观几何参数测量Table 1. Mesoscopic geometric parameters’ measurements of 3D angle-interlock woven UHMWPE fiber/ polyurethane compositesYarn Parameter Number of measurements Average value Variable coefficient Input value Weft Height Hw 408 0.492 mm 0.137 0.469 mm Width Ww 408 1.919 mm 0.042 1.919 mm Space Sw 306 3.651 mm 0.012 3.333* mm Warp Width Wj 300 1.139 mm 0.014 1.111* mm Height Hj 300 0.382 mm 0.143 0.398 mm Inclination θs 255 45.6° 0.074 Notes: * represents data obtained by equation (10). 表1中，经纱高度和纬纱高度测量值的离散程度较其它测量值大一个数量级，这是由于沿复合材料厚度方向上纱线的密实程度不同导致的，材料表面区域纱线间挤压程度小，经纱间距是材料内部区域的2倍，细观结构松散，纱线易变形，而材料内部纱线间挤压程度大，细观结构紧密，纱线形状较稳定。为了使模型中经纱直线段倾角θs和复合材料总厚度t分别与倾角均值和样品实际厚度保持一致，需要对纬纱高度和经纱高度的测量均值进行调整，将调整值作为输入值建立模型。另外，纬纱间距的参数输入值比测量均值小8.7%，原因是纬纱的间距在材料生产过程中是随机变化的，受机织过程“打紧”工序影响，纬纱排列不规整，造成纬纱间距局部偏大或偏小的现象，CT扫描的试件只是材料整体的一小部分，这一小块试件的纬纱间距平均值不能反映整个材料内纬纱间距的平均趋势。本文中纬纱间距和经纱宽度(即经纱间距)的输入值通过纱线密度直接换算得到，如下式所示[7]：
{S_k} = \frac{{10}}{{{P_k}}} (10) 式中，Sk和Pk(k=w, j)分别为纱线间距(mm)和纱线密度(根/cm)，w和j分别代表纬纱和经纱。
1.3 三维角联锁机织复合材料细观实体模型的建立与验证
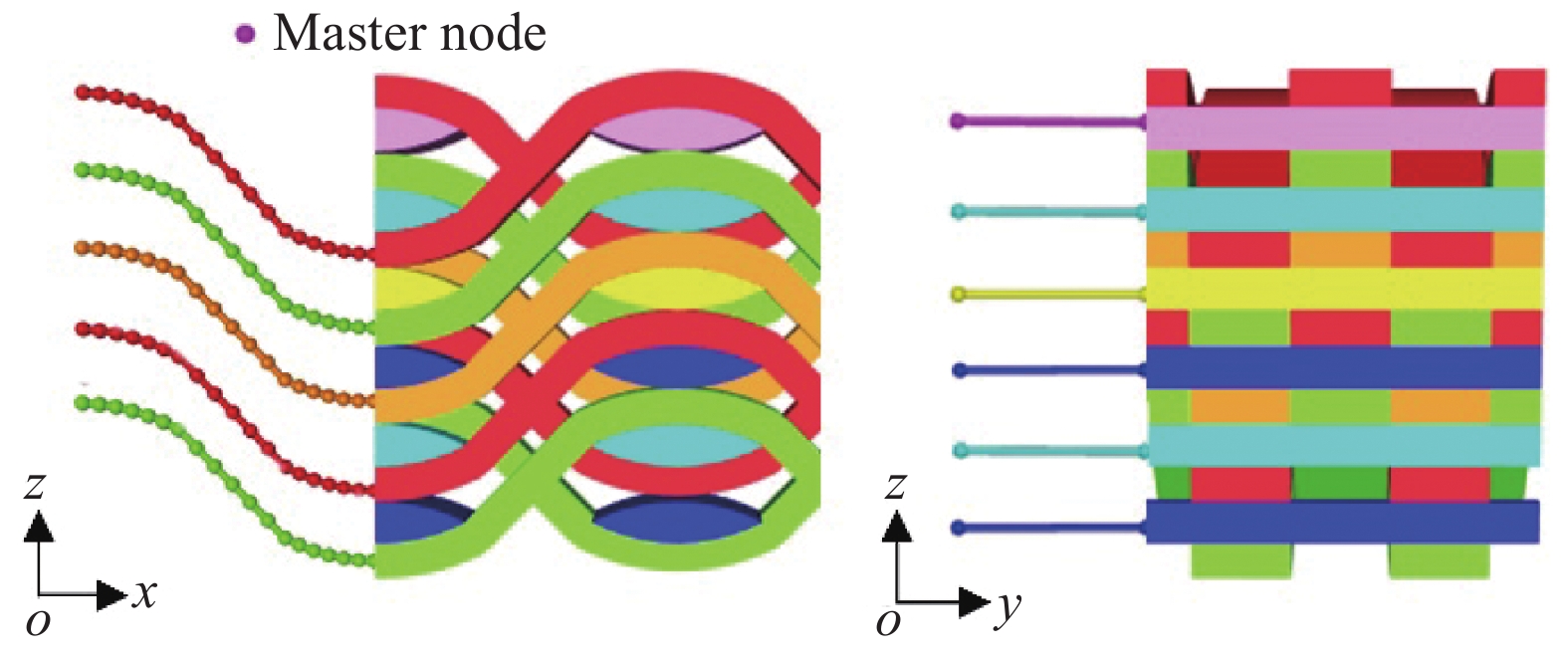
在纺织建模软件TexGen[12-15]中基于CT图像几何参数实测值通过Python语言对三维角联锁机织复合材料的细观实体模型进行参数化建模。建模过程如下：首先定义纱线主节点的坐标及在主节点处的纱线横截面形状和尺寸，然后在主节点间通过插值法来描述完整的纱线路径，其中纬纱路径用线性插值法描述，经纱路径用贝塞尔插值法描述，最后定义一个有界的区域将所需的模型范围截取出来，且认为纱线间的空隙被基体充分填充。TexGen中定义的三维角联锁机织复合材料经纱和纬纱路径及建立的细观实体模型如图3所示，与图1的CT图像进行比较，表明该模型较为真实地表现出三维角联锁机织复合材料经纱和纬纱的空间路径和横截面形状。
![]()
图 3 三维角联锁机织复合材料在纺织建模软件TexGen中纱线路径的定义及细观实体模型Figure 3. Definition of yarn path and microscopic solid model of 3D angle-interlock woven composites in TexGen2. 三维角联锁机织复合材料弹性性能数值预测
2.1 三维角联锁机织复合材料单胞划分方案与组合面单胞模型
三维角联锁机织复合材料的细观结构具有周期性特征，可以沿经向和纬向对复合材料进行划分，提取最小的重复单元，如图4(a)所示，该单元在x方向和y方向上的长度Lx和Ly如下式：
{L_x} = 2{S_{\rm{w}}},{L_y} = 2{S_{\rm{j}}} (11) 沿复合材料厚度方向上，内部区域经纱的密实程度比表面区域大，可以将该单元进一步划分为内单胞和分别位于复合材料上、下表面区域的面单胞，如图4(b)和图4(c)所示，内单胞模型如图4(d)所示。
![]()
图 4 三维角联锁机织复合材料的单胞划分方案Figure 4. Unit-cells division scheme of 3D angle-interlock woven composites内单胞厚度ti和面单胞厚度ts分别如下式所示：
{t_{\rm{i}}} = {H_{\rm{w}}} + {H_{\rm{j}}} (12) {t_{\rm{s}}} = {\rm{1}}{\rm{.5}}{H_{\rm{w}}} + {\rm{2}}{H_{\rm{j}}} (13) 复合材料的总厚度t如下式：
t = n{H_{\rm{w}}} + (n + 1){H_{\rm{j}}} (14) 式中，n代表纬纱层数。
所有内单胞和面单胞的体积占复合材料总体积的比值Vi和Vs分别如下式所示：
{V_{\rm{i}}} = \frac{{(n - 3){t_{\rm{i}}}}}{t} (15) {V_{\rm{s}}} = 1 - {V_{\rm{i}}} (16) 三维角联锁机织复合材料内部区域的细观结构在x、y和z方向上具有周期性，外载作用下复合材料内部区域的应力、应变分布呈周期性变化，变化的周期为单胞各方向的边长，可以对内单胞施加周期性边界条件[16-18]，满足内单胞边界面上的变形协调和应力连续性要求。为减小复合材料表面区域沿厚度方向上细观结构的非周期性和经纱不连续性对面单胞宏观力学性能的数值预测结果造成的误差，利用位于三维角联锁机织复合材料上、下表面区域的面单胞细观结构呈反对称[11]并能互补的特点，可以将上、下表面区域的面单胞沿z方向进行组合，形成组合面单胞，如图5所示。
此时，经纱在组合面单胞厚度方向上是连续的，组合面单胞相当于纬纱层数为3层的三维机织复合材料最小的重复单元。假设组合面单胞上、下侧边界面上具有相同的变形，可以对组合面单胞直接施加周期性边界条件进行数值仿真分析。
![]()
图 5 三维角联锁机织复合材料的组合面单胞模型Figure 5. Integrated surface unit-cell model of 3D angle-interlock woven composites2.2 纤维体积含量的计算
纤维体积含量是影响三维角联锁机织复合材料宏观弹性性能的重要因素之一。内单胞中经纱纤维体积含量Vji和纬纱纤维体积含量Vwi分别如下式：
V_{\rm{j}}^{\rm{i}} = \frac{{4(2{l_{\rm{c}}} + {l_{\rm{s}}}){A_{\rm{j}}}}}{{{L_x}{L_y}{t_{\rm{i}}}}} (17) V_{\rm{w}}^{\rm{i}} = \frac{{4{S_{\rm{j}}}{A_{\rm{w}}}}}{{{L_x}{L_y}{t_{\rm{i}}}}} (18) 式中，Aj和Aw分别为经纱和纬纱内纤维丝的总横截面面积。
组合面单胞中经纱纤维体积含量
V_{\rm{j}}^{\rm{s}} 和纬纱纤维体积含量V_{\rm{w}}^{\rm{s}} 分别如下式：V_{\rm{j}}^{\rm{s}} = \frac{{4(2{l_{\rm{c}}} + {l_{\rm{s}}}){A_{\rm{j}}}}}{{{L_x}{L_y}{t_{\rm{s}}}}} (19) V_{\rm{w}}^{\rm{s}} = \frac{{6{S_{\rm{j}}}{A_{\rm{w}}}}}{{{L_x}{L_y}{t_{\rm{s}}}}} (20) 经纱体系纤维体积含量Vj和纬纱体系纤维体积含量Vw分别如下式：
{V_{\rm{j}}} = V_{\rm{j}}^{\rm{i}}{V_{\rm{i}}} + V_{\rm{j}}^{\rm{s}}{V_{\rm{s}}} (21) {V_{\rm{w}}} = V_{\rm{w}}^{\rm{i}}{V_{\rm{i}}} + V_{\rm{w}}^{\rm{s}}{V_{\rm{s}}} (22) 复合材料内总的纤维体积含量Vf如下式：
{V_{\rm{f}}} = {V_{\rm{j}}} + {V_{\rm{w}}} (23) 经计算得到三维角联锁机织UHMWPE纤维/聚氨酯复合材料内总纤维的体积含量为49.3vol%，与实际值相比，误差为1.65%，证明了本文对三维角联锁机织复合材料细观几何模型所做出的假设是合理的。
2.3 组分材料的基本力学性能与网格划分
三维角联锁机织UHMWPE纤维/聚氨酯复合材料中各组分材料力学性能如表2所示。
表 2 UHMWPE纤维和聚氨酯力学性能参数Table 2. Mechanical properties of UHMWPE fiber and polyurethaneUHWMPE fiber Ea*/GPa Et[19]/GPa Ga[19]/GPa 94 3.5 1.0 Gt[19]/GPa νa[19] νt[19] 1.2 0.29 0.45 Polyurethane Em*/MPa νm[19] 195 0.25 Notes：Ea, Ga and νa—Axial tensile modulus, shear modulus and Passion’s ratio of fiber, respectively；Et, Gt and νt—Transverse tensile modulus, shear modulus and Passion’s ratio of fiber, respectively；Em and νm—Modulus and Poisson’s ratio of matrix, respectively; * represents data obtained by experiments. 假设基体是各向同性材料，纱线由相互平行排列的纤维丝和基体组成，可看作横观各向同性材料，根据Chamis经验公式[20]得到纱线的9个等效弹性常数。TexGen软件中，利用体素网格划分技术将内单胞和组合面单胞模型中的纱线和基体离散为立方体网格[21]，通过对数值解进行收敛性分析，为兼顾计算效率和数值结果的准确性，网格的边长取为0.07 mm，采用8节点六面体减缩积分单元(C3D8R)，TexGen也能自动为纱线单元在局部坐标系下定义材料属性以考虑纱线在不同位置取向的变化。
对内单胞和组合面单胞模型施加周期性边界条件，采用位移荷载的施加方法[17]。内单胞和组合面单胞的有限元模型如图6所示，将各单胞模型分别导入到有限元软件ABAQUS中用Standard分析模块进行数值计算得到内单胞和组合面单胞模型的宏观刚度矩阵，经体积加权平均得到复合材料整体的刚度矩阵C，如下式所示[22]：
![]()
图 6 三维角联锁机织UHWMPE纤维/聚氨酯复合材料的内单胞和组合面单胞有限元模型Figure 6. Interior unit-cell and integrated surface unit-cell finite element model of 3D angle-interlock woven UHWMPE fiber/ polyurethane composites{\boldsymbol{C}} = {\boldsymbol{C}_{\rm{i}}}{V_{\rm{i}}} + {\boldsymbol{C}_{\rm{s}}}{V_{\rm{s}}} (24) 式中：Ci是内单胞的宏观刚度矩阵；Cs是组合面单胞的宏观刚度矩阵。根据刚度矩阵内各元素与弹性常数的关系最后得到整个复合材料的宏观弹性常数[23]。
3. 三维角联锁机织UHWMPE纤维/聚氨酯复合材料经向拉伸实验验证
经向拉伸实验中，为了在三维角联锁机织UHWMPE纤维/聚氨酯复合材料实验件的工作段产生足够大的应力使试件出现破坏，参考文献[20, 24]的做法，其设计方案及经向拉伸实验件分别如图7(a)和7(b)所示。
![]()
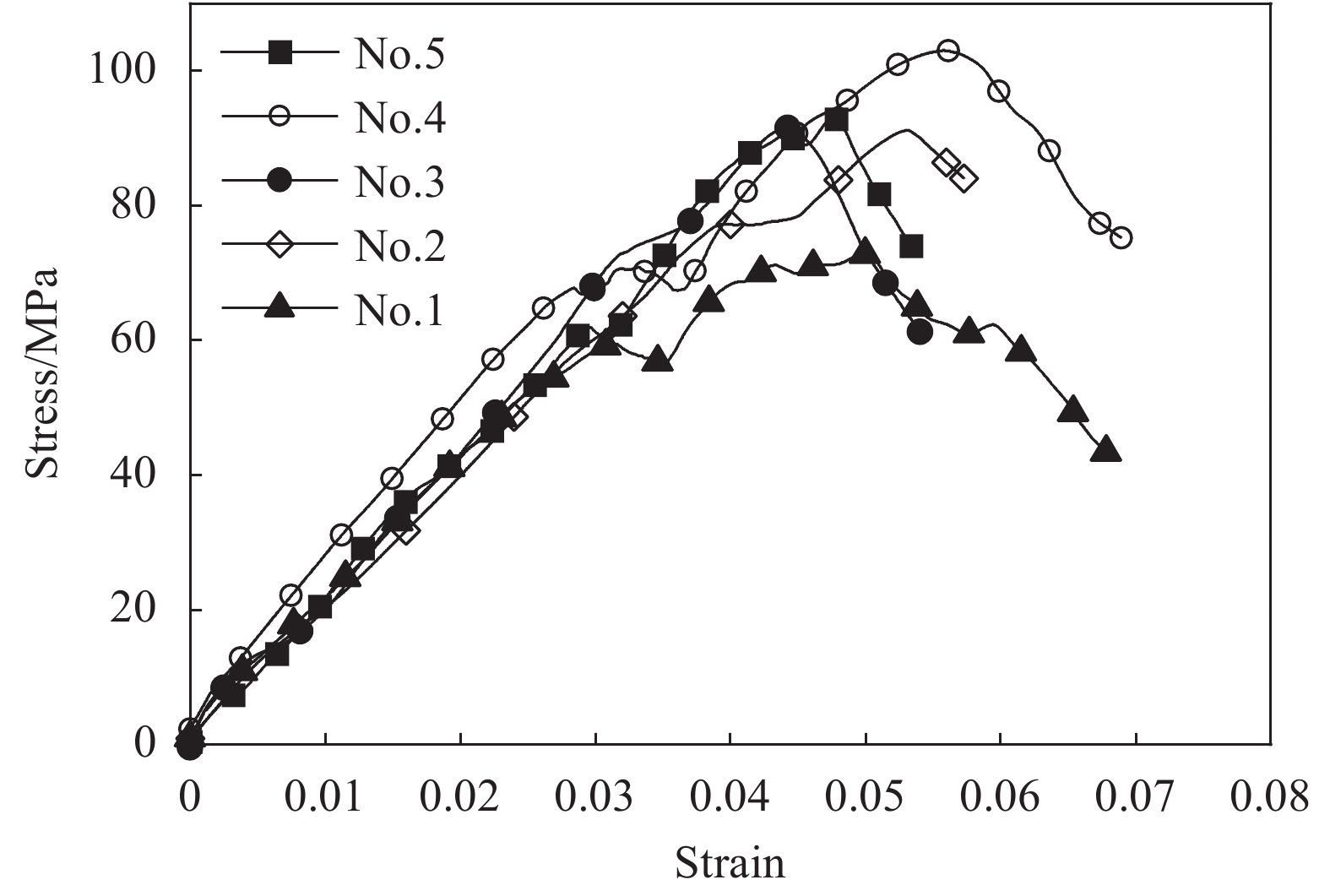
图 7 三维角联锁机织UHWMPE纤维/聚氨酯复合材料试件设计方案及经向拉伸试件Figure 7. Design scheme and warp tensile test specimen of 3D angle-interlock woven UHWMPE fiber/polyurethane composites采用激光切割技术制备了5个试件，试件的长度方向为经向，厚度为5.6 mm，试件端部表面用环氧树脂粘贴5 mm厚的铝片避免在拉伸过程中出现打滑现象。对试件以2 mm/min的加载速率进行经向拉伸，实验所用设备为长春试验机研究所的CSS44200电子万能试验机，复合材料的经向拉伸实验过程如图8所示。图9为该复合材料5个试件的经向拉伸应力-应变曲线。对实验数据进行处理，计算得到各试件的经向拉伸模量，如表3所示。
![]()
图 8 三维角联锁机织UHWMPE纤维/聚氨酯复合材料的经向拉伸实验过程Figure 8. Tensile test process of 3D angle-interlock woven UHWMPE fiber/polyurethane composites in warp direction![]()
图 9 三维角联锁机织UHWMPE纤维/聚氨酯复合材料经向拉伸应力-应变曲线Figure 9. Tensile stress-strain curves of 3D angle-interlock woven UHWMPE fiber/polyurethane composites in warp direction![]()
图 10 三维角联锁机织UHMWPE纤维/聚氨酯复合材料经向拉伸应变为0.001时内单胞和组合面单胞中应力分布情况Figure 10. Stress distribution in interior unit-cell and integrated surface unit-cell of 3D angle-interlock woven UHWMPE fiber/polyurethane composites when the tensile strain in warp direction was 0.001表 3 三维角联锁机织UHWMPE纤维/聚氨酯复合材料试件的经向拉伸模量实验结果Table 3. Experimental results of tensile modulus in warp direction of 3D angle-interlock woven UHWMPE fiber/polyurethane composite specimensSpecimen Ex/GPa Average/GPa Variable coefficient/% No.1 2.02 2.19 5.34 No.2 2.14 No.3 2.27 No.4 2.33 No.5 2.20 Note：Ex—Tensile modulus in x direction. 通过图9可以发现，当应变小于0.03时，三维角联锁机织UHWMPE纤维/聚氨酯复合材料在较大的应变下仍近似线弹性，这是由于复合材料经向拉伸过程中经纱会趋于伸直，具有较强的变形能力，基体刚度小，能随经纱共同变形；当应变达到0.03时，试件的应力-应变曲线开始表现出显著的非线性特征。
4. 结果与分析
4.1 三维角联锁机织UHMWPE纤维/聚氨酯复合材料弹性性能数值预测结果与实验结果比较
基于内单胞和组合面单胞模型进行有限元分析得到的三维角联锁机织UHWMPE纤维/聚氨酯复合材料宏观弹性常数的预测结果如表4所示。
表 4 三维角联锁机织UHWMPE纤维/聚氨酯复合材料弹性常数的数值预测值Table 4. Results of elastic constants of 3D angle-interlock woven UHWMPE fiber/polyurethane composites by numerical analysis methodElastic
constantInterior
unit-cellIntegrated surface
unit-cellOverall Ex/GPa 3.12 1.75 2.39 Ey/GPa 17.21 14.20 15.58 Ez/GPa 0.80 0.46 0.62 Gxz/GPa 0.79 0.29 0.52 Gyz/GPa 0.30 0.18 0.24 Gxy/GPa 0.31 0.20 0.25 νxz 0.35 0.30 0.32 νyz 0.01 0.01 0.01 νxy −0.06 −0.04 −0.05 Notes：Ex, Ey and Ez—Tensile moduli in x, y and z directions, respectively；Gxz, Gyz and Gxy—Shear moduli in xz, yz and xy directions, respectively；νxz, νyz and νxy—Poisson’s ratios in xz, yz and xy directions, respectively. 复合材料经向拉伸模量的预测值比实验结果略大，误差为9.1%，有如下三个原因：(1) 在三维角联锁机织复合材料真实的细观结构中纬纱沿厚度方向上并非层层对齐排列，会存在偏移现象，如图1(a)所示；(2) 在有限元分析中纱线单元与基体单元之间采用共节点连接，忽略了纱线与基体之间的相对滑移[25]；(3) 在复合材料固化过程中聚氨酯基体无法完全渗透进预制件内纱线间所有的间隙，试件中存在大量气泡和空隙导致复合材料的力学性能降低。经计算可以得到，内单胞的纤维体积含量为57.6%，组合面单胞的纤维体积含量为38.5%，因此内单胞各方向的拉伸模量和剪切模量均大于组合面单胞。
由表4可以发现，内单胞的经向拉伸模量比组合面单胞大78%，说明内单胞经向拉伸模量与组合面单胞具有较大差异，仅以内单胞模型作为研究对象进行数值预测会忽略表面区域对复合材料整体弹性性能的影响。另外，复合材料在xy方向上的泊松比νxy为负值，这是由于复合材料经向拉伸时，经纱在复合材料厚度方向上与纬纱相互挤压，通过Chamis经验公式可知纱线的横向模量由基体决定，聚氨酯基体模量小，经纱受挤压时横向会出现较大变形，使得整个复合材料纬向出现正应变。
4.2 三维角联锁机织UHMWPE纤维/聚氨酯复合材料内单胞和组合面单胞经向拉伸的应力云图
经向拉伸应变为0.001时，三维角联锁机织UHMWPE纤维/聚氨酯复合材料的内单胞和组合面单胞模型中经纱、纬纱和基体的应力分布情况如图10所示。可以发现：(1) 内单胞和组合面单胞的应力分布相似，这是由于它们具有相同的细观结构。经纱的最大应力是纬纱最大应力的5倍，是基体最大应力的15倍，这是由于复合材料沿经向拉伸时经纱承担主要载荷，纬纱横向承担少部分荷载，基体的模量远小于纱线，仅起保护纤维、在纱线间传递载荷、为纤维提供侧向支撑的作用；(2) 在内单胞和组合面单胞中，经纱应力主要集中在经纱间的接触面位置，如图10(a)和图10(d)所示；纬纱应力主要集中在沿纬纱宽度方向的端部位置，如图10(b)和图10(e)所示。这是由于复合材料内相邻的经纱直线段朝向不同，经向拉伸时，经纱的伸直变形会使相邻经纱间相互挤压并沿厚度方向错动，同时纬纱端部受经纱伸直变形影响呈波浪状，导致经纱间接触面位置和纬纱端部位置出现应力集中现象。基体与纱线的力学性能差异较大使得基体应力主要集中在基体与经纱交界面处，如图10(c)和图10(f)所示，考虑到基体的强度较小，可以预见经向拉伸载荷较大时在基体与经纱交界面位置的基体先出现破坏。
![]()
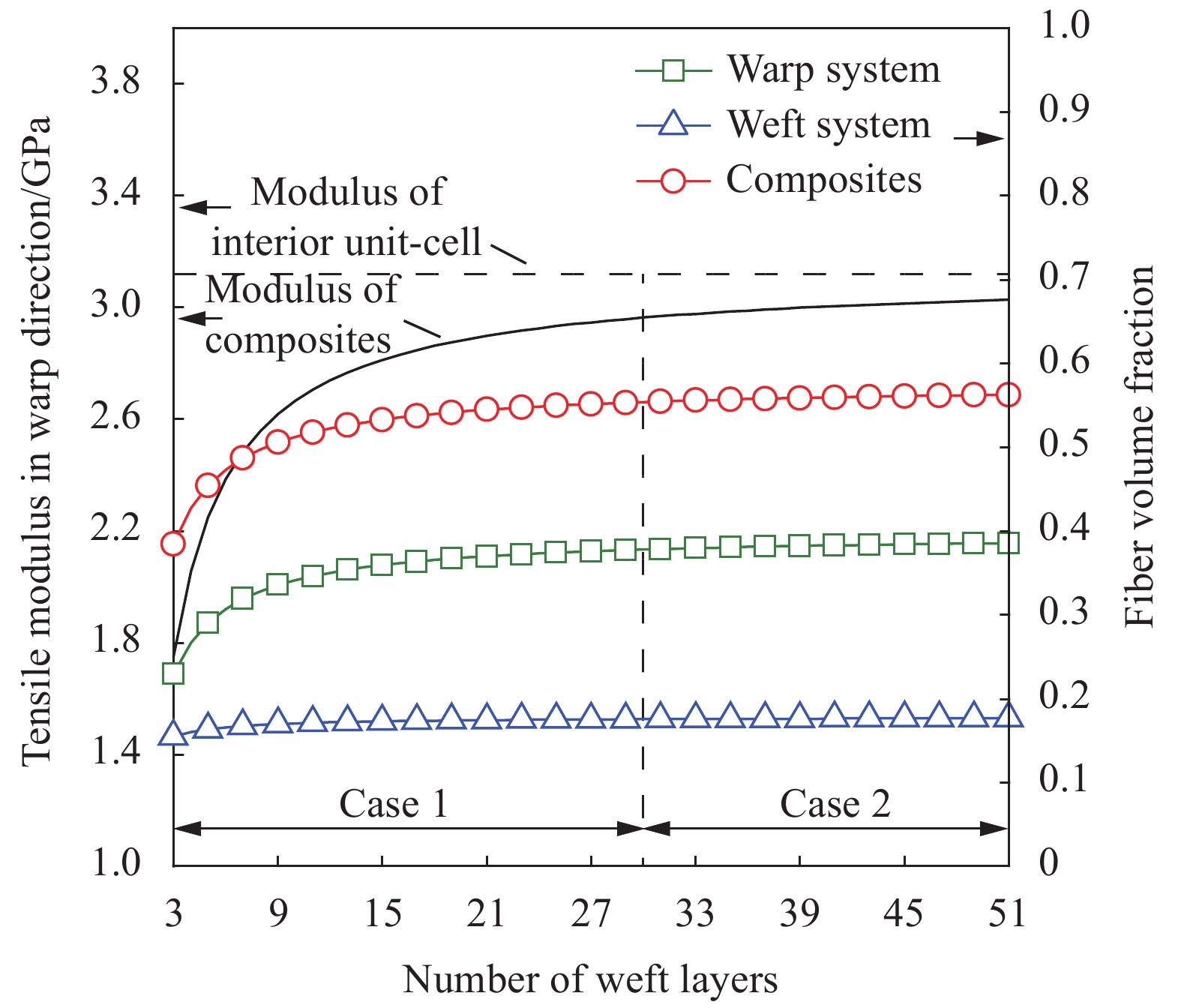
图 11 三维角联锁机织UHWMPE纤维/聚氨酯复合材料经向拉伸模量和纤维体积含量随纬纱层数的变化规律Case 1—Accurate modulus of composites obtained by interior unit-cell and integrated surface unit-cells models； Case 2—Accurate modulus of composites obtained by only interior unit-cell modelFigure 11. Change law of tensile modulus in warp direction and fiber volume fraction of 3D angle-interlock woven UHWMPE fiber/polyurethane composites with the number of weft layers4.3 纬线层数对三维角联锁机织UHMWPE纤维/聚氨酯复合材料经向拉伸模量和纤维体积含量的影响规律
根据内单胞和面单胞随纬纱层数增加各自占复合材料整体体积的比例不同得到三维角联锁机织UHWMPE纤维/聚氨酯复合材料的经向拉伸模量和纤维体积含量随纬纱层数的变化曲线，如图11所示。可以发现，复合材料经向拉伸模量和总纤维体积含量随纬纱层数的增加而增大，经纱体系的纤维体积含量随纬纱层数的变化趋势与总纤维体积含量一致，而纬纱体系的纤维体积含量始终保持在16%左右，这说明复合材料经向拉伸模量的变化由经纱体系的纤维体积含量决定。当纬纱层数小于30层时，复合材料经向拉伸模量随纬纱层数的增加而增大，增长速率逐渐减缓，此时应该考虑表面区域对复合材料整体力学性能的影响，通过内单胞和组合面单胞模型预测复合材料宏观弹性性能更为合理；当纬纱层数大于30层时，复合材料的经向拉伸模量与内单胞相差5%以内，此时仅以内单胞模型作为研究对象预测复合材料的经向拉伸模量既能得到较合理的结果，又可以提升计算效率。
5. 结 论
(1) 基于CT图像对纱线横截面形状和经纱轨迹做出合理假设并得到了几何参数实测数据，建立的三维角联锁机织复合材料的细观实体模型较合理地反映了复合材料的细观结构特征。
(2) 当施加周期性边界条件时，采用组合面单胞形式能减小面单胞宏观力学性能数值预测结果中由材料表面区域细观结构沿厚度方向上的非周期性和经纱不连续性导致的误差。基于内单胞和组合面单胞模型预测的三维角联锁机织超高分子量聚乙烯(UHMWPE)纤维/聚氨酯复合材料的经向拉伸模量与实验值吻合良好，误差为9.1%。内单胞的经向拉伸模量比组合面单胞大78%，说明内单胞与组合面单胞的力学性能具有明显差异。
(3) 三维角联锁机织UHMWPE纤维/聚氨酯复合材料试件在经向拉伸初期，应力-应变曲线近似线性，当应变大于0.03时，应力-应变曲线表现为非线性特征。
(4) 三维角联锁机织UHMWPE纤维/聚氨酯复合材料的内单胞和组合面单胞在经向拉伸下经纱、纬纱和基体的应力分布相似，应力主要集中在经纱间接触面处、纬纱沿宽度方向的端部和经纱与基体的交界面处。
(5) 随着纬纱层数的增加，三维角联锁机织UHMWPE纤维/聚氨酯复合材料的经向拉伸模量、总纤维体积含量和经纱体系纤维体积含量逐渐接近于内单胞。当纬纱层数小于30层时，应该考虑表面区域对复合材料整体力学性能的影响，基于内单胞和组合面单胞模型对三维角联锁机织复合材料弹性性能进行数值预测更为合理。
-
![]()
图 1 三维角联锁机织超高分子量聚乙烯(UHMWPE)纤维/聚氨酯复合材料经向和纬向断面图
Figure 1. Profiles in warp and weft directions of 3D angle-interlock woven ultrahigh molecular weight polyethylene (UHMWPE) fiber/polyurethane composites
![]()
![]()
图 3 三维角联锁机织复合材料在纺织建模软件TexGen中纱线路径的定义及细观实体模型
Figure 3. Definition of yarn path and microscopic solid model of 3D angle-interlock woven composites in TexGen
![]()
图 4 三维角联锁机织复合材料的单胞划分方案
Figure 4. Unit-cells division scheme of 3D angle-interlock woven composites
![]()
图 5 三维角联锁机织复合材料的组合面单胞模型
Figure 5. Integrated surface unit-cell model of 3D angle-interlock woven composites
![]()
图 6 三维角联锁机织UHWMPE纤维/聚氨酯复合材料的内单胞和组合面单胞有限元模型
Figure 6. Interior unit-cell and integrated surface unit-cell finite element model of 3D angle-interlock woven UHWMPE fiber/ polyurethane composites
![]()
图 7 三维角联锁机织UHWMPE纤维/聚氨酯复合材料试件设计方案及经向拉伸试件
Figure 7. Design scheme and warp tensile test specimen of 3D angle-interlock woven UHWMPE fiber/polyurethane composites
![]()
图 8 三维角联锁机织UHWMPE纤维/聚氨酯复合材料的经向拉伸实验过程
Figure 8. Tensile test process of 3D angle-interlock woven UHWMPE fiber/polyurethane composites in warp direction
![]()
图 9 三维角联锁机织UHWMPE纤维/聚氨酯复合材料经向拉伸应力-应变曲线
Figure 9. Tensile stress-strain curves of 3D angle-interlock woven UHWMPE fiber/polyurethane composites in warp direction
![]()
图 10 三维角联锁机织UHMWPE纤维/聚氨酯复合材料经向拉伸应变为0.001时内单胞和组合面单胞中应力分布情况
Figure 10. Stress distribution in interior unit-cell and integrated surface unit-cell of 3D angle-interlock woven UHWMPE fiber/polyurethane composites when the tensile strain in warp direction was 0.001
![]()
图 11 三维角联锁机织UHWMPE纤维/聚氨酯复合材料经向拉伸模量和纤维体积含量随纬纱层数的变化规律
Case 1—Accurate modulus of composites obtained by interior unit-cell and integrated surface unit-cells models； Case 2—Accurate modulus of composites obtained by only interior unit-cell model
Figure 11. Change law of tensile modulus in warp direction and fiber volume fraction of 3D angle-interlock woven UHWMPE fiber/polyurethane composites with the number of weft layers
表 1 三维角联锁机织UHMWPE纤维/聚氨酯复合材料细观几何参数测量
Table 1 Mesoscopic geometric parameters’ measurements of 3D angle-interlock woven UHMWPE fiber/ polyurethane composites
Yarn Parameter Number of measurements Average value Variable coefficient Input value Weft Height Hw 408 0.492 mm 0.137 0.469 mm Width Ww 408 1.919 mm 0.042 1.919 mm Space Sw 306 3.651 mm 0.012 3.333* mm Warp Width Wj 300 1.139 mm 0.014 1.111* mm Height Hj 300 0.382 mm 0.143 0.398 mm Inclination θs 255 45.6° 0.074 Notes: * represents data obtained by equation (10). 
下载: 导出CSV
表 2 UHMWPE纤维和聚氨酯力学性能参数
Table 2 Mechanical properties of UHMWPE fiber and polyurethane
UHWMPE fiber Ea*/GPa Et[19]/GPa Ga[19]/GPa 94 3.5 1.0 Gt[19]/GPa νa[19] νt[19] 1.2 0.29 0.45 Polyurethane Em*/MPa νm[19] 195 0.25 Notes：Ea, Ga and νa—Axial tensile modulus, shear modulus and Passion’s ratio of fiber, respectively；Et, Gt and νt—Transverse tensile modulus, shear modulus and Passion’s ratio of fiber, respectively；Em and νm—Modulus and Poisson’s ratio of matrix, respectively; * represents data obtained by experiments.
下载: 导出CSV
表 3 三维角联锁机织UHWMPE纤维/聚氨酯复合材料试件的经向拉伸模量实验结果
Table 3 Experimental results of tensile modulus in warp direction of 3D angle-interlock woven UHWMPE fiber/polyurethane composite specimens
Specimen Ex/GPa Average/GPa Variable coefficient/% No.1 2.02 2.19 5.34 No.2 2.14 No.3 2.27 No.4 2.33 No.5 2.20 Note：Ex—Tensile modulus in x direction.
下载: 导出CSV
表 4 三维角联锁机织UHWMPE纤维/聚氨酯复合材料弹性常数的数值预测值
Table 4 Results of elastic constants of 3D angle-interlock woven UHWMPE fiber/polyurethane composites by numerical analysis method
Elastic
constantInterior
unit-cellIntegrated surface
unit-cellOverall Ex/GPa 3.12 1.75 2.39 Ey/GPa 17.21 14.20 15.58 Ez/GPa 0.80 0.46 0.62 Gxz/GPa 0.79 0.29 0.52 Gyz/GPa 0.30 0.18 0.24 Gxy/GPa 0.31 0.20 0.25 νxz 0.35 0.30 0.32 νyz 0.01 0.01 0.01 νxy −0.06 −0.04 −0.05 Notes：Ex, Ey and Ez—Tensile moduli in x, y and z directions, respectively；Gxz, Gyz and Gxy—Shear moduli in xz, yz and xy directions, respectively；νxz, νyz and νxy—Poisson’s ratios in xz, yz and xy directions, respectively.
下载: 导出CSV
-
[1] 杨彩云, 李嘉禄. 基于纱线真实形态的三维机织复合材料细观结构及其厚度计算[J]. 复合材料学报, 2005, 22(6):178-182. DOI: 10.3321/j.issn:1000-3851.2005.06.031 YANG Caiyun, LI Jialu. Microstructure and thickness equation of 3d woven composites based on yarn’s true configuration[J]. Acta Materiae Compositae Sinica,2005,22(6):178-182(in Chinese). DOI: 10.3321/j.issn:1000-3851.2005.06.031
[2] 丁辛, 易洪雷. 三维机织结构的几何模型[J]. 复合材料学报, 2003, 20(5):108-113. DOI: 10.3321/j.issn:1000-3851.2003.05.020 DING Xin, YI Honglei. A geometric model of three dimensional woven structures[J]. Acta Materiae Compositae Sinica,2003,20(5):108-113(in Chinese). DOI: 10.3321/j.issn:1000-3851.2003.05.020
[3] 张超, 许希武, 毛春见. 三维编织复合材料渐进损伤模拟及强度预测[J]. 复合材料学报, 2011, 28(2):222-230. ZHANG Chao, XU Xiwu, MAO Chunjian. Progressive damage simulation and strength prediction of 3D braided composites[J]. Acta Materiae Compositae Sinica,2011,28(2):222-230(in Chinese).
[4] 郑君, 温卫东, 崔海涛, 等. 2.5维机织结构复合材料的几何模型[J]. 复合材料学报, 2008, 25(2):143-148. DOI: 10.3321/j.issn:1000-3851.2008.02.024 ZHENG Jun, WEN Weidong, CUI Haitao, et al. Geometric model of 2.5 dimensional woven structures[J]. Acta Materiae Compositae Sinica,2008,25(2):143-148(in Chinese). DOI: 10.3321/j.issn:1000-3851.2008.02.024
[5] 杨振宇, 俸翔, 苏洲, 等. 2.5D编织复合材料细观结构及弹性性能[J]. 宇航材料工艺, 2010, 40(2):67-71. DOI: 10.3969/j.issn.1007-2330.2010.02.018 YANG Zhenyu, FENG Xiang, SU Zhou, et al. Meso-structure and elastic properties of 2.5D braided composites[J]. Aerospace Materials & Technology,2010,40(2):67-71(in Chinese). DOI: 10.3969/j.issn.1007-2330.2010.02.018
[6] 梁仕飞, 矫桂琼, 王波. 三维机织C/C-SiC复合材料弹性性能预测[J]. 复合材料学报, 2011, 28(1):138-142. LIANG Shifei, JIAO Guiqiong, WANG Bo. Prediction of elastic properties of three dimensional woven C/C-SiC composite[J]. Acta Materiae Compositae Sinica,2011,28(1):138-142(in Chinese).
[7] ZHANG D T, CHEN L, WANG Y, et al. Stress field distribution of warp-reinforced 2.5D woven composites using an idealized meso-scale voxel-based model[J]. Journal of Materials Science,2017,52(11):6814-6836. DOI: 10.1007/s10853-017-0921-0
[8] 卢子兴, 周原, 冯志海, 等. 2.5D机织复合材料压缩性能实验与数值模拟[J]. 复合材料学报, 2015, 32(1):150-159. LU Zixing, ZHOU Yuan, FENG Zhiyuan, et al. Experiment and numerical simulation compressive properties of 2.5D woven fabric composites[J]. Acta Materiae Compositae Sinica,2015,32(1):150-159(in Chinese).
[9] ZENG X S, BROWN L P, ENDRUWEIT A, et al. Geometrical modelling of 3D woven reinforcements for polymer composites: Prediction of fabric permeability and composite mechanical properties[J]. Composites Part A: Applied Science and Manufacturing,2014,56:150-160. DOI: 10.1016/j.compositesa.2013.10.004
[10] GREEN S D, MATVEEV M Y, LONG A C, et al. Mechanical modelling of 3D woven composites considering realistic unit cell geometry[J]. Composite Structures,2014,118:284-293. DOI: 10.1016/j.compstruct.2014.07.005
[11] 仲苏洋. 三维机织复合材料损伤演化与失效行为研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. ZHONG Suyang. Investigation of damage evolution and failure of the three-dimensional woven composites[D]. Harbin: Harbin Institute of Technology, 2015(in Chinese).
[12] SHERBURN M. Geometric and mechanical modelling of textiles[D]. Nottingham: University of Nottingham, 2007.
[13] LIN H, BROWN L P, LONG A C. Modelling and simulating textile structures using TexGen[J]. Advanced Materials Research,2011,331:44-47. DOI: 10.4028/www.scientific.net/AMR.331.44
[14] BROWN L P, ENDRUWEIT A, LONG A, et al. Characterisa-tion and modelling of complex textile geometries usingTexGen[C]//13th International Conference on TextileComposites. Milan, Italy: IOP Publishing Ltd, 2018: 1-8.
[15] 孙晓军, 赵晓明, 郑振荣, 等. 新型织物仿真软件TexGen的特点及其应用[J]. 纺织导报, 2013(4):70-73. DOI: 10.3969/j.issn.1003-3025.2013.04.019 SUN Xiaojun, ZHAO Xiaoming, ZHENG Zhenrong, et al. Introduction and application of a new fabric simulation software[J]. China Textile Leader,2013(4):70-73(in Chinese). DOI: 10.3969/j.issn.1003-3025.2013.04.019
[16] ZHANG C, CURIEL-SOSA J L, BUI T Q, Comparison of periodic mesh and free mesh on the mechanical properties prediction of 3D braided composites[J]. Composite Structures, 2017, 159: 667-676.
[17] 赖卫清, 王秀梅, 辛亮亮, 等. 基于RVE方法的二维机织复合材料弹性性能预测[J]. 玻璃钢/复合材料, 2019(6):64-72. LAI Weiqing, WANG Xiumei, XIN Liangliang, et al. Prediction of elastic properties of 2D woven composites based on RVE method[J]. Fiber Reinforced Plastics/Composites,2019(6):64-72(in Chinese).
[18] ZHANG C, XU X W. Finite element analysis of 3D braided composites based on three unit-cells models[J]. Composite Structures,2013,98:130-142. DOI: 10.1016/j.compstruct.2012.11.003
[19] RUSSELL B P, KARTHIKEYAN K, DESHP-ANDE V S, et al. The high strain rate response of ultra high molecular-weight polyethylene: From fibre to laminate[J]. International Journal of Impact Engineering 2013, 60: 1-9.
[20] CHAMIS C C. Mechanics of composites materials: Past, present, and future[J]. Journal of Composites Technology and Research,1989,11(1):3-14. DOI: 10.1520/CTR10143J
[21] ZHANG D T, FENG G Y, SUN M Y, et al. Finite element analysis of mesh size effect of 3D angle-interlock woven composites using voxel-based method[J]. Applied Composite Materials,2018,25(4):905-920. DOI: 10.1007/s10443-018-9723-z
[22] 许善迎, 谭焕成, 关玉璞, 等. 三维四向编织复合材料力学性能预测及实验验证[J]. 材料工程, 2018, 46(6):132-140. DOI: 10.11868/j.issn.1001-4381.2016.001135 XU Shanying, TAN Huancheng, GUAN Yupu, et al. Predication and experimental verification on mechanical properties of three-dimensional and four-direction braided composites[J]. Journal of Materials Engineering,2018,46(6):132-140(in Chinese). DOI: 10.11868/j.issn.1001-4381.2016.001135
[23] SUN Jin, WANG Yu, ZHOU Guangming, et al. Finite element analysis of mechanical properties of 3D surface-core braided composites[J]. Polymer Composites,2018,39(4):1076-1088.
[24] LEVI-SASSON A, MESHI I, MUSTACCHI S, et al. Experimental determination of linear and nonlinear mechanical properties of laminated soft composite material system[J]. Composites Part B: Engineering,2014,57:96-104. DOI: 10.1016/j.compositesb.2013.09.043
[25] 王宇. 三维斜交机织复合材料细观结构与力学性能研究[D]. 南京: 南京航空航天大学, 2017. WANG Yu. Research on microstructure and mechanical properties of 3D nonorthogonal woven composites[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2017(in Chinese).
-
期刊类型引用(2)
1. 李天宇，沈伟，陈立峰，竺铝涛. 三维角联锁机织复合材料的制备及其弯曲压缩失效机制. 纺织学报. 2024(08): 183-189 . 
百度学术
2. 杨斌，王继辉，冯雨薇，杨超，倪爱清. 织物增强复合材料Micro-CT辅助数值仿真技术研究进展. 复合材料学报. 2023(10): 5466-5485 . 本站查看
其他类型引用(1)
-
计量
- 文章访问数: 984
- HTML全文浏览量: 410
- PDF下载量: 84
- 被引次数: 3
