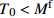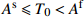形状记忆合金在复合材料损伤监测中的应用

张亚楠; 刘亚冬; 刘兵飞

doi:10.13801/j.cnki.fhclxb.20201111.001

形状记忆合金在复合材料损伤监测中的应用

1.
中国民航大学　机场学院，天津 300300
2.
中国民航大学　中欧航空工程师学院，天津 300300
3.
中国民航大学　航空工程学院，天津 300300

基金项目: 国家自然科学基金(11502284)；中科院重点部署项目(KFZD-SW-435)；中央高校基金(3122015C019)

详细信息

通讯作者:
刘兵飞，博士，副教授，硕士生导师，研究方向为智能材料与结构力学　 E-mail：bingfeiliu2@126.com

中图分类号: TG139.6；TB33
计量
- 文章访问数: 1340
- HTML全文浏览量: 466
- PDF下载量: 96
出版历程
- 收稿日期: 2020-09-02
- 录用日期: 2020-10-27
- 网络出版日期: 2020-11-10
- 刊出日期: 2021-04-07

Application of shape memory alloy in damage monitoring of composite materials

1.
Airport College, Civil Aviation University of China, Tianjin 300300, China
2.
Sino-European Institute of Aviation Engineering, Civil Aviation University of China, Tianjin 300300, China
3.
Faculty of Aerospace Engineering, Civil Aviation University of China, Tianjin 300300, China

摘要

摘要: 复合材料的损伤会对结构的可靠性和安全性造成威胁，近年来引起国内外专家和学者的广泛关注。本文将形状记忆合金(SMA)埋入复合材料试件中，通过对SMA电阻变化与复合材料应变之间的关系进行讨论，建立不同监测条件下复合材料的损伤监测理论模型。基于该模型讨论了不同初始状态下SMA材料的损伤监测行为。研究结果表明：复合材料的损伤与SMA电阻变化呈线性关系，温度荷载在SMA未发生相变时对损伤监测影响较小，在SMA发生相变时对损伤监测影响较大。本研究可为基于SMA的复合材料损伤监测理论的进一步工程应用提供理论指导。
- 形状记忆合金 /
- 复合材料 /
- 损伤监测 /
- 变温 /
- 相变
Abstract: The damage of composite materials poses a threat to the reliability and safety of the structure, and has attracted widespread attention from domestic and foreign experts and scholars in recent years. This study embeded the shape memory alloy (SMA) in the composite material specimen, and discussed the relationship between the SMA resistance change and the composite material strain, established theoretical models of composite damage monitoring under different monitoring conditions. Based on this model, the damage monitoring behavior of SMA materials in different initial states was discussed. The research results show that the damage of the composite material has a linear relationship with the resistance change of the SMA. The temperature load has little influence on the damage monitoring when the SMA does not undergo a phase change, and has a greater influence on the damage monitoring when the SMA undergoes a phase change. The research can provide theoretical guidance for the further engineering application of SMA-based composite damage monitoring theory.
- shape memory alloy /
- composite materials /
- damage monitoring /
- change temperature /
- phase tran-sition

HTML全文

纤维复合材料(Fiber reinforced polymer，FRP)由于其具有优良的材料性能，目前在土木工程结构的修复与加固中得到较广泛的应用^[1-3]。为了充分发挥FRP材料的轻质高强特性，一个有效的方法是将预应力引入到FRP片材中。然而，传统的机械式预应力施加方法存在施工复杂、施工空间狭小、预应力损失较大等缺点，限制了预应力FRP片材的推广与应用^[4-7]。因此，急需研究新的方法对FRP片材引入预应力。

目前，一种性能优异的材料-形状记忆合金(Shape memory alloy，SMA)正在进入土木工程领域^[8-13]，SMA具有两种典型的特性：超弹性性能和形状记忆效应^[14-18]。Zafar等^[18]将超弹性的SMA丝与玻璃纤维复合材料(Glass fiber reinforced polymer，GFRP)纤维及高伸长率树脂相结合，研究复合棒材的基本力学性能和滞回性能。Zheng等^[19-20] 、El-Tahan等^[21]将SMA丝作为加固材料，FRP作为锚固片材，对钢板进行疲劳加固。通过FRP将SMA粘贴在钢板表面，并利用SMA丝的回复性能将预应力引入钢板，以减小钢板的应力幅。此外，超弹性SMA丝特殊的电阻特性被用来制作FRP/SMA组合中的应变传感元件，以监测结构健康状况^[22]。

结合SMA和FRP两种材料的优异性能，本文提出了一种新的FRP/SMA复合材料主动增强技术^[23-25]。该项加固技术所应用的加固层是由SMA丝和FRP片材两种材料组成：SMA丝作为预应力引入介质嵌入到FRP片材内部，利用SMA的回复性能在FRP片材中引入预应力。该项技术克服了机械张拉过程中FRP片材不易夹持，预应力不易施加等问题^[25-27]。

为验证该项技术的可行性，本文开展了SMA丝与碳纤维复合材料(Carbon fiber reinforced polymer， CFRP)片材形成的复合材料的力学性能和可回复性能试验研究。

1. FRP/SMA复合材料的力学性能

FRP/SMA复合材料主动增强技术(图1)的工作原理是利用SMA丝的形状记忆效应将SMA产生的回复力引入加固区。在修复与加固工程中，首先在端部采用FRP片材将SMA丝材锚固于梁底面，同时，在加固区的FRP片材与混凝土梁底面涂刷环氧树脂类粘结材料进行粘结，然后通过SMA丝材的升温回复将预应力引入加固区中的FRP片材中，在环氧树脂固化过程中，FRP片材中的预应力传递到混凝土中，从而改善被加固结构受力性能。

图 1 纤维增强复合材料(FRP)/形状记忆合金(SMA)复合材料预应力增强系统

Figure 1. Fiber reinforced polymer (FRP)/shape memory alloy (SMA) composite prestressed strengthening system

下载: 全尺寸图片幻灯片

1.1 原材料

SMA丝为西安思维金属材料有限公司生产的镍钛(NiTi)合金，直径为0.5 mm和1.0 mm。根据差示扫描量热法测试结果，0.5 mm和1.0 mm丝的奥氏体、马氏体相变温度如表1所示。可以看出，在常温(20℃)的条件下，NiTi丝处于马氏体相。

表 1 材料的物理力学性能

Table 1. Physical and mechanical properties of materials

Material	Diameter φ/mm	Austenite transition temperature/℃		Martensite transition temperature/℃		Phase transition stress/MPa	Strength/ MPa	Elastic modulus/ GPa	Elongation/ %
Material	Diameter φ/mm	Start A_s	Finish A_f	Start M_s	Finish M_f	Phase transition stress/MPa	Strength/ MPa	Elastic modulus/ GPa	Elongation/ %
SMA wire	0.5	106.12	121.40	55.34	27.34	122	982	12.2	78.0
SMA wire	1.0	79.13	105.46	59.00	35.81	117	906	10.4	75.0
CFRP		–	–	–	–	–	3000	247.7	1.2
Epoxy resin		–	–	–	–	–	35	2.2	1.6
Notes: CFRP—Carbon fiber reinfored plastic; A_f—Austenite finish temperature; A_s—Austenite start temperature; M_s—Martensite start temperature; M_f—Martensite finish temperature.

下载: 导出CSV

| 显示表格

图2为0.5 mm和1.0 mm的NiTi合金丝在常温下单调拉伸的典型试验结果。在1.0 mm/min加载速率下，0.5 mm和1.0 mm的丝的应力-应变关系曲线表现出一致性，SMA丝从试验加载到拉断，整个应力-应变曲线可分为4个阶段：从开始加载到SMA丝的应力达到相变开始应力σ_s之前，SMA处于弹性阶段。随着拉伸荷载的增加，SMA丝应力超过相变开始应力σ_s时，触发SMA丝发生相变，此时SMA丝的应力基本不增长而应变持续增加，所对应的相变阶段的应变从1.5%开始一直持续到7%左右。当SMA丝的拉伸应力超过相变结束应力σ_f时，应力-应变曲线表现为明显的上升趋势。而后试件截面发生局部颈缩，变形持续增加，超过了极限抗拉强度后，应力随之下降直至断裂。

图 2 SMA丝单调拉伸应力-应变关系曲线

Figure 2. Stress-strain relationship of SMA wires in monotonic tension

σ_s—Phase transition initiation stress; σ_f—End-phase change stress

下载: 全尺寸图片幻灯片

FRP材料为卡本复合材料(天津)有限公司所生产的CFS-I-300高强I型CFRP单向布，根据《纤维增强复合材料建设工程应用技术规范》^[28]，试件的设计尺寸为250 mm×25 mm×0.167 mm，标距为150 mm。环氧树脂为配套的CFSR-A/B型碳纤维浸渍胶，拉伸测试标准依据GB/T 2567—2008^[29]，标距为50 mm的棒骨试件拉。在2.0 mm/min的加载速率下，CFRP片材试件表现为脆性断裂破坏，拉伸强度为3000.0 MPa，最大拉伸应变量为1.2%，弹性模量为247.7 GPa。环氧树脂胶抗拉强度为35.0 MPa，最大拉伸应变约为1.6%，弹性模量为2.2 GPa。表1给出了所有材料的物理力学性能指标。

1.2 试件设计

FRP/SMA复合材料由一层CFRP片材垫层、一层SMA丝中间夹层及一层CFRP片材覆盖层组成。它们之间使用环氧树脂相互牢固粘结。本文设计了两种FRP/SMA复合材料试件：第一种类型(I类)的复合材料试件是由CFRP片材与SMA丝在全部长度范围内进行复合，用于测试复合材料的力学性能；第二种类型(II类)的复合材料试件是将FRP片材与SMA丝进行部分复合并留出一段非复合区—激活段，用于对SMA丝通电升温，测试复合材料的回复性能，如图3所示。

I类复合材料试件设计了SMA丝的根数和SMA直径两个试验变量，共4组试件；II类复合材料试件的试验变量为SMA丝的初始拉应变，共3组试件，如表2所示。表中符号“FRP/SMA-I、FRP/SMA-II”表示两类试件；“0.5、1.0”表示SMA丝的直径分别为0.5 mm和1.0 mm；“5、10和15”分别表示SMA丝的根数；“4%、6%和8%”分别为SMA丝的初始拉应变。

1.3 试验装置

试验加载装置为电液伺服万能试验机，力传感器量程为300 kN。荷载值通过采集软件自动记录，之后换算成试件的应力值。应变通过TST3827E动静态信号测试分析系统采集。环境温度为20℃，试验过程采用等位移速率控制，设定为2.0 mm/min，拉伸试件直至破坏。

图 3 两类FRP/SMA复合材料试件

Figure 3. Two types of FRP/SMA composite specimens

下载: 全尺寸图片幻灯片

1.4 试验结果与分析

1.4.1 破坏形态

图4为I类FRP/SMA复合材料试件的典型破坏形态，主要有两种：CFRP片材纵向劈裂破坏，如图4(a)所示；CFRP片材中部爆裂破坏，如图4(b)所示。CFRP片材纵向劈裂破坏是随着荷载的增加，试件的拉伸段出现一条贯通的主裂缝，使试件沿着拉伸方向产生过大的剪切力而造成的，破坏形式更类似于CFRP片材的拉伸破坏模式。CFRP片材中部爆裂破坏是随着试验载荷的增加，试件中部CFRP片材中的纤维丝相继达到拉伸强度，断裂并伴随着剧烈的爆裂声的破坏模式。

表 2 两种类型的FRP/SMA复合材料试件

Table 2. Two types of FRP/SMA composite specimens

Specimen type	Specimen	Number of SMA wires	Diameter of SMA/ mm	Prestrain/ %	Length of composite section/ mm
FRP/SMA-I	FRP/SMA-I-0.5-5-4%	5	0.5	4	250
	FRP/SMA-I-0.5-10-4%	10	0.5	4	250
	FRP/SMA-I-0.5-15-4%	15	0.5	4	250
	FRP/SMA-I-1-10-4%	10	1.0	4	250
FRP/SMA-II	FRP/SMA-II-1.0-10-4%	10	1.0	4	2×70
	FRP/SMA-II-1.0-10-6%	10	1.0	6	2×70
	FRP/SMA-II-1.0-10-8%	10	1.0	8	2×70

下载: 导出CSV

| 显示表格

图 4 FRP/SMA复合材料的破坏形态

Figure 4. Failure modes of FRP/SMA composites

下载: 全尺寸图片幻灯片

1.4.2 应力-应变关系曲线

图5给出了I类FRP/SMA复合材料试件单调拉伸直至破坏的应力-应变曲线。可知，所有试件的应力-应变关系曲线在破坏前近似为一条直线。断裂之后，试件仍然有一定的残余强度，主要来自于未断裂的CFRP纤维和SMA丝的贡献。还可以看出，对于发生纵向劈裂破坏的试件，随着SMA丝用量和直径的增加，FRP/SMA复合材料的极限抗拉强度有所降低，而断裂应变基本不变。如极限抗拉强度由FRP/SMA-I-0.5-5试件组的2544.0 MPa(平均值)降低到FRP/SMA-I-1-10试件组的2031.0 MPa(平均值)，对应的最大断裂应变为1.3%~1.4%。值得注意的是，对于发生中部爆裂破坏的试件，其极限抗拉强度的平均值接近CFRP片材的抗拉强度，说明这种破坏模式下，SMA丝对复合材料抗拉强度的贡献非常有限，CFRP起到主要作用。表3给出了I类FRP/SMA复合材料试件的试验结果。

图 5 FRP/SMA复合材料试件的应力-应变曲线

Figure 5. Stress-strain curves of FRP/SMA composite specimen

下载: 全尺寸图片幻灯片

表 3 FRP/SMA复合材料试验与分析结果

Table 3. Test and analysis results of FRP/SMA composites

Specimen	No.	Strength/MPa			Elastic modulus/GPa			Fracture strain/%			Failure mode
Specimen	No.	Test value	Calculated value	Test value/ calculated value	Test value	Calculated value	Test value/ calculated value	Test value	Calculated value	Test value/ calculated value	Failure mode
FRP/SMA-I-0.5- 5-4%	1	2206	2840	0.78	158.7	234.7	0.68	1.39	1.2	1.16	Longitudinal splitting
	2	2617		0.92	186.9		0.80	1.40		1.17
	3	2809		0.98	205.0		0.87	1.37		1.14
FRP/SMA-I-0.5-10-4%	1	2326	2697	0.86	169.7	222.9	0.76	1.32	1.2	1.10	Longitudinal splitting
	2	2566		0.95	192.9		0.87	1.33		1.11
	3	2828		1.05	212.6		0.95	1.28		1.07
FRP/SMA-I-0.5-15-4%	1	2602	3000	0.87	154.9	212.4	0.73	1.68	1.41	1.19	Burst failure
	2	2992		1.04	188.4		0.89	1.65		1.17
	3	2999		1.00	196.0		0.92	1.65		1.17
FRP/SMA-I-1.0-10-4%	1	1968	2078	0.95	145.8	171.8	0.85	1.35	1.2	1.13	Longitudinal splitting
	2	2085		1.00	156.8		0.91	1.33		1.11
	3	2039		0.98	156.8		0.91	1.30		1.08
Average value				0.95			0.85			1.13
Standard deviation				0.08			0.08			0.04
Coefficient of variation				0.08			0.09			0.04

下载: 导出CSV

| 显示表格

根据试验结果，FRP/SMA复合材料在破坏之前的应力-应变关系可以视为线性关系，即应力等于应变与弹性模量的乘积；破坏之后，认为CFRP片材不参与工作，只有SMA丝提供强度，且复合材料破坏时的应变均处于SMA丝相变阶段，因此复合材料的应力取SMA丝的相变应力σ_s，可以给出FRP/SMA复合材料的应力-应变曲线为

${\sigma }_{{\rm{fs}}}=\left\{\begin{array}{l}{E}_{{\rm{fs}}}{\varepsilon }_{{\rm{fs}}}\quad\quad\quad\quad 0\leqslant {\varepsilon }_{{\rm{fs}}}\leqslant {\varepsilon }_{{\rm{fs,u}}}\\ {\sigma }_{{\rm{s}}}\quad\quad\quad\quad\quad\;\;{\varepsilon }_{{\rm{fs}}} > {\varepsilon }_{{\rm{fs,u}}}\end{array}\right.$

(1)

式中： ${\sigma }_{{\rm{fs}}}$ 为FRP/SMA复合材料的应力； ${\varepsilon }_{{\rm{fs}}}$ 为FRP/SMA复合材料的应变； ${\varepsilon }_{{\rm{fs,u}}}$ 为FRP/SMA复合材料的极限拉应变； ${E}_{{\rm{fs}}}$ 为FRP/SMA复合材料的弹性模量； ${\sigma }_{{\rm{s}}}$ 为SMA丝的相变开始应力。

FRP/SMA复合材料的弹性模量可以按照下式计算：

${E}_{{\rm{fs}}}=\frac{{E}_{{\rm{f}}}{A}_{{\rm{fs}}}+{E}_{{\rm{s}}}{A}_{{\rm{ss}}}}{{A}_{{\rm{fs}}}+{A}_{{\rm{ss}}}}$

(2)

式中：E_f、E_s分别是CFRP片材的弹性模量和SMA丝的弹性模量；A_fs、A_ss分别是CFRP片材的截面面积和SMA丝的截面面积。

FRP/SMA复合材料的极限拉应变可以按照下式计算：

${\varepsilon }_{{\rm{fs,u}}}=\left\{\begin{gathered}{\varepsilon }_{{\rm{f}}}\qquad 纵向劈裂 \\ \dfrac{{f}_{{\rm{fs,u}}}}{{E}_{{\rm{fs}}}}\qquad 爆裂破坏 \end{gathered}\right.$

(3)

${f}_{{\rm{fs,u}}}=\left\{\begin{gathered}\frac{{{f}}_{{{\rm{f}}}{{\rm{u}}}}{{A}}_{{{\rm{fs}}}}+{{\sigma }}_{{{\rm{s}}}}{{A}}_{{{\rm{ss}}}}}{{{A}}_{{{\rm{fs}}}}+{{A}}_{{{\rm{ss}}}}}\qquad 纵向劈裂 \\ {{f}}_{{{\rm{f}}}{{\rm{u}}}}\qquad 爆裂破坏 \end{gathered}\right.$

(4)

式中：f_fu、σ_s分别是CFRP片材的极限抗拉强度和SMA丝的相变开始应力；f_fs,u为FRP/SMA复合材料的极限抗拉强度。

表3给出了试验结果与计算结果的比较。可以看出，抗拉强度、弹性模量及断裂应变的试验值与计算值比值的平均值分别为0.95、0.85和1.13，变异系数分别为0.08、0.09和0.04，计算值与试验值吻合较好。然而，弹性模量的计算值略高于试验值，断裂应变的计算值略低于试验值，其原因是每组试验中均有单个试件的抗拉强度相对较低，而断裂应变相差不大，从而造成该试件的弹性模量也相对较低，影响了平均值和变异系数。

2. FRP/SMA复合材料的可回复性能

为了清楚地了解FRP/SMA复合材料的回复性能，本文进行了SMA丝及FRP/SMA复合材料的受限回复试验，采用通电升温的方式获得回复应力。

2.1 SMA丝的回复性能

2.1.1 试件设计

在SMA丝回复性能试验中，设计了7组试件，每组试件包含2个试样，SMA丝试件两夹头之间距离200 mm(图6)。试验变量为SMA丝的直径和初始拉应变水平，直径为0.5 mm和1.0 mm，初始拉应变设计为4%、6%、8%和10%，如表4所示。

图 6 SMA回复试验装置

Figure 6. SMA recovery test device

下载: 全尺寸图片幻灯片

表 4 SMA回复性能试验试件设计与试验结果

Table 4. Design and test results of SMA recovery test specimen

Specimen	Length of SMA/ mm	Diameter of SMA/ mm	Prestrain/ %	Average value of maximum recovery stress/ MPa
SMA-0.5-4%	200	0.5	4	202
SMA-0.5-6%	200	0.5	6	273
SMA-0.5-8%	200	0.5	8	288
SMA-0.5-10%	200	0.5	10	295
SMA-1.0-4%	200	1.0	4	267
SMA-1.0-6%	200	1.0	6	312
SMA-1.0-8%	200	1.0	8	391

下载: 导出CSV

| 显示表格

预先对SMA丝施加初始预拉伸应变，将SMA丝的夹持端用砂纸打磨后用绝缘胶布包裹后放置在电子万能材料试验机的夹具中。电源为直流高压稳压直流电源，采用电流控制并达到设计温度。在升温过程中，采用温度传感器实时监测温度的变化情况。试验中记录SMA丝的回复应力随温度变化的曲线，确定目标电流下SMA丝所能达到的最高应力水平(σ_max)及该应力水平所对应的温度(T_σ)，试验加载装置如图6所示。

2.1.2 试验结果与分析

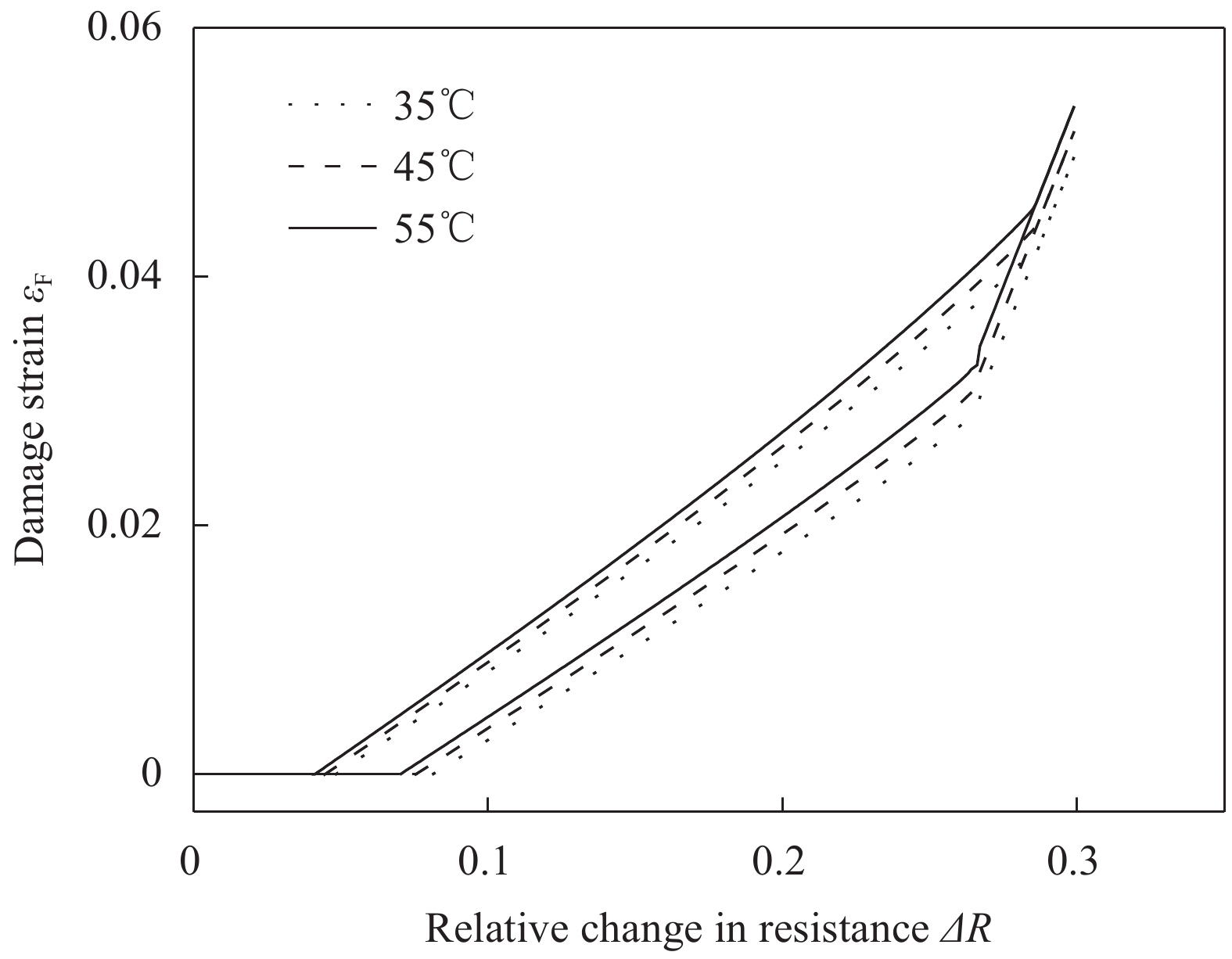
0.5 mm直径的SMA丝在不同初始拉应变水平下的受限回复应力与温度的关系曲线如图7所示。可以看出，随着温度的升高，SMA丝发生奥氏体相变，产生了很大的回复应力，并且其回复应力随温度的升高而迅速增加。当温度大于奥氏体相变结束温度A_f后，回复应力值的增加趋于平缓，此时应力的下降是由温度热膨胀引起的。表4统计了所有试件的最大回复应力。可以看出，当0.5 mm的SMA丝的预应变水平分别为4%、6%、8%和10%时，最大回复应力分别为202 MPa、273 MPa、288 MPa和295 MPa，即随着预拉伸应变水平的增大，最大回复应力也均随之增加。

图 7 0.5 mm SMA丝不同预应变水平情况下回复应力随温度的变化曲线

Figure 7. Recovery stress curves of 0.5 mm SMA wire with different pre-strain levels as a function of temperature

下载: 全尺寸图片幻灯片

1.0 mm直径的SMA丝不同预应变水平下的受限回复应力与温度的关系曲线如图8所示。与0.5 mm直径的SMA丝所表现出来的性质类似，最大回复应力随预拉伸应变水平的增加而增加。但是相比于相同预拉伸应变水平下0.5 mm直径SMA丝，1.0 mm直径的SMA丝的回复应力有明显的提升，如表4所示。可以看出，当1.0 mm的SMA丝的预应变水平分别为4%、6%、8%时，最大回复应力分别为267 MPa、312 MPa和391 MPa。

图 8 1.0 mm SMA丝不同预应变水平情况下回复应力随温度的变化曲线

Figure 8. Recovery stress and temperature curves of 1.0 mm SMA wire with different pre-strain levels

下载: 全尺寸图片幻灯片

2.2 基于Brinson模型的受限回复分析

2.2.1 理论推导

Brinson模型^[30-32]将马氏体分为温度诱发的马氏体和应力诱发的马氏体两部分，相对应的两部分的马氏体体积分数分别用ξ_T和ξ_S表示。受限回复过程中，SMA的马氏体相变开始和结束温度及马氏体逆相变的开始和结束温度都将因应力水平不同而有所改变。考虑应力因素后的马氏体相变开始和结束温度及马氏体逆相变开始和结束温度分别设为M_s^m、M_f^m、A_s^m、A_f^m。

Brinson^[31]根据SMA在相变过程中自由能应达到最小值的原理建立了SMA的本构关系模型，并考虑了应力诱导马氏体含量对本构关系的影响。根据Brinson模型可知，SMA的本构关系可表达为

$\sigma - {\sigma }_{0} = E\left(\xi \right)\varepsilon - E\left({\xi }_{0}\right){\varepsilon }_{0}+\Omega \left(\xi \right){\xi }_{{{S}}} - \Omega \left({\xi }_{0}\right){\xi }_{{{S}}0}+\Theta \left(T - {T}_{0}\right)$

(5)

其中： $E\left(\xi \right)$ 为SMA丝的弹性模量； $\Omega \left(\xi \right)$ 为SMA的相变张量；下标0表示SMA材料的初始状态。

将SMA的回复应力用σ^r表示，则SMA初始状态为σ₀ ^r=0，ε₀=ε_m，ξ₀=1，ξ_S0=ε_m/ε_L，T₀=T_m<M_f。其中，ε_m为SMA拉伸后的残余应变，ε_L为最大可回复应变。由于SMA初始的应力诱发马氏体分数ξ_S0不大于1，故当ε_m略大于ε_L时，取ε_m等于ε_L，即此时有ξ_S0=1。

为便于计算加热受限回复过程中的回复应力，基于Brinson模型对其进行分段推导：

① 当T≤A_s ^m时，没有发生马氏体逆相变，此时受限回复应力与温度之间的关系为

${\sigma }^{{\rm{r}}}-{{\sigma }_{0}^{{\rm{r}}}}=\Theta \left(T-{T}_{{\rm{m}}}\right)$

(6)

② 当T=A_s ^m时，SMA即将发生马氏体逆相变，应力达到临界点，由式(5)可得：

$\sigma _{A_{\rm{s}}^{\rm{m}}}^{\rm{r}} = \Theta \left( {A_{\rm{s}}^{\rm{m}} - {T_{\rm{m}}}} \right)$

(7)

③ 当A_s ^m<T≤A_f ^m时，SMA发生马氏体逆相变，此时SMA初始状态为σ₀ ^r= ${{\sigma }_{{A}_{{\rm{s}}}^{{\rm{m}}}}}^{{\rm{r}}}$ ，ε₀=ε_m，ξ₀=1，ξ_S0=ε_m/ε_L，T₀=A_s ^m。马氏体含量和应力诱发马氏体含量可分别表示为

$\xi =\frac{1}{2}\mathrm{cos}\left[{a}_{{\rm{A}}}\left(T-{A}_{{\rm{s}}}\right)-{\sigma }^{{\rm{r}}}/{C}_{{\rm{A}}}\right]+\frac{1}{2}$

(8)

${\xi }_{{\rm{s}}}=\frac{{\xi }_{{{S}}0}}{2}\mathrm{cos}\left[{a}_{{\rm{A}}}\left(T-{A}_{{\rm{s}}}\right)-{\sigma }^{r}/{C}_{{\rm{A}}}\right]+\frac{{\xi }_{{{S}}0}}{2}$

(9)

SMA刚开始发生马氏体逆相变时，温度为A_s ^m，此时应力诱发马氏体含量仍为ξ_S0， ${a}_{{\rm{A}}}$ 和 ${C}_{{\rm{A}}}$ 为SMA丝的材料常数，根据式(8)和式(9)可得：

${A}_{{\rm{s}}}^{{\rm{m}}}=\frac{{{C}_{{\rm{A}}}A}_{{\rm{s}}}-\Theta {T}_{{\rm{m}}}}{{C}_{{\rm{A}}}-\Theta }$

(10)

当SMA发生马氏体逆相变时，根据式(5)受限回复应力与温度的关系可表示为

$\begin{split} {{{\sigma }^{{\rm{r}}}-\sigma }_{{A}_{{\rm{s}}}^{{\rm{m}}}}}^{{\rm{r}}}=&\mathrm{\Theta }\left(T-{A}_{{\rm{s}}}^{{\rm{m}}}\right)+E\left(\xi \right)\frac{{\varepsilon }_{0}}{2}\\ &\left\{1-\mathrm{cos}\left[{a}_{{\rm{A}}}\left(T-{A}_{{\rm{s}}}\right)-{\sigma }^{{\rm{r}}}/{C}_{{\rm{A}}}\right]\right\} \end{split}$

(11)

当T=A_f ^m时，马氏体逆相变结束，受限回复应力达到临界点，可表示为

${{\sigma }_{{A}_{{\rm{f}}}^{{\rm{m}}}}}^{{\rm{r}}}=\Theta \left({A}_{{\rm{f}}}^{{\rm{m}}}-{A}_{{\rm{s}}}^{{\rm{m}}}\right)+{(E}_{{\rm{A}}}-{E}_{{\rm{M}}}){\varepsilon }_{0}+{\varepsilon }_{{\rm{L}}}{E}_{{\rm{M}}}{\xi }_{{{S}}0}{{+\sigma }_{{{\rm{A}}}_{{\rm{s}}}^{{\rm{m}}}}}^{{\rm{r}}}$

(12)

由式(9)和式(12)可得：

${A}_{{\rm{f}}}^{{\rm{m}}}=\frac{{E}_{{\rm{A}}}{\varepsilon }_{0}+{C}_{{\rm{A}}}{A}_{{\rm{f}}}-\Theta {A}_{{\rm{s}}}^{{\rm{m}}}}{{C}_{{\rm{A}}}-\Theta }$

(13)

当T≥A_f ^m时，马氏体逆相变完成。此时SMA初始状态为：σ₀ ^r= ${{\sigma }_{{{\rm{A}}}_{{\rm{f}}}^{{\rm{m}}}}}^{{\rm{r}}}$ ，ε₀=ε_m，ξ₀=0，T₀=A_s ^f。根据式(5)，受限回复应力与温度的关系可表示为

${\sigma }^{{\rm{r}}}-{{\sigma }_{{{\rm{A}}}_{{\rm{f}}}^{{\rm{m}}}}}^{{\rm{r}}}=\Theta \left(T-{A}_{{\rm{f}}}^{{\rm{m}}}\right)$

(14)

当温度达到A_f^m时，此时SMA丝内部相变已经完成，因此将此时产生的受限回复应力定义为最大受限回复应力。

2.2.2 数值模拟

根据上述分析，对SMA丝受限回复过程性能进行计算，并与试验结果进行了对比，如图9所示。根据试验数据和表1所列的试验参数，可得计算过程中所需的SMA材料参数取值。

图 9 SMA丝回复应力-温度模拟曲线

Figure 9. Stress-temperature simulation curves of SMA wire recovery

下载: 全尺寸图片幻灯片

0.5 mm和1.0 mm的SMA丝在不同预应变水平情况下的最大回复应力的试验平均值和Brinson模型的模拟值进行了比较，如图10所示。可以看出，针对不同预应变水平情况下，升温阶段计算曲线均与试验曲线吻合较好，特别是计算所得最大受限回复应力与试验实测值较接近，表明基于Brinson模型提出的修正模型可较好地描述SMA的升温阶段受限回复性能。

图 10 SMA丝最大回复应力试验值和模拟值比较

Figure 10. Comparison of the test value and simulation value of maximum recovery stress of SMA wire

下载: 全尺寸图片幻灯片

2.3 FRP/SMA复合材料的受限回复性能

2.3.1 试验方案

由前述试验结果可知，直径为1.0 mm的SMA丝的回复应力-温度曲线与预应变水平相关性较好。在制备复合材料试件时，1.0 mm丝有一定的刚度，在操作上更有可行性。因此，在FRP/SMA复合材料回复性能试验中使用的是直径为1.0 mm的SMA丝。试验设计了3组试件，每组试件包含2个试样，试件激活段长度为150 mm，丝直径为1.0 mm，试验变量为初始拉伸应变水平，分别设置了4%、6%和8%。

试验装置及试件细部分别如图11(a)和图11(b)所示。值得注意的是，由于涉及到试件内多根SMA丝同时进行通电加热，使用与丝间距相配套的螺母连接相互临近的丝，这样可将丝串联形成串联电路，如图11(c)和图11(d)所示。加热激活区SMA丝与复合段之间预留绝热段，加热激活段端部与复合段端部的距离为L=10 mm，这可保证复合段不受SMA丝加热的影响。

图 11 FRP/SMA复合材料试件受限回复试验

Figure 11. Restricted recovery test of FRP/SMA composite specimen

下载: 全尺寸图片幻灯片

2.3.2 试验结果与分析

FRP/SMA复合材料试件受限回复应力与温度的关系曲线如图12所示。可知，与SMA丝受限回复试验类似，FRP/SMA复合材料试件的回复表现出首先缓慢上升，当达到奥氏体相变开始温度后回复应力迅速增长，达到奥氏体相变结束温度后回复应力趋于稳定的趋势。复合试件的最大回复应力随预应变水平的增加而增加，但与SMA单丝试件相比，其最大回复应力略有降低。表5统计了所有试件的最大回复应力。可以看出，当FRP/SMA复合材料试件的预应变水平分别为4%、6%、8%时，最大回复应力的平均值分别为247 MPa、284 MPa、358 MPa，即随着预拉伸应变水平的增大，最大回复应力也均随之增加。

图 12 FRP/SMA复合材料试件不同预应变水平情况下回复应力随温度的变化曲线

Figure 12. Recovery stress curve of FRP/SMA composite specimens with different pre-strain levels as a function of temperature

下载: 全尺寸图片幻灯片

表 5 FRP/SMA回复性能试验试件设计与试验结果

Table 5. FRP/SMA recovery test specimen design and test results

Specimen	Length of activated section/ mm	Diameter of SMA/ mm	Prestrain/ %	Average value of maximum recovery stress/MPa
FRP/SMA- II-1.0-4%	150	1.0	4	247
FRP/SMA- II-1.0-6%	150	1.0	6	284
FRP/SMA- II-1.0-8%	150	1.0	8	358

下载: 导出CSV

| 显示表格

3. 结论

(1) 常温下形状记忆合金丝在单调拉伸至断裂的过程中主要经历4个阶段，其最大应变可达0.7以上，极限强度900 MPa以上。随着应变的增加，形状记忆合金(SMA)丝约在应变幅值为7%后进入强化阶段。

(2) 纤维增强复合材料(FRP)/SMA复合材料试件的单轴拉伸基本力学试验研究结果表明，在一定SMA丝掺量范围内，提高掺入SMA丝的数量(体积率)可提高FRP/SMA复合材料试件的最大断裂应变和抗拉强度，且掺入的丝数量越多，断后残余强度越大。掺入丝的直径明显影响FRP/SMA复合材料试件的拉伸弹性模量。

(3) SMA丝的回复应力随温度的变化呈明显的上升趋势，在一定预应变范围内，SMA丝的最大回复应力随预应变水平的增加而增加。0.5 mm的SMA丝的预应变水平为8%时，产生的最大回复应力为297 MPa；1.0 mm的SMA丝的预应变水平为8%时，产生的最大回复应力为392 MPa。

(4) 验证了FRP/SMA复合材料通电回复试验的可行性，FRP/SMA复合材料试件的回复表现出首先缓慢上升，当达到奥氏体相变开始温度后回复应力迅速增长，达到奥氏体相变结束温度后回复应力趋于稳定的趋势。复合试件的最大回复应力与SMA单丝试件表现出类似的现象，但与SMA单丝试件相比，其最大回复应力略有降低。

图 1 埋入形状记忆合金(SMA)的复合材料示意图

Figure 1. Schematic diagram of composite material embedded with shape memory alloys (SMA)

下载: 全尺寸图片幻灯片

图 2 对低温马氏体相升温过程中 (a) 和高温奥氏体相降温过程中 (b) 相变或重定向临界应力与温度之间的关系

Figure 2. Relationship between phase transformation or reorientation critical stress and temperature during the heating process of low-temperature martensite phase (a) cooling process of high-temperature austenite phase (b)

下载: 全尺寸图片幻灯片

图 3 ${T_0} < {M^{\rm{f}}}$ 时SMA损伤应变与电阻相对变化的关系

Figure 3. Relationship between the damage strain and the relative change of resistance at ${T_0} < {M^{\rm{f}}}$ for SMA

下载: 全尺寸图片幻灯片

图 4 ${A^{\rm{s}}} \leqslant {T_0} < {A^{\rm{f}}}$ 时损伤应变与电阻相对变化的关系

Figure 4. Relationship between the damage strain and the relative change of resistance at ${A^{\rm{s}}} \leqslant {T_0} < {A^{\rm{f}}}$

下载: 全尺寸图片幻灯片

图 5 ${M^{\rm{s}}} \leqslant {T_0} < {A^{\rm{s}}}$ 时SMA损伤应变与电阻相对变化的关系

Figure 5. Relationship between the damage strain and the relative change of resistance at ${M^{\rm{s}}} \leqslant {T_0} < {A^{\rm{s}}}$ for SMA

下载: 全尺寸图片幻灯片

图 6 ${A^{\rm{f}}} \leqslant {T_0}$ 时SMA损伤应变与电阻相对变化的关系

Figure 6. Relationship between the damage strain and the relative change of resistance at ${A^{\rm{f}}} \leqslant {T_0}$ for SMA

下载: 全尺寸图片幻灯片

图 7 ${T}_{0}={\rm{-}}80$ ℃时不同应力下SMA损伤应变与温度的关系

Figure 7. Relationship between damage strain and temperature under different stresses and ${T}_{0}={\rm{-}}80$ ℃ for SMA

下载: 全尺寸图片幻灯片

图 8 ${\sigma _{{\rm{SMA}}}} = 150\;{\rm{MPa}}$ 时不同初始温度下SMA损伤应变与温度的关系

Figure 8. Relationship between damage strain and temperature at different initial temperatures and ${\sigma _{{\rm{SMA}}}} = 150\;{\rm{MPa}}$ for SMA

下载: 全尺寸图片幻灯片

图 9 ${T}_{0}={\rm{-}}5$ ℃时加载阶段不同应力下SMA损伤应变与温度的关系

Figure 9. Relationship between damage strain and temperature under different stresses during loading stage and ${T}_{0}={\rm{-}}5$ ℃ for SMA

下载: 全尺寸图片幻灯片

图 10 ${T}_{0}={\rm{-}}5$ ℃时卸载阶段不同应力下SMA损伤应变与温度的关系

Figure 10. Relationship between damage strain and temperature under different stresses during unloading stage and ${T}_{0}={\rm{-}}5$ ℃ for SMA

下载: 全尺寸图片幻灯片

图 11 ${\sigma _{{\rm{SMA}}}} = 450\;{\rm{MPa}}$ 时加载阶段不同初始温度下SMA损伤应变与温度的关系

Figure 11. Relationship between damage strain and temperature at different initial temperatures in the loading stage and ${\sigma _{{\rm{SMA}}}} = 450\;{\rm{MPa}}$ for SMA

下载: 全尺寸图片幻灯片

图 12 ${\sigma _{{\rm{SMA}}}} = 300\;{\rm{MPa}}$ 时卸载阶段不同初始温度下SMA损伤应变与温度的关系

Figure 12. Relationship between damage strain and temperature at different initial temperatures during unloading stage and ${\sigma _{{\rm{SMA}}}} = 300\;{\rm{MPa}}$ for SMA

下载: 全尺寸图片幻灯片

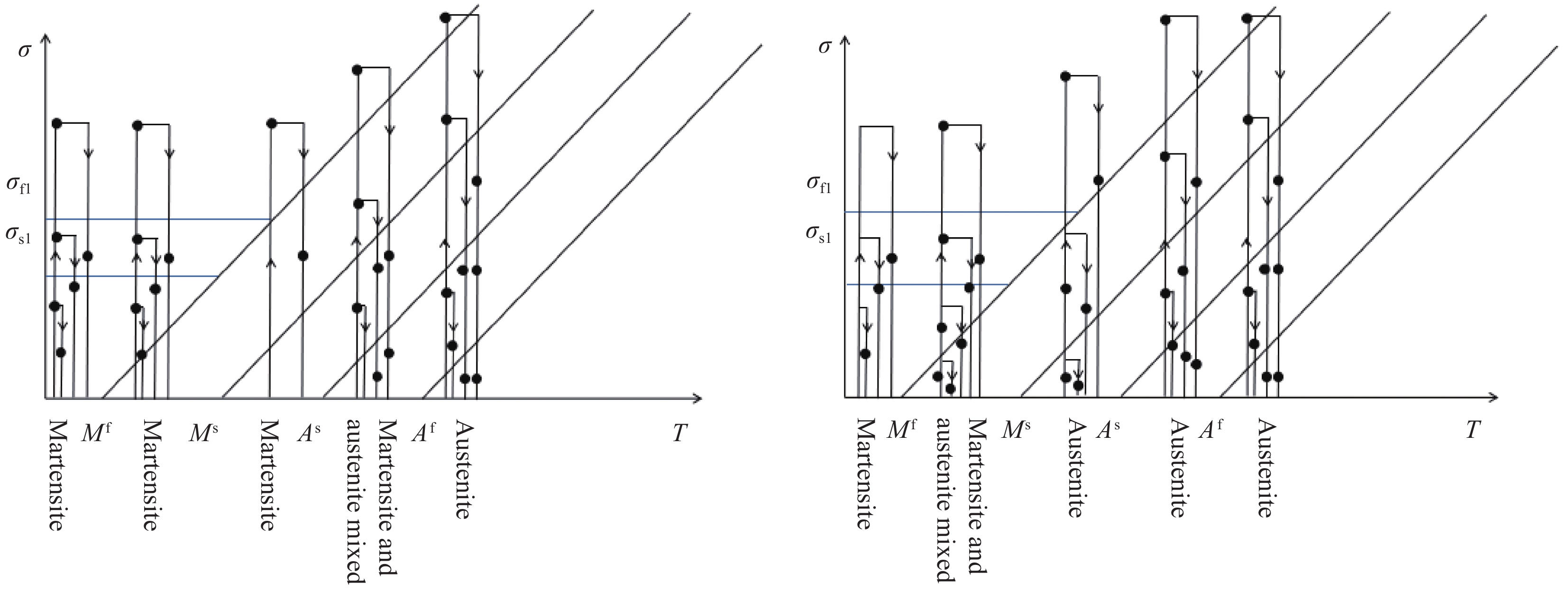
表 1 对初始状态为低温马氏体相的SMA升温过程中的情况分类

Table 1 Classification of the conditions during the heating process of the SMA whose initial state is low-temperature martensite phase

Temperature section	SMA initial state	Loading phase	Composite material	Uninstall phase
${T_0} < {M^{\rm{f}}}$	Martensite	$0 \leqslant {\sigma _{{\rm{SMA}}}} \leqslant {\sigma _{{\rm{s1}}}}$	No damage	$0 \leqslant {\sigma _{{\rm{SMA}}}}$
			Damaged
		${\sigma _{{\rm{s1}}}} < {\sigma _{{\rm{SMA}}}} < {\sigma _{{\rm{f1}}}}$	No damage
			Damaged
		${\sigma _{{\rm{f1}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	No damage
		${\sigma _{{\rm{f1}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	Damaged
${M^{\rm{f}}} \leqslant {T_0} < {M^{\rm{s}}}$	Martensite	$0 \leqslant {\sigma _{{\rm{SMA}}}} \leqslant {\sigma _{{\rm{s1}}}}$	No damage	$0 \leqslant {\sigma _{{\rm{SMA}}}}$
			Damaged
		${\sigma _{{\rm{s1}}}} < {\sigma _{{\rm{SMA}}}} < {\sigma _{{\rm{f1}}}}$	No damage
			Damaged
		${\sigma _{{\rm{f1}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	No damage
		${\sigma _{{\rm{f1}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	Damaged
${M^{\rm{s}}} \leqslant {T_0} < {A^{\rm{s}}}$	Martensite	$0 \leqslant {\sigma _{{\rm{SMA}}}}$	No damage	$0 \leqslant {\sigma _{{\rm{SMA}}}}$
${M^{\rm{s}}} \leqslant {T_0} < {A^{\rm{s}}}$	Martensite	$0 \leqslant {\sigma _{{\rm{SMA}}}}$	Damaged	$0 \leqslant {\sigma _{{\rm{SMA}}}}$
${A^{\rm{s}}} \leqslant {T_0} < {A^{\rm{f}}}$	Martensite and austenite mixed	$0 \leqslant {\sigma _{{\rm{SMA}}}} \leqslant {\sigma _{{\rm{s4}}}}$	No damage	${\sigma _{{\rm{SMA}}}} \geqslant {\sigma _{{\rm{As4}}}}$		$0 \leqslant {\sigma _{{\rm{SMA}}}} < {\sigma _{{\rm{As4}}}}$
			Damaged
		${\sigma _{{\rm{s4}}}} < {\sigma _{{\rm{SMA}}}} < {\sigma _{{\rm{f4}}}}$	No damage
			Damaged
		${\sigma _{{\rm{f4}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	No damage
		${\sigma _{{\rm{f4}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	Damaged
${A^{\rm{f}}} \leqslant {T_0}$	Austenite	$0 \leqslant {\sigma _{{\rm{SMA}}}} \leqslant {\sigma _{{\rm{s5}}}}$	No damage	$\begin{array}{l} {\sigma _{{\rm{SMA}}}} \\ \geqslant {\sigma _{{\rm{As5}}}} \end{array}$	$\begin{array}{l} {\sigma _{{\rm{Af5}}}} < {\sigma _{{\rm{SMA}}}} \\ < {\sigma _{{\rm{As5}}}} \end{array}$		$\begin{array}{l} 0 \leqslant {\sigma _{{\rm{SMA}}}} \\ \leqslant {\sigma _{{\rm{Af5}}}} \end{array}$
			Damaged
		${\sigma _{{\rm{s5}}}} < {\sigma _{{\rm{SMA}}}} < {\sigma _{{\rm{f5}}}}$	No damage
			Damaged
		${\sigma _{{\rm{f5}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	No damage
		${\sigma _{{\rm{f5}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	Damaged
Notes: M^f−Martensitic transformation completion temperature; M^s−Martensitic transformation start temperature; A^s−Austenite transformation start temperature; A^f−Austenite transformation completion temperature; σ_SMA—Stress of the SMA; ${\sigma _{{\rm{s1}}}},{\sigma _{{\rm{f1}}}}$ —SMA begins and completes redirection to critical stress; ${\sigma _{{\rm{f2}}}}$ —SMA completes the critical stress of martensitic transformation in M^f≤T₀＜M^s; ${\sigma _{{\rm{s3}}}},{\sigma _{{\rm{f3}}}}$ —Critical stress for the initiation and completion of martensitic transformation in M^f≤T₀＜A^s of SMA; ${\sigma _{{\rm{s4}}}},{\sigma _{{\rm{f4}}}}$ , ${\sigma _{{\rm{As}}4}},{\sigma _{{\rm{Af4}}}}$ —SMA begins and completes martensitic transformation and austenitic transformation in A^s≤T₀＜A^f section; ${\sigma _{{\rm{s5}}}},{\sigma _{{\rm{f5}}}},{\sigma _{{\rm{As5}}}},{\sigma _{{\rm{Af5}}}}$ —SMA begins and completes martensitic transformation and austenitic transformation in A^f≤T₀ section.

下载: 导出CSV

表 2 对初始状态为高温奥氏体相的SMA降温过程中的情况分类

Table 2 Classification of the conditions during the cooling process of the SMA whose initial state is high-temperature austenite phase

Temperature section	SMA initial state	Loading phase	Composite material	Uninstall phase
${T_0} < {M^{\rm{f}}}$	Martensite	$0 \leqslant {\sigma _{{\rm{SMA}}}} \leqslant {\sigma _{{\rm{s1}}}}$	No damage	$0 \leqslant {\sigma _{{\rm{SMA}}}}$
			Damaged
		${\sigma _{{\rm{s1}}}} < {\sigma _{{\rm{SMA}}}} < {\sigma _{{\rm{f1}}}}$	No damage
			Damaged
		${\sigma _{{\rm{f1}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	No damage
		${\sigma _{{\rm{f1}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	Damaged
${M^{\rm{f}}} \leqslant {T_0} < {M^{\rm{s}}}$	Martensite and austenite mixed	$0 \leqslant {\sigma _{{\rm{SMA}}}} < {\sigma _{{\rm{f2}}}}$	No damage	$0 \leqslant {\sigma _{{\rm{SMA}}}}$
			Damaged
		${\sigma _{{\rm{f2}}}} \leqslant {\sigma _{{\rm{SMA}}}} < \sigma '_{{\rm{s2}}}$	No damage
			Damaged
		$\sigma' _{{\rm{s2}}} \leqslant {\sigma _{{\rm{SMA}}}} < \sigma' _{{\rm{f2}}}$	No damage
			Damaged
		$\sigma' _{{\rm{f2}}} \leqslant {\sigma _{{\rm{SMA}}}}$	No damage
		$\sigma' _{{\rm{f2}}} \leqslant {\sigma _{{\rm{SMA}}}}$	Damaged
${M^{\rm{s}}} \leqslant {T_0} < {A^{\rm{s}}}$	Austenite	$0 \leqslant {\sigma _{{\rm{SMA}}}} \leqslant {\sigma _{{\rm{s3}}}}$	No damage	$0 \leqslant {\sigma _{{\rm{SMA}}}}$
			Damaged
		${\sigma _{{\rm{s3}}}} < {\sigma _{{\rm{SMA}}}} < {\sigma _{{\rm{f3}}}}$	No damage
			Damaged
		${\sigma _{{\rm{f3}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	No damage
		${\sigma _{{\rm{f3}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	Damaged
${A^{\rm{s}}} \leqslant {T_0} < {A^{\rm{f}}}$	Austenite	$0 \leqslant {\sigma _{{\rm{SMA}}}} \leqslant {\sigma _{{\rm{s4}}}}$	No damage	${\sigma _{{\rm{SMA}}}} \geqslant {\sigma _{{\rm{As4}}}}$		$0 \leqslant {\sigma _{{\rm{SMA}}}} < {\sigma _{{\rm{As4}}}}$
			Damaged
		${\sigma _{{\rm{s4}}}} < {\sigma _{{\rm{SMA}}}} < {\sigma _{{\rm{f4}}}}$	No damage
			Damaged
		${\sigma _{{\rm{f4}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	No damage
		${\sigma _{{\rm{f4}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	Damaged
${A^{\rm{f}}} \leqslant {T_0}$	Austenite	$0 \leqslant {\sigma _{{\rm{SMA}}}} \leqslant {\sigma _{{\rm{s5}}}}$	No damage	$\begin{array}{l} {\sigma _{{\rm{SMA}}}} \\ \geqslant {\sigma _{{\rm{As5}}}} \end{array}$	$\begin{array}{l} {\sigma _{{\rm{Af5}}}} < {\sigma _{{\rm{SMA}}}} \\ < {\sigma _{{\rm{As5}}}} \end{array}$		$\begin{array}{l} 0 \leqslant {\sigma _{{\rm{SMA}}}} \\ \leqslant {\sigma _{{\rm{Af5}}}} \end{array}$
			Damaged
		${\sigma _{{\rm{s5}}}} < {\sigma _{{\rm{SMA}}}} < {\sigma _{{\rm{f5}}}}$	No damage
			Damaged
		${\sigma _{{\rm{f5}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	No damage
		${\sigma _{{\rm{f5}}}} \leqslant {\sigma _{{\rm{SMA}}}}$	Damaged

下载: 导出CSV

表 3 与玻璃纤维/不饱和树脂和SMA有关的材料参数^{[16, 18-19]}

Table 3 Material parameters related to glass fiber/unsaturated resin and SMA^{[16, 18-19]}

M^f/℃	M^s/℃	A^s/℃	A^f/℃	E^A/MPa	E^M/MPa	${\alpha ^{\rm{A}}}$ /℃⁻¹	${\alpha ^{\rm{M}}}$ /℃⁻¹	H/%
−85	−52	0.2	28.4	60 000	25 400	1.1×10⁻⁵	6.6×10⁻⁶	3.5
E_G/MPa	C(MPa·℃⁻¹)	${\sigma _{\rm{G}}}$ /MPa	$\sigma _{\rm{s}}^{{\rm{cr}}}$ /MPa	$\sigma _{\rm{f}}^{{\rm{cr}}}$ /MPa	${\alpha_{\rm{G}} }$ /℃⁻¹
33 400	5	417.1	100	170	3×10⁻⁶
Notes: E^A—Elastic modulus of SMA austenite; E^M—Elastic modulus of SMA martensite; ${\alpha ^{\rm{A}}}$ —Thermal expansion coefficient of SMA austenite; ${\alpha ^{\rm{M}}}$ —Thermal expansion coefficient of SMA martensite; H—Maximum recoverable residual strain; E_G—Elastic modulus of glass fiber unsaturated resin; C—Stress influence factor; ${\sigma _{\rm{G}}}$ —Stress on glass fiber unsaturated resin; $\sigma _{\rm{s}}^{{\rm{cr}}}$ —SMA reorientation starts critical stress; $\sigma _{\rm{f}}^{{\rm{cr}}}$ —SMA reorientation ends critical stress; ${\alpha_{\rm{G}} }$ —Thermal expansion coefficient of glass fiber unsaturated resin.

下载: 导出CSV

表 4 与电阻率有关的材料参数^[20]

Table 4 Material parameters related to resistivity^[20]

${C_{{\rm{M1}}}}$ /(Ω·m·℃⁻¹)	${C_{{\rm{M2}}}}$ /(Ω·m)	${C_{{\rm{A1}}}}$ /(Ω·m·℃⁻¹)	${C_{{\rm{A2}}}}$ /(Ω·m)
7×10⁻¹⁰	0.87×10⁻⁶	8×10⁻¹⁰	0.72×10⁻⁶
Note: ${C_{{\rm{M1}}}}$ , ${C_{{\rm{M2}}}}$ , ${C_{{\rm{A1}}}}$ , ${C_{{\rm{A2}}}}$ —Material parameters related to resistivity.

下载: 导出CSV

参考文献(20)

[1]	杜善义. 先进复合材料与航空航天[J]. 复合材料学报, 2007, 24(1):1-12. DOI: 10.3321/j.issn:1000-3851.2007.01.001 DU S Y. Advanced composite materials and aerospace engineering[J]. Acta Materiae Compositae Sinica,2007,24(1):1-12(in Chinese). DOI: 10.3321/j.issn:1000-3851.2007.01.001
[2]	WU F, YAO W X. A fatigue damage model of composite materials[J]. International Journal of Fatigue,2010,32(1):134-138. DOI: 10.1016/j.ijfatigue.2009.02.027
[3]	EI-SABBAGH A, STEUERNAGEL L, ZIEGMANN G. Characterisation of flax polypropylene composites using ultrasonic longitudinal sound wave technique[J]. Composites: Part B,2013,45:1164-1172. DOI: 10.1016/j.compositesb.2012.06.010
[4]	FREEMANTLE R J, HANKINSON N, BROTHERHOOD C J. Rapid phased array ultrasonic imaging of large area composite aerospace structures[J]. Insight,2005,47(3):129-132. DOI: 10.1784/insi.47.3.129.61315
[5]	RYU C H, PARK S H, KIM D H, et al. Nondestructive evaluation of hidden multi-delamination in a glass-fiber-reinforced plastic composite using terahertz spectroscopy[J]. Composite Structures,2016,156:338-347. DOI: 10.1016/j.compstruct.2015.09.055
[6]	HOSOI A, YAMAGUCHI Y, JU Y, et al. Detection and quantitative evaluation of defects in glass fber reinforced plastic laminates by microwaves[J]. Composite Structures, 2015, 128: 134-144.
[7]	KALYANAVALLI V, ABILASHA R T K, SASTIKUMAR D. Long pulse thermography investigations of basalt fiber reinforced composite[J]. NDT & E International,2018,100:84-91.
[8]	周玉敬, 任明伟, 刘刚, 等. 基于FBG传感技术的复合材料T型加筋板低速冲击损伤监测[J]. 复合材料学报, 2019, 36(10):2266-2274. ZHOU Y J, REN M W, LIU G, et al. Low-velocity impact damage monitoring of composite T-stiffened panels based on FBG sensors[J]. Acta Materiae Compositae Sinica,2019,36(10):2266-2274(in Chinese).
[9]	ZHAO H T, ZHANG B M, WU Z J, et al. Infrastructure study for optical fiber grating in smart composite materials[J]. Transducer and Microsystem Technologies,2007,26(12):27-30.
[10]	KAN Q, KANG G. Constitutive model for uniaxial transformation ratchetting of super-elastic NiTi shape memory alloy at room temperature[J]. International Journal of Plasticity,2010,26(3):441-465. DOI: 10.1016/j.ijplas.2009.08.005
[11]	SUN Q P, HWANG K C. Micromechanics modeling for the constitutive behavior of polycrystalline shape memory alloy[J]. Journal of the Mechanics and Physics of Solids,1993,41(1):1-33. DOI: 10.1016/0022-5096(93)90060-S
[12]	WU X D, FAN Y Z, WU J S. A study on the variations of the electrical resistance for NiTi shape memory alloy wires during the thermo-mechanical loading[J]. Materials & Design,2000,21(6):511-515.
[13]	狄生奎, 韩全治, 李慧, 等. SMA在结构健康监测中的应用研究[J]. 低温建筑技术, 2008(4):58-60. DOI: 10.3969/j.issn.1001-6864.2008.04.027 DI S K, HAN Q Z, LI H, et al. Research on the shape memory alloy applied in structural health monitoring[J]. Low Temperature Architecture Technology,2008(4):58-60(in Chinese). DOI: 10.3969/j.issn.1001-6864.2008.04.027
[14]	狄生奎, 花尉攀, 汲生伟, 等. 约束态SMA混凝土梁的裂缝监测及自修复[J]. 建筑材料学报, 2010, 13(2):237-242. DOI: 10.3969/j.issn.1007-9629.2010.02.021 DI S K, HUA W P, JI S W, et al. Self-monitoring and self-repairing of crack in concrete beam with constraint super-elastic SMA[J]. Journal of Building Materials,2010,13(2):237-242(in Chinese). DOI: 10.3969/j.issn.1007-9629.2010.02.021
[15]	袁江, 邱自学, 邵建新, 等. 基于无线射频识别传感标签的形状记忆合金增强复合结构低速冲击响应监测[J]. 机械工程学报, 2012, 48(18):89-96. DOI: 10.3901/JME.2012.18.089 YUAN J, QIU Z X, SHAO J X, et al. Low speed impact test for shape memory alloy-reinforced composite structure based on radio frequency idebtification sensortags[J]. Journal of Mechanical Engineering,2012,48(18):89-96(in Chinese). DOI: 10.3901/JME.2012.18.089
[16]	王庆菲. SMA智能混凝土的裂缝监测与自修复理论研究[D]. 天津: 中国民航大学. 2020. WANG Q F. Theoretical research on crack monitoring and self-repairing mechanism for SMA intelligent concrete materials[D]. Tianjin: Civil Aviation University of China, 2020(in Chinese).
[17]	IKUTA K, TSUKAMOTO M, HIROSE S. Institute of electric and electronic engineer. mathematical model and experimental verification of shape memory alloy for designing micro actuator[C]//Micro Electro Mechanical Systems, 1991, MEMS '91, Proceedings. An Investigation of Micro Structures, Sensors, Actuators, Machines and Robots. IEEE. 1991: 103-108.
[18]	BRINSON L C. One-dimensional constitutive behavior of shape memory alloys: Thermomechanical derivation with non-constant material functions and redefined martensite internal variable[J]. Journal of Intelligent Material Systems and Structures,1993,4(2):229-242. DOI: 10.1177/1045389X9300400213
[19]	詹瑒. 纤维增强复合材料(FRP)格构柱基本性能研究[D]. 南京: 东南大学. 2016. ZHAN Y. Performance evaluation of lattice columns using pultruded fiber-reinforced polymer(FRP) structurak profiles[D]. Nanjing: Southeast University, 2016(in Chinese).
[20]	崔迪, 李宏男, 宋钢兵. NiTi形状记忆合金电阻特性研究[J]. 建筑材料学报, 2008(5):68-74. CUI D, LI H N, SONG G B. Study on electrical resistance properties of NiTi shape memory alloy[J]. Journal of Building Materials,2008(5):68-74(in Chinese).

施引文献(3)

期刊类型引用(3)

1.	何初生，王文炜，姜进科，张吴桐. 基于Arduino的SMA丝材智能修复损伤钢筋混凝土梁试验研究. 桥梁建设. 2024(01): 61-67 . 百度学术
2.	覃清玥，李岩，张文学，陈富琨. 大跨径预应力混凝土连续梁桥加固研究进展. 建材技术与应用. 2024(03): 49-57 . 百度学术
3.	甄静水，王文炜，蔡德成，杜洋洋，间冀明，余雄飞. SMA/预应力CFRP片材增强混凝土梁全过程受力性能分析. 中国科技论文. 2024(10): 1097-1104 . 百度学术