Review on buckling and post-buckling of stiffened composite panels
-
摘要:
复合材料加筋板因其卓越的轻质、高强度和高刚度特性，在航空航天领域的飞机承力构件中得到了广泛应用。随着对材料性能要求的不断提升，深入理解这类结构的屈曲与后屈曲行为变得尤为重要。本文综述了国内外复合材料加筋板屈曲及后屈曲性能的研究进展，系统归纳了理论方法、有限元仿真技术及实验研究方法。研究表明：加筋板的几何参数(如加筋高度和间距)及层合板的铺层顺序显著影响其屈曲性能；同时，考虑材料非线性和几何非线性对准确预测后屈曲行为至关重要。此外，本文探讨了预测复合材料加筋板屈曲和后屈曲失效模式及载荷的关键技术难点。通过分析现有研究的局限性，本文指出了未来可能的研究方向，为复合材料加筋板的屈曲与后屈曲研究及其工程应用提供了理论基础和实践指导。
Abstract:Composite stiffened panels are widely used in aircraft load-bearing components in the aerospace field due to their excellent lightweight, high strength and high stiffness properties. With the continuous improvement of material performance requirements, it is particularly important to have a deep understanding of the buckling and post-buckling behavior of such structures. This article reviews the research progress on buckling and post-buckling properties of composite stiffened panels, and systematically summarizes theoretical approach, finite element simulation technology and experimental research methods. Studies have shown that the geometric parameters (such as height and spacing of stiffeners) and lay-up sequence of stiffened panels significantly affect the buckling performance. At the same time, considering material nonlinearity and geometric nonlinearity is crucial to accurately predict post-buckling behavior. In addition, this article explores the key technical difficulties in predicting buckling and post-buckling failure modes and loads of composite stiffened panels. By analyzing the limitations of existing researches, this article points out possible future research directions, providing a theoretical basis and practical guidance for buckling and post-buckling research on composite stiffened panels and their engineering applications.
-
我国的淡水和河砂资源短缺，但海水和海砂资源十分丰富，这使海水海砂混凝土(Seawater sea-sand concrete，SSC)的研究受到广泛关注[1-3]。由于海水和海砂的掺入，SSC中的氯离子含量较高，容易引发钢筋锈蚀，导致结构使用寿命变短。为此，研究人员引入轻质高强、耐腐蚀性的纤维增强树脂复合材料(Fiber reinforced polymer，FRP)筋[4]替代钢筋，使之与SSC组合。然而，由于FRP筋的弹性模量较低且界面光滑，FRP筋增强SSC结构的裂缝宽度控制能力弱，在正常使用极限状态下通常表现出较大的裂缝宽度[5]，结构耐久性再次受到挑战。另一方面，由于FRP材料的弹脆性，FRP筋不容易弯折，难以现场加工。工程中常见的箍筋往往需要厂家专门制作，这一定程度上影响了FRP筋的广泛应用。此外，FRP箍筋的弯折区域往往是其薄弱点，在受力过程中容易出现过早破坏的情况。
高延性纤维增强水泥基复合材料(Engineered cementitious composites，ECC)的控裂能力突出，单轴受拉状态下的平均裂缝宽度约为0.06 mm[6]。《纤维增强复合材料工程应用技术规范》(GB 50608—2020)[7]规定FRP筋增强混凝土结构的最大裂缝宽度限值为0.5 mm。这表明FRP筋与ECC组合可以较容易地满足规范对裂缝宽度的要求。另一方面，ECC的单轴受拉变形能力优异(通常大于2%[6])，与FRP筋的拉伸变形能力处于同一数量级。同普通混凝土相比，ECC和FRP筋的拉伸变形能力更接近。并且，受拉开裂后的ECC可通过纤维桥接作用持续提供抗力。因此，ECC和FRP筋组合后将拥有相对更好的协调变形能力。
从现有的文献来看，关于FRP筋增强ECC梁的研究偏少且以研究受弯性能为主[8-11]，少量关于抗剪性能的研究成果如下：Li等[8]以剪跨比和纵筋配筋率为变量试验研究了玻璃纤维增强树脂复合材料(Glass fiber reinforced polymer，GFRP)筋增强ECC梁的弯剪性能。结果表明，与高强混凝土梁相比，ECC梁在延性、承载力和损伤容忍度等方面都有显著提高。此外，Yuan等[9]通过四点加载试验发现，无腹筋玄武岩纤维增强树脂复合材料(Basalt fiber reinforced polymer，BFRP)筋增强ECC梁的极限承载力和变形能力与配箍率约为0.51%的BFRP筋增强混凝土梁相当，初步证明采用ECC材料减小配箍率是可行的。但是，以上研究均未以海水海砂ECC(Seawater sea-sand ECC，SSE)为研究对象。
为探究海水海砂ECC梁的抗剪性能，本文采用海水和海砂研制SSE，并对BFRP筋增强海水海砂ECC梁(BFRP/SSE梁)进行剪切试验，分析配箍率和剪跨比对梁破坏形态、抗剪承载力和裂缝宽度等的影响。此外，通过有限元软件ABAQUS研究SSE材料力学性能对无腹筋BFRP/SSE梁抗剪承载力的影响规律。
1. 海水海砂ECC力学性能
1.1 原材料和配合比
SSE的配合比见表1。SSE-0.18、SSE-0.21和SSE-0.27分别是水胶比为0.18、0.21和0.27的海水海砂ECC。作为对照组的SSM-0.21(Seawater sea-sand mortar，SSM)，是采用海水和海砂等材料制备的水泥砂浆，其水胶比与SSE-0.21相同。试验采用的胶凝材料包括普通硅酸盐水泥、石灰石粉(Limestone powder，LP)、硅灰(Silica fume，SF)、粒化高炉矿渣(Ground granulated blast furnace slag，GGBFS)。粒径不超过0.21 mm的海砂被作为细骨料使用。配制人工海水用于拌和混凝土。采用聚羧酸减水剂(Polycarboxylate superplasticizer，PS)以提高拌合物的流动度。
表 1 海水海砂高延性纤维增强水泥基复合材料(SSE)配合比Table 1. Mixing proportions of seawater sea-sand engineered cementitious composites (SSE)Mixture ID Binder material Sea-sand/wt% Seawater/wt% PS/wt% PE fiber/vol% Cement/wt% LP/wt% SF/wt% GGBFS/wt% SSE-0.18 1.00 0.14 0.21 1.07 1.04 0.44 0.015 1.5 SSE-0.21 1.00 0.14 0.21 1.07 1.04 0.51 0.015 1.5 SSE-0.27 1.00 0.14 0.21 1.07 1.04 0.65 0.015 1.5 SSM-0.21 1.00 0.14 0.21 1.07 1.04 0.51 0.015 — Notes: SSE-x—SSE with water/binder ratio of x; SSM-0.21—Seawater sea-sand mortar with water/binder ratio of 0.21; LP—Limestone powder; SF—Silica fume; GGBFS—Ground granulated blast furnace slag; PS—Polycarboxylate superplasticizer; PE—Polyethylene. 聚乙烯(PE)纤维相比聚乙烯醇(PVA)纤维不仅具有更高的抗拉强度和弹性模量，而且裂缝桥接能力也更强[12]。因此，PE/ECC通常比PVA/ECC的抗拉强度和拉伸应变能力更大。这将有利于提升FRP筋增强混凝土梁的抗剪承载力和延性等。此外，PE纤维具有良好的抗氯离子侵蚀性能[12]。海水海砂PE/ECC和淡水河砂PE/ECC显示出相近的力学性能[13]。鉴于此，SSE中使用PE纤维，纤维体积分数为1.5vol%。采用的PE纤维直径为24 μm，长度为18 mm，密度为0.97 g/cm3，抗拉强度为2900 MPa，弹性模量为116 GPa。
1.2 材料试验方法
SSE和SSM-0.21在自然环境中养护28天后进行单轴拉伸试验、单轴压缩试验和弯曲试验，见图1。试件尺寸、位移计布置和加载速率如下所述。值得一提的是，试验采用数字图像相关(Digitalimage correlation，DIC)技术[14]来监测混凝土的裂缝开展情况。
根据JSCE[15]的建议，单轴拉伸试验采用狗骨试件，具体尺寸见文献[16]。如图1(a)所示，2个线性差动变压器(Linear variable differential transformer，LVDT)用于测量试件的轴向拉伸变形，标距为80 mm。试验采用位移控制加载，速率为2 mm/min。
![]()
图 1 材料试验加载装置Figure 1. Setup for material testLVDT—Linear variable differential transformer单轴压缩试验采用棱柱体试件，尺寸为300 mm×100 mm×100 mm。通过2个LVDT监测试件的轴向压缩变形，标距为100 mm，见图1(b)所示。采用荷载控制进行加载，速率为0.5 MPa/s。
如图1(c)所示，弯曲试验采用尺寸为160 mm×40 mm×40 mm的棱柱体试件。跨度为150 mm，支座到加载点的距离为50 mm。通过在跨中布置2个LVDT来测量试件的挠曲变形。与单轴拉伸试验相同，弯曲试验也采用位移控制加载，其速率为2 mm/min。
1.3 材料试验结果及分析
1.3.1 受拉力学性能
如图2所示，SSE单轴受拉破坏形态呈多缝开裂的特点，平均裂缝宽度约为0.2 mm。相反，SSM-0.21破坏时只有一条裂缝出现，平均裂缝宽度为0.52 mm。值得注意的是，以上的平均裂缝宽度是指抗拉强度对应的裂缝宽度平均值。单轴受拉应力-应变曲线表明，SSE表现出明显的应变硬化特点。如图3所示，随水胶比增加，SSE的抗拉强度(平均值，下同)降低，但拉伸应变能力基本提高。这是由于水胶比增加导致基体的强度和断裂韧度降低，SSE的基体更容易开裂。与SSM-0.21相比，SSE显示出优越的抗拉强度和变形能力。例如，在水胶比相同的情况下(即SSE-0.21和SSM-0.21)，抗拉强度提高了79%，拉伸应变能力提高上百倍。这主要是由于纤维提供的桥接作用使SSE经历较长的应变硬化过程。值得一提的是，就拉伸变形能力而言，SSE与FRP筋处于同一水平。
![]()
图 2 SSE单轴受拉应力-应变曲线及破坏形态Figure 2. Tensile stress-strain curves and failure mode of SSE1.3.2 受压力学性能
SSE单轴受压破坏形态见图4。与一般的纤维混凝土类似，SSE受压无剥落破坏发生，保持良好的整体性。此外，SSE受压也表现出多缝开裂的特点。与抗拉强度随水胶比变化的规律相似，水胶比增加，SSE抗压强度降低，见图5。同普通ECC[17]类似，SSE的受压变形能力很强，抗压强度对应的应变约为0.0036。然而，普通混凝土达抗压强度时的应变仅为0.002 (SSE提高幅度约为80%)。
![]()
图 4 SSE单轴受压应力-应变曲线及破坏形态Figure 4. Compressive stress-strain curves and failure mode of SSE1.3.3 受弯力学性能
如图6所示，SSE受弯有明显的多缝开裂特征，并且裂缝数量随水胶比增加而增加。图7为弯曲荷载-挠度曲线，SSE呈明显的挠度硬化特点。随水胶比增加，抗弯强度(图5)降低，但对应的挠度增加。与SSM-0.21相比，SSE的抗弯强度和弯曲变形能力明显提高。
以上表明，SSE与SSM-0.21相比拥有优异的拉伸性能和弯曲性能及良好的受压变形能力。此外，与文献[9]中使用的ECC材料相比，本文研制的SSE抗拉强度更高，拉伸变形能力更好。因此，海水海砂ECC梁有望展现出更好的抗剪性能。
2. BFRP/SSE梁的剪切性能
2.1 BFRP/SSE梁剪切试验概况
2.1.1 试件设计与制作
剪切试验的试件包括BFRP/SSE梁和BFRP筋增强水泥砂浆梁(BFRP/SSM梁)。其中，4根为BFRP/SSE梁(BFRP/SSE-00-1.9、BFRP/SSE-37-1.9、BFRP/SSE-00-1.3和BFRP/SSE-37-1.3)，2根为BFRP/SSM梁(BFRP/SSM-67-1.9和BFRP/SSM-67-1.3)，如表2所示。试验变量为剪跨比和配箍率，采用的剪跨比为1.9和1.3，配箍率为0和0.37%。所有梁的跨度、高度和宽度都相同，分别为900 mm、200 mm和150 mm。截面有效高度均为160 mm。纵向受拉筋和架立筋也都相同，分别是3根直径18 mm的BFRP筋和2根直径8 mm的BFRP筋。BFRP筋力学性能见表3，外观照片见图8。筋材的拉伸应变能力最大为2.32%，比SSE的拉伸变形能力弱。试件尺寸及截面配筋情况详见图9。
表 2 玄武岩纤维增强树脂复合材料(BFRP)/SSE梁和BFRP筋增强水泥砂浆(BFRP/SSM)梁试件的主要参数Table 2. Main parameters of basalt fiber reinforced polymer (BFRP)/SSE beam and BFRP reinforced seawater sea-sand mortar (BFRP/SSM) beam specimensSpecimen ID Span/
mmShear span/
mmShear span
ratioHeight/
mmWidth/
mmCover
thickness/mmConcrete Stirrup
ratio/%Longitudinal tensile
reinforcement ratio/%BFRP/SSM-67-1.9 900 300 1.9 200 150 23 SSM-0.21 0.67 3.17 BFRP/SSE-00-1.9 900 300 1.9 200 150 31 SSE-0.21 — 3.17 BFRP/SSE-37-1.9 900 300 1.9 200 150 25 SSE-0.21 0.37 3.17 BFRP/SSM-67-1.3 900 200 1.3 200 150 23 SSM-0.21 0.67 3.17 BFRP/SSE-00-1.3 900 200 1.3 200 150 31 SSE-0.21 — 3.17 BFRP/SSE-37-1.3 900 200 1.3 200 150 25 SSE-0.21 0.37 3.17 Notes: BFRP/SSE-y—x—SSE with shear span ratio of x and stirrup ratio of y; BFRP/SSM-y—x—Seawater sea-sand mortar with shear span ratio of x and stirrup ratio of y. 表 3 FRP筋力学性能指标Table 3. Mechanical properties of FRP barsType of FRP bar Diameter/mm Elastic modulus/GPa Tensile strength/MPa Tensile strain capacity/% BFRP bar 6 53 1190 2.22 8 57 1127 2.14 18 57 1319 2.32 采用的基体材料为SSE-0.21和SSM-0.21，具体配合比见表1。浇筑试验梁的同时，制作伴随试块，并与梁在同条件下养护90天。测得SSE-0.21和SSM-0.21的抗拉强度分别为6.56 MPa和5.54 MPa，拉伸应变能力为3.92%和0.02%，立方体抗压强度(边长为100 mm)为45 MPa和44 MPa。
2.1.2 加载装置与加载方案
通过四点加载进行剪切试验，加载示意见图9。加载设备为济南川佰仪器设备有限公司生产的电液伺服万能试验机，最大加载力为1000 kN。采用LVDT监测试件的跨中挠度，量程为0~80 mm。单反相机拍照记录试验过程中梁剪跨段的裂缝发展情况，在试验结束后借助DIC分析软件得到裂缝图。此外，加载过程中采用裂缝宽度测量仪监测裂缝宽度。试验以位移控制进行加载，速率为1 mm/min。
![]()
图 9 BFRP/SSE梁和BFRP/SSM梁试件尺寸及配筋Figure 9. Details of BFRP/SSE and BFRP/SSM beam specimens2.2 BFRP/SSE梁剪切试验结果及分析
2.2.1 破坏形态
由于试验采用的纵筋配筋率很高(3.17%)，试件最终因BFRP箍筋断裂或基体材料失效而破坏。破坏模式均为剪切破坏，图10显示了部分代表性试件的破坏形态。在临近破坏时，BFRP/SSM梁剥落破坏严重，甚至在剪跨段内有部分BFRP筋外露的情况出现。与此相反，SSE中的纤维桥接作用使BFRP/SSE梁始终无剥落破坏出现，保持良好的整体性。与BFRP/SSM梁相比，BFRP/SSE梁剪跨段的裂缝数量明显更多，裂缝宽度更小。其中，BFRP/SSE梁裂缝数量多是由于SSE材料自身具有多缝开裂的特点，见图2、图4和图6。在卸载过程中发现，BFRP/SSM梁和BFRP/SSE梁均出现明显的弹性恢复变形。由于后者的裂缝宽度较小，卸载后部分裂缝甚至完全闭合。
![]()
图 10 BFRP/SSE梁和BFRP/SSM梁剪跨段的典型破坏形态Figure 10. Typical failure modes of BFRP/SSE and BFRP/SSM beams in shear span2.2.2 荷载-跨中挠度曲线
试件的荷载-跨中挠度曲线见图11。试件BFRP/SSE-37-1.3的曲线并未被显示，是因为试验过程中LVDT发生故障，导致挠度未被有效记录。由于BFRP筋的线弹性力学特点，荷载-跨中挠度曲线没有出现明显的屈服点。与试件BFRP/SSM-67-1.9相比，试件BFRP/SSE-00-1.9和BFRP/SSE-37-1.9的抗剪承载力分别提升6.37%和59.32%。试件BFRP/SSE-00-1.3和BFRP/SSE-37-1.3的抗剪承载力比试件BFRP/SSM-67-1.3的高73.68%和99.25%。表明采用SSE减小箍筋用量后，梁的抗剪承载力提高，尤其是剪跨比较小时。这是由于纤维通过桥接作用在梁开裂后的斜裂缝面上持续提供剪切抗力，并且纤维的剪切承载力贡献占抗剪承载力的绝大部分[18]。此外，随剪跨比减小，BFRP/SSE梁和BFRP/SSM梁的抗剪承载力均增加。这是由于随剪跨比减小抗剪承载力从主要由混凝土抗拉强度控制逐渐转变为抗压强度控制。采用BFRP箍筋后，BFRP/SSE梁的抗剪承载力增加14.72%~49.77%。
![]()
图 11 BFRP/SSE梁和BFRP/SSM梁荷载-跨中挠度曲线Figure 11. Load versus mid-span deflection curves of BFRP/SSE and BFRP/SSM beams构件的变形过大会妨碍建筑物的使用功能，而变形能力与刚度密切相关。与试件BFRP/SSM-67-1.3相比，试件BFRP/SSE-00-1.3的刚度明显更大，且达峰值荷载时的跨中挠度也更小。试件BFRP/SSE-00-1.9、BFRP/SSE-37-1.9和BFRP/SSM-67-1.9显示出类似的结果。这说明采用SSE材料后可以提高梁的刚度且减小变形。分析认为，受拉开裂后的SSE通过纤维桥接作用继续提供剪切抗力，但水泥砂浆开裂后基本退出工作，这使BFRP/SSE梁的实际有效截面相对更大。
2.2.3 荷载-裂缝宽度曲线
如图12所示，BFRP/SSM梁的裂缝宽度随荷载增加而明显变大，表现出较差的裂缝宽度控制能力。与此相反，由于SSE具有通过多缝开裂实现复合材料优异控裂能力的特点，BFRP/SSE梁的裂缝宽度随荷载增加不明显。Tomlinson等[19]通过将峰值荷载除以1.5得到BFRP筋增强混凝土梁正常使用极限状态的荷载(梁自重很小，可忽略不计)。本文采用这种方法确定BFRP/SSE梁和BFRP/SSM梁的使用荷载，见表4，并在图12中指出相应的裂缝宽度。标准GB 50608—2020[7]规定的最大裂缝宽度限值为0.5 mm，BFRP/SSE梁在正常使用极限状态时的裂缝宽度不大于0.3 mm，满足裂缝宽度要求。然而，BFRP/SSM梁的裂缝宽度过大，部分试件(即BFRP/SSM-67-1.9的裂缝宽度大于0.7 mm)已不满足裂缝宽度的要求。以上结果表明，当采用控裂能力突出的SSE材料后，梁的控裂能力显著增强。
![]()
图 12 BFRP/SSE梁和BFRP/SSM梁荷载-裂缝宽度曲线Figure 12. Load-crack width curves of BFRP/SSE and BFRP/SSM beams表 4 BFRP/SSE梁和BFRP/SSM梁的特征荷载Table 4. Characteristic loads of the tested BFRP/SSE and BFRP/SSM beamsSpecimen ID Cracking load/kN Shear capacity/kN Shear capacity/Cracking load Service load/kN BFRP/SSM-67-1.9 11.5 106.37 9.25 141.82 BFRP/SSE-00-1.9 11.0 113.15 10.29 150.87 BFRP/SSE-37-1.9 12.5 169.47 13.56 225.96 BFRP/SSM-67-1.3 9.0 123.54 13.73 164.71 BFRP/SSE-00-1.3 16.5 214.56 13.00 286.08 BFRP/SSE-37-1.3 16.0 246.15 15.38 328.20 Notes: Shear capacity is equal to half of peak load. Service load is equal to the peak load divided by 1.5. 将试件BFRP/SSE-00-1.9与BFRP/SSE-00-1.3(BFRP/SSE-37-1.9与BFRP/SSE-37-1.3)进行对比，可知剪跨比对梁在正常使用极限状态时的裂缝宽度基本没有影响。此外，通过比较试件BFRP/SSE-00-1.9与BFRP/SSE-37-1.9(BFRP/SSE-00-1.3与BFRP/SSE-37-1.3)后发现，采用箍筋后BFRP/SSE梁在正常使用极限状态时的裂缝宽度变大，这可能是由于箍筋会影响邻近纤维的分散，使SSE桥接裂缝的能力受到影响，最终导致复合材料的控裂能力变弱。
2.2.4 最小配箍率
最小配箍率是为保证梁在剪切开裂后有足够的富余剪切承载能力和正常使用极限状态下的斜裂缝宽度满足要求[20]。如表4所示，与BFRP/SSM梁相比，BFRP/SSE梁的抗剪承载力/开裂荷载比值明显更大。这说明尽管BFRP/SSE梁的配箍率低，但依然具有优良的开裂后剪切承载能力。无腹筋BFRP/SSE梁的抗剪承载力/开裂荷载比值较高(大于10)。出现以上结果的原因为，SSE受拉开裂后能持续提供剪切抗力，以及纤维的剪切承载力贡献占梁抗剪承载力的绝大部分[18]。此外，BFRP/SSE梁在正常使用极限状态时的裂缝宽度小于0.3 mm，见图12，满足规范GB 50608—2020[7]要求。因此，BFRP/SSE梁的最小配箍率可以由海水海砂ECC来保证而不需另外考虑。
2.3 BFRP/SSE梁受剪有限元模拟
2.3.1 材料模型
混凝土塑性损伤(Concrete damaged plasticity，CDP)模型可以模拟材料的非弹性行为和材料断裂过程中发生的不可逆连续介质损伤。因此，在SSE的材料本构模型中选用了CDP模型。如图2所示，与普通ECC[13]类似，SSE单轴受拉表现出明显的应变硬化现象，故单轴受拉应力
σt -应变εt 本构关系采用Han等[21]提出的三折线模型，文献[22]也采用该模型模拟ECC的单轴受拉应力-应变本构关系：σt={Eεt0⩽ (1) 式中：
E 为混凝土的弹性模量；{\sigma _{{\rm{t}}0}} 和{\varepsilon _{{\rm{t}}0}} 为混凝土受拉的初裂应力和应变；{\sigma _{{\rm{tp}}}} 和{\varepsilon _{{\rm{tp}}}} 为抗拉强度及对应的拉应变；{\varepsilon _{{\rm{tu}}}} 为极限拉应变，即拉应力为0时的应变。SSE单轴受压本构关系采用Carreira和Chu[23]提出的材料模型进行计算，模型的应力
{\sigma _{\rm{c}}} -应变{\varepsilon _{\rm{c}}} 关系用下式表示：\frac{{{\sigma _{\rm{c}}}}}{{\sigma _{\rm{c}}'}}{\rm{ = }}\frac{{\beta ({\varepsilon _{\rm{c}}}/\varepsilon _{\rm{c}}')}}{{\beta - 1 + {{({\varepsilon _{\rm{c}}}/\varepsilon _{\rm{c}}')}^\beta }}} (2) 式中：
\sigma _{\rm{c}}' 和\varepsilon _{\rm{c}}' 分别为抗压强度及对应的压应变；\beta 为取决于混凝土受压应力-应变曲线形状的材料参数，可以通过下式计算：\beta {\rm{ = }}{\left(\frac{{\sigma _{\rm{c}}'}}{{32.4}}\right)^3} + 1.55 (3) 与混凝土这种弹塑性材料不同，BFRP筋是一种线弹性材料，单轴受拉应力
{\sigma _{\rm{f}}} -应变{\varepsilon _{\rm{f}}} 曲线呈线性。其本构关系如下：{\sigma _{\rm{f}}}{\rm{ = }}{E_{\rm{f}}}{\varepsilon _{\rm{f}}} (4) 式中：
{E_{\rm{f}}} 为BFRP筋的弹性模量。2.3.2 有限元计算模型
通过有限元软件ABAQUS建立模型，SSE和BFRP筋分别采用C3D8R单元和T3D2单元。借助Embedded命令将BFRP筋笼嵌入到SSE中，不考虑SSE与筋材之间的粘结滑移。综合考虑计算精度和效率，网格尺寸设为20 mm。加载点和支座处设置尺寸为40 mm×20 mm×150 mm的刚性垫块，单元采用C3D8R。垫块与梁之间通过Tie约束将两者的接触面进行耦合，加载点与垫块顶面采用Coupling进行耦合。梁端为简支边界条件，支座约束设置在支座垫块底面的中线上。
2.3.3 模拟结果与试验结果对比
为验证上述有限元模型的可靠性，将BFRP/SSE梁的模拟结果与相应的试验结果进行对比分析。图13为BFRP/SSE梁的等效塑性应变云图。可见，梁的裂缝主要集中在剪跨段且发生剪切破坏，这与试验中梁的裂缝分布和破坏模式吻合(图10)。此外，如表5所示，与试验得到的抗剪承载力和跨中挠度相比，模拟结果的偏差均不超过±8%。因此，模拟结果与试验结果吻合良好，本文建立的有限元模型合理。
![]()
图 13 BFRP/SSE梁等效塑性应变云图Figure 13. Distribution of equivalent plastic strain of BFRP/SSE beams表 5 BFRP/SSE梁模拟结果与试验结果的比较Table 5. Comparison between simulation results and experimental results of BFRP/SSE beamsSpecimen ID Shear capacity/kN Mid-span deflection at shear capacity/mm Experimental
resultSimulation
resultDeviation/
%Experimental
resultSimulation
resultDeviation/
%BFRP/SSE-00-1.9 113.15 104.31 −7.81 9.70 9.61 −0.93 BFRP/SSE-37-1.9 169.47 166.93 −1.50 10.81 11.17 3.33 BFRP/SSE-00-1.3 214.56 214.13 −0.20 8.75 9.40 7.43 BFRP/SSE-37-1.3 246.15 241.70 −1.81 — 10.86 — 图13表明，与试件BFRP/SSE-00-1.9相比，试件BFRP/SSE-37-1.9的海水海砂ECC在纯弯段受压区损伤更加明显。这是由于试件BFRP/SSE-37-1.9采用0.37%的配箍率后剪跨段具有更高的抗剪承载力，其纯弯段承受更大的弯矩作用及梁的纵筋配筋率很高(纵筋不易断裂)。
2.3.4 参数分析
鉴于SSE具有优异的拉伸性能和良好的压缩性能，对SSE抗拉强度、拉伸应变能力和抗压强度进行研究，分析这3个参数对无腹筋BFRP/SSE梁抗剪承载力的影响。参数分析采用的梁尺寸见图9。纵向受拉筋为3根直径18 mm的BFRP筋，架立筋为2根直径8 mm的BFRP筋，筋材力学性能见表3。参数分析以试件BFRP/SSE-00-1.9和BFRP/SSE-00-1.3为基础，其结果如图14所示。当剪跨比从1.3增加到1.9时，梁的抗剪承载力明显减小，这与试验所得规律类似(图11)。
由文献[15]可知，ECC梁抗剪承载力主要由筋材、水泥基材料和纤维组成。其中，纤维所提供的抗剪承载力为
{V_{\rm{f}}}{\rm{ = }}\frac{{{f_{\rm{t}}}bz}}{{\tan \theta }} (5) 式中：
{f_{\rm{t}}} 为ECC材料的抗拉强度；b 为梁截面宽度；z 为受压区作用点到受拉筋中心点之间的距离；\theta 为剪切斜裂缝的倾斜角，通常取45°。因此，随SSE抗拉强度的提高，无腹筋BFRP/SSE梁抗剪承载力缓慢增加，见图14(a)。如图14(b)所示，当SSE拉伸应变能力从4%增加到12%时，梁的抗剪承载力基本不变，表明拉伸应变能力对抗剪承载力基本没有影响。另一方面，纤维掺量与拉伸应变能力通常呈正相关关系[24]，而纤维成本占ECC制备成本的50%以上。因此，可以考虑通过适当减少纤维掺量来降低海水海砂ECC梁的建造成本。
![]()
图 14 各参数对BFRP/SSE梁抗剪承载力的影响Figure 14. Influence of various parameters on shear capacity of BFRP/SSE beams与SSE抗拉强度和拉伸应变能力相比，抗压强度对梁抗剪承载力的影响更加明显，如图14(c)所示。随SSE抗压强度增加，抗剪承载力明显提高。即，抗压强度从30 MPa增加到70 MPa，抗剪承载力提高29.23%(剪跨比为1.9)和19.75%(剪跨比为1.3)。以上表明，提高(无腹筋)BFRP筋增强海水海砂ECC梁抗剪承载力的有效方法是增加抗压强度。
3. 结论
(1) 海水海砂ECC(Seawater sea-sand engineeredcementitious composites，SSE)具有优越的变形能力和多缝开裂的特点，最大拉伸应变可达8.3%，平均裂缝宽度约为0.2 mm，抗压强度对应的应变约为0.36%。
(2) 与配箍率为0.67%的玄武岩纤维增强树脂复合材料(Basalt fiber reinforced polymer，BFRP)筋增强水泥砂浆梁(BFRP/SSM梁)相比，无箍筋或配箍率为0.37%的BFRP筋增强海水海砂ECC(BFRP/SSE)梁抗剪承载力提高6.37%~99.25%，且具有更高的刚度。BFRP/SSE梁在正常使用极限状态下的裂缝宽度小于0.3 mm，满足《纤维增强复合材料工程应用技术规范》(GB 50608—2020)[7]的要求。抗剪承载力、刚度和裂缝宽度的结果表明，无箍筋和少箍筋的海水海砂ECC梁具备足够的抗剪能力。
(3) 无腹筋BFRP/SSE梁开裂后仍具有较高的剪切承载能力，且在正常使用极限状态下裂缝宽度很小，可以考虑在BFRP/SSE梁结构设计中不要求最小配箍率。
(4) 无腹筋BFRP/SSE梁抗剪承载力随SSE抗压强度增加明显。随SSE抗拉强度提高，梁抗剪承载力缓慢增加。SSE拉伸应变能力对抗剪承载力基本没有影响，表明可以通过适当减少纤维掺量来降低BFRP筋增强海水海砂ECC梁的建造成本。
-
![]()
![]()
![]()
![]()
图 12 压剪混合试验夹具示意图
F—Force; T1—Shear load; T2—Compression load
Figure 12. Schematic diagram of compression-shear test fixture
![]()
![]()
![]()
表 1 Camanho和Matthews的材料性能折减模型[29]
Table 1 Material property reduction model of Camanho and Matthews[29]
Failure mode Degradation coefficient Fiber tensile failure E_{11}^{\mathrm{d}}=0.07E_{11} Fiber compression failure E_{11}^{\mathrm{d}}=0.14E_{11} Matrix tensile/shear failure E_{22}^{\mathrm{d}}=0.2E_{22}
G_{12}^{\mathrm{d}}=0.2G_{12} , G_{23}^{\mathrm{d}}=0.2G_{23}Matrix compression/shear failure E_{22}^{\mathrm{d}}=0.4E_{22}
G_{12}^{\mathrm{d}}=0.4G_{12} , G_{23}^{\mathrm{d}}=0.4G_{23}Notes: {E_{11}} and {E_{22}} are the elastic moduli in the fiber and matrix directions; {G_{12}} and {G_{23}} are the shear moduli; \mathrm{d} stands for degradation. 
下载: 导出CSV
Failure mode Degradation coefficient Fiber failure E_{11}^{\mathrm{d}}=0 , E_{22}^{\mathrm{d}}=0 , G_{12}^{\mathrm{d}}=0 Matrix failure E_{22}^{\mathrm{d}}=0 , \nu_{21}^{\mathrm{d}}=0 Fiber-matrix shear failure G_{12}^{\mathrm{d}}=0 , \nu_{12}^{\mathrm{d}}=0 , \nu_{21}^{\mathrm{d}}=0 Notes: E_{11}^{\mathrm{d}} and E_{22}^{\mathrm{d}} are the elastic moduli in the fiber and matrix directions after degradation; G_{12}^{\mathrm{d}} is the shear moduli after degradation; \nu_{12}^{\mathrm{d}} and \nu_{21}^{\mathrm{d}} are poisson’s ratios after degradation.
下载: 导出CSV
-
[1] CHAGRAOUI H, LAZGHAB T, SOULA M. Buckling optimization and post-buckling analysis of omega sub-stiffened composite panels using different cohesive interface properties[J]. Thin-Walled Structures, 2023, 189: 110944. DOI: 10.1016/j.tws.2023.110944
[2] WANG Y, WANG F, JIA S, et al. Experimental and numerical studies on the stability behavior of composite panels stiffened by tilting hat-stringers[J]. Composite Structures, 2017, 174: 187-195. DOI: 10.1016/j.compstruct.2017.04.039
[3] ABRAMOVICH H, WELLER T. Buckling and postbuckling behavior of laminated composite stringer stiffened curved panels under axial compression: Experiments and design guidelines[J]. Journal of Mechanics of Materials and Structures, 2009, 4(7): 1187-1207.
[4] 王海燕, 段世慧, 孙侠生. 复合材料加筋板后屈曲设计技术欧盟研究综述[J]. 航空工程进展, 2015, 6(2): 139-148. DOI: 10.3969/j.issn.1674-8190.2015.02.002 WANG Haiyan, DUAN Shihui, SUN Xiasheng. Review on the EU research projects of design and analysis of stiffened composite panels including post-buckling[J]. Advances in Aeronautical Science and Engineering, 2015, 6(2): 139-148(in Chinese). DOI: 10.3969/j.issn.1674-8190.2015.02.002
[5] 朱菊芬, 陈浩然, 陈绍杰, 等. 复合材料加筋板后屈曲强度工程分析方法探讨[J]. 航空学报, 1991(12): 639-642. DOI: 10.3321/j.issn:1000-6893.1991.12.019 ZHU Jufen, CHEN Haoran, CHEN Shaojie, et al. Engineering method research of post-buckling[J]. Acta Aeronautica et Astronautica Sinica, 1991(12): 639-642(in Chinese). DOI: 10.3321/j.issn:1000-6893.1991.12.019
[6] 张雅倩, 刘轶轩, 吴泳芙, 等. 反对称铺设复合材料层合板非线性后屈曲分析[J]. 应用力学学报, 2023, 40(4): 778-787. ZHANG Yaqian, LIU Yixuan, WU Yongfu, et al. Nonlinear post-buckling analysis of composite laminates with antisymmetric angle-ply[J]. Chinese Journal of Applied Mechanics, 2023, 40(4): 778-787(in Chinese).
[7] 钟博, 王新峰, 于健. 石英纤维与碳纤维混杂加筋壁板剪切后屈曲性能研究[J]. 南京航空航天大学学报, 2023, 55(6): 1111-1117. ZHONG Bo, WANG Xinfeng, YU Jian. Shear post-buckling behavior of quartz fiber and carbon fiber hybrid stiffened panels[J]. Journal of Nanjing University of Aernautics & Astrnautics, 2023, 55(6): 1111-1117(in Chinese).
[8] FENG Y, WANG W, LU S, et al. Axial compressive performances of stiffened composite panels: Experimental and numerical study[J]. Alexandria Engineering Journal, 2023, 71: 115-130. DOI: 10.1016/j.aej.2023.03.047
[9] FENG Y, MA B, CUI R, et al. Effects of hygrothermal environment on the buckling and postbuckling performances of stiffened composite panels under axial compression[J]. Composite Structures, 2020, 242: 112132. DOI: 10.1016/j.compstruct.2020.112132
[10] 邹建超. 纤维复合材料冲击后压缩/剪切的损伤机理及性能预测研究[D]. 大连: 大连理工大学, 2023. ZOU Jianchao. Study on damage mechanism and performance prediction of fiber composites under compression/shear after impact[D]. Dalian: Dalian University of Technology, 2023(in Chinese).
[11] 孙振亚. 基于人工神经网络的复合材料加筋板失效行为预测研究[D]. 大连: 大连理工大学, 2022. SUN Zhenya. Prediction of failure behavior of composite stiffened panels using artificial neural network[D]. Dalian: Dalian University of Technology, 2022(in Chinese).
[12] 王彬文, 艾森, 张国凡, 等. 考虑不确定性的复合材料加筋壁板后屈曲分析模型验证方法[J]. 航空学报, 2020, 41(8): 280-287. WANG Binwen, AI Sen, ZHANG Guofan, et al. Validation method for post-buckling analysis model of stiffened composite panel considering uncertainties[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(8): 223987(in Chinese).
[13] FENG Y, LIU S, ZHANG T, et al. Experimental and theoretical investigation on the shear performance of stiffened composite panel with I-shaped stiffeners[J]. Composite Structures, 2022, 284: 115234. DOI: 10.1016/j.compstruct.2022.115234
[14] 杨钧超, 柴亚南, 陈向明, 等. 复合材料加筋板剪切屈曲与后屈曲承载特性[J]. 科学技术与工程, 2019, 19(7): 289-293. DOI: 10.3969/j.issn.1671-1815.2019.07.048 YANG Junchao, CHAI Yanan, CHEN Xiangming, et al. Shear buckling and post-buckling behavior of composite stiffened panels[J]. Science Technology and Engineering, 2019, 19(7): 289-293(in Chinese). DOI: 10.3969/j.issn.1671-1815.2019.07.048
[15] HAYATDAVOODI A, SHANMUGAM N E. Web buckling and ultimate strength of composite plate girders subjected to shear and bending[J]. International Journal of Structural Stability and Dynamics, 2015, 1450047.
[16] HAYATDAVOODI A, NAZARI M, JAVADI PORDESARI A. Investigation on the collapse behavior of diagonal stiffened composite plate girders subjected to shear loading[J]. International Journal of Steel Structures, 2020, 20(2): 386-399. DOI: 10.1007/s13296-019-00291-7
[17] 高志刚, 冯宇, 马斌麟, 等. 航空复合材料加筋板压缩屈曲及后屈曲力学性能[J]. 航空材料学报, 2020, 40(1): 53-61. DOI: 10.11868/j.issn.1005-5053.2019.000067 GAO Zhigang, FENG Yu, MA Binlin, et al. Compressive bucking and post-bucking mechanical properties of aeronautic composite stiffened panel[J]. Journal of Aeronautical Materials, 2020, 40(1): 53-61(in Chinese). DOI: 10.11868/j.issn.1005-5053.2019.000067
[18] 王菲菲, 崔德刚, 熊强, 等. 复合材料加筋板后屈曲承载能力工程分析方法[J]. 北京航空航天大学学报, 2013, 39(4): 494-497. WANG Feifei, CUI Degang, XIONG Qiang, et al. Engineering analysis of post-buckling loading capability for composite stiffened panels[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(4): 494-497(in Chinese).
[19] 高伟, 刘存, 陈顺强. 变厚度复合材料加筋板轴压试验及分析方法[J]. 航空学报, 2022, 43(11): 148-156. GAO Wei, LIU Cun, CHEN Shunqiang. Axial compression test and analysis method of composite stiffened plates with variable thickness[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(11): 148-156 (in Chinese).
[20] 王春寿, 张笑宇, 詹志新, 等. 复合材料厚板结构压缩稳定性和承载能力分析[J]. 北京航空航天大学学报, 2025, 51(1): 94-101. WANG Chunshou, ZHANG Xiaoyu, ZHAN Zhixin, et al. The analysis of compression stability and load capacity of the thick composite plate structures[J]. Journal of Beijing University of Aeronautics and Astronautics, 2025, 51(1): 94-101(in Chinese).
[21] PEVZNER P, ABRAMOVICH H, WELLER T. Calculation of the collapse load of an axially compressed laminated composite stringer-stiffened curved panel–An engineering approach[J]. Composite Structures, 2008, 83(4): 341-353. DOI: 10.1016/j.compstruct.2007.05.001
[22] 黄晓笛. 复合材料帽形加筋壁板轴压承载能力工程分析[D]. 大连: 大连理工大学, 2023. HUANG Xiaodi. Engineering analysis of axial compression load bearing capacity of composite omega stiffened panels[D]. Dalian: Dalian University of Technology, 2023(in Chinese).
[23] ZHAO W, KAPANIA R K. Buckling analysis of unitized curvilinearly stiffened composite panels[J]. Composite Structures, 2016, 135: 365-382. DOI: 10.1016/j.compstruct.2015.09.041
[24] FERREIRA F P V, TSAVDARIDIS K D, MARTINS C H, et al. Buckling and post-buckling analyses of composite cellular beams[J]. Composite Structures, 2021, 262: 113616. DOI: 10.1016/j.compstruct.2021.113616
[25] 袁坚锋. 基于显式有限元的复合材料加筋板后屈曲分析方法研究[J]. 机械设计与制造工程, 2021, 50(4): 73-76. DOI: 10.3969/j.issn.2095-509X.2021.04.016 YUAN Jianfeng. Research on post-buckling for composite stiffened panel based on explicit FEM[J]. Machine Design and Manufacturing Engineering, 2021, 50(4): 73-76(in Chinese). DOI: 10.3969/j.issn.2095-509X.2021.04.016
[26] 刘存, 张磊, 杨卫平. 舰载机壁板剪切后屈曲承载能力预测与试验验证[J]. 航空学报, 2019, 40(4): 49-57. LIU Cun, ZHANG Lei, YANG Weiping. Post-buckling study and test verification of carrier-based aircraft wing stiffened panels under shear load[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(4): 49-57(in Chinese).
[27] 张连青. 压剪组合载荷下复合材料壁板屈曲性能及后屈曲承载能力分析[D]. 哈尔滨: 哈尔滨工业大学, 2021. ZHANG Lianqing. Analysis of buckling behavior and post-buckling bearing capacity of composite panels under combined compression and shear loads[D]. Harbin: Harbin Institute of Technology, 2021(in Chinese).
[28] 林国伟, 李新祥. 复合材料加筋板后屈曲分析方法及实验验证[J]. 航空材料学报, 2021, 41(4): 149-156. DOI: 10.11868/j.issn.1005-5053.2021.000013 LIN Guowei, LI Xinxiang. Post-buckling analysis method of stiffened composite panels and test verification[J]. Journal of Aeronautical Materials, 2021, 41(4): 149-156(in Chinese). DOI: 10.11868/j.issn.1005-5053.2021.000013
[29] CAMANHO P P, MATTHEWS F L. A progressive damage model for mechanically fastened joints in composite laminates[J]. Journal of Composite Materials, 1999, 33(24): 2248-2280. DOI: 10.1177/002199839903302402
[30] CHANG F K, LESSARD L B. Damage tolerance of laminated composites containing an open hole and subjected to compressive loadings: Part I—Analysis[J]. Journal of Composite Materials, 1991, 25(1): 2-43. DOI: 10.1177/002199839102500101
[31] 崔进, 肖文莹, 李想. 船体复合材料帽型加筋板渐进破坏分析[J]. 舰船科学技术, 2021, 43(3): 20-25. DOI: 10.3404/j.issn.1672-7649.2021.02.004 CUI Jin, XIAO Wenying, LI Xiang. Progressive failure of hat-stringer-stiffened composite panel in the hull[J]. Ship Science and Technology, 2021, 43(3): 20-25(in Chinese). DOI: 10.3404/j.issn.1672-7649.2021.02.004
[32] 邹华民. 含初始分层缺陷复合材料加筋壁板承载性能分析[D]. 大连: 大连理工大学, 2018. ZOU Huamin. Bearing capacity analysis of composite stiffened panels with initial delamination defects [D]. Dalian: Dalian University of Technology, 2018(in Chinese).
[33] 邹华民, 崔向斌, 任明法, 等. 含初始脱粘缺陷复合材料加筋壁板渐进压溃过程的数值模拟[J]. 玻璃钢/复合材料, 2017(11): 12-18. ZOU Huamin, CUI Xiangbin, REN Mingfa, et al. Numerical simulation on progressive collapse process of composite stiffened panel with initial debonding defect[J]. Fiber Reinforced Plastics/Composites, 2017(11): 12-18(in Chinese).
[34] 韩庆, 宋恩鹏, 陆华, 等. 复合材料加筋结构后屈曲的自开发程序[J]. 复合材料学报, 2017, 34(7): 1443-1450. HAN Qing, SONG Enpeng, LU Hua, et al. Self-developed program for post-buckling of composite stiffened structures[J]. Acta Materiae Compositae Sinica, 2017, 34(7): 1443-1450(in Chinese).
[35] ORIFICI A C, HERSZBERG I, THOMSON R S. Review of methodologies for composite material modelling incorporating failure[J]. Composite Structures, 2008, 86(1): 194-210.
[36] 王涛. 基于筋元界面的复合材料帽型加筋板失效分析[D]. 大连: 大连理工大学, 2023. WANG Tao. Failure analysis of composite hat-stiffened panels based on interface failure behavior of stiffener element [D]. Dalian: Dalian University of Technology, 2023(in Chinese).
[37] 李乐坤, 张铁军, 支乐, 等. 湿热环境下复合材料加筋壁板压缩屈曲与后屈曲行为的有限元模拟[J]. 机械工程材料, 2023, 47(8): 93-99. DOI: 10.11973/jxgccl202308015 LI Lekun, ZHANG Tiejun, ZHI Le, et al. Finite element modelling for buckling and post-buckling behavior of composite stiffened panel during compression in hygrothermal environment[J]. Materials for Mechanical Engineering, 2023, 47(8): 93-99(in Chinese). DOI: 10.11973/jxgccl202308015
[38] JI R, ZHAO L, WANG K, et al. Effects of debonding defects on the postbuckling and failure behaviors of composite stiffened panel under uniaxial compression[J]. Composite Structures, 2021, 256: 113121. DOI: 10.1016/j.compstruct.2020.113121
[39] YE Y, ZHU W, JIANG J, et al. Computational modelling of post-buckling behavior of composite T-stiffened panels with different bonding methods[J]. Composites Part B: Engineering, 2019, 166: 247-256. DOI: 10.1016/j.compositesb.2018.11.137
[40] 胡波涛, 柴亚南, 陈向明, 等. 后屈曲复合材料加筋板筋条-蒙皮界面失效表征[J]. 机械强度, 2019, 41(6): 1473-1479. HU Botao, CHAI Yanan, CHEN Xiangming, et al. Stiffener-skin interface failure characterization of the stiffened composite panel at post-buckling stage[J]. Journal of Mechanical Strength, 2019, 41(6): 1473-1479(in Chinese).
[41] VAN DOOREN K, BISAGNI C. Design, analysis and testing of thermoplastic welded stiffened panels to investigate skin-stringer separation in post-buckling[J]. Composites Part B: Engineering, 2023, 267: 111033. DOI: 10.1016/j.compositesb.2023.111033
[42] VAN DOOREN K S, TIJS B H A H, WALESON J E A, et al. Skin-stringer separation in post-buckling of butt-joint stiffened thermoplastic composite panels[J]. Composite Structures, 2023, 304: 116294. DOI: 10.1016/j.compstruct.2022.116294
[43] BERTOLINI J, CASTANIÉ B, BARRAU J J, et al. An experimental and numerical study on omega stringer debonding[J]. Composite Structures, 2008, 86(1): 233-242.
[44] RAIMONDO A, DOESBURG S A, BISAGNI C. Numerical study of quasi-static and fatigue delamination growth in a post-buckled composite stiffened panel[J]. Composites Part B: Engineering, 2020, 182: 107589. DOI: 10.1016/j.compositesb.2019.107589
[45] 田甜, 张帆, 许健. 复合材料加筋壁板压缩试验研究与仿真分析[J]. 科技创新与应用, 2018(5): 45-46. TIAN Tian, ZHANG Fan, XU Jian. Compression test research and simulation analysis of composite stiffened panel[J]. Technology Innovation and Application, 2018(5): 45-46(in Chinese).
[46] 杜洪雨, 奚晓波, 孟力华, 等. 含分层损伤的复合材料层压板后屈曲及低周疲劳分层扩展有限元模拟研究[J]. 玻璃钢/复合材料, 2018(6): 39-43. DU Hongyu, XI Xiaobo, MENG Lihua, et al. Finite element analysis of post-buckled delamination of composite laminate with preliminary debond subjected to static and fatigue loads[J]. Fiber Reinforced Plastics/Composites, 2018(6): 39-43(in Chinese).
[47] DÁVILA C G, BISAGNI C. Fatigue life and damage tolerance of postbuckled composite stiffened structures with initial delamination[J]. Composite Structures, 2017, 161: 73-84. DOI: 10.1016/j.compstruct.2016.11.033
[48] 唐劼尧, 柏敏建. 轴压载荷下复合材料蜂窝夹芯板的稳定性研究[J]. 兵器装备工程学报, 2020, 41(9): 242-246. DOI: 10.11809/bqzbgcxb2020.09.045 TANG Jieyao, BAI Minjian. Stability evaluation on composite honeycomb sandwich panels subjected to compressive loadings[J]. Journal of Ordnance Equipment Engineering, 2020, 41(9): 242-246(in Chinese). DOI: 10.11809/bqzbgcxb2020.09.045
[49] 李晓文, 朱兆一, 李妍, 等. 船舶复合材料加筋板屈曲和后屈曲行为研究[J]. 中国造船, 2020, 61(3): 186-194. DOI: 10.3969/j.issn.1000-4882.2020.03.020 LI Xiaowen, ZHU Zhaoyi, LI Yan, et al. Research on buckling and post buckling behavior of composite stiffened panel for ships[J]. Ship Building of China, 2020, 61(3): 186-194(in Chinese). DOI: 10.3969/j.issn.1000-4882.2020.03.020
[50] KOLANU N R, RAJU G, RAMJI M. Experimental and numerical studies on the buckling and post-buckling behavior of single blade-stiffened CFRP panels[J]. Composite Structures, 2018, 196: 135-154. DOI: 10.1016/j.compstruct.2018.05.015
[51] 孙中雷, 张国凡, 李军鹏. 轴压载荷下复合材料加筋板后屈曲承载能力研究[J]. 航空计算技术, 2016, 46(3): 63-66. DOI: 10.3969/j.issn.1671-654X.2016.03.016 SUN Zhonglei, ZHANG Guofan, LI Junpeng. Study on loading capacity of composite panels under uniaxial compression[J]. Aeronautical Computing Technique, 2016, 46(3): 63-66(in Chinese). DOI: 10.3969/j.issn.1671-654X.2016.03.016
[52] 张修路, 黄文超, 方采文, 等. 飞机复合材料加筋壁板结构屈曲和后屈曲研究[J]. 计算机仿真, 2020, 37(12): 230-234, 408. DOI: 10.3969/j.issn.1006-9348.2020.12.048 ZHANG Xiulu, HUANG Wenchao, FANG Caiwen, et al. The investigation on buckling and post buckling of aircraft composite panel structure[J]. Computer Simulation, 2020, 37(12): 230-234, 408(in Chinese). DOI: 10.3969/j.issn.1006-9348.2020.12.048
[53] 林国伟, 李新祥. 复合材料壁板后屈曲分析失效准则的适用性研究[J]. 机械强度, 2020, 42(3): 565-572. LIN Guowei, LI Xinxiang. Applicability investigation of failure criterion for post-buckling analysis of stiffened composite panels[J]. Journal of Mechanical Strength, 2020, 42(3): 565-572(in Chinese).
[54] LIAN C, WANG P, ZHANG K, et al. Experimental and numerical research on the calculation methods for buckling and post-buckling of aircraft tail inclined stiffened panel under compression load[J]. Aerospace Science and Technology, 2024, 146: 108930. DOI: 10.1016/j.ast.2024.108930
[55] LIAN C, WANG P, CHEN X, et al. Experimental and numerical research on the analysis methods for buckling and post-buckling of inclined stiffened panel under shear load[J]. Thin-Walled Structures, 2024, 195: 111374. DOI: 10.1016/j.tws.2023.111374
[56] 王维阳, 李伟, 曹奇凯. 复合材料加筋板轴压后屈曲及承载有限元分析[J]. 计算机仿真, 2022, 39(5): 474-479. DOI: 10.3969/j.issn.1006-9348.2022.05.095 WANG Weiyang, LI Wei, CAO Qikai. Finite element analysis of post-buckling and bearing capability of composite stiffened plates under axial compression[J]. Computer Simulation, 2022, 39(5): 474-479(in Chinese). DOI: 10.3969/j.issn.1006-9348.2022.05.095
[57] 李小乐. 含开口复合材料层合板的剪切承载及后屈曲渐进损伤研究[D]. 哈尔滨: 哈尔滨工业大学, 2019. LI Xiaole. Bearing characteristics and post-buckling progressive failure behavior of composite laminate with cutout under shear load [D]. Harbin: Harbin Institute of Technology, 2019(in Chinese).
[58] SUN W, GUAN Z, LI Z, et al. Modelling and simulating of the compressive behavior of T-stiffened composite panels subjected to stiffener impact[J]. Composite Structures, 2018, 186: 221-232. DOI: 10.1016/j.compstruct.2017.11.079
[59] 黎汉华. 复合材料格栅加筋结构损伤对力学性能影响研究[D]. 哈尔滨: 哈尔滨工业大学, 2021. LI Hanhua. Influence of damage on mechanical properties of composite grid reinforced structure[D]. Harbin: Harbin Institute of Technology, 2021(in Chinese).
[60] 杨钧超, 王雪明, 陈向明, 等. 低速冲击损伤对复材加筋板压缩性能的影响[J]. 航空学报, 2023, 44(20): 248-263. DOI: 10.7527/S1000-6893.2023.28498 YANG Junchao, WANG Xueming, CHEN Xiangming, et al. Effect of low-velocity impact damage on compressive properties of composite stiffened panels[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(20): 248-263(in Chinese). DOI: 10.7527/S1000-6893.2023.28498
[61] 杨钧超, 陈向明, 邹鹏, 等. 复合材料层合板剪切稳定性试验及强度预测[J]. 复合材料学报, 2023, 40(3): 1707-1717. YANG Junchao, CHEN Xiangming, ZOU Peng, et al. Shear stability test and strength prediction of composite laminates[J]. Acta Materiae Compositae Sinica, 2023, 40(3): 1707-1717(in Chinese).
[62] MASOOD S N, VISHAKH R, VISWAMURTHY S R, et al. Influence of stiffener configuration on post-buckled response of composite panels with impact damages[J]. Composite Structures, 2018, 194: 433-444. DOI: 10.1016/j.compstruct.2018.04.005
[63] WU Q, HU S, TANG X, et al. Compressive buckling and post-buckling behaviors of J-type composite stiffened panel before and after impact load[J]. Composite Structures, 2023, 304: 116339. DOI: 10.1016/j.compstruct.2022.116339
[64] 胡少杰. J型复合材料加筋板压缩屈曲及后屈曲行为研究[D]. 哈尔滨: 哈尔滨工业大学, 2022. HU Shaojie. Research on compression buckling and post-buckling behavior of J-type composite stiffened plate[D]. Harbin: Harbin Institute of Technology, 2022(in Chinese).
[65] WANG X M, CAO W, DENG C H, et al. Experimental and numerical analysis for the post-buckling behavior of stiffened composite panels with impact damage[J]. Composite Structures, 2015, 133: 840-846. DOI: 10.1016/j.compstruct.2015.08.019
[66] 付新卫, 刘瑞同, 戴瑛. 夹具对复合材料加筋板剪切试验屈曲载荷的影响[J]. 力学季刊, 2011, 32(4): 563-569. FU Xinwei, LIU Ruitong, DAI Ying. Effects of support fixture on the buckling loads in shear test of stiffened composites plate[J]. Chinese Quarterly of Mechanics, 2011, 32(4): 563-569(in Chinese).
[67] WANG Y, ZHU S. Effect of stringer design on the stability of stiffened composite panel under in-plane shear: An experimental study[J]. International Journal of Aeronautical and Space Sciences, 2021, 22(3): 590-601. DOI: 10.1007/s42405-020-00332-0
[68] YILDIRIM E G, ÜNAL R. A review on post-buckling behaviors of composites: Crippling phenomenon kompozitlerin son burkulma davranışı üzerine bir i̇nceleme: burkulma sonrası dayanım olgusu[J]. 2024.
[69] 刘达. 加筋板屈曲及后屈曲行为的相移编码条纹投影测量方法研究[D]. 大连: 大连理工大学, 2022. LIU Da. Study on measurement method of buckling and post-buckling behavior of stiffened panels via phase-shift coding fringe projection profilometry[D]. Dalian: Dalian University of Technology, 2022(in Chinese).
[70] 胡嘉桐, 余明. 国产T800H复合材料加筋壁板压缩破坏试验研究及数值仿真分析[J]. 机械设计与研究, 2022, 38(6): 98-103, 109. HU Jiatong, YU Ming. Destruction test and numerical simulation analysis of homegrown T800H composite stiffened panel under compression[J]. Machine Design and Research, 2022, 38(6): 98-103, 109(in Chinese).
[71] 高伟, 刘存, 张文军, 等. 不同长桁截面复合材料加筋板轴压屈曲分析[J]. 力学与实践, 2022, 44(5): 1143-1150. DOI: 10.6052/1000-0879-21-521 GAO Wei, LIU Cun, ZHANG Wenjun, et al. Axial compression buckling of stiffened panel of composite materials with different stringer section[J]. Mechanics in Engineering, 2022, 44(5): 1143-1150(in Chinese). DOI: 10.6052/1000-0879-21-521
[72] 张国凡. 复合材料加筋壁板结构屈曲承载特性研究[D]. 西安: 西北工业大学, 2020. ZHANG Guofan. Study on buckling behavior of stiffened composite panels[D]. Xi'an: Northwestern Polytechnical University, 2020(in Chinese).
[73] 阳奥, 陈普会, 孔斌, 等. 数字图像相关技术在复合材料加筋曲板压缩试验中的应用[J]. 复合材料学报, 2020, 37(10): 2439-2451. YANG Ao, CHEN Puhui, KONG Bin, et al. Application of digital image correlation technology in compression test of stringer stiffened composite curved panels[J]. Acta Materiae Compositae Sinica, 2020, 37(10): 2439-2451(in Chinese).
[74] 王彩英, 白瑞祥, 雷振坤. 工字型加筋复合材料壁板的压缩屈曲行为实验研究[J]. 实验力学, 2018, 33(5): 725-733. DOI: 10.7520/1001-4888-18-030 WANG Caiying, BAI Ruixiang, LEI Zhenkun. Experimental study on compression buckling behavior of I-shaped rib stiffened composite panel[J]. Journal of Experimental Mechanics, 2018, 33(5): 725-733(in Chinese). DOI: 10.7520/1001-4888-18-030
[75] LAURIN F, CHARRIER J S, LÉVÊQUE D, et al. Determination of the properties of composite materials thanks to digital image correlation measurements[J]. Procedia IUTAM, 2012, 4: 106-115. DOI: 10.1016/j.piutam.2012.05.012
[76] NADEEM MASOOD S, VISWAMURTHY S R, GADDIKERI K M. Composites airframe panel design for post-buckling – An experimental investigation[J]. Composite Structures, 2020, 241: 112104. DOI: 10.1016/j.compstruct.2020.112104
[77] 汪厚冰, 李新祥, 魏景超, 等. 复合材料曲面帽形加筋壁板在内压-轴压联合载荷下的屈曲及承载性能[J]. 航空制造技术, 2020, 63(18): 55-64, 81. WANG Houbing, LI Xinxiang, WEI Jingchao, et al. Buckling and post-buckling of curved hat-stiffened composite panels under combined internal pressure and axial compression[J]. Aeronautical Manufacturing Technology, 2020, 63(18): 55-64, 81(in Chinese).
[78] 汪厚冰, 陈昊, 雷安民, 等. 复合材料帽形加筋壁板轴压屈曲与后屈曲性能[J]. 复合材料学报, 2018, 35(8): 2014-2022. WANG Houbing, CHEN Hao, LEI Anmin, et al. Buckling and post-buckling performance of hat-stiffened composite panels under axial compression load[J]. Acta Materiae Compositae Sinica, 2018, 35(8): 2014-2022(in Chinese).
[79] MO Y, GE D, HE B. Experiment and optimization of the hat-stringer-stiffened composite panels under axial compression[J]. Composites Part B: Engineering, 2016, 84: 285-293. DOI: 10.1016/j.compositesb.2015.08.039
[80] 张浩宇, 何宇廷, 冯宇, 等. 先进复合材料薄壁加筋板轴压屈曲特性及后屈曲承载性能[J]. 航空材料学报, 2016, 36(4): 55-63. DOI: 10.11868/j.issn.1005-5053.2016.4.008 ZHANG Haoyu, HE Yuting, FENG Yu, et al. Buckling and post-buckling performance of advanced composite stiffened panel under compression[J]. Journal of Aeronautical Materials, 2016, 36(4): 55-63(in Chinese). DOI: 10.11868/j.issn.1005-5053.2016.4.008
[81] 谭翔飞, 何宇廷, 冯宇, 等. 航空碳纤维树脂基复合材料加筋板压缩屈曲及后屈曲性能[J]. 航空动力学报, 2016, 31(10): 2359-2369. TAN Xiangfei, HE Yuting, FENG Yu, et al. Buckling and post-buckling performance of aeronautic carbon fiber reinforced resin composite stiffened panel under compression[J]. Journal of Aerospace Power, 2016, 31(10): 2359-2369(in Chinese).
[82] ZHU S, YAN J, CHEN Z, et al. Effect of the stiffener stiffness on the buckling and post-buckling behavior of stiffened composite panels–Experimental investigation[J]. Composite Structures, 2015, 120: 334-345. DOI: 10.1016/j.compstruct.2014.10.021
[83] 石经纬, 赵娟, 刘传军, 等. 复合材料翼面壁板剪切稳定性[J]. 复合材料学报, 2020, 37(7): 1590-1600. SHI Jingwei, ZHAO Juan, LIU Chuanjun, et al. Stability of composite stiffened panels in plane shear[J]. Acta Materiae Compositae Sinica, 2020, 37(7): 1590-1600(in Chinese).
[84] 谭翔飞, 何宇廷, 冯宇, 等. 航空复合材料加筋板剪切稳定性及后屈曲承载性能[J]. 复合材料学报, 2018, 35(2): 320-331. TAN Xiangfei, HE Yuting, FENG Yu, et al. Stability and post-buckling carrying capacity of aeronautic composite stiffened panel under shear loading[J]. Acta Materiae Compositae Sinica, 2018, 35(2): 320-331(in Chinese).
[85] 张国凡, 孙侠生, 孙中雷. 复合材料加筋壁板剪切破坏试验与后屈曲分析[J]. 机械科学与技术, 2016, 35(8): 1280-1285. ZHANG Guofan, SUN Xiasheng, SUN Zhonglei. Failure test and post-buckling analysis of composite stiffened panels under shear load[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(8): 1280-1285(in Chinese).
[86] RAY B C. Temperature effect during humid ageing on interfaces of glass and carbon fibers reinforced epoxy composites[J]. Journal of Colloid and Interface Science, 2006, 298(1): 111-117. DOI: 10.1016/j.jcis.2005.12.023
[87] CHEN L, ZHUO Y, XU R, et al. Buckling and post-buckling characteristics of stiffened panels under compression-shear load[J]. Journal of Physics: Conference Series, IOP Publishing, 2022, 2403(1): 012008. DOI: 10.1088/1742-6596/2403/1/012008
[88] 党乐, 郑洁, 杜凯, 等. 复合材料多墙盒段弯扭耦合下的屈曲和后屈曲[J]. 力学季刊, 2022, 43(2): 271-280. DANG Le, ZHENG Jie, DU Kai, et al. Buckling and post buckling of composite multi-wall box section under bending-torsion coupled loads[J]. Chinese Quarterly of Mechanics, 2022, 43(2): 271-280(in Chinese).
[89] 袁菲, 柴亚南, 张阿盈. 复合材料多墙盒段后屈曲的破坏预测方法[J]. 机械强度, 2018, 40(5): 1090-1096. YUAN Fei, CHAI Yanan, ZHANG A'ying. Prediction and damage analysis of the postbuckling for multi-spar composite box[J]. Journal of Mechanical Strength, 2018, 40(5): 1090-1096(in Chinese).
[90] BISAGNI C, DÁVILA C G. Experimental investigation of the postbuckling response and collapse of a single-stringer specimen[J]. Composite Structures, 2014, 108: 493-503. DOI: 10.1016/j.compstruct.2013.09.018
[91] LIU X, HAN K, BAI R, et al. Buckling measurement and numerical analysis of M-type ribs stiffened composite panel[J]. Thin-Walled Structures, 2014, 85: 117-124. DOI: 10.1016/j.tws.2014.08.008
[92] FENG Y, ZHANG H, TAN X, et al. Effect of impact damage positions on the buckling and post-buckling behaviors of stiffened composite panel[J]. Composite Structures, 2016, 155: 184-196. DOI: 10.1016/j.compstruct.2016.08.012
[93] SUN W, GUAN Z, OUYANG T, et al. Effect of stiffener damage caused by low velocity impact on compressive buckling and failure modes of T-stiffened composite panels[J]. Composite Structures, 2018, 184: 198-210. DOI: 10.1016/j.compstruct.2017.09.084
[94] MEEKS C, GREENHALGH E, FALZON B G. Stiffener debonding mechanisms in post-buckled CFRP aerospace panels[J]. Composites Part A: Applied Science and Manufacturing, 2005, 36(7): 934-946. DOI: 10.1016/j.compositesa.2004.12.003
[95] TAN R, XU J, GUAN Z, et al. Experimental study on effect of impact locations on damage formation and compression behavior of stiffened composite panels with L-shaped stiffener[J]. Thin-Walled Structures, 2020, 150: 106707. DOI: 10.1016/j.tws.2020.106707
[96] FENG Y, HE Y, TAN X, et al. Experimental investigation on different positional impact damages and shear-after-impact (SAI) behaviors of stiffened composite panels[J]. Composite Structures, 2017, 178: 232-245. DOI: 10.1016/j.compstruct.2017.06.053
[97] 肖浩, 胡伟平, 张淼, 等. 薄板的后屈曲损伤分析与疲劳寿命预估[J]. 北京航空航天大学学报, 2015, 41(3): 523-529. XIAO Hao, HU Weiping, ZHANG Miao, et al. Post-buckling damage analysis and fatigue life prediction of thin plate[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(3): 523-529(in Chinese).
[98] 张彦军, 朱亮, 杨卫平, 等. 舰载机机身加筋壁板屈曲疲劳试验[J]. 航空学报, 2019, 40(4): 40-48. ZHANG Yanjun, ZHU Liang, YANG Weiping, et al. Buckling fatigue test of fuselage stiffened panel for carrier-based aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(4): 40-48(in Chinese).
[99] 薛景川, 贺恭泰, 宋湘臣, 等. 薄壁结构剪切屈曲疲劳研究[J]. 航空学报, 1989(12): 607-613. DOI: 10.3321/j.issn:1000-6893.1989.12.008 XUE Jingchuan, HE Gongtai, SONG Xiangchen, et al. A study of shear-buckling fatigue for thin-walled structures[J]. Acta Aeronautica et Astronautica Sinica, 1989(12): 607-613(in Chinese). DOI: 10.3321/j.issn:1000-6893.1989.12.008
[100] 成传贤. 飞机壁板屈曲疲劳试验与结果分析[J]. 机械强度, 1988(3): 48-51, 47. CHENG Chuanxian. Buckling fatigue testing and analysis of results of aircraft plate[J]. Mechanical Strength, 1988(3): 48-51, 47(in Chinese).
[101] 苏少普, 常文魁, 陈先民. 飞机典型壁板结构剪切屈曲疲劳试验与分析方法[J]. 航空学报, 2022, 43(5): 274-283. SU Shaopu, CHANG Wenkui, CHEN Xianmin. Fatigue buckling test and analytical approach of aircraft typical panel structures[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(5): 274-283(in Chinese).
-
期刊类型引用(3)
1. 李彦宵，于本田，张占旭，吴明星，谢超. 河砂粒径与纤维类型对ECC力学性能的影响. 混凝土与水泥制品. 2024(02): 51-55+60 . 
百度学术
2. 周甲佳，温金鑫，景川，赵军. CFRP筋增强ECC梁弯曲性能试验研究. 复合材料学报. 2023(02): 978-989 . 本站查看
3. 林培轩，胡苗. 海水海砂对水泥基材料的性能影响分析. 中国建筑金属结构. 2023(01): 99-101 . 百度学术
其他类型引用(5)
-
目的
复合材料具有轻质、高强度和高刚度、抗疲劳、耐高温、成型工艺优良且成本低等优势，如今广泛应用于航空航天领域。复合材料加筋板是飞机机身的主要部件，筋条能够显著提高层合板的屈曲性能。加筋板的主要失效模式是屈曲，但在结构屈曲后并未完全丧失承载能力，为了能够充分利用复合材料加筋板结构的后屈曲承载能力，研究学者们对屈曲与后屈曲行为做了大量研究。本文对近年来有关复合材料加筋板屈曲与后屈曲问题的研究进行了综述，系统地描述了加筋板屈曲后屈曲的处理方法。
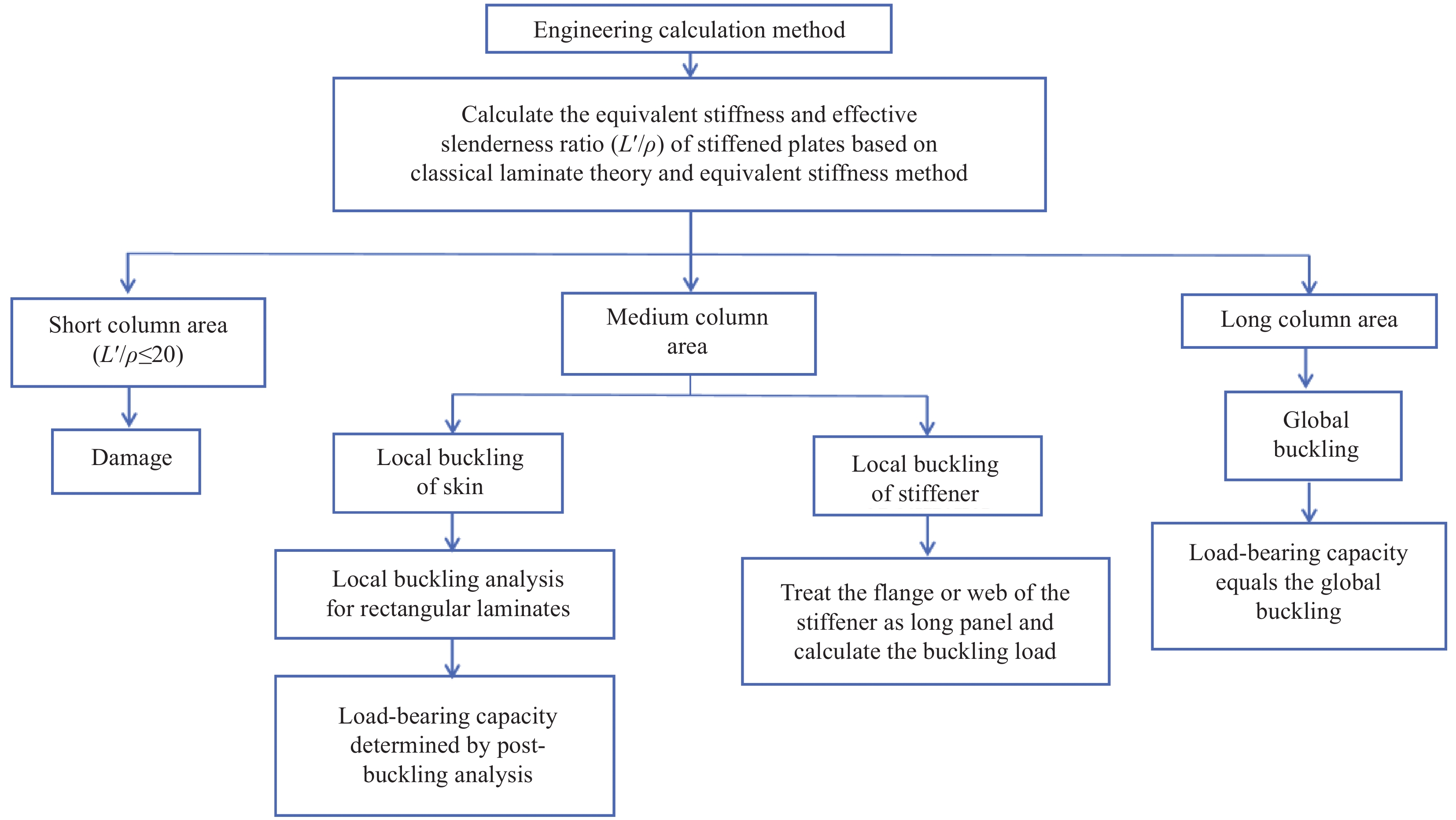
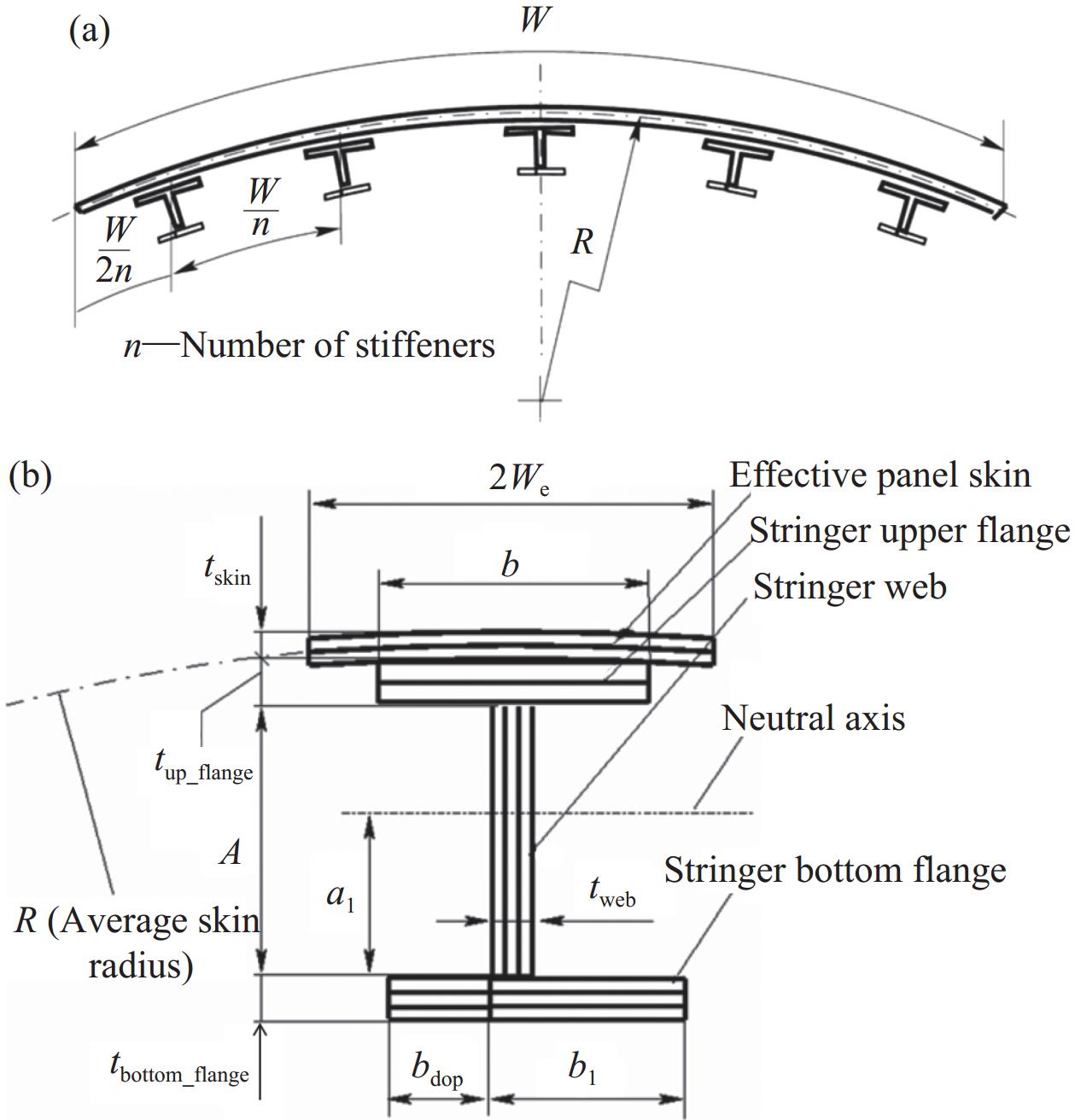
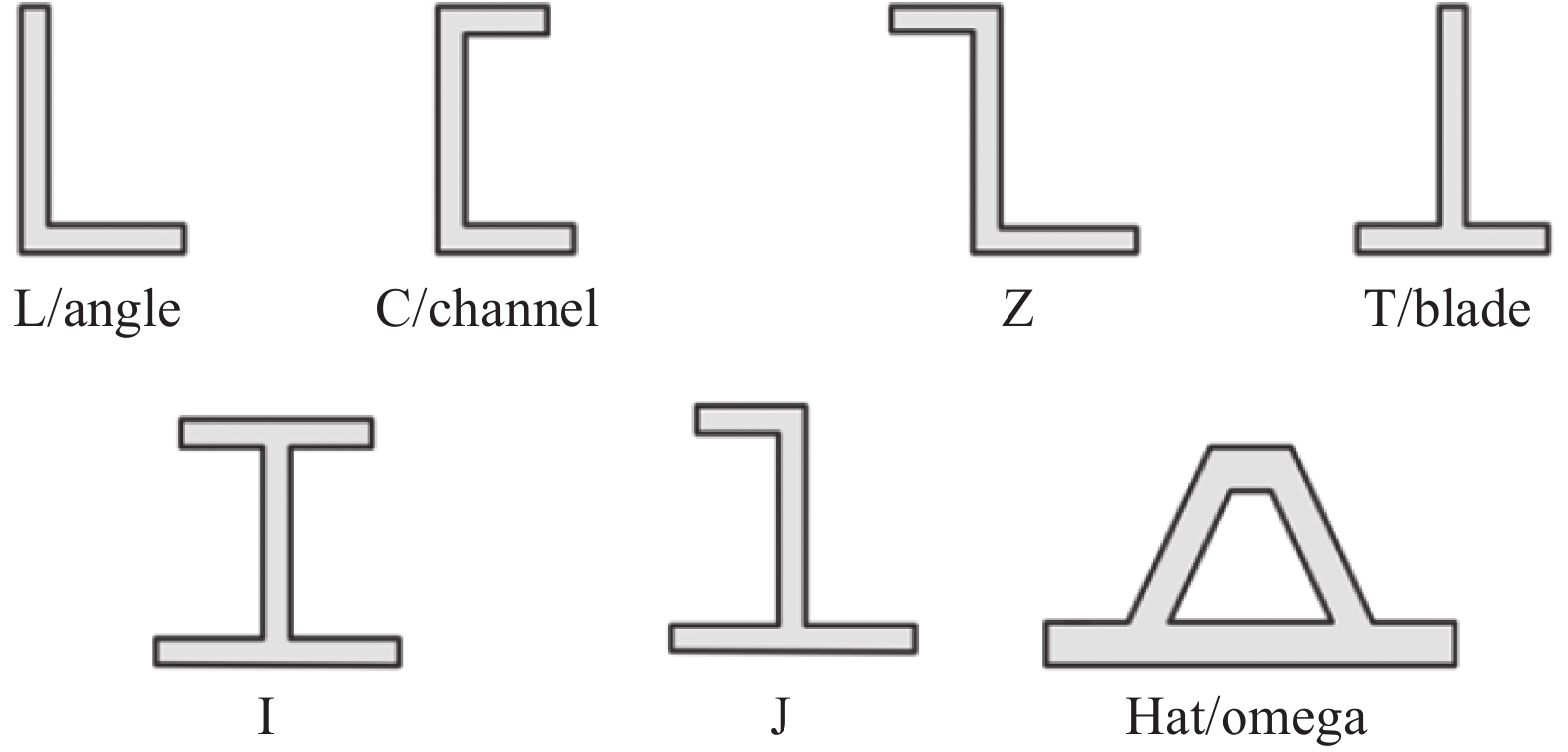
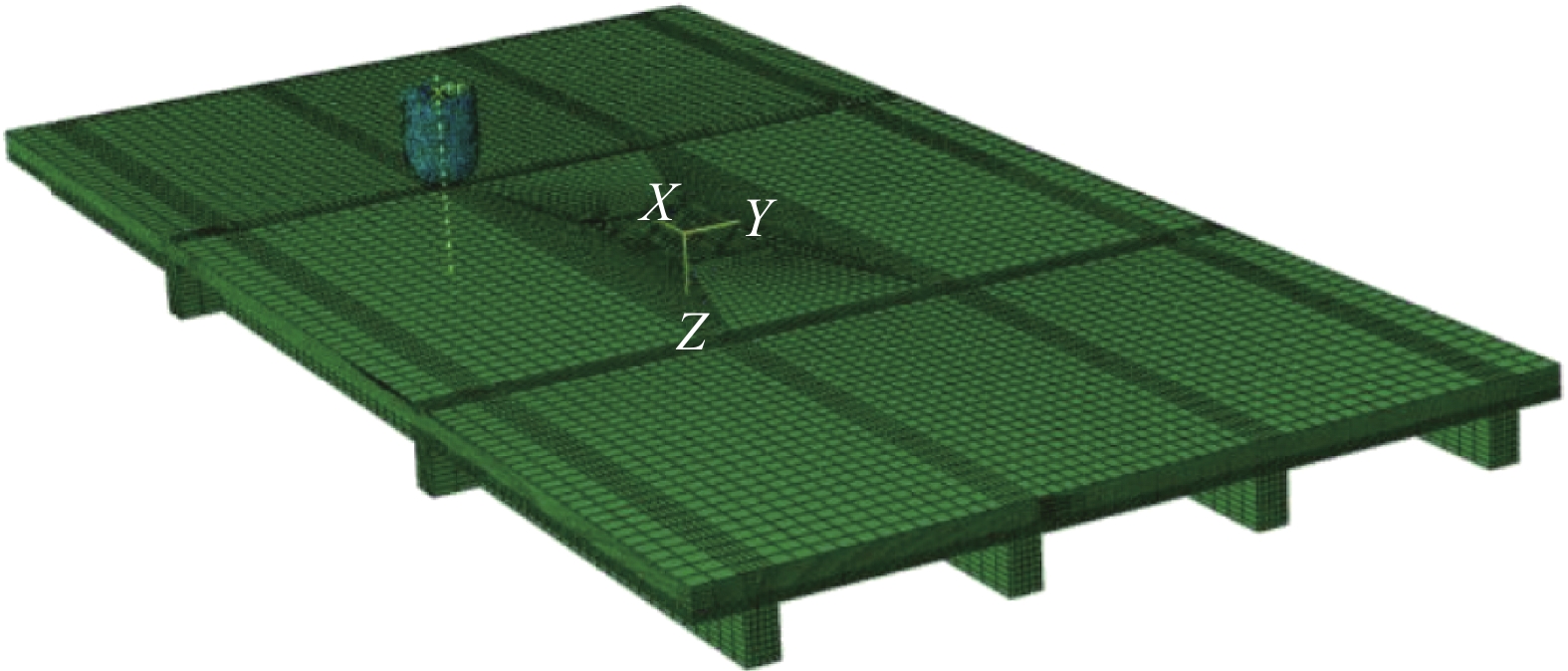
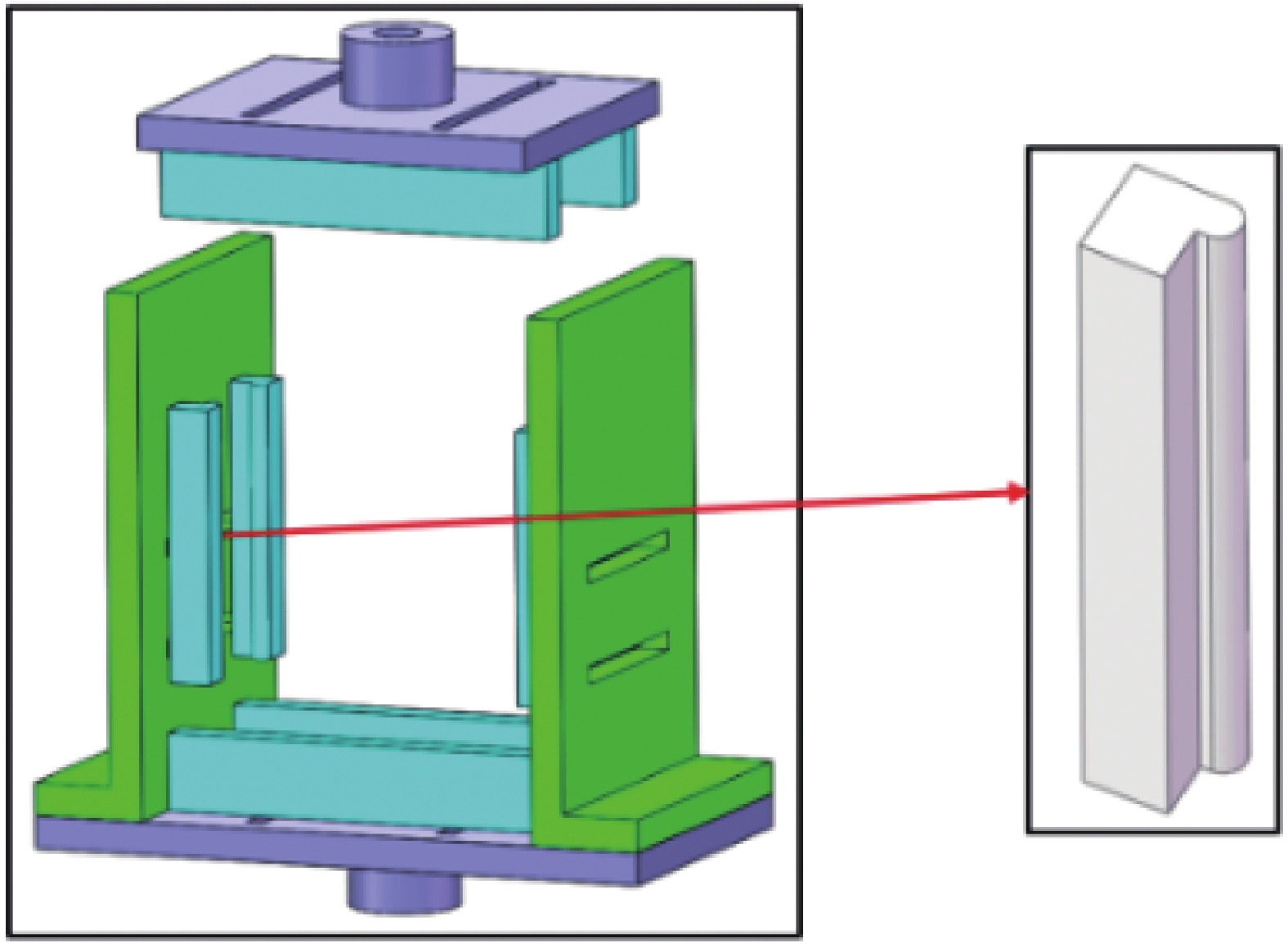
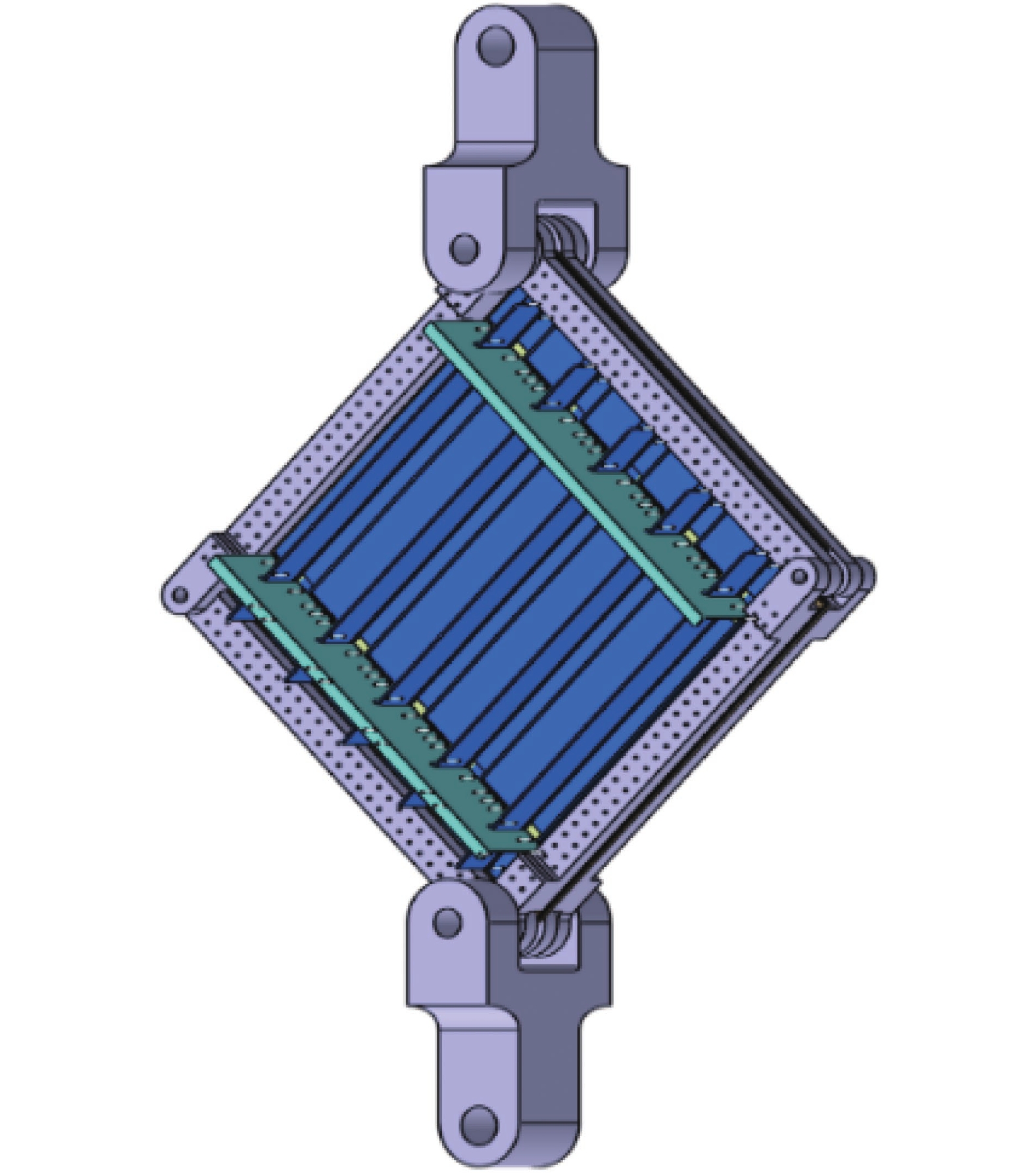
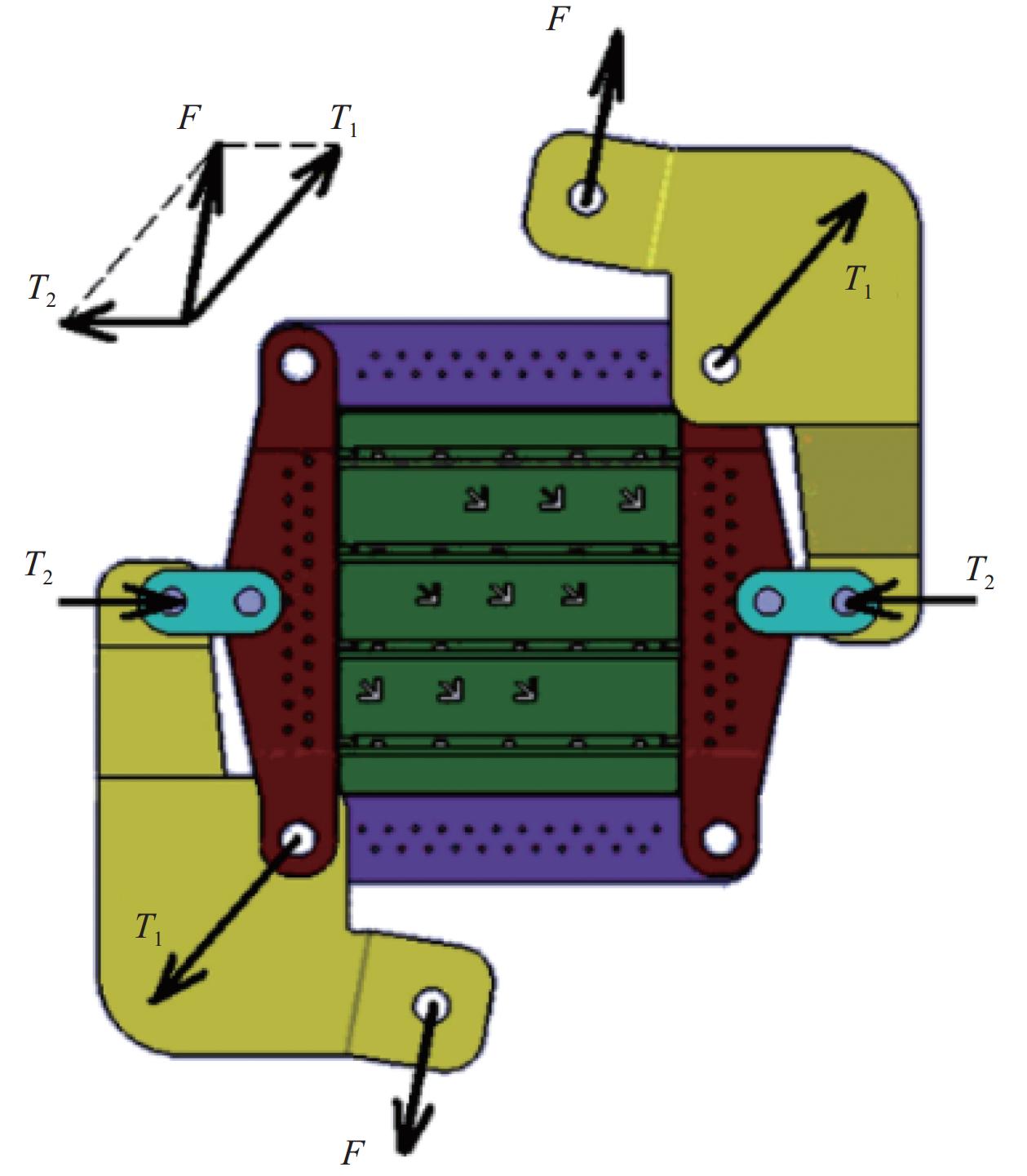
方法本文从复合材料加筋板结构在工程中最常用的三种方法展开介绍：第一部分为常用理论方法介绍及具体公式，并提供有效宽度的处理方法；第二部分详细介绍有限元方法的分析过程，并分别对复合材料加筋板的层内层间模拟方法展开综述；第三部分分别从夹具设计、加载类型以及屈曲疲劳三个方面介绍了屈曲与后屈曲的试验方法。最后分别对三种方法进行优缺点的总结，并对该领域的研究进行了展望。
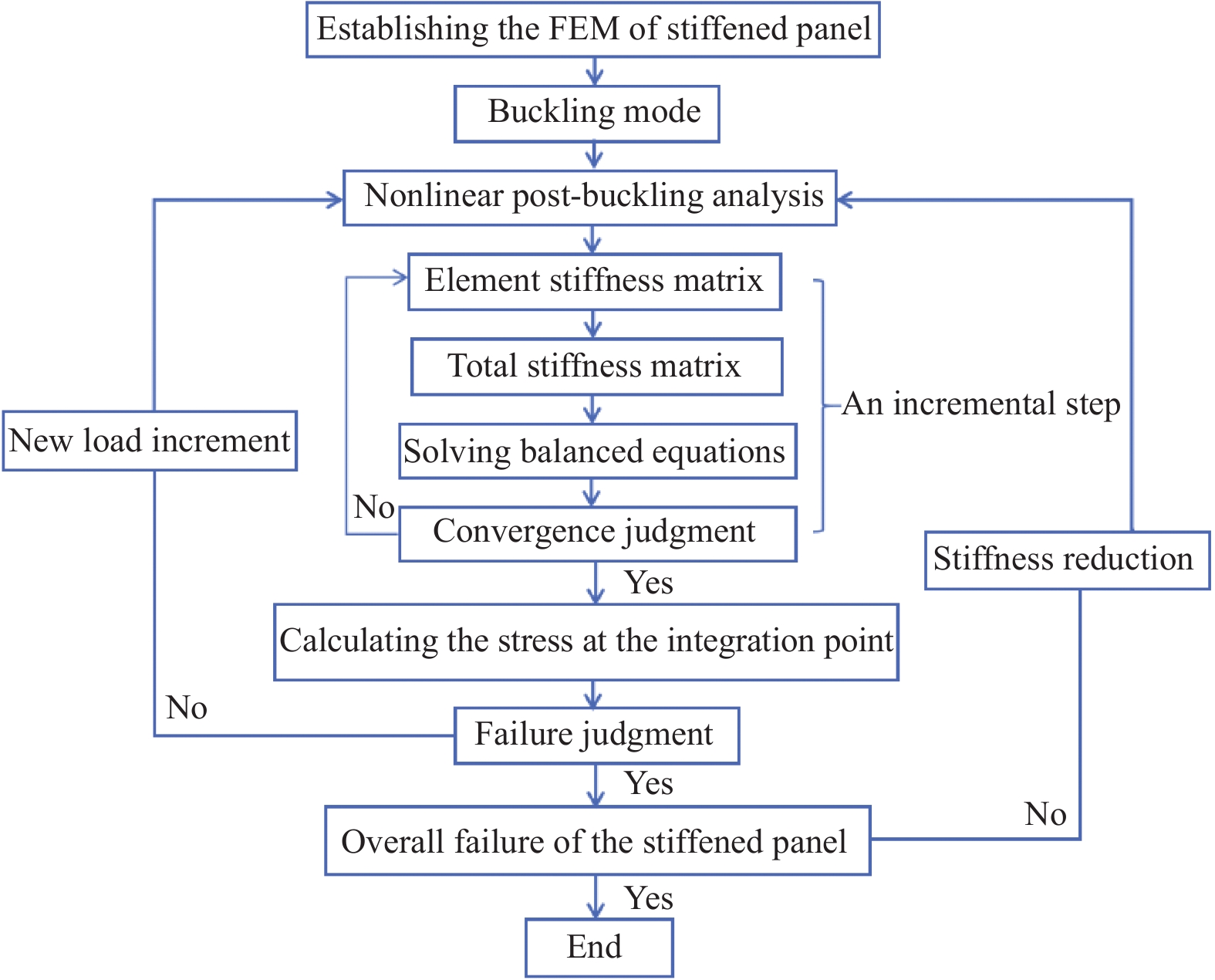
结果理论方法在初步设计阶段具有不可替代的重要性。通过层板理论延伸的分析模型以及工程经验得到的计算公式，可以快速获得加筋板的屈曲与后屈曲载荷，其中最重要的步骤是如何正确地简化模型，这对于加筋板的初步设计具有极高的参考价值。但理论模型和经验公式精度有限，无法完全模拟实际情况，且忽略了复合材料的缺陷。有限元方法能够针对复杂几何形状、特殊边界情况进行求解，选择合适的损伤、失效准则，能够准确模拟加筋板的损伤、失效过程，并得到加筋板的屈曲载荷和极限载荷。其中，渐进损伤分析(Progressive Damage Analysis，PDA)方法是预测复合材料层合板失效过程的有效工具。根据不同情况选取适当的层间损伤模型及失效准则，能够使得有限元分析结果更加精确。试验是研究复合材料加筋板屈曲与后屈曲行为不可或缺的手段。针对不同的载荷类型，包括面内载荷(压缩、剪切、压剪混合)和冲击载荷，通过精心设计的试验夹具、合适的加载方式和先进的试验设备，研究人员能够准确直观地测得加筋板的屈曲/后屈曲失效模式以及关键载荷参数。
结论深入研究加筋板的屈曲与后屈曲性能，挖掘后屈曲承载能力，能够进一步实现飞机轻量化的目标。理论方法通常用理论分析模型及既定公式对加筋板的屈曲和破坏载荷进行计算。其中工程算法速度较快，但精度较低，没办法考虑复杂的边界条件。因此通常用于加筋板初步设计阶段，为设计人员提供一个大致的范围以供参考。有限元方法可以对各种复杂的加筋板外形以及边界条件进行模拟，选取合适的失效准则和建模方法，可以较为准确地预测出加筋板屈曲和后屈曲载荷。合理地使用有限元工具可以减少试验的成本，一般可用于后期设计及验证阶段。试验可以清晰直观地观测到加筋板受载时的失效过程及破坏模式，可以用于最终试验验证以及对有限元方法进行修正。随着科技的飞速发展，未来复合材料加筋板的屈曲与后屈曲分析方法将持续发展，特别是在数值仿真精度的提高、理论模型的完善以及多尺度分析技术的融合等方面，将有显著进展。
计量
- 文章访问数: 166
- HTML全文浏览量: 196
- PDF下载量: 42
- 被引次数: 8
