Deformation control in shape machining of CFRP flexible parts
-
摘要: 碳纤维增强树脂基复合材料(CFRP)柔性件的保形加工是航空航天高端装备制造的重要环节,柔性件的可靠装夹是控制加工变形、降低加工尺寸偏差的前提。首先,在理论分析的基础上,明确了柔性件装夹中夹紧及摩擦约束基本条件,提出了基于悬臂梁理论的“随形-就近”吸盘分布原则。进而,使用“ISIGHT-ABAQUS”联合仿真方法,实现了不同装夹条件及等效切削力作用下CFRP柔性件变形的仿真分析,分析表明:真空吸盘的弹性变形易加大装夹变形,应采用弹性真空吸盘与刚性定位吸盘组合的方式;定位吸盘数量为8、12或16,并“随形-就近”分布时,真空吸盘数量及分布对柔性件变形的影响可忽略。最后,仿真与实验分析了考虑定位几何量偏差时的加工尺寸偏差,仿真与实验结果规律基本一致,优化装夹后的加工尺寸偏差最大降幅达57.7 μm (35%);综上,CFRP柔性件保形加工中变形引起的加工尺寸偏差不容忽略,在“随形-就近”、“定位与真空吸盘组合”原则下优化装夹可以大幅降低变形引起的尺寸偏差。
-
关键词:
- 碳纤维增强树脂基复合材料柔性件 /
- 保形加工 /
- 装夹 /
- 变形 /
- 尺寸偏差
Abstract: The shape machining of carbon fiber reinforced polymer (CFRP) flexible parts is an important process in manufacturing of high-end aerospace equipment. Reliable clamping of the flexible parts is a prerequisite to control the deformation and reduce the dimensional deviation in machining. Firstly, the basic conditions for clamping and friction constraint by theory analysis were given, and a principle of “Following the shape and near the point” for the sucker distribution based on the cantilever beam theory was proposed. Furthermore, based on the “ISIGHT-ABAQUS” co-simulation method, the simulation analysis of the deformation of the CFRP flexible part were taken under different clamping conditions. The research shows that the elastic deformation of the vacuum sucker is easy to increase the clamping deformation, and the combination of the vacuum and positioning suckers should be used. When the numbers of the positioning suckers are 8, 12, or 16, and are distributed according to the principle of “Following the shape and near the point”, the influence of the distribution of the vacuum sucker on the deformation of the flexible part is negligible. Finally, the machining size deviation when considering the positioning geometric deviation was analyzed by the simulation and experiment. The trends in simulation and experiment are consistent with each other, and after the clamping optimization the dimension deviation can be reduced by 57.7 μm (35%). In summary, the machining dimension deviation caused by the deformation in shape machining of CFRP flexible parts cannot be ignored, and then the clamping optimization under the proposed principles of “Following the shape and near the point” and “Combining of positioning and vacuum suckers” can greatly reduce the dimension deviation caused by the deformation.-
Keywords:
- CFRP flexible part /
- shape machining /
- clamping /
- deformation /
- dimensional deviation
-
碳纤维增强树脂基复合材料(CFRP)柔性件(蒙皮、壁板类)的保形加工是航空航天高端装备制造的重要环节,其加工精度直接决定了该类复材件的制造容差水平及后续的装配难度[1]。可见,如何控制此类复材柔性件的加工变形,降低加工误差,是决定设计对制造各环节容差分配的关键。其保形加工能力恰好能满足设计分配的容差要求,甚至远远胜任,降低其他环节的容差控制压力,是先进飞机制造领域追逐的理想目标。
对于此类复材柔性件来说,由于其薄壁弱刚性特征,若装夹不合理,易引起工件不同程度的变形,甚至因装夹刚度不足而引起过大的加工变形,最终导致加工超差。工程中20%~60%的加工误差是由工件装夹不合理引起的[2]。基于“N+2+1”原则的可重构柔性工装系统是目前适应性较好的装夹方式,即在第一基准面上采取N(N>3)个定位元件,通过重复定位解决切边、开窗口等加工中因局部刚性差而易变形的问题。
针对复材柔性件保形加工中装夹变形过大、局部刚度与切削载荷不匹配,导致工件位姿误差大、保形加工精度难保证的问题,国内外学者基于“N+2+1”定位原则,利用合金类柔性件加工变形的仿真与实验数据,结合遗传算法、非线性回归等优化方法,研究了合金类柔性件装夹布局的优化问题[3]。Camelio等[4]从二维梁和三维弹性板理论层面,建立了合金类柔性件的装夹变形机械模型,为最佳定位位置的解析优化问题提供了理论支撑。Vaz等[5]通过开展系列切削过程仿真建模的研究,为合金类柔性件加工中的局部变形求解提供了有益借鉴。
面向工程需求的实验探索可以直接为加工工艺提供参考,Han等[6]开展了多种铝合金柔性件的铣削实验,分析归纳了不同材料属性、厚度下的加工局部变形规律。合金类柔性件装夹变形的实验与仿真研究结果表明:定位件位置分布、装夹顺序及夹紧力施加方式是装夹变形主要影响因素[1, 7-8]。周孝伦等[9]结合有限元仿真与遗传算法,开展了考虑接触与弹性变形的合金类柔性件装夹布局优化研究。Guo等[10]仿真研究了刀具轨迹、夹具分布对合金类柔性件加工变形的影响。陈蔚芳等[11]、倪丽君[12]进一步考虑了切削力、时变工件轮廓和刚度对合金类柔性件加工变形的影响,开展了夹紧元件位置及夹紧力大小优化研究。路冬[13]引入装夹应力、机械应力及热应力等因素的共同作用,仿真与实验研究了航空合金柔性件铣削加工中的工件变形,并结合遗传算法优化了定位点分布,以获得最优装夹布局。Liu等[14]仿真分析了合金类柔性件的铣削变形,研究表明在最大变形处逐个增加定位点可以有效降低变形。袁俊凇[15]仿真分析了辅助支撑位置和夹紧位置分布对柔性件装夹变形的影响。王沙沙[16]应用粒子群算法对柔性件加工中的装夹布局和切削参数开展了优化研究,有效减少了柔性件的加工变形。Hu[17]基于合金柔性件数模与实际测量的外形尺寸数据,仿真分析了多点分布及支撑柱空间几何参数对工件变形的影响,获得了定位分布与切削力耦合作用下的装夹变形及误差数据。赵旭亮[18]在实验数据的基础上,建立了柔性件装夹变形的BP神经网络预测模型。杨元等[19]建立了一种基于支持向量回归机的铝合金蒙皮定位布局优化模型,有效减小有限元计算成本。Matras等[20]通过有限元仿真,重点讨论了铣削进给和装夹分布对加工变形的影响。对CFRP柔性件加工来说,关注的重点多在切削力建模与预测方面[21-22]。仅有Stefan等[23]研究了采用多点夹紧装夹CFRP壁板件时,夹紧点间距对壁板件制孔误差的影响。
综上所述,目前文献中以合金类柔性件的保形加工研究为主,面向复材柔性件保形加工中变形控制的研究较少。因此,本文以CFRP柔性件保形加工变形及其所引起的加工尺寸偏差为研究对象,采用参数化联合仿真及非接触测量实验相结合的方式,研究真空吸附组件(定位吸盘和真空吸盘组合)的位置分布和数量对柔性件变形及尺寸偏差的影响规律,为CFRP柔性件保形加工的装夹方案优化提供可参考的方法与数据支撑。
1. 柔性件装夹理论基础
1.1 柔性件平衡约束
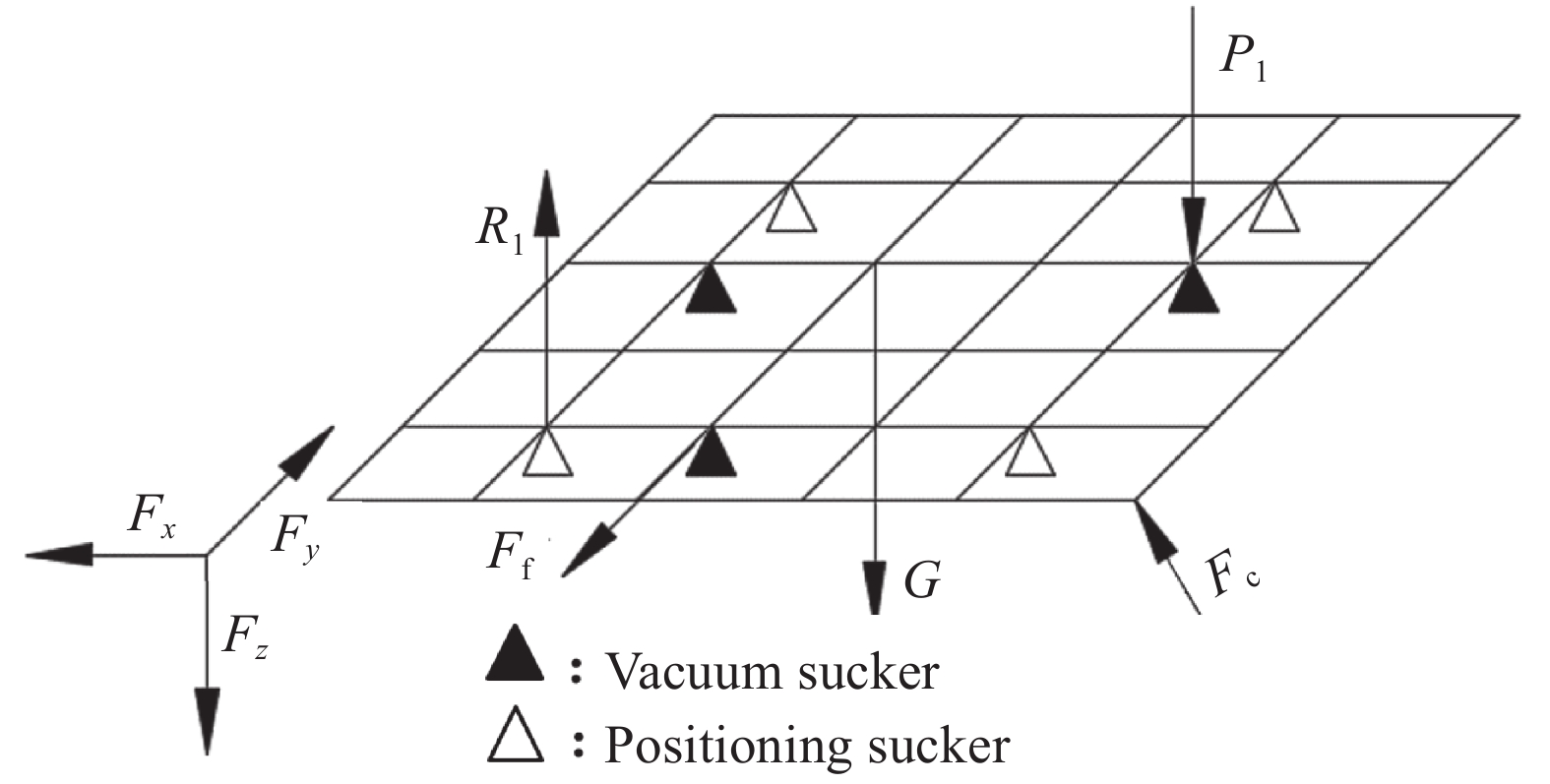
CFRP柔性件保持平衡的充分必要条件是合力与合力矩都为0,也就是要求力平衡和力矩平衡[7],如图1所示。可用数学式表达如下:
![]() 图 1 碳纤维增强树脂基复合材料(CFRP)柔性件约束平衡示意图R1—Reaction force of positioning sucker somewhere; P1—Clamping force of vacuum sucker somewhere; Fx—Tangential force; Fy—Radial force; Fz—Axial force; Ff—Friction; Fc—Milling force; G—Gravity of flexible partsFigure 1. Balance schematic diagram of carbon fiber reinforced polymer (CFRP) flexible part
图 1 碳纤维增强树脂基复合材料(CFRP)柔性件约束平衡示意图R1—Reaction force of positioning sucker somewhere; P1—Clamping force of vacuum sucker somewhere; Fx—Tangential force; Fy—Radial force; Fz—Axial force; Ff—Friction; Fc—Milling force; G—Gravity of flexible partsFigure 1. Balance schematic diagram of carbon fiber reinforced polymer (CFRP) flexible partm∑i=1Ri+n∑j=1Pj+∑Ff+Fc+G=0m∑i=1(rriRi)+n∑j=1(rpjPj)+∑(rfFf)+rcFc+rgG+T=0} (1) 式中:Ri为定位吸盘i处的反作用力;Pj为真空吸盘j的夹紧力;Ff为摩擦力;Fc为铣削力;G为柔性件重力;T为铣削力矩;m为支撑个数;n为夹紧力个数;rc、rf、rg分别为铣削力、摩擦力、柔性件重力的位置矢量;rpj、rri分别为第i个夹紧力和第j个支撑处的位置矢量。
1.2 夹紧约束和摩擦约束条件
1.1节中的平衡约束仅能够确定柔性件处于平衡状态,但并不能借此确定柔性件被夹具固定。当柔性件与支撑脱离接触时,反作用力等于0,装夹失效。为了确保柔性件与支撑充分接触,反作用力应大于0,且为了保证柔性件固定,夹紧力方向应始终朝着柔性件方向[7]。为了确保柔性件在加工过程中不移动,柔性件水平面内受的载荷应小于滑动摩擦力。基于夹紧力对柔性件的约束条件及单个真空吸盘吸附力(37.67 N),由下式分析可得:柔性件被夹紧时需要夹紧吸盘的个数至少为2。
∑Ff+Fx=0;∑Ff+Fy=0∑(rfFf)+rcFx+rcFy=0n∑j=1Pj+Fz+G=0n∑j=1(rpjPj)+rcFz+rgG=0} (2) 式中:Fx为切向力;Fy为径向力;
Fz 为轴向力。1.3 基于悬臂梁理论的定位原则
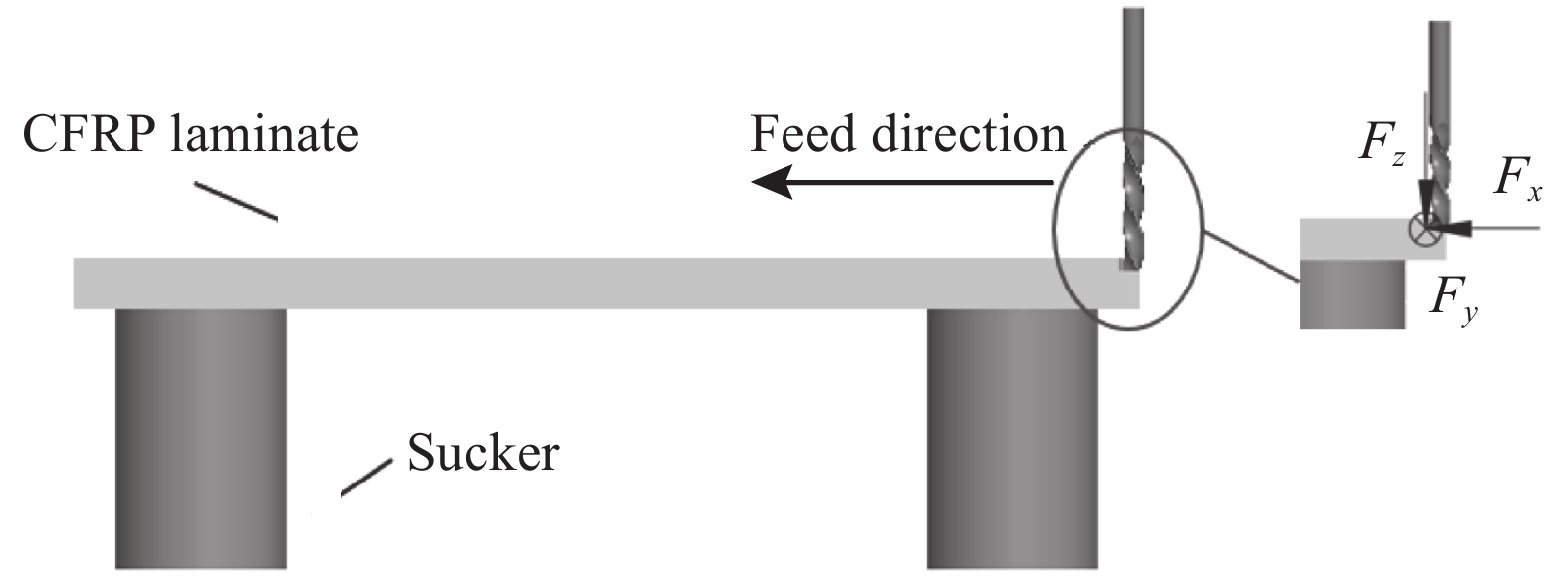
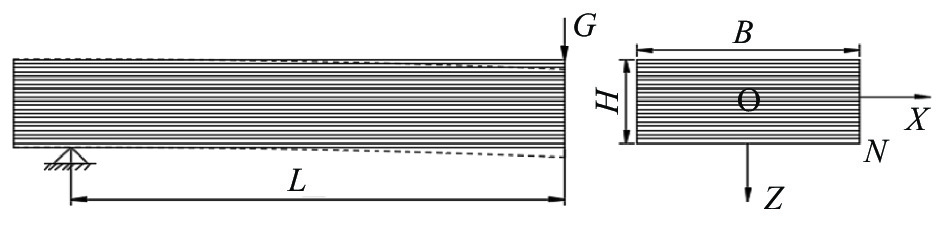
复材板切边时的工况分析如图2所示。本文将其等效为层合板悬臂梁模型,如图3所示。对于均匀厚度的偶数铺层悬臂梁[24],梁的有效抗弯模量由下式计算:
Ef=8N3N/2∑N3((E1)j(3j2−3j+1)) (3) 其中:N为材料铺层层数,即值为32;Ef为梁的有效抗弯模量;E1为碳纤维复合材料的弹性模量;j为第j个支撑处的位置矢量。
截面惯性矩Iyy由下式可得:
Iyy=BH312 (4) 进而由下式计算悬臂梁的最大挠度Wmax与悬臂长度L间关系曲线,如图4所示。
Wmax (5) 式中:B为截面宽度,80 mm;H为截面高度,4 mm;F为铣削力,40 N。
可见,定位吸盘位置应尽可能接近切削位置,悬臂长度L小于60 mm时最大挠度趋于0,即在设置吸盘定位件时应遵循“随形-就近”定位原则。
2. 柔性件装夹有限元模型
2.1 等效模型建立
工程中,切边、开窗口等铣削加工中,铣刀轴线、吸盘定位件轴线均始终与柔性件曲面法线方向保持平行,且柔性件仅发生局部变形,并非整体行为。因此,基于单元化思路,将被加工的局部曲面区域近似为平面的情况,结合现有实验条件,本文以CFRP正方形平面柔性件为基本单元开展仿真及实验研究。
CFRP平面柔性件保形加工等效模型如图5所示,柔性件的装夹采用真空吸盘与定位吸盘组合的方式;通过在复材柔性件的危险位置、沿柔性件平面的法线方向施加与最大切削力幅值相当的静态力,研究在此等效切削力作用及装夹约束下的吸盘分布对柔性件变形的影响。
仿真模型中的CFRP柔性件尺寸为500 mm×500 mm×4 mm,单层厚度0.125 mm,共有32层,铺层方向为[−45,0,45,90]3s,0,0,0,0,0,0,0,0,[−45,0,45,90]3s。吸盘简化为直径80 mm、高100 mm的圆柱体;其中真空吸盘中包含高度为10 mm的橡胶层(弹性体),定位吸盘整体设置为刚体,静态力为集中力作用于加工区域单元节点上。实验样件采用T300/7901单向预浸料经过热固化而成,纤维体积分数达60vol%,其中,CFRP层合板柔性件的力学性能参数及夹紧吸盘橡胶垫材料属性见表1。
CFRP property Value CFRP property Value NBR property Value E11/MPa 125000 G23/MPa 3980 C10 2.767 E22/MPa 11300 v12 0.30 C01 1.439 E33/MPa 11300 v13 0.30 D1 0.014 G12/MPa 5430 v23 0.42 G13/MPa 5430 ρ/(g·cm−3) 1.7 Notes: E—Elastic modulus; G—Shear modulus; v—Poisson's ratio; 1—Direction of fiber; 2—Direction of matrix; 3—Thickness direction of layer; C10, C01, D1—Rivlin coefficient; ρ—Density. 2.2 网格尺寸
模型网格尺寸采用整体均匀、局部细化的原则。柔性件网格采用扫略方式,单元类型为C3D8R(八节点六面体线性减缩积分单元),吸盘部分网格采用扫略、中性轴算法的方式,单元类型为C3D8R。吸盘底部被完全固定,6个自由度均为0。
建模中网格尺寸是否合理,将直接影响仿真计算精度。利用本文提出的联合仿真方法,设置了网格尺寸分别为30、25、20、15、10、5、1 mm的7组仿真实验,讨论了网格尺寸对柔性件位移值的影响规律,如图6所示。
整体来看,不同网格尺寸下的柔性件最大位移值随定位件数量的增加而逐渐减小,仅在采用30 mm网格尺寸时位移值基本不变。随着网格尺寸的减小,柔性件最大位移值呈现增加趋势,且当网格尺寸从5 mm减小至1 mm时,位移值增量明显减小。与此同时,从相邻网格尺寸间柔性件最大位移的差值率来看,如图7所示,25~20 mm之间、5~1 mm之间的位移变化率小,仿真结果稳定性好。因此,兼顾计算成本,该模型中的非加工区域网格尺寸为20 mm,加工区域局部细化网格尺寸为5 mm。
3. 实验设计
3.1 定位与真空吸盘组合原则
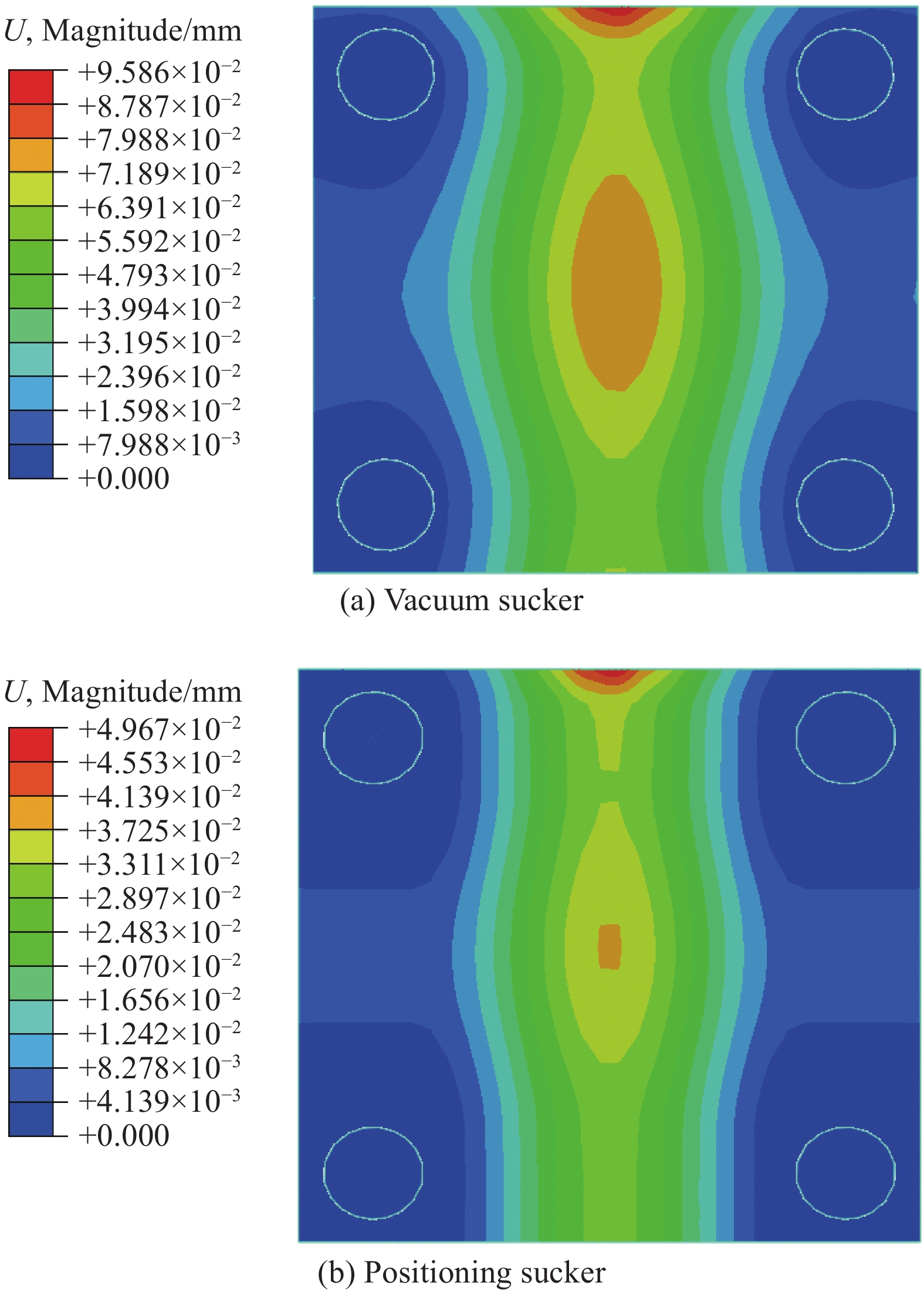
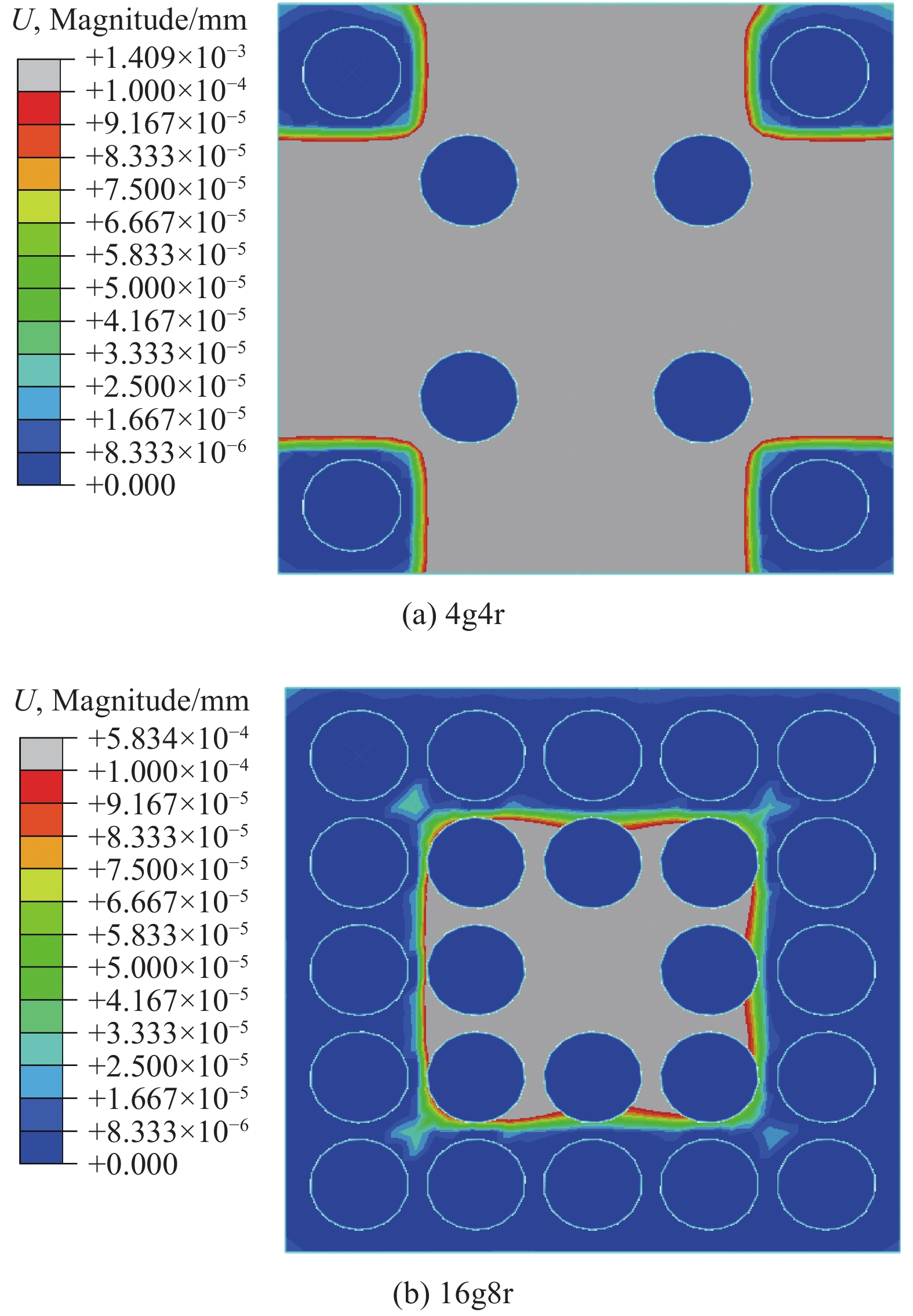
图8为分别采用定位吸盘和真空吸盘装夹下的柔性件变形情况。结果表明:装夹过程中真空吸盘橡胶垫的弹性退让对柔性件位移的影响不容忽视。同时考虑到只采用刚性定位吸盘时,若刚性定位点数目过多,必然会引起柔性件过定位与定位件制造误差之间的矛盾,即离散分布的刚性定位件包络形成的曲面与柔性件自身曲面间的吻合度必然受到定位件误差的影响,过定位点越多,误差协调难度越大,或者误差带来的柔性件变形越复杂。鉴于此,采用刚性定位吸盘与弹性真空吸盘组合更有利于CFRP柔性件的可靠装夹。
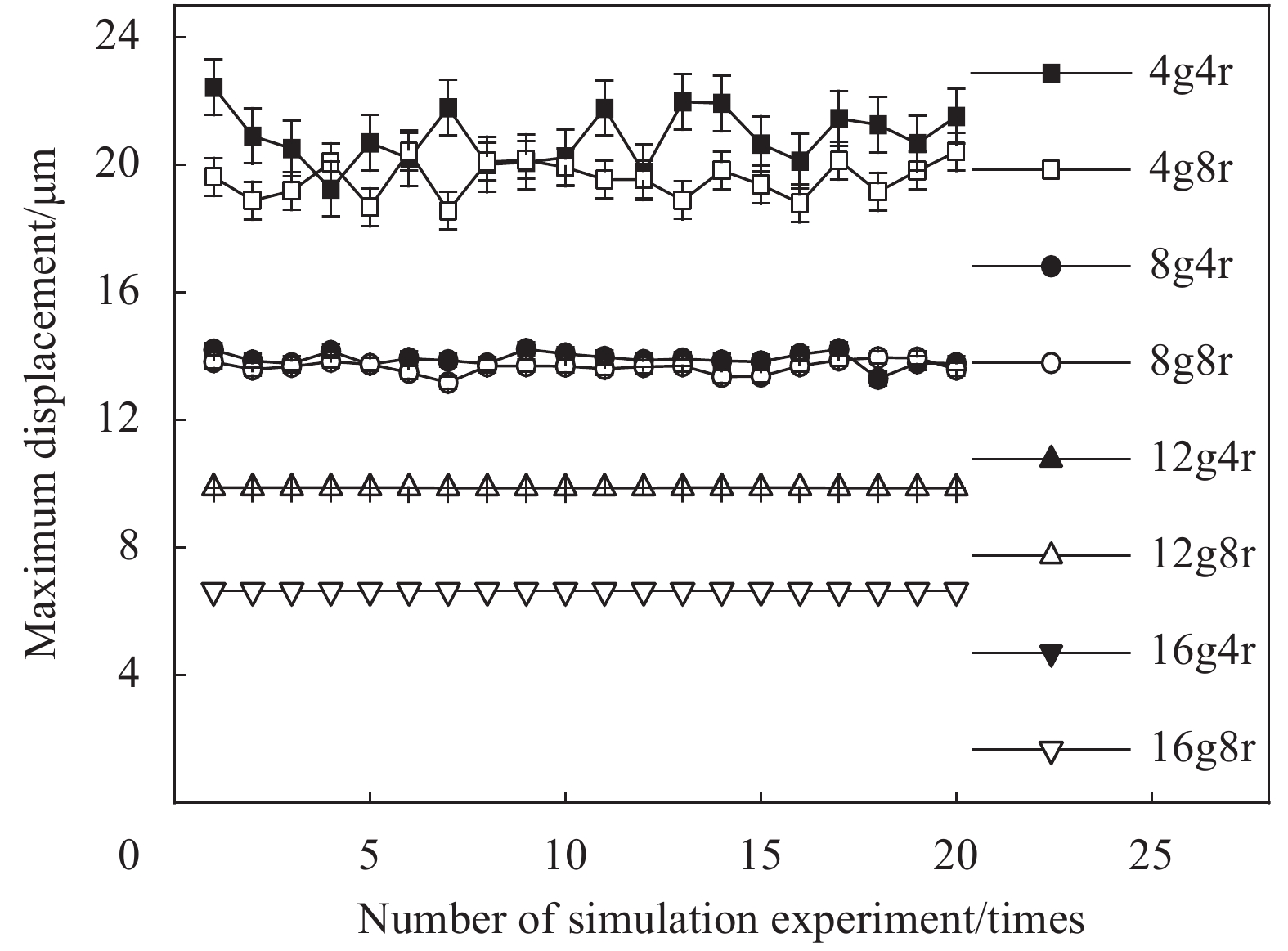
在遵循“随形-就近”原则的前提下,获得了不同数量的定位与真空吸盘组合、随机分布下的柔性件变形数据(160组实验),如图9所示,研究了装夹点随机分布对柔性件变形的影响。以切边为例,静态力施加如图5所示,当定位吸盘数量为8、12、16时,柔性件变形几乎不受真空吸盘分布的影响,且增加真空吸盘的数量,柔性件变形仅减小几微米。可见,定位吸盘与真空吸盘的分布应“随形-就近”,真空吸盘的数量满足夹紧及摩擦约束即可,应重点关注定位吸盘数量对柔性件变形的影响。
3.2 仿真实验设计
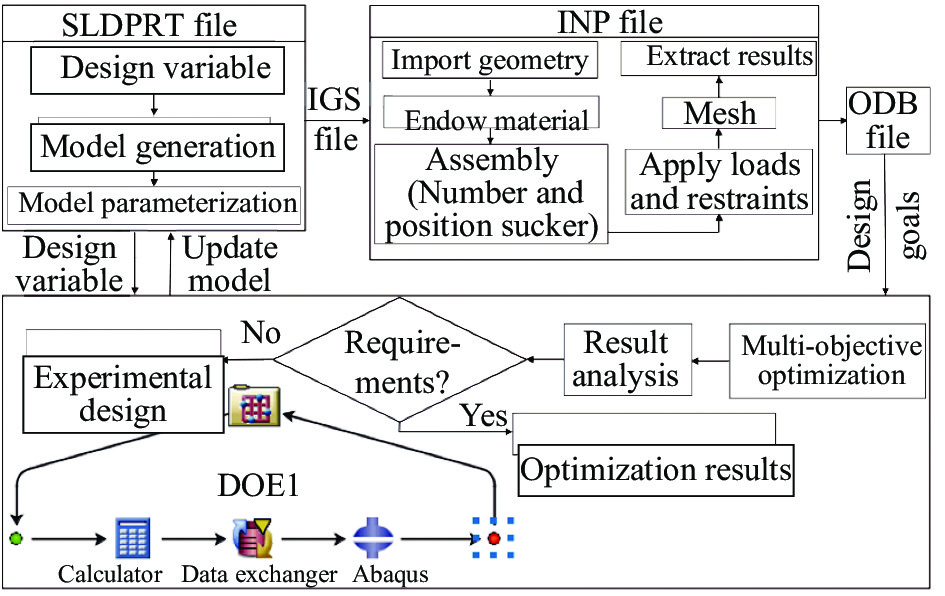
以定位吸盘和真空吸盘组件的位置分布和数量为自变量,CFRP柔性件的最大位移为因变量,设计通过联合仿真实验,如图10所示,分析CFRP柔性件自由状态、理想工装时的柔性件位移及考虑定位几何量偏差时装夹及等效切削力作用下的柔性件位移,从而揭示定位吸盘与真空吸盘的数量及分布对CFRP柔性件变形的影响规律。
依据定位与真空吸盘组合原则,并考虑吸盘几何尺寸(单边最大允许放置吸盘的数量为5个),确定出定位吸盘的数量及分布位置,即定位吸盘应随形、就近分布于柔性件边缘,真空吸盘水平数的设置不需过多。为提高实验效率,采用拉丁超立方方法设计实验,该方法可保证一个因子的每个水平只被研究1次[5],实验设计如表2所示。采用理想工装时,等效静态力下柔性件位移仿真结果的标准偏差如表3所示,表明实验数据可靠。
表 2 实验设计参数Table 2. Parameters of experimental designFactor Level Number of positioning suckers 4 8 12 16 Number of vacuum suckers 4 8 Position distribution of positioning suckers Following the shape and near the point Position distribution of vacuum suckers Random distribution 表 3 采用理想工装时等效静态力作用下的CFRP柔性件位移及标准偏差Table 3. Displacement and standard deviation of CFRP flexible parts under static force by ideal toolingNumber of positioning suckers Number of vacuum suckers Maximum displacement/μm Standard deviation Minimum displacement/μm Standard deviation 4 4 22.430 0.8654 19.240 0.8654 4 8 20.410 0.5899 18.550 0.5899 8 4 14.210 0.2146 13.740 0.2146 8 8 13.950 0.1978 13.590 0.1978 12 4 9.880 0.0036 9.872 0.0036 12 8 9.872 0.0010 9.870 0.0010 16 4 6.650 0.0000 6.650 0.0000 16 8 6.650 0.0000 6.650 0.0000 3.3 验证实验设计
为了验证仿真实验,并获得实验条件下的装夹变形规律,本文设计了包含CFRP壁板件、铝合金型材吸附工装、等效载荷夹具及三维扫描仪的实验系统,如图11所示。铝合金型材吸附工装中设有间距为95 mm吸盘支座阵列分布,以此满足任意位置的定位及夹紧吸盘设置需求。
依次按照仿真实验方案,将CFRP壁板件装夹于铝合金型材吸附工装上,采用悬挂重物的方式施加等效静态力,最后通过双目视觉非接触式测量手段获得不同工况下的柔性件曲面点云数据,如图12所示。
工程中必然存在工装制造及安装误差,如图13所示,导致柔性件偏离理想位置,误差特征如表4所示,δ1为零件1与其接触面间贴合度的随机性误差;δ2、δ3、δ5及δ6为零件本身制造误差,基于标准公差(International tolerance)7级(IT7)精度考虑不同尺寸范围内极限偏差;δ4为装置的定位偏差,该误差是随机性的;δ7为夹紧力不当及不均匀的随机性误差;δ8为测量仪器系统偏差及不可避免的人工测量的随机性误差。
![]() 图 13 实验装置装配尺寸链1—Leveling base; 2—Bottom support profiles; 3—Connecting frame profiles; 4—Connection profiles for suckers; 5—Adapters; 6—Sucker assembly; 7—CFRP laminates; A1—Overall height of the experimental setup; A2—Installation height of leveling base; A3—Installation height of the bottom support profile; A4—Height of the bottom support profile installation position to the upper surface of the connecting frame profile; A5—Installation height of connection profiles for sucker; A6—Adaptor installation height; A7—Sucker assembly installation height; δ—Cumulative errorFigure 13. Assembly dimensional chain of experimental system
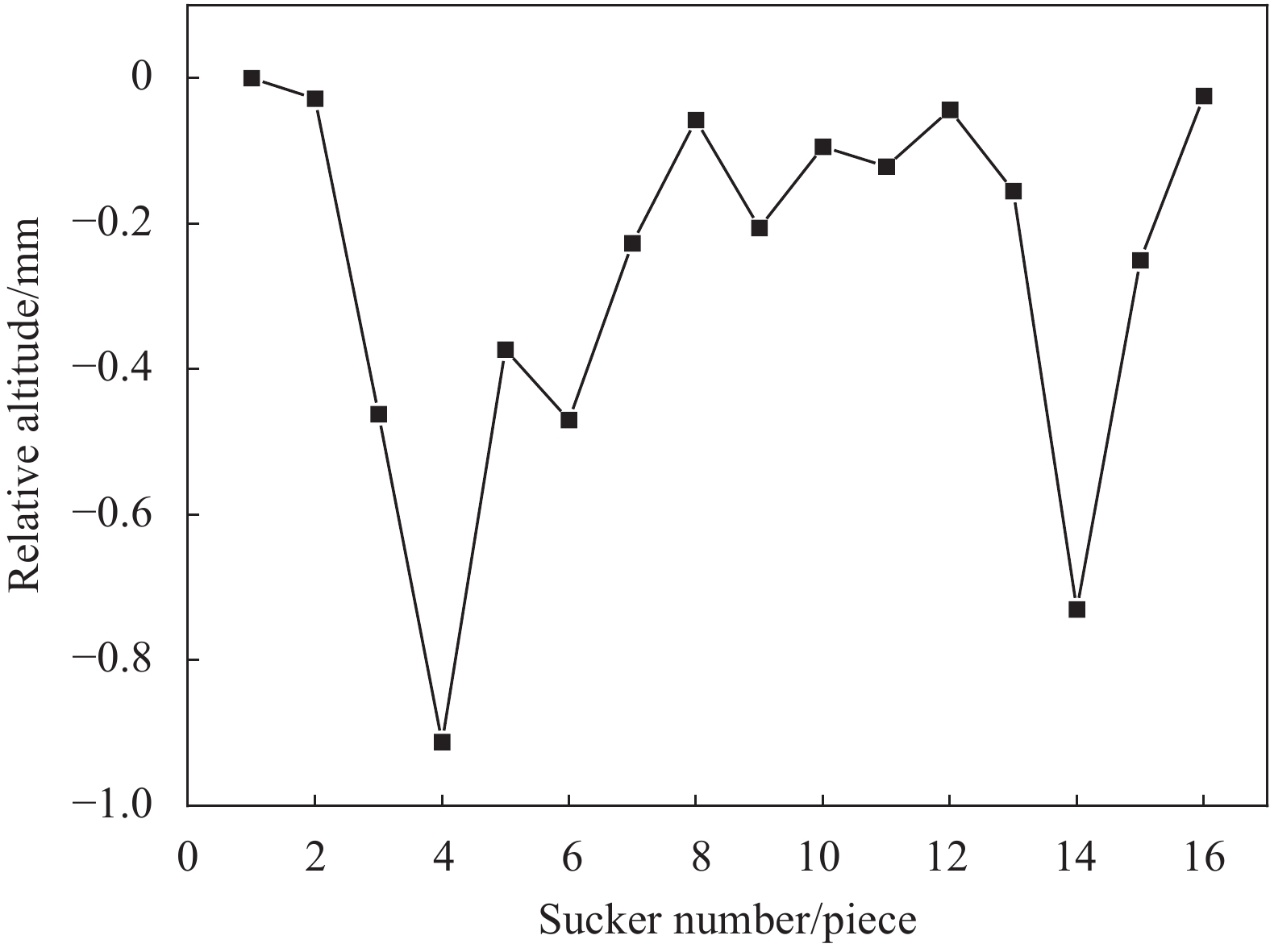
图 13 实验装置装配尺寸链1—Leveling base; 2—Bottom support profiles; 3—Connecting frame profiles; 4—Connection profiles for suckers; 5—Adapters; 6—Sucker assembly; 7—CFRP laminates; A1—Overall height of the experimental setup; A2—Installation height of leveling base; A3—Installation height of the bottom support profile; A4—Height of the bottom support profile installation position to the upper surface of the connecting frame profile; A5—Installation height of connection profiles for sucker; A6—Adaptor installation height; A7—Sucker assembly installation height; δ—Cumulative errorFigure 13. Assembly dimensional chain of experimental system使用北京天远三维科技有限公司OKIO-B三维扫描仪对定位吸盘定位件位置进行测量,获得铝合金型材吸附工装中定位件之间的相对高度,以此反映上述整体误差情况,扫描点云如图14所示。在每个定位件的点云数据中取3个点的平均值作为定位件的最终坐标值,进而获得每一种定位方案下所有定位件的实际高度差,如图15所示。
表 4 实验系统内的尺寸偏差Table 4. Dimensional deviation in the experimental systemDeviation type Deviation Misalignment deviation of part 1 (δ1) — Manufacturing deviation of part 2 (δ2) ±0.3 mm Manufacturing deviation of part 3 (δ3) ±0.3 mm Positioning deviation of the device (δ4) — Manufacturing deviation of part 4 (δ5) ±0.3 mm Manufacturing deviation of part 5 (δ6) ±0.2 mm Deviation caused by clamping force (δ7) — Deviation caused by measuring
instruments and methods (δ8)— Total deviation (δ∑) — 3.4 柔性件位移下的几何偏差
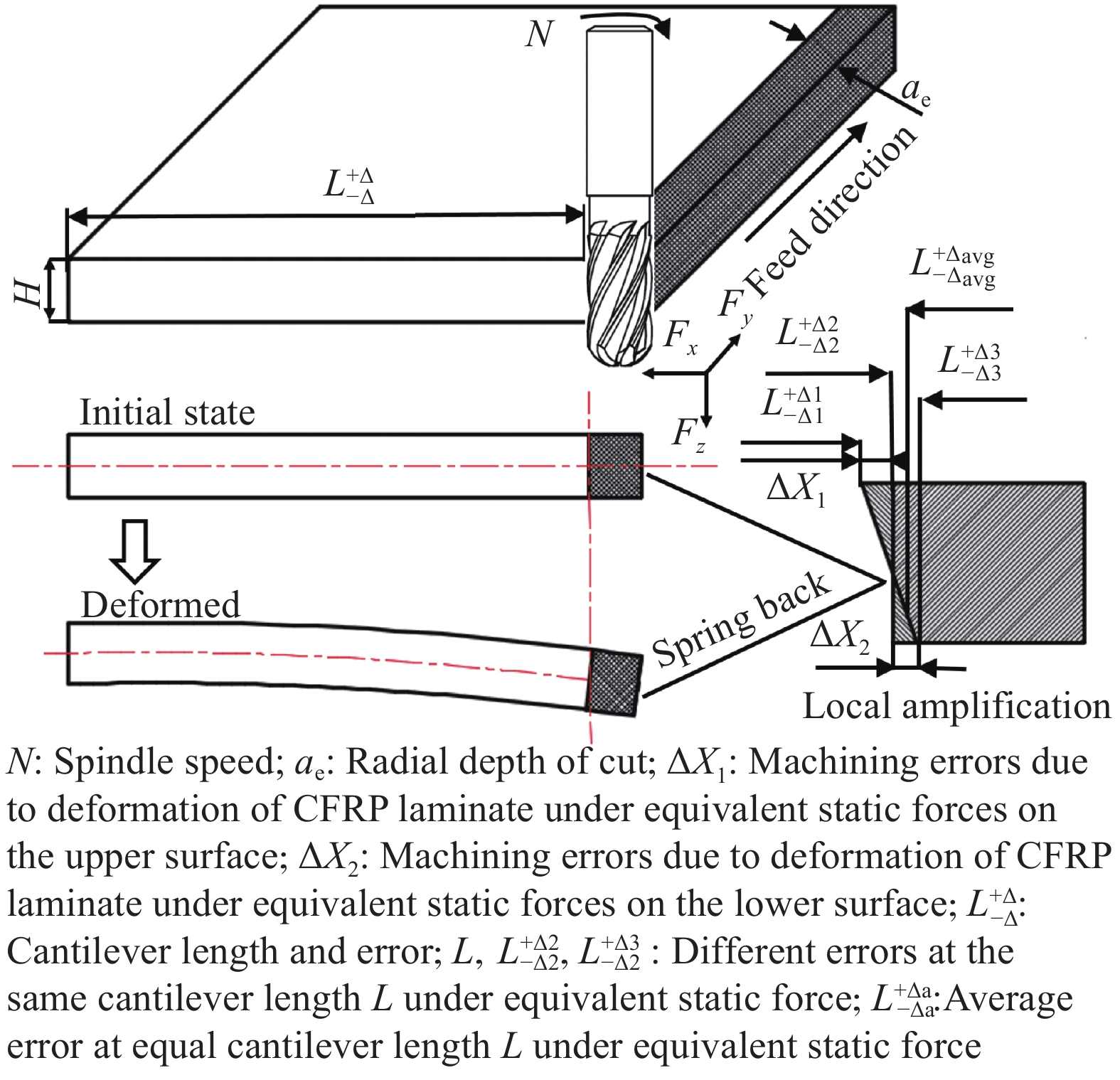
在仿真分析及实验验证获得柔性件位移的基础上,利用悬臂梁理论,可以间接分析柔性件位移对其加工几何偏差的影响,如图16所示。由于柔性件的弯曲,必然导致铣刀与其接触位置及切削深度的变化,实际已加工表面不再垂直于柔性件中性面。本文采用因弯曲变形导致的未切除部分的余量表征柔性件外形尺寸的单向偏差:
\varphi = \frac{{F{L^2}}}{{2{E_{\rm{f}}}{I_{yy}}}} (6) \frac{W}{\theta } = \frac{3}{2}L (7) \Delta X = \frac{H}{2}\sin \theta (8) 式中:ϕ为复合材料悬臂梁转角弧度;θ为等效静态力作用点切线方向转角;ΔX为等效静态力作用下CFRP层合板变形时所产生的长度L方向上的误差;W为复合材料悬臂梁挠度。板的弯曲意味着其悬臂长L减小,实际切边加工中则意味着实际径向切深ae减小,实际的切削量减小,未加工余量增加。
4. 结果与分析
4.1 自由状态、理想工装下柔性件装夹变形规律
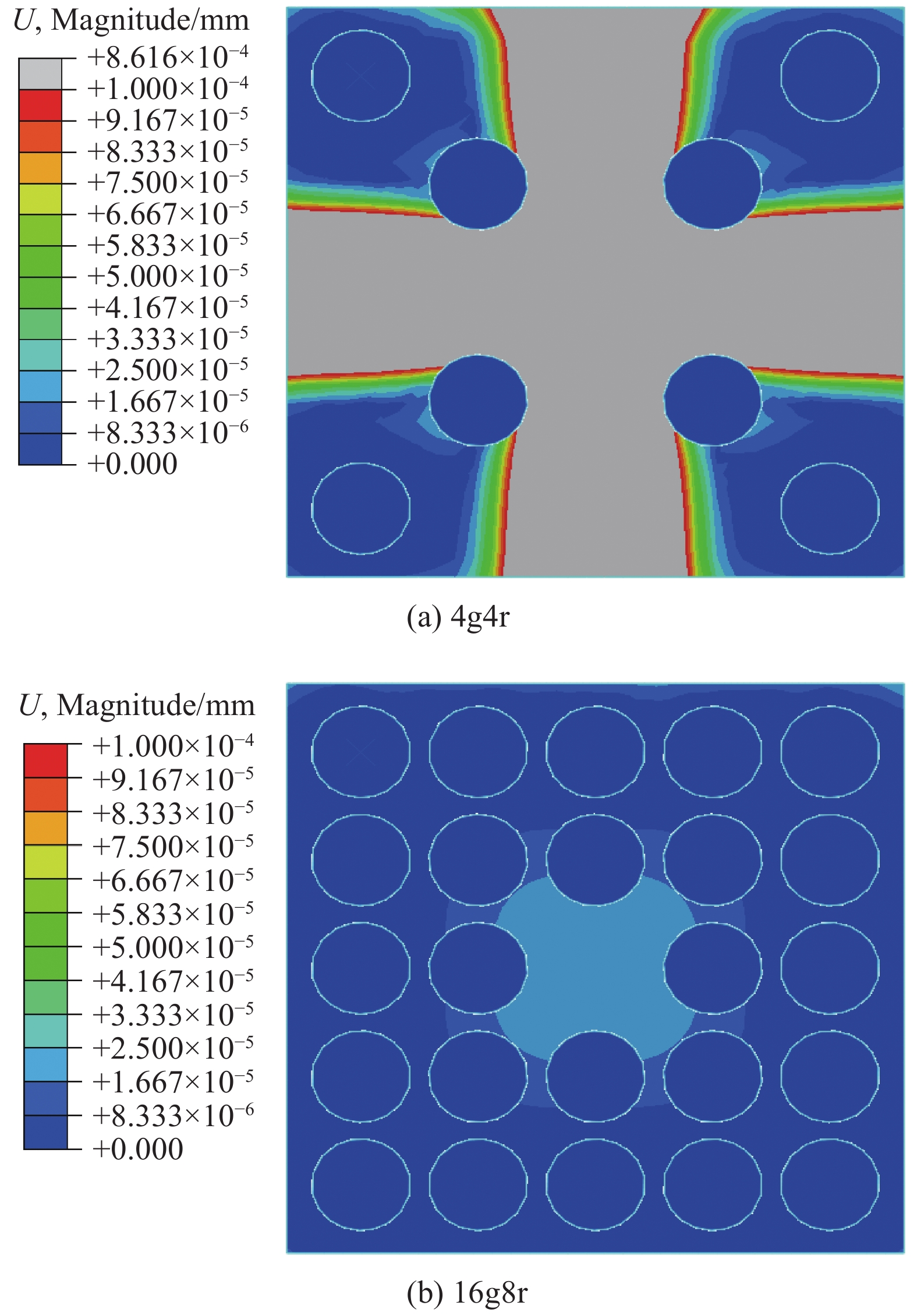
获知CFRP柔性件自由状态及理想工装状态下的变形规律是可靠装夹的前提。自由状态下采用不同装夹方案时的柔性件位移如图17所示,支撑刚度最小的情况,即4个真空吸盘与4个定位吸盘组合,柔性件最大位移仅为0.86 μm,随着定位与夹紧点的增加,最大位移减小至0.10 μm。
理想工装下采用不同装夹方案时的柔性件位移如图18所示,在真空吸盘吸附力作用下,CFRP柔性件中间部位下移相对较大,但整体最大位移皆小于1.50 μm。仿真结果表明,自由状态、理想工装状态下自重、吸附力引起的变形均小于1.5 μm,且随着吸盘数目增加,自重及吸附力作用下的位移趋于一致,如图19所示,证明了“随形-就近”原则分布装夹的合理性。
4.2 虑及定位几何偏差时的柔性件加工变形规律
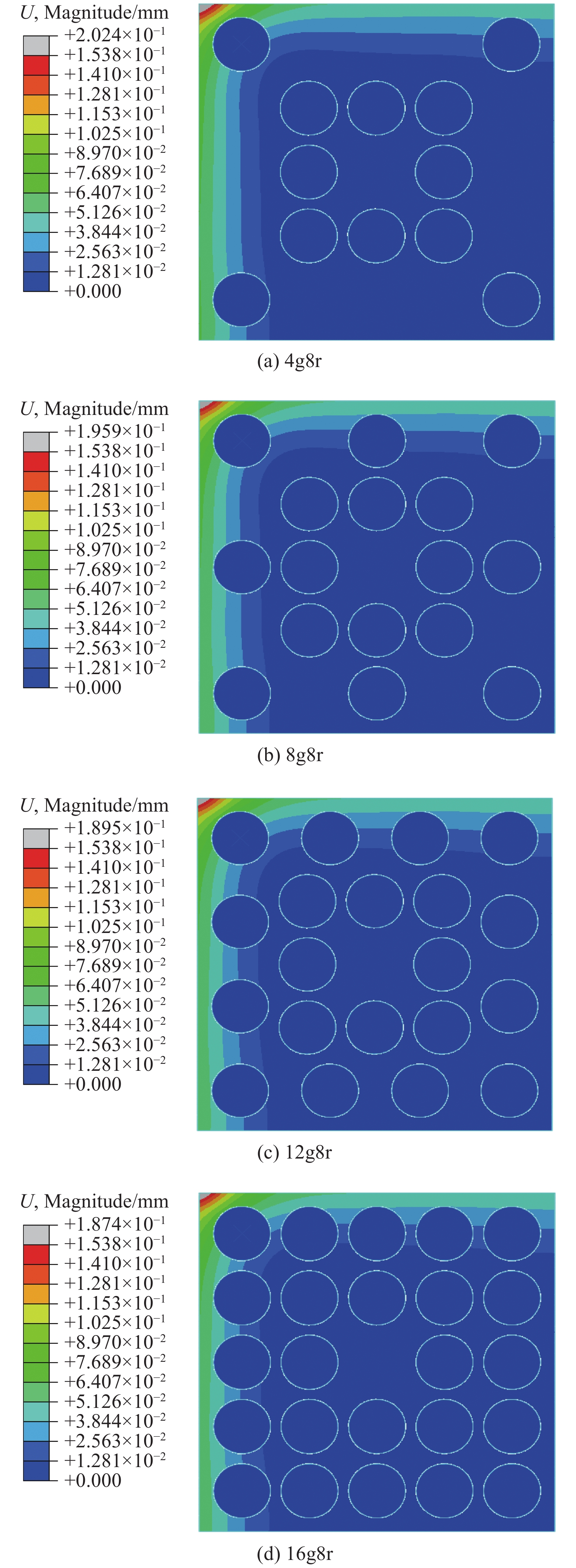
在获得实验系统中定位偏差高度差数据的基础上,仿真分析了切边加工中铣削初始阶段位置A在等效切削力作用下的位移情况,如图20所示。考虑定位偏差时等效切削力作用下的最大位移达到了202.4 μm。可见,实际定位偏差的影响不容忽略。当定位吸盘与真空吸盘数量分别为12、8,分布如图20所示时,柔性件的最大位移减小至189.5 μm。随着吸盘数量的增加,位置A的位移减小至187.4 μm,最大降幅为15.0 μm(近10%)。
验证实验中柔性件的位移由431 μm减小到279.6 μm,降幅为151.4 μm(近40%),如图21所示,结果表明:由于有限元仿真的等效及实验测量误差的存在,仿真与实验数据间存在差异,但柔性件变形规律与实验规律基本保持一致。
不同装夹方案下柔性件仿真与实验加工尺寸偏差的变化规律如图22所示,随着吸盘数量的增加,CFRP柔性件加工尺寸偏差呈减小趋势,上表面仿真值由92.0 μm降至77.7 μm,下表面仿真值由85.3 μm降至70.5 μm,最大降幅为14.8 μm (17.4%);实验值由164.5 μm降至106.8 μm,最大降幅为57.7 μm (35%)。对于仿真与实验之间存在的误差,后续研究中考虑通过边界条件等效中引入工程经验系数予以修正,以此实现基础模型在工程应用中的推广。
5. 结 论
(1) 碳纤维增强树脂基复合材料(CFRP)柔性件装夹中的吸盘应遵循“随形-就近”分布原则,能够更好的抑制CFRP柔性件变形。
(2) 真空吸盘的弹性变形对装夹变形影响不容忽视,应采用带有刚性定位件的定位吸盘与真空吸盘组合的方式。
(3) 定位吸盘数量为8、12、16,并“随形-就近”分布时,真空吸盘数量及分布对柔性件变形的影响可忽略。
(4) 不同装夹方案下柔性件变形及加工尺寸偏差的仿真与实验结果规律基本一致,优化后的柔性件加工尺寸偏差最大降幅达57.7 μm(35%)。
(5) CFRP柔性件保形加工中变形引起的加工尺寸偏差不容忽略,在“随形-就近”、“定位与真空吸盘组合”原则下优化装夹方案可以大幅降低变形引起的尺寸偏差。
-
图 1 碳纤维增强树脂基复合材料(CFRP)柔性件约束平衡示意图
R1—Reaction force of positioning sucker somewhere; P1—Clamping force of vacuum sucker somewhere; Fx—Tangential force; Fy—Radial force; Fz—Axial force; Ff—Friction; Fc—Milling force; G—Gravity of flexible parts
Figure 1. Balance schematic diagram of carbon fiber reinforced polymer (CFRP) flexible part
图 13 实验装置装配尺寸链
1—Leveling base; 2—Bottom support profiles; 3—Connecting frame profiles; 4—Connection profiles for suckers; 5—Adapters; 6—Sucker assembly; 7—CFRP laminates; A1—Overall height of the experimental setup; A2—Installation height of leveling base; A3—Installation height of the bottom support profile; A4—Height of the bottom support profile installation position to the upper surface of the connecting frame profile; A5—Installation height of connection profiles for sucker; A6—Adaptor installation height; A7—Sucker assembly installation height; δ—Cumulative error
Figure 13. Assembly dimensional chain of experimental system
表 1 T300/7901 CFRP[25]及丁腈橡胶(NBR) [26]的材料参数
Table 1 Material property of T300/7901 CFRP [25] and nitrile rubber (NBR)[26]
CFRP property Value CFRP property Value NBR property Value E11/MPa 125000 G23/MPa 3980 C10 2.767 E22/MPa 11300 v12 0.30 C01 1.439 E33/MPa 11300 v13 0.30 D1 0.014 G12/MPa 5430 v23 0.42 G13/MPa 5430 ρ/(g·cm−3) 1.7 Notes: E—Elastic modulus; G—Shear modulus; v—Poisson's ratio; 1—Direction of fiber; 2—Direction of matrix; 3—Thickness direction of layer; C10, C01, D1—Rivlin coefficient; ρ—Density. 表 2 实验设计参数
Table 2 Parameters of experimental design
Factor Level Number of positioning suckers 4 8 12 16 Number of vacuum suckers 4 8 Position distribution of positioning suckers Following the shape and near the point Position distribution of vacuum suckers Random distribution 表 3 采用理想工装时等效静态力作用下的CFRP柔性件位移及标准偏差
Table 3 Displacement and standard deviation of CFRP flexible parts under static force by ideal tooling
Number of positioning suckers Number of vacuum suckers Maximum displacement/μm Standard deviation Minimum displacement/μm Standard deviation 4 4 22.430 0.8654 19.240 0.8654 4 8 20.410 0.5899 18.550 0.5899 8 4 14.210 0.2146 13.740 0.2146 8 8 13.950 0.1978 13.590 0.1978 12 4 9.880 0.0036 9.872 0.0036 12 8 9.872 0.0010 9.870 0.0010 16 4 6.650 0.0000 6.650 0.0000 16 8 6.650 0.0000 6.650 0.0000 表 4 实验系统内的尺寸偏差
Table 4 Dimensional deviation in the experimental system
Deviation type Deviation Misalignment deviation of part 1 (δ1) — Manufacturing deviation of part 2 (δ2) ±0.3 mm Manufacturing deviation of part 3 (δ3) ±0.3 mm Positioning deviation of the device (δ4) — Manufacturing deviation of part 4 (δ5) ±0.3 mm Manufacturing deviation of part 5 (δ6) ±0.2 mm Deviation caused by clamping force (δ7) — Deviation caused by measuring
instruments and methods (δ8)— Total deviation (δ∑) — -
[1] 王运巧, 梅中义, 范玉青. 薄壁弧形件装夹布局有限元优化[J]. 机械工程学报, 2005, 41(6):214-217. DOI: 10.3321/j.issn:0577-6686.2005.06.041 WANG Yunqiao, MEI Zhongyi, FAN Yuqing. Clamping of thin-walled curved parts layout finite element optimization[J]. Journal of Mechanical Engineering,2005,41(6):214-217(in Chinese). DOI: 10.3321/j.issn:0577-6686.2005.06.041
[2] WU N H, CHAN K C, LEONG S S. Static interactions of surface contacts in a fixture-workpiece system[J]. International Journal of Computer Applications in Technology,1997,10(3/4):133-151.
[3] KAYA N. Machining fixture locating and clamping position optimization using genetic algorithms[J]. Computers in Industry,2006,57(2):112-120. DOI: 10.1016/j.compind.2005.05.001
[4] CAMELIO J A, JACK HU S, CEGLAREK D. Impact of fixture design on sheet metal assembly variation[J]. Journal of Manufacturing Systems,2007 , 23 (3):182-193.
[5] VAZ M, OWEN D R J, KALHORI V, et al. Modelling and simulation of machining processes[J]. Archives of Computational Methods in Engineering: State of the Art Reviews,2007,14(2):173-204. DOI: 10.1007/s11831-007-9005-7
[6] HAN B, REN C Z, YANG X Y, et al. Experiment study on deflection of alloy thin-wall workpiece in milling process[J]. Materials Science Forum,2012,697:129-132.
[7] 董辉跃, 柯映林. 铣削加工中柔性件装夹方案优选的有限元模拟[J]. 浙江大学学报工学版, 2004, 38(1):17-21. DONG Huiyue, KE Yinglin. Finite element simulation of optimal clamping scheme for thin-walled parts in milling[J]. Journal of Zhejiang University Engineering Science,2004,38(1):17-21(in Chinese).
[8] 秦国华, 张卫红, 吴竹溪, 等. 多重夹紧力及其作用顺序对工件变形的影响分析与优化技术[J]. 工程力学, 2006, 23(S1):229-235. QIN Guohua, ZHANG Weihong, WU Zhuxi, et al. Analysis and optimization technology of the influence of multiple clamping forces and their action sequence on the deformation of workpiece[J]. Engineering Mechanics,2006,23(S1):229-235(in Chinese).
[9] 周孝伦, 张卫红, 秦国华, 等. 基于遗传算法的夹具布局和夹紧力同步优化[J]. 机械科学与技术, 2005(3):339-342. DOI: 10.3321/j.issn:1003-8728.2005.03.025 ZHOU Xiaolun, ZHANG Weihong, QIN Guohua, et al. Synchronous optimization of fixture layout and clamping force based on genetic algorithm[J]. Mechanical Science and Technology,2005(3):339-342(in Chinese). DOI: 10.3321/j.issn:1003-8728.2005.03.025
[10] GUO H, ZUO D W, WANG S H, et al. Effect of tool path on milling accuracy under given clamp[J]. Transactions of Nanjing University of Aeronautics & Astronautics,2005(3):234-239.
[11] 陈蔚芳, 倪丽君, 王宁生. 夹具布局和夹紧力的优化方法研究[J]. 中国机械工程, 2007(12):1413-1417. DOI: 10.3321/j.issn:1004-132X.2007.12.007 CHEN Weifang, NI Lijun, WANG Ningsheng. Research on optimization method of fixture layout and clamping force[J]. China Mechanical Engineering,2007(12):1413-1417(in Chinese). DOI: 10.3321/j.issn:1004-132X.2007.12.007
[12] 倪丽君. 计算机辅助夹具设计中的装夹优化技术研究[D]. 南京: 南京航空航天大学, 2007. NI Lijun. Research on clamping optimization technology in computer aided fixture design[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007(in Chinese).
[13] 路冬. 航空整体结构件加工变形预测及装夹布局优化[D]. 济南: 山东大学, 2007. LU Dong. Processing deformation prediction and clamping layout optimization of aviation monolithic structure parts[D]. Jinan: Shandong University, 2007(in Chinese).
[14] LIU S G, ZHENG L, ZHANG Z H, et al. Optimization of the number and positions of fixture locators in the peripheral milling of a low-rigidity workpiece[J]. The International Journal of Advanced Manufacturing Technology,2007,33(7):668-676.
[15] 袁俊凇. 复杂薄壁结构件铣削加工变形有限元模拟及装夹布局优选[D]. 上海: 上海交通大学, 2011. YUAN Junsong. Finite element simulation of milling deformation and clamping layout optimization of complex thin-walled structure parts[D]. Shanghai: Shanghai Jiao Tong University, 2011(in Chinese).
[16] 王沙沙. 框类柔性件装夹和切削参数的同步优化[D]. 大连: 大连理工大学, 2012. WANG Shasha. Synchronous optimization of clamping and cutting parameters of frame-type thin-walled parts[D]. Dalian: Dalian University of Technology, 2012(in Chinese).
[17] HU F W. Location issues of thin shell parts in the reconfigurable fixture for trimming operation[J]. Journal of Aerospace Technology and Management,2014,3:319-331.
[18] 赵旭亮. 柔性件装夹变形预测及装夹布局优化方法[D]. 南昌: 南昌航空大学, 2014. ZHAO Xuliang. Clamping deformation prediction and clamping layout optimization method of thin-walled parts[D]. Nanchang: Nanchang Hangkong University, 2014(in Chinese).
[19] 杨元, 王仲奇, 杨勃, 等. 基于SVR的航空柔性件夹具布局优化预测模型[J]. 计算机集成制造系统, 2017, 23(6):1302-1309. YANG Yuan, WANG Zhongqi, YANG Bo, et al. Optimization prediction model of fixture layout for aviation thin-walled parts based on SVR[J]. Computer Integrated Manufacturing Systems,2017,23(6):1302-1309(in Chinese).
[20] MATRAS A, PLAZA M. The FEM simulation of the thin walled aircraft engine corpus deformation during milling[J]. Materials Science , 2016 , 10031: 100310B-1.
[21] 秦旭达, 朱圣富, 李士鹏, 等. 不同纤维方向角时碳纤维增强树脂基复合材料切削力建模[J]. 宇航材料工艺, 2020, 50(6):31-40. QIN Xuda, ZHU Shengfu, LI Shipeng, et al. Modeling of cutting force of carbon fiber reinforced resin matrix compo-sites with different fiber orientation angle[J]. Aerospace Materials Technology,2020,50(6):31-40(in Chinese).
[22] 贾振元, 宿友亮, 张博宇, 等. 基于径向基函数神经网络的CFRP切削力预测[J]. 复合材料学报, 2016, 33(3):516-524. JIA Zhenyuan, SU Youliang, ZHANG Boyu, et al. Prediction of cutting force in CFRP based on radial basis function neural network[J]. Acta Materialia Compositae Sinica,2016,33(3):516-524(in Chinese).
[23] STEFAN K, LEPOLD A, ZANGER F, et al. Experimental investigation of clamping systems and the resulting change of cutting conditions while drilling carbon fiber reinforced plastics[J]. Procedia CIRP,2017,62:15-20. DOI: 10.1016/j.procir.2016.06.089
[24] GIBSON R F. Principles of composite material mechanics[M]. 4th Edition. UK: Taylor and Francis, 2016.
[25] 毛振刚, 侯玉亮, 李成, 等. 搭接长度和铺层方式对CFRP复合材料层合板胶接结构连接性能和损伤行为的影响[J]. 复合材料学报, 2020, 37(1):121-131. MAO Zhengang, HOU Yuliang, LI Cheng, et al. Effect of length and layout pattern on bonding properties and damage behavior of CFRP composite laminates[J]. Acta Materialia Compositae Sinica,2020,37(1):121-131(in Chinese).
[26] 赵小龙, 刁晓勇, 姜国良, 等. 氢化丁腈橡胶本构模型参数确定方法[J]. 合成橡胶工业, 2019, 42(5):352-356. DOI: 10.3969/j.issn.1000-1255.2019.05.005 ZHAO Xiaolong, DIAO Xiaoyong, JIANG Guoliang, et al. Determination of constitutive model parameters of hydrogenated nitrile rubber[J]. Rubber Industry,2019,42(5):352-356(in Chinese). DOI: 10.3969/j.issn.1000-1255.2019.05.005
-
期刊类型引用(0)
其他类型引用(3)
-




 下载:
下载: