Failure study of gradient bimaterial negative Poisson's ratio honeycomb sandwich panels subjected to local impact
-
摘要:
夹芯板结构具有轻质、高抗弯刚度和良好的抗冲击等特性，将负泊松比材料作为夹芯板芯层，可以设计出具有优良动力学特征的防护结构。本文基于提出的双材料曲边内凹负泊松比胞元，通过改变胞元内纵横向材料，构建了正梯度、负梯度、对称正梯度及对称负梯度4种排列的负泊松比多胞蜂窝夹芯板。实验与仿真结果比较说明了本文数值方法的可行性。数值研究了不同排列方式时蜂窝夹芯板在受局部冲击作用下的失效力学性能，考察了冲头冲击速度和芯层梯度排列模式对夹芯板破坏模式、冲头接触力与能量吸收效果的影响。研究表明：芯层排列模式显著影响夹芯板的冲击破坏模式和冲击动力学性能；梯度双材料设计可以显著增强夹芯板的吸能效果。
Abstract:The sandwich panel structure, known for its lightweight nature, high bending stiffness, and exceptional impact resistance, can be tailored with a core layer of negative Poisson's ratio materials. This design approach yields protective structures with outstanding dynamic characteristics. In this paper, a negative Poisson's ratio biomaterial cellular sandwich plate with positive gradient, negative gradient, symmetric positive gradient and symmetric negative gradient was constructed by changing the vertical and horizontal materials in the cell based on the proposed curved edge concave negative Poisson's ratio biomaterial cell. The comparison between experimental results and simulation results demonstrates the feasibility of the numerical method proposed in this paper. The effects of punch impact velocity and gradient arrangement on the failure mode of sandwich plate, punch contact force and energy absorption were investigated. The results show that the impact failure mode and impact dynamic performance of the sandwich panels are significantly affected by the arrangement mode of core layers. This design can significantly enhance the energy absorption effect of sandwich panels.
-
蜂窝材料具有轻质、抗弯、耐冲击等优异的力学性能，被广泛应用于汽车、航天、军事、医疗等工业领域[1]。相较于传统蜂窝材料，具有负泊松比效应的蜂窝结构有着更为优越的吸能效果[2]。自1982年Gibson等[3]设计出最早的内凹六边形负泊松比胞元并推导了其弹性模量及泊松比表达式后，各种各样的胞元结构开始涌现，常见的有重入凹角结构、手性/反手性结构、旋转刚体结构等[4-7]。魏路路等[8]设计了一种结合六边形内凹结构和手性结构的内凹-反手性结构。Jin等[9]将星型内凹结构嵌入六边形内凹结构中，提出了一种负泊松比嵌套结构。常见的负泊松比胞元大多由内凹直杆构成，蒋伟等[10]将曲杆引入到内凹六边形胞元中，构建了一种新型的半圆形内凹结构，这种方法也提供了一种新的设计思路，避免了直杆中出现的应力集中现象。沿着此思路，沈建邦和肖俊华[11]在此基础上提出了一种可变弧角的曲边内凹负泊松比结构，并研究了不同胞元参数对其力学性能的影响。作为最典型的负泊松比结构，内凹型胞元常用于构建蜂窝材料。张新春等[12]采用有限元方法探讨了内凹六边形胞元凹角度数以及冲击速度大小对结构能量吸收性能的影响。Shen等[13]利用有限元软件研究了可变弧角曲边负泊松比结构的面内冲击性能。尤泽华和肖俊华[14]对完全对称的弧边内凹蜂窝负泊松比结构的面内冲击性能进行了详细的数值研究。郭之熙和肖俊华[15]提出了一种全新的多弧段曲边内凹可调泊松比胞元，并基于能量法导出了结构的等效泊松比与等效弹性模量的解析表达式。他们利用仿真软件深入分析了不同冲击速度下结构的冲击变形失效行为和单位质量能量吸收率。
随着负泊松比胞元设计研究的不断深入，人们逐渐认识到单一材料胞元结构设计的局限性。为了克服这些限制，借鉴复合材料设计理念，提出了将不同种材料组合起来以获得优异力学性能的全新胞元设计方案。Li等[16]设计了一种由双材料构成的二维四边形蜂窝结构，并通过实验和数值模拟系统地研究了其热变形行为。研究结果显示，可以通过自由调节结构的胞形来调整其泊松比。He等[17]以双材料三角形网格单元为基础设计了一种新型结构，推导出了通用热弹性方程，建立了有界节点平面网格结构的外力、温度载荷和变形之间的关系，计算了有效泊松比、杨氏模量和热膨胀系数。马芳武等[18]提出了一种双材料双箭头负泊松比结构，在保持胞元几何参数不变的情况下，深入研究了不同速度和参数对面内抗冲击能力和能量吸收能力的影响。此外，不同的排布方式也会显著影响结构的性能，因此梯度设计方法对提升材料的抗冲击性能至关重要。Shao等[19]数值研究了具有厚度梯度排布的内凹负泊松比结构的能量耗散特性，结果表明负梯度排布的结构表现出优异的吸能效果。Li等[20]结合模拟和实验研究了沿横向呈逐层梯度变化的多层蜂窝结构的抗冲击性能。Wu等[21]借助调整内凹蜂窝结构的内凹角度，设计了一系列不同角度梯度排布的模式，系统研究了冲击速度、梯度排布等因素对结构性能的影响，并与均匀排布结构进行了全面对比。研究结果显示，角度梯度内凹蜂窝结构相对于均匀排布结构在吸能效果上表现更为突出。朱冬梅等[22]结合甲虫鞘翅结构提出一种新型负泊松比蜂窝结构，以胞元角度作为梯度变换参数来构造不同梯度排列的新型负泊松比结构，数值分析了其抗冲击性能。张晓楠等[23]提出了一种变截面内凹蜂窝结构，并结合实验与模拟讨论了在不同冲击速度下梯度变截面内凹蜂窝结构的能量吸收性能。
典型的夹芯结构由两个薄面板和一个轻质芯层组成，选择合适的芯层对夹芯结构的性能有显著影响。鉴于负泊松比蜂窝材料优越的力学性能，其逐渐取代了夹芯板的传统芯层，研究人员发现将负泊松比蜂窝结构应用于夹芯板可以显著提高抗冲击能力。王堃等[24]模拟了铝蜂窝夹芯板被刚体低俗冲击的过程，研究了夹芯板各结构参数对夹芯板冲击动态响应的影响。罗伟铭等[25]采用落锤冲击试验研究了铝质夹芯结构在局部冲击载荷作用下的变形模式和吸能特性。Luo等[26]研究了不同泊松比的蜂窝夹芯板的抗弹丸冲击性能。邓云飞等[27]制备并研究了泡沫填充褶皱夹芯结构低速冲击下的响应特性与损伤机制，通过落锤试验机对夹芯板节点与基座两个位置进行了冲击试验。陈鹏宇[28]结合实验与有限元仿真研究了不同冲击速度对内凹弧形蜂窝夹芯板的影响。辛亚军等[29]通过试验和数值模拟对铝蜂窝夹芯板的面外剪切行为和力学性能进行了研究，讨论了其失效模式，并分析了面板厚度、蜂窝胞元尺寸和芯层厚度对夹芯板的影响。Bohara等[30]研究对比了内凹蜂窝夹芯板与传统六边形蜂窝夹芯板的防护性能，证明了内凹蜂窝夹芯板具有更好的防护能力。杨姝等[31]设计制备了两种铝合金材质的夹芯板，结合钢柱冲击试验与有限元数值仿真，研究对比了两类蜂窝夹芯板抗冲击性能。蒋舟顺等[32]提出了一种双向相同力学性能的正弦曲边三维负泊松比夹芯板，并将其应用于防爆保护，数值研究了夹芯板在空爆载荷下的力学性能。郭之熙[33]将梯度蜂窝材料作为芯层构建厚度梯度和角度梯度两种夹芯板结构，讨论了局部冲击时梯度蜂窝夹芯板的失效行为及吸能效果。
目前关于负泊松比芯层夹芯板的研究大多使用单一材料且直杆负泊松比多胞蜂窝结构，本文基于作者提出的双材料曲边内凹负泊松比胞元[34]，基于纵横向材料模量比梯度设计的思想，将梯度双材料曲边内凹负泊松比蜂窝构建为夹芯层，通过改变芯层纵横向材料的模量比构建了正梯度、负梯度、对称正梯度和对称负梯度四种夹芯板结构，研究了夹芯板受局部冲击时的失效行为，讨论了梯度排布和冲击速度对夹芯板抗冲击性能的影响。
1. 梯度双材料负泊松比蜂窝夹芯板
1.1 计算模型
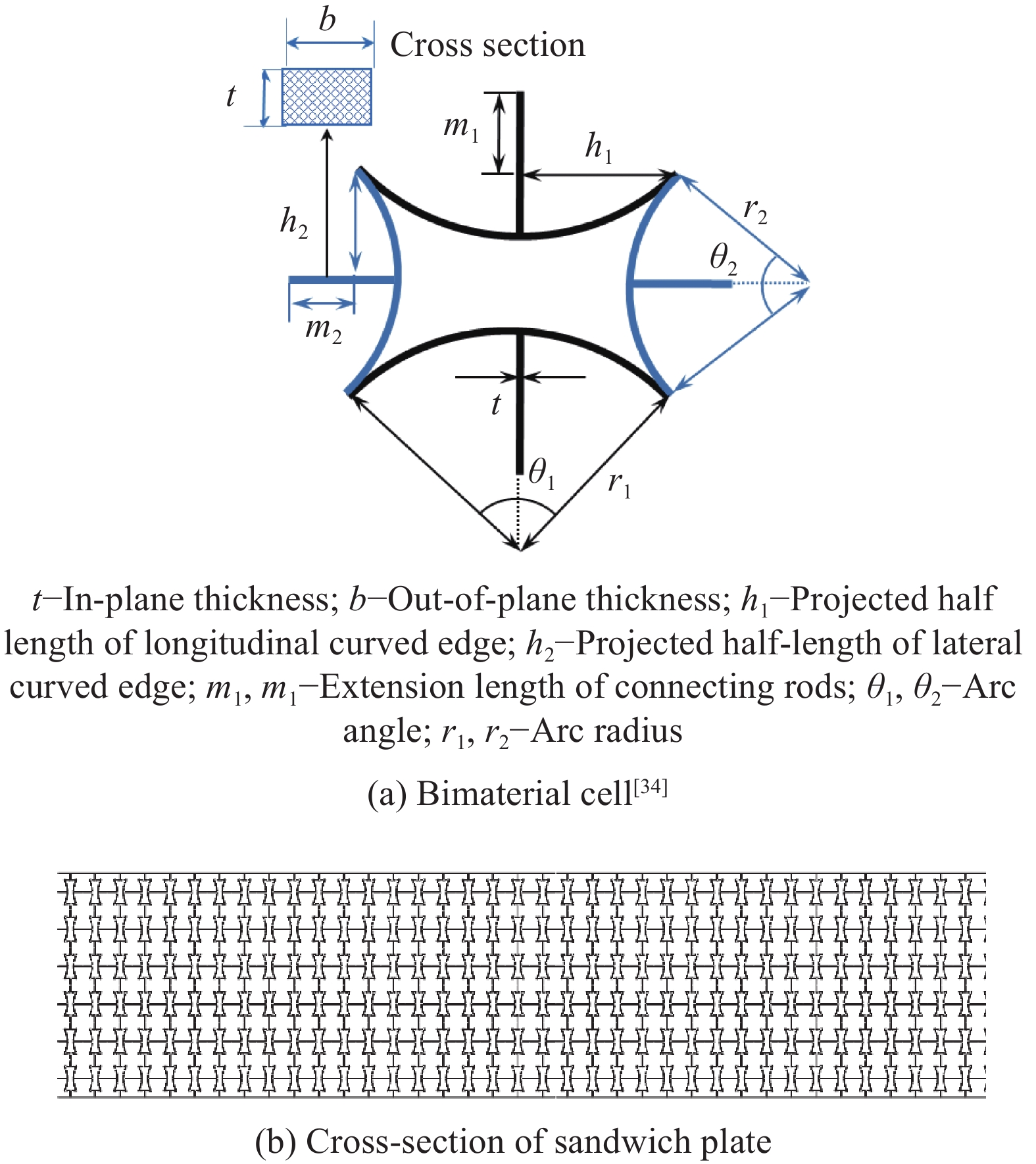
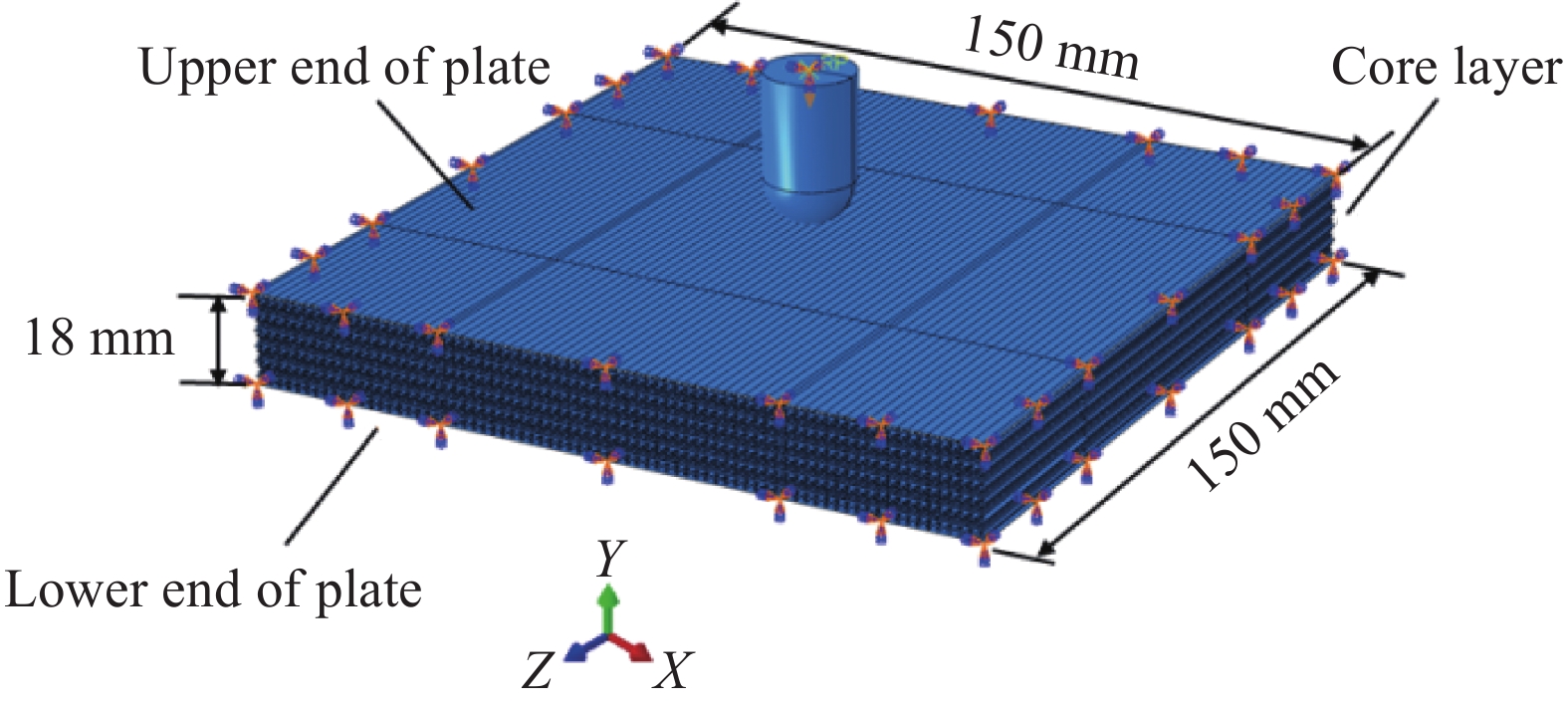
图1为基于提出的双材料曲边内凹胞元(图2(a))构建的夹芯板及其边界条件的模型示意图，其中h1为纵向曲边投影半长，h2为横向曲边投影半长，m1和m1为连接杆伸出长度。纵向曲杆模量E1，圆弧角θ1，半径r1=h1/sin(θ1/2)，横向曲杆模量E2，圆弧角θ2，半径r2=h2/sin(θ2/2)，面内厚度为t，面外厚度为b(垂直纸面)。夹芯板由上下两层板及中间负泊松比夹芯层构成，夹芯层与上下两层板之间设置为绑定约束。夹芯层由6×75个双材料单胞在纵向拉伸后阵列而成。单胞中几何参数为：θ1=30°，θ2=60°，h1=0.5 mm，h2=1 mm，m1=m2=0.5 mm，t=0.1 mm和b=150 mm。
![]()
图 1 梯度双材料负泊松比蜂窝夹芯板与边界条件示意图Figure 1. Schematic diagram of gradient bimaterial honeycomb sandwich plate with negative Poisson's ratio and boundary conditions![]()
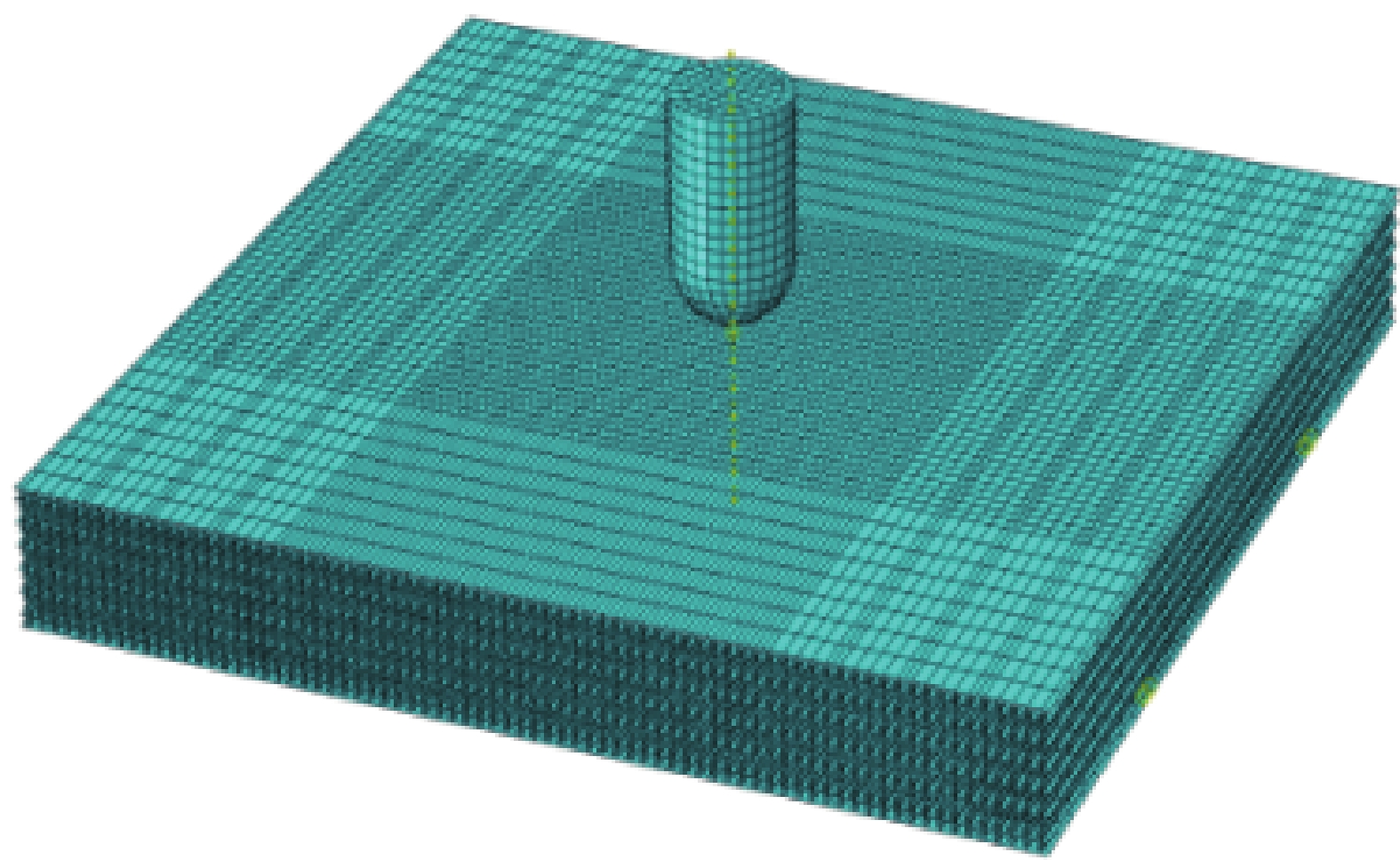
图 2 梯度双材料负泊松比夹芯板示意图Figure 2. Schematic diagram of gradient bimaterial honeycomb sandwich plate with negative Poisson's ratio图1中冲头为半球形冲头，直径为18 mm，长度30 mm，质量18 kg。冲头在上端板上部2 mm中心位置处。固定上下板的四条边，约束冲头x、z方向的位移及旋转，对其施加一个y方向的初速度，全局设置为通用接触，切向无摩擦，法向为硬接触。采用ABAQUS显式动力学对夹芯板进行冲击模拟，冲头设置为离散刚体，面板与夹层为S4R壳单元，考虑控制沙漏现象，将伪应变能控制在3%左右，为兼顾计算准确性与时效，对模型中心70 mm×70 mm部分网格进行细化，计算模型如图3。冲头设置为离散刚体，上下板均为铝板，厚度1 mm。
1.2 梯度双材料设计
夹芯板芯层由单胞阵列组成(图2(b))，面板为铝合金，定义胞元纵横向材料模量比E1/E2=k，数值仿真中采用J-C本构及损伤模型[35]，材料与组合方式见表1和表2，k值取为1.38、1和0.48。
表 1 材料性能Table 1. Material propertiesMaterial Density/
(g·cm−3)Young's
modulus/GPaPoisson's
ratioA/
MPaB/
MPan C m D1 D2 D3 D4 D5 2024 Aluminum 2.7 73 0.33 369 684 0.73 0.0083 1 0.112 0.123 −1.5 0.007 0 Cast-iron 7.2 150 0.3 525 650 0.6 0.0205 1 0.029 0.44 −1.5 0 0 4340 Steel 7.85 207 0.29 910 586 0.26 0.014 1.03 −0.8 2.1 −0.5 0.002 0.61 Notes: A—Initial yield stress at reference strain rate and reference temperature; B, n—Strain hardening modulus and hardening index of the material; C—Material strain rate strengthening parameter; m—Thermal softening index of material; D1, D2, D3, D4, D5—Failure parameters in the damage formula. 表 2 纵横向材料组合方式Table 2. Vertical and horizontal material combinationModulus ratio E1/E2 Vertical/transverse materials 1.38 4340 Steel/Cast-iron 1 Cast-iron/Cast-iron 0.48 2024 Aluminum/Cast-iron 2. 实验与仿真结果
2.1 试件与仿真模型
为了验证本文数值方法的可行性与准确性，作者制备了单层夹芯板进行实验，并将实验结果与仿真结果进行比较。由于条件限制，作者目前无法制备双材料夹芯板，仅利用3D打印技术制备均质曲边内凹负泊松比蜂窝夹芯板，材料为316L不锈钢。夹芯层为1×8胞元阵列结构，单胞几何参数为θ1=θ2=45°，h1=h2=4 mm，m1=m2=1 mm，面内厚度t为0.5 mm，上下板厚度为0.75 mm，图4为制备的试件与相应的仿真计算模型。
2.2 实验平台
图5为实验装置，采用万能试验机(CEAST9350，英斯特朗公司)为加载设备，配备传感器输出载荷位移曲线。为了研究夹芯板的力学性能和失效机制，对夹芯板进行压缩穿透实验，加载速率为2 mm/min，试件位于平台和压板之间，试件下放置空心垫圈，将冲头垂直放置于板上，冲头下压直至穿透夹芯板，通过摄像机(vivo X90)记录压缩过程获取试件穿透过程。
2.3 实验与模拟结果比较
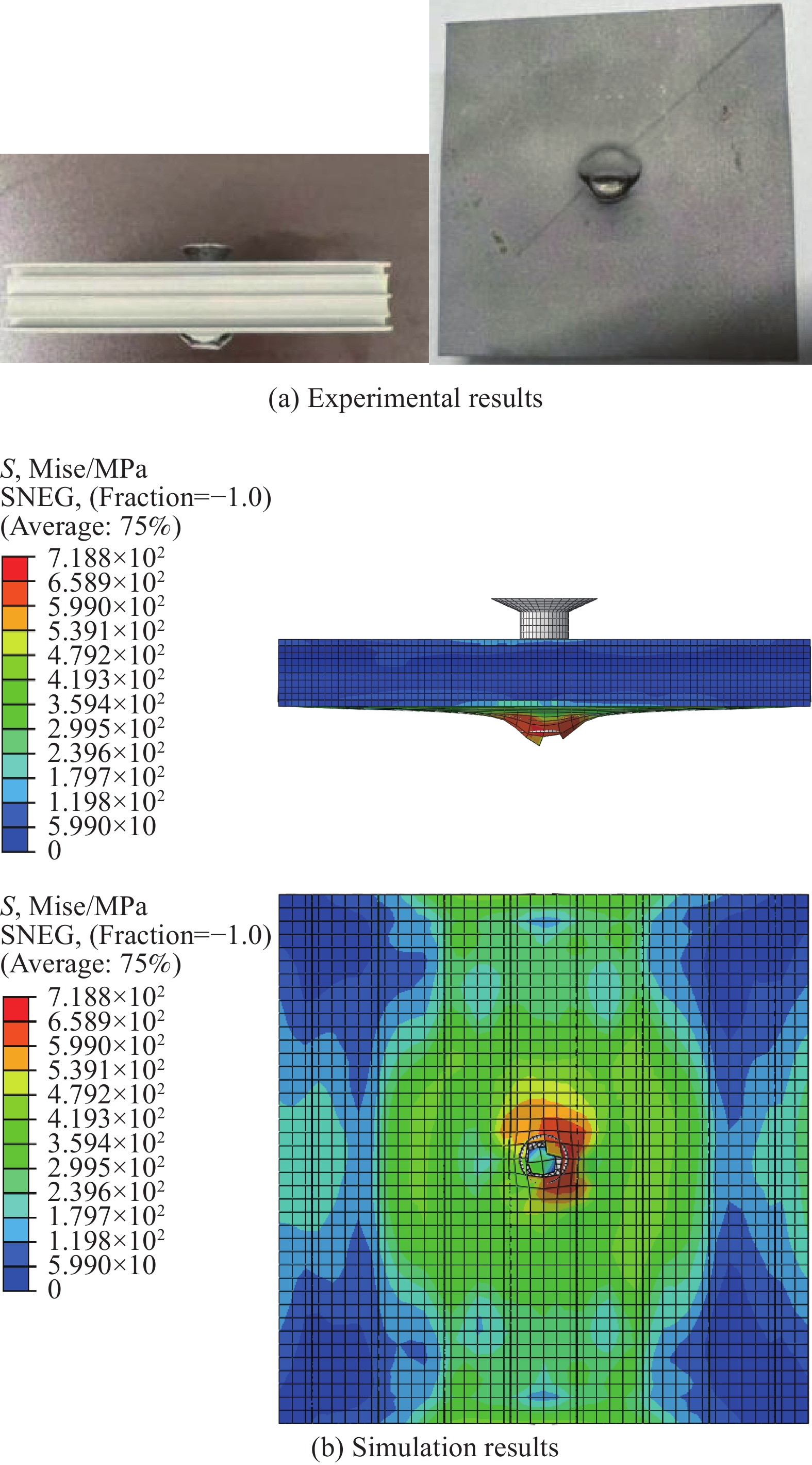
采用ABAQUS显式动力学研究结构的面内冲击性能，边界条件见图1，材料选取与前文一致，冲头为圆柱钉形，设置为离散刚体，长20 mm。冲头初始在上端板上部2 mm中心位置。冲击速度1 m/s，该过程动能小于内能的5%，可近似认为是准静态加载。图6为夹芯板在准静态局部压缩时的穿透破坏模式与应力云图。可以看出压头穿透夹芯板时，实验与模拟的破坏模式非常相似，下端板均呈现出被直接冲破的方式，开裂面较大。原因在于内部夹层的层数较少，使得冲头与底板接触面积较大，且冲头底部为圆形，使得底板被大面积冲破。不同的是，实验中底板未被完全破坏冲出，而仿真中底板则被冲头直接冲破顶出，原因在于实验中冲头的压缩速度较小，使得底板破坏处未被顶出；同时仿真中未考虑冲头与夹层板之间的摩擦，忽略了夹层对冲头阻碍的影响。
![]()
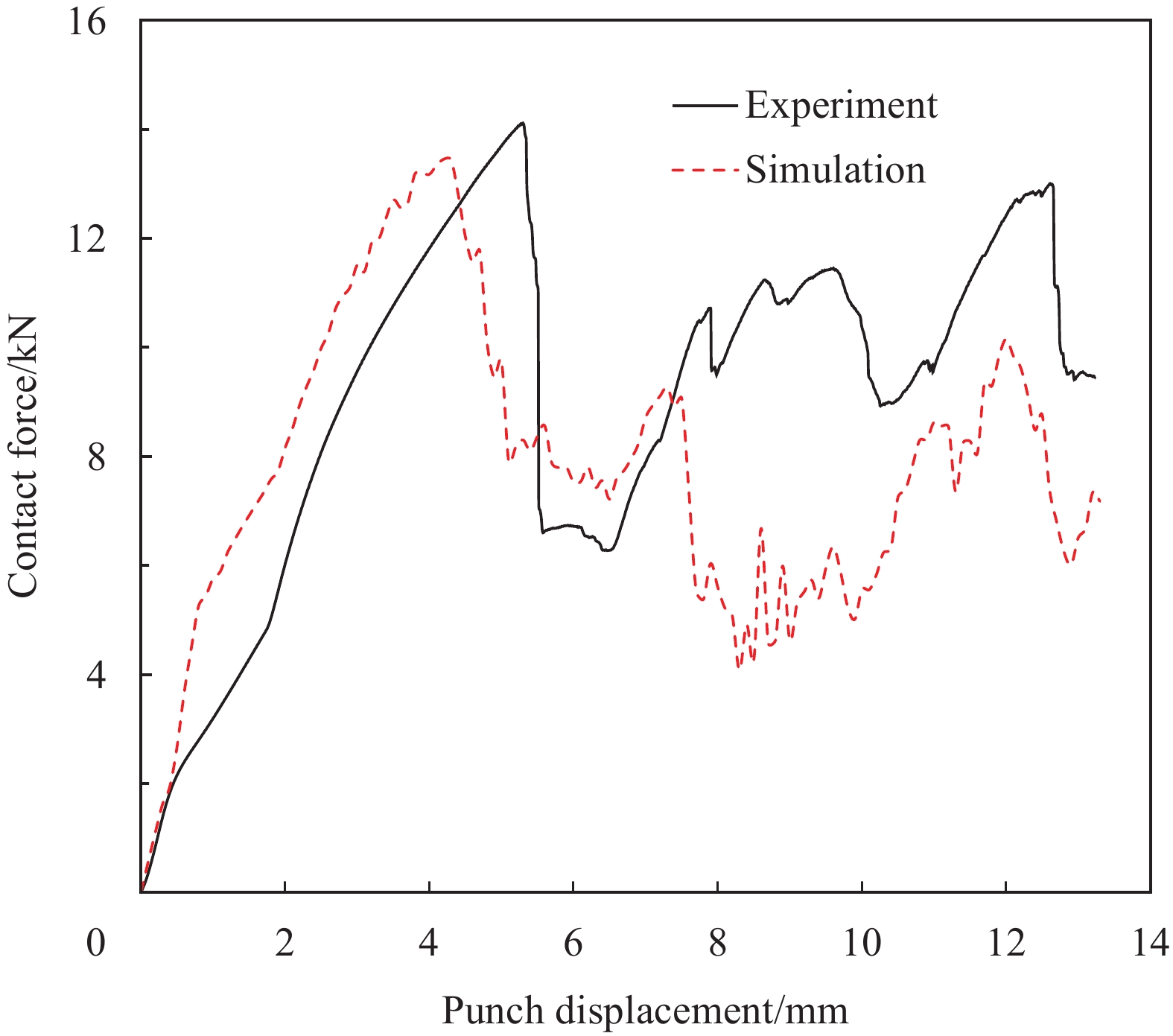
图 6 局部穿透后实验和模拟中夹芯板试件破坏模式Figure 6. Failure modes of sandwich plate specimens in experiment and simulation during local penetrationS, Mise—Von Mises stress; SNEG—Negative normal side of the element图7给出了夹层板局部压缩穿透时实验和模拟的冲头接触力-位移曲线。可以看出二者显示出相似的曲线变化：在冲击前期，冲头接触力迅速增大直到冲破上端板，随后呈现下降趋势。两条曲线经过第一峰值之后，再次上升，不同的是仿真结果先上升而后再下降趋势。原因是冲头穿破上层板后接触芯层时，仿真中忽略了冲头与夹芯板之间摩擦的影响，使得冲头所受阻力小于实验结果。随着冲头位移增加，实验和模拟的接触力再次增大，达到峰值后表示冲头穿破下板，最后接触力逐渐下降。
![]()
图 7 夹芯板局部穿透过程中冲头的接触力-位移曲线Figure 7. Contact force-displacement curves of punch during local penetration of sandwich plate3. 梯度双材料夹芯板及其局部冲击性能数值研究
3.1 梯度排列模式
夹芯板的芯层选取6层(图8)，保持横向材料模量不变，改变纵向材料的模量获得不同模量比k的层阵列胞元(表2材料组合方式)，从而构建出不同梯度排布的夹芯板。4种蜂窝结构具有相同的相对密度与质量。
![]()
图 8 4种梯度双材料蜂窝夹芯结构Figure 8. Four gradient bimaterial honeycomb sandwich structuresk—The E1/E2 of each layer3.2 夹芯板冲击破坏模式
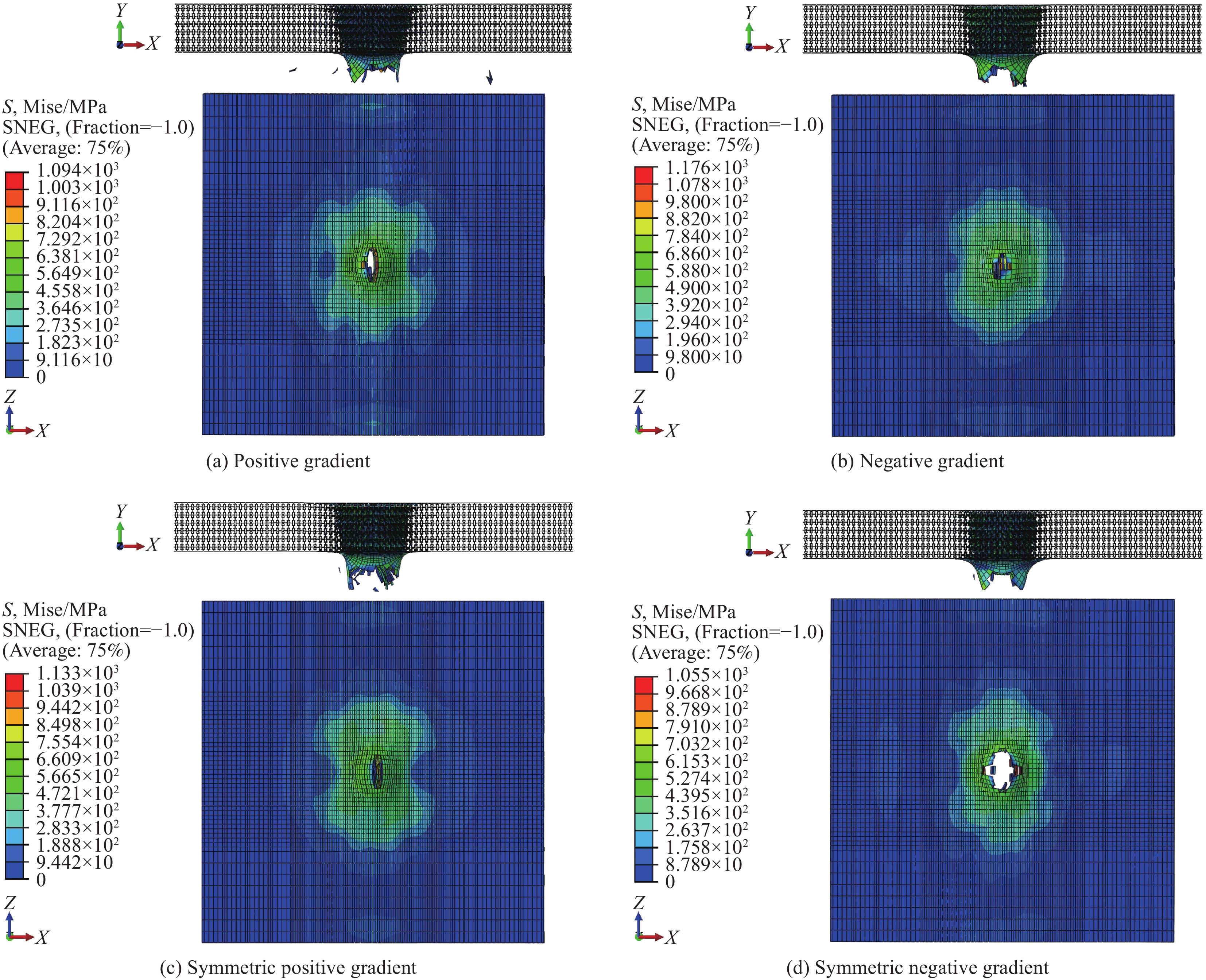
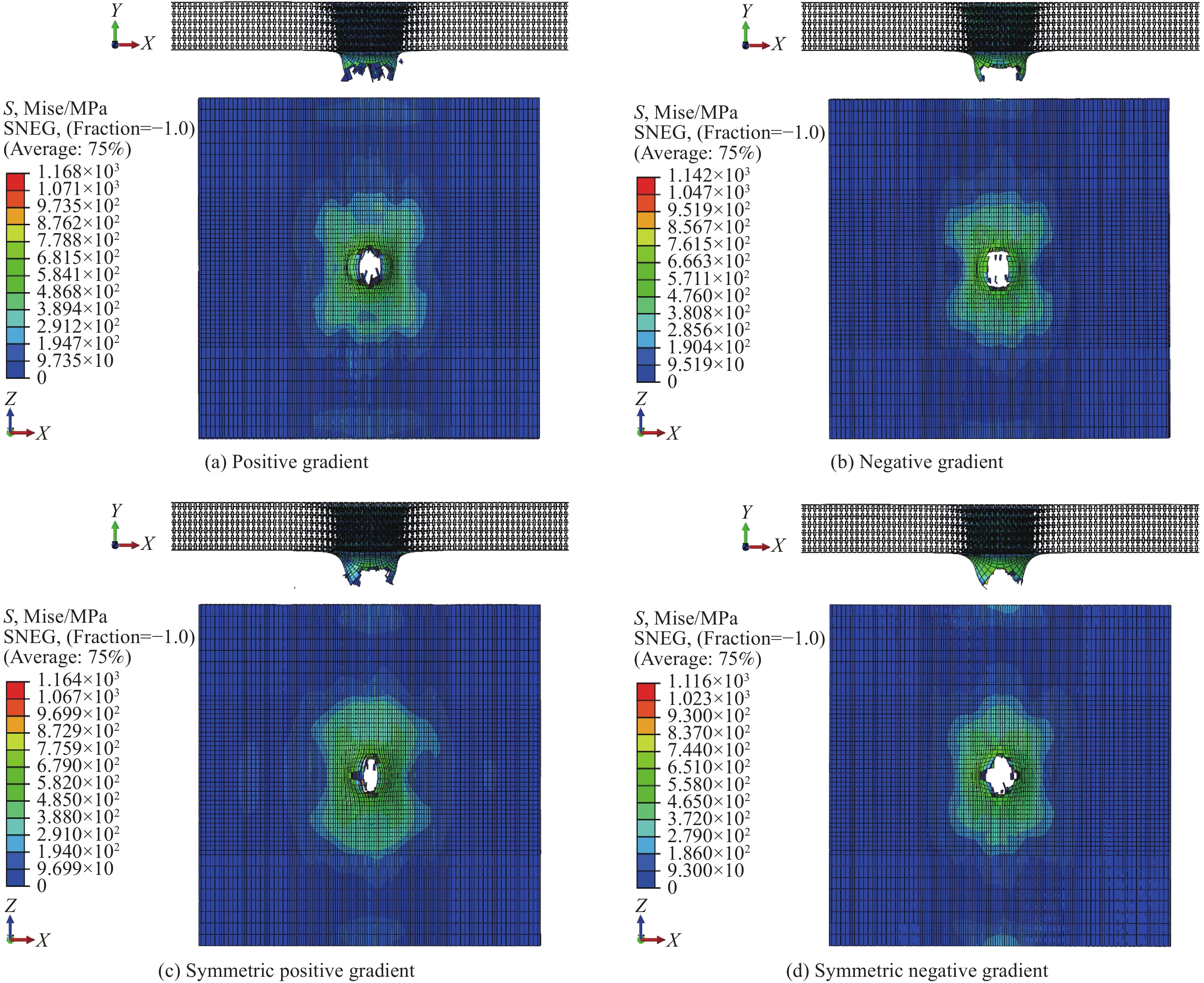
冲头的初速度分别取低速(10 m/s)与高速(30 m/s)对夹芯板进行冲击穿透，4种排布模式夹芯板在不同速度时的穿透破坏如图9和图10。可知，低速(10 m/s)冲击下正梯度与对称正梯度下端板均出现Z方向开裂，而负梯度与对称负梯度则呈现出直接被冲破的方式，开裂面较大。原因为芯层底部胞元纵横向模量比k较高时胞元不易变形，从而使得胞元下端外伸杆向下挤压造成下端板沿Z方向开裂，而当底部胞元k较小时，胞元形变较大，内部胞元受挤压后与底板接触面积增大，使得底板出现被大面积冲破的现象。冲头高速(30 m/s)冲击时，不同排布模式时的底板穿透方式与低速时类似，但由于冲击速度增大，破开处面积明显增大，破坏方式与低速冲击时一致。可知，底板的穿透模式与芯层的排布方式有关，冲击速度显著影响穿透时造成破坏的面积。
![]()
图 9 10 m/s冲击速度时不同芯层排布夹芯板破坏模式Figure 9. Failure modes of sandwich plate with different core arrangement at 10 m/s impact speed![]()
图 10 30 m/s冲击速度时不同芯层排布夹芯板破坏模式Figure 10. Failure modes of sandwich plate with different core arrangement at 30 m/s impact speed3.3 冲头接触力
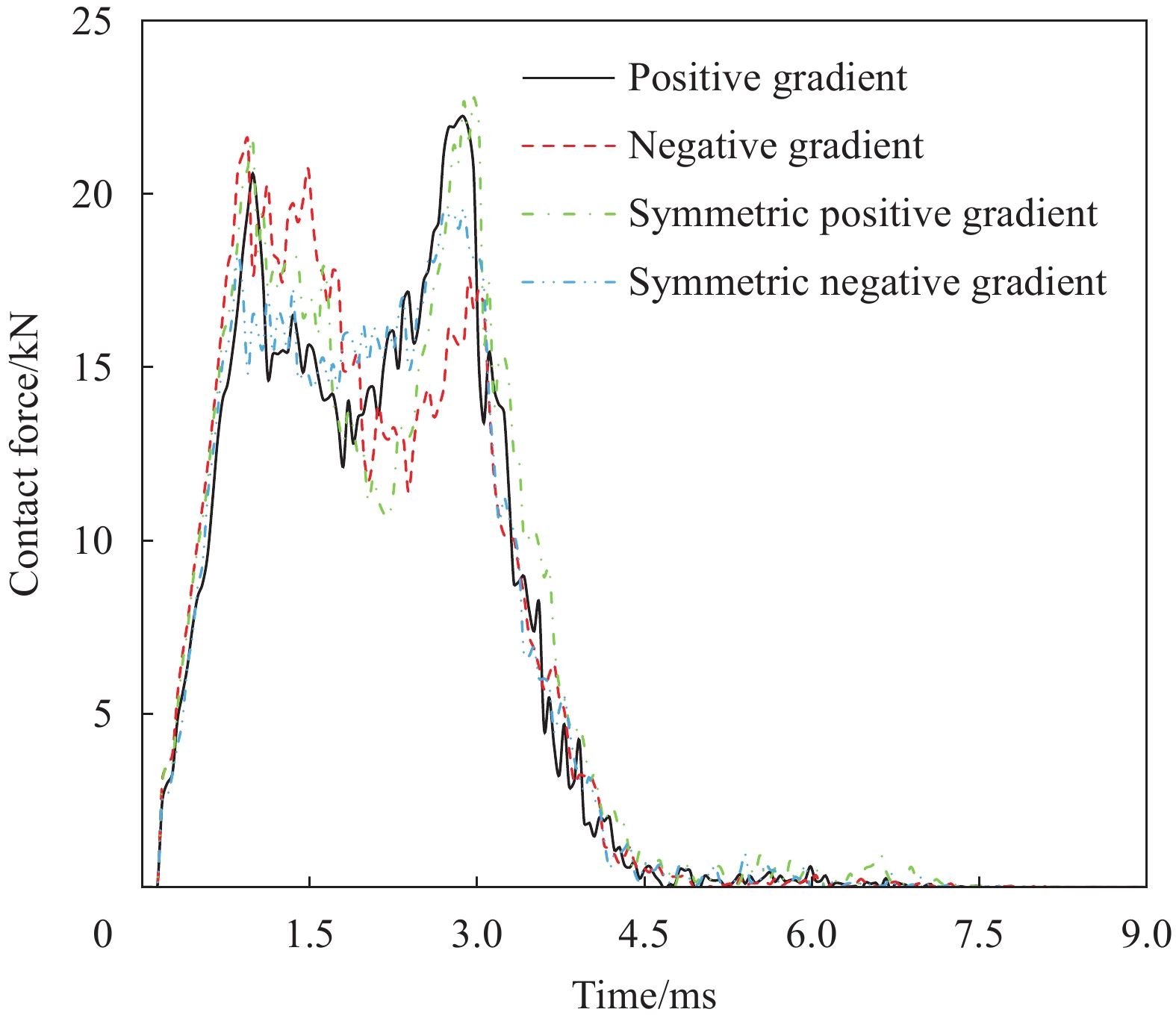
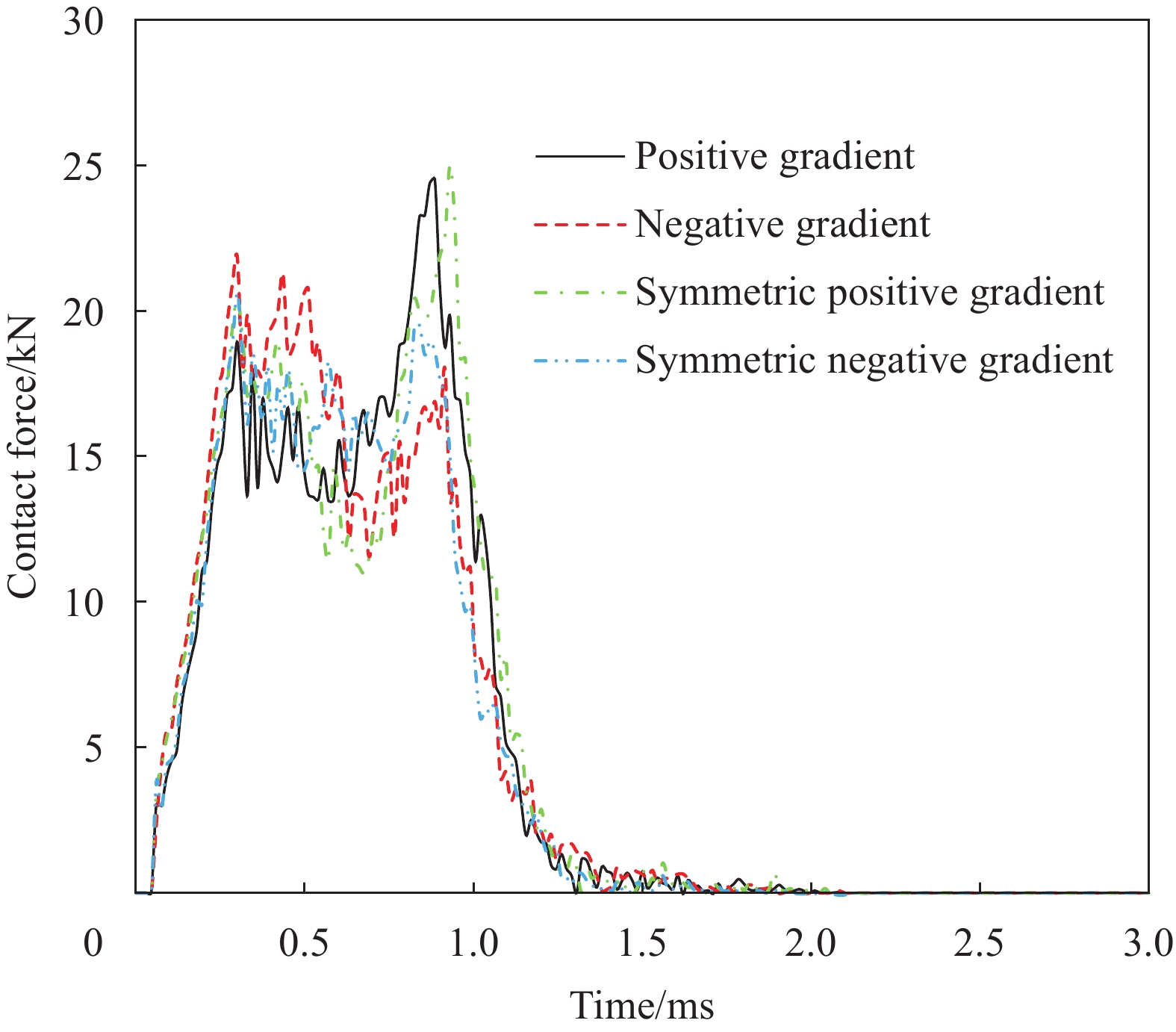
图11和图12给出了不同芯层排布时两种速度冲击下冲头的接触力-时间曲线。可以看出，4种排布模式的夹芯板在承受低、高两种冲击速度时，冲头接触力随时间变化曲线有相同之处也有不同之处。相同之处为：4种模式的变化趋势一致，都会出现两个峰值；第一个峰值出现在上端板被冲破时，可以发现负梯度与对称正梯度的第一个峰值明显大于其他两种，其中负梯度的峰值最大，对称负梯度最小，即上端板遭到破坏时负梯度模式承受冲击力最大。不同之处在于：第二个峰值发生在下端板被冲破时，负梯度的第二个峰值明显小于第一个峰值，而其他3种模式的第二个峰值则明显大于第一个峰值，原因在于前期负梯度模式吸能较多，当下端板被冲破时冲头动能最小，则此时接触力较小。速度高低仅对接触力的峰值大小有影响，而对变化趋势影响不大。
![]()
图 11 10 m/s速度时不同芯层夹芯板的接触力-时间曲线Figure 11. Contact force-time curves of sandwich plates with different core layers at 10 m/s speed![]()
图 12 30 m/s速度时不同芯层夹芯板的接触力-时间曲线Figure 12. Contact force-time curves of sandwich plates with different core layers at 30 m/s speed3.4 夹芯板能量吸收特性
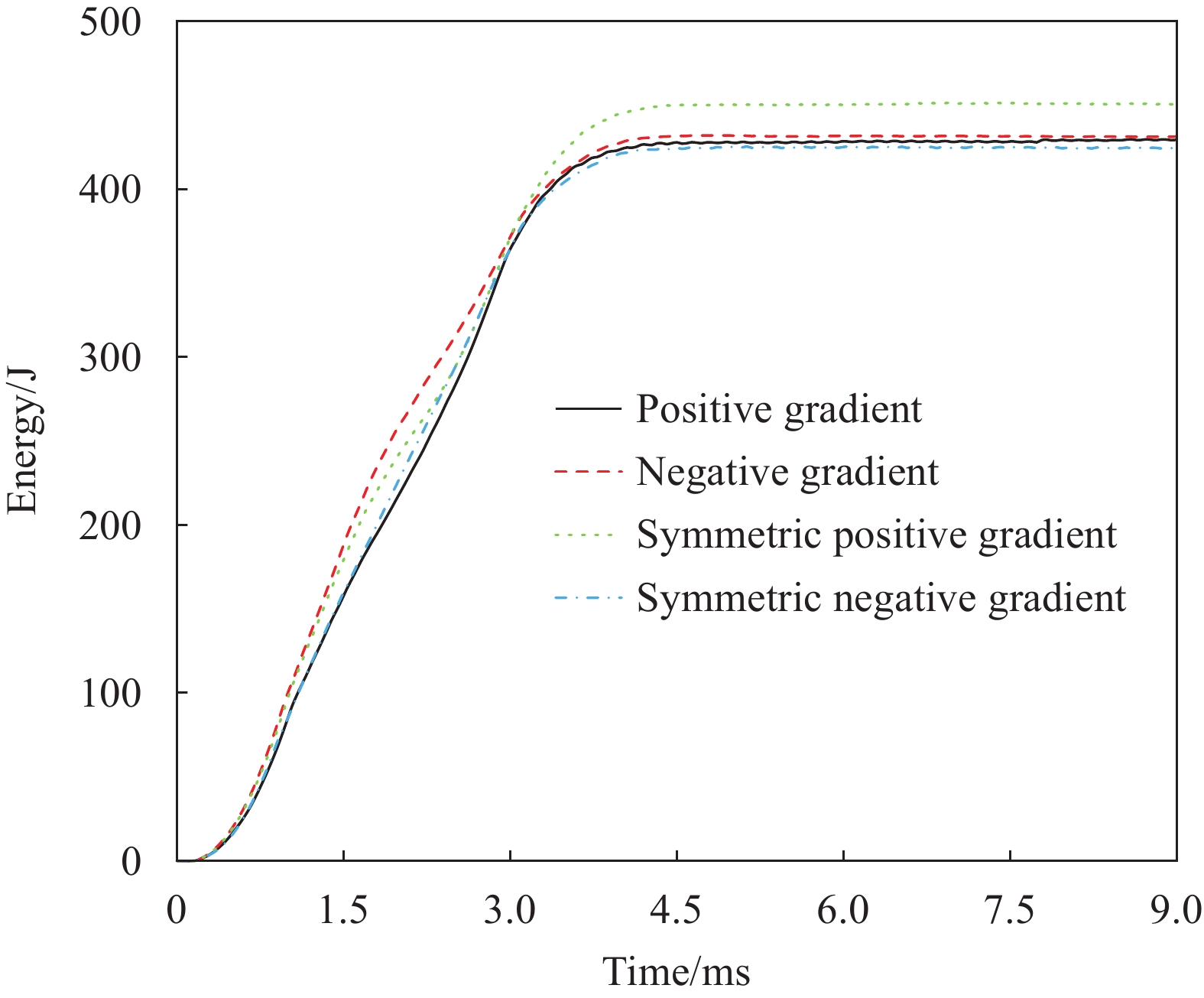
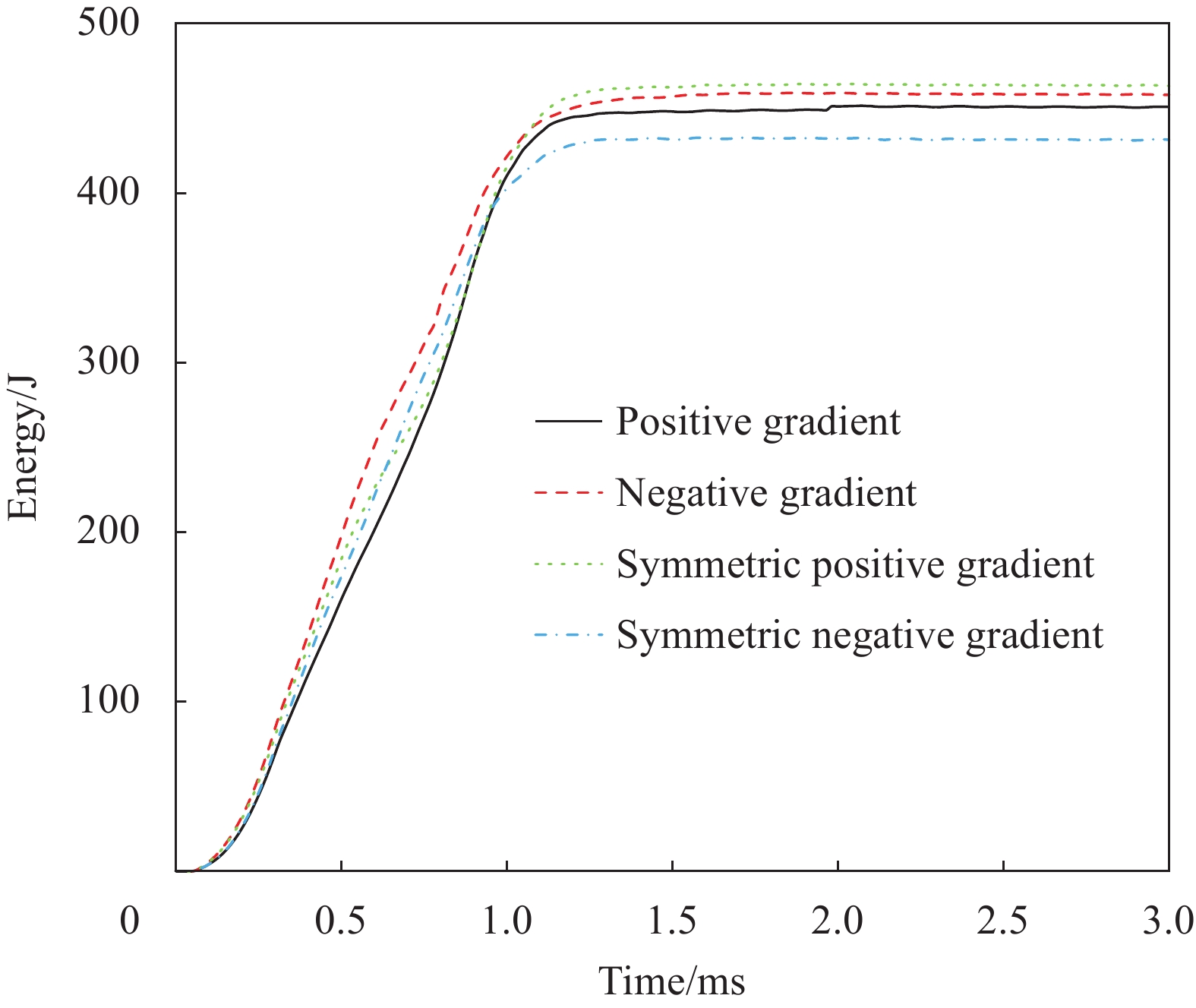
图13和图14给出了低、高冲头速度下不同芯层排布时夹芯板的能量吸收-时间曲线。从图13可以看出，低速冲击时，夹芯板在穿透前期(3 ms之前)负梯度相比于其他排布模式表现出较好的吸能效果，夹芯板被彻底穿透之前负梯度夹芯板的能量吸收最高；随着冲击穿透的持续，夹芯板被彻底穿透破坏，此时对称正梯度夹芯板的能量吸收值明显高于其他3种，其他3种在后期几乎相等。图10显示，高速冲击时，负梯度夹芯板的前期能量吸收同样具有优势，且后期与对称正梯度夹芯板之间的能量吸收差异很小。可知，合理的芯层梯度双材料设计可以使夹芯板结构有效抵抗冲击穿透。
![]()
图 13 10 m/s速度时不同梯度夹芯板的能量吸收Figure 13. Energy absorption of sandwich panels with different gradients at a speed of 10 m/s![]()
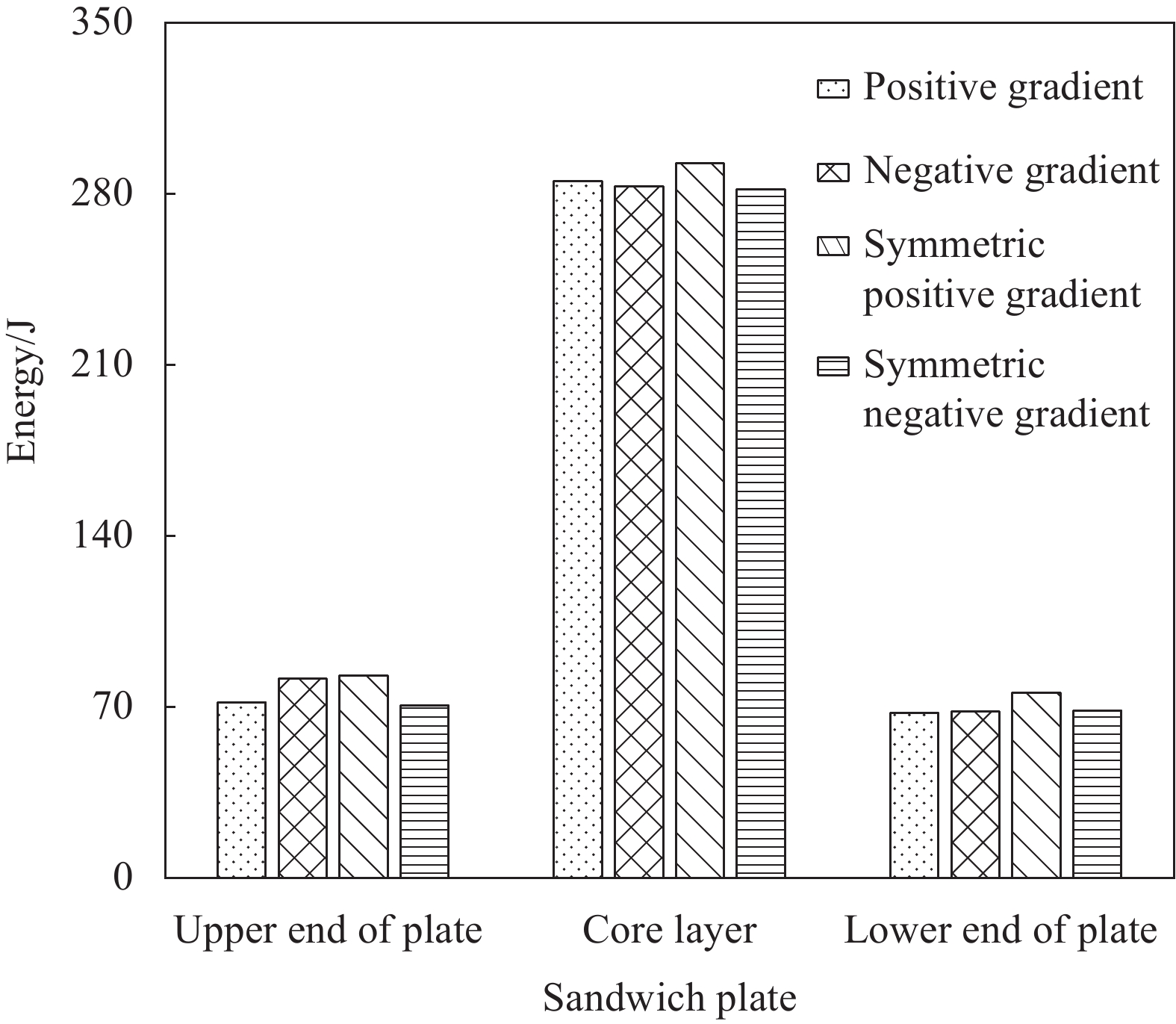
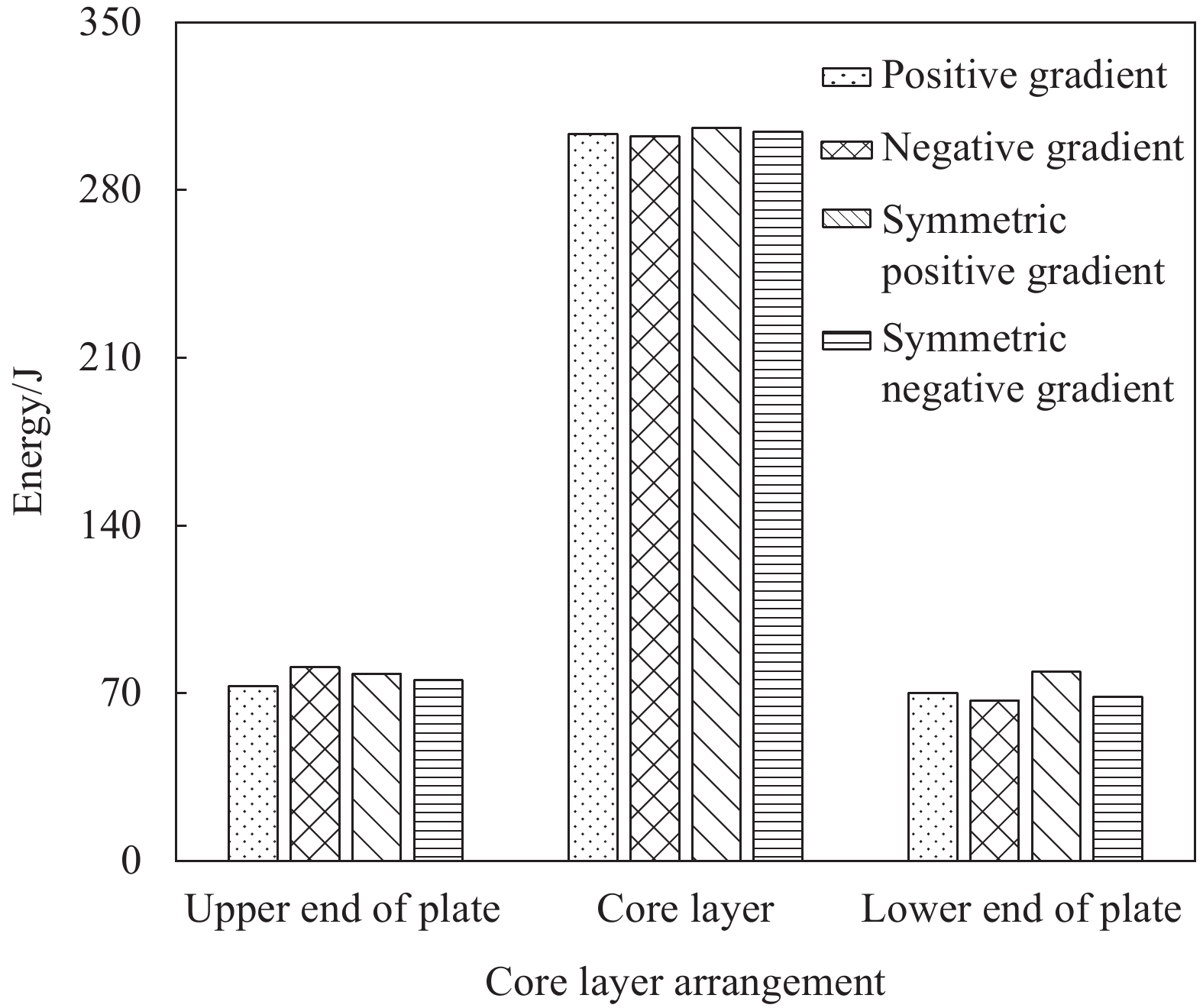
图 14 30 m/s速度时不同梯度夹芯板的能量吸收Figure 14. Energy absorption of sandwich panels with different gradients at a speed of 30 m/s图15和图16给出了低、高速冲击下当接触力为0 (完全穿透)时夹芯板各部分的能量值。由图可知，无论何种芯层排布方式，承受冲击时内部芯层均吸收了最多的能量，下端板吸收的能量略低于上端板。图15表明低速冲击下对称正梯度不仅芯层吸收的能量最多，整体吸收能量也最多。负梯度和对称正梯度的上端板吸收能量效果最好。图16显示高速冲击下4种排列时夹芯板的吸能效果差异减小。
![]()
图 15 10 m/s冲击速度时夹芯板各部分能量吸收值Figure 15. Energy absorption value of each part of the sandwich plate at 10 m/s impact velocity![]()
图 16 30 m/s冲击速度时夹芯板各部分能量吸收值Figure 16. Energy absorption value of each part of the sandwich plate at 30 m/s impact velocity4. 结 论
基于提出的双材料曲边内凹负泊松比胞元，通过改变胞元内杆件的纵横向模量比值，构造了不同排布模式的4种梯度双材料负泊松比蜂窝夹芯板，研究了局部冲击时夹芯板的失效力学性能，分别讨论了冲击速度和芯层排布模式对夹芯板抗冲击力学性能的影响。主要结论为：
(1)夹芯结构下端板的开裂方式与芯层的排布方式有关，底部芯层胞元变形越大，底板开裂面积越大；冲击速度显著影响穿透时造成破坏的面积；
(2)不同排布模式的夹芯板在被穿透时，接触力曲线会出现两个峰值，对应着上下板穿透破裂的时间点，芯层排布方式对第二个峰值的影响较大；
(3)夹芯板的能量吸收曲线先增大随后趋于定值，梯度双材料的结构设计可以显著增强夹芯板的吸能效果，负梯度夹芯板的前期吸能效果最好，穿透时对称正梯度夹芯板的芯层吸能最多。合理的芯层梯度双材料设计可以使夹芯板结构有效抵抗冲击穿透。
-
![]()
图 1 梯度双材料负泊松比蜂窝夹芯板与边界条件示意图
Figure 1. Schematic diagram of gradient bimaterial honeycomb sandwich plate with negative Poisson's ratio and boundary conditions
![]()
图 2 梯度双材料负泊松比夹芯板示意图
Figure 2. Schematic diagram of gradient bimaterial honeycomb sandwich plate with negative Poisson's ratio
![]()
图 6 局部穿透后实验和模拟中夹芯板试件破坏模式
Figure 6. Failure modes of sandwich plate specimens in experiment and simulation during local penetration
S, Mise—Von Mises stress; SNEG—Negative normal side of the element
![]()
图 7 夹芯板局部穿透过程中冲头的接触力-位移曲线
Figure 7. Contact force-displacement curves of punch during local penetration of sandwich plate
![]()
图 8 4种梯度双材料蜂窝夹芯结构
Figure 8. Four gradient bimaterial honeycomb sandwich structures
k—The E1/E2 of each layer
![]()
图 9 10 m/s冲击速度时不同芯层排布夹芯板破坏模式
Figure 9. Failure modes of sandwich plate with different core arrangement at 10 m/s impact speed
![]()
图 10 30 m/s冲击速度时不同芯层排布夹芯板破坏模式
Figure 10. Failure modes of sandwich plate with different core arrangement at 30 m/s impact speed
![]()
图 11 10 m/s速度时不同芯层夹芯板的接触力-时间曲线
Figure 11. Contact force-time curves of sandwich plates with different core layers at 10 m/s speed
![]()
图 12 30 m/s速度时不同芯层夹芯板的接触力-时间曲线
Figure 12. Contact force-time curves of sandwich plates with different core layers at 30 m/s speed
![]()
图 13 10 m/s速度时不同梯度夹芯板的能量吸收
Figure 13. Energy absorption of sandwich panels with different gradients at a speed of 10 m/s
![]()
图 14 30 m/s速度时不同梯度夹芯板的能量吸收
Figure 14. Energy absorption of sandwich panels with different gradients at a speed of 30 m/s
![]()
图 15 10 m/s冲击速度时夹芯板各部分能量吸收值
Figure 15. Energy absorption value of each part of the sandwich plate at 10 m/s impact velocity
![]()
图 16 30 m/s冲击速度时夹芯板各部分能量吸收值
Figure 16. Energy absorption value of each part of the sandwich plate at 30 m/s impact velocity
表 1 材料性能
Table 1 Material properties
Material Density/
(g·cm−3)Young's
modulus/GPaPoisson's
ratioA/
MPaB/
MPan C m D1 D2 D3 D4 D5 2024 Aluminum 2.7 73 0.33 369 684 0.73 0.0083 1 0.112 0.123 −1.5 0.007 0 Cast-iron 7.2 150 0.3 525 650 0.6 0.0205 1 0.029 0.44 −1.5 0 0 4340 Steel 7.85 207 0.29 910 586 0.26 0.014 1.03 −0.8 2.1 −0.5 0.002 0.61 Notes: A—Initial yield stress at reference strain rate and reference temperature; B, n—Strain hardening modulus and hardening index of the material; C—Material strain rate strengthening parameter; m—Thermal softening index of material; D1, D2, D3, D4, D5—Failure parameters in the damage formula. 
下载: 导出CSV
表 2 纵横向材料组合方式
Table 2 Vertical and horizontal material combination
Modulus ratio E1/E2 Vertical/transverse materials 1.38 4340 Steel/Cast-iron 1 Cast-iron/Cast-iron 0.48 2024 Aluminum/Cast-iron
下载: 导出CSV
-
[1] XUE Z Y, HUTCHINSON J W. A comparative study of impulse-resistant metal sandwich plates[J]. International Journal of Impact Engineering, 2004, 30(10): 1283-1305. DOI: 10.1016/j.ijimpeng.2003.08.007
[2] WANG H D, LI X X, LI P, et al. Delta-phosphorene: A two dimensional material with a highly negative Poisson's ratio[J]. Nanoscale, 2017, 9(2): 850-855. DOI: 10.1039/C6NR08550D
[3] GIBSON L J, ASHBY M F, SCHAJER G S, et al. The mechanics of two-dimensional cellular materials[J]. Proceedings of the Royal Society of London A: Mathematical and Physical Sciences, 1982, 382(1782): 25. DOI: 10.1098/rspa.1982.0087
[4] REN X, DAS R, TRAN P, et al. Auxetic metamaterials and structures: A review[J]. Smart Materials and Structures, 2018, 27(2): 023001. DOI: 10.1088/1361-665X/aaa61c
[5] 吴文旺, 肖登宝, 孟嘉旭, 等. 负泊松比结构力学设计, 抗冲击性能及在车辆工程应用与展望[J]. 力学学报, 2021, 53(3): 611-638. DOI: 10.6052/0459-1879-20-333 WU Wenwang, XIAO Dengbao, MENG Jiaxu, et al. Mechanical design, impact energy absorption and applications of auxetic structures in automobile lightweight engineering[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(3): 611-638(in Chinese). DOI: 10.6052/0459-1879-20-333
[6] LI C L, MA N F, DENG Q T, et al. Deformation and energy absorption of the laminated reentrant honeycomb structures under static and dynamic loadings[J]. Mechanics of Advanced Materials and Structures, 2024, 31(11): 2472-2482.
[7] LI X, PENG W T, WU W W, et al. Auxetic mechanical metamaterials: From soft to stiff[J]. International Journal of Extreme Manufacturing, 2023, 5(4): 042003. DOI: 10.1088/2631-7990/ace668
[8] 魏路路, 余强, 赵轩, 等. 内凹-反手性蜂窝结构的面内动态圧溃性能研究[J]. 振动与冲击, 2021, 40(4): 261-269. WEI Lulu, YU Qiang, ZHAO Xuan, et al. Research on the in-plane dynamic collapse performance of concave backhand honeycomb structures[J]. Journal of Vibration and Shock, 2021, 40(4): 261-269(in Chinese).
[9] JIN Y T, QIE Y H, LI N N, et al. Study on elastic mechanical properties of novel 2D negative Poisson's ratio structure: Re-entrant hexagon nested with star-shaped structure[J]. Composite Structures, 2022, 301: 116065. DOI: 10.1016/j.compstruct.2022.116065
[10] 蒋伟, 马华, 王军, 等. 基于环形蜂窝芯结构的负泊松比机械超材料[J]. 科学通报, 2016, 61(13): 1421-1427. DOI: 10.1360/N972015-01314 JIANG Wei, MA Hua, WANG Jun, et al. Mechanical metamaterial with negative Poisson’s ratio based on circular honeycomb core[J]. Chinese Science Bulletin, 2016, 61(13): 1421-1427(in Chinese). DOI: 10.1360/N972015-01314
[11] 沈建邦, 肖俊华. 负泊松比可变弧角曲边内凹蜂窝结构的力学性能[J]. 中国机械工程, 2019, 30(17): 2135-2141. DOI: 10.3969/j.issn.1004-132X.2019.17.017 SHEN Jianbang, XIAO Junhua. Mechanics properties of negative Poisson’s ratio honeycomb structures with variable arc angle curved concave sides[J]. China Mechanical Engineering, 2019, 30(17): 2135-2141(in Chinese). DOI: 10.3969/j.issn.1004-132X.2019.17.017
[12] 张新春, 刘颖, 李娜. 具有负泊松比效应蜂窝材料的面内冲击动力学性能[J]. 爆炸与冲击, 2012, 32(5): 475-482. DOI: 10.3969/j.issn.1001-1455.2012.05.005 ZHANG Xinchun, LIU Ying, LI Na. In-plane dynamic crushing of honeycombs with negative Poisson’s ratio effects[J]. Explosion and Shock Waves, 2012, 32(5): 475-482(in Chinese). DOI: 10.3969/j.issn.1001-1455.2012.05.005
[13] SHEN J B, GE J R, XIAO J H, et al. In-plane impact dynamics of honeycomb structure containing curved reentrant sides with negative Poisson’s ratio effect[J]. Mechanics of Advanced Materials and Structures, 2022, 29(10): 1489-1497. DOI: 10.1080/15376494.2020.1824285
[14] 尤泽华, 肖俊华. 弧边内凹蜂窝负泊松比结构的面内冲击动力学数值研究[J]. 工程力学, 2022, 39(12): 248-256. DOI: 10.6052/j.issn.1000-4750.2021.07.0572 YOU Zehua, XIAO Junhua. Numerical study on in-plane impact dynamics of concave honeycomb structure with negative Poisson’s ratio[J]. Engineering Mechanics, 2022, 39(12): 248-256(in Chinese). DOI: 10.6052/j.issn.1000-4750.2021.07.0572
[15] 郭之熙, 肖俊华. 多弧段曲边内凹蜂窝可调泊松比结构的力学性能研究[J]. 工程力学, 2023, 40(10): 204-212. DOI: 10.6052/j.issn.1000-4750.2022.01.0093 GUO Zhixi, XIAO Junhua. Mechanical properties of multi-arc concave honeycomb structure with adjustable Poisson’s ratio[J]. Engineering Mechanics, 2023, 40(10): 204-212(in Chinese). DOI: 10.6052/j.issn.1000-4750.2022.01.0093
[16] LI D, MA J, DONG L, et al. A bi-material structure with Poisson's ratio tunable from positive to negative via temperature control[J]. Materials Letters, 2016, 181: 285-288. DOI: 10.1016/j.matlet.2016.06.054
[17] HE X B, YU J J, XIE Y. Bi-material re-entrant triangle cellular structures incorporating tailorable thermal expansion and tunable Poisson’s ratio[J]. Journal of Mechanisms and Robotics, 2019, 11(6): 061003. DOI: 10.1115/1.4044335
[18] 马芳武, 梁鸿宇, 王强, 等. 双材料负泊松比结构的面内冲击动力学性能[J]. 吉林大学学报(工学版), 2021, 51(1): 114-121. MA Fangwu, LIANG Hongyu, WANG Qiang, et al. In-plane impact dynamic performance of dual material negative Poisson’s ratio structure[J]. Journal of Jilin University (Engineering and Technology Edition), 2021, 51(1): 114-121(in Chinese).
[19] SHAO Y, MENG J, MA G, et al. Insight into the negative Poisson’s ratio effect of the gradient auxetic reentrant honeycombs[J]. Composite Structures, 2021, 274: 114366. DOI: 10.1016/j.compstruct.2021.114366
[20] LI S, LI X, WANG Z, et al. Finite element analysis of sandwich panels with stepwise graded aluminum honeycomb cores under blast loading[J]. Composites Part A: Applied Science and Manufacturing, 2016, 80: 1-12. DOI: 10.1016/j.compositesa.2015.09.025
[21] WU X, SU Y T, SHI J. In-plane impact resistance enhancement with a graded cell-wall angle design for auxetic metamaterials[J]. Composite Structures, 2020, 247(9): 112451.
[22] 朱冬梅, 鲁光阳, 杜瑶, 等. 新型负泊松比梯度结构缓冲性能[J]. 湖南大学学报(自然科学版), 2023, 50(10): 203-211. ZHU Dongmei, LU Guangyang, DU Yao, et al. Cushioning performance of a new negative Poisson’s ratio gradient structer[J]. Journal of Hunan University (Natural Sciences), 2023, 50(10): 203-211(in Chinese).
[23] 张晓楠, 晏石林, 欧元勋, 等. 负泊松比内凹蜂窝结构梯度设计与动态冲击响应[J]. 振动与冲击, 2023, 42(3): 193-198. ZHANG Xiaonan, YAN Shilin, OU Yuanxun, et al. Gradient design and dynamic impact response of concave honeycomb structures with negative Poisson’s ratio[J]. Journal of Vibration and Shock, 2023, 42(3): 193-198(in Chinese).
[24] 王堃, 孙勇, 彭明军, 等. 基于ANSYS的铝蜂窝夹芯板低速冲击仿真模拟研究[J]. 材料导报, 2012, 26(8): 157-160. DOI: 10.3969/j.issn.1005-023X.2012.08.040 WANG Kun, SUN Yong, PENG Mingjun, et al. Simulation of low-velocity impact of aluminium honeycomb sandwich panels with ANSYS[J]. Materials Reports, 2012, 26(8): 157-160(in Chinese). DOI: 10.3969/j.issn.1005-023X.2012.08.040
[25] 罗伟铭, 石少卿, 廖瑜, 等. 成层式铝蜂窝夹芯结构冲击响应试验研究[J]. 材料导报, 2018, 32(8): 1328-1332. DOI: 10.11896/j.issn.1005-023X.2018.08.023 LUO Weiming, SHI Shaoqing, LIAO Yu, et al. An experimental investigation upon the impact response of the layered aluminum honeycomb sandwich structure[J]. Materials Reports, 2018, 32(8): 1328-1332(in Chinese). DOI: 10.11896/j.issn.1005-023X.2018.08.023
[26] LUO Y, YUAN K, SHEN L, et al. Sandwich panel with in-plane honeycombs in different Poisson's ratio under low to medium impact loads[J]. Reviews on Advanced Materials Science, 2021, 60(1): 145-157. DOI: 10.1515/rams-2021-0020
[27] 邓云飞, 张伟岐, 吴华鹏, 等. 泡沫填充的S型褶皱复合材料夹芯板低速冲击响应特性[J]. 复合材料学报, 2021, 38(8): 2605-2615. DENG Yunfei, ZHANG Weiqi, WU Huapeng, et al. Low-speed impact response of the composite sandwich panels with S-type foldcore filled by foam[J]. Acta Materiae Compositae Sinica, 2021, 38(8): 2605-2615(in Chinese).
[28] 陈鹏宇. 内凹弧形蜂窝夹芯板抗弹性能试验与数值仿真[D]. 大连: 大连理工大学, 2022. CHEN Pengyu. Test and numerical simulation on ballistic impact resistance of re-entrant Circular honeycomb sandwich panel[D]. Dalian: Dalian University of Technology, 2022(in Chinese).
[29] 辛亚军, 孙帅, 杨硕, 等. 铝蜂窝夹芯板面外剪切性能试验研究与数值模拟[J]. 复合材料学报, 2022, 39(12): 6119-6129. XIN Yajun, SUN Shuai, YANG Shuo, et al. Experiment and numerical simulation of out-plane shear performance of aluminum honeycomb sandwich panel[J]. Acta Materiae Compositae Sinica, 2022, 39(12): 6119-6129(in Chinese).
[30] BOHARA R P, LINFORTH S, GHAZLAN A, et al. Performance of an auxetic honeycomb-core sandwich panel under close-in and far-field detonations of high explosive[J]. Composite Structures, 2022, 280: 114907. DOI: 10.1016/j.compstruct.2021.114907
[31] 杨姝, 陈鹏宇, 江峰, 等. 内凹弧形蜂窝夹芯板低速弹道冲击试验与数值仿真[J]. 振动与冲击, 2023, 42(6): 255-262, 297. YANG Shu, CHEN Pengyu, JIANG Feng, et al. Low-speed ballistic impact test and numerical simulation on re-entrant circular honeycomb sandwich panels[J]. Journal of Vibration and Shock, 2023, 42(6): 255-262, 297(in Chinese).
[32] 蒋舟顺, 徐峰祥, 邹震, 等. 爆炸载荷下正弦曲边三维负泊松比夹芯板的动态响应和吸能特性[J]. 爆炸与冲击, 2024, 44(2): 3-20. DOI: 10.11883/bzycj-2023-0214 JIANG Zhoushun, XU Fengxiang, ZOU Zhen, et al. Dynamic response and energy absorption properties of sinusoidally curved three-dimensional negative Poisson’s ratio sandwich panels subjected to blast loading[J]. Explosion and Shock Waves, 2024, 44(2): 3-20(in Chinese). DOI: 10.11883/bzycj-2023-0214
[33] 郭之熙. 梯度负泊松比弧边蜂窝结构力学性能研究[D]. 秦皇岛: 燕山大学, 2023. GUO Zhixi. Study on mechanical properties of gradient negative Poisson’s ratio arc-edge honeycomb structure[D]. Qinhuangdao: Yanshan University, 2023(in Chinese).
[34] 万武举, 肖俊华, 郭之熙. 双材料曲边内凹负泊松比多胞结构的力学性能研究[J]. 工程力学, 2023[2024-04-16]. WAN Wuju, XIAO Junhua, GUO Zhixi. Mechanical properties of arc concave multicell structures of bimaterials with negative Poisson's ratio[J]. Engineering Mechanics, 2023[2024-04-16]. (in Chinese).
[35] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures[J]. Engineering Fracture Mechanics, 1985, 21(1): 31-48.
-
其他相关附件
-
-
负泊松比结构材料具有高抗压性能，在众多领域中具有巨大的潜在应用(如用于航空航天、医疗卫生、建筑等领域的某些特殊零部件)。目前现有的负泊松比胞元大都是由单种材料且直边组成，本文借鉴复合材料设计的思想，考虑结合不同种材料的优势性能，将其应用到负泊松比胞元设计中。相比单材料负泊松比结构，多材料胞元设计能够将负泊松比特性与其他材料所具有的优异性能结合起来，更好地发挥材料的优势。
本文基于作者提出的双材料曲边内凹负泊松比胞元，基于纵横向材料模量比梯度设计的思想，将梯度双材料曲边内凹负泊松比蜂窝构建为夹芯层，通过改变芯层纵横向材料的模量比构建了正梯度、负梯度、对称正梯度和对称负梯度四种夹芯板结构，研究了夹芯板受局部冲击时的失效行为，讨论了梯度排布和冲击速度对夹芯板抗冲击性能的影响。实验与仿真结果比较说明了本文数值方法的可行性。数值研究了不同排列方式时蜂窝夹芯板在受局部冲击作用下的失效力学性能，考察了冲头冲击速度和芯层梯度排列模式对夹芯板破坏模式、冲头接触力与能量吸收效果的影响。研究表明：芯层排列模式显著影响夹芯板的冲击破坏模式和冲击动力学性能；梯度双材料设计可以显著增强夹芯板的吸能效果。所得结果为该类机械超材料的冲击变形失效和吸能效果研究提供了力学依据。
梯度双材料负泊松比蜂窝夹芯板与边界条件示意图
梯度双材料负泊松比夹芯板示意图
局部穿透后实验和模拟中试件破坏模式
计量
- 文章访问数: 169
- HTML全文浏览量: 70
- PDF下载量: 32
