Low frequency bandgap characteristics and application of a novel two-dimensional three-component cement-based phononic-like crystal composite material
-
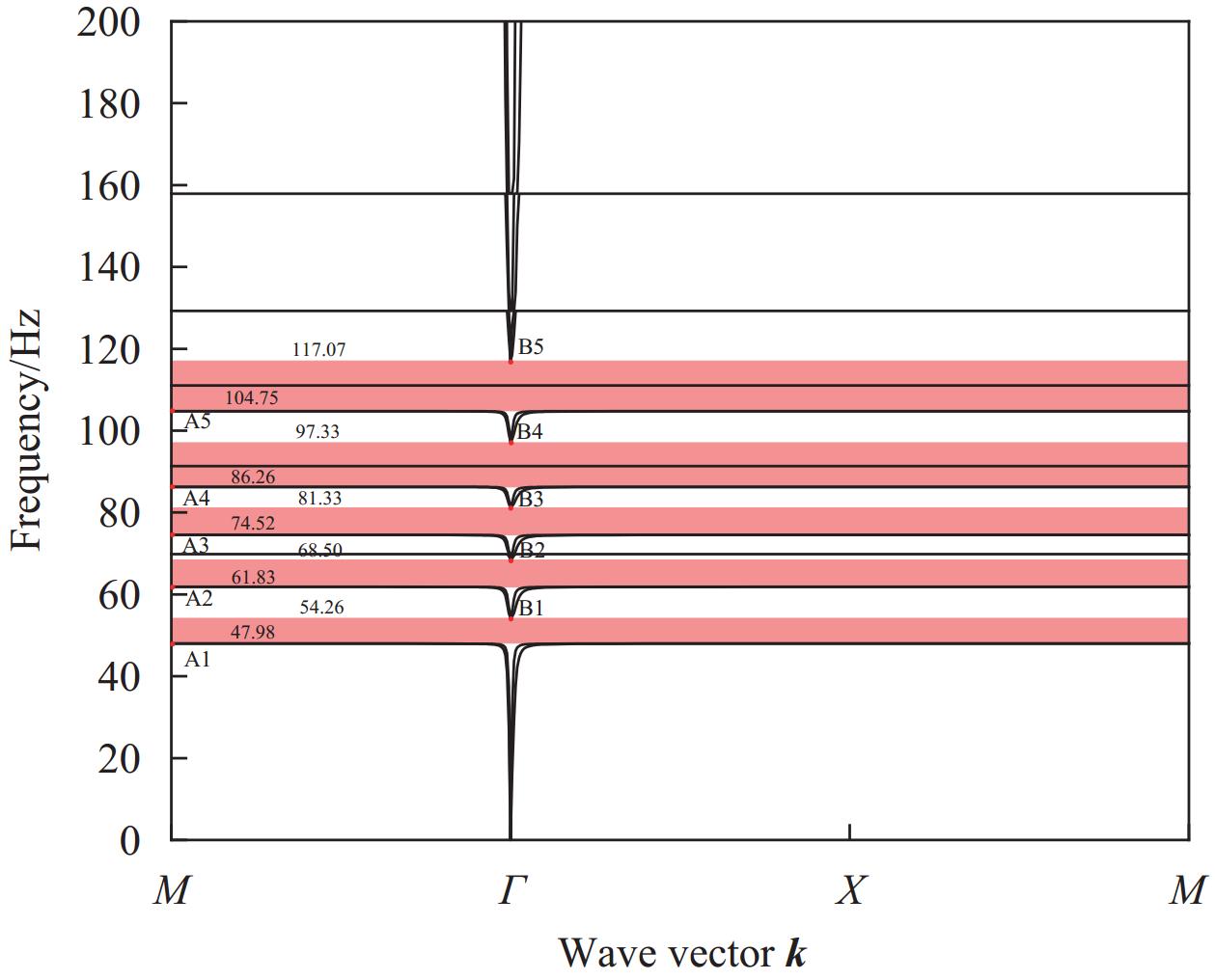
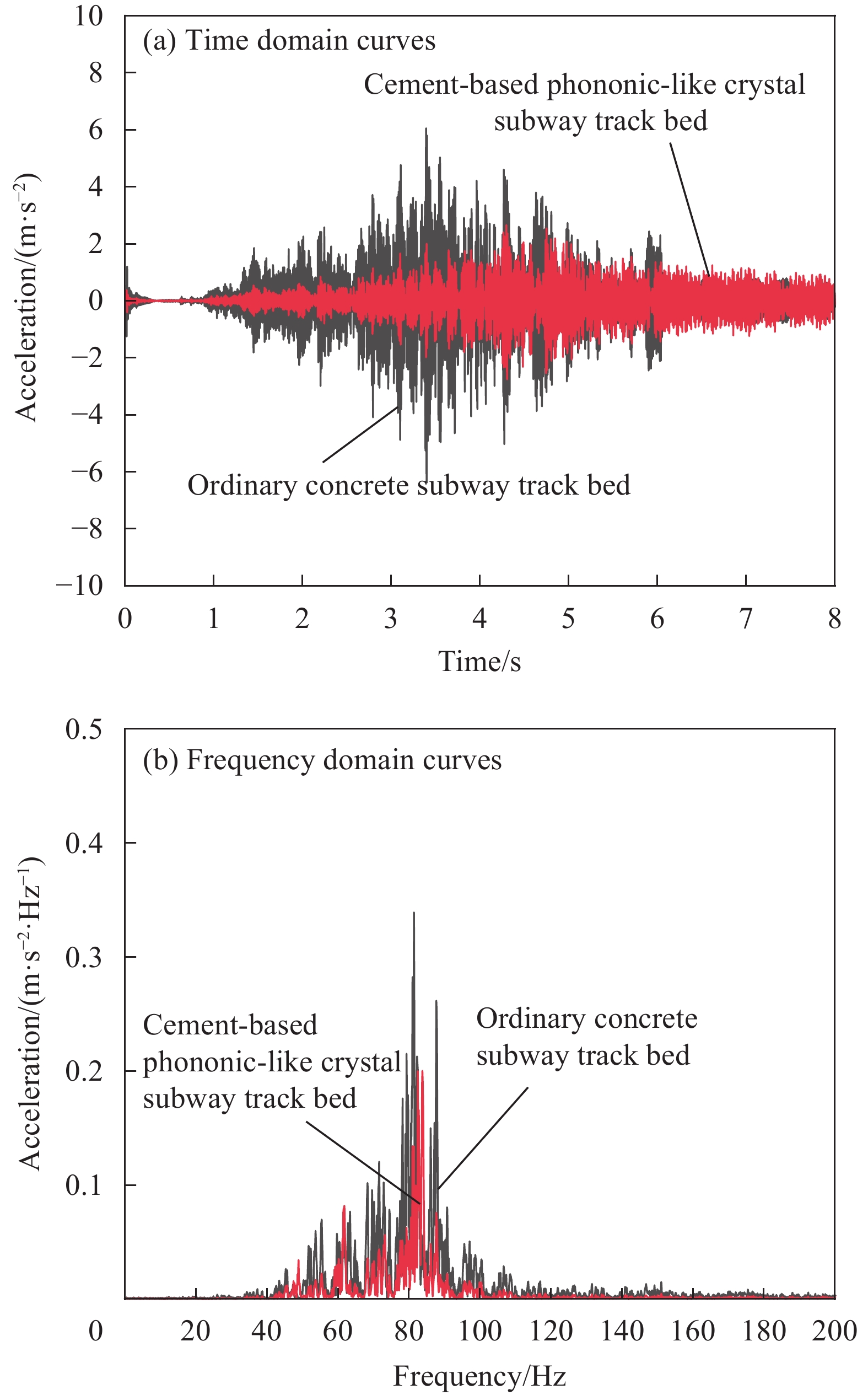
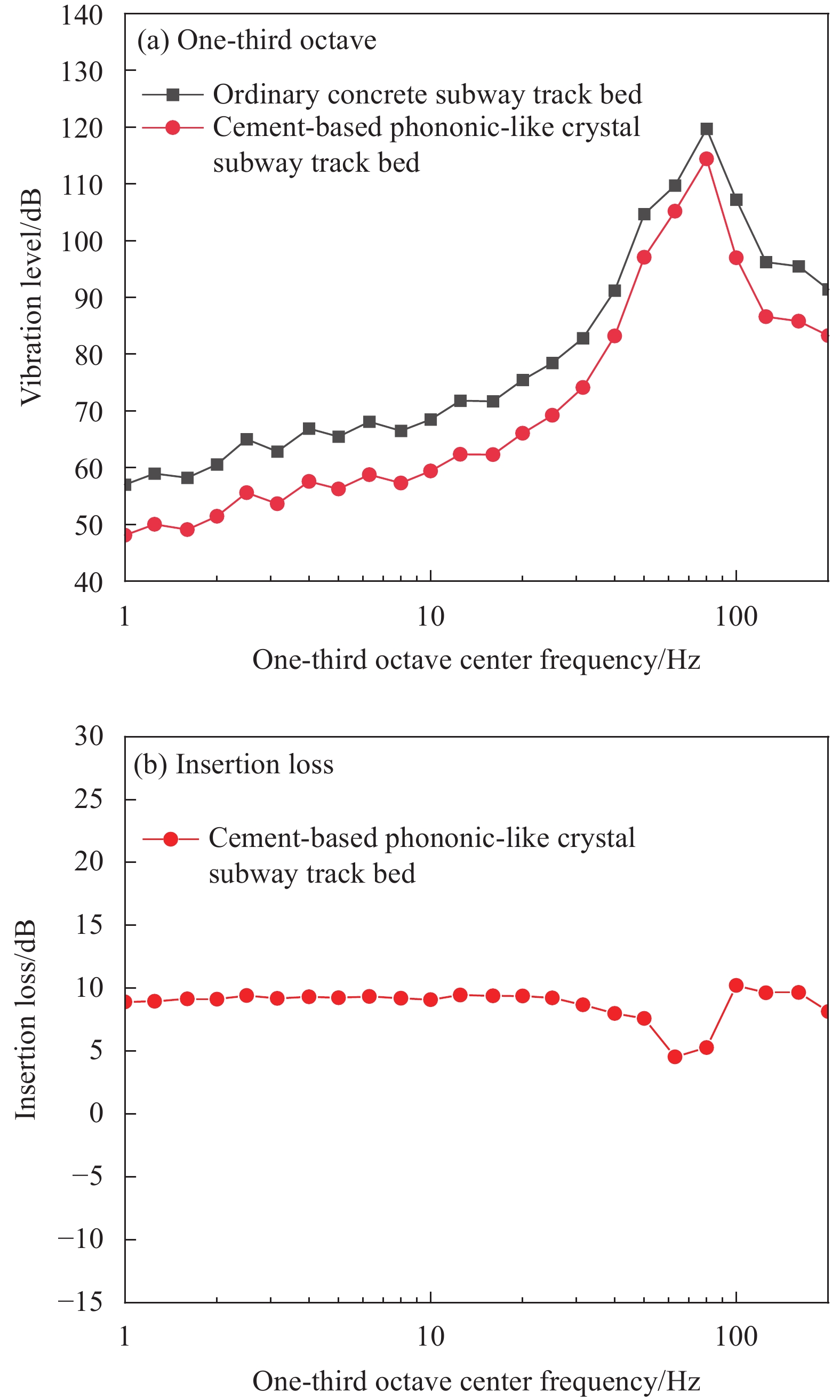
摘要: 为了拓宽混凝土超材料的弹性波带隙宽度和数量，本文基于局域共振理论设计了一种新型二维三组元水泥基拟声子晶体。首先，采用有限元方法计算和研究了该新型二维三组元水泥基拟声子晶体的能带结构、振动模态、位移场和衰减特性。其次，分析了带隙形成机制和影响因素，并根据质量-弹簧系统模型推导了带隙范围的理论估计式。最后，将该水泥基拟声子晶体应用到地铁道床上，分析了水泥基拟声子晶体地铁道床的减振性能。结果表明：该新型二维三组元水泥基拟声子晶体在200 Hz频段内打开了5条低频带隙，在带隙频率范围内，衰减值大多都在10 dB以上，衰减效果较好；带隙的打开与各原胞的振动特征呈现出对应关系，因特定原胞的平移振动触发，由特定原胞与基体的耦合作用的强度所控制；散射体材料的密度、包裹层材料的弹性模量及厚度是影响其带隙的主要因素；由新型二维三组元水泥基拟声子晶体组成的水泥基拟声子晶体地铁道床在1~200 Hz频段内的振动加速度均小于普通混凝土地铁道床，最大插入损失为10.22 dB，插入损失平均值为8.76 dB，具有显著的减振性能。Abstract: In order to widen the width and number of elastic bandgap of concrete metamaterials, a novel two-dimensional three-component cement-based phononic-like crystal was designed based on local resonance theory. Firstly, the finite element method was used to calculate and study the energy band structure, vibration mode, displacement field and attenuation characteristics of the novel two-dimensional three-component cement-based phononic-like crystal. Secondly, the formation mechanism and influencing factors of the bandgap were analyzed, and the theoretical estimation of the bandgap range was derived according to the mass-spring system model. Finally, the cement-based phononic-like crystal was applied to the subway track bed, and the vibration reduction performance of the cement-based phononic-like crystal subway track bed was analyzed. The results show that the novel two-dimensional three-component cement-based phononic-like crystal opens 5 low-frequency bandgaps in the 200 Hz frequency range, and the attenuation values are mostly above 10 dB within the bandgap frequency range, and the attenuation effect is good. The opening of the bandgap corresponds to the vibration characteristics of each primitive cell, which is triggered by the translational vibration of a specific primitive cell and controlled by the strength of the coupling between the specific primitive cell and the matrix. The density of scatterer material, elastic modulus and thickness of cladding material are the main factors affecting the bandgap. In the 1-200 Hz frequency band, the vibration acceleration of the cement-based phononic-like crystal subway track bed composed of the novel two-dimensional three-component cement-based phononic-like crystal is lower than that of the ordinary concrete subway track bed, and the maximum insertion loss is 10.22 dB and the average insertion loss is 8.76 dB, which has remarkable vibration reduction performance.
-
随着全球经济的发展和化石燃料的消耗剧增，全球石油的需求量在逐年增加，多次采油技术得到了更广泛应用[1]，原油采出液的含水率也在逐年增加，正在给中国这一世界最大石油进口国带来严峻的挑战。同时，随着海上油气开发向深海迈进，深海平台的油水分离、采油井井底油水分离等都迫使人们探索新的油水分离技术。
工业生产运输过程中的各类不溶性有机物的泄露和排放导致了各种严重的环境问题[2-5]。例如石油加工和运输过程中的原油和成品泄露导致的水污染。皮革处理、食品加工、冶金、化工等工业生产过程中排放的含油废水。这些含油废水如不经处理直接排放，会对生态系统、农业生产构成严重破坏，危及人类健康，因此需要有效的油水分离技术来解决分离问题。目前主要的油水分离形式包括重力分离、离心、吸附和膜分离等[6-9]。将含油废水进行油水分离后，对废水的后续的处理难度和成本将会大大降低。膜分离技术作为一种先进的水净化技术，由于其经济、节能、易于操作的特点，已经成为一种不可或缺的选择[10-12]。然而，面对愈加复杂的含油污水(轻/重油和水的混合物、水包油乳液和油包水乳液的混合体系)以及不同酸碱环境，单一的除油型、除水型分离材料无法实现按需、高效和可持续的分离。因此，开发先进的智能油水分离材料是解决世界水环境恶化和石油短缺问题的迫切需要。
对某种外界刺激敏感并产生特殊反应的现象称为智能响应。具有可转换润湿行为的人工智能响应界面材料引起了人们越来越多的兴趣[13-15]。研究表明，可转换润湿行为通常可通过调节pH值[16]，改变光源[17]、温度[18]、磁场强度[19]等方式实现。pH响应材料可定义为在其结构中包括弱酸性或碱性基团的聚电解质，酸性或碱性基团如羧基、吡啶、磺酸、磷酸盐、叔胺等通常被称为pH响应基团，这些基团响应于pH的变化。基团会随着环境pH变化而接受或释放质子，导致结构和性质的变化，从而实现材料的pH响应。例如，Liu等[20]合成了一种基于分子印迹聚合物的pH响应型纳米药物，该纳米药物在的模拟肿瘤微环境中表现出良好的 pH 响应性，可通过特定的分子印迹位点选择性地从前列腺肿瘤中螯合睾酮。Surapaneni等[21]合成了一种具有温度和 pH 双重刺激响应的聚N-乙烯基己内酰胺和聚赖氨酸的嵌段共聚物，该共聚物可在两种刺激单独或共同作用下增加细胞对聚合物囊泡的渗透性，用于增强细胞内化和溶酶体靶向药物运送。
光作为一种低成本、绿色环保的刺激方法，使含有光响应基团的材料具有非接触式的遥控特性。光响应性能可以通过引入光响应基团来实现，该基团在特定波长的照射下发生结构变化，从而导致材料的性能发生变化[22-24]。目前常用的光响应基团是偶氮苯及其衍生物。偶氮化合物有两种异构体，一种是稳定态的反式结构，另一种是亚稳态的顺式结构。偶氮苯官能团经紫外线照射后，反式的非极性异构体可以转化为顺式的极性异构体，并且这一过程具有可逆性。由于偶氮苯反式构象的极性较弱，顺式构象的极性较强，在顺反异构体转变的过程中会导致材料的极性发生变化，其亲疏水性也随之变化，可以利用这一特性制备光响应智能转换油水分离材料，因为偶氮苯顺反异构体转换的可逆性，所以亲疏水性能的变化过程也是可逆的[25-28]。Yang等[29]利用偶氮苯聚合物作为衬底，制备一种可光切换的超疏水表面，该表面可受紫外和可见光的影响，使聚合物膜发生亲水到疏水的可逆改变。Du等[30]制备了一种功能化的偶氮苯聚合物，制备的偶氮苯溶液在紫外和可见光交替暴露下表现出偶氮苯的光异构化转变以及亲水到亲油的可逆变化。偶氮苯衍生物因其良好的化学稳定性和多功能性在光响应材料的制备和应用中具有广阔的发展前景[31]。
本文采用可逆加成-断裂链转移(RAFT)一步聚合法，制备得到了具有pH/光刺激响应性能的三元无规共聚物，并将其与无纺布相结合，得到了具有智能化可逆响应性能复合织物的油水分离膜。这种油水分离膜在油水分离、工业复杂废水处理等方面具有巨大的应用潜力。
1. 实验材料及方法
1.1 原材料
四氢呋喃(THF)、盐酸(35%)、甲醇，西陇科学公司；二硫代苯甲酸异丙酯(CDB)，阿拉丁生物技术有限公司；无纺布，深圳瑞都净化公司；偶氮二异丁腈(AIBN)、甲基丙烯酸羟乙酯(HEMA)、甲基丙烯酸二甲氨乙酯(DMAEMA)、对氨基苯甲酸、苯酚、氢氧化钠、亚硝酸钠、三乙胺、丙烯酰氯，麦克林公司。上述试剂均是分析纯，实验用水为去离子水。
1.2 样品表征
傅里叶红外光谱仪(VERTEX 70 Bruker)、 超导核磁共振波谱仪(BRUKER 500 MHz AVANCE NEO)、紫外可见分光光度计(UV-3600 Plus，日本岛津)、扫描电子显微镜(ZEISS GeminiSEM 500，德国卡尔蔡司) 、视频光学接触角测试仪(OCA25 Eastern-Dataphy)。
1.3 智能响应油水分离材料的合成
合成主要分为4个步骤：(1)重氮化-偶联反应；(2)酯化反应；(3)酯水解反应；(4)聚合反应。合成路线见图1。
![]()
图 1 偶氮苯单体及聚合物的合成路线：((a), (b))中间体；(c)单体；(d)聚合物Figure 1. Synthetic route of azobenzene monomer and polymer: ((a), (b)) Intermediate; (c) Monomer; (d) PolymerTEA—Tetrahydrofuran; THF—Triethylamine; AIBN—2, 2'-azobis(2-methylpropionitrile); CDB—Cumyl dithiobenzoate1.3.1 4-(4'-羟基)苯偶氮基苯甲酸的合成
通过重氮化-偶联反应制备4-(4'-羟基)苯偶氮基苯甲酸。将35%的盐酸12 mL与等体积的蒸馏水混合，缓慢滴加到装有对氨基苯甲酸(4.10 g，30 mmol)的烧瓶中搅拌均匀后，将30 mL的NaNO2水溶液(1 mol/L)缓慢滴入烧瓶反应30 min后加300 mL冰水稀释。然后滴加20 mL苯酚(2.94 g，31 mmol)和NaOH (1.72 g，31 mmol)水溶液。0~5℃下反应2 h，用NaOH调节pH至5~6。过滤收集固体，蒸馏水洗涤，得到4-(4'-羟基)苯偶氮基苯甲酸(中间体a)的橘黄色固体6.97 g，产率85%。
1.3.2 丙烯酸-4-((4-(丙烯氧基)苯基)二氮基)苯甲酸酐的合成
将1.3.1制得的偶氮苯(2.42 g，10 mmol)与三乙胺(1.47 mL，10 mmol)溶于25 mL THF并滴加丙烯酰氯(0.8 mL，10 mmol)，室温下反应24 h。滤去生成的盐，浓缩滤液并滴入甲醇中沉淀，得到丙烯酸-4-((4-(丙烯氧基)苯基)二氮基)苯甲酸酐黄色固体1.67 g (中间体b)，产率57%。
1.3.3 4-((4-(丙烯氧基)苯基)二氮基)苯甲酸的合成
将1.3.2中制备的偶氮苯1.51 g溶解在20 mL THF中，用10%的氢氧化钠水溶液调节pH至7~8，室温反应24 h，后用5%的盐酸水溶液调节pH至2~4，过滤并用蒸馏水洗涤，得到橙色固体1.24 g (单体c)，产率83%。
1.3.4 智能双响应聚合物的制备
采用可逆加成-断裂链转移聚合(RAFT)，一步反应制得智能响应聚合物。这种聚合也被称为“活性”/可控自由基聚合。由于其反应条件温和、单体选择范围广、分子设计能力强等优点，已发展成为最通用、最强大的聚合技术之一。
将1.3.3中的产物(1.55 g，5 mmol)与 DMAEMA(0.339 g，2.16 mmol)、HEMA (0.280 g，2.16 mmol)溶于THF后通氮排氧，温度升至70℃后加入AIBN (0.08 g，0.5 mmol)、CDB (0.2 g，0.2 mmol)反应48 h，旋蒸去除溶剂，甲醇洗涤后，干燥，得到橘红色聚合物1.84 g (聚合物d)，产率85%。
1.4 智能响应涂层的制备
将1.3.4中得到的聚合物均匀地涂膜在载玻片上，60℃下真空干燥，用于测量接触角。
1.5 智能油水分离膜的制备
将直径5 cm的无纺布用无水乙醇浸泡并超声清洁表面灰尘和油脂后，浸入未干燥的聚合物中，使聚合物均匀地涂在无纺布表面，60℃下真空干燥48 h，得到智能双响应油水分离膜。
2. 结果与讨论
2.1 表征与形貌
合成的各中间体、单体和聚合物的红外谱图如图2所示。
3452 cm−1处的吸收峰为偶氮苯中苯环上不饱和C—H键的伸缩振动，1606 cm−1为苯环骨架的C=C伸缩振动，807 cm−1为苯环上的C—H面外弯曲振动峰。a、c、d 在2942 cm−1处的吸收峰为羧基的O—H伸缩振动峰；b、c在1721 cm−1处存在C=C的伸缩振动；b在1786 cm−1处存在酸酐的C=O伸缩振动；聚合物d在3250 cm−1左右处存在DMAEMA中叔胺甲基上C—H伸缩振动峰和HEMA中的O—H伸缩振动峰。![]()
图 2 中间体a、b，单体c和聚合物d的傅里叶红外图谱Figure 2. FTIR spectra of azobenzene intermediates a, b, monomer c and polymer d图3为偶氮苯单体及聚合物的1H NMR图，图3(a)中，8.13×10−6、8.01×10−6、7.45×10−6和5.88×10−6处的峰对应单体c结构中为A、B、C和D的氢。图3(b)中，1.13×10−6和1.26×10−6处的氢对应于聚合物d中F和G相应位置的氢，A、B、C和D的氢与单体结构中的峰位置基本一致。
![]()
图 3 偶氮苯单体(a)和聚合物(b)的核磁共振氢谱图Figure 3. 1HNMR spectra of azobenzene monomer (a) and polymer (b)将偶氮苯溶于DMF (0.15 g·L−1)中，用365 nm紫外灯(20 W)照射2 h，使溶液中的单体转化为顺式结构后，分别检测不同照射时间的UV-Vis吸收光谱，吸收光谱随时间变化的关系如图4所示。其中，图4(a)为用LED灯(445 nm，20 W)对溶液进行照射，直至吸光度不再变化的吸收光谱。图4(b)为继续用365 nm紫外灯对溶液进行照射后的吸收光谱。偶氮苯特征吸收峰主要是330~380 nm处的π-π*吸收峰和420~500 nm的n-π*吸收峰。从图4中单体在365 nm和445 nm光照射下吸收光谱的变化情况可以看出，365 nm和445 nm的光照下，随照射时间的增加，单体在溶液中π-π*吸收峰的位置几乎不发生移动，而吸光度会逐渐变化。n-π*特征峰处的吸光度和吸收峰的位置均变化很小。吸光度的变化归因于紫外-可见光照射引起的偶氮苯从顺式到反式的异构化。对比图4(a)与图4(b)中吸收光谱变化，可以看到偶氮苯的顺反异构化是一个可逆的过程。
未经处理的无纺布(图5(a))纤维表面相对光滑。经过涂膜的无纺布(油水分离膜，图5(b))，可以观察到纤维表面及相邻纤维间粘附的聚合物，作为基底的无纺布具有多孔结构和交错的纤维，有利于聚合物的粘附并为油水分离提供了必要的空间。无纺布的柔性还使油水分离膜具有良好的柔韧性，可以承受多次折叠而不损坏。
![]()
图 5 (a)无纺布的SEM图像；(b)油水分离膜的SEM图像Figure 5. (a) SEM image of blank non-woven fabric; (b) SEM image of oil-water separation membrane2.2 智能响应及油水分离测试
将聚合物均匀地涂抹在载玻片上烘干后，分别在自然条件、pH=3的缓冲溶液浸泡、紫外-可见光照射、缓冲溶液浸泡后继续用紫外-可见光照射等情况下进行接触角测量实验，每次滴液的量为5 μL，接触角变化如图6所示。
![]()
图 6 聚合物d的载玻片涂层在不同条件下的接触角变化：(a)自然条件下；(b)经pH=3缓冲溶液浸泡后；(c)经pH=10缓冲溶液浸泡后；(d)经365 nm光照射后；(e)经445 nm光照射后；(f)经pH=3缓冲溶液浸泡并用365 nm紫外光照射后Figure 6. Contact angle variation of polymer d slide coatings under different conditions: (a) The natural state; (b) After immersion with pH=3 buffer solution; (c) After immersion in pH=10 buffer solution; (d) After exposure to 365 nm light; (e) After exposure to 445 nm light; (f) After immersion in pH=3 buffer solution and irradiation with 365 nm ultraviolet light图6显示了聚合物涂层在不同条件下的接触角的变化情况，该变化能够反映涂层材料的智能响应特性。在自然条件下的接触角143.7°，见图6(a)。将其在pH=3的缓冲溶液中浸泡1 h后烘干，接触角变化至109.9°，见图6(b)。该过程的接触角是由聚合物中DMAEMA单元和偶氮苯上羧基质子化共同作用导致的。随后将涂层置于pH=10的缓冲溶液中浸泡1 h后烘干，其接触角恢复至142.2°，见图6(c)，将烘干后的涂层在365 nm (20 W)紫外灯下照射5 min，接触角变化至48.4°，见图6(d)。用LED灯照射15 min后，其接触角恢复至139.3°，如图6(e)所示。该过程接触角的变化是由于聚合物中偶氮苯单元经过紫外-可见光照射后发生构型转化使涂层的润湿性发生转变。最后将涂层置于pH=3的缓冲溶液中浸泡1 h后烘干，然后将其置于365 nm (20 W)紫外灯下照射15 min，该过程由pH响应单元与光响应单元共同作用，其接触角由139.3°变化至19.0°，见图6(f)。
上述过程证明了涂层具有良好的刺激响应能力。以相同的方法重复进行上述实验，接触角的变化如图7所示。实验结果表明，经过多次刺激响应，聚合物涂层发生亲水和疏水的多次转换，且接触角仍可恢复到初始状态，证明了涂层的转换润湿能力具有良好的可逆性。其中，光在转化过程中具有更加显著的效果，这也在随后的油水分离试验中得到证实，切换时间也与偶氮苯单体吸收光谱的转化时间基本对应。由于光照可以在没有物理接触的情况下实现转化，这增强了材料的实际应用的便利性。
![]()
图 7 聚合物d的载玻片涂层在不同pH和光照下的接触角的可逆变化情况Figure 7. Contact angle reversible variation of polymer d slide coatings under different pH and light conditions为了测试光/pH双响应油水分离膜的分离效果，将柠檬黄染色的水100 mL与石油醚以2∶1的体积比混合后倒入滤杯中进行油水分离实验。为加快油/水的分离速度，在0.005 MPa的压力下用抽滤的方法模拟油水分离系统 (图8)。图8(a)中，抽滤30 s后，无色的石油醚被抽滤下来，不再有液体从上方流下，染色的水保留在上方滤杯中。在图8(b)中，用365 nm光照射分离膜12 h，以相同的方法进行油水分离，抽滤25 s后，染色的水被抽滤下来，石油醚被保留在上方。
![]()
图 8 聚合物d无纺布涂层的油水分离实验Figure 8. Oil-water separation experiment of non-woven coating with intelligent response polymer d分别测量分离后上方滤杯中的油或水的体积，计算得到分离效率分别为96.3% (图8(a))和95.8%(图8(b))。实验结果证明了分离膜具有良好的智能转换油水分离能力。
3. 结 论
(1)以合成的偶氮苯、甲基丙烯酸羟乙酯(HEMA)和甲基丙烯酸二甲氨乙酯(DMAEMA)为原料，采用可逆加成-断裂链转移(RAFT)法一步聚合，制得光和pH智能双响应三元无规共聚物。该聚合物以偶氮苯作为光响应单元，DMAEMA作为pH响应单元，HEMA使聚合物具有良好的柔性附着性能，FTIR和1HNMR谱图说明了聚合物的成功合成。
(2)通过在不同条件下的润湿性实验，验证了聚合物涂层的可转换润湿性。紫外线的照射导致偶氮苯单元的分子构型发生转变，结构上的变化导致聚合物的润湿性和渗透性的变化。在仅有pH=3的缓冲溶液浸泡后其最大接触角转变达到33.8°，仅有紫外光照射下其最大接触角转变达到93.8°，而在光和pH的共同作用下，其最大接触角变化可达到120.3°。说明了涂层在光照和pH的刺激下具有优异的刺激响应性。经过亲水与疏水的多次转换实验后，接触角仍可恢复到初始状态，证明了涂层对水的润湿能力切换具有可逆性。
(3)偶氮苯的引入使聚合物对光具有良好的响应性，DMAEMA上含有的叔胺基团和偶氮苯上的羧基共同增强了涂层的pH响应性和抗酸性，可以使涂层应对一些复杂情况下的油水分离，油水分离实验证明涂层在光照下的极性转变，单次分离效率分别达96.3%和95.8%。
综上，通过一步RAFT聚合制备得到的光/pH双响应的聚合物材料，可用来制备智能光/pH双响应油水分离膜，该膜具有优异的可逆刺激响应性能。
-
![]()
图 1 水泥基拟声子晶体原胞结构及第一布里渊区
Figure 1. Cement-based phononic-like crystal primitive cell and first Brillouin region
Rs—Scatterer inner diameter; Rc—Wrapping layerouter diameter; a—Lattice constant; M—Matrix; Γ, M—High symmetry point; kx, ky—Wave vector in the x and y directions
![]()
图 3 传统水泥基声子晶体能带结构
Figure 3. Band structure of traditional cement-based phononic crystal
![]()
图 4 新型二维三组元水泥基拟声子晶体能带结构
Figure 4. Band structure of novel two-dimensional three-component cement-based phononic-like crystal
![]()
图 15 新型二维三组元水泥基拟声子晶体的频率响应函数计算模型
Figure 15. Frequency response function calculation model of novel two-dimensional three-component cement-based phononic-like crystal
![]()
图 16 新型二维三组元水泥基拟声子晶体的频率响应函数
Figure 16. Frequency response function of novel two-dimensional three-component cement-based phononic-like crystal
![]()
图 17 新型二维三组元水泥基拟声子晶体的散射体材料参数对带隙的影响
Figure 17. Effect of scatterer material parameters on bandgap of novel two-dimensional three-component cement-based phononic-like crystal
![]()
图 18 新型二维三组元水泥基拟声子晶体的散射体结构参数对带隙的影响
Figure 18. Effect of scatterer structure parameters on bandgap of novel two-dimensional three-component cement-based phononic-like crystal
![]()
图 19 新型二维三组元水泥基拟声子晶体的包裹层材料参数对带隙的影响
Figure 19. Effect of material parameters of wrapping layer on bandgap of novel two-dimensional three-component cement-based phononic-like crystal
![]()
图 20 新型二维三组元水泥基拟声子晶体的包裹层结构参数对带隙的影响
Figure 20. Effect of structure parameters of wrapping layer on bandgap of novel two-dimensional three-component cement-based phononic-like crystal
![]()
图 21 新型二维三组元水泥基拟声子晶体的水泥砂浆基体材料参数对带隙的影响
Figure 21. Effect of material parameters of cement mortar matrix on bandgap of novel two-dimensional three-component cement-based phononic-like crystal
![]()
图 22 新型二维三组元水泥基拟声子晶体的水泥砂浆基体结构参数对带隙的影响
Figure 22. Effect of structure parameters of cement mortar matrix on bandgap of novel two-dimensional three-component cement-based phononic-like crystal
![]()
图 23 不同散射体形状的新型二维三组元水泥基拟声子晶体的计算模型
Figure 23. Calculation models of novel two-dimensional three-component cement-based phononic-like crystal with different scatterer shapes
![]()
图 24 不同形状散射体的新型二维三组元水泥基拟声子晶体的能带结构
Figure 24. Band structure of novel two-dimensional three-component cement-based phononic-like crystal with different scatterer shapes
![]()
图 25 新型二维三组元水泥基拟声子晶体内部散射体的多形状耦合的计算模型
Figure 25. Calculation models of multi-shape coupling of internal scatterers in novel two-dimensional three-component cement-based phononic-like crystal
![]()
图 26 新型二维三组元水泥基拟声子晶体原胞内部散射体多形状耦合的能带结构
Figure 26. Band structure of multi-shape coupling of internal scatterers in novel two-dimensional three-component cement-based phononic-like crystal
![]()
图 27 单振子和多振子局域共振声子晶体原胞的弹簧-质量系统等效模型
Figure 27. Spring-mass system equivalent models of single-oscillator and multi-oscillator local resonance phononic crystal primitive cell
k0-k5—Equivalent stiffness of oscillators; m0-m5—Equivalent mass of oscillators
![]()
图 28 多振子局域共振声子晶体的无限质量-质量晶格结构
Figure 28. Infinite mass-in-mass lattice structure of local resonance phononic crystal with multiple oscillators
L—Lattice constant
![]()
图 29 等效模型分析法计算结果
Figure 29. Calculation result of equivalent model analysis method
q—Wave vector; a—Lattice constant
![]()
图 30 水泥基拟声子晶体地铁道床和普通混凝土地铁道床计算模型
Figure 30. Calculation models of cement-based phononic-like crystal subway track bed and ordinary concrete subway track bed
![]()
图 31 水泥基拟声子晶体地铁道床和普通混凝土地铁道床时域和频域曲线
Figure 31. Time domain and frequency domain curves of cement-based phononic-like crystal subway track bed and ordinary concrete subway track bed
![]()
图 32 水泥基拟声子晶体地铁道床和普通混凝土地铁道床1/3倍频程及插入损失
Figure 32. One-third octave and insertion loss of cement-based phononic-like crystal subway track bed and ordinary concrete subway track bed
表 1 结构参数
Table 1 Structure parameters
Scatterer i Rs/m Rc/m a/m 1 0.0275 0.033 0.1 2 0.018 0.0216 3 0.013 0.0156 4 0.01 0.012 5 0.007 0.0084 
下载: 导出CSV
表 2 材料参数
Table 2 Material parameters
Component Density
ρ/(kg·m−3)Elastic modulus
E/PaShear modulus
G/PaScatterer 3300 1.2×1011 4.8×1010 Wrapping layer 12 1.34×105 5.93×104 Matrix 2000 3.45×1010 1.44×1010
下载: 导出CSV
表 3 新型二维三组元水泥基拟声子晶体的带隙影响因素及其水平
Table 3 Bandgap influencing factors and their levels of novel two-dimensional three-component cement-based phononic-like crystal
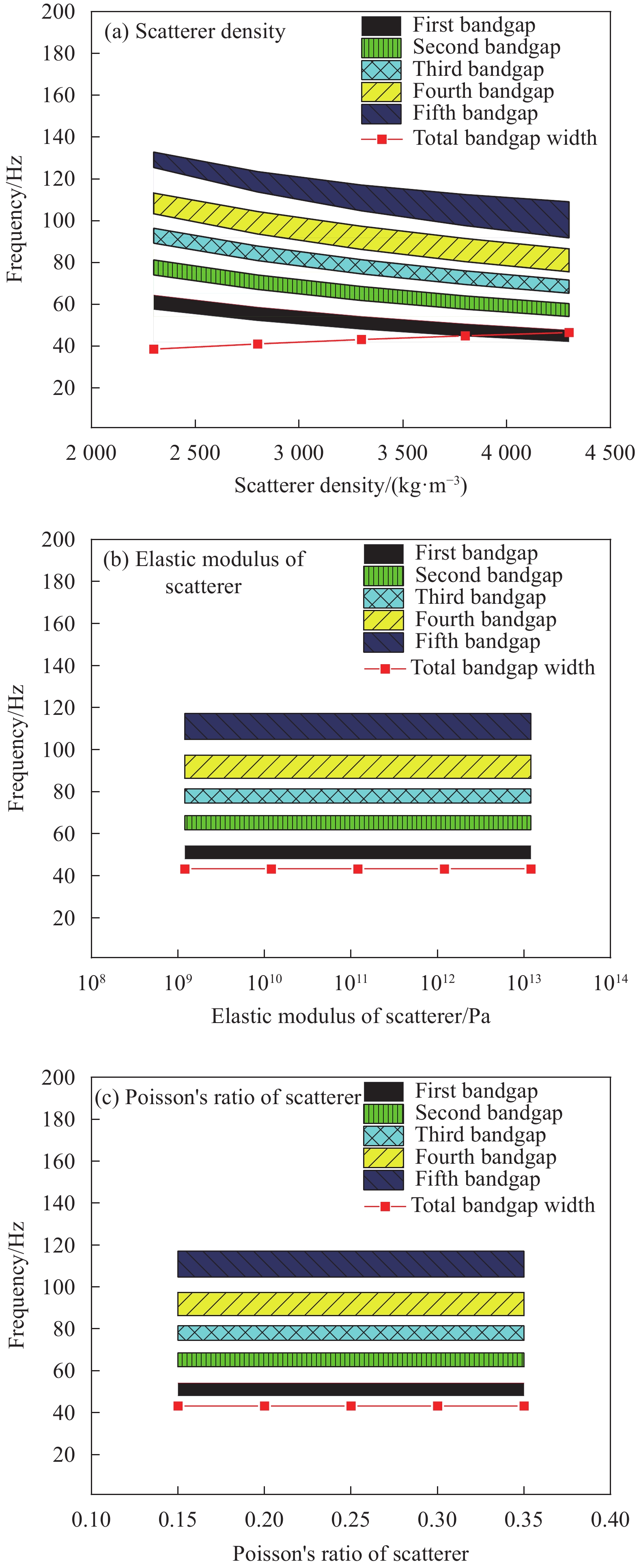
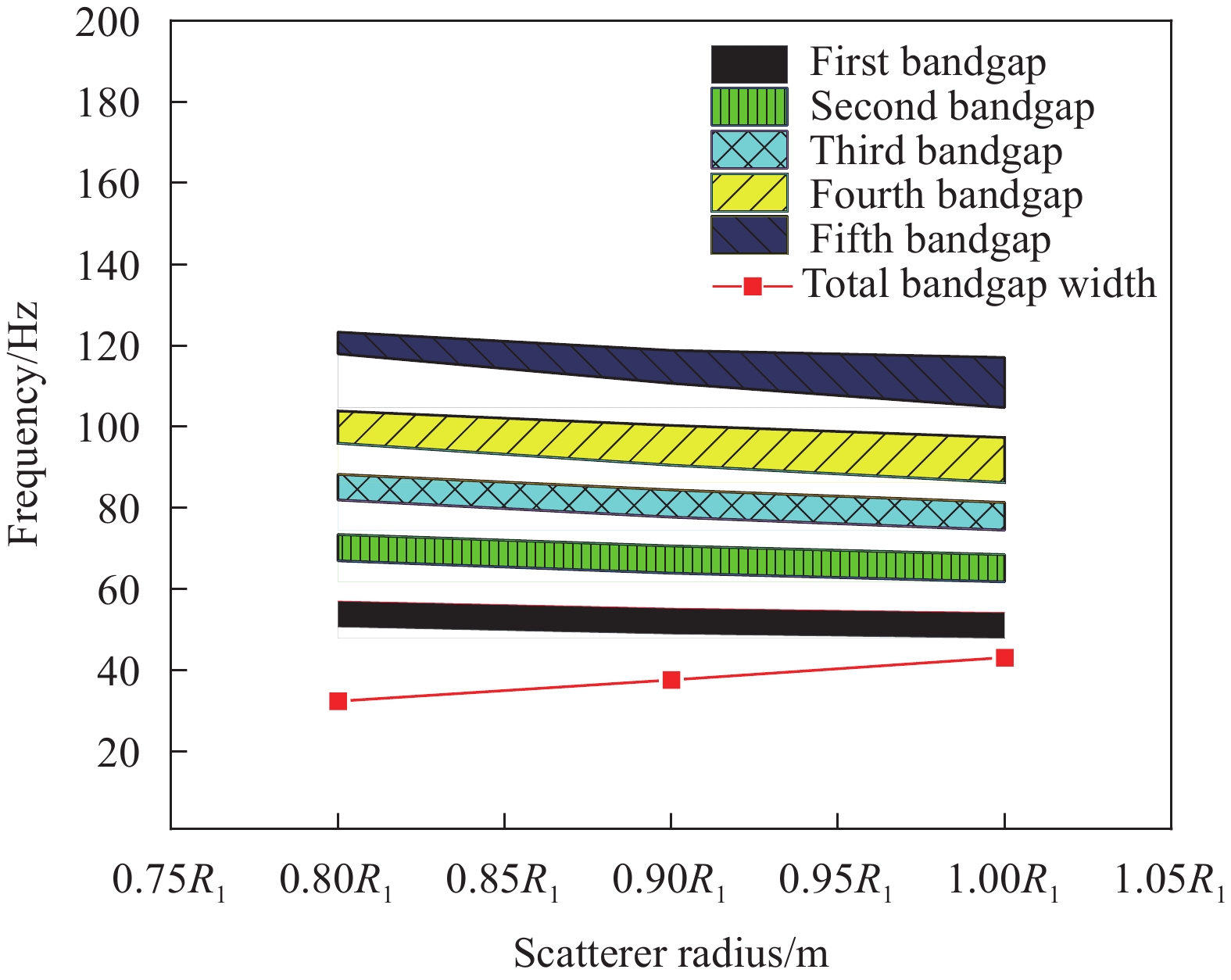
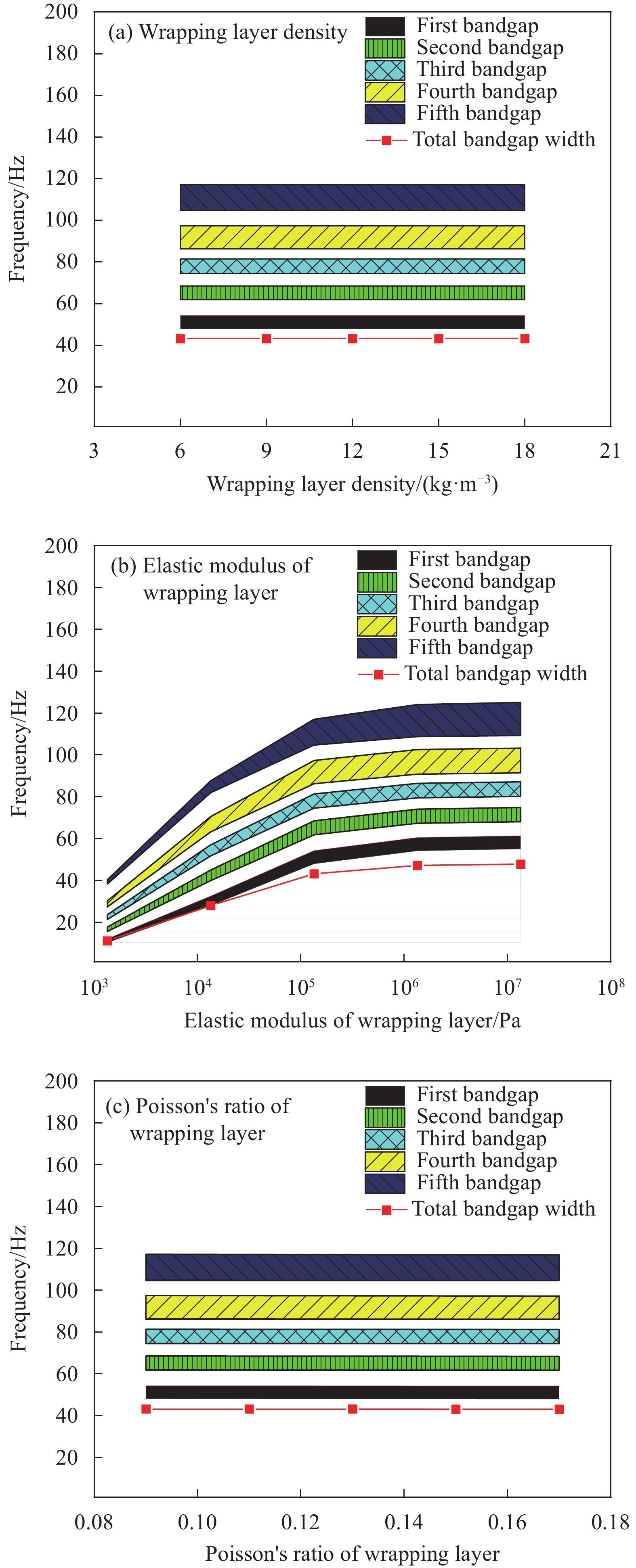
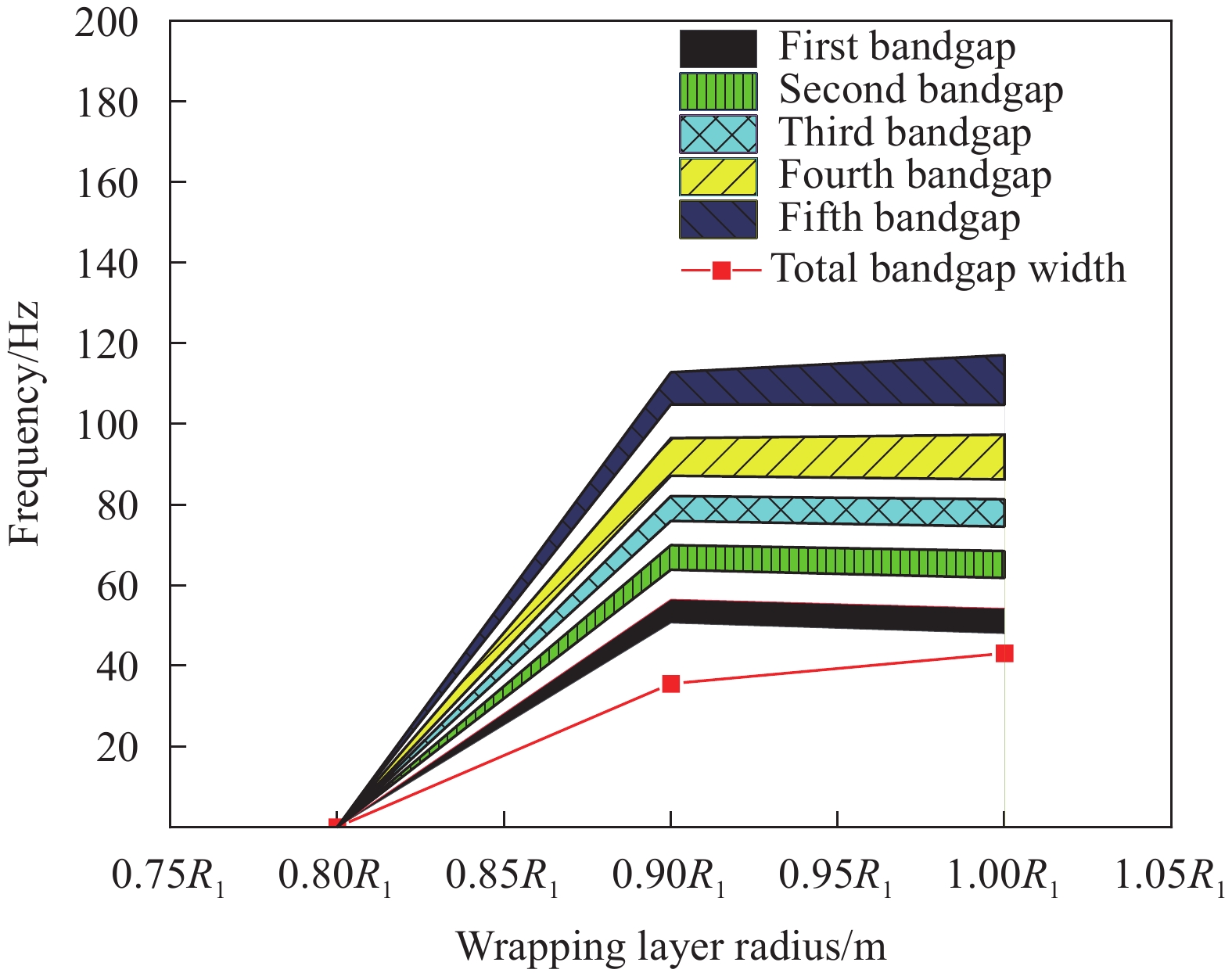
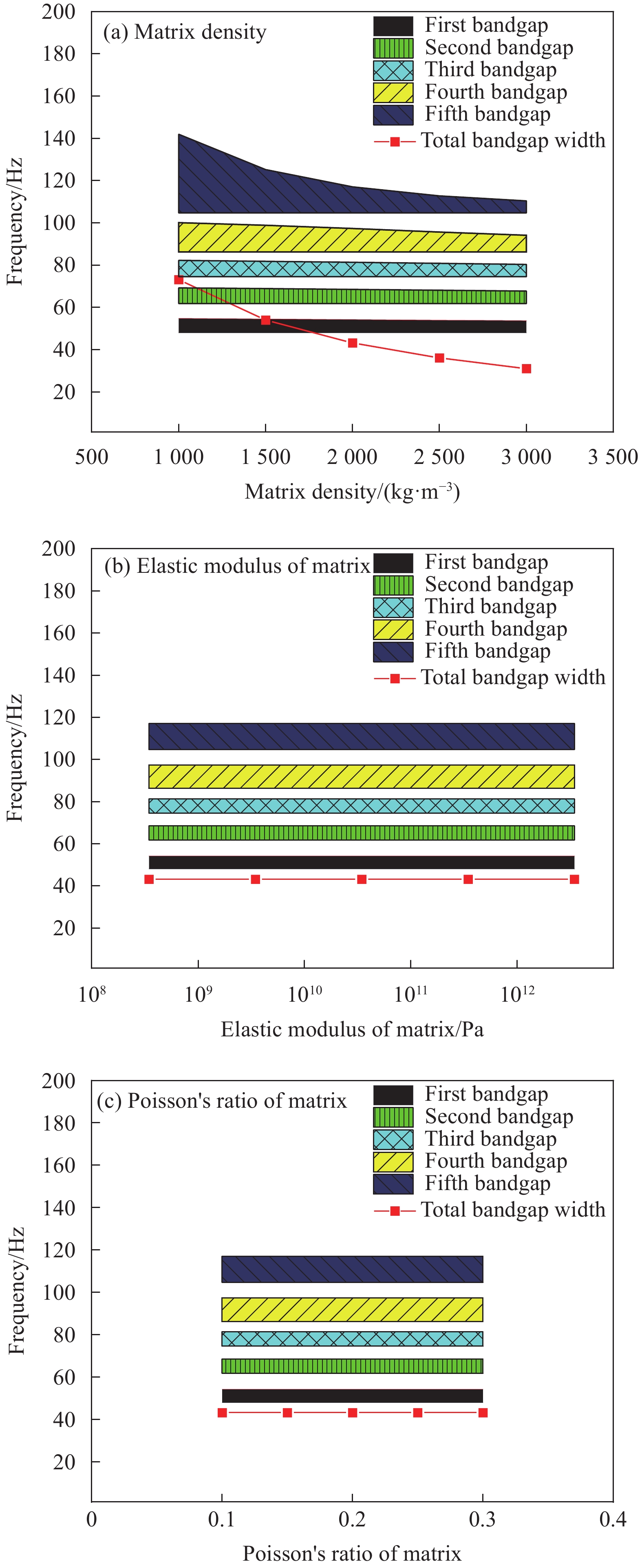
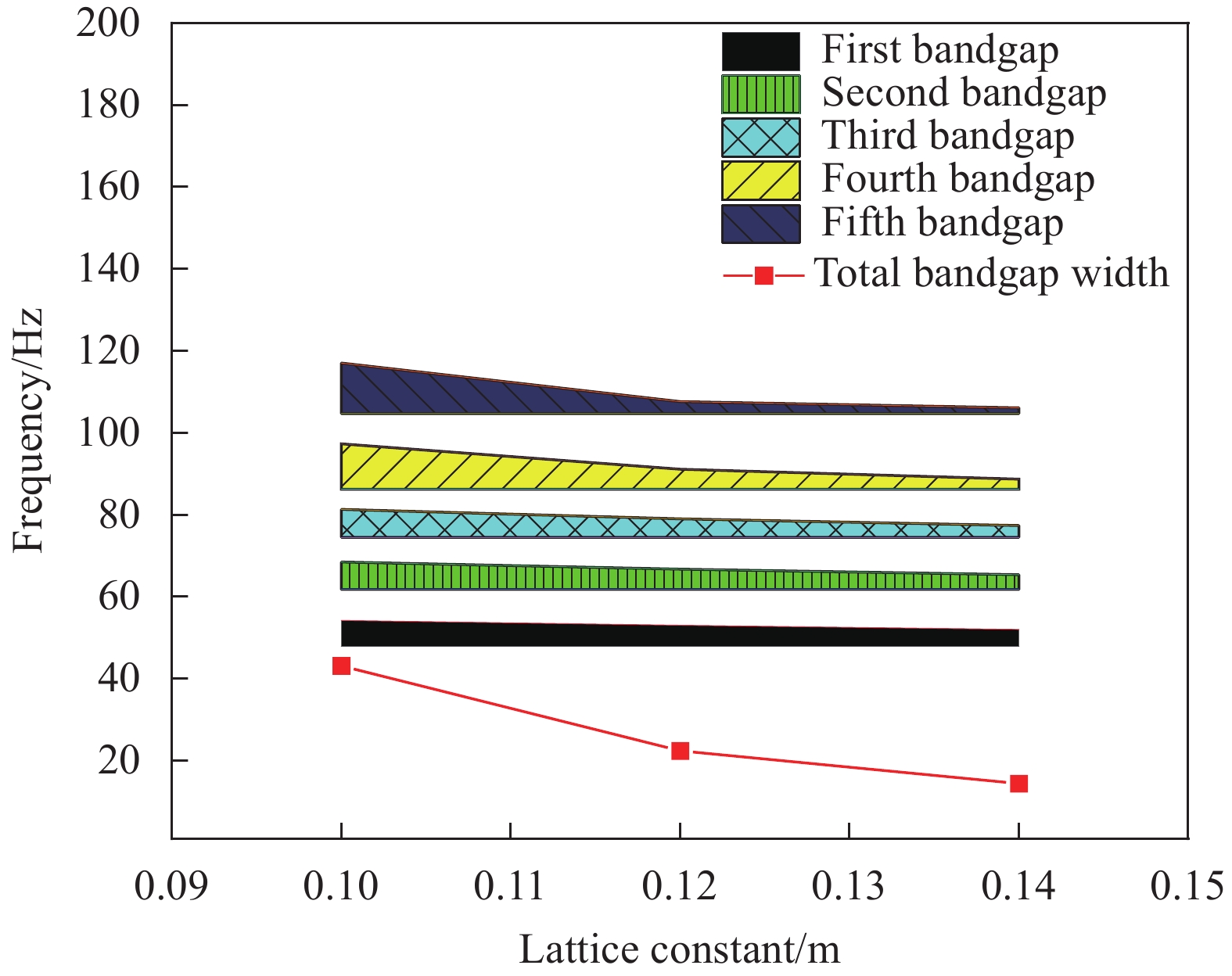
Influence factor Level 1 Level 2 Level 3 Level 4 Level 5 Material parameters Scatterer E/Pa 1.2×109 1.2×1010 1.2×1011 1.2×1012 1.2×1013 ρ/(kg·m−3) 2300 2800 3300 3800 4300 v 0.15 0.20 0.25 0.30 0.35 Wrapping layer E/Pa 1.34×103 1.34×104 1.34×105 1.34×106 1.34×107 ρ/(kg·m−3) 6 9 12 15 18 v 0.09 0.11 0.13 0.15 0.17 Matrix E/Pa 3.45×108 3.45×109 3.45×1010 3.45×1011 3.45×1012 ρ/(kg·m−3) 1000 1500 2000 2500 3000 v 0.10 0.15 0.20 0.25 0.30 Structure parameters Scatterer Rs/m 0.8R1 0.9R1 R1 – – Wrapping layer Rc/m 0.8R2 0.9R2 R2 – – Matrix a/m – – 0.1 0.12 0.14 Notes: R1—Inner diameter of scatterer; R2—Outer diameter of wrapping layer; v—Poisson's ratio.
下载: 导出CSV
-
[1] 陈俊豪, 曾晓辉, 谢友均, 等. 具有减振功能的混凝土超材料的带隙特性[J]. 硅酸盐学报, 2023, 51(5): 1272-1282. CHEN Junhao, ZENG Xiaohui, XIE Youjun, et al. Band gap properties of metaconcrete with vibration reduction function[J]. Journal of the Chinese Ceramic Society, 2023, 51(5): 1272-1282(in Chinese).
[2] JIN H X, HAO H, CHEN W S, et al. Effect of enhanced coating layer on the bandgap characteristics and response of metaconcrete[J]. Mechanics of Advanced Materials and Structures, 2021, 30(1): 175-188.
[3] 韩洁, 路国运, 赵一涛. 超材料混凝土单胞骨料的有阻尼自由振动特性研究[J]. 振动与冲击, 2022, 41(4): 239-245, 269. HAN Jie, LU Guoyun, ZHAO Yitao. A study of damped free vibration characteristics on a metaconcrete unit cell[J]. Journal of Vibration and Shock, 2022, 41(4): 239-245, 269(in Chinese).
[4] XU C, CHEN W S, HAO H, et al. Damping properties and dynamic responses of metaconcrete beam structures subjected to transverse loading[J]. Construction and Building Materials, 2021, 311: 125273. DOI: 10.1016/j.conbuildmat.2021.125273
[5] 靳贺欣, 陈文苏, 郝洪, 等. 超材料混凝土抗冲击效应数值研究[J]. 中国科学: 物理学 力学 天文学, 2020, 50(2): 78-89. JIN Hexin, CHEN Wensu, HAO Hong, et al. Numerical study on impact resistance of metaconcrete[J]. SCIENTIA SINICA Physica, Mechanica & Astronomica, 2020, 50(2): 78-89(in Chinese).
[6] BRICCOLA D, PANDOLFI A. Analysis on the dynamic wave attenuation properties of metaconcrete considering a quasi-random arrangement of inclusions[J]. Frontiers in Materials, 2021, 7: 615189. DOI: 10.3389/fmats.2020.615189
[7] 熊剑荣, 任凤鸣, 田时雨, 等. 超材料混凝土减振性能研究现状与展望[J]. 复合材料学报, 2024, 41(2): 656-671. XIONG Jianrong, REN Fengming, TIAN Shiyu, et al. Status and prospects of research on vibration reduction performance of metaconcrete[J]. Acta Materiae Compositae Sinica, 2024, 41(2): 656-671(in Chinese).
[8] MITCHELL S J, PANDOLFI A, ORTIZ M. Metaconcrete: Designed aggregates to enhance dynamic performance[J]. Journal of the Mechanics and Physics of Solids, 2014, 65: 69-81.
[9] XU C, CHEN W S, HAO H. The influence of design parameters of engineered aggregate in metaconcrete on bandgap region[J]. Journal of the Mechanics and Physics of Solids, 2020, 139: 103929. DOI: 10.1016/j.jmps.2020.103929
[10] 张恩, 路国运, 杨会伟, 等. 超材料混凝土的带隙特征及对冲击波的衰减效应[J]. 爆炸与冲击, 2020, 40(6): 69-77. DOI: 10.11883/bzycj-2019-0252 ZHANG En, LU Guoyun, YANG Huiwei, et al. Band gap features of metaconcrete and shock wave attenuation in it[J]. Explosion and Shock Waves, 2020, 40(6): 69-77(in Chinese). DOI: 10.11883/bzycj-2019-0252
[11] MIRANDA E J P, ANGELIN A F, SILVA F M, et al. Passive vibration control using a metaconcrete thin plate[J]. Cerâmica, 2019, 65(1): 27-33.
[12] 陈俊豪, 曾晓辉, 谢友均, 等. 多重谐振水泥基声子晶体带隙特性研究[J]. 材料导报, 2024, 38(12): 94-102. CHEN Junhao, ZENG Xiaohui, XIE Youjun, et al. Research on band gaps characteristics of multiple resonant cement-based phononic crystals[J]. Materials Reports, 2024, 38(12): 94-102(in Chinese).
[13] LIU Y, AN X Y, CHEN H L, et al. Vibration attenuation of finite-size metaconcrete: Mechanism, prediction and verification[J]. Composites Part A: Applied Science and Manufacturing, 2021, 143: 106294. DOI: 10.1016/j.compositesa.2021.106294
[14] LEI L J, MIAO L C, LI C, et al. The effects of composite primitive cells on band gap property of locally resonant phononic crystal[J]. Modern Physics Letters B, 2021, 35(20): 2150334. DOI: 10.1142/S0217984921503346
[15] GOFFAUX C, SÁNCHEZ-DEHESA J, LAMBIN P. Comparison of the sound attenuation efficiency of locally resonant materials and elastic band-gap structures[J]. Physical Review B, 2004, 70(18): 3352-3359.
[16] GOFFAUX C, SÁNCHEZ-DEHESA J, YEYATI A L, et al. Evidence of Fano-like interference phenomena in locally resonant materials[J]. Physical Review Letters, 2002, 88(22): 225502. DOI: 10.1103/PhysRevLett.88.225502
[17] WANG G, SHAO L H, LIU Y Z, et al. Accurate evaluation of lowest band gaps in ternary locally resonant phononic crystals[J]. Chinese Physics, 2006, 15(8): 1843-1848. DOI: 10.1088/1009-1963/15/8/036
[18] HUANG G L, SUN C T. Band gaps in a multiresonator acoustic metamaterial[J]. Journal of Vibration and Acoustics, 2010, 132(3): 031003. DOI: 10.1115/1.4000784
[19] ZHOU X Q, WANG J, WANG R Q, et al. Effects of relevant parameters on the bandgaps of acoustic metamaterials with multi-resonators[J]. Applied Physics A, 2016, 122(4): 427.
[20] HUANG H H, SUN C T, HUANG G L. On the negative effective mass density in acoustic metamaterials[J]. International Journal of Engineering Science, 2009, 47(4): 610-617. DOI: 10.1016/j.ijengsci.2008.12.007
[21] MIAO L C, LEI L J, LI C, et al. Vibration reduction of phononic-like crystal metaconcrete track bed for underground railway[J]. Journal of Materials in Civil Engineering, 2023, 35(8): 04023254. DOI: 10.1061/JMCEE7.MTENG-15400
-
目的
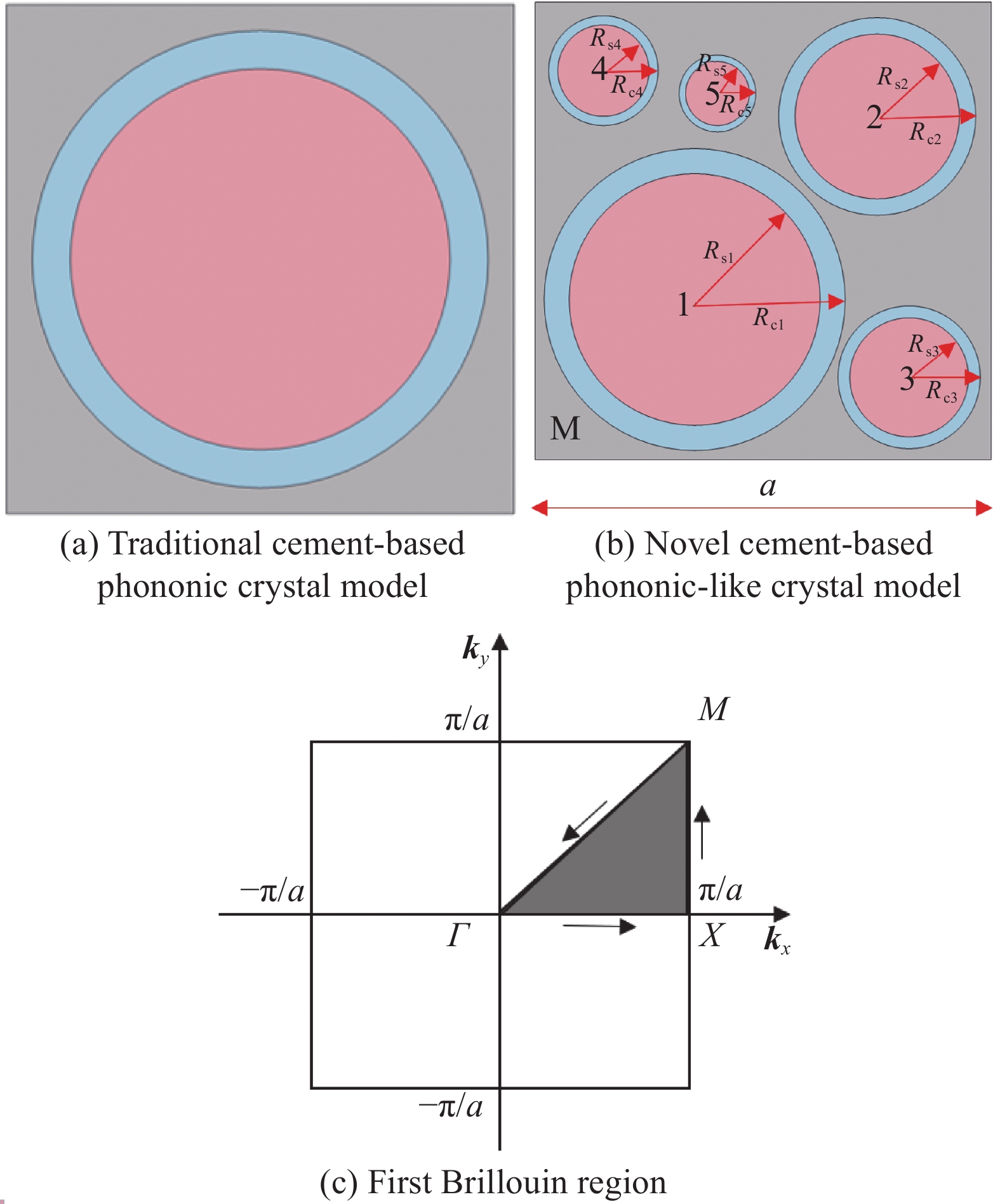
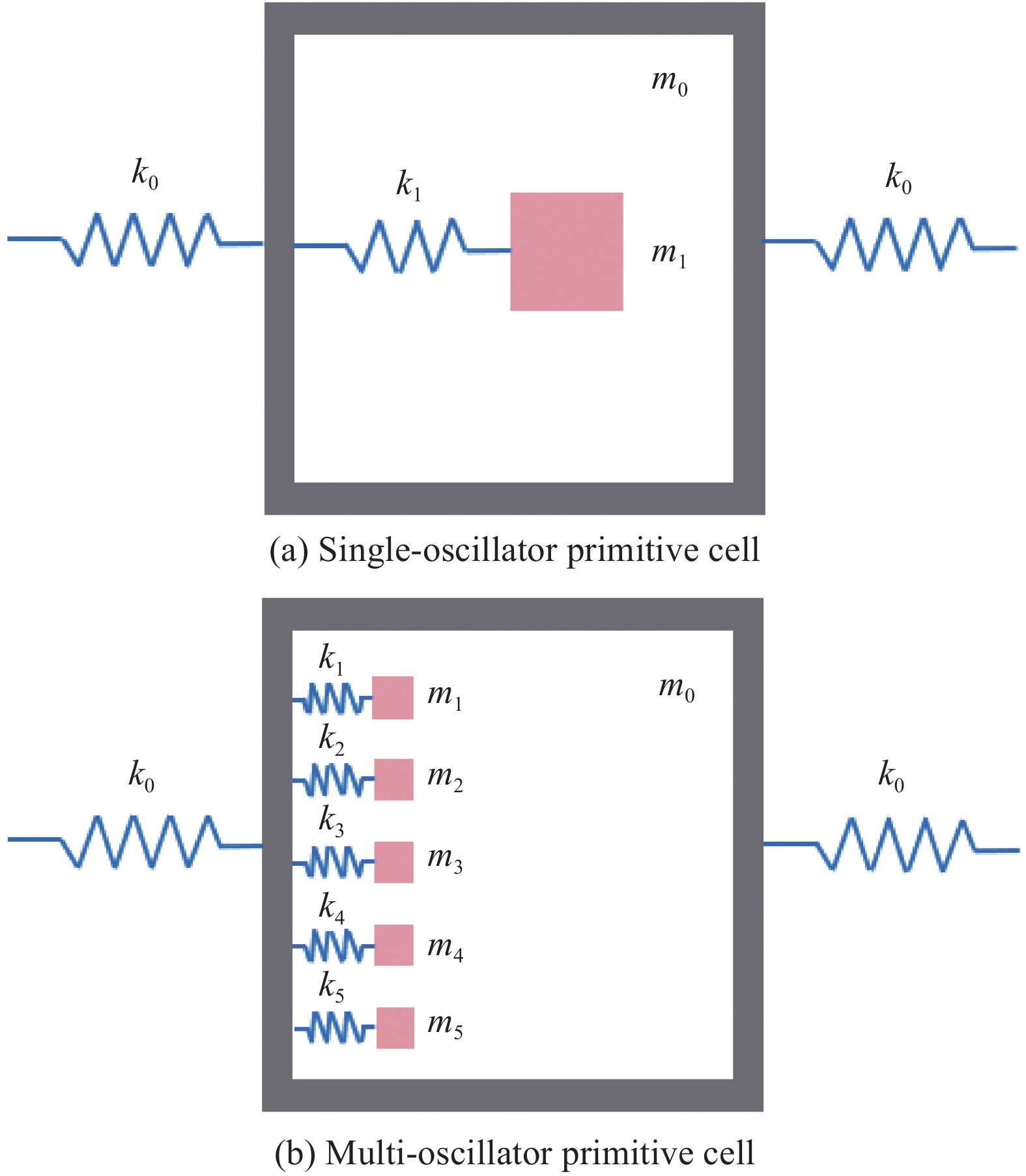
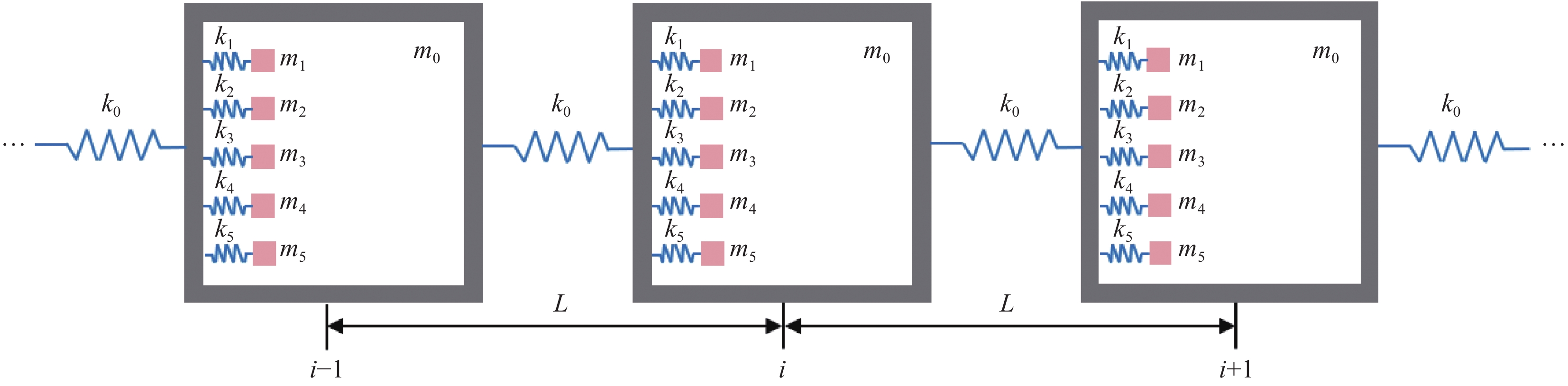
混凝土材料因具有高强耐久、使用方便且性能易调等优势，在建筑、桥梁、铁路轨道和隧道等结构中被广泛应用，但由于其较差的阻尼性能使其在工程结构中发挥的减振隔振效果甚微。水泥基声子晶体带隙的数量和宽度决定了混凝土超材料对弹性波的抑制范围和能力，传统的水泥基声子晶体有且仅有一条带隙，故由其构成的混凝土超材料也就只有一条衰减带，在实际工程应用上具有较大局限性。为了拓宽混凝土超材料对弹性波的衰减范围和数量，本文基于局域共振理论提出了一种新型二维三组元水泥基拟声子晶体，即在传统水泥基声子晶体的基础上，在水泥砂浆基体内部增加多个具有单独包裹层的散射体，形成一种水泥基拟声子晶体结构，使共振单元由单自由度系统变为多自由度系统，从而使混凝土超材料具有多重局域共振的特点。
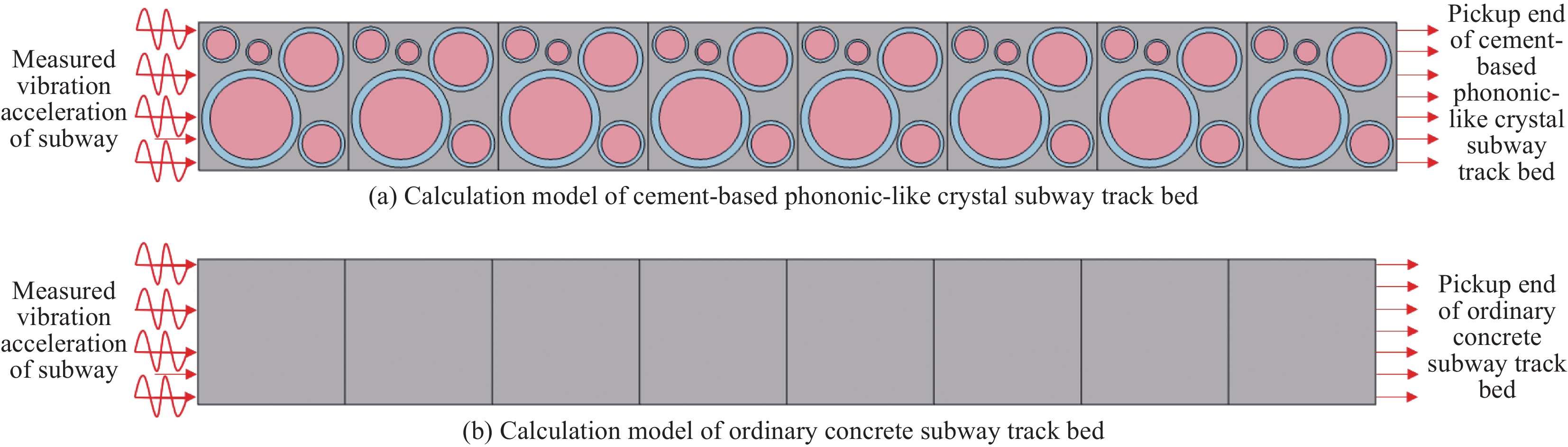
方法首先，采用有限元方法计算和研究了该新型二维三组元水泥基拟声子晶体的能带结构、振动模态、位移场和衰减特性。其次，分析了带隙形成机制和影响因素，并根据质量-弹簧系统模型推导了带隙范围的理论估计式。最后，将该水泥基拟声子晶体复合材料应用到地铁道床上，分析了水泥基拟声子晶体地铁道床的减振性能，以进一步验证新型二维三组元水泥基拟声子晶体复合材料的低频减振带隙功能。
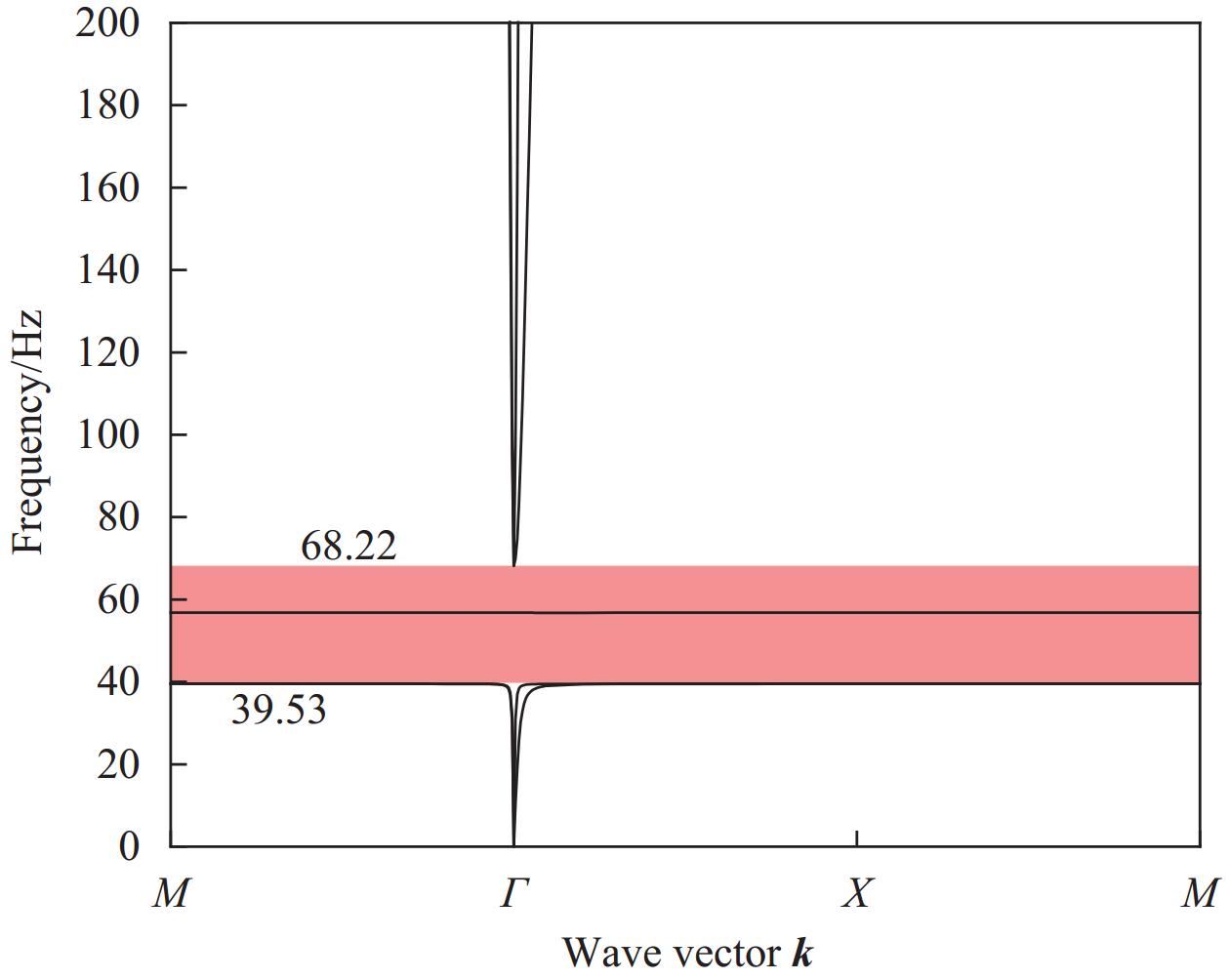
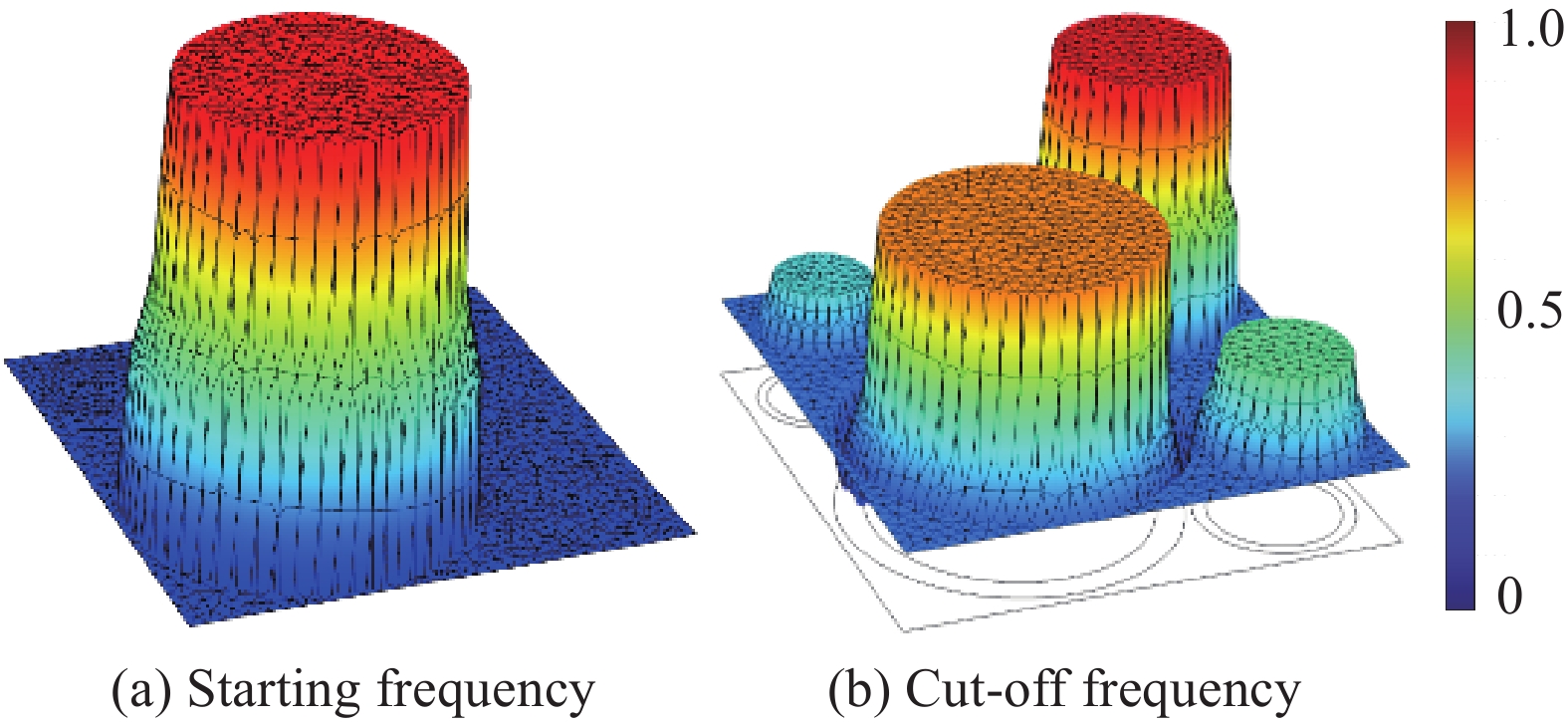
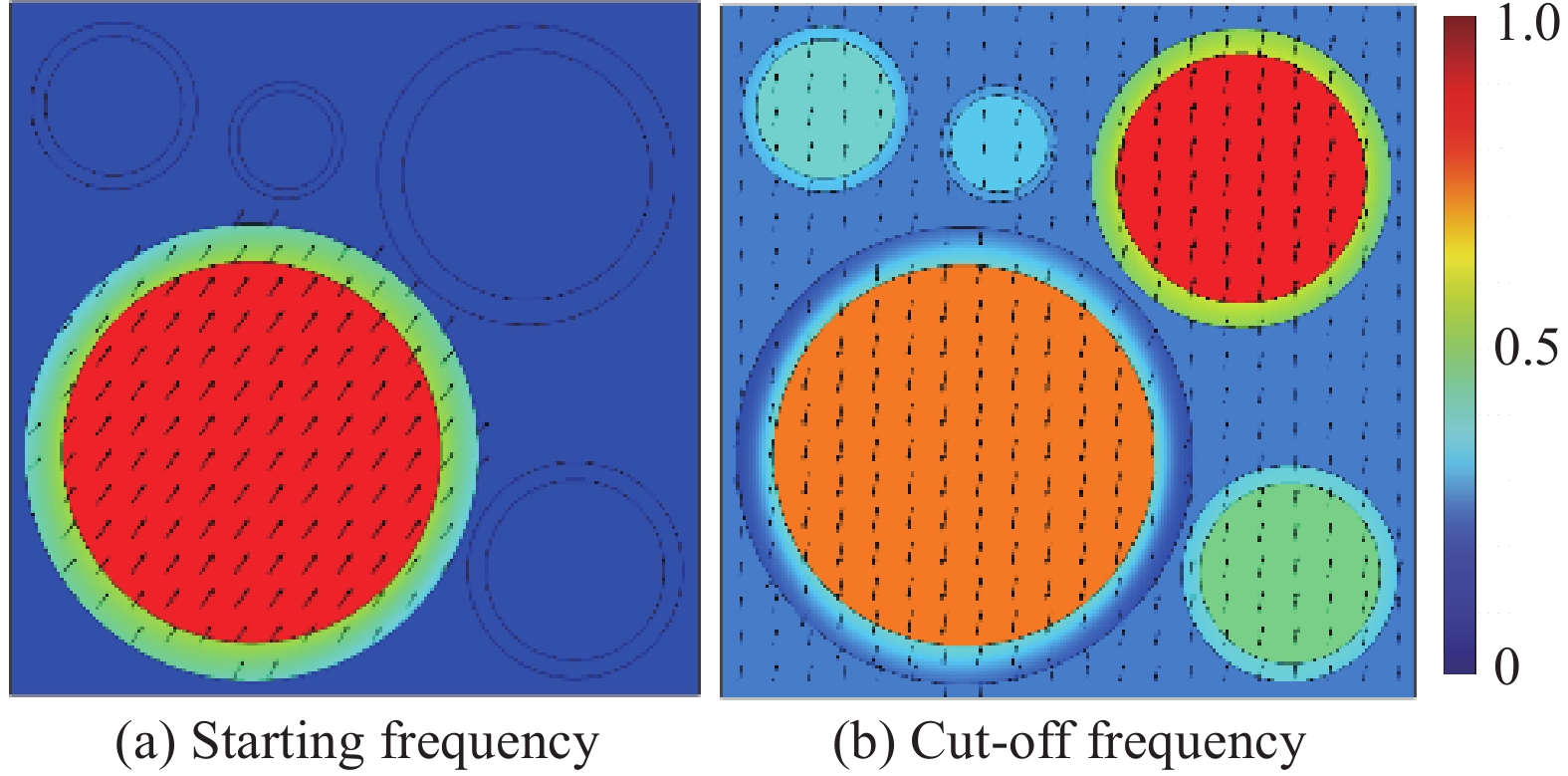
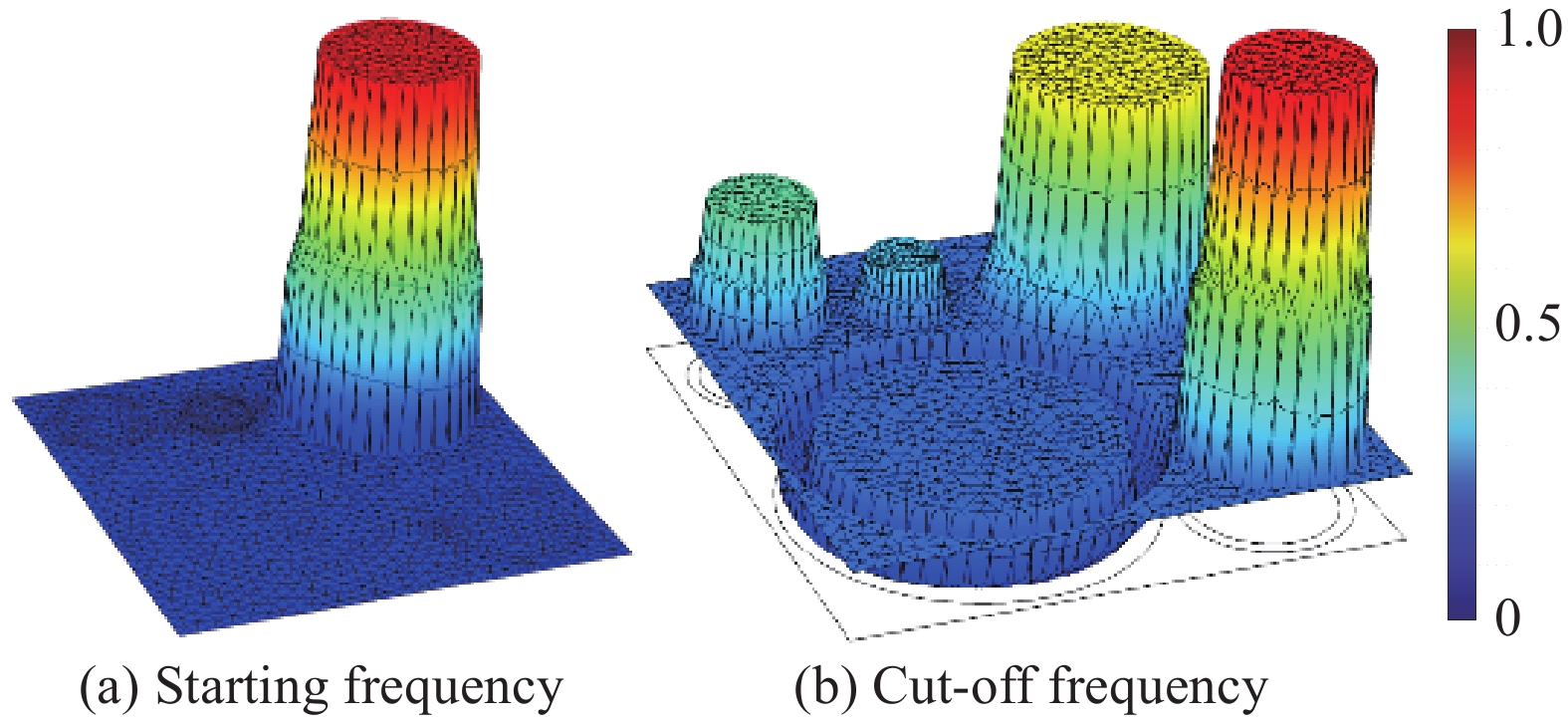
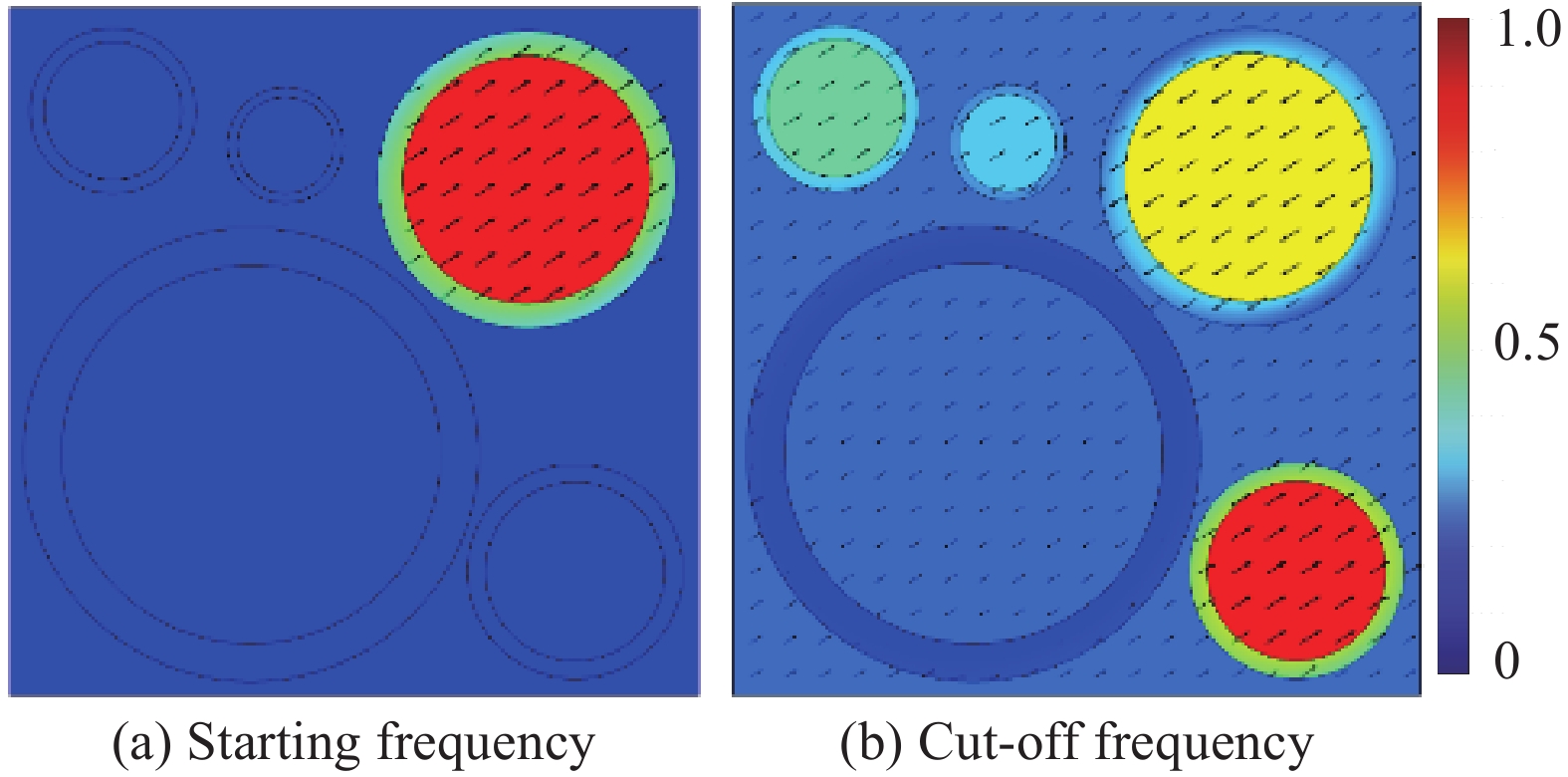
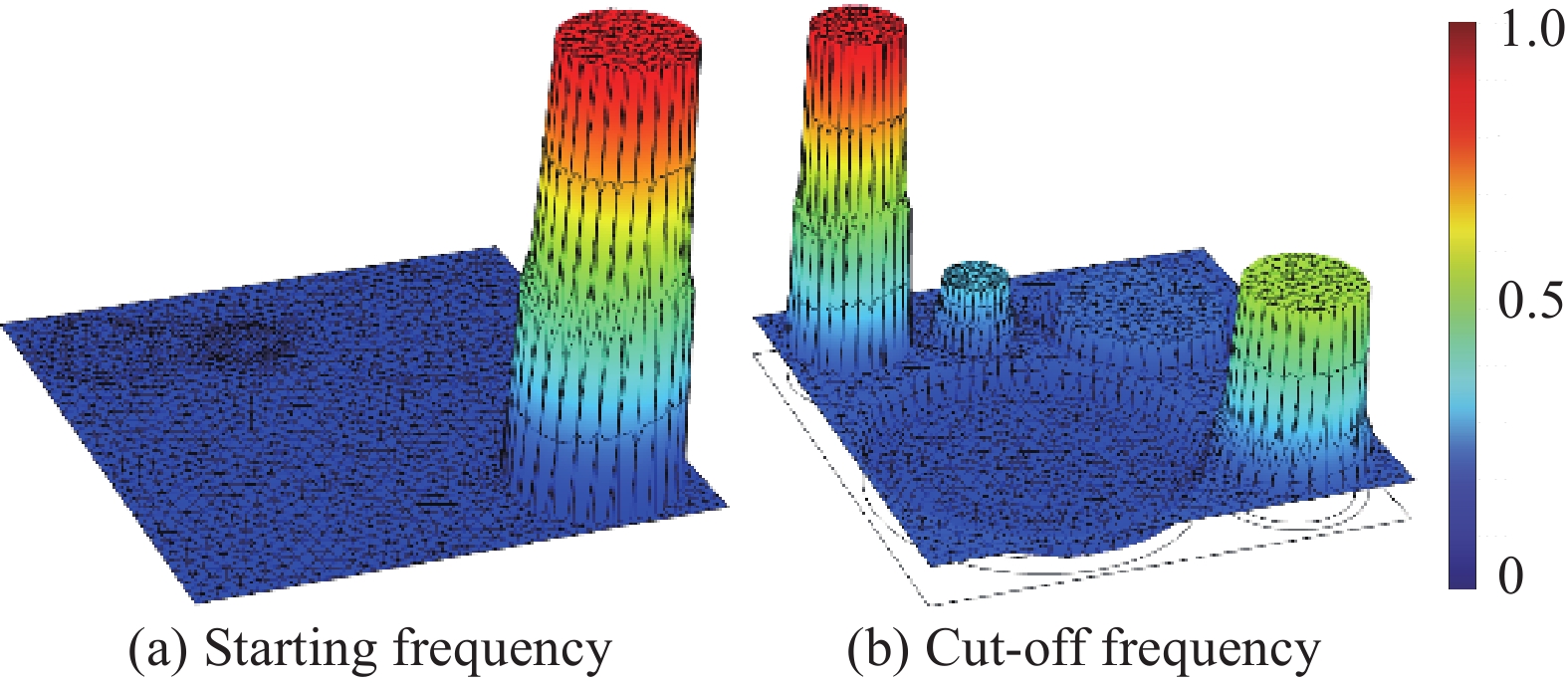
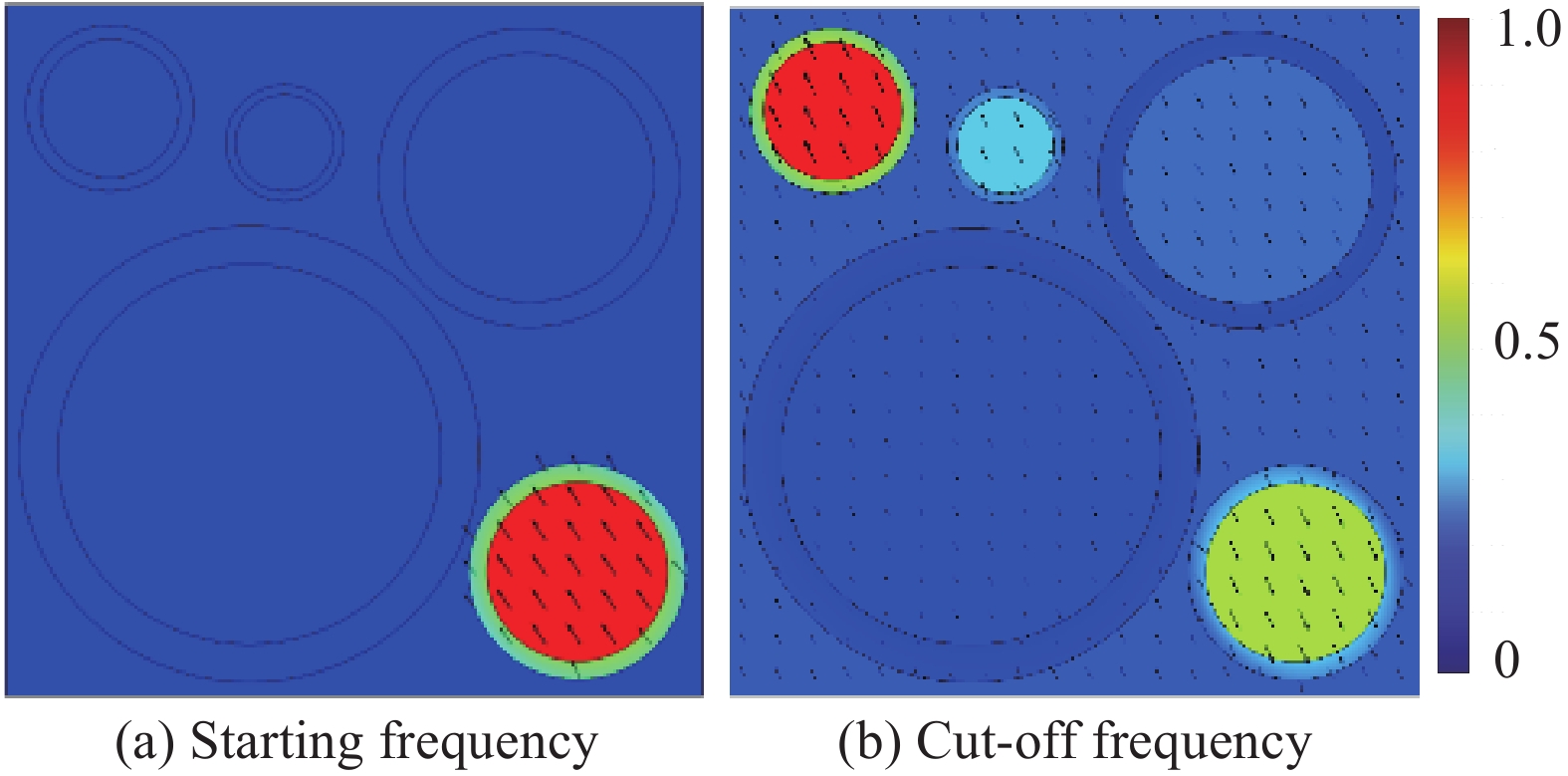
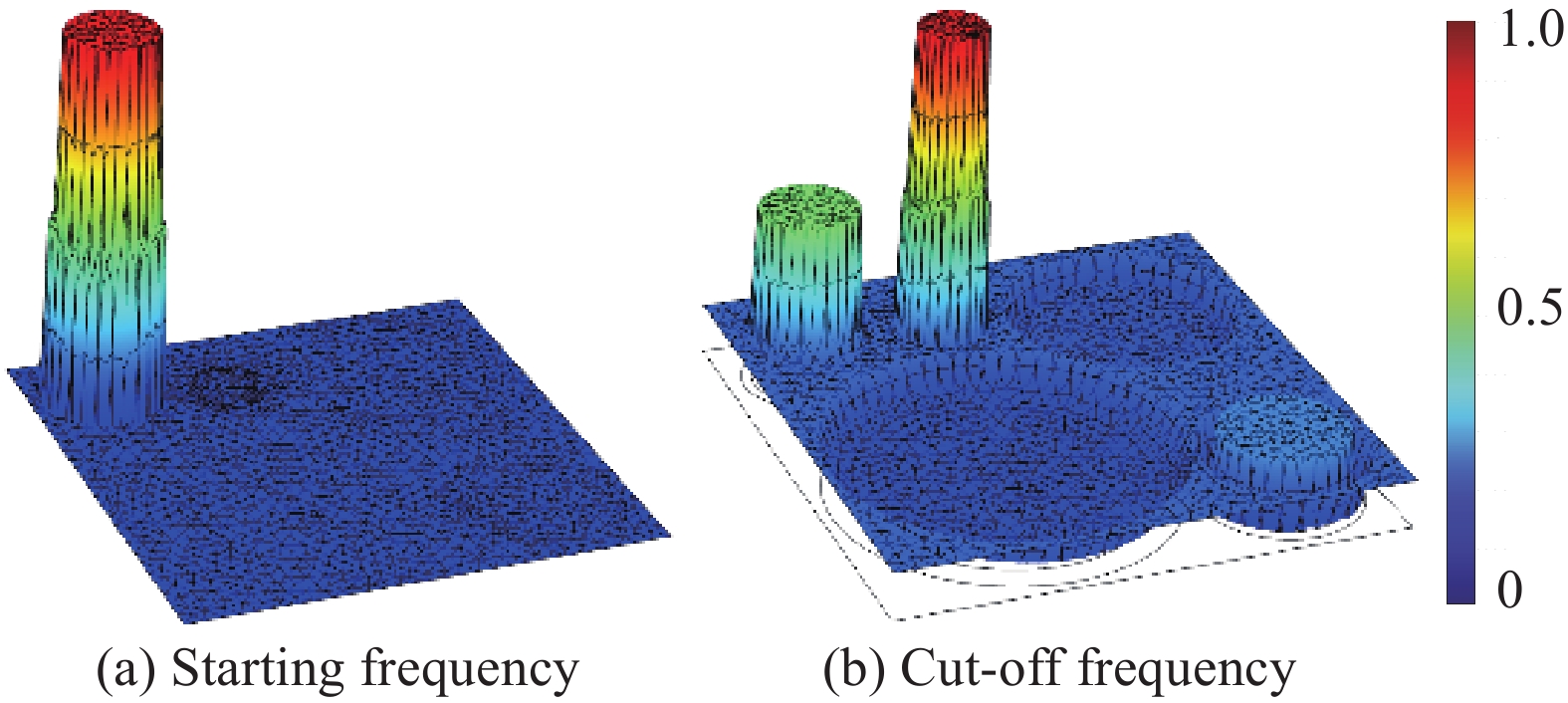
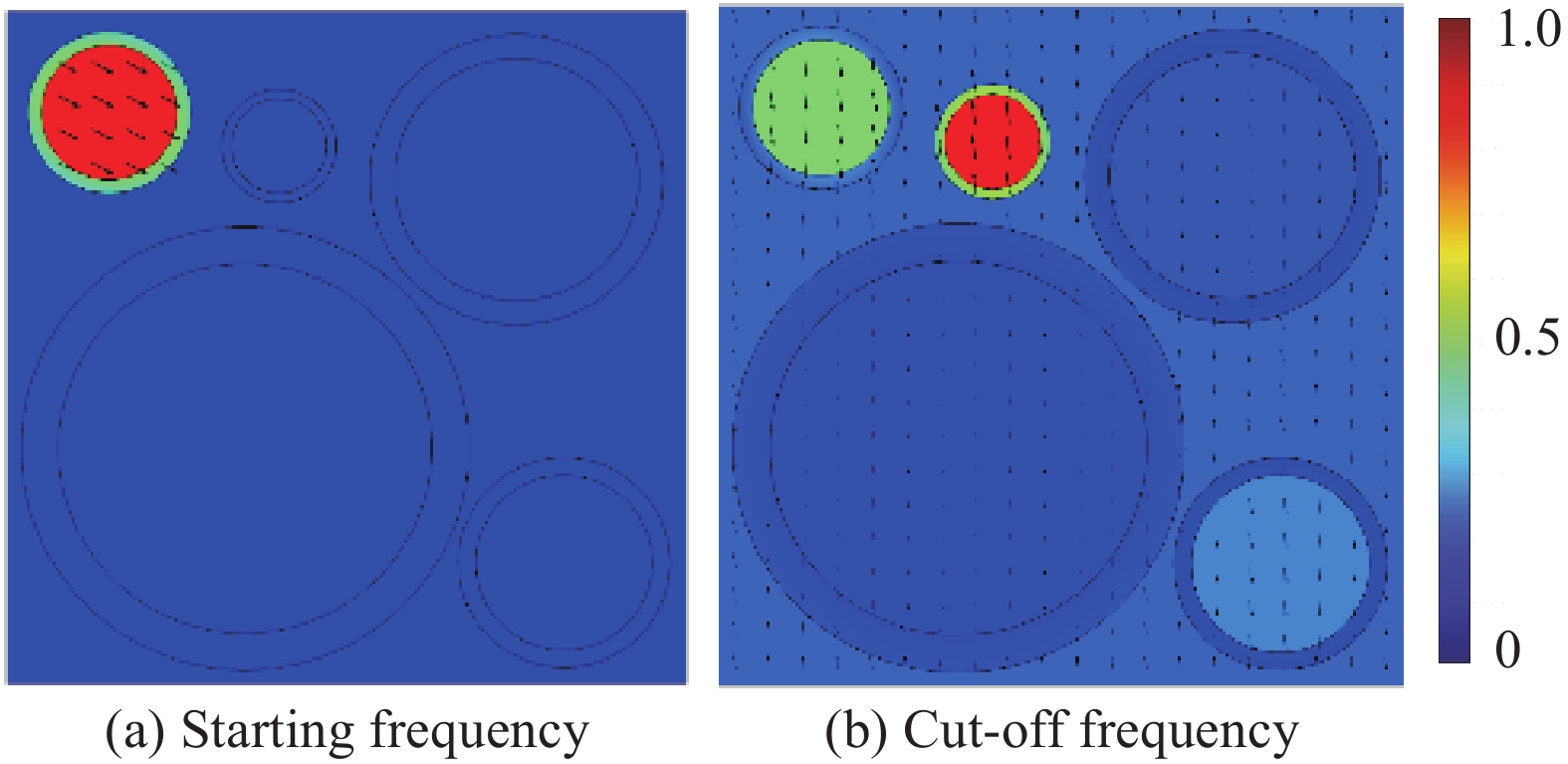
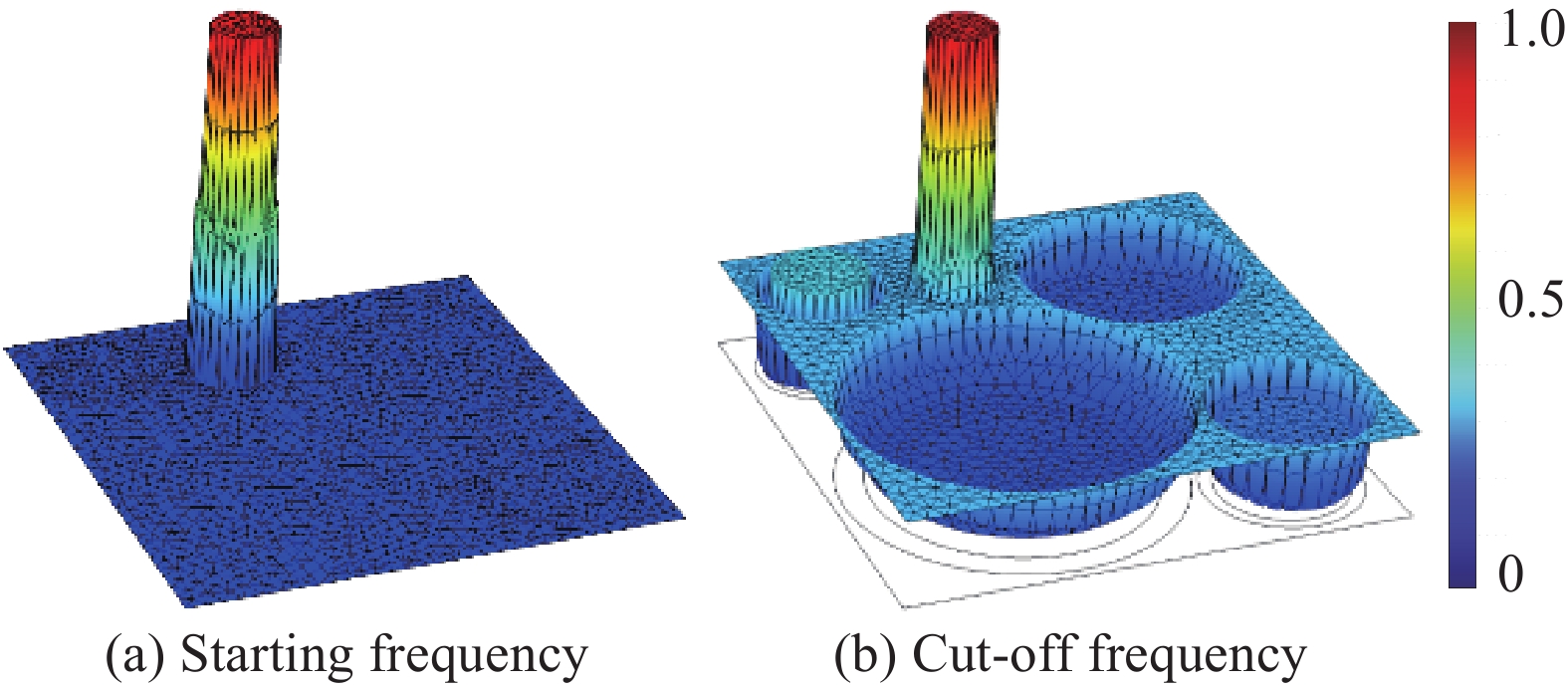
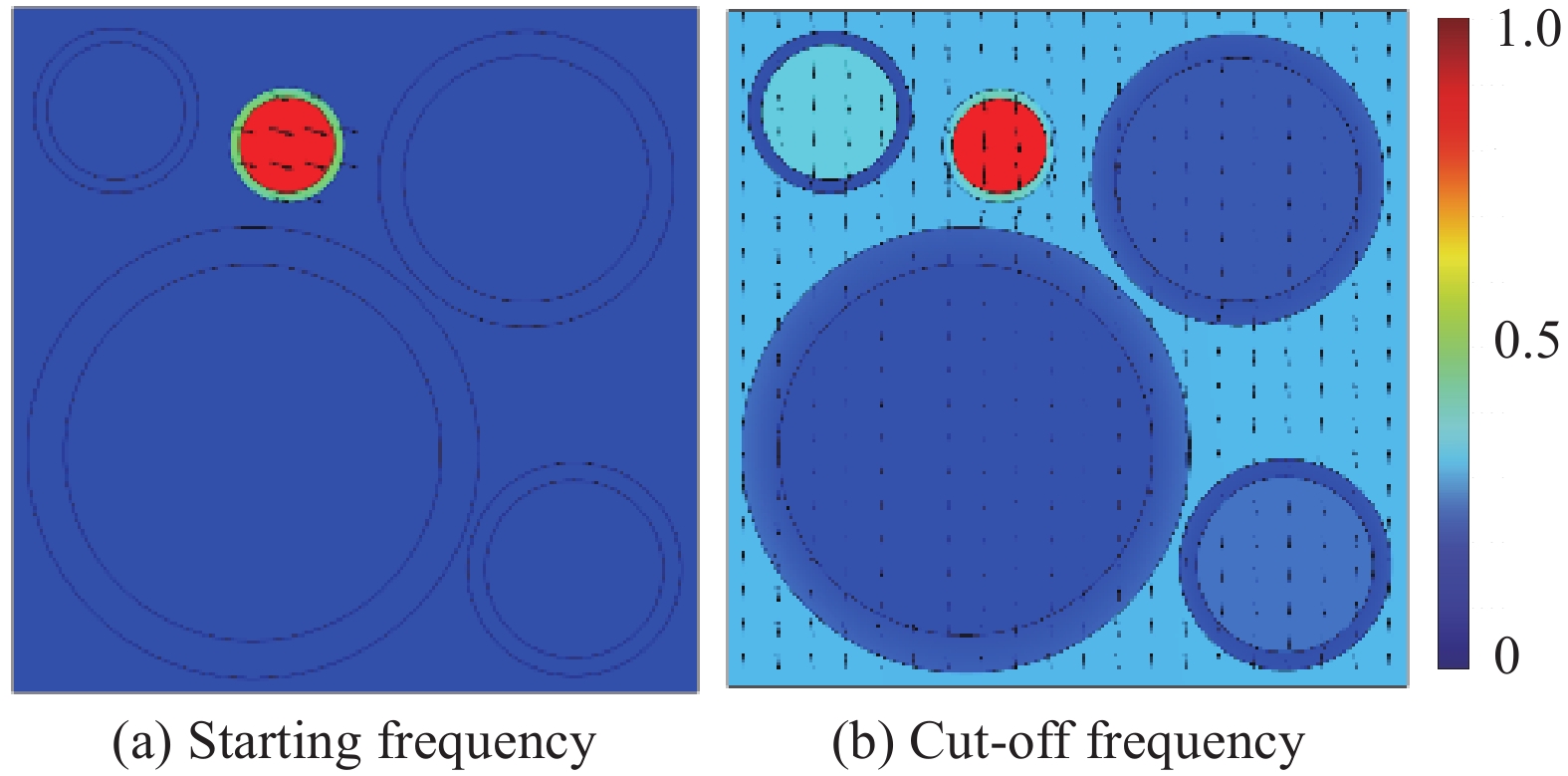
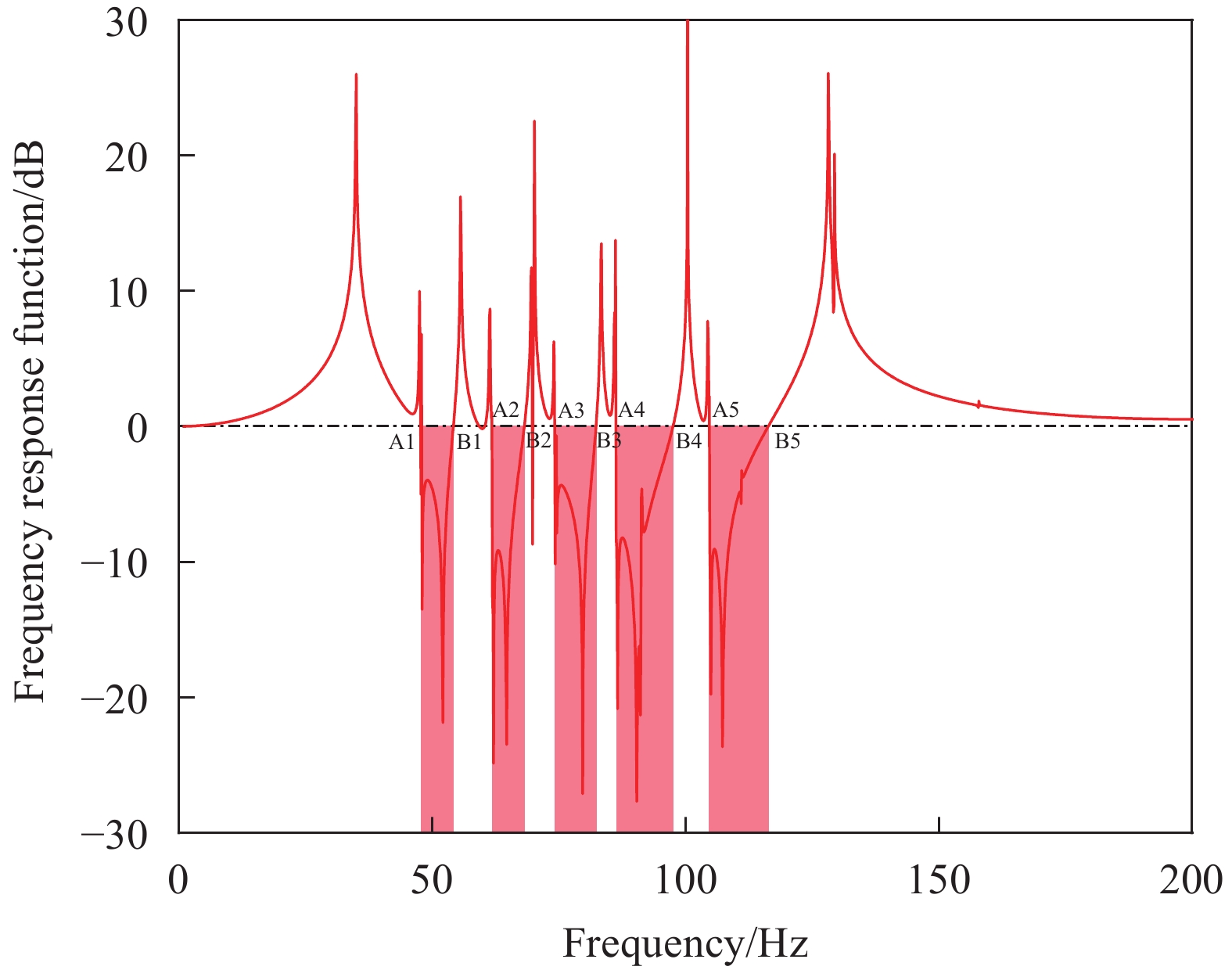
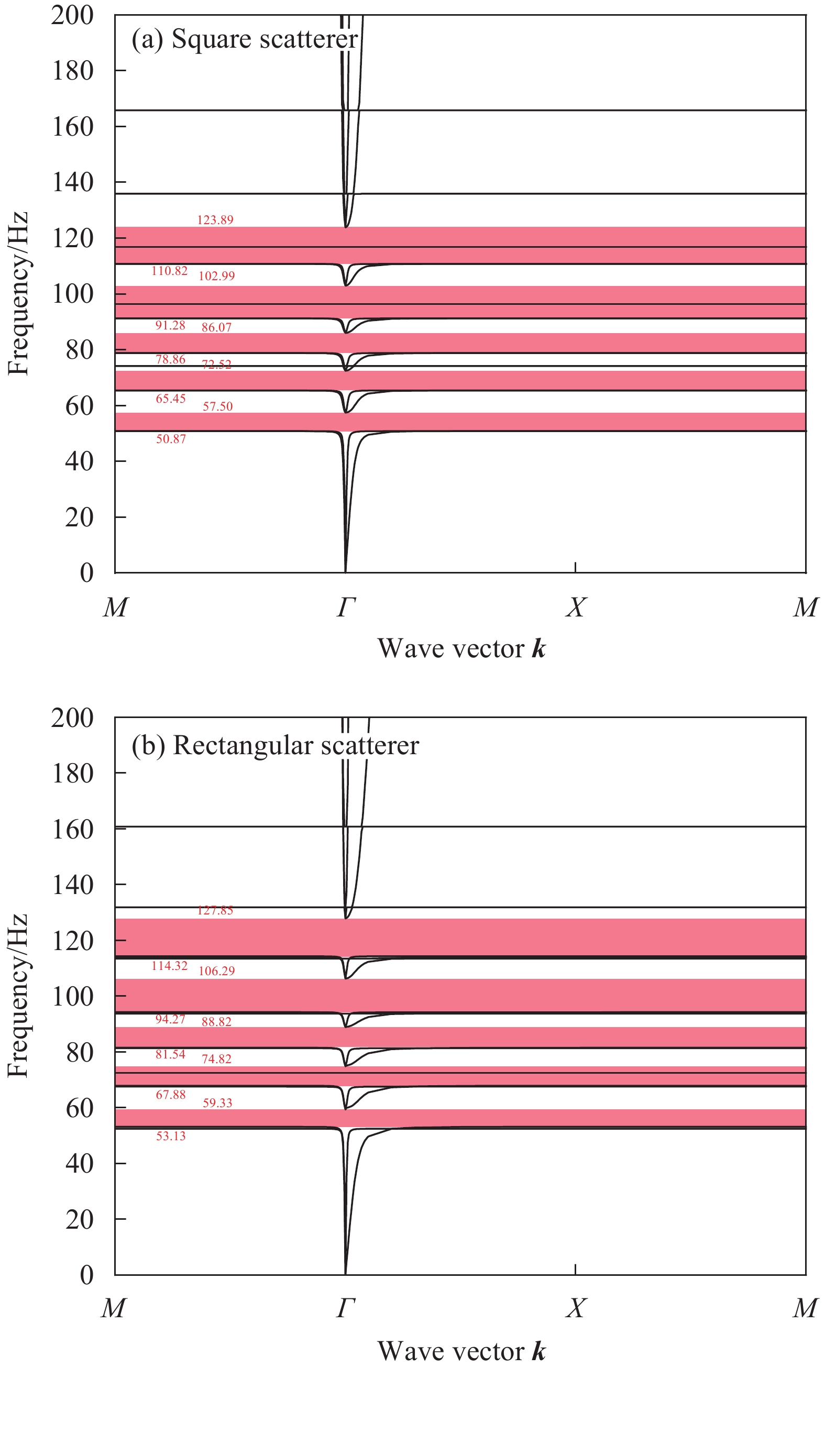
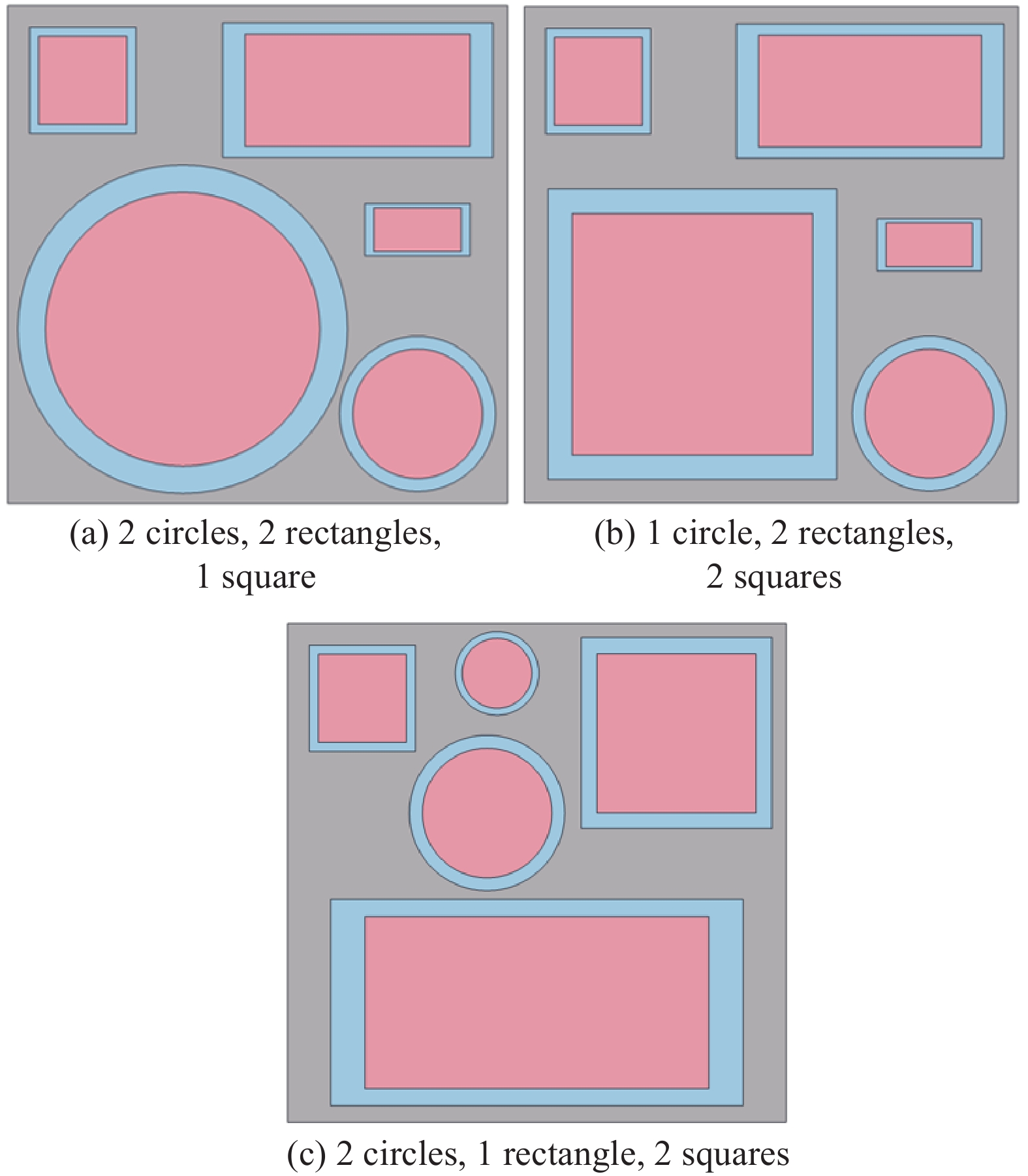
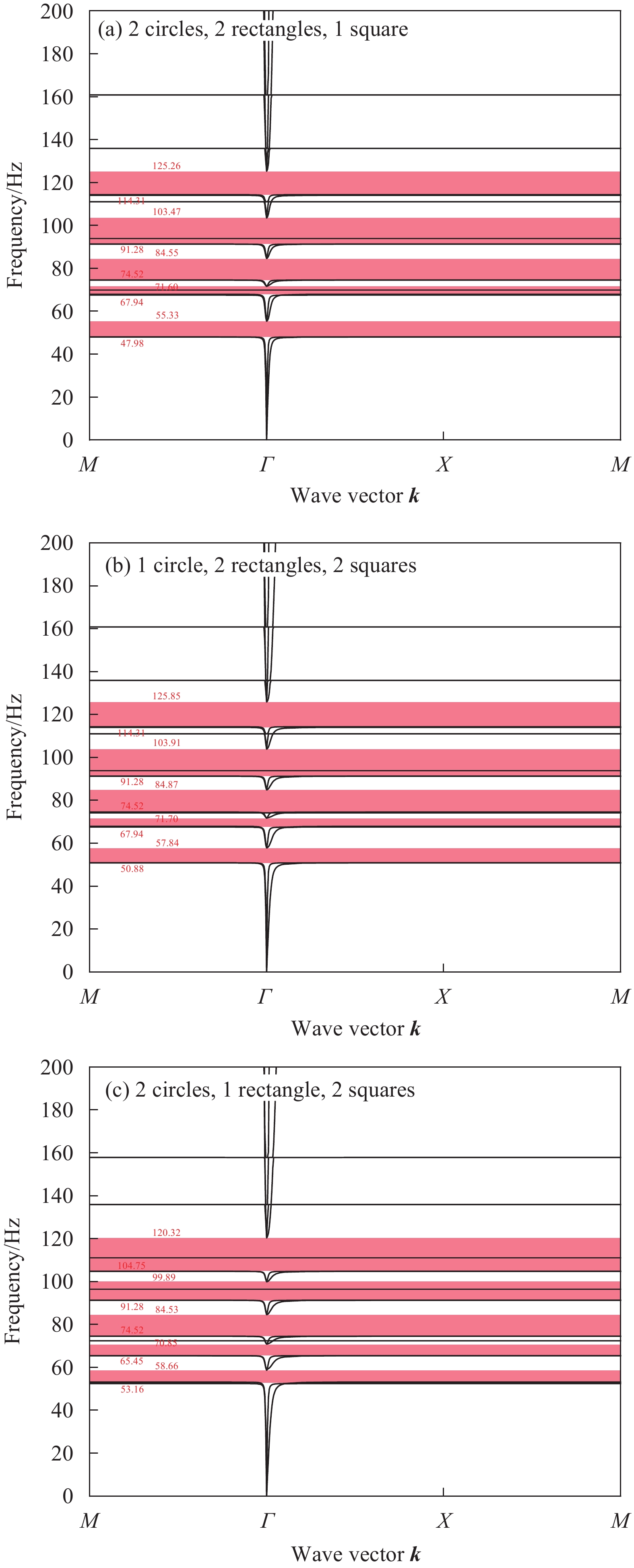
结果该新型二维三组元水泥基拟声子晶体在0~200 Hz频段内打开了5个低频带隙，较传统的水泥基声子晶体相比打开的带隙范围更广，带隙数量更多。新型二维三组元水泥基拟声子晶体低频带隙的打开，与各原胞的振动特征呈现出对应关系，因特定原胞的平移振动触发，由特定原胞与基体的耦合作用的强度所控制。在带隙频率范围内，新型二维三组元水泥基拟声子晶体的衰减值大多都在10 dB以上，且存在多个共振峰，衰减效果较好。新型二维三组元水泥基拟声子晶体的带隙受到散射体、包裹层和水泥砂浆基体的材料参数和结构参数的影响，其中散射体材料的密度、包裹层材料的弹性模量及厚度是影响其带隙的主要因素。此外，散射体的形状和散射体的多形状耦合对新型二维三组元水泥基拟声子晶体的带隙影响甚微。由新型二维三组元水泥基拟声子晶体组成的水泥基拟声子晶体地铁道床在1-200 Hz频段内的振动加速度均小于普通混凝土地铁道床，最大插入损失为10.22 dB，插入损失平均值为8.76 dB，具有显著的减振性能。
结论基于本文提出的新型二维三组元水泥基拟声子晶体模型所研发的水泥基拟声子晶体复合材料打开了低频宽带隙，具有显著的低频减振带隙功能，其在低频振动控制工程领域具有广阔的应用前景。
-
近年来，随着声子晶体复合材料的发展，具有弹性波带隙特性的混凝土超材料吸引了国内外学者们的重视，并开展了广泛的研究。但混凝土超材料具有的带隙范围通常较高，一般在几百到几千赫兹，甚至上万赫兹，且带隙宽度较窄，故在低频振动控制领域(例如：地铁产生的低频振动控制)的工程应用上具有很大局限性。
为了拓宽混凝土超材料对弹性波的衰减范围和数量，即打开低频宽带隙。本文基于局域共振理论提出了一种新型二维三组元水泥基拟声子晶体复合材料，即在传统水泥基声子晶体的基础上，在水泥砂浆基体内部增加多个具有单独包裹层的散射体，形成一种水泥基拟声子晶体结构，使共振单元由单自由度系统变为多自由度系统，从而使混凝土超材料具有多重局域共振的特点。该新型二维三组元水泥基拟声子晶体复合材料在200 Hz频段内打开了5条低频带隙，在带隙频率范围内，衰减值大多都在10 dB以上，衰减效果较好。本文的相关研究成果可为低频振动控制领域的材料研发提供参考。
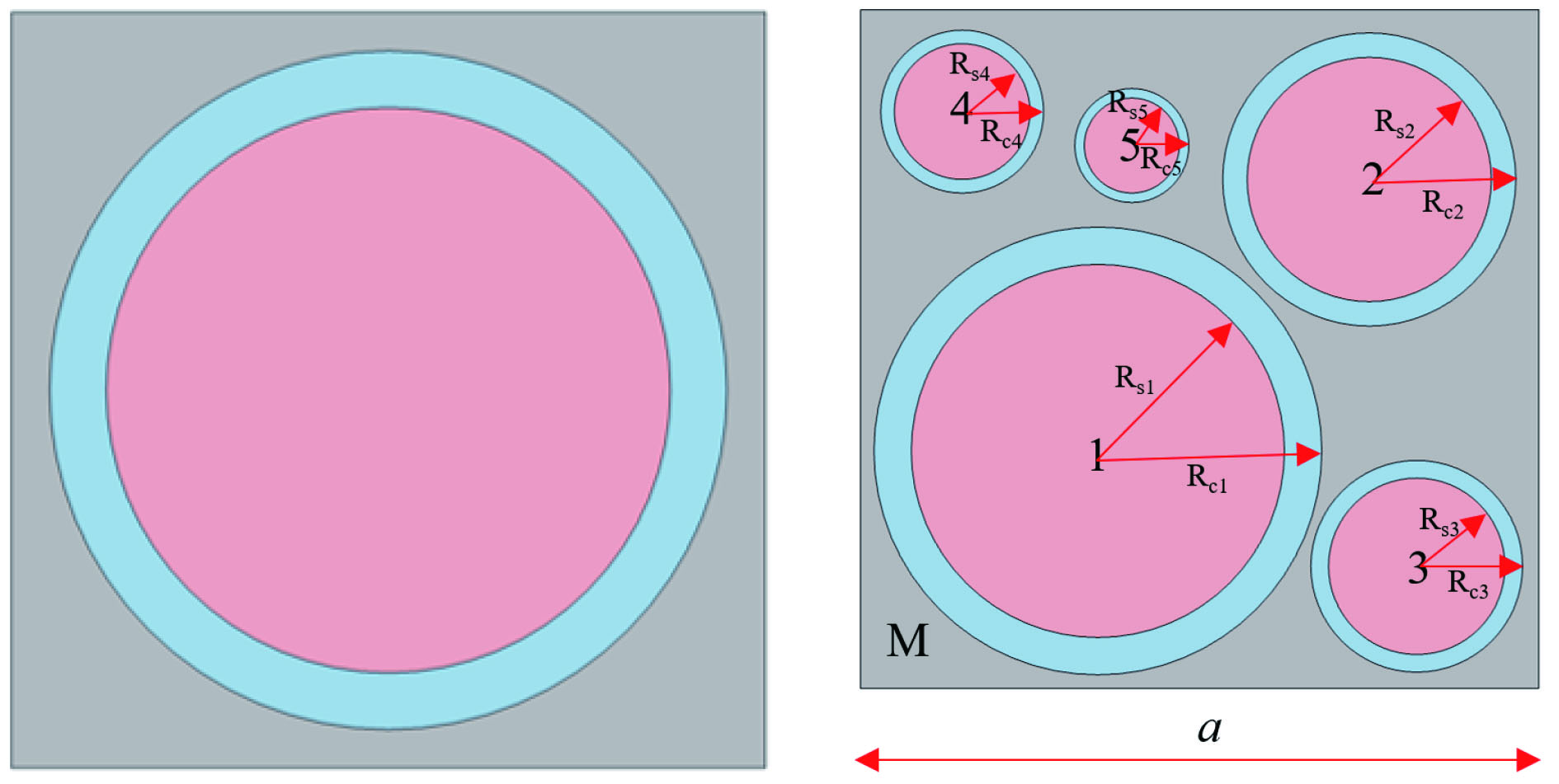
传统水泥基声子晶体模型与新型水泥基拟声子晶体模型
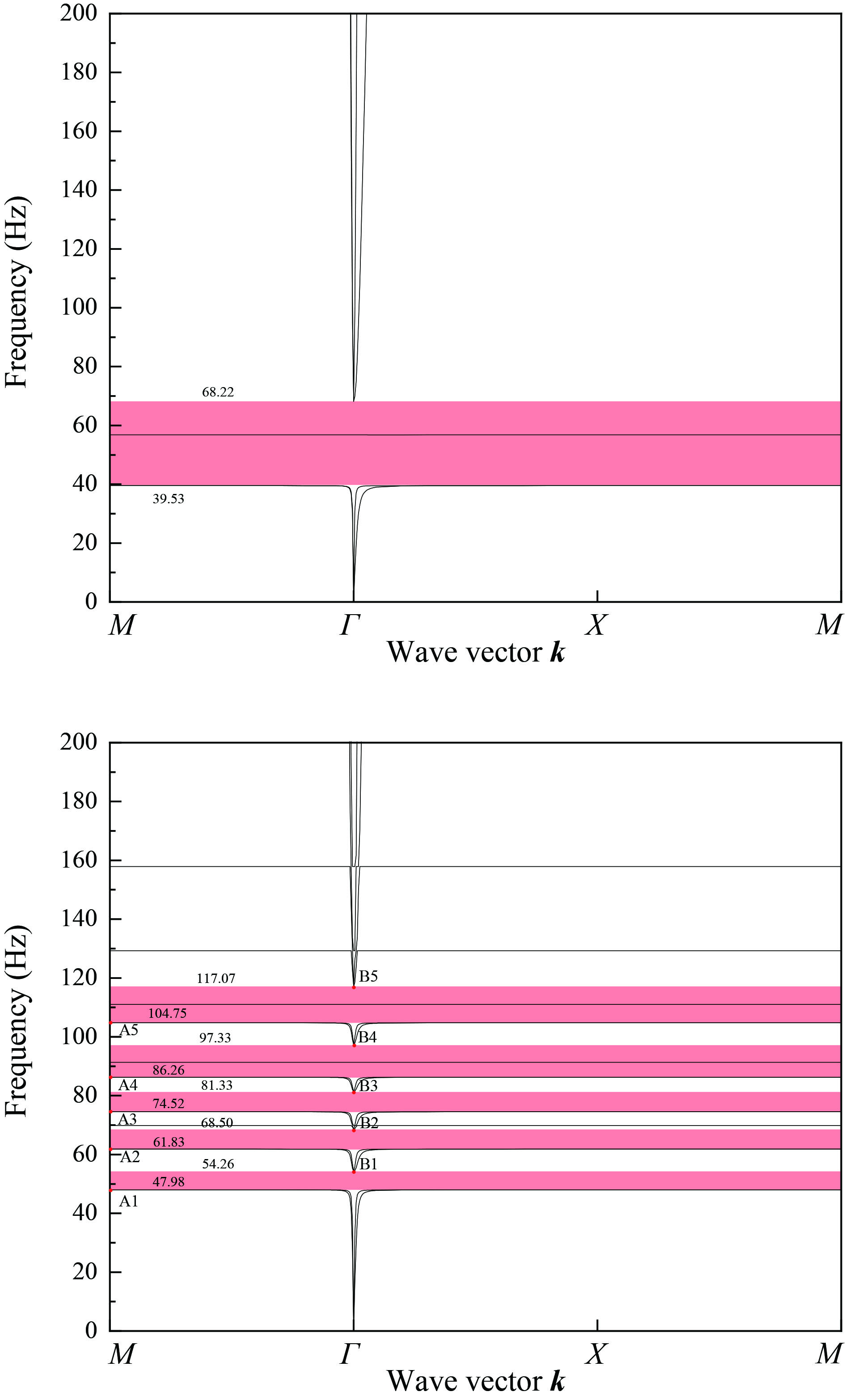
传统水泥基声子晶体复合材料的能带结构与新型二维三组元水泥基拟声子晶体复合材料的能带结构
计量
- 文章访问数: 271
- HTML全文浏览量: 195
- PDF下载量: 27
