AZ31镁合金表面激光熔覆Al-TiC复合涂层微观组织与腐蚀性能

刘奋军; 宁祥; 白艳霞; 申志康; 陈海燕

doi:10.13801/j.cnki.fhclxb.20220410.002

AZ31镁合金表面激光熔覆Al-TiC复合涂层微观组织与腐蚀性能

doi: 10.13801/j.cnki.fhclxb.20220410.002

刘奋军^{1, 2},
宁祥³,
白艳霞³,
申志康⁴,
陈海燕^4, ,

1.
榆林学院　能源工程学院，榆林 719000
2.
榆林学院　榆林市金属基复合材料与再制造技术重点实验室，榆林 719000
3.
榆林学院　化学与化工学院，榆林 719000
4.
西北工业大学　材料学院，西安 710072

基金项目: 国家自然科学基金(51861034；51974260)；榆林市科技局产学研项目(CXY-2022-083；CXY-2020-006-01)；榆林高新区科技创新局产学研项目(CXY-2021-16)；榆林学院高层次人才项目(20 GK06)；中国科学院洁净能源创新研究院-榆林学院联合基金项目(YLU-DNL Fund 2021008)；陕西省教育厅创新团队项目(22JP105)

详细信息

通讯作者:
陈海燕，博士，副教授，博士生导师，研究方向为激光复合钎焊的超精密连接及复合材料制备等　E-mail：hychen@nwpu.edu.cn

中图分类号: TB331
计量
- 文章访问数: 1066
- HTML全文浏览量: 462
- PDF下载量: 57
- 被引次数: 0
出版历程
- 收稿日期: 2022-02-11
- 修回日期: 2022-03-28
- 录用日期: 2022-03-29
- 网络出版日期: 2022-04-12
- 刊出日期: 2023-02-15

Microstructure and corrosion properties of the laser cladding Al-TiC composite coating on AZ31 magnesium alloy

1.
College of Energy Engineering, Yulin University, Yulin 719000, China
2.
Yulin Key Laboratory of Metal Matrix Composites and Remanufacturing Technology, Yulin University, Yulin 719000, China
3.
School of Chemistry and Chemical Engineering, Yulin University, Yulin 719000, China
4.
School of Materials Science and Engineering, Northwestern Polytechnical University, Xi′an 710072, China

Funds: National Natural Science Foundation of China (51861034; 51974260); Technology Bureau of Yulin (CXY-2022-083; CXY-2020-006-01); Technology Bureau of Yulin High-tech Zone (CXY-2021-16); High-level Talent Project of Yulin University (20 GK06); Joint Fund of the Yulin University and the Dalian National Laboratory for Clean Energy (YLU-DNL Fund 2021008); Innovation Team of Education Department of Shaanxi Provincial Government (22JP105)

摘要

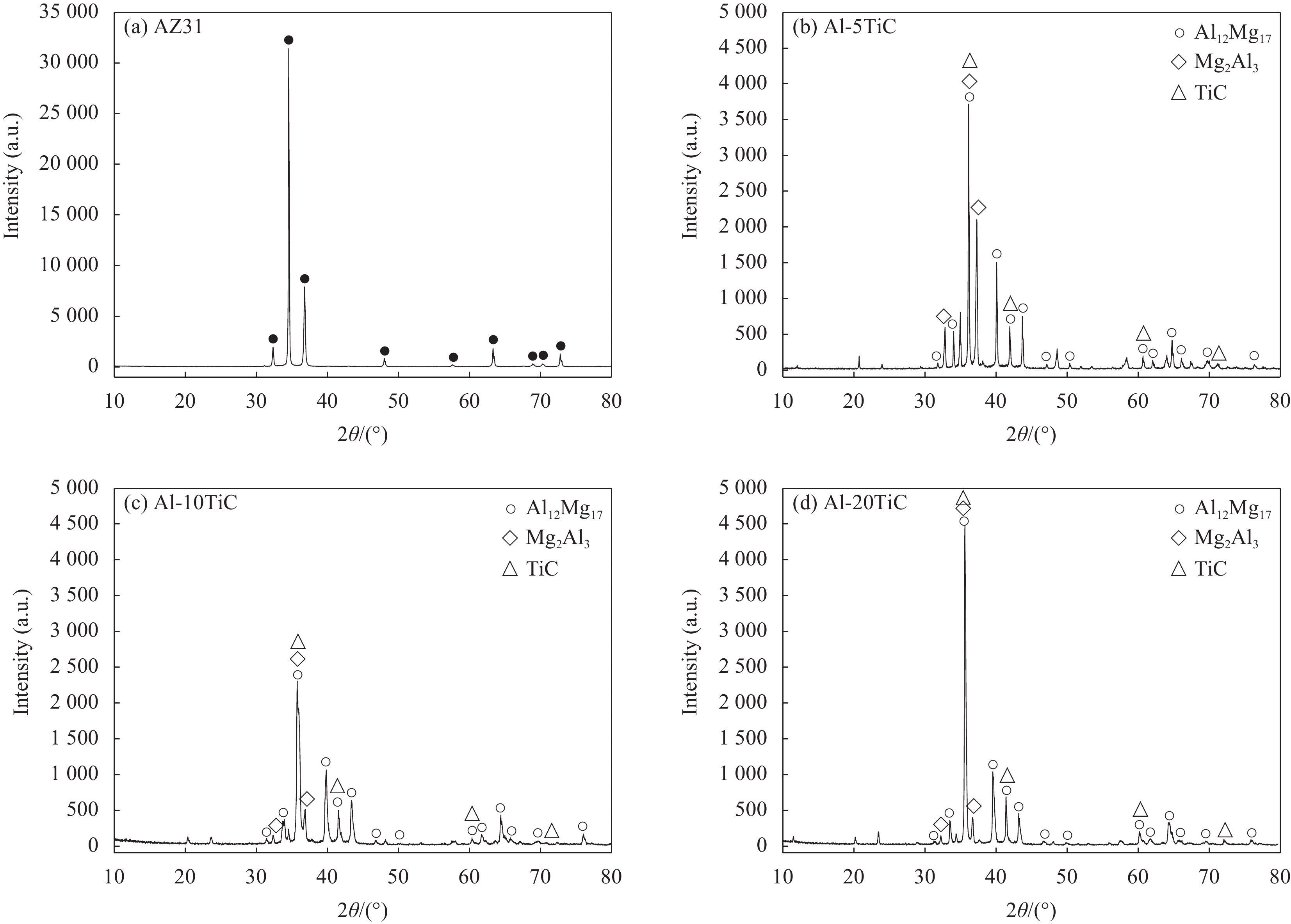
摘要: 为有效改善AZ31镁合金表面的腐蚀性能，本文采用激光熔覆技术在AZ31镁合金表面成功制备了无缺陷的Al-TiC复合涂层。研究了不同成分含量的Al-TiC复合涂层的相组成、微观组织和耐腐蚀性能的影响。结果表明：在Al-TiC复合涂层内形成了大量的Al₁₂Mg₁₇、Mg₂Al₃和TiC相。复合涂层内微观组织呈现出连续网络状分布特征。随着Al-TiC混合粉末中Al含量的减小，复合涂层中Al₁₂Mg₁₇、Mg₂Al₃和TiC相的含量呈递增趋势，网络状分布的微观组织结构变得更加均匀连续。复合涂层与AZ31基体之间形成了良好的冶金结合界面。激光熔覆制备的Al-TiC复合涂层耐腐蚀性能较AZ31基体显著提升。自腐蚀电位由基体的−1.563 V提升至−1.144 V，自腐蚀电流由基体的1.55×10⁻⁴ A减小至2.63×10⁻⁶ A。
- 激光熔覆 /
- Al-TiC复合涂层 /
- AZ31合金 /
- 微观组织 /
- 耐腐蚀性
Abstract: In order to enhance the surface corrosion resistance of the AZ31 magnesium alloy, the defect-free Al-TiC composite coatings were prepared on AZ31 magnesium alloy using laser cladding technology. The influences of Al-TiC compositions with different contents on the phase composition, microstructure and corrosion resistance of the Al-TiC composite coatings were investigated. The results indicate that a large number of Al₁₂Mg₁₇, Mg₂Al₃ and TiC phases are produced in the Al-TiC composite coating. The microstructure of the composite coating characterizes as a continuous network distribution. With the decrease of the Al content in the composite powder, the contents of the Al₁₂Mg₁₇, Mg₂Al₃ and TiC phases in the composite coating gradually increase, and the network-like distribution characteristics of the microstructure in the composite coating become more uniform and continuous. In addition, a sound metallurgical bonding interface is prepared between the composite coating and the AZ31 substrate. The corrosion resistance of the Al-TiC composite coating prepared using the laser cladding technology is significantly enhanced compared to that of the AZ31 substrate. The self-corrosion potential increased from −1.563 V of the AZ31 substrate to −1.144 V of the Al-TiC composite coating, whereas the self-corrosion current decreased from 1.55×10⁻⁴ A to 2.63×10⁻⁶ A.
- laser cladding /
- Al-TiC composite coating /
- AZ31 alloy /
- microstructure /
- corrosion resistance

HTML全文

图 1 Al粉和TiC粉的SEM图像

Figure 1. SEM images of Al and TiC

下载: 全尺寸图片幻灯片

图 2 AZ31和Al-TiC复合涂层XRD图谱

Figure 2. XRD patterns of AZ31 and Al-TiC composite coatings

下载: 全尺寸图片幻灯片

图 3 Al-TiC复合涂层表面 ((a)~(c)) 及横截面 ((d)~(f)) 宏观成型

Figure 3. Surface ((a)-(c)) and cross-sectional ((d)-(f)) morphologies of Al-TiC composite coatings

下载: 全尺寸图片幻灯片

图 4 Al-TiC复合涂层结合界面 ((a)~(c)) 及微观组织 ((d)~(f))

A, B—Test point

Figure 4. Bonding interface ((a)-(c)) and microstructure ((d)-(f)) of Al-TiC composite coatings

下载: 全尺寸图片幻灯片

图 5 Al-TiC复合涂层微观组织

Figure 5. Microstructures of the Al-TiC composite coatings

下载: 全尺寸图片幻灯片

图 6 Al-TiC复合涂层(Al-5TiC)元素分布

Figure 6. Elemental mappings of Al-TiC composite coatings (Al-5TiC)

下载: 全尺寸图片幻灯片

图 8 Al-TiC复合涂层(Al-20TiC)元素分布

Figure 8. Elemental mappings of Al-TiC composite coatings (Al-20TiC)

下载: 全尺寸图片幻灯片

图 7 Al-TiC复合涂层(Al-10TiC)元素分布

Figure 7. Elemental mappings of Al-TiC composite coatings (Al-10TiC)

下载: 全尺寸图片幻灯片

图 9 AZ31和Al-TiC复合涂层耐腐蚀性能

Figure 9. Corrosion resistance of AZ31 and Al-TiC composite coatings

下载: 全尺寸图片幻灯片

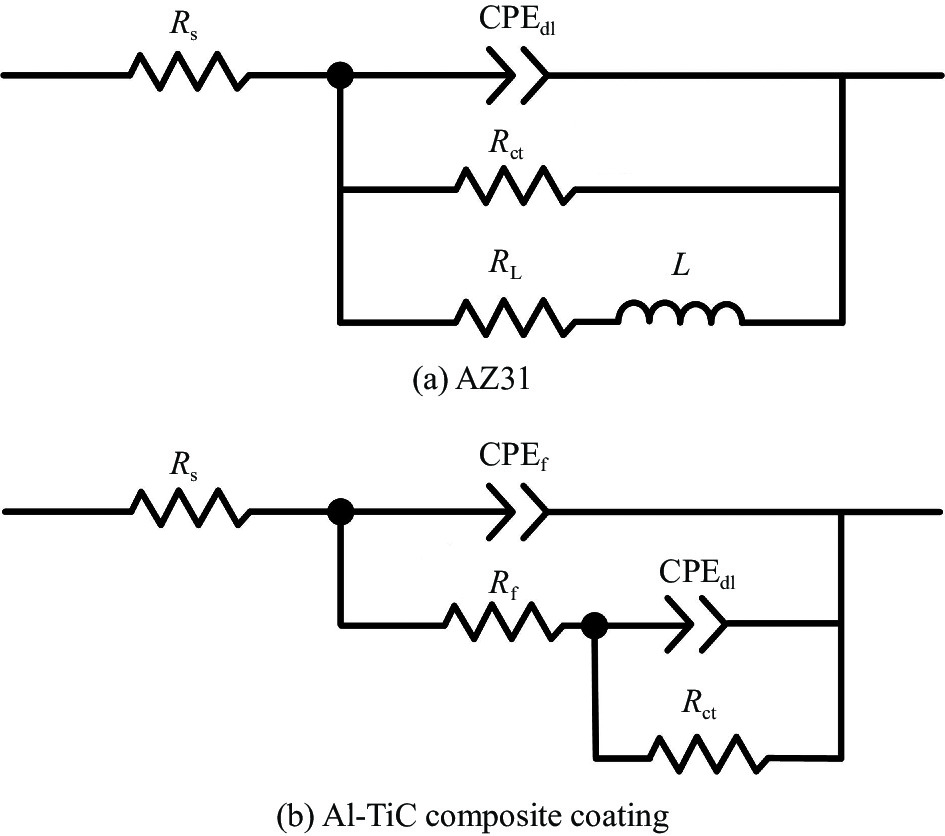
图 10 AZ31和Al-TiC复合涂层的EIS等效电路图

R_s—Solution resistance; CPE_f—Al-TiC composite coating capacitance; R_f—Al-TiC composite coating resistance; CPE_dl—Electric double layer capacitor; R_ct—Charge transfer resistance; L—Inductance; R_L—Inductor resistance

Figure 10. EIS equivalent circuit diagram of AZ31 and Al-TiC composite coatings

下载: 全尺寸图片幻灯片

图 11 AZ31和Al-TiC复合涂层表面腐蚀形貌

Figure 11. Corrosion morphologies of AZ31 and Al-TiC composite coatings

下载: 全尺寸图片幻灯片

表 1 Al-TiC复合涂层具体粉末配比

Table 1. Specific ratios of the Al-TiC composite coatings

Sample	Powders and powder ratio
Sample	Al/wt%	TiC/wt%
Al-5TiC	95	5
Al-10TiC	90	10
Al-20TiC	80	20

下载: 导出CSV

表 2 A点和B点的EDS测试结果

Table 2. EDS analysis of point A and point B

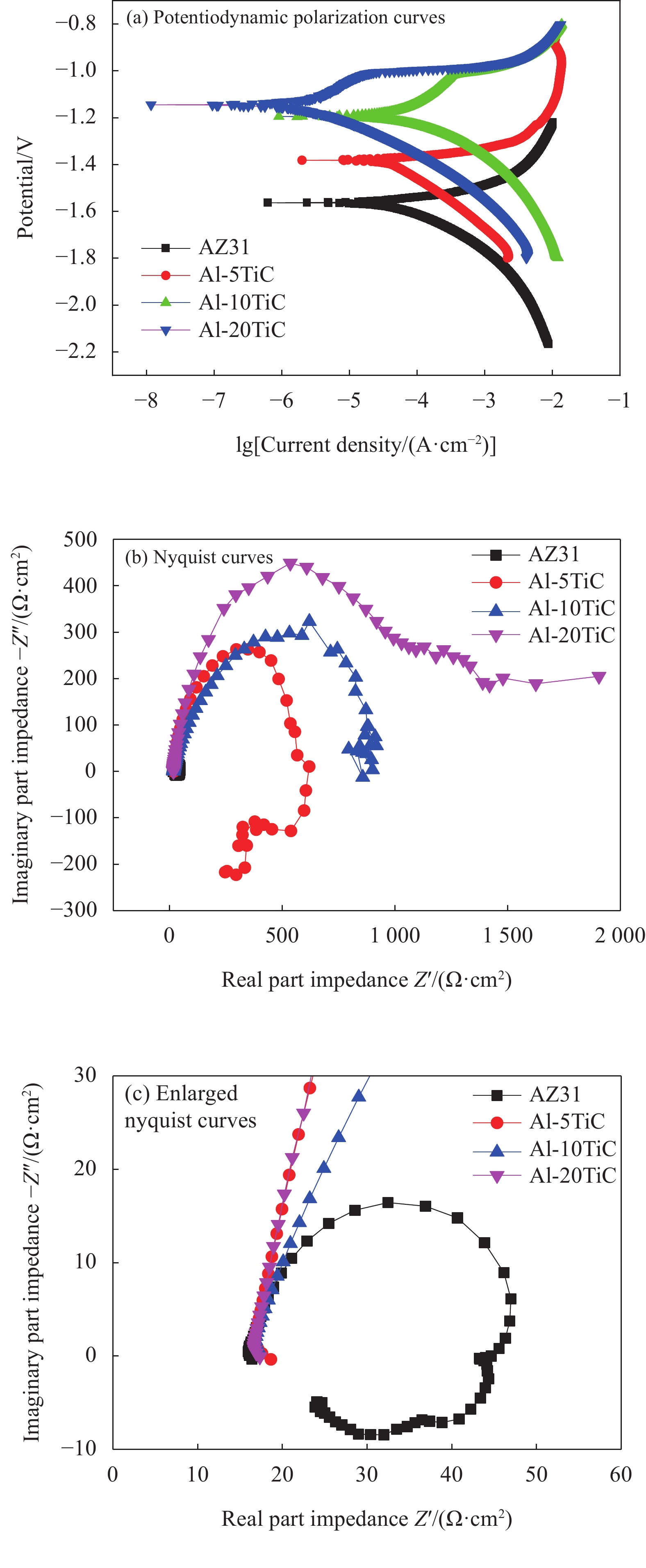
Point	Mg/at%	Al/at%	Zn/at%	TiC/at%	C/at%
A	38.32	32.43	0.80	2.48	25.96
B	47.97	33.04	0.85	0.09	18.05

下载: 导出CSV

表 3 AZ31和Al-TiC复合涂层的自腐蚀电位和自腐蚀电流

Table 3. Self-corrosion potential and self-corrosion current of the AZ31 and Al-TiC composite coatings

Sample	Self-corrosion potential/V	Self-corrosion current/A
AZ31	−1.563	1.55×10⁻⁴
Al-5TiC	−1.381	2.30×10⁻⁴
Al-10TiC	−1.195	7.55×10⁻⁵
Al-20TiC	−1.144	2.63×10⁻⁶

下载: 导出CSV

表 4 等效电路模型拟合的电化学参数

Table 4. Electrochemical parameters fitted by the equivalent circuit model

Parameter	R_s/(Ω·cm²)	CPE_f/(Ω·cm²·Sⁿ)	n_f	R_f/(Ω·cm²)	CPE_dl/(Ω·cm²·Sⁿ)	n_dl	R_ct/(Ω·cm²)	L/(H·cm²)	R_L/(Ω·cm²)
AZ31	16.50	–	–	–	7.69×10⁻⁶	0.91	27.6	13.46	10.29
Al-5TiC	16.99	7.38×10⁻⁶	0.95	118.5	4.36×10⁻⁶	0.89	452.2	–	–
Al-10TiC	15.96	3.04×10⁻⁵	0.76	506.5	3.22×10⁻⁵	0.85	416.3	–	–
Al-20TiC	16.47	1.83×10⁻⁵	0.87	1045.0	1.01×10⁻⁴	0.68	774.8	–	–
Notes: n_f—CPE_f index; n_dl—CPE_dl index.

下载: 导出CSV

参考文献(31)

[1]	JOOST W J, KRAJEWSKI P E. Towards magnesium alloys for high-volume automotive applications[J]. Scripta Materialia,2017,128:107-112. doi: 10.1016/j.scriptamat.2016.07.035
[2]	CHEN J X, TAN L L, YU X M, et al. Mechanical properties of magnesium alloys for medical application: A review[J]. Journal of the Mechanical Behavior of Biomedical Materials,2018,87:68-79. doi: 10.1016/j.jmbbm.2018.07.022
[3]	赵聪铭, 邓坤坤, 聂凯波, 等. 挤压包覆轧制对SiCp增强镁合金(AZ91)复合板显微组织和力学性能的影响[J]. 复合材料学报, 2020, 37(1):164-172. ZHAO Congming, DENG Kunkun, NIE Kaibo, et al. Effect of extrusion-cladding rolling on microstructure and mecha-nical property of SiCp reinforced magnesium alloy (AZ91) clad plate[J]. Acta Materiae Compositae Sinica,2020,37(1):164-172(in Chinese).
[4]	FRIEDRICH H, SCHUMANN S. Research for a new age of magnesium in the automotive industry[J]. Journal of Materials Processing Technology, 2001, 117: 276-281.
[5]	PARDO A, MERINO M C, COY A E, et al. Corrosion behaviour of magnesium/aluminium alloys in 3.5wt%NaCl[J]. Corrosion Science,2008,50(3):823-834. doi: 10.1016/j.corsci.2007.11.005
[6]	PAITAL S M, BHATTACHARYA A, MONCAYO M, et al. Improved corrosion and wear resistance of Mg alloys via laser surface modification of Al on AZ31 B[J]. Surface and Coatings Technology,2012,206(8-9):2308-2315. doi: 10.1016/j.surfcoat.2011.10.009
[7]	BALAKRISHNAN M, DINAHARAN I, PALANIVEL R, et al. Synthesize of AZ31/TiC magnesium matrix composites using friction stir processing[J]. Journal of Magnesium and Alloys,2015,3:76-78. doi: 10.1016/j.jma.2014.12.007
[8]	NIE X M, SHEN H Y, FU J Z, et al. Effective control of microstructure evolution in AZ91 D magnesium alloy by SiC nanoparticles in laser powder-bed fusion[J]. Materials and Design,2021,206:109787. doi: 10.1016/j.matdes.2021.109787
[9]	LIU F J, LI Y P, SUN Z Y, et al. Corrosion resistance and tribological behavior of particles reinforced AZ31 magnesium matrix composites developed by friction stir processing[J]. Journal of Materials Research and Technology,2021,11:1019-1030. doi: 10.1016/j.jmrt.2021.01.071
[10]	YANG L Q, LI Z Y, ZHANG Y Q, et al. Al-TiC in situ compo-site coating fabricated by low power pulsed laser cladding on AZ91 D magnesium alloy[J]. Applied Surface Science,2018,435:1187-1198. doi: 10.1016/j.apsusc.2017.11.240
[11]	LIU H X, XU Q, WANG C Q, et al. Corrosion and wear behavior of Ni60 CuMoW coatings fabricated by combination of laser cladding and mechanical vibration processing[J]. Journal of Alloys and Compounds,2015,621:357-363. doi: 10.1016/j.jallcom.2014.10.030
[12]	WENG F, YU H J, CHEN C Z, et al. Microstructures and wear properties of laser cladding Co-based composite coatings on Ti-6Al-4V[J]. Materials and Design,2015,80:174-181. doi: 10.1016/j.matdes.2015.05.005
[13]	王鑫, 潘希德, 牛强, 等. AZ33 M镁合金激光熔覆制备了Al-Si涂层的组织和性能[J]. 金属热处理, 2021, 46(5):202-206. WANG Xin, PAN Xide, NIU Qiang, et al. Microstructure and properties of laser clad Al-Si coating on AZ33 M magnesium alloy[J]. Heat Treatment of Metals,2021,46(5):202-206(in Chinese).
[14]	靳坤, 张英乔, 张涛, 等. AZ91 D镁合金表面激光熔覆Al-Ti-Ni/C涂层的电化学腐蚀行为[J]. 电焊机, 2019, 49(10): 83-87. JIN Kun, ZHANG Yingqiao, ZHANG Tao, et al. Electroche-mical corrosion behavior of laser cladding Al-Ti-Ni/C coating on AZ94 D magnesium alloy[J]. Electric Welding Machine, 2019, 49(10): 83-87(in Chinese).
[15]	刘德坤, 张可敏, 刘应瑞. AZ31镁合金表面Al-Ti-TiB₂激光熔覆层的组织和性能[J]. 机械工程材料, 2018, 42(10):24-28, 33. doi: 10.11973/jxgccl201810005 LIU Dekun, ZHANG Kemin, LIU Yingrui. Microstructure and properties of Al-Ti-TiB₂ laser-cladding layer on surface of AZ31 Magnesium Alloy[J]. Materials for Mechani-cal Engineering,2018,42(10):24-28, 33(in Chinese). doi: 10.11973/jxgccl201810005
[16]	LIN P Y, ZHANG Z H, REN L Q. The mechanical properties and microstructures of AZ91 D magnesium alloy processed by selective laser cladding with Al powder[J]. Optics and Laser Technology,2014,60:61-68. doi: 10.1016/j.optlastec.2013.12.024
[17]	AYDIN F, SUN Y, TURAN M E. Influence of TiC content on mechanical, wear and corrosion properties of hot-pressed AZ91/TiC composites[J]. Journal of Composite Materials,2020,54:141-152. doi: 10.1177/0021998319860570
[18]	ZHENG B J, CHEN X M, LIAN J S. Microstructure and wear property of laser cladding Al+SiC powders on AZ91 D magnesium alloy[J]. Optics and Laser Technology,2010,48:526-532. doi: 10.1016/j.optlaseng.2010.01.001
[19]	MASSALSKI T B, OKAMOTO H, SUBRAMAMIAN P R, et al. Binary alloy phase diagrams[M]. 2nd Edition. Metals Park: ASM International, 1990: 170.
[20]	LIU F J, JI Y, MENG Q S, et al. Microstructure and corrosion resistance of laser cladding and friction stir processing hybrid modification Al-Si coatings on AZ31 B[J]. Vacuum,2016,133:31-37. doi: 10.1016/j.vacuum.2016.08.010
[21]	LIU F J, JI Y, SUN Z Y, et al. Enhancing corrosion resistance of Al-Cu/AZ31 composites synthesized by a laser cladding and FSP hybrid method[J]. Materials and Manufacturing Processes, 2019, 34: 1458-1466.
[22]	朱红梅, 龚文娟, 易志威. AZ91镁合金表面激光熔覆Al-Cu 合金涂层的组织与性能[J]. 中国有色金属学报, 2016, 26(7):1498-1504. ZHU Hongmei, GONG Wenjuan, YI Zhiwei. Microstructure and property of laser cladding Al-Cu alloy coating on surface of AZ91 magnesium alloy[J]. The Chinese Journal of Nonferrous Metals,2016,26(7):1498-1504(in Chinese).
[23]	孙琪, 李志勇, 张英乔, 等. AZ91 D 镁合金表面激光熔覆Al-TiC涂层组织和性能的研究[J]. 表面技术, 2017, 46(1):40-44. SUN Qi, LI Zhiyong, ZHANG Yingqiao, et al. Microstructure and properties of laser cladding Al-TiC coating on AZ91 D magnesium alloy[J]. Surface Technology,2017,46(1):40-44(in Chinese).
[24]	SONG G L, ATRENS A. Corrosion mechanisms of magnesium alloys[J]. Advanced Engineering Materials,1999,1(1):11-33. doi: 10.1002/(SICI)1527-2648(199909)1:1<11::AID-ADEM11>3.0.CO;2-N
[25]	刘奋军, 张媛媛, 刘建勃, 等. 镁合金表面高转速搅拌摩擦加工区的微观组织和耐腐蚀性能[J]. 表面技术, 2021, 50(3):330-337. LIU Fenjun, ZHANG Yuanyuan, LIU Jianbo, et al. Microstructure and corrosion resistance of high rotating speed friction stir processed zone on magnesium alloy[J]. Surface Technology,2021,50(3):330-337(in Chinese).
[26]	楚志兵, 吕阳阳, 唐宾, 等. 表面渗铝改性镁合金的轧制组织性能[J]. 复合材料学报, 2015, 32(5):1374-1380. CHU Zhibing, LV Yangyang, TANG Bin, et al. Structure and properties on surface of aluminizing-modification magnesium alloy in rolling[J]. Acta Materiae Compositae Sinica,2015,32(5):1374-1380(in Chinese).
[27]	JALILVAND M N, MAZAHERI Y. Effect of mono and hybrid ceramic reinforcement particles on the tribological behavior of the AZ31 matrix surface composites developed by friction stir processing[J]. Ceramics International,2020,46:20345-20356. doi: 10.1016/j.ceramint.2020.05.123
[28]	LIU F J, LIU J B, JI Y, et al. Microstructure, mechanical properties, and corrosion resistance of friction stir welded Mg-Al-Zn alloy thick plate joints[J]. Welding in the World,2021,65:229-241. doi: 10.1007/s40194-020-01012-z
[29]	LIU F J, JI Y, BAI Y X. Influence of multipass high rotating speed friction stir processing on microstructure evolution, corrosion behavior and mechanical properties of stirred zone on AZ31 alloy[J]. Transactions of Nonferrous Metals Society of China,2020,30:3263-3273. doi: 10.1016/S1003-6326(20)65459-0
[30]	BU R, JIN A X, SUN Q, et al. Study on laser cladding and properties of AZ63-Er alloy for automobile engine[J]. Journal of Materials Research and Technology,2020,9(3):5154-5160. doi: 10.1016/j.jmrt.2020.03.032
[31]	ARTHANARI S, LI Y H, NIE L, et al. Microstructural evolution and properties analysis of laser surface melted and Al/SiC cladded magnesium-rare earth alloys[J]. Journal of Alloys and Compounds,2020,848:156598. doi: 10.1016/j.jallcom.2020.156598