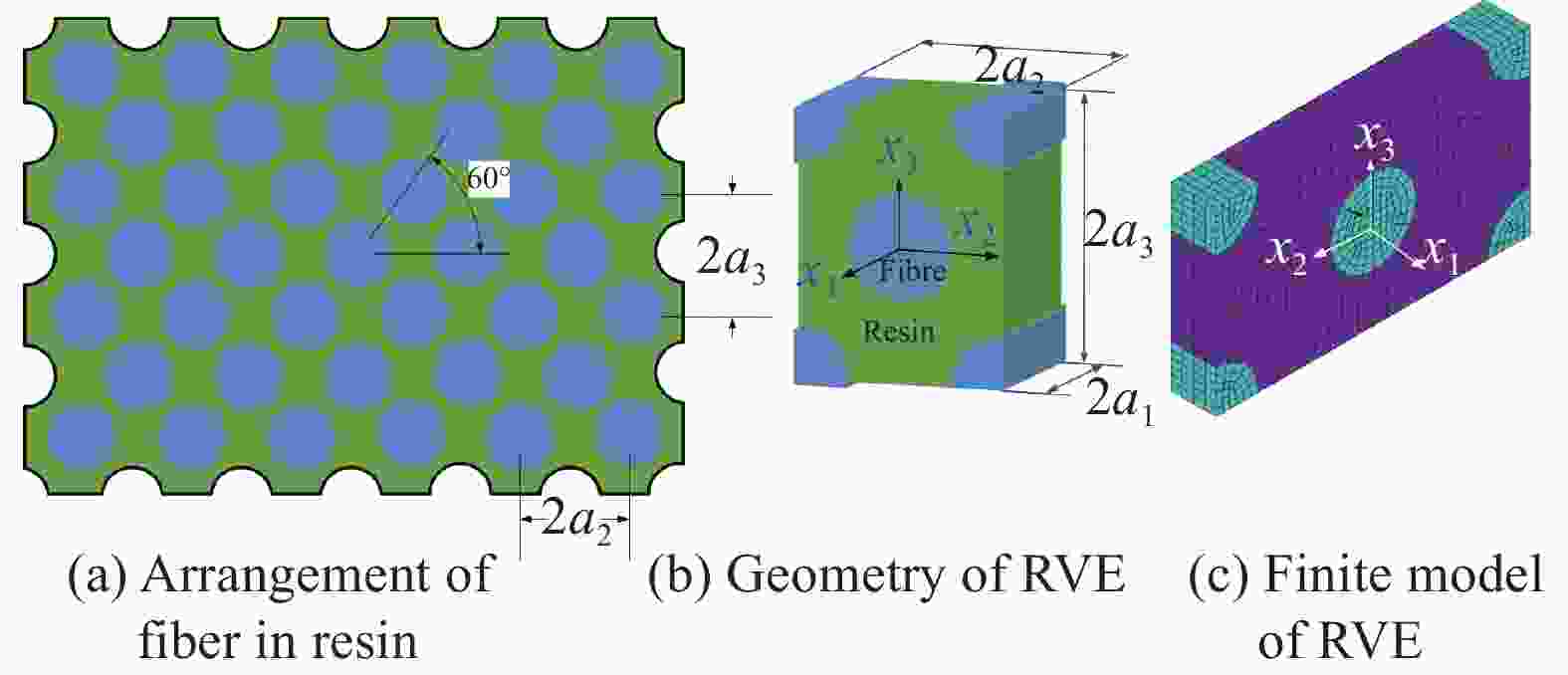
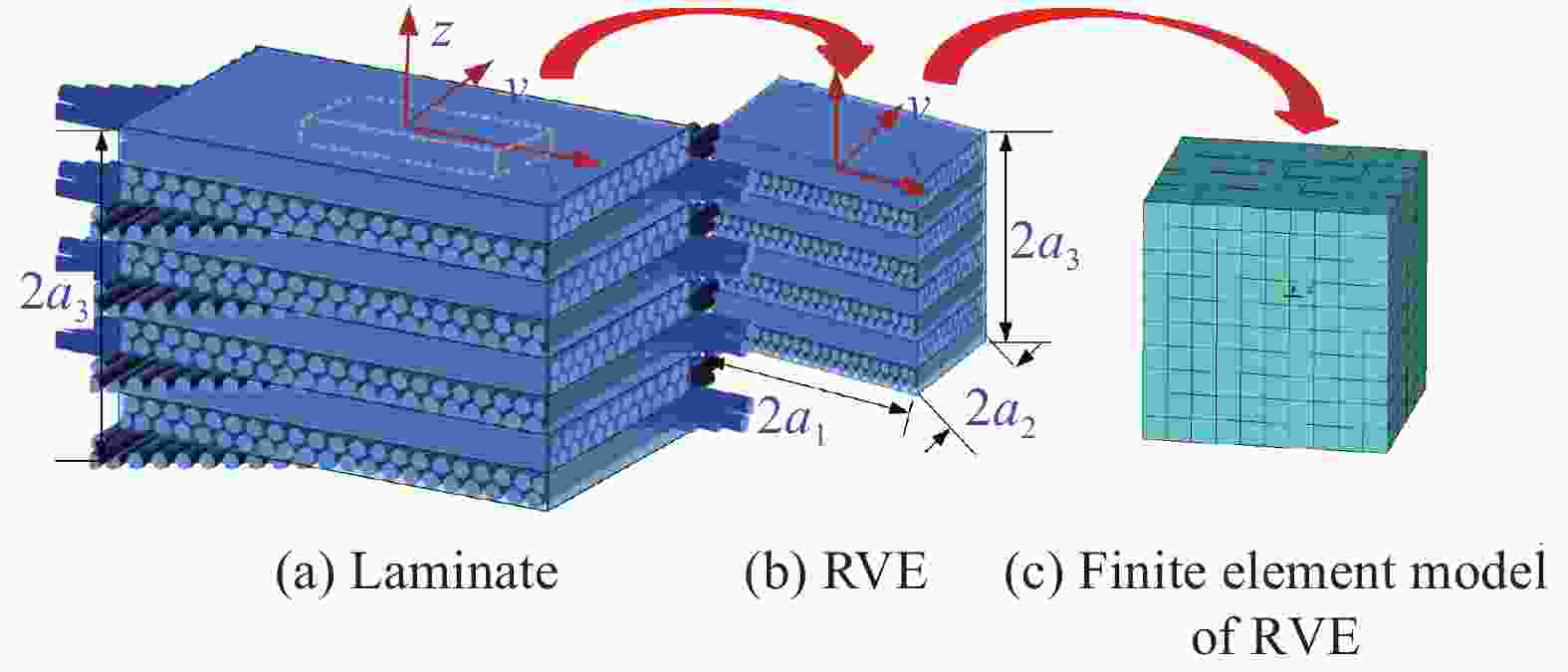
Prediction of anisotropic coefficient of thermal expansion for laminated composite using multiscale numerical models
-
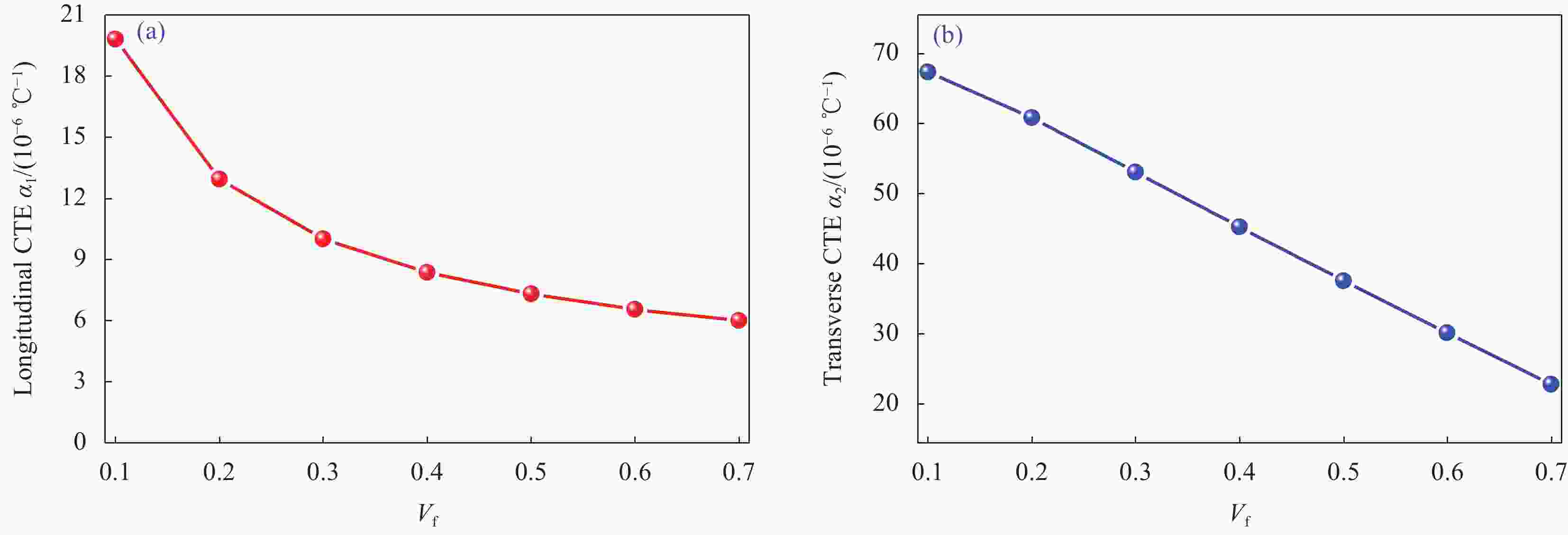
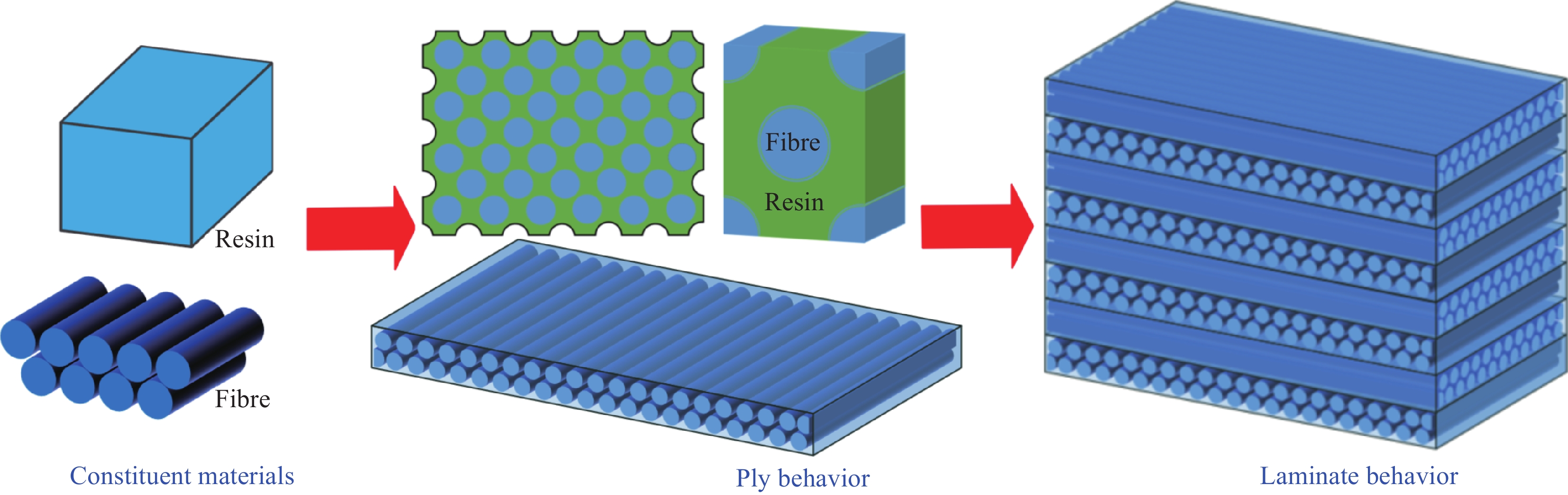
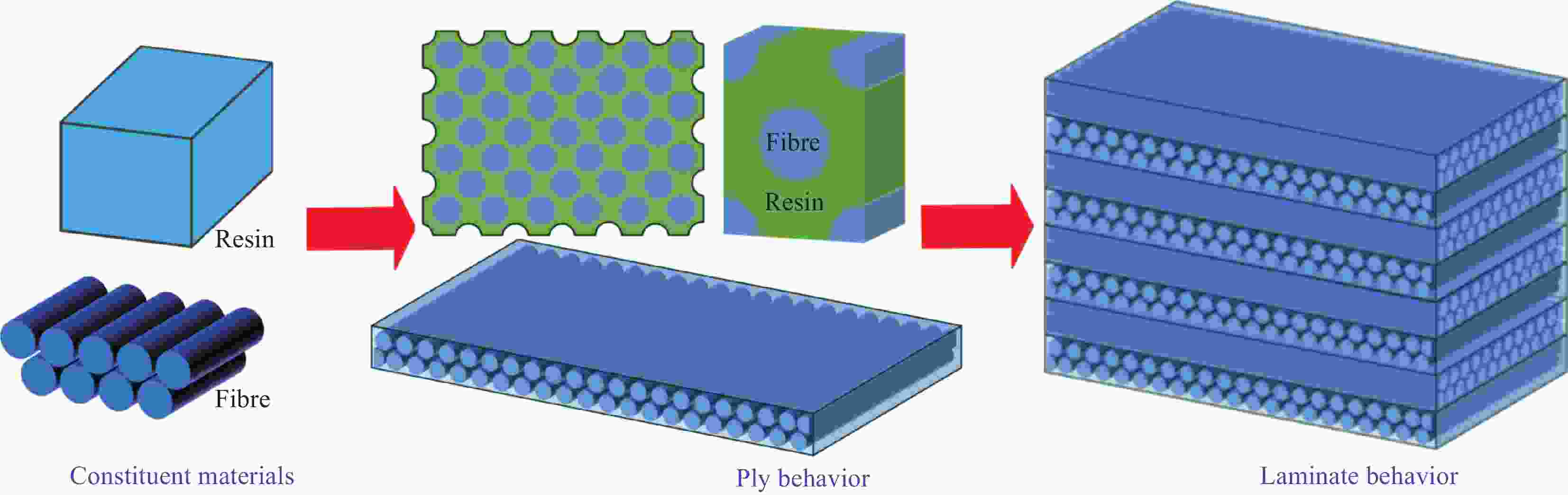
摘要: 依据复合材料内部纤维在基体内的排布规律及层合板铺层特性，基于多尺度方法，建立单层板和层合板代表性体积单元(RVE)模型，施加相应的边界条件，预测单层板的热膨胀系数和工程常数，进而预测复合材料层合板各向异性的等效热膨胀系数。通过与实验数据对比发现，基于正六边形单层板RVE模型预测的热膨胀系数，相比理论预测值，整体更接近实验值，其中预测的单向T300/5208碳纤维增强环氧树脂基复合材料、P75/934碳纤维增强环氧树脂基复合材料和C6000/Pi碳纤维增强环氧树脂基复合材料的横向热膨胀系数与实验结果的误差分别只有3%、1%和2%；采用单层板RVE预测的单向ECR/Derakane 510C玻璃纤维增强乙烯基酯树脂基复合材料的工程常数与实验值最大相差7.5%；层合板RVE模型预测的正交AS4/8552碳纤维增强环氧树脂基复合材料厚度方向的热膨胀系数与实验结果误差可以忽略，只有0.08%。最后以大型复合结构常用的正交铺层结构为研究对象，基于给出的单层板和层合板RVE模型预测了不同铺层复合材料烟道层合板的等效热膨胀系数，环向铺层比例对厚度方向的热膨胀系数影响较小。Abstract: Representative volume element (RVE) in lamina and laminate levels were build based on the arrays of fiber into resin and stacking sequences in laminated composites. In combination with the specified boundary conditions in RVE models, coefficient of thermal expansions (CTEs) and engineering constants for lamina were predicted, followed by an evaluation of anisotropic CTEs for laminate using multiscale method. The results show that numerically predicted CTEs match well with experimental data as compared to theoretically calculated value as a whole, especially for the numerically predicated CTEs of unidirectional T300/5208, P75/934 and C6000/Pi carbon fiber reinforced epoxy resin matrix composites with a difference of 3%, 1% and 2%, respectively. And the predicted engineering constants using RVE model for unidirectional ECR/Derakane 510C glass fiber reinforced vinyl ester resin matrix composites were also in good agreement with experimentally measured results, with a maximum difference of 7.5%. Meanwhile, the difference between experimental results and forecasted CTEs in through-thickness direction for cross-ply AS4/8552 carbon fiber reinforced resin matrix composites using RVE model of laminated composites is nearly negligible with a difference of 0.08%. Finally, the equivalent CTEs of laminated composite with different stacking sequences were estimated using RVE models of lamina and laminate levels for cross-ply composite structures in large large-scale structures, and the results reveal that CTEs in through-thickness direction are weakly related to the ratio of stacking sequences in hoop direction.
-
Key words:
- RVE /
- numerical simulation /
- laminate /
- cross-ply /
- multiscale
-
图 1 预测层合板各向异性热膨胀系数总体框架
Figure 1. Framework for predicting anisotropic coefficient of thermal expansions of laminated composites
图 2 单层板代表性体积单元(RVE)模型
Figure 2. Representative volume element (RVE) model of lamina
a1, a2 and a3—Dimension in three direction; x1, x2 and x3—Coordinate axes
图 4 HMS/Glass复合材料RVE模型的位移云图：(a)纵向方向； (b)横向方向
MX—Max; MN—Min
Figure 4. Contour of displacement for RVE model of HMS/Glass composites: (a) In longitudinal direction; (b) In transverse direction
图 5 拉伸模量(a)和剪切模量(b)实验测试
Figure 5. Experimental testing for tensile (a) and shear (b) moduli
图 6 ECR/Derakane 510C复合材料单层板RVE模型在横向(a)和纵向(b)方向应力云图
Figure 6. Contour of stress in RVE model of unidirectional lamina for ECR/Derakane 510C composites in longitudinal (a) and transverse (b) direction
图 7 AS4/8552 复合材料层合板RVE在x方向(a)和z方向(b)位移云图
Figure 7. Displacement contour of laminate in x direction (a) and z direction (b) for AS4/8552 composites
图 8 单向ECR/Derakane 510C复合材料纵向(a)和横向(b)热膨胀系数随纤维体积含量Vf的变化
Figure 8. Change of coefficient of thermal expansion (CTE) with fiber volume fraction Vf for unidirectional ECR/Derakane 510C composites in longitudinal (a) and transverse (b) direction
Constituent material E1/GPa E2/GPa G12/GPa G23/GPa ν12 ν23 α1/(10−6℃−1) α2/(10−6℃−1) T300 carbon fiber 233.04 23.10 8.96 8.27 0.20 0.4 −0.54 10.08 5208 epoxy 4.34 — 1.59 — 0.37 — 43.92 — P75 carbon fiber 550.20 9.51 6.89 3.38 0.20 0.4 −1.35 6.84 934 epoxy 4.34 — 1.59 — 0.37 — 43.92 — CE339 epoxy 4.34 — 1.59 — 0.37 — 63.36 — C6000 carbon fiber 233.04 23.10 8.96 8.27 0.20 0.4 −0.54 10.08 PMR15 polyimide 3.45 — 1.31 — 0.35 — 36.00 — HMS carbon fiber 379.21 6.21 7.58 2.21 0.20 0.4 −0.99 6.84 Borosilicate glass 62.74 — 26.20 — 0.20 — 3.24 — Notes: E1 and E2—Moduli in “1” and “2” direction; G12 and G23—Shear moduli in “1-2” plane and “2-3” plane direction; ν12 and ν23—Poisson’s ratio in “1-2” plane and “2-3” plane direction; α1 and α2—Coefficients of thermal expansion in “1” and “2” direction. 
下载: 导出CSV
表 2 各复合材料预测与实验测试值的比较
Table 2. Comparison of experimental data with predicted values of composites
Composite α1/(10−6℃−1) α2/(10−6℃−1) Experimental[23] SH/CH(Error) Predicted(Error) Experimental[23] SH(Error) CH(Error) Predicted(Error) T300/5208
(Vf=0.68)−0.113 −0.153(35%) −0.091(19%) 25.236 27.540(9%) 18.900(25%) 24.383(3%) P75/934
(Vf=0.48)−1.051 −0.967(8%) −0.922(12%) 34.524 35.460(3%) 23.220(33%) 34.045(1%) P75/930
(Vf=0.65)−1.076 −1.159(8%) −1.128(5%) 31.716 26.640(16%) 17.154(46%) 25.018(21%) P75/CE339
(Vf=0.54)−1.021 −0.918(10%) −0.859(16%) 47.412 44.640(6%) 28.080(41%) 42.732(10%) C6000/Pi
(Vf=0.63)−0.212 −0.225(6%) −0.192(9%) 22.428 25.740(15%) 18.000(20%) 22.062(2%) HMS/Glass
(Vf=0.47)−0.414 −0.324(22%) −0.324(22%) 3.780 5.976(58%) 5.427(44%) 4.479(18%) Notes: Vf —Fiber volume fraction; SH are the predicted values using Eq.(11)-(12); CH are the predicted values using Eq.(11) and Eq.(13).
下载: 导出CSV
表 3 ECR/Derakane 510C 复合材料组分材料的性能参数
Table 3. Properties of constituent materials for ECR/Derakane 510C composites
Property E/GPa ν ECR glass fiber 80.00 0.20 Derakane 510C 3.35 0.35 Notes: E—Modulus; ν—Poisson’s ratio.
下载: 导出CSV
表 4 单向ECR/Derakane 510C复合材料工程常数预测值与试验结果对比
Table 4. Comparison of numerical results with experimental values for engineering constants of unidirectional ECR/Derakane 510C composites
Iterm E1/GPa E2/GPa G12/GPa G23/GPa ν12 ν23 Numerical 34.03 7.32 2.71 2.51 0.282 0.333 Experimental 31.63 7.40 2.69 − 0.281 − Error/% 7.50 1.10 0.74 − 0.350 −
下载: 导出CSV
表 5 单层AS4/8552碳纤维增强树脂基复合材料力学性能参数[27]
Table 5. Parameters of mechanical properties of unidirectional AS4/8552 composites[27]
E1
/GPaE2
/GPaG12=G13=G23
/GPaν12=ν13 ν23 α1
/(10−6℃−1)α2
/(10−6℃−1)135 9.5 4.9 0.3 0.45 0.00 32.6 Note: G13—Shear moduli in “1-3” plane direction, respectively; 1—Longitudinal direction; 2—Transverse direction; 3—Thickness direction.
下载: 导出CSV
表 6 AS4/8552复合材料层合板仿真数据与文献[27]实验结果对比
Table 6. Comparisons of numerical results and experimental values from literature [27] of laminated AS4/8552 composite
Equivalent CTEs αx
/(10−6℃−1)αy
/(10−6℃−1)αz
/(10−6℃−1)Numerical 2.68 2.68 45.16 Experimental[27] 2.70 2.70 45.20 Error/% 0.70 0.70 0.08 Notes: αx, αy and αz—Coefficients of thermal expansion in x, y and z direction, respectively; CTEs—Coefficient of thermal expansions.
下载: 导出CSV
表 7 ECR/Derakane 510C复合材料单向布和纤维缠绕层单层板力学性能
Table 7. Mechanical properties of lamina composed of unidirectional fabrics and filament wound roving for ECR/Derakane 510C composites
Engineering constant Unidirectional fabric layer Filament wound layer E1/MPa 38690 31630 E2=E3/MPa 9100 7400 G12=G13/MPa 3370 2690 G23/MPa 3594 2888 ν12=ν13 0.266 0.281 ν23 0.266 0.281
下载: 导出CSV
表 8 ECR/Derakane 510C复合材料烟道层合板等效热膨胀系数
Table 8. Equivalent CTEs of laminate in ECR/Derakane 510C composite duck
Stacking sequence αx
/10−6℃−1αy
/10−6℃−1αz
/10−6℃−1RVE CLT RVE CLT RVE [0/90/90]s 18.02 18.40 11.80 13.38 42.93 [0/90]s 14.60 14.19 14.88 16.14 44.64 [0/0/90]s 12.23 11.39 19.42 19.89 45.55 [0/0/0/90]s 11.25 10.29 22.67 22.41 45.63 Note: CLT—Classic laminate theory.
下载: 导出CSV
-
[1] DING A, WANG J, NI A, et al. A new analytical solution for cure-induced spring-in of L-shaped composite parts[J]. Composites Science and Technology, 2019, 171: 1-12. [2] 丁安心, 王继辉, 倪爱清, 等. 热固性树脂基复合材料固化变形解析预测研究进展[J]. 复合材料学报, 2018, 35(6): 1361-1376.DING Anxin, WANG Jihui, NI Aiqing, et al. A review of analytical prediction of cure-induced distortions in thermoset composites[J]. Acta Materiae Compositae Sinica, 2018, 35(6): 1361-1376(in Chinese). [3] 李云波, 李宗利, 姚希望, 等. 含孔洞和裂隙混合缺陷的干燥水泥砂浆导热系数相互作用直推预测模型[J]. 复合材料学报, 2022, 39(1): 361-370.LI Yunbo, LI Zongli, YAO Xiwang, et al. Interaction direct deduction prediction model of thermal conductivity of dry cement mortar with mixed defects of cavities and cracks[J]. Acta Materiae Compositae Sinica, 2022, 39(1): 361-370(in Chinese). [4] 周龙伟, 赵丽滨. 基于失效机制的单向纤维增强树脂复合材料退化模型[J]. 复合材料学报, 2019, 36(6): 1389-1397.ZHOU Longwei, ZHAO Libin. Failure mechanisms based degradation model of unidirectional fiber reinforced polymer composites[J]. Acta Materiae Compositae Sinica, 2019, 36(6): 1389-1397(in Chinese). [5] GAO Z, CHEN L. A review of multi-scale numerical modeling of three-dimensional woven fabric[J]. Composite Structures, 2021, 263: 113685. [6] FU Y, YAO X, GAO X. Micro-mesoscopic prediction of void defect in 3D braided composites[J]. Composites Part A: Applied Science and Manufacturing, 2021, 147: 106450. [7] SUN C, VAIDYA R. Prediction of composite properties from a representative volume element[J]. Composites Science and Technology, 1996, 56(2): 171-179. [8] GARNICH M R, KARAMI G. Finite element micromecha-nics for stiffness and strength of wavy fiber composites[J]. Journal of Composite Materials, 2004, 38(4): 273-292. [9] GARNICH M R, KARAMI G. Localized fiber waviness and implications for failure in unidirectional composites[J]. Journal of Composite Materials, 2005, 39(14): 1225-1245. [10] 张元冲, HARDING J. 平面织物复合材料机械性能的数值细观力学分析[J]. 应用力学学报, 1989(4): 20-27, 114.ZHANG Yuanchong, HARDING J. A numerical micromechanics analysis of the mechanical properties of a plain weave composite[J]. Chinese Journal of Applied Mechanics, 1989(4): 20-27, 114(in Chinese). [11] 吕毅, 吕国志, 吕胜利. 细观力学方法预测单向复合材料的宏观弹性模量[J]. 西北工业大学学报, 2007, 24(6): 787-790.LV Yi, LV Guozhi, LV Shengli. Semi-theoretical and engi-neering prediction of macroscopic elastic moduli of unidirectional composites[J]. Journal of Northwestern Polytechnical University, 2007, 24(6): 787-790(in Chinese). [12] 左中鹅, 王瑞, 徐磊. 基于有限单元法的平纹织物复合材料强度预测: 1. RVE的有限元模型[J]. 纺织学报, 2009(12): 45-49.ZUO Zhong'e, WANG Rui, XU Lei. Mechanical strength prediction of plain woven fabric composite: 1. Finite element model of composite RVE[J]. Journal of Textile Research, 2009(12): 45-49(in Chinese). [13] LU J, ZHU P, JI Q, et al. Identification of the mechanical properties of the carbon fiber and the interphase region based on computational micromechanics and Kriging metamodel[J]. Computational Materials Science, 2014, 95: 172-180. [14] 马学仕. 基于均匀化理论的周期性复合材料有效性能预测[D]. 南京: 南京航空航天大学, 2013.MA Xueshi. Homogenization method to calculation of effective properties for periodic composite materials[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013(in Chinese). [15] GHOSH S, MUKHOPADHYAY S N. A material based finite element analysis of heterogeneous media involving dirichlet tessellations[J]. Computer Methods in Applied Mecha-nics and Engineering, 1993, 104(2): 211-247. [16] TRIAS D, COSTA J, MAYUGO J, et al. Random models versus periodic models for fibre reinforced composites[J]. Computational Materials Science, 2006, 38(2): 316-324. [17] LUCIANO R, BARBERO E J. Formulas for the stiffness of composites with periodic microstructure[J]. International Journal of Solids and Structures, 1994, 31(21): 2933-2944. [18] RAMM E, RANK E, RANNACHER R, et al. Error-controlled adaptive finite elements in solid mechanics[M]. Chichester: John Wiley & Sons, 2003. [19] 赵琳. 基于单胞解析模型与渐进损伤分析的复合材料强度预报[D]. 哈尔滨: 哈尔滨工业大学, 2012.ZHAO Lin. Strength prediction of composites based on unit cell analytic model and progressive damage analysis[D]. Harbin: Harbin Institute of Technology, 2012(in Chinese). [20] 张超, 许希武, 严雪. 纺织复合材料细观力学分析的一般性周期性边界条件及其有限元实现[J]. 航空学报, 2013, 34(7): 1636-1645.ZHANG Chao, XU Xiwu, YAN Xue. General periodic boundary conditions and their application to micromechanical finite element analysis of textile composites[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(7): 1636-1645(in Chinese) [21] SUN C, LIAO W. Analysis of thick section composite laminates using effective moduli[J]. Journal of Composite Materials, 1990, 24(9): 977-993. [22] SUN C, LI S. Three-dimensional effective elastic constants for thick laminates[J]. Journal of Composite Materials, 1988, 22(7): 629-639. [23] BOWLES D E, TOMPKINS S S. Prediction of coefficients of thermal expansion for unidirectional composites[J]. Jour-nal of Composite Materials, 1989, 23(4): 370-388. [24] SCHAPERY R A. Thermal expansion coefficients of compo-site materials based on energy principles[J]. Journal of Composite Materials, 1968, 2(3): 380-404. [25] CHAMIS C. Simplified composite micromechanics equations of hygral, thermal, and mechanical properties[J]. Transactions of the Asae, 1984, 39(3): 999-1004. [26] 中国国家标准化管理委员会. 纤维增强塑料拉伸性能试验方法: GB/T 1447—2005[S]. 北京: 中国标准出版社, 2005.Standardization Administration of the People's Republic of China. Fiber-reinforced plastics composites—Determination of tensile properties: GB/T 1447—2005[S]. Beijing: China Standards Press, 2005(in Chinese). [27] WISNOM M R, POTTER K D, ERSOY N. Shear-lag analysis of the effect of thickness on spring-in of curved compo-sites[J]. Journal of Composite Materials, 2007, 41(11): 1311-1324. -
下载:
点击查看大图
计量
- 文章访问数: 2019
- HTML全文浏览量: 830
- PDF下载量: 275
- 被引次数: 0
