Micro-mechanics analytical method for composite out-of-plane wrinkle with double fiber-waviness
-
摘要: 复合材料由于其高比模量、高比强度和疲劳寿命长等突出的优点被广泛应用于航空航天领域，但在制备过程中易产生褶皱缺陷，并对复合材料层合板的刚度、强度产生负面影响。本文主要研究含有单波纹和双波纹外部褶皱的复合材料力学性能。提出一种解析方法计算单波纹和双波纹褶皱细观力学模型的等效材料属性，通过与数值模型结果的对比与分析，发现含褶皱层合板的等效模量随波纹比绝对值的增大而减小。当波纹比绝对值相同时，含凹陷褶皱的层合板等效模量比含凸起褶皱的层合板等效模量低。不同厚度的含有褶皱的层合板等效模量曲线存在交汇点，交汇点两侧等效模量随厚度变化的趋势相反，且双波纹褶皱与单波纹褶皱的交汇点不同。Abstract: Composites are widely used in aerospace industry because of their outstanding advantages, such as high specific modulus, high specific strength and long fatigue life. However, composite often encounters wrinkle defects in the manufacturing process. The existence of wrinkle defects has negative impacts on the stiffness and strength of composite laminates. The mechanical properties of composites with wrinkle of single and double fiber-waviness were studied in this paper. Analytical and numerical methods were used to calculate the effective material properties of single and double fiber-waviness wrinkle with micro-mechanical models. Through the comparison and analyses of the prediction results from micro-mechanical models, it is shown that when the absolute value of waviness ratio increases, the effective modulus of the laminate with wrinkle decreases. When the absolute value of waviness ratio is the same, the effective modulus of the laminate with concave wrinkle is lower than that with convex wrinkle. There is an intersection point among the effective modulus curves obtained from wrinkled laminates with different thicknesses. The variation of effective modulus associated with laminates thickness is opposite on the two sides of intersection point. The intersection point of wrinkle with double fiber-waviness is different from that of single fiber-waviness.
-
图 3 实际制备过程中出现的双波纹褶皱
Figure 3. Double-fiber-waviness wrinkle in the actual production process
图 4 单波纹褶皱模型：(a)凸起褶皱；(b)凹陷褶皱
Figure 4. Single-fiber-waviness wrinkle model: (a) Convex wrinkle; (b) Concave wrinkle
H—Wrinkle height; L—Wrinkle wavelength; t—Laminate thickness; t1—Thickness of wrinkle-free zone; φ—Out-of-plane orientation angle
图 5 双波纹褶皱模型：(a) 含有凸起褶皱；(b) 含有凸起褶皱和凹陷褶皱
Figure 5. Double-fiber-waviness wrinkle model: (a) Containing convex wrinkle; (b) Containing convex and concave wrinkle
H1—Wrinkle height (Left); L1—Wrinkle wavelength (Left); H2—Wrinkle height (Right); L2—Wrinkle wavelength (Right)
图 6 含褶皱层合板两步均质化过程
Figure 6. Two-step homogenization procedure for wrinkled composite laminates
图 7 含褶皱复合材料有限元模型示意图
RP—Reference point
Figure 7. Schematic illustration of finite element model of wrinkled composites
图 8
${[0]_{{\text{5s}}}}$ 铺层AS4/8552单波纹褶皱层合板等效材料属性随H/L的变化情况Figure 8. Change of the effective material properties versus H/L of AS4/8552 single-fiber-waviness wrinkle laminate with
${[0]_{{\text{5s}}}}$ layup
图 9 不同铺层AS4/8552单波纹褶皱的等效模量
$E_{xx}^{**}$ 随H/L的变化趋势Figure 9. Variation trend of
$E_{xx}^{**}$ for AS4/8552 single-fiber-waviness wrinkle of different layers versus H/L
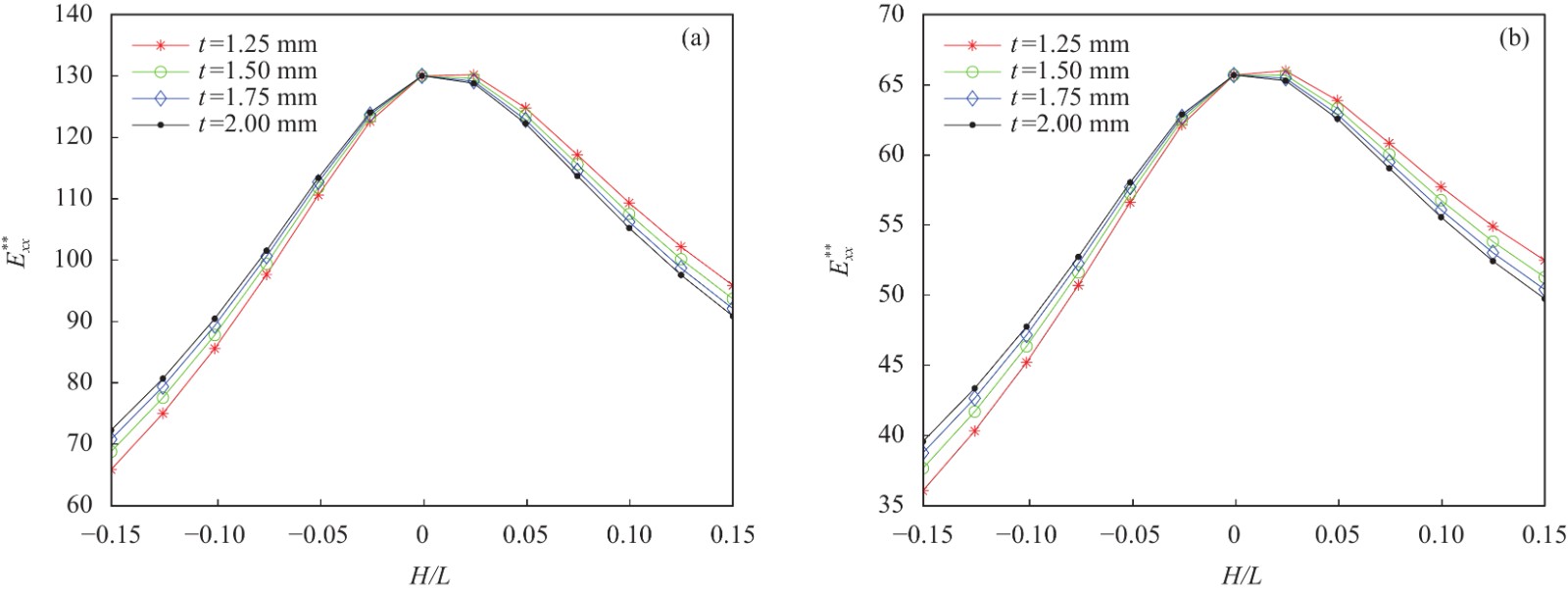
图 10 不同厚度AS4/8552单波纹褶皱
$E_{xx}^{**}$ 随$H/L$ 的变化情况：(a)${[0]_{{\text{5s}}}}$ 铺层；(b)$ {[0/45/90/ - 45/0]_{\text{s}}} $ 铺层Figure 10. Variations of
$E_{xx}^{**}$ versus$H/L$ for AS4/8552 single-fiber-waviness wrinkle of different thicknesses: (a)${[0]_{{\text{5s}}}}$ layup; (b)$ {[0/45/90/ - 45/0]_{\text{s}}} $ layup
图 11
${[0]_{{\text{5s}}}}$ 铺层AS4/8552双波纹褶皱层合板等效材料属性随${H_2}/{L_2}$ 的变化情况Figure 11. Change of the effective material properties versus
${H_2}/{L_2}$ of AS4/8552 double-fiber-waviness wrinkle laminate with${[0]_{{\text{5s}}}}$ layup
图 12 不同铺层AS4/8552双波纹褶皱的
$E_{xx}^{**}$ 随${H_2}/{L_2}$ 的变化情况Figure 12. Variations of
$E_{xx}^{**}$ for AS4/8552 double-fiber-waviness wrinkle of different layers versus${H_2}/{L_2}$ 
图 13 不同厚度AS4/8552双波纹褶皱的
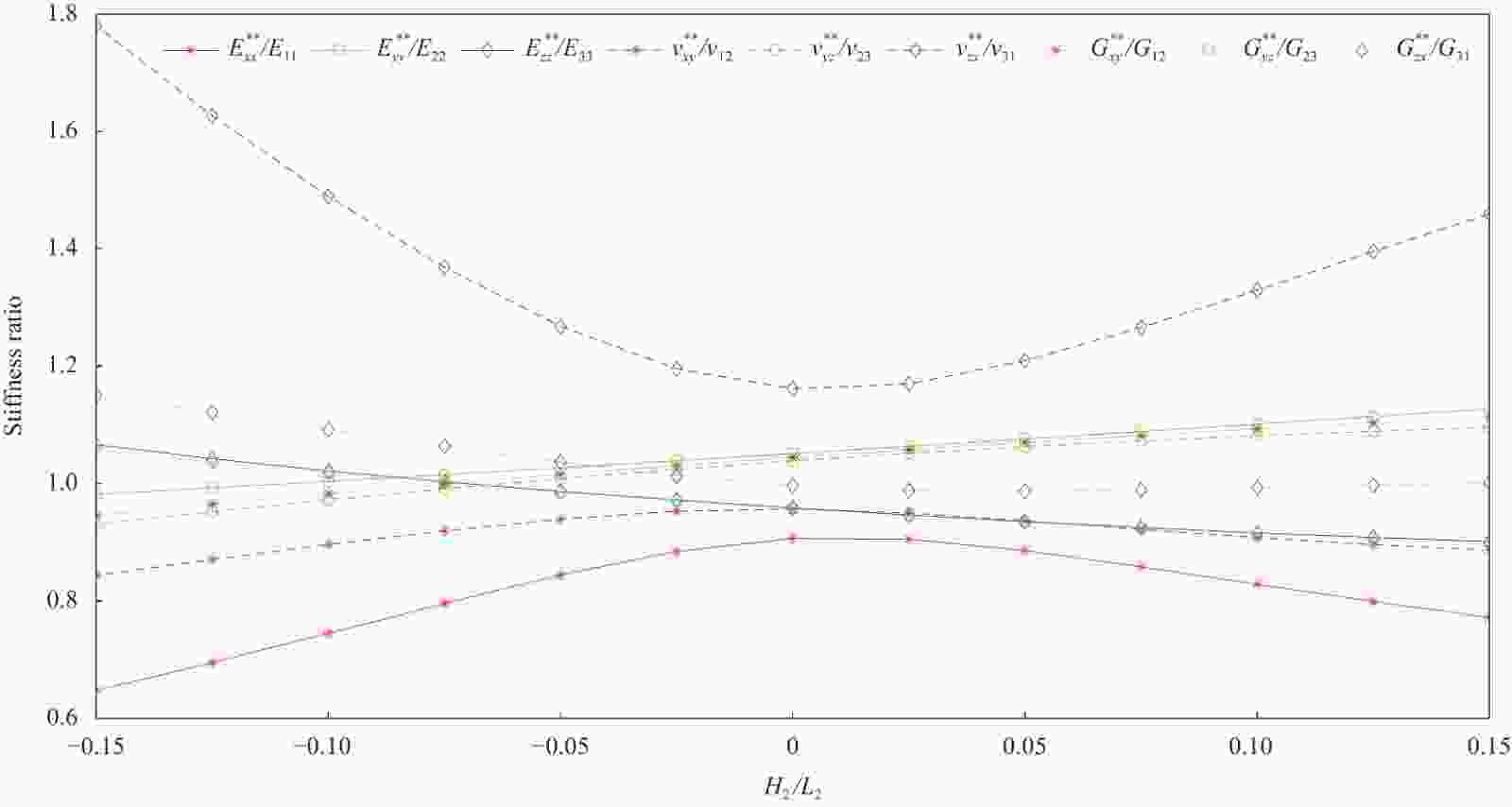
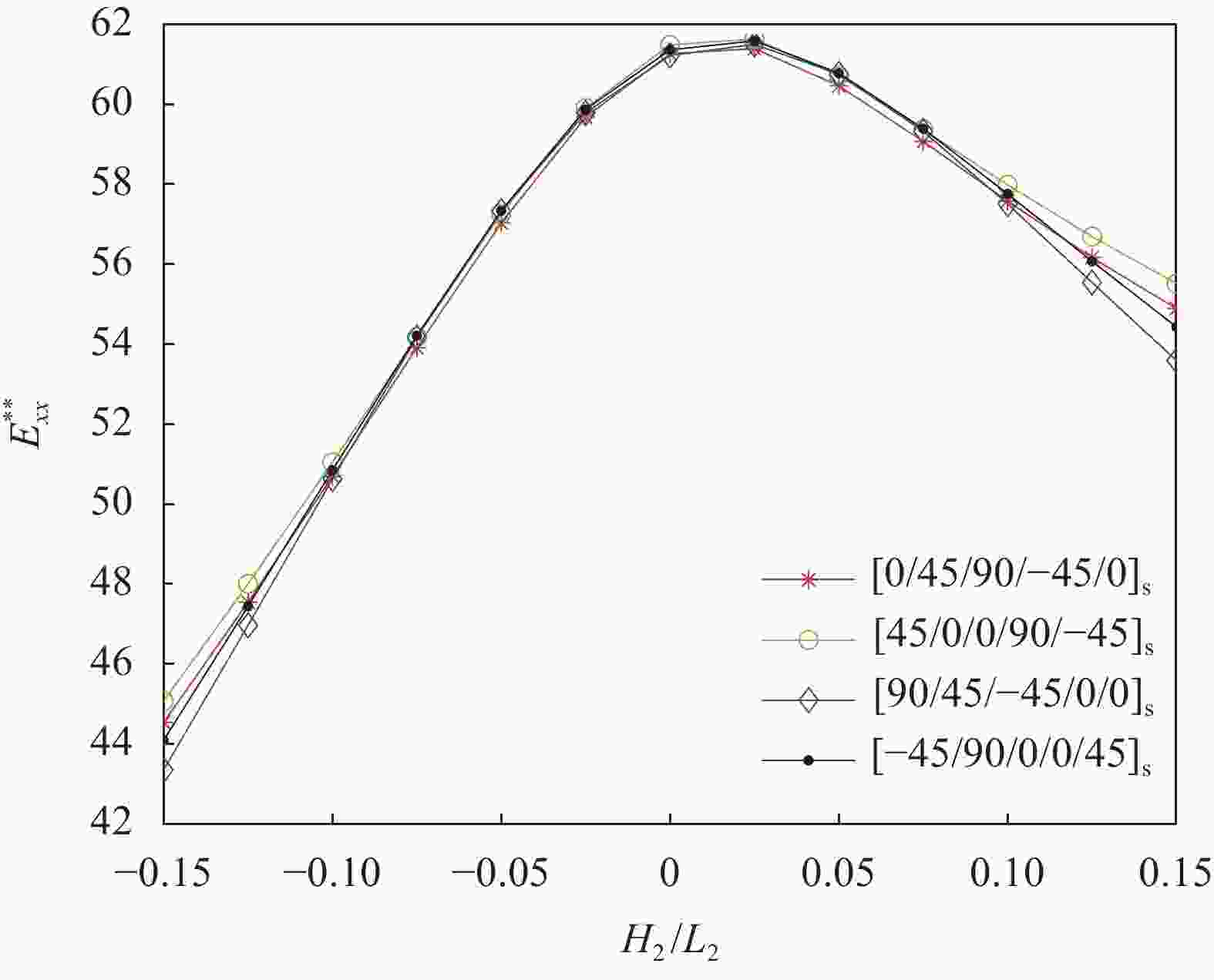
$E_{xx}^{**}$ 随${H_2}/{L_2}$ 的变化情况：(a)${[0]_{{\text{5s}}}}$ 铺层，${H_1}/{L_1}{\text{ = 0}}{\text{.10}}$ ； (b)$ {[0/45/90/ - 45/0]_{\text{s}}} $ 铺层，${H_1}/{L_1}{\text{ = 0}}{\text{.10}}$ ；(c)${[0]_{{\text{5s}}}}$ 铺层，${H_1}/{L_1}{{ = - }}0.10$ a, b, c—Intersection point
Figure 13. Variations of
$E_{xx}^{**}$ versus${H_2}/{L_2}$ for AS4/8552 double-fiber-waviness wrinkle of different thicknesses: (a)${[0]_{{\text{5s}}}}$ layup,${H_1}/{L_1} = 0.10$ ; (b)$ {[0/45/90/ - 45/0]_{\text{s}}} $ layup,${H_1}/{L_1} = 0.10$ ; (c)${[0]_{{\text{5s}}}}$ layup,${H_1}/{L_1} = - 0.10$ 表 1 碳纤维/环氧树脂复合材料AS4/8552的力学性能
Table 1. Mechanical properties of AS4/8552 carbon fiber/epoxy composites
$ \begin{gathered} {\text{ }}E_{11} /{\text{GPa}} \end{gathered} $ $ \begin{gathered} {\text{ }}E_{22}^{} {\text{/GPa}} \end{gathered} $ $\begin{gathered} {\text{ } }E_{33}^{} {\text{/GPa} } \end{gathered}$ $ \begin{gathered} {\text{ }}G_{12}^{} {\text{/GPa}} \end{gathered} $ $ \begin{gathered} {\text{ }}G_{13}^{} {\text{/GPa}} \end{gathered} $ $ \begin{gathered} {\text{ }}G_{23}^{} {\text{/GPa}} \end{gathered} $ ${v_{12}}$ ${v_{13} }$ ${v_{23}}$ 130 8.5 8.5 4.2 4.2 3.7 0.35 0.35 0.43 Notes: E—Tensile modulus; G—Shear modulus; $v $—Poisson's ratio; 1, 2, 3—Longitudinal, transverse and thickness directions of materials. 
下载: 导出CSV
表 2
${[0]_{{\text{5s}}}}$ 铺层AS4/8552单波纹褶皱模型通过解析和数值方法获得的等效材料属性Table 2. Effective material properties of AS4/8552 single-fiber-waviness wrinkle model with
${[0]_{{\text{5s}}}}$ layup obtained by analytical and numerical methodsEffective material properties $ H/L{{ = - 0}}{\text{.2 mm/}}3.0\;{\text{mm}} $ $ H/L{\text{ = 0}}{\text{.2 mm/}}3.0\;{\text{mm}} $ Analytical method Numerical method Error/% Analytical method Numerical method Error/% $E_{xx}^{**}{\text{/GPa}}$ 113.174 112.988 0.160 128.069 127.232 0.660 $ E_{yy}^{**}{\text{/GPa}} $ 7.939 7.937 0.025 9.071 9.072 –0.011 $ E_{zz}^{**}{\text{/GPa}} $ 9.140 9.168 –0.310 7.992 8.012 –0.250 $ v_{yz}^{**} $ 0.3990 0.3980 0.25 0.4560 0.4560 0.00 $ v_{zx}^{**} $ 0.0270 0.0246 9.76 0.0240 0.0218 10.09 $ v_{xy}^{**} $ 0.3410 0.3260 4.60 0.3400 0.3260 4.29 $ G_{yz}^{**}{\text{/GPa}} $ 3.976 2.178 82.55 3.477 2.678 29.84 $ G_{zx}^{**}{\text{/GPa}} $ 4.713 3.540 33.14 4.139 3.256 27.12 $ G_{xy}^{**}{\text{/GPa}} $ 3.908 3.890 0.46 4.469 4.450 0.43 Note: **—After two steps homogenization.
下载: 导出CSV
表 3
$ {[0/45/90/ - 45/0]_{\text{s}}} $ 铺层AS4/8552单波纹褶皱模型通过解析和数值方法获得的等效材料属性Table 3. Effective material properties of AS4/8552 single-fiber-waviness wrinkle model with
${[0/45/90/ - 45/0]_{\text{s}}}$ layup obtained by analytical and numerical methodsEffective material properties $ H/L{\text{ = 0}}{\text{.2 mm/3}}{\text{.0 mm}} $ Analytical method Numerical method Error/% $E_{xx}^{**}{\text{/GPa}}$ 65.172 66.398 −1.85 $ E_{yy}^{**}{\text{/GPa}} $ 45.170 45.616 −0.98 $ E_{zz}^{**}{\text{/GPa}} $ 9.348 9.372 −0.26 $ v_{yz}^{**} $ 0.3870 0.3790 2.11 $ v_{zx}^{**} $ 0.0515 0.0476 8.19 $ v_{xy}^{**} $ 0.3100 0.3050 1.64 $ G_{yz}^{**}{\text{/GPa}} $ 3.668 3.044 20.50 $ G_{zx}^{**}{\text{/GPa}} $ 3.838 2.989 28.40 $ G_{xy}^{**}{\text{/GPa}} $ 16.387 16.750 −2.17
下载: 导出CSV
表 4
${[0]_{{\text{5s}}}}$ 铺层 AS4/8552双波纹褶皱模型通过解析和数值方法获得的等效材料属性Table 4. Effective material properties of AS4/8552 double-fiber-waviness wrinkle model with
${[0]_{{\text{5s}}}}$ layup obtained by analytical and numerical methodsEffective material properties $ {H_1}/{L_1}=0.2\;{\text{mm/}}3.0\;{\text{mm}} $ $ {H_2}/{L_2}=0.1\;{\text{mm/}}3.0\;{\text{mm}} $ $ {H_2}/{L_2}= - 0.1\;{\text{mm/}}3.0\;{\text{mm}} $ Analytical method Numerical methods Error/% Analytical method Numerical methods Error/% $ E_{xx}^{**}{\text{/GPa}} $ 129.570 131.622 −1.560 125.396 127.513 −1.660 $ E_{yy}^{**}{\text{/GPa}} $ 8.924 8.926 −0.022 8.649 8.642 0.081 $ E_{zz}^{**}{\text{/GPa}} $ 8.113 8.125 −0.150 8.401 8.412 −0.130 $ v_{yz}^{**} $ 0.4500 0.4500 0.00 0.4350 0.4340 0.23 $ v_{zx}^{**} $ 0.0234 0.0219 6.70 0.0242 0.0223 8.52 $ v_{xy}^{**} $ 0.3430 0.3500 −2.00 0.3430 0.3380 1.48 $ G_{yz}^{**}{\text{/GPa}} $ 3.530 2.612 35.14 3.654 2.487 46.92 $ G_{zx}^{**}{\text{/GPa}} $ 4.133 2.540 62.72 4.270 2.563 66.60 $ G_{xy}^{**}{\text{/GPa}} $ 4.402 4.389 0.30 4.253 4.239 0.14
下载: 导出CSV
表 5
$ {[0/45/90/ - 45/0]_{\text{s}}} $ 铺层AS4/8552双波纹褶皱模型通过解析和数值方法获得的等效材料属性Table 5. Effective material properties of AS4/8552 double-fiber-waviness wrinkle model with
$ {[0/45/90/ - 45/0]_{\text{s}}} $ layup obtained by analytical and numerical methodsEffective material properties $ {H_1}/{L_1}{\text{ = }}0.2\;{\text{mm/}}3.0\;{\text{mm}} $ $ {H_2}/{L_2}{\text{ = }}0.1\;{\text{mm/2}}.0\;{\text{mm}} $ $ {H_2}/{L_2}{ = - }0.1\;{\text{mm/2}}.0\;{\text{mm}} $ Analytical method Numerical methods Error/% Analytical method Numerical methods Error/% $ E_{xx}^{**}{\text{/GPa}} $ 65.029 64.571 0.71 62.784 63.684 −1.41 $ E_{yy}^{**}{\text{/GPa}} $ 44.681 44.660 0.05 44.156 43.630 1.21 $ E_{zz}^{**}{\text{/GPa}} $ 9.464 9.483 −0.20 9.572 9.752 −1.85 $ v_{yz}^{**} $ 0.3830 0.3840 −0.26 0.3780 0.3730 1.34 $ v_{zx}^{**} $ 0.0514 0.0505 1.78 0.0538 0.0494 8.91 $ v_{xy}^{**} $ 0.3120 0.3110 −0.32 0.3060 0.3120 −1.92 $ G_{yz}^{**}{\text{/GPa}} $ 3.710 2.972 24.83 3.763 2.375 58.44 $ G_{zx}^{**}{\text{/GPa}} $ 3.872 2.410 60.66 3.942 2.877 37.02 $ G_{xy}^{**}{\text{/GPa}} $ 16.275 16.171 0.64 15.820 15.867 0.30
下载: 导出CSV
-
[1] CHUN H, SHIN J, DANIEL I M. Effects of material and geometric nonlinearities on the tensile and compressive behavior of composite materials with fiber waviness[J]. Composite Science Technology,2001,61:125-134. doi: 10.1016/S0266-3538(00)00201-3 [2] TAKEDA T. Micromechanics model for three-dimensional effective elastic properties of composite laminates with ply wrinkles[J]. Composite Structures,2018,189:419-427. doi: 10.1016/j.compstruct.2017.10.086 [3] ALVES M P, CIMINI JUNIOR C A, HA S K. Fiber waviness and its effect on the mechanical performance of fiber reinforced polymer composites: An enhanced review[J]. Composites Part A: Applied Science and Manufacturing,2021,149:106526. doi: 10.1016/j.compositesa.2021.106526 [4] KULKARNI P, MALI K D, SINGH S. An overview of the formation of fiber waviness and its effect on the mechanical performance of fiber reinforced polymer composites[J]. Composites Part A: Applied Science and Manufacturing,2020,137:106013. doi: 10.1016/j.compositesa.2020.106013 [5] MUKHOPADHYAY S, JONES M I, HALLETT S R. Compres-sive failure of laminates containing an embedded wrinkle: Experimental and numerical study[J]. Composites Part A: Applied Science and Manufacturing,2015,73:132-142. doi: 10.1016/j.compositesa.2015.03.012 [6] ZHU J, WANG J, ZU L. Influence of out-of-plane ply waviness on elastic properties of composite laminates under uniaxial loading[J]. Composite Structures, 2015, 132: 440-450. [7] 朱俊, 吴维清, 欧阳佳斯, 等. 面外波纹对复合材料层合板弹性性能的影响[J]. 复合材料学报, 2016, 33(9):1981-1988.ZHU Jun, WU Weiqing, OUYANG Jiasi, et al. Influence of out-of-plane waviness on elastic properties of composite laminates[J]. Acta Materiae Compositae Sinica,2016,33(9):1981-1988(in Chinese). [8] 欧阳佳斯, 倪爱清, 朱俊, 等. 均一波纹单向复合材料板的力学性能研究[J]. 玻璃钢/复合材料, 2016(3):38-43.OUYANG Jiasi, NI Aiqing, ZHU Jun, et al. The mechanical behavior of unidirectional composite laminates[J]. Fiber Reinforced Plastics/Composites,2016(3):38-43(in Chinese). [9] 吴维清, 朱俊, 王继辉, 等. 纤维波纹对复合材料层合板刚度影响研究[J]. 玻璃钢/复合材料, 2015(12):41-47.WU Weiqing, ZHU Jun, WANG Jihui, et al. Effects of fiber waviness on the stiffness of composite laminates[J]. Fiber Reinforced Plastics/Composites,2015(12):41-47(in Chinese). [10] 曾文浩, 何鹏, 刘菲, 等. 含纤维波纹缺陷复合材料层合板的损伤分析[J]. 复合材料学报, 2019, 36(2):330-336.ZENG Wenhao, HE Peng, LIU Fei, et al. Damage analysis for composite laminate with fiber waviness[J]. Acta Materiae Compositae Sinica,2019,36(2):330-336(in Chinese). [11] GARNICH M R, KARAMI G. Finite element micromechanics for stiffness and strength of wavy fiber composites[J]. Journal of Composite Material, 2004, 38(4): 273–292. [12] XIE N, SMITH R, MUKHOPADHYA S. A numerical study on the influence of composite wrinkle defect geometry on compressive strength[J]. Materials and Design,2018,140:7-20. doi: 10.1016/j.matdes.2017.11.034 [13] 郑亦媚, 程吉, 王轩, 等. 褶皱层数对玻璃纤维层合板拉伸性能的影响[J]. 兵器材料科学与工程, 2021, 44(1):104-110.ZHENG Yimei, CHENG Ji, WANG Xuan, et al. Effect of different wrinkled layers on tensile properties of glass fiber reinforced laminates[J]. Ordnance Material Science and Engineering,2021,44(1):104-110(in Chinese). [14] BARBERO E J, BARBERO J C. Determination of material properties for progressive damage analysis of carbon/epoxy laminates[J]. Mechanics of Advanced Materials and Structures,2019,26:938-947. doi: 10.1080/15376494.2018.1430281 [15] 于晓东, 胡海晓, 贾欲明. 褶皱缺陷影响L型层合板失效行为: 实验和数值研究[J]. 复合材料学报, 2020, 37(8):1932-1943.YU Xiaodong, HU Haixiao, JIA Yuming, et al. Impact of wrinkle defects on failure behavior of L-shaped laminates: Experimental and numerical study[J]. Acta Materiae Compositae Sinica,2020,37(8):1932-1943(in Chinese). [16] WANG Y, ZHU S, LI H, et al. Experimental and numerical study on the compressive failure of composite laminates with fiber waviness defects[J]. Polymers,2021,13:3204. doi: 10.3390/polym13193204 [17] OMAIREY S L, DUNNING P D, SRIRAMULA S. Development of an ABAQUS plugin tool for periodic RVE homogenization[J]. Engineering with Computers,2019,35:567-577. doi: 10.1007/s00366-018-0616-4 [18] HU H, CAO D, CAO Z, et al. Experimental and numerical investigations of wrinkle effect on failure behavior of curved composite laminates[J]. Composite Structures, 2021, 261: 113541. -
下载:
点击查看大图
计量
- 文章访问数: 1028
- HTML全文浏览量: 783
- PDF下载量: 76
- 被引次数: 0
