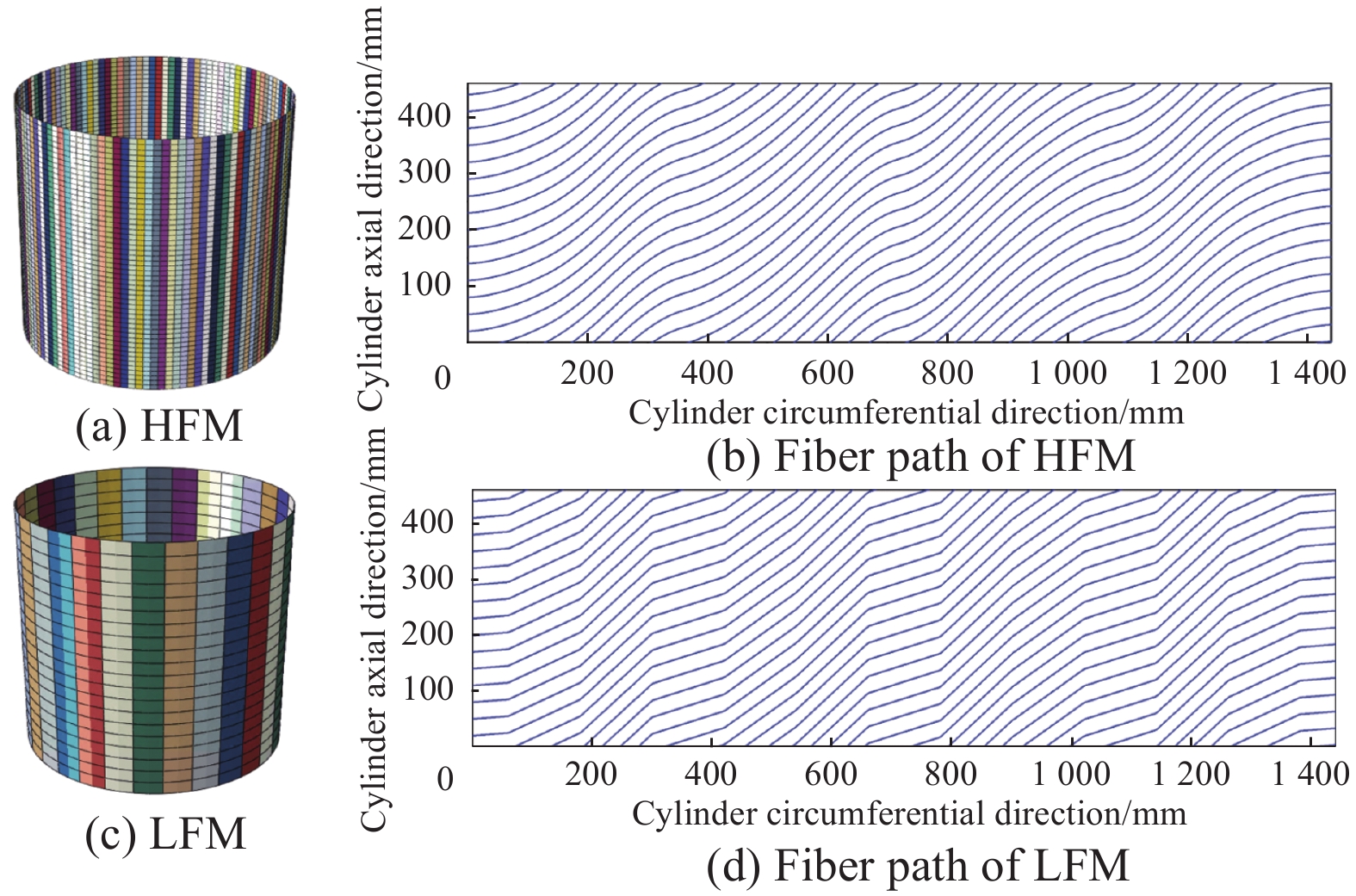
Variable-fidelity transfer learning model for efficient buckling analysis of variable stiffness composite cylindrical shells
-
摘要: 相较于传统直线铺层设计的复合材料筒壳结构，变刚度复合材料筒壳结构通过曲线纤维路径铺层，可以极大地增加复合材料的设计空间，进而获得更优的抗屈曲能力。为了准确描述曲线纤维路径，需要针对变刚度复合材料筒壳建立精细有限元模型，因此对屈曲分析和优化效率带来了较大的挑战。本论文以变刚度复合材料筒壳结构的线性屈曲及后屈曲承载力快速预测为目标，提出了一种变保真度迁移学习模型的构建方法。首先，针对变刚度复合材料筒壳结构建立合适的高保真度、低保真度模型；然后，基于大量低保真度样本数据作为源域样本集建立并训练深度神经网络，得到预训练模型；最后，以少量高保真度样本数据作为目标域样本集对最后一层神经网络参数进行微调，训练得到变保真度迁移学习模型。变刚度复合材料筒壳线性屈曲和后屈曲算例结果表明，在达到相同的预测精度水平时，变保真度迁移学习模型比直接采用高保真度样本数据构建的代理模型分别节约了47.7%和62.3%的计算成本，验证了提出方法的高效率优势。同时，与基于桥函数构建的变保真度代理模型和Co-Kriging进行比较，所提出方法在不同高保真度、低保真度样本数据组合下均具有更优精度，验证了提出方法的高精度优势。Abstract: Compared with the traditional design method of composite cylindrical shells with straight fiber laminate, variable stiffness composite cylindrical shells can greatly increase the design space of composite material and thus achieve higher buckling loads by means of the curved fiber laminate. To describe the curved fiber path precisely, it is necessary to establish high-fidelity detailed finite element model for variable stiffness composite cylindrical shells. Therefore, it brings great challenges to the efficiency of buckling analysis and optimization of variable stiffness composite cylindrical shells. In this paper, a variable-fidelity transfer learning model was proposed for the fast prediction of linear buckling load and post-buckling load of variable stiffness composite cylindrical shells. Firstly, the appropriate high-fidelity model and low-fidelity model of variable stiffness composite cylindrical shells were constructed. Then, the deep neural network was established and trained with a large number of low-fidelity samples as the source dataset, and the pre-trained model was obtained. Finally, the last layer was retained by fine-tuning with a small number of high-fidelity samples as the target dataset, and the variable-fidelity transfer learning model was constructed after the retraining on the pre-trained model. The example results of linear buckling and post-buckling load prediction of variable stiffness composite cylindrical shells indicate that, the computational cost of variable-fidelity transfer learning model can reduce by 47.7% and 62.3% than surrogates built by the high-fidelity samples directly when achieving similar prediction accuracy, showing the advantage of high prediction efficiency of the proposed method. Besides, compared with the variable-fidelity surrogate models built by the bridge function and Co-Kriging, the proposed method shows the best prediction accuracy with different combinations of high-fidelity and low-fidelity samples, which demonstrates the advantage of high prediction accuracy of the proposed method.
-
强韧、轻质复合多级结构材料在能源储存转化、环境治理、生物医学及航天等战略领域的应用越来越受关注[1-4]，其中二维多级层状结构材料独特的电子限域效应赋予这类材料独特的物理、化学性质及丰富的科学内涵，在众多的领域都有重要的应用前景，特别是电子器件、光电器件等方面[5-6]。但人工合成材料不能像天然材料(贝壳、骨骼等)一样通过大量的相互作用对结构基元进行精准的调控，以致各结构基元在受力时应力不能有效传递导致材料断裂，影响力学性质、进而限制材料的应用[7-10]。
受自然界启发，研究工作者发展了大量具有强韧力学性能的二维层状结构材料，通常采取的方案是将高强度的无机纳米片与高柔性的有机聚合物通过层-层(LBL)组装、真空抽滤组装、空气诱导组装、冰模板等方法复合，得到类贝壳珍珠层的“砖-泥”结构[11-13]。如Shin等[14]将还原石墨烯氧化物(RGOF)与碳纳米管(SWNT)复合，用RGOF-SWNT复合体填充聚乙烯醇(PVA)，获得了具有强韧性的RGOF-SWNT-PVA复合膜材料。Cao等[15]鉴于电磁屏蔽材料对厚度与力学性能的需要，选择Ti3C2Tx (MXene)与纤维素纳米纤维(CNF)为功能基元通过真空抽滤自组装的方法得到了高电磁屏蔽效率的复合膜材料，同时保证了材料的强度和韧性。Yoo等[16]通过静电组装氮化硼(BNNS)与明胶获得机械强度媲美人体骨密质的复合膜，且表现出优异的生物相容性，有望应用于组织工程与骨内植入领域。Woo等[17]利用交联剂(CA) 将片层氧化石墨烯(GO)通过化学键相连，形成仿贝壳结构的GO/CA层状复合薄膜，由于GO之间强大的共价键网络，复合薄膜表现出优异的力学性能，在航空航天、电子保护器、渗透膜等领域有潜在应用。过去研究者们采用纳米填充质增强聚合物薄膜的工作在拉伸强度上都有明显的提升，但断裂伸长率却变化不大甚至有所降低，导致复合薄膜的韧性提升被限制。究其原因在于结构基元之间可作为牺牲性成键的相互作用力较少，也将其归结为应力传递效率较低。综上所述，发展一种普适性的复合膜增强增韧方法仍然具有一定的挑战性[18-20]。
利用聚乙烯亚胺(PEI)修饰过后的纤维素纳米晶(PCNC)与蒙脱土纳米片(MMT)静电自组装得到MMT-PCNC组装体，将其分散到PVA水溶液中并搅拌均匀，随后倒入培养皿中利用溶剂蒸发法成膜。得到的MMT-PCNC/PVA复合膜拉伸强度与断裂伸长率同步增加，性能平衡。此法提高了材料的应力传递效率，有效增加了复合膜的拉伸强度；同时利用多重弱相互作用实现了断裂强度、断裂伸长率以及韧性的同步提升。
1. 实验材料及方法
1.1 原材料
蒙脱土粉末购买于浙江丰虹新材料有限公司，棉浆浆板购买于河北中国纸业公司，浓硫酸(98%)购买于北京化学试剂厂，聚乙烯醇(PVA，醇解度为87%~89%，AR)在阿拉丁上海有限公司购买，聚乙烯亚胺(PEI，Mw=10000，AR)购买于阿达玛斯试剂有限公司。实验过程中所用到的试剂都未经任何处理。
1.2 PCNC的制备
晶态纳米纤维素(Cellulose nanocrystals, CNC)悬浮液制备方法参考文献[21]制得，PEI修饰的CNC具体制备过程如下：取10 mL PEI水溶液(3.0wt%)加入到5 mL CNC悬浮液(3.0wt%)中，室温下连续搅拌1 h，随后用浓盐酸将混合溶液pH调到1.3以增强CNC与PEI之间的离子相互作用。继续搅拌十分钟后，将混合溶液高速离心20 min(13000 r/min)，弃去上层清液，将沉淀用超纯水(18.2 MΩ·cm，Mill-Q Corp)洗涤三次，去掉未发生相互作用的游离PEI聚合物。最后再将沉淀加入水中，超声30 min重新分散，8000 r/min低速离心8 min，去掉CNC聚集体，收集上层清液得到单分散的CNC悬浮液，浓度为1.0wt%，命名为PCNC。
1.3 MMT悬浮液的制备
将2 g MMT粉末加入到500 mL超纯水中，连续溶解搅拌一周后静置72 h，收集上层清液得到剥离充分的MMT纳米片备用，浓度为0.2wt%。
1.4 MMT-PCNC组装体的制备
将MMT (0.2wt%)悬浮溶液逐滴加入到PCNC (1.0wt%)悬浮溶液中，持续搅拌24 h，得到MMT-PCNC组装体悬浮液，控制MMT与PCNC的质量比分别为1∶1、1∶2、1∶4。得到不同MMT、PCNC质量比的组装体，分别命名为1MMT-1PCNC、1MMT-2PCNC、1MMT-4PCNC，具体组成见表1。
1.5 MMT-PCNC/PVA复合膜的制备
将上述组装体悬浮液加入到PVA水溶液中，搅拌过夜，使组装体分散均匀，组装体含量控制为PVA质量的20%。将混合液置于直径为60 mm的聚乙烯塑料培养皿中室温干燥2天，得到柔性MMT-PCNC/PVA复合膜。
表 1 蒙脱土-纤维素纳米晶(MMT-PCNC)组装体的组成Table 1. Compositions of the montmorillonite-cellulose nanocrystal (MMT-PCNC) assembliesSample 1MMT-1PCNC 1MMT-2PCNC 1MMT-4PCNC Composition Mass fraction Mass ratio Mass ratio Mass ratio MMT 0.2% 1 1 1 PCNC 1.0% 1 2 4 1.6 样品性能及表征
SEM结果在JSM-6510A上获得，样品用导电胶粘贴于样品台表面，喷金60 s，电压设置为20 kV，电流设置为86 μA[22]。TEM结果在FEI Tecnai G2S-Twin上获得，样品滴于200 mm铜网上，室温晾干，加速电压为200 kV。溶液的Zeta电势常温下在Malvern Zetasizer Nano-ZS90上获得，样品浓度为0.1wt%[23]。傅立叶红外光谱(FTIR)测试在Bruker IFS 66v/S红外光谱仪上进行，扫描范围为 400~4000 cm−1，扫描速度为4 cm−1，制样过程参考文献[24]，样品采用KBr压片，测试前置于60℃烘箱干燥1 h。力学性能测试在万能材料测试机(Instron 5944, UK)上进行，所用传感器为2000 N，拉伸速率为5 mm·min−1，夹距为10 mm。所有的样品测试均在常温下进行，样品长度约为50 mm、宽度约为5 mm、厚度约为0.3 mm，每组样品重复测量3次。
2. 结果与讨论
2.1 MMT-PCNC组装体的形成过程
图1(a)~1(c)分别为CNC、PCNC、MMT悬浮溶液置于室温下一个月之后的光学照片，从图中可以看到溶液基本都呈乳白色，无沉淀产生，说明所有的溶液均非常稳定。CNC由硫酸水解制得，表面含有磺酸基，带负电，Zeta电势分析得到CNC的电势值为−21.3 mV。加入PEI对其进行修饰后，在其表面引入了氨基，带正电，Zeta电势分析显示，PEI修饰过后的CNC (PCNC)电势值由−21.3 mV增加到35.4 mV。对MMT进行Zeta电势表征得到，其电势值为−31.3 mV，与PCNC所带电荷相反，数值匹配，为静电相互作用驱动形成MMT-PCNC组装体提供了必要的条件(图1(d))。
对修饰前后的CNC进行TEM表征，可以看到PCNC仍为棒状结构，长度与直径相比较CNC有明显的增加(图2)。经过统计，平均长度由164 nm增加到206 nm，平均直径由22 nm增加到26 nm (图3)，说明PEI聚电解质已成功包覆于CNC的表面，形成PCNC。
![]()
图 1 显示悬浮液稳定性的光学照片: (a) 晶态纳米纤维素(CNC)；(b) PCNC；(c) MMT；(d) 相应悬浮液的Zeta电势值Figure 1. Photographs showing the stability of suspensions: (a) Cellulose nanocrystals (CNC); (b) PCNC; (c) MMT; (d) Zeta potentials of corresponding suspensions![]()
图 2 CNC修饰前后的形貌表征: CNC (a)和PCNC (b)的TEM图像Figure 2. Morphology before and after CNC modification: TEM images of pristine CNC (a) and PCNC (b)![]()
图 3 CNC (a)和PCNC (b)的长度分布图; CNC (c)和PCNC (d)的直径分布图Figure 3. Diameter distributions of CNC (a) and PCNC (b); Length distributions of CNC (c) and PCNC (d)将不同质量比的PCNC与MMT悬浮液混合，得到不同质量比的MMT-PCNC组装体悬浮液(1MMT-2PCNC、1MMT-1PCNC、1MMT-4PCNC)，组装后发现三组不同配比的溶液均不同程度的发生聚沉，出现明显颗粒感，说明两种结构基元发生相互作用，且组装以后尺寸变大。以1MMT-2PCNC组装体为例，分别对组装前后的结构基元(MMT纳米片、PCNC纳米棒和1MMT-2PCNC组装体)进行TEM表征(图4)。如图4(a)所示，MMT呈分散、不规则片层结构，横向尺寸大约有100~1000 nm。在1MMT-2PCNC组装体的TEM图像中可以看到PCNC纳米棒附着于MMT纳米片的表面及边缘上，取向各异，在MMT表面上形成一层稠密的PCNC层(图4(c)及插图)。组装体的尺寸取决于原始MMT与PCNC的尺寸。
![]()
图 4 MMT-PCNC组装体的形成过程: MMT (a)、PCNC (b)和1MMT-2PCNC组装体 (c)的TEM图像Figure 4. Tracking the formation of MMT-PCNC: TEM images of MMT (a), PCNC (b) and supramolecular ensemble of 1MMT-2PCNC (c)2.2 MMT-PCNC/PVA复合膜的形貌
图5为不同MMT-PCNC/PVA复合膜的SEM图像。如图所示，纯PVA薄膜截面致密，无有序结构。而由不同MMT、PCNC质量比的组装体所构成的复合膜均具有明显层状结构，为干燥成膜过程中MMT纳米片组装而成，由图5(c)、5(d)可见，层间具有明显PCNC附着(图中箭头所指)，表明由于较强的静电相互作用，使MMT-PCNC组装体在成膜过程中得以有效保存，但由于层间还存在PVA分子，使得PCNC被部分覆盖，电镜下只观察到棒状尖端。图5(b)中，由于PCNC含量相对较少，未在截面处观察到明显PCNC结构。
![]()
图 5 不同MMT-PCNC/PVA复合膜的SEM图像: (a) 纯PVA薄膜；(b) 1MMT-1PCNC/PVA；(c) 1MMT-2PCNC/PVA；(d) 1MMT-4PCNC/PVAFigure 5. SEM images of MMT-PCNC/PVA: (a) Pure PVA film; (b) 1MMT-1PCNC/PVA; (c) 1MMT-2PCNC/PVA; (d) 1MMT-4PCNC/PVA2.3 MMT-PCNC/PVA复合膜的力学性能
对复合膜及纯PVA膜进行力学性能的测试(图6)，测试结果总结于表2中。如图6所示，相比较纯PVA膜，MMT-PCNC作为增强质对复合膜的力学性能产生正影响，拉伸强度、断裂伸长率、韧性都不同程度的增加，杨氏模量均略有下降；其中，1MMT-1PCNC/PVA复合膜拉伸强度增长最为明显，为196%；1MMT-2PCNC/PVA复合膜的断裂伸长率、韧性增加最为明显(图6插图)，分别为175%和900%。这些均得益于复合膜内部的弱相互作用[25-26]：MMT与PCNC之间通过静电组装，使组装体内部存在大量静电相互作用；MMT-PCNC组装体表面携带羟基和氨基，易与PVA分子侧基羟基形成氢键，增加了组装体与基体的界面相互作用[27]。这些弱相互作用在复合膜受到拉伸时首先断裂，充当牺牲性成键，使复合膜内部的MMT、PCNC产生滑移，断裂伸长率提高，进而提升韧性[28-29]；其次，附着于MMT表面的PCNC通过静电与氢键相互作用将MMT与PVA连接，形成具有砖-泥结构的片层复合膜，当应力作用于膜上时，可在这些刚性结构基元之间有效传递，从而增加复合膜的强度。二者协同作用使材料单位应变时所需的应力减小，即刚性减小。
![]()
图 6 不同MMT和PCNC质量比的组装体复合膜力学性能Figure 6. Mechanical properties of hybrid films with varying weight ratio of MMT and PCNC表 2 MMT-PCNC/PVA复合膜的力学性能Table 2. Mechanical properties of the MMT-PCNC/PVA hybrid filmsHybrid films of filler/PVA Elongation-at-break
/%Tensile strength
/MPaYoung’s modulus
/MPaToughness
/(MJ·m−3)PVA 28±3 26±3 101±13 3±1 1MMT-1PCNC/PVA 50±4 77±7 97±6 27±6 1MMT-2PCNC/PVA 77±4 63±8 100±3 30±9 1MMT-4PCNC/PVA 42±2 54±9 92±7 13±2 为了证实氢键的存在，对1MMT-2PCNC/PVA复合膜、纯PVA膜以及冷冻干燥的纯CNC进行了红外分析。如图7所示，在3000~3500 cm−1区域内出现的透过峰归属于PVA羟基伸缩振动，对比几个样品—OH的透过峰峰位可以发现，1MMT-2PCNC/PVA复合膜的峰位较纯CNC和PVA向低波数方向移动。过去研究表明[30-33]，氢键的形成是导致羟基峰位发生偏移的主要原因。PEI修饰的CNC表面存在大量的氨基，MMT表面也有一定量的羟基，因此组装体1MMT-2PCNC与PVA之间势必会形成氢键，导致羟基峰发生移动。在1025 cm−1、1733 cm−1以及2945 cm−1波数处出现的峰分别归属于PVA的C—OH、C=O以及脂肪质C—H的伸缩振动[34]，在1256 cm−1、1370 cm−1以及1446 cm−1处出现的峰分别归属于PVA的C—H、O—H的弯曲振动以及C—H非平面摇摆振动[35-37]。CNC在3382 cm−1、2915 cm−1、1649 cm−1及1055 cm−1处分别出现明显的透过峰，其中3382 cm−1、2915 cm−1归属于CNC的O—H与C—H的伸缩振动，1649 cm−1归属于CNC吡喃糖环的伸缩振动，而1055 cm−1归属于CNC中吸附了水分子的羟基伸缩振动[38]。
![]()
图 7 通过纯PVA、CNC以及1MMT-2PCNC/PVA复合膜的FTIR图谱显示1MMT-2PCNC和PVA之间氢键的形成Figure 7. FTIR spectra of CNC, PVA and hybrid films of 1MMT-2PCNC/PVA showing multiple hydrogen bonds between 1MMT-2PCNC and PVA为了进一步研究自组装体改善聚合物薄膜力学性能的强韧化机制，人为破坏薄膜表面造成裂纹进行SEM测试。如图8(a)所示，裂纹均非直线传播，而是随着主裂纹的扩展出现了明显的微裂纹偏转(图8(a)中白色折线)，说明MMT、PCNC、PVA之间存在强烈的相互作用，与之前分析一致。存在于片层之间的PCNC通过静电以及氢键作用将PVA和MMT相互连接，当应力施加时充当桥连剂，阻止裂纹扩展，随着应力增大，裂纹将沿着纳米纤维发生偏转，直至最终断裂，这一过程将导致裂纹路径增大，消耗更多的能量，实现复合材料的强韧化[26, 39]。
![]()
图 8 1MMT-2PCNC/PVA复合膜断裂形态的SEM图像和断裂示意图：(a) 断裂过程中裂纹扩展的SEM图像(白色折线表示裂纹偏转)；(b) 断裂模型示意图Figure 8. SEM image of fracture morphologies of 1MMT-2PCNC/PVA hybrid films and the proposed fracture model: (a) SEM image of crack propagation occurred during fracture (White line indicate crack propagation); (b) Schematic illustration of the fracture model通过观察组装体中MMT与PCNC的不同比例组装体对薄膜力学性能的影响发现，随着组装体中PCNC含量的增加，拉伸强度逐渐减弱，当MMT与PCNC比例为1∶4时，断裂伸长率也明显下降(图6)，原因可能是随着PCNC含量的增加，组装体质量加重，更易发生聚沉，且当其分布于聚合物基体中时，不易分散均匀，导致复合膜力学性能下降[40-41]。
3. 结 论
(1) 组装体1MMT(蒙脱土)-1PCNC(纤维素纳米晶)和1MMT-2PCNC对PVA(聚乙烯醇)力学性能增强较为明显，拉伸强度分别增加196%、142%；断裂伸长率增幅分别为79%、175%；韧性增幅分别为800%、900%；复合膜杨氏模量略有下降。
(2) MMT-PCNC/PVA复合膜中存在多种弱相互作用(静电相互作用、氢键)，给应力的传递提供了有效的途径，同时引起裂纹偏转，达到消耗能量的目的，使其在拉伸强度提高的同时断裂伸长率也得到提升。本文提出了一种新的合理设计构筑先进复合纳米材料的思路，即用自组装的方法制备组装体，并利用组装体中存在的大量弱相互作用提升聚合物薄膜的力学性质，从而拓展其应用。
-
![]()
![]()
图 2 变保真度迁移学习模型建立方法
Figure 2. Establishment method of variable-fidelity transfer learning model
HFM—High-fidelity model; LFM—Low-fidelity model; n, m—Number of LFM and HFM sample points
![]()
图 3 变刚度复合材料筒壳纤维路径 (a) 与设计变量(b) 示意图
Figure 3. Schematic diagram of fiber path (a) and design variables (b) of variable stiffness composite cylindrical shell
α—Circumferential azimuth angle; θ—Fiber orientation angle; M—Moment; T1-T7—Continuous design variables
![]()
图 4 变刚度复合材料筒壳高保真度模型(HFM) ((a), (b)) 与低保真度模型(LFM) ((c), (d)) 示意图
Figure 4. Schematic diagram of high-fidelity model (HFM) ((a), (b)) and low-fidelity model (LFM) ((c), (d)) for variable stiffness composite cylindrical shell
![]()
图 5 变刚度复合材料筒壳HFM (a) 与LFM (b) 一阶屈曲模态
Figure 5. First buckling modes of HFM (a) and LFM (b) for variable stiffness composite cylindrical shell
Mcr—Critical buckling moment
![]()
图 6 变刚度复合材料筒壳算例各代理模型回归系数 R2 (a) 和相对均方根误差RRMSE (b) 预测精度
Figure 6. Prediction accuracy of regression square R2 (a) and relative root mean square error
RRMSE (b) for various surrogates of variable stiffness composite cylindrical shell ![]()
图 7 含缺陷变刚度复合材料筒壳HFM (a)、LFM (b) 与缺陷分布示意图 (c)
Figure 7. Schematic diagram of HFM (a), LFM (b) and imperfection distribution (c) of variable-stiffness composite cylindrical shell with imperfection
![]()
图 8 含缺陷变刚度复合材料筒壳HFM (a) 与LFM (b) 屈曲模态
Figure 8. Buckling modes of HFM (a) and LFM (b) for variable stiffness composite cylindrical shell with imperfection
Pco—Collapse load
![]()
图 9 含缺陷变刚度复合材料筒壳算例各代理模型 R2 (a) 和 RRMSE (b) 预测精度
Figure 9. Prediction accuracy of R2 (a) and RRMSE (b) for various surrogates of variable stiffness composite cylindrical shell with imperfection
表 1 变刚度复合材料筒壳材料属性
Table 1 Material properties of variable stiffness composite cylindrical shell
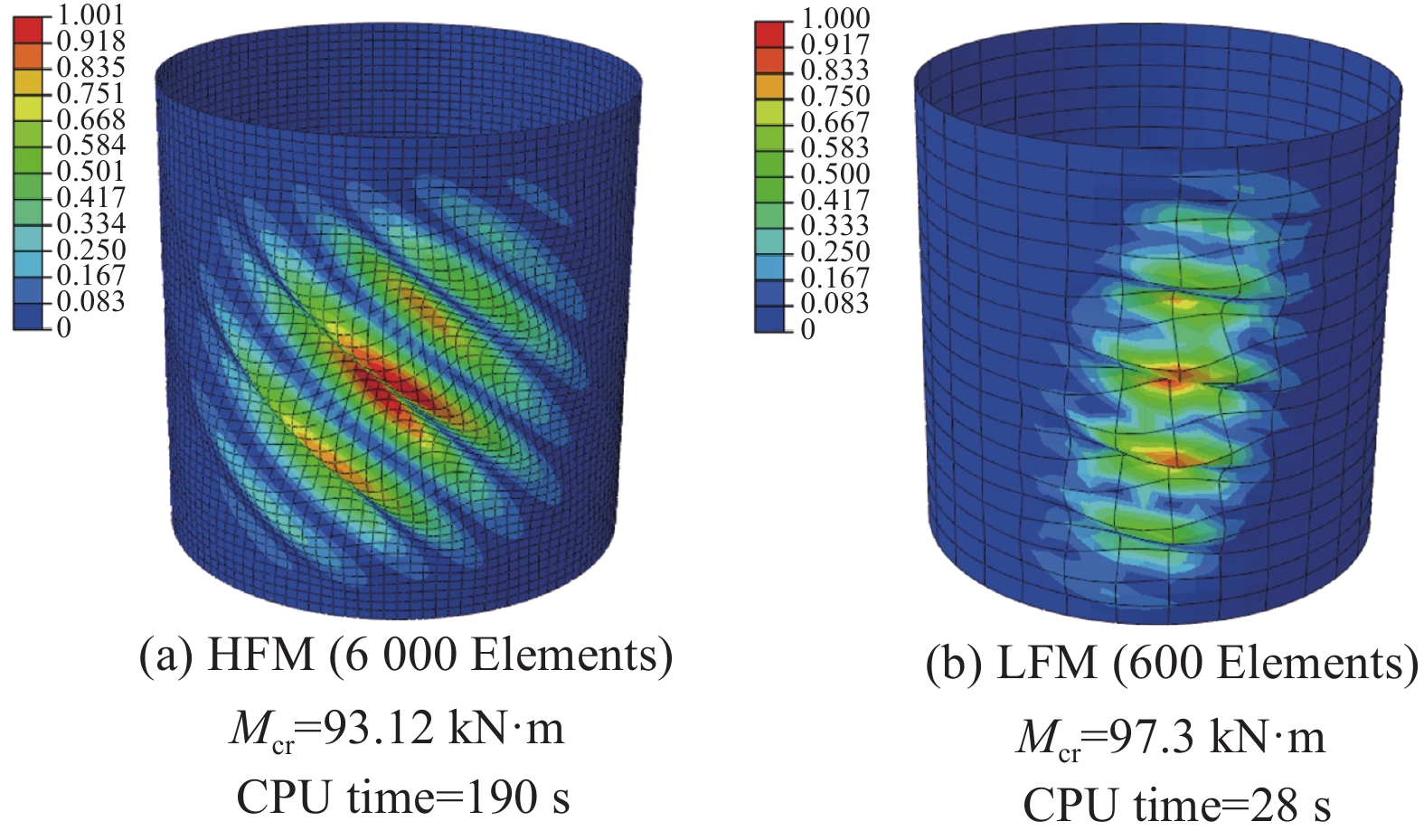
Property Value E1/GPa 134 E2/GPa 7.71 E3/GPa 7.71 G12/GPa 4.31 G13/GPa 4.31 G23/GPa 2.76 v12 0.301 v13 0.301 v23 0.396 Thickness of each ply/mm 0.127 Notes: E1, E2, E3—Modulus of elasticity of direction 1, direction 2 and direction 3, respectively; G12, G13, G23—Shear elasticity of direction 12, direction 13 and direction 23, respectively; ν12, ν13, ν23—Poisson's ratio of direction 12, direction 13 and direction 23, respectively. 
下载: 导出CSV
表 2 不同网格数量下变刚度复合材料筒壳结构屈曲载荷与计算耗时
Table 2 Buckling load and computational cost with different number of elements of variable stiffness composite cylindrical shell
Number of elements Buckling load/(kN∙m) CPU time/s 600 97.30 28 840 95.46 37 1000 94.46 45 1800 93.78 65 3600 93.22 120 6000 93.12 190 7500 93.09 230 — 93.10 (Rouhi[40]) — Note: CPU—Central processing unit.
下载: 导出CSV
表 3 变刚度复合材料筒壳算例各代理模型预测精度与计算耗时
Table 3 Prediction accuracy and computational cost of various surrogates for variable stiffness composite cylindrical shell
Kriging RBF-VFSM Co-Kriging Proposed method CPU time/min R2 RRMSE R2 RRMSE R2 RRMSE R2 RRMSE 30HFM 0.272 0.849 — — — — — — 95.0 90HFM 0.691 0.548 — — — — — — 285.0 180HFM 0.850 0.380 — — — — — — 570.0 200LFM 0.549 0.661 — — — — — — 93.3 300LFM 0.542 0.668 — — — — — — 140.0 30HFM+300LFM — — 0.529 0.691 0.780 0.481 0.823 0.418 235.0 50HFM+300LFM — — 0.661 0.580 0.838 0.393 0.871 0.360 298.3 Notes: R2—Regression square; RRMSE—Relative root mean square error; RBF-VFSM—BRF-based variable-fidelity surrogate model.
下载: 导出CSV
表 4 含缺陷变刚度复合材料筒壳材料属性
Table 4 Material properties of variable stiffness composite cylindrical shell with imperfection
Property Value E1/GPa 124.4 E2/GPa 8.69 E3/GPa 8.69 G12/GPa 4.83 G13/GPa 4.83 G23/GPa 4.83 v 0.347 Thickness of each ply/mm 0.124
下载: 导出CSV
表 5 不同网格数量下含缺陷变刚度复合材料筒壳后屈曲载荷与计算耗时
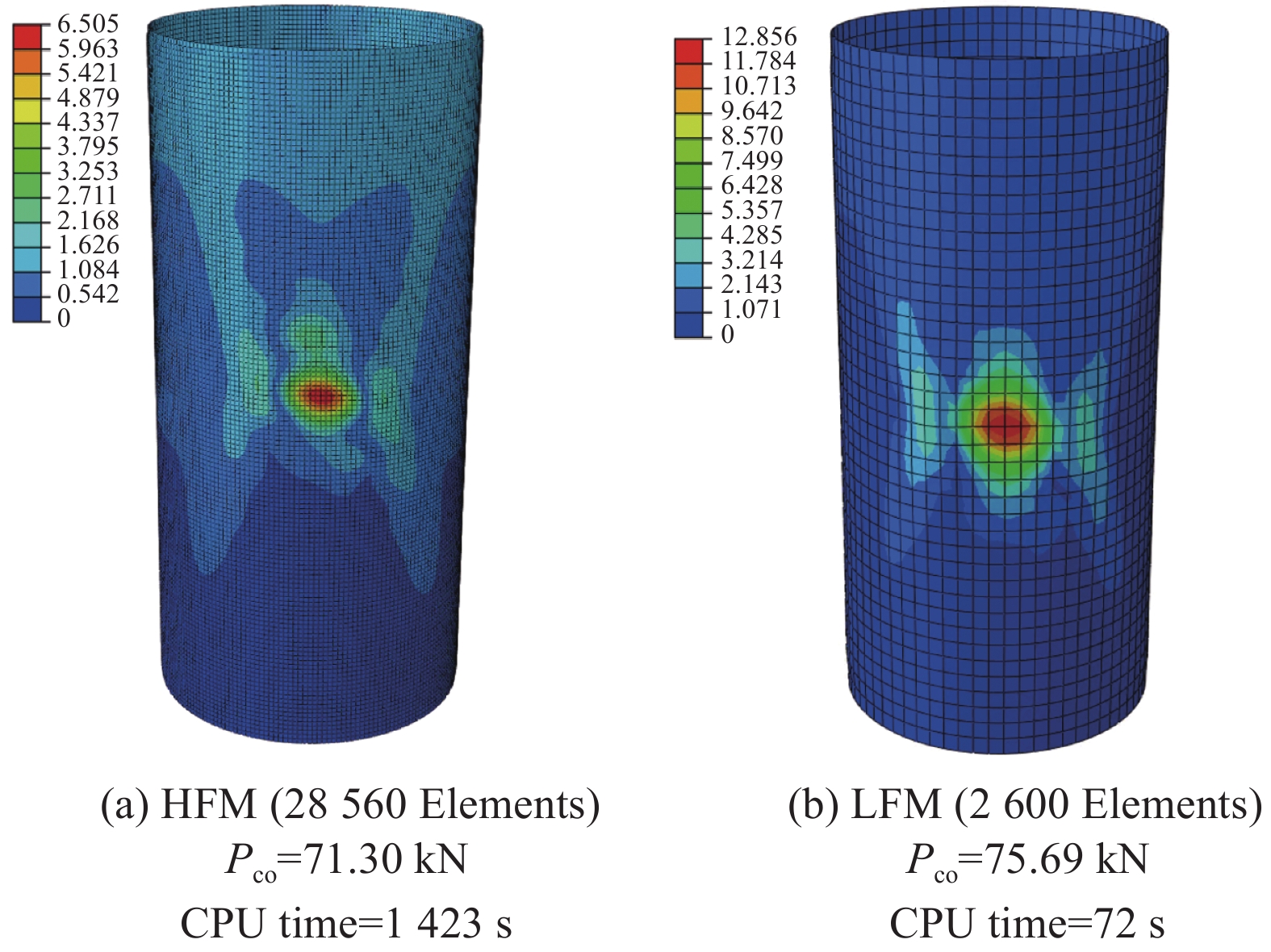
Table 5 Post-buckling load and computational cost with different number of elements for variable stiffness composite cylindrical shell with imperfection
Number of elements Buckling load/(kN∙m) CPU time/s 2600 75.69 72 4000 75.27 104 7000 74.98 176 9600 74.65 267 15000 73.96 505 21600 73.50 895 28560 71.30 1423 — 71.20 [42] —
下载: 导出CSV
表 6 含缺陷变刚度复合材料筒壳算例各代理模型预测精度与计算耗时
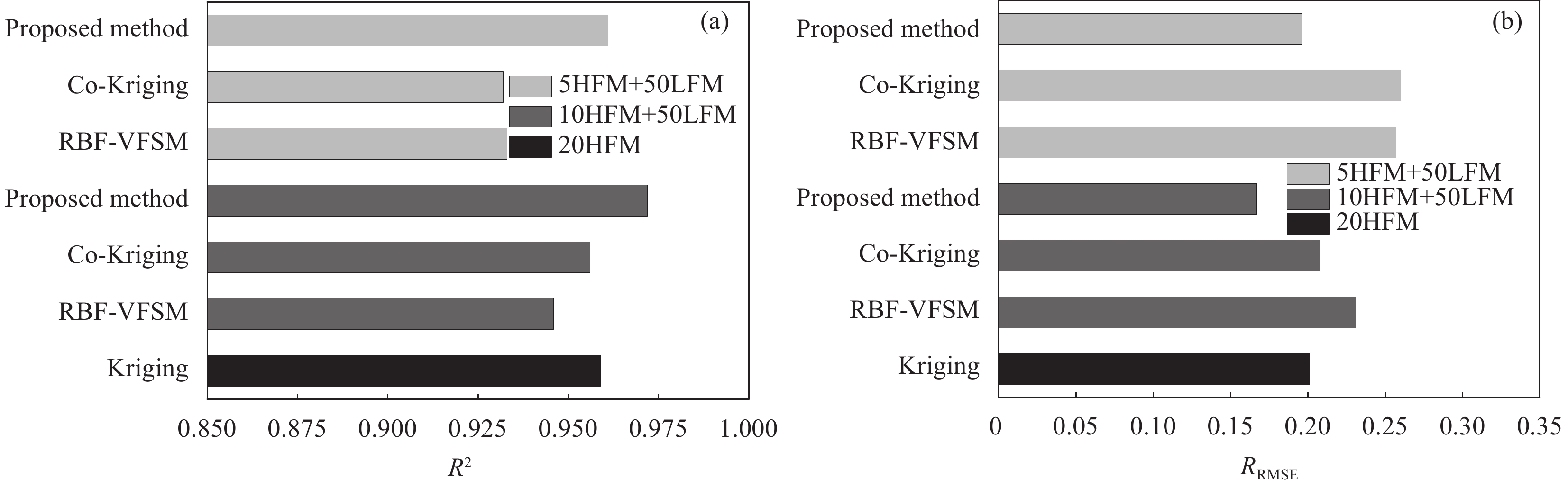
Table 6 Prediction accuracy and computational cost of various surrogates for variable stiffness composite cylindrical shell with imperfection
Kriging RBF-VFSM Co-Kriging Proposed method CPU time/min R2 RRMSE R2 RRMSE R2 RRMSE R2 RRMSE 5HFM 0.744 0.503 — — — — — — 118.6 10HFM 0.915 0.290 — — — — — — 237.2 20HFM 0.959 0.201 — — — — — — 474.3 50LFM 0.843 0.395 — — — — — — 60.0 100LFM 0.842 0.395 — — — — — — 120.0 5HFM+50LFM — — 0.933 0.257 0.932 0.260 0.961 0.196 178.6 10HFM+50LFM — — 0.946 0.231 0.956 0.208 0.972 0.167 297.2
下载: 导出CSV
-
[1] CROFT K, LESSARD L, PASINI D, et al. Experimental study of the effect of automated fiber placement induced defects on performance of composite laminates[J]. Composites Part A: Applied Science and Manufacturing,2011,42(5):484-491. DOI: 10.1016/j.compositesa.2011.01.007
[2] 董安琪, 肇研, 赵新青. 自动铺放工艺制备罐外固化复合材料的力学行为[J]. 复合材料学报, 2018, 35(5):1095-1104. DONG Anqi, ZHAO Yan, ZHAO Xinqing. Mechanical performance of out-of-autoclave composites manufactured by automated fiber placement[J]. Acta Materiae Compositae Sinica,2018,35(5):1095-1104(in Chinese).
[3] GÜRDAL Z, TATTING B F, WU C K. Variable stiffness composite panels: Effects of stiffness variation on the in-plane and buckling response[J]. Composites Part A: Applied Science and Manufacturing,2008,39(5):911-922. DOI: 10.1016/j.compositesa.2007.11.015
[4] SETOODEH S, ABDALLA M M, IJSSELMUIDEN S T, et al. Design of variable-stiffness composite panels for maxi-mum buckling load[J]. Composite Structures,2009,87(1):109-117. DOI: 10.1016/j.compstruct.2008.01.008
[5] 孔斌, 顾杰斐, 陈普会, 等. 变刚度复合材料结构的设计、制造与分析[J]. 复合材料学报, 2017, 34(10):2121-2133. KONG Bin, GU Jiefei, CHEN Puhui, et al. Design, manufacture and analysis of variable-stiffness composite structures[J]. Acta Materiae Compositae Sinica,2017,34(10):2121-2133(in Chinese).
[6] Rolls-Royce Engine Company. Step inside our factory of the future[EB]. (2021-01-14) [2021-04-22]. Website: www.rolls-royce.com/media/ourstories/discover/2020/step-inside-our-actory-of-the-future.aspx.
[7] QUEIPO N V, HAFTKA R T, SHYY W, et al. Surrogate-based analysis and optimization[J]. Progress in Aerospace Sciences,2005,41(1):1-28. DOI: 10.1016/j.paerosci.2005.02.001
[8] FORRESTER A I J, KEANE A J. Recent advances in surrogate-based optimization[J]. Progress in Aerospace Sciences,2009,45(1):50-79.
[9] 王莉, 刘国强, 肖迎春. 基于代理模型的复合材料加筋壁板分层损伤定量监测方法[J]. 复合材料学报, 2020, 37(2): 302-308. WANG Li, LIU Guoqiang, XIAO Yingchun. Quantitative monitoring method for delamination damage of stiffened composite panel based on surrogate model[J]. Acta Mater-iae Compositae Sinica, 2020, 37(2): 302-308(in Chinese).
[10] 魏星, 陈莘莘, 张洪峰, 等. 基于代理模型的指数型功能梯度板固有频率优化[J]. 复合材料学报, 2019, 36(8):1886-1892. WEI Xing, CHEN Shenshen, ZHANG Hongfeng, et al. Frequency optimization of power-law functionally graded plates via surrogate model[J]. Acta Materiae Compositae Sinica,2019,36(8):1886-1892(in Chinese).
[11] NIK M A, FAYAZBAKHSH K, PASINI D, et al. A compara-tive study of metamodeling methods for the design opti-mization of variable stiffness composites[J]. Composite Structures,2014,107:494-501. DOI: 10.1016/j.compstruct.2013.08.023
[12] ROUHI M, GHAYOOR H, HOA S V, et al. Computational efficiency and accuracy of multi-step design optimization method for variable stiffness composite structures[J]. Thin-Walled Structures,2017,113:136-143. DOI: 10.1016/j.tws.2017.01.019
[13] PASSOS A G, LUERSEN M A, STEEVES C A. Optimal curved fibre orientations of a composite panel with cutout for improved buckling load using the efficient global optimization algorithm[J]. Engineering Optimization,2017,49(8):1354-1372. DOI: 10.1080/0305215X.2016.1256052
[14] YE F, WANG H, LI G. Variable stiffness composite material design by using support vector regression assisted efficient global optimization method[J]. Structural and Multidisciplinary Optimization,2017,56(1):203-219. DOI: 10.1007/s00158-017-1658-8
[15] HAN Z H, GÖRTZ S. Hierarchical kriging model for variable-fidelity surrogate modeling[J]. AIAA Journal,2012,50(9):1885-1896. DOI: 10.2514/1.J051354
[16] HAN Z H, ZIMMERMAN N, GÖRTZ S. Alternative cokriging method for variable-fidelity surrogate modeling[J]. AIAA Journal,2012,50(5):1205-1210. DOI: 10.2514/1.J051243
[17] ZHOU Q, SHAO X, JIANG P, et al. An active learning metamodeling approach by sequentially exploiting difference information from variable-fidelity models[J]. Advanced Engineering Informatics,2016,30(3):283-297. DOI: 10.1016/j.aei.2016.04.004
[18] ZHOU Q, SHAO X, JIANG P, et al. An active learning variable-fidelity metamodelling approach based on ensemble of metamodels and objective-oriented sequential sampling[J]. Journal of Engineering Design,2016,27(4/6):205-231. DOI: 10.1080/09544828.2015.1135236
[19] TIAN K, LI Z, MA X, et al. Toward the robust establishment of variable-fidelity surrogate models for hierarchical stiffened shells by two-step adaptive updating approach[J]. Structural and Multidisciplinary Optimization,2020,61:1515-1528. DOI: 10.1007/s00158-019-02432-2
[20] GUO Q, HANG J, WANG S, et al. Buckling optimization of variable stiffness composite cylinders by using multi-fide-lity surrogate models[J]. Thin-Walled Structures,2020,156:107014. DOI: 10.1016/j.tws.2020.107014
[21] GUO Q, HANG J, WANG S, et al. Design optimization of variable stiffness composites by using multi-fidelity surro-gate models[J]. Structural and Multidisciplinary Optimization,2021,63(1):439-461. DOI: 10.1007/s00158-020-02684-3
[22] 郑君. 基于变可信度近似的设计优化关键技术研究[D]. 武汉: 华中科技大学, 2014. ZHENG Jun. Research on key technology of variable-fide-lity approximation-based design optimization[D]. Wuhan: Huazhong University of Science and Technology, 2014(in Chinese).
[23] CHOI S, ALONSO J J, KROO I M. Two-level multifidelity design optimization studies for supersonic jets[J]. Journal of Aircraft,2009,46(3):776-790. DOI: 10.2514/1.34362
[24] HAFTKA R T. Combining global and local approximations[J]. AIAA Journal,1991,29(9):1523-1525. DOI: 10.2514/3.10768
[25] GISELLE F G M, PARK C, KIM N H, et al. Issues in deciding whether to use multifidelity surrogates[J]. AIAA Journal,2019,57(5):1-16.
[26] HAN Z H, ZIMMERMANN R, GORETZ S. A new cokriging method for variable-fidelity surrogate modeling of aerodynamic data[C]. Florida: 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 2010: 1225.
[27] 韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11):3197-3225. HAN Zhonghua. Kriging surrogate model and its application to design optimization: A review of recent progress[J]. Acta Aeronautica et Astronautica Sinica,2016,37(11):3197-3225(in Chinese).
[28] SINGH K, KAPANIA R K. Accelerated optimization of curvilinearly stiffened panels using deep learning[J]. Thin-Walled Structures,2021,161(3):107418.
[29] ZHANG X, XIE F, JI T, et al. Multi-fidelity deep neural network surrogate model for aerodynamic shape optimization[J]. Computer Methods in Applied Mechanics and Engineering,2021,373:113485. DOI: 10.1016/j.cma.2020.113485
[30] 李妙玲, 仝军锋, 赵红霞. 基于遗传算法和神经网络的C/C复合材料等温CVI工艺参数优化模型[J]. 复合材料学报, 2016, 33(11):2666-2673. LI Miaoling, TONG Junfeng, ZHAO Hongxia. Optimization model for isothermal CVI process parameters for C/C composites based on genetic algorithm and neural network[J]. Acta Materiae Compositae Sinica,2016,33(11):2666-2673(in Chinese).
[31] 王春红, 赵玲, 白肃跃, 等. 改进Back Propagation神经网络预测麻纤维/UP复合材料的界面性能[J]. 复合材料学报, 2015, 32(6):1696-1702. WANG Chunhong, ZHAO Ling, BAI Suyue, et al. Prediction of bast fiber/UP composites interfacial property by improved back propagation neural network[J]. Acta Materiae Compositae Sinica,2015,32(6):1696-1702(in Chinese).
[32] SHU L, JIANG P, SONG X, et al. Novel approach for selecting low-fidelity scale factor in multifidelity meta-modeling[J]. AIAA Journal,2019,57(12):5320-5330. DOI: 10.2514/1.J057989
[33] PARK C, HAFTKA R T, KIM N H. Low-fidelity scale factor improves bayesian multi-fidelity prediction by reducing bumpiness of discrepancy function[J]. Structural and Multidisciplinary Optimization,2018,58(2):399-414. DOI: 10.1007/s00158-018-2031-2
[34] COURBARIAUX M, BENGIO Y, DAVID J P. Binaryconnect: Training deep neural networks with binary weights during propagations[J]. Advances in Neural Information Processing Systems, 2015, 28: 3123-3131.
[35] ZOU D, CAO Y, ZHOU D, et al. Gradient descent optimizes over-parameterized deep ReLU networks[J]. Machine Learning,2019,109(6):1-26.
[36] PAN S J, YANG Q. A survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2009, 22(10): 1345-1359.
[37] TIAN K, LI Z, HUANG L, et al. Enhanced variable-fidelity surrogate-based optimization framework by gaussian process regression and fuzzy clustering[J]. Computer Methods in Applied Mechanics and Engineering,2020,366:113045. DOI: 10.1016/j.cma.2020.113045
[38] LU J, BEHBOOD V, HAO P, et al. Transfer learning using computational intelligence: A survey[J]. Knowledge-Based Systems,2015,80:14-23. DOI: 10.1016/j.knosys.2015.01.010
[39] JANG H, PLIS S M, CALHOUN V D, et al. Task-specific feature extraction and classification of fMRI volumes using a deep neural network initialized with a deep belief network: Evaluation using sensorimotor tasks[J]. Neuro Image,2017,145:314-328. DOI: 10.1016/j.neuroimage.2016.04.003
[40] ROUHI M, GHAYOOR H, HOA S V, et al. Effect of structural parameters on design of variable-stiffness composite cylinders made by fiber steering[J]. Composite Structures,2014,118(1):472-481.
[41] LI Z C, TIAN K, LI H Q, et al. A competitive variable-fidelity surrogate-assisted CMA-ES algorithm using data mining techniques[J]. Aerospace Science and Technology, 2021, 119: 107084.
[42] WHITE S C, WEAVER P M, WU K C. Post-buckling analyses of variable-stiffness composite cylinders in axial compression[J]. Composite Structures,2015,123:190-203. DOI: 10.1016/j.compstruct.2014.12.013
[43] WU K, TATTING B K, SMITH B H, et al. Design and manufacturing of tow-steered composite shells using fiber placement[C]. California: 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2009: 1-18.
-
计量
- 文章访问数: 1773
- HTML全文浏览量: 631
- PDF下载量: 161
