Investigation on effect of crack geometry on permeability of fiber/concrete based on fractal theory
-
摘要: 分形维数可以表征裂缝形态，能够用来分析混凝土裂缝断面的粗糙程度。裂缝形态对开裂混凝土的渗透性有重要影响，为研究这种影响，利用劈裂试验获得不同宽度的裂缝，使用不同的纤维种类，并设置多种纤维掺量，得到粗糙程度不同的裂缝断面，通过水渗透试验测量不同裂缝宽度时混凝土的渗透系数。采用激光扫描仪扫描裂缝断面并重构3D断面几何形态，采用立方体覆盖法计算断面分形维数。采用分形维数将实测裂缝宽度和有效裂缝宽度联系起来，联立达西定律和泊肃叶定律建立开裂混凝土渗透系数和分形维数的函数关系。结果表明：使用相同的网格划分法，分形维数随着纤维掺量的增加而增大；渗透系数随着纤维掺量的增加而减小；函数关系式中分形维数的指数绝对值和修正系数都随裂缝宽度增加而减小。Abstract: Fractal dimension can characterize the geometric properties of cracks and can be used to analyze the rupture surface roughness of concrete. Crack geometry plays an important role in water permeability of cracked concrete. In order to investigate this effect, a series of crack widths were obtained through feedback controlled splitting test and a variety of rupture surface roughness was achieved by adjusting fiber types and fiber contents. Water permeability test was performed to measure the permeability coefficients under different crack widths. 3D rupture surface was re-established after scanning the real rupture surface via laser scanning device. The fractal dimension was calculated based on the cube covering method. The function between fractal dimension and water permeability coefficient was established by correlating the measured crack width and the effective crack width and solving Darcy’s Law and Poiseuille’s Law simultaneously. The results show that fractal dimension calculated by the same meshing approach increases as the fiber content increases. Water permeability coefficient reduces with the rise of the fiber content. The results also demonstrate that both the absolute value of the exponential of fractal dimension and the correction factor in the function decreases with crack width increasing.
-
Key words:
- fractal dimension /
- permeability /
- rupture surface roughness /
- cracked concrete /
- fiber
-
图 6 纤维/混凝土渗透系数-裂缝宽度曲线
Figure 6. Permeability coefficient-crack width curves of fiber/concrete
图 9 纤维/混凝土渗透系数与分形维数的关系(裂缝宽度
$ w$ =150 μm)Figure 9. Relationship between permeability coefficient and fractal dimension of fiber/concrete (Crack width
$ w$ =150 μm)
图 10 纤维/混凝土影响因子与实测裂缝宽度的关系
Figure 10. Relationship between influence factor andmeasured crack width of fiber/concrete
图 11 修正系数φ与实测裂缝宽度的关系
Figure 11. Relationship between correction factor φ and measured crack width
表 1 钢纤维(SF)性能参数
Table 1. Performance parameters of steel fiber (SF)
Type Form Length/mm Diameter/mm Aspect ratio Elastic modulus/GPa Tensile strength/MPa Pieces/kg RC-65/35 Hooked 35 0.55 65 200 1 345 14 500 
下载: 导出CSV
表 2 聚丙烯长纤维(PP)性能参数
Table 2. Performance parameters of macro polypropylene fiber (PP)
Type Tensile strength/MPa Elastic modulus/GPa Elongation/% Length/mm Diameter/mm Pieces/kg WK-8 490 5 <30 30 0.4 96 000
下载: 导出CSV
表 3 混凝土配比
Table 3. Mix proportion of concrete
kg·m–3 Cement Fly ash Coarse aggregate (5–10 mm) Fine aggregate (0–5 mm) Water Superplasticizer 390 155 848 822 272.5 7.6
下载: 导出CSV
表 4 纤维/混凝土试件编号、纤维掺量和根数
Table 4. Specimen number, fiber contents and pieces of fiber/concrete
Specimen number SF content/vol% SF/(pieces·m–3) PP fiber content/vol% PP fiber/(pieces·m–3) PP0.5/concrete 0 0 0.50 432 000 PP0.75/concrete 0 0 0.75 648 000 SF0.5/concrete 0.50 569 125 0 0 SF0.75/concrete 0.75 853 688 0 0 SF1/concrete 1.00 1 138 250 0 0 SF0.5-PP0.5/concrete 0.50 569 125 0.50 432 000 SF0.5-PP0.75/concrete 0.50 569 125 0.75 648 000 SF0.75-PP0.5/concrete 0.75 853 688 0.50 432 000
下载: 导出CSV
表 5 不同裂缝宽度下纤维/混凝土的渗透系数k
Table 5. Permeability coefficients k of fiber/concrete under different crack width
μm·s–1 Specimen 100 μm 125 μm 150 μm 175 μm 200 μm 225 μm 250 μm PP0.5/concrete 8.50 13.00 19.90 28.40 39.90 49.30 59.80 PP0.75/concrete 5.50 7.65 10.80 15.40 21.90 30.00 41.80 SF0.5/concrete 0.27 0.70 1.84 2.68 3.88 5.91 8.96 SF0.75/concrete 0.07 0.26 0.97 1.73 3.18 4.94 7.54 SF1/concrete 0.01 0.05 0.23 0.70 1.59 3.17 6.19 SF0.5-PP0.5/concrete 0.19 0.47 1.20 1.92 3.03 4.94 7.75 SF0.5-PP0.75/concrete 0.04 0.12 0.35 0.61 1.38 2.50 4.57 SF0.75-PP0.5/concrete 0.01 0.04 0.10 0.38 0.42 1.78 2.39
下载: 导出CSV
表 6 纤维/混凝土裂缝断面分形维数
Table 6. Fractal dimensions of rupture surface of fiber/concrete
Specimen Fractal
dimension DChange in
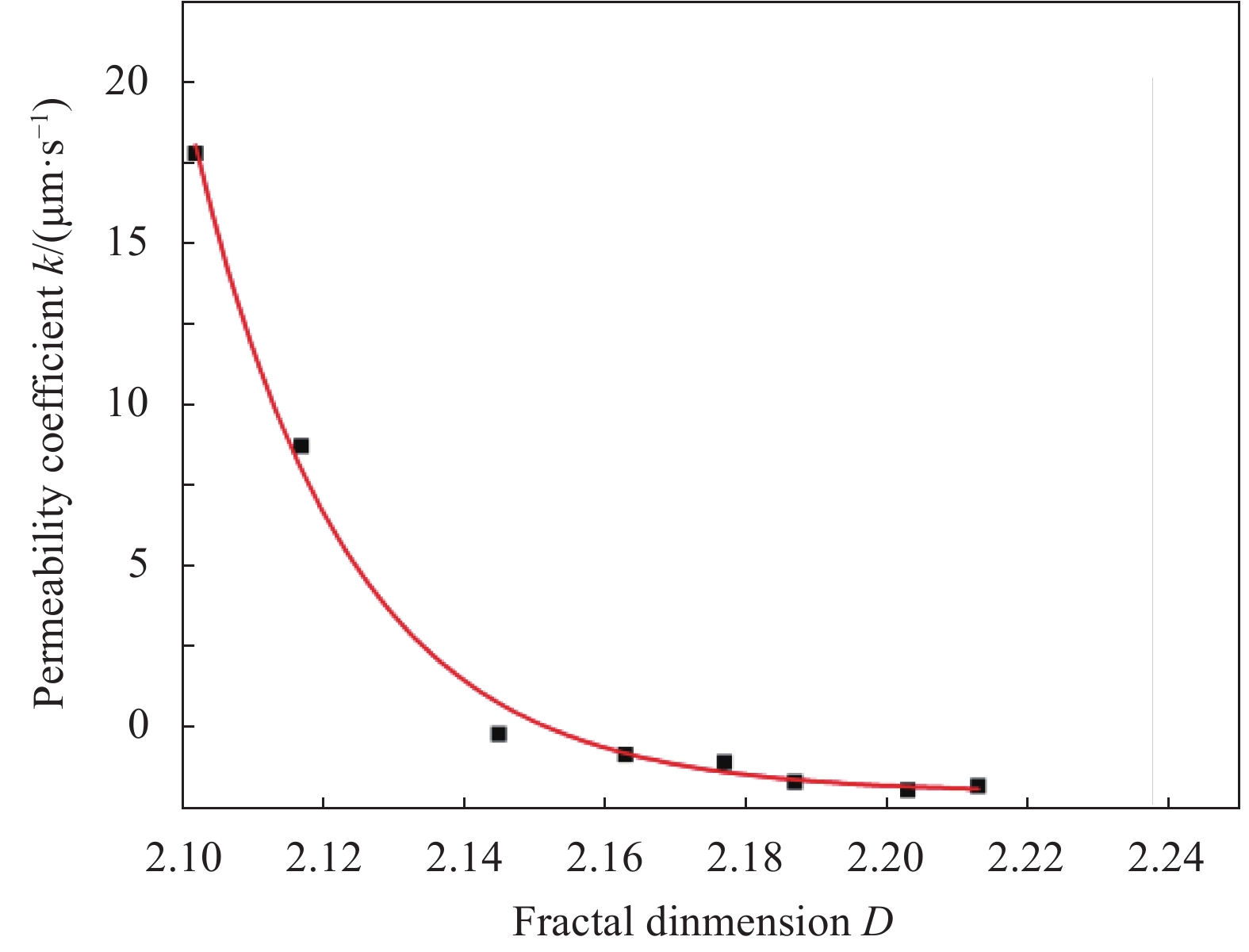
decimal of D/%PP0.5/concrete 2.114 0 PP0.75/concrete 2.129 13.16 SF0.5/concrete 2.157 37.72 SF0.75/concrete 2.189 65.79 SF1/concrete 2.225 97.37 SF0.5-PP0.5/concrete 2.175 53.51 SF0.5-PP0.75/ concrete 2.199 74.56 SF0.75-PP0.5/ concrete 2.215 88.60
下载: 导出CSV
表 7 不同裂缝宽度条件下纤维/混凝土渗透系数与分形维数的关系
Table 7. Relationship between permeability coefficient and fractal dimension of fiber/concrete under different crack width
Crack width/μm R2 Relationship 100 0.95 $k = 1.05 {\rm{1}}{0^{37}} {D^{ - 123}}$ 125 0.98 $k = 6.99 {\rm{1}}{0^{2{\rm{9}}}} {D^{ - 101}}$ 150 0.99 $k = {\rm{1}}.25 {\rm{1}}{0^{{\rm{29}}}} {D^{ - 98}}$ 175 0.99 $k = {\rm{4}}.24 {\rm{1}}{0^{{\rm{28}}}} {D^{ - 96}}$ 200 0.99 $k = {\rm{5}}.97 {\rm{1}}{0^{{\rm{27}}}} {D^{ - 93}}$ 225 0.98 $k = {\rm{3}}.04 {\rm{1}}{0^{{\rm{23}}}} {D^{ - 79}}$ 250 0.97 $k = {\rm{2}}.36 {\rm{1}}{0^{{\rm{20}}}} {D^{ - 69}}$
下载: 导出CSV
表 8 不同实测裂缝宽度的lgφ
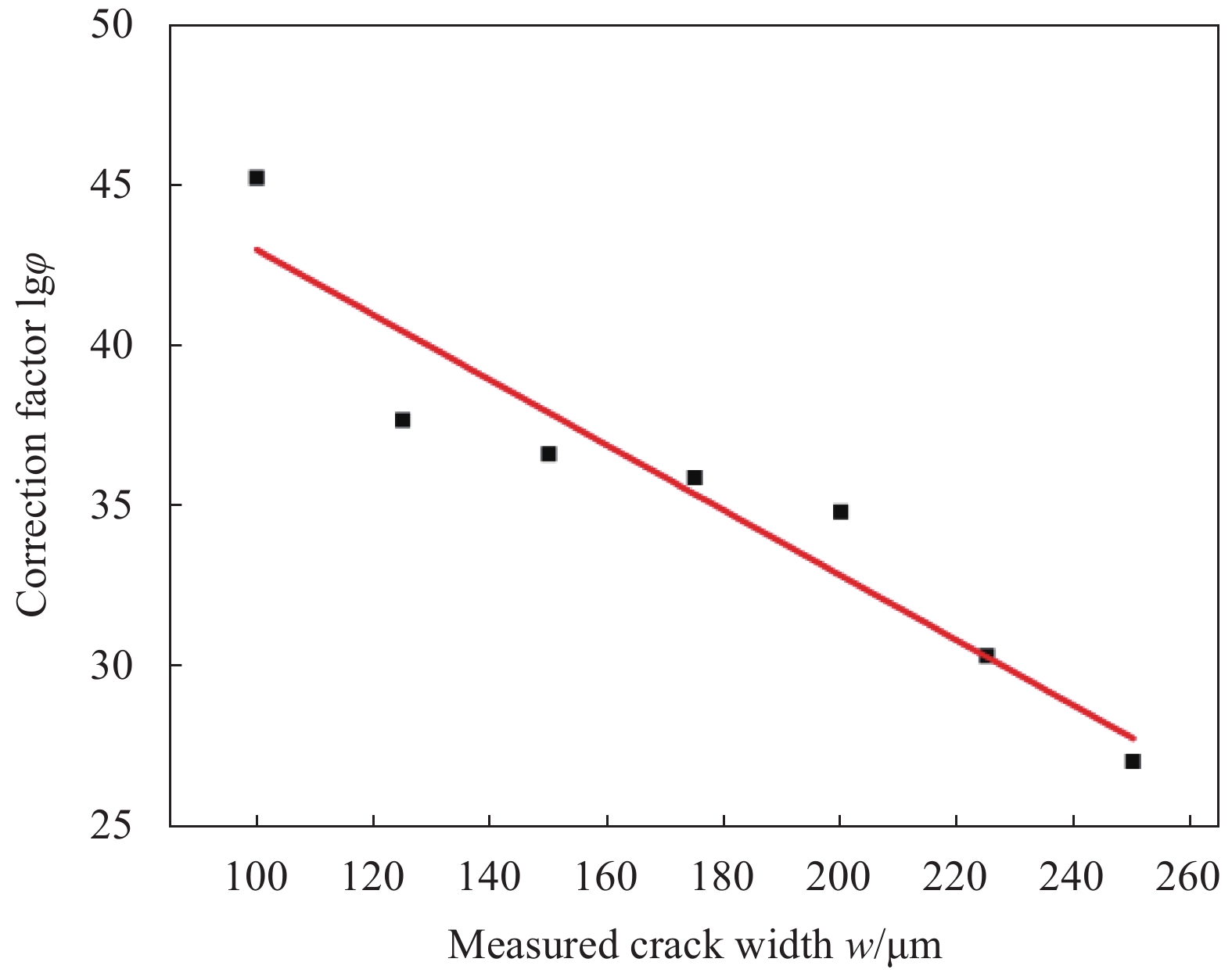
Table 8. lgφ for different measured crack width
Measured crack width $ w$/μm lgφ 100 45.12 125 37.56 150 36.49 175 35.75 200 34.67 225 30.17 250 26.88
下载: 导出CSV
-
[1] HOSEIINI M, BINDIGANAVILE V, BANTHIA N. The effect of mechanical stress on permeability of concrete: A review[J]. Cement and Concrete Composites,2009,31(4):213-220. doi: 10.1016/j.cemconcomp.2009.02.003 [2] LIU Q F, FENG G L, XIA J, et al. Ionic transport features in concrete composites containing various shaped aggregates: A numerical study[J]. Composite Structures,2018,183:371-380. doi: 10.1016/j.compstruct.2017.03.088 [3] SHIN K J, BAE W, CHOI S W, et al. Parameters influencing water permeability coefficient of cracked concrete specimens[J]. Construction and Building Materials,2017,151:907-915. doi: 10.1016/j.conbuildmat.2017.06.093 [4] LI X, LI D, XU Y. Modeling the effects of microcracks on water permeability of concrete using 3D discrete crack network[J]. Composite Structures,2019,210:262-273. doi: 10.1016/j.compstruct.2018.11.034 [5] DESMETTRE C, CHARRON J P. Water permeability of reinforced concrete with and without fiber subjected to staticand constant tensile loading[J]. Cement and Concrete Research,2012,42(7):945-952. doi: 10.1016/j.cemconres.2012.03.014 [6] BANTHIA N, BHARGAVA A. Permeability of stressed concrete and role of fiber reinforcement[J]. ACI Materials Journal,2007,104(1):70-76. [7] CHOINSKA M, KHELIDJ A, CHATZIGEORGIOU G, et al. Effects and interactions of temperature and stress-level related damage on permeability of concrete[J]. Cement and Concrete Research,2007,37(1):79-88. doi: 10.1016/j.cemconres.2006.09.015 [8] WANG K, JANSEN D C, SHAH S P, et al. Permeability study of cracked concrete[J]. Cement and Concrete Research,1997,27(3):381-393. doi: 10.1016/S0008-8846(97)00031-8 [9] YI S T, HYUN T Y, KIM J K. The effects of hydraulic pressure and crack width on water permeability of penetration crack-induced concrete[J]. Construction and Building Materials,2011,25(5):2576-2583. doi: 10.1016/j.conbuildmat.2010.11.107 [10] DING Y, LI D, ZHANG Y. Quantitative analysis of macro steel fiber influence on crack geometry and water permeability of concrete[J]. Construction and Building Materials,2018,187:325-335. [11] PICANDET V, KHELIDJ A, BELLEGOU H. Crack effects on gas and water permeability of concretes[J]. Cement and Concrete Research,2009,39(6):537-547. doi: 10.1016/j.cemconres.2009.03.009 [12] AKHAVAN A, SHAFAATIAN S M H, RAJABIPOUR F. Quantifying the effects of crack width, tortuosity, and roughness on water permeability of cracked mortars[J]. Cement and Concrete Research,2012,42(2):313-320. doi: 10.1016/j.cemconres.2011.10.002 [13] 丁一宁, 李林泽, 曾伟. 纤维对混凝土的损伤、裂缝曲折度及裂缝恢复的影响[J]. 复合材料学报, 2019, 36(10):2439-2447.DING Yining, LI Linze, ZENG Wei. Fibers effects on the concrete damage, crack tortuosity and crack recovery[J]. Acta Materiae Compositae Sinica,2019,36(10):2439-2447(in Chinese). [14] RESTUCCIA L, REGGIO A, FERRO G A, et al. Fractal analysis of crack paths into innovative carbon-based cementitious composites[J]. Theoretical and Applied Fracture Mechanics,2017,90:133-141. doi: 10.1016/j.tafmec.2017.03.016 [15] 殷新龙, 孙洪泉, 薛祯钰, 等. 橡胶混凝土梁裂缝分形理论分析[J]. 土木建筑与环境工程, 2013, 35(s2):157-159.YIN Xinlong, SUN Hongquan, XUE Zhenyu, et al. Study of cracks on rubber concrete beams based on fractal theory[J]. Journal of Civil, Architectural & Environmental Engineering,2013,35(s2):157-159(in Chinese). [16] 蒋赏, 徐港, 赵恬悦. 冻融损伤混凝土梁抗力性能演化的裂缝分形特征[J]. 水电能源科学, 2018, 36(1):124-127.JIANG Shang, XU Gang, ZHAO Tianyue. Fractal characteristics of fracture resistance evolution of concrete beam subjected to freeze-thaw damage[J]. Water Resources and Power,2018,36(1):124-127(in Chinese). [17] ISSA M A, ISSAM A, ISLAM M S, et al. Fractal dimension: A measure of fracture roughness and toughness of concrete[J]. Engineering Fracture Mechanics,2003,70(1):125-137. doi: 10.1016/S0013-7944(02)00019-X [18] 李冬, 丁一宁. 结构型纤维对开裂混凝土渗透性能的影响[J]. 土木工程学报, 2017, 50(10):62-68.LI Dong, DING Yining. Effects of macro fibers on the permeability of cracked concrete[J]. China Civil Engineering Journal,2017,50(10):62-68(in Chinese). [19] 中国工程建设标准化协会. 纤维混凝土试验方法标准: CECS 13∶2009[S]. 北京: 中国计划出版社, 2010.China Association for Engineering Construction Standardization. Standard test methods for fiber reinforced concrete: CECS 13∶2009[S]. Beijiing: China Planning Press, 2010(in Chinese). [20] ZHOU H W, XIE H. Direct estimation of the fractal dimensions of a fracture surface of rock[J]. Surface Review and Letter,2003,10(5):751-762. doi: 10.1142/S0218625X03005591 [21] MANDELBROT B B. The fractal geometry of nature[M]. New York: WH Freeman and Co., 1983. [22] WHITE F M. Fluid mechanics[M]. 9th Edition. New York: McGraw-Hill, 2003. [23] RASTIELLO G, BOULAY C, PONT D S, et al. Real-time water permeability evolution of a localized crack in concrete under loading[J]. Cement and Concrete Research,2014,56:20-28. doi: 10.1016/j.cemconres.2013.09.010 -
下载:
点击查看大图
计量
- 文章访问数: 1753
- HTML全文浏览量: 782
- PDF下载量: 66
- 被引次数: 0
