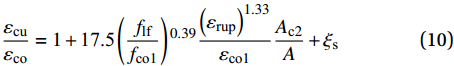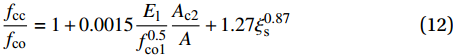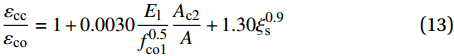钢管混凝土-FRP管海水海砂混凝土组合柱轴压模型

缪坤廷; 魏洋; 朱超; 丁明珉; 郑开启

doi:10.13801/j.cnki.fhclxb.20211206.003

钢管混凝土-FRP管海水海砂混凝土组合柱轴压模型

南京林业大学　土木工程学院，南京 210037

基金项目: 江苏省研究生科研与实践创新计划(KYCX21_0880)；国家自然科学基金(51778300)；江苏省自然科学基金(BK20191390)；江苏省重点研发计划(BE2020703)；江苏省六大人才高峰项目(JZ-017)；江苏省高校“青蓝工程”项目(2020)

详细信息

通讯作者:
魏洋，博士，教授，博士生导师，研究方向为约束混凝土结构　E-mail:wy78@njfu.edu.cn

中图分类号: U445.7
计量
- 文章访问数: 1167
- HTML全文浏览量: 602
- PDF下载量: 82
出版历程
- 收稿日期: 2021-11-01
- 修回日期: 2021-11-18
- 录用日期: 2021-11-29
- 网络出版日期: 2021-12-06
- 刊出日期: 2022-10-31

Model for stress-strain curves of concrete filled steel tube-seawater and sea sand concrete filled FRP tube composite columns under axial load

College of Civil Engineering, Nanjing Forestry University, Nanjing 210037, China

摘要

摘要: 提出一种钢管混凝土-纤维增强复合材料(FRP)管海水海砂混凝土(SWSSC)组合柱新型结构，其由外侧钢管、夹层普通混凝土、内侧FRP管和核心SWSSC构成。在轴向荷载作用下，夹层普通混凝土受到钢管的约束，而核心SWSSC受到钢管和FRP管的共同约束，考虑到两部分混凝土的不同约束机制，在现有的FRP-钢复合管约束混凝土的计算模型的基础上，本文提出了钢管混凝土-FRP管SWSSC组合柱的峰值点和极限点的计算模型；并利用FRP-钢复合管约束混凝土的应力-应变曲线模型，得到了钢管混凝土-FRP管SWSSC组合柱的应力-应变预测曲线；在72个钢管混凝土-FRP管SWSSC组合柱的轴压试验结果的基础上，对建议的模型进行了验证与评估。结果表明，提出的模型可以较好地预测钢管混凝土-FRP管SWSSC组合柱的应力-应变曲线。最后，利用提出的应力-应变曲线模型对钢管混凝土-FRP管SWSSC组合柱的轴压性能进行了参数化分析。
- FRP管 /
- 钢管混凝土柱 /
- 海水海砂混凝土 /
- 单调轴压 /
- 计算模型
Abstract: A novel structure termed as concrete filled steel tube-seawater and sea sand concrete (SWSSC) filled fiber reinforced polymer (FRP) tube composite columns was proposed, which was composed of outer steel tube, sandwiched ordinary concrete, inner FRP tube and core SWSSC. The sandwiched ordinary concrete was confined by the outer steel tube, while the core SWSSC was confined by both steel tube and FRP tube under axial compression. Considering the different confinement mechanism of two kinds of concrete, the calculation models of peak point and ultimate point of concrete filled steel tube-SWSSC filled FRP tube composite columns were proposed based on the existing calculation model of concrete-filled FRP-steel composite tube columns. And the predicted stress-strain curve model was obtained by using the stress-strain curve model of concrete-filled FRP-steel compo-site tube columns. The proposed model was verified and evaluated on the basis of the existing test results. The results show that the proposed model can predict the stress-strain curve of concrete filled steel tube-SWSSC filled FRP tube composite columns well. Finally, based on the proposed stress-strain model, the axial compression behavior of concrete filled steel tube-SWSSC filled FRP tube composite columns with different parameters was analyzed.
- FRP tube /
- concrete-filled steel tube /
- seawater and sea sand concrete /
- monotonic axial compression /
- calculation model

HTML全文

为了综合利用海水海砂混凝土(SWSSC)，发挥钢管混凝土的传统优势，提出了一种钢管混凝土-纤维增强复合材料(FRP)管SWSSC组合柱新型结构，其由外部钢管、夹层普通混凝土、内部FRP管和核心SWSSC构成，即将FRP管约束SWSSC柱设置于钢管混凝土柱截面内部。这种新型结构兼具钢管混凝土^[1-3]及FRP约束混凝土^[4-6]的优势，主要有以下优点：SWSSC的使用，减少了普通混凝土的用量，节约了日益短缺的淡水和河砂资源；内部FRP管的设置保证了SWSSC不会对外部的钢管产生不利影响；夹层中的普通混凝土为实际工程中设置纵向钢筋、梁-柱连结筋等钢构件提供了可能；结构的承载能力、抗震性能和变形能力都有一定的增强；结构内部FRP管布置形式的多样性，可以适应复杂的工程实际，如对于内置多根FRP管结构，其在空间布置上更加灵活多变，FRP管可以根据实际受力需要布置于截面的不同位置，如关键的受压区域，多根FRP管的参数可以相同或变化。

目前，已经有很多学者针对类似结构的力学性能进行了研究，研究主要着眼于结构的轴压承载力^[7-15]。李广悦^[11]对钢-混凝土-碳纤维增强复合材料(CFRP)-混凝土实心组合短柱的轴压性能进行了试验研究，并通过将钢管和FRP管的约束作用统一考虑，得到了钢-混凝土-CFRP-混凝土实心组合短柱的承载力计算公式；Li等^[12]通过有限元分析，对钢管、混凝土和FRP管之间的作用机制进行了分析，并得出了夹层混凝土和核心混凝土分担荷载的计算公式；Li等^[13]认为内置FRP管的钢管混凝土柱的承载力为夹层混凝土在钢管约束下的承载力和核心混凝土在FRP管约束下的承载力叠加而成，并提出了可以预测内置FRP管的钢管混凝土柱全曲线的理论模型；张海镇^[14]提出的承载力计算公式将内置FRP管的钢管混凝土柱的承载力分解为钢管的承载力、夹层混凝土在钢管约束作用下的承载力和核心混凝土在FRP管与钢管共同约束作用下的承载力；陶毅等^[15]利用双剪统一强度理论和Von-Mises屈服准则提出了两种针对内置FRP约束混凝土芯柱的方钢管混凝土的承载力的计算公式，两个模型均能较好地预测该结构的轴压承载力。

在上述研究中，夹层混凝土和核心混凝土往往为同一种混凝土，且内管仅为一根，无法满足复杂的工程实际的要求，并且当前尚无针对内置FRP管约束混凝土的钢管混凝土柱的应力-应变曲线的预测模型。因此，本文基于现有的FRP-钢复合圆管约束混凝土的峰值点和极限点的计算公式^[16]，建立了钢管混凝土-FRP管SWSSC组合柱相应的计算公式，并利用作者提出的针对FRP-钢复合管约束混凝土柱的全曲线模型^[17]，对钢管混凝土-FRP管SWSSC组合柱的应力-应变曲线进行了预测。预测结果与试验结果的对比表明，提出的应力-应变曲线可以较好地预测钢管混凝土-FRP管SWSSC组合柱的应力-应变全曲线，具有良好的精确性和通用性。

1. 机制分析

1.1 基本假定

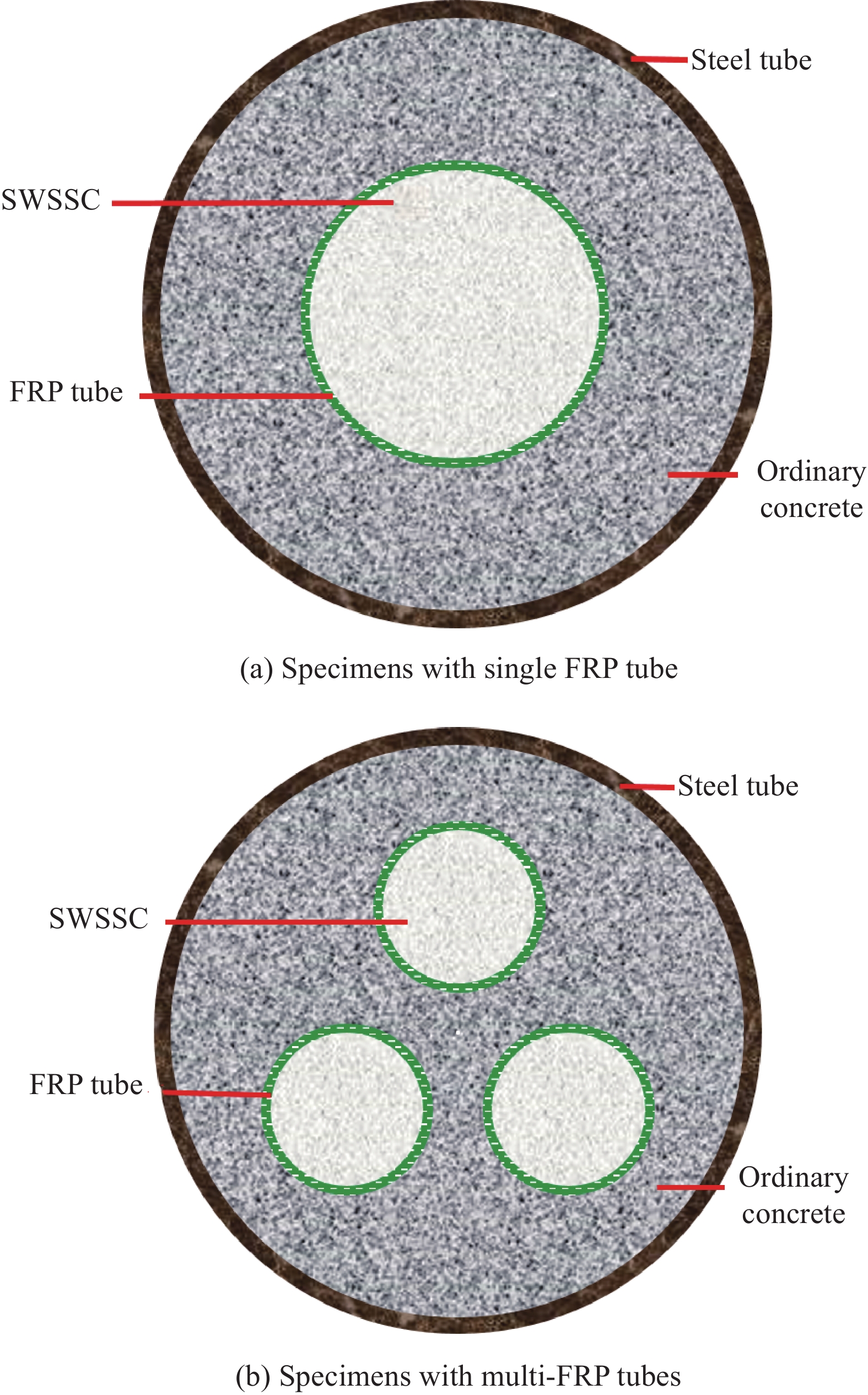
为了将钢管混凝土-FRP管SWSSC组合柱更加广泛地推广于工程实际，使提出的模型既适用于内置单根FRP管的结构(图1(a))，又适用于内置多根FRP管的结构(图1(b))，在计算该结构的应力-应变曲线时提出以下假定：

图 1 钢管混凝土-纤维增强复合材料(FRP)管海水海砂混凝土(SWSSC)组合柱试件示意图

Figure 1. Schematic diagram of concrete filled steel tube-seawater and sea sand concrete (SWSSC) filled fiber reinforced polymer (FRP) tube composite columns

下载: 全尺寸图片幻灯片

本文认为钢管混凝土-FRP管SWSSC组合柱的力学性能与FRP管的位置和数量无关，仅仅与FRP管约束的混凝土的面积有关^[18]。因此，可以通过等面积法将内置数根FRP管约束SWSSC的钢管混凝土柱处理为内置单根FRP管约束SWSSC的钢管混凝土柱，如下式：

${D}_{\text{f}}{{'}}\text=\sqrt{n}{D}_{\text{f}}$

(1)

式中：D_f为原钢管混凝土-FRP管SWSSC组合柱中FRP管的管径；n为原钢管混凝土-FRP管SWSSC组合柱中的FRP管的个数；D_f′为处理后的钢管混凝土-FRP管SWSSC组合柱内部FRP管的管径。

1.2 约束机制分析

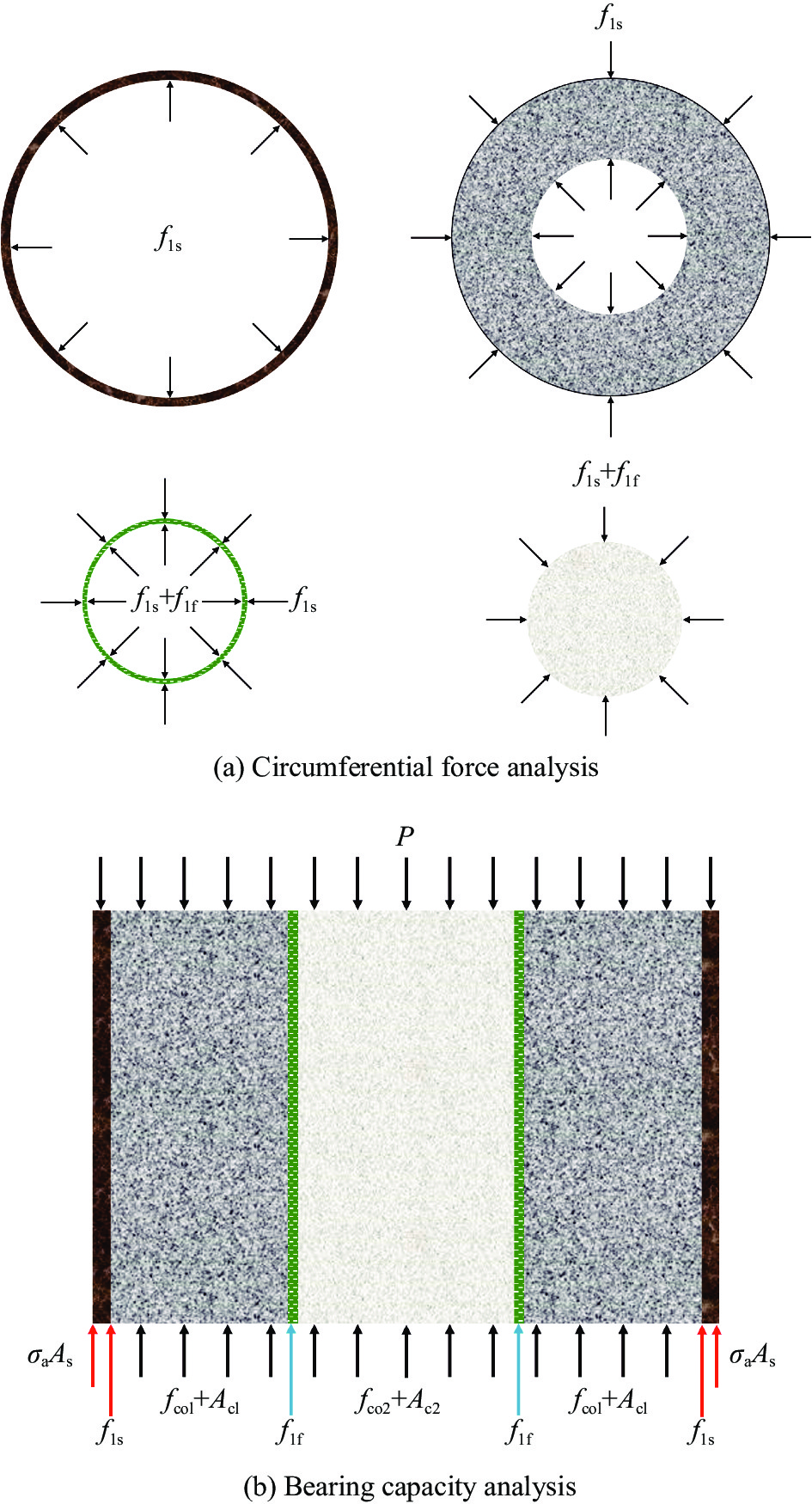
钢管混凝土-FRP管SWSSC组合柱中的钢管、普通混凝土、FRP管和SWSSC之间的相互作用如图2(a)所示。夹层普通混凝土仅受到外侧钢管的侧向约束，而核心SWSSC既受到外侧钢管的侧向约束，又受到FRP管的侧向约束。

图 2 钢管混凝土-FRP管SWSSC组合柱约束机制分析图

Figure 2. Analysis diagram of confinement mechanism for concrete filled steel tube-SWSSC filled FRP tube composite columns

P—Axial load; f_lf—Confining pressure provided by FRP tube; f_ls—Confining pressure provided by the steel tube; σ_a—Axial stress of steel tube; A_s—Sectional area of steel tube; f_co1—Compressive strength of sandwiched concrete; A_c1—Sectional area of sandwiched concrete; f_co2—Compressive strength of core concrete; A_c2—Sectional area of core concrete

下载: 全尺寸图片幻灯片

钢管混凝土-FRP管SWSSC组合柱在轴向荷载作用下的受力状态如图2(b)所示。在轴向荷载的作用下，钢管混凝土-FRP管SWSSC组合柱的极限强度由钢管、普通混凝土和SWSSC构成。其中，钢管在轴向荷载作用下，既可以承受轴向荷载，产生轴向应力σ_a，又可以为核心混凝土和夹层混凝土提供侧向约束力f_ls。而FRP管由于其厚度较小，不承受轴向荷载，仅仅为核心混凝土提供侧向约束力f_lf。

1.3 约束系数

在许多当前钢管约束混凝土的研究中^[19-22]，引入了套箍系数ξ_s，即将钢管的纵向承载与侧向约束综合考虑。能够体现出截面构造和材料性能变化对于钢管约束效果的影响，其计算公式如下：

$\xi_{\mathrm{s}} = \frac{{{A_{\text{s}}}{f_{\text{y}}}}}{{{A_{\text{c}}}{f_{{\text{co}}}}}}$

(2)

式中：A_s和A_c分别为钢管和混凝土的横截面积；f_y为钢管的屈服强度；f_co为素混凝土的轴心抗压强度。

在轴向荷载作用下，FRP管仅对混凝土起到侧向约束的作用，因此FRP有效约束系数ξ_f被引入^[23]表示FRP管的侧向约束作用，其计算公式如下：

$\xi_{\mathrm{f}} = \frac{{{A_{\text{f}}}{f_{\text{f}}}}}{{{A_{\text{c}}}{f_{{\text{co}}}}}}$

(3)

式中：A_f为FRP管的横截面积；f_f为FRP的拉伸强度。

2. 模型提出

2.1 钢管混凝土-FRP管SWSSC组合柱典型应力-应变关系曲线

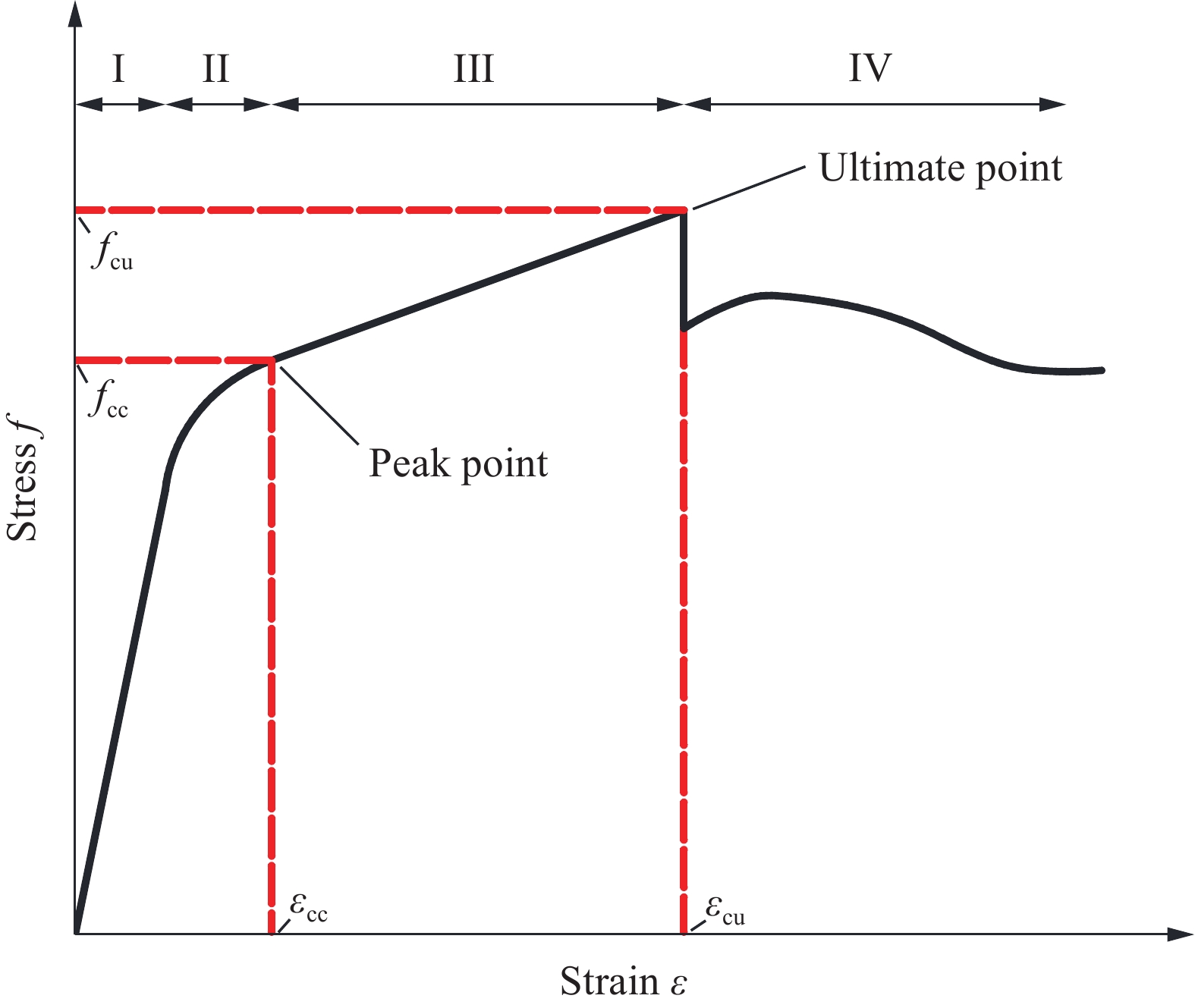
与FRP-钢复合管约束混凝土类似，钢管混凝土-FRP管SWSSC组合柱的应力-应变曲线如图3所示。钢管混凝土-FRP管SWSSC组合柱的应力-应变曲线主要由四个阶段组成：在第一个阶段，钢管混凝土-FRP管SWSSC组合柱主要由钢管提供约束，应力随着应变的增加呈现线性增加；从第二个阶段开始，钢管开始屈服，FRP管开始提供约束，应力的增加逐渐减缓；随后钢管混凝土-FRP管SWSSC组合柱的应力-应变曲线进入第二个线性增长阶段，在这个阶段，钢管由于屈服，仅提供一个恒定的侧向约束，因此这个阶段的约束主要由FRP管提供；随着荷载达到极限值，FRP管断裂，试件进入残余阶段。在这个阶段中，对于内置多根FRP管的钢管混凝土-FRP管SWSSC组合柱，由于其多根FRP管的断裂往往不同步，其应力-应变曲线在遭遇极限点的急剧下降之后，会呈现轻微的上升然后再次下降，这是与普通FRP-钢复合管约束混凝土平缓下降应力-应变曲线的轻微区别之处。如本文内置多根FRP管的钢管混凝土-FRP管SWSSC组合柱，其内部有3根FRP管，试件破坏时往往是其中1根FRP管断裂，其他的FRP管仍然可以继续提供约束。因此，在残余阶段中，试件的应力-应变曲线可能会出现2~3次的突降。最后，当所有FRP管都断裂后，试件重新回归到仅由钢管提供约束的阶段，试件的应力-应变曲线呈现平缓的下降趋势。

图 3 钢管混凝土-FRP管SWSSC组合柱典型应力-应变曲线

Figure 3. Typical stress-strain curves of concrete filled steel tube-SWSSC filled FRP tube composite columns

f_cu—Ultimate stress of specimens; f_cc—Peak stress of specimens; ε_cu—Ultimate strain of specimens; ε_cc—Peak strain of specimens

下载: 全尺寸图片幻灯片

2.2 钢管混凝土-FRP管SWSSC组合柱应力-应变曲线模型

张依睿等^[17]提出了针对FRP-钢管复合约束混凝土的应力-应变全曲线通用模型。由于FRP-钢管复合约束混凝土的应力-应变曲线与钢管混凝土-FRP管SWSSC组合柱的应力-应变曲线相似，因此提出的通用模型也适用于预测钢管混凝土-FRP管SWSSC组合柱的应力-应变曲线。

该模型主要由两个部分组成，即分为FRP断裂前后两个阶段。在FRP断裂前，混凝土既受到钢管的约束，又受到FRP的约束，因此在Popovics模型^[24]的基础上，通过引入两个常数(0.01和−0.1)和一个影响系数c来描述FRP管和钢管对于混凝土的约束效果：

${f_{\text{c}}} = \frac{{{{x}}a}}{{a - 1 + {x^{a(x + 0.01)^{-0.1}+ c}}}}{f_{{\text{cc}}}}$

(4)

式中：f_c为钢管混凝土-FRP管SWSSC组合柱的应力；f_cc为钢管混凝土-FRP管SWSSC组合柱的峰值应力；x为钢管混凝土-FRP管SWSSC组合柱极限应变与峰值应变的比值；c的计算与文献[17]相同；a=E_cs/(E_cs−E_sec)，E_cs和E_sec可用下式计算：

${E_{{\text{cs}}}}{\text{ = }}\frac{{{A_{\text{c}}}{E_{\text{c}}} + {A_{\text{s}}}{E_{\text{s}}}}}{A}, {E_{\sec }} = \frac{{{f_{{\text{cc}}}}}}{{{\varepsilon _{{\text{cc}}}}}}$

(5)

式中：E_cs为应力-应变曲线的初始斜率，即第一个阶段的斜率；E_sec为应力-应变曲线的二次斜率，即第二个线性增长阶段的斜率；E_c和E_s分别为混凝土和钢管的弹性模量；A为钢管混凝土-FRP管SWSSC组合柱的横截面面积；ε_cc为钢管混凝土-FRP管SWSSC组合柱的峰值应变。

当FRP管断裂后，钢管混凝土-FRP管SWSSC组合柱仅由钢管提供约束，因此第四阶段的应力-应变曲线可以直接利用Popovics模型：

${f_{\text{c}}} = \frac{{x a}}{{a - 1 + {x^a}}}{f_{{\text{cc}}}}$

(6)

2.3 钢管混凝土-FRP管SWSSC组合柱极限应力

钢管混凝土-FRP管SWSSC组合柱的极限应力即为试件的极限承载力除以试件的截面面积。试件的极限承载力主要由两部分构成，即为夹层普通混凝土在钢管约束下的承载力和核心SWSSC在钢管环绕FRP管共同约束下的承载力。针对FRP-钢复合管约束混凝土的强度预测，通过引入ξ_s综合考虑钢管的纵向应力和侧向约束，采用ξ_f反映FRP管的侧向约束，将钢套箍系数ξ_s和FRP有效约束系数ξ_f简单叠加，从而得到FRP-钢复合管约束混凝土的极限应力^[25]：

$\frac{{{f_{{\text{cu}}}}}}{{{f_{{\text{co}}}}}} = 1 + 1.27{\xi _{\text{s}}} + 1.28{\xi _{\text{f}}}$

(7)

其中，f_cu为钢管混凝土-FRP管SWSSC组合柱的极限应力。

在FRP-钢复合管约束混凝土的极限应力模型的基础上，根据新型钢管混凝土-FRP管SWSSC组合柱结构中两部分混凝土的不同约束受力机制，其极限应力可计算如下：

${f}_{\text{cu}}=\frac{(1+1.27{\xi }_{\text{s}}){A}_{\text{sc}1}{f}_{\text{co}1}+(1+1.27{\xi }_{\text{s}}+1.28{\xi }_{\text{f}}){A}_{\text{cf}2}{f}_{\text{co}2}}{A}$

(8)

$\xi_{\mathrm{s}} = \frac{{{A_{\text{s}}}{f_{\text{y}}}}}{{{A_{{\text{c}}1}}{f_{{\text{co}}1}}}},\xi_{\mathrm{f}} = \frac{{{A_{\text{f}}}{f_{\text{f}}}}}{{{A_{{\text{c}}2}}{f_{{\text{co}}2}}}}$

(9)

式中：A_c1和A_c2为夹层混凝土和核心混凝土的横截面积；A_sc1为夹层混凝土的横截面积加上钢管的横截面积；A_cf2为核心混凝土的横截面积加上FRP管的横截面积；f_co1为夹层混凝土的轴心抗压强度；f_co2为核心混凝土的轴心抗压强度。

2.4 钢管混凝土-FRP管SWSSC组合柱极限应变

与钢管混凝土-FRP管SWSSC组合柱的极限应力相似，FRP管的侧向约束和钢管的套箍系数是决定钢管混凝土-FRP管SWSSC组合柱的极限应变的两个重要因素。由于钢管混凝土-FRP管SWSSC组合柱的FRP管设置在结构的内部，而不是在钢管的表面，FRP管对于结构极限应变的贡献会有一定的减弱；另外，由于FRP管约束的核心混凝土面积小于结构整体的横截面积，需引入A_c2/A使其等效。综上，在建立的FRP-钢复合管混凝土极限应变计算公式的基础上^[16]，可得到钢管混凝土-FRP管SWSSC组合柱的极限应变公式：

$\frac{{{\varepsilon _{{\text{cu}}}}}}{{{\varepsilon _{{\text{co}}}}}} = 1 + {\text{17}}{\text{.5}} \left(\frac{{{f_{{\text{lf}}}}}}{{{f_{{\text{co}}1}}}}\right){^{0.39}}\frac{{{{\left( {{\varepsilon _{{\text{rup}}}}} \right)}^{1.33}}}}{{{\varepsilon _{{\text{co}}1}}}}\frac{{{A_{{\text{c}}2}}}}{A} + {\xi _{\text{s}}}$

(10)

${f_{{\rm{lf}}}} = \frac{{2{E_{\rm{f}}}{t_{\rm{f}}}{\varepsilon _{\rm{f}}}}}{{D{'_{\rm{f}}}}}$

(11)

式中：f_lf为FRP管的侧向约束；ε_rup为FRP管的断裂应变；E_f为FRP管的弹性模量；t_f为FRP管的厚度；ε_f为FRP管的极限拉伸应变；ε_cu为钢管混凝土-FRP管SWSSC组合柱的极限应变；ε_co为素混凝土的极限应变；ε_co1为夹层混凝土的极限应变。

2.5 钢管混凝土-FRP管SWSSC组合柱峰值应力及峰值应变

对于FRP-钢复合管混凝土柱的峰值应力和峰值应变，一般认为其与FRP管的约束刚度密切相关，并需考虑钢管的套箍作用影响^[16]。与FRP-钢复合管约束混凝土柱相比，钢管混凝土-FRP管SWSSC组合柱内部的FRP管不能充分发挥约束作用，因此钢管混凝土-FRP管SWSSC组合柱的峰值点会早于FRP-钢复合管约束混凝土柱的峰值点出现，因此对FRP-钢复合管混凝土柱的峰值应力和峰值应变模型进行修正，可得到钢管混凝土-FRP管SWSSC组合柱的峰值应力和峰值应变的计算公式如下：

$\frac{{{f_{{\text{cc}}}}}}{{{f_{{\text{co}}}}}} = 1 + 0.0015\frac{{{E_{\text{l}}}}}{{f_{{\text{co}}1}^{0.5}}}\frac{{{A_{{\text{c}}2}}}}{A} + 1.27\xi _{\text{s}}^{0.87}$

(12)

$\frac{{{\varepsilon _{{\text{cc}}}}}}{{{\varepsilon _{{\text{co}}}}}} = 1 + 0.0030\frac{{{E_{\text{l}}}}}{{f_{{\text{co}}1}^{0.5}}}\frac{{{A_{{\text{c}}2}}}}{A} + 1.30\xi _{\text{s}}^{0.9}$

(13)

${E_{\rm{l}}} = \frac{{2{E_{\rm{f}}}{t_{\rm{f}}}}}{{D{'_{\rm{f}}}}}$

(14)

式中，E_l为FRP管提供的侧向约束。

3. 模型验证

3.1 试验概况

为了验证上述模型的准确性，对于72个钢管混凝土-FRP管SWSSC组合柱进行了轴压试验，其中36个为内置单根FRP管的试件，36个为内置三根分布式FRP管的试件。试验的变化参数主要包括：钢管厚度(4.5 mm和6.0 mm)，FRP管层数(2层、3层和4层)和FRP管管径(内置单根FRP管的结构的FRP管径为70、90和110 mm，内置三根FRP管的结构的FRP管径为35、45和55 mm)。试件参数如表1所示，部分试件的试验过程和破坏模式如图4所示。表1中试件命名规则如下：“S”后的数字代表钢管的厚度，“D”后的数字代表FRP管的管径，“I”和“III”分别代表内置FRP管的个数为1个和3个，“C”后的数字代表FRP管的层数。

试验所用的钢管为无缝碳钢，两种厚度的钢管的屈服强度分别为317.6 MPa和325.4 MPa；FRP管采用CFRP，名义厚度为0.167 mm，极限抗拉强度为3475.9 MPa，极限抗拉应变为0.014，弹性模量为243.6 GPa。为了简化试件制作，最大程度减少试验误差，试验中所用的普通混凝土均用SWSSC代替，SWSSC的圆柱体轴心抗压强度为31.4 MPa。

表 1 钢管混凝土-FRP管SWSSC组合柱试件的具体参数

Table 1. Detailed parameters of concrete filled steel tube-SWSSC filled FRP tube composite columns

Specimens	Steel thickness/ mm	FRP tube diameter/ mm	FRP tube layers	FRP tube numbers	Specimens	Steel thickness/ mm	FRP tube diameter/ mm	FRP tube layers	FRP tube numbers
S4.5D70IC2	4.5	70	2	1	S4.5D35IIIC2	4.5	35	2	3
S4.5D70IC3	4.5	70	3	1	S4.5D35IIIC3	4.5	35	3	3
S4.5D70IC4	4.5	70	4	1	S4.5D35IIIC4	4.5	35	4	3
S4.5D90IC2	4.5	90	2	1	S4.5D45IIIC2	4.5	45	2	3
S4.5D90IC3	4.5	90	3	1	S4.5D45IIIC3	4.5	45	3	3
S4.5D90IC4	4.5	90	4	1	S4.5D45IIIC4	4.5	45	4	3
S4.5D110IC2	4.5	110	2	1	S4.5D55IIIC2	4.5	55	2	3
S4.5D110IC3	4.5	110	3	1	S4.5D55IIIC3	4.5	55	3	3
S4.5D110IC4	4.5	110	4	1	S4.5D55IIIC4	4.5	55	4	3
S6.0D70IC2	6.0	70	2	1	S6.0D35IIIC2	6.0	35	2	3
S6.0D70IC3	6.0	70	3	1	S6.0D35IIIC3	6.0	35	3	3
S6.0D70IC4	6.0	70	4	1	S6.0D35IIIC4	6.0	35	4	3
S6.0D90IC2	6.0	90	2	1	S6.0D45IIIC2	6.0	45	2	3
S6.0D90IC3	6.0	90	3	1	S6.0D45IIIC3	6.0	45	3	3
S6.0D90IC4	6.0	90	4	1	S6.0D45IIIC4	6.0	45	4	3
S6.0D110IC2	6.0	110	2	1	S6.0D55IIIC2	6.0	55	2	3
S6.0D110IC3	6.0	110	3	1	S6.0D55IIIC3	6.0	55	3	3
S6.0D110IC4	6.0	110	4	1	S6.0D55IIIC4	6.0	55	4	3
Notes: Labels of the specimens are as follows: The first letter “S” denotes steel tube, the second number such as “6.0” denotes the thickness of the steel tube; the second letter and number such as “D90” denotes the diameter of the FRP tube; the number “I” denotes the number of the FRP tube; the third letter and number such as “C2” denotes the number of FRP layers. For example, “S6.0D55IIIC3” indicates that the thickness of the steel tube is 6.0 mm, diameter of the FRP tube is 55 mm, the number of FRP tube is 3, and number of layers of the FRP tube is 3.

下载: 导出CSV

| 显示表格

图 4 部分钢管混凝土-FRP管SWSSC组合柱试件的试验过程及破坏模式

Figure 4. Test process and failure modes of concrete filled steel tube-SWSSC filled FRP tube composite column specimens

下载: 全尺寸图片幻灯片

3.2 钢管混凝土-FRP管SWSSC组合柱极限点及峰值点验证

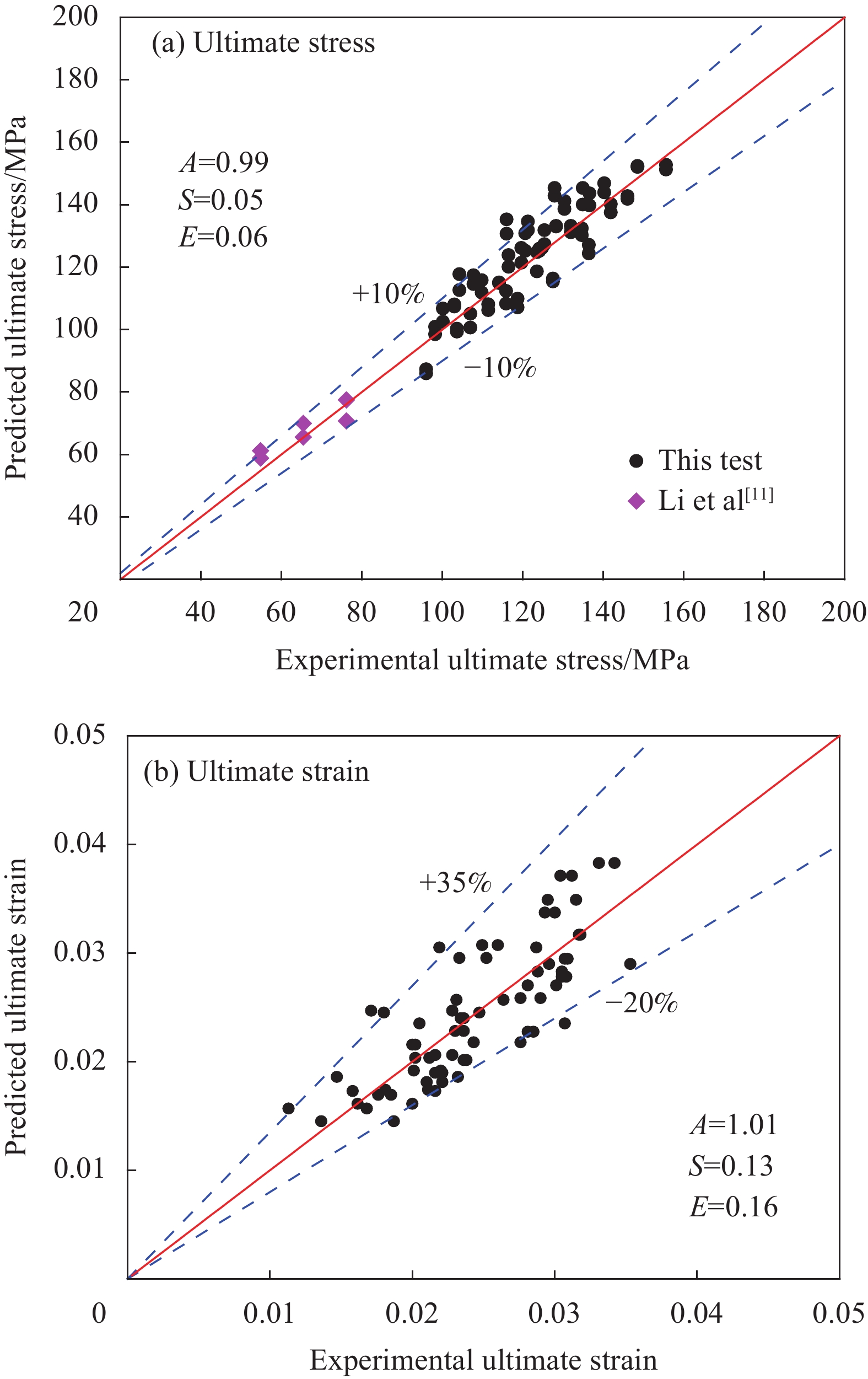
采用本文建议公式计算得出的极限应力与试验值的对比如图5所示。在验证极限应力模型时，收集了文献[11]中的6个圆截面钢-混凝土-CFRP-混凝土实心组合短柱的轴压试验数据。其试验概况如下：钢管厚度为2 mm，屈服强度为293 MPa，外径为260 mm；内置单根FRP管，FRP管采用CFRP，极限抗拉强度为3718.1 MPa，极限抗拉应变为0.014，弹性模量为292.0 GPa，外径为200 mm；混凝土强度为43.1 MPa。

由图5(a)可知，极限应力的预测值与试验值比值的平均值A为0.99，标准差S为0.05，绝对平均误差E为0.06。大部分试件的误差均位于±10%以内。说明提出的极限应力计算模型可以较精确地预测钢管混凝土-FRP管SWSSC组合柱的极限应力。钢管混凝土-FRP管SWSSC组合柱的极限应变可以通过式(10)计算。由图5(b)可知，极限应变的预测值与试验值比值的平均值为1.01，标准差为0.13，绝对平均误差为0.16。误差位于−20%~35%之间，说明提出的极限应变计算模型可以较好地预测钢管混凝土-FRP管SWSSC组合柱的极限应变。

图 5 钢管混凝土-FRP管SWSSC组合柱极限点模型评估

Figure 5. Evaluation of ultimate point model for concrete filled steel tube-SWSSC filled FRP tube composite columns

A—Average of theoretical value to experiment value ratio; S—Standard deviation; E—Absolute average error

下载: 全尺寸图片幻灯片

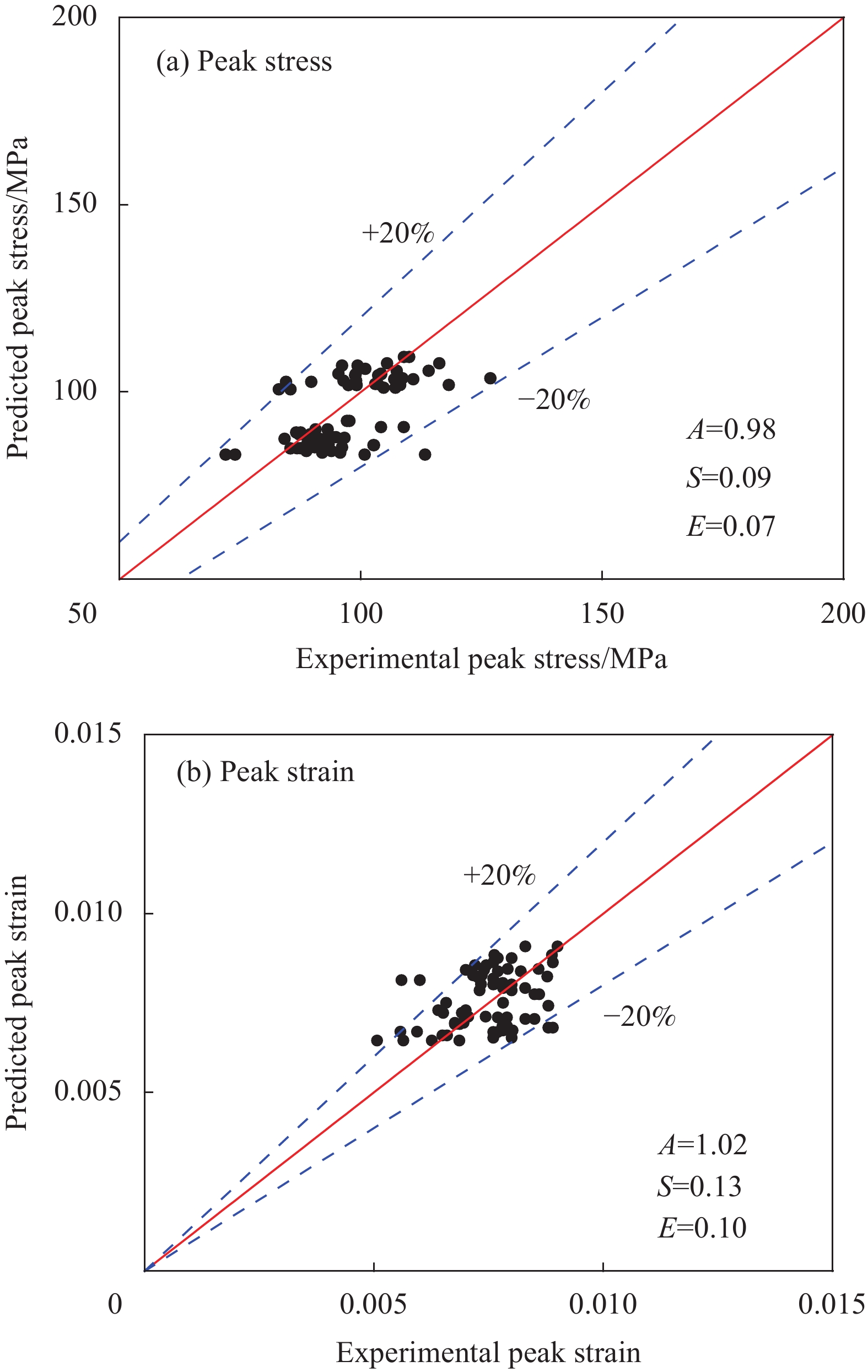
本文建议钢管混凝土-FRP管SWSSC组合柱的峰值点模型的验证与评估如图6所示。从图6(a)可以看出，有个别试件的峰值应力与峰值应变的理论与试验误差超过了20%，但是绝大多数试件的误差位于−20%~20%之间。峰值应力的预测值与试验值比值的平均值为0.98，标准差为0.09，绝对平均误差为0.07。峰值应变的预测值与试验值比值的平均值为1.02，标准差为0.13，绝对平均误差为0.10。因此，本文提出的峰值应变与峰值应力模型预测的计算值与试验值较吻合。

图 6 钢管混凝土-FRP管SWSSC组合柱峰值点模型评估

Figure 6. Evaluation of peak point model for concrete filled steel tube-SWSSC filled FRP tube composite columns

下载: 全尺寸图片幻灯片

3.3 钢管混凝土-FRP管SWSSC组合柱应力-应变模型验证

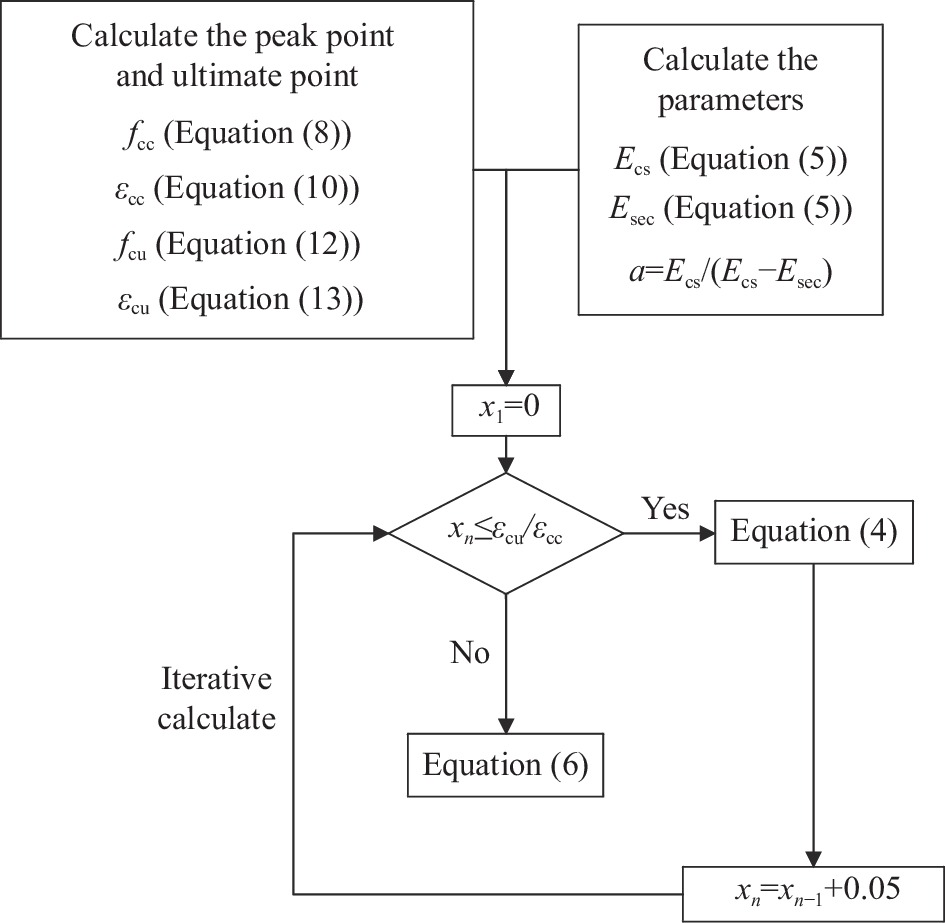
图7展示了钢管混凝土-FRP管SWSSC组合柱的应力-应变曲线计算流程图。具体的计算过程如下：

(1) 将钢管混凝土-FRP管SWSSC组合柱的基本参数(钢管厚度、外径、FRP管管径、FRP管层数、混凝土抗压强度等)代入公式，计算出极限应力、极限应变、峰值应力与峰值应变的计算值；并利用公式，计算出复合弹性模量和割线模量。

(2) 比较x与ε_cu/ε_cc的大小，若x $\leqslant$ ε_cu/ε_cc，说明FRP管尚未断裂，则代入公式计算钢管混凝土-FRP管SWSSC组合柱的应力f_c及钢管混凝土-FRP管SWSSC组合柱的应变ε_c；若x>ε_cu/ε_cc，说明FRP管已断裂，则代入公式计算f_c及ε_c。

(3) 对x进行迭代计算，每次迭代x的值增加0.05，最后将计算得到的f_c及ε_c连接起来，即得到完整的应力-应变曲线。

图 7 钢管混凝土-FRP管SWSSC组合柱计算流程图

Figure 7. Flow chart of model calculation for concrete filled steel tube-SWSSC filled FRP tube composite columns

E_cs—Initial stiffness of stress-strain curves (i.e. the slope of initial stage of stress-strain curves); E_sec—Second stiffness of stress-strain curves (i.e. the slope of second linear strengthening stage of stress-strain curves); x_n—nth iteration point

下载: 全尺寸图片幻灯片

根据上述流程对钢管混凝土-FRP管SWSSC组合柱进行计算，即可以得到钢管混凝土-FRP管SWSSC组合柱的预测应力-应变曲线图。部分试件的试验应力-应变曲线与预测应力-应变曲线的对比如图8所示。可以看出，钢管混凝土-FRP管SWSSC组合柱的计算应力-应变曲线和试验应力-应变曲线的趋势和形状均较吻合，试验应力-应变曲线的四个阶段(即初始线性阶段、屈服过渡阶段、线性强化阶段和残余)均可以较好地从计算应力-应变曲线中反映出来。计算应力-应变曲线的峰值点和极限点与试验应力-应变曲线的峰值点和极限点也较接近。因此，提出的应力-应变曲线模型具有较好的精度，可以精确地预测钢管混凝土-FRP管SWSSC组合柱的应力-应变曲线。

图 8 钢管混凝土-FRP管海水海砂混凝土组合柱应力-应变曲线模型验证

Figure 8. Verification of stress-strain curves model for concrete filled steel tube-SWSSC filled FRP tube composite columns

下载: 全尺寸图片幻灯片

3.4 钢管混凝土-FRP管SWSSC组合柱参数化分析

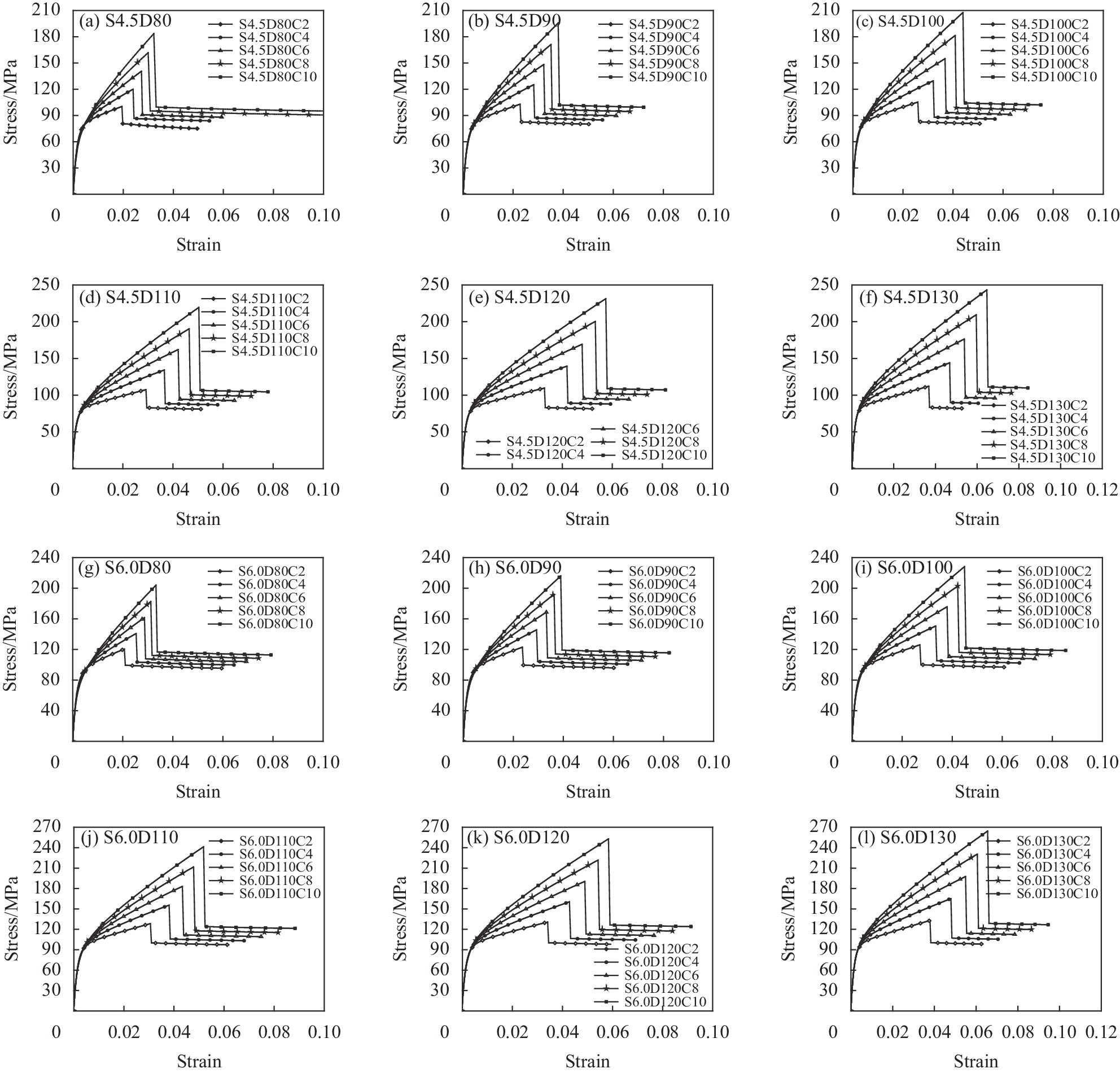
为了研究FRP管层数和FRP管管径对于钢管混凝土-FRP管SWSSC组合柱在轴向荷载作用下的应力-应变关系的影响，本文利用提出的应力-应变曲线模型对钢管混凝土-FRP管SWSSC组合柱进行了参数化分析。具体的试件参数如下：试件外径159 mm，钢管厚度(4.5 mm和6.0 mm)，FRP管层数(2、4、6、8和10层)，FRP管管径(80~130 mm)，混凝土强度31.4 MPa，钢管屈服强度317.6 MPa和325.4 MPa，FRP采用CFRP，其极限强度为3475.9 MPa。在本文提出的模型中，内置多根FRP管的结构均可以等效处理为内置单根FRP管的结构，因此在参数化分析中，选取的试件均为内置单根FRP管的钢管混凝土-FRP管SWSSC组合柱。

图9展示了相同钢管厚度、相同FRP管管径和不同FRP管层数情况下试件的应力-应变曲线。图9中各试件的编号与表1相似，以“S4.5D80C2”为例，S4.5D80C2代表钢管厚度为4.5 mm，FRP管管径为80 mm，FRP层数为2层的试件。可知，FRP管层数的增加对于试件初始刚度几乎没有影响，而随着钢管厚度的增加，试件的初始钢管会有一定的提高，说明在初始阶段，主要由钢管提供约束，而FRP管尚未发挥约束效果直至钢管开始屈服。FRP管层数对于钢管混凝土-FRP管SWSSC组合柱的应力-应变曲线的影响主要体现在第二个线性上升阶段，试件应力-应变曲线的第三阶段的斜率随着FRP管层数的提高而提高，试件的极限应力和极限应变也随着FRP管层数的提高而提高。

图 9 钢管混凝土-FRP管SWSSC组合柱参数化分析

Figure 9. Parametric analysis of concrete filled steel tube-SWSSC filled FRP tube composite columns

下载: 全尺寸图片幻灯片

表2展示了FRP管管径对于试件力学性能的影响，表中的提高比代表了FRP管管径的增加对于试件承载力的增益效果。可以看出，对于FRP管层数和钢管厚度相同的钢管混凝土-FRP管SWSSC组合柱，FRP管的管径对于试件的极限应力有一定的增益效果。例如，对于钢管厚度为6.0 mm和FRP管层数为2层的试件，当FRP管管径从80 mm增加到130 mm时，试件的承载力增加了1.83%~1.98%。这是由于随着FRP管管径的提升，核心被约束的混凝土的面积也随之增加。且对于FRP管层数相同的试件，随着FRP管管径的增大，FRP管管径的增加对于试件承载力的增益效果会相应的减少。例如，对于钢管厚度为4.5 mm和FRP管层数为2层的试件，当FRP管管径从80 mm增加到90 mm，试件的承载力增加了2.37%，而当FRP管管径从120 mm增加到130 mm，试件的承载力增加了2.16%。

表 2 钢管混凝土-FRP管SWSSC组合柱参数变化的影响

Table 2. Influence of parameter variation of concrete filled steel tube-SWSSC filled FRP tube composite columns

Specimens	Two-layers		Four-layers		Six-layers		Eight-layers		Ten-layers
Specimens	Ultimate stress/MPa	Increase ratio/%	Ultimate stress/MPa	Increase ratio/%	Ultimate stress/MPa	Increase ratio/%	Ultimate stress/MPa	Increase ratio/%	Ultimate stress/MPa	Increase ratio/%
S4.5D80	100.62	−	120.64	−	141.30	−	162.61	−	184.59	−
S4.5D90	103.01	2.37	125.40	3.95	148.44	5.06	172.13	5.86	196.49	6.45
S4.5D100	105.39	2.31	130.16	3.80	155.58	4.81	181.66	5.53	208.39	6.06
S4.5D110	107.77	2.26	134.93	3.66	162.73	4.59	191.18	5.24	220.30	5.71
S4.5D120	110.15	2.21	139.69	3.53	169.88	4.39	200.71	4.98	232.21	5.41
S4.5D130	112.53	2.16	144.46	3.41	177.02	4.21	210.24	4.75	244.12	5.13
S6.0D80	121.11	−	141.23	−	162.01	−	183.44	−	205.54	−
S6.0D90	123.50	1.98	146.02	3.39	169.19	4.44	193.02	5.22	217.51	5.82
S6.0D100	125.90	1.94	150.81	3.28	176.38	4.25	202.60	4.96	229.49	5.51
S6.0D110	128.29	1.90	155.61	3.18	183.57	4.08	212.19	4.73	241.47	5.22
S6.0D120	130.69	1.87	160.40	3.08	190.76	3.92	221.78	4.52	253.45	4.96
S6.0D130	133.09	1.83	165.19	2.99	197.95	3.77	231.36	4.32	265.44	4.73
Notes: The labels of the specimens are as follows: the first letter “S” denotes steel tube, the second number such as “6.0” denotes the thickness of the steel tube; the second letter and number such as “D90” denotes the diameter of the FRP tube. For example, “S6.0D90” indicates that the thickness of the steel tube is 6.0 mm, diameter of the FRP tube is 90 mm.

下载: 导出CSV

| 显示表格

4. 结论

(1) 新型钢管混凝土-纤维增强复合材料(FRP)管海水海砂混凝土(SWSSC)组合柱由外侧钢管、夹层普通混凝土、内侧FRP管和核心SWSSC构成。其中，夹层普通混凝土仅受到钢管约束，核心SWSSC既受到钢管的约束，又受到FRP管的约束。

(2) 在FRP-钢复合管约束混凝土的极限应力计算模型的基础上，将钢管混凝土-FRP管SWSSC组合柱的极限承载力分为夹层混凝土和核心混凝土两个部分，提出了钢管混凝土-FRP管SWSSC组合柱的极限应力计算公式。

(3) 考虑到FRP管的管径小于钢管，约束效果略有削弱，提出了钢管混凝土-FRP管SWSSC组合柱的极限应变、峰值应力和峰值应变的计算模型，并利用已有的试验数据，对上述模型进行了评估，结果表明提出的计算模型与试验数据较吻合。

(4) 利用作者提出的FRP-钢复合管约束混凝土的应力-应变曲线模型，对钢管混凝土-FRP管SWSSC组合柱的应力-应变曲线进行了预测，预测曲线与试验曲线较吻合，有较好的适用性与通用性。

(5) 在提出的应力-应变曲线模型的基础上，对钢管混凝土-FRP管SWSSC组合柱的力学性能进行了参数化分析。结果表明，FRP管管径和层数的增加均对新型钢管混凝土-FRP管SWSSC组合柱的承载力和变形能力有积极影响。

图 1 钢管混凝土-纤维增强复合材料(FRP)管海水海砂混凝土(SWSSC)组合柱试件示意图

Figure 1. Schematic diagram of concrete filled steel tube-seawater and sea sand concrete (SWSSC) filled fiber reinforced polymer (FRP) tube composite columns

下载: 全尺寸图片幻灯片

图 2 钢管混凝土-FRP管SWSSC组合柱约束机制分析图

Figure 2. Analysis diagram of confinement mechanism for concrete filled steel tube-SWSSC filled FRP tube composite columns

下载: 全尺寸图片幻灯片

图 3 钢管混凝土-FRP管SWSSC组合柱典型应力-应变曲线

Figure 3. Typical stress-strain curves of concrete filled steel tube-SWSSC filled FRP tube composite columns

f_cu—Ultimate stress of specimens; f_cc—Peak stress of specimens; ε_cu—Ultimate strain of specimens; ε_cc—Peak strain of specimens

下载: 全尺寸图片幻灯片

图 4 部分钢管混凝土-FRP管SWSSC组合柱试件的试验过程及破坏模式

Figure 4. Test process and failure modes of concrete filled steel tube-SWSSC filled FRP tube composite column specimens

下载: 全尺寸图片幻灯片

图 5 钢管混凝土-FRP管SWSSC组合柱极限点模型评估

Figure 5. Evaluation of ultimate point model for concrete filled steel tube-SWSSC filled FRP tube composite columns

A—Average of theoretical value to experiment value ratio; S—Standard deviation; E—Absolute average error

下载: 全尺寸图片幻灯片

图 6 钢管混凝土-FRP管SWSSC组合柱峰值点模型评估

Figure 6. Evaluation of peak point model for concrete filled steel tube-SWSSC filled FRP tube composite columns

下载: 全尺寸图片幻灯片

图 7 钢管混凝土-FRP管SWSSC组合柱计算流程图

Figure 7. Flow chart of model calculation for concrete filled steel tube-SWSSC filled FRP tube composite columns

下载: 全尺寸图片幻灯片

图 8 钢管混凝土-FRP管海水海砂混凝土组合柱应力-应变曲线模型验证

Figure 8. Verification of stress-strain curves model for concrete filled steel tube-SWSSC filled FRP tube composite columns

下载: 全尺寸图片幻灯片

图 9 钢管混凝土-FRP管SWSSC组合柱参数化分析

Figure 9. Parametric analysis of concrete filled steel tube-SWSSC filled FRP tube composite columns

下载: 全尺寸图片幻灯片

表 1 钢管混凝土-FRP管SWSSC组合柱试件的具体参数

Table 1 Detailed parameters of concrete filled steel tube-SWSSC filled FRP tube composite columns

Specimens	Steel thickness/ mm	FRP tube diameter/ mm	FRP tube layers	FRP tube numbers	Specimens	Steel thickness/ mm	FRP tube diameter/ mm	FRP tube layers	FRP tube numbers
S4.5D70IC2	4.5	70	2	1	S4.5D35IIIC2	4.5	35	2	3
S4.5D70IC3	4.5	70	3	1	S4.5D35IIIC3	4.5	35	3	3
S4.5D70IC4	4.5	70	4	1	S4.5D35IIIC4	4.5	35	4	3
S4.5D90IC2	4.5	90	2	1	S4.5D45IIIC2	4.5	45	2	3
S4.5D90IC3	4.5	90	3	1	S4.5D45IIIC3	4.5	45	3	3
S4.5D90IC4	4.5	90	4	1	S4.5D45IIIC4	4.5	45	4	3
S4.5D110IC2	4.5	110	2	1	S4.5D55IIIC2	4.5	55	2	3
S4.5D110IC3	4.5	110	3	1	S4.5D55IIIC3	4.5	55	3	3
S4.5D110IC4	4.5	110	4	1	S4.5D55IIIC4	4.5	55	4	3
S6.0D70IC2	6.0	70	2	1	S6.0D35IIIC2	6.0	35	2	3
S6.0D70IC3	6.0	70	3	1	S6.0D35IIIC3	6.0	35	3	3
S6.0D70IC4	6.0	70	4	1	S6.0D35IIIC4	6.0	35	4	3
S6.0D90IC2	6.0	90	2	1	S6.0D45IIIC2	6.0	45	2	3
S6.0D90IC3	6.0	90	3	1	S6.0D45IIIC3	6.0	45	3	3
S6.0D90IC4	6.0	90	4	1	S6.0D45IIIC4	6.0	45	4	3
S6.0D110IC2	6.0	110	2	1	S6.0D55IIIC2	6.0	55	2	3
S6.0D110IC3	6.0	110	3	1	S6.0D55IIIC3	6.0	55	3	3
S6.0D110IC4	6.0	110	4	1	S6.0D55IIIC4	6.0	55	4	3
Notes: Labels of the specimens are as follows: The first letter “S” denotes steel tube, the second number such as “6.0” denotes the thickness of the steel tube; the second letter and number such as “D90” denotes the diameter of the FRP tube; the number “I” denotes the number of the FRP tube; the third letter and number such as “C2” denotes the number of FRP layers. For example, “S6.0D55IIIC3” indicates that the thickness of the steel tube is 6.0 mm, diameter of the FRP tube is 55 mm, the number of FRP tube is 3, and number of layers of the FRP tube is 3.

下载: 导出CSV

表 2 钢管混凝土-FRP管SWSSC组合柱参数变化的影响

Table 2 Influence of parameter variation of concrete filled steel tube-SWSSC filled FRP tube composite columns

Specimens	Two-layers		Four-layers		Six-layers		Eight-layers		Ten-layers
Specimens	Ultimate stress/MPa	Increase ratio/%	Ultimate stress/MPa	Increase ratio/%	Ultimate stress/MPa	Increase ratio/%	Ultimate stress/MPa	Increase ratio/%	Ultimate stress/MPa	Increase ratio/%
S4.5D80	100.62	−	120.64	−	141.30	−	162.61	−	184.59	−
S4.5D90	103.01	2.37	125.40	3.95	148.44	5.06	172.13	5.86	196.49	6.45
S4.5D100	105.39	2.31	130.16	3.80	155.58	4.81	181.66	5.53	208.39	6.06
S4.5D110	107.77	2.26	134.93	3.66	162.73	4.59	191.18	5.24	220.30	5.71
S4.5D120	110.15	2.21	139.69	3.53	169.88	4.39	200.71	4.98	232.21	5.41
S4.5D130	112.53	2.16	144.46	3.41	177.02	4.21	210.24	4.75	244.12	5.13
S6.0D80	121.11	−	141.23	−	162.01	−	183.44	−	205.54	−
S6.0D90	123.50	1.98	146.02	3.39	169.19	4.44	193.02	5.22	217.51	5.82
S6.0D100	125.90	1.94	150.81	3.28	176.38	4.25	202.60	4.96	229.49	5.51
S6.0D110	128.29	1.90	155.61	3.18	183.57	4.08	212.19	4.73	241.47	5.22
S6.0D120	130.69	1.87	160.40	3.08	190.76	3.92	221.78	4.52	253.45	4.96
S6.0D130	133.09	1.83	165.19	2.99	197.95	3.77	231.36	4.32	265.44	4.73
Notes: The labels of the specimens are as follows: the first letter “S” denotes steel tube, the second number such as “6.0” denotes the thickness of the steel tube; the second letter and number such as “D90” denotes the diameter of the FRP tube. For example, “S6.0D90” indicates that the thickness of the steel tube is 6.0 mm, diameter of the FRP tube is 90 mm.

下载: 导出CSV

参考文献(25)

[1]	韦建刚, 周俊, 罗霞, 等. 高强钢管超高强混凝土柱抗震性能试验研究[J]. 工程力学, 2021, 38(7):30-40, 51. WEI J G, ZHOU J, LUO X, et al. Experimental study on quasi-static behavior of ultrahigh strength concrete filled high strength steel tubular columns[J]. Engineering Mechanics,2021,38(7):30-40, 51(in Chinese).
[2]	颜燕祥. 方钢管UHPC短柱轴压性能试验研究[J]. 建筑结构, 2021, 51(12):117-123. YAN Y X. Experimental study on behavior of square UHPC filled short steel tube columns subjected to axial compression[J]. Building Structure,2021,51(12):117-123(in Chinese).
[3]	魏洋, 柏佳文, 张依睿, 等. 矩形开槽钢管混凝土柱的受压承载性能[J]. 东南大学学报(自然科学版), 2020, 50(2):237-243. DOI: 10.3969/j.issn.1001-0505.2020.02.005 WEI Y, BAI J W, ZHANG Y R, et al. Compressive behaviors of rectangular concrete-filled slotted steel tubular columns[J]. Journal of Southeast University (Natural Science Edition),2020,50(2):237-243(in Chinese). DOI: 10.3969/j.issn.1001-0505.2020.02.005
[4]	郭晓云, 陈杰, 唐永明. 不同纤维增强复合材料加固混凝土短柱轴心受压承载力试验研究[J]. 复合材料科学与工程, 2021, 8:66-72. GUO X Y, CHEN J, TANG Y M. Experimental study on axial compression bearing capacity of concrete short column strengthened with different fiber reinforced composites[J]. Composites Science and Engineering,2021,8:66-72(in Chinese).
[5]	马高, 曾志虎. BFRP约束损伤混凝土棱柱体轴压力学性能研究[J]. 防灾减灾工程学报, 2020, 40(6):910-918. MA G, ZENG Z H. Axial compression behavior of pre-damaged concrete prisms confined with BFRP[J]. Journal of Disaster Prevention and Mitigation Engineering,2020,40(6):910-918(in Chinese).
[6]	WEI Y, XU P F, ZHANG Y R, et al. Compressive behaviour of FRP-steel wire mesh composite tubes filled with seawater and sea sand concrete[J]. Construction and Building Materials, 2021, 314(Part B): 125608.
[7]	赵均海, 张焕青, 李莹萍. 等角八边形中空夹层钢管混凝土短柱承载力统一解[J]. 应用力学学报, 2021, 38(3):1054-1061. ZHAO J H, ZHANG H Q, LI Y P. Unified solutions on bearing capacity of concrete-filled double skin steel tubular stub column with equal-angle octagon[J]. Chinese Jour-nal of Applied Mechanics,2021,38(3):1054-1061(in Chinese).
[8]	LONG Y L, LI W T, DAI J G, et al. Experimental study of concrete-filled CHS stub columns with inner FRP tubes[J]. Thin-Walled Structures,2018,122:606-621. DOI: 10.1016/j.tws.2017.10.046
[9]	ZHANG Y R, WEI Y, BAI J W, et al. A novel seawater and sea sand concrete filled FRP-carbon steel composite tube column: Concept and behavior[J]. Composite Structures,2020,246(8):112421.
[10]	柏佳文, 魏洋, 张依睿, 等. 新型碳纤维增强复合材料-钢复合管海水海砂混凝土圆柱轴压试验[J]. 复合材料学报, 2021, 38(9):3084-3093. BAI J W, WEI Y, ZHANG Y R, et al. Axial compression behavior of new seawater and sea sand concrete filled circular carbon fiber reinforced polymer-steel composite tube columns[J]. Acta Materiae Compositae Sinica,2021,38(9):3084-3093(in Chinese).
[11]	李广悦. 圆截面钢-混凝土-CFRP-混凝土实心组合短柱轴压力学性能研究[D]. 沈阳: 沈阳建筑大学, 2011. LI G Y. Study on mechanical properties of circular steel-concrete-CFRP-concrete solid composite short columns under axial compression[D]. Shenyang: Shenyang Jianzhu University, 2011(in Chinese).
[12]	LI G C, LANG Y, YANG Z J. Behavior of high strength CFSST stub columns with inner CFRP tube under axial compres-sive load[J]. Advanced Steel Construction,2011,7(3):239-254.
[13]	LI Y L, ZHAO X L. Hybrid double tube sections utilising seawater and sea sand concrete, FRP and stainless steel[J]. Thin-Walled Structures,2020,149:106643. DOI: 10.1016/j.tws.2020.106643
[14]	张海镇. 内置FRP-UHPC芯柱的钢管混凝土组合柱轴压力学性能研究[D]. 西安: 西安建筑科技大学, 2017. ZHANG H Z. Research on the mechanical properties of concrete-filled steel tube columns with FRP-UHPC core columns subjected to axial compression[D]. Xi’an: Xi’an University of Architecture and Technology, 2017(in Chinese).
[15]	陶毅, 张海镇, 史庆轩, 等. 内置FRP约束混凝土的方钢管混凝土轴压承载力[J]. 土木建筑与环境工程, 2017, 39(2):43-49. TAO Y, ZHANG H Z, SHI Q X, et al. Bearing capacity of steel tube-concrete-FRP-concrete composite columns[J]. Journal of Civil and Environmental Engineering,2017,39(2):43-49(in Chinese).
[16]	ZHANG Y R, WEI Y, BAI J W, et al. Stress-strain model of an FRP-confined concrete filled steel tube under axial compression[J]. Thin-Walled Structures,2019,142:149-159. DOI: 10.1016/j.tws.2019.05.009
[17]	张依睿, 魏洋, 柏佳文, 等. 纤维增强聚合物复合材料-钢复合圆管约束混凝土轴压性能预测模型[J]. 复合材料学报, 2019, 36(10):2478-2485. ZHANG Y R, WEI Y, BAI J W, et al. Models for predicting axial compression behavior of fiber reinforced polymer-steel composite circular tube confined concrete[J]. Acta Materiae Compositae Sinica,2019,36(10):2478-2485(in Chinese).
[18]	YU T, TENG J G, WONG Y L. Stress-strain behavior of concrete in hybrid FRP-concrete-steel double-skin tubular columns[J]. Journal of Structural Engineering,2010,136:379-389. DOI: 10.1061/(ASCE)ST.1943-541X.0000121
[19]	WEI Y, JIANG C, WU Y F. Confinement effectiveness of circular concrete-filled steel tubular columns under axial compression[J]. Journal of Constructional Steel Research,2019,158:15-27. DOI: 10.1016/j.jcsr.2019.03.012
[20]	曾翔, 吴晚博, 霍静思, 等. 圆铝合金管混凝土短柱轴心受压承载力研究[J]. 工程力学, 2021, 38(2):52-60. ZENG X, WU W B, HUO J S, et al. The axial strength of concrete-filled aluminum alloy circular tubular stub columns[J]. Engineering Mechanics,2021,38(2):52-60(in Chinese).
[21]	HAN L H, YAO G H, ZHAO X L. Tests and calculations for hollow structural steel (HSS) stub columns filled with self-consolidating concrete (SCC)[J]. Journal of Constructional Steel Research,2005,61:1241-1269. DOI: 10.1016/j.jcsr.2005.01.004
[22]	HAN L H, YAO G H, ZHONG T. Performance of concrete-filled thin-walled steel tubes under pure torsion[J]. Thin-Walled Structures,2007,45:24-36. DOI: 10.1016/j.tws.2007.01.008
[23]	JIANG T, TENG J G. Analysis-oriented stress-strain models for FRP-confined concrete[J]. Engineering Structures, 2007, 29: 2968-2986.
[24]	POPOVICS S. A numerical approach to the complete stress-strain curve of concrete[J]. Cement & Concrete Research,1973,3(5):583-599.
[25]	WEI Y, WU G, LI G F. Performance of circular concrete-filled fiber-reinforced polymer-steel composite tube columns under axial compression[J]. Journal of Reinforced Plastics and Composites,2014,33:1911-1928. DOI: 10.1177/0731684414550836

施引文献(9)

期刊类型引用(3)

1.	吴沛宗，江振兴，杨泽铭，林嘉祥. FRP增强海水海砂混凝土结构研究进展. 混凝土. 2024(08): 48-54+62 . 百度学术
2.	杨来运，方海，谢红磊，李奔奔. 多腔矩形纤维增强复合材料约束混凝土组合短柱受压性能. 复合材料学报. 2023(12): 6910-6921 . 本站查看
3.	原野，王震宇，王代玉. 配置新型封闭缠绕式GFRP箍筋混凝土梁的受剪性能试验. 复合材料学报. 2022(11): 5074-5085 . 本站查看