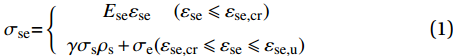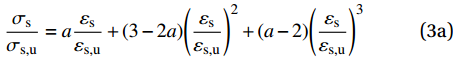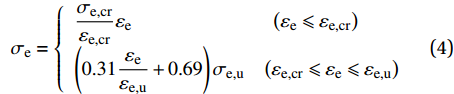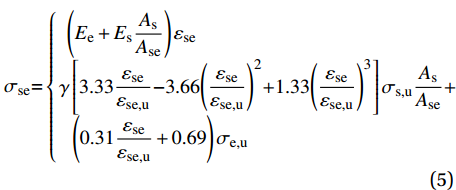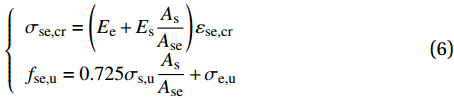Tensile stress-strain relationship of engineered cementitious composites reinforced by high-strength stainless steel wire mesh
-
摘要: 为了研究高强不锈钢绞线网增强工程水泥基复合材料(Engineered cementitious composites，EEC)的受拉性能，考虑高强不锈钢绞线配筋率、ECC抗拉强度、高强不锈钢绞线网增强ECC试件宽度3个影响因素，对设计的27个高强不锈钢绞线网增强ECC试件进行了单轴拉伸试验。试验结果表明，高强不锈钢绞线网增强ECC受拉试件的开裂应力和极限应力随着钢绞线配筋率、ECC抗拉强度的增大而增大；增大试件宽度对试件的开裂应力和极限应力几乎无影响。基于试验结果，提出并建立了高强不锈钢绞线网增强ECC受拉本构模型，推导了开裂应力和极限应力计算公式。经验证，计算结果与试验结果吻合良好，说明所建立的受拉本构模型可准确描述高强不锈钢绞线网增强ECC的受拉应力-应变关系。
-
关键词:
- 高强不锈钢绞线网增强工程水泥基复合材料 /
- 应力-应变关系 /
- 本构模型 /
- 拉伸性能 /
- 试验
Abstract: In order to study the tensile performance of the engineered cementitious composites (EEC) reinforced by high high-strength stainless steel wire mesh, the parameters of reinforcement ratio of high-strength stainless steel stranded wire, tensile strength of ECC and width of ECC reinforced by high high-strength stainless steel wire mesh specimen were considered, and the uniaxial tensile tests of total of 27 test pieces were carried out. The test results show that the cracking stress and ultimate stress of the specimens increase with the increase of the steel strand reinforcement ratio and ECC tensile strength. The crack stress and ultimate stress of the specimens are almost not affected by increasing the width of the specimen. Based on the test results, the tensile constitutive model of high-strength stainless steel stranded wire mesh reinforced ECC and the formulas for calculating the cracking stress and ultimate stress were proposed. It is proved that the calculated results are in good agreement with the experimental results, which indicates that the established tensile constitutive model can accurately describe the tensile stress-strain relationship of ECC reinforced by high-strength stainless steel wire mesh. -
工程用水泥基复合材料(Engineered cementitious composites，ECC)是一种通过微观力学和断裂力学原理对材料体系进行系统设计和优化的短纤维乱向水泥基复合材料[1-2]，国内外学者围绕ECC的受拉、受弯等基本力学性能开展了大量相关研究工作，并取得了众多优异成果[3-8]。然而ECC的抗拉强度仍然有限，用于结构加固时对构件的抗拉、抗弯承载力和抗裂性能的增强效果有限，仍需与性能优异的增强材料共同使用，为此，众多学者相继开展筋材、网材等用于增强ECC受力性能的研究。
Fischer等[9]、Mihashi等[10]进行了钢筋增强ECC单轴拉伸试验，结果表明，钢筋增强ECC试件裂缝分布更加均匀，减小了裂缝宽度，提高了变形能力。郑宇宙等[11]、朱忠锋等[12]对纤维增强ECC复合材料进行了单轴拉伸试验，结果表明，增强材料可以明显改善ECC的受拉性能，其轴向刚度、极限承载力也得到了显著提高。但是已研究的增强材料中，采用普通钢筋时，ECC的优越性能不能完全发挥，使用纤维编织网增强材料又降低了经济性。而高强不锈钢绞线抗拉强度高，具有良好的耐腐蚀性能和经济性。相关学者对高强不锈钢绞线加固混凝土结构的研究表明，其能有效提高加固构件的抗弯、抗剪承载力和刚度[13-17]。目前该加固技术已成功应用于实际工程，并取得了优异的效果[18-19]。
综上分析，高强不锈钢绞线网是由不锈钢绞线编制而成，本身具有很强的耐腐蚀、抗锈蚀能力；ECC具有良好的裂缝分散能力，正常使用状态裂缝宽度很小[1-10]，二者结合后，可以使ECC开裂后钢绞线不发生锈蚀，耐久性好。因此，朱俊涛等[20]提出了新型高性能复合材料“高强不锈钢绞线网增强ECC”。已对高强不锈钢绞线网与ECC的粘结锚固性能[21-22]进行了试验和理论研究，结果表明，在试验所得的粘结滑移曲线中，平均粘结应力达到峰值开始微下降至峰值的85%左右之后，即进入延性强化段，该阶段平均粘结应力不再降低，仅滑移量呈水平线增长，说明高强不锈钢绞线网与ECC具有良好的粘结锚固性能。为了尽快使该复合材料在实际工程中得到应用，本文对高强不锈钢绞线网增强ECC的受拉性能进行试验和理论研究。
1. 试验概况
1.1 试件设计及材性试验
为了研究ECC抗拉强度、高强不锈钢绞线网受拉方向配筋率及高强不锈钢绞线网增强ECC试件宽度三个影响因素对高强不锈钢绞线增强ECC抗拉性能的影响，共设计了9组试件，每组3个共27个试件，各组试件参数见表1。为了避免试件在加载过程中在变截面处应力集中破坏，本试验受拉试件均采用哑铃型试件，试件变截面处为弧形，试件示意图如图1所示。试验中ECC的两种配合比见刘伟康[5]研究成果，试件标准养护28天。对预留的ECC受拉薄板试件(280 mm×40 mm×15 mm)进行拉伸试验，得到两种ECC配合比的抗拉性能，各组试件的ECC抗拉性能见表2。高强不锈钢绞线直径均为2.4 mm，对其进行拉伸试验(3根)，得到高强不锈钢绞线应力-应变曲线如图2所示。
表 1 高强不锈钢绞线网增强工程水泥基复合材料(ECC)试件参数Table 1. Parameters of engineered cementitious composites(ECC) reinforced by high-strength stainless steel wire mesh specimensGroup number Test section width bc /mm Steel strand spacing/mm Reinforcement ratio of steel strand TC12 80 50 0.0028 TC22 70 40 0.0032 TC32 60 30 0.0037 TC42 50 20 0.0048 TC52 90 30 0.0037 TD12 80 50 0.0028 TD22 70 40 0.0032 TD32 60 30 0.0037 TD42 50 20 0.0048 ![]()
图 1 高强不锈钢绞线网增强ECC试件设计详图(虚线表示钢绞线)Figure 1. Design details of ECC reinforced by high-strength stainless steel wire mesh specimens (Dotted line indicates steel strand)表 2 ECC受拉试验结果Table 2. Tensile test results of ECCGroup number Tensile strength/MPa Ultimate tensile strain Cracking stress/MPa Cracking strain TC12 3.53 0.0179 2.45 0.000204 TC22 3.53 0.0179 2.45 0.000204 TC32 3.53 0.0179 2.45 0.000204 TC42 3.53 0.0179 2.45 0.000204 TC52 3.53 0.0179 2.45 0.000204 TD12 3.46 0.0297 2.39 0.000189 TD22 3.46 0.0297 2.39 0.000189 TD32 3.46 0.0297 2.39 0.000189 TD42 3.46 0.0297 2.39 0.000189 ![]()
图 2 高强不锈钢绞线应力-应变曲线Figure 2. Stress-strain curves of high-strength stainless steel strand1.2 加载及测试方法
单轴拉伸试验采用100 kN电液伺服万能试验机。试验加载采用位移控制，加载速率为0.2 mm/min。试件正反面分别粘贴应变片，测试区段两侧面分别布置量程为30 mm的位移计。
1.3 试验现象及机制分析
高强不锈钢绞线网增强ECC试件受拉试验的加载装置如图3(a)所示。当荷载达到极限荷载的25%~30%时，在试件接近中间位置表面出现一条细微裂缝(如图3(b)所示)，宽度仅为0.02 mm。随着荷载的增加，试件表面不断出现新的裂缝，已有的裂缝宽度缓慢增大；当荷载增加到极限荷载的85%~90%，裂缝数量达到饱和状态(如图3(c)所示)，试件表面布满相互平行的细微裂缝，此时各试件的最大裂缝宽度为0.2~0.28 mm，该状态的荷载远远超过了规范GB 50010—2010[23]规定的正常使用极限状态。继续加载，试件表面不再出现新裂缝，已有裂缝变宽。达到极限荷载时，试件表面的某条裂缝发展成主裂缝，同时伴随着明显的纤维拔出和断裂声，随后主裂缝处的纵向高强不锈钢绞线拉断。试件破坏形态如图3(d)所示。
![]()
图 3 高强不锈钢绞线网增强ECC试件受拉破坏过程Figure 3. Tensile failure process of ECC reinforced by high-strength stainless steel wire mesh specimens分析上述试验现象发现，高强不锈钢绞线的加入增加了ECC裂缝分散能力，其机制主要是钢绞线表面的螺旋进一步限制了ECC裂缝的开展，使受拉试件在达到极限承载力的85%~90%时，最大裂缝宽度依然满足规范GB 50010—2010[23]中正常使用极限状态裂缝要求。充分表明了本文研究的新型复合材料高强不锈钢绞线网增强ECC具有良好的抗裂性能；验证了高强不锈钢筋网和ECC具有很好的粘结性能。
2. 试验结果及分析
2.1 试验结果
各组高强不锈钢绞线网增强ECC试件拉伸试验结果见表3 (试验值均取同一组试件的平均值，应力为试验拉力除以受力面积)。
表 3 高强不锈钢绞线网增强ECC试件拉伸试验结果Table 3. Tensile test results of ECC reinforced by high-strength stainless steel wire mesh specimensGroup number Cracking stress/MPa Cracking strain Ultimate tensile stress/MPa Ultimate tensile strain Elastic modulus/MPa TC12 2.20 0.000156 7.09 0.030874 14 471 TC22 2.25 0.000162 7.94 0.034056 14 122 TC32 2.41 0.000171 8.77 0.030581 14 492 TC42 2.56 0.000182 10.65 0.034815 14 578 TC52 2.54 0.000181 8.82 0.033683 14 642 TD12 1.97 0.000145 6.41 0.031929 14 216 TD22 1.99 0.000149 7.81 0.043660 14 727 TD32 2.07 0.000139 8.62 0.041116 14 460 TD42 2.19 0.000159 10.30 0.035051 14 496 2.1.1 试件宽度对高强不锈钢绞线网增强ECC受拉性能的影响
对比表3中TC32组和TC52组试件，结果表明，增大截面宽度对受拉试件的开裂应力和极限应力几乎没有影响。
2.1.2 高强不锈钢绞线配筋率对高强不锈钢绞线网增强ECC受拉性能的影响
对比表3中TC12~TC42及TD12~TD42试件的试验结果可知，随着高强不锈钢绞线配筋率的增大，受拉试件的开裂应力略有增大，极限应力明显增大。
2.1.3 ECC抗拉强度对高强不锈钢绞线网增强ECC受拉性能的影响
对比表3中TC12组与TD12组、TC22组与TD22组、TC32组与TD32组及TC42组与TD42组试件结果可知，随着ECC抗拉强度的增大，受拉试件的开裂应力和极限应力均明显增大。
2.2 高强不锈钢绞线网增强ECC受拉应力-应变曲线
高强不锈钢绞线网增强ECC试件在单轴荷载作用下的受拉应力-应变曲线如图4所示。可知，高强不锈钢绞线网增强ECC试件受拉应力-应变曲线呈现出明显的两阶段特征，故可将其分为两个阶段：(1)可表征为弹性阶段，从试件开始加载到试件开裂为止，为峰值的25%~30%。在该阶段ECC和不锈钢绞线均处于弹性工作状态；应力-应变曲线接近为直线；(2)可表征为弹塑性阶段，对应于试件ECC开裂至完全破坏(纵向高强不锈钢绞线拉断)。该阶段应力-应变曲线为非线性关系，试件表现出明显的弹塑性性质。此阶段主要是ECC裂缝出现和发展，由于裂缝处的聚乙烯醇(PVA)纤维尚未从水泥基中拔出或拉断，而高强不锈钢绞线表面的螺旋增大了与ECC的粘结力。因此，该阶段ECC和高强不锈钢绞线依然共同承担拉力，亦是高强不锈钢绞线网增强ECC受拉的主要阶段。由图4还可以看出，极限应力是开裂应力的3~5倍，极限应变为开裂应变的200倍以上，达到3%~5%，超过了本文采用的ECC和高强不锈钢绞线本身的极限拉应变，显示了该新型高性能复合材料优越的变形能力。
![]()
图 4 高强不锈钢绞线网增强ECC试件受拉应力-应变曲线Figure 4. Tensile stress-strain curves of ECC reinforced by high-strength stainless steel wire mesh specimens3. 高强不锈钢绞线网增强ECC受拉本构模型
3.1 模型提出
由图4可知，高强不锈钢绞线网增强ECC受拉应力-应变曲线可分为弹性阶段(OA段)和应变硬化阶段(AB段)。弹性阶段即认为应力-应变为线性关系；弹塑性(应变硬化)阶段应力由ECC和钢绞线共同承担，其本构模型由二者应力-应变关系组合而成。同时考虑该阶段高强不锈钢绞线网和ECC可能产生相对滑移，用γ表示钢绞线的应力发挥系数。本文提出了高强不锈钢绞线网增强ECC受拉本构模型，如图5所示。其表达式如下：
![]()
图 5 高强不锈钢绞线网增强ECC受拉应力-应变曲线模型Figure 5. Tensile stress-strain curve model of ECC reinforced by high-strength stainless steel wire meshσse={Eseεse(εse⩽ (1) 式中：σse、σse,cr和σse,u分别为高强不锈钢绞线网增强ECC试件的受拉应力、开裂应力和极限拉应力；σe和σs分别为ECC和高强不锈钢绞线的应力；Ese为高强不锈钢绞线网增强ECC的弹性模量；εse、εse,cr和εse,u分别为高强不锈钢绞线网增强ECC试件的受拉应变、开裂应变和极限拉应变；γ为高强不锈钢绞线的应力发挥系数；ρs为高强不锈钢绞线的配筋率。
3.2 模型参数分析
3.2.1 弹性阶段
高强不锈钢绞线网增强ECC受拉试件开裂前，由高强不锈钢绞线和ECC共同承担外部荷载；该阶段高强不锈钢绞线网与ECC间无滑移。根据应变协调原理得出弹性阶段高强不锈钢绞线网增强ECC受拉试件的弹性模量Ese如下式：
{E_{\rm{se}}} = {E_{\rm{e}}} + {E_{\rm{s}}}\frac{{{A_{\rm{s}}}}}{{{A_{\rm{se}}}}} (2) 式中：Ee和Es分别为ECC和高强不锈钢绞线的弹性模量；Ase和As分别为高强不锈钢绞线网增强ECC和高强不锈钢绞线的截面面积。
3.2.2 弹塑性阶段
首先建立高强不锈钢绞线受拉本构模型。对本试验得到的高强不锈钢绞线应力-应变曲线(图2)采用三次多项式进行拟合，如下式：
\frac{{{\sigma _{\rm{s}}}}}{{{\sigma _{\rm{s,u}}}}} = a\frac{{{\varepsilon _{\rm{s}}}}}{{{\varepsilon _{\rm{s,u}}}}} + (3 - 2a){\left( {\frac{{{\varepsilon _{\rm{s}}}}}{{{\varepsilon _{\rm{s,u}}}}}} \right)^2} + (a - 2){\left( {\frac{{{\varepsilon _{\rm{s}}}}}{{{\varepsilon _{\rm{s,u}}}}}} \right)^3}\tag{3a} (3a) 式中：σs,u为高强不锈钢绞线的极限拉应力；εs和εs,u分别为高强不锈钢绞线应变和极限拉应变。
根据式(3a)，基于最小二乘法对试验数据进行回归分析，得到待定常数a的值。对三组数据进行拟合，其值分别为3.37、3.26和3.36。由拟合结果可知，各组值较接近，故可取其平均值a=3.33。将a代入式(3a)，则有：
\frac{{{\sigma _{\rm{s}}}}}{{{\sigma _{\rm{s,u}}}}} = 3.33\frac{{{\varepsilon _{\rm{s}}}}}{{{\varepsilon _{\rm{s,u}}}}} - 3.66{\left( {\frac{{{\varepsilon _{\rm{s}}}}}{{{\varepsilon _{\rm{s,u}}}}}} \right)^2} + 1.33{\left( {\frac{{{\varepsilon _{\rm{s}}}}}{{{\varepsilon _{\rm{s,u}}}}}} \right)^3}\tag{3b} (3b) ECC的受拉应力-应变关系采用刘伟康[5]的研究成果，如下式：
\!\!\!\!\!\!\quad{\sigma _{\rm{e}}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{\sigma _{\rm{e,cr}}}}}{{{\varepsilon _{\rm{e,cr}}}}}{\varepsilon _{\rm{e}}}}&{\;\;\left( {{\varepsilon _{\rm{e}}} \leqslant {\varepsilon _{\rm{e,cr}}}} \right)}\\ {\left( {0.31\dfrac{{{\varepsilon _{\rm{e}}}}}{{{\varepsilon _{\rm{e,u}}}}} + 0.69} \right){\sigma _{\rm{e,u}}}}&{\left( {{\varepsilon _{\rm{e,cr}}} \leqslant {\varepsilon _{\rm{e}}} \leqslant {\varepsilon _{\rm{e,u}}}} \right)} \end{array}} \right. (4) 式中：σe,cr和σe,u为ECC的开裂应力和极限拉应力；εe、εe,cr和εe,u为ECC的应变、开裂应变和极限拉应变。
3.2.3 高强不锈钢绞线应力发挥系数γ
将式(2)、式(3b)和式(4)代入式(1)，则高强不锈钢绞线网增强ECC受拉本构关系可表示为
{\sigma _{\rm{se}}}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {\left( {{E_{\rm{e}}} + {E_{\rm{s}}}\dfrac{{{A_{\rm{s}}}}}{{{A_{\rm{se}}}}}} \right){\varepsilon _{\rm{se}}}} \\ \begin{array}{l} \!\!\!\!\!\!\!\!\gamma \left[ {{\rm{3}}{\rm{.33}}\dfrac{{{\varepsilon _{\rm{se}}}}}{{{\varepsilon _{\rm{se,u}}}}}{\rm{ - 3}}{\rm{.66}}{{\left( {\dfrac{{{\varepsilon _{\rm{se}}}}}{{{\varepsilon _{\rm{se,u}}}}}} \right)}^2}{\rm{ + 1}}{\rm{.33}}{{\left( {\dfrac{{{\varepsilon _{\rm{se}}}}}{{{\varepsilon _{\rm{se,u}}}}}} \right)}^3}} \right]{\sigma _{\rm{s,u}}}\dfrac{{{A_{\rm{s}}}}}{{{A_{\rm{se}}}}} +\\ \!\! \left( {{\rm{0}}{\rm{.31}}\dfrac{{{\varepsilon _{\rm{se}}}}}{{{\varepsilon _{\rm{se,u}}}}} + 0.69} \right){\sigma _{\rm{e,u}}} \\ \end{array} \end{array}} \right. (5) 基于应变协调，高强不锈钢绞线网增强ECC的开裂应变与ECC相等，即εse,cr=εe,cr；同时高强不锈钢绞线网增强ECC受拉试件的破坏形态为纵向高强不锈钢绞线拉断破坏，其极限应变主要取决于高强不锈钢绞线的极限应变大小，即εse,u=εs,u。
分别将开裂状态和破坏状态的应变值代入式(5)，利用MATLAB软件进行分析，得到式(5)中高强不锈钢绞线应力发挥系数γ的值，如表4所示。可知，各组值较接近，故取其平均值(0.725)作为式(5)中γ的值。
表 4 高强不锈钢绞线应力发挥系数γ取值Table 4. Value of stress development coefficient γ of high-strength stainless steel strandGroup number γ R2 TC12 0.73 0.9267 TC22 0.72 0.9459 TC32 0.76 0.9607 TD12 0.71 0.9157 TD22 0.72 0.9755 TD32 0.71 0.9325 3.2.4 开裂应力和抗拉强度公式
基于高强不锈钢绞线网增强ECC受拉试件的本构关系模型(式(5))，推导出高强不锈钢绞线网增强ECC受拉试件的开裂应力和极限拉应力即抗拉强度的计算公式：
\left\{ {\begin{array}{*{20}{l}} {{\sigma _{\rm{se,cr}}} = \left( {{E_{\rm{e}}} + {E_{\rm{s}}}\dfrac{{{A_{\rm{s}}}}}{{{A_{\rm{se}}}}}} \right){\varepsilon _{\rm{se,cr}}}} \\ {{f_{\rm{se,u}}} = 0.725{\sigma _{\rm{s,u}}}\dfrac{{{A_{\rm{s}}}}}{{{A_{\rm{se}}}}} + {\sigma _{\rm{e,u}}}} \end{array}} \right. (6) 式中，fse,u为高强不锈钢绞线网增强ECC受拉试件的极限应力，即抗拉强度。
3.3 模型验证
为验证本文提出的高强不锈钢绞线网增强ECC受拉本构模型，将试验得出的应力-应变曲线与式(5)计算的应力-应变曲线进行对比，如图6所示。将试验得出的开裂应力和极限拉应力(抗拉强度)与式(6)计算的结果进行对比，如表5所示。
表 5 试验与式(6)计算得到的高强不锈钢绞线网增强ECC试件开裂应力和极限应力的对比Table 5. Comparison of cracking stress and ultimate tensile stress of ECC reinforced by high-strength stainless steel wire mesh specimens obtained by test and equation (6)Group number Cracking stress/MPa Ultimate tensile stress/MPa T C R T C R TC12 2.20 2.26 0.97 7.09 6.79 1.04 TC22 2.25 2.27 0.99 7.94 7.25 1.10 TC32 2.41 2.28 1.06 8.77 7.87 1.11 TC42 2.56 2.30 1.11 10.65 9.19 1.16 TC52 2.54 2.28 1.11 8.82 7.87 1.12 TD12 1.97 1.94 1.01 6.41 6.58 0.97 TD22 1.99 1.95 1.02 7.81 7.03 1.11 TD32 2.07 1.96 1.06 8.62 7.63 1.13 TD42 2.19 1.98 1.11 10.30 8.90 1.16 Notes: T—Test value; C—Calculated value; R—T/C. ![]()
图 6 高强不锈钢绞线网增强ECC受拉本构模型验证Figure 6. Verification of tensile constitutive model of ECC reinforced by high-strength stainless steel wire mesh从图6可看出，本文提出的本构模型与试验应力-应变曲线整体趋势完全一致。其中，本文所提的受拉本构关系曲线的弹性阶段与试验值基本重合，符合良好；其弹塑性阶段与试验曲线弯曲度均吻合较好(TD42稍有差别)，仅试验在ECC开裂后，荷载有微小波动，属于正常情况。因此，本文提出的高强不锈钢绞线网增强ECC受拉本构模型能较准确地预测受拉应力-应变关系全曲线。表5中的高强不锈钢绞线网增强ECC受拉试件的开裂应力试验值与计算值比值的平均值为1.05，标准差为0.05，变异系数为0.05；极限应力试验值与计算值比值的平均值为1.10，标准差为0.06，变异系数为0.05，说明本文提出的式(6)计算结果和试验值吻合良好。
综上所述，本文提出的高强不锈钢绞线网增强ECC受拉本构模型和开裂应力、抗拉强度计算公式可用于反映高强不锈钢绞线网增强ECC受拉状态的应力-应变关系和分析其受拉性能。
4. 结 论
对高强不锈钢绞线网增强工程水泥基复合材料(Engineered cementitious composites，EEC) 的受拉性能进行试验和理论研究，提出了其受拉本构关系模型。
(1)高强不锈钢绞线表面的螺旋进一步限制了ECC裂缝的开展，增加了ECC裂缝的分散能力，使受拉试件在达到极限承载力的85%时，最大裂缝宽度依然小于规范GB 50010—2010[23]中正常使用极限状态裂缝要求。充分显示了高强不锈钢绞线网增强ECC的良好抗裂性能。
(2)高强不锈钢绞线网增强ECC受拉应力-应变曲线分为弹性阶段和弹塑性阶段，弹塑性阶段是其主要受拉阶段，该阶段是ECC和钢绞线共同受拉至钢绞线拉断，极限应变可达到3%~5%，显示了该新型复合材料优越的变形能力。
(3)随着ECC抗拉强度提高和纵向钢绞线配筋率增大，高强不锈钢绞线网增强ECC的开裂应力和极限拉应力(抗拉强度)均增大。
(4)所建立的受拉本构模型及模型参数计算公式与试验结果吻合良好，能够较好地反映高强不锈钢绞线网增强ECC的受拉应力-应变关系，预测其受力状态；所提出的高强不锈钢绞线网增强ECC受拉开裂应力、抗拉强度的计算公式与试验结果吻合良好，可以用于分析该新型复合材料受拉性能。
-
![]()
图 1 高强不锈钢绞线网增强ECC试件设计详图(虚线表示钢绞线)
Figure 1. Design details of ECC reinforced by high-strength stainless steel wire mesh specimens (Dotted line indicates steel strand)
![]()
图 2 高强不锈钢绞线应力-应变曲线
Figure 2. Stress-strain curves of high-strength stainless steel strand
![]()
图 3 高强不锈钢绞线网增强ECC试件受拉破坏过程
Figure 3. Tensile failure process of ECC reinforced by high-strength stainless steel wire mesh specimens
![]()
图 4 高强不锈钢绞线网增强ECC试件受拉应力-应变曲线
Figure 4. Tensile stress-strain curves of ECC reinforced by high-strength stainless steel wire mesh specimens
![]()
图 5 高强不锈钢绞线网增强ECC受拉应力-应变曲线模型
Figure 5. Tensile stress-strain curve model of ECC reinforced by high-strength stainless steel wire mesh
![]()
图 6 高强不锈钢绞线网增强ECC受拉本构模型验证
Figure 6. Verification of tensile constitutive model of ECC reinforced by high-strength stainless steel wire mesh
表 1 高强不锈钢绞线网增强工程水泥基复合材料(ECC)试件参数
Table 1 Parameters of engineered cementitious composites(ECC) reinforced by high-strength stainless steel wire mesh specimens
Group number Test section width bc /mm Steel strand spacing/mm Reinforcement ratio of steel strand TC12 80 50 0.0028 TC22 70 40 0.0032 TC32 60 30 0.0037 TC42 50 20 0.0048 TC52 90 30 0.0037 TD12 80 50 0.0028 TD22 70 40 0.0032 TD32 60 30 0.0037 TD42 50 20 0.0048 
下载: 导出CSV
表 2 ECC受拉试验结果
Table 2 Tensile test results of ECC
Group number Tensile strength/MPa Ultimate tensile strain Cracking stress/MPa Cracking strain TC12 3.53 0.0179 2.45 0.000204 TC22 3.53 0.0179 2.45 0.000204 TC32 3.53 0.0179 2.45 0.000204 TC42 3.53 0.0179 2.45 0.000204 TC52 3.53 0.0179 2.45 0.000204 TD12 3.46 0.0297 2.39 0.000189 TD22 3.46 0.0297 2.39 0.000189 TD32 3.46 0.0297 2.39 0.000189 TD42 3.46 0.0297 2.39 0.000189
下载: 导出CSV
表 3 高强不锈钢绞线网增强ECC试件拉伸试验结果
Table 3 Tensile test results of ECC reinforced by high-strength stainless steel wire mesh specimens
Group number Cracking stress/MPa Cracking strain Ultimate tensile stress/MPa Ultimate tensile strain Elastic modulus/MPa TC12 2.20 0.000156 7.09 0.030874 14 471 TC22 2.25 0.000162 7.94 0.034056 14 122 TC32 2.41 0.000171 8.77 0.030581 14 492 TC42 2.56 0.000182 10.65 0.034815 14 578 TC52 2.54 0.000181 8.82 0.033683 14 642 TD12 1.97 0.000145 6.41 0.031929 14 216 TD22 1.99 0.000149 7.81 0.043660 14 727 TD32 2.07 0.000139 8.62 0.041116 14 460 TD42 2.19 0.000159 10.30 0.035051 14 496
下载: 导出CSV
表 4 高强不锈钢绞线应力发挥系数γ取值
Table 4 Value of stress development coefficient γ of high-strength stainless steel strand
Group number γ R2 TC12 0.73 0.9267 TC22 0.72 0.9459 TC32 0.76 0.9607 TD12 0.71 0.9157 TD22 0.72 0.9755 TD32 0.71 0.9325
下载: 导出CSV
表 5 试验与式(6)计算得到的高强不锈钢绞线网增强ECC试件开裂应力和极限应力的对比
Table 5 Comparison of cracking stress and ultimate tensile stress of ECC reinforced by high-strength stainless steel wire mesh specimens obtained by test and equation (6)
Group number Cracking stress/MPa Ultimate tensile stress/MPa T C R T C R TC12 2.20 2.26 0.97 7.09 6.79 1.04 TC22 2.25 2.27 0.99 7.94 7.25 1.10 TC32 2.41 2.28 1.06 8.77 7.87 1.11 TC42 2.56 2.30 1.11 10.65 9.19 1.16 TC52 2.54 2.28 1.11 8.82 7.87 1.12 TD12 1.97 1.94 1.01 6.41 6.58 0.97 TD22 1.99 1.95 1.02 7.81 7.03 1.11 TD32 2.07 1.96 1.06 8.62 7.63 1.13 TD42 2.19 1.98 1.11 10.30 8.90 1.16 Notes: T—Test value; C—Calculated value; R—T/C.
下载: 导出CSV
-
[1] LI V C, LEUNG C K Y. Steady-state and multiple cracking of short random fiber composite[J]. Journal of Engineering Mechanics,1992,118(11):2246-2264. DOI: 10.1061/(ASCE)0733-9399(1992)118:11(2246)
[2] LI V C, STANG H, KRENCHEL H. Micromechanics of crack bridging in fibre-reinforced concrete[J]. Materials & Structures,1993,26(8):486-494.
[3] 徐世烺 , 李贺东. 超高韧性水泥基复合材料直接拉伸试验研究[J]. 土木工程学报, 2009, 42(9):32-41. DOI: 10.3321/j.issn:1000-131X.2009.09.005 XU Shilang, LI Hedong. Uniaxial tensile experiments of ultra-high toughness cementitious composite[J]. China Civil Engineering Journal,2009,42(9):32-41(in Chinese). DOI: 10.3321/j.issn:1000-131X.2009.09.005
[4] 蔡向荣. 超高韧性水泥基复合材料基本力学性能和应变硬化过程理论分析[D]. 大连: 大连理工大学, 2010. CAI Xiangrong. The basic mechanical performance and strain hardening process theoretical analysis of ultra high toughness cementitious composites[D]. Dalian: Dalian University of Technology, 2010(in Chinese).
[5] 刘伟康. ECC受压和受拉性能及本构模型研究[D]. 郑州: 郑州大学, 2018. LIU Weikang. Study on the compression and tensile properties and the constitutive model of ECC[D]. Zhengzhou: Zhengzhou University, 2018(in Chinese).
[6] 王新玲, 李苗浩夫, 李可. ECC圆柱体轴心受压性能试验研究[J]. 建筑科学, 2019, 35(5):59-63. WANG Xinling, LI Miaohaofu, LI Ke. Experimental research on the axial compression performance of ECC cylinders[J]. Building Science,2019,35(5):59-63(in Chinese).
[7] 李艳, 刘泽军. 高韧性PVA-FRCC单轴受压力学性能及本构关系[J]. 建筑材料学报, 2014, 17(4):606-612. DOI: 10.3969/j.issn.1007-9629.2014.04.008 LI Yan, LIU Zejun. Study on mechanical performance and constitutive equation of high toughness PVA-FRCC under uniaxial compression[J]. Journal of Building Materials,2014,17(4):606-612(in Chinese). DOI: 10.3969/j.issn.1007-9629.2014.04.008
[8] SUTHIWARAPIRAK P, MATSUMOTO T, KANDA T. Flexural fatigue failure characteristics of an engineered cementitious composite and polymer cement mortars[J]. Journal of materials, concrete structures and pavements,2002,718(718):121-134.
[9] FISCHER G, LI V C. Influence of matrix ductility on tension-stiffening behavior of steel reinforced engineering cementitious composites (ECC)[J]. ACI Structural Journal,2002,99(1):104-114.
[10] MIHASHI H, OTSUKA K, AKITA H, et al. Bond behavior of a deformed bar in high-performance fiber-reinforced cement composites (HPFRCC)[C]//11th International Conference on Fracture, 2005, 2: 1494-1499.
[11] 郑宇宙, 王文炜, 李剑锋, 等. 复材格栅-高延性纤维水泥基受拉本构关系模型[J]. 工业建筑, 2016, 46(5):12-17. ZHENG Yuzhou, WANG Wenwei, LI Jianfeng, et al. The constitutive relationship model of ECC composite strengthened with FRP grid under axial loading[J]. Industrial Construction,2016,46(5):12-17(in Chinese).
[12] 朱忠锋, 王文炜. 玄武岩格栅增强水泥基复合材料单轴拉伸力学性能试验及本构关系模型[J]. 复合材料学报, 2017, 34(10):2367-2374. ZHU Zhongfeng, WANG Wenwei. Experiment on the uniaxial tensile mechanical behavior of basalt grid reinforced engineered cementitious composites and its constitutive model[J]. Acta Materiae Compositae Sinica,2017,34(10):2367-2374(in Chinese).
[13] 聂建国, 王寒冰, 张天申, 等. 高强不锈绞线网-渗透性聚合砂浆抗弯加固的试验研究[J]. 建筑结构学报, 2005, 26(2):1-9. DOI: 10.3321/j.issn:1000-6869.2005.02.001 NIE Jianguo, WANG Hanbing, ZHANG Tianshen, et al. Experimental study on flexural behavior of RC beams strengthened with stainless steel wire mesh and permeability polymer mortar[J]. Journal of Building Structures,2005,26(2):1-9(in Chinese). DOI: 10.3321/j.issn:1000-6869.2005.02.001
[14] 胡新舒. 高强钢绞线加固钢筋混凝土梁抗弯疲劳性能的试验研究[D]. 北京: 清华大学, 2004. HU Xinshu. Experimental study on bending fatigue behavior of RC beams strengthened by stainless steel wires[D]. Beijing: Tsinghua University, 2004(in Chinese).
[15] 林于东, 宗周红, 林秋峰. 高强钢绞线网-聚合物砂浆加固混凝土及预应力混凝土梁的抗弯性能试验研究[J]. 工程力学, 2012, 29(9):141-149. LIN Yudong, ZONG Zhouhong, LIN Qiufeng. Experiment study on flexural behavior of RC/PRC beams strengthened with high strength steel wire mesh and permeable polymer mortar[J]. Engineering Mechanics,2012,29(9):141-149(in Chinese).
[16] 郭瑞, 蔡联亨, 潘毅, 等. 聚合物水泥砂浆-碳纤维网格加固层与混凝土界面的黏结性能试验研究[J]. 建筑结构学报, 2018, 39(9):167-174. GUO Rui, CAI Lianheng, PAN Yi, et al. Experimental study on bonding behavior of interface between concrete and CFRP grid-PCM[J]. Journal of Building Structures,2018,39(9):167-174(in Chinese).
[17] 聂建国, 蔡奇, 张天申, 等. 高强不锈钢网-渗透性聚合砂浆抗剪加固的试验研究[J]. 建筑结构学报, 2005, 26(2):10-17. DOI: 10.3321/j.issn:1000-6869.2005.02.002 NIE Jianguo, CAI Qi, ZHANG Tianshen, et al. Experimental study on shear behavior of RC beams strengthened with stainless steel wire mesh and permeability polymer mortar[J]. Journal of Building Structures,2005,26(2):10-17(in Chinese). DOI: 10.3321/j.issn:1000-6869.2005.02.002
[18] 王亚勇, 姚秋来, 巩正光, 等. 高强钢绞网-聚合物砂浆在郑成功纪念馆加固工程的应用[J]. 建筑结构, 2005, 35(8):41-42. WANG Yayong, YAO Qiulai, GONG Zhengguang, et al. Application of strengthened technology by composite cover combined with high strength wire cable mesh and polymeric mortar in Zheng Chenggong memorial strengthening engineering[J]. Building Structure,2005,35(8):41-42(in Chinese).
[19] 王大愚, 仝胜强, 朱同然, 等. 中国美术馆加固改造综合施工技术[J]. 施工技术, 2009, 38(6):60-62. WANG Dayu, TONG Shengqiang, ZHU Tongran, et al. Comprehensive construction technology of reinforcement and reconstruction in China Art Gallery[J]. Construction Technology,2009,38(6):60-62(in Chinese).
[20] 朱俊涛, 李燚 , 王新玲. 考虑横向钢绞线影响的钢绞线网/工程水泥基复合材料黏结性能试验研究[J]. 工业建筑, 2018, 48(11):143-148. ZHU Juntao, LI Yi, WANG Xinling. Experimental study on bonding performance of stainless steel wire mesh/ECC with horizontal steel wire[J]. Industrial Construction,2018,48(11):143-148(in Chinese).
[21] 周擎威. 高强不锈钢绞线与ECC粘结锚固性能试验研究[D]. 郑州: 郑州大学, 2018. ZHOU Qingwei. Experimental study on bonding performance of high-strength stainless steel stranded wire and ECC[D]. Zhengzhou: Zhengzhou University, 2018(in Chinese).
[22] 朱俊涛, 赵亚楼, 李燚, 等. 高强不锈钢绞线网与工程水泥基复合材料粘结锚固性能试验[J]. 复合材料学报, 2020, 37(7):1731-1742. ZHU Juntao, ZHAO Yalou, LI Yi, et al. Experiment on bonding and anchoring performance between high-strength stainless steel wire mesh and engineered cementitious composites[J]. Acta Materiae Compositae Sinica,2020,37(7):1731-1742(in Chinese).
[23] 中华人民共和国住房和城乡建筑部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2015. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2015(in Chinese).
-
期刊类型引用(16)
1. 王新玲，李世伟，金蕾蕾，范家俊. 高强不锈钢绞线网/ECC约束高强混凝土受压本构模型. 工程力学. 2023(09): 153-160 . 
百度学术
2. 王新玲，罗鹏程，钱文文，李可. 高强不锈钢绞线网增强工程水泥基复合材料薄板受弯承载力研究. 建筑结构学报. 2022(01): 164-172 . 百度学术
3. 姚淇耀，陆宸宇，彭林欣，滕晓丹，罗月静. 氯盐侵蚀作用下BFRP筋增强海砂ECC的拉伸及弯曲性能试验. 复合材料学报. 2022(03): 1215-1227 . 本站查看
4. 朱俊涛，张凯，邹旭岩，李可，张普. 钢绞线与水泥基复合材料局部黏结滑移模型. 哈尔滨工程大学学报. 2022(04): 541-548 . 百度学术
5. 王新玲，李赟璞，李苗浩夫，范家俊. 高强不锈钢绞线网增强ECC加固RC短柱轴心受压试验. 复合材料学报. 2022(05): 2308-2317 . 本站查看
6. 朱俊涛，张凯，王新玲，李可. 高强钢绞线网增强ECC与混凝土界面黏结-滑移关系研究. 工程力学. 2022(09): 204-214 . 百度学术
7. 李可，王宇，李志强，朱俊涛. 高强钢绞线网增强ECC加固无损RC梁受弯承载力研究. 建筑结构学报. 2022(12): 82-90 . 百度学术
8. 李可，李思辰，周擎威，王新玲. 高强钢绞线与工程水泥基复合材料黏结性能试验. 沈阳工业大学学报. 2022(06): 706-713 . 百度学术
9. 惠迎新，王文炜，朱忠锋. FRP-ECC复合约束混凝土圆柱反复受压力学性能. 复合材料学报. 2022(11): 5586-5598 . 本站查看
10. 王新玲，陈永杰，钱文文，李可，朱俊涛. 高强不锈钢绞线网增强工程水泥基复合材料弯曲性能试验. 复合材料学报. 2021(04): 1292-1301 . 本站查看
11. 王春红，左祺，支中祥，徐磊，SARANI Zakaria，SHERAZ Hussain Siddique Yousfani. 聚乙烯醇乳液改性对汉麻秸秆纤维/水泥基复合材料性能的影响. 复合材料学报. 2021(05): 1567-1575 . 本站查看
12. 朱俊涛，赵奎，邹旭岩，王新玲，李可，张哲. 高强不锈钢绞线网在ECC中的搭接性能. 土木与环境工程学报(中英文). 2021(03): 174-182 . 百度学术
13. 朱俊涛，侯晶强，王新玲，李可. 基于损伤演化的钢绞线网/ECC黏结滑移关系. 华中科技大学学报(自然科学版). 2021(06): 103-108 . 百度学术
14. 范建伟，李可，王新玲. 高性能复合材料“高强钢绞线/ECC”板受弯试验分析. 建筑科学. 2021(09): 130-136 . 百度学术
15. 王新玲，卫垚鑫，范建伟，朱俊涛. 新型复合材料“高强钢绞线网/ECC约束素混凝土”受压性能试验研究. 复合材料学报. 2021(11): 3904-3911 . 本站查看
16. 王新玲，赵要康，周擎威，朱俊涛. 高强不锈钢绞线与ECC黏结滑移性能研究. 华中科技大学学报(自然科学版). 2020(12): 108-113 . 百度学术
其他类型引用(2)
-
计量
- 文章访问数: 1618
- HTML全文浏览量: 510
- PDF下载量: 79
- 被引次数: 18
