Enhanced theory and finite element method for wrinkling analysis of composite sandwich structure
-
摘要: 复合材料软核夹芯结构承受面内载荷，面板可能出现褶皱。一旦面板出现褶皱，夹芯结构将失去承载能力。因此，需要发展准确的理论模型预测软核夹芯结构褶皱行为。夹芯结构褶皱是典型三维(3D)问题，鲜有高阶模型能准确预测此类问题。为此，提出考虑局部形变和三维效应的增强型高阶模型。基于此理论，推导了梁单元公式，并分析了不同边界条件复合材料夹芯结构的起皱行为。通过与准三维弹性解和三维有限元解对比，提出方法的准确性得到验证。为了提高夹芯结构抗起皱能力，尝试使用复合材料面板代替金属面板。数值分析结果表明，发展的增强型高阶模型可以准确分析复合材料夹芯结构褶皱行为，并且使用复合材料面板可有效提升夹芯结构抗起皱能力。Abstract: Panels wrinkling behaviors may occur when composite soft-core sandwich structures subjected to coplanar compression loads. Once the panels wrinkling appears, the sandwich structures will lose its load-bearing capacity. Therefore, it is necessary to develop an accurate model to predict the wrinkling behaviors of soft-core sandwich structures. Sandwich structure wrinkling is a typical three-dimensional (3D) problem, and few high-order models can accurately predict such issues. Therefore, this paper proposed an enhanced higher-order model including the local deformation and the 3D effects. Based on the proposed theory, the beam element formulation was derived, and the wrinkling behaviors of sandwich structures with different boundary conditions were analyzed. By comparing with the quasi-3D elasticity solution and the 3D finite element results, accuracy of the proposed method has been verified. In order to improve the capability of sandwich structures resisting the wrinkling deformation, this work attempted to use composite face sheets instead of metal panel in the sandwich structure. Numerical results show that the developed enhanced high-order model can accurately predict the wrinkling behaviors of the composite sandwich structures, and the use of composite panels can effectively resist the wrinkling behaviors of sandwich structures.
-
Keywords:
- composite /
- sandwich structures /
- enhanced higher-order theory /
- wrinkling /
- beam element
-
蜂窝夹层结构具有比模量大、隔音、隔热、吸能强、成本低等优点，在航空航天、交通运输、土木建筑、海洋船舶等许多领域都有广泛的应用[1]。碳纤维增强树脂复合材料（CFRP）蒙皮-铝蜂窝夹层板主要通过蜂窝芯和蒙皮的变形、损伤及内能形式将冲击能量加以耗散，从而达到吸能的目的[2-3]。CFRP板和铝蜂窝在生产和使用过程中都容易受到低速冲击的影响，而且蜂窝夹层板在低速冲击下的损伤一般是目视不可见的，但这种损伤却能够明显降低零部件的寿命和强度[4-5]。因此，研究结构参数对CFRP蒙皮-铝蜂窝夹层结构低速冲击性能的影响很有必要。
国内外有大量关于蜂窝夹层板在不同载荷下力学性能的研究[6-11]。Zhang等[12]通过摆锤冲击试验和数值模拟方法研究了铝蜂窝夹层结构在低速冲击下的动力学特性，并得出结论：蜂窝芯是主要的吸能构件。Chen等[13]通过落锤式低速冲击试验与数值模拟方法验证了试验与仿真结果的一致性，并探究了CFRP面板-Nomex蜂窝夹层结构的损伤机制。A. Riccio等[14]结合落锤冲击试验和仿真模型探究了亚麻天然纤维蜂窝的吸能效果，试验与仿真结果吻合较好。Sun等[15]通过解析法研究了金属蒙皮蜂窝夹层板在低速冲击下的动态响应，通过与已有的试验结果对比，证明了其解析法的可靠性。Vincenzo Crupi等[16]结合试验方法和数值模型，研究了玻璃纤维增强树脂复合材料（GFRP）面板对低速冲击下铝蜂窝结构动力学性能的影响，发现GFRP面板是增强蜂窝夹层板能量吸收和承载能力的重要构件。Inés Ivañez等[17]基于材料用户子程序建立了CFRP面板-铝蜂窝夹层梁低速冲击有限元模型，通过多次试验对比验证了仿真模型的有效性，并得出结论：蜂窝夹层结构受低速冲击时，冲击能量较大时，蒙皮吸能较多，冲击能量较小时，蜂窝芯吸能较多。
目前对不同材料蜂窝夹层板在低速冲击下动态响应的研究有很多[18-22]，但CFRP蒙皮-铝蜂窝夹层板在低速冲击下的损伤模式相对较复杂，关于建立该类型夹层板在低速冲击下的精细化仿真模型，以探究其结构参数对抗低速冲击性能的影响以及各组件损伤对吸能占比的研究比较少，研究结构参数对该类型蜂窝夹层板低速冲击性能的影响，对其在实际工程中的应用及结构参数优化有重要的指导意义。本文使用半球头式落锤冲击试验平台和高速摄像分析平台，进行了蜂窝芯单元边长对CFRP蒙皮-铝蜂窝夹层板抗低速冲击性能影响的试验探究，根据试验结果验证了所建仿真模型的准确性。利用该数值模型进一步探究了蜂窝芯高度、蒙皮厚度和蜂窝芯壁厚等结构参数对蜂窝夹层板低速冲击性能的影响。
1. 试 验
1.1 试验材料及设备
基于D7766/D7766M—11标准[23]，搭建了如图1所示的CFRP蒙皮-铝蜂窝夹层板落锤冲击试验平台，平台主要构成设备包括：XBL-300型落锤式低速冲击试验机及数据采集装置，厂家为长春科新试验仪器有限公司。其中，控制平台、落锤、夹具和防二次冲击装置是试验机的主要构件。使用的i-speed 2系列高速摄像机及配备的ProAnalyst数码分析软件由Xcitex公司提供，如图2所示。
试件蒙皮均采用由威海光威复合材料有限公司提供的CFRP层合板，CFRP蒙皮是型号为T300/7901的碳纤维增强环氧树脂复合材料，铺层顺序为(45/-45/0)2s，单层厚度为0.1 mm，单块蒙皮长L=100 mm，宽W=100 mm，厚Tf =1.2 mm；铝蜂窝采用Al 3003-H19铝箔粘接而成，蜂窝芯壁厚Tc=0.06 mm，铝芯高Hc=20 mm，正六边形蜂窝芯单元边长Lc=2 mm、4 mm、6 mm；蜂窝芯与蒙皮之间采用LJM-170胶膜进行粘接；夹层板总体尺寸为100 mm×100 mm×22.4 mm。图3为蜂窝夹层板的几何构型示意图及试件，表1为T300/7901层合板的材料参数[24]，表2为Al 3003-H19铝箔的材料参数。
表 1 CFRP蒙皮的材料参数Table 1. Mechanical properties of CFRP laminatesT300/7901 Value Adhesive Value E1/MPa 125 000 GCn/(N⋅mm−1) 0.52 E2,E3/MPa 11 300 GCs,GCt/(N⋅mm−1) 0.92 G12,G13/MPa 5 430 σn,max 50 {G_{23}}{\rm{/MPa}} 3 979 {\sigma _{{\rm{s}},\max }}{\rm{/MPa}} 94 ν12, ν23 0.3 {\sigma _{{\rm{t}},\max }}{\rm{/MPa}} 94 ν23 0.42 {K_{\rm{n}}}{\rm{/(N}} \cdot {\rm{m}}{{\rm{m}}^{ - {\rm{3}}}}{\rm{)}} 100 000 {X_{\rm{T}}}{\rm{/MPa}} 2 000 {K_{\rm{s} } },{K_{\rm{t} } }{\rm{/(N} } \cdot {\rm{m} }{ {\rm{m} }^{ - {\rm{3} } } }{\rm{)} } 100 000 {X_{\rm{C}}}{\rm{/MPa}} 1 100 {Y_{\rm{T}}},{Z_{\rm{T}}}{\rm{/MPa}} 80 {Y_{\rm{C}}},{Z_{\rm{T}}}{\rm{/MPa}} 280 S{\rm{/MPa}} 120 Notes: Ei(i=1,2,3) is Young’s modulus in i direction; Gij(i,j=1,2,3) is shear modulus in i-j plane; νij(i,j=1,2,3) is Poisson’s ratio in i-j plane; Xt/Xc and Yt/Yc are the tensile/compressive strengths in 1 and 2 directions, respectively; S is shear strength; G_{\rm{n}}^{\rm{C}} is toughness in tension; G_{\rm{s}}^{\rm{C}}and G_{\rm{t}}^{\rm{C}} are toughness components in shear; σn,max is maximum nominal stress of normal-only mode; σs,max and σt,max are maximum nominal stress in 1 and 2 directions, respectively; Kn is stiffness in tension; Ks and Kt are stiffness components in shear. 表 2 Al 3003-H19铝箔材料参数Table 2. Material properties of Al3003-H19 aluminum alloy foilProperty Value Density/(kg·m−3) 2 730 Young’s modulus/GPa 70 Poisson’s ratio 0.3 Yield strength/MPa 183 ![]()
图 3 碳纤维增强树脂复合材料（CFRP）蒙皮-铝蜂窝夹层板几何构型示意图及试件Figure 3. Schematic of geometric configurations and specimens of aluminum honeycomb sandwich plates with carbon fiber reinforced polymer (CFRP) face sheets1.2 试验过程
在进行落锤冲击试验时，用夹具将试件固定，设置好落锤下降高度后进行冲击试验。落锤完成冲击时，防二次冲击装置会立刻夹紧落锤。冲击时压力传感器采集的冲击力数据由数据采集装置记录并保存；同时通过高速摄像机记录冲击过程，以便使用ProAnalyst数码分析软件获得落锤在冲击过程中的运动数据。冲击过程中的冲击试验参数：落锤质量m=2.5 kg，半球形冲头直径为25 mm，落锤下降高度h=0.48 m，理论冲击能量为E=11.76 J。由于落锤在下降过程中存在摩擦，通过高速摄像平台测得落锤接触夹层板时初始冲击速度为3.0 m/s，即实际冲击能量为11.25 J。
2. 数值计算模型
2.1 CFRP层合板本构模型
2.1.1 CFRP层合板层内渐进损伤模型
本文引用文献[24-25]中基于渐进损伤力学（CDM）方法对受损的CFRP蒙皮进行刚度退化，此方法定义了损伤因子Df，其值随着材料损伤的扩展而逐渐增大。层合板损伤后利用基于应力描述的三维Hashin准则进行损伤判定：
纤维拉伸失效
\left( {{\sigma _{11}} \geqslant 0} \right) ：{\left( {\frac{{{\sigma _{11}}}}{{{X_{\rm{T}}}}}} \right)^2} + \frac{1}{{{S^2}}}\left( {\sigma _{12}^2 + \sigma _{13}^2} \right) \geqslant 1 (1) 纤维压缩失效
\left( {{\sigma _{11}} < 0} \right) ：{\left( {\frac{{{\sigma _{11}}}}{{{X_{\rm{C}}}}}} \right)^2} \geqslant 1 (2) 基体开裂失效
\left( {{\sigma _{22}} + {\sigma _{33}} \geqslant 0} \right) ：\frac{1}{{Y_{\rm{T}}^2}}{\left( {{\sigma _{22}} + {\sigma _{33}}} \right)^2} + \frac{1}{{{S^2}}}\left( {\sigma _{23}^2 - {\sigma _{22}}{\sigma _{23}}} \right) + \frac{1}{{{S^2}}}\left( {\sigma _{12}^2 + \sigma _{13}^2} \right) \geqslant 1 (3) 基体压溃失效
\left( {{\sigma _{22}} + {\sigma _{33}} < 0} \right) ：\begin{split} \frac{1}{{{Y_{\rm{C}}}}}\left[ {{{\left( {\frac{{{Y_{\rm{C}}}}}{{2S}}} \right)}^2} - 1} \right]\left( {{\sigma _{22}} + {\sigma _{33}}} \right) + \frac{1}{{4{S^2}}}{\left( {{\sigma _{22}} + {\sigma _{33}}} \right)^2} + \\ \frac{1}{{{S^2}}}\left( {\sigma _{23}^2 - {\sigma _{22}}{\sigma _{23}}} \right) + \frac{1}{{{S^2}}}\left( {\sigma _{12}^2 + \sigma _{13}^2} \right) \geqslant 1 \end{split} (4) 其中，σij（i，j=1,2,3）为CFRP面板单元的各个方向应力张量。
2.1.2 CFRP层合板层间胶层损伤模型
基于内聚力（Cohesive）单元的双线性本构模型，建立了CFRP层合板胶层模型以模拟CFRP层合板的分层损伤。内聚力单元的双线性本构模型如图4所示[26-28]，σ轴表示单元的应力，δ横轴表示单元的相对分离位移。当δ<δ0时，内聚力单元未破坏，其应力和相对位移呈线性关系，刚度为K，即O→A段；当δ0≤δ<δmax时，内聚力单元发生部分破坏，卸载时单元进入线性软化阶段，如图4中虚线部分，此时刚度为(1-Df)K，Df为损伤因子，即O→A→B→O段，如重加载，初始阶段内聚力单元的σ与δ的关系即对应O→B段；当δ≥δmax时，内聚力单元完全失效。
A点表示材料开始出现损伤，其对应的损伤准则为
{\left( {\frac{{{{\left( {{t_{\rm{n}}}} \right)}^2}}}{{t_{\rm{n}}^0}}} \right)^2} + {\left( {\frac{{{{\left( {{t_{\rm{s}}}} \right)}^2}}}{{t_{\rm{s}}^0}}} \right)^2} + {\left( {\frac{{{{\left( {{t_{\rm{t}}}} \right)}^2}}}{{t_{\rm{t}}^0}}} \right)^2} \geqslant 1 (5) 其中，
t_{\rm{n}}^0 、t_{\rm{s}}^0 、t_{\rm{t}}^0 分别表示内聚力单元的法向和两个切向强度。AB段表示内聚力单元的损伤扩展，本文选择与试验吻合度较高的基于能量释放率的B-K准则[24]：G_{\rm{n}}^{\rm{C}} + \left( {G_{\rm{s}}^{\rm{C}} - G_{\rm{n}}^{\rm{C}}} \right){\left( {\frac{{{G_{\rm{S}}}}}{{{G_{\rm{T}}}}}} \right)^\eta } = {G^{\rm{C}}} (6) 其中：GS=Gs+Gt，GT=Gn+GS，
G_{\rm{s}}^{\rm{C}} = G_{\rm{t}}^{\rm{C}} ；Gi（i=n,s,t）为Cohesive单元的应变能释放率；G_i^{\rm{C}} 为单元的临界应变能释放率；GC对应图4中△OAC的面积，即单元开裂对应的总临界能释放率；η为单元材料修正系数。2.2 CFRP蒙皮-铝蜂窝夹层板低速冲击有限元模型
基于CFRP层合板本构模型和用户材料子程序VUMAT，在ABAQUS有限元分析软件上建立蜂窝夹层板在低速冲击下的精细化仿真模型，如图5所示，蜂窝夹层板结构参数如表3所示。其中，层合板采用C3D8R单元，层间胶层采用COH3D8单元，铝蜂窝芯采用S4R壳单元；夹具和落锤均设置为刚体，夹具限制所有自由度，落锤仅保留冲击方向的自由度；假设蒙皮与蜂窝芯始终保持粘接，其接触类型设置为“Tie”，冲头与蒙皮采用“面-面接触”；为了节约计算成本，仅对临近冲击区域蒙皮进行网格细化，细化区域网格大小为1.5 mm×1.5 mm，其余区域网格大小为3 mm×3 mm，蜂窝芯网格大小为1 mm×2 mm。
表 3 CFRP蒙皮-铝蜂窝夹层板的结构参数Table 3. Structural parameters of aluminum honeycomb sandwich plate with CFRP face sheetsLabel Cell side length {L_{\rm{c}}}/mm Core height {H_{\rm{c}}}/mm Facesheet thickness {T_{\rm{f}}}/mm Cell wall thickness {T_{\rm{c}}}/mm A1 2 20 1.2 0.06 A2 4 20 1.2 0.06 A3 6 20 1.2 0.06 B1 4 10 1.2 0.06 B2 4 20 1.2 0.06 B3 4 30 1.2 0.06 C1 4 20 1.2 0.06 C2 4 20 1.8 0.06 C3 4 20 2.4 0.06 D1 4 20 1.2 0.06 D2 4 20 1.2 0.10 D3 4 20 1.2 0.14 ![]()
图 5 CFRP蒙皮-铝蜂窝夹层板的低速冲击有限元模型Figure 5. Finite element model of aluminum honeycomb sandwich plate with CFRP face sheets for low-velocity impact simulation3. 模型验证
为了证明数值模拟方法所建有限元模型的准确性，以本文的试验参数为参照，将数值模拟计算结果与试验结果进行对比。在保证其他参数相同的条件下，蜂窝芯单元边长Lc=2 mm、4 mm、6 mm的CFRP蒙皮-铝蜂窝夹层板在质量m=2.5 kg、下降高度h=0.46 m的半球头落锤的冲击下（仿真中设置落锤初始速度为3 m/s），仿真与试验的接触力历程对比如图6所示，通过高速摄像平台采集分析了落锤的速度历程，仿真与试验速度历程对比如图7所示。
![]()
图 6 试验与仿真中CFRP蒙皮-铝蜂窝夹层板的接触力历程对比Figure 6. Comparison of experimental and numerical contact force historiesof aluminum honeycomb sandwich plate with CFRP face sheets![]()
图 7 试验与仿真中落锤的速度历程对比Figure 7. Comparison of experimental and numerical velocity histories of the impactor通过对比图6和图7的仿真和试验数据可知：在相同能量的冲击作用下，三种蜂窝芯单元边长夹层板在仿真中的接触力峰值分别为4 037 N、3 666 N和2 854 N，试 验d接触力峰值分别为3 799 N、3 476 N和2 811 N，仿真和试验接触力峰值的偏差分别为6.24%、5.47%和1.53%；仿真和试验的接触时长的差值分别为0.72 ms、0.40 ms和0.11 ms。试验与仿真在接触力历程和速度历程的总体趋势方面具有良好的一致性。
将A组所有受冲击后的蜂窝夹层板由冲击区域的中心纵向切开，会发现受冲击位置的上蒙皮与芯层之间的胶层脱粘，蜂窝芯存在折叠和屈曲，上蒙皮的下表面均有部分基体开裂的现象。试验与仿真的蜂窝芯损伤深度对比如表4所示，不同蜂窝芯单元边长的夹层板在相同的冲击能量下得到了三种不同的变形深度，A组试验中受低速冲击区域蜂窝芯变形深度分别为2.15 mm、2.77 mm和4.32 mm，仿真中的蜂窝芯变形深度δ分别为2.20 mm、3.03 mm和4.10 mm。仿真与试验得到夹层板的蜂窝芯变形量之间的偏差分别为2.33%、9.39%和5.09%。由于本文设置的低速冲击能量较小，下蒙皮未发生任何形式的损伤，故不再在文中赘述其受载情况。
表 4 试验与仿真中蜂窝芯损伤深度δ的对比Table 4. Comparison of experimental and numerical deformations δ of honeycomb coresLabel Top face sheet Cross-section Experiment Simulation-Honeycomb core A1 
A2 
A3 
综上所述，所搭建的低速冲击有限元仿真模型可以较为准确地预测低速冲击下CFRP蒙皮-铝蜂窝夹层板的动力学响应。
图8为三种不同蜂窝芯边长的CFRP蒙皮-铝蜂窝夹层板在质量m=2.5 kg、初始冲击速度为3 m/s的半球头落锤的冲击下，有限元模型预测的A组落锤动能历程，图9为预测的接触力-位移关系。可知，相同冲击能量下的蜂窝芯边长Lc分别为2 mm、4 mm、6 mm的CFRP蒙皮-铝蜂窝夹层板的最大变形深度依次增大，分别为5.26 mm、6.25 mm、7.40 mm。
![]()
图 8 A组CFRP 蒙皮-铝蜂窝夹层板试件落锤的动能历程对比Figure 8. Comparison of kinetic energy histories of the impactor for group A aluminum honeycomb sandwich plate with CFRP face sheets specimens![]()
图 9 A组CFRP 蒙皮-铝蜂窝夹层板试件落锤的接触力-位移对比Figure 9. Comparison of contact force-central displacement histories of the impactor for group A aluminum honeycomb sandwich plate with CFRP face sheets specimens通过分析可知：随着蜂窝芯单元边长的增大，夹层板受冲击时，落锤动能减小速率逐渐降低，接触时长逐渐增加，接触力峰值随之减小，夹层板受冲击位置的变形深度随之增大。可见，增大蜂窝芯单元的边长会降低蜂窝夹层板的刚度，但其吸能效果会随之增强。
4. 结构参数对CFRP蒙皮-铝蜂窝夹层板吸能的影响
4.1 蜂窝芯高度对CFRP蒙皮-铝蜂窝夹层板吸能的影响
为了确定在低速冲击载荷下，蜂窝芯高度Hc对CFRP蒙皮-铝蜂窝夹层板吸能特性的影响，在仿真中使用了Hc=10 mm、20 mm、30 mm三种不同高度的蜂窝芯，蜂窝芯单元边长Lc=4 mm，蒙皮厚度Tf=1.2 mm，蜂窝芯壁厚Tc=0.06 mm，其余条件保持不变。图10为该工况下落锤的接触力历程对比，图11为落锤的动能历程对比，图12为落锤的接触力-位移关系对比。
![]()
图 10 B组CFRP 蒙皮-铝蜂窝夹层板试件落锤的接触力历程对比Figure 10. Comparison of contact force histories of the impactor for group B aluminum honeycomb sandwich plate with CFRP face sheets specimens![]()
图 11 B组CFRP 蒙皮-铝蜂窝夹层板试件落锤的动能历程对比Figure 11. Comparison of kinetic energy histories of the impactor for group B aluminum honeycomb sandwich plate with CFRP face sheets specimens![]()
图 12 B组CFRP 蒙皮-铝蜂窝夹层板试件落锤的接触力-位移对比Figure 12. Comparison of contact force-central displacement histories of the impactor for group B aluminum honeycomb sandwich plate with CFRP face sheets specimens由图10~12可知：在蜂窝芯高度Hc=10 mm、20 mm、30 mm的该组仿真中，三种蜂窝夹层板在低速冲击载荷下，落锤的接触力峰值分别为3852N、3666N、3674N，接触时长分别为5.81 ms、5.85 ms、5.82 ms，最大变形深度分别为6.25 mm、6.26 mm、6.38 mm，且落锤的接触力历程、动能历程和接触力-位移的图形几乎保持一致。B组仿真中预测的蜂窝夹层板冲击损伤如表5所示。可知，蜂窝芯受冲击区域的最终变形量δ分别为2.97 mm、3.03 mm和3.08 mm，其变形量相差较小。由该组仿真结果可见，蜂窝芯高度的变化对于CFRP蒙皮-铝蜂窝夹层板的刚度和抗低速冲击性能影响不大。
表 5 仿真预测的B组CFRP蒙皮-铝蜂窝夹层板冲击损伤Table 5. Simulation predicted impact damage of group B aluminum honeycomb sandwich plate with CFRP face sheetsLabel Cross-section Honeycomb sandwich plate Honeycomb core B1 
B2 
B3 
4.2 蒙皮厚度对CFRP蒙皮-铝蜂窝夹层板吸能的影响
为了确定蒙皮厚度Tf对低速冲击载荷下CFRP蒙皮-铝蜂窝夹层板吸能特性的影响，在仿真中使用了Tf=1.2 mm、1.8 mm、2.4 mm三种不同厚度的CFRP蒙皮，蜂窝芯单元边长为4 mm，蜂窝芯高度Hc=20 mm，蜂窝芯壁厚Tc=0.06 mm，其余条件保持不变。图13为该工况下落锤的接触力历程对比，图14为落锤的动能历程对比，图15为落锤的接触力-位移关系对比。
![]()
图 13 C组CFRP 蒙皮-铝蜂窝夹层板试件落锤的接触力历程对比Figure 13. Comparison of contact force histories of the impactor for group C aluminum honeycomb sandwich plate with CFRP face sheets specimens![]()
图 14 C组CFRP 蒙皮-铝蜂窝夹层板试件落锤的动能历程对比Figure 14. Comparison of kinetic energy histories of the impactor for group C aluminum honeycomb sandwich plate with CFRP face sheets specimens![]()
图 15 C组CFRP 蒙皮-铝蜂窝夹层板试件落锤的接触力-位移对比Figure 15. Comparison of contact force-central displacement histories of the impactor for group C aluminum honeycomb sandwich plate with CFRP face sheets specimens由图13~15可知：在蒙皮厚度Tf=1.2 mm、1.8 mm、2.4 mm的该组仿真中，三种蜂窝夹层板在相同冲击能量的低速冲击载荷下，落锤的接触力峰值分别为3666N、3923N、4314N，接触时长分别为5.85 ms、5.13 ms、4.28 ms，最大变形深度分别为6.26 mm、5.14 mm、4.39 mm。C组仿真中预测的蜂窝夹层板冲击损伤如表6所示。可知，蜂窝芯受冲击区域的最终变形量δ分别为3.03 mm、2.41 mm和2.13 mm。随着蜂窝夹层板蒙皮厚度的增大，冲击时，落锤动能的减小速率随之增大，接触时间随之减少，接触力的峰值随之增大，夹层板受冲击区域的变形量随之减小。可见，蒙皮厚度的增加会使蜂窝夹层板的刚度增大，吸能效果随之降低。
表 6 仿真预测的C组CFRP蒙皮-铝蜂窝夹层板冲击损伤Table 6. Simulation predicted impact damage of group C aluminum honeycomb sandwich plate with CFRP face sheetsLabel Cross-section Honeycomb sandwich plate Honeycomb core C1 
C2 
C3 
4.3 蜂窝芯壁厚对CFRP蒙皮-铝蜂窝夹层板吸能的影响
为了探究低速冲击载荷下，蜂窝芯壁厚Tc对CFRP蒙皮-铝蜂窝夹层板吸能特性的影响，在仿真中使用了Tc=0.06 mm、0.10 mm、0.14 mm三种不同壁厚的蜂窝芯，蜂窝芯单元边长为4 mm，蜂窝芯高度Hc=20 mm，蒙皮厚度Tf=1.2 mm，其余条件保持不变。图16为该工况下落锤的接触力历程对比，图17为落锤的动能历程对比，图18为落锤的接触力-位移关系对比。
![]()
图 16 DCFRP 蒙皮-铝蜂窝夹层板组试件落锤的接触力历程对比Figure 16. Comparison of contact force histories of the impactor for group D aluminum honeycomb sandwich plate with CFRP face sheets specimens![]()
图 17 DCFRP 蒙皮-铝蜂窝夹层板组试件落锤的动能历程对比Figure 17. Comparison of kinetic energy histories of the impactor for group D specimens![]()
图 18 D组CFRP 蒙皮-铝蜂窝夹层板试件落锤的接触力-位移对比Figure 18. Comparison of contact force-central displacement histories of the impactor for group D aluminum honeycomb sandwich plate with CFRP face sheets specimens根据图16~18可知：在蜂窝芯壁厚Tc=0.06 mm、0.10 mm、0.14 mm的该组仿真中，三种蜂窝夹层板在相同冲击能量的低速冲击载荷下，落锤的接触力峰值分别为3666N、4153N、4454N，接触时长分别为5.85 ms、5.31 ms、4.99 ms，最大变形深度分别为6.26 mm、5.50 mm、5.28 mm。仿真预测的D组蜂窝夹层板冲击损伤如表7所示。可知，蜂窝芯受冲击区域的最终变形量δ分别为3.03 mm、2.83 mm和2.77 mm。随着蜂窝夹层板蜂窝芯壁厚的增大，在低速冲击下，落锤动能的减小速率随之增大，接触时间随之减少，落锤与夹层板之间的接触力峰值随之增大，夹层板受冲击区域的变形量随之减小。可见，增加蜂窝芯的壁厚会使蜂窝夹层板的刚度增大，抗低速冲击的性能增强。
表 7 仿真预测的D组CFRP蒙皮-铝蜂窝夹层板冲击损伤Table 7. Simulation predicted impact damage of group D aluminum honeycomb sandwich plate with CFRP face sheetsLabel Cross-section Honeycomb sandwich plate Honeycomb core D1 
D2 
D3 
4.4 各组件吸能占比
表8为不同结构参数的CFRP蒙皮-铝蜂窝夹层板在相同能量的低速冲击下，各组件的吸能占比情况。可知：在本文设置的较低能量级冲击载荷下，CFRP蒙皮-铝蜂窝夹层板的吸能占比均大于60%，足以证明蜂窝夹层结构具有较好的冲击吸能特性；在该规格的冲击条件下，CFRP蒙皮-铝蜂窝夹层板最主要的吸能组件是铝蜂窝芯，上蒙皮吸能次之，下蒙皮吸能最少。由A组夹层板吸能占比分析可知，随着蜂窝芯单元边长的增大，蜂窝芯吸能占比逐渐增大，上蒙皮吸能占比逐渐减小，夹层板总吸能逐渐增大；由B组数据分析可知，随着蜂窝芯高度的增大，蜂窝芯吸能占比逐渐增大，上蒙皮吸能逐渐减少，夹层板总吸能逐渐增大；由C组数据分析可知，随着蒙皮厚度的增大，蜂窝芯层吸能占比逐渐减小，上蒙皮吸能占比逐渐增大，夹层板总吸能逐渐增大；由D组数据分析可知，随着蜂窝芯壁厚的增大，蜂窝芯吸能占比逐渐减小，上蒙皮吸能占比逐渐增大，夹层板总吸能逐渐增大。综上所述，在本文所设置的载荷条件下，增大蜂窝芯单元边长、蜂窝芯高度、蒙皮厚度和蜂窝芯壁厚，均能增加蜂窝夹层板的吸能量。然而吸能效果需结合碰撞时的接触时长、接触力峰值、变形损伤深度和吸能量综合考虑，故需结合图表才能得到合理的结论。
表 8 不同结构参数的CFRP蒙皮-铝蜂窝夹层板组件吸能占比Table 8. Absorbed energy rates by components of aluminum honeycomb sandwich plate with CFRP face sheets with different structural parameters% Parameters Cell side length {L_{\rm{c}}} Core height {H_{\rm{c}}} Facesheet thickness {T_{\rm{f}}} Cell wall thickness {T_{\rm{c}}} A1 A2 A3 B1 B2 B3 C1 C2 C3 D1 D2 D3 Upper plate 20.43 17.29 16.49 19.53 17.29 16.04 17.29 26.97 31.72 17.29 20.88 30.02 Honeycomb 45.16 50.01 58.60 38.45 50.01 57.35 50.01 43.20 39.78 50.01 45.61 41.75 Lower plate 1.88 1.70 2.51 2.15 1.70 1.70 1.70 1.08 0.72 1.70 2.69 3.32 Impactor 32.53 31.00 22.40 39.87 31.00 24.91 31.00 28.05 27.78 31.00 30.82 24.91 Sandwich plate 67.37 69.00 77.60 60.13 69.00 75.09 69.00 71.95 72.22 69.00 69.18 75.09 5. 结 论
建立了碳纤维增强树脂复合材料（CFRP）蒙皮-铝蜂窝夹层板精细化低速冲击仿真模型，通过对比不同蜂窝芯边长的夹层板在相同冲击能量下的仿真与试验结果，证明了试验与仿真结果具有较好的一致性。进而利用该数值模型探究了蜂窝芯高度、蒙皮厚度和蜂窝芯壁厚等结构参数对于蜂窝夹层板低速冲击性能的影响。
（1）随着蜂窝芯单元边长的增大，夹层板受冲击时，落锤动能减小速率逐渐降低，接触时长逐渐增加，接触力峰值随之减小，夹层板受冲击位置的变形深度随之增大。可见，蜂窝芯单元边长尺寸的增大会降低蜂窝夹层板的刚度，但其吸能效果会随之增强。
（2）蜂窝夹层板的芯层高度对夹层板的刚度及抗低速冲击性能影响较小。
（3）增大蜂窝夹层板的蒙皮厚度，可以提高夹层板的刚度，但会降低夹层板的吸能效果。
（4）增大蜂窝芯壁厚，会提高蜂窝夹层板的刚度和抗低速冲击性能。
（5）在本文的低速冲击条件下，CFRP蒙皮-铝蜂窝夹层板的蜂窝芯是主要的吸能组件，上蒙皮吸能占比次之，下蒙皮吸能最少。
-
![]()
图 1 三层夹芯梁截面
tc—Thickness of the core layer; tf—Thickness of the panel layer
Figure 1. Three-layer sandwich beam section
![]()
图 2 构建的高阶单元收敛率
BE18—Enhanced higher-order model; 3D-FEM—Three-dimensional finite element method
Figure 2. Convergence rate of constructed higher-order elements
![]()
图 3 三层铝面板夹芯梁屈曲和褶皱载荷(芯材与面板厚度之比tc/tf =50，夹芯梁长厚比a/h=2)
Figure 3. Buckling and wrinkling loads for three-layer sandwich beam with aluminum face sheets (Ratio of core thickness to panel thickness is tc/tf=50, ratio of length to thickness is a/h=2)
![]()
图 4 使用当前模型和3D有限元模型(3D-FEM)计算得到的三层铝面板夹芯梁屈曲行为的位移模态
Figure 4. Displacement modes for buckling behaviors of a three-layer aluminum panel sandwich beam calculated by using the current model and 3D finite element method (3D-FEM)
m—Number of half waves
![]()
图 5 使用当前模型和3D-FEM计算得到的三层铝面板夹芯梁褶皱行为的位移模态
Figure 5. Displacement modes for wrinkling behaviors of a three-layer aluminum panel sandwich beam calculated by using the current model and 3D-FEM
![]()
图 6 材料参数和几何参数对三层铝面板夹芯梁屈曲和褶皱载荷影响
Figure 6. Influence of material properties and geometric parameters on buckling and wrinkling loads of three-layer sandwich beam with aluminum face sheets
![]()
图 7 几何参数对三层铝面板夹芯梁屈曲和褶皱载荷影响
Figure 7. Influence of geometric parameters on buckling and wrinkling loads of three-layer sandwich beam with aluminum face sheets
表 1 3D有限元边界条件
Table 1 Boundary condition for 3D finite element
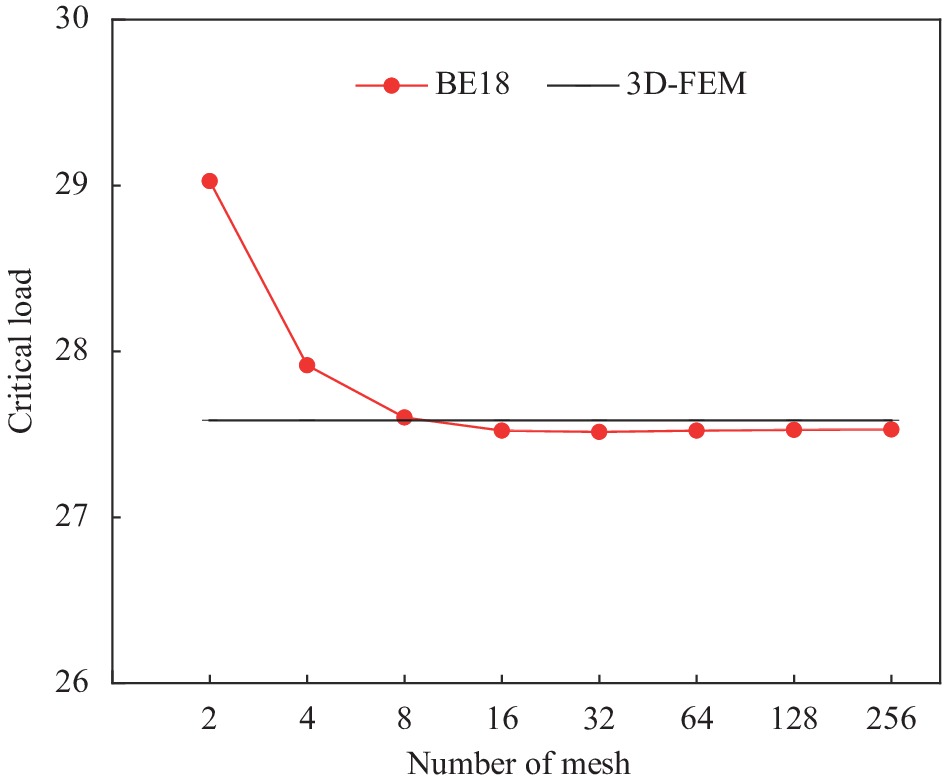
x=0 x=a y=0 y=1 U2=U3=UR3=0 U3=UR3=0 U2=0 U2=0 Notes: a—Length of the sandwich beam; U2, U3, UR3—Translational and rotational degrees of freedom in ABAQUS, respectively. 
下载: 导出CSV
表 2 三层铝面板夹芯梁屈曲载荷
Table 2 Buckling load of three-layer sandwich beam with aluminum panels
tc/tf a/h 3D-FEM
(270000 elements)BE18
(64 elements)HYF11[20] HYF21[20] HOST[21] Allen[22] 5 2 6.6111 6.7131(1.54) 6.2220(5.89) 37.551(468.00) 37.238(463.26) 6.3544(3.88) 5 14.7065 14.838(0.89) 14.320(2.63) 159.0500(981.49) 159.3200(983.33) 14.385(2.19) 10 41.6580 41.8190(0.39) 41.0840(1.38) 329.6300(691.28) 321.2600(671.18) 41.1150(1.30) 25 2 1.5342 1.5600(1.68) 1.5299(0.28) 2.3207(51.26) 2.3112(50.64) 1.5923(3.79) 5 9.0749 9.1046(0.33) 9.0314(0.48) 13.1300(44.68) 13.1130(44.50) 9.0971(0.24) 10 31.6490 31.6550(0.02) 31.0960(1.75) 42.4330(34.07) 42.4360(34.08) 31.1590(1.55) 50 2 1.4432 1.4640(1.44) 1.4419(0.09) 1.8335(27.04) 1.8301(26.81) 1.5074(4.45) 5 8.5657 8.6504(0.99) 8.5553(0.12) 10.3110(20.38) 10.3010(20.26) 8.6191(0.62) 10 27.5850 27.5220(0.23) 26.7620 (2.98) 30.7460(11.46) 30.7690(11.54) 26.8490(2.67) Notes: tc/tf—Core and panel thickness ratio; a/h—Span thickness ratio of sandwich beam; BE18—Present model; HYF11—Quasi-3D model; HYF21 and HOST—Higher-order models; Allen represents the model proposed by Allen.
下载: 导出CSV
表 3 三层铝面板夹芯梁褶皱载荷
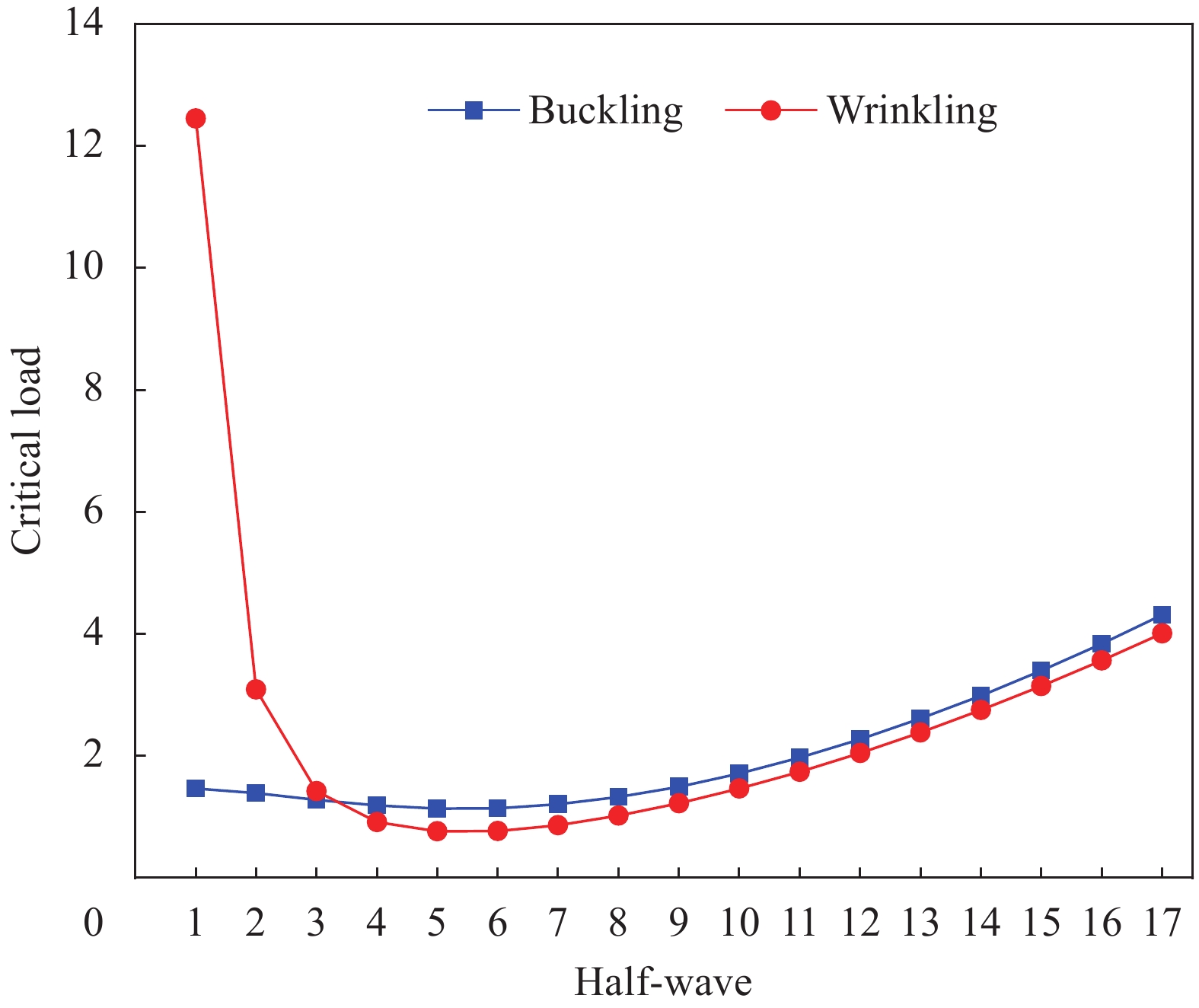
Table 3 Wrinkling loads of three-layer sandwich beam with aluminum panels
tc/tf a/h 3D-FEM
( 270000 elements)BE18
(480 elements)HYF11[20] HYF21[20] Allen[22] 50 2 0.7311 (5) 0.7632 (5) 0.7073 (6) 0.8074 1.3020 (9) 5 4.5097 (13) 4.7147 (14) 4.3583 (14) 5.0048 8.1376 (23) 10 18.0910 (27) 18.8830 (27) 17.4330 (28) 20.0190 – 100 2 0.2610 (9) 0.2845 (9) 0.2517 (9) 0.3121 0.6638(9) 5 1.6318 (22) 1.7768 (22) 1.5736 (23) 1.9480 4.1486 (22) 10 6.5273 (44) 7.1612 (43) 6.2921 (45) 7.7921 16.594 (45) Note: Numbers in brackets represent half-wave numbers.
下载: 导出CSV
表 4 三层复合材料夹芯梁屈曲载荷
Table 4 Buckling load of three-layer composite sandwich beam
tc/tf a/h 3D-FEM
(270000 elements)BE18
(240 elements)BHSDT[24] RHSDT[25] 25 2 11.301 11.457 14.951 15.525 5 64.288 64.441 85.873 89.282 10 239.100 239.200 313.650 325.220 50 2 10.016 10.135 13.442 12.360 5 61.853 61.978 80.805 73.963 10 222.560 222.510 280.980 259.830 Notes: BHSDT—Higher order model proposed by Babu et al[24]; RHSDT—Higher-order model proposed by Reddy[25].
下载: 导出CSV
表 5 三层复合材料夹芯梁褶皱载荷
Table 5 Wrinkling load of three-layer composite sandwich beam
tc/tf a/h SS CC 3D-FEM
(270000 elements)BE18
(480 elements)3D-FEM
(270000 elements)BE18
(480 elements)50 2 7.5768 (4) 8.0174 (4) 8.0246 (4) 8.5964 (4) 5 46.4130 (11) 49.2650 (11) 47.1010 (11) 50.0860 (11) 10 185.7200 (22) 197.4900 (22) 186.4300 (21) 198.3100 (21) 100 2 2.7004 (7) 2.8531 (7) 2.7806 (7) 2.9505 (7) 5 16.8350 (18) 17.8290 (18) 16.9290 (18) 17.9370 (18) 10 7.3330 (36) 1.7410 (36) 7.4410 (36) 1.8490 (36) Notes: SS—Simply supported boundary conditions; CC—Clamped supported boundary conditions; Numbers in brackets represent half-wave numbers.
下载: 导出CSV
-
[1] 杜冰, 刘后常, 潘鑫, 等. 热塑性复合材料夹芯结构熔融连接研究进展[J]. 复合材料学报, 2022, 39(7):3044-3058. DOI: 10.13801/j.cnki.fhclxb.20220228.001 DU Bing, LIU Houchang, PAN Xin, et al. Progress in fusion bonding of thermoplastic composite sandwich structures[J]. Acta Materiae Compositae Sinica,2022,39(7):3044-3058(in Chinese). DOI: 10.13801/j.cnki.fhclxb.20220228.001
[2] 熊健, 李志彬, 刘惠彬, 等. 航空航天轻质复合材料壳体结构研究进展[J]. 复合材料学报, 2021, 38(6):1629-1650. DOI: 10.13801/j.cnki.fhclxb.20210107.002 XIONG Jian, LI Zhibin, LIU Huibin, et al. Advances in aerospace lightweight composite shell structure[J]. Acta Materiae Compositae Sinica,2021,38(6):1629-1650(in Chinese). DOI: 10.13801/j.cnki.fhclxb.20210107.002
[3] JI W, WAAS A M. Global and local buckling of a sandwich beam[J]. Journal of Engineering Mechanics,2007,133(2):230-237. DOI: 10.1061/(ASCE)0733-9399(2007)133:2(230)
[4] VADAKKE V, CARLSSON L A. Experimental investigation of compression failure of sandwich specimens with face/core debond[J]. Composites Part B: Engineering,2004,35:583-590. DOI: 10.1016/j.compositesb.2003.10.004
[5] KHALILI S M R, KHEIRIKHAH M M, FARD K M. Buckling analysis of composite sandwich plates with flexible core using improved high-order theory[J]. Mechanics of Advanced Materials and Structures,2015,22(4):233-247. DOI: 10.1080/15376494.2012.736051
[6] BENSON A S, MAYERS J. General instability and face wrinkling of sandwich plates-Unified theory and applications[J]. AIAA Journal, 1967, 5(4): 729-739.
[7] HADI B K, MATTHEWS F L. Development of Benson-Mayers theory on the wrinkling of anisotropic sandwich panels[J]. Composite Structures,2000,49(4):425-434. DOI: 10.1016/S0263-8223(00)00077-5
[8] DAFEDAR J B, DESAI Y M, MUFTI A A. Stability of sandwich plates by mixed, higher-order analytical formulation[J]. International Journal of Solids and Structures,2003,40(17):4501-4517. DOI: 10.1016/S0020-7683(03)00283-X
[9] LOPATIN A V, MOROZOV E V. Symmetrical facing wrinkling of composite sandwich panels[J]. Journal of Sandwich Structures & Materials,2008,10(6):475-497.
[10] JI W, WAAS A M. Wrinkling and edge buckling in orthotro-pic sandwich beams[J]. Journal of Engineering Mechanics,2008,134(6):455-461. DOI: 10.1061/(ASCE)0733-9399(2008)134:6(455)
[11] HU H, BELOUETTAR S, POTIER-FERRY M, et al. A novel finite element for global and local buckling analysis of sandwich beams[J]. Composite Structures,2009,90(3):270-278. DOI: 10.1016/j.compstruct.2009.02.002
[12] YU K, HU H, TANG H, et al. A novel two-dimensional finite element to study the instability phenomena of sandwich plates[J]. Computer Methods in Applied Mechanics and Engineering,2015,283:1117-1137. DOI: 10.1016/j.cma.2014.08.006
[13] DOUVILLE M A, LE GROGNEC P. Exact analytical solutions for the local and global buckling of sandwich beam-columns under various loadings[J]. International Journal of Solids and Structures,2013,50:2597-2609. DOI: 10.1016/j.ijsolstr.2013.04.013
[14] D'OTTAVIO M, POLIT O. Linearized global and local buckling analysis of sandwich struts with a refined quasi-3D model[J]. Acta Mechanica,2015,226(1):81-101. DOI: 10.1007/s00707-014-1169-2
[15] D'OTTAVIO M, POLIT O, JI W, et al. Benchmark solutions and assessment of variable kinematics models for global and local buckling of sandwich struts[J]. Composite Structures,2016,156:125-134. DOI: 10.1016/j.compstruct.2016.01.019
[16] VESCOVINI R, D'OTTAVIO M, DOZIO L, et al. Buckling and wrinkling of anisotropic sandwich plates[J]. International Journal of Engineering Science,2018,130:136-156. DOI: 10.1016/j.ijengsci.2018.05.010
[17] HUANG Q, LIU Y, HU H, et al. A Fourier-related double scale analysis on the instability phenomena of sandwich plates[J]. Computer Methods in Applied Mechanics and Engineering,2017,318:270-295. DOI: 10.1016/j.cma.2017.01.021
[18] CHEN X, NIE G, WU Z. Global buckling and wrinkling of variable angle tow composite sandwich plates by a modified extended high-order sandwich plate theory[J]. Composite Structures,2022,292:115639. DOI: 10.1016/j.compstruct.2022.115639
[19] 朱秀杰, 郑坚, 熊超, 等. 基于精确板理论的复合材料格栅/波纹夹芯结构屈曲特性[J]. 复合材料学报, 2022, 39(1):399-411. DOI: 10.13801/j.cnki.fhclxb.20210309.003 ZHU Xiujie, ZHENG Jian, XIONG Chao, et al. Buckling characteristics of composite grid/corrugated sandwich structure based on refined plate theory[J]. Acta Materiae Compositae Sinica,2022,39(1):399-411(in Chinese). DOI: 10.13801/j.cnki.fhclxb.20210309.003
[20] DAFEDAR J B, DESAI Y M. Stability of composite and sandwich struts by mixed formulation[J]. Journal of Engineering Mechanics,2004,130(7):762-770. DOI: 10.1061/(ASCE)0733-9399(2004)130:7(762)
[21] KANT T, PATIL H S. Buckling loads of sandwich columns with a higher-order theory[J]. Journal of Reinforced Plastics and Composites,1991,10(1):102-109. DOI: 10.1177/073168449101000107
[22] ALLEN H G. Analysis and design of structural sandwich panels[M]. Oxford: Pergamon Press, 1969.
[23] SZE K Y, CHEN R, CHEUNG Y K. Finite element model with continuous transverse shear stress for composite laminates in cylindrical bending[J]. Finite Elements in Analysis & Design,1998,31(2):153-164.
[24] BABU R T, VERMA S, SINGH B N, et al. Dynamic analysis of flat and folded laminated composite plates under hygrothermal environment using a nonpolynomial shear deformation theory[J]. Composite Structures,2021,274:114327. DOI: 10.1016/j.compstruct.2021.114327
[25] REDDY J N. A simple higher-order theory for laminated composite plates[J]. Journal of Applied Mechanics,1984,51(12):745-752.
-
期刊类型引用(0)
其他类型引用(4)
-
目的
夹芯结构广泛应用于航空航天和航海等领域。对于承受复杂载荷的夹芯结构，褶皱失效行为可能比其它失效模式更早发生。因此，需要构造准确高效的理论模型和数值分析方法研究夹芯结构的屈曲和褶皱失效行为。
方法为研究夹芯梁的屈曲和起皱行为，本文构建了考虑局部形变和横法向应变的增强型高阶模型，该模型满足面内位移和横向剪切应力层间连续条件及自由表面条件。基于构建的理论模型，构造两节点梁单元并分析夹芯结构屈曲和褶皱问题。通过两种算例研究了三层夹芯梁的屈曲和起皱行为。为了评估所提出模型的性能，将本模型的计算结果和准三维弹性解与 ABAQUS的三维有限元解进行比较。为了说明夹芯梁的屈曲和褶皱行为之间的区别，给出了使用本模型和三维有限元计算的屈曲和起皱行为对应的位移模态。进一步使用发展的方法分析了材料参数和几何参数对夹芯梁褶皱临界载荷和屈曲临界载荷的影响规律。
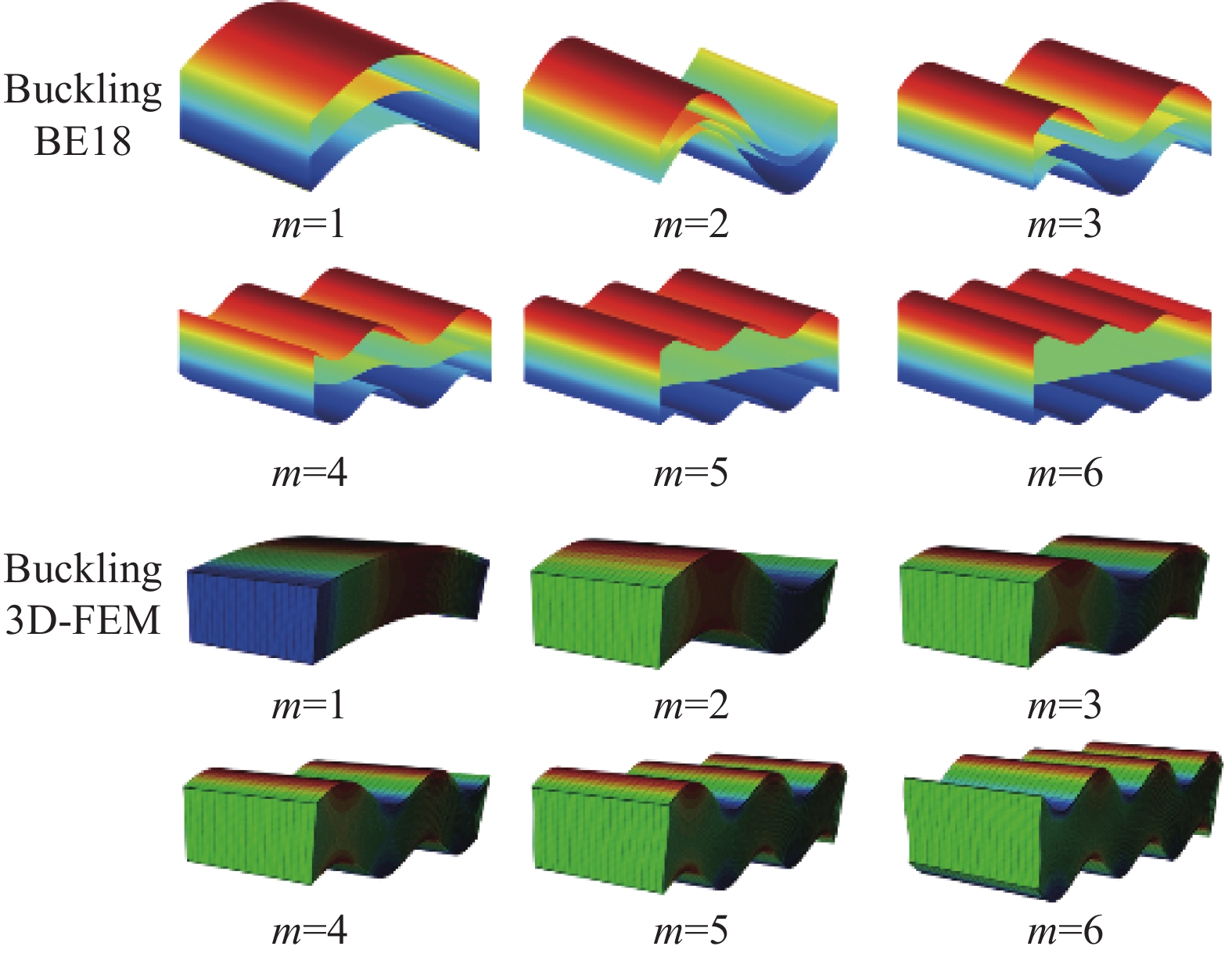
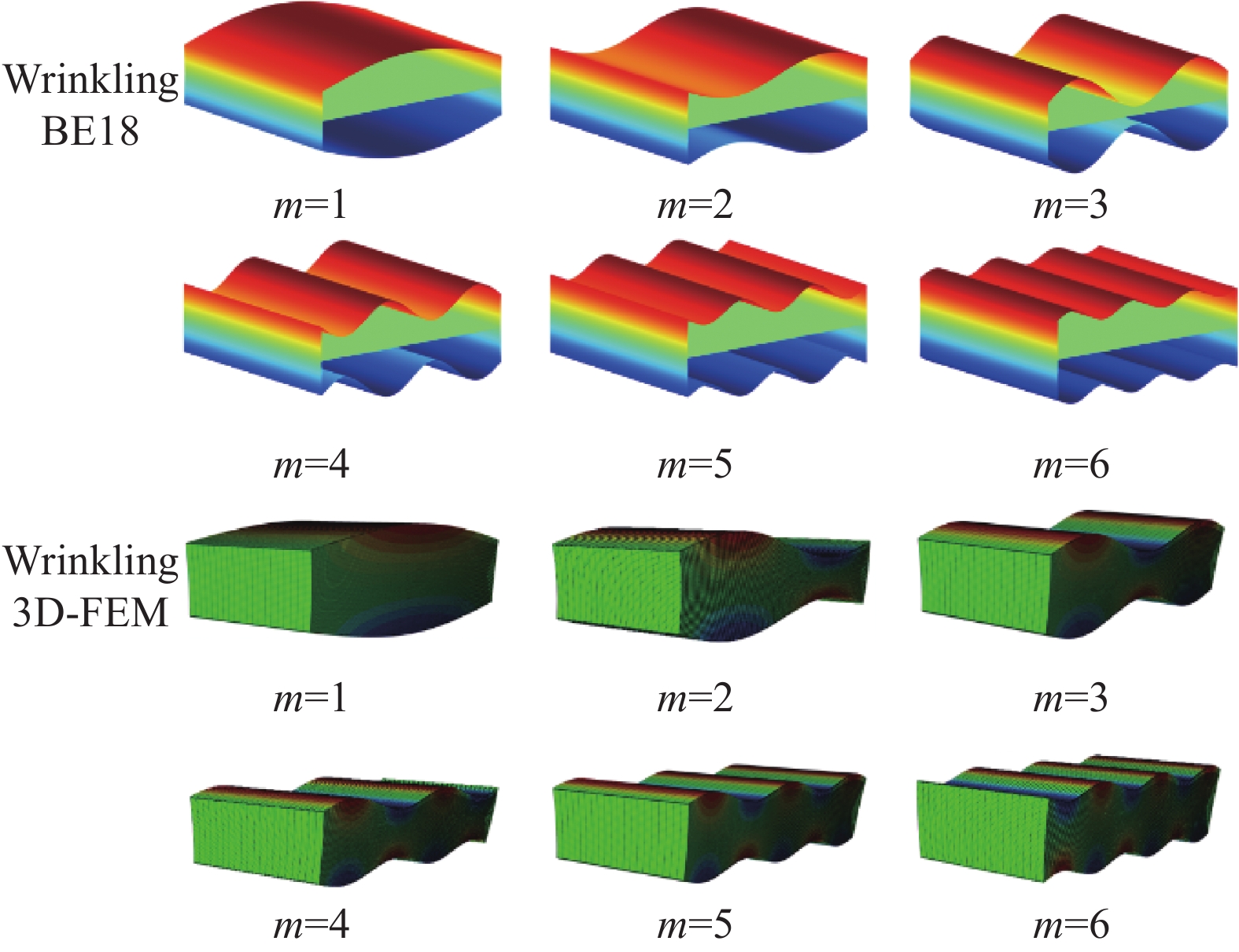
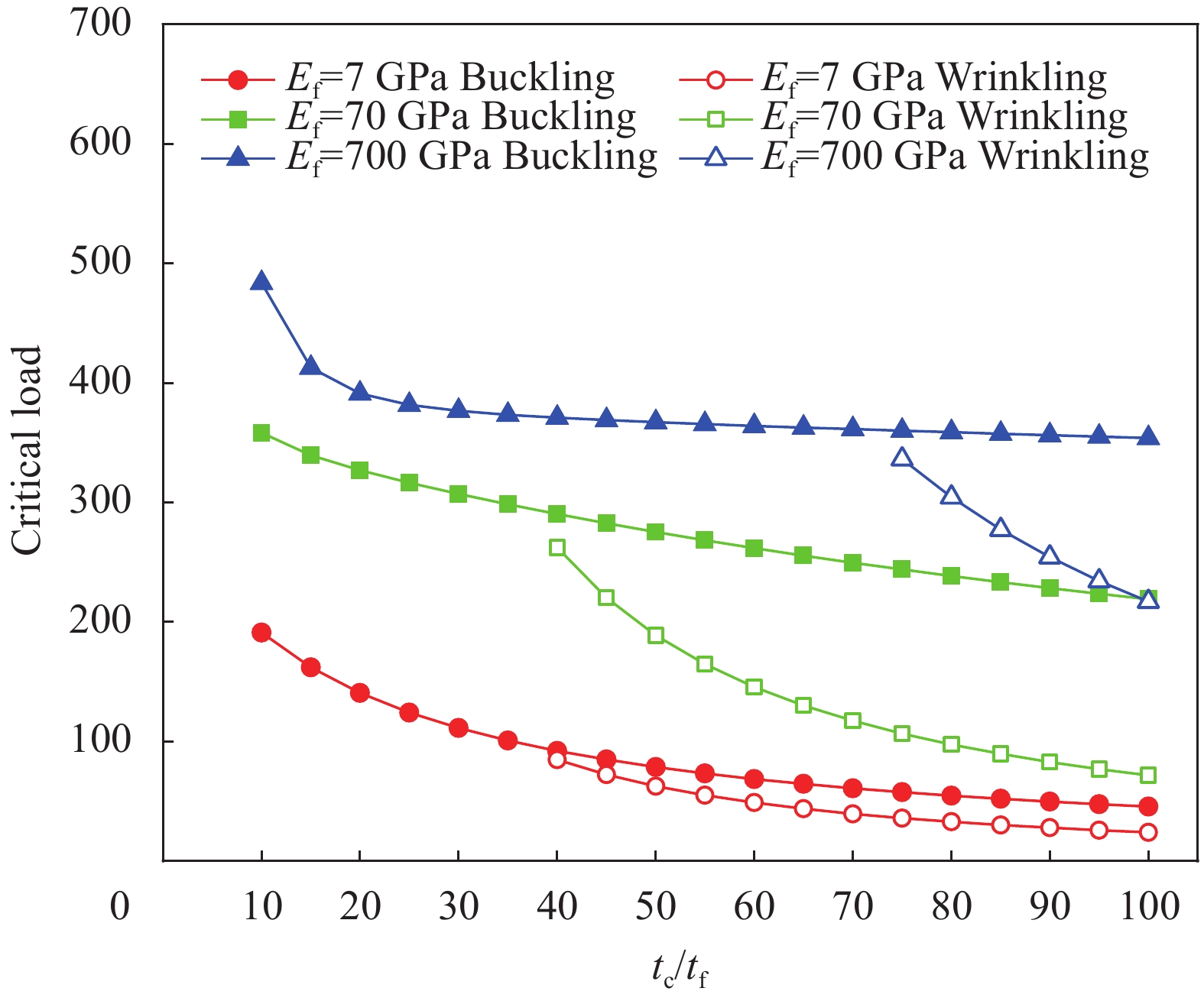
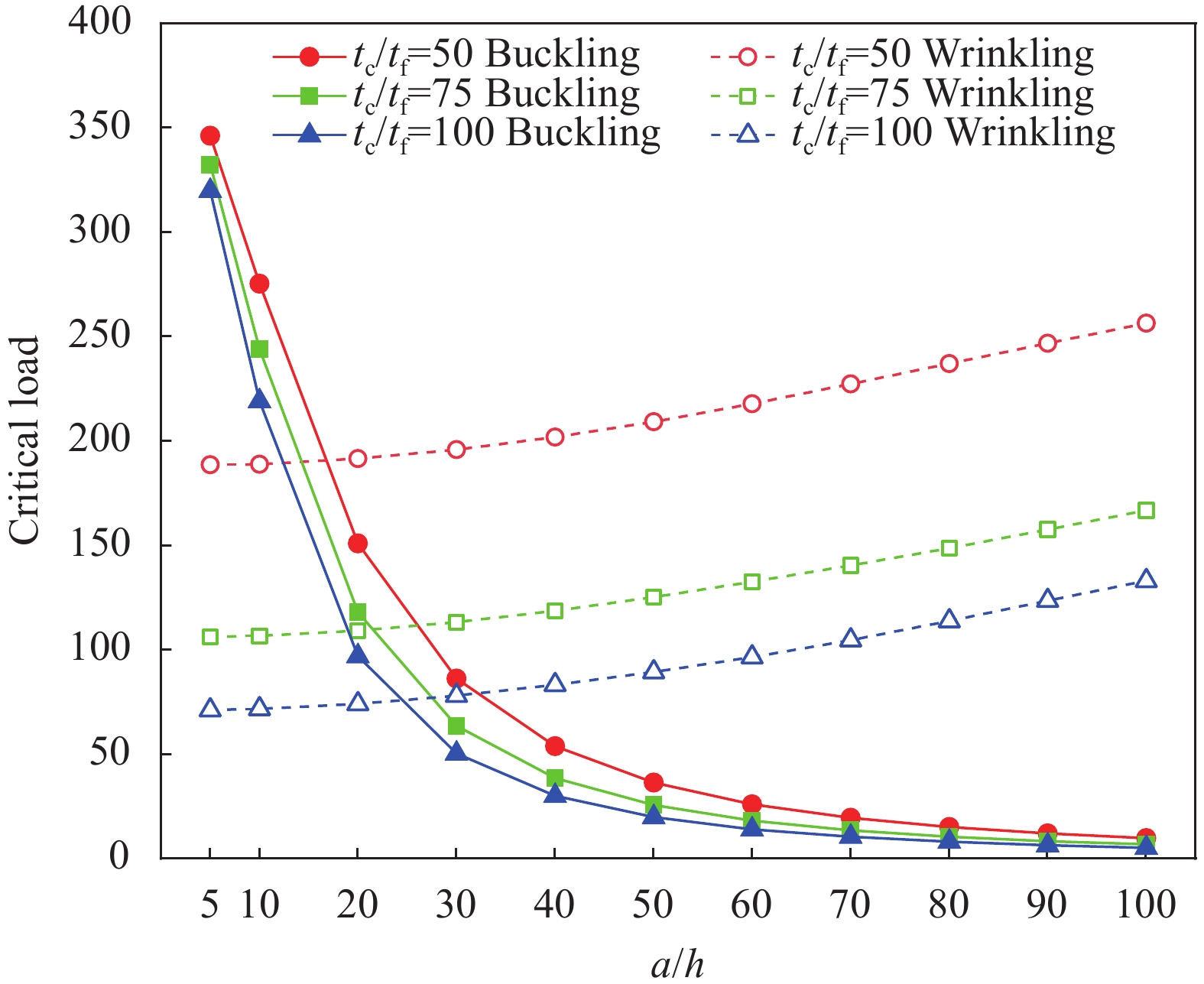
结果首先将本模型的计算结果和准三维弹性解与 ABAQUS的三维有限元解进行比较，验证了本模型的有效性和准确性。使用本模型和三维有限元计算得到的三层铝面板夹芯梁屈曲和起皱行为对应的位移模态，对于屈曲行为，中平面的变形与上下表面的变形一致。对于起皱行为，由于中平面仅受压缩变形，但是上、下表面受到弯曲变形，所以中平面的变形与上下表面的变形完全不同。之后，进一步分析了面板弹性模量，夹芯层和面板厚度比()、夹芯梁长厚比()等参数对夹芯梁褶皱临界载荷和屈曲临界载荷的影响规律。结果表明，通过提高表面层弹性模量可有效提高屈曲和褶皱载荷，随着长厚比()的增加，褶皱载荷缓慢增加，而屈曲载荷降低，相比于屈曲载荷，夹芯层和表面层厚度比()对褶皱载荷有更大影响。此外，使用本模型和三维有限元法分析了三层复合材料夹芯梁的屈曲行为，使用本模型、现有高阶模型以及三维有限元法分析了三层复合材料夹芯梁的屈曲行为，结果表明本模型的预测结果与三维有限元结果误差最小。随后，研究了不同边界条件下三层复合材料夹芯梁的褶皱行为。在简支边界条件下，起皱行为将会先于固支边界条件下发生。而且，使用复合材料面板的夹芯结构能有效增强抵抗褶皱行为的能力。
结论本文提出的增强型高阶模型可以合理地预测夹芯梁的屈曲和起皱行为。与现有高阶模型相比，本模型预测屈曲和褶皱临界载荷的数值分析结果相对三维有限元解的误差更小。夹芯梁起皱行为的发生与夹芯梁结构几何参数、载荷边界条件以及面板材料参数相关。夹芯梁的起皱最小临界载荷随着夹芯梁长厚比增加而提高，随着夹芯层和面板的厚度比的增加而减小。在简支边界条件下，夹芯梁起皱行为将会先于固支边界条件下发生。相较于使用金属面板，使用纤维方向弹性模量大于金属面板弹性模量的复合材料面板，能有效增强夹芯梁抵抗起皱的能力。
-
夹芯结构广泛应用于航空航天和航海等领域。但由于面板和芯材的力学性能和几何尺寸差异较大，夹芯结构失效行为与其他复合材料结构的失效行为不同。对于承受复杂载荷的夹芯结构，褶皱失效行为可能比其他失效模式更早发生。
本文针对夹芯梁在承受面内压缩载荷时容易发生屈曲和起皱的行为，构建了考虑局部形变和横法向应变的增强型高阶模型，该模型满足面内位移和横向剪切应力层间连续条件及自由表面条件。基于构建的理论模型，构造两节点梁单元公式并分析夹芯结构屈曲和褶皱问题。为了研究屈曲行为和褶皱行为之间的差异，使用本模型和三维有限元计算得到的屈曲和起皱行为对应的位移模态绘制在
图1 中。对于屈曲行为，中平面的变形与上下表面的变形一致。对于褶皱行为，由于中平面仅受压缩变形，但是上、下表面受到弯曲变形，所以中平面的变形与上下表面的变形完全不同。通过算例验证了所构建模型的准确性。数值分析结果表明，发展的模型计算夹芯结构的屈曲和褶皱行为有较高的精度，与三维有限元方法相比，本文构造的模型具有较高计算效率。相较于使用金属面板，使用纤维方向弹性模量大于金属面板弹性模量的复合材料面板，能有效增强夹芯梁抵抗起皱的能力。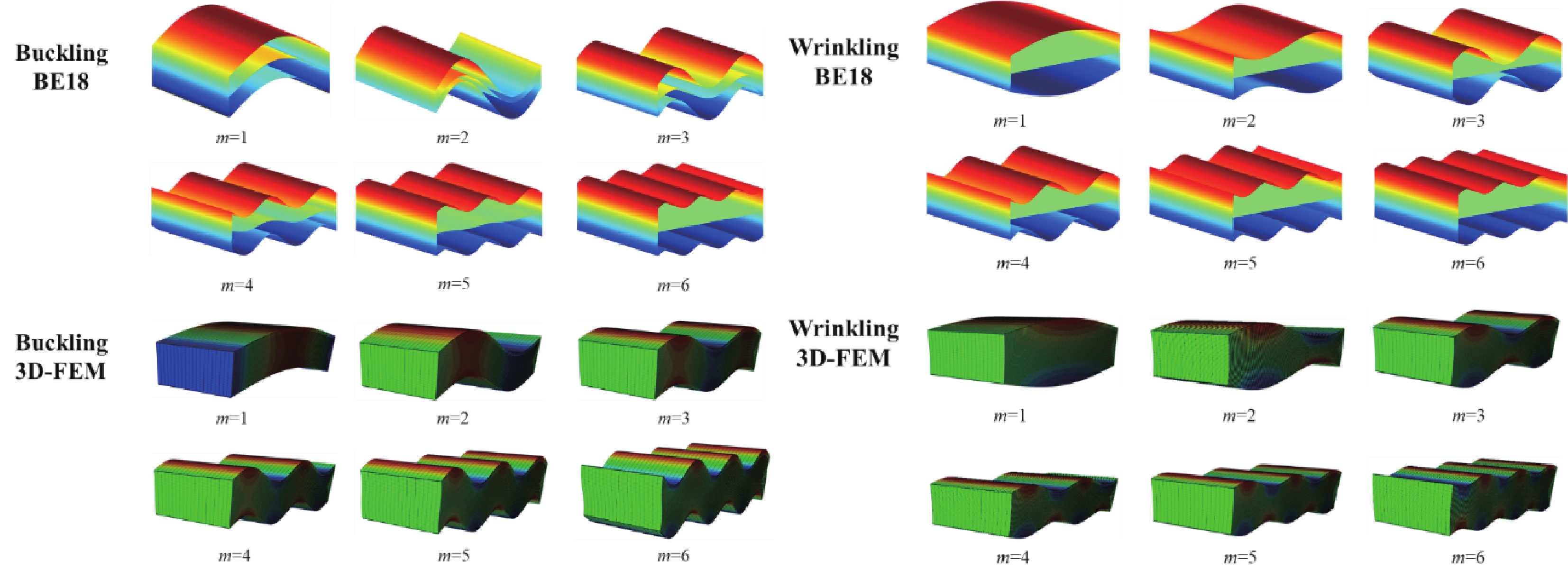
使用本文提出的模型和三维有限元计算得到的屈曲和褶皱行为的位移模态
计量
- 文章访问数: 1100
- HTML全文浏览量: 433
- PDF下载量: 102
- 被引次数: 4
