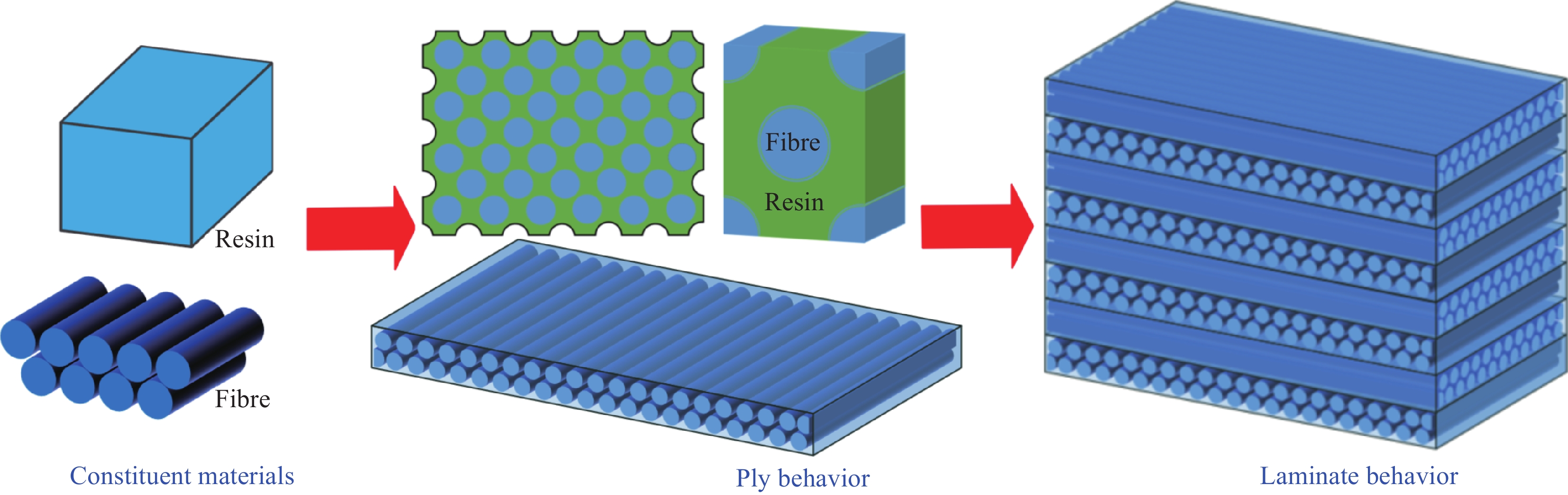
Prediction of anisotropic coefficient of thermal expansion for laminated composite using multiscale numerical models
-
摘要: 依据复合材料内部纤维在基体内的排布规律及层合板铺层特性,基于多尺度方法,建立单层板和层合板代表性体积单元(RVE)模型,施加相应的边界条件,预测单层板的热膨胀系数和工程常数,进而预测复合材料层合板各向异性的等效热膨胀系数。通过与实验数据对比发现,基于正六边形单层板RVE模型预测的热膨胀系数,相比理论预测值,整体更接近实验值,其中预测的单向T300/5208碳纤维增强环氧树脂基复合材料、P75/934碳纤维增强环氧树脂基复合材料和C6000/Pi碳纤维增强环氧树脂基复合材料的横向热膨胀系数与实验结果的误差分别只有3%、1%和2%;采用单层板RVE预测的单向ECR/Derakane 510C玻璃纤维增强乙烯基酯树脂基复合材料的工程常数与实验值最大相差7.5%;层合板RVE模型预测的正交AS4/8552碳纤维增强环氧树脂基复合材料厚度方向的热膨胀系数与实验结果误差可以忽略,只有0.08%。最后以大型复合结构常用的正交铺层结构为研究对象,基于给出的单层板和层合板RVE模型预测了不同铺层复合材料烟道层合板的等效热膨胀系数,环向铺层比例对厚度方向的热膨胀系数影响较小。Abstract: Representative volume element (RVE) in lamina and laminate levels were build based on the arrays of fiber into resin and stacking sequences in laminated composites. In combination with the specified boundary conditions in RVE models, coefficient of thermal expansions (CTEs) and engineering constants for lamina were predicted, followed by an evaluation of anisotropic CTEs for laminate using multiscale method. The results show that numerically predicted CTEs match well with experimental data as compared to theoretically calculated value as a whole, especially for the numerically predicated CTEs of unidirectional T300/5208, P75/934 and C6000/Pi carbon fiber reinforced epoxy resin matrix composites with a difference of 3%, 1% and 2%, respectively. And the predicted engineering constants using RVE model for unidirectional ECR/Derakane 510C glass fiber reinforced vinyl ester resin matrix composites were also in good agreement with experimentally measured results, with a maximum difference of 7.5%. Meanwhile, the difference between experimental results and forecasted CTEs in through-thickness direction for cross-ply AS4/8552 carbon fiber reinforced resin matrix composites using RVE model of laminated composites is nearly negligible with a difference of 0.08%. Finally, the equivalent CTEs of laminated composite with different stacking sequences were estimated using RVE models of lamina and laminate levels for cross-ply composite structures in large large-scale structures, and the results reveal that CTEs in through-thickness direction are weakly related to the ratio of stacking sequences in hoop direction.
-
Keywords:
- RVE /
- numerical simulation /
- laminate /
- cross-ply /
- multiscale
-
碳纤维增强聚合物复合材料(CFRP)具有高强、质轻、抗疲劳性能好和施工方便等优点,目前不仅被广泛应用于钢筋混凝土结构的加固中,同时也用在砌体结构的加固中[1-6]。CFRP加固砌体结构是通过CFRP与砌体材料界面间的粘结力,使两种材料组合在一起协同工作并传递荷载。因此,CFRP与砌体材料之间良好的粘结性能是保证CFRP与砌体结构共同受力变形的基础[7-8]。关于CFRP加固砌体结构,国内外学者做了大量研究,而关于CFRP-砌体界面性能只有少部分学者进行了研究并提出不同的界面粘结-滑移模型,这些模型基本上能准确模拟粘结界面的受力情况[9],但对于冻融环境下界面粘结-滑移模型未见公开报道。在冻融环境中,粘土砖的性能会随着时间的推移有所退化,在一定程度上会影响界面粘结性能,最终引起不可避免的耐久性问题[10-12]。因此,对冻融循环作用下CFRP与粘土砖之间粘结性能进行相应研究具有十分重要的意义。
通过简单可靠的单剪试验探究了冻融循环作用下CFRP-粘土砖界面在外力作用的破坏过程及破坏形态,得到了界面剥离承载力在循环作用下的变化规律,通过试验测得的应变得到了冻融循环过程中剪应力的发展及分布规律,并给出了考虑冻融循环影响的界面粘结-滑移关系。
1. 实验材料及方法
1.1 试件设计及制作
试验所使用碳纤维增强聚合物复合材料(CFRP)和树脂均为上海滠口实业有限公司生产,其主要性能如表1所示。试验所使用粘土砖的抗压强度平均值为9.28 MPa,吸水率约为17.58%,平均密度约为1 700 kg/m3。试验所用胶粘剂为SKO-碳纤维浸渍胶,其主要性能如表2所示。
表 1 碳纤维增强聚合物复合材料(CFRP)的性能Table 1. Properties of carbon fiber reinforced polymer(CFRP)Sample Tensile
strength/MPaModulus/
GPaElongation/
%Thickness/
mmCFRP ≥3 500 220 1.458 0.111 表 2 粘结树脂的性能Table 2. Properties of impregnation resinTensile shear strength/MPa Tensile strength/GPa Compressive strength/MPa Bending strength/MPa Positive tensile bond strength/MPa Modulus/MPa Elongation/% 24.29 40.12 73.62 72.95 4.44 2 605.7 2.45 本试验选用的粘土砖尺寸为235 mm×115 mm×55 mm,CFRP片材粘贴在粘土砖的一个表面(如图1所示),CFRP粘贴尺寸设计为6种规格,试件的具体参数如表3所示。
表 3 CFRP-粘土砖单剪试验试件参数Table 3. Specimen parameters of CFRP-clay brick specimens for single shear testCFRP size(Length×width)/mm Number of CFRP-clay brick specimen 0 cycle 20 cycles 40 cycles 60 cycles 80 cycles 80×50 5 5 5 5 5 100×80 5 5 5 5 5 80×80 5 5 5 5 5 100×80 5 5 5 5 5 80×100 5 5 5 5 5 100×100 5 5 5 5 5 参照CECS 146—2003[13]中相关要求将CFRP粘贴在粘土砖表面。为防止粘土砖出现局部拉剪破坏,粘结CFRP时在加载端留出30 mm非粘结区,制作完成的试件如图1所示,标准试件示意图如图2所示。
1.2 实验装置及加载程序
冻融循环试验参照GB/T 2542—2012[14]进行。将试件清理干净,在鼓风干燥箱内烘干达到质量要求后,将其在20℃的水中浸泡24 h后取出拭干水分,在冷冻箱内温度降至−15℃时开始计时。每次冷冻时间为3 h,融化2 h,控制冷冻温度为(−17±2)℃,融化水的温度控制在(15±2)℃。冻融循环次数分别取0次、20次、40次、60次和80次。
所有试件的单剪试验均在济南恒思盛大仪器有限公司生产的WDW-50微机控制电子万能试验机上通过自制单剪试验盒进行(如图3(a)所示),通过电脑控制加载速度,由荷载传感器输出CFRP与粘土砖的粘结荷载,CFRP的应变值通过江苏东华DH3816静态应变测试系统采集(如图3(b)所示)。为了使CFRP片材在加载过程中受力均匀,在试件加载端片材上下各粘贴一层30 mm长的CFRP加强片,加强片与试件同宽。加载过程采用位移控制,加载速率为0.5 mm/min。在CFRP试件拉伸前,先施加约为破坏荷载5%的预拉荷载(约为0.4 kN),检查夹具、拉力机和应变采集系统运行是否正常。
2. 试验现象
2.1 冻融循环对CFRP-烧结粘土砖界面的作用效果
试验发现,在经过若干次冻融循环后,CFRP-烧结粘土试件界面发生了较为明显的变化,以粘贴长度×宽度为80 mm×50 mm的单剪试件为例,图4为不同冻融循环作用下CFRP-烧结粘土砖界面破坏情况。可知,室温下试件破坏发生后,CFRP片材上粘有大颗粒粘土砖碎屑(如图4(a)所示);冻融20次和40次的试件破坏后,CFRP片材上粘有的粘土砖颗粒较小(如图4(b)所示);冻融60次后,其中2个试件破坏面较40次严重,界面上粘有大量粘土砖颗粒(如图4(c)所示),另1个试件与冻融40次的形态基本相同;冻融80次后,试件破坏发生在粘土砖,界面发生剪切破坏(如图4(d)所示),说明冻融循环作用对界面粘结性能有不利影响。
表4为粘贴长度×宽度为80 mm×50 mm的CFRP-粘土砖单剪试件试验结果。可以看出,随着冻融次数的增加,界面承载力逐渐降低,60次冻融后减小了约12%,表明冻融循环作用对CFRP-粘土砖的界面承载力有着不利影响。因此,当使用CFRP对粘土砖结构进行加固时,如果是在北方寒冷地区应适当考虑界面粘结折减系数。
表 4 CFRP-粘土砖界面承载力平均值和降低幅度Table 4. Average interfacial bearing capacity and reduction of CFRP-brick specimensCFRP size(Length×width)/mm Interfacial baring capacity/kN Decrease of bearing capacity/% 0 cycle 20 cycles 40 cycles 60 cycles 80 cycles 0 cycle 20 cycles 40 cycles 60 cycles 80 cycles 80×50 7.63 7.52 6.85 5.93 5.34 — 1.44 10.22 22.28 30.01 100×50 7.95 7.88 7.07 6.95 6.43 — 0.88 11.07 12.58 19.12 120×50 8.12 8.15 7.26 7.06 6.65 — –0.37 10.59 13.05 18.10 80×80 12.40 12.00 11.40 11.00 10.30 — 3.23 8.06 11.29 16.94 100×80 13.00 12.80 12.30 11.60 10.50 — 1.54 5.38 10.77 19.23 120×80 13.50 13.20 12.50 11.70 11.00 — 2.22 7.41 13.33 18.52 从试验及文献分析可知,造成界面承载力降低的原因主要有两点:(1)冻融作用导致粘土砖自身材料强度降低而引起CFRP-粘土砖试件粘结强度降低;(2) CFRP-粘土砖之间的胶体面层的粘结性能退化。由于CFRP的特殊构造,其聚合物基体的孔径较小,冻融循环作用下,其孔隙中的水不会冻结[15]。因此,可能是胶体吸水后,在冻融作用下,当溶胀和温度应力共同作用时,界面产生微裂纹,从而导致介质水在界面上冻结产生应力。
2.2 CFRP-粘土砖单剪试验破坏形态
由于本次试验在CFRP-粘土砖试件加载端预留了30 mm非粘结区,所有CFRP-粘土砖试件均是CFRP与粘土砖之间发生界面剥离而破坏的,没有发生CFRP布的撕裂破坏,也没有发生粘土砖的拉剪破坏。
所有CFRP-粘土砖试件剥离破坏是由纤维布传递荷载到粘土砖,从而使粘土砖内部产生的微小裂缝逐渐发展导致的。对于没有经过冻融循环的CFRP-粘土砖试件,其破坏过程是初始加载时除了碳纤维布开始绷紧外,试件并无明显变化,加载端的应变基本呈线性增加;当荷载增加至剥离荷载的40%左右时,可以听到“噼啪声”,加载端附近的应变迅速增加,粘土砖内部微裂缝逐渐开展,试件开始发生局部粘结破坏,总的粘结面积开始减少;随着荷载的进一步增大,应变急速增加,剥离深度也在加大,距离加载端较远处应变片的应变也逐渐增大,说明剥离逐渐向自由端发展。当剩余的粘结面积不足以抵抗荷载时,破坏瞬间发生。而在冻融循环作用下,破坏具有相似性,只是由于粘土砖与胶层之间的界面被削弱、粘土砖材料本身强度降低,开裂速度较未经循环试件更迅速,破坏更突然。
3. 结果与分析
3.1 冻融循环作用下粘土砖孔隙结构损伤
粘土砖为多孔材料,在水冻作用下,粘土砖内部孔隙中的水分子会出现冻结现象,造成孔隙体积膨胀,从而使粘土砖内部出现较大的微孔隙损伤和拉应力,使砖体的缝隙和节理出现加深和扩大;当粘土砖处于融化状态时,粘土砖内部微孔隙会出现迁移现象。当粘土砖在不同温度下进行反复冻结和溶解时,张力使孔隙壁的损伤不断加剧,最终造成砖体损伤。这种损伤反映到CFRP-粘土砖的粘结上,便会出现粘结退化现象。
图5为不同冻融循环作用下粘土砖孔隙度变化。图6为不同冻融循环作用下粘土砖弛豫时间T2谱分布。从图5可以看出,随着冻融循环次数的增加,粘土砖的孔隙度逐渐增大。由图6可知,随着冻融循环次数的增加,T2谱的峰值向右移动,说明大孔径比例增加,冻融使冻胀力逐渐大于颗粒间的粘聚力,造成砖样的孔隙发育和扩展程度加剧。
由CFRP-粘土砖单剪试验结果分析可知,冻融作用下,粘结界面破坏模式的变化与粘土砖微观变化是相统一的(如图4所示)。从单剪试件的破坏过程可以看出,不同冻融次数下,CFRP-粘土砖试件破坏后,粘土砖的表层破坏模式不尽相同。未经冻融的CFRP-粘土砖试件以CFRP粘结区域内靠近加载端部位的粘土砖剪切破坏为主。剪切破坏面被拉出的近似三角形粘土砖块与CFRP粘结较好,其余部位CFRP粘有大量被拉下的粘土砖碎屑与颗粒,破坏面一般在粘土砖基层一侧,深度约为2~5 mm。经过冻融循环的CFRP-粘土砖试件在冻融次数较低时,破坏模式与未受冻融的CFRP-粘土砖试件基本一致,冻融达到40次后,在加载端出现三角破坏区的概率随之减小,破坏以界面剥离破坏为主;当冻融时间达到60次时,所有试件均为剥离破坏,加载端不再出现三角破坏区,在CFRP上粘下的粘土砖层越来越均匀;当冻融时间达到80次时,在加载端出现类似三角区域的破坏情况,说明粘土砖的强度减弱。
3.2 CFRP-粘土砖界面承载力及平均粘结强度
图7为CFRP-粘土砖界面承载力随冻融循环次数的变化曲线。由表4和图7可知,随着冻融循环次数的增加,CFRP-粘土砖界面承载力总体呈下降趋势,而后期的下降速度要快于前期。同时,还可以看到,在CFRP的粘结宽度及冻融循环次数相同的情况下,当粘结长度从80 mm增加至120 mm时,CFRP-粘土砖界面承载力增加的幅度并不大,但当粘结宽度从50 mm增加到80 mm时,CFRP-粘土砖界面承载力却提高了60%~70%,说明CFRP的粘结宽度是影响界面承载力的主要因素之一,与以混凝土为基材的复合材料结果相似[16-18]。
在不考虑相关几何参数因素对试件界面粘结性能的影响下,通过界面粘结强度平均值来考察界面在冻融循环作用下的劣化情况,界面粘结强度平均值计算如下:
τf=PuA (1) 式中:
τf 为试件平均粘结强度(MPa);Pu为CFRP-粘土砖界面承载力(kN);A为粘结面积(mm2)。图8为CFRP-粘土砖界面平均粘结强度曲线。可知,平均粘结强度曲线根据长度和宽度组合分为三组,同一长度不同宽度的图形在位置上比较接近,再次证明粘结宽度对承载力的贡献较大,即只要保证粘结长度足够,CFRP-粘土砖试件的平均粘结强度基本和粘结宽度呈正相关关系。
3.3 CFRP-粘土砖界面剪应力的分布规律
由于试验无法得到粘结界面上任意点的应变值,因此在计算中以两个相邻应变片之间的平均剪应力作为界面剪应力。由于CFRP非常薄,可以假定CFRP在轴向力方向上的应力
σf 在横截面内是均匀分布的,并假定相邻两应变片间的应变线性分布,现取长度为微元长度dx的CFRP单元作为对象进行研究,CFRP-烧结粘土砖界面单元体剪应力分布如图9所示。由力的平衡条件可以得到粘结剪应力的计算公式为
τ(x)=dFbfdx=dσfdxtf=Eftfdεxdx=Eftfεi+1−εiΔxi (2) 式中:F为界面承载力;
bf 、tf 、Ef 和εi 分别为CFRP片材的宽度、厚度、弹性模量和应变。由于各个试件剪应力的分布具有一定相似性,因此以粘贴长度×宽度为80 mm×50 mm的单剪试件为例,其不同冻融循环作用下的剪应力分布如图10所示。可知,当荷载较小时,剪应力的峰值出现在加载端,而粘结剪应力只分布在距加载端20 mm左右的范围内;当荷载逐渐增加时,加载端附近的剪应力也随之逐渐增加,增加到峰值后剪应力开始向远端传递,此时的剪应力集中分布在一定区域内,区域外剪应力几乎为零,这一区域即为有效粘结区域,该区域的长度称为“有效粘结长度”,本试验中有效粘结长度基本保持不变,大约为60~80 mm,且其不随CFRP粘结尺寸及冻融循环次数而变化,说明随着荷载的增加,有效粘结区域在破坏过程中会以近似不变的长度由加载端向自由端平行移动,从而使剥离区域逐渐增加,直至试件破坏,与CFRP-混凝土试件的研究结果一致[19-20]。
3.4 CFRP-粘土砖界面粘结-滑移本构关系
为建立准确可靠的粘结-滑移曲线,需要进一步了解界面剥离机制及破坏过程中粘结剪应力与滑移值的变化情况,即
ττmax−ss0 曲线。其中,滑移值为CFRP与粘土砖的位移差,计算如下:s(x)=s(0)+∫x0ε(u)du (3) 式中:
s(0) 为最大剪应力对应的滑移值;s(x) 为CFRP上任一点滑移值;ε 为应变值。关于粘结-滑移关系,目前国内外学者对纤维增强聚合物复合材料(FRP)-混凝土界面深入研究较多,而对于FRP-粘土砖的研究鲜见报道。粘结-滑移模型的提出有试验方法、有限元模拟方法、理论推导方法等,图11为几种典型粘结-滑移关系模型曲线。由图11(a)可以看到,直角三角形模型属于早期模型,把界面近似看做弹性体,缺点是忽略了界面在加载后期的软化行为;由图11(b)~11(d)可知,粘结-滑移关系模型均为两阶段曲线模型,曲线由上升段和下降段组成,目前对CFRP-混凝土界面的研究大多采用该类型曲线模型。通过对比发现,图11(d)的Popovics模型比较适合本试验数据,如下式:
ττmax (4) 通过式(4)拟合效果较好(拟合系数n=3.032),可以较准确地表示CFRP-粘土砖面粘结-滑移的有关特征,如图12所示。可以看出,CFRP-粘土砖界面粘结-滑移曲线分为上升段和下降段,上升段为强化阶段,下降段为软化阶段。开始加载时,界面粘结剪应力和滑移均不大,粘结-滑移曲线近似呈线性关系,试件处于弹性状态;随着粘结剪应力逐步增大,粘结-滑移曲线表现出非线性,此时滑移量增加速度较剪应力增加速度要快,当界面逐渐达到最大剪应力,界面的粘结不足以抵抗剪应力时,试件开始出现滑移;当粘结剪应力增大至最大后,曲线进入下降段,此时剪应力下降速度和滑移量增加的速度均较快,且滑移量增加的速度越来越大,当粘结应力几乎为零时,滑移量达到最大值,此时CFRP和粘土砖在界面处完全剥离。对比Popovics曲线和实验数据可以发现,Popovics模型可以较好地描述CFRP-粘土砖界面粘结-滑移关系,上升段试验数据点几乎与Popovics模型曲线重合,下降段的试验数据分布于Popovics模型曲线两侧,但偏差较小,表明采用Popovics模型来描述CFRP-粘土砖界面的粘结-滑移本构关系是较准确的。
4. 结 论
分析了冻融循环作用和粘结尺寸对CFRP-粘土砖界面承载力及粘结强度的影响,通过试验数据和理论比较,建立了考虑冻融循环影响下的CFRP-粘土砖界面粘结-滑移模型。
(1)在冻融循环作用下,CFRP-粘土砖界面的破坏模式是由剪切破坏转变为粘结剥离破坏,剥离是从CFRP加载端开始逐渐向自由端发展。相对于长度,CFRP的宽度对试件界面承载力影响更为显著。
(2)随着冻融循环次数的增加,CFRP-粘土砖界面承载力总体呈下降趋势,而后期的下降速度要快于前期。
(3) CFRP-粘土砖界面粘结剪应力分布曲线具有相似性,当荷载水平逐渐增加,剪应力也随之逐渐增大,并从加载端向自由端传递,且所有剪应力集中分布在一定的“有效粘结区域”内,而区域外的剪应力几乎为零,有效粘结区域的长度约为60~80 mm,且与冻融循环次数无关。
(4) CFRP-粘土砖界面粘结-滑移关系有明显的上升段和下降段,上升段为强化阶段,下降段为软化阶段,Popovics模型可以很好地描述CFRP-粘土砖的界面粘结-滑移关系。
-
Constituent material E1/GPa E2/GPa G12/GPa G23/GPa ν12 ν23 α1/(10−6℃−1) α2/(10−6℃−1) T300 carbon fiber 233.04 23.10 8.96 8.27 0.20 0.4 −0.54 10.08 5208 epoxy 4.34 — 1.59 — 0.37 — 43.92 — P75 carbon fiber 550.20 9.51 6.89 3.38 0.20 0.4 −1.35 6.84 934 epoxy 4.34 — 1.59 — 0.37 — 43.92 — CE339 epoxy 4.34 — 1.59 — 0.37 — 63.36 — C6000 carbon fiber 233.04 23.10 8.96 8.27 0.20 0.4 −0.54 10.08 PMR15 polyimide 3.45 — 1.31 — 0.35 — 36.00 — HMS carbon fiber 379.21 6.21 7.58 2.21 0.20 0.4 −0.99 6.84 Borosilicate glass 62.74 — 26.20 — 0.20 — 3.24 — Notes: E1 and E2—Moduli in “1” and “2” direction; G12 and G23—Shear moduli in “1-2” plane and “2-3” plane direction; ν12 and ν23—Poisson’s ratio in “1-2” plane and “2-3” plane direction; α1 and α2—Coefficients of thermal expansion in “1” and “2” direction. 表 2 各复合材料预测与实验测试值的比较
Table 2 Comparison of experimental data with predicted values of composites
Composite α1/(10−6℃−1) α2/(10−6℃−1) Experimental[23] SH/CH(Error) Predicted(Error) Experimental[23] SH(Error) CH(Error) Predicted(Error) T300/5208
(Vf=0.68)−0.113 −0.153(35%) −0.091(19%) 25.236 27.540(9%) 18.900(25%) 24.383(3%) P75/934
(Vf=0.48)−1.051 −0.967(8%) −0.922(12%) 34.524 35.460(3%) 23.220(33%) 34.045(1%) P75/930
(Vf=0.65)−1.076 −1.159(8%) −1.128(5%) 31.716 26.640(16%) 17.154(46%) 25.018(21%) P75/CE339
(Vf=0.54)−1.021 −0.918(10%) −0.859(16%) 47.412 44.640(6%) 28.080(41%) 42.732(10%) C6000/Pi
(Vf=0.63)−0.212 −0.225(6%) −0.192(9%) 22.428 25.740(15%) 18.000(20%) 22.062(2%) HMS/Glass
(Vf=0.47)−0.414 −0.324(22%) −0.324(22%) 3.780 5.976(58%) 5.427(44%) 4.479(18%) Notes: Vf —Fiber volume fraction; SH are the predicted values using Eq.(11)-(12); CH are the predicted values using Eq.(11) and Eq.(13). 表 3 ECR/Derakane 510C 复合材料组分材料的性能参数
Table 3 Properties of constituent materials for ECR/Derakane 510C composites
Property E/GPa ν ECR glass fiber 80.00 0.20 Derakane 510C 3.35 0.35 Notes: E—Modulus; ν—Poisson’s ratio. 表 4 单向ECR/Derakane 510C复合材料工程常数预测值与试验结果对比
Table 4 Comparison of numerical results with experimental values for engineering constants of unidirectional ECR/Derakane 510C composites
Iterm E1/GPa E2/GPa G12/GPa G23/GPa ν12 ν23 Numerical 34.03 7.32 2.71 2.51 0.282 0.333 Experimental 31.63 7.40 2.69 − 0.281 − Error/% 7.50 1.10 0.74 − 0.350 − 表 5 单层AS4/8552碳纤维增强树脂基复合材料力学性能参数[27]
Table 5 Parameters of mechanical properties of unidirectional AS4/8552 composites[27]
E1
/GPaE2
/GPaG12=G13=G23
/GPaν12=ν13 ν23 α1
/(10−6℃−1)α2
/(10−6℃−1)135 9.5 4.9 0.3 0.45 0.00 32.6 Note: G13—Shear moduli in “1-3” plane direction, respectively; 1—Longitudinal direction; 2—Transverse direction; 3—Thickness direction. 表 6 AS4/8552复合材料层合板仿真数据与文献[27]实验结果对比
Table 6 Comparisons of numerical results and experimental values from literature [27] of laminated AS4/8552 composite
Equivalent CTEs αx
/(10−6℃−1)αy
/(10−6℃−1)αz
/(10−6℃−1)Numerical 2.68 2.68 45.16 Experimental[27] 2.70 2.70 45.20 Error/% 0.70 0.70 0.08 Notes: αx, αy and αz—Coefficients of thermal expansion in x, y and z direction, respectively; CTEs—Coefficient of thermal expansions. 表 7 ECR/Derakane 510C复合材料单向布和纤维缠绕层单层板力学性能
Table 7 Mechanical properties of lamina composed of unidirectional fabrics and filament wound roving for ECR/Derakane 510C composites
Engineering constant Unidirectional fabric layer Filament wound layer E1/MPa 38690 31630 E2=E3/MPa 9100 7400 G12=G13/MPa 3370 2690 G23/MPa 3594 2888 ν12=ν13 0.266 0.281 ν23 0.266 0.281 表 8 ECR/Derakane 510C复合材料烟道层合板等效热膨胀系数
Table 8 Equivalent CTEs of laminate in ECR/Derakane 510C composite duck
Stacking sequence αx
/10−6℃−1αy
/10−6℃−1αz
/10−6℃−1RVE CLT RVE CLT RVE [0/90/90]s 18.02 18.40 11.80 13.38 42.93 [0/90]s 14.60 14.19 14.88 16.14 44.64 [0/0/90]s 12.23 11.39 19.42 19.89 45.55 [0/0/0/90]s 11.25 10.29 22.67 22.41 45.63 Note: CLT—Classic laminate theory. -
[1] DING A, WANG J, NI A, et al. A new analytical solution for cure-induced spring-in of L-shaped composite parts[J]. Composites Science and Technology, 2019, 171: 1-12.
[2] 丁安心, 王继辉, 倪爱清, 等. 热固性树脂基复合材料固化变形解析预测研究进展[J]. 复合材料学报, 2018, 35(6): 1361-1376. DING Anxin, WANG Jihui, NI Aiqing, et al. A review of analytical prediction of cure-induced distortions in thermoset composites[J]. Acta Materiae Compositae Sinica, 2018, 35(6): 1361-1376(in Chinese).
[3] 李云波, 李宗利, 姚希望, 等. 含孔洞和裂隙混合缺陷的干燥水泥砂浆导热系数相互作用直推预测模型[J]. 复合材料学报, 2022, 39(1): 361-370. LI Yunbo, LI Zongli, YAO Xiwang, et al. Interaction direct deduction prediction model of thermal conductivity of dry cement mortar with mixed defects of cavities and cracks[J]. Acta Materiae Compositae Sinica, 2022, 39(1): 361-370(in Chinese).
[4] 周龙伟, 赵丽滨. 基于失效机制的单向纤维增强树脂复合材料退化模型[J]. 复合材料学报, 2019, 36(6): 1389-1397. ZHOU Longwei, ZHAO Libin. Failure mechanisms based degradation model of unidirectional fiber reinforced polymer composites[J]. Acta Materiae Compositae Sinica, 2019, 36(6): 1389-1397(in Chinese).
[5] GAO Z, CHEN L. A review of multi-scale numerical modeling of three-dimensional woven fabric[J]. Composite Structures, 2021, 263: 113685.
[6] FU Y, YAO X, GAO X. Micro-mesoscopic prediction of void defect in 3D braided composites[J]. Composites Part A: Applied Science and Manufacturing, 2021, 147: 106450.
[7] SUN C, VAIDYA R. Prediction of composite properties from a representative volume element[J]. Composites Science and Technology, 1996, 56(2): 171-179.
[8] GARNICH M R, KARAMI G. Finite element micromecha-nics for stiffness and strength of wavy fiber composites[J]. Journal of Composite Materials, 2004, 38(4): 273-292.
[9] GARNICH M R, KARAMI G. Localized fiber waviness and implications for failure in unidirectional composites[J]. Journal of Composite Materials, 2005, 39(14): 1225-1245.
[10] 张元冲, HARDING J. 平面织物复合材料机械性能的数值细观力学分析[J]. 应用力学学报, 1989(4): 20-27, 114. ZHANG Yuanchong, HARDING J. A numerical micromechanics analysis of the mechanical properties of a plain weave composite[J]. Chinese Journal of Applied Mechanics, 1989(4): 20-27, 114(in Chinese).
[11] 吕毅, 吕国志, 吕胜利. 细观力学方法预测单向复合材料的宏观弹性模量[J]. 西北工业大学学报, 2007, 24(6): 787-790. LV Yi, LV Guozhi, LV Shengli. Semi-theoretical and engi-neering prediction of macroscopic elastic moduli of unidirectional composites[J]. Journal of Northwestern Polytechnical University, 2007, 24(6): 787-790(in Chinese).
[12] 左中鹅, 王瑞, 徐磊. 基于有限单元法的平纹织物复合材料强度预测: 1. RVE的有限元模型[J]. 纺织学报, 2009(12): 45-49. ZUO Zhong'e, WANG Rui, XU Lei. Mechanical strength prediction of plain woven fabric composite: 1. Finite element model of composite RVE[J]. Journal of Textile Research, 2009(12): 45-49(in Chinese).
[13] LU J, ZHU P, JI Q, et al. Identification of the mechanical properties of the carbon fiber and the interphase region based on computational micromechanics and Kriging metamodel[J]. Computational Materials Science, 2014, 95: 172-180.
[14] 马学仕. 基于均匀化理论的周期性复合材料有效性能预测[D]. 南京: 南京航空航天大学, 2013. MA Xueshi. Homogenization method to calculation of effective properties for periodic composite materials[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013(in Chinese).
[15] GHOSH S, MUKHOPADHYAY S N. A material based finite element analysis of heterogeneous media involving dirichlet tessellations[J]. Computer Methods in Applied Mecha-nics and Engineering, 1993, 104(2): 211-247.
[16] TRIAS D, COSTA J, MAYUGO J, et al. Random models versus periodic models for fibre reinforced composites[J]. Computational Materials Science, 2006, 38(2): 316-324.
[17] LUCIANO R, BARBERO E J. Formulas for the stiffness of composites with periodic microstructure[J]. International Journal of Solids and Structures, 1994, 31(21): 2933-2944.
[18] RAMM E, RANK E, RANNACHER R, et al. Error-controlled adaptive finite elements in solid mechanics[M]. Chichester: John Wiley & Sons, 2003.
[19] 赵琳. 基于单胞解析模型与渐进损伤分析的复合材料强度预报[D]. 哈尔滨: 哈尔滨工业大学, 2012. ZHAO Lin. Strength prediction of composites based on unit cell analytic model and progressive damage analysis[D]. Harbin: Harbin Institute of Technology, 2012(in Chinese).
[20] 张超, 许希武, 严雪. 纺织复合材料细观力学分析的一般性周期性边界条件及其有限元实现[J]. 航空学报, 2013, 34(7): 1636-1645. ZHANG Chao, XU Xiwu, YAN Xue. General periodic boundary conditions and their application to micromechanical finite element analysis of textile composites[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(7): 1636-1645(in Chinese)
[21] SUN C, LIAO W. Analysis of thick section composite laminates using effective moduli[J]. Journal of Composite Materials, 1990, 24(9): 977-993.
[22] SUN C, LI S. Three-dimensional effective elastic constants for thick laminates[J]. Journal of Composite Materials, 1988, 22(7): 629-639.
[23] BOWLES D E, TOMPKINS S S. Prediction of coefficients of thermal expansion for unidirectional composites[J]. Jour-nal of Composite Materials, 1989, 23(4): 370-388.
[24] SCHAPERY R A. Thermal expansion coefficients of compo-site materials based on energy principles[J]. Journal of Composite Materials, 1968, 2(3): 380-404.
[25] CHAMIS C. Simplified composite micromechanics equations of hygral, thermal, and mechanical properties[J]. Transactions of the Asae, 1984, 39(3): 999-1004.
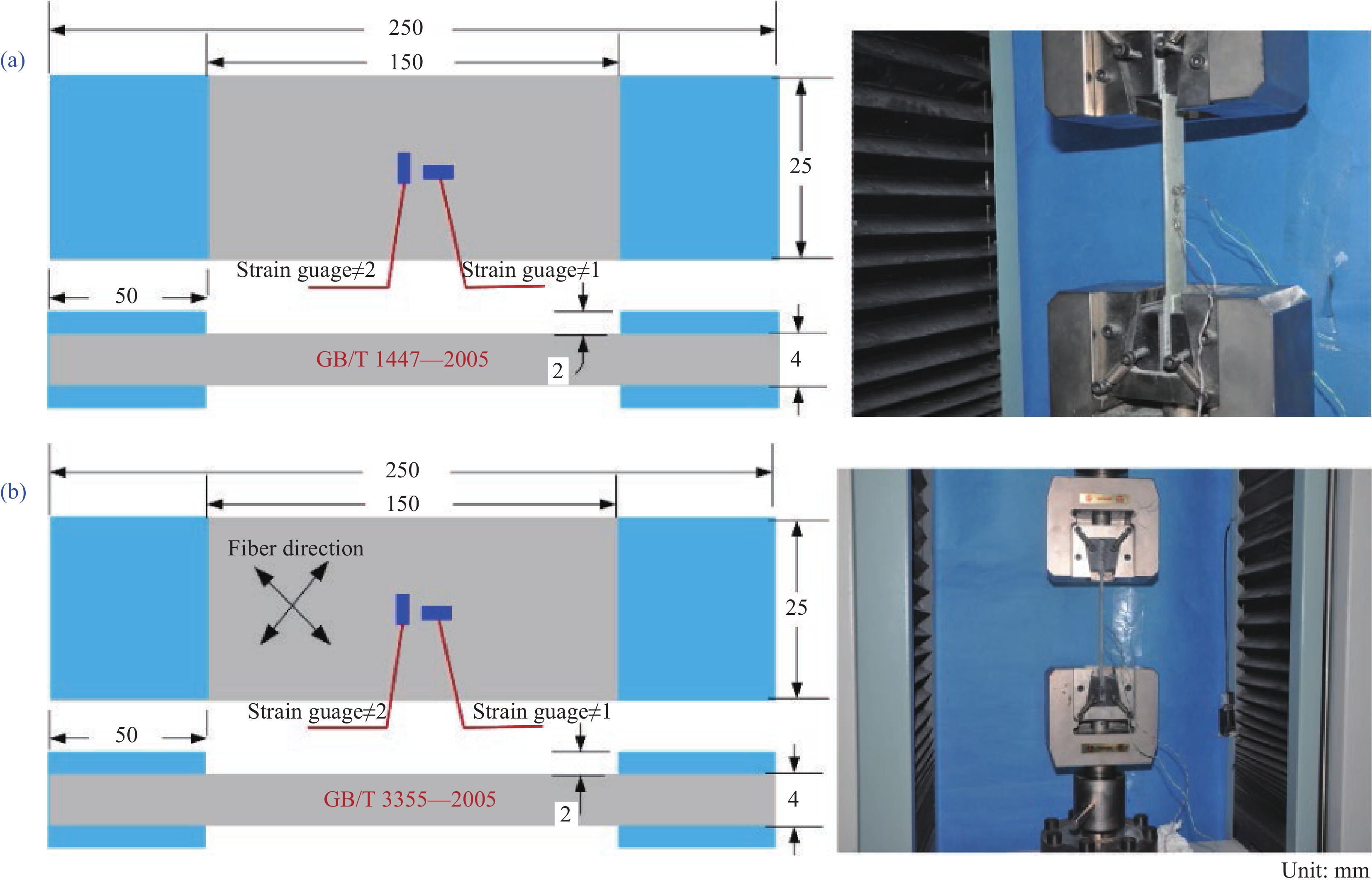
[26] 中国国家标准化管理委员会. 纤维增强塑料拉伸性能试验方法: GB/T 1447—2005[S]. 北京: 中国标准出版社, 2005. Standardization Administration of the People's Republic of China. Fiber-reinforced plastics composites—Determination of tensile properties: GB/T 1447—2005[S]. Beijing: China Standards Press, 2005(in Chinese).
[27] WISNOM M R, POTTER K D, ERSOY N. Shear-lag analysis of the effect of thickness on spring-in of curved compo-sites[J]. Journal of Composite Materials, 2007, 41(11): 1311-1324.
-




 下载:
下载: