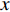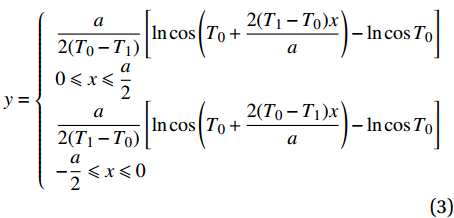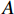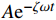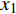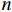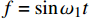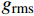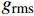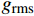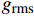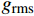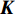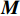Influences of fiber angle on the vibration damping performance of variable angle laminates
-
摘要: 自动铺丝技术可以实现复杂曲率曲线铺放,可极大提高角度设计的自由度。本文以改善复合材料层合板动态特性为目的,对变角度层合板的减振性能进行了研究分析。首先对不同角度变化变角度层合板进行自由衰减试验,研究了纤维角度变化与变角度层合板阻尼比的关系。然后对含相应角度变角度夹层板进行随机试验,研究了层合板随机激励条件下的振动响应,并采用共振峰处传递函数(Transition function,TF)和拾振点加速度总均方根(Root mean square,RMS)两种指标评价减振效果。结果表明:层合板阻尼比在纤维变化角度为±<45|60>时最大,纤维变化角度为±<73|88>时最小。基于RMS减振评价指标,±<45|60>夹层板较传统直线板减振性能提高27.13%;基于共振峰TF减振评价指标,纤维角度变化对不同共振峰减振效果规律差异明显。研究表明,变角度层合板减振性能明显优于传统直线层合板,相关实验结果将对变角度层合板减振设计及优化提供一定的参考意义。Abstract: With the development of automated fiber placement technology, it is possible to lay complex curves which greatly increase the freedom of angle design. In this paper, with the purpose of improving the dynamic characteristics of composite laminates, the vibration damping performance of variable angle laminates was studied and analyzed. Firstly, the free attenuation experiment was carried out to study the relationship between the change of fiber angle and damping ratio of variable angle laminates. Then, the vibration response of variable angle laminates under random excitation was studied by random experiments. The transition function (TF) at the formant and the root mean square (RMS) of the acceleration at the pick-up point of vibration were used to evaluate the effect of vibration reduction. The results show that the damping ratio of laminates is the largest when the fiber angle is ±<45|60> and the least when the fiber angle is ±<73|88>. Based on the vibration reduction evaluation index of RMS, the vibration reduction performance of ±<45|60> sandwich laminate is 27.13% higher than the traditional linear laminate; Based on the formant vibration reduction evaluation index of TF, the vibration reduction effect of different formants is obviously different with the fiber change. The results show that the vibration reduction performance of the variable angle laminates is obviously better than that of the traditional linear laminates. The relevant experimental results will be helpful for the design and optimization of vibration reduction of variable angle laminates.
-
Keywords:
- advanced composites /
- variable angle /
- vibration damping /
- damping /
- vibration response
-
碳纤维增强树脂基复合材料以其优良的特性在航空航天领域应用越来越广泛。复合材料构件轻量化设计,除了对其强度严格要求外,动力学性能也是关键指标[1]。飞行器飞行过程中,和空气摩擦,受空气扰动,不可避免会产生振动。为了减低这种振动,一方面,要具有良好的气动外形,另一方面在结构和材料方面的减振效果也要好。自动铺丝技术(Automated fiber placement, AFP)等新型制造技术的发展[2],为复合材料层合板角度和铺层设计带来了更大的空间。纤维曲线铺放时,纤维角在面内连续变化,改变纤维路径可合理调整复合材料层合板的频率和相应的振型[3],改善复合材料层合板的阻尼性能[4]。因此,对变角度复合材料层合板的减振研究具有重要意义。
孔斌等[5]综述了变刚度复合材料结构的设计、制造与分析的研究进展,相比于常规复合材料结构,变刚度复合材料结构有其特殊之处。Abdalla等[6]基于经典层合板理论,采用有限元法研究了纤维曲线层合板的频率最大化问题。聂国隽等[7]基于弹性薄板的小挠度理论,采用微分求积法研究了纤维曲线铺放的复合材料层合板的自由振动问题。孙士平等[8]对不同边界条件下丝束变角度层合板的频率性能进行了参数化分析与优化。欧阳小穗等[9]研究了高速流场中的曲线纤维变刚度层合复合材料壁板非线性颤振响应,通过调整曲线纤维路径可以改变复合材料壁板的颤振特性。
考虑振动时,阻尼是重要特性,复合材料的阻尼系数大于金属材料的阻尼系数,对阻尼的主要贡献是基体的黏弹性[10],因此,在振动环境中,复合材料构件的能耗更多,减振效果优于金属材料。文献[11]综述了纤维增强树脂基复合材料的阻尼机理。D.A. Pereira[12-13]从数值计算和实验初步验证了变角度同时调整层合板频率和阻尼的可能性,并研究多目标优化提高合层压板的基本模态频率和相应的比阻尼能力。
目前,变角度层合板的阻尼减振研究仍处于探索阶段。本文以变角度层合板和含相应角度变角度夹层板为研究对象,利用实验方法研究纤维角度变化对复合材料层合板阻尼性能和振动响应的影响,探究纤维增强树脂复合材料的阻尼减振新途径。
1. 实验理论基础
1.1 纤维方向角的定义
本文采用由Gürdal和Olmedo[14-15]定义的复合材料纤维曲线铺放的经典参考路径,纤维沿着参考坐标系线性变化,形成的路径便是纤维曲线铺放的参考路径,如图1及下式所示:
θ(x)=2a(T1−T0)|x|+T0 (1) 参考路径曲线的斜率为
dydx=tan[θ(x)] (2) 将曲线与
x 轴夹角的表达式代入式(2),积分可得参考路径曲线的轨迹为y={a2(T0−T1)[lncos(T0+2(T1−T0)xa)−lncosT0]0⩽ (3) 其中:T0为位于层合板中心纤维的起始角;T1为位于层合板两边纤维的终止角;
a 为层合板x 轴方向的长度。连续铺层正曲线铺层记为+<T0|T1>,与之对应的负曲线铺层记为−<T0|T1>。为覆盖整个铺层,沿y轴平移参考路径曲线得到其他路径的位置。当T0=T1时,为传统直线层合板。航空航天中使用的材料,不但需要较高的刚度还要有一定的阻尼。然而,对于相同的材料具有高阻尼和高刚度是相互矛盾的关系[16]。对于复合材料变角度层合板而言,可以通过合理调整面内纤维角度θ连续变化来保证刚度的同时提升阻尼性能,这对于复合材料减振设计具有重要的工程意义。
1.2 时域阻尼测试方法
阻尼是反映结构系统振动过程中能量耗散特征的参数,其本质是振动系统能量的转换,即从机械能转换为热能或其他能量形式的过程[17]。
自由振动衰减法是时域测量系统阻尼的一种经典方法。根据振动学原理,一个结构系统的阻尼特性决定了其振动能量消耗的快慢,假设结构系统共振时(不论复合材料结构还是单一材料结构),当其各阶模态互不耦合时,可以将其看作单自由度系统,并可通过自由振动衰减法来获取其阻尼参数[18]。即首先利用振动激励设备,激发其达到某阶共振状态,然后在切断激励源后,研究其时域信号衰减的快慢程度,进而从时域测试角度来客观评价其阻尼参数的大小。
以下以单自由度系统为例加以说明,有阻尼单自由度系统的衰减响应可表达为
x = {{A}}{{\rm{e}}^{ - \zeta \omega t}}\sin \left( {\sqrt {1 - {\zeta ^2}} {\kern 1pt} {\kern 1pt} \omega t + \varphi } \right) (4) 式中:
{{A}} 为振幅;t 为衰减时间;\varphi 为相位差角。有阻尼系统的自由振动不再是等幅的简谐振动,理论上是振幅被限制在{{A}}{{\rm{e}}^{ - \zeta \omega t}} 之内,并按时间指数衰减的振动,最终完全消失。通常表征阻尼如:对数衰减率δ、损耗因子η、阻尼比ζ等,在小阻尼情况下,各个参量之间有如下关系:\delta {\rm{ = }}\frac{1}{n}\ln \left| {\frac{{{x_1}}}{{{x_{n{\rm{ + }}1}}}}} \right|{\rm{ = }}\frac{{2{\rm{{\text{π}} }}\zeta }}{{\sqrt {1{\rm{ - }}{\zeta ^2}} }} (5) 式中,
{x_1} 、{x_{n + 1}} 为相隔n 个周期的两个振幅。2. 试验材料及方法
2.1 原材料
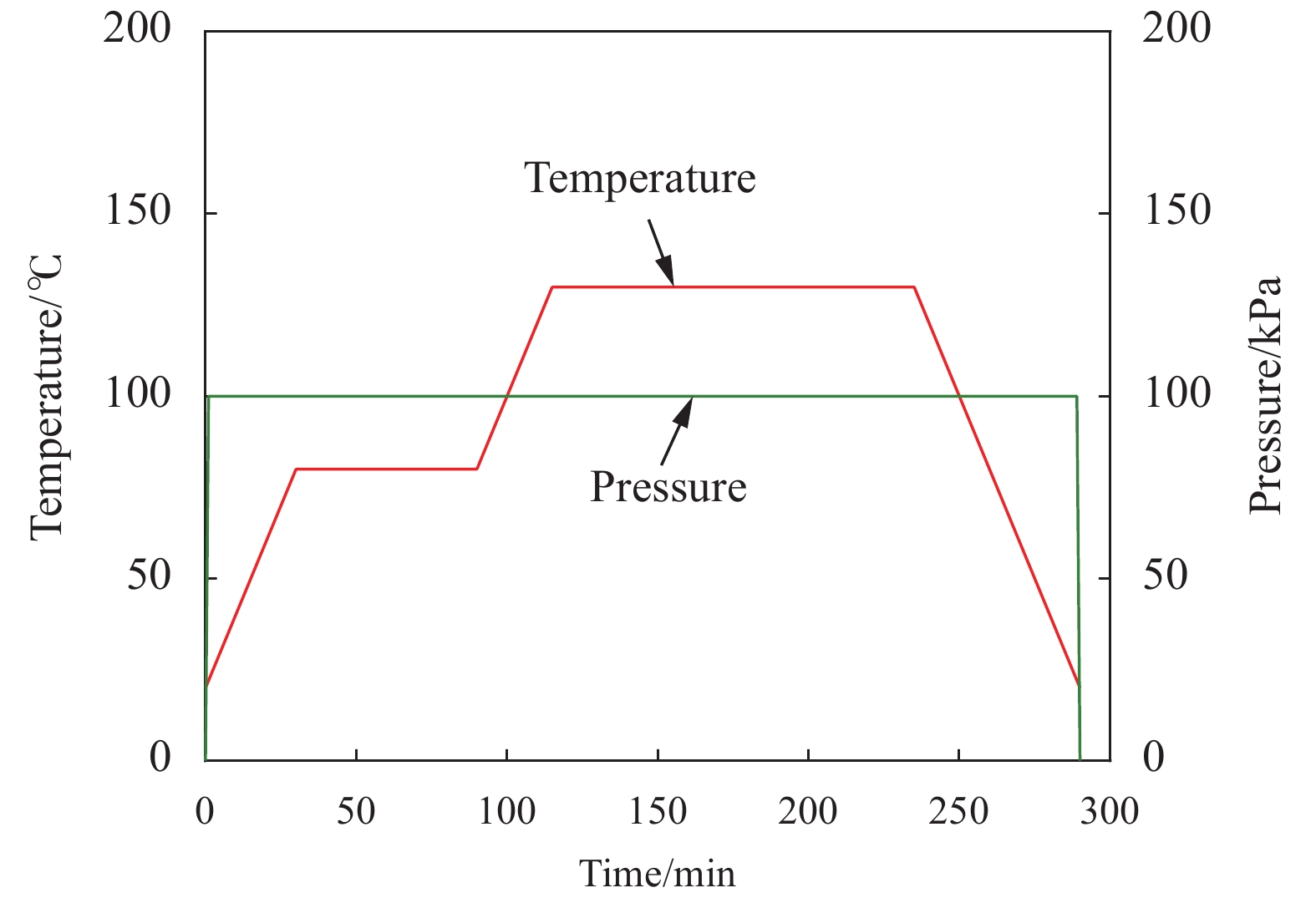
试件采用江苏恒神EM118系列碳纤维增强树脂预浸料制备,材料密度为1.85 g/cm3,单层厚度为0.15 mm,材料的弹性参数如表1所示。该预浸料采用真空袋压工艺固化,固化温度为130℃,固化工艺曲线如图2所示。
表 1 EM118碳纤维增强树脂预浸料的弹性基础参数Table 1. Elastic fundation parameters of EM118 carbon fiber reinforced resin prepregE1/GPa E2/GPa G12/GPa G13/GPa G23/GPa {v_{12}} 140 7.50 3.69 3.69 2.77 0.27 2.2 纤维曲线铺放变角度层合板制备
纤维曲线铺放复合材料变角度层合板的铺层设计应满足对称均衡性,本文曲线铺放采用交叉铺层设计,研究纤维角度变化对交叉曲线铺放变角度层合板阻尼性能和振动响应的影响,并以传统直线层合板(铺层顺序为[45/−45/0/90]s)为基准分析减振效果。变角度层合板表示为[±<T0|T1>]2s,同一铺层中纤维角度连续变化,不同位置纤维角度不同。变角度夹层板采用直线和曲线混合铺放,表示为[±θ/±<T0|T1>]2s,θ为直线铺层角度。
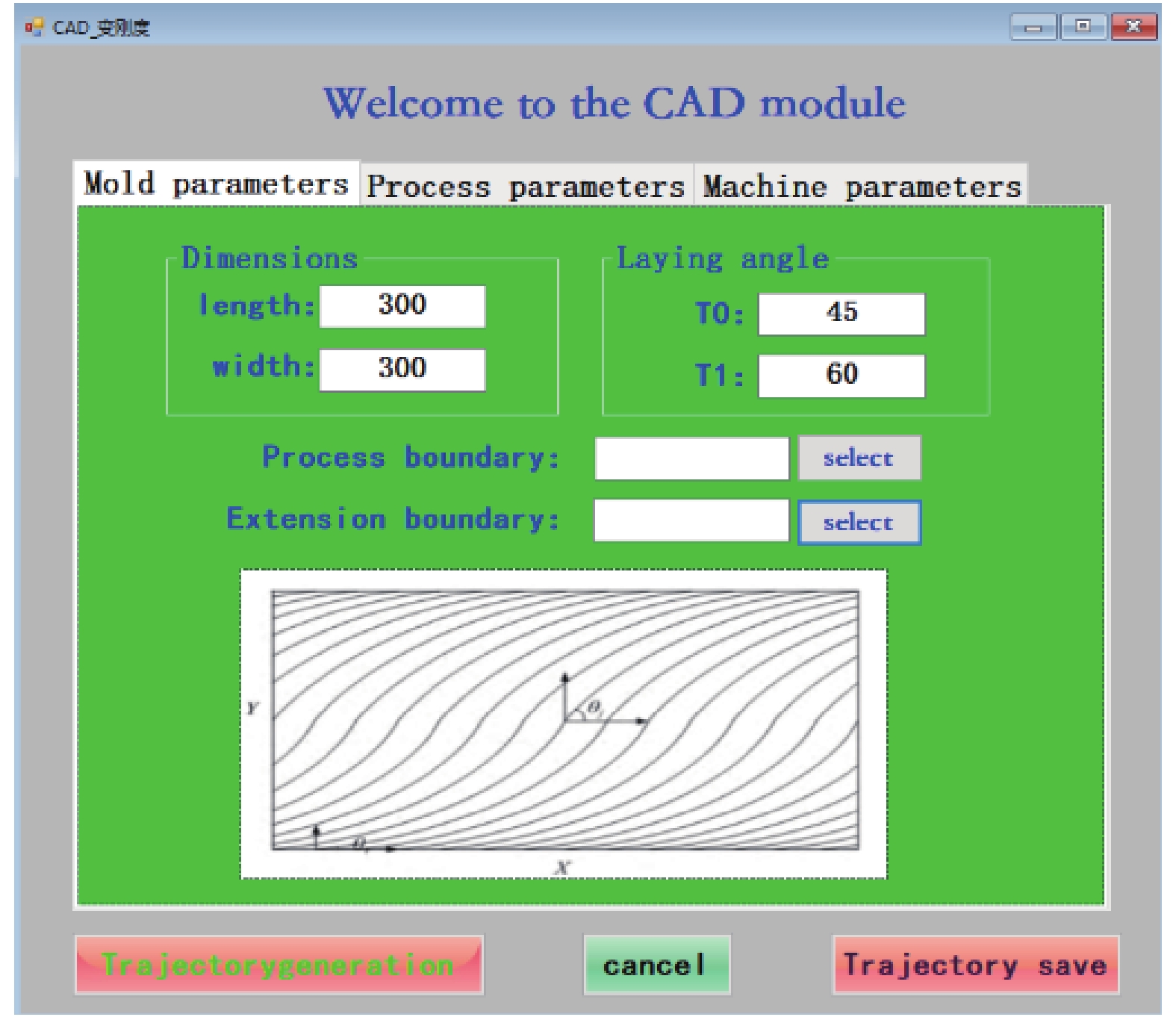
纤维曲线轨迹设计,根据式(3)基于VB.NET语言编写变角度轨迹规划软件,对CATIA二次开发形成人机交互界面实现轨迹可视化,输入设计参数T0、T1生成轨迹;输入铺放工艺参数完成NC代码输出。图3为软件界面,图4为生成的连续铺层±<45|60>的铺放中心轨迹线。
为研究纤维曲线铺放角度变化与复合材料层合板减振效果的关系,本文采用自动铺丝技术制备了变角度层合板6块,铺层顺序为[±<0|15>]2s、[±<15|30>]2s、[±<30|45>]2s、[±<45|60>]2s、[±<60|75>]2s、[±<73|88>]2s。对每块变角度层合板进行悬臂自由振动衰减实验,计算出不同纤维变化角度层合板的阻尼比。通过自由振动衰减法测得不同变角度层合板的阻尼比变化趋势与纤维曲线角度变化之间的关系,变角度层合板阻尼比越大,能量在传输过程中消耗的越多,其减振效果越好。
为研究变角度层合板在外界激励条件下的振动响应情况和验证不同纤维曲线铺层在变角度夹层板中的减振效果,制备6块变角度夹层板[±45/±<0|15>]s、[±45/±<15|30>]s、[±45/±<30|45>]s、[±45/±<45|60>]s、[±45/±<60|75>]s、[±45/±<73|88>]s,对其进行随机振动试验,得出随机激励条件下的加速度响应结果。从铺层纤维变化角度方面,阻尼比大的变角度层合板,在含有相应纤维角度变化铺层的夹层板较含其他纤维角度变化铺层的夹层板,减振效果更好。
本文制备所有试验件尺寸均为300 mm×300 mm,铺层数为8层,总厚度为1.2 mm。变角度层合板铺放工艺性需考虑以下三个问题[19-20]:(1) 曲率半径,曲率半径过小,在铺放时由于面内弯曲而导致丝束内侧出现褶皱,影响预浸料的性能;(2) 角度偏差;(3) 间隙和重叠。本文所有曲线铺层均采用自动铺丝设备的丝束切断/重送技术铺叠,丝束覆盖比例为50%覆盖[5]。为减小曲线铺放角度偏差和间隙、搭接面积,采用单丝束宽度为3.175 mm窄丝铺放。该预浸料所允许的最小曲率半径为700 mm,在铺放过程中采用单边切断法,即不改变丝束带中心线上半部分的丝束数,只切断中心线下半部分的丝束。直线铺层采用预浸料宽带手糊成型。图5为实际铺放的变角度复合材料层合板。试件自动铺丝制备完成,根据EM118碳纤维增强树脂预浸料固化工艺完成层合板固化,图6为固化的变角度层合板。
2.3 试验过程
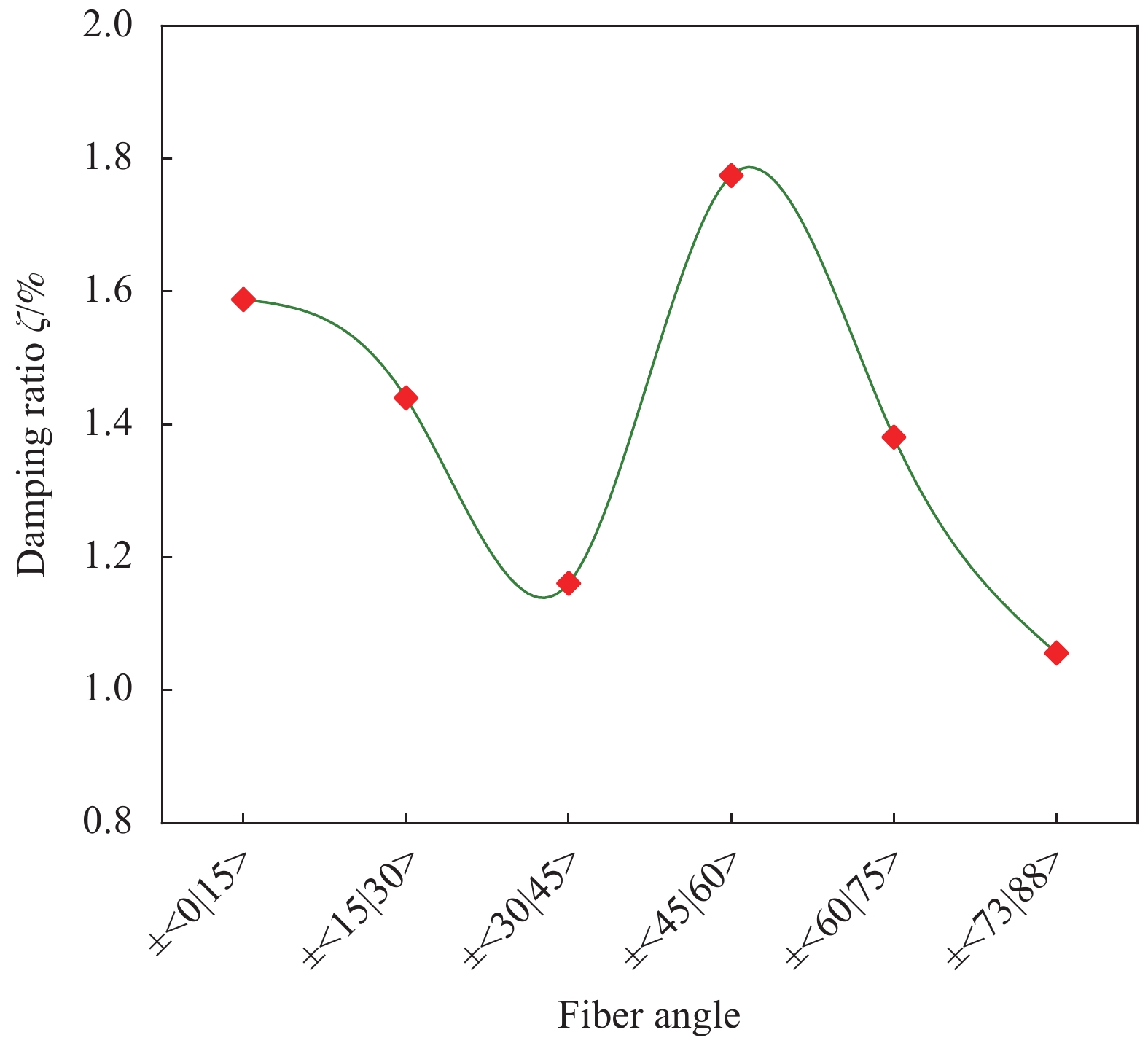
如图7所示,采用一端固支悬臂梁的自由振动衰减法测量阻尼性能,悬臂长度为270 mm。具体措施为:首先将复合材料变角度层合板在激振区域内平均分为9个点,在5号点对称面(光滑面)安装一个轻质的量程50 g的ICP传感器。采用逐点激励、单点测量的方法,使用力锤激振器从1号点至9号依次敲击,每个位置敲击5次,获得每个点的响应信号,信号传递到动态分析仪中,通过数字计算机对采集到的数据进行分析计算得出变角度层合板9个点的求和频响函数,从而分析出层合板的一阶固有频率;然后利用激振器在8号点施加
f = \sin{{\omega _1}t} 简谐载荷激发其达到共振状态,并在其稳定一段时间后,停止激励,采用型号为LMS SC316数采分析仪记录变角度层合板一阶固有频率对应的共振状态下的时域衰减的加速度信号。每块变角度层合板均进行3次衰减实验,对所测3次实验的结果进行平均作为每种实验工况下的实验结果。为对比不同层合板减振效果,所有变角度夹层板随机激励实验控制点位置均安装在试件8号点位置,采用型号为MODAL25+MB500VI的激振器提供振动源,随机控制方式均采用单点最大值方式控制,振动控制设备为8通道M+P振动控制仪。5号点为拾振点,测试分析软件为LMS.Test.Lab 11B,随机激励频域范围为4~1600 Hz,功率谱密度(PSD)定值输入0.00005 g2/Hz。
3. 结果与讨论
3.1 纤维角度变化对变角度层合板阻尼性能的影响
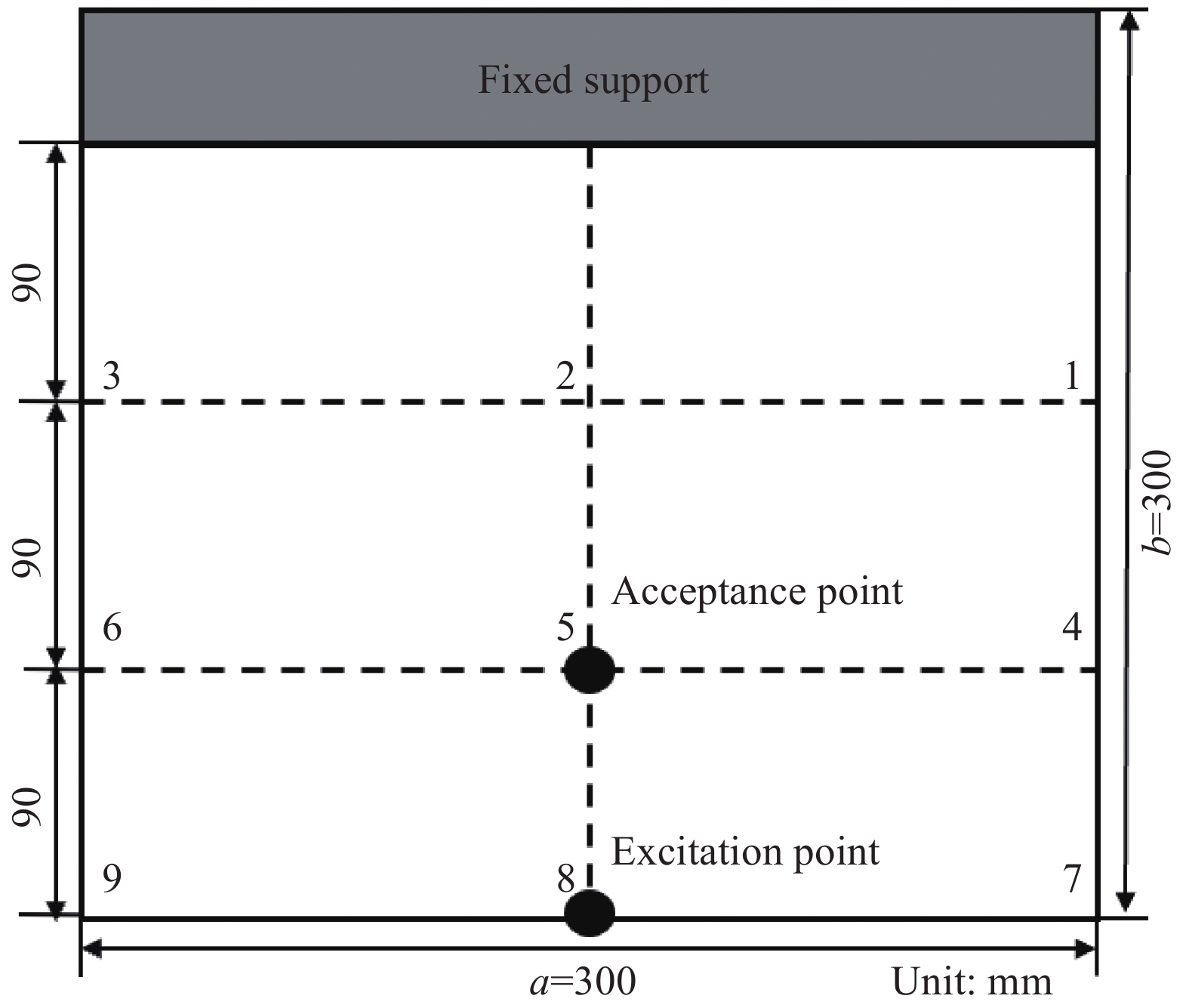
图8为6组纤维曲线铺放层合薄板的自由衰减曲线。根据振动衰减波形,利用式(5)计算出不同角度变化下复合材料变角度层合板的阻尼比,计算中采用相隔30个周期的两个振幅。结果如表2所示。
表 2 EM118碳纤维增强树脂复合材料变角度层合板阻尼比Table 2. Damping ratio of EM118 carbon fiber reinforced resin variable angle composite laminatesFiber curve composite laminate Damping ratio ζ/% [±<0|15>]2s 1.588 [±<15|30>]2s 1.440 [±<30|45>]2s 1.161 [±<45|60>]2s 1.775 [±<60|75>]2s 1.381 [±<73|88>]2s 1.056 复合材料变角度层合板阻尼比越大,其减振性能越好。从表2可以看出变角度层合板T0至T1在45~60°之间变化时阻尼比最大,为1.775%;变角度层合板T0至T1在73~88°之间变化时阻尼比最小,为1.056%。因此,变角度层合板[±<45|60>]2s的减振效果最好,[±<73|88>]2s的减振效果最差。
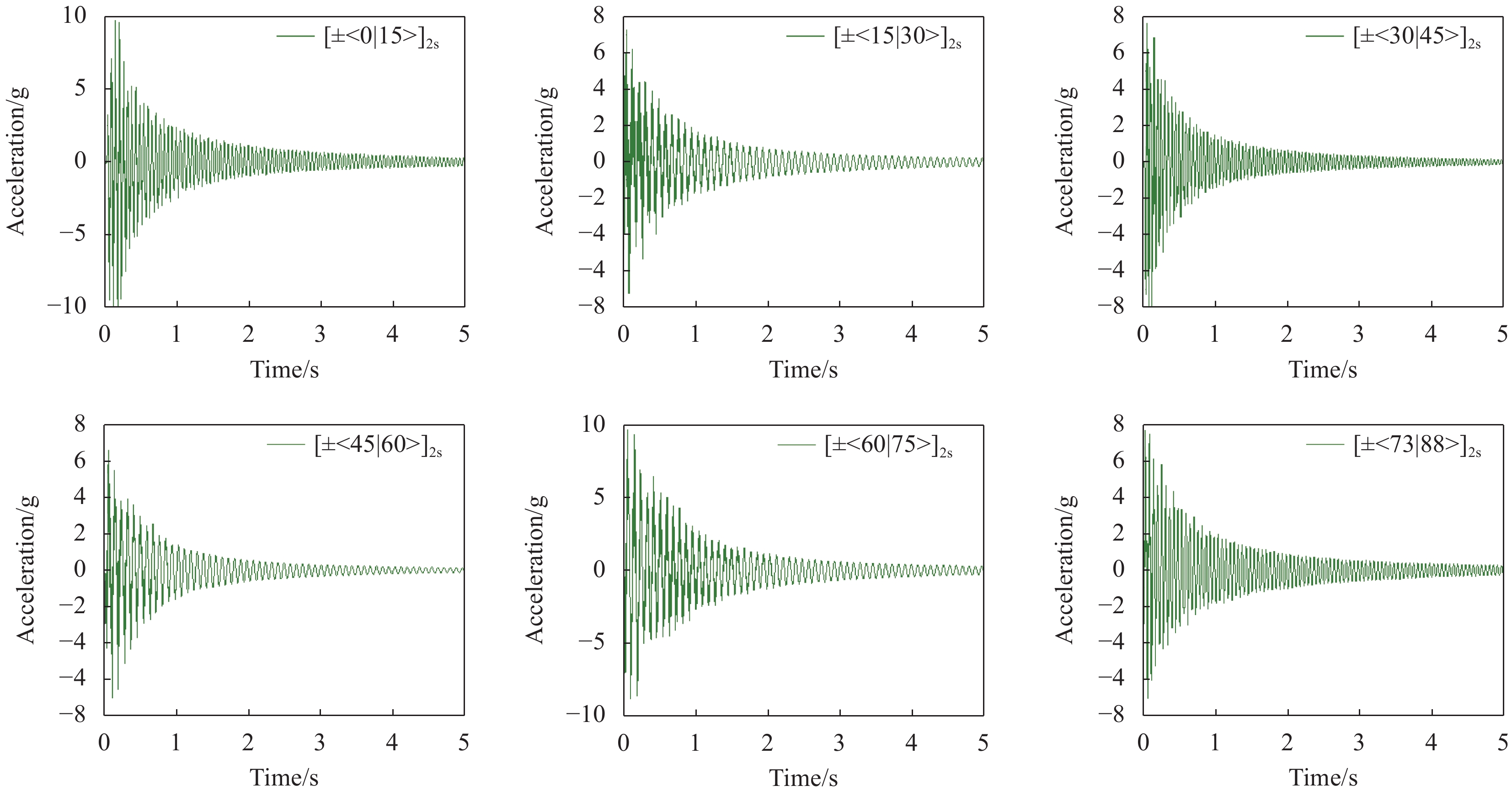
复合材料变角度层合板阻尼比随纤维角度变化的趋势如图9所示。可以看出,纤维角度变化在±<0|15>和±<45|60>附近获得良好的减振效果,随着纤维铺放角度的增加,复合材料变角度层合板的阻尼比先减小后增大,纤维变化角度为±<45|60>时阻尼比达到最大,纤维角度继续增加,层合板阻尼比逐渐减小,在纤维变化角度为±<73|88>时,层合板的阻尼比达到最小。说明纤维角度变化对阻尼性能影响显著,纤维角连续变化导致不同位置和方向上能量耗散不同,不同变角度层合板振动衰减率发生变化,阻尼性能产生差异。此外,变角度层合板与传统直线层合板相比,面内纤维长度增大纤维内摩擦增大、与树脂间界面强度的变化以及制造工艺产生的间隙、重叠缺陷等,对材料的振动能量耗散也起较大作用,其阻尼特性也有所变化[11]。另一方面,碳纤维增强树脂基复合材料作为黏弹性材料,本身具有的阻尼性能可以消耗一部分能量,起到阻尼减振的作用。
3.2 角度变化对变角度层合板振动响应的影响
依次对每块纤维曲线变角度夹层板进行随机激励试验,通过加速度传感器得到的激振信号传递到动态分析仪进行分析,采用共振峰处加速度响应的传递函数值作为减振评价指标。
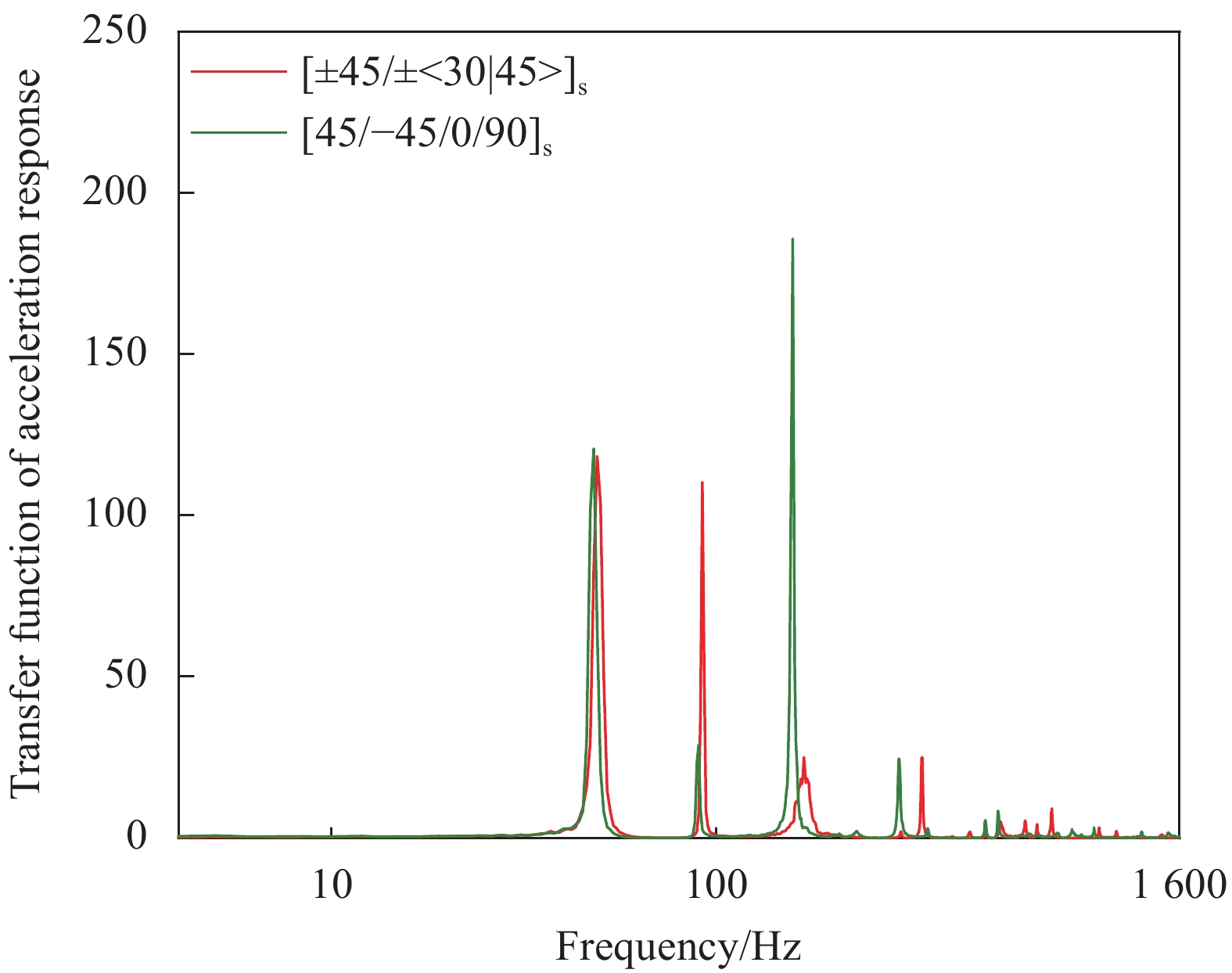
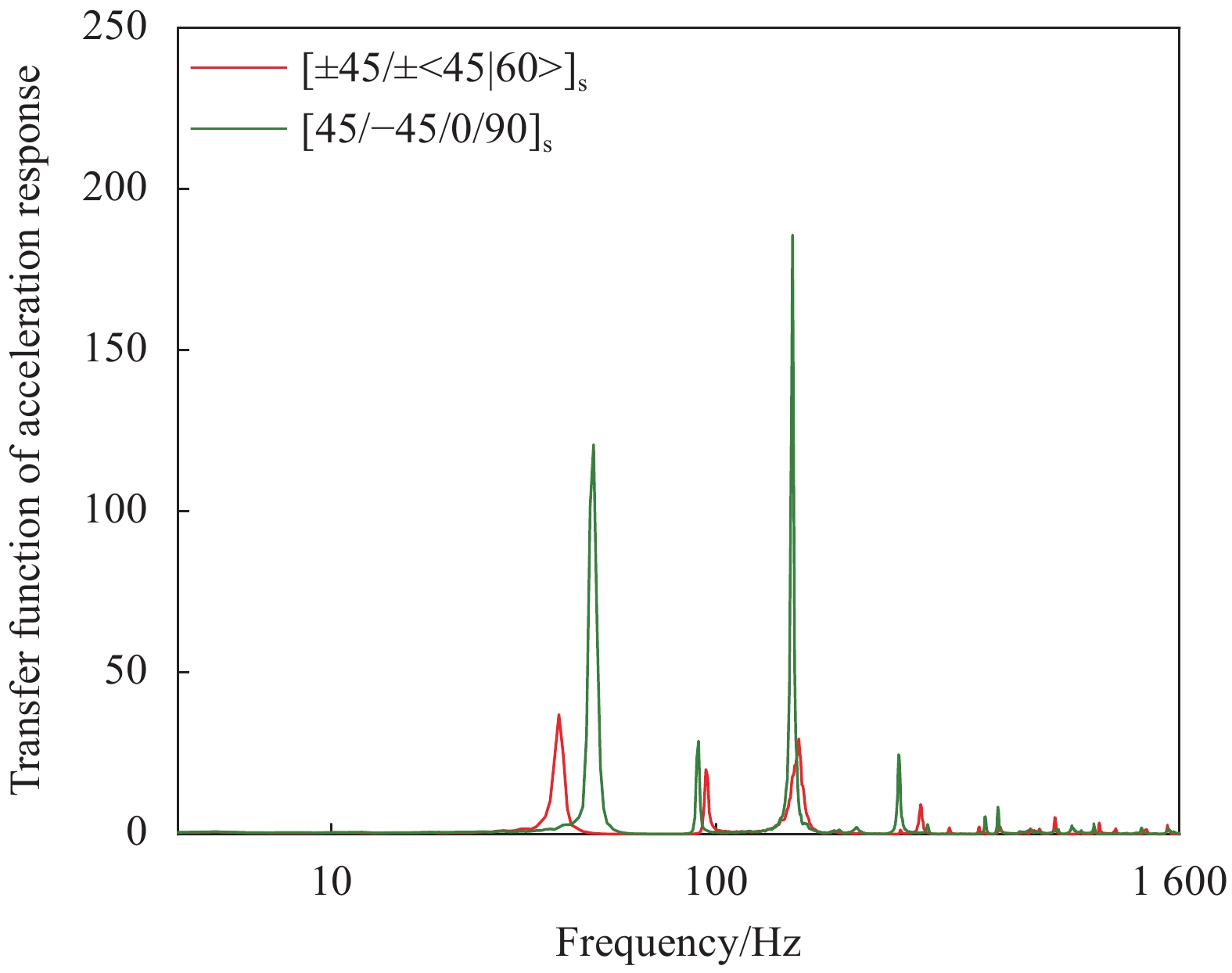
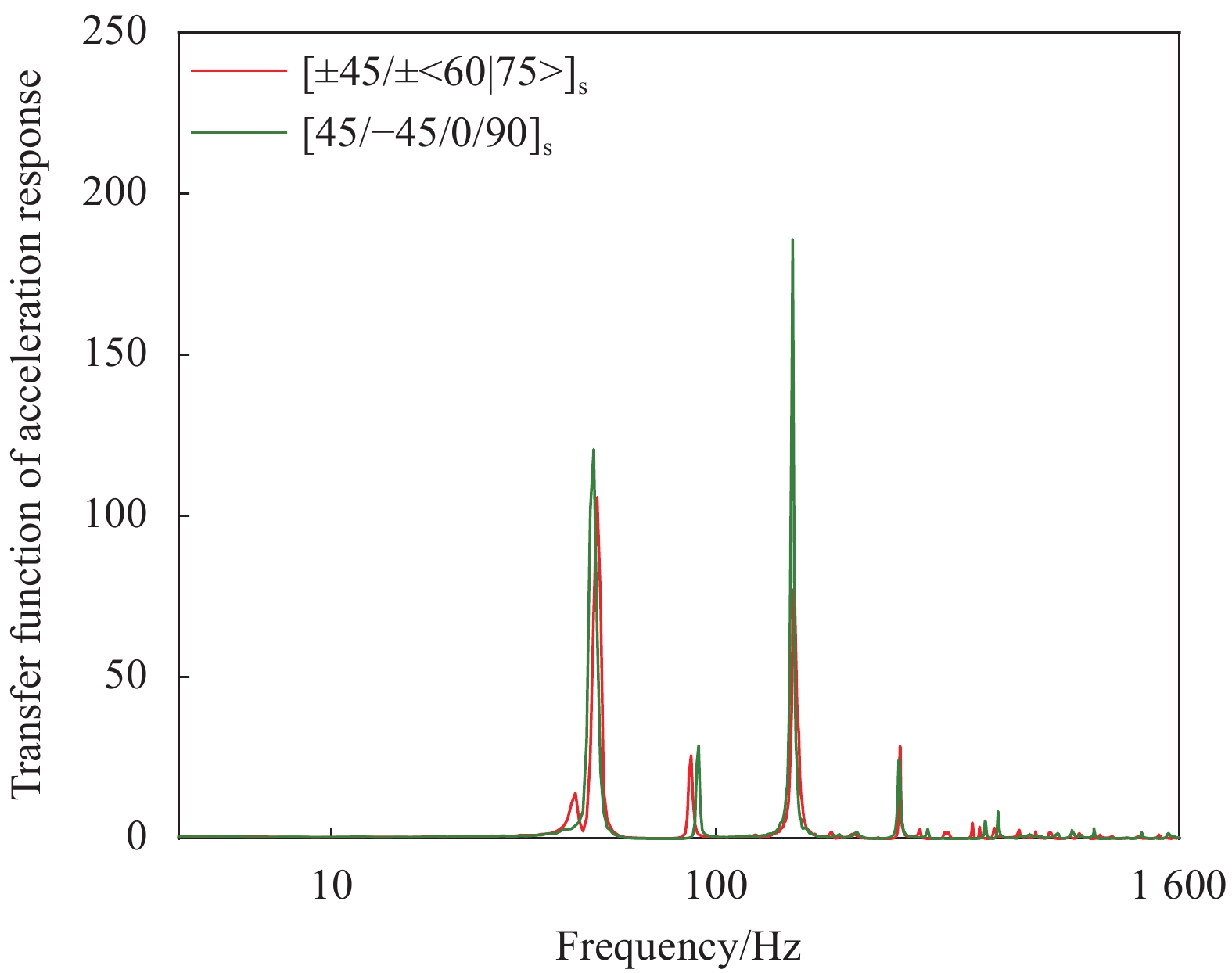
图10~15是随机激励条件下6块纤维曲线夹层板与传统直线层合板的测点振动加速度传递函数图。可以发现:6块纤维曲线夹层板与传统直线层合板的主要共振峰位置几乎重合,主要的共振频率分别为48 Hz、90 Hz、158 Hz。主要原因是,基于经典层合板理论[21],外侧铺层对层合板刚度影响较大,该铺层顺序下纤维角度对纤维曲线变角度夹层板共振频率和模态振型影响较小。
但相同随机激励条件下,不同夹层板各共振峰处加速度响应产生显著差异。在48 Hz处共振峰处加速度响应,变角度夹层板在0°~75°范围变化,峰值较传统直线板呈现不同程度降低,±<45|60>降低最显著,减振性能最佳;±<73|88>反而增大,减振性能变差;在90 Hz处共振峰处加速度响应,纤维曲线夹层板在45°~75°范围变化,峰值较传统直线板降低,其他角度反而增大;在158 Hz处共振峰处响应均不同程度降低,±<45|60>降低最显著。总体含±<45|60>曲线设计层合板共振时抑振响应能力最好。
表3列出了各纤维角度变化下夹层板,相同位置测点不同共振峰处响应的传递函数值(Transition function,TF)及减振效果评价[(传统直线层合板响应值−变角度夹层板响应值)/传统直线层合板响应值]。结果表明,随机激励下,基于拾振点不同共振峰处传递函数的减振效果规律差异明显。在3个共振峰处,含±<45|60>曲线夹层板减振效果均为最优,分别为69.32%、30.61%、94.89%,这主要是由于该曲线角度对应的变角度层合板阻尼性能最好,抑制响应。48 Hz附近,0~75°变化范围均获得了减振效果,减振效果变化趋势与纤维曲线铺放复合材料层合板阻尼比随纤维角度变化趋势一致;158 Hz附近,各曲线铺层夹层板较传统直线层合板均获得减振效果。90 Hz附近,改变纤维曲线角度减振效果较差。
表 3 EM118碳纤维增强树脂变角度层合板随机激励测点加速度响应共振峰值处传递函数值及减振效果Table 3. Value of transfer function and vibration reduction effect at the resonance peak of the acceleration response of the random excitation measuring point of EM118 carbon fiber reinforced resin variable angle laminatesComposite layer sequence Near 48 Hz Near 90 Hz Near 158 Hz Transition function Vibration reduction effect/% Transition function Vibration reduction effect/% Transition function Vibration reduction effect/% [45/−45/0/90]s 120.747 − 28.873 − 185.817 − [±45/±<0|15>]s 39.817 67.02 101.510 −251.57 89.800 51.67 [±45/±<15|30>]s 67.944 43.73 47.002 −62.79 171.014 7.97 [±45/±<30|45>]s 118.434 1.92 110.382 −282.30 25.029 86.53 [±45/±<45|60>]s 37.043 69.32 20.034 30.61 9.504 94.89 [±45/±<60|75>]s 105.821 12.36 25.855 10.45 77.399 58.35 [±45/±<73|88>]s 255.780 −111.83 47.988 −66.20 185.373 0.24 3.3 角度变化对变角度层合板振动强度的影响
通常用均方根值来评价结构振动的能量水平,均方根值
{g_{{\rm{rms}}}} 的表达式为{g_{{\rm{rms}}}}{\rm{ = }}\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{x_i}^2} } (6) 采用拾振点加速度响应的均方根值作为减振评价指标。表4列出了不同含曲线铺层夹层板在相同随机激励条件下的加速度均方根及减振效果[(传统直线层合板
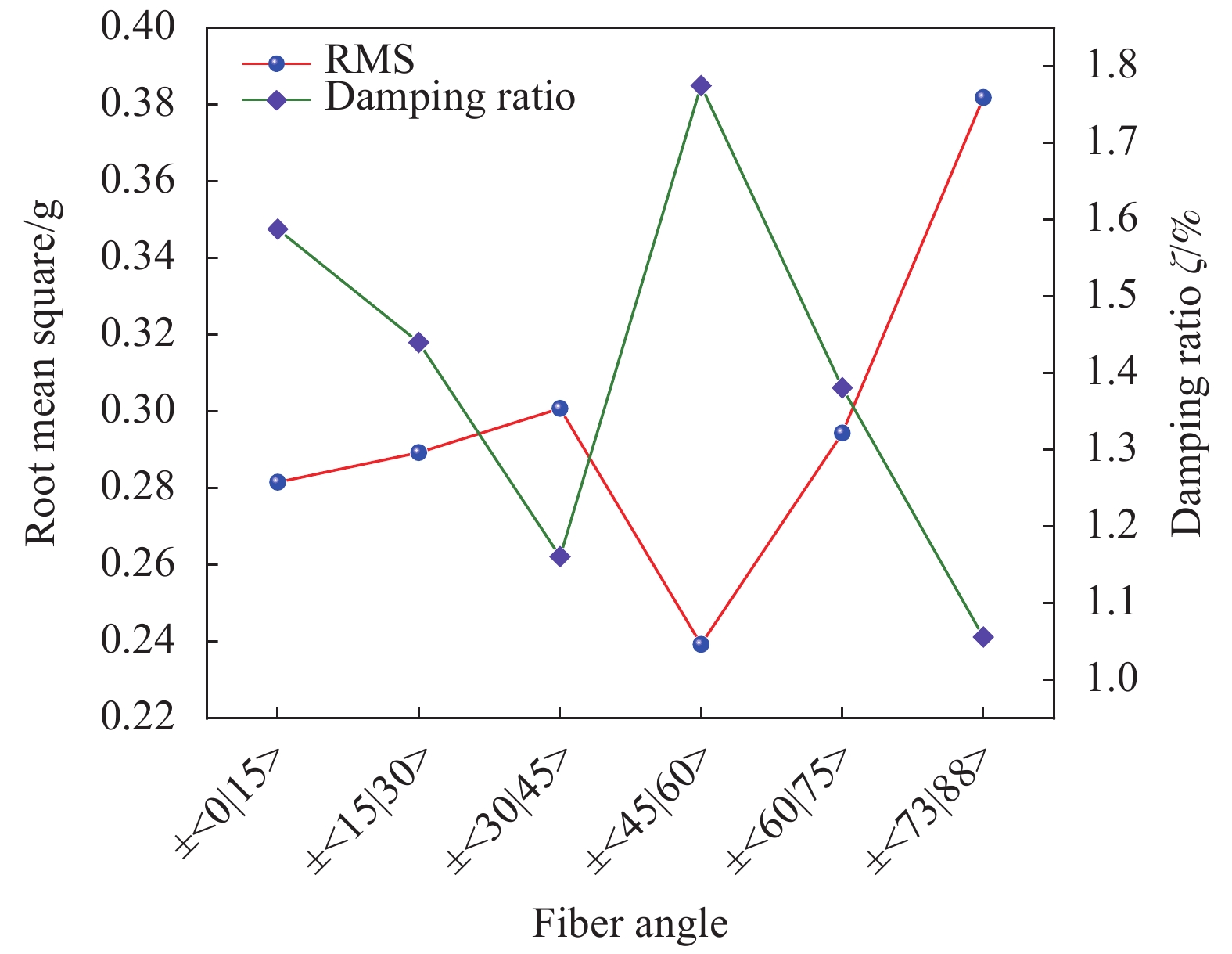
{g_{{\rm{rms}}}} −含曲线铺层变角度夹层板{g_{{\rm{rms}}}} ) /传统直线层合板{g_{{\rm{rms}}}} ]。可以发现:以测点实测加速度响应的{g_{{\rm{rms}}}} 为减振评价指标,相同能量输入下除了含±<73|88>曲线夹层板未获得减振效果,含其它曲线角度夹层板较传统直线板均获得了减振效果,其中±<45|60>最优,减振性能提高27.13%。图16为变角度层合板自由衰减实验与随机激励实验结果对比。可以发现,含自由衰减试验中阻尼比大的纤维曲线对应的夹层板,{g_{{\rm{rms}}}} 小,减振效果好。这是由于该变角度夹层板的阻尼性能较传统直线层合板得到改善,对共振峰处响应抑制明显,层合板振动能量水平降低,提高了减振效果。表 4 EM118碳纤维增强树脂变角度层合板随机激励测点响应加速度均方根值及减振效果Table 4. Random excitation measuring point response acceleration RMS and vibration reduction effect of EM118 carbon fiber reinforced resin variable angle laminatesComposite layer sequence Root mean square/g Vibration reduction effect/% [45/−45/0/90]s 0.3284 − [±45/±<0|15>]s 0.2816 14.25 [±45/±<15|30>]s 0.2893 11.91 [±45/±<30|45>]s 0.3008 8.40 [±45/±<45|60>]s 0.2393 27.13 [±45/±<60|75>]s 0.2944 10.35 [±45/±<73|88>]s 0.3819 −16.29 3.4 刚度和阻尼对变角度层合板减振性能的影响
刚度和阻尼都是影响结构振动的重要因素,相关研究表明增大刚度和阻尼均可有效降低复合材料层合板振动响应,提高减振性能。纤维角度变化后,变角度层合板除了阻尼发生变化外,刚度也会改变。因此进一步分析角度变化后刚度和阻尼分别对变角度层合板减振的影响。
为降低分析难度,本文根据固有频率近似推算层合板的等效刚度[22],根据频率方程:
{\boldsymbol{K}} - {\omega ^2}{\boldsymbol{M}}{\kern 1pt} {\kern 1pt} {\rm{ = }}{\kern 1pt} {\kern 1pt} 0 (7) 则刚度之比为
\left| {\frac{{{K_1}}}{{{K_2}}}} \right|{\rm{ = }}\left| {\frac{{\omega _1^2{M_1}}}{{\omega _2^2{M_2}}}} \right| (8) 式中:
{\boldsymbol{K}} 为等效刚度;ω为固有频率;{\boldsymbol{M}} 为质量。若以传统直线层合板的等效刚度和质量为基准量,则其它复合材料变角度层合板的相对刚度和相对质量如表5所示。
由表4可得,各层合板减振性能大小关系为:CFRP-VS4>CFRP-VS1>CFRP-VS2>CFRP-VS5>CFRP-VS3>CFRP-T1>CFRP-VS6。由表5可以发现,各层合板相对刚度大小关系为:CFRP-VS5>CFRP-VS3>CFRP-T1>CFRP-VS6>CFRP-VS1>CFRP-VS4>CFRP-VS2,这主要是由于纤维角度变化改变了刚度分布;各层合板相对阻尼大小关系为:CFRP-VS4>CFRP-VS1> CFRP-VS2>CFRP-VS5>CFRP-VS3>CFRP-T1>CFRP-VS6,这主要是由于纤维角度变化改变了层合板阻尼性能。
表 5 不同EM118碳纤维增强树脂变角度层合板相对刚度和相对质量Table 5. Relative stiffness and relative mass of EM118 carbon fiber reinforced resin laminated plates with different variable anglesComposite layer
sequenceNumber Relative stiffness Relative mass Relative damping Relative stiffness
to mass ratio[45/−45/0/90]s CFRP-T1 1 1 1 1 [±45/±<0|15>]s CFRP-VS1 0.884 1.006 1.490 0.879 [±45/±<15|30>]s CFRP-VS2 0.622 0.993 1.348 0.626 [±45/±<30|45>]s CFRP-VS3 1.031 1.011 1.087 1.020 [±45/±<45|60>]s CFRP-VS4 0.663 1.004 1.662 0.660 [±45/±<60|75>]s CFRP-VS5 1.039 0.997 1.293 1.042 [±45/±<73|88>]s CFRP-VS6 0.949 0.990 0.989 0.959 由以上关系对比发现,含±<45|60>变角度夹层板刚度为传统直线层合板的0.663倍,阻尼为传统直线层合板1.662倍,刚度下降的同时减振性能仍然提高,主要原因是虽然刚度下降不利于抑制振动响应,但该角度变化下阻尼性能提高最大,有效降低了共振峰幅值,整体振动水平降低,减振性能最好,提高27.13%;含±<0|15>和±<15|30>变角度夹层板规律类似。
含±<73|88>变角度夹层板刚度为传统直线层合板的0.949倍,阻尼为传统直线层合板的0.989倍,刚度和阻尼均降低,减振性能最差,降低−16.29%。同时可以发现,含±<60|75>角度夹层板和含±<30|45>角度夹层板较传统直线层合板刚度和阻尼都有提高,因此获得了减振效果。但从数据对比可以发现,阻尼贡献略大于刚度贡献。由图16可以发现,含自由衰减试验中阻尼比大的纤维曲线对应的变角度夹层板,
{g_{{\rm{rms}}}} 小,减振效果好。以上分析可得,不同纤维曲线变化层合板的刚度和阻尼对减振性能贡献不同,不改变层合板厚度和尺寸,纤维曲线设计确实可以改善动态响应获得减振效果。同时变角度层合板较传统直线层合板阻尼和刚度设计空间更大,其优势在于不改变厚度和尺寸情况下,通过纤维曲线设计可调节层合板刚度和阻尼来改善动态响应获得减振效果或保证层合板刚度不下降的同时优化阻尼来抑制共振峰响应,从而降低整体层合板振动能量水平,提高减振效果。
4. 结 论
主要探究了纤维曲线铺放角度变化与EM118碳纤维增强树脂复合材料层合板的减振性能关系。采用自由振动衰减法研究纤维角度变化与曲线变角度层合板阻尼比的关系;以拾振点共振峰处的传递函数和加速度均方根值为评价指标,研究了含不同曲线铺层变角度夹层板在随机激励条件下的减振效果。主要结论如下:
(1) 通过对变角度层合板[±<0|15>]2s、[±<15|30>]2s、[±<30|45>]2s、[±<45|60>]2s、[±<60|75>]2s、[±<73|88>]2s进行自由衰减实验分析,并计算得到每块层合板的阻尼比。通过自由衰减实验发现变角度层合板阻尼比在纤维变化角度为±<45|60>变化时最大,纤维变化角度为±<73|88>之间变化时层合板阻尼比最小;
(2) 随机激励条件下,基于拾振点不同共振峰处传递函数的减振效果规律差异明显;以拾振点加速度响应均方根(Root mean square,RMS)为减振评价指标,除了含±<73|88>曲线夹层板未获得减振效果,含其它曲线角度夹层板较传统直线板均获得了减振效果,其中±<45|60>最优,减振性能提高27.13%;
(3) 变角度层合板减振性能明显优于传统直线层合板,不改变层合板厚度和尺寸,纤维曲线设计确实可以改善动态响应获得减振效果。不同纤维曲线变化下其刚度和阻尼对减振性能贡献不同,改善阻尼有利于抑制振动响应。本文相关试验结果对变角度层合板减振设计和优化有一定的参考意义;
(4) 变角度层合板减振设计优势在于其阻尼和刚度设计空间更大,不改变厚度和尺寸情况下,也可通过纤维曲线铺层设计改善其动态响应获得减振效果。另外也可发现相同厚度和尺寸下,可通过设计曲线铺层来保证层合板刚度不下降的同时提升阻尼来抑制共振峰响应,从而降低整体层合板振动能量水平,提高减振效果。
-
表 1 EM118碳纤维增强树脂预浸料的弹性基础参数
Table 1 Elastic fundation parameters of EM118 carbon fiber reinforced resin prepreg
E1/GPa E2/GPa G12/GPa G13/GPa G23/GPa {v_{12}} 140 7.50 3.69 3.69 2.77 0.27 表 2 EM118碳纤维增强树脂复合材料变角度层合板阻尼比
Table 2 Damping ratio of EM118 carbon fiber reinforced resin variable angle composite laminates
Fiber curve composite laminate Damping ratio ζ/% [±<0|15>]2s 1.588 [±<15|30>]2s 1.440 [±<30|45>]2s 1.161 [±<45|60>]2s 1.775 [±<60|75>]2s 1.381 [±<73|88>]2s 1.056 表 3 EM118碳纤维增强树脂变角度层合板随机激励测点加速度响应共振峰值处传递函数值及减振效果
Table 3 Value of transfer function and vibration reduction effect at the resonance peak of the acceleration response of the random excitation measuring point of EM118 carbon fiber reinforced resin variable angle laminates
Composite layer sequence Near 48 Hz Near 90 Hz Near 158 Hz Transition function Vibration reduction effect/% Transition function Vibration reduction effect/% Transition function Vibration reduction effect/% [45/−45/0/90]s 120.747 − 28.873 − 185.817 − [±45/±<0|15>]s 39.817 67.02 101.510 −251.57 89.800 51.67 [±45/±<15|30>]s 67.944 43.73 47.002 −62.79 171.014 7.97 [±45/±<30|45>]s 118.434 1.92 110.382 −282.30 25.029 86.53 [±45/±<45|60>]s 37.043 69.32 20.034 30.61 9.504 94.89 [±45/±<60|75>]s 105.821 12.36 25.855 10.45 77.399 58.35 [±45/±<73|88>]s 255.780 −111.83 47.988 −66.20 185.373 0.24 表 4 EM118碳纤维增强树脂变角度层合板随机激励测点响应加速度均方根值及减振效果
Table 4 Random excitation measuring point response acceleration RMS and vibration reduction effect of EM118 carbon fiber reinforced resin variable angle laminates
Composite layer sequence Root mean square/g Vibration reduction effect/% [45/−45/0/90]s 0.3284 − [±45/±<0|15>]s 0.2816 14.25 [±45/±<15|30>]s 0.2893 11.91 [±45/±<30|45>]s 0.3008 8.40 [±45/±<45|60>]s 0.2393 27.13 [±45/±<60|75>]s 0.2944 10.35 [±45/±<73|88>]s 0.3819 −16.29 表 5 不同EM118碳纤维增强树脂变角度层合板相对刚度和相对质量
Table 5 Relative stiffness and relative mass of EM118 carbon fiber reinforced resin laminated plates with different variable angles
Composite layer
sequenceNumber Relative stiffness Relative mass Relative damping Relative stiffness
to mass ratio[45/−45/0/90]s CFRP-T1 1 1 1 1 [±45/±<0|15>]s CFRP-VS1 0.884 1.006 1.490 0.879 [±45/±<15|30>]s CFRP-VS2 0.622 0.993 1.348 0.626 [±45/±<30|45>]s CFRP-VS3 1.031 1.011 1.087 1.020 [±45/±<45|60>]s CFRP-VS4 0.663 1.004 1.662 0.660 [±45/±<60|75>]s CFRP-VS5 1.039 0.997 1.293 1.042 [±45/±<73|88>]s CFRP-VS6 0.949 0.990 0.989 0.959 -
[1] SABA N, JAWAID M, ALOTHMAN OY, et al. A review on dynamic mechanical properties of natural fibre reinforced polymer composites[J]. Construction and Building Materials,2016(106):149-159.
[2] 肖军, 李勇, 李建龙. 自动铺放技术在大型飞机复合材料结构件制造中的应用[J]. 航空制造技术, 2008(1):50-53. DOI: 10.3969/j.issn.1671-833X.2008.01.009 XIAO Jun, LI Yong, LI Jianlong. Application of automatic fiber placement in manufacture of composite structures in large aircraft[J]. Aeronautical Manufacturing Technology,2008(1):50-53(in Chinese). DOI: 10.3969/j.issn.1671-833X.2008.01.009
[3] AKHAVAN H, RIBEIRO P. Natural modes of vibration of variable stiffness composite laminates with curvilinear fibers[J]. Composite Structures,2011,93(11):3040-3047. DOI: 10.1016/j.compstruct.2011.04.027
[4] 尹先桃, 漆文凯. 变刚度复合材料层合板阻尼性能优化[C]. 中国航空学会第八届航空发动机可靠性学术交流, 2015: 459-463. YIN Xiantao, QI Wenkai. Research on damping properties optimization of variable-stiffness plate[C]. Journal of Physics Conference Series, 2015: 459-463 (in Chinese).
[5] 孔斌, 顾杰斐, 陈普会, 等. 变刚度复合材料结构的设计、制造与分析[J]. 复合材料学报, 2017, 34(10):2121-2133. KONG Bin, GU Jiefei, CHEN Puhui, et al. Design, manufacture and analysis of variable stiffness composite structures[J]. Journal of Composite Materials,2017,34(10):2121-2133(in Chinese).
[6] ABDALLA M, SETOODHE S, GRDAL Z. Design of variable stiffness composite panels for maximum fundamental frequency using lamination parameters[J]. Computers & Strutures,2008,86(9):870-878.
[7] 聂国隽, 朱佳瑜. 纤维曲线铺放的复合材料层合板的自由振动分析[J]. 力学季刊, 2016, 37(2):274-283. NIE Guojun, ZHU Jiayu. Free vibration analysis of composite laminates with curvilinear fibers[J]. Chinese Quarterly of Mechanics,2016,37(2):274-283(in Chinese).
[8] 孙士平, 邓同强, 胡政. 丝束变角度层合板频率性能的参数化分析与优化[J]. 玻璃钢/复合材料, 2016, 8:27-32. SUN Shiping, DENG Tongqiang, HU Zheng. Par ametric analysis and optimization of frequency property of variable angle tow laminates[J]. Fiber Reinforced Plastics/Composites,2016,8:27-32(in Chinese).
[9] 欧阳小穗, 刘毅. 高速流场中变刚度复合材料层合板颤振分析[J]. 航空学报, 2018, 39(3):221539. OUTANG X S, LIU Y. Panel flutter of variable stiffness composite laminates in supersonic flow[J]. Acta Aeronautica et Astronautica Sinica,2018,39(3):221539(in Chinese).
[10] TREVISO A, VAN GENECHTEN B, MUNDO D, et al. Damping in composite materials: Properties and models[J]. Composites Part B: Engineering,2015,78:144-152. DOI: 10.1016/j.compositesb.2015.03.081
[11] TANG X, YAN X. A review on the damping properties of fiber reinforced polymer composites[J]. Journal of Industrial Textiles,2020,49(6):693-721.
[12] PEREIRA D A, GUIMARÃES T A M, RESENDE H B, et al. Numerical and experimental analyses of modal frequency and damping in tow-steered CFRP laminates[J]. Composite Structures,2020,244(4):112190.
[13] PEREIRA D A, SALES T P, RADE D A. Multi-objective frequency and damping optimization of tow-steered composite laminates[J]. Composite Structures,2020,256:112932.
[14] GÜRDAL Z, OLMEDO R. In-plane response of laminates with spatially varying fiber orientations variable stiffness concept[J]. AIAA Journal,1993,31(4):751-758. DOI: 10.2514/3.11613
[15] GÜRDAL Z, TATTING B F, WU C K. Variable stiffness composite panels: Effects of stiffness variation on the in-plane and buckling response[J]. Composites Part A: Applied Science and Manufacturing,2008,39(5):911-922. DOI: 10.1016/j.compositesa.2007.11.015
[16] 漆文凯, 程博. 复合材料层合板阻尼预测分析与验证[J]. 振动测试与诊断, 2013, 33(6):1049-1053. QI Wenkai, CHENG Bo. Predictive analysis and verification of damping for composite laminates[J]. Journal of Vibration, Measurement & Diagnosis,2013,33(6):1049-1053(in Chinese).
[17] DHIKARI S, WOODHOUSE J. Identification of damping: Part1, Viscous damping[J]. Journal of Sound and Vibration,2001,243(1):43-61. DOI: 10.1006/jsvi.2000.3391
[18] 李晖, 孙伟, 常永乐, 等. 具有振幅依赖性的纤维增强复合薄板非线性阻尼的时域测试方法[J]. 振动与冲击, 2018, 37(5): 169-174. LI Hui, SUN Wei, CHANG Yongle, et al. Time domain test method for nonlinear damping of a fiber-reinforced composite thin plate with amplitude dependence. Journal of Vibration and Shock [J], 2018, 37(5): 169-174. (in Chinese).
[19] FALCÓ O, MAYUGO J A, LOPES C S, et al. Variable-stiffness composite panels: As-manufactured modeling and its influence on the failure behavior[J]. Composites Part B: Engineering,2014,56:660-669. DOI: 10.1016/j.compositesb.2013.09.003
[20] PEETERS D M J, LOZANO G G, ABDALLA M M. Effect of steering limit constraints on the performance of variable stiffness laminates[J]. Computers & Structures,2018,196:94-111.
[21] REDDY J N. Mechanics of laminated composite plates and shells: theory and analysis [M]. Boca Raton: CRC Press, 2004: 81-376.
[22] 刘建良, 梅志远, 唐宇航, 等. 几种典型复合材料板振动特性综合对比分析及设计规律研究[J]. 振动与冲击, 2019, 38(15):65-72. LIU Jianliang, MEI Zhiyuan, TANG Yuhang, et al. Comprehensive comparative analysis for vibration characteristics of several typical composite panels and their design law[J]. Journal of Vibration and Shock,2019,38(15):65-72(in Chinese).
-
期刊类型引用(5)
1. 王显峰,阳铭广,刘琛,高文明,孙颖,叶帆. 变刚度复合材料层合板研究进展. 南京航空航天大学学报. 2024(01): 17-30 .  百度学术
百度学术
2. 王婷婷,高军鹏,张宝艳,马兆丹,王伟翰,许虎. 纤维增强聚合物阻尼复合材料研究进展. 材料工程. 2024(11): 1-11 .  百度学术
百度学术
3. 叶帆,王显峰,王东立,高天成,张浩天,冯天洋. 不同铺层数量下的纤维角度曲线变化复合材料层合板振动特性研究. 复合材料科学与工程. 2023(01): 44-54 .  百度学术
百度学术
4. 张桂明,沈志强,祖磊,王华毕,张骞,夏献钊,耿洪波,潘杰,邹李清. 基于蚁群算法的变刚度层合板角度优化分析. 复合材料科学与工程. 2023(01): 5-15 .  百度学术
百度学术
5. 彭运松,罗兴宇,李想,张浩天,张晨旭,段少华. 变角度混杂复合材料层合板振动特性研究. 当代化工研究. 2023(21): 58-61 .  百度学术
百度学术
其他类型引用(6)
-





 下载:
下载: