A cyclic plasticity-damage model for predicting ratcheting behavior of composite materials
-
摘要: 构建循环塑性本构模型并揭示其微观机制，目前仍然是复合材料力学研究富有挑战性的课题。本文提出了一种循环塑性-损伤模型，用以预测在循环载荷作用下纤维增强复合材料的应力-应变响应。该模型是在作者前期提出的描述非线性滞后行为的弹塑性本构模型的基础上的进一步扩展。它可以预测加载时的非线性响应、卸载和重加载时的迟滞行为及大量循环下的棘轮现象。作为基准问题验证，将Kawai等的实验数据与本文模型的数值预测进行了比较。结果表明，该模型能够模拟碳纤维/环氧树脂单向复合材料在偏轴循环加载下的棘轮行为。
-
关键词:
- 纤维增强聚合物复合材料 /
- 循环塑性 /
- 迟滞行为 /
- 棘轮效应 /
- 疲劳损伤
Abstract: It is still a challenging problem to establish a constitutive model for cyclic plasticity and reveal its microscopic mechanism. A cyclic plasticity-damage model was proposed in this study to predict the stress-strain response of fiber reinforced polymer under cyclic loading. This model is a further extension of the elastic-plastic constitutive model to describe the nonlinear hysteresis behavior proposed by the authors. It can predict the nonlinear responses during loading, hysteresis behavior during unloading and reloading and the ratcheting phenomena under a large number of cycles. As a benchmark problem verification, the experimental data by Kawai et al, were compared with the numerical prediction of the model in this paper. The results show that the model can simulate the ratcheting behavior of carbon fiber/epoxy unidirectional composite under off-axis cyclic loading. -
随着超高速飞行器马赫数的不断提升，对飞行器电缆罩等结构件的质量、力学承载性能、抗静电性能和防热性能等都提出了更为苛刻的要求[1]。传统的飞行器耐高温与承载部件大多采用金属材料，并在表面涂覆涂层来实现防热，这种结构存在质量大、隔热差及耐用性难保证等缺点，难以满足结构-功能一体化的设计需求[2-3]。纤维增强树脂基复合材料由于其丰富的结构设计性、优异的热-力性能和低成本加工与维护等优势，已成为耐高温领域的理想候选材料[4-5]。
为满足纤维增强树脂基复合材料高承载-功能一体化的使用需求，通常采取纤维混杂和使用三维纺织结构的方式[6-7]。例如，碳纤维(CF)和玻璃纤维(GF)混杂不仅能在力学性能上实现互补，提高其承载效率，还可以对纤维进行合理的排布和编织，获得更低的电阻率和导热系数[8-9]。此外，2.5D机织复合材料作为一种新型三维纺织结构复合材料，其纬纱平行排列，经纱在垂直于纬纱的方向以一定角度进行交织。在受力过程中，结构中的经纱可以阻碍裂纹的扩展，有效阻止分层现象发生[10-11]。在使用过程中，2.5D机织复合材料常处于极端热环境下，由高温引起的热应力集中和热变形过大常常导致复合材料提前失效，因此，研究2.5D机织复合材料的热-力学行为具有重要的理论和实践意义[12-13]。
近几十年来，热固性树脂的快速发展，大大加快了纤维增强树脂基复合材料高温力学性能的研究。Ruggles-Wrenn等[14]研究了二维层合和三维正交机织碳/聚酰亚胺复合材料在329℃下的拉伸-压缩疲劳行为。Zhao等[15]围绕2.5D机织碳/双马来酰亚胺树脂(简称为双马树脂)复合材料进行了常温和高温下纬向拉伸疲劳研究，分析了温度和疲劳载荷分别对2.5D机织碳/双马复合材料性能的影响。Song等[16]探究了温度对2.5D机织碳/双马复合材料拉伸性能影响，并分析了其微观损伤模式和高温下的损伤机制。Dang等[17]探究了2.5D机织碳/环氧复合材料温度效应下的弯曲失效机制，发现室温和高温下2.5D机织碳/环氧复合材料的主要破坏机制均包括纤维的断裂、基体开裂和界面脱粘，但高温下因基体软化，试样损伤更加严重。曹淼[18]为研究2.5D机织碳/环氧复合材料的热氧稳定性和层间性能，开展了不同老化时间下的层间剪切和冲击后弯曲力学性能测试，并分析了其力学性能随老化时间退化规律。Rathore等[19]研究了温度对碳-玻纤/环氧层合复合材料弯曲性能的影响，随着温度的升高，复合材料的强度和刚度都持续下降，且碳纤维铺层数更多的复合材料力学性能下降速度更快。于洋等[20]研究了高温老化对三维正交碳-玻纤/双马复合材料的三点弯曲和层间剪切力学性能影响，结果发现Z向纱线可以有效阻挡层间裂纹的扩展，减缓材料的老化速率。目前，学者们针对2.5D机织复合材料的热-力学行为研究主要围绕非混杂结构，而关于2.5D机织混杂结构复合材料在高温环境下的损伤及混杂协同机制的研究还鲜有报道[21-22]。
本文设计制备了2.5D机织碳纤维-玻璃纤维/双马来酰亚胺树脂复合材料(简称为2.5D机织混杂复合材料)，并根据复合材料的动态热机械性能设定了力学性能测试温度上限，开展了不同温度场(25℃、150℃、240℃、300℃)下2.5D机织混杂复合材料的三点弯曲和层间剪切力学性能测试。借助光学显微镜和扫描电镜对试样的断口形貌进行了观测，阐明了2.5D机织混杂复合材料的高温力学行为及损伤机制，以期为三维纺织复合材料的多功能-承载一体化设计和应用提供数据依据。
1. 实验和测试
1.1 实验材料与试样制备
2.5D机织混杂复合材料增强体选用日本东丽公司生产的T300-3 K型碳纤维和南京玻璃纤维研究设计院生产的E型玻璃纤维，并通过多层角联织机完成织造，基体选用航天材料及工艺研究所研制的R801双马树脂。其中，复合材料截面和预制体结构示意图如图1所示，碳纤维、玻璃纤维和双马树脂性能如表1所示。此外，2.5D机织混杂复合材料增强体的混杂方式为夹芯混杂，整个结构一共有6层，中间4层为玻璃纤维，顶层和底层为碳纤维，增强体编织参数如表2所示。并采用树脂传递模塑工艺(RTM)制备2.5D机织混杂复合材料，树脂注射温度为100℃，固化工艺为：170℃ 2 h、210℃ 3 h、230℃ 3 h，常温冷却，并利用下式计算复合材料的纤维体积分数，结果见表2。
Vf=1−M−mρabH (1) 式中：Vf为纤维体积含量(vol%)；M为复合材料质量(g)；m为增强体质量(g)；ρ为双马树脂密度(g·cm−3)；a、b、H分别对应着复合材料的长(mm)、宽(mm)、厚(mm)。
![]()
图 1 2.5D机织混杂复合材料截面和预制体结构示意图Figure 1. Schematic diagram of 2.5D woven hybrid composite material section and precast structure表 1 复合材料各组分性能参数Table 1. Performance parameters of each component of composite materialsMaterial Type Tensile strength/MPa Tensile modulus/GPa Elongation at break/% Density/(g·cm−3) Carbon fiber (CF) T300-3 K 3530 230 2.1 1.8 Glass fiber (GF) E 3400 73 4.8 2.54 Bismaleimide R801 90 4.2 2.5 1.25 表 2 2.5D机织混杂复合材料参数Table 2. 2.5D woven hybrid composite material parametersYarn Fiber linear
density/texLayer Preformed unit
density/(yarn·cm−1)Composite
thickness/mmFiber volume
fraction/vol%Warp (CF) 200 2 8 1.85 49.87 Warp (GF) 144 4 8 Weft (CF) 200 3 4 Weft (GF) 144 4 8 1.2 测试与表征
1.2.1 复合材料力学性能测试
采用DMA Q800型动态热机械分析仪(DMA)对复合材料动态热机械性能进行测试。试样尺寸为50 mm×10 mm×1.85 mm (长×宽×厚)，加载方式为三点弯曲，测试频率为1 Hz，升温速率为5℃/min，测试温度范围为25℃(室温)~350℃。最终根据复合材料热力学性能设定三点弯曲和层间剪切性能测试温度。
复合材料三点弯曲力学性能测试参照标准GB/T 1449—2005[23]，试样尺寸为70 mm×10 mm×1.85 mm (长×宽×厚)，加载速率为1 mm/min，经向加载，测试跨距为54 mm。弯曲强度σ3b、弯曲模量E的计算公式如下所示：
σ3b=3PL2WH2 (2) E=KL34WH3 (3) 式中：P为最大弯曲载荷(N)；L为三点弯曲的测试跨距(mm)；W为复合材料试样的宽度(mm)；H为复合材料的厚度(mm)；K为三点弯曲载荷-位移曲线的斜率值。
复合材料层间剪切力学性能测试参照标准JC/T 773—2010[24]，试样尺寸为20 mm×10 mm×1.85 mm (长×宽×厚)，加载速率为1 mm/min，经向加载，测试跨距为10 mm，层间剪切强度τm计算公式如下所示：
τm=3P4WH (4) 复合材料的三点弯曲和层间剪切实验均在MTS Criterion C44电子万能试验机(美特斯工业系统(中国)有限公司)上进行，实验温度为25、150、240和300℃。其中，高温下的力学性能测试需借助高温炉进行加热，升热速率为10℃/min，当温度达到设定温度时，保温30 min，使试样受热均匀。每个温度下测试3个试样，取平均值。试样形状尺寸和实验加载图如图2所示。
![]()
图 2 高温力学性能测试设备及加载方式Figure 2. High temperature mechanical properties test equipment and loading method1.2.2 损伤表征
采用深圳超眼的DM4带屏显微镜和日本日立SU8100型场发射扫描电子显微镜(SEM)对三点弯曲和层间剪切加载后试样的宏细观损伤形貌进行观测。
2. 结果与讨论
2.1 2.5D机织混杂复合材料动态热机械性能
图3为2.5D机织混杂复合材料的DMA曲线，其在高温下的动态力学性能可通过储能模量和损耗因子来表征，其中，储能模量反映材料刚度，损耗因子反映材料形变过程能量耗损大小[25]。测试结果表明，随着温度的升高，2.5D机织混杂复合材料的储能模量逐渐降低，损耗因子先增后减。当温度为300℃时，储能模量保留率仍有72.32%，表现出优异的耐高温性能。当温度升高到304℃左右时，储能模量开始急剧下降，此时的温度为复合材料的玻璃化转变温度(Tg)。基于此，将2.5D机织混杂复合材料三点弯曲和层间剪切力学性能最高测试温度设为300℃。
2.2 2.5D机织混杂复合材料三点弯曲力学行为及失效分析
2.2.1 三点弯曲力学行为
图4(a)为不同温度下2.5D机织混杂复合材料的三点弯曲载荷-位移曲线。可以看出，2.5D机织混杂复合材料表现出明显的温度效应，随着温度升高，曲线的斜率以及峰值载荷都逐渐下降。在25℃下，初始阶段曲线呈线性上升，在第一次达到峰值载荷后略有下降，这代表试样开始出现损伤，但此时复合材料并未失效，随着载荷重新分配，曲线再次上升。在150℃和240℃高温场中，复合材料载荷-位移曲线与室温下相似，载荷在达到峰值后，也未完全失效，但同室温下相比，载荷波动更加缓和，塑性特征更加显著。在300℃下，此时温度接近复合材料的玻璃化转变温度，树脂开始从玻璃态向高弹态转变，纤维/基体界面结合力减弱，应力传递效率降低，曲线斜率及峰值载荷有明显下降[19]。
![]()
图 4 不同温度下2.5D机织混杂复合材料三点弯曲力学性能：(a) 载荷-位移曲线；(b) 弯曲强度和弯曲模量Figure 4. Three-point bending mechanical properties of 2.5D woven hybrid composites at different temperatures: (a) Load-displacement curves; (b) Flexural strength and flexural modulus图4(b)为不同温度下2.5D机织混杂复合材料的弯曲强度和模量。可以看出，随着温度升高，2.5D机织混杂复合材料的弯曲强度和模量逐渐下降。复合材料在150、240和300℃下的平均弯曲强度分别为261.20、251.63和237.30 MPa，相较于25℃下试样的弯曲强度(308.43 MPa)分别降低了15.31%、18.42%和23.06%；150、240和300℃下的平均弯曲模量分别为27.98、21.14和9.33 GPa，相较于25℃下试样的弯曲模量(31.11 GPa)分别降低了10.06%、32.05%和70.01%。可以看出，相较于弯曲模量，弯曲强度对温度的敏感性更低。
2.2.2 三点弯曲断裂形貌与损伤机制
图5为不同温度下2.5D机织混杂复合材料三点弯曲测试后受压面、受拉面和侧面的损伤形貌。可以看出，随着温度升高，试样受压面和受拉面上的损伤逐渐减弱，从侧面观察到试样的损伤主要集中在试样的上半部分并沿经纱方向扩展，主要的损伤模式包括纱线断裂、基体裂纹、纤维/基体脱粘和分层等。
![]()
图 5 不同温度下2.5 D机织混杂复合材料弯曲损伤宏观形貌Figure 5. Macromorphologies of bending damage of 2.5 D woven hybrid composites at different temperatures在25℃下，2.5D机织混杂复合材料表面受损严重，树脂发生脆性失效，典型的破坏模式是受压面的纤维剪切断裂和受拉面的基体开裂。侧面可以看到基体出现细微裂纹、纤维扭结断裂及树脂与纤维束间发生轻微脱粘。其中，纤维的断裂主要集中在复合材料的顶层，这是由于CF断裂应变较低，在弯曲载荷作用下比GF更容易出现损伤。试样底层未发生明显破坏，表现出较好的抗拉性能。随着温度升高(150℃)，载荷对试样表面的损伤相对减弱，基体破坏面积减少，在试样的侧面可以看到基体裂纹数量增多且伴有层间裂纹并沿着经纱方向扩展。在240℃下，试样侧面的基体裂纹继续扩张并向厚度方向延展，中间层GF出现局部扭结带，纤维/基体界面脱粘现象更加显著。在300℃下，复合材料韧性增强，试样受拉面仅有局部微裂纹产生，没有出现明显的纤维断裂。但由于复合材料界面粘结强度降低，试样出现了更大面积的脱粘现象。
为进一步研究2.5D机织混杂复合材料在不同温度下的弯曲破坏模式和损伤特征，使用SEM对试样进行细观损伤形貌观测，如图6所示。可以看出，温度对2.5D机织混杂复合材料的损伤影响显著。在25℃下，可以观察到树脂基体的开裂及纤维束的剪切断裂，且断面较整齐，具有明显的脆性特征。在150℃下，断口中存在明显纤维抽拔，纤维上树脂呈鳞片状附着在其表面，界面剥离特征明显。240℃下，复合材料逐渐表现出塑性特性，可见局部基体发生塑性开裂，界面强度降低，纤维发生扭转和开裂。在300℃下，由于分子热运动加剧，基体软化，复合材料的界面结合状况更差，微裂纹沿复合材料的经纱和纬纱方向扩散，纤维与基体分离严重。
![]()
图 6 不同温度下2.5D机织混杂复合材料弯曲损伤SEM图像Figure 6. SEM images of bending damage of 2.5D woven hybrid composites at different temperatures由以上研究可以看出，2.5D机织混杂复合材料在弯曲载荷作用下，试样上侧承受压缩应力，下侧承受拉伸应力，同时伴随着面内剪切作用，复合材料弯曲受力示意图如图7(a)所示。因此，当2.5D机织混杂复合材料受到弯曲载荷时，上侧受压缩应力作用发生局部损伤。随着载荷的增加，纤维束上的纤维微裂纹增加并且不断地沿着轴向扩展。同时，下侧基体受拉开裂，整个破坏是从受压面外侧到受拉面内侧的渐进过程，屈曲状态相反的经纱起主要的承载作用，如图7(b)所示。当温度升至300℃时，由于树脂基体软化，界面黏附力降低，更容易出现脱粘现象。同时，由于软化后的树脂对内部纤维的保护，试样没有明显的纤维断裂，承载主体由纤维向树脂基体转变[26]。此外，纤维和基体热膨胀系数存在一定差异，且碳纤维热膨胀系数(−1×10−6~1×10−6 K−1)和双马树脂热膨胀系数(4.4×10−5 K−1)差异比玻璃纤维(5×10−6~12×10−6 K−1)和双马树脂差异更大。随着温度升高，纤维比树脂以更慢的速率膨胀，会在界面处产生热应力并出现损伤，且碳纤维和双马树脂间的界面损伤更加严重[19, 27]。在弯曲载荷的作用下，损伤开始相互结合并扩展，最终导致复合材料高温下的失效，如图7(c)所示。
![]()
图 7 2.5D机织混杂复合材料弯曲受力及损伤示意图：(a) 受力图；(b) 25℃损伤示意图；(c) 300℃损伤示意图Figure 7. Schematic diagram of bending force and damage of 2.5D woven hybrid composites: (a) Force diagram; (b) Schematic diagram of damage at 25℃; (c) Schematic diagram of damage at 300℃2.3 2.5D机织混杂复合材料层间剪切力学行为及失效分析
2.3.1 层间剪切力学行为
短梁剪切测试被广泛用于表征材料层间剪切行为，在测试时通过缩小试样弯曲跨厚比来增加内部剪切应力，使试样发生层间破坏从而获得层间剪切强度[28]。图8(a)为不同温度下2.5D机织混杂复合材料层间剪切载荷-位移曲线。可以发现，随着温度的升高，纤维和基体间的结合作用减弱，试样抗剪切性能逐渐下降，4条曲线的峰值载荷和斜率逐渐减小并呈塑性断裂特征。在25℃下，试样初始阶段载荷-位移曲线呈近似线性关系，纤维/基体界面保持良好的力学性能。载荷达到峰值后会小幅度下降，这代表试样可能出现了基体开裂和纤维断裂损伤。但试样并未失效，继续加载过程中由于损伤累积，应力呈波动下降直至最终失效，表现出较好的断裂韧性。在150℃和240℃下，试样载荷-位移曲线同室温下相似，此时测试温度没有达到复合材料的玻璃化转变温度，纤维和树脂基体的性能并未受到严重影响。在300℃下，2.5D机织混杂复合材料层间剪切力学性能下降较为明显，这是由于复合材料失效主要由纤维和基体的界面状态决定。此时温度接近复合材料的玻璃化转变温度，基体出现软化，并且由于纤维与其外围树脂热膨胀系数差异导致纤维/基体界面处的的应力传递效率进一步降低。
![]()
图 8 不同温度下2.5D机织混杂复合材料层间剪切力学性能：(a) 载荷-位移曲线；(b) 剪切强度Figure 8. Interlayer shear mechanical properties of 2.5D woven hybrid composites at different temperatures: (a) Load-displacement curves; (b) Shear strength不同温度下复合材料的层间剪切强度如图8(b)所示，可知，2.5D机织混杂复合材料层间剪切强度随温度升高不断下降，说明温度对试样层间剪切性能有着显著影响。复合材料在150、240和300℃下的平均弯曲强度分别为30.53、29.72和26.03 MPa，相较于25℃下试样的层间剪切强度(32.11 MPa)分别降低了4.92%、7.47%和18.93%。试样在各温度场下的剪切强度变化不大，表现出优异的层间剪切性能。
2.3.2 层间剪切断裂形貌与损伤机制
图9为不同温度下2.5D机织混杂复合材料层间剪切测试后的侧面损伤形貌。可以看出，短梁试样上半部分受压出现纱线与基体界面开裂，下半部分呈拉伸破坏并存在明显的分层现象。随着温度升高，界面退化引起损伤范围增大，导致试样最终失效。主要的损伤模式为纱线断裂、基体开裂、界面脱粘及分层等。
在25℃下，由于剪切应力作用，基体产生微裂纹并在材料内部传播，在纤维/基体界面处发生应力集中，引起分层和基体开裂。由于试样接结经纱在厚度和面内方向的分布，抑制了分层的扩展。试样未出现明显弯折，表明复合材料内部损伤并不严重。在150℃下，试样底部出现了明显的纤维断裂和大面积的界面开裂，其中，CF的断口较为平整，而GF抽拔现象比较严重。在240℃下，试样出现了大面积的界面脱粘和开裂现象，并集中在受压面和受拉面处。在300℃下，基体抵抗变形的能力减弱，试样发生塑性变形。由于纤维和基体的主要作用分别是承载和传递载荷，软化的基体不能有效将来自压头的压应力传递给纤维束，使纤维与树脂界面脱粘和分层破坏进一步加重，层间裂纹、层内横向裂纹和层内纵向裂纹交织在一起，并由表面向内部扩展。
![]()
图 9 不同温度下2.5D机织混杂复合材料层间剪切侧面损伤形貌Figure 9. Morphology of 2.5D woven hybrid composites with interlayer shear side damage at different temperatures为进一步研究2.5D机织混杂复合材料在不同温度条件下层间剪切破坏模式和损伤特征，使用SEM对试样进行细观损伤形貌的观测，如图10所示。可以看出，2.5D机织混杂复合材料的失效模式随着温度的升高发生了较大的改变。在25℃下，复合材料表现出较大的脆性，试样断口附近存在大量基体碎屑。同时，纤维表面附有较多树脂，表现出良好的界面黏结性能。在150℃下，纤维表面相对光滑，树脂较少，此时树脂开始软化，界面结合作用减弱。在240℃下，复合材料的界面结合状况更差，纤维束与树脂接触面分离，大量纤维断裂。在300℃下，基体对纤维的黏附力下降，可以清楚地看到纤维的抽拔以及纤维从基体上剥离的轨迹。
![]()
图 10 不同温度下2.5D机织混杂复合材料层间剪切损伤SEM图像Figure 10. SEM images of interlaminar shear damage of 2.5D woven hybrid composites at different temperatures短梁法在测定2.5D机织混杂复合材料层间剪切强度时，不仅存在层间剪切应力，还有弯曲应力、横向剪切应力和局部挤压应力等[29]，如图11(a)所示。室温下，2.5D机织混杂复合材料试样上侧受压缩应力作用，基体内部出现微小裂纹，纤维产生扭结而断裂，下侧在拉伸应力和剪切应力作用下发生脱粘，进而表现出分层破坏。由于复合材料内部纤维与基体界面黏结良好，有效地阻止了裂纹的扩展和分层破坏，试样失效部分较少，如图11(b)所示。在300℃高温环境下，由于纤维/基体界面性能减弱，软化的基体不能将弯曲载荷及时有效传递给增强体纤维束，在剪切应力作用下更容易产生分层破坏，复合材料损伤区域增大。同时，高温下基体抵抗变形的能力减弱，试样发生塑性变形，纤维弯折程度加大，进而出现应力集中，造成纱线断裂。此外，下侧经纱在拉伸应力作用下会向内收缩，并对相邻纬纱产生挤压，导致其发生相应的挤压破坏，如图11(c)所示。界面开裂区域多、失效部分少，增强体承载大部分剪切应力，与基体之间的应力差异增大，树脂裂纹沿经纱方向扩展。
![]()
图 11 2.5D机织混杂复合材料层间剪切受力及损伤示意图：(a) 受力图；(b) 25℃损伤示意图；(c) 300℃损伤示意图Figure 11. Schematic diagram of interlaminar shear force and damage of 2.5D woven hybrid composites: (a) Force diagram; (b) Schematic diagram of damage at 25℃; (c) Schematic diagram of damage at 300℃3. 结 论
(1) 2.5D机织碳纤维-玻璃纤维/双马来酰亚胺树脂复合材料具有优异的耐高温性能。通过DMA测得该复合材料玻璃化转变温度Tg为304℃，当测试温度升至300℃时，其储能模量保留率仍有72.32%，表现出良好的热稳定性。
(2) 2.5D机织碳纤维-玻璃纤维/双马来酰亚胺树脂复合材料具有明显的温度效应。温度上升导致纤维/基体界面结合力减弱，复合材料的弯曲强度、弯曲模量和层间剪切强度逐渐下降，承载主体由纤维向树脂基体转变。
(3) 2.5D机织碳纤维-玻璃纤维/双马来酰亚胺树脂复合材料的三点弯曲失效为压缩应力、拉伸应力和剪切应力耦合作用下的结果，整个破坏是一个从受压面外侧到受拉面内侧的渐进过程。弯曲载荷下，2.5D机织混杂复合材料的室温破坏模式以局部的纤维断裂和基体开裂为主，而高温破坏模式则以纤维/基体界面脱粘为主导。
(4) 2.5D机织碳纤维-玻璃纤维/双马来酰亚胺树脂复合材料的层间剪切失效为层间剪切应力、弯曲应力、横向剪切应力和局部挤压应力多力耦合作用下的结果。剪切载荷下，2.5D机织混杂复合材料的室温破坏模式主要为分层破坏。而随着温度升高，树脂由脆性失效变为韧性失效，复合材料也因基体软化出现塑性变形，基体开裂、界面脱粘及分层破坏决定了材料的最终失效。
-
![]()
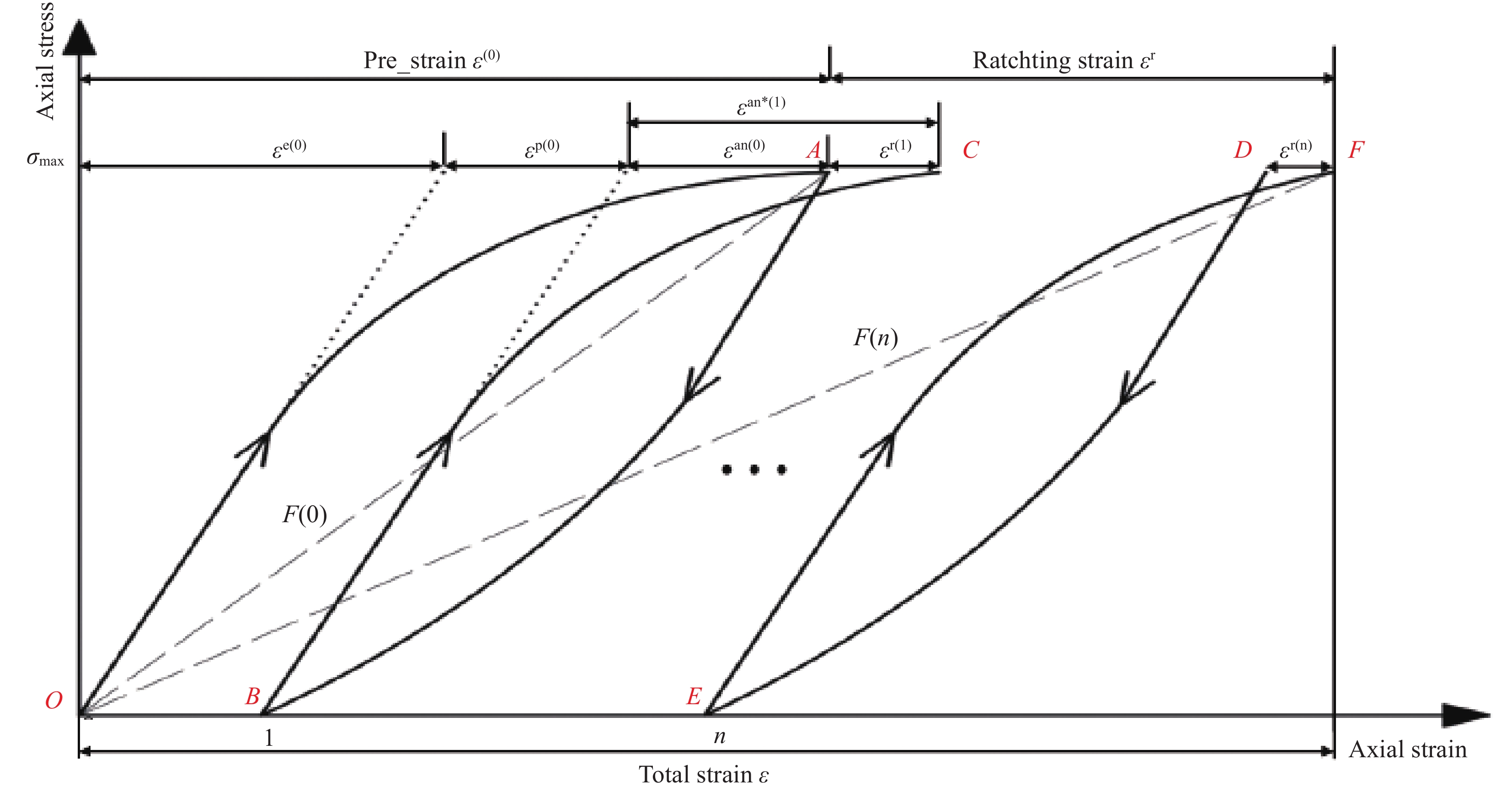
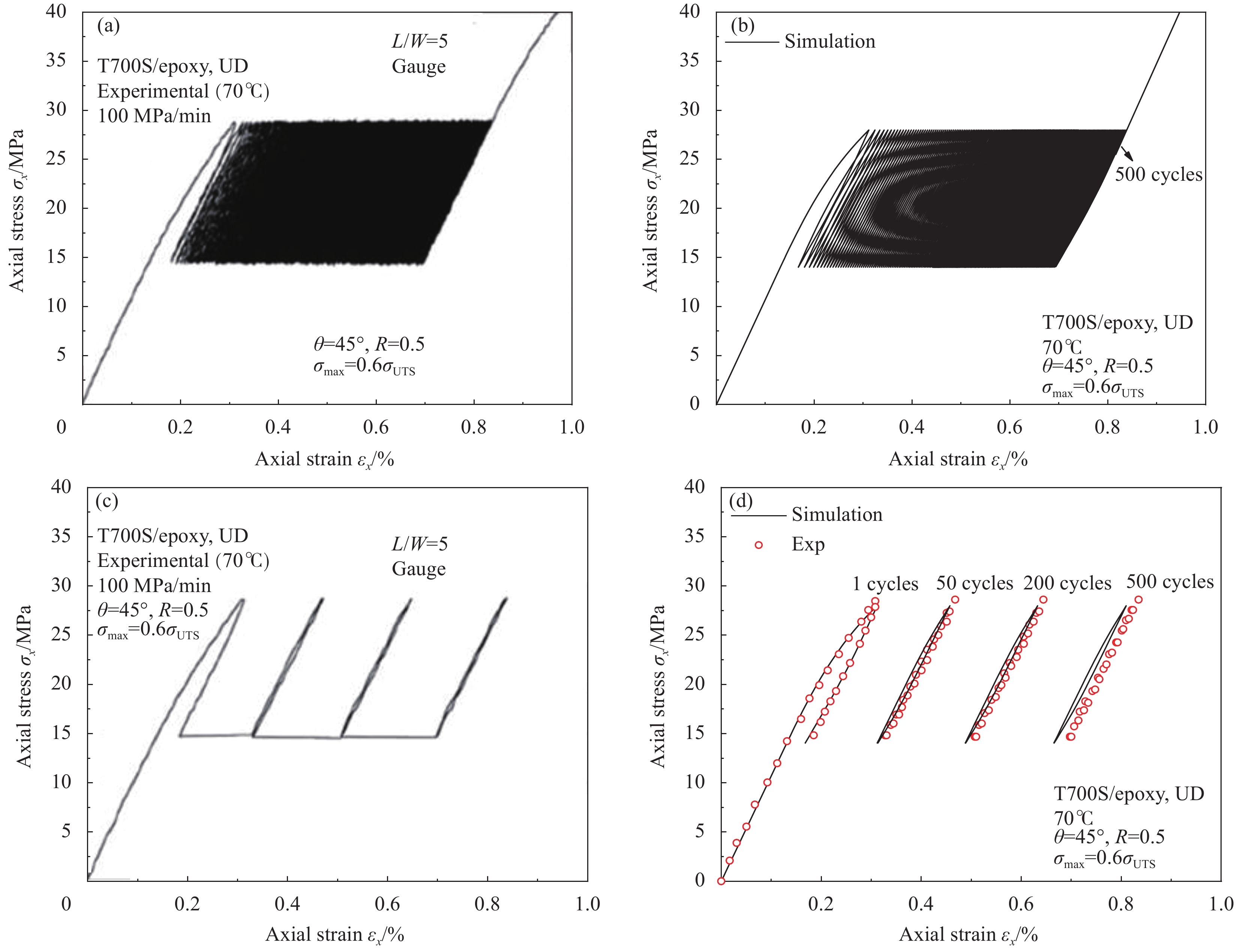
图 1 单向纤维增强聚合物复合材料(FRP)在偏轴循环载荷下应力-应变曲线的典型特征
Figure 1. Typical features of stress-strain curves for unidirectional fiber reinforced polymer (FRP) laminates under off-axis cycle loading
σmax—Maximum stress; ε, εe, εp, εan, εr, εan*—Total, elastic, plastic, anelastic, ratcheting and sum of anelastic and ratcheting strain; F(n)—Fatigue modulus
![]()
图 2 循环过程中迟滞回环的不同演化
Figure 2. Different evolution of hysteresis loops during cyclic loading
![]()
![]()
![]()
![]()
![]()
![]()
表 1 碳纤维/环氧树脂复合材料性能和模型参数(70 ℃)
Table 1 Properties and model parameters of carbon fiber/epoxy composites (70℃)
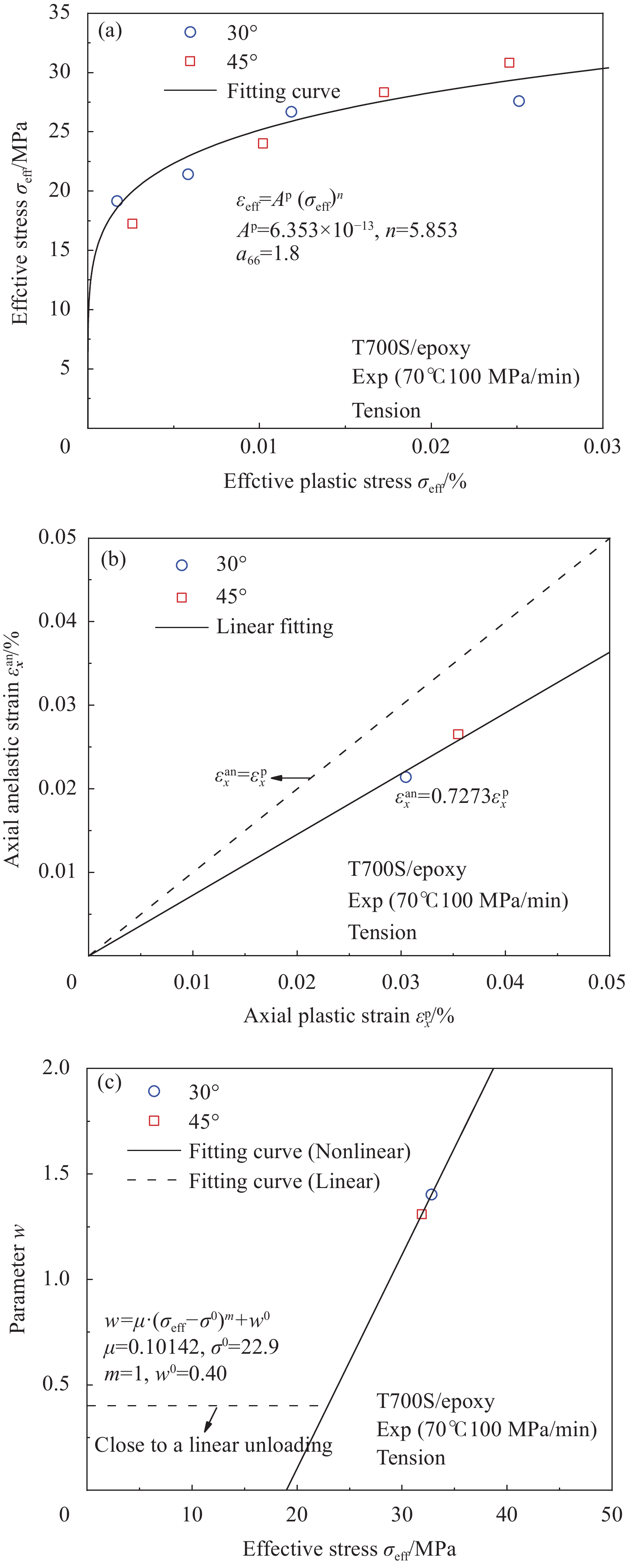
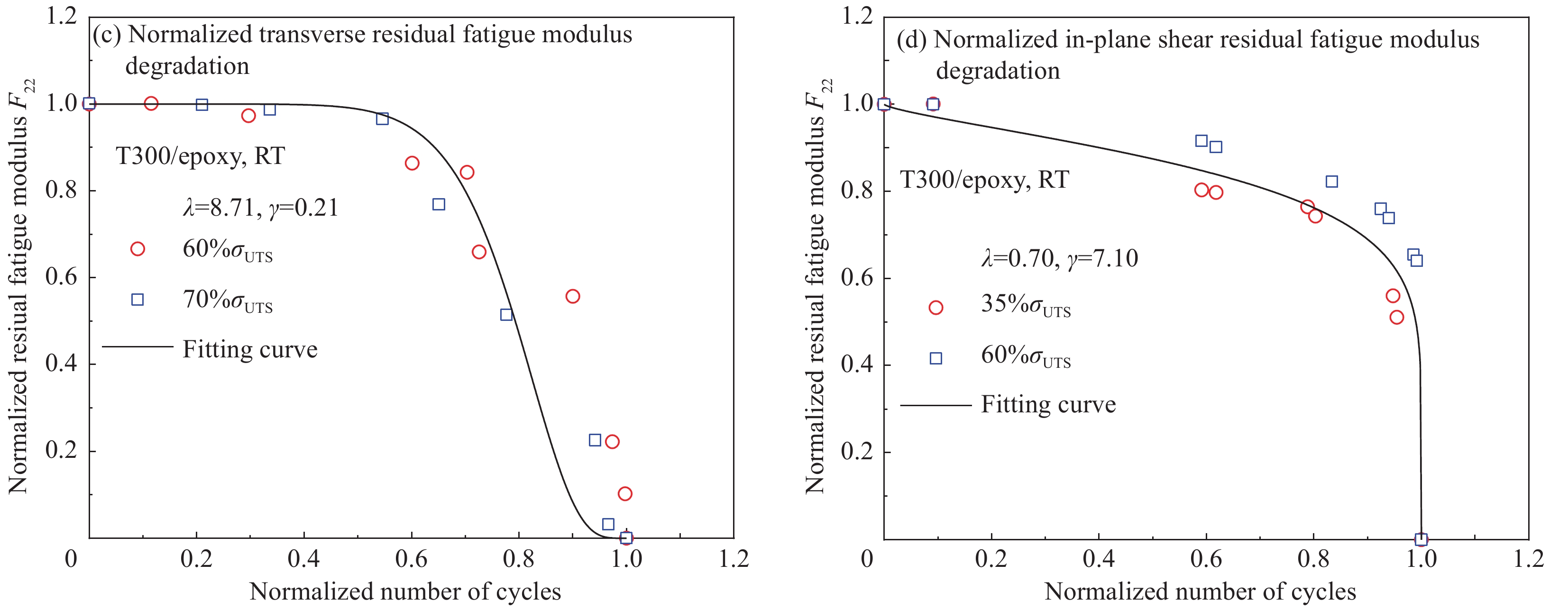
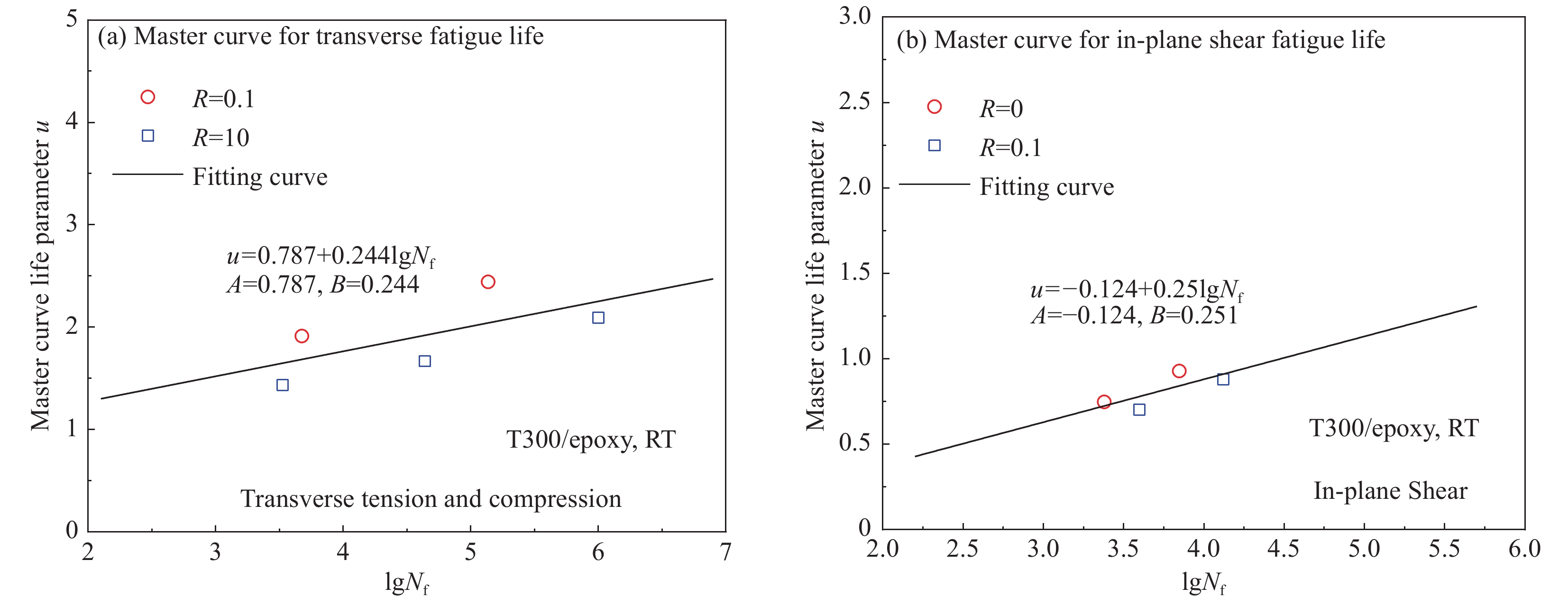
Material property Model parameter Cycle plastic Fatigue damage E1/GPa 124 a66 1.8 λ22 1.62 E2/GPa 7.93 Ap 6.35×10−13 γ22 0.21 G12/GPa 3.74 Aan 4.62×10−13 λ12 0.70 μ12 0.35 n 5.853 γ12 7.10 YT/MPa 33.4 μ 0.10142 A22 0.787 *YC/MPa 123 m 1 B22 0.244 S12/MPa 24.1 σ0 22.9 A12 −0.124 w0 0.40 B12 0.251 Notes:E1—Longitudinal modulus; E2—Transverse modulus; G12—Shear modulus; u12—Poisson’s ratio; YT—Transverse tensile strength; *YC—Transverse compress strength, from the data of our research group; S12—Shear strength;
a66—Shear/transverse plasticity ratio; Ap, Aan, n—Plasticity and anelasticity during initial loading; μ, m, σ0, w0—Hysteresis loop;
λ22, γ22—Transverse fatigue modulus degradation; λ12, γ12—In-plane shear fatigue modulus degradation; A22, B22—Transverse fatigue life; A12,B12—In-plane shear fatigue life.
下载: 导出CSV
-
[1] 罗祖道, 王震鸣. 复合材料力学进展[M]. 北京: 北京大学出版社, 1992. LUO Z D, WANG Z M. Progress in composite material mechanics[M]. Beijing: Peking University Press, 1992(in Chinese).
[2] FALLAHI H, TAHERI-BEHROOZ F, ASADI A. Nonlinear mechanical response of polymer matrix composites: A review[J]. Polymer Reviews,2020,60(1):42-85. DOI: 10.1080/15583724.2019.1656236
[3] KAWAI M, ZHANG J Q, XIAO Y, et al. Modeling of tension-compression asymmetry in off-axis nonlinear rate-dependent behavior of unidirectional carbon/epoxy composites[J]. Journal of Composite Materials, 2010, 44(1): 75-94.
[4] WANG J, XIAO Y. Some improvements on Sun–Chen’s one-parameter plasticity model for fibrous composites-Part I: Constitutive modelling for tension-compression asymmetry response[J]. Journal of Composite Materials,2017,51(3):405-418. DOI: 10.1177/0021998316644853
[5] WANG J, XIAO Y, KAWAI M. Parameter identification problem in one-parameter plasticity model for fibrous compo-sites[J]. Advanced Composite Materials,2019,28:29-51.
[6] DROZDOV A D. Cyclic thermo-viscoplasticity of high density polyethylene[J]. International Journal of Solids and Structures,2010,47(11-12):1592-1602. DOI: 10.1016/j.ijsolstr.2010.02.021
[7] WANG J, XIAO Y, INOUE K, et al. Modeling of nonlinear response in loading-unloading tests for fibrous composites under tension and compression[J]. Composite Structures,2019,207:894-908. DOI: 10.1016/j.compstruct.2018.09.054
[8] 薛康, 肖毅, 王杰, 等. 单向纤维增强聚合物复合材料压缩渐进破坏[J]. 复合材料学报, 2019, 36(6):1398-1412. XUE K, XIAO Y, WANG J, et al. Compression progressive failure of unidirectional fiber reinforced polymer compo-sites[J]. Acta Materiae Compositae Sinica,2019,36(6):1398-1412(in Chinese).
[9] LV J X, XIAO Y, ZHOU Y, et al. Characterization and modeling of the creep behavior of fiber composites with tension and compression asymmetry[J]. International Journal of Mechanical Sciences,2020,170:105340. DOI: 10.1016/j.ijmecsci.2019.105340
[10] OHNO N. Recent topics in constitutive modeling of cyclic plasticity and viscoplasticity[J]. Applied Mechanics Reviews, 1990, 43(11): 283-295.
[11] OHNO N. Recent progress in constitutive modeling for ratchetting[J]. Journal of the Society of Materials Science Japan,1997,46(3Appendix):1-9. DOI: 10.2472/jsms.46.3Appendix_1
[12] 陈旭, 焦荣, 田涛. 棘轮效应预测及其循环本构模型研究进展[J]. 力学进展, 2003, 33(4):461-470. DOI: 10.3321/j.issn:1000-0992.2003.04.003 CHEN X, JIAO R, TIAN T. Research advances of ratcheting effects and cyclic constitutive models[J]. Advances in Mechanics,2003,33(4):461-470(in Chinese). DOI: 10.3321/j.issn:1000-0992.2003.04.003
[13] KANG G Z. Ratchetting: Recent progresses in phenomenon observation, constitutive modeling and application[J]. International Journal of Fatigue,2008,30(8):1448-1472. DOI: 10.1016/j.ijfatigue.2007.10.002
[14] FREDERICK C O, ARMSRRONG P J. A mathematical representation of the multiaxial Bauschinger effect[J]. High Temperature Technology, 1998, 24(1): 1-26.
[15] BOWER A F. Cyclic hardening properties of hard-drawn copper and rail steel[J]. Journal of the Mechanics and Physics of Solids,1989,37(4):455-470. DOI: 10.1016/0022-5096(89)90024-0
[16] CHABOCHE J L. On some modifications of kinematic hardening to improve the description of ratchetting effects[J]. International Journal of Plasticity,1991,7(7):661-678. DOI: 10.1016/0749-6419(91)90050-9
[17] OHNO N, WANG J D. Kinematic hardening rules with critical state of dynamic recovery, Part I: Formulation and basic features for ratchetting behavior[J]. International Journal of Plasticity,1993,9(3):375-390. DOI: 10.1016/0749-6419(93)90042-O
[18] OHNO N, WANG J D. Kinematic hardening rules with critical state of dynamic recovery, Part II: Application to experiments of ratchetting behavior[J]. International Journal of Plasticity,1993,9(3):391-403. DOI: 10.1016/0749-6419(93)90043-P
[19] JIANG Y, SEHITOGLU H. Multiaxial cyclic ratchetting under multiple step loading[J]. International Journal of Plasticity,1994,10(8):849-870. DOI: 10.1016/0749-6419(94)90017-5
[20] KANG G Z, GUO S, DONG C. Numerical simulation for uniaxial cyclic deformation of discontinuously reinforced metal matrix composites[J]. Materials Science & Engineering A,2006,426(1-2):66-76.
[21] VOYIADJIS G Z, THIAGARAJAN G. A cyclic anisotropic-plasticity model for metal matrix composites[J]. International Journal of Plasticity,1995,12(1):69-91.
[22] 王艳锋, 康国政, 刘宇杰, 等. 玻璃长纤维增强树脂基复合材料的单轴时间相关棘轮行为实验研究[J]. 复合材料学报, 2009, 26(6):161-166. DOI: 10.3321/j.issn:1000-3851.2009.06.027 WANG Y F, KANG G Z, LIU Y J, et al. Experimental study on uniaxial time-dependent ratcheting of continuous glass fiber reinforced polymer composites[J]. Acta Materiae Compositae Sinica,2009,26(6):161-166(in Chinese). DOI: 10.3321/j.issn:1000-3851.2009.06.027
[23] 刘煦, 朱志武, 康国政, 等. 碳纤维增强 PEEK 树脂基复合材料的单轴时相关循环特性实验研究[J]. 复合材料学报, 2012, 29(1):28-34. LIU X, ZHU Z W, KANG G Z, et al. Experimental study on uniaxial time-dependent cyclic character of carbon fiber reinforced PEEK resin matrix composite[J]. Acta Materiae Compositae Sinica,2012,29(1):28-34(in Chinese).
[24] SAKAI M, UDA N, KUNOO K. Experimental observation on low cycle fatigue behavior of symmetric angle-ply CFRP laminate[J]. Journal of the Japan Society for Aeronautical and Space Sciences, 2006, 54(635): 555-562
[25] KAWAI M, KIGURE T, SUZUKI T. Off-axis ratcheting behavior of unidirectional CFRP laminate at high temperature and its phenomenological modeling[J]. Journal of the Japan Society for Composite Materials, 2011, 37(2): 46-57.
[26] SUZUKI T, KAWAI M. Off-axis ratcheting behavior of unidirectional carbon/epoxy laminate under asymmetric cyclic loading at high temperature[C]// Proceedings of the 12th Japan International SAMPE Symposium & Exhibition (JISSE-12), Tokyo, 2011.
[27] RUI Y, SUN C T. Cyclic plasticity in AS4/PEEK composite laminates[J]. Journal of Thermoplastic Composite Materials,1993,6(4):312-322.
[28] ZHU C, SUN C T. Micromechanical characterization of cyclic plasticity of IM7/5260 composite at various temperatures[J]. Journal of Reinforced Plastics and Composites,1998,17(3):184-204. DOI: 10.1177/073168449801700301
[29] ZHU C, SUN C T. A viscoplasticity model for characterizing loading and unloading behavior of polymeric composites[M]//Time dependent and nonlinear effects in polymers and composites. West Conshohocken: ASTM International, 2000.
[30] SHOKRIEH M M, LESSARD L B. Multiaxial fatigue behaviour of unidirectional plies based on uniaxial fatigue experiments I—Modelling[J]. International Journal of Fatigue, 1997, 19(3): 201-207.
[31] LEE L J, YANG J N, SHEU D Y. Prediction of fatigue life for matrix-dominated composite laminates[J]. Composites Science and Technology,1993,46(1):21-28. DOI: 10.1016/0266-3538(93)90077-T
[32] 沈媛臻, 肖毅. 微动损伤对复合材料螺栓连接预紧力松弛的影响[J]. 复合材料学报, 2019, 36(2):400-409. SHEN Y Z, XIAO Y. Effects of fretting damage on pre load relaxation in bolted composite joints[J]. Acta Materiae Composite Sinica,2019,36(2):400-409(in Chinese).
[33] 成磊. 复合材料疲劳损伤的定量评估[D]. 上海: 同济大学, 2018. CHENG L. Quantitative assessment on fatigue damage of composite materials[D]. Shanghai: Tongji University, 2018(in Chinese).
-
期刊类型引用(1)
1. 李新娅，王宁，卢佳浩，张鹏，夏兆鹏，侯耒. 基于改进Weibull模型的高强缝合锚钉缝线强度预测. 现代纺织技术. 2024(06): 52-60 . 
百度学术
其他类型引用(1)
-
计量
- 文章访问数: 1456
- HTML全文浏览量: 826
- PDF下载量: 143
- 被引次数: 2
