Axial compression performance of pultruded GFRP tube based on casing buckling restraint
-
摘要: 为解决复合材料空间桁架结构部分关键压杆失稳引发的连续性倒塌问题,提出了一种由不锈钢套管及螺栓连接系组成的玻璃纤维增强树脂复合材料(GFRP)管整体失稳套管屈曲约束装置。为分析该套管屈曲约束装置对拉挤型GFRP管轴压性能的影响,对3个GFRP管试件和4个套管屈曲约束GFRP管试件进行了轴压试验,观察了试件的受力过程和破坏形态,获得了荷载-位移曲线和荷载-应变曲线,对比研究了两者的极限承载力和破坏模式,同时利用有限元模型分析了不同内核长细比、内核与套管间隙及套管壁厚对GFRP管轴压性能的影响。结果表明:该套管屈曲约束装置能有效约束GFRP管整体失稳变形,其极限承载力和延性均得到提升,并使GFRP管从失稳破坏向材料强度破坏发展;内核长细比越大,套管屈曲约束GFRP管极限承载力相比于内核失稳临界荷载的相对提升幅值越高,约束效果越好;内核与套管间隙越大,GFRP管延性越好,但其极限承载力会降低;套管壁厚过薄会降低GFRP管极限承载力,过厚则约束效果不明显。Abstract: In order to solve the problem of continuous collapse caused by the instability of the key compression struts in fiber reinforced polymer (FRP) space truss structure, a casing buckling restrained brace for the overall instability of glass fiber reinforced polymer (GFRP) tubes composed of stainless steel casing and bolt connection system was proposed. In order to analyze the influence of the casing buckling restrained brace on the axial compression performance of pultruded GFRP tubes, axial compression tests were carried out on three GFRP tube specimens and four GFRP tube specimens with casing buckling-restrained brace. The loading course and failure form of specimens were observed, and the load-displacement curves and load-strain curves were obtained, and the ultimate bearing capacity and failure mode were compared. At the same time, the finite element model was used to analyze the influence of different slenderness ratios of GFRP tubes, core and casing gaps and casing thicknesses on the axial compression performance of GFRP tubes. The results show that: the casing buckling restrained brace can effectively restrain the overall instability deformation of GFRP tubes, its ultimate bearing capacity and ductility are improved, and the GFRP tubes develop from instability failure to material strength failure; the larger the slenderness ratio of the core, the higher the ultimate bearing capacity of the GFRP tubes due to buckling of the casing compared with the critical load of the core instability, and the better the restraint effect; the greater the gap between the inner core and the casing, the better the ductility of the GFRP tube, but its ultimate bearing capacity will be reduced; too thin casing thickness will reduce the ultimate bearing capacity of GFRP tubes, but too thick will have no obvious restraint effect.
-
纤维增强树脂复合材料(FRP)拉挤型材是由纤维和基体材料按一定比例经拉挤工艺制成,具有轻质、高强、耐腐蚀、质量稳定等优点,已开始广泛应用于桥梁[1-2]、建筑体系[3]等各类承载结构中,且多采用空间桁架结构形式。在拉挤型FRP空间桁架结构中,FRP杆件轴向受力,有利于发挥FRP拉挤型材较优的顺纤维方向承载性能;但当FRP空间桁架结构中的部分关键杆件受压时,由于其较低的纵向弹性模量[4],整体失稳是其常见的失效模式[5]。因此,国内外学者对FRP构件性能开展了大量研究。Goodman等[6]对3根FRP圆管进行了轴心受压试验,研究表明大长细比的杆件整体屈曲荷载与欧拉屈曲荷载相近;Hashem等[7]研究了玻璃纤维增强树脂复合材料(GFRP)柱的轴压稳定性,认为
l/r⩾ 的试件将发生整体失稳,l/r < 50 的试件发生局部屈曲和材料压坏破坏形式;Hewson[8]、Zureick等[9]研究了拉挤GFRP构件在轴压作用下的弯曲屈曲和扭转屈曲,发现当纵向弹性模量与纵横向剪切模量比值较大时,需考虑横向剪切变形的影响,并提出修正后欧拉公式;南波等[10]以拉挤型碳纤维增强树脂复合材料(CFRP)管轴压试验和考虑Hashin破坏准则的有限元模型(FEM)为基础,对长杆的力学性能进行参数化分析,发现CFRP管极限承载力随着长细比的增大呈现下降趋势,稳定系数随着长细比的增大而减小。陈静芬[11]指出若要准确预测复合材料的破坏荷载,描述复合材料力学行为的本构关系应同时包含塑性效应和材料属性退化两个特征,为此建立了一个同时考虑塑性效应和损伤累积导致材料属性退化的复合材料弹塑性损伤本构模型。FRP层合结构在工程中也有重要应用,郭小农等[12]对6根CFRP增强铝合金叠层复合材料短柱进行了轴压试验,根据弹性力学推导了试件的荷载-压缩变形曲线,与试验曲线吻合较好,并建立逐层精细化和整体等效简化两种FEM,经试验验证能很好地模拟CFRP/Al短柱的轴压性能;金福松等[13]针对贯穿脱层碳纤维增强树脂层合板产生面外屈曲后的特点,提出了一个基于刚度等效理论来分析损伤层合板结构失效的力学性能,结果表明:该方法充分考虑了脱层带来的刚度降低及分层界面处非线性抗穿透约束影响,不仅简化推导过程和节省计算量,而且解释了深层次的力学机制。当FRP空间桁架结构中部分关键压杆整体失稳后[14-15],杆件将迅速失效并失去承载能力,进而结构荷载传递路径改变,容易导致空间桁架结构连续性倒塌或破坏;此外,弹性失稳导致FRP关键压杆在杆件跨中产生较大的二阶弯矩,跨中应力水平激增导致该区域材料发生强度破坏,而FRP杆件其余部分强度未得到有效利用;再加上拉挤型FRP材料不具备塑性变形能力,杆件整体失稳将最终导致脆性破坏,使复合材料结构往往延性不足。有鉴于此,相关学者提出了改善受压杆件屈曲性能的装置及方式,如抑制屈曲支撑、限制力装置、套管屈曲约束装置及更换性能更优材料、增大压杆截面等。总的来说,抑制屈曲支撑主要用作框架结构的抗震消能支撑,限制力装置因结构复杂性及不可靠性使应用受到制约,更换材料可能出现难以预料的内力或变形集中,增大压杆截面方式对于提高延性承载能力没有明显帮助,而套管屈曲约束装置因其构造简单、设计方便及可靠性强等优点而被广泛使用。该装置通过外套管约束受压内核的屈曲变形,使受压内核发生高阶屈曲模态,内核可以达到相当高的应力水平,从而极大提高了内核的受压承载能力及延性变形能力。
Prasad[16]做了典型套管构件的缩尺模型试验,与传统的受压构件相比,套管构件的受压承载力有大幅度提高,且在高阶模态下这种受压承载力的提高越大;Sridhara[17]通过试验与理论研究了套管构件中柔性套管约束下内核的受压承载力,认为受压内核应力可以达到屈服应力,而套管应力达到其屈服应力时,内核不能再承受继续增加的荷载。申波等[18-19]针对轴压套管构件,研究了初弯曲内核与柔性套筒未接触、点接触、线接触、线接触屈曲后等变形过程,利用小挠度二阶平衡微分方程推导了内核与套筒挠度、弯矩、剪力、接触力等参量关系的计算公式;张晨辉等[20]建立了轴压作用下钢套管构件的非线性有限元分析模型,发现当轴向压力增大,内核弯矩最大截面逐渐向内核端部移动;黄炳生等[21]对5根钢管和7根套管加固钢管进行了单调加载静力试验,研究了长细比、初应力比、径厚比对负荷套管加固钢管受压性能的影响,发现套管能有效提高构件的刚度、屈服承载力和稳定承载力,且长细比越大、径厚比越小,提高效果越显著。
上述文献中的套管屈曲约束装置,套管与内核均是钢质构件,还未见内核为FRP材料的屈曲约束装置。鉴于GFRP空间桁架结构会因部分关键压杆失稳而发生连续性倒塌,在GFRP关键压杆外部用螺栓连接了不锈钢套管,提出了一种由不锈钢套管和GFRP管内核组成的套管屈曲约束组合构件,两者各司其职−内核承受轴向荷载,套管约束内核屈曲变形。一方面,经过尺寸优化的套管屈曲约束装置占整个空间桁架结构重量的比重会随着大跨结构的规模变大而降低;另一方面,套管及螺栓连接系均采用耐腐蚀材料,可实现整体结构较好的耐腐蚀性;再者,套管屈曲约束装置还可以作为结构健康监测的有效手段,采用通用电流传感器来监测内核与套管是否发生接触,可用于暴雪及强风等极端荷载工况情况下的安全预警。因此,在FRP空间桁架结构的关键压杆上加装套管屈曲约束装置具有较好的工程应用价值。该装置在不改变原复合材料压杆轴向刚度的情况下,构件可实现刚度与强度的独立设计,两者可单独进行调整,增加原结构的设计灵活性。
本文首先对3个GFRP管试件和两种间隙的4个套管屈曲约束试件分别进行了轴压试验,根据试验现象和荷载-位移、荷载-应变曲线,对比分析了两者的极限承载力和破坏模式;接着建立了两种FEM,在与试验结果对比验证的基础上,揭示组合构件的破坏机制;最后通过参数化分析,研究了内核长细比、内核与套管间隙及套管壁厚对套管屈曲约束装置极限承载力和延性的影响。本文分析套管屈曲约束装置对复合材料空间桁架结构性能影响,可以更加清楚地了解其对GFRP管轴压性能的影响及组合管在轴压作用下的破坏机制,对复合材料空间桁架结构的性能改进及防倒塌设计等研究具有重要基础性意义。
1. 套管屈曲约束GFRP管轴压试验
1.1 屈曲约束装置基本构造
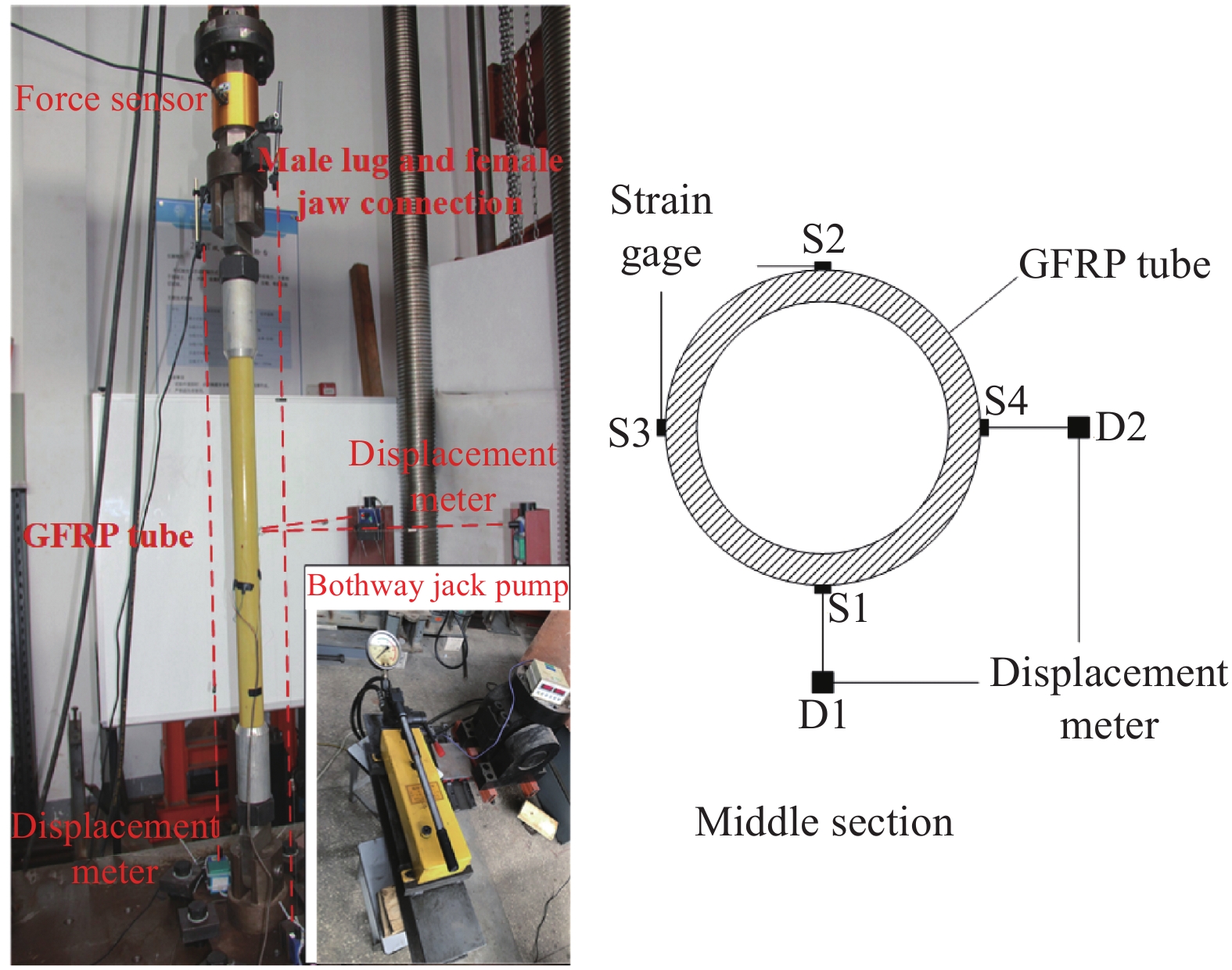
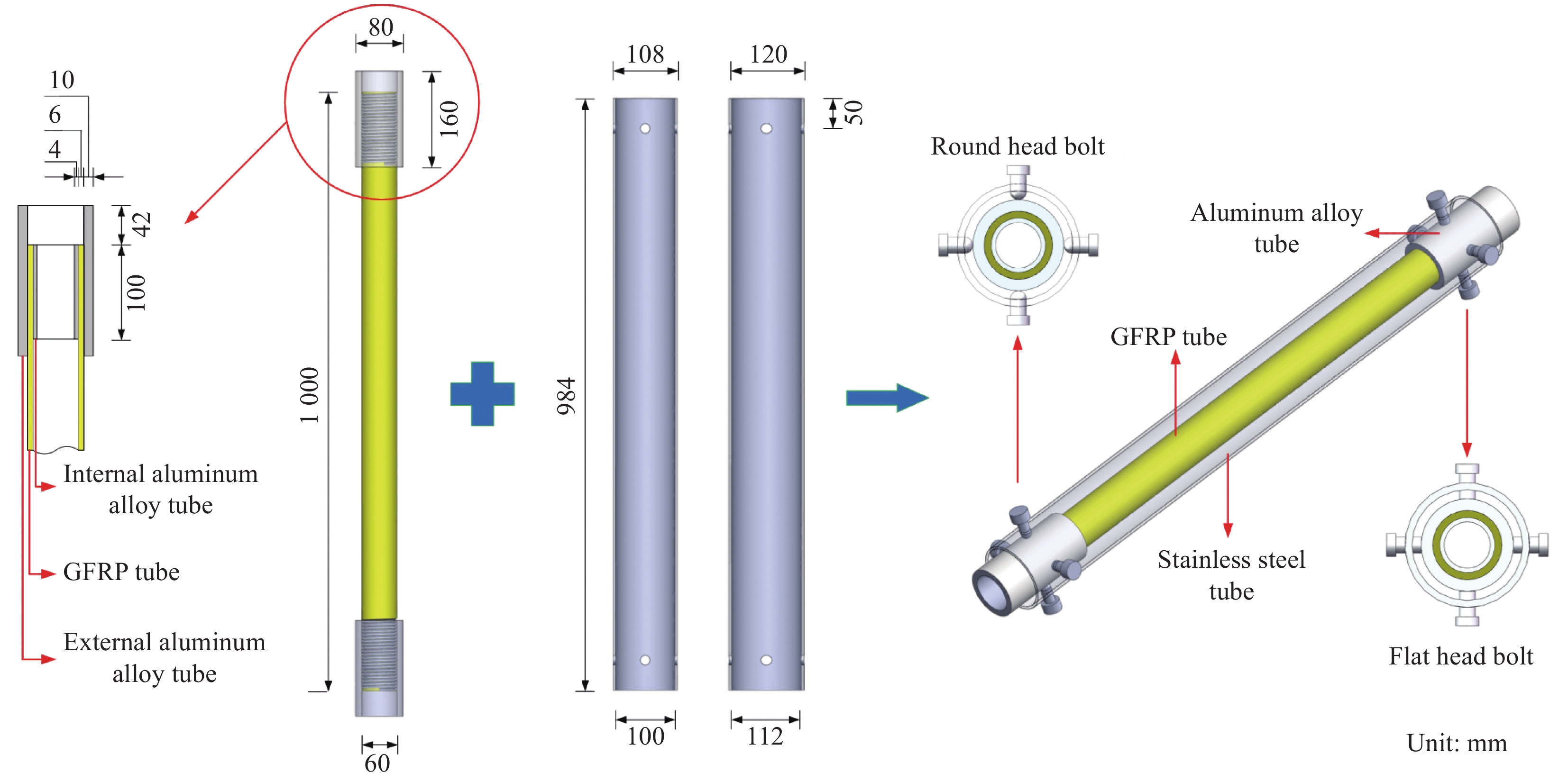
套管屈曲约束装置的基本构造如图1所示。该装置由GFRP管内核、不锈钢套管及螺栓连接系组成,内核要比套管稍长且两者之间存在间隙。
为防止轴压试验时GFRP管端部发生破坏,在GFRP管两端的外部与内部均采用铝合金套筒进行加强。GFRP管和铝合金套筒之间采用预紧力齿连接技术来实现可靠连接,即在GFRP管两端的外部和内部加工出螺旋齿,在铝合金套筒上分别加工出与之相配合的螺旋齿,并通过施加预紧力进行连接[22-23]。
外套管采用厚度4 mm的不锈钢无缝钢管,并选取两种外径以实现内核与套管间的不同间隙。在套管距顶端和底端50 mm处,各设置4个直径为M16的圆孔,并在圆孔位置焊接M16螺帽,圆孔及螺帽内部开设M16内螺纹。采用4个M16平头螺栓及4个M16圆头螺栓实现GFRP管内核与不锈钢外套管的连接,平头螺栓紧定稍紧以实现固定铰支连接,圆头螺栓紧定稍松以实现滑动铰支连接,如此在轴力作用下不锈钢外套管不受轴力。
GFRP拉挤管由南京经略复合材料有限公司生产,纤维质量分数为80wt%,基体材料采用聚氨酯以提高拉挤型材中玻璃纤维的含量,进而提高型材弹性模量。GFRP、铝合金、不锈钢的材料参数与文献[24]相同,如表1。
表 1 玻璃纤维增强树脂复合材料(GFRP)、铝合金及不锈钢的材料力学参数Table 1. Mechanical parameters of glass fiber reinforced polymer (GFRP), aluminum alloy and stainless steelMaterial Elastic modulus/GPa Poisson’s ratio GFRP {E_1} = 63.0, {E_{\rm{2}}}{\rm{ = }}{E_{\rm{3}}}{\rm{ = 14}}{\rm{.2}}, {G_{{\rm{12}}}}{\rm{ = }}{G_{{\rm{13}}}}{\rm{ = 13}}{\rm{.0}}, {G_{{\rm{23}}}}{\rm{ = 9}}{\rm{.4}} {v_{12}} = {v_{13}} = 0.25, {v_{23}} = 0.27 Al alloy {E_{{\rm{Al}}}}{\rm{ = 65}}{\rm{.0}} {v_{{\rm{Al}}}} = 0.{\rm{3}} Stainless steel {E_{{\rm{SS}}}}{\rm{ = 200}}{\rm{.0}} {v_{{\rm{SS}}}} = 0.{\rm{3}} Notes: {E_{\rm{1}}}—Elastic modulus of 1-axis; {E_{\rm{2}}}—Elastic modulus of 2-axis; {E_{\rm{3}}}—Elastic modulus of 3-axis; {G_{{\rm{12}}}}—Shear modulus of plane 12; {G_{{\rm{13}}}}—Shear modulus of plane 13; {G_{{\rm{23}}}}—Shear modulus of plane 23; {v_{12}},{v_{13}}—Major Poisson’s ratio; {v_{23}}—Minor Poisson’s ratio; {E_{{\rm{Al}}}}—Elastic modulus of Al alloy; {v_{{\rm{Al}}}}—Poisson’s ratio of Al alloy; {E_{{\rm{SS}}}}—Elastic modulus of stainless steel; {v_{{\rm{SS}}}}—Poisson’s ratio of stainless steel. 1.2 加载及量测装置
对3个GFRP管和4个带套管屈曲约束装置(Buckling restrained brace,BRB)GFRP管进行轴压试验。除内核与套管的间隙不同,其余尺寸均一致,将3个GFRP管试件编号为GFRP1~GFRP3,将4个带BRB试件根据内核与套筒间距的大小分别编号为L-B-1(Large gap BRB)、L-B-2及S-B-1(Small gap BRB)、S-B-2,试件编号见表2。
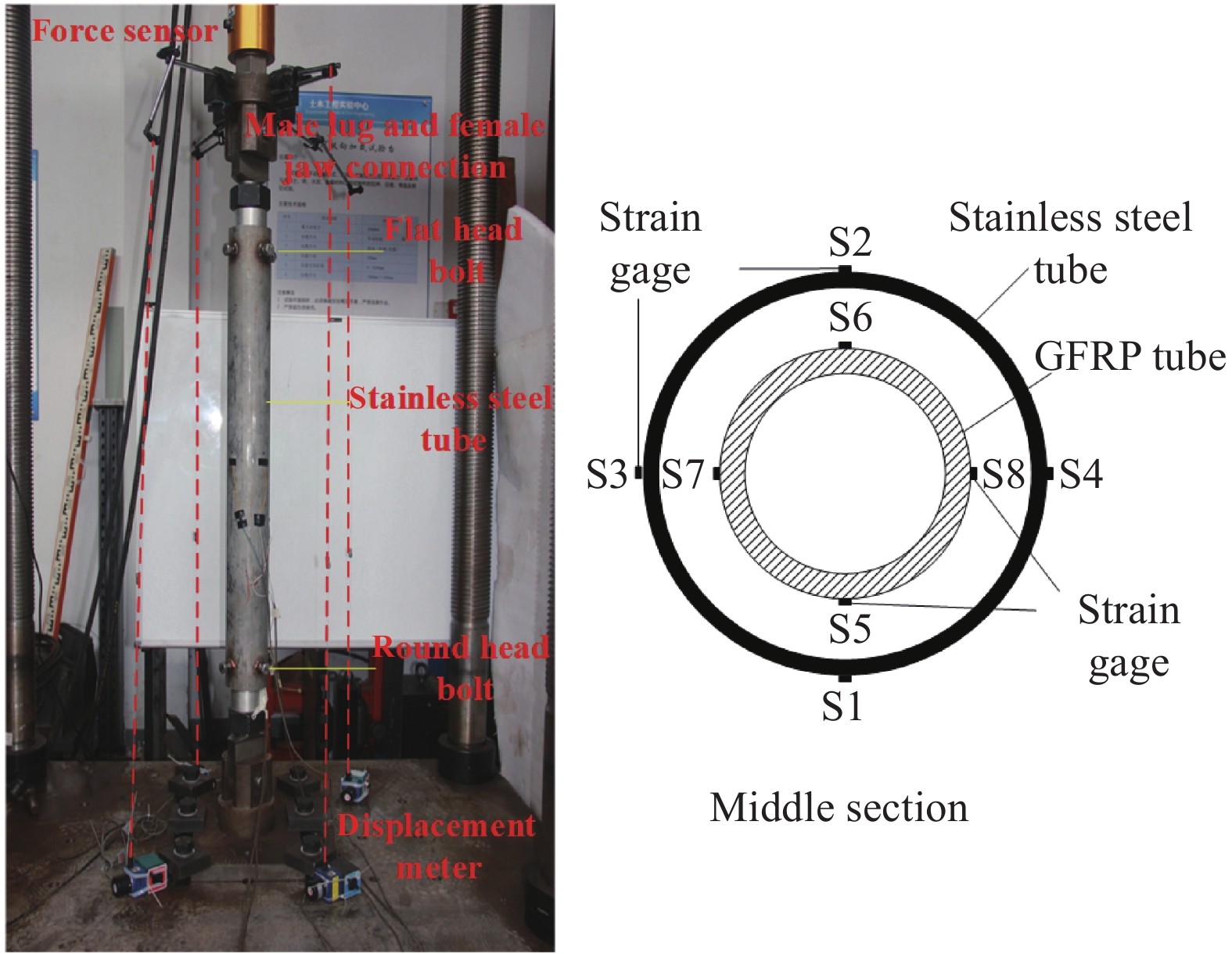
表 2 GFRP管及带套管屈曲约束装置(BRB)管试件的编号及尺寸Table 2. Number and size of GFRP and buckling restrained brace (BRB) tubesmm Number Outer sleeve GFRP tube DO L T DO L T GFRP1 — — — 60 1000 6 GFRP2 GFRP3 L-B-1 120 984 4 60 1000 6 L-B-2 S-B-1 108 S-B-2 Notes: L—Length; DO—Outer diameter; T—Thickness; L-B—Large gap BRB; S-B—Small gap BRB. 试验均在液压双向加载试验台上进行,试验台与试件两端采用销钉穿过单双耳形式连接模拟铰支,配置荷载传感器实时显示荷载值。利用泰州市江苏东华测试技术股份有限公司生产的东华DH3816静态应变仪采集数据,包括荷载、位移和应变。试件应变测点及位移计布置如图2、图3所示,其中试件中部应变片用来测量轴向应变,竖向位移计用来测量轴向位移,面内位移计(D1)用来获取试件横向位移,面外位移计(D2)用于监测试件是否发生面外变形。
1.3 结果与讨论
1.3.1 GFRP管试件
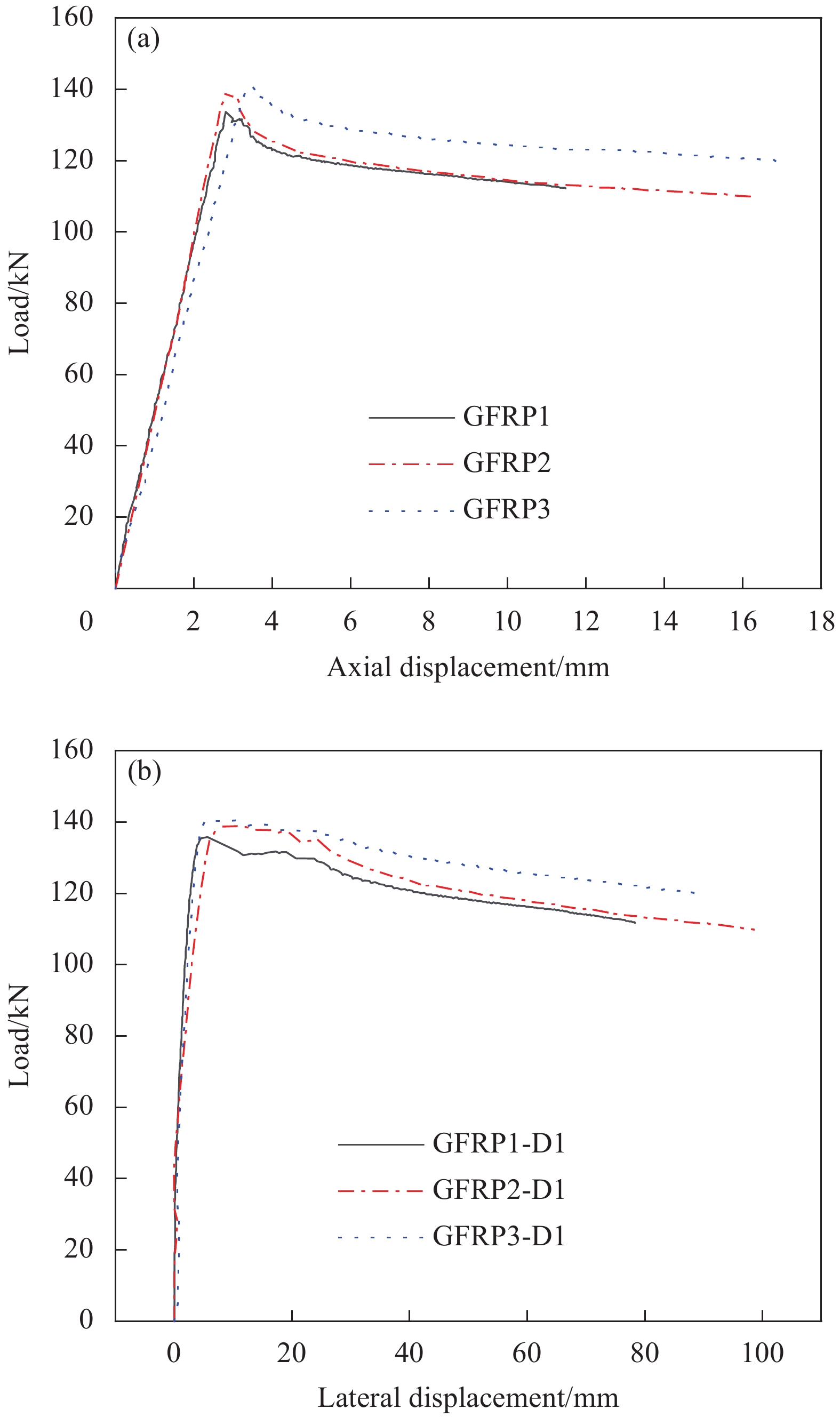
3根GFRP管轴压试验的破坏过程和荷载-位移曲线相似,图4为其中一根GFRP管轴压试验典型破坏过程。图5为轴压下GFRP管荷载-位移曲线。试验加载初期,试件保持挺直状态(如图4(a)所示),荷载与位移呈线性增长关系,说明试件处于弹性工作阶段。当荷载加至约130 kN时,试件发生整体失稳,单双耳处可见明显相对转动(如图4(b)所示)。失稳后荷载无法继续增加,并表现出下降趋势,而轴向缩短及横向挠曲明显增大。随着加载继续进行,试件持续产生撕裂声,试件突然发生破坏并伴有巨大响声,在GFRP管表面产生多条纵向贯穿裂缝(如图4(c)所示),最终破坏模式为失稳破坏。试验结束卸载后,试件恢复至挺直状态(如图4(d)所示)。3根GFRP管的极限荷载值分别为:133.7 kN、138.9 kN、140.6 kN。
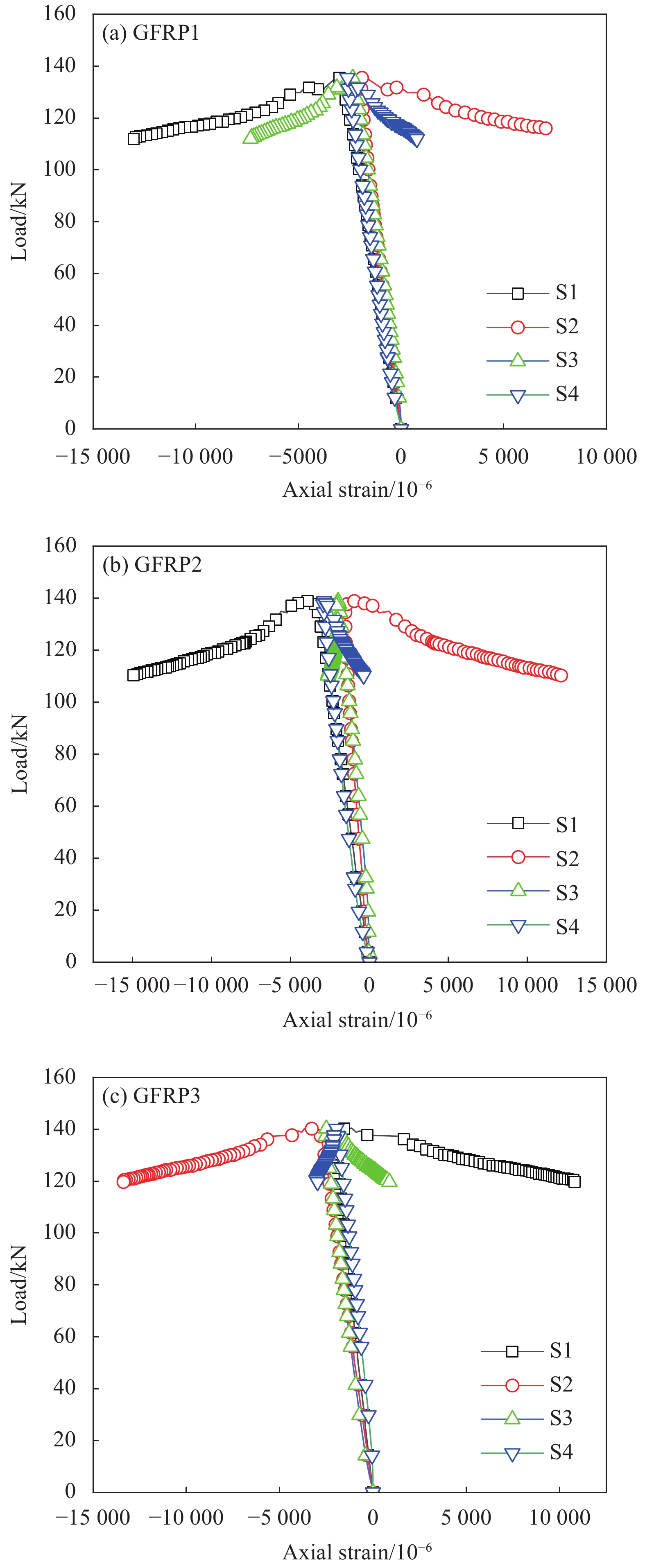
图6为轴压下3根GFRP管的荷载-轴向应变曲线,可以看出:3根GFRP管在中部截面4个位置处的荷载-应变曲线变化趋势一致。加载前期,荷载与应变呈线性关系,试件处于弹性阶段,各截面对称面上的应变值均较小且相近。达到失稳临界荷载后,应变值逐渐增大,荷载与应变呈非线性关系。其中,S1和S2曲线分别向正值与负值迅速发展,该现象由失稳后杆件跨中显著增加的二阶弯矩引起;S3和S4曲线因GFRP管存在初始缺陷及单双耳安装误差等具有不同的变化趋势。
1.3.2 套管屈曲约束装置试件
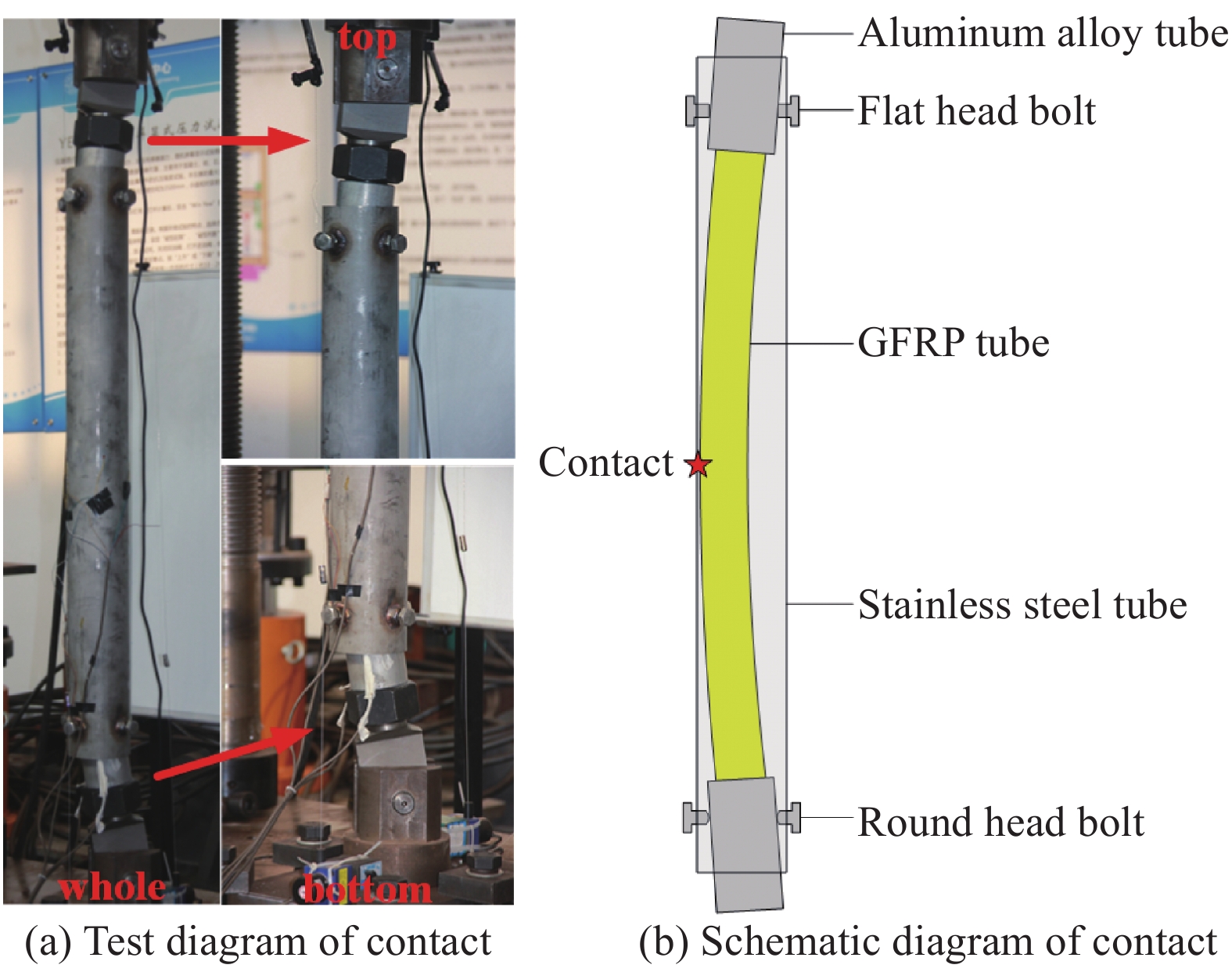
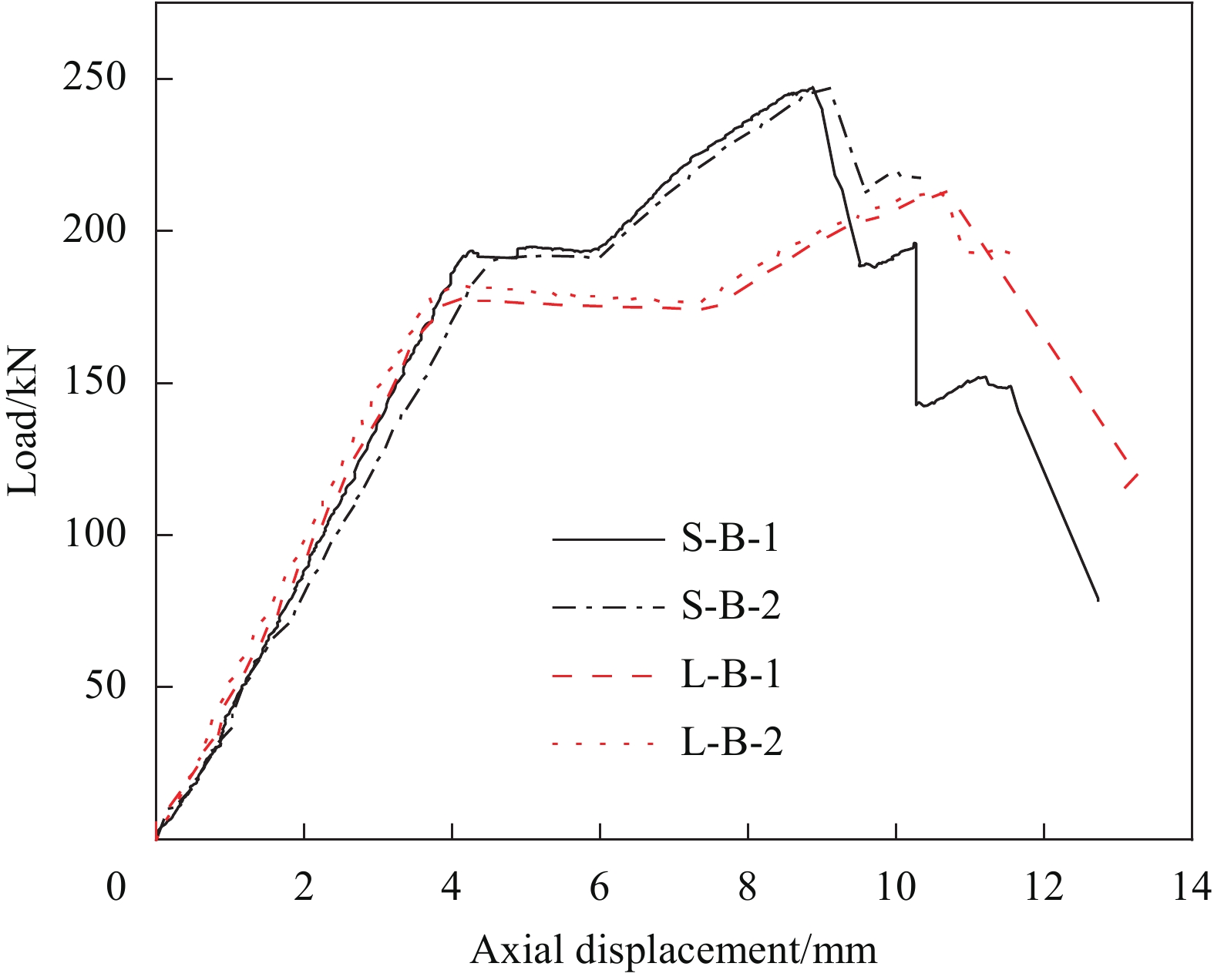
图7为内核与套管接触的试验图与示意图,图8为轴压下4个带套管屈曲约束装置GFRP管的荷载-轴向位移曲线。试验加载初期未见试件变形响应,荷载-位移曲线均处于线性且斜率基本一致;当内核发生失稳后,明显可见内核端部中轴线与套管中轴线偏移,曲线变为平台段,且大间隙试件的平台段长于小间隙试件;继续加载,内核与套管发生接触,两者共同受力,曲线进入后接触段,先呈线性增长至极限承载力,再下降直至试件破坏,其中此段线性斜率小于初始曲线斜率且小间隙试件极限承载力较高。4个试件的极限荷载值分别为:247.4 kN、247.3 kN、212.9 kN、212.6 kN。其荷载-位移曲线包含线性段、平台段及后接触段,曲线线型与低屈服点钢材应力-应变曲线相似,表明通过加装约束装置可使线弹性的GFRP材料产生类似于钢材弹塑性本构。
试验结束后取出内核GFRP管,可以看出试件S-B-1、S-B-2及L-B-1于GFRP管与铝合金套筒相接处发生全截面压溃(如图9(a)、9(b)、9(c)),相应位置材料发生粉末压碎,试件L-B-2在连接处产生纵向裂纹(如图9(d)),该裂纹自GFRP管与铝合金套筒连接处萌生,并向GFRP管中部发展。由于加套管屈曲约束装置后GFRP管二阶挠曲受到约束,内核破坏模式为截面承压强度破坏。
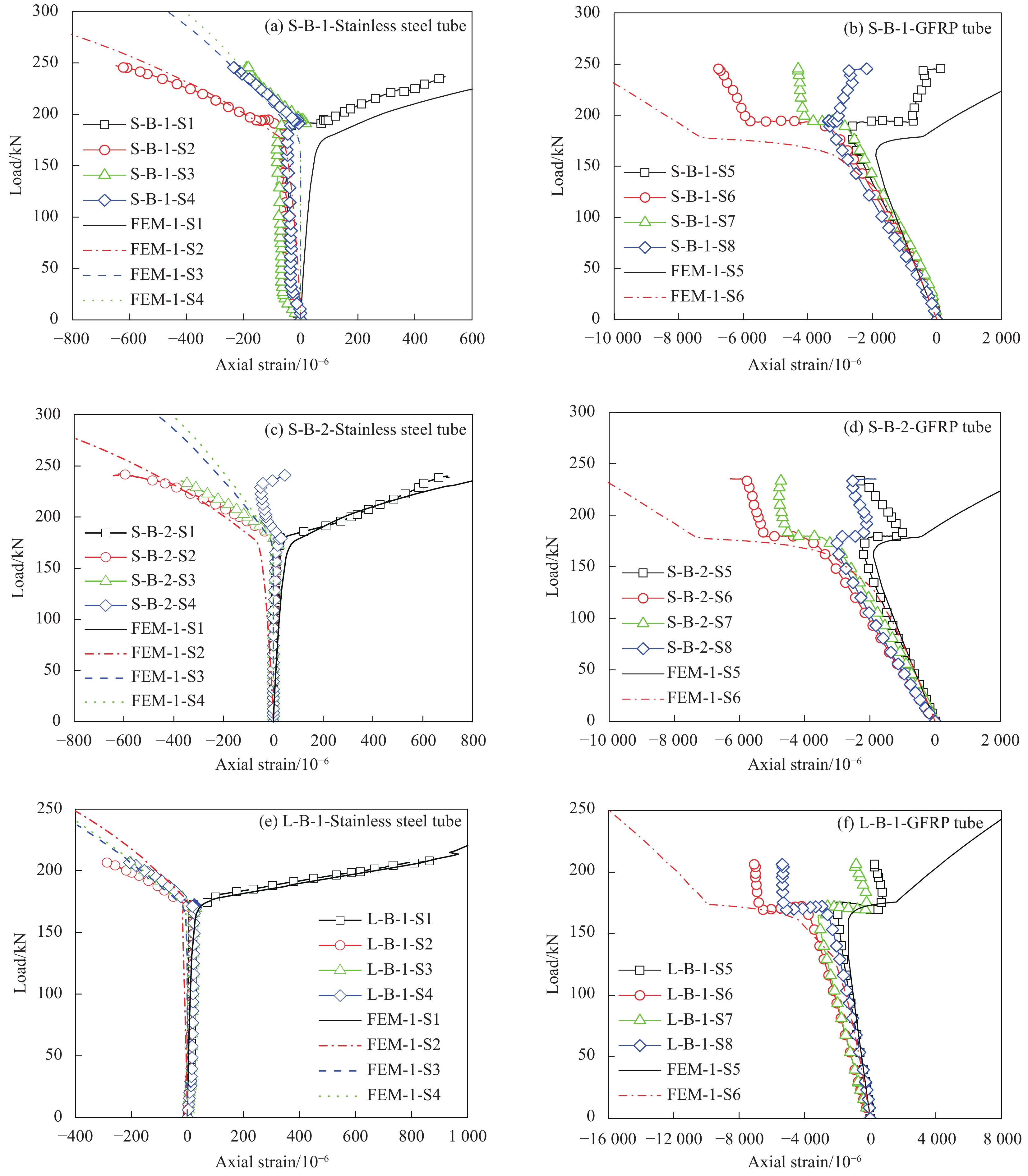
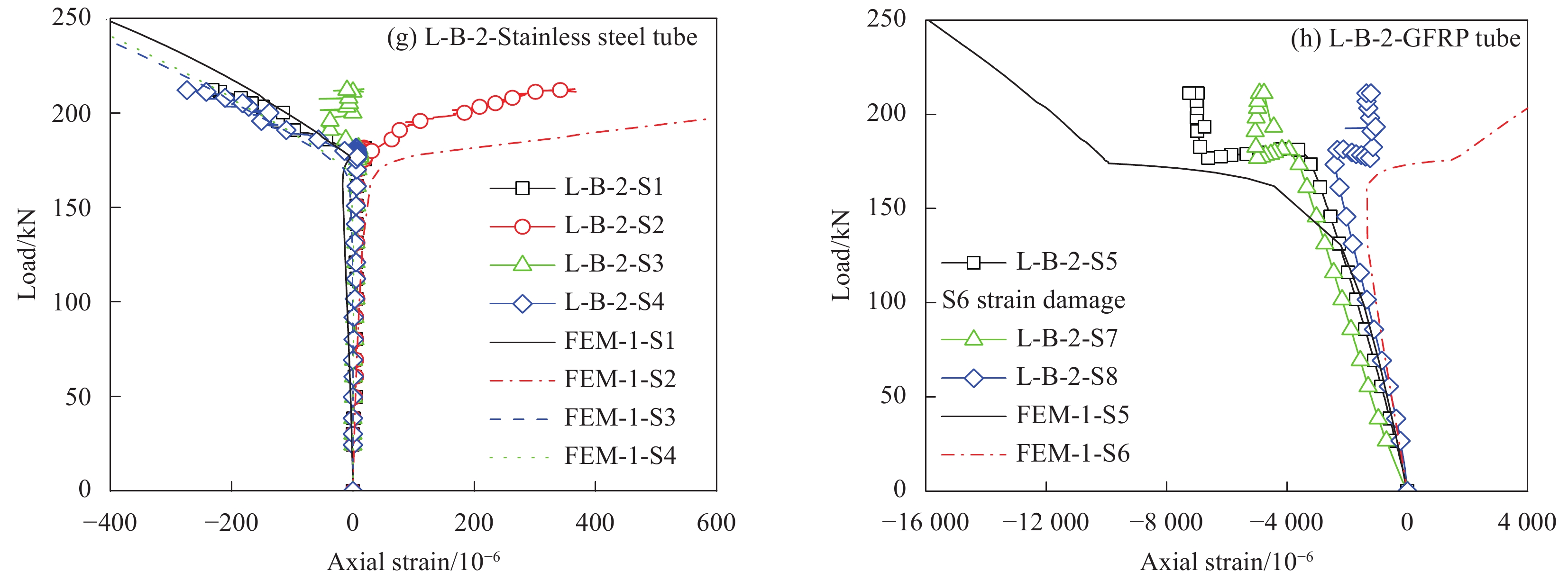
图10为轴压下带套管屈曲约束装置GFRP管的荷载-轴向应变曲线,通过荷载-应变曲线判定各试件中部截面的应变分布和发展情况。加载初期,不锈钢套管上的应变值很小,而GFRP管上荷载与应变呈线性增长,表明初期套管不承受轴力,由GFRP管内核承受轴力。当内核发生失稳后,内核与套管接触,套管的荷载与应变呈线性增长,而GFRP管的荷载-应变曲线先保持水平后线性上升,直至试件破坏。其中,套管处于弹性状态,远未到屈服强度,说明套管参与共同作用小,仅起到横向约束作用,试件极限承载力按GFRP管取值。
综上,GFRP管在轴压作用下易发生整体失稳破坏。而在加装套管屈曲约束装置轴压试验中,套管可以约束内核GFRP管横向变形,能有效提高GFRP管极限承载能力及延性,使GFRP管从失稳破坏向材料强度破坏发展,其中小间隙试件的极限承载力提高幅度大于大间隙试件,而大间隙试件表现出来的延性优于小间隙试件。两组试验的极限承载力和破坏模式对比见表3。
表 3 GFRP管与带屈曲约束装置GFRP管轴压试验结果对比Table 3. Comparison of the axial compression test results between GFRP tubes and GFRP tubes with BRBSpecimen Ultimate load/kN Average load/kN Increase coefficient/% Variation/% Failure mode GFRP1 133.7 137.7 — 1.85 Buckling failure GFRP2 138.9 GFRP3 140.6 S-B-1 247.4 247.4 79.66 0.02 Strength failure S-B-2 247.3 L-B-1 212.9 212.8 54.54 0.05 L-B-2 212.6 2. 有限元分析
2.1 套管屈曲约束GFRP管FEM建立
利用ANSYS软件建立套管屈曲约束装置试件的有限元模型(FEM)如图11所示。模型采用8节点三维实体单元(SOLID185)对GFRP管、铝合金套筒和不锈钢套管进行建模,并采用体扫掠方式实现规则六面体网格划分。不锈钢套管与GFRP管及铝合金套筒之间的接触行为采用了一对接触单元(TARGE170和CONTA174)进行模拟,将不锈钢套管内表面定义为接触单元TARGE170,将GFRP管和铝合金套筒的外表面定义为接触单元CONTA174,并定义法向接触均为硬接触。由于试验中单双耳的存在使荷载并未直接施加于试件端面,于是在模型两端设置两参考点,各参考点与模型端面采用刚体绑定,并将荷载施加在参考点上。边界条件模拟试验情况,底部放松
x 向转角变形,顶部放松同向转角变形和纵向位移,其余自由度约束。为了更好模拟带套管屈曲约束装置GFRP管在轴向荷载作用下的受力行为,先对GFRP管进行特征值屈曲分析,根据美国土木工程复合材料制造协会颁布的标准[25]取H/500 (H为试件总长度)的一阶屈曲模态作为初始缺陷加到FEM上,后进行非线性计算。上述FEM能基本反映内核与套管之间的相对关系及约束作用,但实际试验中螺栓连接的约束作用是较复杂的。当GFRP管内核发生失稳后,内核端部对套管端部将产生较大的相对作用,这一相对作用会产生局部塑性变形,使螺栓对GFRP管内核约束作用减弱,而实际试验中在螺栓连接部位焊接螺帽予以增强,故实际螺栓约束作用介于套管弹性约束和塑性约束之间,且还与螺栓的拧紧程度和局部变形有关。FEM中采用梁单元(BEAM188)对螺栓进行简化处理,并将内核与套管上重合节点的自由度耦合约束。
建立两种FEM,分别命名为FEM-1和FEM-2。FEM-1模型中全部材料均取线弹性本构模型,由此局部相对作用力不产生塑性变形,即不产生局部刚度减弱;FEM-2模型中铝合金套筒和不锈钢套管采用其实际弹塑性本构模型,而对于GFRP管,考虑到其局部应力达到材料强度极限时,局部区域材料失效且刚度丧失,为近似反映上述材料强度的承载响应及破坏模式,GFRP管采用理想弹塑性本构模型;近似以GFRP管的压缩强度为限值,当局部应力达到该值时,材料刚度降低为零。
2.2 套管屈曲约束GFRP管FEM验证
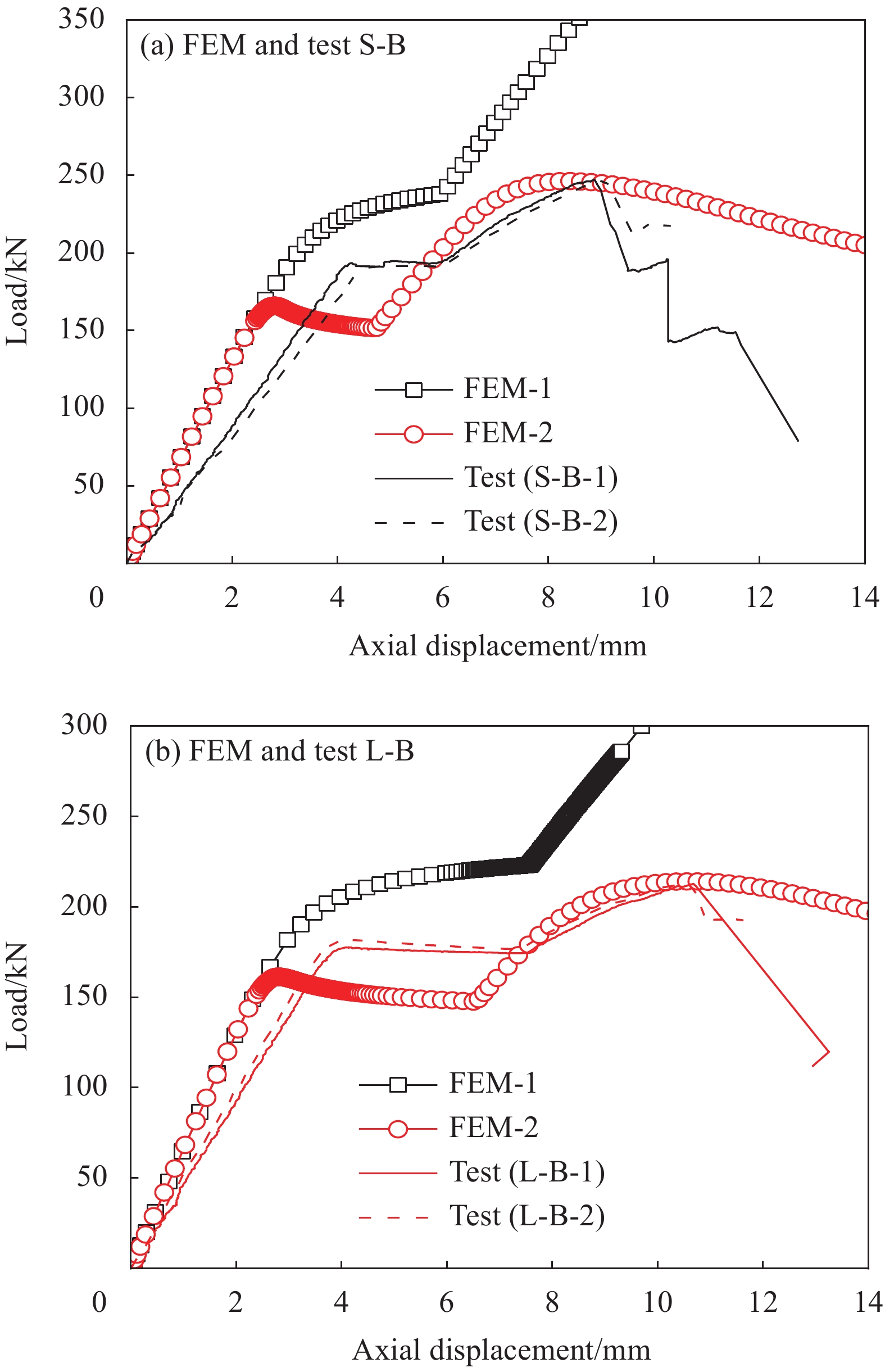
将FEM-1和FEM-2计算得到的荷载-轴向位移曲线与试验曲线进行对比,如图12所示。可见考虑材料塑性本构与否对试件初始轴向刚度影响不大。将FEM-1模型得到的荷载-轴向应变曲线与试验曲线进行对比,如图10所示,可知与试验结果较吻合。但考虑套管塑性后使GFRP管内核失稳临界荷载变小,且随着内核挠曲发展,荷载-位移曲线平台段存在轻微的下降趋势,与实验得到的结果一致。这一现象是由于内核失稳导致套管在螺栓连接处产生较大的塑性变形,使螺栓约束作用降低,且随着失稳发展,螺栓约束作用逐步降低,从而引起试件对应承受的轴向荷载轻微降低。试验得到的内核失稳临界荷载位于两种FEM计算结果之间,表明上述模型分析的正确性。
随着内核与套管发生接触,两种FEM得到的荷载-位移曲线呈现出不同发展趋势。FEM-1模型曲线呈现不断上升趋势,若GFRP管强度足够高,则其承载力可不断提高,其极限承载力可采用Tsai-Wu失效准则进行判定。FEM-2模型曲线呈现先上升后下降趋势,当GFRP管局部应力达到材料强度极限时,局部将完全失去刚度并发展为塑性铰,因此曲线极值点可近似看作试件极限承载力。从图12可知,采用有限元FEM-2模型得到的极限荷载值与试验结果十分接近,与S-B试验组平均值相差2.03%,与L-B试验组平均值相差1.86%。
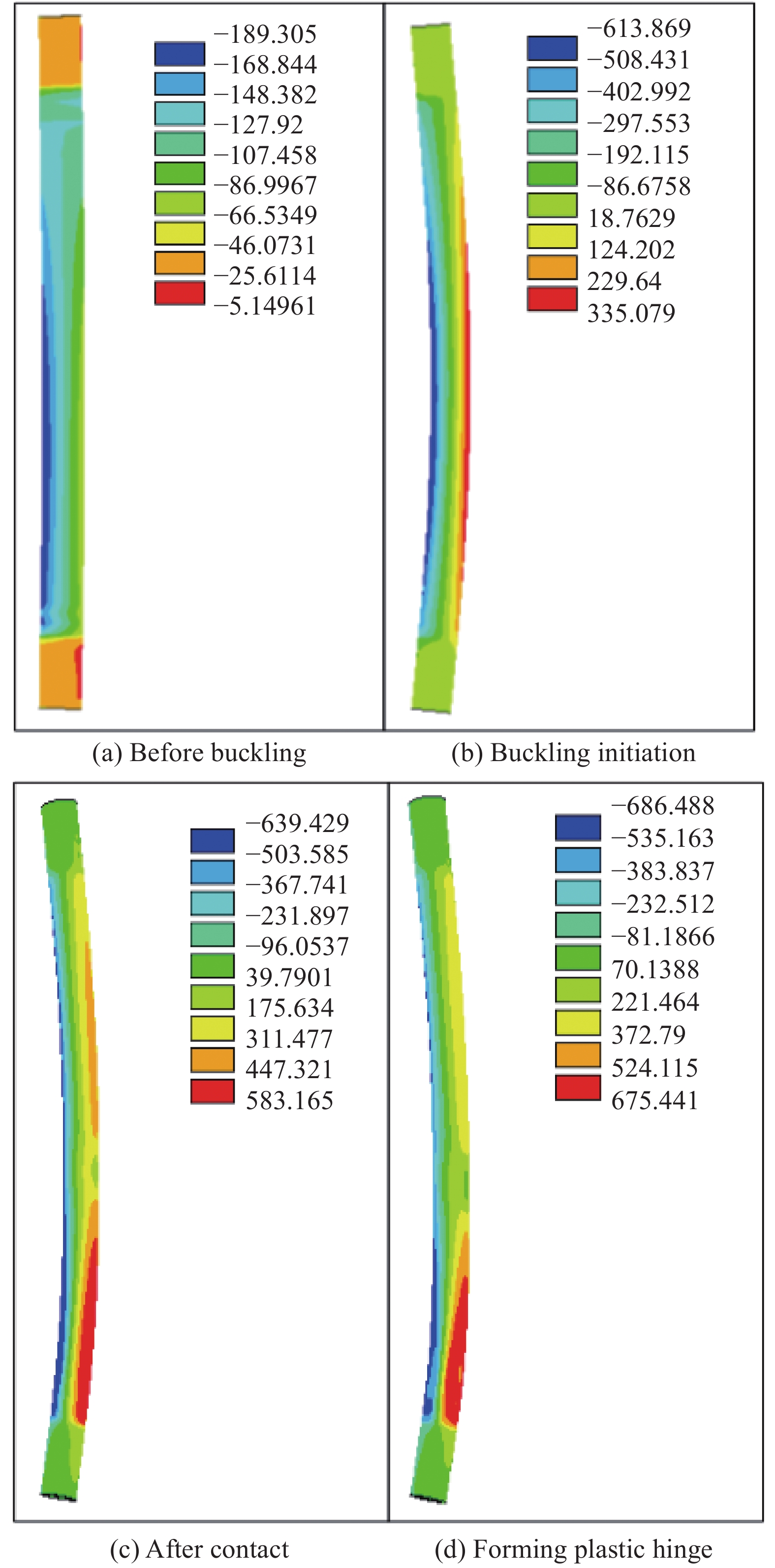
图13为FEM-2模型中L-B试件的GFRP管内核在加载过程中典型阶段的轴向应力图。图14为FEM-2模型中S-B试件失效后套管及GFRP管的变形云图和应力云图。失稳前,GFRP管全截面受压应力;失稳后,GFRP管拉伸侧正应力迅速增长;GFRP管与套管接触后,将产生横向接触力,使GFRP管中部应力降低;继续加载,在GFRP管端部产生一塑性铰,使试件失去进一步承载能力。套管屈曲约束装置失效后,套管和GFRP管在端部的变形和应力均达到了最大值,最终导致GFRP管失去承载能力,在端部发生了破坏,与试验破坏位置吻合。
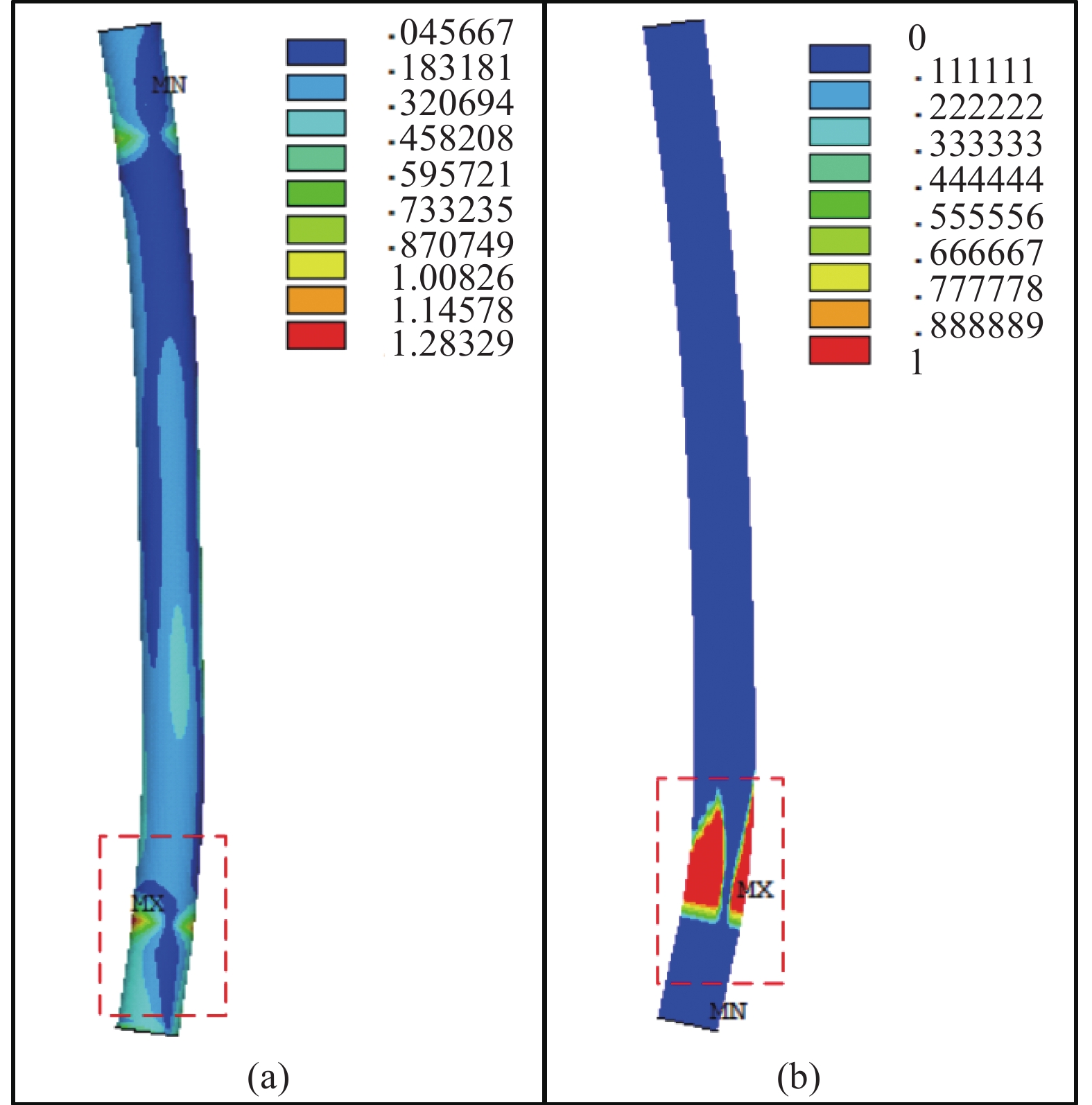
实际上从承载机制本质上说,套管仅起到横向约束作用,极限承载力最终取决于内核截面强度,故可用FEM-2模型进行试件极限承载力的近似预测。将FEM-1模型中反Tsai-Wu强度比系数If云图与FEM-2模型中塑性分布云图进行对比,如图15所示。可见两种FEM中GFRP管内核失效位置是一致的,且与试验的破坏发展位置吻合,进一步表明了FEM-2模型在预测试件失效方面的可行性。
综上,FEM的变形特征、破坏位置及极限荷载值等均与试验结果相符合,证明了FEM的正确性和有效性,因此可采用FEM-2模型分析组合构件承载力及装置应用效果,并进行参数化分析。
3. 套管屈曲约束GFRP管轴压性能影响因素
影响套管屈曲约束装置轴压性能的主要参数是内核长细比、内核与套管间隙及套管壁厚,若均采用试验方法验证的话,既不经济又费时间。因此本文采用经试验验证的FEM进行参数化分析,研究各参数对套管屈曲约束装置轴压性能的影响。
3.1 内核长细比
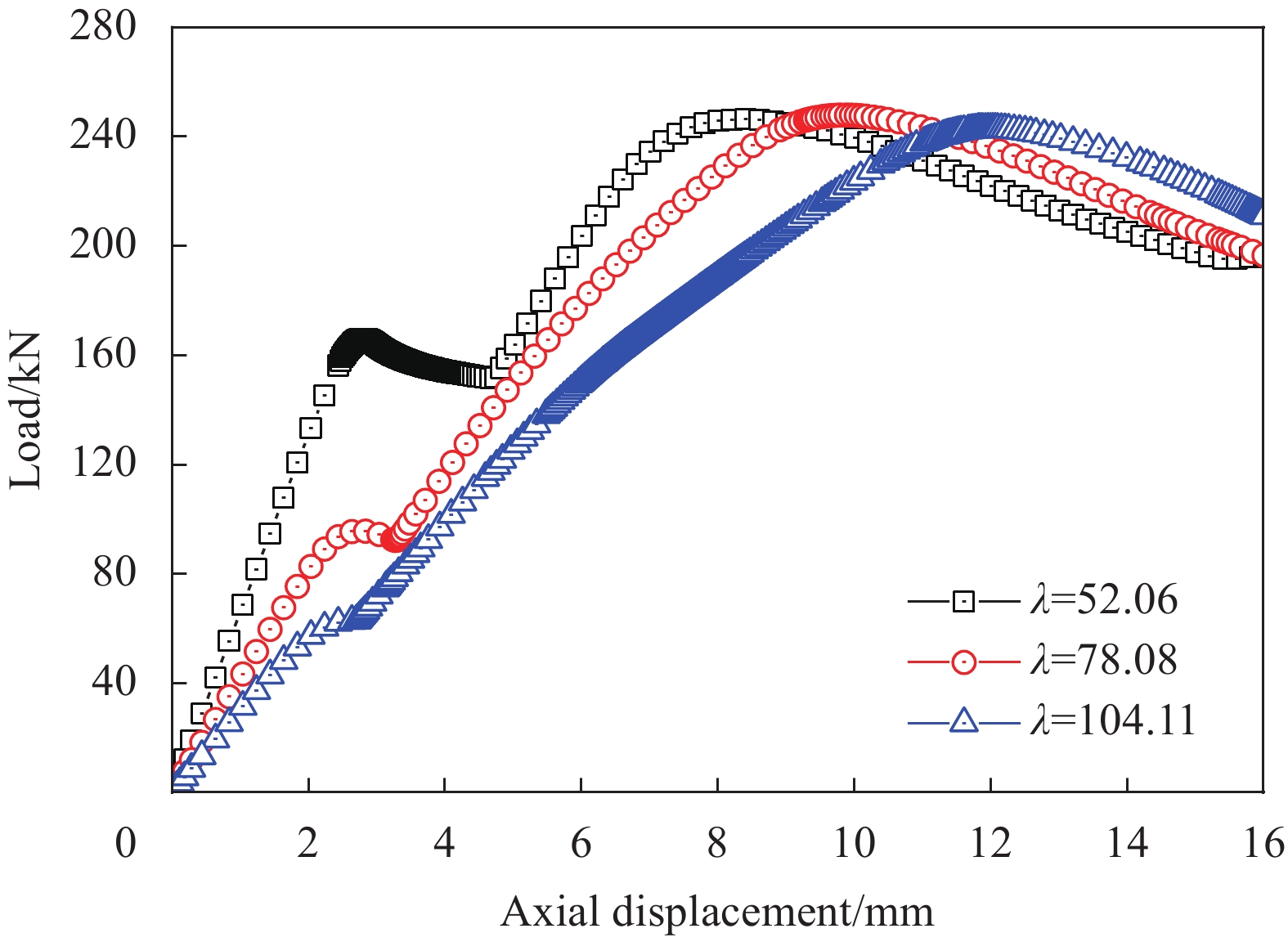
考虑GFRP管内核长细比变化时,屈曲约束装置对内核GFRP管约束效果及轴压性能的影响。分别取试验试件GFRP管长度的1.0、1.5及2.0倍,对应长细比分别为
\lambda =52.06、78.08及104.11,不锈钢套管也随之变长,其余尺寸与试验S-B试件一致。利用上述FEM-2进行计算,得到的荷载-轴向位移曲线如图16所示。可见,在其它条件不变情况下,由于内核GFRP管长细比变化,三种GFRP管的线刚度不同;随着长细比增大,失稳临界荷载值下降且曲线平台段变短,这是由于内核GFRP管长细比增大后,更小的轴向荷载将会引起更大的横向挠曲。不同长细比的GFRP管加装套管屈曲约束装置后,其极限承载力相比于GFRP管失稳临界荷载的相对提升幅值不同,具体表现为:当内核GFRP管长细比为52.06、78.08、104.11时,套管屈曲约束GFRP管极限承载力相比于内核失稳临界荷载的相对提升幅值分别为49%、161%、286%。
因此,内核GFRP管长细比越大,套管屈曲约束GFRP管极限承载力相比于内核失稳临界荷载的相对提升幅值越高,约束效果越好,这是由于试件长细比越大,试件越易发生失稳,套管的约束作用发挥越充分。
3.2 内核与套管间隙
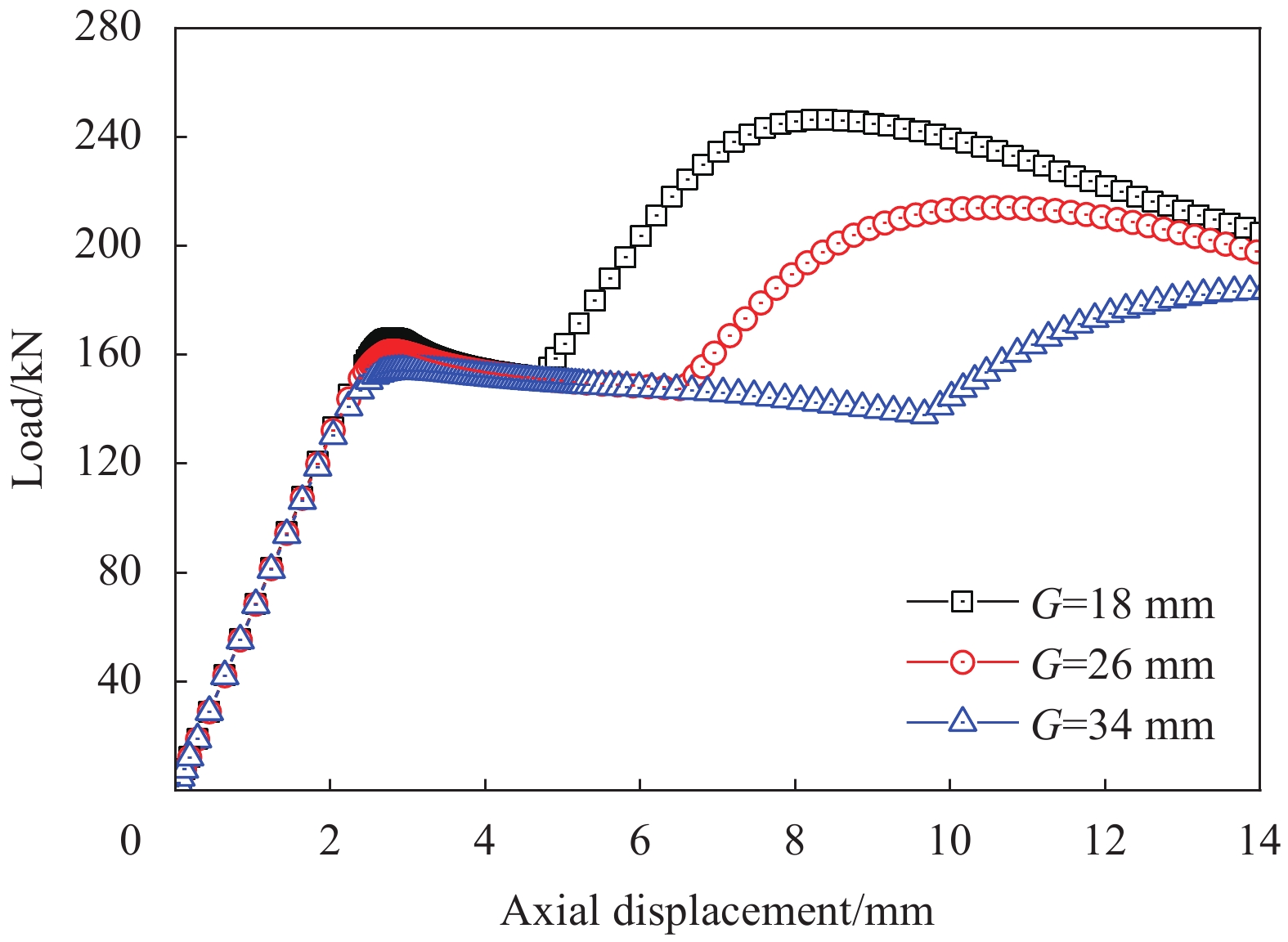
考虑内核与套管间隙变化时,屈曲约束装置对内核GFRP管约束效果及轴压性能的影响。分别取内核与套管间隙G=18 mm、26 mm、34 mm,其余尺寸与试验试件一致。利用上述有限元FEM-2模型进行计算,得到的荷载-轴向位移曲线如图17所示。
可见,在其他条件不变情况下,内核与套管间隙变化,对屈曲约束装置的初始轴向刚度没有影响,这是由于套管不承受轴向荷载,由内核承受轴向荷载。随着内核与套管间隙增大,内核GFRP管失稳临界荷载值降低,曲线平台段变长,其极限承载力也降低,这与试验结果相一致。这是由于当内核GFRP管失稳与套管接触后,较大的间隙使轴力对内核GFRP端部产生了较长的力臂,进而产生了更大的附加弯矩,最终导致了屈曲约束装置极限承载力的下降。
因此,内核与套管间隙越大,在荷载-轴向位移曲线上可以产生更长的平台段,为内核GFRP管的延性提供储备,这对于线弹性GFRP材料是有益的,但必须考虑间隙增大的同时会对组合构件的极限承载力产生不利影响,在实际使用中应按需求进行择优综合选取。
3.3 套管壁厚
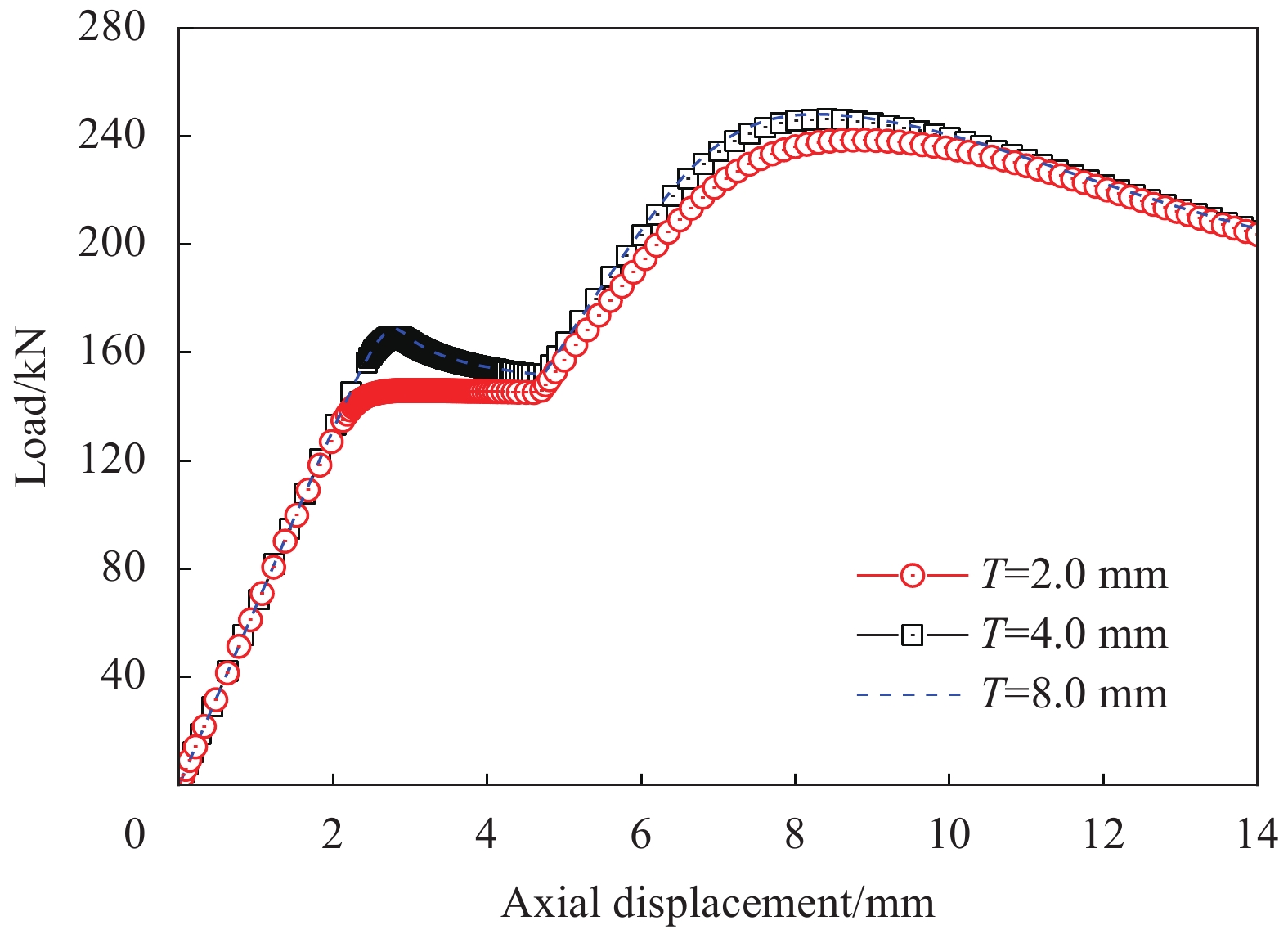
考虑套管壁厚变化时,屈曲约束装置对内核GFRP管约束效果及轴压性能的影响。分别取套管壁厚T=2.0 mm、4.0 mm、8.0 mm,其余尺寸与试验试件一致。利用FEM-2模型进行计算,得到的荷载-轴向位移曲线如图18所示。
可见,在其它条件不变情况下,当采用不同套管壁厚时,试件初始刚度不变。当壁厚为2.0 mm时,内核GFRP管失稳临界荷载降低,且套管屈曲约束装置的极限承载力略微降低,这是由于套管壁厚变薄,接触后的局部变形变大,内核GFRP管侧向挠曲增大,导致底部弯矩增加,从而使套管屈曲约束装置极限承载力下降。当套管壁厚为4.0 mm、8.0 mm时,荷载-位移曲线几乎重合。
因此,本试验选取套管壁厚为4.0 mm是合适的,当套管壁厚变薄时,不仅会对内核GFRP管失稳临界荷载有影响,还使套管屈曲约束装置的极限承载力降低;而套管壁厚过厚时,套管对内核GFRP管约束作用没有明显提升。故在设计套管屈曲约束装置时,应根据内核材料、内核长细比等因素综合选取壁厚,过薄会对内核失稳临界荷载和构件极限承载力产生不利影响,过厚则使约束效果提升不明显。
4. 结 论
为解决复合材料空间桁架结构部分关键压杆失稳引发的连续性倒塌问题,提出了一种由不锈钢套管及螺栓连接系组成的玻璃纤维增强树脂复合材料(GFRP)管整体失稳套管屈曲约束装置,通过轴压试验和有限元模拟分析了套管屈曲约束装置对GFRP管轴压性能的影响,是拉挤型复合材料压杆轴向承载性能提升的初步探索,且是分析套管屈曲约束装置对复合材料空间桁架结构性能影响的基础性研究,结论如下:
(1) GFRP管在轴压作用下易发生整体失稳,失稳后轴向缩短和横向挠曲明显增大,跨中产生较大的二阶弯矩,导致管件迅速失效并失去承载力,破坏时管体产生多条纵向贯穿裂缝,呈现脆性破坏和弹性失稳特征;
(2) 对于带套管屈曲约束装置的GFRP组合构件,内核GFRP管承受轴向荷载,套管约束内核屈曲侧向挠曲。轴向压力增大时,内核失稳后与套管发生接触,GFRP管二阶挠曲受到约束,内核上弯矩最大的截面逐渐向端部移动,在压力与弯矩共同作用下,内核GFRP管在端部发生了强度破坏,而套管一直处于弹性阶段。套管屈曲约束装置能有效约束内核GFRP管整体失稳变形,其轴压承载力和延性有大幅提高;
(3) 基于内核GFRP管采用理想弹塑性本构建立的套管屈曲约束组合构件有限元模型(FEM),其数值计算结果与试验结果吻合较好;
(4) 参数化分析表明,内核GFRP管长细比越大,套管屈曲约束GFRP管极限承载力相比于内核失稳临界荷载的相对提升幅值越高,约束效果越好;内核与套管间隙越大,其产生的较大弯矩易导致极限承载力下降,但组合构件延性越好;套管壁厚应适中选取,过薄会降低内核失稳临界荷载和构件极限承载力,过厚则约束效果提升不明显。
设计试验件内核GFRP管的长细比较小,其屈曲承载力与其全截面强度承载力较接近;此外,不锈钢外套管厚度设计得较厚,自重较重。本文的研究工作是拉挤型复合材料压杆轴向承载性能提升的初步探索,下一步可尝试采用铝合金、缠绕复合材料管等轻质材料取代本文不锈钢外套管,以进一步减轻组合构件自重;进行套管屈曲约束装置的优化设计,内核可采用CFRP、混杂纤维等强度更优型材,并开展大长细比内核下组合构件的承载性能试验,研究内核失稳模态跃升的实现条件及相应作用机制。
-
表 1 玻璃纤维增强树脂复合材料(GFRP)、铝合金及不锈钢的材料力学参数
Table 1 Mechanical parameters of glass fiber reinforced polymer (GFRP), aluminum alloy and stainless steel
Material Elastic modulus/GPa Poisson’s ratio GFRP {E_1} = 63.0, {E_{\rm{2}}}{\rm{ = }}{E_{\rm{3}}}{\rm{ = 14}}{\rm{.2}}, {G_{{\rm{12}}}}{\rm{ = }}{G_{{\rm{13}}}}{\rm{ = 13}}{\rm{.0}}, {G_{{\rm{23}}}}{\rm{ = 9}}{\rm{.4}} {v_{12}} = {v_{13}} = 0.25, {v_{23}} = 0.27 Al alloy {E_{{\rm{Al}}}}{\rm{ = 65}}{\rm{.0}} {v_{{\rm{Al}}}} = 0.{\rm{3}} Stainless steel {E_{{\rm{SS}}}}{\rm{ = 200}}{\rm{.0}} {v_{{\rm{SS}}}} = 0.{\rm{3}} Notes: {E_{\rm{1}}}—Elastic modulus of 1-axis; {E_{\rm{2}}}—Elastic modulus of 2-axis; {E_{\rm{3}}}—Elastic modulus of 3-axis; {G_{{\rm{12}}}}—Shear modulus of plane 12; {G_{{\rm{13}}}}—Shear modulus of plane 13; {G_{{\rm{23}}}}—Shear modulus of plane 23; {v_{12}},{v_{13}}—Major Poisson’s ratio; {v_{23}}—Minor Poisson’s ratio; {E_{{\rm{Al}}}}—Elastic modulus of Al alloy; {v_{{\rm{Al}}}}—Poisson’s ratio of Al alloy; {E_{{\rm{SS}}}}—Elastic modulus of stainless steel; {v_{{\rm{SS}}}}—Poisson’s ratio of stainless steel. 表 2 GFRP管及带套管屈曲约束装置(BRB)管试件的编号及尺寸
Table 2 Number and size of GFRP and buckling restrained brace (BRB) tubes
mm Number Outer sleeve GFRP tube DO L T DO L T GFRP1 — — — 60 1000 6 GFRP2 GFRP3 L-B-1 120 984 4 60 1000 6 L-B-2 S-B-1 108 S-B-2 Notes: L—Length; DO—Outer diameter; T—Thickness; L-B—Large gap BRB; S-B—Small gap BRB. 表 3 GFRP管与带屈曲约束装置GFRP管轴压试验结果对比
Table 3 Comparison of the axial compression test results between GFRP tubes and GFRP tubes with BRB
Specimen Ultimate load/kN Average load/kN Increase coefficient/% Variation/% Failure mode GFRP1 133.7 137.7 — 1.85 Buckling failure GFRP2 138.9 GFRP3 140.6 S-B-1 247.4 247.4 79.66 0.02 Strength failure S-B-2 247.3 L-B-1 212.9 212.8 54.54 0.05 L-B-2 212.6 -
[1] ZHANG D D, ZHAO Q L, HUANG Y X, et al. Flexural properties of a lightweight hybrid FRP-aluminum modular space truss bridge system[J]. Composite Structures,2014,108:600-615. DOI: 10.1016/j.compstruct.2013.09.058
[2] 冯鹏, 田野, 覃兆平. 纤维增强复合材料拉挤型材桁架桥静动力性能研究[J]. 工业建筑, 2013, 43(6):36-41. FENG P, TIAN Y, QIN Z P. Static and dynamic behavior of a truss bridge made of FRP pultruded profiles[J]. Industrial Construction,2013,43(6):36-41(in Chinese).
[3] ALEXANDER V, ALEXANDER S, FAUSTO T, et al. Pultruded materials and structures: A review[J]. Journal of Composite Materials,2020,54(26):1-37.
[4] 周龙伟, 赵丽滨. 基于失效机制的单向纤维增强树脂复合材料退化模型[J]. 复合材料学报, 2019, 36(6):1389-1397. ZHOU L W, ZHAO L B. Failure mechanisms based degradation model of unidirectional fiber reinforced polymer composites[J]. Acta Materiae Compositae Sinica,2019,36(6):1389-1397(in Chinese).
[5] 朱锐杰, 李峰, 刘加顺. 基于能量法的变截面层合管整体稳定承载力计算方法[J]. 复合材料学报, 2017, 34(10):2211-2219. ZHU R J, LI F, LIU J S. A method for calculating bearing capacity of laminated tube with variable cross section based on energy method[J]. Acta Materiae Compositae Sinica,2017,34(10):2211-2219(in Chinese).
[6] GOODMAN J W, GISKSMAN J A. Structural evaluation of long boron composite column[J]. Composite Materials: Testing and Designing,1969,460:460-469.
[7] HASHEM Z A, YUAN R L. Short vs. long column behavior of pultruded glass-fiber reinforced polymer composites[J]. Construction and Building Materials,2001,15(8):369-378. DOI: 10.1016/S0950-0618(01)00018-6
[8] HEWSON P. Buckling of pultruded glass fiber-reinforced channel sections[J]. Composites Structures,1978,9(1):56-60.
[9] ZUREICK A H, SCOTT D W. Short-Term behavior and design of fiber-reinforced polymeric slender members under axial compression[J]. Journal of Composites for Construction,1997,1(4):140-149. DOI: 10.1061/(ASCE)1090-0268(1997)1:4(140)
[10] 南波, 武岳, 孙浩田. 拉挤型CFRP管轴压性能[J]. 哈尔滨工程大学学报, 2015, 36(6):779-783. NAN B, WU Y, SUN H T. Buckling behavior of pultruded carbon fiber reinforced polymer pipes under axial compressive load[J]. Journal of Harbin Engineering University,2015,36(6):779-783(in Chinese).
[11] 陈静芬. 基于弹塑性损伤本构模型的复合材料层合板破坏荷载预测[J]. 复合材料学报, 2017, 36(4):773-785. CHEN J F. Failure loads prediction of composite laminates using a combined elastoplastic damage model[J]. Acta Materiae Compositae Sinica,2017,36(4):773-785(in Chinese).
[12] 郭小农, 王丽, 罗永峰, 等. CFRP增强铝合金叠层复合材料短柱力学性能[J]. 复合材料学报, 2021, 38(4): 1115-1127. GUO X N, WANG L, LUO Y F, et al. Mechanical properties of CFRP reinforced aluminum alloy laminated composite stub column[J]. Acta Materiae Compositae Sinica, 2021, 38(4): 1115-1127(in Chinese).
[13] 金福松, 薛江红, 夏飞, 等. 考虑多尺度界面力学特性的损伤复合材料层合板分岔屈曲性能的等代化[J]. 复合材料学报, 2019, 36(5):1132-1142. JIN F S, XUE J H, XIA F, et al. An equivalent model on bifurcation buckling of delaminated composite laminates with multiscale interfacial behaviors[J]. Acta Materiae Compositae Sinica,2019,36(5):1132-1142(in Chinese).
[14] FÜLÖP A, IVÁNYI M. Experimentally analyzed stability and ductility behaviour of a space-truss roof system[J]. Thin-Walled Structures,2004,42(2):309-320. DOI: 10.1016/S0263-8231(03)00062-4
[15] YANG X, BAI Y, DING F X. Structural performance of a large-scale space frame assembled using pultruded GFRP composites[J]. Composites Structures,2015,133:986-996. DOI: 10.1016/j.compstruct.2015.07.120
[16] PRASAD B K. Experimental investigation of sleeved column[C]. Proc. 33rd AIAA/ASCE Structures, Structural Dynamics and Materials Conference, Dallas USA: AIAA/ASCE, 1992: 991-999.
[17] SRIDHARA B N. Sleeved compression member: USA, 5175972[P]. 1993-5-1.
[18] 申波, 马克俭, 邓长根. 轴压套管构件静力稳定的理论与试验研究[J]. 工程力学, 2013, 30(3):8-16. SHEN B, MA K J, DENG C G. Theoretical and experimental investigations on the static stability of a sleeved column[J]. Engineering Mechanics,2013,30(3):8-16(in Chinese).
[19] 申波. 轴压套管构件静力稳定性能的理论与试验研究[D]. 上海: 同济大学, 2007. SHEN B. Theoretical and experimental investigations on the static stability of sleeved compression members[D]. Shanghai: Tongji University, 2007(in Chinese).
[20] 张晨辉, 邓长根, 应武挡. 轴压套管构件的典型破坏模式与极限承载力[J]. 东南大学学报(自然科学版), 2019, 49(2):311-320. DOI: 10.3969/j.issn.1001-0505.2019.02.016 ZHANG C H, DENG C G, YING W D. Typical failure mode and ultimate bearing capacity of sleeved compression member under axial compression[J]. Journal of Southeast University(Natural Science Edition),2019,49(2):311-320(in Chinese). DOI: 10.3969/j.issn.1001-0505.2019.02.016
[21] 黄炳生, 崔海涛, 杨放, 等. 套管加固圆钢管轴心受压性能试验研究[J]. 建筑结构学报, 2020, 41(9):198-206. HUANG B S, CUI H T, YANG F, et al. Experimental study on axial compressive behavior of circular steel tubes strengthened by sleeved pipe[J]. Journal of Building Structures,2020,41(9):198-206(in Chinese).
[22] 李峰, 朱锐杰, 刘建邦, 等. 一种复合材料管屈曲约束装置: 中国, 201921953198[P]. 2020-7-21. LI F, ZHU R J, LIU J B, et al. A buckling restrained brace for composite tube: China, 201921953198[P]. 2020-7-21(in Chinese).
[23] LI F, ZHAO Q L, GAO Y F, et al. A prediction method of the failure load and failure mode for composite pre-tightened tooth connections based on the characteristic lengths[J]. Composite Structures,2016,154:684-693. DOI: 10.1016/j.compstruct.2016.06.036
[24] ZHU R J, LI F, SHAO F, et al. Static and dynamic behaviour of a hybrid PFRP-aluminium space truss girder: Experimental and numerical study[J]. Composite Structures,2020,243:112226. DOI: 10.1016/j.compstruct.2020.112226
[25] ASCE. Pre-standard for load and resistance factor design of pultruded fiber reinforced polymer structures[S]. Arlington: American Composites Manufacturers Association, 2010.
-
期刊类型引用(4)
1. 杨文伟,周海洋,王痛快,陈志伟. CFRP不同约束方式下拉挤型GFRP管混凝土组合柱的承载性能. 土木与环境工程学报(中英文). 2025(02): 141-150 .  百度学术
百度学术
2. 侍荣德,丁超峰. 拉挤型轴压GFRP圆管端部加固方式研究. 四川建材. 2022(01): 86-87 .  百度学术
百度学术
3. 罗振敏,邓婕,王涛,杨勇,王煦青,林峰. 玻璃纤维薄壁圆管复合结构的制备工艺及其性能研究进展. 塑料工业. 2022(01): 20-25 .  百度学术
百度学术
4. 刘龙刚,杨瑞娟. 基于有限元分析的受压构件计算与验证. 自动化与仪器仪表. 2022(10): 9-13+17 .  百度学术
百度学术
其他类型引用(0)
-




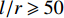

 下载:
下载: