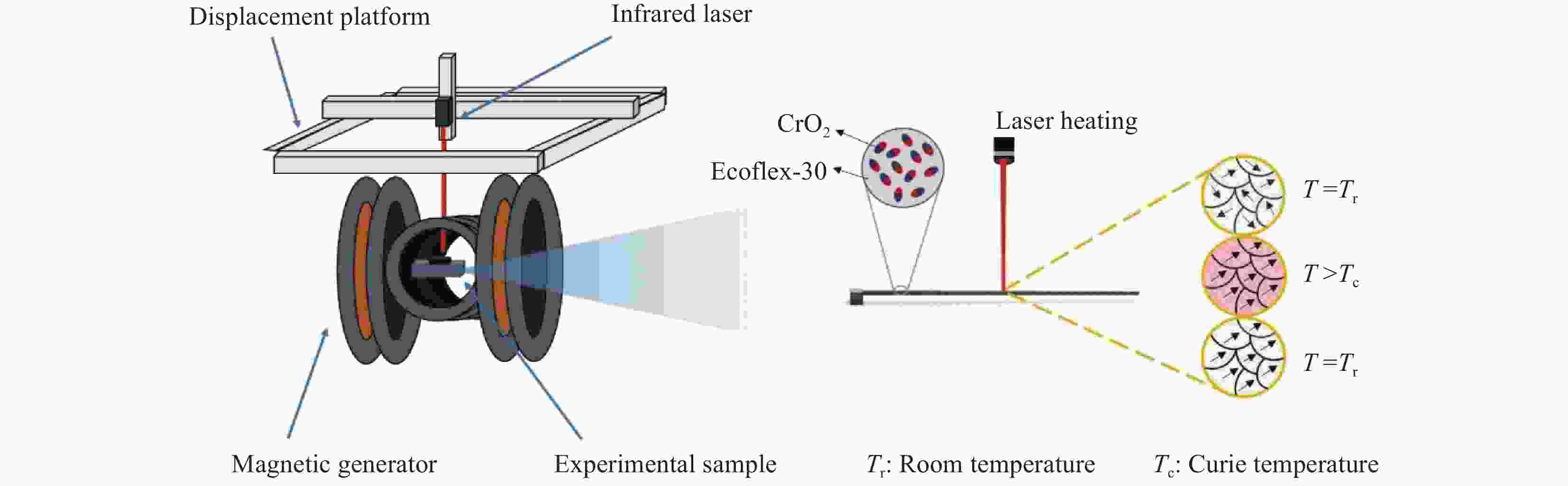
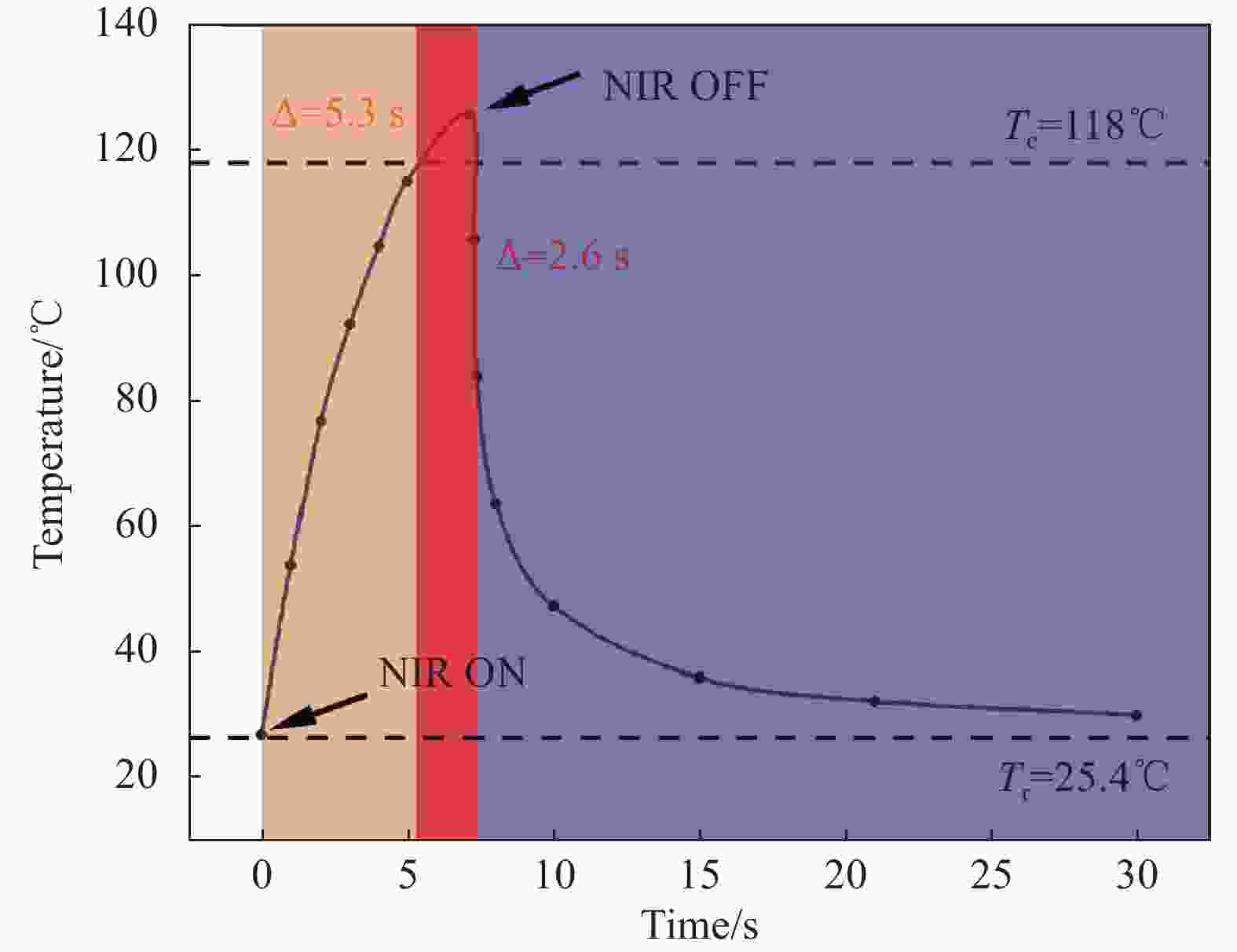
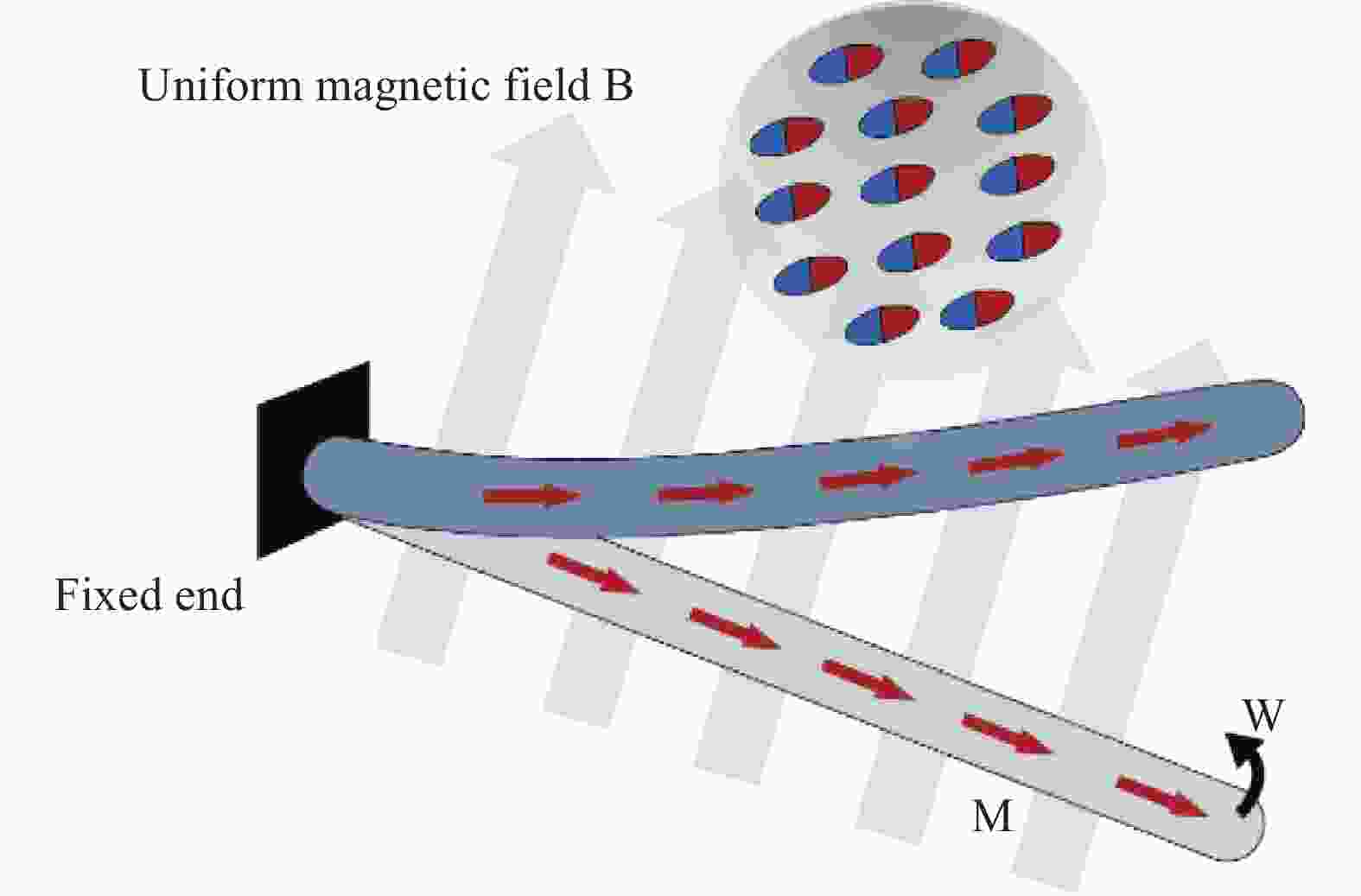
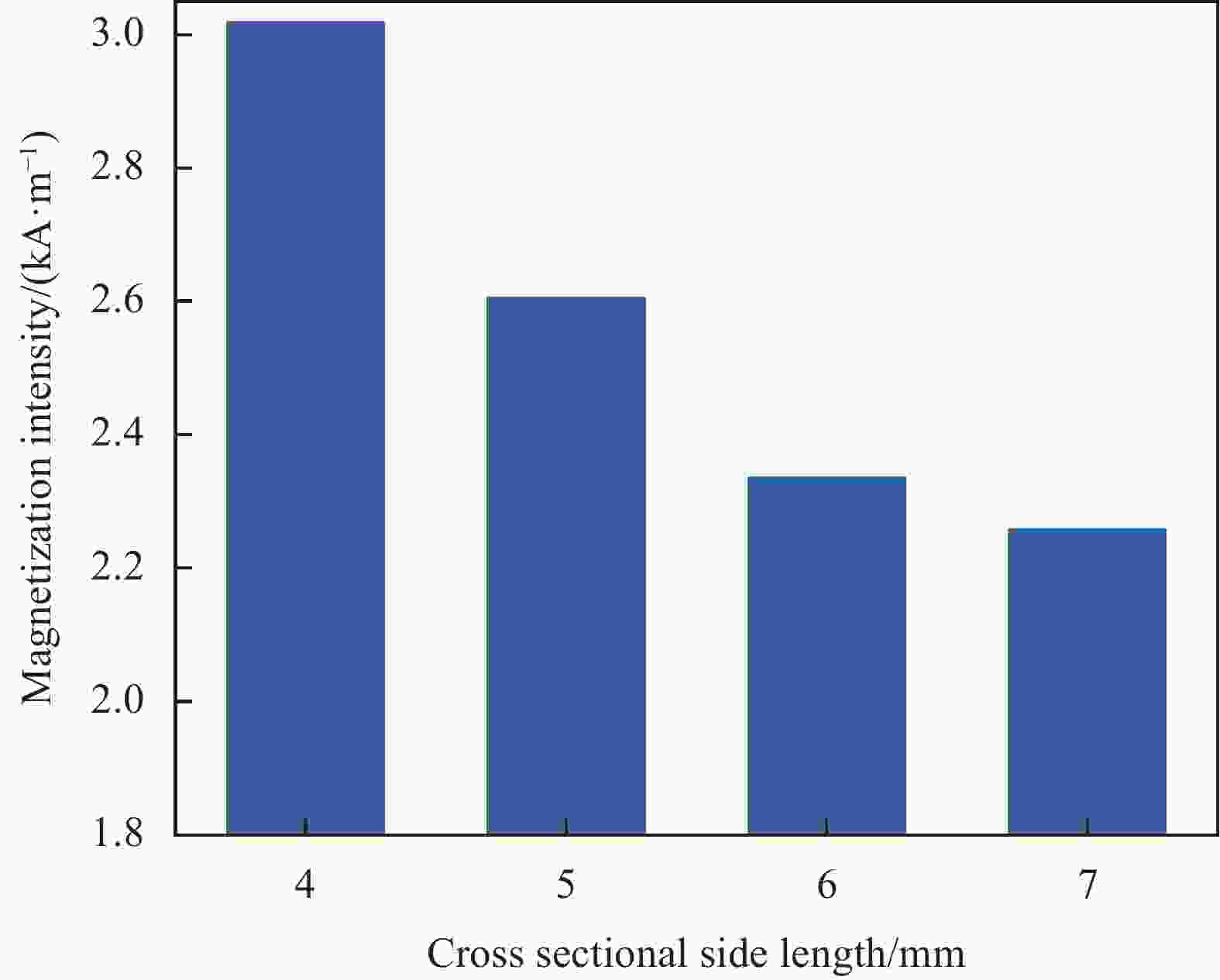
Reprogrammable magnetic domains and optimized design of a hard magnetic soft continuum
-
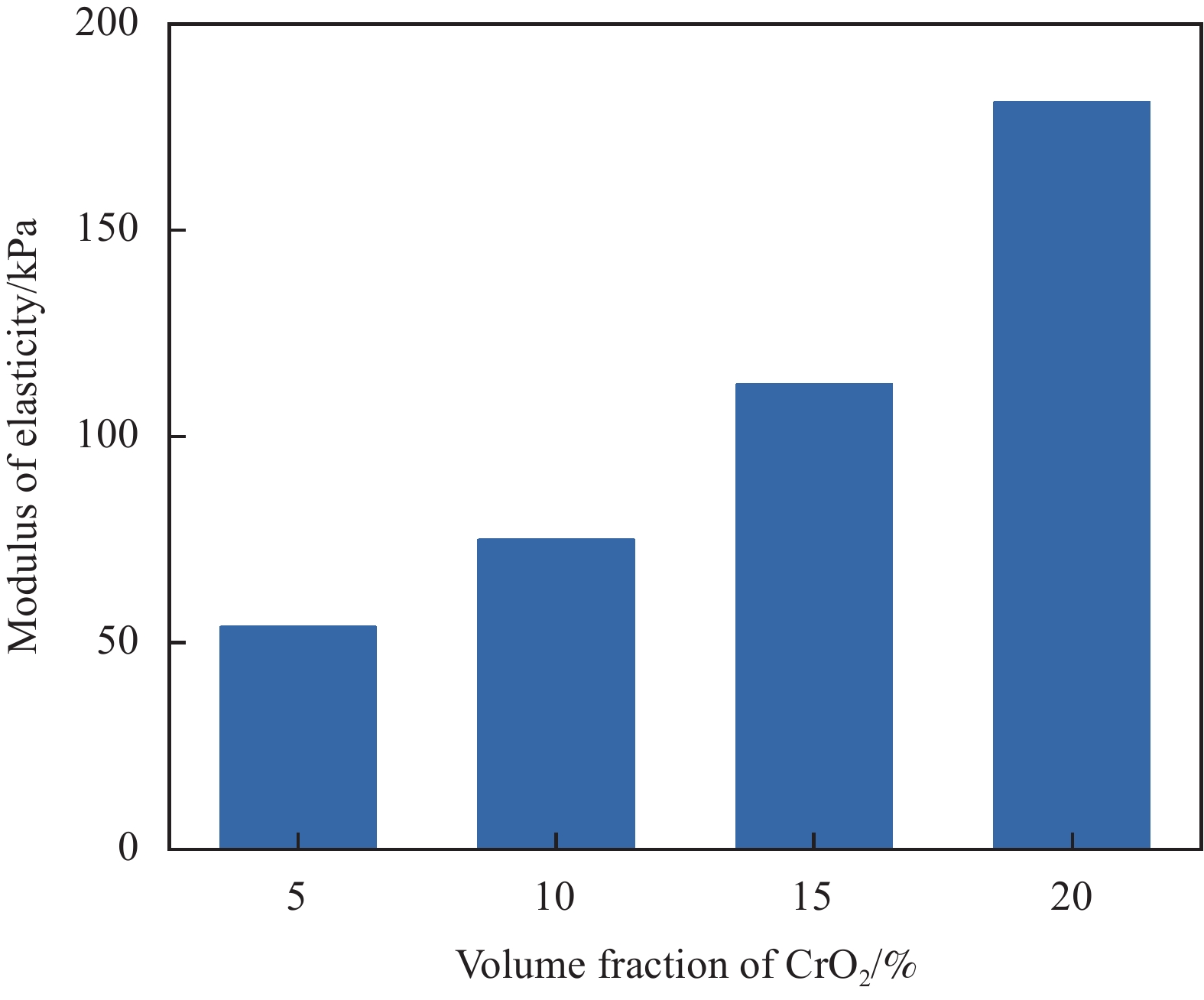
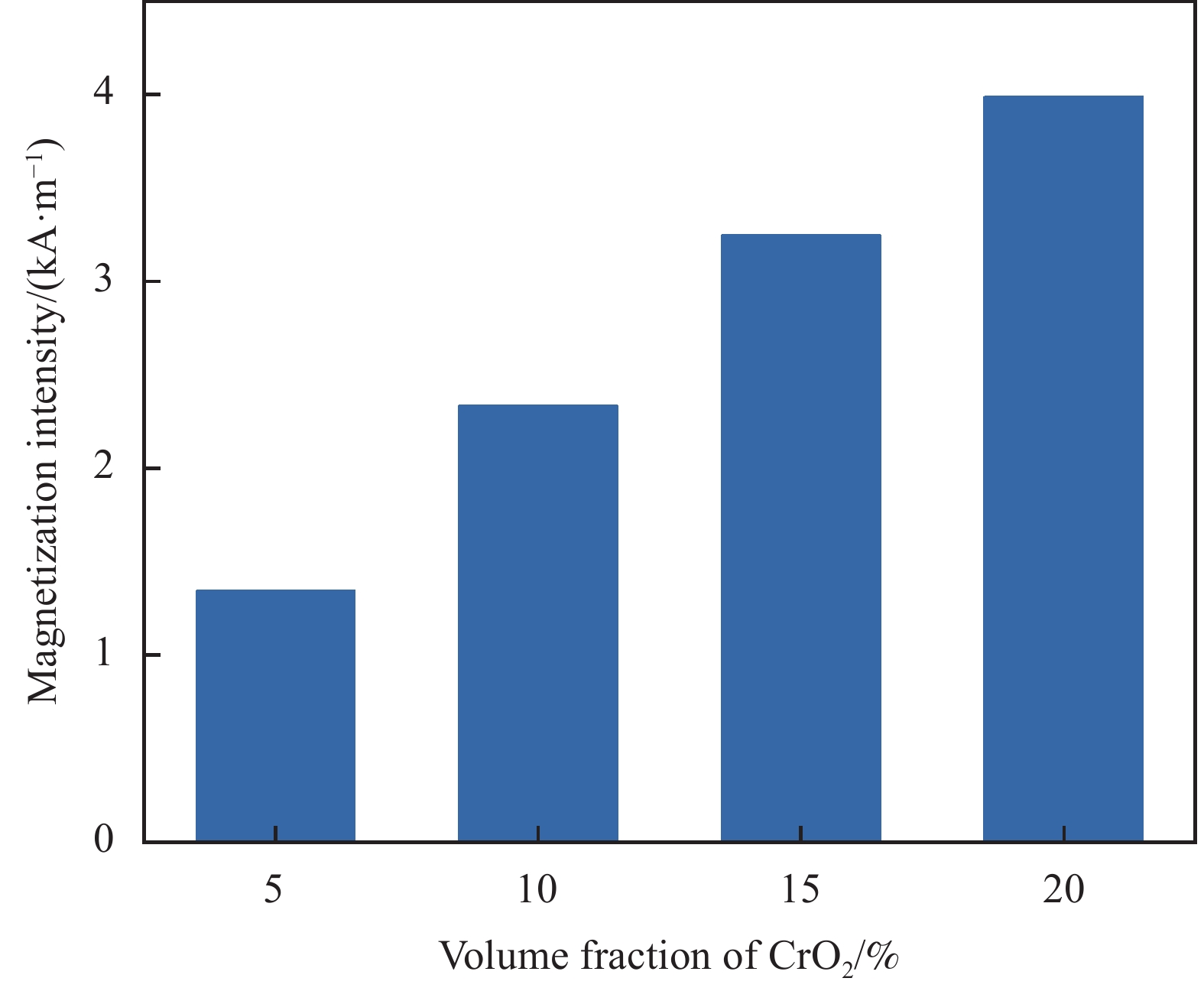
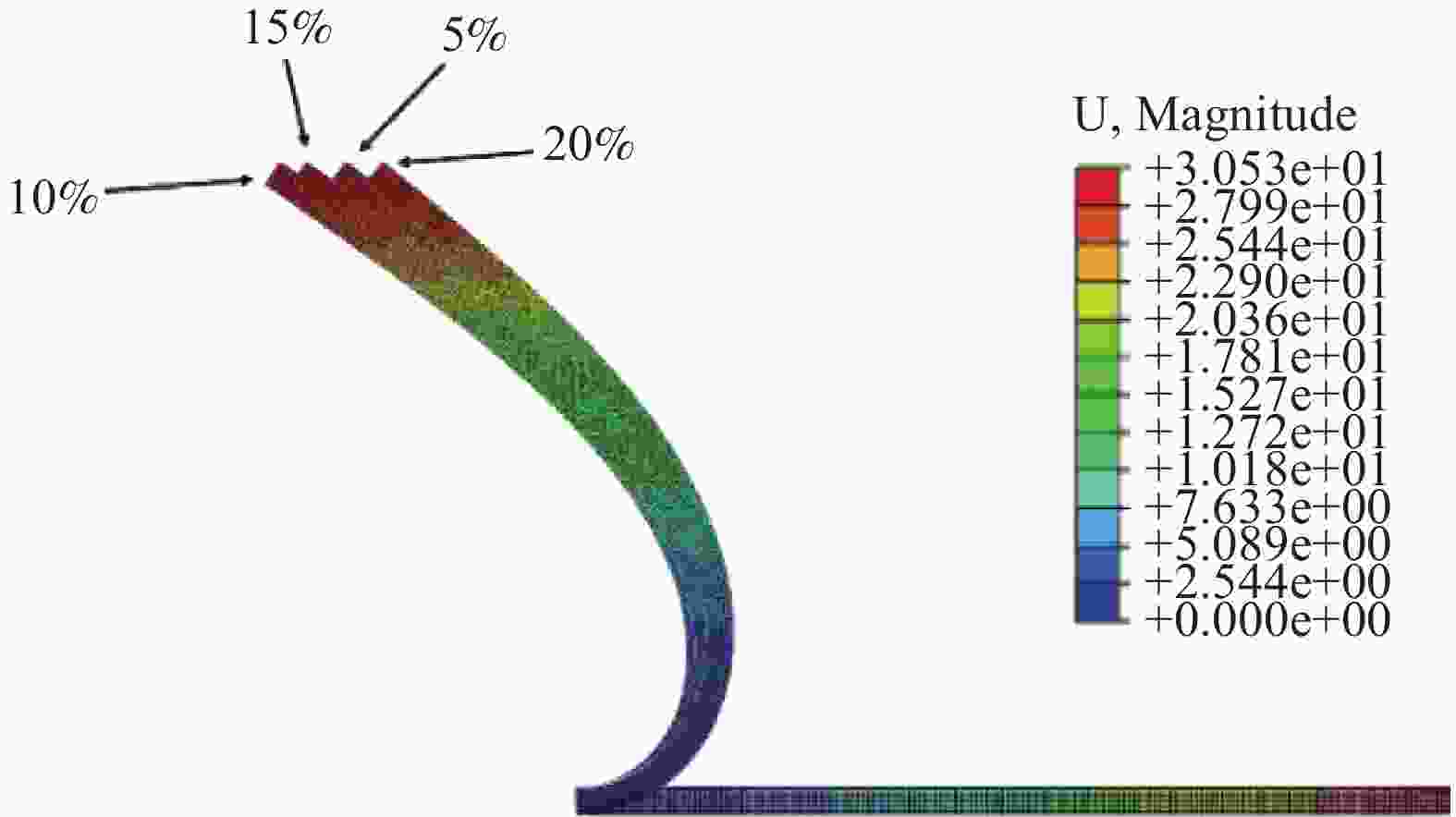
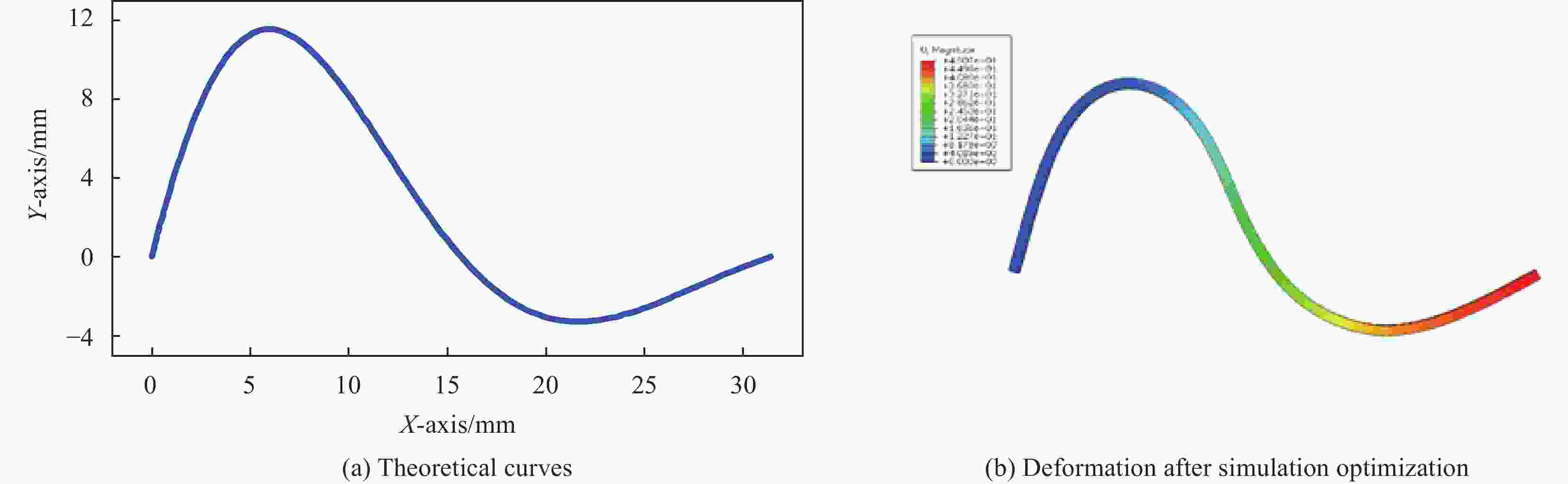
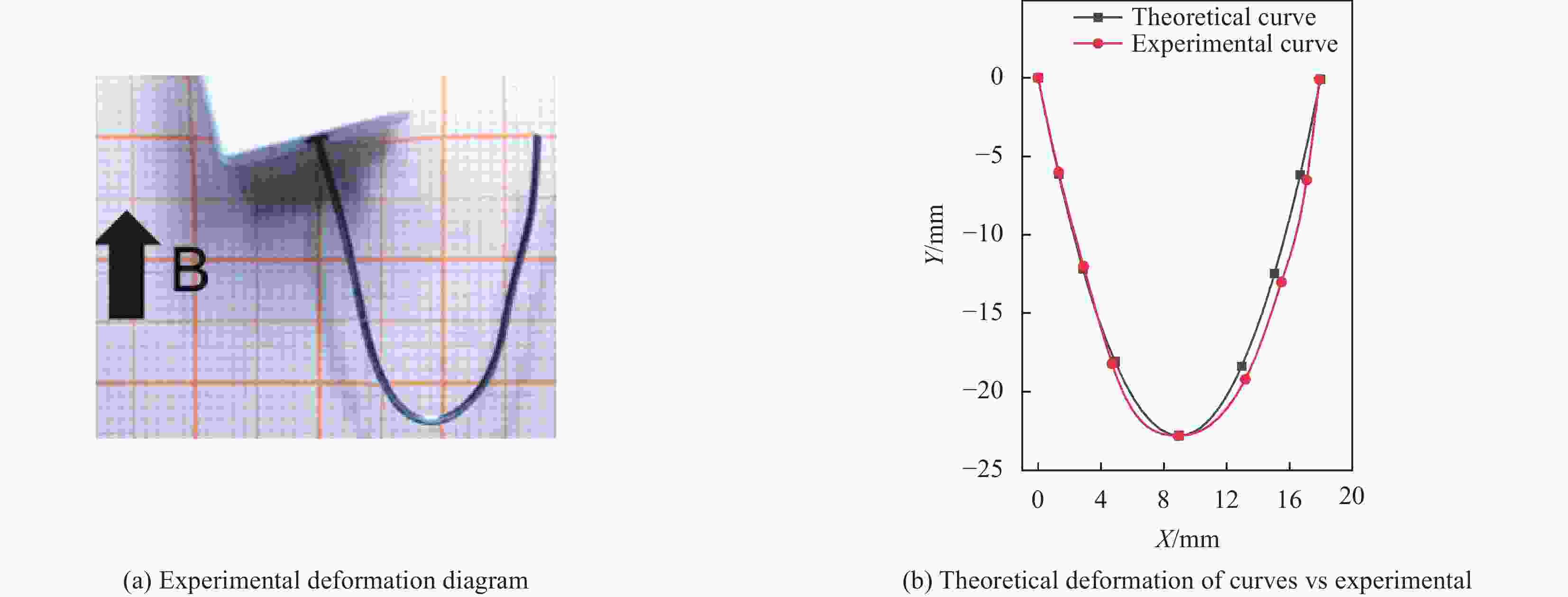
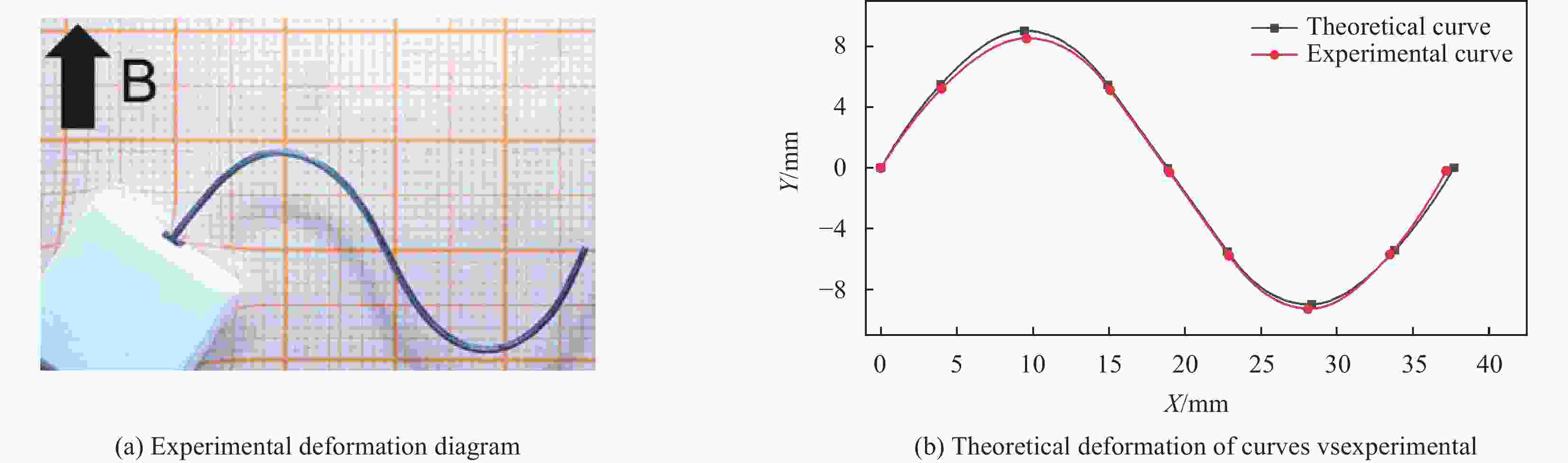
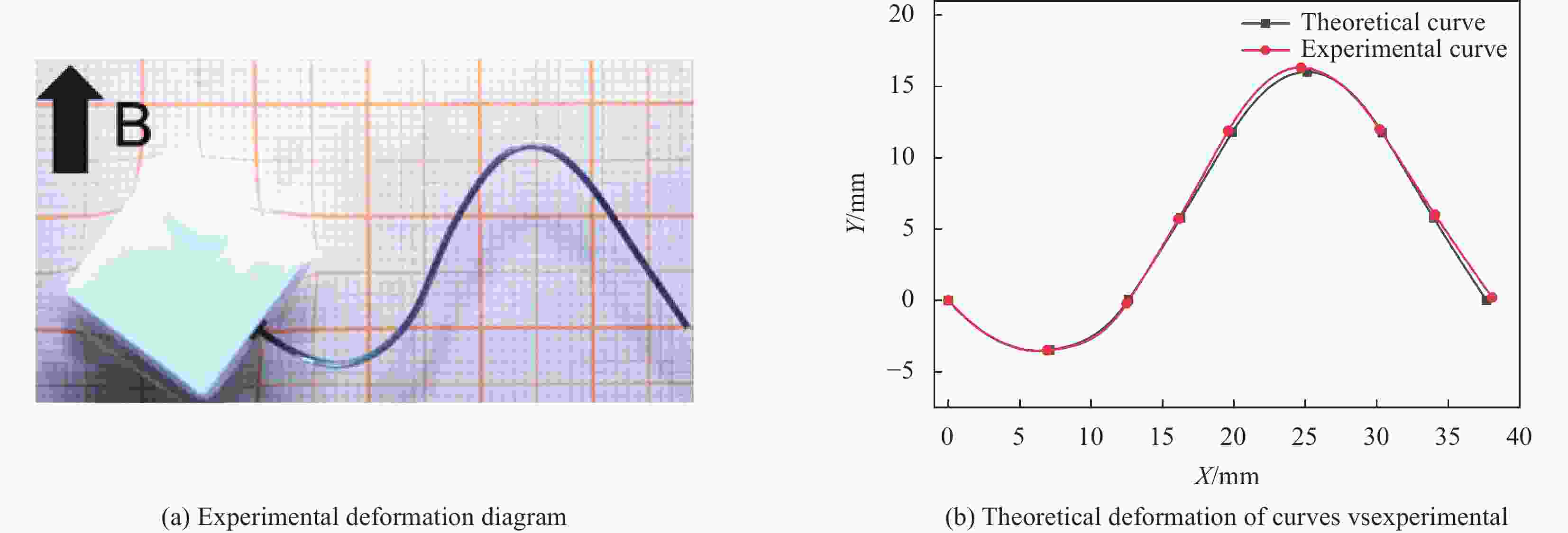
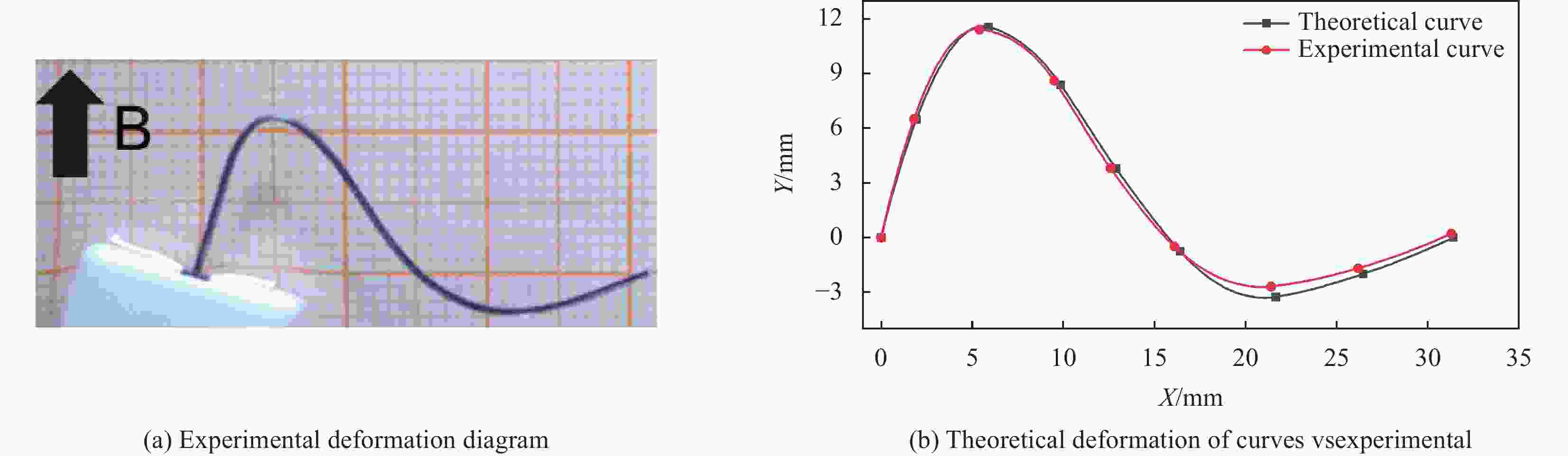
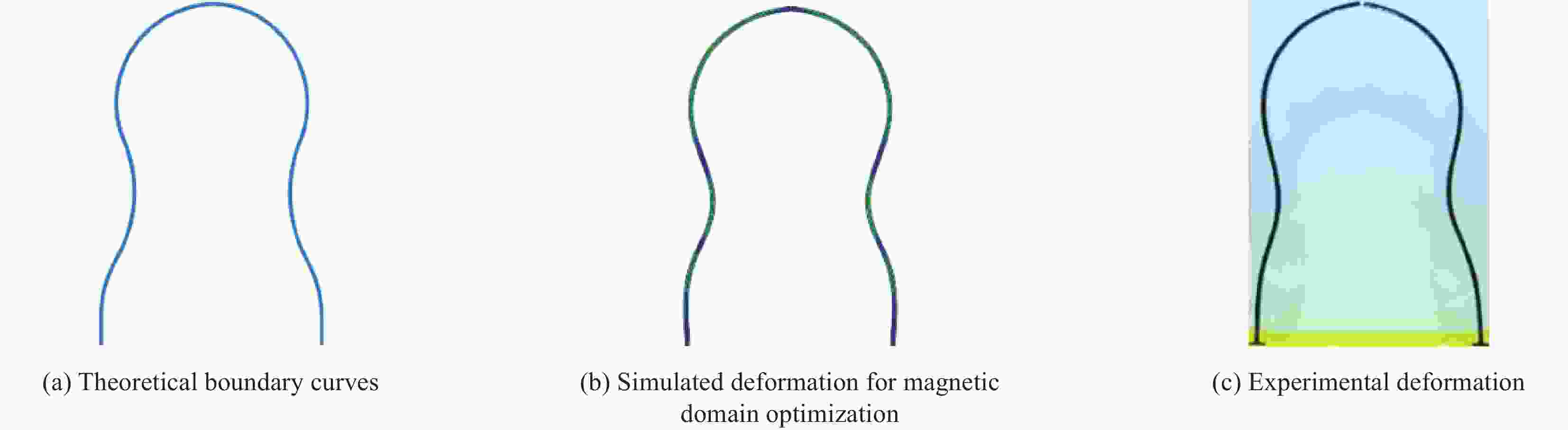
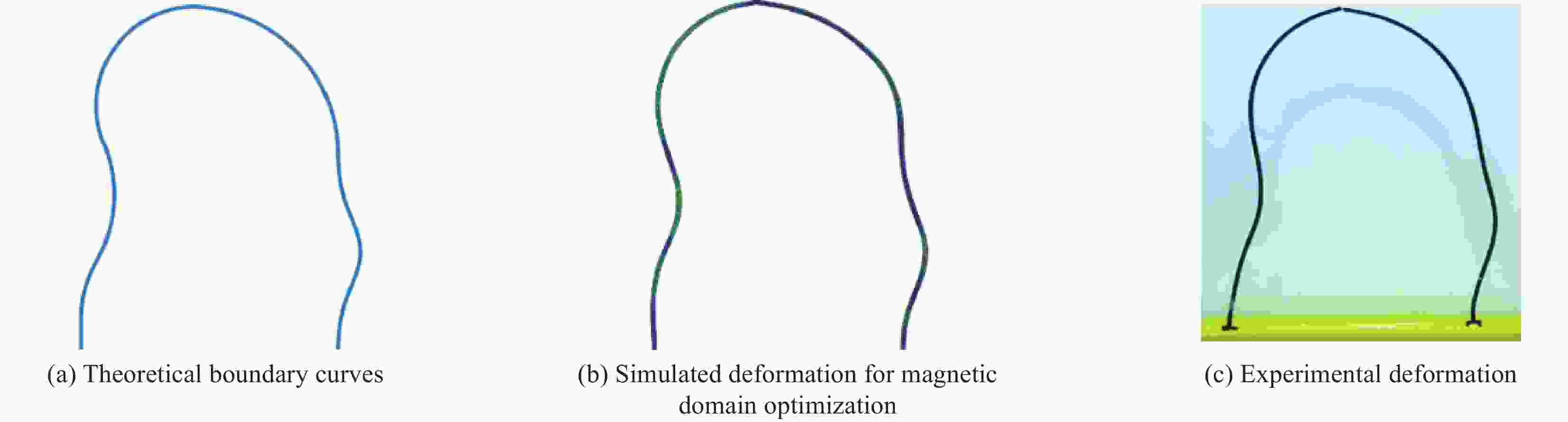
摘要: 硬磁软材料是一种新型的磁驱动复合材料,其中硬磁软连续体具有响应快、变形大、生物安全性好的特点,在生物医疗,仿生,软体触手等领域获得了广泛的关注。然而,现有的硬磁软连续体通过脉冲磁场磁化,磁畴模式单一,难以满足复杂的变形需求,此外如何解决硬磁软连续体在复杂变形下的磁畴优化设计问题也是当前的重要挑战。针对该问题,本文开发了基于二氧化铬的硬磁软连续体,通过激光直写实现了复杂磁畴模式的可重构编程。而后针对不同变形需求的磁畴分段设计问题,对尺寸大小、磁粉含量和磁畴方向进行优化设计。最后针对多种变形需求进行磁畴的优化设计并通过实验进行验证,同时进行功能化展示。Abstract: Hard magnetic soft materials are a new type of magnetically driven composite materials, in which the hard magnetic soft continuum is characterized by fast response, large deformation, and good biosafety, and has gained wide attention in the fields of biomedicine, bionics, and soft body tentacles. However, the existing hard magnetic soft continuum is magnetized by pulsed magnetic field with a single magnetic domain mode, which is difficult to meet the demand of complex deformation, in addition, how to solve the problem of optimizing the design of magnetic domains of hard magnetic soft continuum under the complex deformation is also an important challenge nowadays. In order to address this problem, this paper developed a hard magnetic soft continuum based on chromium dioxide, and realized the reconfigurable programming of complex magnetic domain patterns through laser direct writing. Then, for the design issues of magnetic domain according to different deformation requirements, optimization design was carried out on dimensions, magnetic powder content, and magnetic domain orientation. Finally, the optimized design of magnetic domains for various deformation requirements was verified by experiments and demonstrated functionally.
-
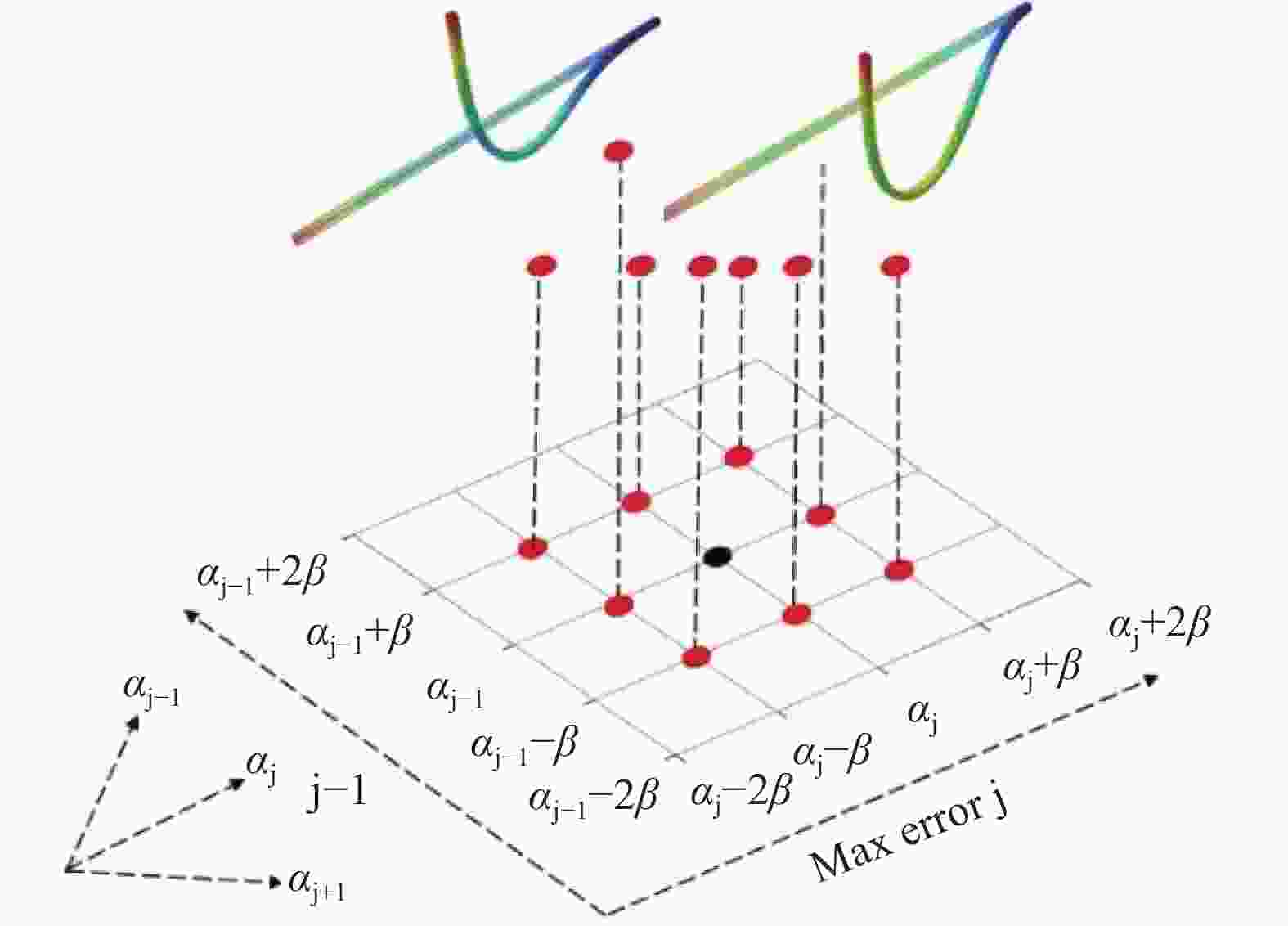
表 1 磁畴优化算法
Table 1. Magnetic Domain Optimization Algorithm
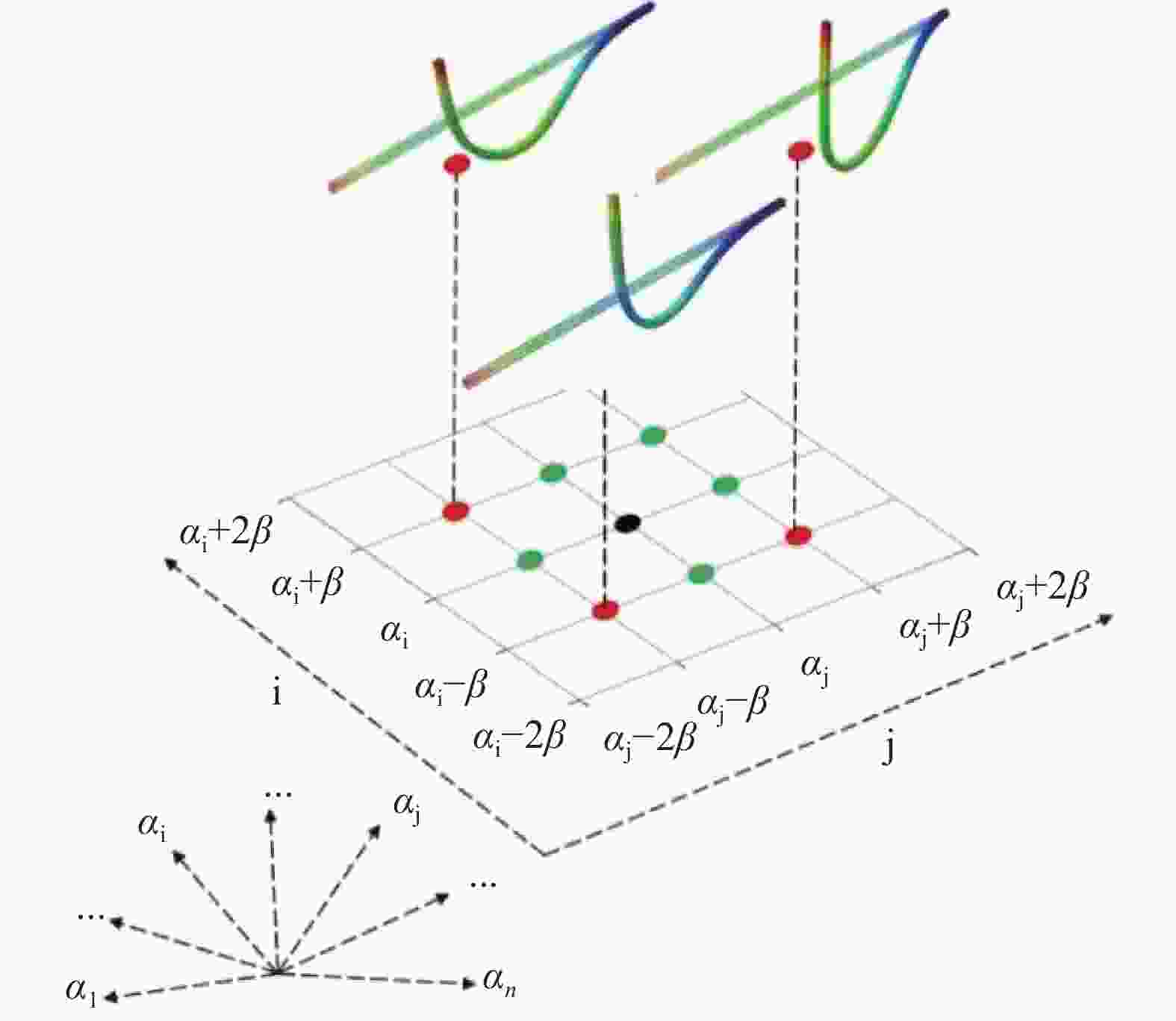
A Random optimization algorithm combining neighborhood optimization with adaptive step size: Input: Target curve
Output: Optimal magnetic domain direction parameters for fitting the corresponding target curve of hard magnetic soft continuum
1: Divide the target curve according to the length of the finite element mesh, so that the target curve nodes correspond one-to-one with the corresponding finite element nodes;
2: Set a marker for the number of repeated iterations, Rt=0;
3: Randomly initialize the direction of magnetic domains $ \left({\alpha }_{1},{\alpha }_{2},\dots {\alpha }_{n}\right) $ Generate 30 samples;
4: if Rt < 3 do
5: Perform finite element simulation;
6: Calculate the average node error D between each deformed sample and the theoretical curve;
Obtain the contemporary optimal solution $ {D}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{t}} $, and compare the sizes of $ {D}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{t}-1} $ and $ {D}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{t}} $;
7: if $ {D}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{t}} < {D}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{t}-1} $ do
8: Use random optimization algorithm, Rt =0;
Update iterative magnetic domain step size $ \beta =4\mathrm{*}{D}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{t}} $;
Update the current optimal magnetic domain direction parameter group $ \left({\alpha }_{1},{\alpha }_{2},\dots {\alpha }_{\mathrm{n}}\right) $;
Update magnetic domain direction parameters, $ {\alpha }_{\mathrm{i}}^{\mathrm{t}+1}={\alpha }_{{\mathrm{o}\mathrm{p}\mathrm{t}}_{\mathrm{i}}}+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}\left(-\beta ,0,\beta \right) $;
Generate 30 new samples;
end
9: if $ {D}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{t}-1} < {D}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{t}} $ do
10: Use neighborhood optimization algorithm, Rt = Rt +1;
Update iterative magnetic domain step size $ \beta =4\mathrm{*}{D}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{t}-1} $;
Calculate the average node error $ ({d}_{1},{d}_{2},\dots ,{d}_{\mathrm{n}}) $ for each segment of the sample corresponding to$ {D}_{\mathrm{m}\mathrm{i}\mathrm{n}}^{\mathrm{t}-1} $;
Sort the error segments in descending order, and select the segment j in the Rt position;
Update magnetic domain direction parameters,$ {\alpha }_{\mathrm{i}}^{\mathrm{t}+1}={\alpha }_{{\mathrm{o}\mathrm{p}\mathrm{t}}_{\mathrm{i}}}+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\left(-\beta ,0,\beta \right) $,$ i=j-1,j,j+1 $; Generate new samples;
end
11: end
12:Output the current optimal magnetic domain direction parameter set $ \left({\alpha }_{{\mathrm{o}\mathrm{p}\mathrm{t}}_{1}},{\alpha }_{{\mathrm{o}\mathrm{p}\mathrm{t}}_{2}},\dots {\alpha }_{{\mathrm{o}\mathrm{p}\mathrm{t}}_{\mathrm{n}}}\right) $表 2 不同函数构型的分段磁化方向和分段长度
Table 2. Segmented magnetization directions and segment lengths for different functional configurations
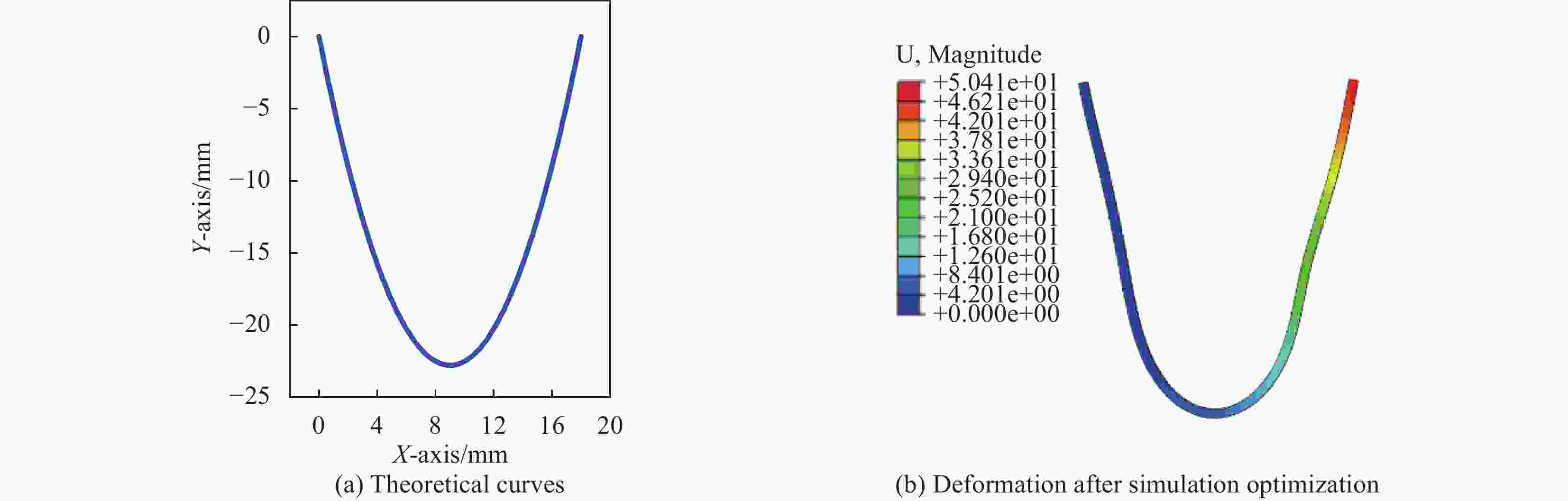
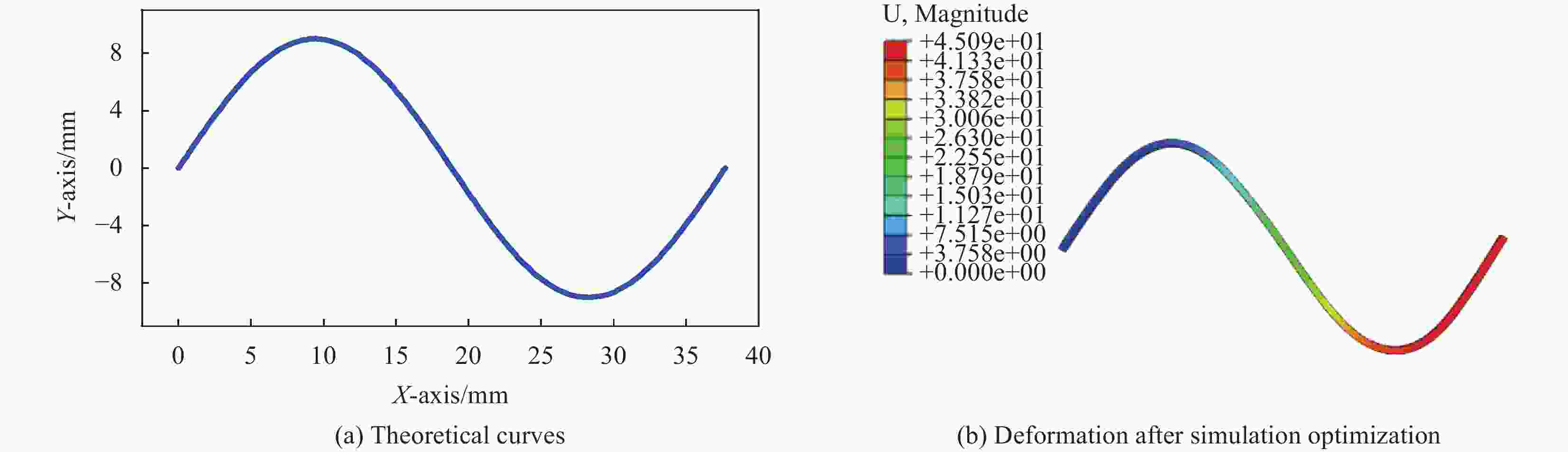
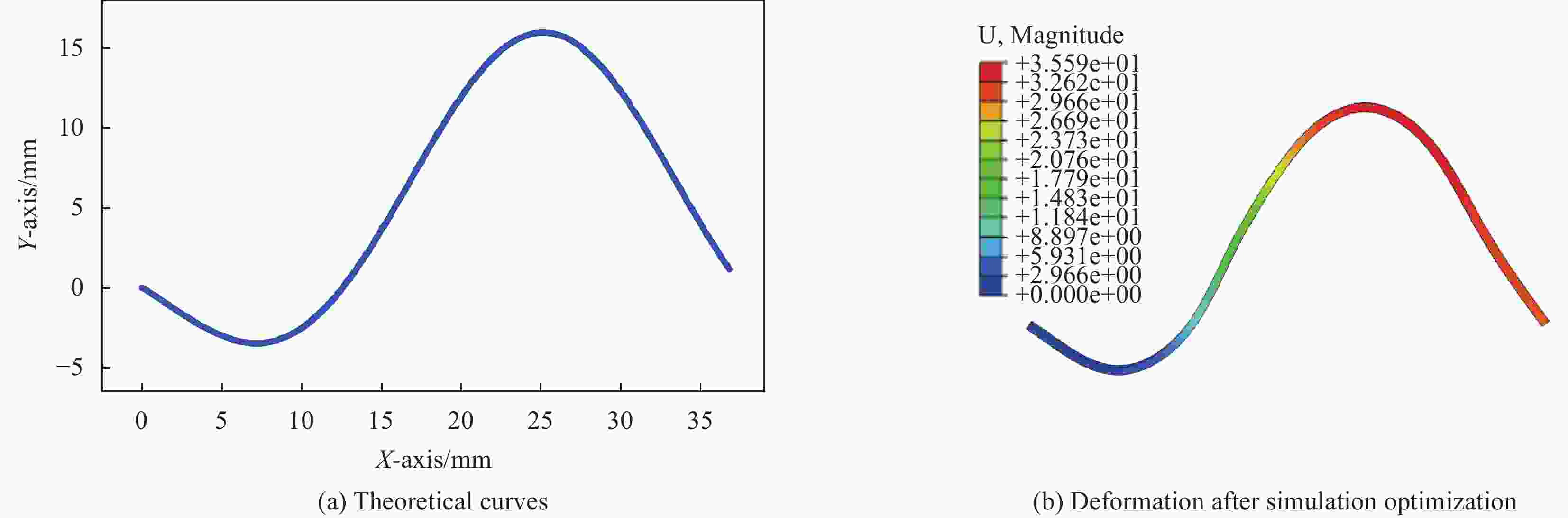
Catenary function type Magnetic domain direction/(°) 158 168 183 185 2 -16 28 6 fractional length/mm 6.3 6.3 6.3 6.4 6.4 6.3 6.3 6.3 sin function type Magnetic domain direction/(°) 31 9 173 147 154 170 -22 45 fractional length/mm 6.7 6.7 6.8 6.8 6.8 6.8 6.7 6.7 sinc function type Magnetic domain direction/(°) 172 30 9 30 6 170 164 141 fractional length /mm 8 6.8 6.8 7 7 7 7 6.9 Damping function type Magnetic domain direction/(°) 7 -20 177 186 163 119 51 53 fractional length/mm 6.7 6.8 5.6 5.6 5.6 5.7 5.2 5.2 表 3 对称结构物体左侧的分段磁化方向和分段长度
Table 3. Direction of segment magnetization and segment length on the left side of a symmetrically structured object
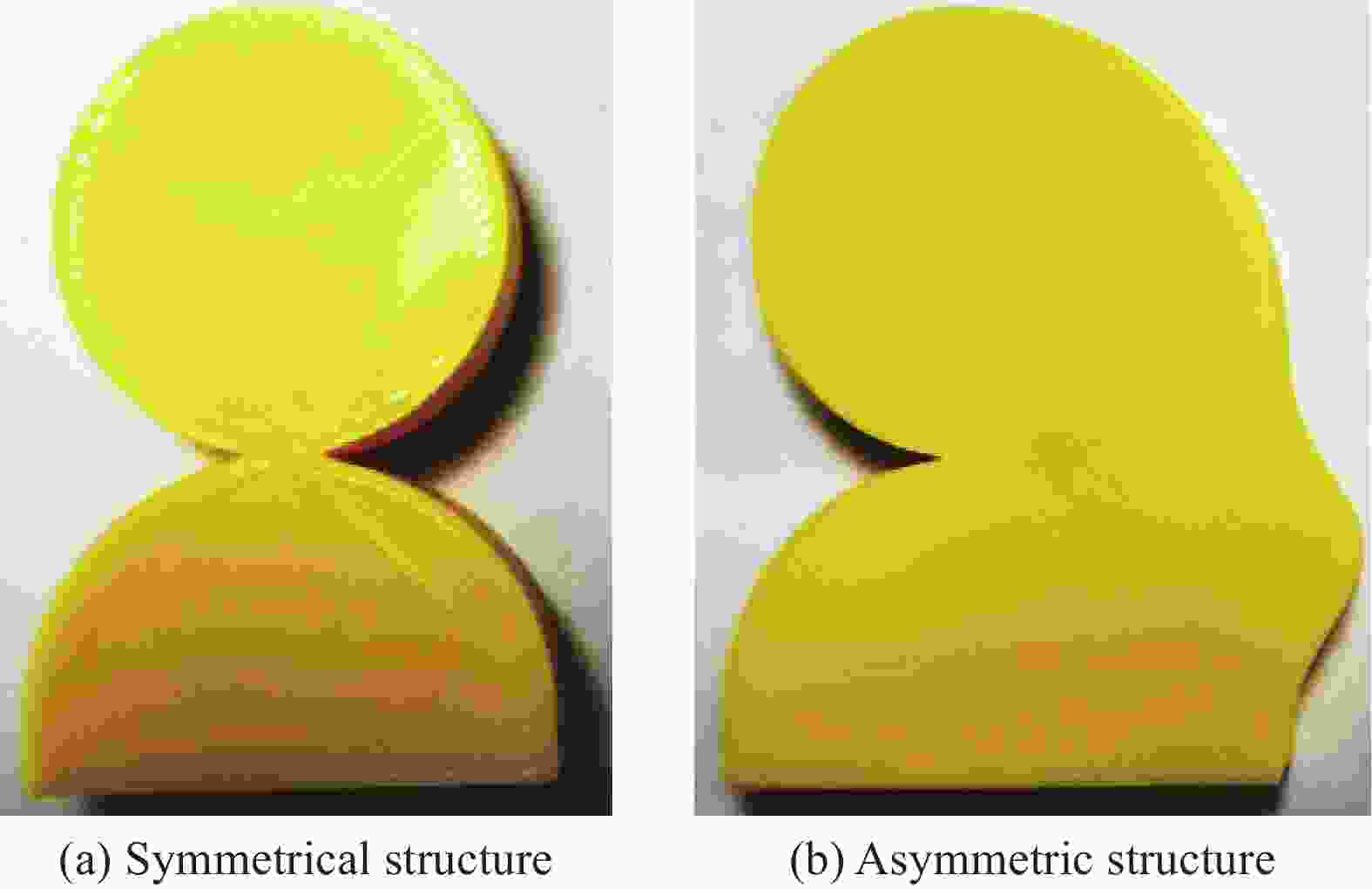
Magnetic domain direction/(°) −27 −6 13 70 17 −37 −39 −17 22 15 54 54 100 Fractional length/mm 4.2 4.2 4.2 4.3 4.3 4.5 4.5 4.6 4.1 4.1 4.1 4.1 4.1 表 4 非对称结构物体右侧的分段磁化方向和分段长度
Table 4. Segmented magnetization directions and segment lengths on the right side of an asymmetrically structured object
Magnetic domain direction/(°) −4 51 45 −63 −25 0 21 −12 −22 55 48 −70 Fractional length/mm 4.7 4.7 4.8 4.7 4.7 4.8 5.1 5.1 5.1 5.1 5.1 5.1 -
[1] 邓攀, 吴志, 孙纪烨, 等. 4D打印磁响应形状记忆环氧树脂基复合材料制备与性能[J]. 复合材料学报, 2024, 41(3): 1226-1234.DENG Pan, WU Zhi, SUN Ji ye, et al. Preparation and properties of 4D printed magnetoresponsive shape memory epoxy resin-based composites[J]. Acta Materiae Compositae Sinica, 2024, 41(3): 1226-1234. (in chinese [2] 圣宇, 欧兴成, 黄嘉琪, 等. 3D打印磁控柔性抓手[J]. 复合材料学报, 2023, 40(05): 2670-2679.SHENG Yu, OU Xing Cheng, HUNAG Jia Qi, et al. 3D printing magnetic soft gripper[J]. Acta Materiae Compositae Sinica. 2023, 40(05): 2670-2679(in chinese [3] PITTIGLIO G, OREKHOV A L, DA VEIGA T, et al. Closed loop static control of multi-magnet soft continuum robots[J]. IEEE Robotics and Automation Letters, 2023. [4] WANG L, GUO C F, ZHAO X. Magnetic soft continuum robots with contact forces[J]. Extreme Mechanics Letters, 2022, 51: 101604. doi: 10.1016/j.eml.2022.101604 [5] LIN D, JIAO N, WANG Z, et al. A magnetic continuum robot with multi-mode control using opposite-magnetized magnets[J]. IEEE Robotics and Automation Letters, 2021, 6(2): 2485-2492. doi: 10.1109/LRA.2021.3061376 [6] WANG Z, WENG D, LI Z, et al. A Magnetic-Controlled Flexible Continuum Robot with Different Deformation Modes for Vascular Interventional Navigation Surgery; proceedings of the Actuators, F, 2023 [C]. MDPI. [7] LLOYD P, KOSZOWSKA Z, DI LECCE M, et al. Feasibility of fiber reinforcement within magnetically actuated soft continuum robots[J]. Frontiers in Robotics and AI, 2021, 8: 715662. doi: 10.3389/frobt.2021.715662 [8] KIM Y, PARADA G A, LIU S, et al. Ferromagnetic soft continuum robots[J]. Science robotics, 2019, 4(33): eaax7329. doi: 10.1126/scirobotics.aax7329 [9] LIU D, LIU X, CHEN Z, et al. Magnetically driven soft continuum microrobot for intravascular operations in microscale[J]. Cyborg and Bionic Systems, 2022, 2022: 9850832-9850840. [10] NI Y, SUN Y, ZHANG H, et al. Data-Driven Navigation of Ferromagnetic Soft Continuum Robots Based on Machine Learning[J]. Advanced Intelligent Systems, 2023, 5(2): 2200167. doi: 10.1002/aisy.202200167 [11] LUM G Z, YE Z, DONG X, et al. Shape-programmable magnetic soft matter[J]. Proceedings of the National Academy of Sciences, 2016, 113(41): E6007-E6015. [12] CAO X, XUAN S, SUN S, et al. 3D printing magnetic actuators for biomimetic applications[J]. ACS Applied Materials & Interfaces, 2021, 13(25): 30127-30136. [13] WANG L, ZHENG D, HARKER P, et al. Evolutionary design of magnetic soft continuum robots[J]. Proceedings of the National Academy of Sciences, 2021, 118(21): e2021922118. doi: 10.1073/pnas.2021922118 [14] SUN Y, ZHANG H, ZHAO Y, et al. Locally Reprogrammable Magnetic Micropillars with On Demand Reconfiguration and Multi Functionality[J]. Advanced Materials Technologies, 2023, 8(22): 2300773. doi: 10.1002/admt.202300773 [15] LI M, KIM T, GUIDETTI G, et al. Optomechanically actuated microcilia for locally reconfigurable surfaces[J]. Advanced Materials, 2020, 32(40): 2004147. doi: 10.1002/adma.202004147 [16] ALAPAN Y, KARACAKOL A C, GUZELHAN S N, et al. Reprogrammable shape morphing of magnetic soft machines[J]. Science advances, 2020, 6(38): eabc6414. doi: 10.1126/sciadv.abc6414 [17] MELNIKOV N, PARADEZHENKO G, RESER B. Magnetic susceptibility in metals above the Curie temperature[J]. Journal of Magnetism and Magnetic Materials, 2021, 525: 167559. doi: 10.1016/j.jmmm.2020.167559 [18] BASTOW T J, HILL A J, NAIRN K M, et al. Cr 53 solid-state nuclear magnetic resonance: New observations and comprehensive correlations as a probe of valence and magnetic states[J]. Physical Review Materials, 2023, 7(11): 114410. doi: 10.1103/PhysRevMaterials.7.114410 [19] DADGAR-RAD F, HOSSAIN M. Large viscoelastic deformation of hard-magnetic soft beams[J]. Extreme Mechanics Letters, 2022, 54: 101773. doi: 10.1016/j.eml.2022.101773 [20] DADGAR-RAD F, HOSSAIN M. Finite deformation analysis of hard-magnetic soft materials based on micropolar continuum theory[J]. International Journal of Solids and Structures, 2022, 251: 111747. doi: 10.1016/j.ijsolstr.2022.111747 [21] 彭帆, 马维力. 硬磁软材料的磁致变形数值研究[J]. 复合材料学报, 2024: 1-8,DOI: 10.13801/j.cnki.fhclxb.20240004.001.PENG Fan, MA Wei Li, et al. Numerical research on magnetostrictive deformation of hard magnetic soft materials[J], 2024: 1-8, DOI: 10.13801/j.cnki.fhclxb.20240004.001.(in chinese). [22] WANG L, KIM Y, GUO C F, et al. Hard-magnetic elastica[J]. Journal of the Mechanics and Physics of Solids, 2020, 142: 104045. doi: 10.1016/j.jmps.2020.104045 [23] GARCIA-GONZALEZ D, HOSSAIN M. Microstructural modelling of hard-magnetic soft materials: Dipole–dipole interactions versus Zeeman effect[J]. Extreme Mechanics Letters, 2021, 48: 101382. doi: 10.1016/j.eml.2021.101382 [24] ZHAO R, KIM Y, CHESTER S A, et al. Mechanics of hard-magnetic soft materials[J]. Journal of the Mechanics and Physics of Solids, 2019, 124: 244-263. doi: 10.1016/j.jmps.2018.10.008 [25] NARAYANAN P, PRAMANIK R, AROCKIARAJAN A. Micromechanics-based constitutive modeling of hard-magnetic soft materials[J]. Mechanics of Materials, 2023, 184: 104722. doi: 10.1016/j.mechmat.2023.104722 -

 点击查看大图
点击查看大图
计量
- 文章访问数: 65
- HTML全文浏览量: 36
- 被引次数: 0




 下载:
下载: