Prediction of ultimate axial strain of FRP-confined concrete based on gene expression programming
-
摘要: 纤维增强树脂复合材料(FRP)以其质量轻、强度高、耐腐蚀和施工方便等优势被广泛应用于混凝土结构性能提升和受损构件加固中。FRP约束混凝土的极限条件是选择FRP种类、选择FRP厚度及确定包裹层数等必须要考虑的因素，现有极限应力模型的预测结果能够较好反地映真实情况，而现有极限轴向应变模型的预测精度偏低，故本文对极限轴向应变进行了研究。由于影响FRP约束混凝土极限轴向应变的因素较多，许多研究人员提出的模型在输入参数的选择上存在较大差异，故本文在通过基因表达式编程建立极限轴向应变模型的同时还探讨了不同输入形式对模型预测精度的影响。采用决定系数及平均绝对误差等5种统计指标对模型预测结果进行评价，并将其与现有模型进行对比分析。研究结果表明：原始数据和新数据组合的输入形式对应的模型具有最高的预测精度，因此在模型输入参数的选择上不能仅考虑原始数据或者新数据；与其他研究人员所提模型相比，本文所提模型预测精度更高，其决定系数为0.893，平均绝对误差等指标均在0.35以下。
-
关键词:
- 基因表达式编程 /
- 纤维增强树脂复合材料 /
- 混凝土柱 /
- FRP约束混凝土 /
- 极限轴向应变
Abstract: Fiber reinforced polymer (FRP) is widely used in enhancing the performance of concrete structures and strengthening damaged components due to its advantages of light weight, high strength, corrosion resistance and convenient construction. The ultimate conditions of FRP-confined concrete are the important factors that must be considered in the selection of FRP types, FRP thickness and the number of covering layer. The prediction results of the existing ultimate stress model can better reflect the real situation, while the prediction accuracy of the existing ultimate axial strain model is low, so the ultimate axial strain was studied. Since there are many factors that affect the ultimate axial strain of FRP-confined concrete, the models proposed by many researchers have large differences in the choice of input parameters. Therefore, the influence of different input forms on the prediction accuracy of ultimate axial strain model was discussed while the ultimate axial strain model was established by gene expression programming. Five statistical indicators such as coefficient of determination and mean absolute error were used to evaluate the prediction results of model, which was compared with the existing prediction models. The research results show that the model corresponding to the input form of the combination of original data and new data has the highest prediction accuracy, so the selection of model input parameters should not only consider the original data or new data. Compared with the models proposed by other researchers, the prediction accuracy of the model proposed in this article is the highest. The coefficient of determination is 0.893, and the mean absolute error and other indicators are all below 0.35. -
图 1 基因表达式编程(GEP)语言示意图
Figure 1. Diagram of gene expression programming (GEP) language
d0—Ultimate axial strain of unconfined concrete; d1—Stiffness ratio; d2—Strain ratio; d3—Ultimate axial strain of FRP-confined concrete; 3Rt—Function symbol; c2—Constant
图 2 FRP约束混凝土极限轴向应变模型最优参数确定
Figure 2. Determination of optimal parameters of ultimate axial strain model of FRP-confined concrete
图 3 不同输入形式下的FRP约束混凝土极限轴向应变模型的预测结果与试验结果对比
Figure 3. Comparison between experimental and prediction results of ultimate axial strain models of FRP-confined concrete under different input forms
图 4 模型C (GEP模型)的表达式树(Sub-ET)
Figure 4. Expression trees (Sub-ET) of model C (GEP model)
Inv—Inverse; c0, c3, c7—Constant
图 5 FRP约束混凝土GEP模型的参数敏感性分析结果
Figure 5. Parameter sensitivity analysis results of GEP model for FRP-confined concrete
图 6 各FRP约束混凝土极限轴向应变模型的预测结果与试验结果对比
Figure 6. Comparison between experimental and prediction results of ultimate axial strain models of FRP-confined concrete
表 1 FRP约束混凝土的极限轴向应变模型
Table 1. Ultimate axial strain models of FRP-confined concrete
Model and year Ultimate axial strain Ahmad et al [23]
(2020)${\varepsilon _{ { { {\rm{cu} } } } } } = (1.85 + 7.46\rho _{ {\varepsilon } }^{ { {1} }{ {.171} } }\rho _{ {{\rm{k}}} }^{ { {0} }{ {.71} } }){\varepsilon _{ { { {\rm{co} } } } } }$ Yu et al[24]
(2011)${\varepsilon _{ { { {\rm{cu} } } } } } = 0.0033 + 0.6{\left( \dfrac{ { {E_l} } }{ {f_{ { {{\rm{co}}} } }^{ {'} } } }\right)^{0.8} }{({\varepsilon _{ { { {\rm{h} },{\rm{rup} } } } } })^{1.45} }$ Benzaid et al [25]
(2010)${\varepsilon _{ { {{\rm{cu}}} } } } = 2{\varepsilon _{ { {{\rm{co}}} } } } + 7.6\dfrac{ { {f_l} } }{ {f_{ { {{\rm{co}}} } }^{ {'} } } }{\varepsilon _{ { {{\rm{co}}} } } }$ Teng et al [26]
(2009)${\varepsilon _{ { {{\rm{cu}}} } } } = 1.75{\varepsilon _{ { {{\rm{co}}} } } } + 6.5{\varepsilon _{ { {{\rm{co}}} } } }\rho _{ {\varepsilon } }^{ { {1} }{ {.45} } }\rho _{ {{\rm{k}}} }^{ { {0} }{ {.8} } }$ Al-Tersawy et al [27] (2007) ${\varepsilon _{ { {{\rm{cu}}} } } } = 2{\varepsilon _{ { {{\rm{co}}} } } } + 8.16{\left( \dfrac{ { {f_l} } }{ {f_{ { {{\rm{co}}} } }^{ {'} } } }\right)^{0.34} }{\varepsilon _{ { {{\rm{co}}} } } }$ Ilki et al [28]
(2004)${\varepsilon _{ { {{\rm{cu}}} } } } = {\varepsilon _{ { {{\rm{co}}} } } } + 20{\left( \frac{ { {f_l} } }{ {f_{ { {{\rm{co}}} } }^{ {'} } } }\right)^{0.5} }{\varepsilon _{ { {{\rm{co}}} } } }$ Xiao et al[29]
(2000)${\varepsilon _{ { { {\rm{cu} } } } } } = \dfrac{ { {\varepsilon _{ { { {\rm{h} },{\rm{rup} } } } } } - 0.0005} }{ {7{ {\left( \dfrac{ { {E_l} } }{ {f_{ { {{\rm{co}}} } }^{ {'} } } }\right)}^{ - 0.8} } } }$ Samaan et al [30]
(1998)${\varepsilon _{ { {{\rm{cu}}} } } } = \dfrac{ {f_{ { {{\rm{cc}}} } }^{ {'} } - 0.872f_{ { {{\rm{co}}} } }^{ {'} } - 0.371{f_l} - 6.258} }{ {245.61f{ {_{ { {{\rm{co}}} } }^{ {'} } }^{0.2} } + 1.3456\dfrac{ { {E_{ { {{\rm{FRP}}} } } }T} }{D} } }$ Mander et al [31]
(1988)${\varepsilon _{ { { {\rm{cu} } } } } } = \left( 1 + 5\left( \dfrac{ {f_{ { { {\rm{cc} } } } }^{ {'} } } }{ {f_{ { {{\rm{co}}} } }^{ {'} } } } - 1\right)\right){\varepsilon _{ { { {\rm{co} } } } } }$ Notes:$f_{ { {{\rm{cc}}} } }'$—Peak strength of FRP-confined concrete; ${\varepsilon _{ { {{\rm{cu}}} } } }$—Ultimate axial strain of FRP-confined concrete; $f_{ { {{\rm{co}}} } }^{ {'} }$—Peak strength of unconfined concrete; ${\varepsilon _{ { {{\rm{co}}} } } }$—Peak strain of unconfined concrete; $D$—Diameter of the concrete core; $T$—Total thickness of the FRP jacket; ${E_{ { {{\rm{FRP}}} } } }$—Elastic modulus of the FRP jacket; ${\varepsilon _{ { {{\rm{h,rup}}} } } }$—Hoop rapture strain of the FRP jacket; $ {f_l} $—Confining stress; ${\rho _{ {{\rm{k}}} } }$—Stiffness ratio; $ {\rho _{{\varepsilon }}} $—Strain ratio; El—Restraint stiffness; See Table 2 for variable units. 
下载: 导出CSV
表 2 FRP约束普通混凝土圆柱体试验数据的统计参数
Table 2. Statistical parameters of test data of FRP-confined normal concrete cylinder
Parameter Min Max Median Average Standard
deviation$D$/mm 100 200 152 146.080 17.816 $H$/mm 200 788 305 314.106 94.341 $f_{ { {{\rm{co}}} } }^{ {'} }$/MPa 26.2 55.2 42 40.577 7.100 ${\varepsilon _{ { {{\rm{co}}} } } }$/% 0.16 0.42 0.239 0.249 0.047 ${E_{\rm{c}}}$/GPa 24.21 35.14 29.77 29.692 2.731 $T$/mm 0.11 5.21 0.495 0.794 0.882 ${E_{ { {{\rm{FRP}}} } } }$/GPa 13.6 629.6 105 154.604 113.36 ${\varepsilon _{ { {{\rm{h}},{\rm{rup}}} } } }$/% 0.19 3.09 1.08 1.208 0.504 ${\rho _{ {{\rm{k}}} } }$ 2.555 38.114 9.324 10.683 7.153 $ {\rho _{{\varepsilon }}} $ 0.010 0.369 0.049 6.430 5.659 $ {f_l} $/MPa 0.905 13.435 4.333 4.922 2.154 ${\varepsilon _{ { {{\rm{cu}}} } } }$/% 0.4 5.55 1.61 1.830 1.005 Notes: H—Height of the concrete core; Ec—Elastic modulus of the concrete core.
下载: 导出CSV
表 3 FRP约束普通混凝土圆柱体试验数据的皮尔逊相关性分析结果
Table 3. Results of Pearson correlation analysis of test data of FRP-confined normal concrete cylinder
${\rho _{ {{\rm{k}}} } }$ $ {\rho _{{\varepsilon }}} $ $ {f_l} $ ${\varepsilon _{ { {{\rm{cu}}} } } }$ $D$ −0.223** −0.064 −0.017 −0.121 $H$ −0.041 −0.131 −0.108 −0.127 $f_{ { {{\rm{co}}} } }^{ {'} }$ −0.211** 0.039 0.136 −0.029 ${\varepsilon _{ { {{\rm{co}}} } } }$ −0.163* −0.181* −0.180* 0.236** ${E_{\rm{c}}}$ −0.198** 0.089 0.151 −0.003 $T$ 0.161* 0.356** 0.553** 0.297** ${E_{ { {{\rm{FRP}}} } } }$ 0.509** −0.544** −0.031 −0.165* ${\varepsilon _{ { {{\rm{h}},{\rm{rup}}} } } }$ −0.395** 0.926** 0.086 0.377** ${\rho _{ {{\rm{k}}} } }$ 1 −0.334** 0.669** 0.379** $ {\rho _{{\varepsilon }}} $ −0.334* 1 0.165* 0.301** $ {f_l} $ 0.669** 0.165* 1 0.653** ${\varepsilon _{ { {{\rm{cu}}} } } }$ 0.379** 0.301* 0.653** 1 Notes: **—Correlation is significant at the 0.01 level (2-tailed);
*—Correlation is significant at the 0.05 level (2-tailed).
下载: 导出CSV
表 4 FRP约束混凝土极限轴向应变模型的参数设置
Table 4. Parameters setting of ultimate axial strain model of FRP-confined concrete
Parameter types Setting Parameter types Setting Population
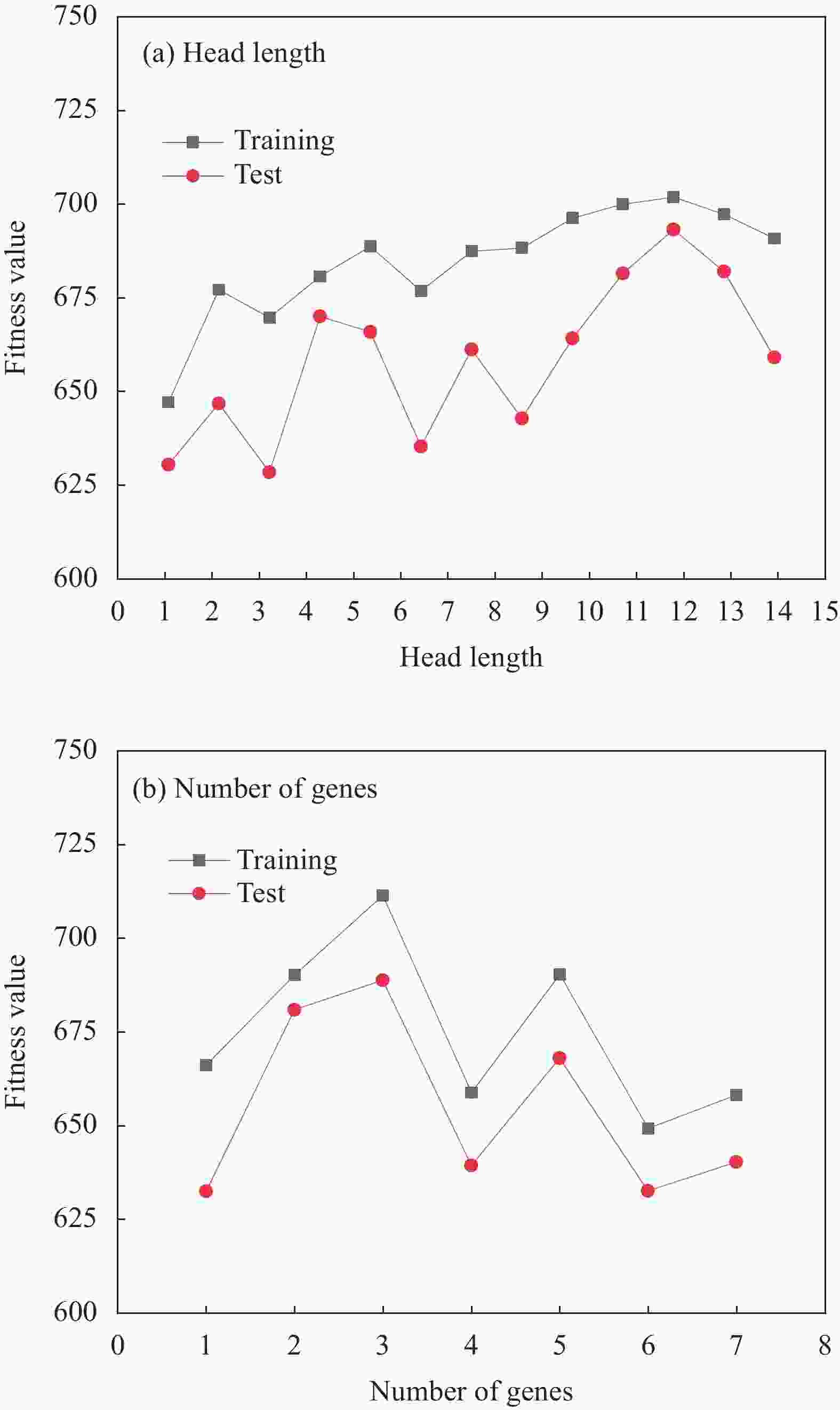
size50 Gene transposition rate 0.3 Head
length12 Gene recombination rate 0.3 Gene
number3 One-point recombination rate 0.4 Chromosome length 45 Two-point recombination rate 0.4 Connection function Addition (+) Insertion sequence transposition rate 0.3 Mutation
rate0.044 Root insertion sequence transposition rate 0.3
下载: 导出CSV
表 5 FRP约束混凝土极限轴向应变模型的输入形式
Table 5. Input informs of ultimate axial strain model of FRP-confined concrete
No. Model Ultimate axial strain ${\varepsilon _{ { {{\rm{cu}}} } } }$ 1 A ${\varepsilon _{ { {{\rm{cu}}} } } } = {f}(D,H,f_{ { {{\rm{co}}} } }^{ {'} },{\varepsilon _{ { {{\rm{co}}} } } },{E_{ {{\rm{c}}} } },T,{E_{ { {{\rm{FRP}}} } } },{\varepsilon _{ { {{\rm{h}},{\rm{rup}}} } } })$ 2 B ${\varepsilon _{ { {{\rm{cu}}} } } } = {f}({f_l},{\rho _{ {\varepsilon } } },{\rho _{ {{\rm{k}}} } })$ 3 C ${\varepsilon _{ { {{\rm{cu}}} } } } = {f}({\varepsilon _{ { {{\rm{co}}} } } },{\rho _{ {\varepsilon } } },{\rho _{ {{\rm{k}}} } })$ 4 D ${\varepsilon _{ { {{\rm{cu}}} } } } = {f}(f_{ { {{\rm{co}}} } }^{ {'} },{\varepsilon _{ { {{\rm{co}}} } } },{f_l})$ 5 E ${\varepsilon _{ { {{\rm{cu}}} } } } = {f}({\varepsilon _{ { {{\rm{co}}} } } },T,{E_{ { {{\rm{FRP}}} } } },{\varepsilon _{ { {{\rm{h}},{\rm{rup}}} } } },{f_l},{\rho _{ {\varepsilon } } },{\rho _{ {{\rm{k}}} } })$
下载: 导出CSV
表 6 不同输入形式下的FRP约束混凝土极限轴向应变模型的预测结果
Table 6. Prediction results of ultimate axial strain models of FRP-confined concrete under different input forms
Model $ {R^{\text{2}}} $ MAE RRSE RMSE MAPE A 0.487 0.414 0.721 0.682 0.257 B 0.561 0.533 0.841 0.796 0.299 C 0.893 0.228 0.334 0.316 0.160 D 0.705 0.362 0.543 0.514 0.260 E 0.740 0.543 0.762 0.721 0.353 Notes: R2—Determination coefficient; MAE—Mean absolute error; RRSE—Relative square root error; RMSE—Root mean square error; MAPE—Mean absolute percentage error.
下载: 导出CSV
表 7 FRP约束混凝土GEP模型的参数重要性分析结果
Table 7. Parameter importance analysis results of GEP model for FRP-confined concrete
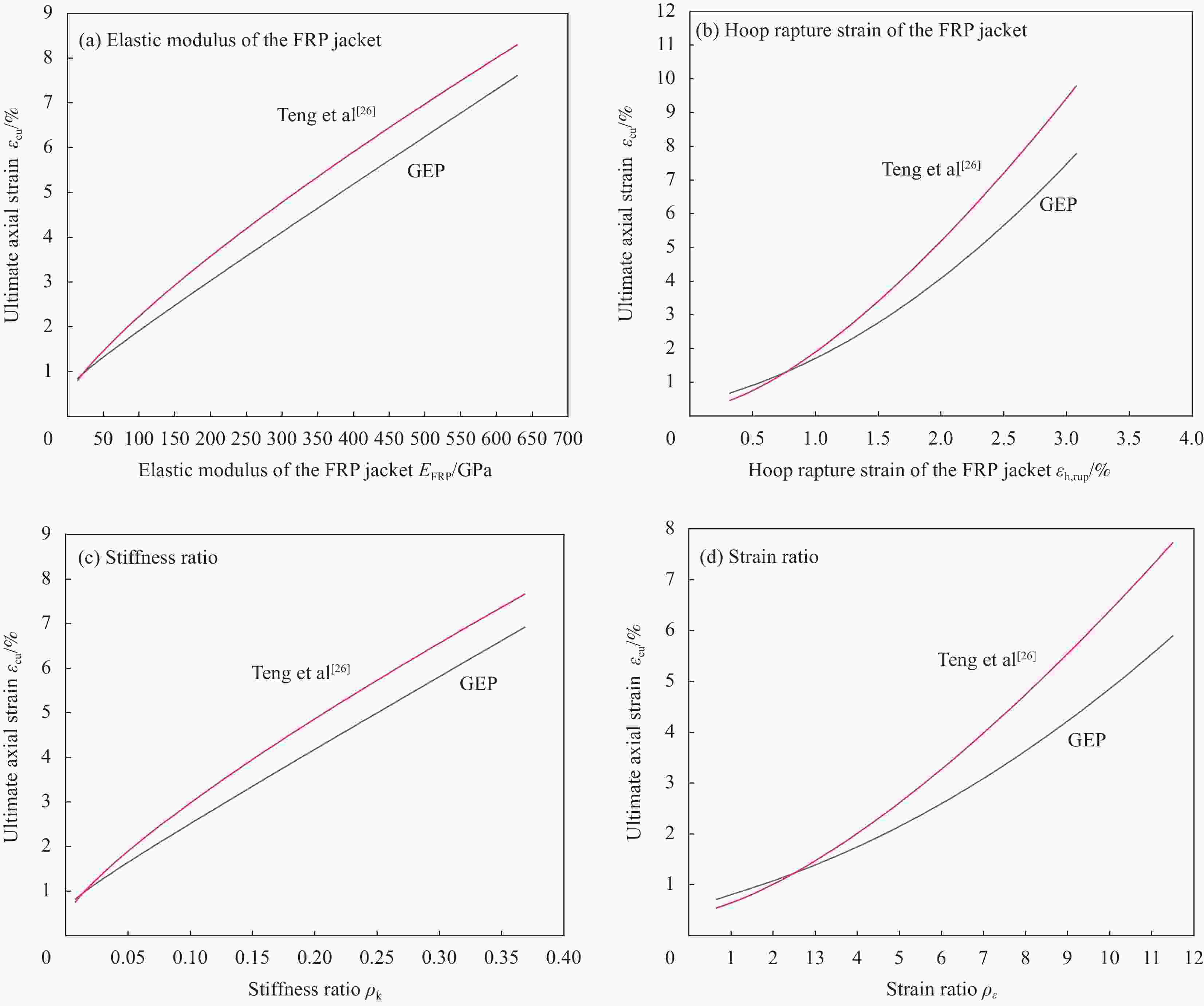
Model Parameter $ {R^{{2}}} $ Conclusion
GEPWithout ${\varepsilon _{ { {{\rm{co}}} } } }$ 0.496
${\rho _{ {{\rm{k}}} } } > {\rho _{ {\varepsilon } } } > {\varepsilon _{ { {{\rm{co}}} } } }$Without ${\rho _{ {{\rm{k}}} } }$ 0.112 Without $ {\rho _{{\varepsilon }}} $ 0.397 Without ${\varepsilon _{ { {{\rm{co}}} } } }$ 0.522 Teng et al [26] Without ${\rho _{ {{\rm{k}}} } }$ 0.118 ${\rho _{ {{\rm{k}}} } } > {\rho _{ {\varepsilon } } } > {\varepsilon _{ { {{\rm{co}}} } } }$ Without $ {\rho _{{\varepsilon }}} $ 0.245
下载: 导出CSV
表 8 各FRP约束混凝土极限轴向应变模型的预测结果
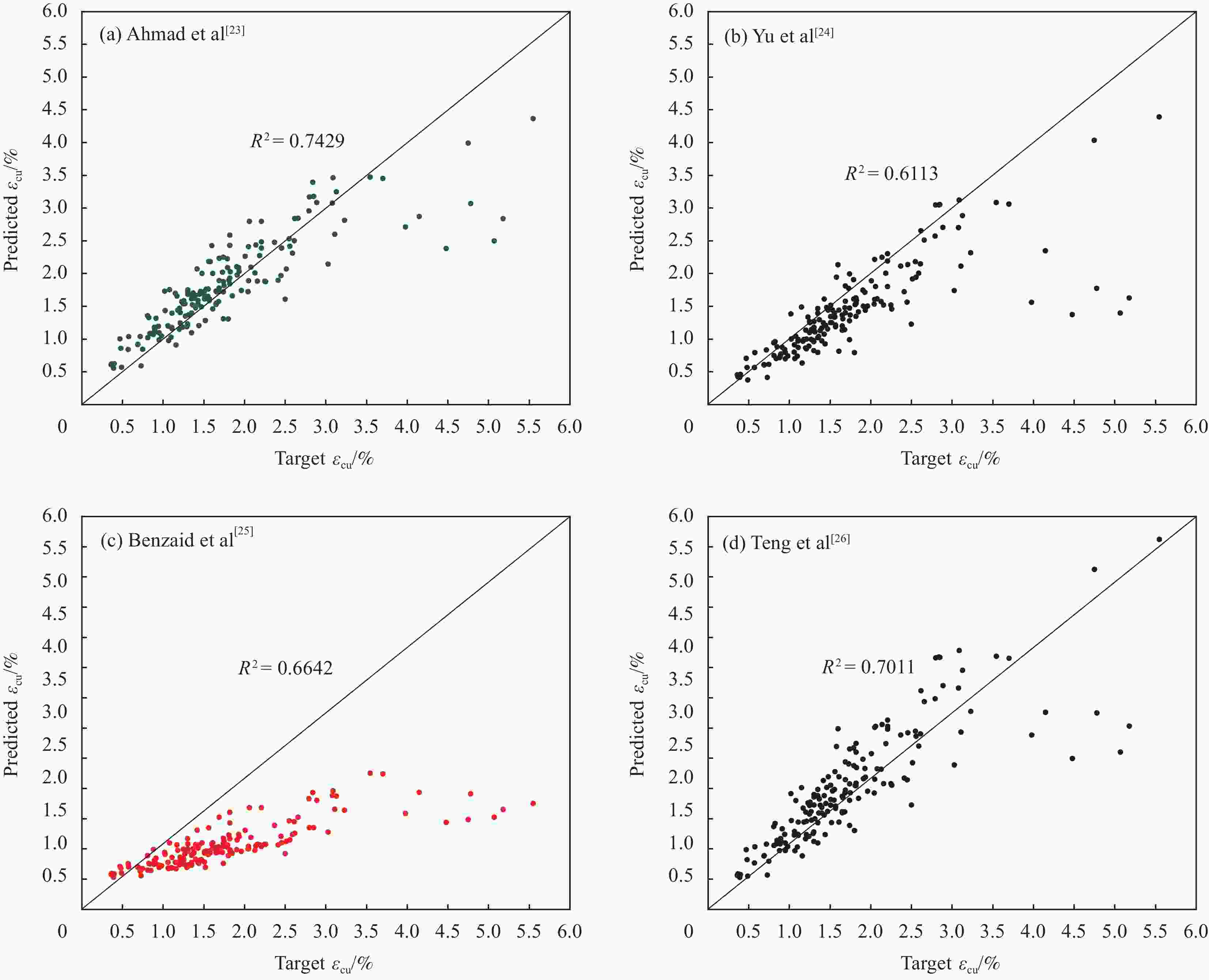
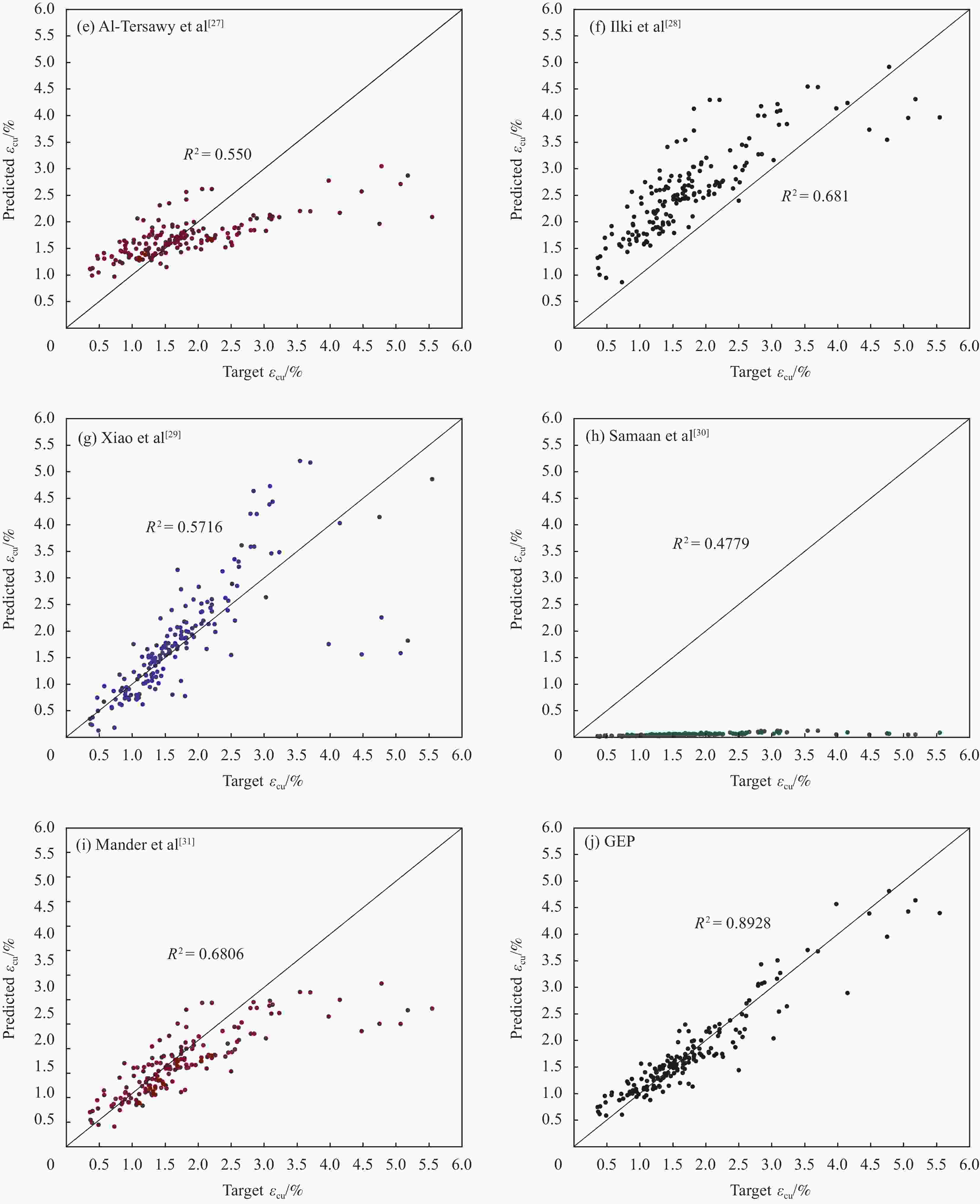
Table 8. Prediction results of ultimate axial strain models of FRP-confined concrete
Model $ {R^{\text{2}}} $ MAE RRSE RMSE MAPE GEP 0.893 0.228 0.334 0.316 0.160 Ahmad et al[23] 0.743 0.327 0.524 0.496 0.206 Yu et al[24] 0.611 0.394 0.721 0.683 0.199 Benzaid et al[25] 0.664 0.814 1.129 1.068 0.410 Teng et al[26] 0.701 0.357 0.563 0.533 0.208 Al-Tersawy et al[27] 0.550 0.513 0.767 0.726 0.348 Ilki et al[28] 0.682 0.881 1.029 0.974 0.671 Xiao et al[29] 0.572 0.412 0.742 0.702 0.213 Samaan et al[30] 0.478 1.713 2.061 1.950 0.971 Mander et al[31] 0.681 0.379 0.544 0.613 0.204
下载: 导出CSV
-
[1] GULER S. Axial behavior of FRP-wrapped circular ultra-high performance concrete specimens[J]. Structural Engineering and Mechanics,2014,50(6):709-722. doi: 10.12989/sem.2014.50.6.709 [2] WANG W, WU C, LIU Z, et al. Compressive behavior of ultra-high performance fiber rein-forced concrete (UHPFRC) confined with FRP[J]. Composite Structures,2018,204:419-437. doi: 10.1016/j.compstruct.2018.07.102 [3] ZHOU Y, LIU X, XING F, et al. Axial compressive behavior of FRP-confined light weight aggregate concrete: An experimental study and stress-strain relation model[J]. Construction and Building Materials,2016,119:1-15. doi: 10.1016/j.conbuildmat.2016.02.180 [4] 李家齐, 李诗娴, 胡皓, 等. FRP约束玄武岩纤维再生混凝土圆柱力学性能试验研究[J]. 混凝土, 2018(12):57-61. doi: 10.3969/j.issn.1002-3550.2018.12.015LI Jiaqi, LI Shixian, HU Hao, et al. Experimental study and finite element analysis on mechanical properties of FRP confined basalt fiber reinforced recycled concrete circular columns[J]. Concrete,2018(12):57-61(in Chinese). doi: 10.3969/j.issn.1002-3550.2018.12.015 [5] LAM L, TENG J G. Design-oriented stress-strain model for FRP-confined concrete[J]. Construction and Building Materials,2003,17(6-7):471-489. doi: 10.1016/S0950-0618(03)00045-X [6] AHMAD S M, SHAH S P. Stress-strain curves of concrete confined by spiral reinforcement[J]. Civil and Environmental Engineering,1982,79(6):484-490. [7] MOZUMDER R A, ROY B, LASKAR A I. Support vector regression approach to predict the strength of FRP confined concrete[J]. Arabian Journal for Science and Engineering,2017,42(3):1129-1146. doi: 10.1007/s13369-016-2340-y [8] KAMGAR R, NADERPOUR H, JANKOWSKI R. A proposed soft computing model for ultimate strength estimation of FRP-confined concrete cylinders[J]. Applied Science-Basel,2020,10(5):1769. doi: 10.3390/app10051769 [9] CEVIK A, CABALAR A F. A genetic-programming-based formulation for the strength enhancement of fiber-reinforced-polymer-confined concrete cylinders[J]. Journal of Applied Polymer Science,2008,110(5):3087-3095. doi: 10.1002/app.28839 [10] CEVIK A, GOGUS M T, GUZELBZY I H, et al. Soft computing based formulation for strength enhancement of CFRP confined concrete cylinders[J]. Advance in Engineering Software,2010,41(4):527-536. doi: 10.1016/j.advengsoft.2009.10.015 [11] GANDOMI A H, ALAVI A H, SAHAB M G. New formulation for compressive strength of CFRP confined concrete cylinders using linear genetic programming[J]. Materials and Structures,2010,43(7):963-983. doi: 10.1617/s11527-009-9559-y [12] MANSOURI I, OZBAKKALOGLU T, KISI O, et al. Predicting behavior of FRP-confined concrete using neuro fuzzy, neural network, multivariate adaptive regression splines and M5 model tree techniques[J]. Materials and Structures,2016,49(10):4319-4334. doi: 10.1617/s11527-015-0790-4 [13] ZHAO J L, YU T, TENG J G. Stress-strain behavior of FRP-confined recycled aggregate concrete[J]. Journal of Composites Construction,2014,19(3):4014-4054. [14] CHEN G M, HE Y H, JIANG T, et al. Behavior of CFRP-confined recycled aggregate concrete under axial compression[J]. Construction and Building Materials,2016,111:85-97. doi: 10.1016/j.conbuildmat.2016.01.054 [15] JIANG T, TENG J G. Analysis-oriented models for FRP confined concrete: A comparative assessment[J]. Engineering Structures,2007,29(11):2968-2986. doi: 10.1016/j.engstruct.2007.01.010 [16] CUI C, SHEIKH S A. Experimental study of normal-and high-strength concrete confined with fiber-reinforced polymers[J]. Journal of Composites Construction,2010,14(5):553-561. doi: 10.1061/(ASCE)CC.1943-5614.0000116 [17] 马高, 刘康. 基于BP神经网络CFRP约束混凝土抗压强度预测[J]. 湖南大学学报(自然科学版), 2021, 48(9):88-97.MA Gao, LIU Kang. Prediction of compressive strength of CFRP-confined concrete columns based on BP neural network[J]. Journal of Hunan University (Natural Sciences),2021,48(9):88-97(in Chinese). [18] FERREIRA C. Gene expression programming: A new adaptive algorithm for solving problems[J]. Complex Systems,2001,13(2):87-129. doi: 10.48550/arXiv.cs/0102027 [19] FERREIRA C. Gene expression programming[M]. Portugal: Angora do Heroismo, 2002. [20] MITCHELL M. An introduction to genetic algorithms[M]. London: MIT Press, 1996. [21] FERREIRA C. Mutation, transposition, and recombination: An analysis of the evolutionary dynamics[C]. 4th International Work Shop on Frontiers in Evolutionary Algorithm. North Carolin: Research Triangle Park, 2001: 614-617. [22] WANG Y C. A review of gene expression programming algorithms and their applications[J]. Computer Applications and Software,2010,27(6):23-26. [23] AHMAD A, PLEVRIS V, KHAN Q U Z. Prediction of properties of FRP-confined concrete cylinders based on artificial neural networks[J]. Crystals,2020,10(9):811. doi: 10.3390/cryst10090811 [24] YU T, TENG J G. Design of concrete-filled FRP tubular columns: Provisions in the Chinese technical code for infrastructure application of FRP composites[J]. Journal of Composites Construction,2011,15(3):451-461. [25] BENZAID R, MESBAH H, CHIKH N E. FRP-confined concrete cylinders: Axial compression experiments and strength model[J]. Journal Reinforced Plastics and Composites,2010,29(16):2469-2488. doi: 10.1177/0731684409355199 [26] TENG J G, JIANG T, LAM L, et al. Refinement of a design-oriented stress-strain model for FRP-confined concrete[J]. Journal of Composites Construction,2009,13(4):269-278. doi: 10.1061/(ASCE)CC.1943-5614.0000012 [27] Al-TERSAWY S H, HODHOD O A, HEFNAWY A A. Reliability and code calibration of RC short columns confined with CFRP wraps[C]. In Proc. 8th Int. Symp. on Fiber Reinforced Polymer Reinforcement for Concrete Structures. Patras, Greece: University of Patras, 2007: 560-563. [28] ILKI A, KUMBASAR N, KOC V. Low strength concrete members externally confined with FRP sheets[J]. Structural Engineering and Mechanics,2004,18(2):167-194. doi: 10.12989/sem.2004.18.2.167 [29] XIAO Y, WU H. Compressive behavior of concrete confined by carbon fiber composite jackets[J]. Journal of Materials in Civil Engineering,2000,12(2):139-146. doi: 10.1061/(ASCE)0899-1561(2000)12:2(139) [30] SAMAAN M, MIRMIRAN A, SHAHAWY M. Model of concrete confined by fiber composites[J]. Journal of Structural Engineering,1998,124(9):1025-1031. doi: 10.1061/(ASCE)0733-9445(1998)124:9(1025) [31] MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering,1988,114(8):1804-1826. doi: 10.1061/(ASCE)0733-9445(1988)114:8(1804) [32] YASMIN M, AHMED A, ROZEN H. Predictive model to the bond strength of FRP-to-concrete under direct pullout using gene expression programming[J]. Journal of Civil Engineering and Management,2019,25(8):773-784. doi: 10.3846/jcem.2019.10798 [33] AIRE C, GETTU R, CASAS J R. Study of the compressive behavior of concrete confined by fiber reinforced composites[C]. Composites in Constructions, Proceedings of the International Conference. Lisse, Netherlands: A. A. Balkema, 2001: 239-243. -
下载:
点击查看大图
图(7) / 表(8)
计量
- 文章访问数: 874
- HTML全文浏览量: 397
- PDF下载量: 39
- 被引次数: 0
