Advances in solid polymer electrolyte matrices for lithium-ion batteries
-
摘要: 固态聚合物电解质(SPE)因具有安全性高、机械强度高与电极界面接触性良好等优势,在固态锂离子电池有更广泛的应用前景。聚合物基质在SPE中作主体,起着骨架支撑和促进锂离子的解离和运输作用,是SPE中不可缺少的部分。本文综述了目前对聚合物基质最新的改性策略,以提升SPE的电化学性能和力学性能。通过调节聚合物基质结构、形貌、制备工艺以及添加无机填料方面来改善聚合物基质的结晶度和锂离子传输通道,提升SPE的电化学性能,有望为固态锂离子电池商业化做出贡献。Abstract: Solid state polymer electrolyte (SPE) has a wider application prospect in solid state lithium ion batteries due to its advantages of high safety, high mechanical strength and good contact with electrode interface. Polymer matrix is an indispensable part of SPE as the main body, which plays the roles of skeleton support and promotion of lithium ion dissociation and transport. This paper reviews the latest modification strategies of polymer matrix to enhance the electrochemical and mechanical properties of SPEs. Improving the crystallinity and lithium ion transport channels of the polymer matrix by modifying its structure, morphology, preparation process, and addition of inorganic fillers to enhance the electrochemical performance of SPEs is expected to contribute to the commercialisation of solid-state lithium-ion batteries.
-
夹层结构因其轻质、热力学性能优异等特点,近几十年来在飞行器、核反应堆、集成电路等领域得到广泛应用。与蜂窝[1]、泡沫[2-3]等夹层结构相比,功能梯度材料(FGM)夹层结构通过使组分材料在空间上连续分布,可消除相邻层界面的接触热阻和应力失配,因此FGM夹层结构常被用于高温工程领域。深入了解FGM夹层结构的传热过程,对其设计和制造具有重要意义。
在FGM夹层结构的初步设计中,由于结构厚度较其他两个方向的尺寸小得多,因此常常将传热问题简化为沿厚度方向的一维问题[4]。Daikh等[5]给出了Dirichlet边界条件下FGM夹层板的一维稳态热传导问题的解析解。Dini等[6]考虑表面热对流和内部热源的作用,研究了旋转FGM夹层圆盘的径向稳态温度分布。由于高温会严重影响FGM的热工参数,因此传热分析需要考虑热工参数温度依赖性的影响,这将导致传热问题变成非线性问题。Shen和Li[7]考虑组分材料热工参数的温度依赖性,研究了FGM夹层板的非线性稳态热传导问题。
以上工作仅研究了FGM夹层结构的稳态传热问题。然而,稳态分析得到的结构内温度分布处于平衡状态,这在整个加热过程中可能无法实现或者维持。因此,稳态分析可能会高估结构内温度分布,导致设计过于保守。为了能尽可能减少结构自重,有必要对非线性瞬态传热过程进行准确预测。Pandey等[8-9]采用有限差分法(FDM)研究了Dirichlet边界条件下FGM夹层板的一维非线性瞬态热传导问题。结果表明,数值结果与文献结果吻合良好。然而,Malekzadeh等[10]指出,传统数值方法如FDM[8-9]和有限元法[11]需要非常小的时间步长,以确保结果的收敛性和准确性,但这样会导致计算耗时。
微分求积法(DQM)是一种求解微分方程的数值方法,该方法无需像有限元法那样推导弱形式的控制方程,因此可以大幅减少高阶近似中的公式化工作量[12]。相较于传统数值方法如FDM,DQM已被证明具有高精度和高计算效率的优势[10]。在已有工作中,学者主要采用DQM求解单域问题[13-15]。然而,DQM并不适用于求解由于荷载、材料和尺寸等不连续造成的多域问题。为了求解这类多域问题,Wang等[16]和Chen等[17]基于传统的DQM提出了微分求积单元法(DQEM)。基于DQEM,Malekzadeh等[18]分析了FGM夹层壳的稳态传热问题。Dai等[19]通过在空间域上应用DQEM并在时间域上应用Newmark法,给出了含FGM层的多层热防护系统的瞬态温度分布。然而Malekzadeh等[18]和Dai等[19]仅仅考虑了热传导系数的温度依赖性,却假定其他热工参数(如密度和比热容)为常量。在高温环境中,这种假设可能会造成一定的误差。
本文首次尝试采用增量微分求积单元法(IDQEM)分析时变热边界条件下FGM夹层板的一维非线性瞬态传热问题。考虑了所有热工参数的温度依赖性及时变热边界条件,以提高板内温度场预测的准确性。为应用IDQEM,将时间域和空间域都划分为若干子域。采用微分求积技术对任一时间子域内的控制方程、初始条件、界面条件及边界条件进行离散处理,并基于矩阵原理对离散方程进行修改,最后采用Newton-Raphson迭代法近似求解,获得单个时间子域内的夹层板温度解。采用递推的方式,即可获得整个受热过程的温度分布。数值算例验证了本方法的快速收敛和高精度优势,并讨论了一些关键参数对FGM夹层板温度分布的影响。
1. FGM夹层板的传热模型
1.1 FGM夹层板的热工参数
图1为一块FGM夹层板,其底层、芯层和顶层分别为金属单相材料、FGM材料和陶瓷单相材料。夹层板的总厚度为H,各单层厚度为Hs (s = 1、2、3)。考虑组分材料热工参数的温度依赖性,通常表述为[20]
Pm(T)=Pm0(Pm−1T−1+1+Pm1T+Pm2T2+Pm3T3),Pc(T)=Pc0(Pc−1T−1+1+Pc1T+Pc2T2+Pc3T3) (1) 其中:Pm和Pc分别代表金属和陶瓷的有效热工参数;Pmk和Pck(k=−1、0、1、2、3)分别为金属和陶瓷热工参数的温度系数;T为温度。令ˉPm0=Pm0,ˉPc0=Pc0,ˉPmj=PmjPm0,ˉPcj=PcjPc0 (j=−1、1、2、3),则式(1)可以改写为
Pm(T)=3∑k=−1ˉPmkTk,Pc(T)=3∑k=−1ˉPckTk (2) 对于夹层板的任意第s (s = 1、2、3)层,可基于局部坐标x(s)(图1(b)),采用Voigt混合幂率模型来表征其有效热工参数P(s),即
P(s)(x(s),T)=Pm(T)+[Pc(T)−Pm(T)]V(s)(x(s)) (3) 其中,V(s)为第s层陶瓷材料的体积分数。对于不同层,V(s)的取值分别为
V(1)(x(1))=0, 0⩽ (4) 其中,η为FGM层的体积分数指数。
1.2 FGM夹层板的传热方程
本文FGM夹层板的传热分析基于以下两个假设:(1)上下表面的热边界条件不沿板面方向变化;(2)板厚相对于长度和宽度方向尺寸足够小。因此,板的传热问题可以简化为沿厚度方向的一维问题。基于局部坐标 {x^{(s)}} ,第s层的热传导方程为[8]
\begin{split} & \left[\mathit{\lambda}^{(s)}(x^{(s)},T)T_{,x}^{(s)}(t,x^{(s)})\right]_{,x}= \\ & \quad\rho^{(s)}(x^{(s)},T)c^{(s)}(x^{(s)},T)\dot{T}^{(s)}(t,x^{(s)}) \end{split} (5) 其中:变量顶部的点表示对时间的偏导;下标中的逗号表示对其后位置坐标的偏导;t为时间;T(s)、λ(s)、ρ(s)、c(s)分别为第s层的温度、热传导系数、密度、比热容。
假设初始时刻板内温度 T_0^{(s)} 任意分布,即
{T^{(s)}}(0,{x^{(s)}}) = T_0^{(s)}({x^{(s)}}) (6) 由相邻层的温度和热通量连续条件,得
{T^{(s)}}(t,{H_s}) = {T^{(s + 1)}}(t,0) ,\quad s = 1, 2 (7) T_{,x}^{(s)}(t,{H_s}) = T_{,x}^{(s + 1)}(t,0) ,\quad s = 1, 2 (8) 假设夹层板底面受自然对流作用,而上表面受气动加热和热辐射共同作用,则边界条件为
- {\lambda ^{(1)}}(0,T)T_{,x}^{(1)}(t,0) = {h_{{\text{bot}}}}\left[ {{T^{(1)}}(t,0) - {T_{{\text{bot}}}}(t)} \right] (9) {\lambda ^{(3)}}({H_3},T)T_{,x}^{(3)}(t,{H_3}) = \qquad{q_{{\text{top}}}}(t) - \sigma \varepsilon \left\{ {{{\left[ {{T^{(3)}}(t,{H_3})} \right]}^4} - T_{{\text{top}}}^4(t)} \right\} (10) 其中:Tbot为下部时变环境温度;hbot为下表面对流换热系数;Ttop为上部时变环境温度;qtop为上表面气动加热生成的时变热流;σ为Stephan-Boltzmann常数;ε为辐射率。需要说明的是,本方法还可将其他类型的热边界条件考虑在内,简单起见这里不再赘述。
2. 增量微分求积单元法
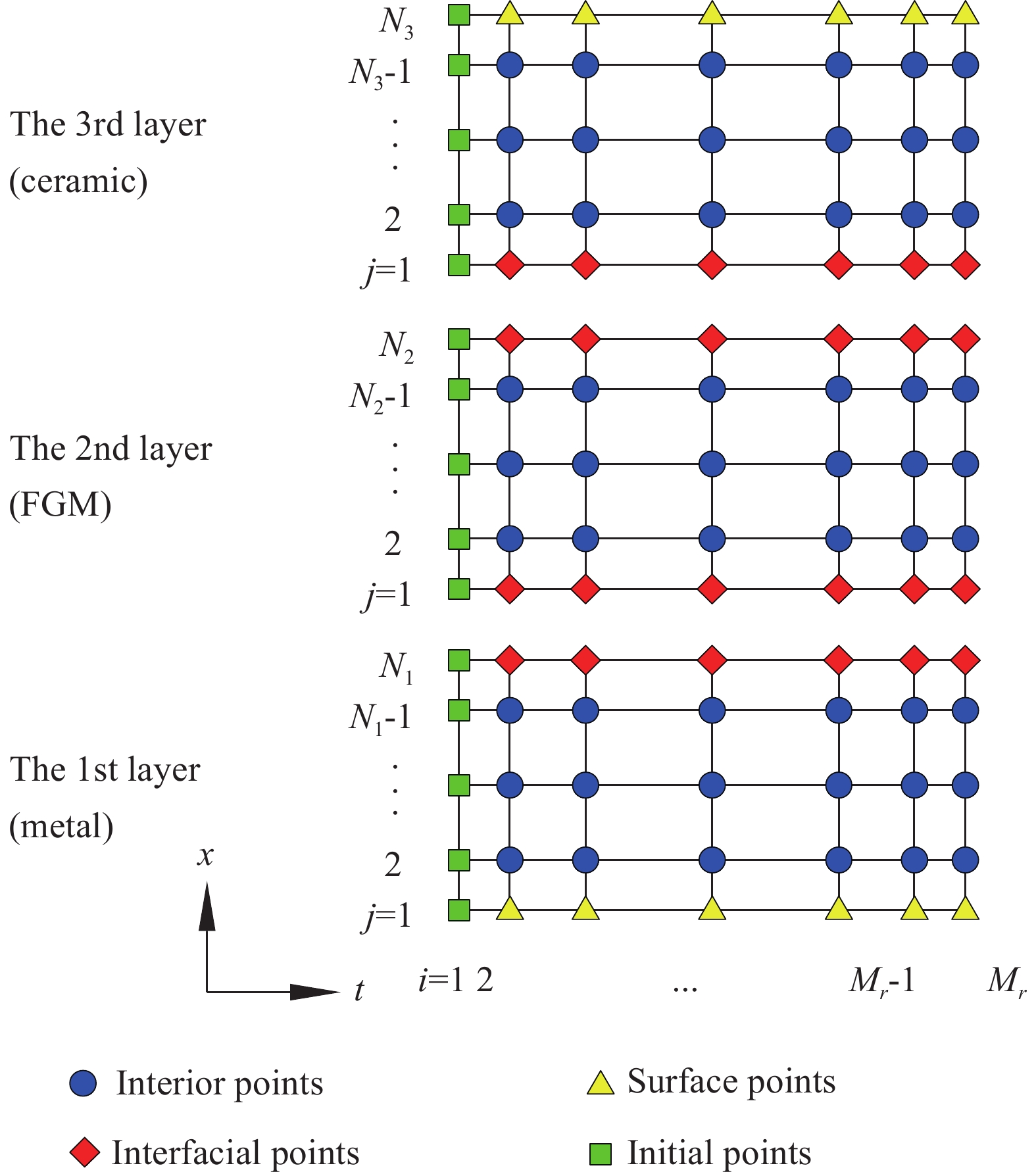
式(5)~(10)形成了FGM夹层板的瞬态传热定解问题。由于材料热工参数具有温度依赖性,同时辐射条件式(10)中含有温度的4次方项,因此该问题属于非线性问题,可采用IDQEM求解。为应用该方法,首先将整个加热过程划分为p (p ≥ 1)个时间子域,其中第r (r = 1、2、···、p)个子域的时长 \Delta {t_r} 由时变热边界条件确定;同时沿层界面将夹层板划分为3个空间子域,如图2所示。将第r个时间子域和第s个空间子域分别离散为 {M_r} 和 {N_s} 个节点,则时间域和空间域上的总节点数分别为 M = \displaystyle\sum\nolimits_{r = 1}^p {{M_r}} 和 N = \displaystyle\sum\nolimits_{s = 1}^3 {{N_s}} 个。节点分布规则依据Gauss-Lobatto-Chebyshev点[21]:
t_i^{(r)} = \frac{{\Delta {t_r}}}{2}\left[ {1 - \cos \frac{{\left( {i - 1} \right){\text{π}} }}{{{M_r} - 1}}} \right] , i = 1, 2, …, {M_r} ; x_j^{(s)} = \frac{{{H_s}}}{2}\left[ {1 - \cos \frac{{\left( {j - 1} \right){\text{π}} }}{{{N_s} - 1}}} \right] , j = 1, 2, …, {N_s} (11) 则节点 (t_i^{(r)},x_j^{(s)}) 处的温度导数可以离散为[21]
\frac{{{\partial ^{{k_t}}}}}{{\partial {{({t^{(r)}})}^{{k_t}}}}}\frac{{{\partial ^{{k_x}}}}}{{\partial {{({x^{(s)}})}^{{k_x}}}}}T_{i,j}^{(r,s)} = \sum\limits_{m = 1}^{{M_r}} {\sum\limits_{n = 1}^{{N_s}} {A_{i,m}^{({k_t},r)}B_{j,n}^{({k_x},s)}T_{m,n}^{(r,s)}} } (12) 其中:T_{i,j}^{(r,s)} = T(t_i^{(r)},x_j^{(s)}) ;A_{i,m}^{({k_t},r)} 为待求温度在节点处对t的kt阶偏导权系数;B_{j,n}^{({k_x},s)} 为待求温度在节点处对x的kx阶偏导权系数。
将式(12)代入式(5),则第r(r = 1、2、···、p)个时间子域的控制方程离散形式为
\begin{split} \tilde \lambda _{i,j}^{(r,s)}&{\left( {\sum\limits_{n = 1}^{{N_s}} {B_{j,n}^{(1,s)}T_{i,n}^{(r,s)}} } \right)^2} + \hat \lambda _{i,j}^{(r,s)}\sum\limits_{n = 1}^{{N_s}} {B_{j,n}^{(1,s)}T_{i,n}^{(r,s)}}+\\ & \lambda _{i,j}^{(r,s)}\sum\limits_{n = 1}^{{N_s}} {B_{j,n}^{(2,s)}T_{i,n}^{(r,s)}} = \rho _{i,j}^{(r,s)}c_{i,j}^{(r,s)}\sum\limits_{m = 1}^{{M_r}} {A_{i,m}^{(1,r)}T_{m,j}^{(r,s)}} , \\ &i = 2, 3, …, {M_r} ; j = 2, 3, …, {N_s} - 1 ; s = 1, 2, 3 \end{split} (13) 其中: \lambda _{i,j}^{(r,s)} 、 \rho _{i,j}^{(r,s)} 、 c_{i,j}^{(r,s)} 为相应热工参数在节点 (t_i^{(r)},x_j^{(s)}) 处的值; \tilde \lambda _{i,j}^{(r,s)} 和 \hat \lambda _{i,j}^{(r,s)} 分别为 {\lambda ^{(r,s)}} 在节点处对T和x的偏导。由式(3), \lambda _{i,j}^{(r,s)} 、 \rho _{i,j}^{(r,s)} 、 c_{i,j}^{(r,s)} 、 \tilde \lambda _{i,j}^{(r,s)} 、 \hat \lambda _{i,j}^{(r,s)} 可以分别表示为
\begin{gathered} P_{i,j}^{(r,s)} = \left[ {\sum\limits_{k = - 1}^3 {\left( {\bar P_k^{\text{c}} - \bar P_k^{\text{m}}} \right){{\left( {T_{i,j}^{(r,s)}} \right)}^k}} } \right]{V^{(s)}}(x_j^{(s)}) + \\ \qquad \sum\limits_{k = - 1}^3 {\bar P_k^{\text{m}}{{\left( {T_{i,j}^{(r,s)}} \right)}^k}} ,{\text{ }}P = \lambda ,{\text{ }}\rho ,{\text{ }}c, \\ \end{gathered} \begin{gathered} \tilde \lambda _{i,j}^{(r,s)} = \left[ {\sum\limits_{k = - 1}^3 {k\left( {\bar \lambda _k^{\text{c}} - \bar \lambda _k^{\text{m}}} \right){{\left( {T_{i,j}^{(s)}} \right)}^{k - 1}}} } \right]{V^{(s)}}(x_j^{(s)}) + \\ \qquad\sum\limits_{k = - 1}^3 {k\bar \lambda _k^{\text{m}}{{\left( {T_{i,j}^{(s)}} \right)}^{k - 1}}} , \\ \end{gathered} \hat \lambda _{i,j}^{(r,s)} = \left[ {\sum\limits_{k = - 1}^3 {k\left( {\bar \lambda _k^{\text{c}} - \bar \lambda _k^{\text{m}}} \right){{\left( {T_{i,j}^{(s)}} \right)}^{k - 1}}} } \right]{\hat V^{(s)}}(x_j^{(s)}) (14) 其中, {\hat V^{(s)}}(x_j^{(s)}) 是 {V^{(s)}} 在节点 x = x_j^{(s)} 处对x的导数。根据 {V^{(s)}} 的表达式(4),可得 {\hat V^{(s)}}(x_j^{(s)}) 为
{\hat V^{(1)}}(x_j^{(1)}) = 0 , {\hat V^{(2)}}(x_j^{(2)}) = \frac{\eta }{{{H_2}}}{\left( {\frac{{x_j^{(2)}}}{{{H_2}}}} \right)^{\eta - 1}} , {\hat V^{(3)}}(x_j^{(3)}) = 0 (15) 类似地,可将第r(r = 1、2、···、p)个时间子域的初始条件式(6)、界面条件式(7)和(8)及边界条件式(9)和(10)离散为
式(6):T_{1,j}^{(r,s)} = T_0^{(r,s)}(x_j^{(s)}) , j = 1, 2, …, {N_s} ; s = 1, 2, 3 (16) 式(7):T_{i,{N_s}}^{(r,s)} = T_{i,1}^{(r,s + 1)} , i = 2, 3, …, {M_r} ; s = 1, 2 (17) \begin{split} 式(8):& \sum\limits_{n = 1}^{{N_s}} {B_{{N_s},n}^{(1,s)}T_{i,n}^{(r,s)}} = \sum\limits_{n = 1}^{{N_{s + 1}}} {B_{1,n}^{(1,s + 1)}T_{i,n}^{(r,s + 1)}} ,\\ & i = 2, 3, …, {M_r} ; s = 1, 2 \end{split} (18) \begin{split} 式(9):&- \lambda _{i,1}^{(r,1)}\sum\limits_{n = 1}^{{N_1}} {B_{1,n}^{(1,1)}T_{i,n}^{(r,1)}} = {h_{{\text{bot}}}}\left[ {T_{i,1}^{(r,1)} - T_{{\text{bot}}}^{(r)}(t_i^{(r)})} \right] , \end{split} \qquad\quad i = 2, 3, …, {M_r} (19) \begin{split} 式(10):& \lambda _{i,{N_3}}^{(r,3)}\sum\limits_{n = 1}^{{N_3}} {B_{{N_3},n}^{(1,3)}T_{i,n}^{(r,3)}} = q_{{\text{top}}}^{(r)}(t_i^{(r)})-\\ & \sigma \varepsilon \left\{ {{{\left( {T_{i,{N_3}}^{(r,3)}} \right)}^4} - {{\left[ {T_{{\text{top}}}^{(r)}(t_i^{(r)})} \right]}^4}} \right\} , i = 2, 3, …, {M_r} \end{split} (20) 由图2可知,离散式(13)和式(16)~(20)建立在对应时间和空间子域的不同节点上(如式(13)中的待求节点温度位于圆点,而式(16)中的待求节点温度位于方点),因此直接求解这些离散式比较困难。基于矩阵理论,提出一种修正方法以使每个离散式都能建立在对应时间和空间子域的全部节点上。修正后的离散式(13)和式(16)~(20)可以写成如下矩阵方程的形式:
式(13):{\boldsymbol{\tilde \lambda }}_{\text{d}}^{(r,s)} \circ {\left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,s)}} {{{{\bar {\boldsymbol{B}}}}}}_{:,2:{N_s} - 1}^{(1,s)}} \right)^{\circ 2}} + \qquad\quad\;\; {\boldsymbol{\hat \lambda }}_{\text{d}}^{(r,s)} \circ \left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,s)}}{{\bar {\boldsymbol{B}}}}_{:,2:{N_s} - 1}^{(1,s)}} \right)+ \qquad\quad\;\;{\boldsymbol{\lambda }}_{\text{d}}^{(r,s)} \circ \left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,s)}}{{\bar {\boldsymbol{B}}}}_{:,2:{N_s} - 1}^{(2,s)}} \right) - {\boldsymbol{\rho }}_{\text{d}}^{(r,s)} \circ {\boldsymbol{c}}_{\text{d}}^{(r,s)} \circ \qquad\quad\;\; \begin{split} & \left( {{\boldsymbol{A}}_{2:{M_r},:}^{(1,r)}{{\boldsymbol{T}}^{(r,s)}}{\boldsymbol{\tilde I}}_{:,2:{N_s} - 1}^{(s)}} \right) = {{\boldsymbol{0}}}_{2:{M_r},2:{N_s} - 1}^{(r,s)} , \\ & s = 1, 2, 3 \end{split} (21) \begin{split} 式(16): {\boldsymbol{I}}_{1,:}^{(r)}{{\boldsymbol{T}}^{(r,s)}}{{\boldsymbol{\tilde I}}^{(s)}} = {{\boldsymbol{T}}^{({\text{ini}},r,s)}} ,s = 1, 2, 3 \end{split} (22) \begin{split} 式(17): {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,s)}}{\boldsymbol{\tilde I}}_{:,{N_s}}^{(s)} = {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,s + 1)}}{\boldsymbol{\tilde I}}_{:,1}^{(s + 1)} , s = 1, 2 \end{split} (23) \begin{split} 式(18):& {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,s)}}{{\bar {\boldsymbol{B}}}}_{:,{N_s}}^{(1,s)} = {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,s + 1)}}{{\bar {\boldsymbol{B}}}}_{:,1}^{(1,s + 1)} ,\\ & s = 1, 2 \end{split} (24) 式(19): - {\boldsymbol{\lambda }}_{{\text{bot}}}^{(r,1)} \circ \left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,1)}}{{\bar {\boldsymbol{B}}}}_{:,1}^{(1,1)}} \right)= \qquad\qquad\quad {h_{{\text{bot}}}}\left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,1)}}{\boldsymbol{\tilde I}}_{:,1}^{(1)} - {\boldsymbol{T}}_{2:{M_r}}^{({\text{bot}},r)}} \right) , (25) 式(20): {\boldsymbol{\lambda }}_{{\text{top}}}^{(r,3)} \circ \left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,3)}}{{\bar {\boldsymbol{B}}}}_{:,{N_3}}^{(1,3)}} \right)= \qquad\quad\quad{\boldsymbol{q}}_{2:{M_r}}^{({\text{top}},r)} - \sigma \varepsilon \left[ {{{\left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,3)}}{\boldsymbol{\tilde I}}_{:,{N_3}}^{(3)}} \right)}^{ \circ 4}} - {{\left( {{\boldsymbol{T}}_{2:{M_r}}^{({\text{top}},r)}} \right)}^{ \circ 4}}} \right] (26) 其中: {{\boldsymbol{T}}^{(r,s)}} 为待求温度 T_{i,j}^{(r,s)} 形成的 {M_r} \times {N_s} 矩阵; {{\boldsymbol{T}}^{({\text{ini}},r,s)}} 为初始温度 T_0^{(r,s)}(x_j^{(s)}) 形成的 {N_s} \times 1 向量; {{\boldsymbol{T}}^{({\text{bot}},r)}} 、 {{\boldsymbol{T}}^{({\text{top}},r)}} 、 {{\boldsymbol{q}}^{({\text{top}},r)}} 分别为下部环境温度 T_{{\text{bot}}}^{(r)}(t_i^{(r)}) 、上部环境温度 T_{{\text{top}}}^{(r)}(t_i^{(r)}) 、上部热流 q_{{\text{top}}}^{(r)}(t_i^{(r)}) 形成的 {M_r} \times 1 向量; {{{\boldsymbol{0}}}^{(r,s)}} 为 {M_r} \times {N_s} 零矩阵; {{\boldsymbol{I}}^{(r)}} 和 {{\boldsymbol{\tilde I}}^{(s)}} 分别为 {M_r} 阶和 {N_s} 阶单位矩阵; {{\boldsymbol{A}}^{(1,r)}} 和 {{\boldsymbol{B}}^{({k_x},s)}} ( {k_x} = 1,{\text{ 2}} )分别为权系数 A_{i,j}^{(1,r)} 和 B_{i,j}^{({k_x},s)} 形成的 {M_r} 阶和 {N_s} 阶矩阵; {{{\bar {\boldsymbol{B}}}}^{({k_x},s)}} 为 {{\boldsymbol{B}}^{({k_x},s)}} 的转置矩阵;其他表征热工参数的矩阵表达式见附录;矩阵或向量的下标表示索引范围,如 {\boldsymbol{I}}_{2:{M_r},:}^{(r)} 表示提取 {M_r} 阶矩阵 {{\boldsymbol{I}}^{(r)}} 的第二行到最后一行元素所形成的 ({M_r} - 1) \times {M_r} 矩阵;运算符\circ 表示Hadamard积,其定义为
{\left( {{\boldsymbol{X}} \circ {\boldsymbol{Y}}} \right)_{i,j}} = {{\boldsymbol{X}}_{i,j}}{{\boldsymbol{Y}}_{i,j}} , {\left( {{{\boldsymbol{X}}^{ \circ k}}} \right)_{i,j}} = {\left( {{{\boldsymbol{X}}_{i,j}}} \right)^k} (27) 其中,X和Y为同型矩阵。
为求解联立矩阵方程式(21)~(26),可采用Kronecker积 \otimes [22]将其转化为如下代数方程:
式(21): {\text{vec}}({\boldsymbol{\tilde \lambda }}_{\text{d}}^{(r,s)}) \circ {\left[ {{\boldsymbol{B}}_{2:{N_s} - 1,:}^{(1,s)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s)}})} \right]^{ \circ 2}}+ \qquad\qquad\quad {\text{vec}}({\boldsymbol{\hat \lambda }}_{\text{d}}^{(r,s)}) \circ \left[ {{\boldsymbol{B}}_{2:{N_s} - 1,:}^{(1,s)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s)}})} \right]+ \qquad\qquad\quad {\text{vec}}({\boldsymbol{\lambda }}_{\text{d}}^{(r,s)}) \circ \left[ {{\boldsymbol{B}}_{2:{N_s} - 1,:}^{(2,s)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s)}})} \right]- \qquad\qquad\quad \begin{split} & {\text{vec}}({\boldsymbol{\rho }}_{\text{d}}^{(r,s)}) \circ {\text{vec}}({\boldsymbol{c}}_{\text{d}}^{(r,s)}) \circ \left[ {{\boldsymbol{\tilde I}}_{2:{N_s} - 1,:}^{(s)} \otimes {\boldsymbol{A}}_{2:{M_r},:}^{(1,r)}} \right.\\ & \left.{{\text{vec}}({{\boldsymbol{T}}^{(r,s)}})} \right] = {\text{vec}}({{\boldsymbol{0}}}_{2:{M_r},2:{N_s} - 1}^{(r,s)}) ,\\ & s = 1, 2, 3 \end{split} (28) 式(22): {{\boldsymbol{\tilde I}}^{(s)}} \otimes {\boldsymbol{I}}_{1,:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s)}}) = {\text{vec}}({{\boldsymbol{T}}^{({\text{ini}},r,s)}}) , \qquad\qquad\quad s = 1, 2, 3 (29) 式(23): {\boldsymbol{\tilde I}}_{{N_s},:}^{(s)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s)}})= \qquad\qquad\quad{\boldsymbol{\tilde I}}_{1,:}^{(s + 1)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s + 1)}}) , s = 1, 2 (30) 式(24): {\boldsymbol{B}}_{{N_s},:}^{(1,s)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s)}})= \qquad\qquad\quad{\boldsymbol{B}}_{1,:}^{(1,s + 1)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s + 1)}}) , s = 1, 2 (31) 式(25): - {\text{vec}}({\boldsymbol{\lambda }}_{{\text{bot}}}^{(r,1)}) \circ \left[ {{\boldsymbol{B}}_{1,:}^{(1,1)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,1)}})} \right]= \qquad\qquad\quad{h_{{\text{bot}}}}\left[ {{\boldsymbol{\tilde I}}_{1,:}^{(1)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,1)}}) - {\boldsymbol{T}}_{2:{M_r}}^{({\text{bot}},r)}} \right] (32) 式(26): {\text{vec}}({\boldsymbol{\lambda }}_{{\text{top}}}^{(r,3)}) \circ \left[ {{\boldsymbol{B}}_{{N_3},:}^{(1,3)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,3)}})} \right] = \qquad\qquad\quad \begin{split} &{\boldsymbol{q}}_{2:{M_r}}^{({\text{top}},r)} - \sigma \varepsilon \left\{ {{\left[ {{\boldsymbol{\tilde I}}_{{N_3},:}^{(3)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,3)}})} \right]}^{ \circ 4}} -\right. \\ &\left.{{{\left( {{\boldsymbol{T}}_{2:{M_r}}^{({\text{top}},r)}} \right)}^{ \circ 4}}} \right\} \end{split} (33) 其中,vec(∙)为向量化算子;热工参数矩阵的向量化表达式见附录。
由式(28)~(33)可得如下非线性代数方程组:
\left[ {{\boldsymbol{E}}_{\text{L}}^{(r)} + {\boldsymbol{E}}_{{\text{NL}}}^{(r)}({\boldsymbol{T}}_{{\text{sum}}}^{(r)})} \right]{\boldsymbol{T}}_{{\text{sum}}}^{(r)} = {{\boldsymbol{f}}^{(r)}} (34) 其中:向量 {{\boldsymbol{f}}^{(r)}} 包含了初始条件、界面条件及边界条件; {\boldsymbol{E}}_{\text{L}}^{(r)} 为线性刚度矩阵; {\boldsymbol{E}}_{{\text{NL}}}^{(r)} 为非线性刚度矩阵,由如下待求温度向量决定:
{\boldsymbol{T}}_{{\text{sum}}}^{(r)} = {\left\{ {\begin{array}{*{20}{c}} {{\text{vec}}({{\boldsymbol{T}}^{(r,1)}})}&{{\text{vec}}({{\boldsymbol{T}}^{(r,2)}})}&{{\text{vec}}({{\boldsymbol{T}}^{(r,3)}})} \end{array}} \right\}^{\text{T}}} (35) 采用Newton-Raphson迭代法求解式(34),即可得第r个时间子域内FGM夹层板的温度分布,该时间子域最终时刻的温度分布可作为下一个子域的初始温度条件。从第一个时间子域递推到最后一个子域,即可得到整个受热过程的温度分布。
本文仅分析了FGM夹层板的一维非线性瞬态传热问题,但本方法仍可用于二、三维问题的计算。以二维问题为例,仅需在板长方向上布置节点,则二维瞬态传热控制方程仍然可以被离散处理,最后得到的非线性代数方程组也可以采用Newton-Raphson迭代法进行求解。这些内容将在后续工作中开展。
3. 收敛性与比较
考虑两种类型的金属-陶瓷复合FGM夹层板,第一类为不锈钢和氮化硅复合(记为SUS304/Si3N4),第二类为钛合金和氧化锆复合(记为Ti-6Al-4V/ZrO2)。表1给出了组分材料热工参数的温度系数[23-26]。如无特别说明,假设初始时刻夹层板处于均匀的温度场T0 = 300 K。
Material Property P0 P−1 P1 P2 P3 SUS304 λ/(W∙(m∙K)−1) 15.379 0 −1.264 × 10−3 2.092×10−6 −7.223×10−10 c/(J∙(kg∙K)−1) 496.56 0 −1.151×10−3 1.636×10−6 −5.863×10−10 ρ/(kg∙m−3) 8166.0 0 0 0 0 Si3N4 λ/(W∙(m∙K)−1) 13.723 0 −1.032× 10−3 5.466 × 10−7 −7.876×10−11 c/(J∙(kg∙K)−1) 555.11 0 1.016×10−3 2.920×10−7 −1.670×10−10 ρ/(kg∙m−3) 2370.0 0 0 0 0 Ti-6Al-4V λ/(W∙(m∙K)−1) 1.0000 0 1.704×10−2 0 0 c/(J∙(kg∙K)−1) 625.30 0 −4.224×10−4 7.179×10−7 0 ρ/(kg∙m−3) 4420.0 0 0 0 0 ZrO2 λ/(W∙(m∙K)−1) 1.7000 0 1.276×10−4 6.648×10−8 0 c/(J∙(kg∙K)−1) 487.34 0 3.049×10−4 −6.037×10−8 0 ρ/(kg∙m−3) 5700.0 0 0 0 0 Notes: λ, c, ρ—Thermal conductivity, specific heat, and density, respectively; Pk (k = −1, 0, 1, 2, 3)—Temperature coefficients; SUS304, Si3N4, Ti-6Al-4V, and ZrO2 denote stainless steel, silicon nitride, titanium alloy, and zirconia, respectively. 3.1 收敛性
由于本文基于IDQEM,因此需要研究数值结果的收敛性。考虑一块体积分数指数为η = 0.2、总厚度为H = 1 mm的1-2-1型SUS304/Si3N4夹层板,其中1-2-1表示底层、芯层、顶层的厚度之比,即芯层厚度为底层和顶层厚度的2倍。在后续算例中,仍然沿用这种格式表示各层厚度之比。夹层板上表面受热冲击作用,其上下表面温度分别为Tc = 400 K和Tm = 300 K。为应用IDQEM,假定底层、芯层、顶层对应的空间子域的节点数分别为N1 = 0.25N、N2 = 0.5N、N3 = 0.25N。由于热边界条件不随时间变化,因此无需进行时间域的划分(即p = 1)。表2给出了SUS304/Si3N4夹层板温度解的收敛结果及计算效率。可以看出,随着节点数M和N的增加,数值结果快速收敛,但计算效率随之降低。当M × N = 20 × 28时,以5位有效数字表示的结果已不再变化,且此时计算效率也较高。此外,当仅采用12 × 20个节点时,精度已经令人满意。因此在后续算例中,如无特别说明,节点数取为20 × 28。
表 2 体积分数指数η = 0.2时SUS304/Si3N4夹层板x = 0.75H处的温度结果(单位:K)Table 2. Temperature results at x = 0.75H for the SUS304/Si3N4 sandwich slab with volume fraction index η = 0.2 (Unit: K)Time Temporal grid point number Spatial grid point number N = 12 N = 20 N = 28 N = 36 t = 0.01 s M = 4 342.16 ( 0.0312 s)342.96 ( 0.0625 s)342.98 ( 0.0938 s)342.99 ( 0.1154 s)M = 12 342.16 ( 0.1406 s)343.01 ( 0.1719 s)343.00 ( 0.2193 s)343.01 ( 0.4688 s)M = 20 342.16 ( 0.1875 s)343.01 ( 0.3281 s)343.01 ( 0.5806 s)343.01 ( 1.0312 s)M = 28 342.16 ( 0.2031 s)343.01 ( 0.5156 s)343.01 ( 1.1562 s)343.01 ( 2.1094 s)t = 0.03 s M = 4 362.95 ( 0.0469 s)362.80 ( 0.0712 s)362.81 ( 0.1024 s)362.80 ( 0.1193 s)M = 12 362.87 ( 0.1562 s)362.69 ( 0.1736 s)362.68 ( 0.2056 s)362.68 ( 0.5021 s)M = 20 362.87 ( 0.1719 s)362.70 ( 0.3598 s)362.69 ( 0.6006 s)362.69 ( 1.0156 s)M = 28 362.87 ( 0.2031 s)362.70 ( 0.5469 s)362.69 ( 1.0625 s)362.69 ( 2.2188 s)Notes: M and N—Total numbers of grid points in the temporal and spatial domains, respectively; The content in parentheses represents the central processing unit (CPU) time. 3.2 比 较
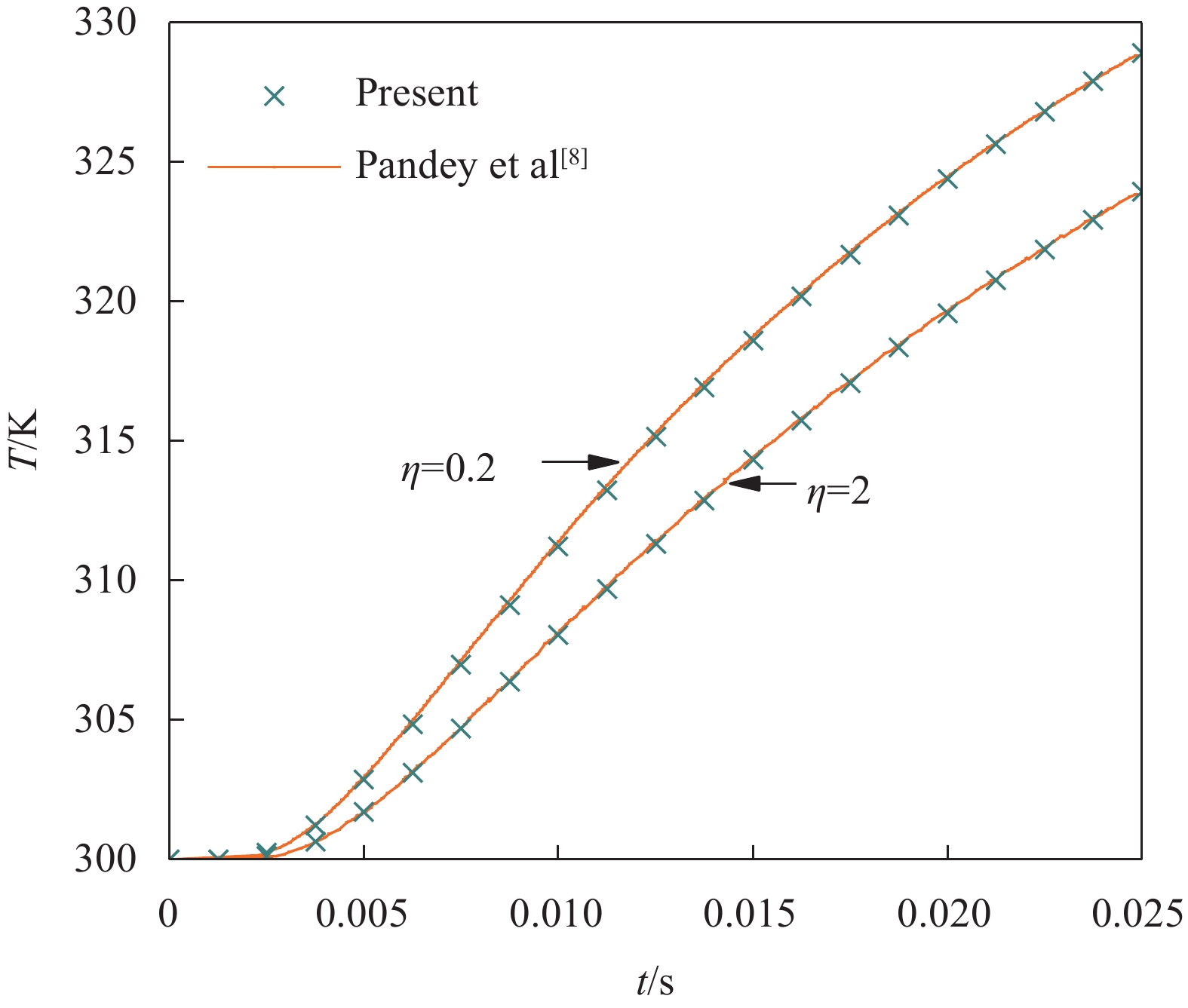
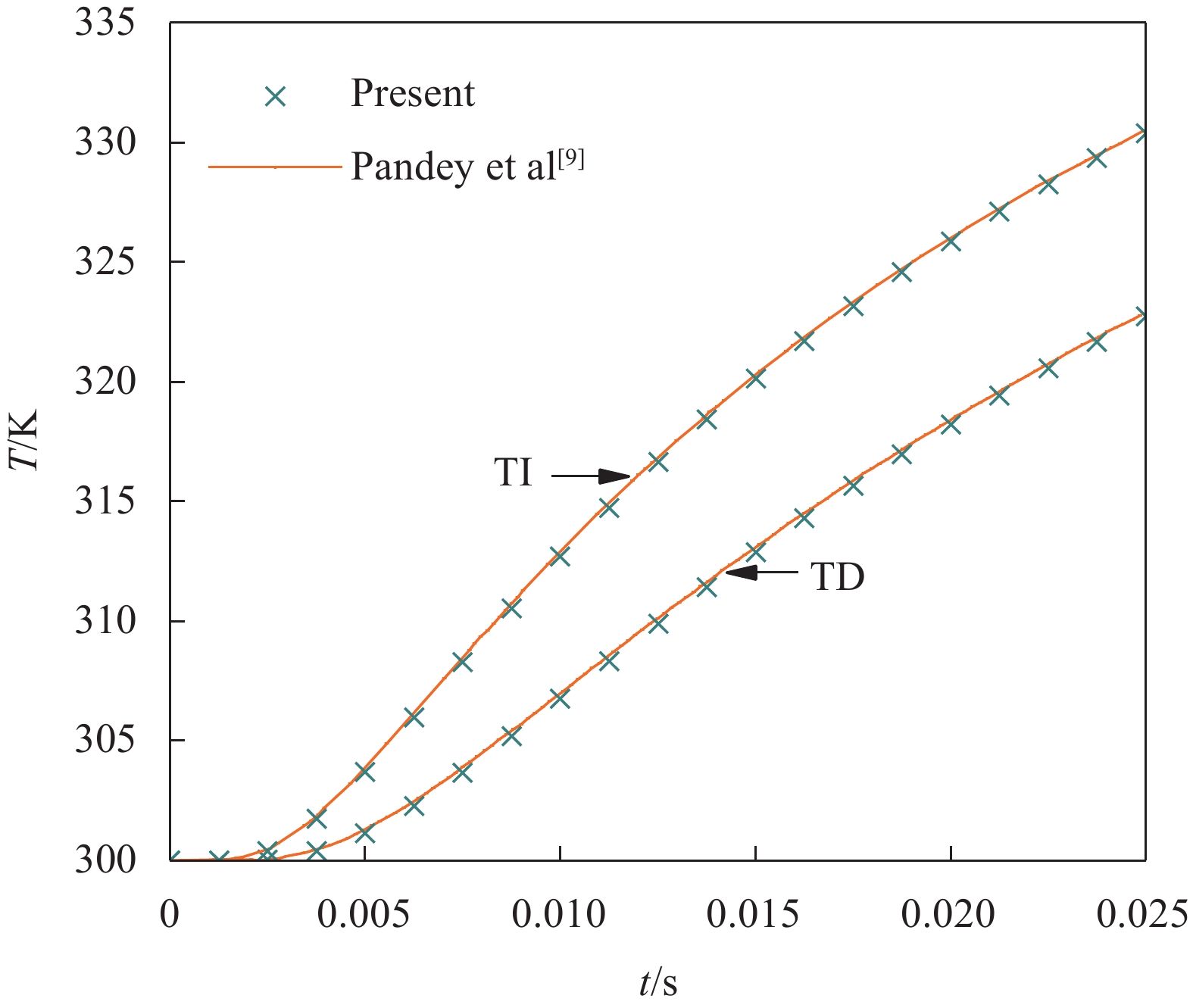
Pandey和Pradyumna[8-9]采用FDM开展了上述SUS304/Si3N4夹层板的非线性瞬态传热分析,其结果可用来验证本文IDQEM解的正确性。图3给出了η = 0.2和2两种情况下1-2-1型夹层板x = 0.5H处温度解的对比结果。图4给出考虑材料热工参数温度依赖性(TD)与不考虑温度依赖性(TI)两种状态下1-8-1型夹层板(η = 2)x = 0.5H处温度解的对比结果,其中TI状态下的热工参数取T = 0 K时的值。可以看出,IDQEM的预测结果与FDM结果具有很好的一致性。
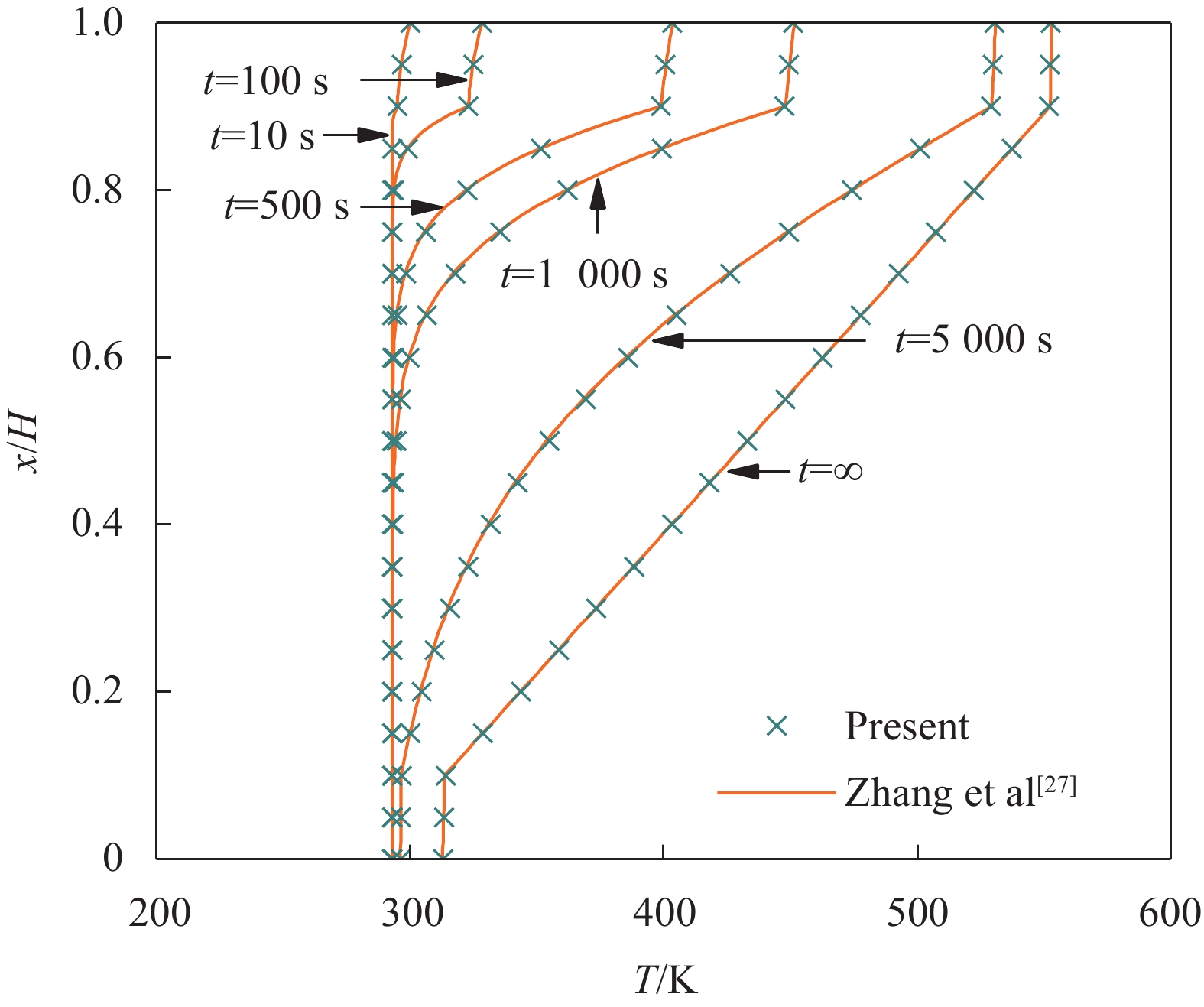
若将夹层板芯层材料由FGM换成均质材料,并忽略各组分材料热工参数的温度依赖性,则本文关于FGM夹层板的非线性问题将退化为普通夹层板的线性问题。对于此类问题,可采用一些解析方法求解,其结果可用于验证本文IDQEM解的正确性。Zhang等[27]采用Laplace变换法研究了对流条件下夹层板的瞬态温度解析解,其中材料热工参数、尺寸和热边界条件为λ(1) = λ(3) = 54.33 W∙(m∙K)−1,λ(2) = 1.33 W∙(m∙K)−1,c(1) = c(3) = 440 J∙(kg∙K)−1,c(2) = 900 J∙(kg∙K)−1,ρ(1) = ρ(3) =
7850 kg∙m−3,ρ(2) =2300 kg∙m−3,H1 = H3 = 20 mm,H2 = 160 mm,hbot = htop = 100 W∙m−2∙K−1,T0 = Tbot = 293 K,Ttop = 573 K。图5给出温度分布对比结果。可以看出,本文数值解与解析解具有很好的一致性。Malekzadeh等[18]和Dai等[19]采用DQEM分析了含FGM层构件的传热问题,但都仅考虑了热传导系数的温度依赖性,而假定其他热工参数为常量。为分析这种假定对数值结果精度和计算效率的影响,采用本方法讨论两种情况下的结果:(1) 仅考虑热传导系数的温度依赖性,其他热工参数取T0 = 300 K时的值(Case 1);(2) 考虑全部热工参数的温度依赖性(Case 2)。仍以3.1节的夹层板为例,表3给出了两种情况下数值结果与CPU计算时间的对比。可以看出,Case 1的结果总是比Case 2的大,最大误差达到1.76%,但两种情况下计算效率并无显著差异。
表 3 两种情况下数值结果和CPU计算时间的对比Table 3. Comparison of numerical results and CPU time in the two casesPosition Time/s Case 1/K Case 2/K Error CPU time of Case 1/s CPU time of Case 2/s x = 0.25H 0.01 302.43 301.40 0.34% 0.6094 0.6310 0.03 314.28 312.23 0.66% 0.5938 0.5781 x = 0.75H 0.01 349.05 343.01 1.76% 0.6094 0.6310 0.03 365.93 362.69 0.89% 0.5938 0.5781 Notes: In Case 1, only the thermal conductivity is considered to be TD; In Case 2, all the thermophysical properties are considered to be TD. 4. FGM夹层板传热的参数分析
4.1 材料温度依赖性对FGM夹层板传热的影响
考虑上述SUS304/Si3N4夹层板受3种不同上表面温度Tc = 400 K、500 K、600 K作用,而下表面温度保持为Tm = 300 K。为研究材料热工参数温度依赖性对瞬态传热的影响,图6给出了t = 0.01 s和0.02 s两种时刻下的温度分布。作为对比,同时绘制了TD和TI两种状态下结果,其中TI状态下的热工参数取T0 = 300 K时的值。可以看出,随着Tc的上升,TD和TI两种状态下的温度分布差异越来越大,这是由于两种状态下材料热工参数的差异随温度的上升而增大。同时可以发现,同一时刻同一表面温度作用下,TI状态下的内部温度总是比TD状态下的高。为解释这种现象,图7绘制了Tc = 600 K时夹层板的热扩散率α(α = λ/ρc)的时空分布。可以发现,对于陶瓷层和FGM层,TI状态下的α比TD下的大得多,导致TI状态具有更快的传热速度,进而具有更高的内部温度。因此在SUS304/Si3N4夹层板的设计中,忽略材料热工参数的温度依赖性将高估板内温度分布,从而导致设计过于保守。
为进一步说明TD和TI两种状态下的温度差异,图8给出了t = 0.01 s、0.02 s、0.03 s这3种时刻下x = 0.5H处的温度T与上表面温度Tc上的关系。可以看出,TI状态下T随着Tc的上升线性增大,而TD状态下T随着Tc的上升非线性增大。当Tc达到600 K时,3种时刻下的温度差异分别达到了12.00%、12.21%、10.41%。因此在预测FGM夹层板的温度分布时,需要考虑材料热工参数的温度依赖性,特别是在高温工况下。在接下来的算例中,仅考虑TD状态下的温度结果。
4.2 体积分数指数对FGM夹层板传热的影响
考虑一块总厚度为H = 120 mm的1-2-1型Ti-6Al-4V/ZrO2夹层板。板的下表面受自然对流作用,上表面受气动加热和热辐射共同作用,其中hbot = 2 W∙m−2∙K−1,Tbot = 300 K,qtop = 80 kW∙m−2,Ttop = 4 K,σ = 5.67 × 10−8 W∙m−2∙K−4,ε = 0.8。图9给出3种不同体积分数指数η = 0.2、1、5情况下夹层板下表面(x = 0)和上表面(x = H)的温度变化。可以看出,当t ≤ 250 s时,温度几乎不受η影响;随着加热时间的增长,η的影响越发显著。这是由于在早期阶段,传热主要发生在陶瓷层,因此传热不受η影响;随着时间的增长,整个夹层板都被加热,因此η对温度分布的影响越发显著。当t =
2000 s时,随着η从0.2增加到5,下表面温度从350 K增加到414 K,而上表面温度从1036 K减少到1021 K。为解释这种现象,图10绘制了不同体积分数指数η时夹层板的热扩散率α的时空分布。可以发现,随着η的增加,FGM层中陶瓷含量将会增加,导致FGM层整体具有更高的热扩散率,进而加快热传导。因此,体积分数指数对FGM夹层板的瞬态传热有着重要影响。4.3 热边界条件对FGM夹层板传热的影响
考虑上述1-2-1型Ti-6Al-4V/ZrO2夹层板(η = 2)受时变热流作用[28],其余热边界条件与4.2节相同。图11给出了时变热流曲线,该曲线可用三次函数qtop = a3t3 + a2t2 + a1t + a0分段拟合,表4给出了分段区间及拟合系数。可以看出,整个加热过程可以划分为4个时间子域,取各子域节点数为M1 = 5、M2 = 4、M3 = 11、M4 = 8。
表 4 时变热流的多项式拟合Table 4. Polynomial fits for the time-dependent heat fluxTime/s a0 a1 a2/10−3 a3/10−6 0-431.1 0 0.003196 1.021 −1.383 431.1-660.2 −228.7 1.595 −2.670 1.471 660.2- 1561 253.4 − 0.5961 − 0.6477 − 0.2043 1561 -2200 − 1257 2.307 −1.212 0.1929 Note: ak (k = 0, 1, 2, 3)—Fitting coefficients. 图12对比了时变热流(图11)和恒定热流qtop = 80 kW∙m−2作用下夹层板的温度时空分布。可以看出,靠近上部陶瓷层等温线更密集,表示温度梯度更大。图12(a)表明,当夹层板受恒定热流作用时,温度随着t和x的增加单调上升。然而从图12(b)可以看出,由于外界热流先增后减,因此等温线在约
1430 s后出现“U”型转折。此外,恒定热流情况下,整个加热过程中上下表面的最大温度分别约为1025 K和436 K;在时变热流情况下,整个加热过程中上下表面的最大温度分别约为1149 K和425 K。上下表面的巨大温差表明了FGM夹层板的优异隔热效果。5. 结 论
(1) 增量微分求积单元法具有快速收敛性,与已有文献的解析和数值结果的对比验证了本方法的正确性。
(2) 对于SUS304/Si3N4夹层板,不考虑材料热工参数温度依赖性状态较考虑温度依赖性状态具有更快的热传导,且两种状态下的温度差异随着表面温度的上升而增加。当上表面温度为600 K时,时间t = 0.01 s、0.02 s、0.03 s的中部温度差异分别达到了12.00%、12.21%、10.41%。因此,材料热工参数的温度依赖性是准确预测板内温度分布的关键因素,尤其是在高温分析中。忽略材料热工参数的温度依赖性将高估板内温度分布,从而导致设计过于保守。
(3) 在早期阶段,功能梯度材料(FGM)芯层的体积分数指数η对夹层板的温度分布几乎无影响,但随着加热时间的增长,η对温度分布的影响越发显著。当t =
2000 s时,随着η从0.2增加到5,下表面温度从350 K增加到414 K,而上表面温度从1036 K减少到1021 K。(4) 当FGM夹层板受恒定热流作用时,其内部温度随着时间和位置的变化单调变化。然而当热流随时间先增后减时,等温线出现“U”型转折。
附录:
式(21)、(25)和(26)中,表征热工参数的矩阵的表达式为
{\boldsymbol{P}}_{\text{d}}^{(r,s)} = \sum\limits_{k = - 1}^3 {\bar P_k^{\text{m}}{{\left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,s)}}{\boldsymbol{\tilde I}}_{:,2:{N_s} - 1}^{(s)}} \right)}^{ \circ k}}} + {\boldsymbol{V}}_{2:{M_r},2:{N_s} - 1}^{(s)} \circ \left[ {\sum\limits_{k = - 1}^3 {\left( {\bar P_k^{\text{c}} - \bar P_k^{\text{m}}} \right){{\left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,s)}}{\boldsymbol{\tilde I}}_{:,2:{N_s} - 1}^{(s)}} \right)}^{ \circ k}}} } \right],{\text{ }}P = \lambda ,{\text{ }}\rho {\text{, }}c, {\boldsymbol{\tilde \lambda }}_{\text{d}}^{(r,s)} = \sum\limits_{k = - 1}^3 {k\bar \lambda _k^{\text{m}}{{\left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,s)}}{\boldsymbol{\tilde I}}_{:,2:{N_s} - 1}^{(s)}} \right)}^{ \circ (k - 1)}}} + \left[ {\sum\limits_{k = - 1}^3 {k\left( {\bar \lambda _k^{\text{c}} - \bar \lambda _k^{\text{m}}} \right){{\left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,s)}}{\boldsymbol{\tilde I}}_{:,2:{N_s} - 1}^{(s)}} \right)}^{ \circ (k - 1)}}} } \right] \circ {\boldsymbol{V}}_{2:{M_r},2:{N_s} - 1}^{(s)} , {\boldsymbol{\hat \lambda }}_{\text{d}}^{(r,s)} = \left[ {\sum\limits_{k = - 1}^3 {\left( {\bar \lambda _k^{\text{c}} - \bar \lambda _k^{\text{m}}} \right){{\left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,s)}}{\boldsymbol{\tilde I}}_{:,2:{N_s} - 1}^{(s)}} \right)}^{ \circ k}}} } \right] \circ {\boldsymbol{\hat V}}_{2:{M_r},2:{N_s} - 1}^{(s)} , {\boldsymbol{\lambda }}_{{\text{bot}}}^{(r,1)} = \sum\limits_{k = - 1}^3 {\bar \lambda _k^{\text{m}}{{\left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,1)}}{\boldsymbol{\tilde I}}_{:,1}^{(1)}} \right)}^{ \circ k}}} + \left[ {\sum\limits_{k = - 1}^3 {\left( {\bar \lambda _k^{\text{c}} - \bar \lambda _k^{\text{m}}} \right){{\left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,1)}}{\boldsymbol{\tilde I}}_{:,1}^{(1)}} \right)}^{ \circ k}}} } \right] \circ {\boldsymbol{V}}_{2:M,1}^{(1)} , {\boldsymbol{\lambda }}_{{\text{top}}}^{(r,3)} = \sum\limits_{k = - 1}^3 {\bar \lambda _k^{\text{m}}{{\left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,3)}}{\boldsymbol{\tilde I}}_{:,{N_3}}^{(3)}} \right)}^{ \circ k}}} + \left[ {\sum\limits_{k = - 1}^3 {\left( {\bar \lambda _k^{\text{c}} - \bar \lambda _k^{\text{m}}} \right){{\left( {{\boldsymbol{I}}_{2:{M_r},:}^{(r)}{{\boldsymbol{T}}^{(r,3)}}{\boldsymbol{\tilde I}}_{:,{N_3}}^{(3)}} \right)}^{ \circ k}}} } \right] \circ {\boldsymbol{V}}_{2:M,{N_3}}^{(3)} 式(28)、(32)和(33)中,热工参数矩阵的向量化表达式为
\begin{split} {\text{vec}}({\boldsymbol{P}}_{\text{d}}^{(r,s)}) =& \sum\limits_{k = - 1}^3 {\bar P_k^{\text{m}}{{\left[ {{\boldsymbol{\tilde I}}_{2:{N_s} - 1,:}^{(s)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s)}})} \right]}^{ \circ k}}} + \left\{ {\sum\limits_{k = - 1}^3 {\left( {\bar P_k^{\text{c}} - \bar P_k^{\text{m}}} \right){{\left[ {{\boldsymbol{\tilde I}}_{2:{N_s} - 1,:}^{(s)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s)}})} \right]}^{ \circ k}}} } \right\}\circ \\& {\text{vec}}({\boldsymbol{V}}_{2:{M_r},2:{N_s} - 1}^{(s)}) , P = \lambda ,{\text{ }}\rho {\text{, }}c , \end{split} \begin{split} {\text{vec}}({\boldsymbol{\tilde \lambda }}_{\text{d}}^{(r,s)}) =& \sum\limits_{k = - 1}^3 {k\bar \lambda _k^{\text{m}}{{\left[ {{\boldsymbol{\tilde I}}_{2:{N_s} - 1,:}^{(s)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s)}})} \right]}^{ \circ (k - 1)}}} + \left\{ {\sum\limits_{k = - 1}^3 {k\left( {\bar \lambda _k^{\text{c}} - \bar \lambda _k^{\text{m}}} \right){{\left[ {{\boldsymbol{\tilde I}}_{2:{N_s} - 1,:}^{(s)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s)}})} \right]}^{ \circ (k - 1)}}} } \right\} \circ\\ & {\text{vec}}({\boldsymbol{V}}_{2:{M_r},2:{N_s} - 1}^{(s)}) , \end{split} {\text{vec}}({\boldsymbol{\hat \lambda }}_{\text{d}}^{(r,s)}) = \left\{ {\sum\limits_{k = - 1}^3 {\left( {\bar \lambda _k^{\text{c}} - \bar \lambda _k^{\text{m}}} \right){{\left[ {{\boldsymbol{\tilde I}}_{2:{N_s} - 1,:}^{(s)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,s)}})} \right]}^{ \circ k}}} } \right\} \circ {\text{vec}}({\boldsymbol{\hat V}}_{2:{M_r},2:{N_s} - 1}^{(s)}) , {\text{vec}}({\boldsymbol{\lambda }}_{{\text{bot}}}^{(r,1)}) = \sum\limits_{k = - 1}^3 {\bar \lambda _k^{\text{m}}{{\left[ {{\boldsymbol{\tilde I}}_{1,:}^{(1)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,1)}})} \right]}^{ \circ k}}} + \left\{ {\sum\limits_{k = - 1}^3 {\left( {\bar \lambda _k^{\text{c}} - \bar \lambda _k^{\text{m}}} \right){{\left[ {{\boldsymbol{\tilde I}}_{1,:}^{(1)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,1)}})} \right]}^{ \circ k}}} } \right\} \circ {\text{vec}}({\boldsymbol{V}}_{2:M,1}^{(1)}) , {\text{vec}}({\boldsymbol{\lambda }}_{{\text{top}}}^{(r,3)}) = \sum\limits_{k = - 1}^3 {\bar \lambda _k^{\text{m}}{{\left[ {{\boldsymbol{\tilde I}}_{{N_3},:}^{(3)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,3)}})} \right]}^{ \circ k}}} + \left\{ {\sum\limits_{k = - 1}^3 {\left( {\bar \lambda _k^{\text{c}} - \bar \lambda _k^{\text{m}}} \right){{\left[ {{\boldsymbol{\tilde I}}_{{N_3},:}^{(3)} \otimes {\boldsymbol{I}}_{2:{M_r},:}^{(r)}{\text{vec}}({{\boldsymbol{T}}^{(r,3)}})} \right]}^{ \circ k}}} } \right\} \circ {\text{vec}}({\boldsymbol{V}}_{2:M,{N_3}}^{(3)}) -
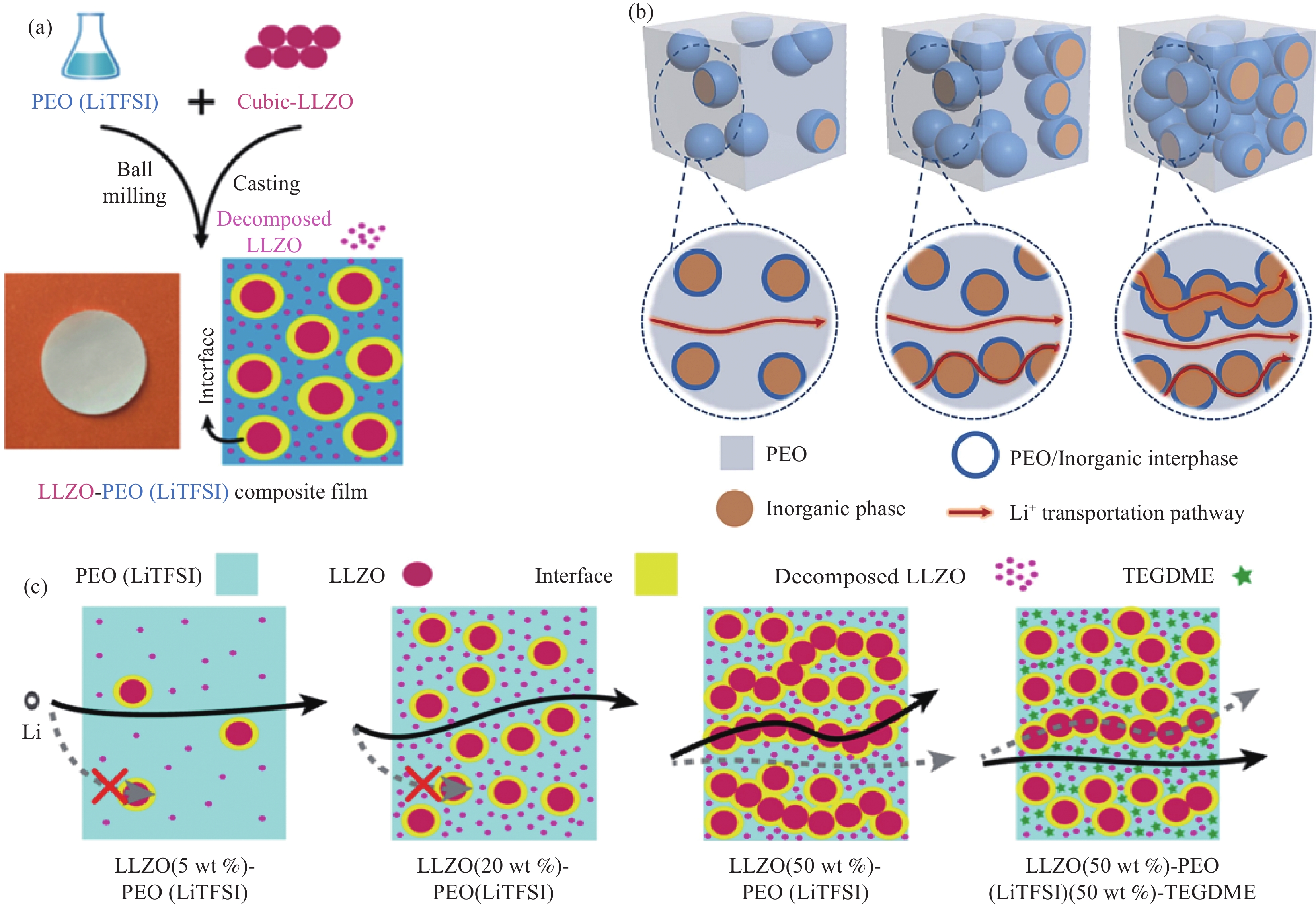
图 4 无机填料LLZO与PEO形成CPE示意图(a)[52]、Li+分布在PEO基体中;PEO基体和PEO/陶瓷界面处;PEO基体和陶瓷相及PEO/陶瓷界面处的传导途径示意图(b)[51]、Li+在LLZO -PEO -LiTFSI不同比例的复合电解质中的路径示意图(c)[52]
Figure 4. Inorganic filler LLZO and PEO form CPE diagram(a)[52], Li+ is distributed in the PEO matrix; PEO matrix and PEO / ceramic interface; the conduction pathway diagram of PEO matrix and ceramic phase and PEO / ceramic interface(b)[51], the path diagram of Li+ in LLZO-PEO-LiTFSI composite electrolyte with different proportions(c) [52]
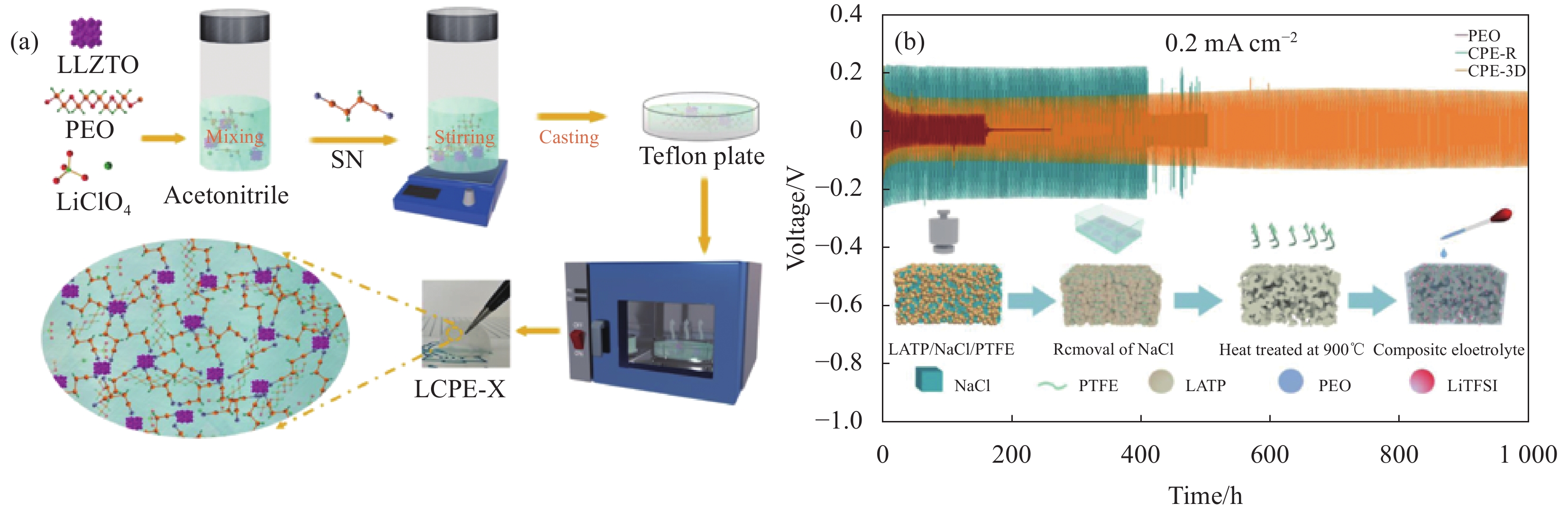
图 5 采用溶液浇铸法制备PEO- LiClO4-LLZTO复合固态电解质流程示意图(a)[46]制备三维多孔导LATP骨架和抑制锂枝晶生长示意图(b)[50]
Figure 5. Preparation of PEO-LiClO4-LLZTO composite solid electrolyte by solution casting process schematic diagram(a)[53], preparation of three-dimensional porous LATP skeleton and inhibition of lithium dendrite growth schematic diagram(b)[50]
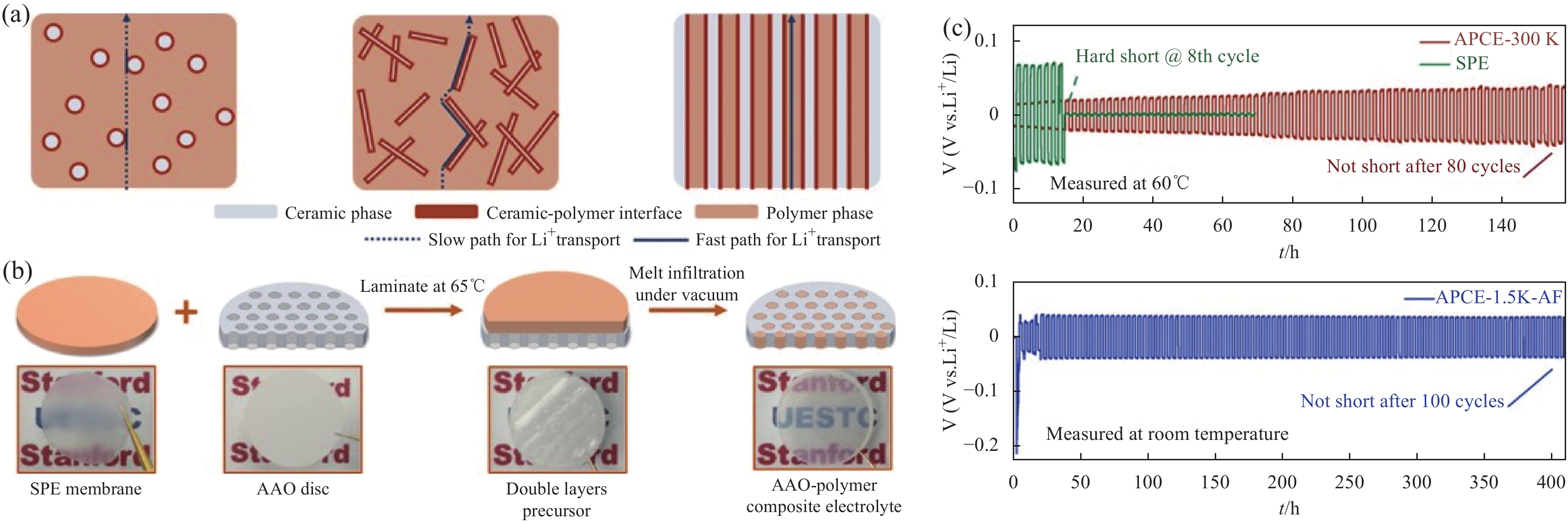
图 9 AAO -聚合物复合电解质的结构设计和电化学性能测试: 内部锂离子传输通道示意图(a)、复合电解质的制备工艺示意图(b)、APCE的在0.25 mA / cm2电流密度下测得的锂对称电池中锂沉积/剥离示意图(c)[62]
Figure 9. The structure design and electrochemical performance test of AAO-polymer composite electrolyte: schematic diagram of internal lithium ion transport channel (a), schematic diagram of preparation process of composite electrolyte (b), schematic diagram of lithium deposition / stripping in lithium symmetric battery measured by APCE at a current density of 0.25 mA / cm2 (c)[62]
表 1 PEO与其他聚合物共混后离子电导率[13]
Table 1 The ionic conductivity of PEO after blending with other polymers was studied [13]
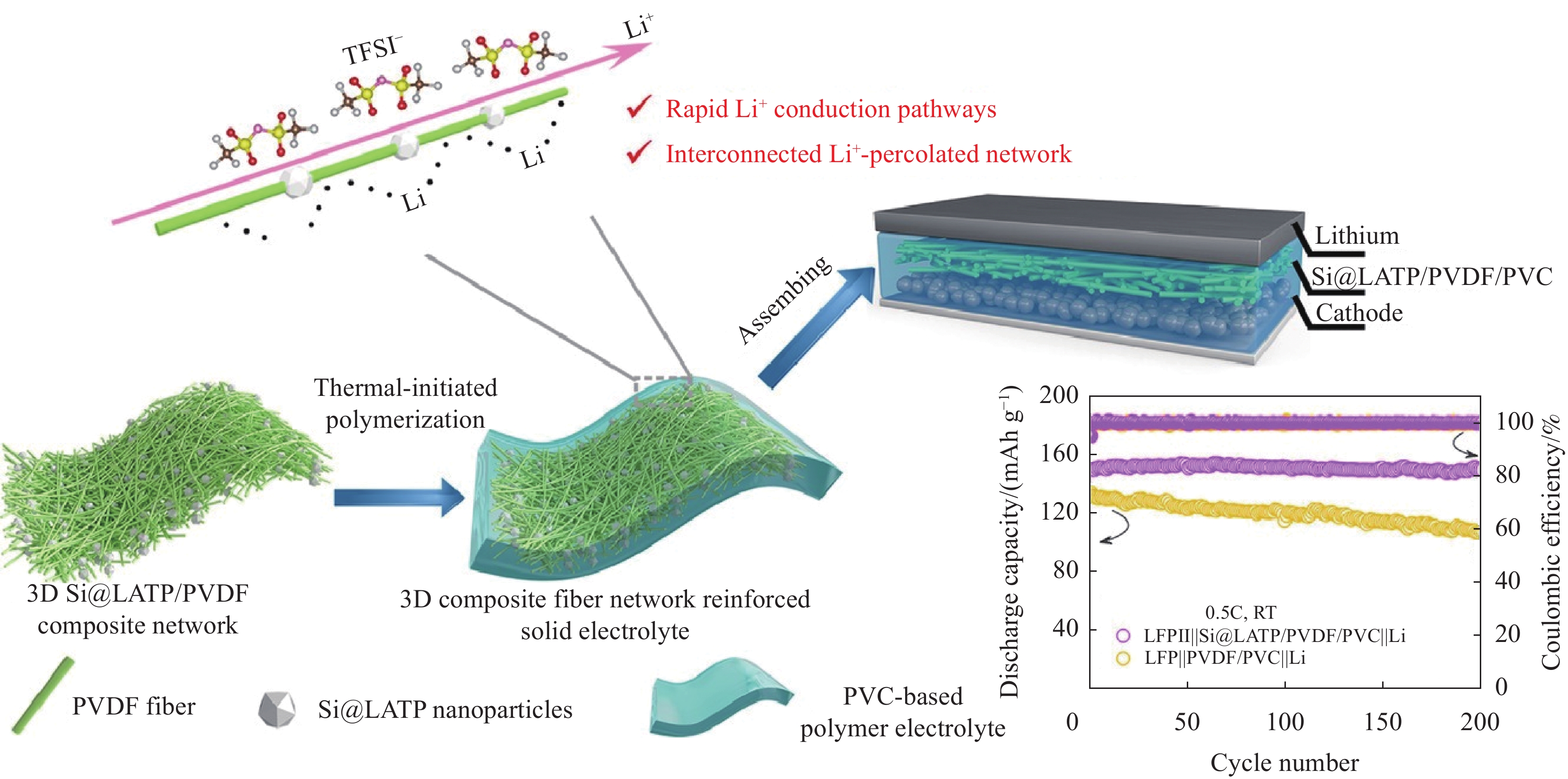
polymer matrix lithium salt temperature/
℃Ionic conductivity/
(S·cm−1)PEO/MEEP LiBF4 25 4 × 10−6 PEO/PES LiClO4 25 1.0 × 10−5 PEO/PET LiClO4 25 2.0 × 10−5 PEO/PVDF LiClO4 30 2.6 × 10−5 PEO/PVDF LiTFSI 30 4.9 × 10−3 -
[1] 王蔼廉, 计文希, 陈婧, 等. 锂电池用固态电解质研究进展[J]. 高分子通报, 2019, (9): 1-14. WANG Gelian, JI Wenxi, CHEN Jing, et al. Research progress of solid electrolyte for lithium battery[J]. Polymer bulletin, 2019, (9): 1-14(in Chinese).
[2] CHENG H, SHAPTER J G, LI Y, et al. Recent progress of advanced anode materials of lithium-ion batteries[J]. Journal of Energy Chemistry, 2021, 57: 451-468. DOI: 10.1016/j.jechem.2020.08.056
[3] 邢宝林, 鲍倜傲, 李旭升, 等. 锂离子电池用石墨类负极材料结构调控与表面改性的研究进展[J]. 材料导报, 2020, 34(15): 15063-15068. DOI: 10.11896/cldb.19080114 XING Baolin, BAO Chouao, LI Xusheng, et al. Research Progress on Structure Regulation and Surface Modification of Graphite Anode Materials for Lithium Ion Batteries[J]. Materials Review, 2020, 34(15): 15063-15068(in Chinese). DOI: 10.11896/cldb.19080114
[4] MA S, JIANG M, TAO P, et al. Temperature effect and thermal impact in lithium-ion batteries: A review[J]. Progress in Natural Science-Materials International, 2018, 28(6): 653-666. DOI: 10.1016/j.pnsc.2018.11.002
[5] 詹元杰, 武怿达, 晓威, 等. 基于碳酸酯基电解液的4.5V电池[J]. 储能科学与技术, 2020, 9(02): 319-330. ZHAN Yuanjie , WU Yida, XIAO Wei, et al. 4.5 V Li-ion battery with a carbonate ester-based electrolyte[J]. Energy Storage Science and Technology, 2020, 9(02): 319-330(in Chinese).
[6] 吴晨, 周颖, 朱晓龙, 等. 锂金属电池用高浓度电解液体系研究进展[J]. 物理化学学报, 2021, 37 (02): 36-52. WU Chen, ZHOU Ying, ZHU Xiaolong , et al. Research Progress on High Concentration Electrolytes for Li Metal Batteries[J]. Acta Physico-Chimica Sinica, 2021, 37 (02): 36-52(in Chinese).
[7] DU G, ZHENG L, ZHANG Z, et al. Overview of research on thermal safety of lithium-ion batteries[J]. Energy Storage Science and Technology, 2019, 8(3): 500-505.
[8] ZHANG J, DONG T, YANG J, et al. Research progress, challenge and perspective of all-solid-state polymer lithium batteries[J]. Energy Storage Science and Technology, 2018, 7(5): 861-868.
[9] MINDEMARK J, LACEY M J, BOWDEN T, et al. Beyond PEO—Alternative Host Materials for Li+ Conducting Solid Polymer Electrolytes[J]. Progress in Polymer Science 2018, 81: 114-143.
[10] LIU J, YUAN H, LIU H, et al. Unlocking the Failure Mechanism of Solid State Lithium Metal Batteries[J]. Advanced Energy Materials, 2022, 12(4): 2100748. DOI: 10.1002/aenm.202100748
[11] CHEN X, GUAN Z, CHU F, et al. Air-stable inorganic solid-state electrolytes for high energy density lithium batteries: Challenges, strategies, and prospects[J]. Infomat, 2022, 4(1): 12248. DOI: 10.1002/inf2.12248
[12] MA J, CHEN B, WANG L, et al. Progress and prospect on failure mechanisms of solid-state lithium batteries[J]. Journal of Power Sources, 2018, 392: 94-115. DOI: 10.1016/j.jpowsour.2018.04.055
[13] XUE Z, HE D, XIE X. Poly (ethylene oxide)-based electrolytes for lithium-ion batteries[J]. Journal of Materials Chemistry A, 2015, 3(38): 19218-19253. DOI: 10.1039/C5TA03471J
[14] ZHAO N, KHOKHAR W, BI Z, et al. Solid garnet batteries[J]. Joule, 2019, 3(5): 1190-1199. DOI: 10.1016/j.joule.2019.03.019
[15] DUAN H, ZHENG H, ZHOU Y, et al. Stability of garnet-type Li ion conductors: An overview[J]. Solid State Ionics, 2018, 318: 45-53. DOI: 10.1016/j.ssi.2017.09.018
[16] FAN X, ZHONG C, LIU J, et al. Opportunities of flexible and portable electrochemical devices for energy storage: expanding the spotlight onto semi-solid / solid electrolytes[J]. Chemical Reviews, 2022, 122(23): 17155-17239. DOI: 10.1021/acs.chemrev.2c00196
[17] 谷琪, 刘夏夏, 周鑫宇, 等. 用于锂金属电池的聚合物固态电解质的研究进展[J]. 化学学报, 2024, 82(04): 449-457. GU Qi, LIU Xiaxia , ZHOU Xinyu , et al. Recent Progress on Polymer Solid Electrolytes for Lithium Metal Batteries[J]. Atca Chimica Sinica, 2024, 82(04): 449-457(in Chinese).
[18] 王青磊, 王涵, 马静, 等. 聚环氧乙烷聚合物固态电解质的现状及改性策略[J]. 高分子材料科学与工程, 2022, 38(04): 165-173. WANG Qinglei , WANG Han, MA Jing, et al. Current Situation and Modification Strategy of Poly(ethylene oxide) Polymer Solid State Electrolyte. Polymer Materials Science and Engineering, 2022, 38(04): 165-173(in Chinese).
[19] 宋彦, 马静, 秦恩博, 等. 聚合物固态电解质的研究进展[J]. 盐湖研究, 2023, 52(10): 1-12. SONG Yan, MA Jing, QING Enbo, et al. Research Progress of Polymer Solid Electrolyte[J]. Journal of salt lake research, 2023, 52(10): 1-12(in Chinese).
[20] MANTHIRAM A, YU X, WANG S. Lithium battery chemistries enabled by solid-state electrolytes[J]. Nature Reviews Materials, 2017, 2(10): 16103.
[21] 王永勤, 薛旭金, 郭贤慧, 等. PEO基聚合物电解质的研究进展[J]. 塑料工业, 2017, 45(09): 1-8. WANG Yongqin , XUE Xujin , GUO Xianhui , et al. Research Progress on PEO-based Polymer Electrolyte[J]. China plastics industry, 2017, 45(09): 1-8.
[22] WANG R, MEI H, REN W, et al. New Progress of the Research on the Modification of PEO Polymer Matrix and Its High-performance Solid Polymer Electrolyte Materials[J]. Materials Review, 2016, 30(6A): 63-67.
[23] ZHAO X D, ZHU W, LI J R, et al. Research Progress in PEO Based Polymer Electrolytes of All Solid State Lithium Ion Battery[J]. Materials Review, 2014, 28(7): 13-17+44.
[24] YU X Y, LI M, WEI L, et al. Application of Polyacrylonitrile in the Electrolytes of Lithium Metal Battery[J]. Progress in Chemistry, 2023, 35(3): 390-406.
[25] 刘汉奎, 刘芹, 贾维尚, 等. PEO-PAN-PEO三明治结构新型固态聚合物电解质的研究[J]. 四川大学学报(自然科学版), 2018, 55(04): 833-837. LIU Hankui , LIU Qin, JIA Weishang , et al. A novel all-solid-state polymer electrolyte basedon PEO-PAN-PEO sandwich structure[J]. Journal of Sichuan University (Natural Science Edition), 2018, 55(04): 833-837(in Chinese).
[26] 唐致远, 王占良. 聚丙烯腈基聚合物电解质[J]. 化学通报, 2002, 65(6): 379-384. TANG Zhiyuan, WANG Zhanliang. Polyacrylonitrile-based polymer electrolyte[J]. Chemistry, 2002, 65(6): 379-384(in Chinese).
[27] LIU F, HASHIM N A, LIU Y, et al. Progress in the production and modification of PVDF membranes[J]. Journal of membrane science, 2011, 375(1-2): 1-27. DOI: 10.1016/j.memsci.2011.03.014
[28] KANG G , CAO Y , Application and modification of poly (vinylidene fluoride)(PVDF) membranes–a review[J]. Journal of membrane science, 2014, 463: 145-165.
[29] CHOI W, KANG Y, KIM I J, et al. Stable Cycling of a 4 V Class Lithium Polymer Battery Enabled by In Situ Cross-Linked Ethylene Oxide/Propylene Oxide Copolymer Electrolytes with Controlled Molecular Structures[J]. ACS Applied Materials & Interfaces, 2021, 13(30): 35664-35676.
[30] 臧玉莉, 石琨, 邹雷, 等. 3D交联复合结构凝胶聚合物电解质制备研究[J]. 电源技术, 2022, 46(01): 30-33. ZANG Yuli , SHI Kun, ZOU Lei, et al. Preparation of 3D cross-linked gel composite polymer electrolytes[J]. Journal of Power Sources, 2022, 46(01): 30-33(in Chinese).
[31] 张政, 贾弼超, 贺艳兵. PVDF基聚合物固态电解质的组成与改性研究[J]. 电池工业, 2024, 28(03), 1-13. ZHANG Zheng, JIA Bichao , HE Yanbing . Composition and modification designs of PVDF-based polymer solid-state electrolytes[J]. Chinese Battery Industry, 2024, 2024, 28(03), 1-13(in Chinese).
[32] 薄扩, 李志义, 魏炜, 等. 超临界法制备PVDF-HFP-PEO共混聚合物电解质及其性能研究[J]. 现代化工, 2022, 42(12): 229-234. BAO Kuo, LI Zhiyi , WEI Wei, et al. Preparation of PVDF-HFP-PEO blending polymer electrolyte by supercritical method and study on its properties[J]. Modern Chemical Industry, 2022, 42(12): 229-234(in Chinese).
[33] HE C, LIU J, LI J, et al. Blending based polyacrylonitrile/poly(vinyl alcohol) membrane for rechargeable lithium ion batteriers[J]. Journal of Membrane Science, 2018, 560: 30-37. DOI: 10.1016/j.memsci.2018.05.013
[34] REDDEPPA N, SHARMA A K, RAO V V R N, et al. Preparation and characterization of pure and KBr doped polymer blend (PVC/PEO) electrolyte thin films[J]. Microelectronic Engineering, 2013, 112: 57-62. DOI: 10.1016/j.mee.2013.05.015
[35] ZOU L, SHI K, LIU H, et al. Polybenzimidazole-reinforced polyethylene oxide-based polymer-in-salt electrolytes enabling excellent structural stability and superior electrochemical performance for lithium metal batteries[J]. Chemical Engineering Journal, 2023, 465: 142794. DOI: 10.1016/j.cej.2023.142794
[36] 宋鑫, 高志浩, 骆林, 等. 全固态锂电池有机-无机复合电解质研究进展[J]. 复合材料学报, 2023, 40(4): 1857-1878. SONG Xin, GAO Zhihao, LUO Lin, et al. Research progress of organic-inorganic composite electrolytes for all-solid-state lithium batteries[J]. Atca Materiae Compositae Sinica, 2023, 40(4): 1857-1878(in Chinese).
[37] 刘聪, 钟霖峰, 宫萧琪, 等. 固态锂电池用有机-无机复合电解质的研究进展[J]. 复合材料学报, 2024, 41(1): 1-15. LIU Cong, ZHONG Linfeng, GONG Xiaoqi, et al. Research progress of organic-inorganic composite electrolytes for solid-state lithium batterie[J]. Atca Materiae Compositae Sinica, 2024, 41(1): 1-15(in Chinese).
[38] TANG S, GUO W, FU Y. Advances in composite polymer electrolytes for lithium batteries and beyond[J]. Advanced Energy Materials, 2021, 11(2): 2000802. DOI: 10.1002/aenm.202000802
[39] LIANG H, WANG L, WANG A, et al. Tailoring practically accessible polymer/inorganic composite electrolytes for all-solid-state lithium metal batteries: a review[J]. Nano-Micro Letters, 2023, 15(1): 42. DOI: 10.1007/s40820-022-00996-1
[40] 李香莉, 肖凯军, 郭祀远. PVDF/Al2O3杂化膜的制备与性能表征[J]. 华南理工大学学报(自然科学版), 2010, 38(07): 112-116. LI Xiangli , XIAO Kaijun , GUO Siyuan. Preparation and Characterization of Hybrid PVDF /Al2O3 Membrane[J]. Journal of South China University of Technology (Natural Science Edition) , 2010, 38(07): 112-116(in Chinese).
[41] DAMIN G, YICAI L, LIU Y, et al. Research on the Electrochemical Properties of PEO8-LiClO4-SiO2-SCA[J]. Acta Chimica Sinica, 2010, 68(22): 2367-2372.
[42] CROCE F, SETTIMI L, SCROSATI B. Superacid ZrO2-added, composite polymer electrolytes with improved transport properties[J]. Electrochemistry communications, 2006, 8(2): 364-368. DOI: 10.1016/j.elecom.2005.12.002
[43] WANG C, YANG T, ZHANG W, et al. Hydrogen bonding enhanced SiO2/PEO composite electrolytes for solid-state lithium batteries[J]. Journal of Materials Chemistry A, 2022, 10(7): 3400-3408. DOI: 10.1039/D1TA10607D
[44] NGUYEN Q H, PARK M G, Nguyen H L, et al. Cubic garnet solid polymer electrolyte for room temperature operable all-solid-state-battery[J]. Journal of Materials Research and Technology, 2021, 15: 5849-5863. DOI: 10.1016/j.jmrt.2021.11.055
[45] HUANG J, HUANG Y, ZHANG Z, et al. Li6.7La3Zr1.7Ta0. 3O12 reinforced PEO/PVDF-HFP based composite solid electrolyte for all solid-state lithium metal battery[J]. Energy & Fuels, 2020, 34(11): 15011-15018.
[46] ZHANG X, FU C, CHENG S, et al. Novel PEO-based composite electrolyte for low-temperature all-solid-state lithium metal batteries enabled by interfacial cation-assistance[J]. Energy Storage Materials, 2023, 56: 121-131. DOI: 10.1016/j.ensm.2022.12.048
[47] LIU K, ZHANG R, SUN J, et al. Polyoxyethylene (PEO)| PEO–perovskite| PEO composite electrolyte for all-solid-state lithium metal batteries[J]. ACS applied materials & interfaces, 2019, 11(50): 46930-46937.
[48] ZHU P, YAN C, DIRICAN M, et al. Li0.33La0.557TiO3 ceramic nanofiber-enhanced polyethylene oxide-based composite polymer electrolytes for all-solid-state lithium batteries[J]. Journal of Materials Chemistry A, 2018, 6(10): 4279-4285. DOI: 10.1039/C7TA10517G
[49] ZHAI H, XU P, NING M, et al. A flexible solid composite electrolyte with vertically aligned and connected ion-conducting nanoparticles for lithium batteries[J]. Nano Letters, 2017, 17(5): 3182-3187. DOI: 10.1021/acs.nanolett.7b00715
[50] WANG G, LIU H, LIANG Y, et al. Composite polymer electrolyte with three-dimensional ion transport channels constructed by NaCl template for solid-state lithium metal batteries[J]. Energy Storage Materials, 2022, 45: 1212-1219. DOI: 10.1016/j.ensm.2021.11.021
[51] SUY, XU F, ZHANG X, et al. Rational design of high-performance PEO/ceramic composite solid electrolytes for lithium metal batteries[J]. Nano-Micro Letters, 2023, 15(1): 82. DOI: 10.1007/s40820-023-01055-z
[52] ZHENG J, Hu Y Y. New insights into the compositional dependence of Li-ion transport in polymer–ceramic composite electrolytes[J]. ACS applied materials & interfaces, 2018, 10(4): 4113-4120.
[53] WANG X, ZHAO C, LIU B, et al. Creating Edge Sites within the 2D Metal-Organic Framework Boosts Redox Kinetics in Lithium–Sulfur Batteries[J]. Advanced Energy Materials, 2022, 12(42): 2201960. DOI: 10.1002/aenm.202201960
[54] SUN W, TANG X, YANG Q, et al. Coordination-induced interlinked covalent-and metal–organic-framework hybrids for enhanced lithium storage[J]. Advanced Materials, 2019, 31(37): 1903176. DOI: 10.1002/adma.201903176
[55] SHEN L, WU H B, LIU F, et al. Creating lithium-ion electrolytes with biomimetic ionic channels in metal–organic frameworks[J]. Advanced Materials, 2018, 30(23): 1707476. DOI: 10.1002/adma.201707476
[56] YUAN Y, CHEN L, LI Y, et al. Functional LiTaO3 filler with tandem conductivity and ferroelectricity for PVDF-based composite solid-state electrolyte[J]. Energy Materials and Devices, 2023, 1(1): 9370004. DOI: 10.26599/EMD.2023.9370004
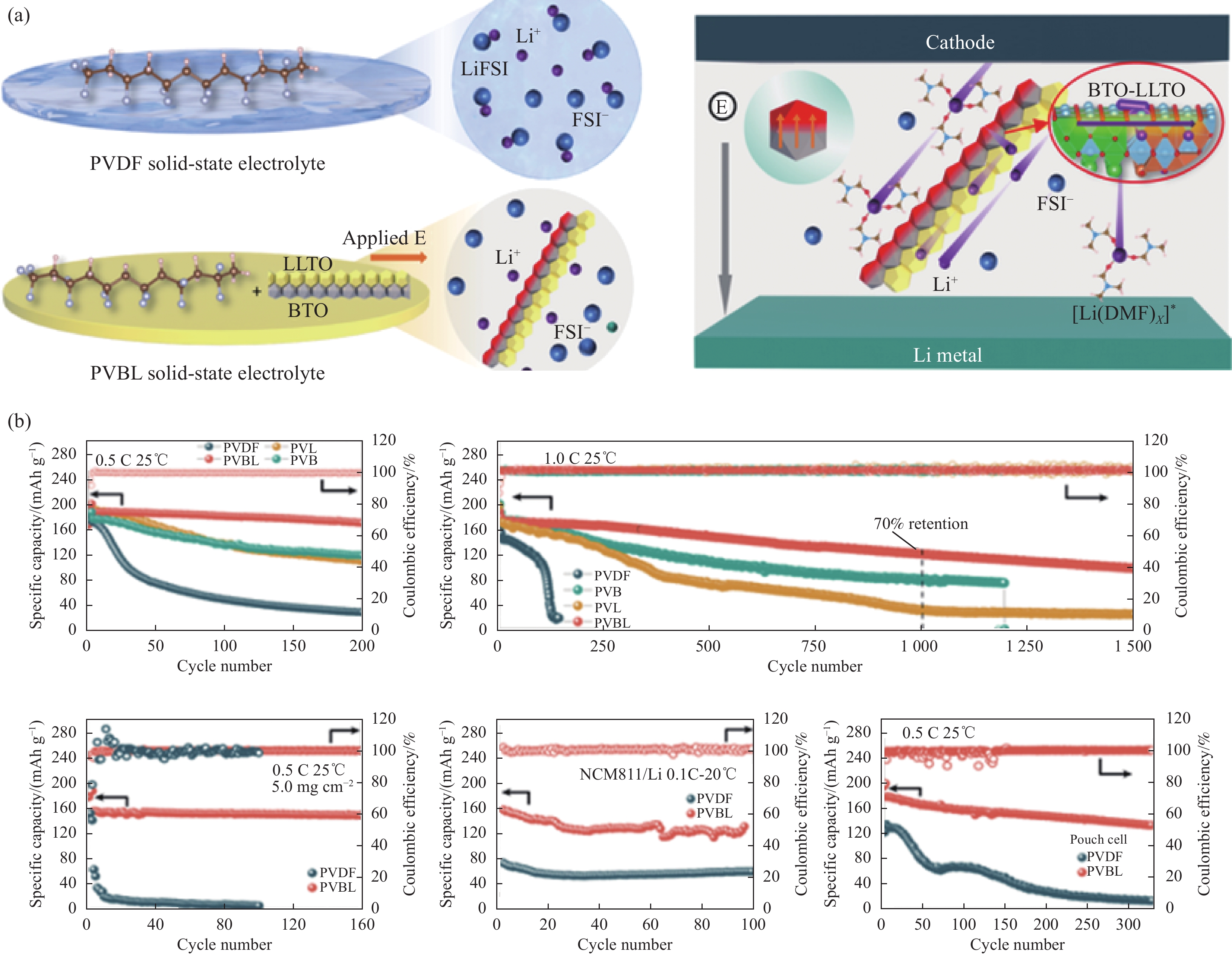
[57] SHI P, MA J, LIU M, et al. A dielectric electrolyte composite with high lithium-ion conductivity for high-voltage solid-state lithium metal batteries[J]. Nature Nanotechnology, 2023, 18(6): 602-610. DOI: 10.1038/s41565-023-01341-2
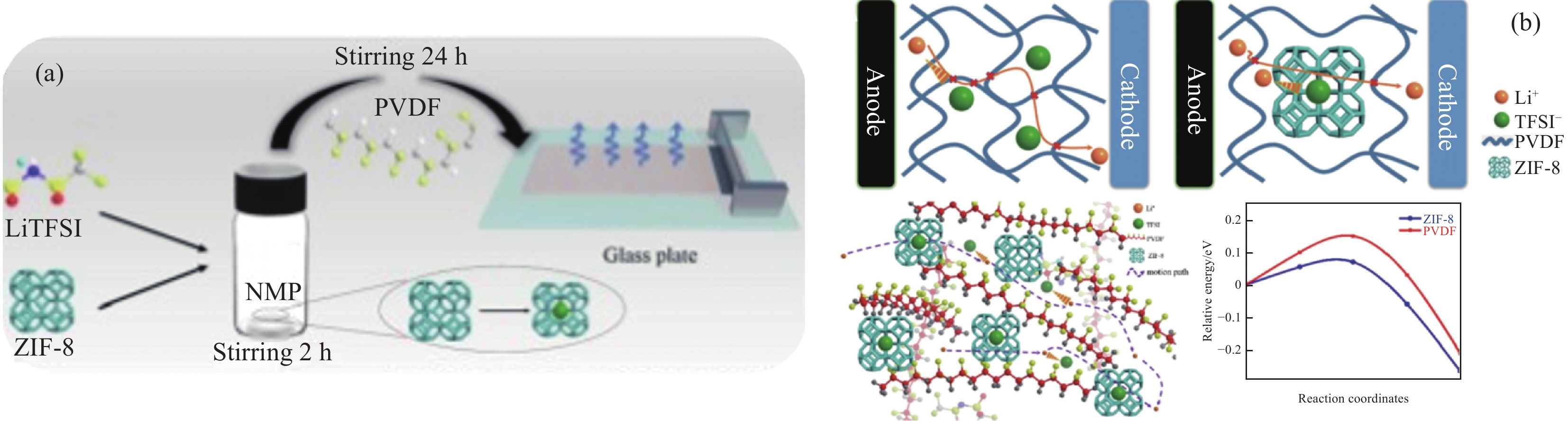
[58] HUANG W, WANG S, ZHANG X, et al. Universal F4-Modified Strategy on Metal–Organic Framework to Chemical Stabilize PVDF-HFP as Quasi-Solid-State Electrolyte[J]. Advanced Materials, 2023, 35(52): 2310147. DOI: 10.1002/adma.202310147
[59] JIANG Y, XU C, XU K, et al. Surface modification and structure constructing for improving the lithium ion transport properties of PVDF based solid electrolytes[J]. Chemical Engineering Journal, 2022, 442: 136245. DOI: 10.1016/j.cej.2022.136245
[60] FURUKAWA H, CORDOVA K E, KEEFFE M, et al. The chemistry and applications of metal-organic frameworks[J]. Science, 2013, 341(6149): 1230444. DOI: 10.1126/science.1230444
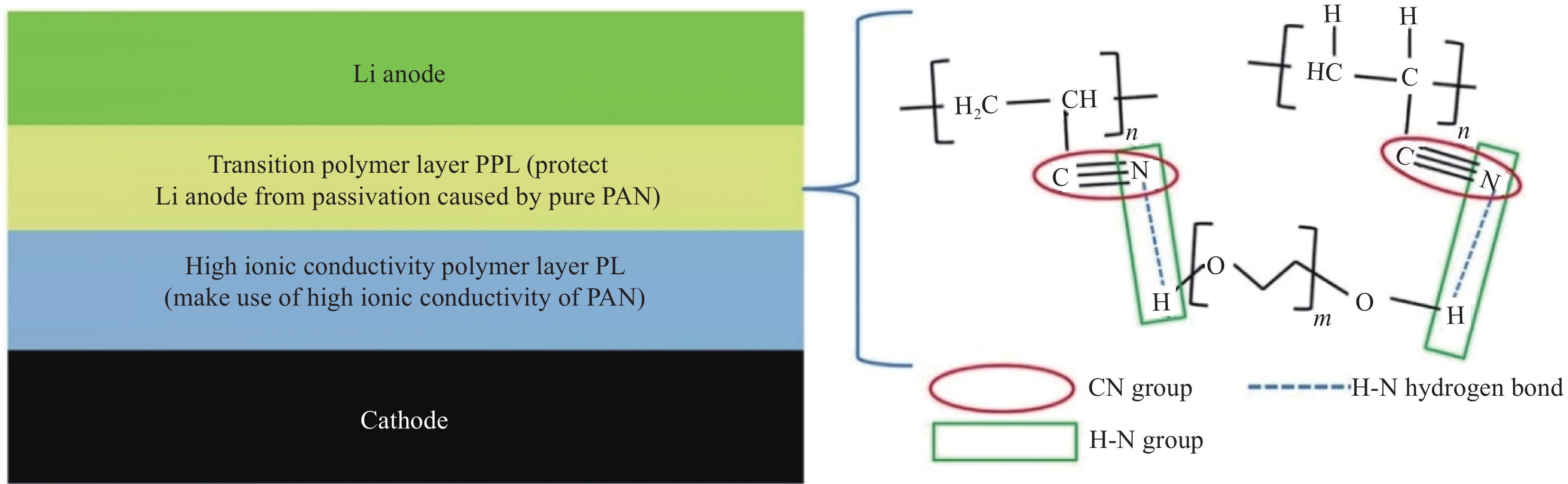
[61] WANG X, HAO X, XIA Y, et al. A polyacrylonitrile (PAN)-based double-layer multifunctional gel polymer electrolyte for lithium-sulfur batteries[J]. Journal of membrane science, 2019, 582: 37-47. DOI: 10.1016/j.memsci.2019.03.048
[62] ZHANG X, XIE J, SHI F, et al. Vertically aligned and continuous nanoscale ceramic–polymer interfaces in composite solid polymer electrolytes for enhanced ionic conductivity[J]. Nano letters, 2018, 18(6): 3829-3838. DOI: 10.1021/acs.nanolett.8b01111
[63] LIU Y, ZENG Q, LI Z, et al. Recent development in topological polymer electrolytes for rechargeable lithium batteries[J]. Advanced Science, 2023, 10(15): 2206978. DOI: 10.1002/advs.202206978
[64] WANG S, ZHANG L, ZENG Q, et al. Cellulose microcrystals with brush-like architectures as flexible all-solid-state polymer electrolyte for lithium-ion battery[J]. ACS Sustainable Chemistry & Engineering, 2020, 8(8): 3200-3207.
[65] REN S, ZHENG T, ZHOU Q, et al. Preparation and ionic conductivity of composite polymer electrolytes based on hyperbranched star polymer[J]. Ionics, 2014, 20: 1225-1234. DOI: 10.1007/s11581-013-1061-4
[66] LI S, ZHANG H, CHEN W, et al. Toward commercially viable Li-S batteries: Overall performance improvements enabled by a multipurpose interlayer of hyperbranched polymer-grafted carbon nanotubes[J]. ACS applied materials & interfaces, 2020, 12(23): 25767-25774.
[67] XU H, WANG A, LIU X, et al. A new fluorine-containing star-branched polymer as electrolyte for all-solid-state lithium-ion batteries[J]. Polymer, 2018, 146: 249-255. DOI: 10.1016/j.polymer.2018.05.045
[68] OSMAN Z, MDISA K B, AHMAD A, et al. A comparative study of lithium and sodium salts in PAN-based ion conducting polymer electrolytes[J]. Ionics, 2010, 16: 431-435. DOI: 10.1007/s11581-009-0410-9
[69] 康树森, 杨程响, 杨泽林, 等. 旋涂法制备 PEO-PAN-PMMA 三组分共混凝胶聚合物电解质[J]. 化学学报, 2020, 78(12): 1441. DOI: 10.6023/A20080356 KANG Shusen, YANG Chengxiang, YANG Zelin, et al. Blending Based PEO-PAN-PMMA Gel Polymer Electrolyte Prepared by Spaying Casting for Solid-state Lithium Metal Batteries[J]. Acta Chimica sinic, 2020, 78(12): 1441(in Chinese) DOI: 10.6023/A20080356
[70] 徐疆兰. 锂离子电池用PAN/TPU/PPC三元凝胶聚合物电解质的制备与研究[D]. 湘潭: 湘潭大学, 2019. XU Jianglan. Preparation and Study of Ternary PAN/TPU/PPC Gel Polymer Electrolytes for Lithium Ion Battery[D]. Xiangtan: Xiangtan University, 2019.
[71] VIJAYAKUMAR V, ANOTHUMAKKOOL B, KURUNGO S, et al. In situ polymerization process: an essential design tool for lithium polymer batteries[J]. Energy & environmental science, 2021, 14(5): 2708-2788.
[72] HUANG S, CUI Z, QIAO L, et al. An in-situ polymerized solid polymer electrolyte enables excellent interfacial compatibility in lithium batteries[J]. Electrochimica Acta, 2019, 299: 820-827. DOI: 10.1016/j.electacta.2019.01.039
[73] LEI Z, QIU Q, SHEN J, et al. Room-Temperature Solid-State Lithium Metal Batteries Using Metal Organic Framework Composited Comb-Like Methoxy Poly (ethylene glycol) Acrylate Solid Polymer Electrolytes[J]. Macromolecular Materials and Engineering, 2021, 306(10): 2100336. DOI: 10.1002/mame.202100336
[74] JIN Y, ZONG X, ZHANG X, et al. Constructing 3D Li+ percolated transport network in composite polymer electrolytes for re- chargeable quasi-solid-state lithium batteries[J]. Energy Storage Materials, 2022, 49: 433-444. DOI: 10.1016/j.ensm.2022.04.035
[75] 何双莉, 苏子秋, 李德阳, 等. PAN基耐高压聚合物电解质的制备及性能研究[J]. 北京服装学院学报(自然科学版), 2022, 42(2): 27-32. HE Shuangli, SU Ziqiu, LI Deyang, et al. Preparation and Performance of PAN-based High Voltage Polymer Electrolyte[J]. Journal of Beijing Institute of Fashion Technology( Natural Science Edition), 2022, 42(2): 27-32(in Chinese).
[76] MA T, CUI Z, WU Y, et al. Preparation of PVDF based blend microporous membranes for lithium ion batteries by thermally induced phase separation: I. Effect of PMMA on the membrane formation process and the properties[J]. Journal of Membrane Science, 2013, 444: 213-222. DOI: 10.1016/j.memsci.2013.05.028
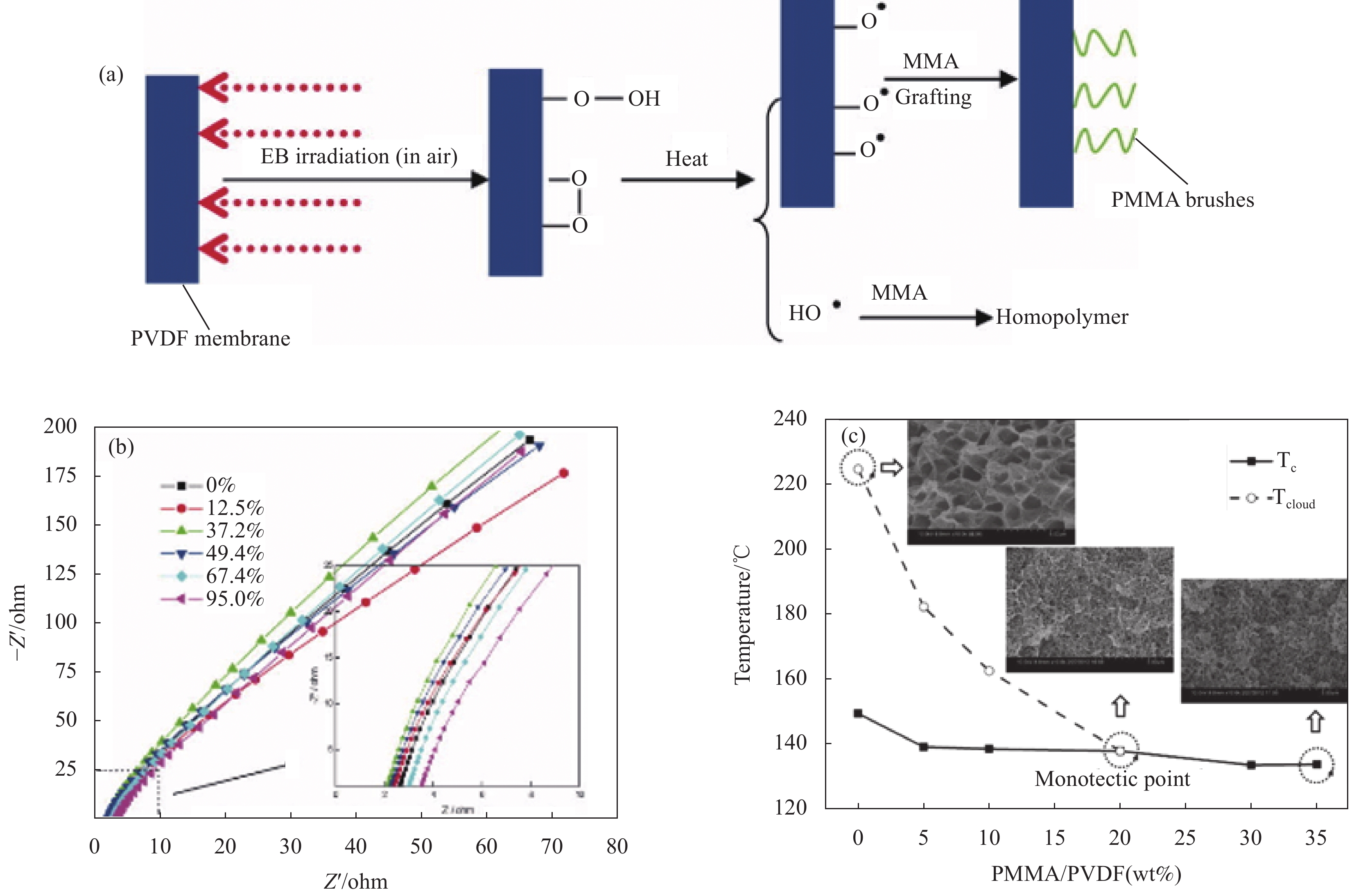
[77] LI Z, WEI J, SHAN F, et al. PVDF/PMMA brushes membrane for lithium-ion rechargeable batteries prepared via preirradiation grafting technique[J]. Journal of Polymer Science Part B: Polymer Physics, 2008, 46(7): 751-758. DOI: 10.1002/polb.21408
-
目的
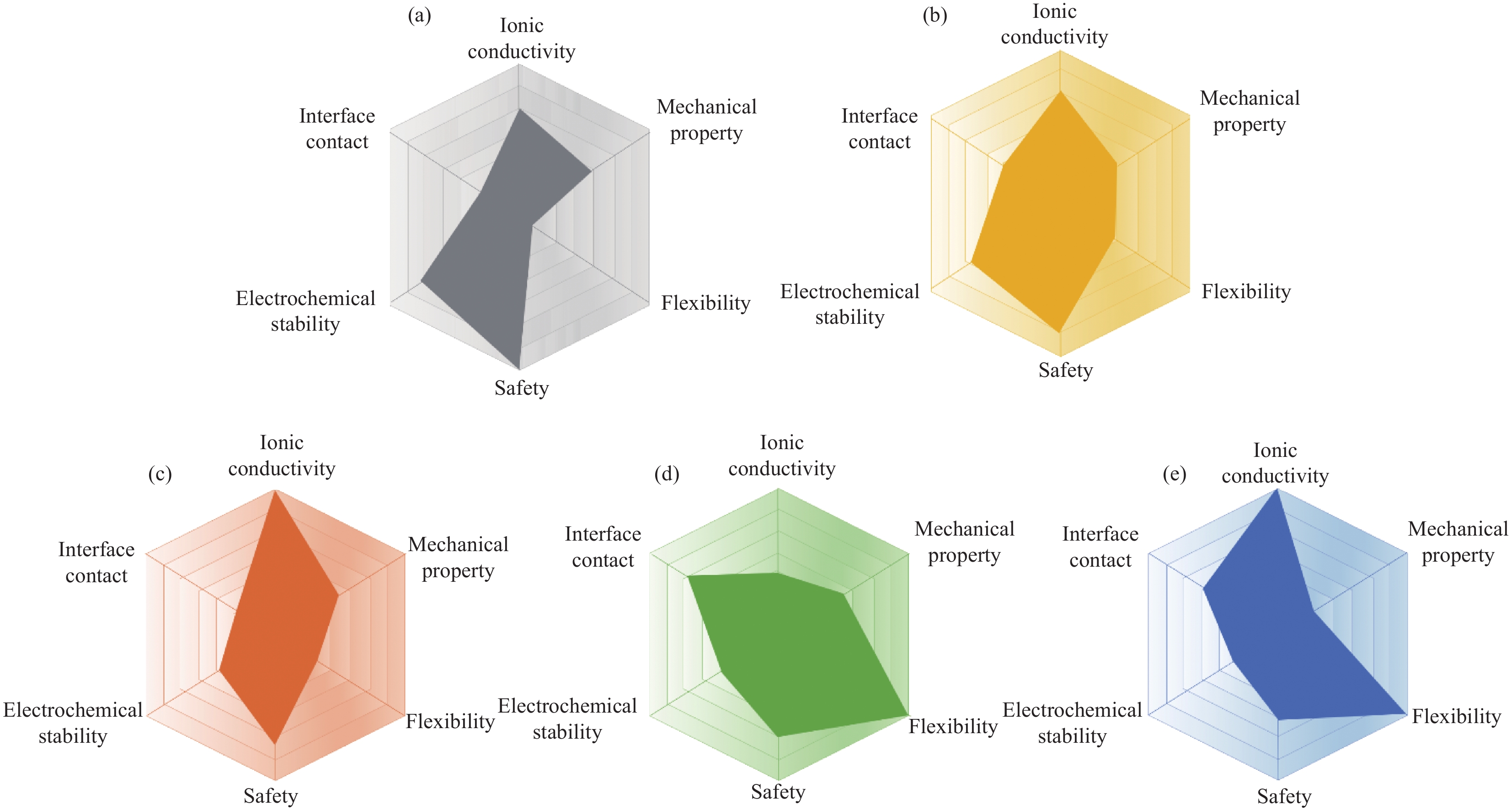
锂离子电池常用的是碳酸酯基类的有机电解液,易燃易挥发,且在循环过程中易造成电池容量衰减,缩短使用寿命,因此,寻找电化学性能优异,安全稳定的电解质材料是提高锂离子电池服役性能的关键。固态聚合物电解质(Solid polymer electrolyte, SPE)由于高安全性、良好的电极界面接触性而受到研究者的广泛关注,但离子电导率偏低以及机械性能差等问题限制了其在锂离子电池中的应用。本文通过综述对固态聚合物电解质基质的改性策略,来提升SPE的综合性能,使其应用在未来固态锂电池的商业化生产中。
方法目前常见的聚合物基质普遍存在离子电导率较低且机械性能不佳的困扰,采取的措施主要有交联、共混、添加无机纳米填料、优化几何结构、改善制备工艺等方面来解决困难。(1)交联改性是通过对聚合物分子结构的简单交联,而共混改性是通过将几种不同的聚合物进行共混,阻止聚合物分子链段的结晶重排,破坏基质的排列规整性,降低基质的结晶度提高了SPE的离子电导率和热稳定性。(2)在基质中添加无机纳米填料,为锂离子迁移提供额外的路径,可以有效提高SPE的离子电导率。此外,利用无机填料的高机械模量,还可为SPE提供了更好的拉伸性能,抵抗电池循环过程中枝晶生长带来的安全问题。无机填料主要分为惰性填料、活性填料以及功能性填料。其中活性填料和功能性填料是目前研究者重点关注的对象。活性填料主要为无机陶瓷类电解质,具有安全性高,离子电导率高的优点。功能性填料主要指某些金属框架填料(如MOF等),能为锂离子传输提供更多的传输通道,且抑制锂枝晶生长。(3)通过优化陶瓷相和聚合物基体的几何结构,改善界面接触性,提高离子电导率。其中非线性拓扑结构的聚合物电解质具有更多的锂离子传输通道和更好的柔韧性,能更好的改善SPE的综合性能。(4)制备工艺对SPE的性能也有影响。制备工艺常用的溶液浇铸法、旋涂法、静电纺丝法、原位聚合法以及热致相分离法。采用合适的制备工作可提高SPE的离子电导率和界面稳定性。其中采用原位聚合法可构建无枝晶的电解质结构,提供更多的锂离子传输通道,抑制锂枝晶生成,提高循环稳定性。
结果通过对聚合物基质的进行交联改性,调节基质几何结构、采用合适的制备工艺以及添加无机填料等方面来改善聚合物基质的结晶度,增加锂离子传输通道,达到提升 SPE的电化学性能,有望促进固态锂离子电池商业化的生产。
结论固态聚合物电解质替代液态电解质,提高锂离子电池使用的安全性,在未来有更广泛的应用前景。尽管目前研究人员采用不同方式改性聚合物基质来提升SPE的机械性能和电化学性能,但在以下方面仍存在一些挑战。(1)需深入研究锂离子的传输机制。采用先进的表征技术和计算模拟技术,全面地分析离子传输机制,为高性能SPE的开发提供理论指导。(2)改进SPE的结构设计,增强界面接触稳定性,进而提高全固态电池的电化学性能。(3)开发新型拓扑聚合物提高电池性能。(4)提高离子电导率。固态电解质的离子电导率仍然低于传统的液态电解质。采用更多的改性策略,提供更多的Li的运输通道,提高离子电导率。(5)减少SPE膜厚度。目前,SPE膜的厚度(100-200μm)仍远高于商业聚丙烯隔膜的厚度(30μm)。还需改善制备工艺获得超薄电解质膜,提高电池性能。





 下载:
下载: