Research progress on optimization design methods for continuous fiber direction and path of composites
-
摘要: 连续纤维增强复合材料因其优异的比刚度、比强度等特性,在航空航天、国防军工、医疗器件等高端装备领域得到了广泛的关注和应用。其中,纤维方向对连续纤维增强复合材料的力学性能有着重要影响,但是由于常规制造工艺的局限,纤维路径通常沿0°、45°、90°等规律一致的方向来设定,连续纤维增强复合材料的优势无法被充分利用。如今,3D打印技术促进了制造具有复杂曲线纤维路径复合材料的发展,其对应的纤维方向及路径优化设计方法正逐步引起国内外专家学者的重点关注。本文围绕纤维增强复合材料的纤维方向及路径优化设计方法,介绍了正交各向异性材料方向优化理论,回顾了纤维角度优化方法,总结了现有纤维路径规划算法,探讨了相关前沿问题并做出了未来展望。本文为高性能连续纤维增强复合材料的优化设计和制造提供了重要信息,有助于推动高性能连续纤维增强复合材料的快速发展和广泛应用。Abstract: Continuous fiber reinforced composites have gained wide attention and application in high-end equipment fields such as aerospace, defense, and medical devices, due to their excellent specific stiffness, specific strength, and other properties. The fiber orientation has a significant impact on the mechanical performance of continuous fiber reinforced composites. However, due to the limitations of conventional manufacturing processes, the fiber paths are usually set along regular directions such as 0°, 45°, 90°, etc., which hinders the full utilization of the advantages of continuous fiber reinforced composites. Nowadays, the development of 3D printing technology has facilitated the manufacturing of composites with complex curved fiber paths, and the corresponding optimization methods for fiber orientation and path design have gradually attracted attention from experts and scholars worldwide. In this article, we focus on the optimization methods for fiber orientation and path design of fiber reinforced composites. We introduce the theory of orthogonal anisotropic material direction optimization, review the methods for fiber angle optimization, summarize the existing fiber path planning algorithms, discuss relevant cutting-edge issues, and provide future prospects. This review provides important information for the design optimization and manufacturing of high-performance continuous fiber reinforced composites, which will contribute to the rapid development and wide application of continuous fiber reinforced composites.
-
Key words:
- composites /
- 3D printing /
- fiber orientation /
- fiber path /
- optimal design
-
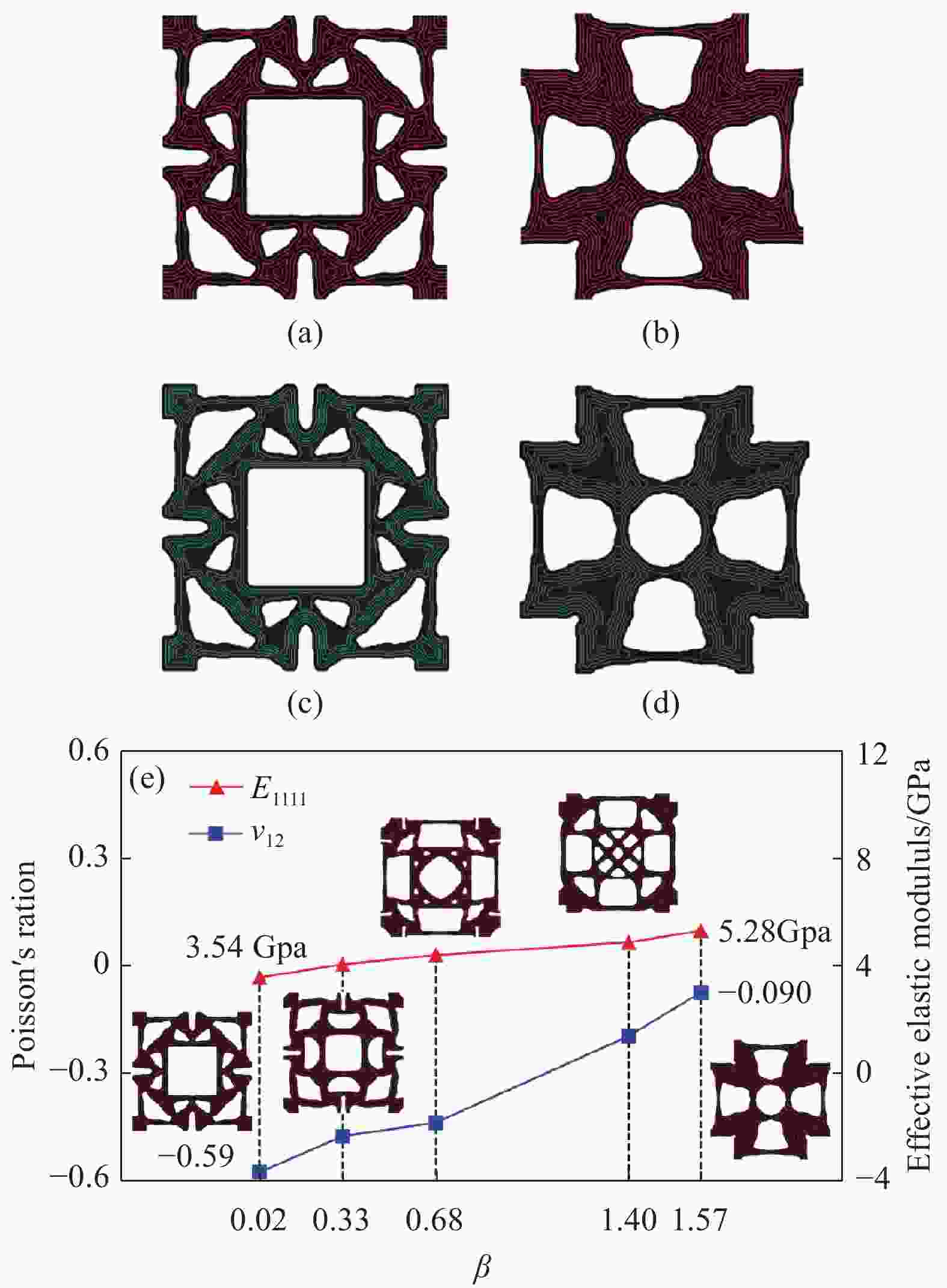
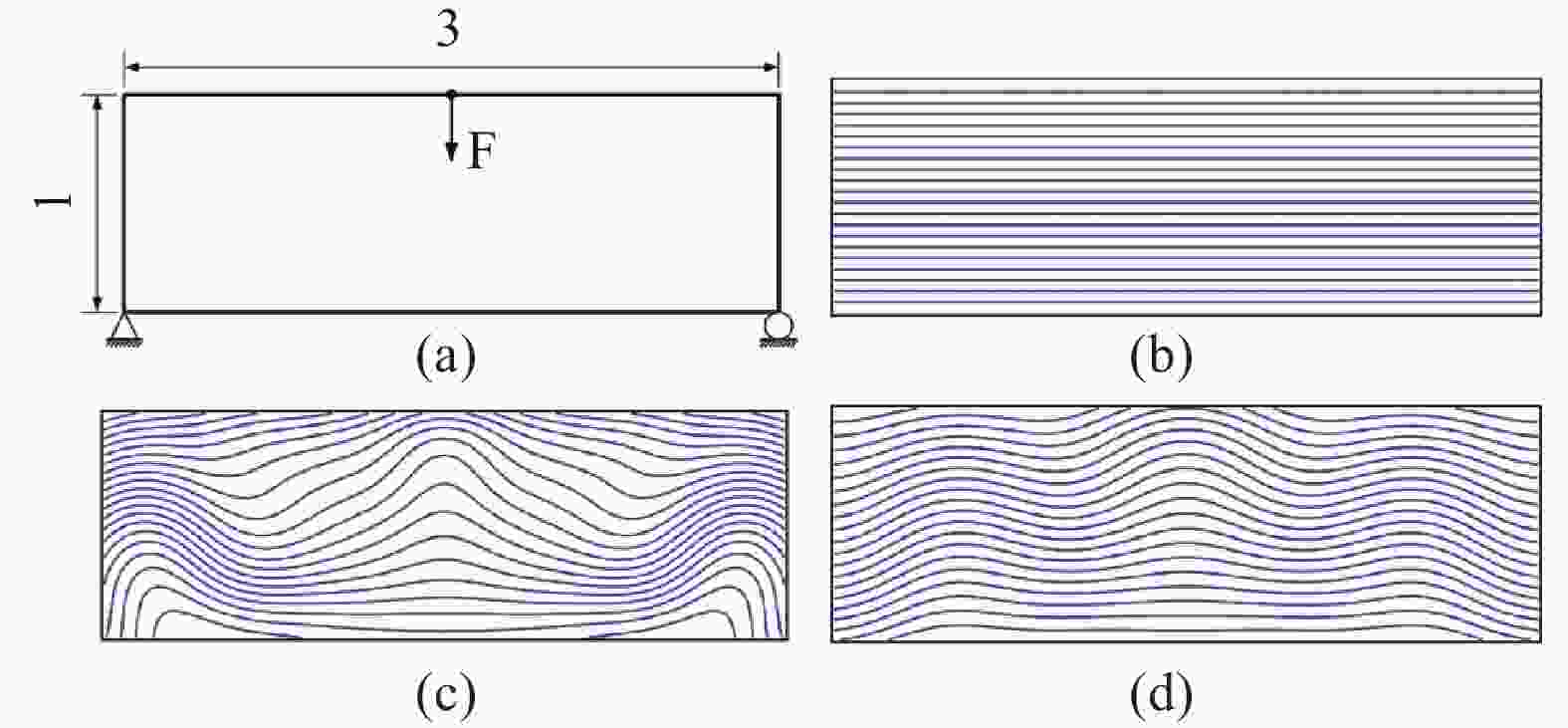
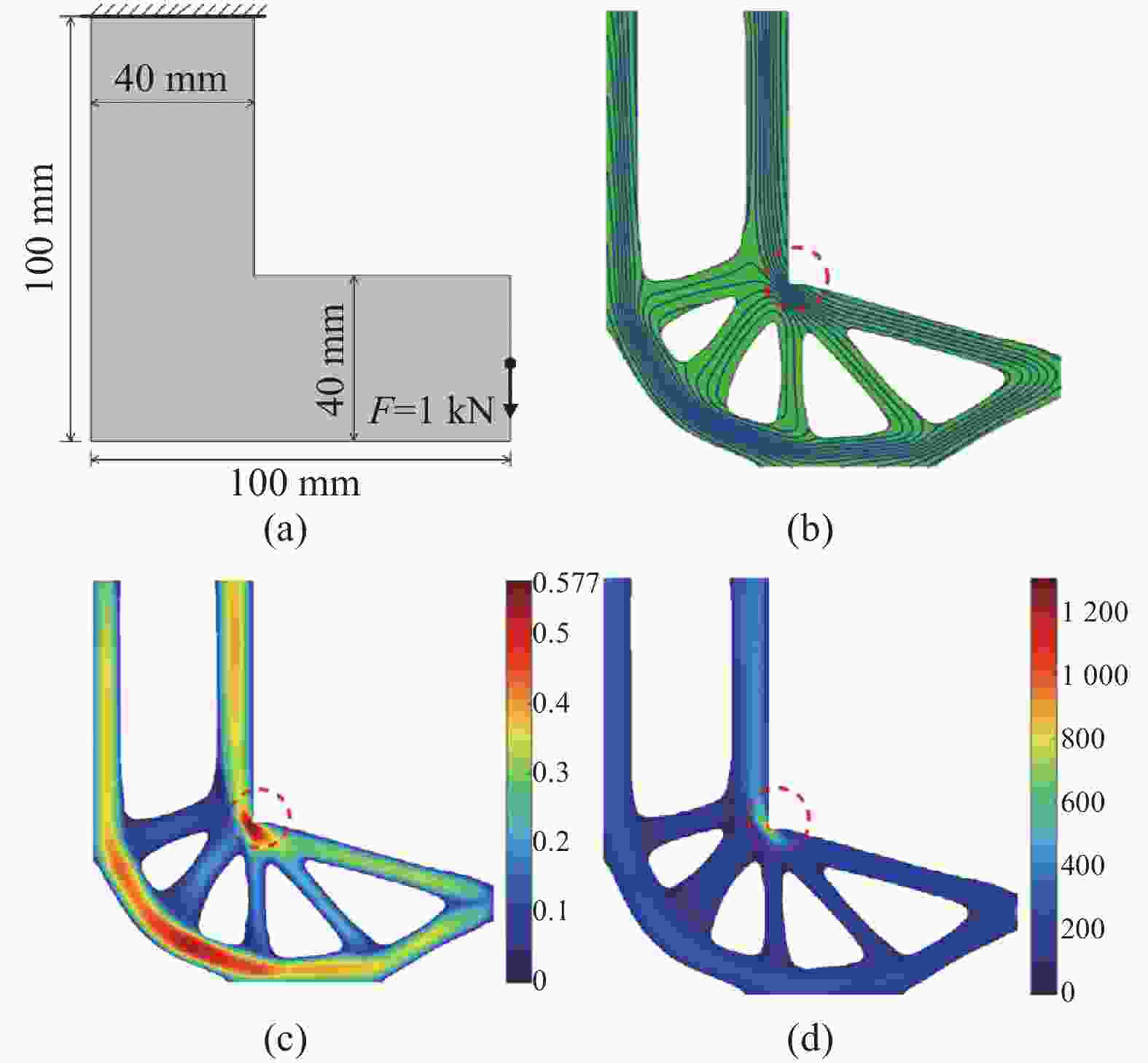
图 1 CFRC拓扑设计:(a)四点弯曲梁[40],(b) 具有负泊松比效应的超结构[41],(c) 三维悬臂梁结构[42],(d) 多载荷情况下的三维梁结构[42]
Figure 1. Topological design CFRC: (a) Four-point bending beam[40],(b) Meta-structures with negative Poisson’s ratio[41], (c) Three-dimension cantilever beam[42], (d) Three-dimension beam structure under multiple-loads[42]
图 6 不同子区间数量情况下悬臂梁的优化结果[71]:(a) 1个子集;(b) 2个子集;(c) 3个子集
Figure 6. Optimization results of cantilever beams under different number of subintervals: (a) One subinterval; (b) Two subintervals; (c) Three subintervals
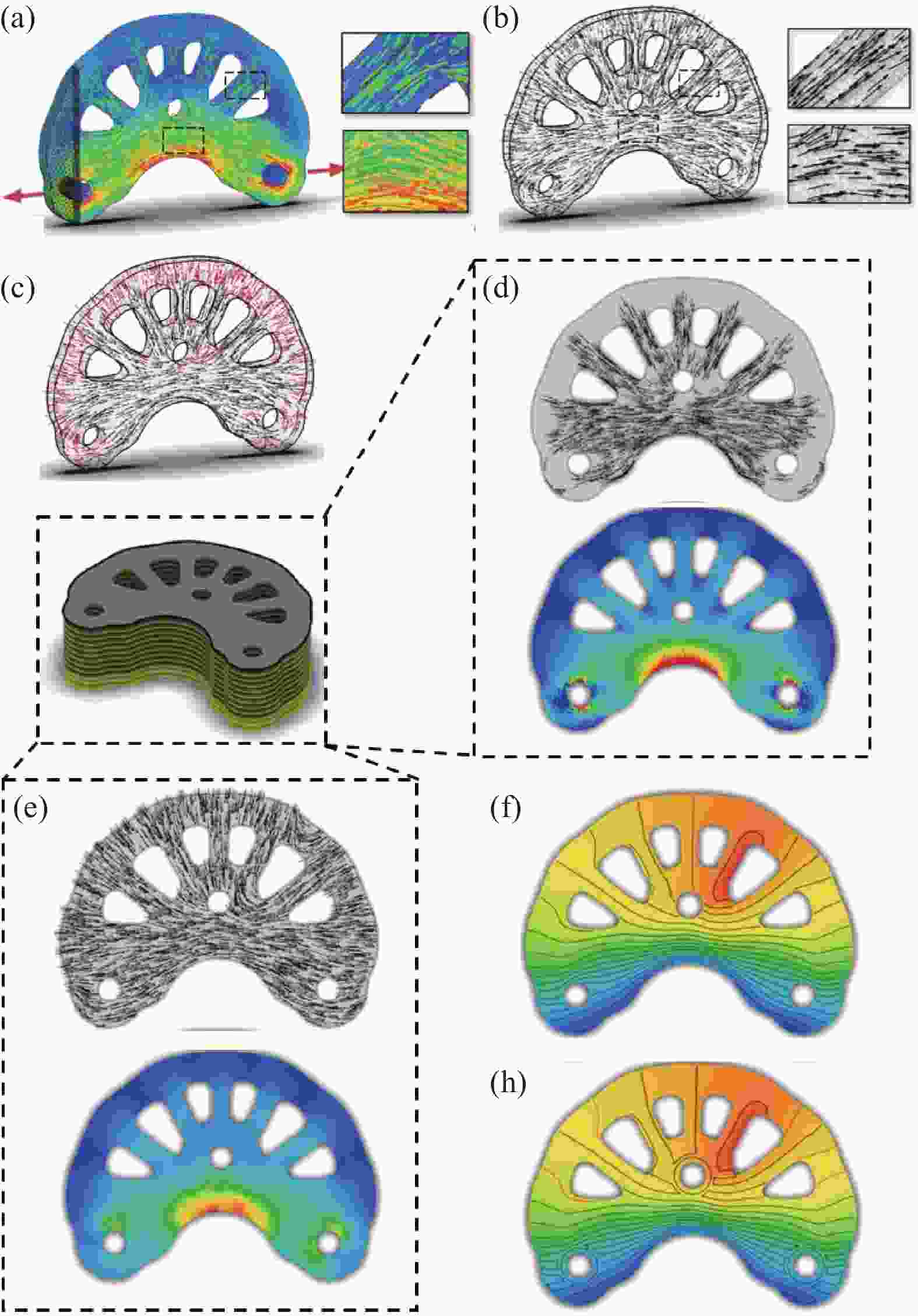
图 15 基于LSF的连续纤维增强复合材料超结构设计:(a)(b) 复合材料超结构中基于LSF得到的连续纤维路径;(c)(d)复合材料超结构的3D打印纤维路径;(e) 复合材料超结构力学性能随调控参数的变化[41]
Figure 15. Design of continuous fiber reinforced meta-composites based on LSF: (a)(b) Continuous fiber path of meta-composite based on LSF; (c)(d) Actually printing path of meta-composite; (e) Variation of mechanical properties of meta-composite versus tailorable parameter[41]
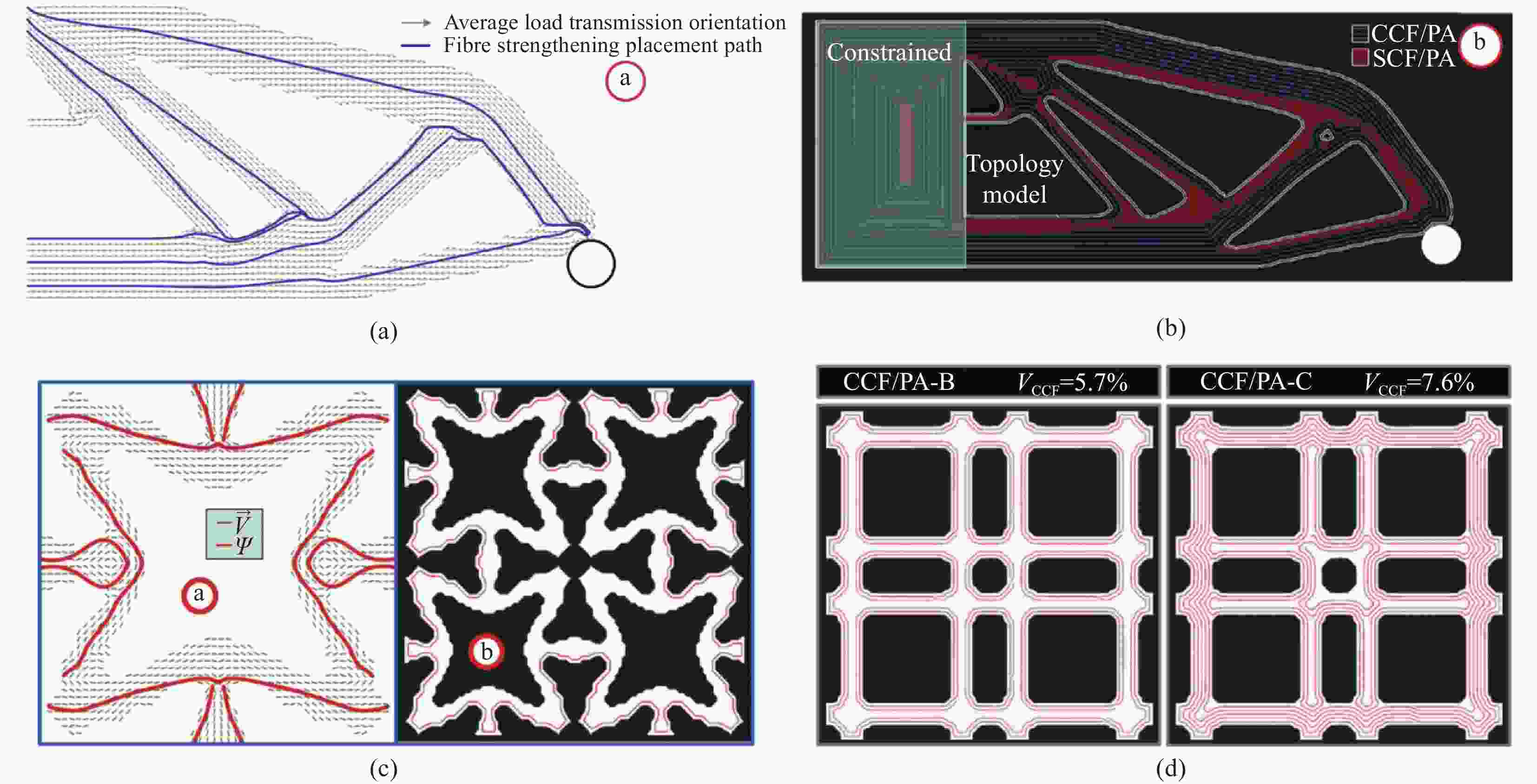
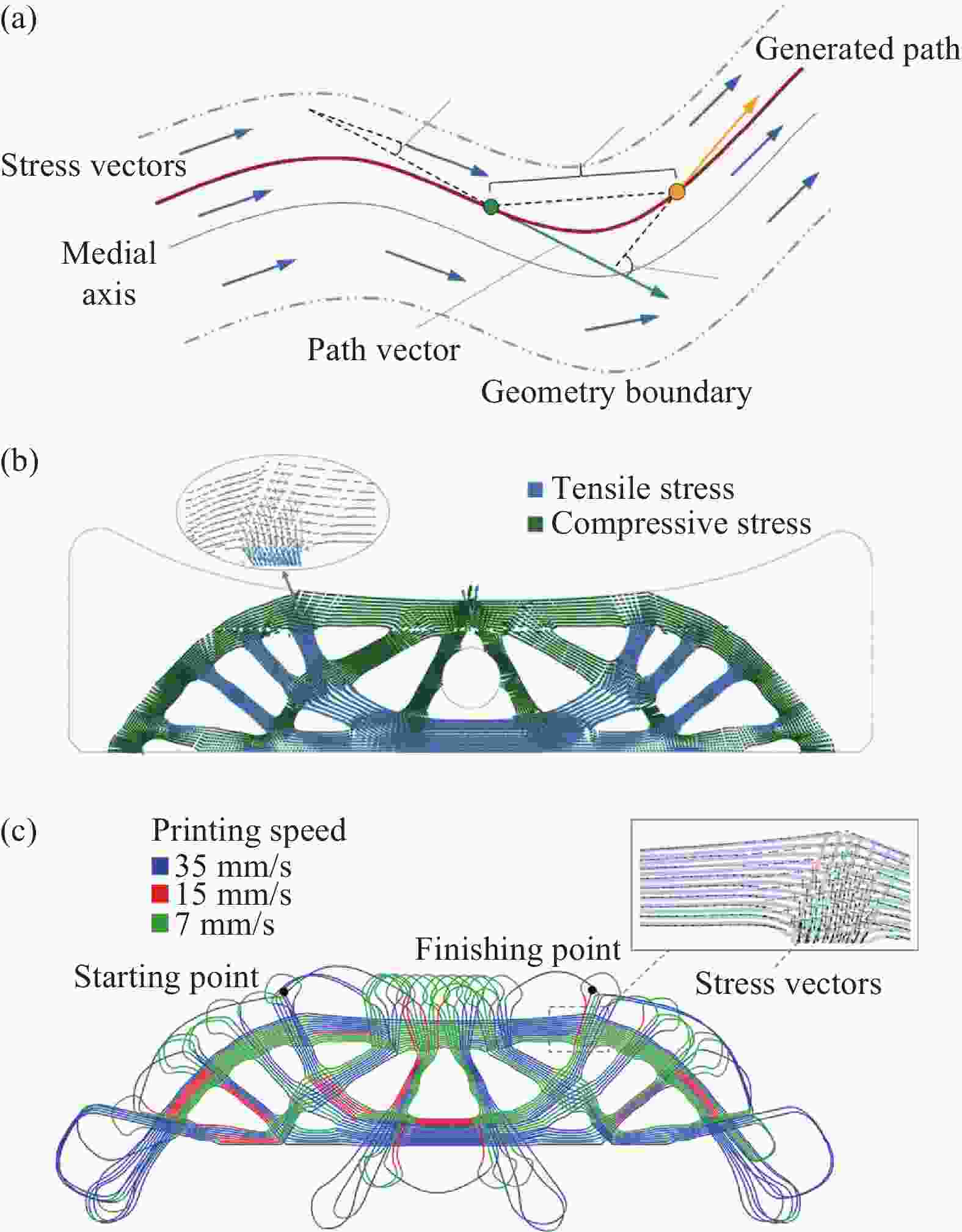
图 19 基于流线方法所设计的连续纤维路径:(a) 复合材料悬臂梁的平均载荷传递方向和连续纤维路径;(b) 复合材料悬臂梁的连续纤维打印路径;(c) 具有负泊松比效应的复合材料超结构;(d) 高弹性模量复合材料格栅结构的连续纤维打印路径[11,116]
Figure 19. Continuous fiber paths designed based on streamline methods: (a) The average load transmission orientation and continuous fiber paths of the cantilever beam; (b) The continuous fiber printing paths of the cantilever beam; (c) The meta-structures with negative Poisson’s ratio; (d) The composite grid structures of enhanced effective elastic modulus and their continuous fiber printing paths [11,116]
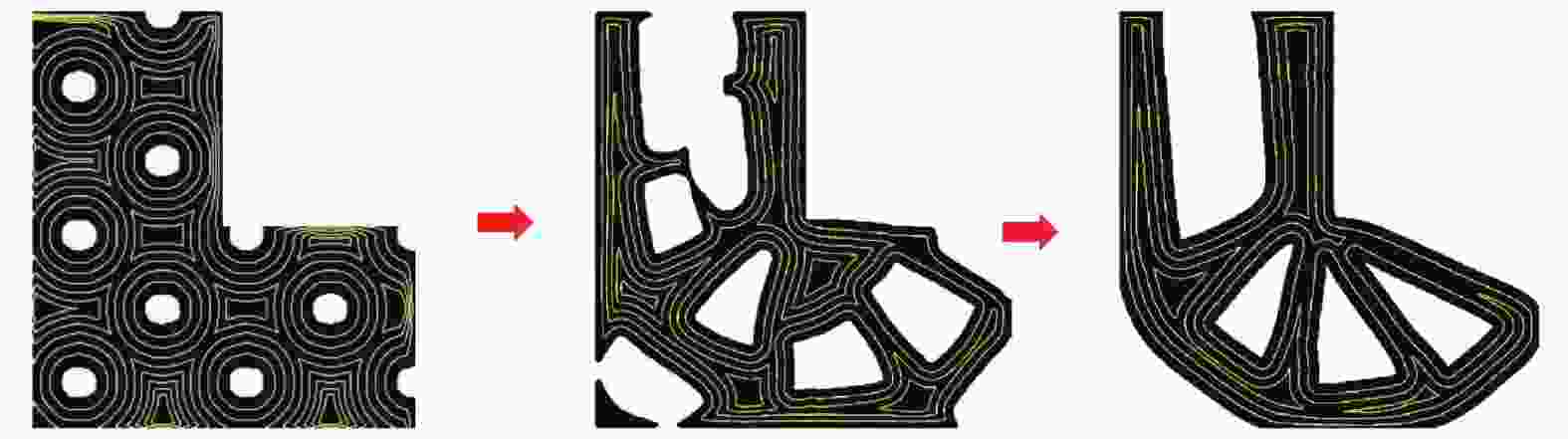
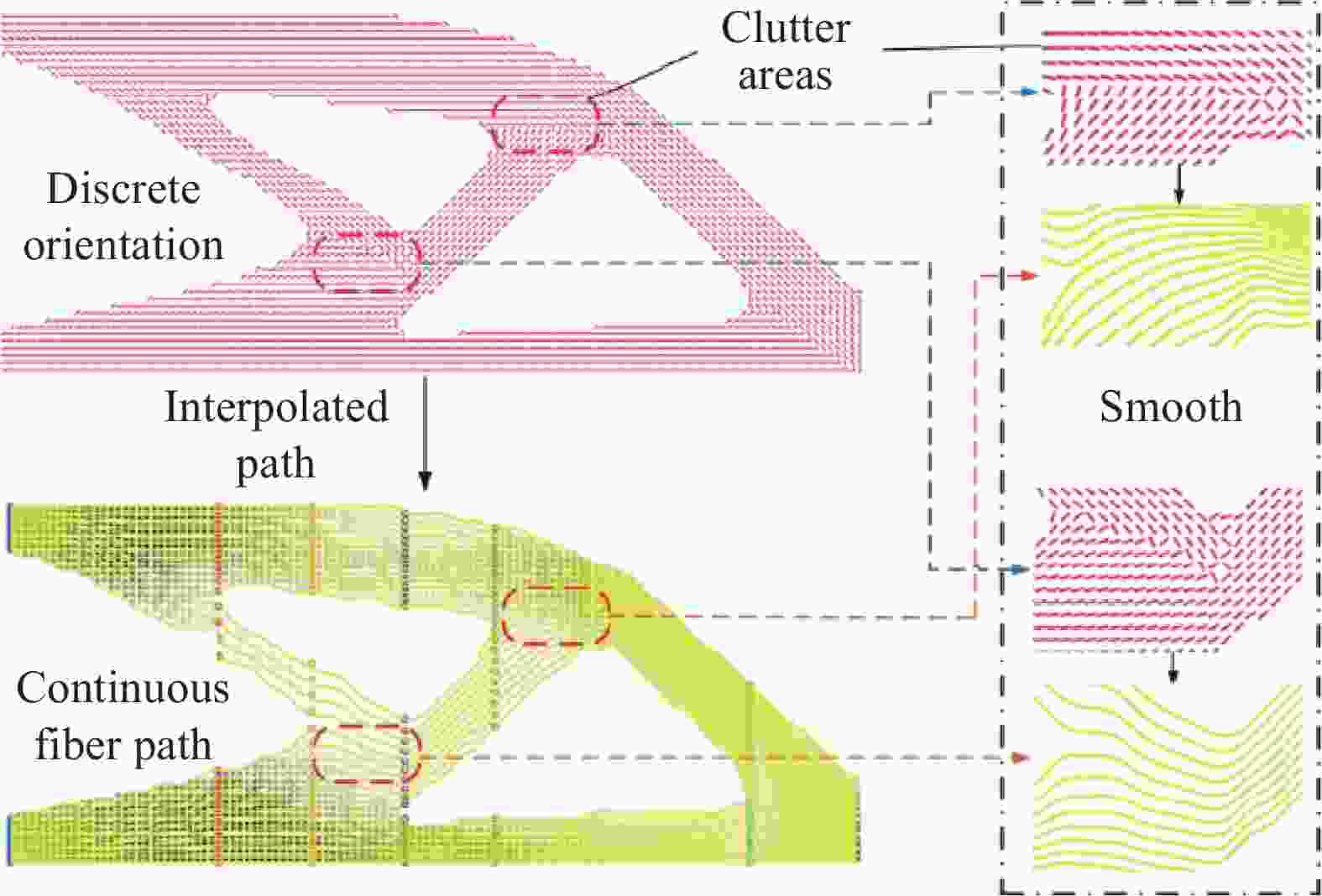
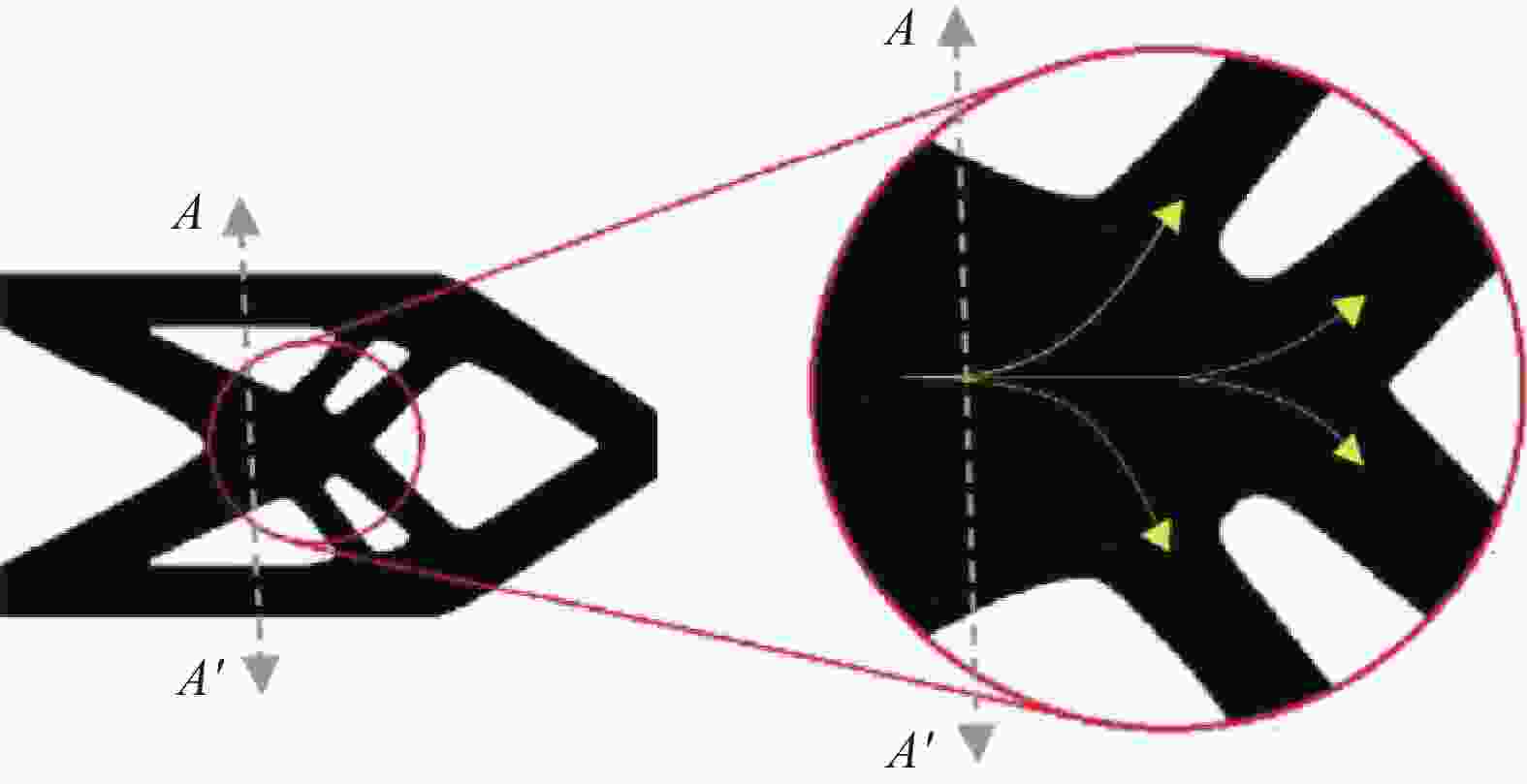
图 21 基于应力场的连续纤维打印路径规划算法:(a) 求解主应力矢量场;(b) 基于MST确定的主应力矢量场;(c) 识别主应力矢量紊乱的区域;(d) 移除混乱的主应力矢量;(e) 完整的主应力矢量场;(f) 连续纤维路径;(g) 最终的纤维打印路径[118]
Figure 21. Continuous fiber printing path planning algorithm based on stress field; (a) Solving the principal stress vector field; (b) Principal stress vectors field determined by MST; (c) Identify the region of disturbed principal stress vector; (d) Remove the principal stress vector from the disturbed area; (e) Full principal stress vector field; (f) Continuous fiber path; (g) Final fiber printing path[118]
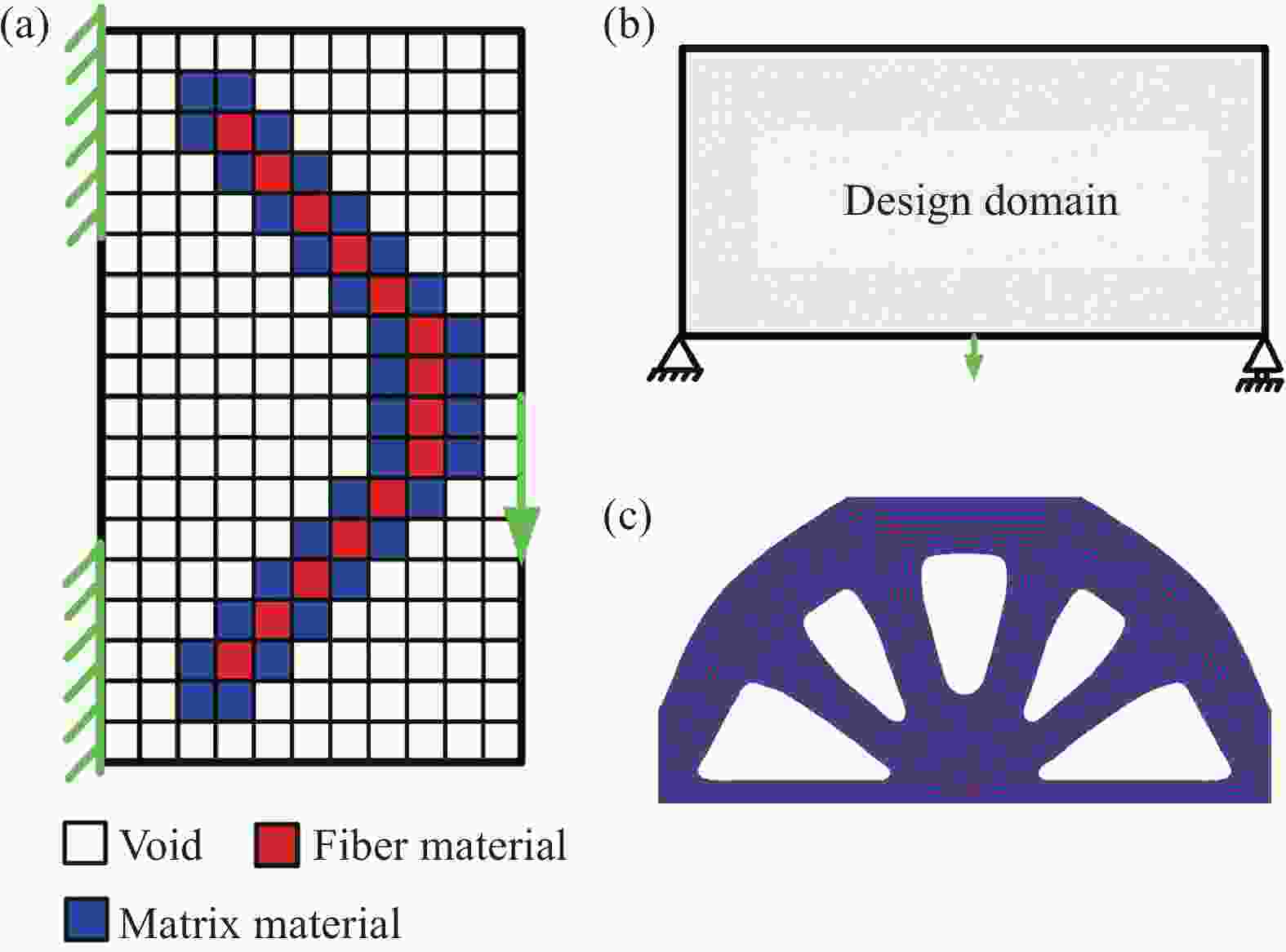
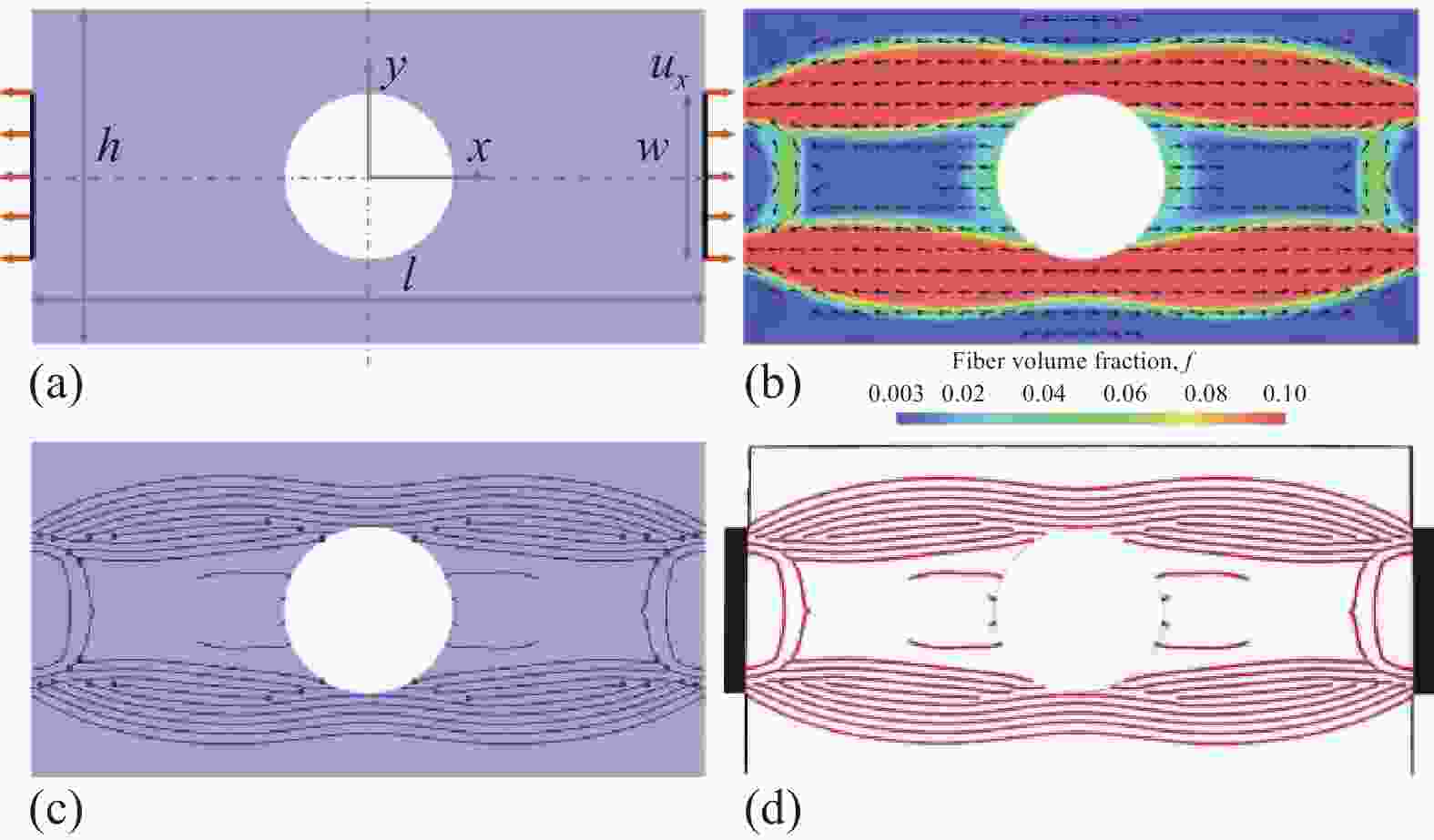
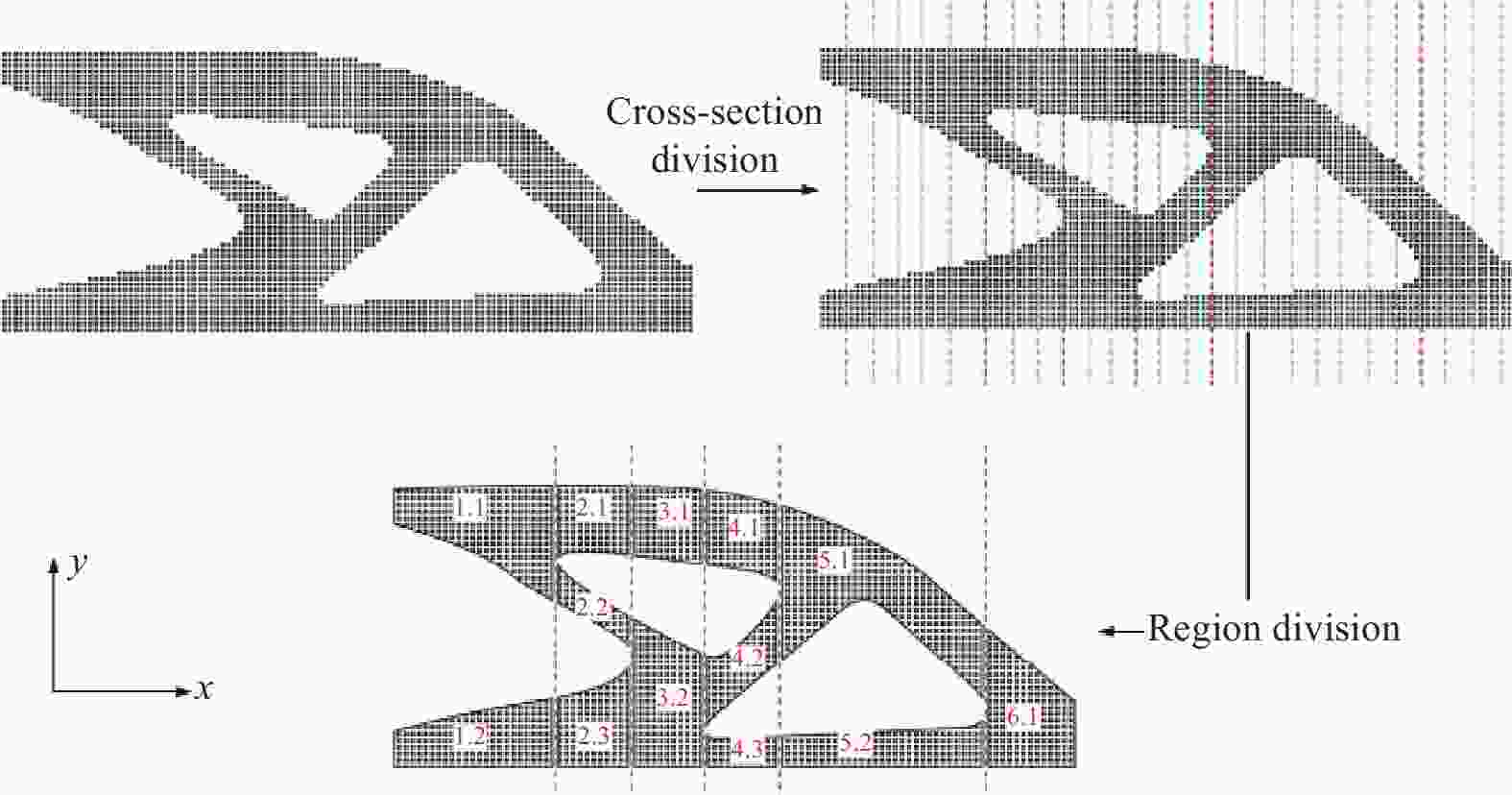
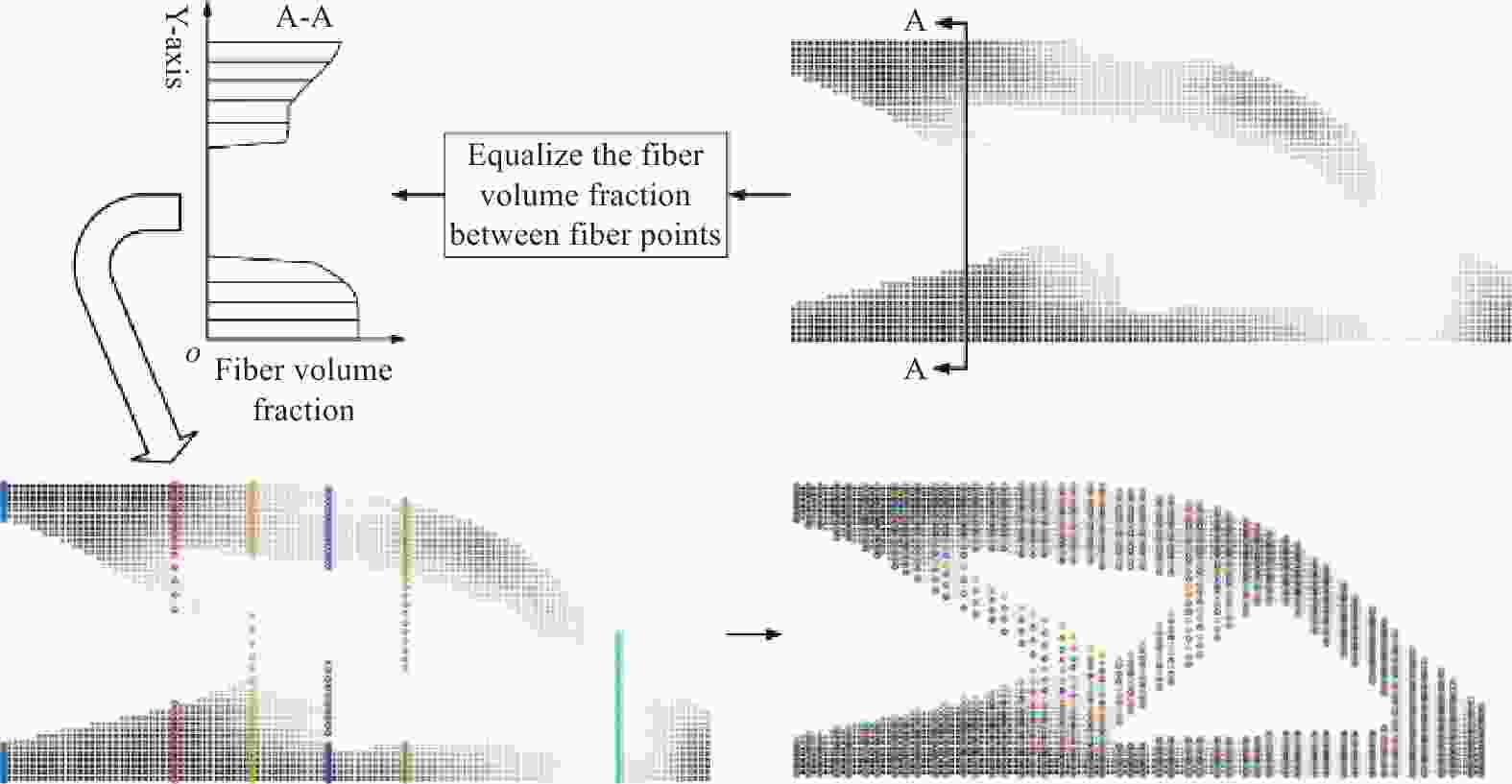
图 23 含有孔洞的复合材料平板优化设计:(a) 设计域和载荷;(b) 优化得到的纤维方向和纤维含量;(c) 根据材料汇编算法得到的纤维路径;(d) 用于可视化的3D打印样件[120]
Figure 23. Design optimization of a composite plate structure with a hole: (a) Design domain and loads; (b) Optimized fiber direction and fiber content; (c) Fiber path obtained by material compilation; (d) 3D printed sample for visualization[120]
表 1 基于应力方法得到的纤维极值角度
Table 1. Fiber extreme angle obtained from stress based method
Cases Condition Extreme angle 1 $ d > 0 $
and
4$ {d}^{2}\left[{({\sigma }_{1}-{\sigma }_{2})}^{2}+4{\sigma }_{12}^{2}\right] > {c}^{2}{\left({\sigma }_{1}+{\sigma }_{2}\right)}^{2} $$ {\theta }_{1}=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(\dfrac{2 b{\gamma }_{12}+\sqrt{4{b}^{2}\left[{({\varepsilon }_{1}-{\varepsilon }_{2})}^{2}+{\gamma }_{12}^{2}\right]-{a}^{2}{\left({\varepsilon }_{1}+{\varepsilon }_{2}\right)}^{2}}}{2 b\left({\varepsilon }_{1}-{\varepsilon }_{2}\right)-a({\varepsilon }_{1}+{\varepsilon }_{2})}\right) $
$ {\theta }_{1}=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(\dfrac{2 b{\gamma }_{12}+\sqrt{4{b}^{2}\left[{({\varepsilon }_{1}-{\varepsilon }_{2})}^{2}+{\gamma }_{12}^{2}\right]-{a}^{2}{\left({\varepsilon }_{1}+{\varepsilon }_{2}\right)}^{2}}}{2 b\left({\varepsilon }_{1}-{\varepsilon }_{2}\right)-a({\varepsilon }_{1}+{\varepsilon }_{2})}\right) $2 $ d > 0 $
and
4$ {d}^{2}\left[{({\sigma }_{1}-{\sigma }_{2})}^{2}+4{\sigma }_{12}^{2}\right] < {c}^{2}{\left({\sigma }_{1}+{\sigma }_{2}\right)}^{2} $$ {\theta }_{1}={\theta }_{I} $
$ {\theta }_{1}={\theta }_{II} $3 $ d < 0 $ $ {\theta }_{1}={\theta }_{I} $ 表 2 基于应变方法得到的纤维极值角度
Table 2. Fiber extreme angle obtained from strain based method
Cases Condition Extreme angle 1 $ b < 0 $
and
4$ {b}^{2}\left[{({\varepsilon }_{1}-{\varepsilon }_{2})}^{2}+4{\varepsilon }_{12}^{2}\right] > {a}^{2}{\left({\varepsilon }_{1}+{\varepsilon }_{2}\right)}^{2} $$ {\theta }_{1}=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(\dfrac{2 b{\gamma }_{12}+\sqrt{4{b}^{2}\left[{({\varepsilon }_{1}-{\varepsilon }_{2})}^{2}+{\gamma }_{12}^{2}\right]-{a}^{2}{\left({\varepsilon }_{1}+{\varepsilon }_{2}\right)}^{2}}}{2 b\left({\varepsilon }_{1}-{\varepsilon }_{2}\right)-a({\varepsilon }_{1}+{\varepsilon }_{2})}\right) $
$ {\theta }_{1}=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left(\dfrac{2 b{\gamma }_{12}-\sqrt{4{b}^{2}\left[{({\varepsilon }_{1}-{\varepsilon }_{2})}^{2}+{\gamma }_{12}^{2}\right]-{a}^{2}{\left({\varepsilon }_{1}+{\varepsilon }_{2}\right)}^{2}}}{2 b\left({\varepsilon }_{1}-{\varepsilon }_{2}\right)-a({\varepsilon }_{1}+{\varepsilon }_{2})}\right) $2 $ b < 0 $
and
4$ {b}^{2}\left[{({\varepsilon }_{1}-{\varepsilon }_{2})}^{2}+4{\varepsilon }_{12}^{2}\right] > {a}^{2}{\left({\varepsilon }_{1}+{\varepsilon }_{2}\right)}^{2} $$ {\theta }_{1}={\theta }_{I} $ 表 3 不同情况下的极值角度[55]
Table 3. The extreme angle under different circumstance.
Extreme angle $ {\theta }_{e} $ Relatively “low” shear stiffness $ {\alpha }_{3} > 0 $ Relatively “high” shear stiffness $ {\alpha }_{3} < 0 $ $ \gamma < -1 $ $ -1 < \gamma < 1 $ $ \gamma > 1 $ $ \gamma < -1 $ $ -1 < \gamma < 1 $ $ \gamma > 1 $ $ {0}^\circ $ Global min Global max Global max Global max Local min Globa min $ {90}^\circ $ Global max Local max Global min Global min Global min Global max $ \mathrm{cos}\left(2{\theta }_{e}\right)=-\gamma $ Global min Global max 表 4 DFOO 算法以及一个离散单元所需设计变量个数
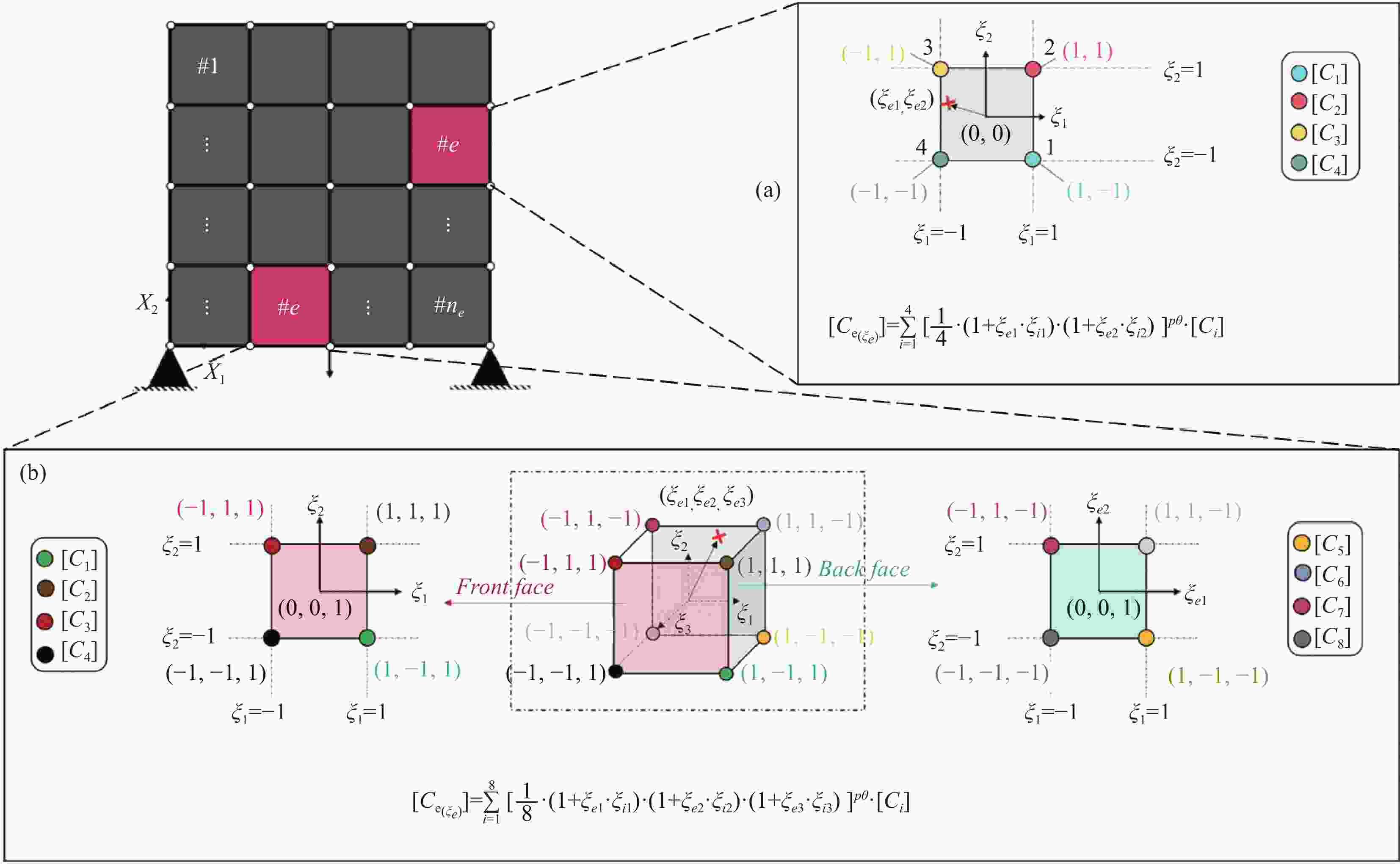
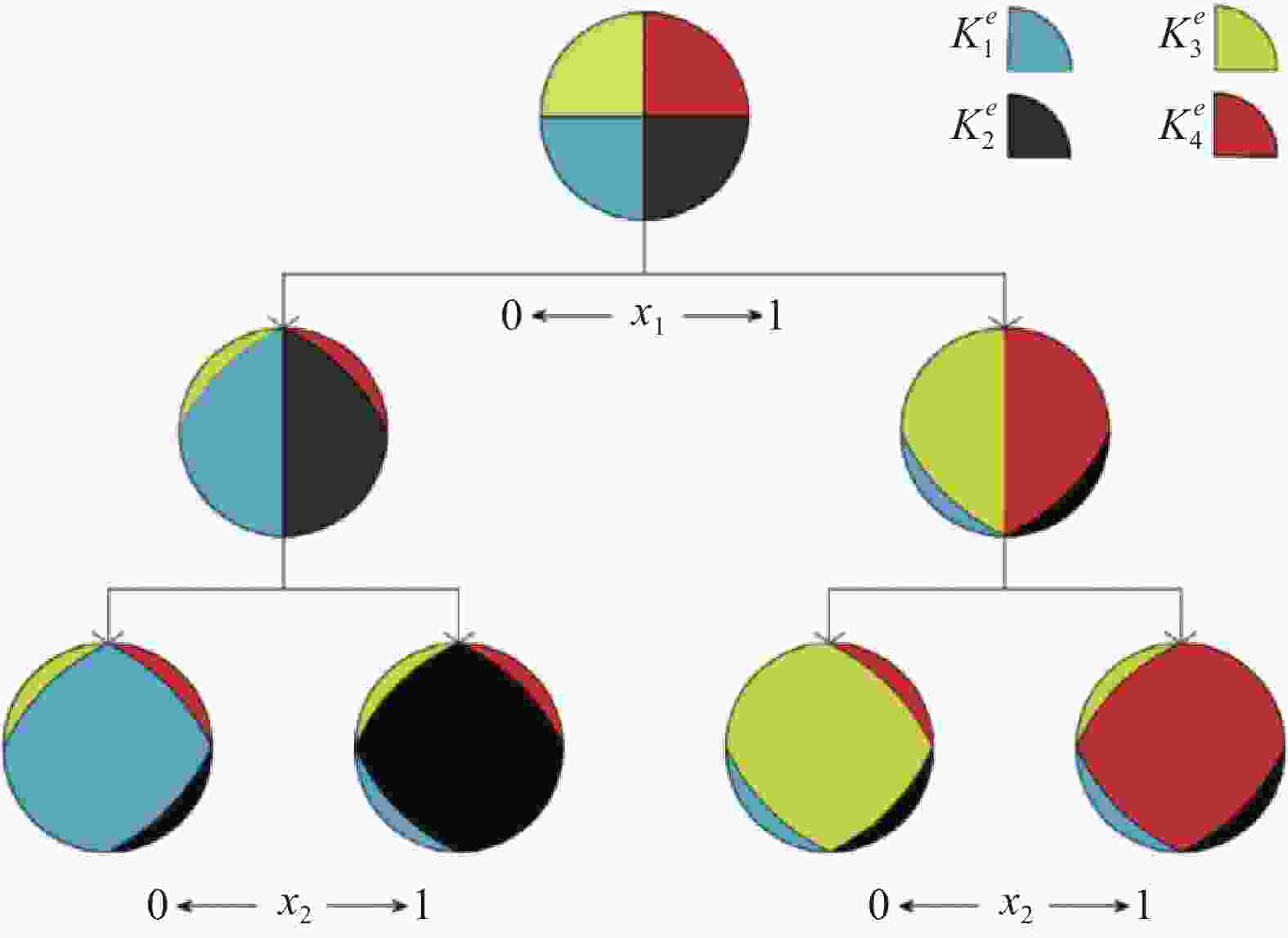
Table 4. DFOO algorithms and the number of required design variables for a discrete element.
Method The number of design variables required Discrete material optimization (DMO)[59] $ {n}_{e} $ Shape function with penalization (SFP) [60] $ {n}_{e}/2 $ Bi-value coding parameterization (BCP) [61] $ \left\lceil {{log}_{2}{n}_{e}} \right\rceil $ Bipartite interpolation optimization (BIO) [62] $\left\lceil {{log}_{2}{n}_{e}} \right\rceil $ Normal distribution fiber optimization (NDFO)[63] 1 表 5 若干种处理CFOO问题的方法及其优缺点
Table 5. Several approaches to CFOO and their advantages and disadvantages
Method Advantage Disadvantage Reference Shepard interpolation for fiber angle The continuity of fiber angle is guaranteed The optimization result depends on the
initial design;
Ends at local optimal solution[69] Gradient descent method Superior convergence properties Poor continuity of fiber angles [70] Discrete-continuous
parameterizationThe solution space is complete;
It reduces the risk of local optimalDifficulty in determining the number of subintervals [71] Principal stress orientation interpolated continuous fiber angle Reduce the phenomenon of local fiber
discontinuity;
Higher convergence efficiencyOptimization results depend on the
direction of principal stress[72] Full-scale topology
optimizationThe difficulty of optimization is low;
Can generate continuous fiber pathsHigh computational cost [73] Deep neural network models Reduces the number of optimization iterations and decreases computational costs Post-processing step required;
Problem-dependent[74] 表 6 三类连续纤维路径优化设计方法
Table 6. Three types of continuous fiber path optimization design methods
Method Optimized variables The representation of fiber paths Advantage Disadvantage Based on continuous and differentiable functions Functional
coefficientsFunction trajectory Convenient for adding
manufacturing
constraintsLow design freedom;
Optimization results depend on the selection of fiber representation functionsBased on level set function Level set function
or expansion
coefficientIso-contours of level set function Fiber paths without gaps and overlaps Fiber path may occur sharp corners Based on stress vector fields Stream function Streamline More robust and
StraightforwardPost-processing step required -
[1] Safari F, Kami A, Abedini V. 3D printing of continuous fiber reinforced composites: A review of the processing, pre- and post-processing effects on mechanical properties[J]. Polymers and Polymer Composites, 2022, 30: 09673911221098734. [2] Tian L, Zhang P, Xian G. Continuous fiber reinforced thermoplastic composite pultrusion with in situ polymerizable methyl methacrylate: A review[J]. Polymer Composites, 2023, 44(8): 4345-4369. doi: 10.1002/pc.27427 [3] Tuan Rahim T N A, Abdullah A, Md Akil H, et al. The improvement of mechanical and thermal properties of polyamide 12 3D printed parts by fused deposition modelling[J]. Express Polymer Letters, 2017, 11: 963-982. doi: 10.3144/expresspolymlett.2017.92 [4] Alaimo G, Marconi S, Costato L, et al. Influence of meso-structure and chemical composition on FDM 3D-printed parts[J]. Composites Part B: Engineering, 2017, 113. [5] Chacón J M, Caminero M, García-Plaza E, et al. Additive manufacturing of PLA structures using fused deposition modelling: Effect of process parameters on mechanical properties and their optimal selection[J]. Materials & design, 2017, 124: 143-157. [6] Lee C U, Vandenbrande J, Goetz A E, et al. Room temperature extrusion 3D printing of polyether ether ketone using a stimuli-responsive binder[J]. Additive Manufacturing, 2019, 28: 430-438. doi: 10.1016/j.addma.2019.05.008 [7] Zhao F, Li D, Jin Z. Preliminary Investigation of Poly-Ether-Ether-Ketone Based on Fused Deposition Modeling for Medical Applications[J]. Materials, 2018, 11(2). [8] Zhang J, Lin G, Vaidya U, et al. Past, present and future prospective of global carbon fibre composite developments and applications[J]. Composites Part B:Engineering, 2023, 250: 110463. doi: 10.1016/j.compositesb.2022.110463 [9] Jones F R, Huff N T. 19 - The structure and properties of glass fibers[M]//Bunsell A R. Handbook of Properties of Textile and Technical Fibres (Second Edition). Woodhead Publishing, 2018: 757-803. [10] Mukherjee M, Das C K, Kharitonov A P. Influence of Fluorinated and Oxy-Fluorinated Short Kevlar Fiber Loading on the Properties of Ethylene Propylene Matrix Composites[J]. Materials and Manufacturing Processes, 2006, 21(8): 892-898. doi: 10.1080/10426910600837780 [11] Chen Y, Ye L. Designing and tailoring effective elastic modulus and negative Poisson’s ratio with continuous carbon fibres using 3D printing[J]. Composites Part A:Applied Science and Manufacturing, 2021, 150: 106625. doi: 10.1016/j.compositesa.2021.106625 [12] Chen Y, Ye L, Dong H. Lightweight 3D carbon fibre reinforced composite lattice structures of high thermal-dimensional stability[J]. Composite Structures, 2023, 304: 116471. doi: 10.1016/j.compstruct.2022.116471 [13] Chen Y, Klingler A, Fu K, et al. 3D printing and modelling of continuous carbon fibre reinforced composite grids with enhanced shear modulus[J]. Engineering Structures, 2023, 286: 116165. doi: 10.1016/j.engstruct.2023.116165 [14] Chen Y, He Q. 3D-printed short carbon fibre reinforced perforated structures with negative Poisson’s ratios: Mechanisms and design[J]. Composite Structures, 2020, 236: 111859. doi: 10.1016/j.compstruct.2020.111859 [15] Iragi M, Pascual-González C, Esnaola A, et al. Ply and interlaminar behaviours of 3D printed continuous carbon fibre-reinforced thermoplastic laminates; effects of processing conditions and microstructure[J]. Additive Manufacturing, 2019, 30: 100884. doi: 10.1016/j.addma.2019.100884 [16] Saeed K, McIlhagger A, Harkin-Jones E, et al. Predication of the in-plane mechanical properties of continuous carbon fibre reinforced 3D printed polymer composites using classical laminated-plate theory[J]. Composite Structures, 2021, 259(113226)[2023-06-15]. [17] 田振生, 刘大伟, 李刚, 等. 连续纤维增强热塑性树脂预浸料的研究进展[J]. 玻璃钢/复合材料, 2013(53-58).Tian Zhensheng, Liu Dawei, Li Gang, et al. Research progress of continuous fiber reinforced thermoplastic prepregs[J]. Fiber Reinforced Plastics/Composites, 2013(53-58) (in Chinese). [18] 何亚飞, 刘文博, 王荣国. 树脂基复合材料成型工艺的发展[J]. 纤维复合材料, 2011, 28(7-13).He Yafei, Liu Wenbo, Wang Rongguo. The Development of Polymer Composites Forming Process[J]. FIBER COMPOSITES, 2011, 28(7-13) (in Chinese) [19] Liu G, Xiong Y, Zhou L. Additive manufacturing of continuous fiber reinforced polymer composites: Design opportunities and novel applications[J]. Composites Communications, 2021, 27: 100907. doi: 10.1016/j.coco.2021.100907 [20] 曹丰, 曾志勇, 黄建, 等. 连续纤维增强复合材料的3D打印工艺及应用进展[J]. 中国科学:技术科学, 2023, 53(1815-1833): 1815-1833).Cao F, Zeng Z Y, Huang J, et al. Printing process and application progress of 3D printing continuous fiber reinforced composites[J]. Sci Sin Tech, 2023, 53(1815-1833): 1815-1833(in Chinese). [21] 龙昱, 李岩, 付昆昆. 3D打印纤维增强复合材料工艺和力学性能研究进展[J]. 复合材料学报, 2022, 39(9): 4196-4212).LONG Yu, LI Yan, FU Kunkun. Recent advances in 3D printed fiber reinforced composites: Processing technique and mechanical performance[J]. Acta Materiae Compositae Sinica, 2022, 39(9): 4196-4212(in Chinese). [22] 胡艺伟, 李亚智, 李彪, 等. 纤维增强聚合物基复合材料熔融堆积成型技术的研究进展及产品的力学性能[J]. 复合材料学报, 2021, 38(4): 979-996).HU Yiwei, LI Yazhi, LI Biao, et al. 3D printed fibre-reinforced polymer composites−Review of the fused deposition modeling process and mechanical performance of products[J]. Acta Materiae Compositae Sinica, 2021, 38(4): 979-996(in Chinese). [23] 周子彦, 范天翔, 张慧颖, 等. 3D打印连续碳纤维/聚醚酮酮复合材料工艺及其性能调控[J]. 复合材料学报, 2023, 40(9): 5070-5084).ZHOU Ziyan, FAN Tianxiang, ZHANG Huiying, et al. Process and performance control of 3D printed continuous carbon fiber/poly(ether ketone ketone) composites[J]. Acta Materiae Compositae Sinica, 2023, 40(9): 5070-5084(in Chinese). [24] 任佳军, 孙颖, 鞠博文, 等. 纤维增强热塑性复合材料3D打印研究进展[J]. 复合材料科学与工程, 2023(122-128).REN Jiajun, SUN Ying, JU Bowen, et al. Research progress in 3D printing of fiber-reinforced thermoplastic composites[J]. Composites science and engineering. 2023(122-128)(in Chinese). [25] Cano-Vicent A, Tambuwala M M, Hassan Sk S, et al. Fused deposition modelling: Current status, methodology, applications and future prospects[J]. Additive Manufacturing, 2021, 47: 102378. doi: 10.1016/j.addma.2021.102378 [26] 邢悦陈, 何鹏飞, 李竞龙, 等. 连续纤维增强聚合物复合材料增材制造工艺研究进展[J]. 复合材料学报, 2023, 40(7): 3703-3721).XING Yue, HE Pengfei, LI Jinglong, et al. Additive manufacturing for continuous fiber-reinforced polymer composites: A review on processing technique[J]. Acta Materiae Compositae Sinica, 2023, 40(7): 3703-3721(in Chinese). [27] Köhler T, Röding T A, Gries T, et al. An Overview of Impregnation Methods for Carbon Fibre Reinforced Thermoplastics[J]. Key Engineering Materials, 2017, 742: 473-481. doi: 10.4028/www.scientific.net/KEM.742.473 [28] Struzziero G, Barbezat M, Skordos A A. Consolidation of continuous fibre reinforced composites in additive processes: A review[J]. Additive Manufacturing, 2021, 48: 102458. doi: 10.1016/j.addma.2021.102458 [29] Fuji W, Wang G, Ning F, et al. Fiber–matrix impregnation behavior during additive manufacturing of continuous carbon fiber reinforced polylactic acid composites[J]. Additive Manufacturing, 2020, 37: 101661. [30] Dikshit V, Goh G D, Nagalingam A P, et al. Recent progress in 3D printing of fiber-reinforced composite and nanocomposites[C]. 2020. [31] Parandoush P, Zhou C, Lin D. 3D Printing of Ultrahigh Strength Continuous Carbon Fiber Composites[J]. Advanced Engineering Materials, 2019, 21(2): 1800622. doi: 10.1002/adem.201800622 [32] Chang B, Li X, Parandoush P, et al. Additive manufacturing of continuous carbon fiber reinforced poly-ether-ether-ketone with ultrahigh mechanical properties[J]. Polymer Testing, 2020, 88: 106563. doi: 10.1016/j.polymertesting.2020.106563 [33] Hoa S, Abdali M, Jasmin A, et al. Development of a new flexible wing concept for Unmanned Aerial Vehicle using corrugated core made by 4D printing of composites[J]. Composite Structures, 2022, 290: 115444. doi: 10.1016/j.compstruct.2022.115444 [34] Hoyt R P. SpiderFab: An Architecture for Self-Fabricating Space Systems[M]//AIAA SPACE 2013 Conference and Exposition. American Institute of Aeronautics and Astronautics. [35] Rinaldi M, Ghidini T, Cecchini F, et al. Additive layer manufacturing of poly (ether ether ketone) via FDM[J]. Composites Part B:Engineering, 2018, 145: 162-172. doi: 10.1016/j.compositesb.2018.03.029 [36] Sigmund O, Maute K. Topology optimization approaches: A comparative review[J]. Structural and Multidisciplinary Optimization, 2013, 48(6): 1031-1055. doi: 10.1007/s00158-013-0978-6 [37] Xie Y M, Steven G P. A simple evolutionary procedure for structural optimization[J]. Computers & Structures, 1993, 49(5): 885-896. [38] Bendsøe M P, Sigmund O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics (Ingenieur Archiv), 1999, 69(9-10): 635-654. doi: 10.1007/s004190050248 [39] Sethian J A, Wiegmann A. Structural Boundary Design via Level Set and Immersed Interface Methods[J]. Journal of Computational Physics, 2000, 163(2): 489-528. doi: 10.1006/jcph.2000.6581 [40] Almeida Jr. J H S, Christoff B G, Tita V, et al. A concurrent fibre orientation and topology optimisation framework for 3D-printed fibre-reinforced composites[J]. Composites Science and Technology, 2023, 232: 109872. doi: 10.1016/j.compscitech.2022.109872 [41] Li G, Chen Y, Wei G. Continuous fiber reinforced meta-composites with tailorable Poisson’s ratio and effective elastic modulus: Design and experiment[J]. Composite Structures, 2024, 329: 117768. doi: 10.1016/j.compstruct.2023.117768 [42] Qiu Z, Li Q, Luo Y, et al. Concurrent topology and fiber orientation optimization method for fiber-reinforced composites based on composite additive manufacturing[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 395: 114962. doi: 10.1016/j.cma.2022.114962 [43] 李岩, 龙昱, 郝潞岑, 等, 肖建庄. 3D打印纤维增强复合材料力学性能研究进展[J]. 力学季刊, 2022, 43(731-750).LI Yan, LONG Yu, HAO Lucen, et al. Recent Advances in the Mechanical Properties of 3D Printed Fiber-Reinforced Composites[J]. Chinese Quarterly of Mechanics, 2022, 43(731-750)(in Chinese). [44] 杨来侠, 刘波, 刘腾飞, 等. 3D 打印连续纤维增强聚碳酸酯复合材料预浸丝制备与性能[J]. 复合材料学报, 2023, 40(10): 5654-5665.YANG Laixia, LIU Bo, LIU Tengfei, et al. Preparation and properties of 3D printing continuous fiber reinforced polycarbonate composite prepreg filaments[J]. Acta Materiae Compositae Sinica, 2023, 40(10): 5654-5665(in Chinese). [45] Frketic J, Dickens T, Ramakrishnan S. Automated manufacturing and processing of fiber-reinforced polymer (FRP) composites: An additive review of contemporary and modern techniques for advanced materials manufacturing[J]. Additive Manufacturing, 2017, 14: 69-86. doi: 10.1016/j.addma.2017.01.003 [46] Goh G D, Yap Y L, Agarwala S, et al. Recent Progress in Additive Manufacturing of Fiber Reinforced Polymer Composite[J]. Advanced Materials Technologies, 2019, 4(1): 1800271. doi: 10.1002/admt.201800271 [47] Pedersen P. Bounds on elastic energy in solids of orthotropic materials[J]. Structural optimization, 1990, 2(1): 55-63. doi: 10.1007/BF01743521 [48] Pedersen P. Combining material and element rotation in one formula[J]. Communications in Applied Numerical Methods, 1990, 6: 549-555. doi: 10.1002/cnm.1630060708 [49] Pedersen P. On optimal orientation of orthotropic materials[J]. Structural optimization, 1989, 1(2): 101-106. doi: 10.1007/BF01637666 [50] Thomsen J. Optimization of composite discs[J]. Structural optimization, 1991, 3(2): 89-98. doi: 10.1007/BF01743277 [51] Gea H C, Luo J H. On the stress-based and strain-based methods for predicting optimal orientation of orthotropic materials[J]. Structural and Multidisciplinary Optimization, 2004, 26(3): 229-234. [52] Gibiansky L V, Cherkaev A V. Microstructures of Composites of Extremal Rigidity and Exact Bounds on the Associated Energy Density[M]//Cherkaev A, Kohn R. Topics in the Mathematical Modelling of Composite Materials. Boston, MA: Birkhäuser, 1997: 273-317. [53] Suzuki K, Kikuchi N. A homogenization method for shape and topology optimization[J]. Computer Methods in Applied Mechanics and Engineering, 1991, 93(3): 291-318. doi: 10.1016/0045-7825(91)90245-2 [54] Majak J, Hannus S. Orientational Design of Anisotropic Materials Using the Hill and Tsai–Wu Strength Criteria[J]. Mechanics of Composite Materials, 2003, 39(6): 509-520. doi: 10.1023/B:MOCM.0000010623.38596.3e [55] Pedersen P. On optimal orientation of orthotropic materials[J]. Structural optimization, 1989, 1(2): 101-106. doi: 10.1007/BF01637666 [56] Moita J S, Infante Barbosa J, Mota Soares C M, et al. Sensitivity analysis and optimal design of geometrically non-linear laminated plates and shells[J]. Computers & Structures, 2000, 76(1): 407-420. [57] Vanderplaats G N. Numerical Optimization Techniques[C]//Mota Soares C A. Computer Aided Optimal Design: Structural and Mechanical Systems. Berlin, Heidelberg: Springer, 1987: 197-239. [58] Bruyneel M, Fleury C. Composite structures optimization using sequential convex programming[J]. Advances in Engineering Software, 2002, 33(7): 697-711. [59] Stegmann J, Lund E. Discrete material optimization of general composite shell structures[J]. International Journal for Numerical Methods in Engineering, 2005, 62(14): 2009-2027. doi: 10.1002/nme.1259 [60] Bruyneel M. SFP—a new parameterization based on shape functions for optimal material selection: application to conventional composite plies[J]. Structural and Multidisciplinary Optimization, 2011, 43(1): 17-27. doi: 10.1007/s00158-010-0548-0 [61] Gao T, Zhang W, Duysinx P. A bi-value coding parameterization scheme for the discrete optimal orientation design of the composite laminate[J]. International Journal for Numerical Methods in Engineering, 2012, 91(1): 98-114. doi: 10.1002/nme.4270 [62] Zhang L, Guo L, Sun P, et al. A generalized discrete fiber angle optimization method for composite structures: Bipartite interpolation optimization[J]. International Journal for Numerical Methods in Engineering, 2023, 124(5): 1211-1229. doi: 10.1002/nme.7160 [63] Kiyono C Y, Silva E C N, Reddy J N. A novel fiber optimization method based on normal distribution function with continuously varying fiber path[J]. Composite Structures, 2017, 160: 503-515. doi: 10.1016/j.compstruct.2016.10.064 [64] Sigmund O. A 99 line topology optimization code written in Matlab[J]. Structural and Multidisciplinary Optimization, 2001, 21(2): 120-127. doi: 10.1007/s001580050176 [65] Andreassen E, Clausen A, Schevenels M, et al. Efficient topology optimization in MATLAB using 88 lines of code[J]. Structural and Multidisciplinary Optimization, 2011, 43(1): 1-16. doi: 10.1007/s00158-010-0594-7 [66] Bruyneel M, Duysinx P, Fleury C, et al. Extensions of the Shape Functions with Penalization Parameterization for Composite-Ply Optimization[J]. AIAA Journal, 2011, 49: 2325-2329. doi: 10.2514/1.J051225 [67] A topology-based in-plane filtering technique for the combined topology and discrete fiber orientation optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2023, 417: 116400. [68] Ma T. Why Do Local Methods Solve Nonconvex Problems?[M]. arXiv, 2021[2023-11-06]. http://arxiv.org/abs/2103.13462. [69] Xia Q, Shi T. Optimization of composite structures with continuous spatial variation of fiber angle through Shepard interpolation[J]. Composite Structures, 2017, 182: 273-282. doi: 10.1016/j.compstruct.2017.09.052 [70] Shen Y, Branscomb D. Orientation optimization in anisotropic materials using gradient descent method[J]. Composite Structures, 2020, 234: 111680. doi: 10.1016/j.compstruct.2019.111680 [71] Luo Y, Chen W, Liu S, et al. A discrete-continuous parameterization (DCP) for concurrent optimization of structural topologies and continuous material orientations[J]. Composite Structures, 2020, 236: 111900. doi: 10.1016/j.compstruct.2020.111900 [72] Ye H, Dong Y, Yang J, et al. Concurrent optimization method of principal stress orientation interpolated continuous fiber angle (PSO-CFAO) and structural topology[J]. Composite Structures, 2023, 325: 117572. doi: 10.1016/j.compstruct.2023.117572 [73] Li H, Gao L, Li H, et al. Full-scale topology optimization for fiber-reinforced structures with continuous fiber paths[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 377: 113668. doi: 10.1016/j.cma.2021.113668 [74] Li Y, Ge W, Liu B, et al. Collaborative optimization of composite structure and fiber orientation through real-time correction of deep neural network (DNN) models with elite samples[J]. Mechanics of Advanced Materials and Structures, 2023, 0: 1-13. [75] Guo X, Zhou K. Topology optimization for variable stiffness design of fiber-reinforced composites with bi-modulus materials[J]. Optimization and Engineering, 2023, 24(4): 2745-2762. doi: 10.1007/s11081-023-09791-2 [76] Nakagawa Y, Mori K ichiro, Maeno T. 3D printing of carbon fibre-reinforced plastic parts[J]. The International Journal of Advanced Manufacturing Technology, 2017, 91(5): 2811-2817. [77] Li N, Li Y, Liu S. Rapid prototyping of continuous carbon fiber reinforced polylactic acid composites by 3D printing[J]. Journal of Materials Processing Technology, 2016, 238: 218-225. doi: 10.1016/j.jmatprotec.2016.07.025 [78] Akarçay E. Fabrication of continuous carbon, glass and Kevlar fibre reinforced polymer composites using additive manufacturing[J]. 2019: 146-152. [79] Lu C, Qi M, Islam S, et al. Mechanical performance of 3D-printing plastic honeycomb sandwich structure[J]. International Journal of Precision Engineering and Manufacturing-Green Technology, 2018, 5(1): 47-54. doi: 10.1007/s40684-018-0005-x [80] Hao W, Liu Y, Zhou H, et al. Preparation and characterization of 3D printed continuous carbon fiber reinforced thermosetting composites[J]. Polymer Testing, 2018, 65: 29-34. doi: 10.1016/j.polymertesting.2017.11.004 [81] Mohammadizadeh M, Imeri A, Fidan I, et al. 3D printed fiber reinforced polymer composites - Structural analysis[J]. Composites Part B:Engineering, 2019, 175: 107112. doi: 10.1016/j.compositesb.2019.107112 [82] 张荣耀, 钱波, 刘钢. 连续碳纤维3D打印的路径规划研究进展[J]. 复合材料科学与工程, 2023(112-120).ZHANG Rongyao, QIAN Bo, LIU Gang. Research progress in path planning continuous carbon fiber 3D printing[J]. Composites science and engineering. 2023(112-120)(in Chinese). [83] Heidari-Rarani M, Rafiee-Afarani M, Zahedi A M. Mechanical characterization of FDM 3D printing of continuous carbon fiber reinforced PLA composites[J]. Composites Part B:Engineering, 2019, 175: 107147. doi: 10.1016/j.compositesb.2019.107147 [84] Baumann F, Scholz J, Fleischer J. Investigation of a New Approach for Additively Manufactured Continuous Fiber-reinforced Polymers[J]. Procedia CIRP, 2017, 66: 323-328. doi: 10.1016/j.procir.2017.03.276 [85] Ding D, Pan Z (Stephen), Cuiuri D, et al. A tool-path generation strategy for wire and arc additive manufacturing[J]. The International Journal of Advanced Manufacturing Technology, 2014, 73(1): 173-183. [86] Ye W, Lin G, Wu W, et al. Separated 3D printing of continuous carbon fiber reinforced thermoplastic polyimide[J]. Composites Part A:Applied Science and Manufacturing, 2019, 121: 457-464. doi: 10.1016/j.compositesa.2019.04.002 [87] Dutra T A, Ferreira R T L, Resende H B, et al. Mechanical characterization and asymptotic homogenization of 3D-printed continuous carbon fiber-reinforced thermoplastic[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2019, 41(3): 133. doi: 10.1007/s40430-019-1630-1 [88] 谭瑞诗, 刘明尧, 张帆, 等. 碳纤维长纤3D打印的连续性路径规划算法[J]. 机械设计与制造, 2019(1-4).TAN Ruishi, LIU Mingyao, ZHANG Fan, et al, Continuous Path Planning Algorithm for Carbon Fiber Composite Material 3D Printing[J]. Machinery Design & Manufacture, 2019(1-4)(in Chinese). [89] 任东改. 基于Bayazit算法的3D打印路径规划研究[J]. 数字印刷, 2019(50-57).REN Donggai, Research on 3D Printing Path Planning Based on Bayazit Algorithm[J]. DIGITAL PRINTING, 2019(50-57)(in Chinese). [90] Han J. An efficient approach to 3D path planning[J]. Inf. Sci., 2019, 478: 318-330. doi: 10.1016/j.ins.2018.11.045 [91] 蔚晟楠, 张帆, 谭跃刚, 等. 碳纤维3D打印的全局连续费马螺旋路径规划算法[J]. 机械设计与研究, 2023, 39(166-172).YU Shengnan, ZHANG Fan, TAN Yuegang, et al. A Global Continuous Fermat Spiral Path Planning Method for Carbon Fiber 3D Printing[J]. Machine Design and Research, 2023, 39(166-172)(in Chinese). [92] 周祖德, 陈飞, 张帆, 等. 连续碳纤维3D打印的高效螺旋偏置填充算法[J]. 武汉理工大学学报, 2017, 39(81-87).ZHOU Zude, CHEN Fei, ZHANG Fan, et al. Efficient Spiral Bias Filling Algorithm for ContinuousCarbon Fiber 3D Printing[J]. Journal of wuhan university of technology, 2017, 39(81-87)(in Chinese). [93] 易雪涛, , 谭跃刚, 王茂森, 等. 连续碳纤维复合材料选择性增强的3D打印切片方法研究[J]. 数字制造科学, 2021, 19(16-21).YI Xuetao, TAN Yuegang, WANG Maosen, et al. Selective Enhancement Slicing Method for 3D Printing of Continuous Carbon Fiber Composite Material[J]. Digital manufacture science, 2021, 19(16-21)(in Chinese). [94] Backer W D, Sinkez P, Chhabra I, et al. In-Process Monitoring of Continuous Fiber Additive Manufacturing through Force/Torque Sensing on the Nozzle[M]//AIAA Scitech 2020 Forum. [95] Ming Y, Duan Y, Wang B, et al. A Novel Route to Fabricate High-Performance 3D Printed Continuous Fiber-Reinforced Thermosetting Polymer Composites[J]. Materials (Basel, Switzerland), 2019, 12(9): E1369. doi: 10.3390/ma12091369 [96] Serra T, Ortiz-Hernandez M, Engel E, et al. Relevance of PEG in PLA-based blends for tissue engineering 3D-printed scaffolds[J]. Materials Science and Engineering:C, 2014, 38: 55-62. doi: 10.1016/j.msec.2014.01.003 [97] Arian Nik M, Fayazbakhsh K, Pasini D, et al. Surrogate-based multi-objective optimization of a composite laminate with curvilinear fibers[J]. Composite Structures, 2012, 94(8): 2306-2313. doi: 10.1016/j.compstruct.2012.03.021 [98] Passos A G, Luersen M A, Steeves C A. Optimal curved fibre orientations of a composite panel with cutout for improved buckling load using the Efficient Global Optimization algorithm[J]. Engineering Optimization, 2017, 49(8): 1354-1372. doi: 10.1080/0305215X.2016.1256052 [99] Buckling analysis and optimisation of variable angle tow composite plates[J]. Thin-Walled Structures, 2012, 60: 163-172. [100] Parnas L, Oral S, Ceyhan Ü. Optimum design of composite structures with curved fiber courses[J]. Composites Science and Technology, 2003, 63(7): 1071-1082. doi: 10.1016/S0266-3538(02)00312-3 [101] Hao P, Liu C, Yuan X, et al. Buckling optimization of variable-stiffness composite panels based on flow field function[J]. Composite Structures, 2017, 181: 240-255. doi: 10.1016/j.compstruct.2017.08.081 [102] Huang G, Wang H, Li G. An efficient reanalysis assisted optimization for variable-stiffness composite design by using path functions[J]. Composite Structures, 2016, 153: 409-420. doi: 10.1016/j.compstruct.2016.06.043 [103] Tanaka H, Mori Y, Kumekawa N, et al. Multi-objective optimization of weight and strength of laminated composites using gap-less and overlap-less variable thickness fiber placement[J]. Composite Structures, 2021, 276: 114562. doi: 10.1016/j.compstruct.2021.114562 [104] Matsuzaki R, Mitsui K, Hirano Y, et al. Optimization of curvilinear fiber orientation of composite plates and its experimental validation[J]. Composite Structures, 2021, 255: 112956. doi: 10.1016/j.compstruct.2020.112956 [105] Wang S, Wang M Y. Radial basis functions and level set method for structural topology optimization[J]. International Journal for Numerical Methods in Engineering, 2006, 65(12): 2060-2090. doi: 10.1002/nme.1536 [106] Tian Y, Shi T, Xia Q. A parametric level set method for the optimization of composite structures with curvilinear fibers[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 388: 114236. doi: 10.1016/j.cma.2021.114236 [107] Brampton C J, Wu K C, Kim H A. New optimization method for steered fiber composites using the level set method[J]. Structural and Multidisciplinary Optimization, 2015, 52(3): 493-505. doi: 10.1007/s00158-015-1256-6 [108] Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science (2nd edition)[J]. Kybernetes, 2000, 29(2): 239-248. [109] Sethian J A. Fast Marching Methods[J]. SIAM Review, 1999, 41(2): 199-235. doi: 10.1137/S0036144598347059 [110] Liu J, Yu H. Concurrent deposition path planning and structural topology optimization for additive manufacturing[J]. Rapid Prototyping Journal, 2017, 23(5): 930-942. doi: 10.1108/RPJ-05-2016-0087 [111] Xu Y, Gao Y, Wu C, et al. Concurrent optimization of topological configuration and continuous fiber path for composite structures — A unified level set approach[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 399: 115350. doi: 10.1016/j.cma.2022.115350 [112] Tian Y, Shi T, Xia Q. Optimization with manufacturing constraints for composite laminates reinforced by curvilinear fibers through a parametric level set method[J]. Composite Structures, 2023, 321: 117310. doi: 10.1016/j.compstruct.2023.117310 [113] Li G, Tian Y, Yang K, et al. A partition of unity level set method with moving knot CS-RBFs for optimizing variable stiffness composites[J]. Chinese Journal of Aeronautics, 2023, 36(4): 565-572. doi: 10.1016/j.cja.2023.02.012 [114] Papapetrou V S, Patel C, Tamijani A Y. Stiffness-based optimization framework for the topology and fiber paths of continuous fiber composites[J]. Composites Part B:Engineering, 2020, 183: 107681. doi: 10.1016/j.compositesb.2019.107681 [115] Niu X, Yang T, Du Y, et al. Tensile properties of variable stiffness composite laminates with circular holes based on potential flow functions[J]. Archive of Applied Mechanics, 2016, 86. [116] Chen Y, Ye L. Topological design for 3D-printing of carbon fibre reinforced composite structural parts[J]. Composites Science and Technology, 2021, 204: 108644. doi: 10.1016/j.compscitech.2020.108644 [117] Yan X, Lai M, Huang D, et al. Manufacturing-oriented topological design of CFRC structures with variable fiber volume and orientation[J]. Composite Structures, 2023, 310: 116779. doi: 10.1016/j.compstruct.2023.116779 [118] Chen X, Fang G, Liao W H, et al. Field-Based Toolpath Generation for 3D Printing Continuous Fibre Reinforced Thermoplastic Composites[J]. Additive Manufacturing, 2022, 49: 102470. doi: 10.1016/j.addma.2021.102470 [119] Wang T, Li N, Link G, et al. Load-dependent path planning method for 3D printing of continuous fiber reinforced plastics[J]. Composites Part A:Applied Science and Manufacturing, 2021, 140: 106181. doi: 10.1016/j.compositesa.2020.106181 [120] Boddeti N, Tang Y, Maute K, et al. Optimal design and manufacture of variable stiffness laminated continuous fiber reinforced composites[J]. Scientific Reports, 2020, 10(1): 16507. doi: 10.1038/s41598-020-73333-4 [121] Zhang F, Li B, Wo W, et al. Topology Design of 3D Printing Continuous Fiber-Reinforced Structure Considering Strength and Non-Equidistant Fiber[J]. Advanced Engineering Materials, n/a(n/a): 2301340. [122] Huang Y, Tian X, Zheng Z, et al. Multiscale concurrent design and 3D printing of continuous fiber reinforced thermoplastic composites with optimized fiber trajectory and topological structure[J]. Composite Structures, 2022, 285: 115241. doi: 10.1016/j.compstruct.2022.115241 [123] Wan Q, Yang W, Wang L, et al. Global continuous path planning for 3D concrete printing multi-branched structure[J]. Additive Manufacturing, 2023, 71: 103581. doi: 10.1016/j.addma.2023.103581 -

 点击查看大图
点击查看大图
计量
- 文章访问数: 369
- HTML全文浏览量: 106
- 被引次数: 0





 下载:
下载: