不同衬经纱占比的三维角联锁机织增强复合材料弯曲性能

王颖杰; 王海楼; 张伟

doi:10.13801/j.cnki.fhclxb.20220811.005

不同衬经纱占比的三维角联锁机织增强复合材料弯曲性能

doi: 10.13801/j.cnki.fhclxb.20220811.005

王颖杰^1,,
王海楼^{1, 2, ,},
张伟^{1, 2}

1.
南通大学　纺织服装学院，南通 226019
2.
南通大学　安全防护用特种纤维复合材料研发国家地方联合工程研究中心，南通 226019

基金项目: 国家自然科学基金(11802144)；江苏省高等学校基础科学(自然科学)重大项目(21 KJA540001)；江苏高校“青蓝工程”National Natural Science Foundation of China (11802144); Major Program of Basic Science (Natural Science) of Higher Education of Jiangsu Province (21KJA540001); Jiangsu University “Qinglan Project”

详细信息

通讯作者:
王海楼，博士，副教授，硕士生导师，研究方向为纺织结构复合材料　E-mail: wanghl1130@ntu.edu.cn

中图分类号: TB332
计量
- 文章访问数: 674
- HTML全文浏览量: 322
- PDF下载量: 42
- 被引次数: 0
出版历程
- 收稿日期: 2022-06-06
- 修回日期: 2022-07-12
- 录用日期: 2022-07-31
- 网络出版日期: 2022-08-12
- 刊出日期: 2023-06-15

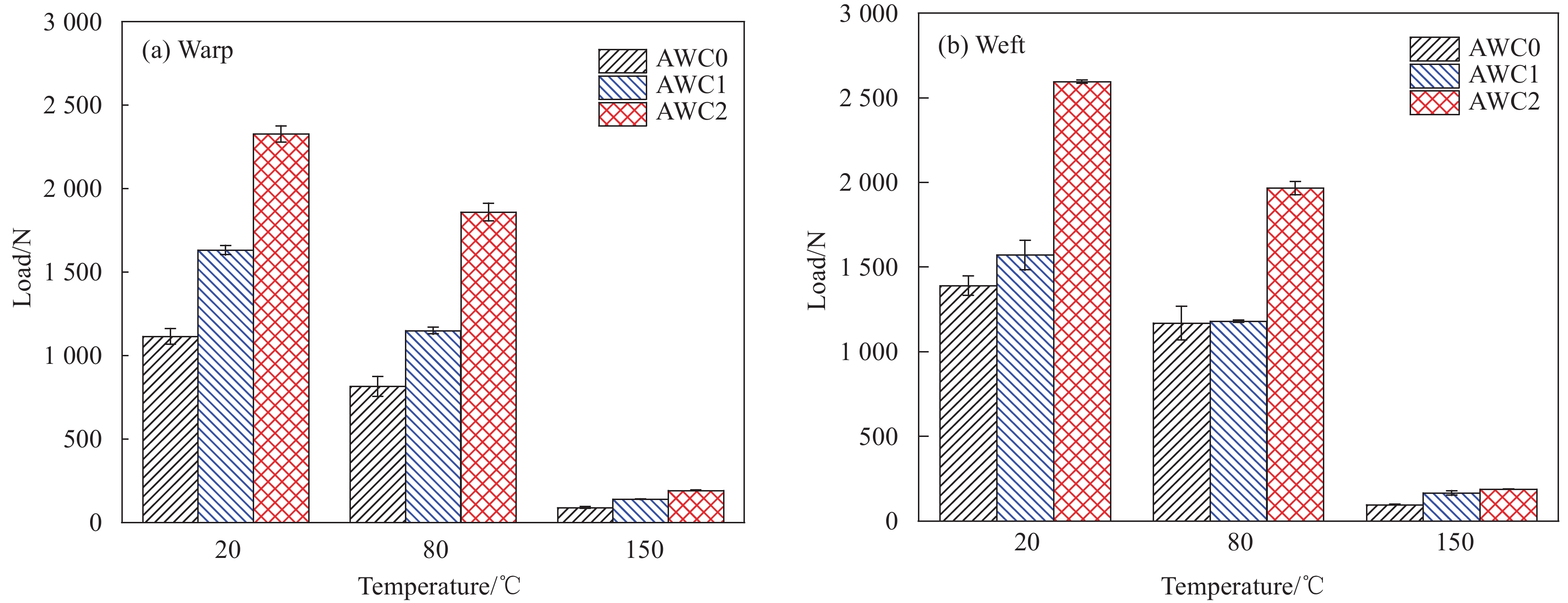
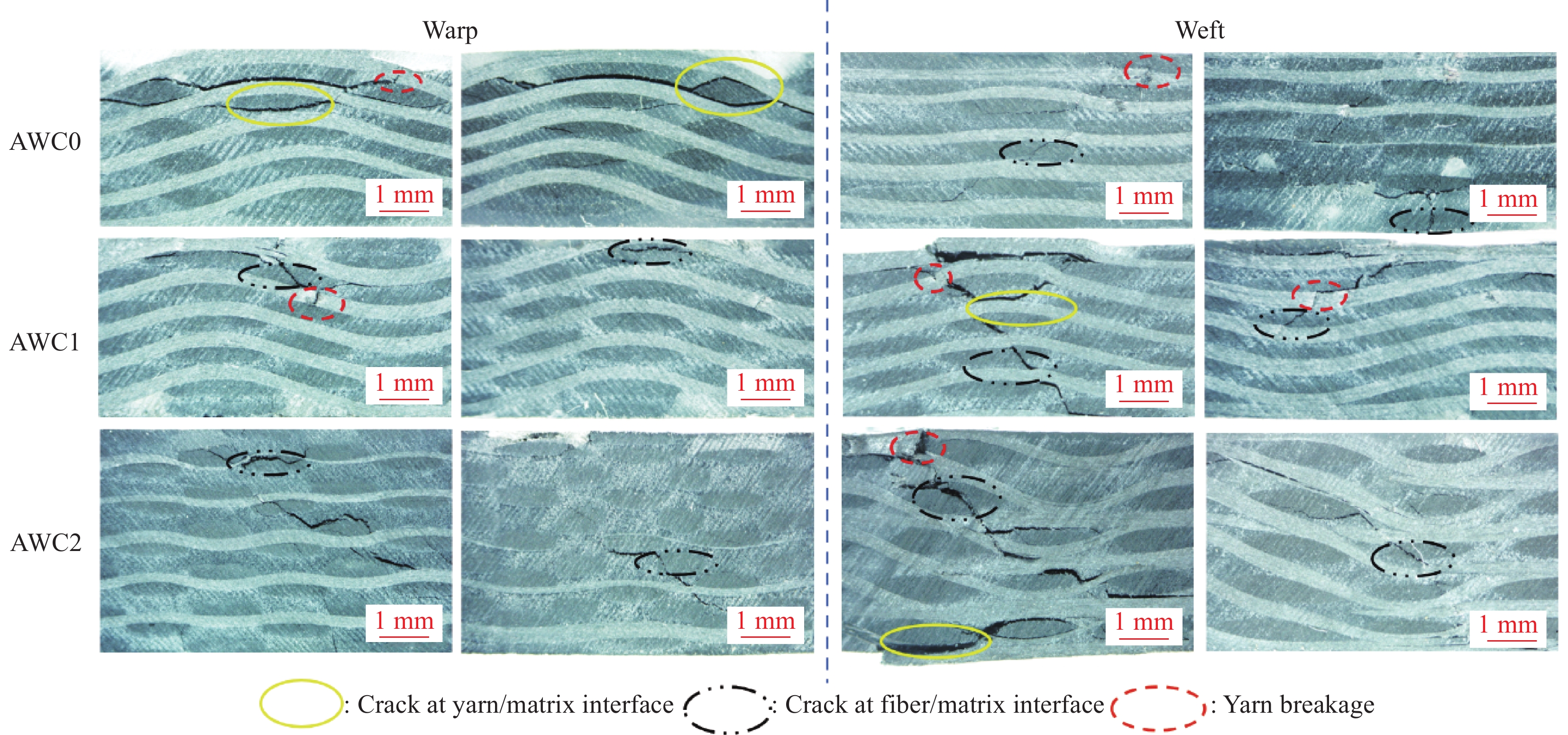
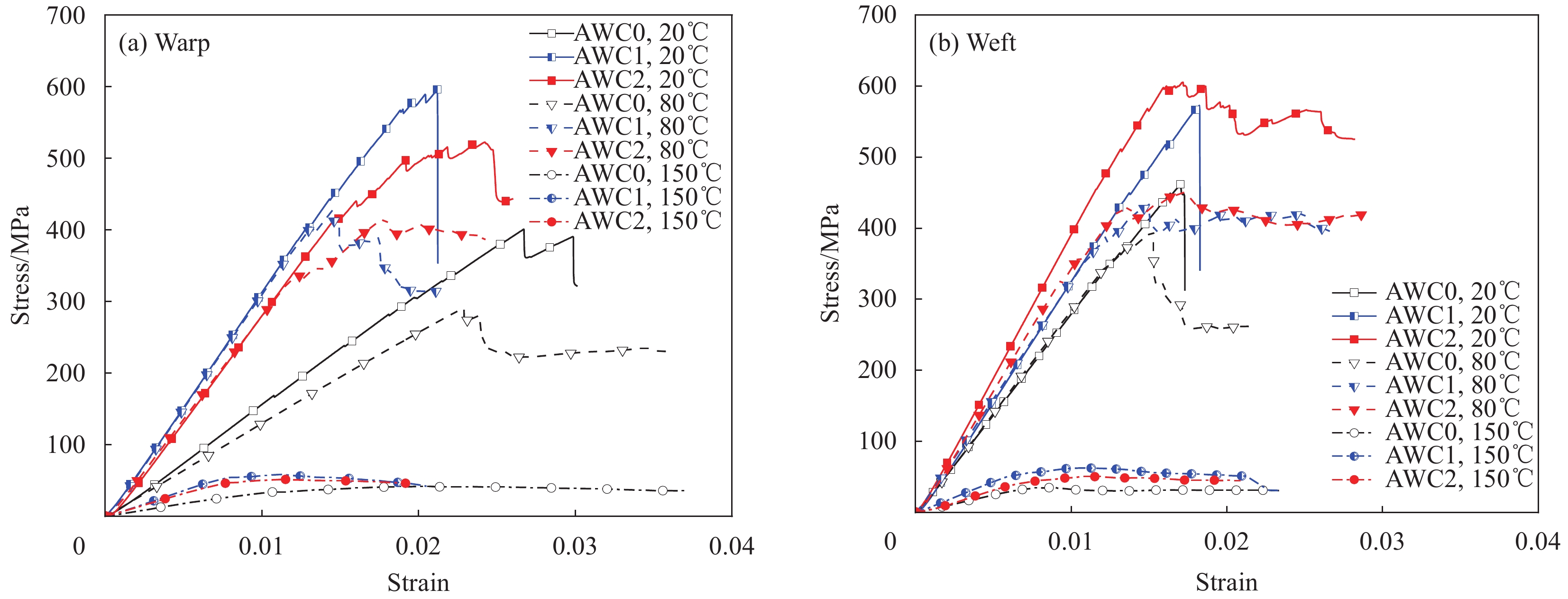
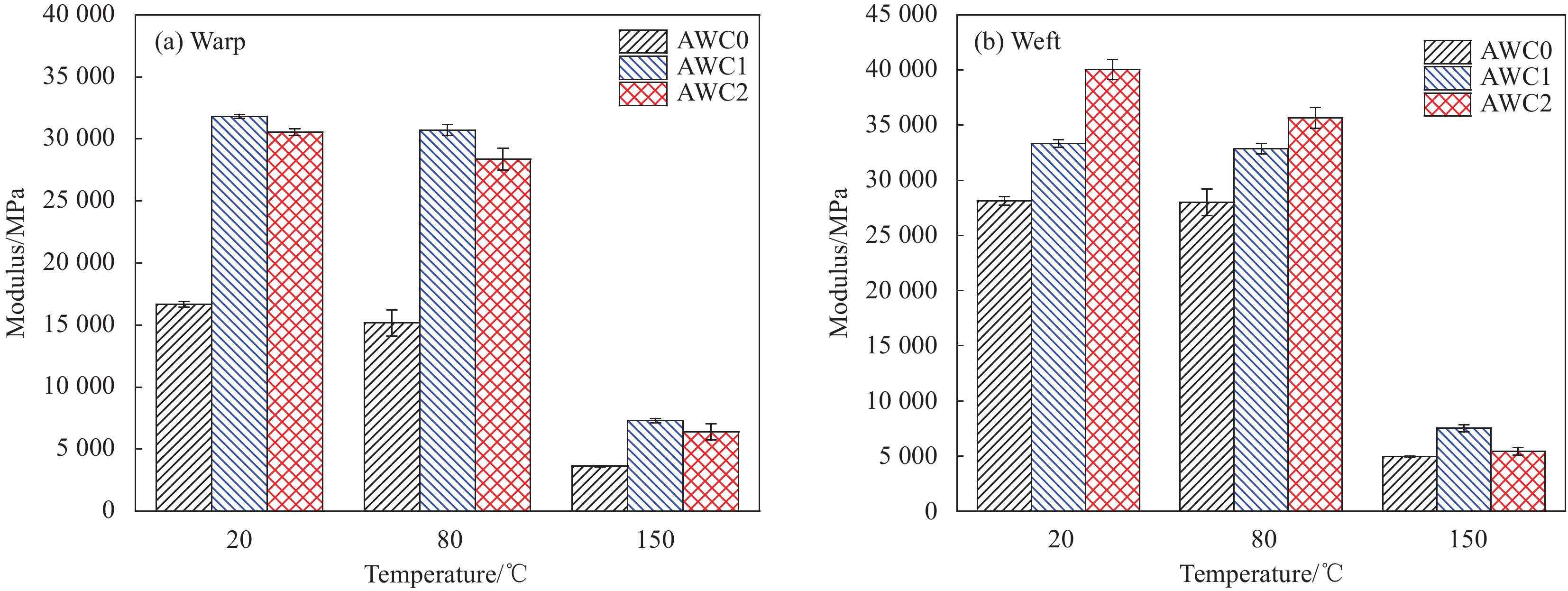
Bending properties of three-dimensional angle interlocking woven reinforced composites with different proportions of warp insertion

WANG Yingjie^1
,,
WANG Hailou^{1, 2
, ,},
ZHANG Wei^{1, 2}

1.
School of Textile and Clothing, Nantong University, Nantong 226019, China
2.
National & Local Joint Engineering Research Center of Technical Fiber Composites for Safety and Protection, Nantong 226019, China

摘要

摘要: 三维角联锁机织增强复合材料(3DAWCs)具有优异的结构整体性和力学性能。为探究3DAWCs中衬经纱对力学性能的影响，本文设计并制备不同衬经纱占比的3DAWCs，研究不同温度场中不同衬经纱占比3DAWCs的弯曲性能。衬经纱与经纱比例包括：0∶1、1∶1和2∶1。温度场包括：20℃、80℃和150℃。研究结果表明：衬经纱对3DAWCs厚度、纱线形态、载荷-挠度曲线形态、弯曲强度、损伤分布均影响显著；随衬经纱占比增加，3DAWCs的厚度和最大弯曲载荷增加，但1∶1型和2∶1型试样的弯曲强度相差较小；随温度升高，试样弯曲性能下降，但在不同温度场中，不同衬经占比试样的经纬向弯曲性能对温度的敏感性不同。
- 三维角联锁机织物 /
- 衬经纱 /
- 复合材料 /
- 弯曲性能 /
- 温度
Abstract: 3D woven reinforced composites have good structural integrity and mechanical properties. In order to explore the influence of warp insertion on mechanical properties of three-dimensional angle interlocking woven reinforced composites (3DAWCs), 3DAWCs with different proportions of warp insertion were designed and prepared in this paper. The bending properties of 3DAWCs with different proportions of warp insertion were studied in different temperature fields. The ratios of warp insertion to warp are 0∶1, 1∶1 and 2∶1. The testing temperatures include 20°C, 80°C and 150°C. The results show that the warp insertion have a significant effect on 3DAWC’s thickness, shape of yarn, shape of load-deflection curve, bending strength and damage distribution. The thickness and maximum bending load of 3DAWCs increase with the increase of the proportion of warp insertion, but the difference of bending strength between 1∶1 and 2∶1 is minor. The bending properties of the specimen decrease with the increase of temperature. In different temperature fields, the warp and weft bending properties of samples with different warp insertion ratios have different sensitivities to temperature.
- 3D angle interlocking woven /
- warp insertion /
- composite /
- bending property /
- temperature

HTML全文

图 1 织物结构和纱线排列

Figure 1. Textile structures and yarn arrangement

下载: 全尺寸图片幻灯片

图 2 三维角联锁机织物

Figure 2. Three-dimensional angle interlocking woven perform

下载: 全尺寸图片幻灯片

图 3 弯曲试样

Figure 3. Sample for bending test

下载: 全尺寸图片幻灯片

图 4 3DAWC中的纱线形态

Figure 4. Curve shape of yarn in 3DAWC

下载: 全尺寸图片幻灯片

图 5 3DAWC经向试样和纬向试样弯曲载荷-挠度曲线

Figure 5. Bending load-displacement curves of 3DAWC in warp and weft directions

下载: 全尺寸图片幻灯片

图 6 3DAWC经向试样和纬向试样最大弯曲载荷

Figure 6. Maximum bending load of 3DAWC in warp and weft directions

下载: 全尺寸图片幻灯片

图 7 3DAWC经向试样弯曲失效过程(20℃)

Figure 7. Bending failure process of 3DAWC in warp direction (20℃)

下载: 全尺寸图片幻灯片

图 12 3DAWC弯曲后的两个侧面形貌(20℃)

Figure 12. Two side surface morphologies of 3DAWC after bending (20℃)

下载: 全尺寸图片幻灯片

图 8 3DAWC纬向试样弯曲失效过程(20℃)

Figure 8. Bending failure process of 3DAWC in weft direction(20℃)

下载: 全尺寸图片幻灯片

图 9 3DAWC经纬向试样弯曲应力-应变曲线

Figure 9. Bending stress-strain curves of 3DAWC in warp and weft directions

下载: 全尺寸图片幻灯片

图 10 3DAWC经纬向试样弯曲强度

Figure 10. Bending strength of 3DAWC in warp and weft directions

下载: 全尺寸图片幻灯片

图 11 3DAWC经纬向试样弯曲模量

Figure 11. Bending modulus of 3DAWC in warp and weft directions

下载: 全尺寸图片幻灯片

图 13 不同温度下AWC1试样弯曲后两个侧面形貌

Figure 13. Two side surface morphologies of AWC1 after bending at different temperatures

下载: 全尺寸图片幻灯片

表 1 碳纤维性能参数

Table 1. Performance parameters of carbon fiber

Density/ (g·cm⁻³)	Breakage elongation/%	Tensile strength/MPa	Tensile modulus/GPa
1.79	2.1	4900	230

下载: 导出CSV

表 2 环氧树脂性能参数

Table 2. Performance parameters of epoxy resin

Density/ (g·cm⁻³)	Compressive strength/MPa	Compressive modulus/MPa	Glass transition temperature/℃
1.12	117	2166	110-120

下载: 导出CSV

表 3 三维角联锁机织物(3DAWF)的结构参数

Table 3. Structural parameters of three-dimensional angle interlocking woven (3DAWF)

Symbol	Warp insertion: Warp	Weave density in weft direction/(ends·cm⁻¹)	Weave density in warp direction/(ends·cm⁻¹)	Warp yarn volume fraction/vol%	Warp insertion yarn volume fraction/vol%
AWF0	0∶1	20	20	20.6	0
AWF1	1∶1	20	20	12.9	12.9
AWF2	2∶1	20	20	7.8	13.2

下载: 导出CSV

表 4 不同衬经占比三维角联锁机织增强复合材料(3DAWC)厚度

Table 4. Thickness of three-dimensional angle interlocking woven reinforced composites (3DAWC) with different proportion of warp insertion

Sample	Thickness/mm
AWC0	4.05
AWC1	4.14
AWC2	5.15

下载: 导出CSV

参考文献(26)

[1]	薛有松, 薛凌明, 孙宝忠, 等. 碳纤维三维角联锁机织复合材料弯曲作用下的力阻响应[J]. 复合材料学报, 2023, 40(3):1468-1476. doi: 10.13801/j.cnki.fhclxb.20220516.006 XUE Yousong, XUE Lingming, SUN Baozhong, et al. Piezoresistive effect of carbon fiber three-dimensional angle interlocking woven composites under bending[J]. Acta Materiae Compositae Sinica,2023,40(3):1468-1476(in Chinese). doi: 10.13801/j.cnki.fhclxb.20220516.006
[2]	郭玉路, 关留祥, 李嘉禄, 等. 航空发动机复合材料叶片用3D机织预制体研究进展[J]. 复合材料学报, 2018, 35(10):748-759. GUO Yulu, GUAN Liuxiang, LI Jialu, et al. Research progress on 3D woven preforms for aero-engine composite blades[J]. Acta Materiae Compositae Sinica,2018,35(10):748-759(in Chinese).
[3]	郭瑞卿, 张一帆, 吕庆涛, 等. 多层多向层联三维机织复合材料的拉伸性能[J]. 复合材料学报, 2020, 37(10):2409-2417. GUO Ruiqing, ZHANG Yifan, LU Qingtao, et al. Tensile properties of multilayer multidirectional laminated three-dimensional woven composites[J]. Acta Materiae Compositae Sinica,2020,37(10):2409-2417(in Chinese).
[4]	WIELHORSKI Y, MENDOZA A, RUBINO M, et al. Numerical modeling of 3D woven composite reinforcements: A review[J]. Composites Part A: Applied Science and Manufacturing,2022,154:106729. doi: 10.1016/j.compositesa.2021.106729
[5]	BANDARU A K, AHMAD S, BHATNAGAR N. Ballistic performance of hybrid thermoplastic composite armors reinforced with Kevlar and basalt fabrics[J]. Composites Part A: Applied Science and Manufacturing, 2017, 97: 151-165.
[6]	DONG K, LIU K, PAN L, et al. Experimental and numerical investigation on the thermal conduction properties of 2.5D angle-interlock woven composites[J]. Composite Structures, 2016, 154: 319-333.
[7]	KUO W. The role of loops in 3D fabric composites[J]. Composites Science and Technology,2000,60(9):1835-1849. doi: 10.1016/S0266-3538(00)00075-0
[8]	LEE L, RUDOV-CLARK S, MOURITZ A P, et al. Effect of weaving damage on the tensile properties of three-dimensional woven composites[J]. Composite Structures,2002,57(1):405-413.
[9]	王忠远, 蔡长春, 王振军, 等. 三维角联锁机织铝基复合材料面内拉伸力学行为与失效机制[J]. 复合材料学报, 2021, 38(9):2989-2999. WANG Zhongyuan, CAI Changchun, WANG Zhenjun, et al. In-plane tensile mechanical behavior and failure mechanism of three-dimensional angle interlocking woven aluminum matrix composites[J]. Acta Materiae Compositae Sinica,2021,38(9):2989-2999(in Chinese).
[10]	LAPEYRONNIE P, LE G P, BINETRUY C, et al. Homogenization of the elastic behavior of a layer-to-layer angle-interlock composite[J]. Composite Structures,2011,93(11):2795-2807. doi: 10.1016/j.compstruct.2011.05.025
[11]	JIN L, NIU Z, JIN B C, et al. Comparisons of static bending and fatigue damage between 3D angle-interlock and 3D orthogonal woven composites[J]. Journal of Reinforced Plastics and Composites,2012,31(14):935-945. doi: 10.1177/0731684412450626
[12]	姚思远, 陈秀华. 三维机织复合材料在拉压循环载荷下的疲劳性能[J]. 复合材料学报, 2018, 35(10):2706-2714. YAO Siyuan, CHEN Xiuhua. Fatigue behaviors of 3D woven composites under tension-compression cyclic loading[J]. Acta Materiae Compositae Sinica,2018,35(10):2706-2714(in Chinese).
[13]	王琦, 蒋秋梅, 杨旭锋, 等. 三维机织复合材料残余应力/应变多尺度分析及工艺参数优化[J]. 复合材料学报, 2021, 38(4):1167-1176. WANG Qi, JIANG Qiumei, YANG Xufeng, et al. Multiscale analysis and process parameters optimization of residual stress/strain of 3D woven composite[J]. Acta Materiae Compositae Sinica,2021,38(4):1167-1176(in Chinese).
[14]	郭兴峰. 三维机织物[M]. 北京: 中国纺织出版社, 2015. GUO Xingfeng. 3D woven fabric[M]. Beijing: China Textile Press, 2015(in Chinese).
[15]	陆慧中, 孙颖, 焦亚男, 等. 典型多向2.5D机织预制体近净形编织结构设计[J]. 复合材料学报, 2021, 38(9):3101-3109. LU Huizhong, SUN Ying, JIAO Yanan, et al. Design of near-net-shape braided structure of typical multi-directional 2.5D woven preform[J]. Acta Materiae Compositae Sinica,2021,38(9):3101-3109(in Chinese).
[16]	冯古雨, 钱坤, 曹海建, 等. 衬经结构对角联锁机织复合材料拉伸力学性能的影响[J]. 玻璃钢/复合材料, 2017(7):45-48. FENG Guyu, QIAN Kun, CAO Haijian, et al. Effect of warp lining structure on tensile mechanical properties of angular interlocking woven composites[J]. Fiberglass/Composite Materials,2017(7):45-48(in Chinese).
[17]	杨梦琪, 陈晓钢, 高强. 三维角联锁织物的可模塑性能研究[J]. 产业用纺织品, 2020, 38(5):27-31. doi: 10.3969/j.issn.1004-7093.2020.05.006 YANG Mengqi, CHEN Xiaogang, GAO Qiang. Study on moldability of 3D corner interlocking fabrics[J]. Technical Textiles,2020,38(5):27-31(in Chinese). doi: 10.3969/j.issn.1004-7093.2020.05.006
[18]	LI J, FAN W, LIU T, et al. The temperature effect on the inter-laminar shear properties and failure mechanism of 3D orthogonal woven composites[J]. Textile Research Journal,2020,90:2806-2817.
[19]	DANG M, LI D, JIANG L. Temperature effects on mechanical response and failure mechanism of 3D angle-interlock woven carbon/epoxy composites[J]. Composites Communications,2020,18:37-42. doi: 10.1016/j.coco.2020.01.001
[20]	SONG L, WEN W, CUI H. Experimental and numerical investigation of mechanical behaviors of 2.5D woven composites at ambient and un-ambient temperatures[J]. Composite Structures, 2018.
[21]	SORRENTINO L, DE VASCONCELLOS D S, D'AURIA M, et al. Effect of temperature on static and low velocity impact properties of thermoplastic composites[J]. Composites Part B: Engineering,2017,113:100-110. doi: 10.1016/j.compositesb.2017.01.010
[22]	WANG S, ZHANG J, ZHOU Z, et al. Compressive and flexural behavior of carbon fiber-reinforced PPS composites at elevated temperature[J]. Mechanics of Advanced Materials and Structures,2020,27(4):286-294. doi: 10.1080/15376494.2018.1472334
[23]	RICCIARDI M R, PAPA I, IMPERO F, et al. Low-temperature effect on the impact and flexural behaviour of basalt composite laminates[J]. Composite Structures,2020,249:112607. doi: 10.1016/j.compstruct.2020.112607
[24]	VIEILLE B, CHABCHOUB M, GAUTRELET C. Influence of matrix ductility and toughness on strain energy release rate and failure behavior of woven-ply reinforced thermoplastic structures at high temperature[J]. Composite Part B: Engineering,2017,132:125-140.
[25]	WANG M, CAO M, WANG H, et al. Drop-weight impact behaviors of 3-D angle interlock woven composites after thermal oxidative aging[J]. Composite Structures,2017,82223(16):31556.
[26]	中国国家标准化管理委员会. 纤维增强塑料弯曲性能实验方法: GB/T 1449—2005[S]. 北京: 中国标准出版社, 2005. Standardization Administration of the People's Republic of China. Test method for flexural properties of fiber-reinforced plastics: GB/T 1449—2005[S]. Beijing: China Standard Press, 2005(in Chinese).