复合材料夹芯结构褶皱增强理论和有限元方法

张森林; 吴振; 任晓辉

复合材料夹芯结构褶皱增强理论和有限元方法

1.
西北工业大学　航空学院, 西安 710072
2.
西安航空学院　机械工程学院, 西安 710065

基金项目: 国家自然科学基金 (12172295)

详细信息

通讯作者:
吴振，博士，博士生导师，研究方向为复合材料结构力学　E-mail: wuzhenhk@nwpu.edu.cn

中图分类号: TB333
计量
- 文章访问数: 195
- HTML全文浏览量: 101
- PDF下载量: 7
- 被引次数: 0
出版历程
- 收稿日期: 2022-09-22
- 修回日期: 2022-10-19
- 录用日期: 2022-11-02
- 网络出版日期: 2022-11-19
- 刊出日期: 2023-08-15

Enhanced theory and finite element method for wrinkling analysis of composite sandwich structure

1.
School of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China
2.
School of Mechanical Engineering, Xi′an Aeronautical University, Xi′an 710065, China

Funds: National Natural Science Foundation of China(12172295)

摘要

摘要: 夹芯结构广泛应用于航空航天和航海等领域。但由于面板和芯材的力学性能和几何尺寸差异较大，夹芯结构失效行为与其他复合材料结构的失效行为不同。对于承受复杂载荷的夹芯结构，褶皱失效行为可能比其他失效模式更早发生。本文针对夹芯梁在承受面内压缩载荷时容易发生屈曲和起皱的行为，构建了考虑局部形变和横法向应变的增强型高阶模型，该模型满足面内位移和横向剪切应力层间连续条件及自由表面条件。基于构建的理论模型，构造两节点梁单元公式并分析夹芯结构屈曲和褶皱问题。为了研究屈曲行为和褶皱行为之间的差异，使用本模型和三维有限元计算得到的屈曲和起皱行为对应的位移模态绘制在图1中。对于屈曲行为，中平面的变形与上下表面的变形一致。对于褶皱行为，由于中平面仅受压缩变形，但是上、下表面受到弯曲变形，所以中平面的变形与上下表面的变形完全不同。通过算例验证了所构建模型的准确性。数值分析结果表明，发展的模型计算夹芯结构的屈曲和褶皱行为有较高的精度，与三维有限元方法相比，本文构造的模型具有较高计算效率。相较于使用金属面板，使用纤维方向弹性模量大于金属面板弹性模量的复合材料面板，能有效增强夹芯梁抵抗起皱的能力。1使用本文提出的模型和三维有限元计算得到的屈曲和褶皱行为的位移模态
- 复合材料 /
- 夹芯结构 /
- 增强型高阶理论 /
- 褶皱 /
- 梁单元
Abstract: Panels wrinkling behaviors may occur when composite soft-core sandwich structures subjected to coplanar compression loads. Once the panels wrinkling appears, the sandwich structures will lose its load-bearing capacity. Therefore, it is necessary to develop an accurate model to predict the wrinkling behaviors of soft-core sandwich structures. Sandwich structure wrinkling is a typical three-dimensional (3D) problem, and few high-order models can accurately predict such issues. Therefore, this paper proposed an enhanced higher-order model including the local deformation and the 3D effects. Based on the proposed theory, the beam element formulation was derived, and the wrinkling behaviors of sandwich structures with different boundary conditions were analyzed. By comparing with the quasi-3D elasticity solution and the 3D finite element results, accuracy of the proposed method has been verified. In order to improve the capability of sandwich structures resisting the wrinkling deformation, this work attempted to use composite face sheets instead of metal panel in the sandwich structure. Numerical results show that the developed enhanced high-order model can accurately predict the wrinkling behaviors of the composite sandwich structures, and the use of composite panels can effectively resist the wrinkling behaviors of sandwich structures.
- composite /
- sandwich structures /
- enhanced higher-order theory /
- wrinkling /
- beam element

HTML全文

图 1 三层夹芯梁截面

Figure 1. Three-layer sandwich beam section

下载: 全尺寸图片幻灯片

图 2 构建的高阶单元收敛率

Figure 2. Convergence rate of constructed higher-order elements

下载: 全尺寸图片幻灯片

图 3 三层铝面板夹芯梁屈曲和褶皱载荷 (芯材与面板厚度之比t_c/t_f =50, 夹芯梁长厚比a/h=2)

Figure 3. Buckling and wrinkling loads for three-layer sandwich beam with aluminum face sheets (ratio of core thickness to panel thickness is t_c/t_f =50, ratio of length to thickness is a/h=2)

下载: 全尺寸图片幻灯片

图 4 使用当前模型和三维有限元计算得到的三层铝面板夹芯梁屈曲行为的位移模态

Figure 4. Displacement modes for buckling behaviors of a three-layer aluminum panel sandwich beam calculated by using the current model and 3 D-FEM

下载: 全尺寸图片幻灯片

图 5 使用当前模型和三维有限元计算得到的三层铝面板夹芯梁褶皱行为的位移模态

Figure 5. Displacement modes for wrinkling behaviors of a three-layer aluminum panel sandwich beam calculated by using the current model and 3 D-FEM

下载: 全尺寸图片幻灯片

图 6 材料参数和几何参数对三层铝面板夹芯梁屈曲和褶皱载荷影响

Figure 6. Influence of material properties and geometric parameters on buckling and wrinkling loads of three-layer sandwich beam with aluminum face sheets

下载: 全尺寸图片幻灯片

图 7 几何参数对三层铝面板夹芯梁屈曲和褶皱载荷影响

Figure 7. Influence of and geometric parameters on buckling and wrinkling loads of three-layer sandwich beam with aluminum face sheets

下载: 全尺寸图片幻灯片

表 1 三维有限元边界条件

Table 1. Boundary condition for 3 D finite element

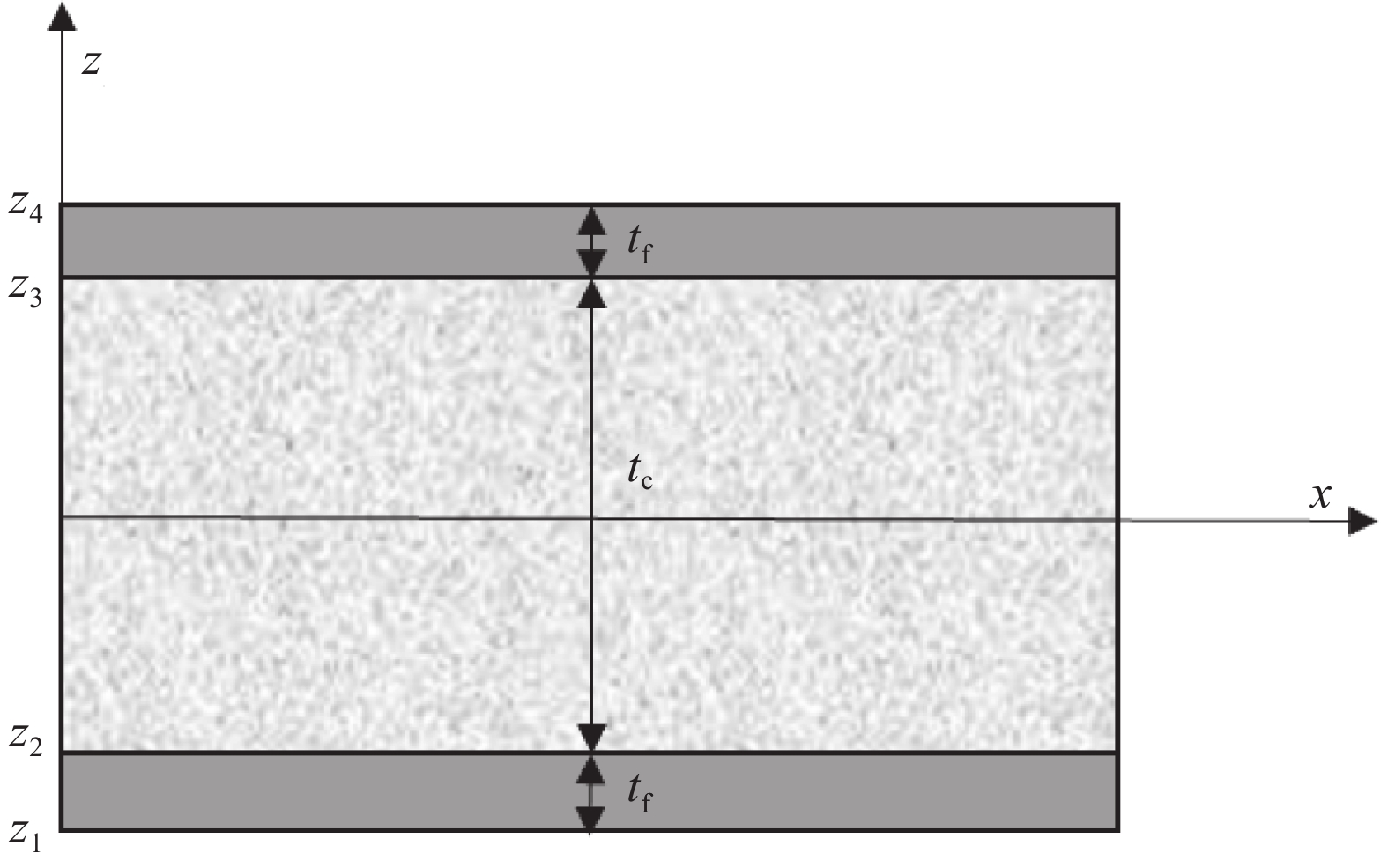
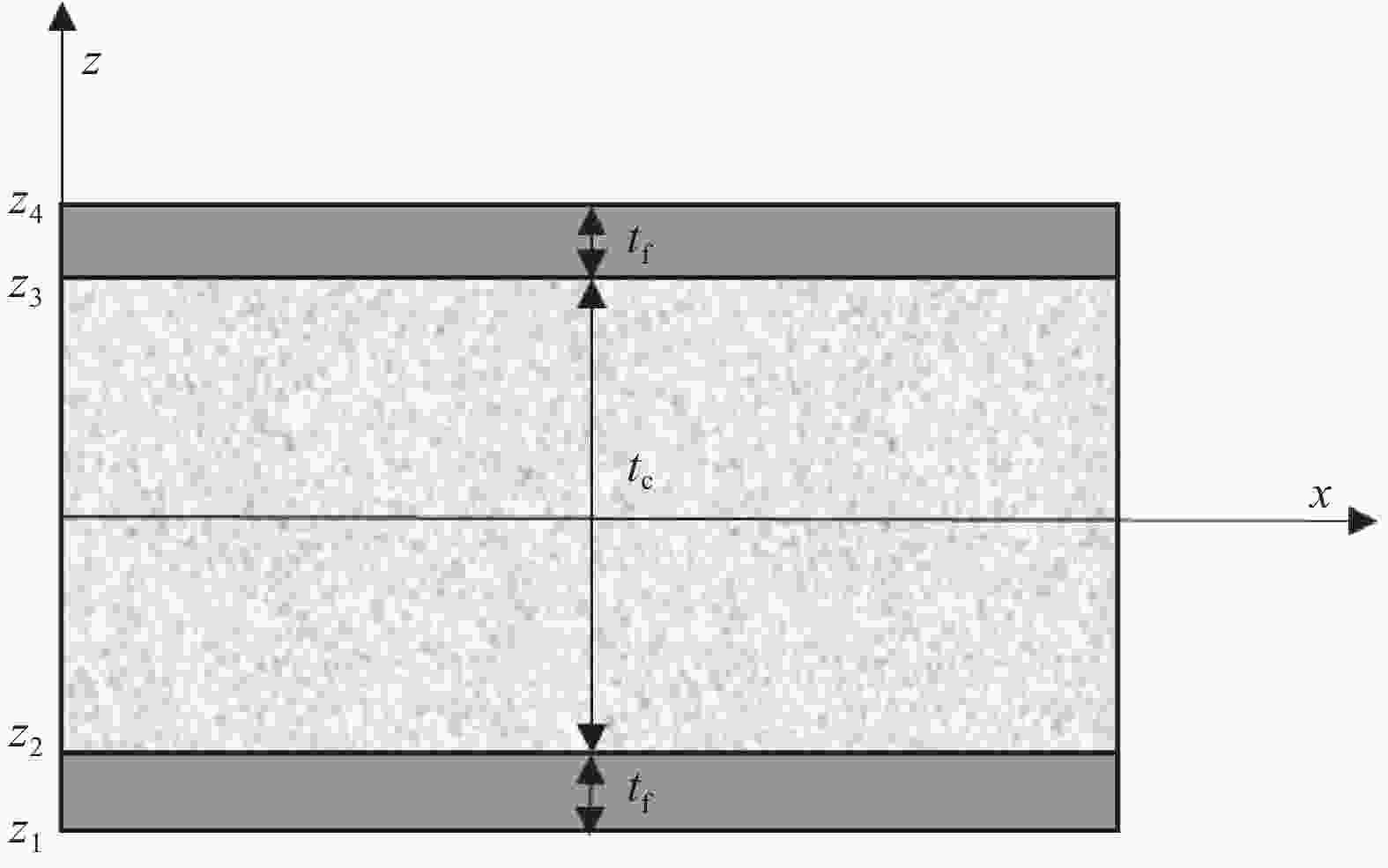
x=0	x=a	y=0	y=1
U2=U3=UR3=0	U3=UR3=0	U2= 0	U2= 0

下载: 导出CSV

表 2 三层铝面板夹芯梁屈曲载荷

Table 2. Buckling load of three-layer sandwich beam with aluminum panels

t_c/t_f	a/h	3 D-FEM (270000 elements)	BE18 (64 elements)	HYF11^[20]	HYF21^[20]	HOST^[21]	Allen^[22]
5	2	6.6111	6.7131 (1.54)	6.2220 (5.89)	37.551 (468.00)	37.238 (463.26)	6.3544 (3.88)
	5	14.7065	14.838 (0.89)	14.320 (2.63)	159.05 (981.49)	159.32 (983.33)	14.385 (2.19)
	10	41.658	41.819 (0.39)	41.084 (1.38)	329.63 (691.28)	321.26 (671.18)	41.115 (1.30)
25	2	1.5342	1.5600 (1.68)	1.5299 (0.28)	2.3207 (51.26)	2.3112 (50.64)	1.5923 (3.79)
	5	9.0749	9.1046 (0.33)	9.0314 (0.48)	13.130 (44.68)	13.113 (44.50)	9.0971 (0.24)
	10	31.649	31.655 (0.02)	31.096 (1.75)	42.433 (34.07)	42.436 (34.08)	31.159 (1.55)
50	2	1.4432	1.4640 (1.44)	1.4419 (0.09)	1.8335 (27.04)	1.8301 (26.81)	1.5074 (4.45)
	5	8.5657	8.6504 (0.99)	8.5553 (0.12)	10.311 (20.38)	10.301 (20.26)	8.6191 (0.62)
	10	27.585	27.522 (0.23)	26.762 (2.98)	30.746 (11.46)	30.769 (11.54)	26.849 (2.67)
Notes: BE18 is the present model; HYF11 is the quasi-3 D model; HYF21 and HOST are the higher-order models; Allen represents the model proposed by Allen.

下载: 导出CSV

表 3 三层铝面板夹芯梁褶皱载荷

Table 3. Wrinkling loads of three-layer sandwich beam with aluminum panels

t_c/t_f	a/h	3 D-FEM (270000 elements)	BE18 (480 elements)	HYF11^[20]	HYF21^[20]	Allen^[22]
50	2	0.7311 (5)	0.7632 (5)	0.7073 (6)	0.8074	1.3020 (9)
	5	4.5097 (13)	4.7147 (14)	4.3583 (14)	5.0048	8.1376 (23)
	10	18.091 (27)	18.883 (27)	17.433 (28)	20.019	--
100	2	0.2610 (9)	0.2845 (9)	0.2517 (9)	0.3121	0.6638(9)
	5	1.6318 (22)	1.7768 (22)	1.5736 (23)	1.9480	4.1486 (22)
	10	6.5273 (44)	7.1612 (43)	6.2921 (45)	7.7921	16.594 (45)
Note: Numbers in brackets represent half-wave numbers.

下载: 导出CSV

表 4 三层复合材料夹芯梁屈曲载荷

Table 4. Buckling load of three-layer composite sandwich beam

t_c/t_f	a/h	3 D-FEM (270000 elements)	BE18 (240 elements)	BHSDT^[24]	RHSDT^[25]
25	2	11.301	11.457	14.951	15.525
	5	64.288	64.441	85.873	89.282
	10	239.10	239.20	313.65	325.22
50	2	10.016	10.135	13.442	12.360
	5	61.853	61.978	80.805	73.963
	10	222.56	222.51	280.98	259.83
Notes: BHSDT is the higher order model proposed by Babu et al. ^[24]; RHSDT is

下载: 导出CSV

表 5 三层复合材料夹芯梁褶皱载荷

Table 5. Wrinkling load of three-layer composite sandwich beam

t_c/t_f	a/h	SS		CC
t_c/t_f	a/h	3 D-FEM (270000 elements)	BE18 (480 elements)	3 D-FEM (270000 elements)	BE18 (480 elements)
50	2	7.5768 (4)	8.0174 (4)	8.0246 (4)	8.5964 (4)
	5	46.413 (11)	49.265 (11)	47.101 (11)	50.086 (11)
	10	185.72 (22)	197.49 (22)	186.43 (21)	198.31 (21)
100	2	2.7004 (7)	2.8531 (7)	2.7806 (7)	2.9505 (7)
	5	16.835 (18)	17.829 (18)	16.929 (18)	17.937 (18)
	10	67.333 (36)	71.741 (36)	67.441 (36)	71.849 (36)
Note: Numbers in brackets represent half-wave numbers.the higher-order model proposed by Reddy ^[25].

下载: 导出CSV

参考文献(25)

[1]	杜冰, 刘后常, 潘鑫, 等. 热塑性复合材料夹芯结构熔融连接研究进展[J]. 复合材料学报, 2022, 39(7):3044-3058. doi: 10.13801/j.cnki.fhclxb.20220228.001 DU Bing, LIU Houchang, PAN Xin, et al. Progress in fusion bonding of thermoplastic composite sandwich structures[J]. Acta Materiae Compositae Sinica,2022,39(7):3044-3058(in Chinese). doi: 10.13801/j.cnki.fhclxb.20220228.001
[2]	熊健, 李志彬, 刘惠彬, 等. 航空航天轻质复合材料壳体结构研究进展[J]. 复合材料学报, 2021, 38(6):1629-1650. doi: 10.13801/j.cnki.fhclxb.20210107.002 XIONG Jian, LI Zhibin, LIU Huibin, et al. Advances in aerospace lightweight composite shell structure[J]. Acta Materiae Compositae Sinica,2021,38(6):1629-1650(in Chinese). doi: 10.13801/j.cnki.fhclxb.20210107.002
[3]	Ji W, Waas A M. Global and Local Buckling of a Sandwich Beam[J]. Journal of Engineering Mechanics,2007,133(2):230-237. doi: 10.1061/(ASCE)0733-9399(2007)133:2(230)
[4]	Vadakke V, Carlsson L A. Experimental investigation of compression failure of sandwich specimens with face/core debond[J]. Composites Part B:Engineering,2004,35:583-590. doi: 10.1016/j.compositesb.2003.10.004
[5]	Khalili S M R, Kheirikhah M M, Fard K M. Buckling Analysis of Composite Sandwich Plates with Flexible Core Using Improved High-Order Theory[J]. Mechanics of Advanced Materials and Structures,2015,22(4):233-247. doi: 10.1080/15376494.2012.736051
[6]	Benson A S, Mayers J, General instability and face wrinkling of sandwich plates-Unified theory and applications[J]. AIAA Journal, 1967, 5(4): 729-739.
[7]	Hadi B K, Matthews F L. Development of Benson–Mayers theory on the wrinkling of anisotropic sandwich panels[J]. Composite Structures,2000,49(4):425-434. doi: 10.1016/S0263-8223(00)00077-5
[8]	Dafedar J B, Desai Y M, Mufti A A. Stability of sandwich plates by mixed, higher-order analytical formulation[J]. International Journal of Solids and Structures,2003,40(17):4501-4517. doi: 10.1016/S0020-7683(03)00283-X
[9]	Lopatin A V, Morozov E V. Symmetrical facing wrinkling of composite sandwich panels[J]. Journal of Sandwich Structures & Materials,2008,10(6):475-497.
[10]	Ji W, Waas A M. Wrinkling and edge buckling in orthotropic sandwich beams[J]. Journal of Engineering Mechanics,2008,134(6):455-461. doi: 10.1061/(ASCE)0733-9399(2008)134:6(455)
[11]	Hu H, Belouettar S, Potier-ferry M, et al. A novel finite element for global and local buckling analysis of sandwich beams[J]. Composite Structures,2009,90(3):270-278. doi: 10.1016/j.compstruct.2009.02.002
[12]	Yu K, Hu H, Tang H, et al. A novel two-dimensional finite element to study the instability phenomena of sandwich plates[J]. Computer Methods in Applied Mechanics and Engineering,2015,283:1117-1137. doi: 10.1016/j.cma.2014.08.006
[13]	Douville M A, Le Grognec P. Exact analytical solutions for the local and global buckling of sandwich beam-columns under various loadings[J]. International Journal of Solids and Structures,2013,50:2597-2609. doi: 10.1016/j.ijsolstr.2013.04.013
[14]	D’ottavio M, Polit O. Linearized global and local buckling analysis of sandwich struts with a refined quasi-3 D model[J]. Acta Mechanica,2015,226(1):81-101. doi: 10.1007/s00707-014-1169-2
[15]	D’ottavio M, Polit O, Ji W, et al. Benchmark solutions and assessment of variable kinematics models for global and local buckling of sandwich struts[J]. Composite Structures,2016,156:125-134. doi: 10.1016/j.compstruct.2016.01.019
[16]	Vescovini R, D’ottavio M, Dozio L, et al. Buckling and wrinkling of anisotropic sandwich plates[J]. International Journal of Engineering Science,2018,130:136-156. doi: 10.1016/j.ijengsci.2018.05.010
[17]	Huang Q, Liu Y, Hu H, et al. A Fourier-related double scale analysis on the instability phenomena of sandwich plates[J]. Computer Methods in Applied Mechanics and Engineering,2017,318:270-295. doi: 10.1016/j.cma.2017.01.021
[18]	Chen X, Nie G, Wu Z. Global buckling and wrinkling of variable angle tow composite sandwich plates by a modified extended high-order sandwich plate theory[J]. Composite Structures,2022,292:115639. doi: 10.1016/j.compstruct.2022.115639
[19]	朱秀杰, 郑坚, 熊超, 等. 基于精确板理论的复合材料格栅/波纹夹芯结构屈曲特性[J]. 复合材料学报, 2022, 39(1):399-411. doi: 10.13801/j.cnki.fhclxb.20210309.003 ZHU Xiujie, ZHENG Jian, XIONG Chao, et al. Buckling characteristics of composite grid/corrugated sandwich structure based on refined plate theory[J]. Acta Materiae Compositae Sinica,2022,39(1):399-411(in Chinese). doi: 10.13801/j.cnki.fhclxb.20210309.003
[20]	Dafedar J B, Desai Y M. Stability of composite and sandwich struts by mixed formulation[J]. Journal of Engineering Mechanics,2004,130(7):762-770. doi: 10.1061/(ASCE)0733-9399(2004)130:7(762)
[21]	Kant T, Patil H S. Buckling loads of sandwich columns with a higher-order theory[J]. Journal of Reinforced Plastics and Composites,1991,10(1):102-109. doi: 10.1177/073168449101000107
[22]	Allen, HG. Analysis and design of structural sandwich panels[M]. London: Pergamon Press. 1969.
[23]	Sze K Y, Chen R, Cheung Y K. Finite element model with continuous transverse shear stress for composite laminates in cylindrical bending[J]. Finite Elements in Analysis & Design,1998,31(2):153-164.
[24]	Babu R T, Verma S, Singh B N, et al. Dynamic analysis of flat and folded laminated composite plates under hygrothermal environment using a nonpolynomial shear deformation theory[J]. Composite Structures,2021,274:114327. doi: 10.1016/j.compstruct.2021.114327
[25]	Reddy J N. A simple higher-order theory for laminated composite plates[J]. Journal of Applied Mechanics,1984,51(12):745-752.