Flexural behavior of concrete-filled circular CFRP-steel tube with flange-sleeve joints
-
摘要:
在钢管混凝土外侧粘贴碳纤维增强复合材料(CFRP)形成的CFRP-钢管混凝土拱架具有高承载力与刚度的优点，用于高应力、极软岩、强采动和断层破碎带等不良地质条件下的大断面隧道支护。本文提出了一种新型法兰-套管组合连接形式，用于CFRP-钢管混凝土拱架的节点。通过四点弯曲试验研究了法兰厚度(20 mm、30 mm、40 mm)对CFRP-钢管混凝土节点破坏模式、抗弯承载力、刚度等弯曲性能的影响。试验结果表明：试件的破坏模式均为CFRP沿轴向剥离破坏，法兰-套管节点完好，该连接方式有效；法兰厚度为20 mm时，抗弯承载力和刚度与无节点试件的基本一致，且抗弯承载力和刚度随着法兰厚度的增加而增大。通过有限元分析，研究法兰厚度、套管长度和套管壁厚对CFRP-钢混凝土节点弯曲性能影响规律。有限元结果表明：内聚力模型能较好地模拟CFRP剥离过程；法兰厚度对节点力学特性影响显著，套管长度和壁厚对节点力学特性影响较小；对于工程中常用的直径为140 mm的CFRP-钢管混凝土拱架节点，建议法兰厚度取20 mm，套管长度取200 mm，套管壁厚取5.5 mm。
Abstract:The concrete filled circular CFRP-steel tube arch formed by pasting carbon fiber reinforced polymer (CFRP) on the outer side of the concrete filled steel tube has higher bearing capacity and stiffness, and can be used for tunnel support under adverse geological conditions such as high stress, extremely soft rock, strong mining, and fault fracture zones. This article proposes a new type of flange-sleeve joint, which is used for concrete filled circular CFRP-steel tube arch in tunnel engineering. The influence of different flange thicknesses (20 mm, 30 mm, 40 mm) on the failure mode, flexural bearing capacity of concrete filled CFRP-steel tube joint under four-point bending was experimentally studied. The results show that the failure mode of the specimens is CFRP axial delamination, and the flange-sleeve joint is intact, indicating that this connection method is effective; When the flange thickness is 20 mm, the bending bearing capacity and stiffness of the specimen are basically the same as those of the node free specimen, and the bending bearing capacity and stiffness increase with the increase of flange thickness. Based on ABAQUS finite element analysis, a comparison was made with experimental results, and parameterized analysis was conducted using flange thickness, casing length, and casing wall thickness as variables. The finite element results indicate that the cohesive zone model can effectively simulate the delamination process of CFRP; The thickness of the flange has a significant influence on the mechanical properties of the joint, while the length and wall thickness of the sleeve have a relatively small influence on the mechanical properties of the joint; For specimens with a steel tube diameter of 140 mm and a CFRP thickness of 3 mm, it is recommended to take a flange thickness of 20 mm, a sleeve length of 200 mm, and a sleeve wall thickness of 5.5 mm.
-
乙烯-四氟乙烯(ETFE)薄膜凭借其良好的物理特性及力学性能，在新型建筑、能源等领域中已被广泛应用。在实际工程应用中，ETFE膜结构的撕裂破坏可归结为内部因素与外部环境因素的协同作用。膜面处膜材在制造与安装过程中，不可避免地会存在微小孔洞、细微折痕和微裂纹等初始缺陷，以及偶发的外来飞致物刺穿引起的切缝；这使膜材在预应力、极端风荷载及雨雪荷载的复合作用下，极易产生应力集中而诱发缺陷不断扩展，最终膜材撕裂损伤，严重情况下甚至会引发膜结构的整体失效，对结构安全构成重大威胁。并且当膜材在中心区域处受到集中载荷或存在制造缺陷时，极有可能会出现显著的中心撕裂行为[1, 2]。因此，除了需对ETFE薄膜的常规力学性能进行研究，也有必要对其撕裂力学行为开展深入研究。
吴明儿[3-5]、崔家春[6, 7]、胡建辉[8]、Zhang[9]、Surholt[10]和Zhao[11-13]等分别对ETFE薄膜进行了系列试验与分析，揭示了薄膜的单轴和双轴力学行为，研究了弹性模量、屈服强度、断裂强度和徐变等力学参数和规律。整体上，现有研究多集中在ETFE母材的粘-弹塑性行为及本构关系等，在撕裂性能的研究尚十分欠缺。而随着ETFE膜结构的社会需求增长，对其撕裂性能研究的欠缺势必会阻碍ETFE膜结构的进一步应用和发展。另外，国内外学者已对织物类膜材的撕裂强度及破坏规律开展了深入研究[14-20]，可为ETFE薄膜撕裂力学性能的研究提供一定参考。Chen等[14, 15]对层压织物进行了系统的单轴撕裂试验，分析了切缝长度、切缝角度、偏轴角对其撕裂行为和撕裂强度的影响；Sun等[18, 19]深入研究了单轴拉伸下切缝长度和切缝角度对PTFE涂层织物撕裂性能的影响；Zhang等[20]论证了切口样式、切缝尺寸和试样尺寸对PVC涂层织物单轴中心撕裂特性的影响。
鉴于此，本文针对典型ETFE薄膜，进行单轴中心撕裂试验，研究切缝长度、切缝角度和切口样式对ETFE薄膜的破坏形态特征及撕裂力学行为的影响。另外，数字图像相关(DIC)技术具有全场测量、非接触、高分辨率等优势[21-23]，可为撕裂力学行为分析提供准确可靠的数据支撑，将用于薄膜撕裂全过程薄膜位移场和应变场的测量与重构。所得结论可为ETFE薄膜材料的撕裂力学性能研究和ETFE膜结构的安全性评估提供有益参考。
1. 试验概况
1.1 试验材料及试件尺寸
试验采用ETFE #250/NJ/
1600 /NT薄膜，其厚度为250μm，密度为1.75 g·cm−3。材料由乙烯和四氟乙烯聚合生成，无色透明，具有优秀的耐化学腐蚀性能和自洁性能[24]。考虑到当前暂无专门的ETFE膜材撕裂性能检测标准，因此参照GB/T 1040.3-2006[25]，以ETFE薄膜单轴拉伸试验的长条形试件的尺寸，直接作为单轴中心撕裂试验的试样尺寸，以实现测试需求。试件尺寸为150 mm×25 mm，夹持端长为25 mm，有效测试区域为100 mm×25 mm。散斑区域设置为50 mm×25 mm，散斑直径为0.5 mm。其中，切缝长度为5 mm，切缝方向角以膜材机器展开方向(MD)的垂直线为基准线，逆时针旋转θ。试件示意图如图1所示。另外，为保证试件在拉伸过程中的滑移量可控，采用在试件夹持端处使用粘结剂粘附砂纸的方法，通过增大夹具与试件接触面之间的摩擦系数，提升夹持的稳定性与可靠性。![]()
图 1 含中心切缝的乙烯-四氟乙烯(ETFE)薄膜典型试件示意图Figure 1. Schematic diagram of a typical specimen of ethylene tetrafluoroethylene (ETFE) foils with a central slit1.2 试验设备
试验选用深圳三思UTM4000型电子万能试验机和尼康D3200高像素照相机。其中，试验机位移速率范围为0.001~500.000 mm·min−1；变形测量范围为10~800 mm，±1‰变形精度；拉压力传感器量程为200 N、精度为0.2 N；尼康D3200高像素照相机拥有
2400 万像素。含中心切缝的ETFE薄膜加载过程中的夹持示意图如图2所示。试验中先对试件施加5 N的预张力，再匀速(50 mm·min−1)加载至试件破坏，并记录试件在试验过程中的变形、荷载和图像数据。![]()
图 2 含中心切缝的ETFE薄膜加载过程中的夹持示意图Figure 2. Clamping schematic of ETFE foils with a central slit during loading1.3 试验工况及环境
试验工况设置为切缝长度、切缝角度和切口样式。其中，切缝长度以2.5 mm为梯度，选取为2.5、5.0、7.5、10.0、12.5和15.0 mm；切缝角度以MD方向为基准，逆时针每旋转15°为一个梯度，选取0°、15°、30°、45°、60°、75°和90°七个角度；切口样式则将典型试件的“一”形切缝更换为其它切口样式，且切口样式可分为开放性切缝(如“一、V、X和十”形等)和封闭性切口(如圆形、椭圆形和矩形切口等)[26]；不同切缝角度和切口样式的示意图如图3所示。每个工况的有效试件为3个，以保证试验的有效性。
![]()
图 3 切缝角度和切口样式的切缝示意图(单位：mm)Figure 3. Slit diagram of slit angles and notch shapes (Unit: mm)试验温度控制在(20±2.0)℃，相对湿度控制在(65±4.0)%。
2. 试验结果及分析
2.1 撕裂过程及破坏形态
ETFE薄膜在不同工况下典型撕裂过程如图4所示，其膜面含散斑贴膜以便于观察，三种工况下的ETFE薄膜的撕裂过程均呈现出4个特征状态：
![]()
图 4 不同工况下ETFE薄膜典型撕裂过程：(a)切缝长度、(b)切缝角度和(c)切口样式Figure 4. Typical tearing process of ETFE foils under different conditions: (a) Slit length; (b) Slit angle; (c) Notch shape(ⅰ)切缝初始状态：在外加5 N预张力时，因其外加荷载较小，切缝保持未张开状态。
(ⅱ)切缝张开状态：随着外加荷载不断增加，切缝逐渐张开，切缝张开形状近似呈现椭圆形；薄膜在切缝尖端上下邻域展现出显著的面外屈曲现象。
(ⅲ)极限撕裂状态：随着外加荷载进一步增大，切缝开口进一步扩大，面外屈曲现象也变得更加明显，薄膜的塑性变形显著增加；其切缝尖端处由于应力集中效应显著，会形成撕裂三角区，出现明显的颈缩现象，并且切缝开始沿着垂直于加载方向扩展。
(ⅳ)完全破坏状态：在薄膜到达极限撕裂状态以后，随着荷载的增大，切缝扩展速度加剧，薄膜的承载能力不断下降，薄膜最终达到完全破坏状态，丧失所有承载能力，并且不同切口样式导致薄膜呈现的破坏形态各异。
图5为ETFE薄膜在切缝张开状态下的切缝邻域εxy应变云图，该云图可直观的展现出薄膜面外屈曲的位置分布及其方向。据图可知，薄膜的面外屈曲的位置集中分布于切口上下邻域；εxy应变云图集中区呈现“X”型分布，其中，“X”型的中心点与切口的中心点重合。在构成“X”型的同一边上，面外屈曲的方向相同；而在构成“X”型的不同边上，面外屈曲的方向相反。随着切缝长度变化，薄膜面外屈曲的位置几乎保持不变。随着切缝角度变化，面外屈曲的位置仍处于切口上下邻域，随之发生相同角度的倾斜。随着切口样式变化，切口会沿着拉伸方向发生不同的张开变形，从而使薄膜面外屈曲的位置随之变化。
2.2 切缝长度影响
不同切缝长度的ETFE薄膜的撕裂抗力-位移曲线如图6(a)所示，撕裂曲线随切缝长度改变存在规律性衍变，但存在典型共同特征，不妨提取典型撕裂曲线对ETFE薄膜撕裂力学行为进行深入阐释(见图6(b))。
![]()
图 5 不同工况下ETFE薄膜切缝邻域的εxy应变云图Figure 5. εxy strain nephogram of ETFE foils in the neighborhood of the slit under different conditions![]()
图 6 不同切缝长度的ETFE薄膜撕裂抗力-位移曲线及其典型撕裂曲线Figure 6. Tearing strength-displacement curves and typical tearing curve of ETFE foils with different slit lengths如图6(a)所示，随着切缝长度增大，撕裂抗力-位移曲线的撕裂前段的斜率不发生变化。在撕裂抗力上升阶段，曲线斜率增加的部分随切缝长度增大而逐渐消失；当切缝长度为2.5 mm、5.0 mm时，可明显观察到曲线斜率上升的趋势，而当切缝长度增大至7.5 mm后，曲线的斜率随着位移的增大而越来越小，无法观察到曲线斜率上升。在撕裂后段，当薄膜的切缝长度从2.5 mm增大到15.0 mm，薄膜有效承载截面不断减小，其极限撕裂抗力从130.74 N下降至57.94 N，下降55.68%；断裂位移由45.48 mm下降至11.05 mm，下降75.70%。
如图6(b)所示，典型撕裂曲线以4个特征点为界，可分为3个特征阶段。其中，初始点O为曲线与纵轴的交点，类屈服点A为曲线斜率首次发生变化点，峰值点B为曲线撕裂抗力最大点和破坏点C为曲线与横轴的交点；4特征点分别与典型撕裂过程的4个特征状态相对应。
(OA)撕裂前段：曲线从不为零的初始点O开始，对应着试验前施加的预张力状态；在该阶段ETFE薄膜呈现出显著的线弹性行为，薄膜的初始弹性模量较大。
(AB)撕裂抗力上升阶段：曲线到达类屈服点A后，斜率迅速减小，明显小于撕裂前段的斜率，开始出现较大的塑性变形；随着位移增大，薄膜内部结构会充分发生变化，撕裂抗力不断增加，曲线斜率明显上升；随后由于变形继续增大导致刚度下降，撕裂抗力增加的速度变缓，曲线斜率又开始下降至零。
(BC)撕裂后段：曲线到达峰值点B时，薄膜达到极限撕裂抗力，开始发生显著的撕裂扩展；随着位移增加，撕裂抗力不断下降，并且撕裂扩展的速度不断加快，撕裂抗力下降幅度逐渐变大，最终下降到破坏点C，对应着薄膜完全破坏。
2.3 切缝角度影响
不同切缝角度的ETFE薄膜撕裂抗力-位移曲线如图7所示。随着切缝角度增大，撕裂抗力-位移曲线的撕裂前段的斜率不发生变化，并且类屈服点对应的位移由1.52 mm上升至1.57 mm，撕裂前段所历经的位移仅增加1.97%，曲线几乎同时进入下一阶段。在撕裂抗力上升阶段，不同切缝角度的薄膜的曲线均会呈现出斜率增大的趋势，并且撕裂抗力上升阶段随切缝角度增加而显著变长。在撕裂后段，当切缝角度由0°增大至90°时，对应的等效切缝长度[27]由5 mm减少至0 mm，其极限撕裂抗力由107.69 N上升至134.25 N，断裂位移由24.39 mm上升至79.90 mm。
可见，随着切缝角度的增大，对应的等效切缝长度随之减小，薄膜的承载途径逐渐恢复，用来承受拉伸荷载的有效截面增大，薄膜的极限撕裂强度增强，使薄膜不易到达极限撕裂状态，使得其断裂位移也随之增大。并且当切缝长度保持为5 mm时，切缝角度由0°增大到90°，其极限撕裂抗力和断裂位移分别上升了24.66%和227.59%，断裂位移的变化率远大于极限撕裂抗力的变化率。因此，切缝角度的改变对薄膜的极限撕裂抗力影响较小，而会显著影响薄膜完全破坏时对应的断裂位移。
![]()
图 7 不同切缝角度的ETFE薄膜撕裂抗力-位移曲线Figure 7. Tearing strength-displacement curves for ETFE foils with different slit angles图8为不同切缝角度的ETFE薄膜的切缝尖端邻域的竖向应变场云图。据图可知，当预制切缝长度为5 mm的“一”形切缝时，薄膜在切缝邻域出现明显的应变集中区(红色区域)，并且其应变集中区分布于切缝尖端邻域上，随切缝角度的增加而发生相应的偏转。这是由于薄膜在预制初始切缝后，在切缝尖端邻域，随着拉伸应力的增大，切缝张开导致薄膜沿着切缝方向发生横向收缩，并且在切缝上下邻域处发生面外屈曲，薄膜会向面外凸出，导致切缝尖端邻域处承受的应力远高于其它区域，从而使薄膜在该区域处的竖向应变较大而出现应变集中区。因此，随着切缝角度的增大，薄膜切缝张开所致的横向收缩效应及面外屈曲现象发生相应的变化，使薄膜的应变集中区始终分布于切缝尖端邻域，从而使得薄膜的应变集中区发生相应的偏转。
![]()
图 8 不同切缝角度的ETFE薄膜切缝尖端邻域的竖向应变场云图Figure 8. Vertical strain field nephograms in the neighborhood of the slit tip of ETFE foils with different slit angles2.4 切口样式影响
图9为不同切口样式的ETFE薄膜的撕裂抗力-位移曲线。不同切口样式对薄膜撕裂曲线的撕裂后段影响显著，导致含不同切口样式的薄膜在完全破坏时，整体上表现出两种破坏模式：类脆性破坏和类延性破坏。如图9(a)和图9(f)所示，对于无切缝和含圆形切口的ETFE薄膜，撕裂曲线到达峰值点后立即发生破坏，在撕裂后段历经的位移占整个撕裂过程发生的位移比例极小；并且在试验过程中可听到轻脆的崩断声，薄膜突然发生破坏，展现出类脆性破坏特性。而对于图9其它切口样式的ETFE薄膜，则呈现类延性破坏特性。撕裂曲线到达峰值点后，薄膜虽然达到了极限撕裂强度，但并不会立即发生断裂破坏；薄膜的切缝不断扩展，有效承载截面逐渐减小，薄膜在历经较大的位移后才完全破坏，可观察到明显预兆。
![]()
图 9 不同切口样式的ETFE薄膜撕裂抗力-位移曲线Figure 9. Tearing strength-displacement curves of ETFE foils with different notch shapes图10为撕裂试样典型损伤模式示意图。可知，含切口的ETFE薄膜，在拉伸撕裂过程中，切口破坏了薄膜的完整性，使薄膜较易出现面外屈曲和颈缩，从而使薄膜在切口邻域处出现显著的大变形区。这会导致薄膜的应力分布不均匀，在大变形区出现应力集中，从而引发撕裂，使薄膜在切口尖端处出现撕裂三角区，薄膜的承载性能下降。并随着撕裂三角区的逐渐扩展，薄膜的有效承载区域不断减小，薄膜的承载性能逐渐下降为零。并且，不同切口样式会使薄膜的大变形区不同，从而使其应力集中各不相同，导致不同切口样式使薄膜承载性能的衰减程度各异。
![]()
图 10 典型撕裂试样损伤模式示意图：(a)“一”形切缝和(b)圆形切口Figure 10. Schematic representation of typical damage modes of the tearing specimens: (a) “—” shaped slit ,and (b) circle notch图11为不同切口样式的ETFE薄膜对应的极限撕裂抗力。对于含开放性切缝的薄膜，相较于无切缝薄膜，含“V、X和十”形切缝的薄膜的极限撕裂抗力均约为138.13 N，下降40.58%，而含“一”形切缝的薄膜仅为107.25 N，下降53.86%。因此，当切缝的横向尺寸相同时，“一”形切缝贯穿了薄膜的主要受力方向，应力集中显著，对薄膜的极限撕裂强度的不利影响最大。对于含封闭性切口的薄膜，相较于无切缝薄膜，含圆形和椭圆形切口的薄膜的极限撕裂强度约为151.88 N，下降34.66%，含矩形-I切口的薄膜仅为115.19 N，下降50.44%。因此，当切口的横向尺寸相同时，矩形-I切口由于具有直角边缘等特性，使薄膜的应力集中程度远大于含圆形和椭圆形切口的薄膜，使薄膜承载性能的衰减程度更大。另外，含矩形-II切口的薄膜的极限撕裂强度为129.63 N，相较于无切缝薄膜的下降44.23%。可见，当切口几何外形相同时，对于横向尺寸较大的切口，其周围的应力集中区域较大，薄膜较易产生撕裂扩展，故对薄膜极限撕裂强度的不利影响更大。
![]()
图 11 不同切口样式的ETFE薄膜极限撕裂抗力Figure 11. Ultimate tearing strength of ETFE foils with different notch shapes3. 结 论
结合系列试验与数字图像相关(DIC)技术，深入分析了乙烯-四氟乙烯(ETFE)薄膜的单轴中心撕裂行为，主要结论如下：
(1) ETFE薄膜的典型撕裂扩展过程呈现出4个特征状态；不同切缝参数显著影响薄膜面外屈曲的位置和破坏形态，但不影响薄膜切缝扩展的方向始终为垂直于加载方向；
(2) ETFE薄膜的撕裂抗力-位移曲线随不同工况的变化而发生非线性衍变，但存在典型共同特征，可划分为3个特征阶段：撕裂前段、撕裂抗力上升阶段和撕裂后段；
(3)当切缝长度从2.5 mm增大到15.0 mm时，薄膜的有效承载截面变小，其极限撕裂强度和断裂位移分别减小了55.75%和75.70%；当切缝角度从0°增大到90°时，薄膜承载途径逐渐恢复，其极限撕裂强度增大了24.67%，而断裂位移却增大了227.59%；
(4)切口样式使薄膜在完全破坏时呈现出类脆性破坏特征或类延性破坏特征。当横向尺寸相同时，在开放性切缝中，“一”形切缝贯穿薄膜主要受力方向，应力集中显著，对薄膜极限撕裂强度的不利影响最大；在封闭性切口中，与光滑边缘切口相比，直角边缘切口使薄膜的应力集中效应更显著，使薄膜易在切口尖角处发生撕裂，造成薄膜承载性能的显著衰减。所得结论可为相关均质性膜材的撕裂力学性能研究和膜结构的安全性评估提供有益参考。
-
![]()
图 2 法兰-套管组合连接碳纤维复合材料(CFRP)-钢管混凝土
Figure 2. Flange-sleeve combination connection of concrete-filled carbon fiber reinforced polymer (CFRP)-steel tube
![]()
图 3 加载测试装置
Figure 3. Loading and testing system
LVDT—Linear variable displacement transducer
![]()
图 7 试件B-1~B-3截面高度轴向应变分布
Figure 7. Axial strain distribution with cross-section height of specimens B-1-B-3
Mu—Ultimate bending moment at specimen failure
![]()
图 8 圆CFRP-钢管混凝土梁有限元模型
Figure 8. Finite element model of concrete-filled circular CFRP-steel tube beam
![]()
图 9 试件B-1~B-4有限元模型和试验荷载-跨中挠度曲线
Figure 9. Load-midspan deflection curves of finite element model and experiment of specimens B-1-B-4
![]()
图 10 试件B-1~B-4有限元模型和试验荷载-轴向应变曲线
Figure 10. Load-axial strain curves of finite element model and experiment of specimens B-1-B-4
![]()
图 11 峰值荷载时试件B-1和B-2的有限元模型应力云图
Figure 11. Stress nephogram of finite element model of specimens B-1 and B-2 under maximum load
S—Stress; S33—Axial stress component in the specimen
![]()
图 12 B-2套管内胶层损伤云图
Figure 12. Damage nephogram of B-2 adhesive inside sleeve
QUADSCRT—Under the quadratic nominal stress damage initiation criterion, the damage initiation threshold for cohesive elements is 1. Damage initiates in the element when this value is reached
![]()
图 13 不同法兰厚度下试件的荷载-跨中挠度曲线
Figure 13. Load-midspan deflection curves of specimens under different flange thicknesses
![]()
图 14 套管长度和厚度对试件荷载-跨中挠度曲线的影响
Figure 14. Influence of the length and thickness of sleeve on the load-midspan deflection curves of specimens
表 1 法兰-套管节点的主要参数
Table 1 Main parameters of flange-sleeve joints
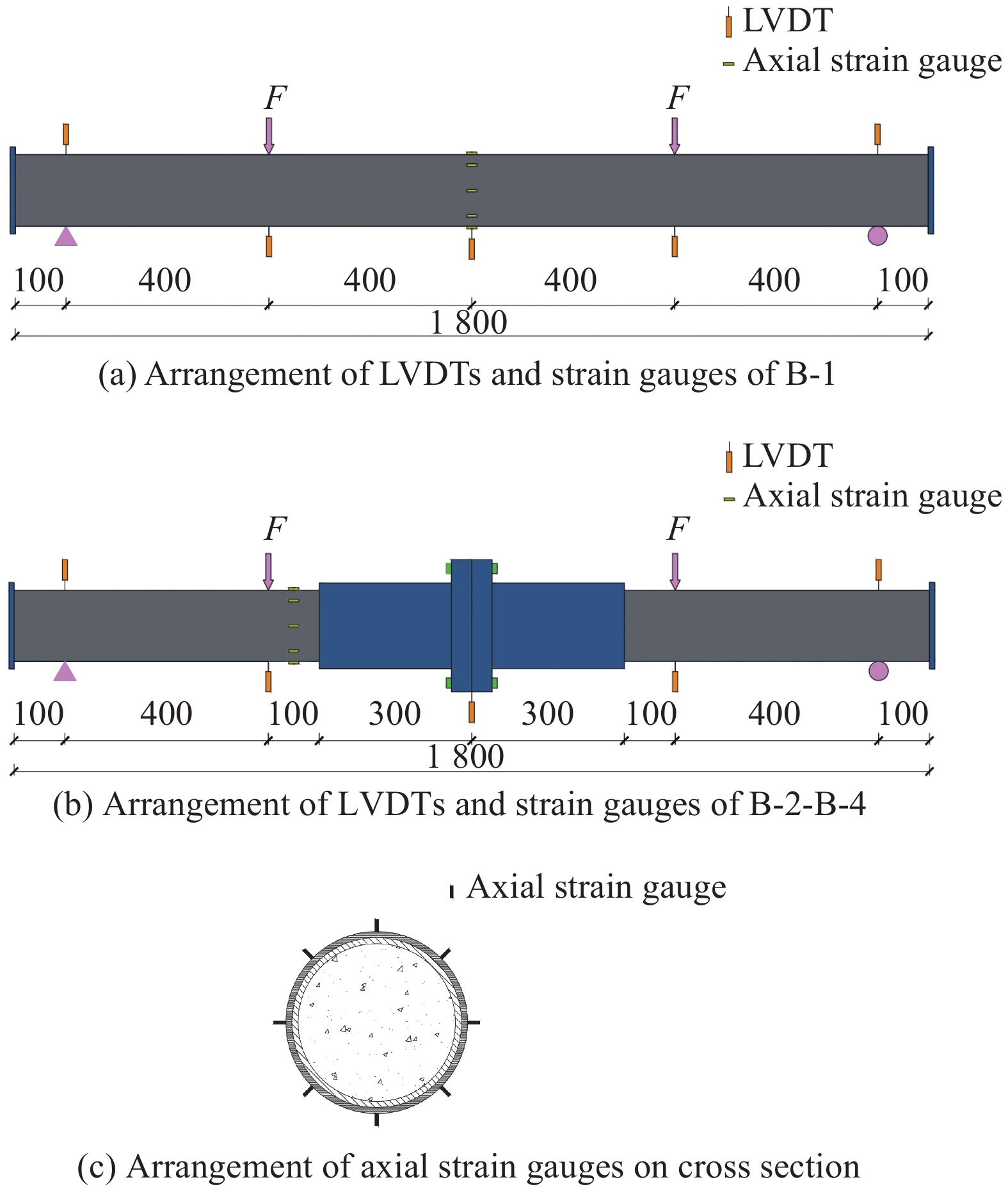
Specimen Thickness of flange/mm Diameter of bolt/mm Length of flange-sleeve/mm Thickness of sleeve/mm B-1 — — — — B-2 20 33 300 8 B-3 30 33 300 8 B-4 40 33 300 8 
下载: 导出CSV
表 2 碳纤维布力学性能
Table 2 Mechanical properties of CFRP sheet
Thickness/
mmTensile
strength/MPaYoung's
modulus/GPaElongation
rate/%0.167 3400 240 1.6
下载: 导出CSV
表 3 钢材力学性能
Table 3 Mechanical properties of steel
Yield strength/MPa Tensile strength/MPa Young's modulus/GPa Poisson's rate 290 405 200 0.3
下载: 导出CSV
表 4 环氧树脂胶力学性能
Table 4 Mechanical properties of epoxy resin adhesive
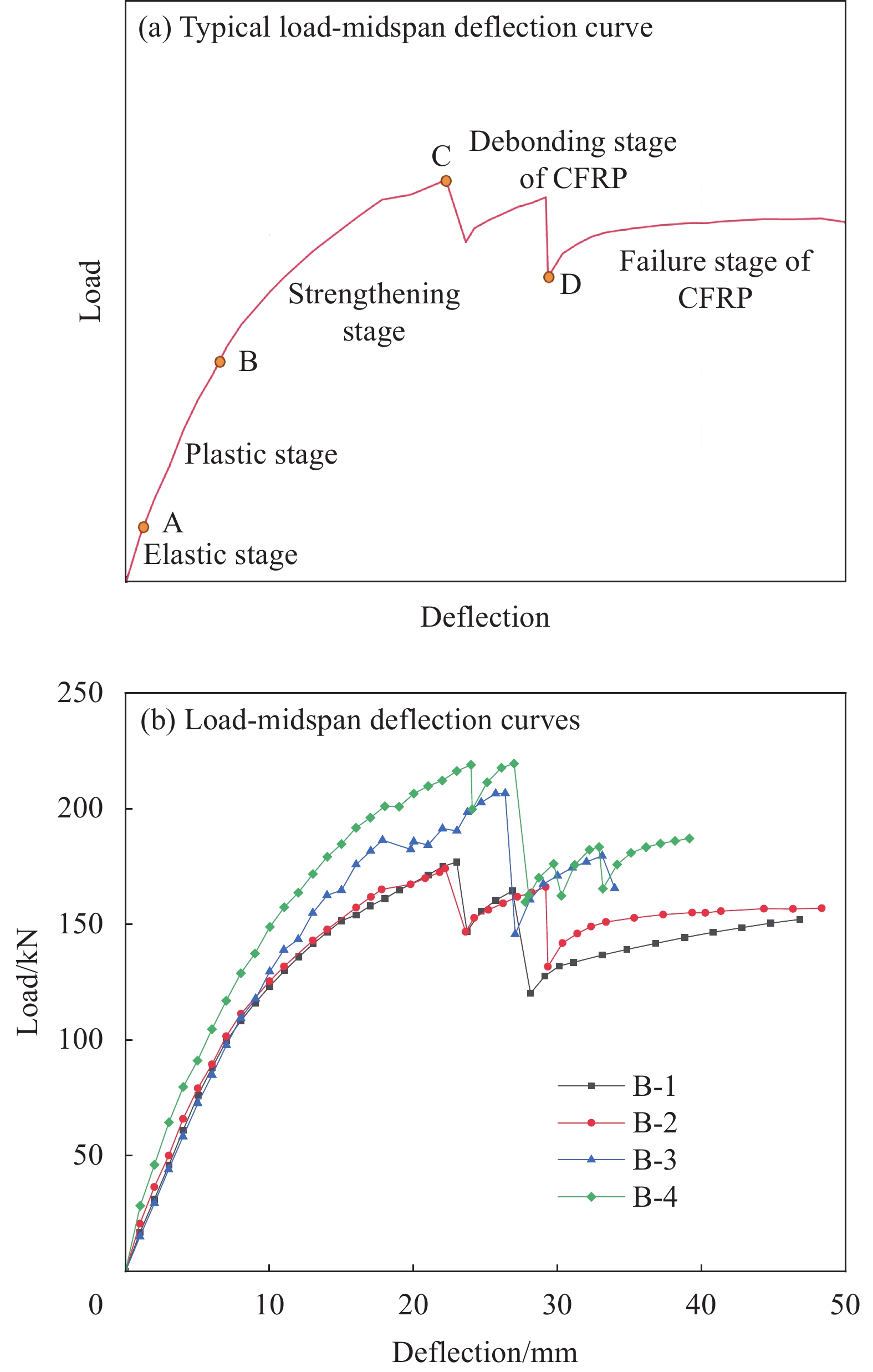
Tensile strength/MPa Young's modulus/MPa Elongation rate/% 50 2500 4
下载: 导出CSV
表 5 试件B-1~B-4各阶段特征荷载与变形
Table 5 Characteristic loads and deformations at each stage of specimens B-1-B-4
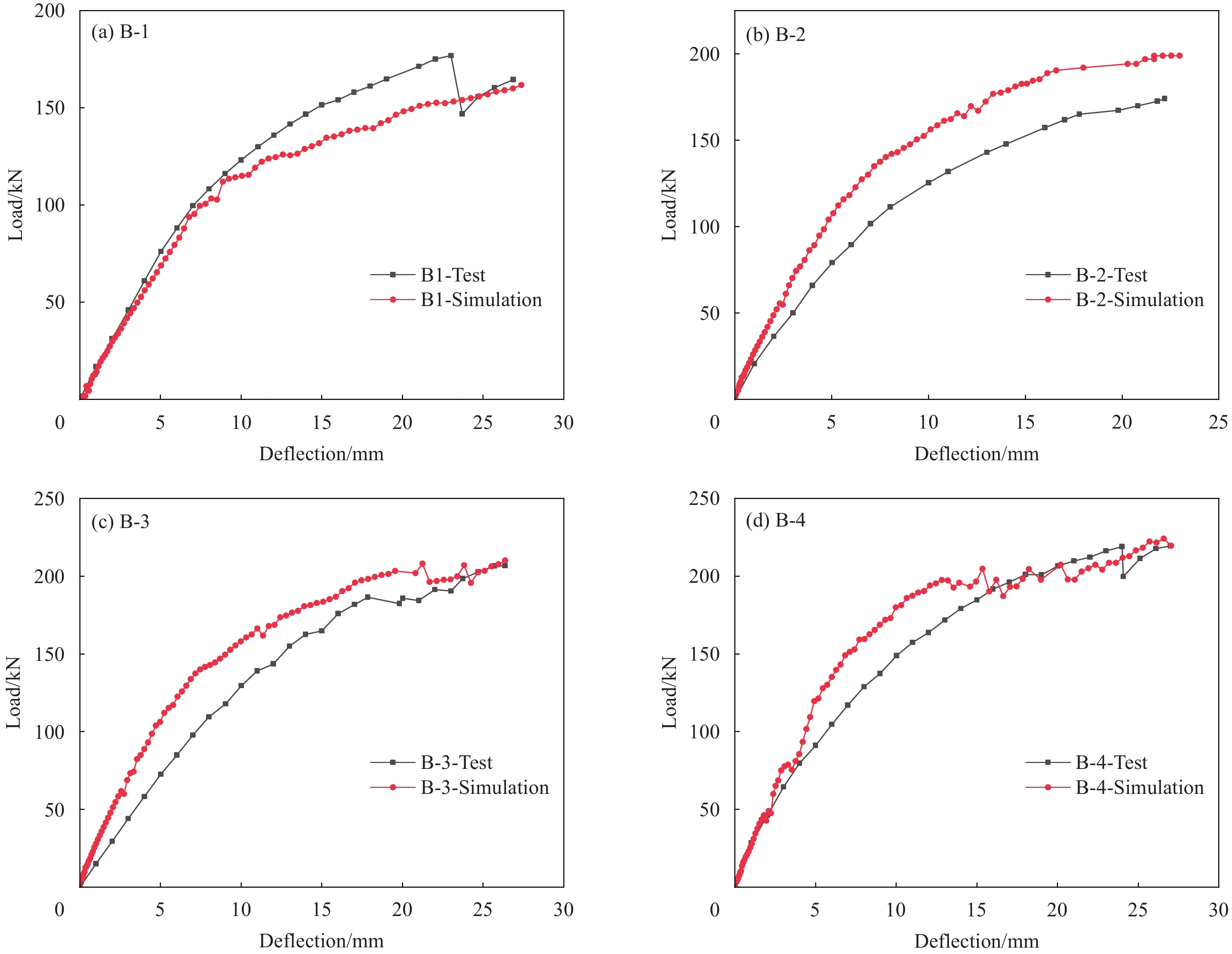
Specimen Eigenvalue Point A Point B Point C Point D Load ratio of point C to point D B-1 Load/kN 15.6 100.7 176.9 120.2 1.47 Deflection/mm 0.9 7.1 23.0 28.1 B-2 Load/kN 15.6 94.0 174.2 131.7 1.32 Deflection/mm 0.7 6.3 22.2 29.3 B-3 Load/kN 19.8 126.4 206.6 145.6 1.42 Deflection/mm 1.3 9.7 26.4 34.0 B-4 Load/kN 24.2 114.2 218.9 165.4 1.32 Deflection/mm 0.7 6.7 24.0 33.1
下载: 导出CSV
表 6 有限元模型和试验极限荷载对比
Table 6 Comparison of ultimate load between finite element model and test
Specimen Ultimate load of
test PT/kNUltimate load of
simulation PF/kNRatio of ultimate
load PT/PFB-1 176.9 160.3 0.91 B-2 174.2 198.9 1.14 B-3 206.6 210.0 1.02 B-4 218.9 211.8 0.97
下载: 导出CSV
-
[1] 王琦, 许硕, 江贝, 等. 地下工程约束混凝土支护理论与技术研究进展[J]. 煤炭学报, 2020, 45(8): 2760-2776. WANG Qi, XU Shuo, JIANG Bei, et al. Research progress of confined concrete support theory and technology for underground engineering[J]. Journal of China Coal Society, 2020, 45(8): 2760-2776(in Chinese).
[2] 王琦, 肖宇驰, 江贝, 等. 交通隧道高强约束混凝土拱架性能研究与应用[J]. 中国公路学报, 2021, 34(9): 263-272. DOI: 10.3969/j.issn.1001-7372.2021.09.022 WANG Qi, XIAO Yuchi, JIANG Bei, et al. Research and application of high strength confined concrete arch in traffic tunnel[J]. China Journal of Highway and Transport, 2021, 34(9): 263-272(in Chinese). DOI: 10.3969/j.issn.1001-7372.2021.09.022
[3] ZHANG W, LI W, YANG N, et al. Determination of the bearing capacity of a concrete-filled steel tubular arch support for tunnel engineering: Experimental and theoretical studies[J]. KSCE Journal of Civil Engineering, 2017, 21(7): 1-14.
[4] 赵卫平, 何宇翔, 徐国正, 等. 钢管混凝土支架节点压弯承载性能数值模拟[J]. 煤炭学报, 2024, 49(S2): 647-658. ZHAO Weiping, HE Yuxiang, XU Guozheng, et al. Numerical simulation of compression bending bearing property of concrete filled steel tubular support joints[J]. Journal of China Coal Society, 2024, 49(S2): 647-658(in Chinese).
[5] 滕锦光. 新材料组合结构[J]. 土木工程学报, 2018, 51(12): 1-11. TENG Jinguang. New-material hybrid structures[J]. China Civil Engineering Journal, 2018, 51(12): 1-11(in Chinese).
[6] MIYANO Y, NAKADA M. Accelerated testing methodology for durability of CFRP[J]. Composites Part B: Engineering, 2020, 191: 107977. DOI: 10.1016/j.compositesb.2020.107977
[7] 李为腾, 王乾, 杨宁, 等. 钢管混凝土拱架在巷道支护中的发展与现状[J]. 土木工程学报, 2016, 49(11): 97-114, 128. LI Weiteng, WANG Qian, YANG Ning, et al. Development and present status of concrete filled steel tubular supporting arch in mine roadway[J]. China Civil Engineering Journal, 2016, 49(11): 97-114, 128(in Chinese).
[8] 鹿伟, 江贝, 王琦, 等. 深部软岩巷道方钢约束混凝土拱架基本构件力学特性及参数影响机制研究[J]. 采矿与安全工程学报, 2020, 37(3): 473-480. LU Wei, JIANG Bei, WANG Qi, et al. Mechanical characteristics and parameter influencing mechanism of square steel confined concrete arch components in deep soft rock roadway[J]. Journal of Mining & Safety Engineering, 2020, 37(3): 473-480(in Chinese).
[9] TENG J G, YU T, FERNANDO D. Strengthening of steel structures with fiber-reinforced polymer composites[J]. Journal of Constructional Steel Research, 2012, 78: 131-143. DOI: 10.1016/j.jcsr.2012.06.011
[10] HE J, XIAN G J. Debonding of CFRP-to-steel joints with CFRP delamination[J]. Composite Structures, 2016, 153: 12-20. DOI: 10.1016/j.compstruct.2016.05.100
[11] XIA S H, TENG J G. Behaviour of FRP-to-steel bonded joints[C]//International Institute for FRP in Construction (IIFC). Proceedings of the International Symposium on Bond Behaviour of FRP in Structures, BBFS 2005. Hongkong: Iifc Secretariat, 2005: 419-426.
[12] 国家市场监督管理总局. 金属材料 拉伸试验 第1部分: 室温试验方法: GB/T 228.1—2021[S]. 北京: 中国标准出版社, 2021. State Administration for Market Regulation. Metallic materials—Tensile testing: Part 1: Method of test at room temperature: GB/T 228.1—2021[S]. Beijing: Standards Press of China, 2021(in Chinese).
[13] 中华人民共和国住房和城乡建设部. 混凝土物理力学性能试验方法标准: GB/T 50081—2019[S]. 北京: 中国建筑工业出版社, 2019. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for test methods of concrete physical and mechanical properties: GB/T 50081—2019[S]. Beijing: China Architecture & Building Press, 2019(in Chinese).
[14] American Concrete Institute. Building code requirements for structural concrete and commentary: ACI 318[S]. Farmington Hills, Michigan: ACI, 2011.
[15] 武芳文, 刘一帆, 何岚清, 等. 钢纤维磷酸镁水泥混凝土梁受弯性能研究[J]. 中国公路学报, 2023, 36(9): 106-118. WU Fangwen, LIU Yifan, HE Lanqing, et al. Flexural performance of steel fiber magnesium phosphate cement concrete beams[J]. China Journal of Highway and Transport, 2023, 36(9): 106-118(in Chinese).
[16] TAO Z, WANG Z B, YU Q. Finite element modelling of concrete-filled steel stub columns under axial compression[J]. Journal Construction Steel Research, 2013, 89: 121-131. DOI: 10.1016/j.jcsr.2013.07.001
[17] BAŽANT Z P, BECQ-GIRAUDON E. Statistical prediction of fracture parameters of concrete and implications for choice of testing standard[J]. Cement & Concrete Research, 2002, 32(4): 529-556.
[18] Comite Euro-international Du Beton. CEB-FIP model code 1990[S]. London: Thomas Telford Ltd., 1993.
[19] TAO Z, WANG X Q, UY B. Stress-strain curves of structural and reinforcing steels after exposure to elevated temperatures[J]. Journal of Materials in Civil Engineering, 2013, 25(9): 1306-1316. DOI: 10.1061/(ASCE)MT.1943-5533.0000676
[20] CAMPILHO R D S G, MOURA M F S F D, DOMINGUES J J M S. Using a cohesive damage model to predict the tensile behaviour of CFRP single-strap repairs[J]. International Journal of Solids and Structures, 2008, 45(5): 1497-1512. DOI: 10.1016/j.ijsolstr.2007.10.003
[21] WANG H T, WU G. Bond-slip models for CFRP plates externally bonded to steel substrates[J]. Composite Structures, 2018, 184: 1204-1214. DOI: 10.1016/j.compstruct.2017.10.033
[22] TENG J G, FERNANDO D, YU T. Finite element modelling of debonding failures in steel beams flexurally strengthened with CFRP laminates[J]. Engineering Structures, 2015, 86: 213-224. DOI: 10.1016/j.engstruct.2015.01.003
-
其他相关附件
-
-
在钢管混凝土外侧粘贴碳纤维增强复合材料形成的CFRP-钢管混凝土拱架具有更高的承载力与刚度，用于高应力、极软岩、强采动和断层破碎带等不良地质条件下的大断面隧道支护。隧道支护的拱架是通过多段拱构件在现场拼装而成，而拼装的节点往往是拱架结构的薄弱位置。因此，拱架连接方式与节点性能成为了研究的热点。
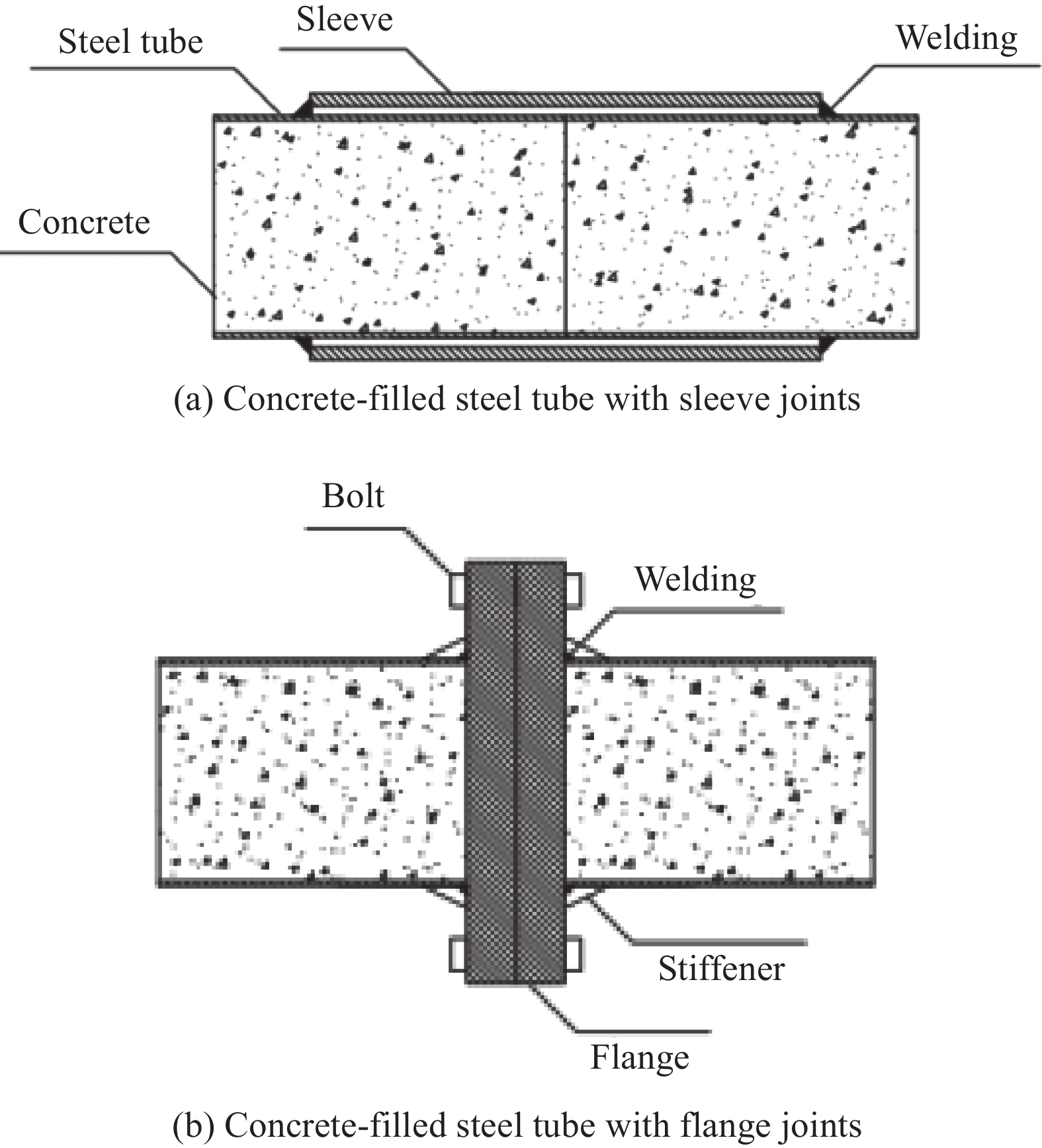
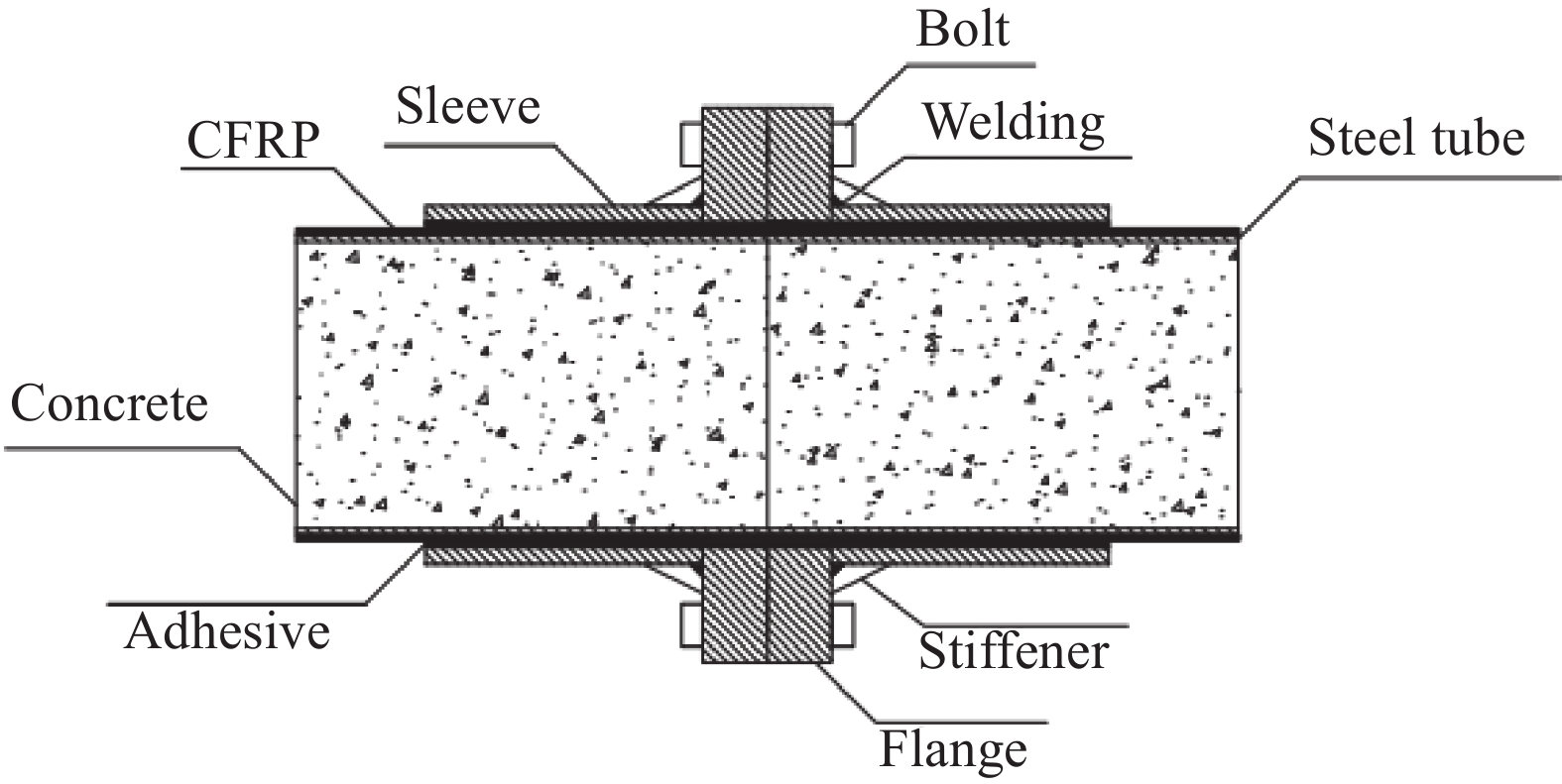
本文提出一种新型法兰-套管组合连接方式，用于圆截面CFRP-钢管混凝土拱架的连接，该连接方式不仅实现了荷载传递和分段装配，同时也实现了“强节点，弱构件”。在弯曲荷载作用下，试件的破坏模式为CFRP剥离破坏，法兰-套管节点完好。在法兰-套管节点的关键参数中，法兰厚度对试件的承载力影响显著，而套管长度和套管壁厚对试件的极限承载力影响较小。
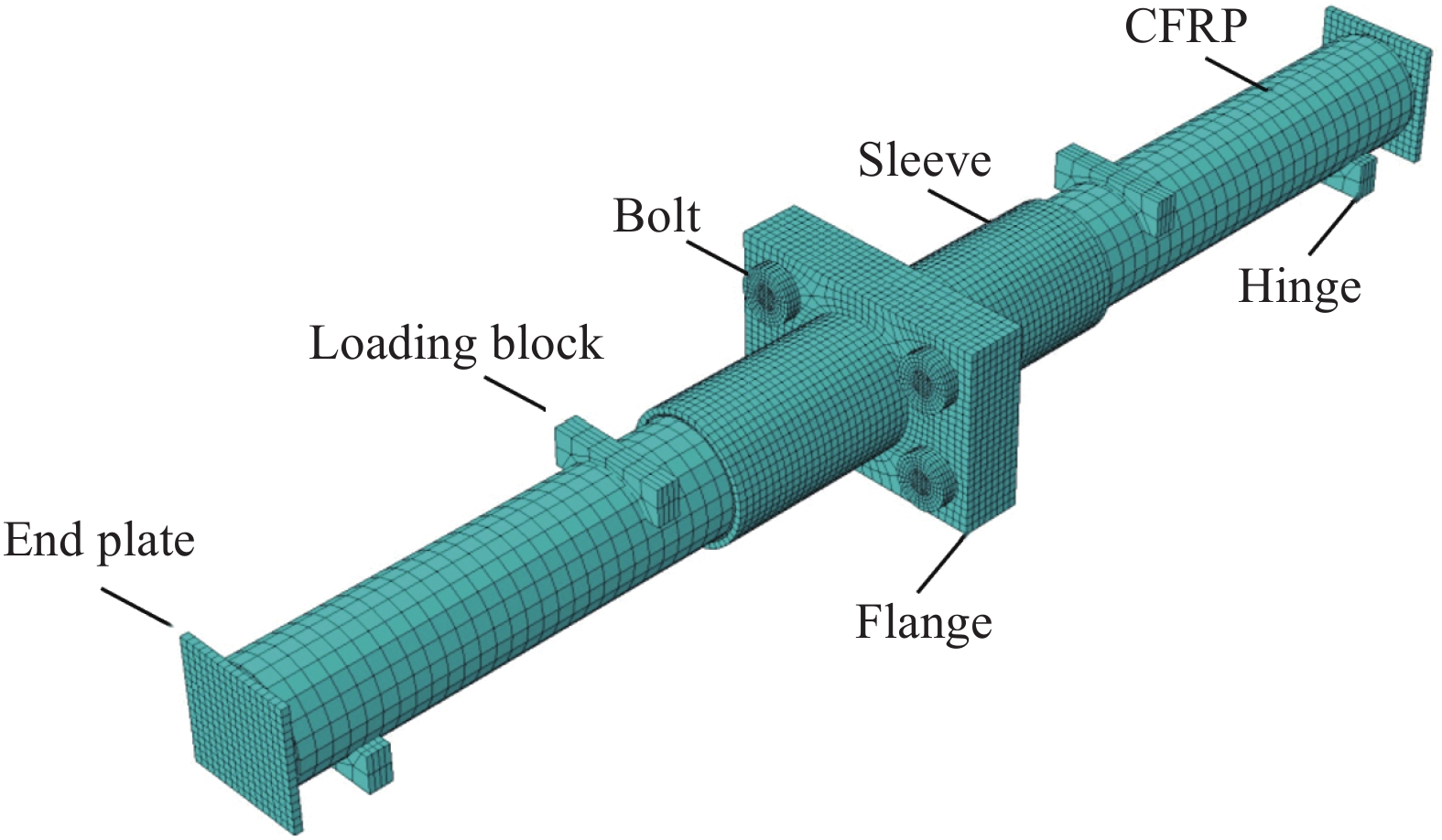
法兰-套管组合连接的圆CFRP-钢管混凝土节点
计量
- 文章访问数: 118
- HTML全文浏览量: 86
- PDF下载量: 5
