Field tests and load-displacement models of GFRP bars and steel bars for anti-floating anchors
-
摘要: 玻璃纤维增强聚合物(Glass fiber reinforced polymer，GFRP)锚杆是从非金属锚杆中发展出的新型复合材料锚杆，具有自重轻、抗拉强度高、造价低、抗腐蚀性能好、抗电磁干扰能力强等优点。基于某中风化花岗岩场地的GFRP筋及钢筋抗浮锚杆的破坏性拉拔试验，对抗浮锚杆在拉拔过程中锚杆杆体及锚固体的位移进行测量，分析了不同材质、不同锚固长度的抗浮锚杆的承载性能及杆体、锚固体相对滑移量的差异，对比不同荷载-位移模型并获得了最适宜岩石抗浮锚杆的荷载-位移模型。试验结果表明：在中风化花岗岩中，相同锚固长度下的GFRP抗浮锚杆比钢筋抗浮锚杆的破坏荷载增加13%~14%，GFRP抗浮锚杆更易发生杆体拔出破坏，锚固系统仍有残余承载力未发挥，使用GFRP锚杆代替钢筋锚杆具有可行性；与锚固长度为4.5 m的GFRP抗浮锚杆相比，锚固长度为6.5 m的锚杆杆体相对于锚固体的滑移量更大，增大GFRP抗浮锚杆的锚固长度可有效增加其相对滑移量，但提升钢筋抗浮锚杆的锚固长度对其破坏形态无明显影响；双曲线函数及幂函数荷载-位移曲线模型与实测值吻合度较差，指-幂函数曲线模型对本次试验锚杆的破坏荷载预测精度最高，曲线整体走势较一致。Abstract: Glass fiber reinforced polymer (GFRP) anchor is a new type of composite anchor developed from non-metallic anchors. It has the advantages of light weight, high tensile strength, low cost, good corrosion resistance and strong electromagnetic interference resistance. Based on the destructive pull test of GFRP anchors and reinforced anti-floating anchor conducted on a medium-weathered granite site, the displacement of the anchor body and anchor solid during the drawing process of the anti-floating anchor was measured. The bearing capacity of anti-floating anchors with different materials and different anchoring lengths and the relative slip between anchor body and anchor were analyzed. The different load-displacement models were compared and the most suitable load-displacement model for rock anti-floating anchors was sought. The test results show that: In medium-weathered granite, the GFRP anti-floating anchors at the same anchoring length increase the failure load by 13% to 14% compared with the reinforced anti-floating anchors. GFRP anti-floating anchors are more prone to pull-out and failure of the anchor body, and the residual bearing capacity of the anchoring system is still not exerted. It is feasible to use GFRP anchors instead of steel anchors. Compared with the GFRP anti-floating anchor with an anchoring length of 4.5 m, the anchor body with an anchoring length of 6.5 m has a greater slippage relative to the anchor solid. Increasing the anchoring length of the GFRP anti-floating anchor can effectively increase its relative slip, and increasing the anchoring length has no obvious effect on the failure mode of the reinforced anti-floating anchor. The hyperbolic function and power function load-displacement curve models are in poor agreement with the measured values, while the finger-power function curve model has the highest accuracy in predicting the failure load of the anchors in this test, and the overall trend of the curve is more consistent.
-
碳纤维增强复合材料(Carbon fiber reinforced plastic，CFRP)具有质量轻和强度高等优点，被广泛应用于航空航天等领域[1]。火箭与飞机等大型飞行器的关键结构处多采用CFRP，以减轻质量和增强结构强度[2]。在长期服役过程中，受内部载荷与外部环境影响，CFRP结构会出现裂纹等损伤，当损伤达到一定程度后会导致结构突然断裂，造成严重的安全事故，因此有必要对CFRP进行结构健康监测[3]。为此，相关学者提出了结构健康监测(Structural health monitoring， SHM)技术，将传感器布置在结构上或集成于结构中，实时采集监测信号，评估结构健康状态，及时发现损伤[4-5]。其中，损伤成像技术因能直观呈现结构损伤位置及大小，被广泛用于CFRP结构的损伤监测中[6]。兰姆(Lamb)波是一种特殊的超声导波，因具有对损伤敏感与传播距离远的特点，常被用作SHM技术中的信息载体[7]。已有研究表明[8]，Lamb波可用于不同材料体系、铺层方向、尺寸和厚度范围的CFRP结构损伤成像。
基于Lamb波，Wang等[9]提出延时叠加(Delay and sum，DAS)成像法，其原理为延时叠加所有路径的散射信号并转换为像素值进行成像，但叠加后损伤与无损区域信号差异较小，结果会存在大量伪影。Yu等[10]基于自编码器提取信号能量差特征构建权重因子并施加于DAS信号模型中抑制噪声与非损伤信号，越靠近损伤权重因子越大，抑制效果越好，定位精度越高。去噪后信号最大均方误差仅为1.252×10−4，加权DAS成像法在加筋CFRP的损伤定位精度提高了92.77%，但自编码网络处理时间较长，后续可改进网络，提升运行效率。Li等[11]基于损伤反射率和频散关系建立频域逆散射模型并提出频域DAS成像法，在频域中考虑频散关系，基于此补偿信号频散，减少由频散导致的误差和伪影。在铝板双损伤的定位误差和伪影分别减少了38.5%、47%和55.6%、54.7%，因回波信号较弱，该方法在单激励多传感时不利于多损伤成像，后续可结合能充分利用信号能量的全聚焦法改进。Hall等[12]在DAS成像法的基础上提出最小方差无失真响应(Minimum variance distortionless response，MVDR)成像法，引入权重系数约束非期望信号(干扰信号)，如机械运行导致的机械噪声、结构振动导致的振动噪声、环境温度与气流变化导致的环境噪声、电子设备产生的电磁噪声、边界反射及非损伤路径信号等与损伤无关的信号，通过权重系数将其最小化，进而减少伪影。Hua等[13]基于激励与散射信号的相关性计算对角加载系数，减小人为经验取值误差，位置越远离损伤该系数越小，对信号正则化处理时的方向误差容忍度越小，得到的像素值则越小，因此可减少伪影。实验表明相比经验取值的MVDR成像法能减少至少80%的伪影，但该方法信号处理过程复杂，未来可优化处理过程，降低算法复杂性。Su等[14]基于路径信号与损伤的相互作用关系和传感阵列建立近场模型，提出近场MVDR成像法，利用非损伤信号与损伤相互作用小的原理使其在模型中的输出最小化，减少由此类信号导致的误差。该方法在CFRP损伤成像实验中的损伤方向角度和定位最大误差分别为1°和1.2 cm，但其未考虑各向异性的影响，后续可考虑该特性的影响以提升模型准确性。
综上所述，相关学者针对DAS与MVDR成像法进行了研究与改进，提高了方法的损伤成像与定位性能，但无损区域还存在非损伤路径信号叠加形成的干扰信号，因此还会存在伪影。为此，Levine等[15-16]借鉴信号处理领域中压缩感知(Compressed sensing，CS)理论[17]的稀疏表示技术，参考该技术中的信号稀疏性原理[18]，基于监测区域损伤稀疏的先验性，提出了稀疏重建(Sparse reconstruction，SR)成像法。基于Lamb波散射模型构造原子并组成字典，结合该字典、实测散射信号与稀疏解变量构建SR模型，求解该模型得到稀疏解并转换为像素值实现损伤成像。
目前，基于SR成像法的损伤成像得到了学者们的广泛研究。Golato等[19-20]在Lamb波散射模型中加入S0模态与边界反射部分来构造新原子，使其更接近于实测信号，以提高模型适配率，降低单模态或损伤位于边界情况下的损伤误判率，但其未考虑结构复杂性，未来可考虑不同结构的影响，进一步完善模型。Zhang等[21]提出自适应SR成像法，设定稀疏度值初值并以迭代前后的信号能量差为依据自适应更新稀疏度值，基于该值选择可能含有损伤信息的原子组成新字典，以此提高损伤成像精度，但算法迭代时间较长，后续可考虑优化迭代过程，降低迭代时间。Xu等[22]提出频域Lamb波散射模型，以此构造频域字典，结合该字典的SR成像法可在大幅减少字典维数的同时减少伪影，但模型未考虑各向异性，在CFRP上的应用有待研究。上述研究对象均为铝板，对于各向异性的CFRP中的损伤监测，Hua等[23]通过设计不同激励信号实现激励器的同步激励，降低激励时间，提高数据采集率，并依据线性特性建立同步激励Lamb波散射模型，提高了损伤成像性能，但不能量化损伤，对此，该学者建立传感路径的椭圆影响范围并结合椭圆定位法得到损伤范围边界点，基于此原理将字典修改为可表示一定面积范围损伤的结构[24]，实验表明结合改进字典的SR成像法可得到用于定量化评估的损伤轮廓，但成像轮廓与实际轮廓有一定偏差，后续可考虑优化字典结构，完善成像轮廓。Xu等[25]构建信号分解和特征提取字典，基于信号分解字典分解损伤散射信号，得到代表损伤信息的稀疏解并结合特征提取字典重构出特征信号，最后结合DAS成像法实现成像，相比原信号可减少伪影，但其未考虑频散与多模态，后续研究可考虑频散与多模态，提升字典准确性。Wu等[26]取只含S0模态的信号首波包前半部分代替原信号，将结构分为若干扇形区域并视扇形内的群速度一致，以降低各向异性与多模态效应的影响，提升模型的准确度，进而提高成像精度，但因模态分离简单，信号还有存在其他模态，只能定位单个损伤，后续可研究更加精确的模态分离方法，使其能定位多损伤。
上述基于SR成像法的研究虽可有效提升CFRP损伤的成像效果，但成像结果中依然可能会因原子失配而导致伪影，甚至损伤误判。对于此，Xu等[27-28]与徐冠基等[29]基于原子与实测信号的相关性，构建相关性权重因子并施加于稀疏解变量，以提高原子适配率，但其只考虑信号间的波形相关性，当原子与实测信号差距较大时，依然会导致损伤误判。针对上述问题，本文结合MVDR和SR成像法，提出一种基于MVDR加权的SR成像法，称为MVDR-SR成像法。利用MVDR成像法对CFRP损伤进行初始成像，基于成像结果构建MVDR权重因子，不需考虑信号的相关性，可减少信号差距过大而导致的原子失配，降低损伤误判的概率。所提出的方法以MVDR权重因子对稀疏解变量进行加权，用基追踪去噪(Basic pursuit denoise，BPDN)算法求解加权SR模型得到最优稀疏解，将其转换为像素值，实现CFRP损伤成像。
1. Lamb波线性传播与散射模型
1.1 Lamb波线性传播模型
Lamb波在CFRP结构中传播时，由于各向异性的影响，传播过程是一个复杂的非线性过程，难以用数学表达式进行表示。当CFRP结构铺层较多，铺层方向按角度均匀分布时，可以缩小各层之间的力学性能差距，将其近似为准各向同性的CFRP结构，进而可将Lamb波的传播模型简化为线性传播模型[30]。
假设Lamb波激励信号为u(t)，其传播距离d后接收传感器接收到的响应信号表示为
W(ω)=∑m√drefdU(ω)e−jkm(ω)d (1) 其中：W(ω)为频域响应信号；U(ω)为频域激励信号；ω为角频率；km(ω)为对应模态的群速度；m表示Lamb波的模态；j为虚数单位；dref为参考距离，ref表示参考。当有多个模态时，则响应信号为所有模态响应信号的相加。
对式(1)取傅里叶逆变换，得到的时域响应信号如下式所示：
w(t)=F−1{W(ω)}=∑m√drefd12π∫+∞−∞U(ω)ejωte−jkm(ω)ddω (2) 其中，F−1{}为傅里叶逆变换。
1.2 Lamb波线性散射模型
Lamb波散射过程如图1所示，将激励传感器视为激励源，接收传感器视为接收源，损伤视为散射源。假设激励源位于p点处，接收源位于q点处，散射源位于h点处。从激励源激励信号u(t)，以激励源为中心，向四周传播。一部分信号被接收源直接接收，称为直达信号，一部分信号到达损伤处发生波的散射，产生散射入射波，传播后被接收源接收，称为散射信号。结合式(1)，q处的接收源接收到的响应信号表示为
Wh(ω)=Wdirect(ω)+Wscatter(ω)=∑m√drefr3U(ω)e−jkm(ω)r3+∑m√drefr1U(ω)e−jkm(ω)r1×Hm(ω)√drefr2U(ω)e−jkm(ω)r2 (3) 其中：Wh(ω)为接收源接收的频域响应信号；Wdirect(ω)为频域直达信号；Wscatter(ω)为频域散射信号；r1为激励源至散射源的距离；r2为散射源至接收源的距离；r3为激励源至接收源的距离；H(ω)为散射系数，由于损伤类型信息未知，一般将H(ω)设置为1[15]。
![]()
图 1 Lamb波散射示意图Figure 1. Scattering plot of Lamb waver1 —Distance from the excitation source to the scattering source; r2 —Distance from the scattering source to the receiving source; r3—Distance from the excitation source to the receiving source损伤散射信号表示为存在损伤时的损伤响应信号减去未有损伤时的基准信号得到的差信号，由式(2)和式(3)可得损伤散射信号，表示为
wscatter(t)=F−1{Wh(ω)−Wdirect(ω)}=F−1{∑m√drefr1U(ω)e−jkm(ω)r1×Hm(ω)√drefr2U(ω)e−jkm(ω)r2}=∑mdref2π√r1r2∫+∞−∞U(ω)ejωte−jkm(ω)(r1+r2)dω (4) 其中，wscatter(t)为时域散射信号，为方便表示不同激励-传感路径的散射信号，定义散射信号传播算子Q，其表示如下：
yp,q(t)=Qp,q{U(ω)} (5) 其中，yp,q(t)为p-q路径的散射信号。
2. 加权稀疏重建成像法
2.1 MVDR成像法
利用MVDR成像法进行成像时，首先需依据损伤散射信号幅值大小区分期望与干扰信号，幅值较大说明信号经过损伤，为损伤路径方向信号，即所期望的信号，反之为干扰信号。其次将监测区域划分为X×Y=M个网格点，计算网格点处的方向向量，结合表示信号相关性的协方差矩阵得到该点处的权重系数，并依据协方差矩阵的信号元素顺序依次施加于信号中，对干扰信号进行约束，通过最小化信号的方差在实现期望信号不变的同时最小化干扰信号，降低其在成像时的影响。因减少了干扰信号的影响，更多的考虑了期望信号，MVDR成像法具有较好的稳定性。
第i个网格点的MVDR像素值计算如下所示：
P_{\mathrm{MV}}^i=\vec{\boldsymbol{w}}_i^{\mathrm{T}}\boldsymbol{R}_i\vec{\boldsymbol{w}}_i^{ }=\vec{\boldsymbol{w}}_i^{\mathrm{T}}\vec{\boldsymbol{r}}_i^{ }\vec{\boldsymbol{r}}_i^{\mathrm{T}}\vec{\boldsymbol{w}}_i^{ } (6) 其中：i的范围为 1 \leqslant i \leqslant M ；“T”表示转置； P_{{{\mathrm{MV}}}}^i 表示为第i个网格点处的像素值； {\vec {\boldsymbol{r}}_i} 为所有散射信号组成的向量； {\boldsymbol{R}}_i^{} 是 {\vec {\boldsymbol{r}}_i} 的协方差矩阵，表示信号之间的相关性； {\vec {\boldsymbol{w}}_i} 是权重系数。
为使损伤位置像素值不变的同时使无损区域的像素值最小，权重系数的选择需满足以下约束条件：
\mathrm{min}\; \overrightarrow{\boldsymbol{w}}_i^{\mathrm{T}}\boldsymbol{R}_i\overrightarrow{\boldsymbol{w}}_i\; \quad\mathrm{s}.\mathrm{t}.\text{ }\overrightarrow{\boldsymbol{w}}_i^{\mathrm{T}}\overrightarrow{\boldsymbol{e}}_i=1 (7) 其中， \vec {\boldsymbol{e}}_i^{} 为第i个网格点处的方向向量，为一个单位列向量，描述了 {\vec {\boldsymbol{r}}_i} 中的信号幅值关系。该向量的取值与损伤反射系数有关，由于损伤类型信息未知，通常将损伤反射系数简化为1[31]。
利用拉格朗日乘数[32]，得到式(7)的最优解为
{\vec {\boldsymbol{w}}_i} = \frac{{{\boldsymbol{R}}_i^{ - 1}{{\vec {\boldsymbol{e}}}_i}}}{{\vec {\boldsymbol{e}}_i^H{\boldsymbol{R}}_i^{ - 1}{{\vec {\boldsymbol{e}}}_i}}} (8) 其中， {\boldsymbol{R}}_i^{ - 1} 是 {\boldsymbol{R}}_i^{} 的逆矩阵，为避免矩阵求逆过程中出现病态矩阵，需通过对角加载对矩阵求逆进行正则化处理：
{\boldsymbol{R}}_i^{ - 1} = {\left( {{{\boldsymbol{R}}_i} + f\lambda {\boldsymbol{I}}} \right)^{ - 1}} (9) 其中，{\boldsymbol{I}}为 N 阶单位矩阵； \lambda 为阵的最大特征值；f为对角加载系数，参考以往研究，本文中f选择为 {10^{ - 4}} [32]。
由于将损伤反射系数简化为1，MVDR成像法中得到的权重系数存在一定误差，不能完全消除干扰信号的影响，因此成像结果中还存在伪影。
2.2 稀疏重建成像法
SR算法是一种基于稀疏条件求解模型逆问题的技术[15]，基于SR算法的成像指求解SR模型的逆问题，得到最优稀疏解并转换为像素值进行成像的过程。其原理为求解过程中将实测散射信号与字典中的原子信号进行匹配，得到信号与字典所有原子之间的匹配系数，即为所求的稀疏解。
假设结构监测区域布置有激励源s与接收源r，同样将监测区域均匀划分为X \times Y = M个网格点，并假设每个网格点都是潜在的散射源，则s - r路径的散射信号可以视为该路径传播的信号在所有潜在散射源处的理论散射信号的线性组合[27]，如下式所示：
{y_{s,r}}(t) = \sum\limits_{i = 1}^M {{a_{s,i,r}}(t)} {x_i} (10) 其中， {y_{s,r}}(t) 表示s - r路径的散射信号， {x_i} 表示第 i 个网格点对应的稀疏解变量； {a_{s,i,r}}(t) 表示s - r路径信号在第 i 个散射源散射后的理论散射信号，可基于1.2节的Lamb波散射模型计算得到。
由式(4)与式(5)得到 {a_{s,i,r}}(t) 的表达式如下：
\begin{split} {a_{{s,i,r}}}(t) =& {Q_{{i,r}}}\{ {Q_{{s,i}}}[U(\omega )]\} \\ =& \sum\limits_m {\frac{{{d_{{\mathrm{ref}}}}}}{{2{\text{π}} \sqrt {{{\left\| {s - i} \right\|}_2}{{\left\| {r - i} \right\|}_2}} }}} \\ &\int_{ - \infty }^{ + \infty } U (\omega ){{\text{e}}^{{\mathrm{j}}{\omega }{\mathrm{t}}}}{{\text{e}}^{ - {\mathrm{j}}{k_m}({\omega })({{\left\| {{s - i}} \right\|}_2} + {{\left\| {{r - i}} \right\|}_2})}}{\text{d}}\omega \\ \end{split} (11) 考虑监测区域中有 N 个压电传感器，则总共有 N \times {(}N{ - 1)} 个激励-传感路径，所有路径散射信号都用式(10)进行表示并按照行方向进行级联，可得到下式的矩阵形式：
{\left[ {\begin{array}{*{20}{c}} {{y_{1,2}}(t)} \\ {{y_{1,3}}(t)} \\ \vdots \\ {{y_{s,r}}(t)} \\ \vdots \\ {{y_{(N{ - 1),}N}}(t)} \end{array}} \right]_{N{(}N{ - 1)} \times {1}}} = {\left[ {\begin{array}{*{20}{c}} {{a_{1,1,2}}}&{{a_{1,2,2}}}& \cdots &{{a_{{1,}i{,2}}}}& \cdots &{{a_{{1,}M{,2}}}} \\ {{a_{1,1,3}}}&{{a_{1,2,3}}}& \cdots &{{a_{{1,}i{,3}}}}& \cdots &{{a_{{1,}M{,3}}}} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {{a_{s{,1,}r}}}&{{a_{s{,2,}r}}}& \cdots &{{a_{s{,}i{,}r}}}& \cdots &{{a_{s{,}M{,}r}}} \\ \vdots & \vdots & \ddots & \cdots & \ddots & \vdots \\ {{a_{N{ - 1,1,}N}}}&{{a_{N{ - 1,2,}N}}}& \cdots &{{a_{N{ - 1,}i{,}N}}}& \cdots &{{a_{N{ - 1,}M{,}N}}} \end{array}} \right]_{N{(}N{ - 1)} \times M}}{\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \\ \vdots \\ {{x_i}} \\ \vdots \\ {{x_M}} \end{array}} \right]_{M \times {1}}} (12) 将式(12)表示为向量形式，可得到如下线性表达式：
{\boldsymbol{y}} = {\boldsymbol{Ax}} (13) 其中： {\boldsymbol{y}} 为所有散射信号组成的列向量； {\boldsymbol{A}} 为所有潜在散射源的理论散射信号 {{\boldsymbol{a}}_{s,r}} 组成的字典矩阵，其中第 i 列向量表示第 i 个原子； {\boldsymbol{x}} 为稀疏解变量组成的列向量。在实际中，划分的网格数远远大于路径数，即 N \times {(}N{ - 1)} \ll M ， {\boldsymbol{y}} = {\boldsymbol{Ax}} 为欠定方程，具有无穷多解，因此求解过程实质为寻优过程。在字典 {\boldsymbol{A}} 中匹配出与 {\boldsymbol{y}} 最相似的少数列向量的组合，即最优原子的组合，其对应的匹配系数即为最优的稀疏解。
SR成像法中原子与信号的匹配实际上是比较信号波形的相似性，其主要利用信号幅值信息，对信号取包络后能得到信号幅值的整体变化趋势，反映出信号的幅值变化特性，对于相位变化不敏感。因此，为便于分析，减少原子与信号间的相位差对结果的影响，往往用信号的包络代替原始信号[16]。目前，提取信号包络的常用方法有小波变换法、峰值检测方法、滤波法和希尔伯特变换法。相比其他方法，希尔伯特变换法具有提取精度高，适用性强和平滑性好的优点，可用于非平稳信号的包络分析，是最常用的包络提取方法。对信号进行希尔伯特变换后能得到其对应的解析信号，通过对解析信号取绝对值后就能得到准确的信号幅值信息，进而得到准确的信号包络。因具有上述优点，在SR成像法中基于希尔伯特变换法来提取信号包络，其表达式如下式所示：
{\boldsymbol{y}}_{}^{{\mathrm{ENV}}} = abs[H({\boldsymbol{y}})]\begin{array}{*{20}{c}} {}&{{\boldsymbol{A}}_{}^{{\mathrm{ENV}}} = abs[H({\boldsymbol{A}})]} \end{array} (14) 其中： H(\cdot) 表示希尔伯特变换； abs(\cdot) 表示取绝对值运算； {{\boldsymbol{y}}^{{\mathrm{ENV}}}} 与 {{\boldsymbol{A^{ENV}}}} 分别表示{\boldsymbol{y}}与{\boldsymbol{A}}的包络。
在稀疏的前提下，式(13)可由以下基于{l_0}范数的最小化模型进行求解[33]：
\widehat{{\boldsymbol{x}}}=\mathrm{argmin}{\Vert {\boldsymbol{x}}\Vert }_{0}\;\;\;{\text{ s}}.{\text{t}}.\text{ }{\Vert {\boldsymbol{y-Ax}}\Vert }_{2}^{2} < {\sigma }^{2} (15) 其中， \hat x 表示得到的最优稀疏解；{l_0}范数项 \Vert x{\Vert }_{0} 表示 x 中非零值的个数； {\sigma ^2} 为正则化参数；由于{l_0}范数的求解是一个NP难的问题，不能直接求解，可将其转化为基于{l_1}范数的最小化模型进行求解：
\widehat{{\boldsymbol{x}}}=\mathrm{argmin}{\Vert {\boldsymbol{x}}\Vert }_{1}\;\;\;{\text{ s}}.{\text{t}}.\text{ }{\Vert {\boldsymbol{y-Ax}}\Vert }_{2}^{2} < {\sigma }^{2} (16) {l_1}范数是凸函数，式(16)是一个典型的凸优化求解问题，BPDN算法是解决上述凸优化问题的经典方法[34]，因此本文基于BPDN算法求解式(16)。得到 \hat {\boldsymbol{x}} 并按正比关系转换为像素值，按X \times Y的方式排列映射成像。
由于损伤区域稀疏，得到的 \hat {\boldsymbol{x}} 中大部分为零值，只有少数稀疏解为非零值，零值稀疏解对应的区域不会成像，因此可以最大程度上消除伪影。
2.3 MVDR加权的稀疏重建成像法
由前述可知，利用MVDR与SR成像法可分别对结构中存在的损伤进行成像。MVDR成像法成像稳定，但会存在一定的伪影，SR成像法可以消除大部分伪影，但稳定性较差[28]。因此，本文利用MVDR成像法成像稳定的优点，构建MVDR权重因子，将其施加于SR成像法中的稀疏解变量中，改变损伤网格点和无损网格点对应的原子分别与实测散射信号的匹配概率，解决SR成像法中导致成像不稳定的原子失配问题。
在{l_1}范数中，对向量元素进行加权，相当于对元素施加惩罚项，当惩罚项越大时，则匹配到该项元素的概率越小，求解后得到此项元素的匹配系数越趋向于零值[27]。基于此，本文对稀疏解变量施加权重因子以改变原子与散射信号的匹配概率的原理为：给第 i 个稀疏解变量施加的权重因子越大，则对其施加的惩罚项越大，寻优中其对应的原子与散射信号的匹配概率越小，最后得到的稀疏解变量数值越趋向于零值，转换后其对应的网格点的像素值则越趋向于零值。
基于式(6)所得结果，定义MVDR权重因子如下式所示：
{v_i} = \frac{1}{{{E_i}}} (17) 其中： {v_i} 为第 i 个网格点对应的MVDR权重因子； {E_i} 为基于MVDR成像法得到的第 i 个网格点的归一化像素值，表示如下：
{E_i} = \frac{{P_{{\mathrm{MV}}}^i}}{{\max ({{\boldsymbol{P}}_{{\mathrm{MV}}}})}} (18) 其中： P_{{{\mathrm{MV}}}}^i 为基于式(6)得到的第 i 个网格点像素值； \max ({{\boldsymbol{P}}_{{{\mathrm{MV}}}}}) 表示所有网格点像素值的最大值。
上述所提的MVDR权重因子 {v_i} 是基于MVDR成像结果进行构建，其包含损伤位置范围信息，相比现有权重因子更符合实际损伤情况。当网格点越远离损伤位置时，得到的 {E_i} 越小，可知 {v_i} 就越大，由前述的加权原理可知将此 {v_i} 施加于对应的 {x_i} 后可以降低其对应的原子信号与散射信号的匹配概率，进而使该 {x_i} 值趋向于零值。反之当网格点靠近损伤位置时，其对应的 {x_i} 值越大。
以定义的MVDR权重因子 {v_i} 对式(16)中的稀疏解变量加权，可得到下式：
{\left\| x \right\|_{1,v}} = \sum\limits_{i = 1}^{M} {{v_i}\left| {{x_i}} \right|} (19) 其中， {\left\| x \right\|_{1,v}} 为基于加权稀疏解变量的{l_1}范数。
基于前述分析，将MVDR权重因子施加于SR成像法的稀疏解变量中，在模型求解时可对损伤网格点对应的稀疏解变量施加小的MVDR权重因子，提高其对应的原子与散射信号的匹配概率，同时对无损网络点对应的稀疏解变量施加大的MVDR权重因子，降低其原子与散射信号的匹配概率，使SR模型求解时的原子匹配更加准确，降低原子失配率，使寻优过程中能准确匹配到损伤网格点对应的原子，解决SR成像法中的原子失配问题，准确得到表示损伤网格点的少数稀疏解，并使其余稀疏解变量趋向于零，进而减少伪影、降低误判风险、提升成像精度和稳定性。
结合式(19)，式(16)可转换为下式：
\widehat{{\boldsymbol{x}}}=\mathrm{argmin}{\Vert {\boldsymbol{x}}\Vert }_{1,v}\;\;\;{\text{ s}}.{\text{t}}.\text{ }{\Vert {\boldsymbol{y-Ax}}\Vert }_{2}^{2} < {\sigma }^{2} (20) 其中，正则化参数{\sigma ^2}是影响成像稀疏度与精度的参数，在SR模型求解中控制原子与实测信号匹配时允许的误差值，其取值范围为 0 < {\sigma ^2} < \left\| y \right\|_2^2 [28]，在该范围内选择最优值以保证成像性能。通过求解式(20)得到加权后的最优稀疏解进行成像。
图2为本文所提出的MVDR-SR成像法流程图，首先将监测区域划分为X \times Y个网格，其次设置稀疏解变量 {\boldsymbol{x}} 和构建字典 {\boldsymbol{A}} ，与散射信号{\boldsymbol{y}}组成SR模型，同时基于MVDR成像法获得网格点的像素值 {\boldsymbol{P}}_{{{\mathrm{MV}}}}^{} 构建MVDR权重因子{\boldsymbol{v}}，对 {\boldsymbol{x}} 进行加权，得到加权SR模型，最后采用BPDN算法进行求解，得到最优稀疏解 \hat {\boldsymbol{x}} 并转换为像素值实现成像。
![]()
图 2 最小方差无失真响应(MVDR)-稀疏重建(SR)成像法流程Figure 2. Flowchart of the minimum variance distortionless response (MVDR)-sparse reconstruction (SR) imaging methodBPDN—Basic pursuit denoise3. 实验验证
3.1 碳纤维复合材料损伤实验
为验证本文所提出的方法的有效性，进行CFRP损伤成像实验，所用数据为Open Guided Waves开源平台提供的CFRP层合板模拟损伤数据集[35]。实验试件为16层CFRP层合板，如图3(a)所示[35]，尺寸为500 mm×500 mm×2 mm，铺层为 {\left[ {45/0/ - 45/90/ - 45/0/45/90} \right]_{\mathrm{S}}} ，S表示对称，铺层方向均匀分布，且为对称分布，可将其看为准各向同性板，在板的上下两端分别布置6个直径10 mm的圆形薄膜式压电传感器，用于Lamb波的激励与接收。为验证所采用的实验试件是否为健康无损的CFRP层合板，通过工业CT技术对此CFRP层合板进行扫描，得到的X射线结果如图3(b)所示[35]，左边界黑色区域为扫描时固定CFRP层合板的支架，长条形阴影为粘贴的胶带，中间为指示方向的铜线箭头，上下两端6个黑色圆形为粘贴的传感器，0°、90°和±45°的阴影线表明层压板的方向。除上述出现的阴影部分外，板中无其他阴影部分，说明所使用的试件为健康无损的CFRP层合板。其单层铺层材料为T700 M21型CFRP，材料性能参数如表1所示[35]。
在板表面粘贴直径10 mm、厚度2.35 mm、质量0.5 g的铝制圆柱块来模拟损伤，以模拟Lamb波遇到真实损伤的散射情况。为分析不同位置下损伤的成像效果，本文选择4个不同典型位置的模拟损伤分别进行损伤成像实验。图4为传感器/损伤坐标示意图，以CFRP板左下角为坐标原点，底边界为x轴，左边界为y轴建立x-y轴坐标系，两轴范围均为0~500 mm，并将传感器位置与损伤位置标注其中，上下两边蓝色圆形表示传感器位置，中间的红色圆形表示损伤位置，T代表传感器，D代表损伤。其中损伤D1靠近边界与上方传感器，损伤D2靠近上方传感器，损伤D3位于中间位置，损伤D4靠近下方传感器。
表 1 T700 M21型CFRP参数Table 1. Material parameters of T700 M21 CFRPParameter Value Parameter Value {E_{{11}}}/GPa 125.5±2.4 {v_{{12}}} 0.37±0.08 {E_{{22}}}/GPa 8.7±0.1 {v_{{23}}} 0.45±0.02 {G_{{12}}}/GPa 4.135 \rho /(kg·m−3) 1571 ±2Notes: E11, E22—Elasticity modulus; G12—Shear modulus; v12, v23—Poisson's ratio; ρ—Density. 基于图4得到的12个压电传感器与4个不同模拟损伤位置的实际坐标分别如表2和表3所示。
表 2 传感器坐标Table 2. Sensor coordinateSensor Coordinate/mm Sensor Coordinate/mm T1 (450, 470) T7 (450, 30) T2 (370, 470) T8 (370, 30) T3 (290, 470) T9 (290, 30) T4 (210, 470) T10 (210, 30) T5 (130, 470) T11 (130, 30) T6 (50, 470) T12 (50, 30) Notes: T represents sensor; The subscript represents the sequence number. 表 3 损伤坐标Table 3. Damage coordinateDamage Coordinate/mm Damage Coordinate/mm D1 (65, 415) D2 (265, 412) D3 (320, 260) D4 (250, 75) Notes: D represents damage; The following number represents the serial number. 实验中，板中布置的12个压电传感器采用顺序依次激励的形式，按照此种方式顺序激励后一共得到66条激励-传感路径。如图5所示，实验中采用的激励信号为汉宁窗调制的5波峰、中心频率为60 kHz的窄带正弦调制信号，其表达式为
\begin{gathered} s(t) = A\sin ({\omega _{{\mathrm{c}}}}t)[1 - \cos ({\omega _{{\mathrm{c}}}}t/n)] \\ \quad [H(t) - H(t - 2{{\text{π}} }n/{\omega _{{\mathrm{c}}}})] \\ \end{gathered} (21) 其中： A 为信号幅值系数；t为采样时间序列； \omega_{\mathrm{c}} 为信号中心频率；n为信号周期数，即波峰数；H(t)为单位阶跃函数，用于生成汉宁窗。
根据信号频率调谐技术[36]，在此频率下，可近似认为激励信号只有A0模态，因此构造字典时只考虑A0模态，简化字典构建的复杂度。实验时，设置的信号采样率为10 MHz，在无损伤情况下采集所有激励-传感路径的响应信号，以此作为基准信号，将模拟损伤的铝块分别放置在不同的损伤位置，采集损伤响应信号，将其与获得的基准信号相减，得到损伤散射信号。
进行成像实验时，选择整个CFRP板为监测区域，并将其划分为100×100个网格点，即
10000 个网格点，每一网格点大小为5 mm×5 mm，成像分辨率为5 mm。成像中第i个网格点的归一化像素值可由下式得到：I_i=\left\{\begin{array}{*{20}{l}}\mathrm{lg}\dfrac{\left|x_i\right|}{\text{max}(|\boldsymbol{x}|)}, & \mathrm{if}\mathrm{\text{ }lg}\dfrac{\left|x_i\right|}{\text{max}(|\boldsymbol{x}|)} > -1 \\ -1, & \mathrm{other\text{ }}\end{array}\right. (22) 其中，{I_i}是第i个网格点像素值归一化后的值，范围为−1 ~ 0。
为评估损伤定位的效果，定义定位误差指标：
r\mathrm{_e}=\sqrt{(y^*-y_0)^2+(x^*-x_0)^2} (23) 其中： r_{\mathrm{e}} 为误差； ({x_0},{y_0}) 为损伤实际位置； ({x^ * },{y^ * }) 为成像中像素值最大的位置。
3.2 不同正则化参数成像实验结果及分析
在SR成像法中，正则化参数 {\sigma ^2} 是影响成像性能的重要参数，其取值与信号中的噪声水平、原子与信号的相似度有关，在不同的实验环境下， {\sigma ^2} 的取值不同。由于实验环境噪声等因素的影响，信号与原子本身之间就已存在一定误差，因此 {\sigma ^2} 往往需要选择较大值，但因不能准确确定信号之间的误差大小，以往研究中确定该值的方式是在 {\sigma ^2} 的取值范围 0 < {\sigma ^2} < \left\| {\boldsymbol{y}} \right\|_2^2 内按照 {\sigma ^2} 的不同取值进行多次损伤成像实验，以损伤的成像效果为依据确定 {\sigma ^2} 的具体取值。鉴于以往研究中对于 {\sigma ^2} 的取值均大于或等于0.5 \left\| {\boldsymbol{y}} \right\|_2^2 [18, 28, 37]，本文结合以往研究对正则化参数的选择将取值范围缩小，设定为0.5 \left\| {\boldsymbol{y}} \right\|_2^2 < {\sigma ^2} < \left\| {\boldsymbol{y}} \right\|_2^2 。此外，为确定 {\sigma ^2} 的具体取值，本节选择损伤D4为实验损伤，在取值范围内分别设置 {\sigma ^2} 为0.55 \left\| {\boldsymbol{y}} \right\|_2^2 、0.75 \left\| {\boldsymbol{y}} \right\|_2^2 与0.95 \left\| {\boldsymbol{y}} \right\|_2^2 进行成像实验，通过实验分析不同大小 {\sigma ^2} 对于SR成像法与MVDR-SR成像法成像效果的影响，并依据成像效果确定 {\sigma ^2} 的取值。
图6为基于不同 {\sigma ^2} 下SR和MVDR-SR成像法得到的D4损伤成像结果，左侧为基于SR成像法的成像结果，右侧为MVDR-SR成像法的成像结果。归一化像素值越大，颜色越趋向于深红色，表明存在损伤的可能性越大。图像中白色实心圆点为传感器在图像中的位置，白色空心圆圈为损伤在图像中的真实位置。由图可看出，在相同 {\sigma ^2} 下，MVDR-SR成像法结果均为最优，说明对稀疏解变量加权后，可提高损伤网格点原子的匹配概率，同时降低无损网格点原子的匹配概率，进而使大部分无损区域对应的稀疏解变量为零，消除伪影。当正则化参数取值到0.75后，MVDR-SR成像结果中的伪影几乎全部消除，验证本文所提出的方法在选择到合适的 {\sigma ^2} 后，可以与本文实验环境相适应，对损伤进行准确的成像与定位。
![]()
图 6 D4处不同正则化参数下的SR与MVDR-SR成像法成像结果Figure 6. SR and MVDR-SR imaging results under different regularization parameters at D4表4为两种方法在不同正则化参数下的成像定位结果，由结果可知，MVDR-SR成像法定位误差最大为19.0 mm，在3种不同正则化参数下，MVDR-SR成像法得到的定位结果均小于SR成像法，且分别降低了72.9 mm、77.4 mm与14.7 mm，证明所提出的方法在不同正则化参数下具有更高的定位精度。
表 4 D4处不同正则化参数σ2下的SR与MVDR-SR成像法定位结果Table 4. Location results of SR and MVDR-SR imaging methods under different regularization parameters σ2 at D4{\sigma ^2} SR MVDR-SR Imaging
center/mmLocation error/mm Imaging
center/mmLocation error/mm 0.55\left\| {\boldsymbol{y}} \right\|_2^2 (187.5, 7.5) 91.9 (257.5, 92.5) 19.0 0.75\left\| {\boldsymbol{y}} \right\|_2^2 (187.5, 7.5) 91.9 (257.5, 87.5) 14.5 0.95\left\| {\boldsymbol{y}} \right\|_2^2 (247.5, 97.5) 22.6 (247.5, 82.5) 7.9 3.3 不同损伤位置成像实验结果及分析
为分析在不同损伤位置下的MVDR、SR与MVDR-SR成像方法的成像效果，分别使用上述3种成像法对4个不同典型位置的损伤进行成像实验。结合3.2节对于不同正则化参数成像实验所得结果，将SR成像法与MVDR-SR成像法中的正则化参数选择为{\sigma ^2} = 0.9\left\| {\boldsymbol{y}} \right\|_2^2。
图7~图10分别为D1~D4这4个不同位置损伤下基于MVDR、SR与MVDR-SR这3种成像方法的成像结果。图7(a)~图10(a)为MVDR成像结果，由成像结果可看出MVDR成像稳定，尤其靠近传感器的损伤，效果更好，且靠近边界时并未由于边界反射而出现损伤误判，其原因是加入了权重系数，降低了干扰信号的影响，更多的考虑了期望方向信号，因此成像会较为稳定，但由于权重系数存在误差，未能完全消除干扰信号，因此在无损区域依然会有伪影，且由于主要成像范围较大，难以准确定位损伤位置，降低了损伤成像性能。基于SR成像法的成像结果如图7(b)~图10(b)所示，与MVDR成像法相比，其消除了大量的伪影，原因为该方法是基于稀疏性的原理，得到大部分稀疏解都为零值，因此可以消除大部分伪影，而当损伤分别靠近边界和中间位置时，会分别由于边界反射和信号叠加严重而造成损伤位置的误判。其原因是边界反射信号或无损路径信号会叠加在损伤路径信号上，对损伤散射信号造成严重的干扰，改变损伤散射信号波形，使实测散射信号与理论散射信号组成的原子差距变大，出现原子失配问题，进而导致成像位置存在偏差，甚至误判，稳定性和精度较差。最后如图7(c)~图10(c)所示为基于MVDR-SR成像法得到的成像结果，与上述两种方法所得结果相比，无损区域的伪影几乎全部消除，且在4个不同典型位置处都能准确定位损伤，其原因为该方法构建的MVDR权重因子不用考虑信号间的差异，因此无论损伤位于何处都可以稳定地反映出损伤范围信息，将其施加于SR成像法的稀疏解变量后可以提高损伤网格点原子的匹配概率，解决由于边界反射或信号叠加干扰而导致的原子失配问题，消除由于原子失配而导致的损伤误判现象，同时也消除MVDR成像法中因干扰信号导致的伪影，验证本文所提出的MVDR-SR成像法的有效性，具有更好的成像性能。同时也验证该方法适用于长宽范围0~500 mm，厚度范围0~2 mm，准各向同性条件下的CFRP结构，可对结构中不同位置的损伤进行准确的成像与定位。
表5为3种成像法在不同位置的损伤定位结果，由表中结果可知，本文所提出的MVDR-SR成像法最大定位误差为7.9 mm，均小于或等于其余两种成像法的最小误差，在不同损伤位置处的损伤定位效果均为最好，结果证明此方法的损伤定位有效性。
表 5 3种成像法在不同损伤位置成像定位结果Table 5. Imaging positioning results of the three imaging methods at different damage localizationsDamage MVDR SR MVDR-SR Imaging
center/mmLocation error/mm Imaging
center/mmLocation error/mm Imaging
center/mmLocation error/mm D1 (82.5, 412.5) 17.6 (2.5, 387.5) 68.2 (62.5, 412.5) 3.5 D2 (267.5, 432.5) 20.7 (262.5, 402.5) 9.8 (257.5, 412.5) 7.5 D3 (307.5, 257.5) 12.7 (492.5, 257.5) 172.5 (312.5, 257.5) 7.9 D4 (247.5, 67.5) 7.9 (247.5, 97.5) 22.6 (247.5, 82.5) 7.9 4. 结 论
(1) 结合最小方差无失真(MVDR)和稀疏重建(SR)成像法，提出了MVDR-SR成像法。以MVDR成像法得到的成像结果为基础进行构建MVDR权重因子，其含有损伤范围信息，更符合实际损伤情况，将其施加于SR成像法中的稀疏解变量，提升了现有SR成像法的原子适配率，减少由于原子失配问题导致的损伤误判和伪影；
(2) 在同样的正则化参数下，MVDR-SR成像法相比SR成像法得到的碳纤维增强复合材料(CFRP)层合板损伤成像效果更好，伪影更少，定位误差最大为19.0 mm。在0.55 \left\| y \right\|_2^2 、0.75 \left\| y \right\|_2^2 与0.95 \left\| y \right\|_2^2 这3种不同正则化参数下，损伤定位误差相比SR成像法则分别降低了72.9 mm、77.4 mm与14.7 mm；
(3) 与MVDR成像法和SR成像法相比， MVDR-SR成像法在CFRP层合板中4个不同典型位置的损伤成像效果更好，有效消除伪影，更加直观反映出损伤位置，最大定位误差为7.9 mm，均优于其他两种成像法。此外，当损伤靠近边界时，MVDR-SR成像法可消除边界影响，对损伤进行准确成像；
(4) 本文所提的MVDR-SR成像法可用于如飞机等飞行器的关键CFRP结构的健康监测，对由于长期服役而出现的损伤进行准确的成像与定位，具有重要的应用价值。但目前CFRP的SR成像研究对象大多都为简单的CFRP结构，而实际应用中的CFRP结构多为加筋与弯曲等复杂结构，因此，该领域后续研究可考虑不同几何结构对信号及模型的影响，提高方法在复杂CFRP结构的成像性能。
-
![]()
图 6 抗浮锚杆上拔过程中锚固体受力示意图
Figure 6. Schematic diagram of anchorage body force in the process of anti-floating anchor pulling up
P—Uplift load of the anti-floating anchor rod; Fc—Interaction force between the anti-floating anchor rod and the mortar; Fc’—Interaction force between the mortar and the soil
![]()
图 7 抗浮锚杆锚固体荷载-位移曲线
Figure 7. Load-displacement curves of anti-floating anchor anchorage body
![]()
图 8 抗浮锚杆杆体、锚固体荷载-位移差曲线
Figure 8. Load-displacement difference curves of anchorage body and rod body of anti-floating anchor
![]()
图 9 抗浮锚杆荷载-位移(Q-s)曲线模型对比
Figure 9. Comparison of load-displacement (Q-s) curve models of anti-floating anchors
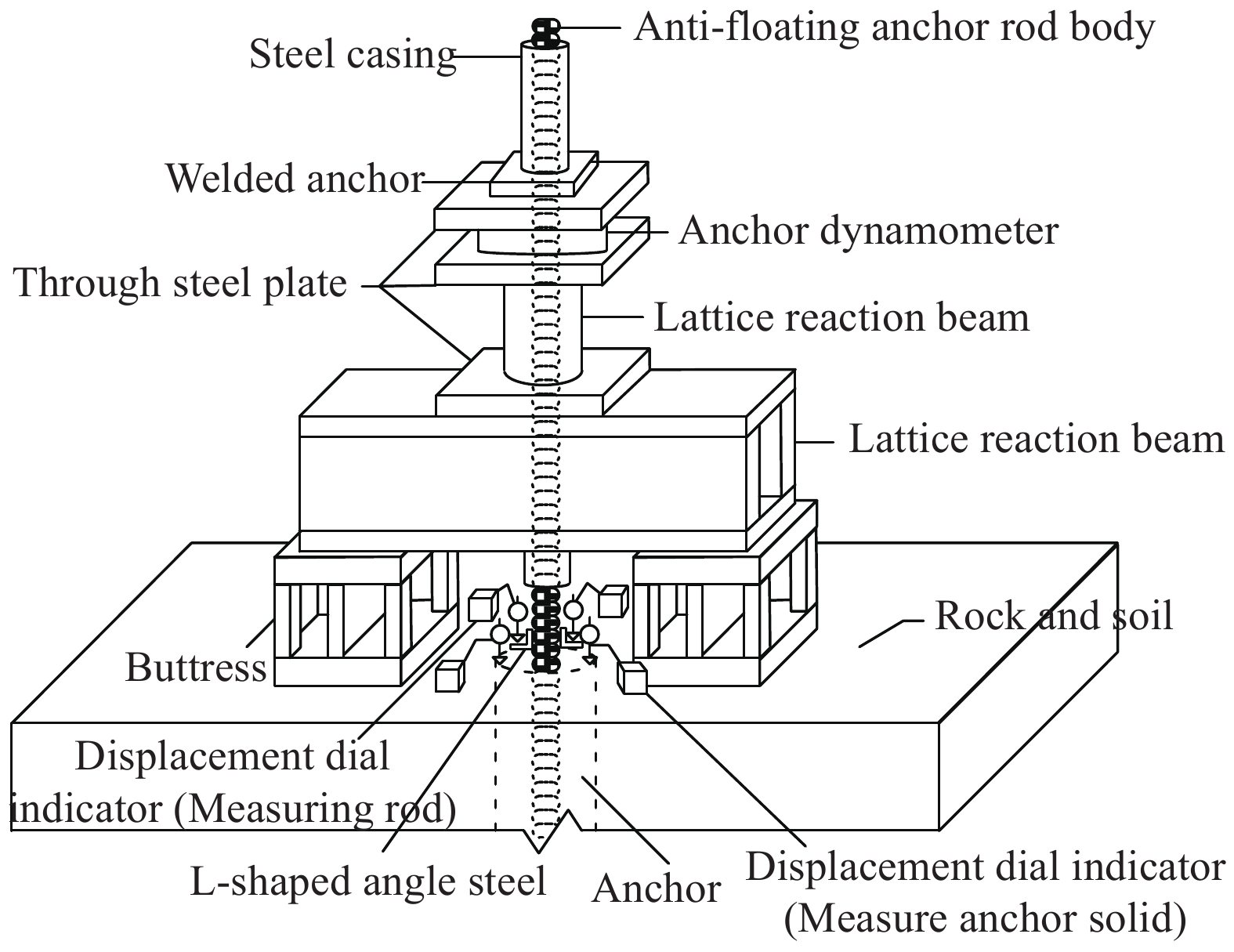
表 1 试验锚杆主要力学参数
Table 1 Main mechanical parameters of test bolt
Anchor material Tensile capacity/kN Tensile strength/MPa Shear strength/MPa Elastic modulus/GPa GFRP 416 675 150 41 Rebar 351 570 277 210 Note: GFRP—Glass fiber reinforced ploymer. 
下载: 导出CSV
表 2 抗浮锚杆试验参数
Table 2 Anti-floating anchor test parameters
Anchor number Anchor rod diameter/mm Total length of anchor rod/mm Length of anchoring section/mm GFRP6.5-1 28 8000 6500 GFRP6.5-2 28 8000 6500 GFRP6.5-3 28 8000 6500 GFRP4.5-1 28 6000 4500 GFRP4.5-2 28 6000 4500 GFRP4.5-3 28 6000 4500 S6.5-1 28 8000 6500 S6.5-2 28 8000 6500 S6.5-3 28 8000 6500 S4.5-1 28 6000 4500 S4.5-2 28 6000 4500 S4.5-3 28 6000 4500 Notes: GFRP6.5—GFRP anti-floating anchors with an anchorage length of 6.5 m; GFRP4.5—GFRP anti-floating anchors with an anchorage length of 4.5 m; S—Steel bar.
下载: 导出CSV
表 3 试验结果统计
Table 3 Test results statistics
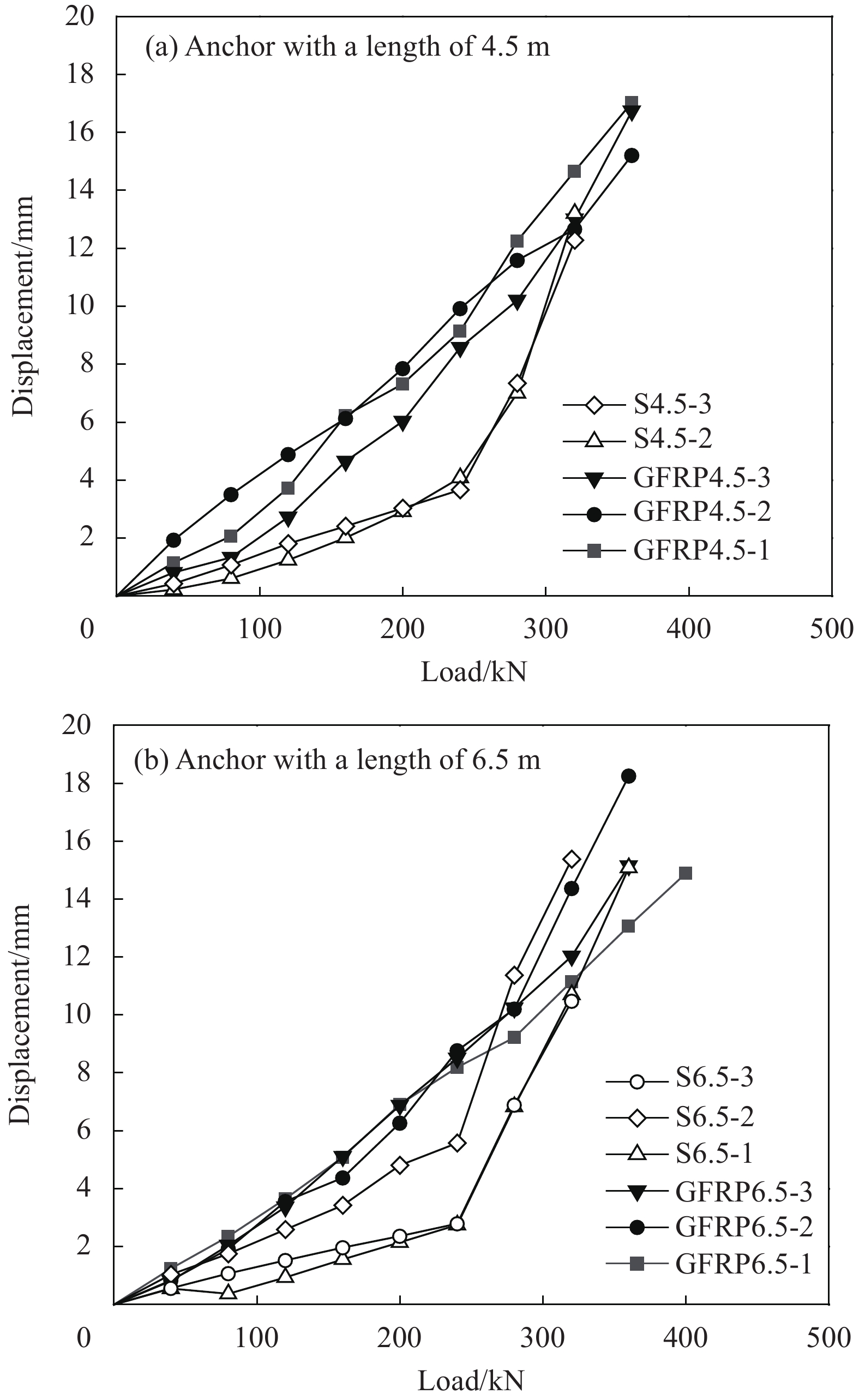
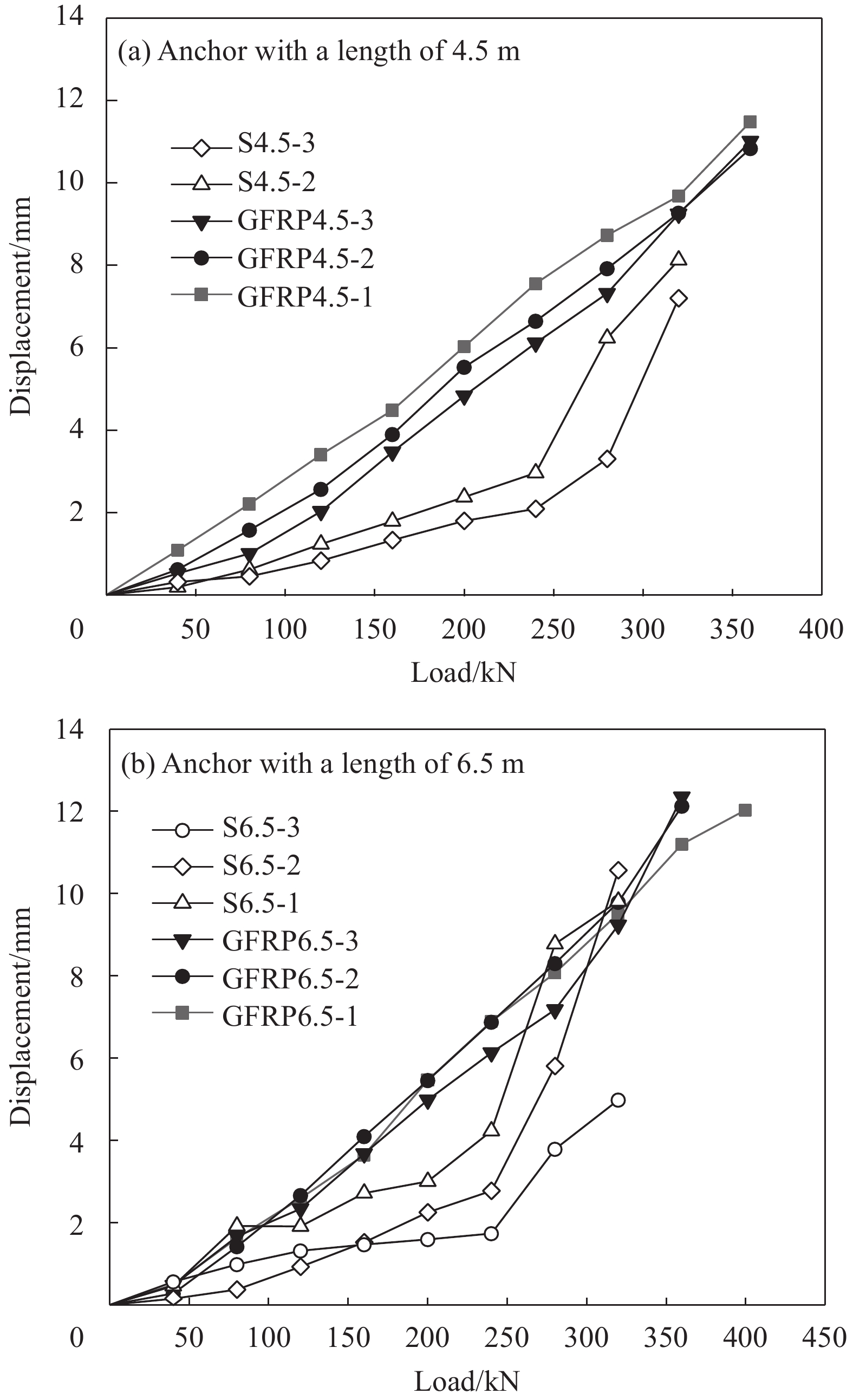
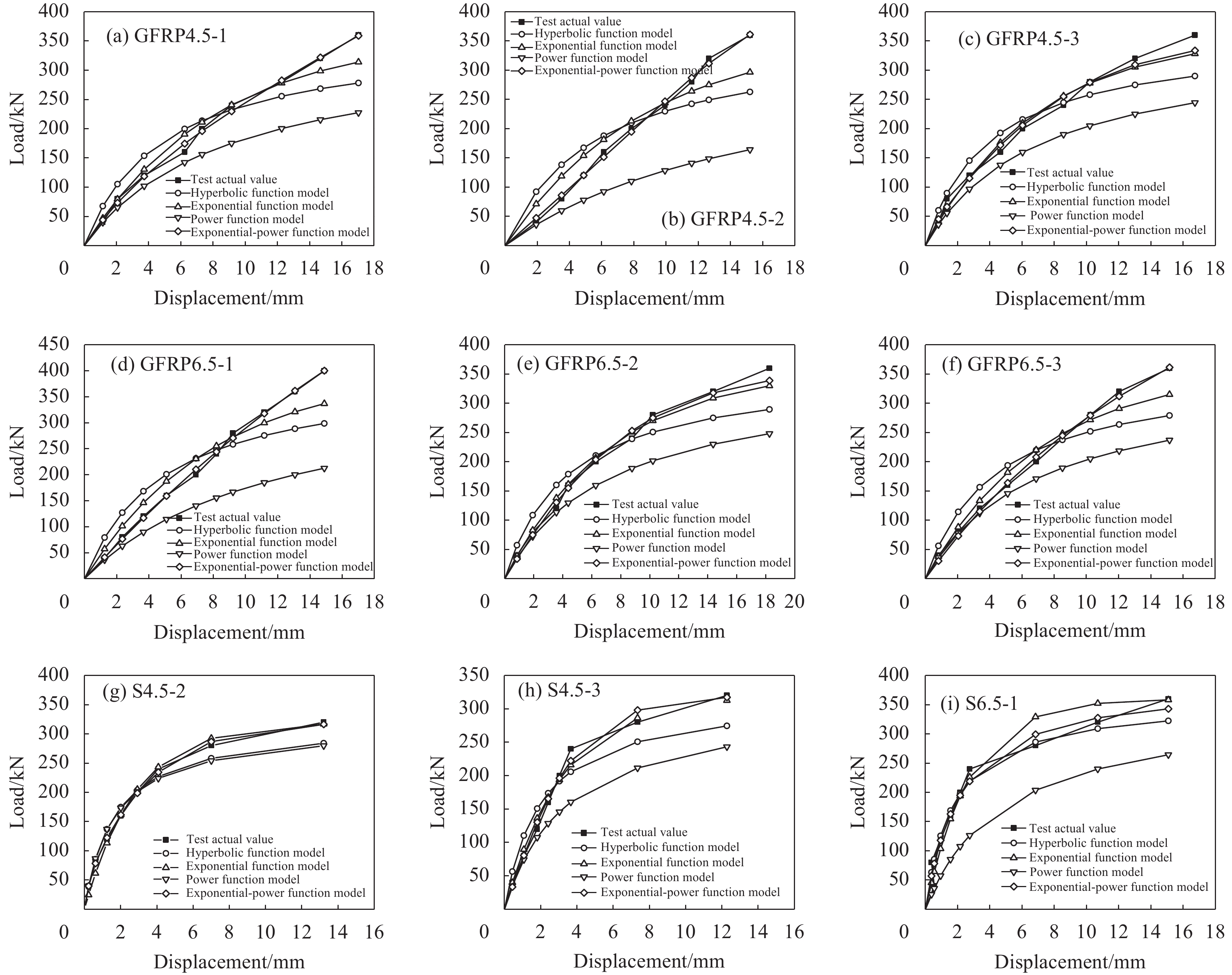
Anchor number Anchor length/m Failure load/kN Maximum rod lift/mm Anchor solid limit lift/mm Destruction form GFRP4.5-1 4.5 381 17.03 12.67 Shear slip failure GFRP4.5-2 4.5 394 15.21 11.47 Disconnect failure GFRP4.5-3 4.5 375 16.74 11.35 Shear slip failure GFRP6.5-1 6.5 412 14.89 12.25 Disconnect failure GFRP6.5-2 6.5 387 18.26 13.27 Shear slip failure GFRP6.5-3 6.5 398 15.16 12.45 Disconnect failure S4.5-1 4.5 320 58.05 15.89 Shear slip failure S4.5-2 4.5 331 13.21 8.47 Disconnect failure S4.5-3 4.5 323 12.28 8.13 Disconnect failure S6.5-1 6.5 362 15.09 11.67 Disconnect failure S6.5-2 6.5 342 15.39 12.16 Disconnect failure S6.5-3 6.5 339 10.49 7.58 Disconnect failure
下载: 导出CSV
表 4 抗浮锚杆各Q-s模型极限承载力计算精度
Table 4 Calculation accuracy of ultimate bearing capacity of each Q-s models of anti-floating anchors
Anchor
numberMeasured
ultimate
bearing
capacity/kNHyperbolic function
modelExponential function
modelPower function
modelExponential-power
function modelPredictive
value/kNRelative
error/%Predictive
value/kNRelative
error/%Predictive
value/kNRelative
error/%Predictive
value/kNRelative
error/%GFRP4.5-1 360 278.23 −22.71 313.99 −12.78 227.57 −36.79 359.07 −0.26 GFRP4.5-2 360 262.85 −26.99 296.55 −17.63 164.16 −54.40 361.07 0.30 GFRP4.5-3 360 290.05 −19.43 328.15 −8.85 244.42 −32.11 333.78 −7.28 GFRP6.5-1 400 298.83 −25.29 337.03 −15.74 212.65 −46.84 400.46 0.11 GFRP6.5-2 360 289.59 −19.56 329.96 −8.34 248.10 −31.08 338.92 −5.86 GFRP6.5-3 360 279.14 −22.46 315.20 −12.44 236.94 −34.18 361.56 0.43 S4.5-2 320 284.07 −11.23 316.87 −0.98 279.69 −12.60 316.57 −1.07 S4.5-3 320 274.58 −14.19 312.61 −2.31 243.22 −23.99 317.41 −0.81 S6.5-1 320 322.31 0.72 358.41 12.00 264.35 −17.39 343.00 7.19 S6.5-2 360 265.38 −26.28 305.39 −15.17 202.11 −43.86 315.21 −12.44 S6.5-3 320 273.44 −14.55 313.01 −2.18 217.35 −32.08 319.78 −0.07
下载: 导出CSV
表 5 抗浮锚杆各Q-s模型计算参数
Table 5 Calculation parameters of each Q-s models of anti-floating anchors
Anchor
numberHyperbolic function
model αExponential function
model β/mm−1Power function
model Ki/(kN·mm−1)Exponential-power function model a b k GFRP4.5-1 4.0254 −0.1454 34.4828 0.0023 −0.0729 −0.9053 GFRP4.5-2 5.6219 −0.1141 20.6718 0.2949 −0.0660 186.4119 GFRP4.5-3 4.0374 −0.1449 49.3827 0.2360 3.8378 −0.9430 GFRP6.5-1 5.0408 −0.1242 32.1285 −0.0224 −0.0673 0.3136 GFRP6.5-2 4.4397 −0.1360 47.6191 0.2325 1.0623 −0.8018 GFRP6.5-3 4.3914 −0.1374 49.3827 0.0031 −0.0664 −0.9239 S4.5-2 1.6707 −0.3502 173.9130 0.4572 1.8488 −0.8234 S4.5-3 2.0314 −0.3069 91.9540 0.4843 0.0940 0.4394 S6.5-1 1.7642 −0.3595 72.7273 0.1578 0.0407 −0.7045 S6.5-2 3.1663 −0.2006 38.2775 0.3956 110.2263 −0.9961 S6.5-3 1.7852 −0.3648 70.1754 0.8980 0.2717 1.2221 Note: a, b, k—Parameters to be fitted.
下载: 导出CSV
-
[1] KUANG Z, ZHANG M Y, BAI X Y. Load-bearing characteristics of fibreglass uplift anchors in weathered rock[J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering,2020,173(1):49-57. DOI: 10.1680/jgeen.18.00195
[2] LI F, ZHAO Q L, CHEN H S, et al. Interface shear stress analysis of bond FRP tendon anchorage under different boundary conditions[J]. Composite Interfaces,2011,18(2):91-106. DOI: 10.1163/092764411X571427
[3] 白晓宇, 张明义, 匡政, 等. 全长黏结GFRP抗浮锚杆荷载分布函数模型研究[J]. 中南大学学报(自然科学版), 2020, 51(7):1977-1988. DOI: 10.11817/j.issn.1672-7207.2020.07.023 BAI Xiaoyu, ZHANG Mingyi, KUANG Zheng, et al. Load distribution function model of full-length bond GFRP anti-floating anchor[J]. Journal of Central South University (Science and Technology),2020,51(7):1977-1988(in Chinese). DOI: 10.11817/j.issn.1672-7207.2020.07.023
[4] ALVES J, EL-RAGABY A, EL-SALAKAWY E. Durability of GFRP bars’ bond to concrete under different loading and environmental conditions[J]. Journal of Composites for Construction,2010,15(3):249-262.
[5] 贾金青, 宋二祥. 滨海大型地下工程抗浮锚杆的设计与试验研究[J]. 岩土工程学报, 2002, 24(6):769-771. DOI: 10.3321/j.issn:1000-4548.2002.06.021 JIA Jinqing, SONG Erxiang. Design and Experimental study of anti-floating anchor rods for large-scale underground engineering in binhai[J]. Chinese Journal of Geotechnical Engineering,2002,24(6):769-771(in Chinese). DOI: 10.3321/j.issn:1000-4548.2002.06.021
[6] 张乐文, 汪稔. 岩土锚固理论研究之现状[J]. 岩土力学, 2002, 23(5):627-631. DOI: 10.3969/j.issn.1000-7598.2002.05.022 ZHANG Lewen, WANG Ren. Current status of research on rock-soil anchoring theory[J]. Rock and Soil Mechanics,2002,23(5):627-631(in Chinese). DOI: 10.3969/j.issn.1000-7598.2002.05.022
[7] 白晓宇, 郑晨, 张明义, 等. 大直径GFRP抗浮锚杆蠕变试验及蠕变模型[J]. 岩土工程学报, 2020, 42(7):1304-1311. BAI Xiaoyu, ZHENG Chen, ZHANG Mingyi, et al. Creep tests and standard linear solid model for large-diameter glass fiber-reinforced polymer anti-floating anchors[J]. Chinese Journal of Geotechnical Engineering,2020,42(7):1304-1311(in Chinese).
[8] TASTANI S P, PANTAZOPOU S J. Bond of GFRP bars in concrete: Experimental study and analytical interpretation[J]. Journal of Composites for Construction,2006,10(5):381-391. DOI: 10.1061/(ASCE)1090-0268(2006)10:5(381)
[9] 黄生文, 邱贤辉, 罗文兴. GFRP锚杆锚固特性研究[J]. 长沙理工大学学报(自然科学版), 2009, 6(3):33-39. HUANG Shengwen, QIU Xianhui, LUO Wenxing. Research on anchoring characteristics of GFRP anchor rod[J]. Journal of Changsha University of Science and Technology (Natural Science Edition),2009,6(3):33-39(in Chinese).
[10] 张明义, 寇海磊, 白晓宇, 等. 玻璃纤维增强聚合物抗浮锚杆抗拔性能试验研究与机制分析[J]. 岩土力学, 2014, 35(4):1069-1076. ZHANG Mingyi, KOU Hailei, BAI Xiaoyu, et al. Experimental research and mechanism analysis of the anti-floating anchor rod pull-out performance of glass fiber reinforced polymer[J]. Rock and Soil Mechanics,2014,35(4):1069-1076(in Chinese).
[11] KOU H L, GUO W, ZHANG M Y. Pullout performance of GFRP anti-floating anchor in weathered soil[J]. Tunnelling and Underground Space Technology, 2015, 49: 408-416.
[12] 尤志嘉, 付厚利, 尤春安, 等. 土层锚固体应力传递机制[J]. 岩土力学, 2018, 39(1):85-92. YOU Zhijia, FU Houli, YOU Chun’an, et al. Stress transfer mechanism of soil anchorage[J]. Rock and Soil Mechanics,2018,39(1):85-92(in Chinese).
[13] GOORANORIMI O, SUARIS W, NANNI A. A model for the bond-slip of a GFRP bar in concrete[J]. Engineering Structures,2017,146:34-42. DOI: 10.1016/j.engstruct.2017.05.034
[14] 中国建筑科学研究院. 建筑基坑支护技术规程: JGJ120—2012[S]. 北京: 中国建筑工业出版社, 2012. China Academy of Building Research. Technical specification for foundation pit support: JGJ120—2012[S]. Beijing: China Building Industry Press, 2012(in Chinese).
[15] 中国建筑科学研究院. 建筑地基基础设计规范: GB50007—2011[S]. 北京: 中国建筑工业出版社, 2011. China Academy of Building Research. Code for design of building foundation: GB50007—2011[S]. Beijing: China Building Industry Press, 2011(in Chinese).
[16] HYETT A J, BAWDEN W F, MACSPORRAN G R, et al. A constitutive law for bond failure of fully-grouted cable bolts using a modified Hoek cell[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1995,32(1):11-36.
[17] 付文光, 柳建国, 杨志银. 抗浮锚杆及锚杆抗浮体系稳定性验算公式研究[J]. 岩土工程学报, 2014, 36(11):1971-1982. DOI: 10.11779/CJGE201411002 FU Wenguang, LIU Jianguo, YANG Zhiyin. Study on the formula for checking the stability of anti-floating anchor rod and anti-floating system of anchor rod[J]. Chinese Journal of Geotechnical Engineering,2014,36(11):1971-1982(in Chinese). DOI: 10.11779/CJGE201411002
[18] 王贤能, 曾卫东, 徐金台. 岩石抗浮锚杆的应用及分析[C]//中国岩石力学与工程学会第七次学术大会论文集. 西安, 2002: 831−835. WANG Xianneng, ZENG Weidong, XU Jintai. Application and analysis of rock anti-floating anchor[C]// Proceedings of the Seventh Academic Conference of Chinese Society of Rock Mechanics and Engineering. Xi’an, 2002: 831−835.
[19] 贾金青, 宋二祥. 滨海大型地下工程抗浮锚杆的设计与试验研究[J]. 岩土工程学报, 2002, 24(6):669-771. JIA Jinqing, SONG Erxiang. Design and experimental study of anti-floating anchor in Binhai large underground project[J]. Journal of Geotechnical Engineering,2002,24(6):669-771(in Chinese).
[20] 陈根全. 锚杆桩的抗拔试验[J]. 工程勘察, 1997, 25(2):15-16. CHEN Genquan. Uplift test of anchor pile[J]. Engineering Survey,1997,25(2):15-16(in Chinese).
[21] 赵卫平, 朱彬荣. 高温后HSC粘结滑移基础参数测量与3D有限元数值模拟[J]. 工程力学, 2017, 34(4):177-186. ZHAO Weiping, ZHU Binrong. Measurement of HSC bond slip foundation parameters and 3D finite element numerical Simulation after high temperature[J]. Engineering Mechanics,2017,34(4):177-186(in Chinese).
[22] 刘凌锋. FRP管与混凝土的粘结性能试验研究[D]. 南京: 东南大学, 2016. LIU Lingfeng. Experimental Study on bond performance of FRP pipe and concrete[D]. Nanjing: Southeast University, 2016(in Chinese).
[23] 张季如, 唐保付. 锚杆荷载传递机理分析的双曲函数模型[J]. 岩土工程学报, 2002, 24(2):188-192. DOI: 10.3321/j.issn:1000-4548.2002.02.013 ZHANG Jiru, TANG Baofu. Hyperbolic function model to analyze load transfer mechanism on bolts[J]. Chinese Journal of Geotechnical Engineering,2002,24(2):188-192(in Chinese). DOI: 10.3321/j.issn:1000-4548.2002.02.013
[24] 应志民, 张洁, 尚岳全. 锚杆荷载-位移曲线的指数函数模型研究[J]. 岩土力学, 2005, 26(8):1331-1334. DOI: 10.3969/j.issn.1000-7598.2005.08.028 YING Zhimin, ZHANG Jie, SHANG Yuequan. Exponential model for simulating load-displacement curve of anchor rod[J]. Rock and Soil Mechanics,2005,26(8):1331-1334(in Chinese). DOI: 10.3969/j.issn.1000-7598.2005.08.028
[25] 许宏发, 钱七虎, 金丰年. 描述抗拔桩荷载-位移曲线的幂函数模型[J]. 岩土工程学报, 2000, 22(5):622-624. DOI: 10.3321/j.issn:1000-4548.2000.05.026 XU Hongfa, QIAN Qihu, JIN Fengnian. Power function model to describe load-displacement curve of tension pile[J]. Chinese Journal of Geotechnical Engineering,2000,22(5):622-624(in Chinese). DOI: 10.3321/j.issn:1000-4548.2000.05.026
[26] 孙晓云, 张涛, 王明明, 等. 基于改进指-幂混合函数模型的锚杆承载力预测方法研究[J]. 岩石力学与工程学报, 2015, 34(8):1641-1649. SUN Xiaoyun, ZHANG Tao, WANG Mingming, et al. A revised model for predicting the bearing capacity of rock bolts based on mixed exponential and power unction[J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(8):1641-1649(in Chinese).
-
计量
- 文章访问数: 1400
- HTML全文浏览量: 465
- PDF下载量: 59
