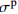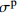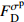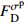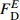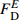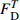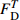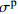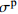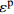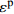钢-塑钢混杂纤维再生混凝土单轴压缩动态力学性能试验

冯俊杰; 尹冠生; 刘柱; 梁建红; 张云杰; 牛志强; 王鹏博

doi:10.13801/j.cnki.fhclxb.20211221.002

钢-塑钢混杂纤维再生混凝土单轴压缩动态力学性能试验

1.
长安大学　理学院，西安 710064
2.
陕西铁投工程检测科技有限公司，西安 710304
3.
郑州科技学院　土木建筑工程学院，郑州 450064

基金项目: 长安大学博士研究生创新能力培养资助项目(300203211121)；陕西省交通运输厅交通科研项目(21-67K)；长安大学相变蓄能建筑材料创新开放实验室项目(2018CXSY06)；河南省科技厅科技攻关项目(182102311091)；郑州科技学院自然科学项目(2017-XYZK-002)

详细信息

通讯作者:
尹冠生，博士，教授，博士生导师，研究方向为混凝土结构　E-mail: yings@chd.edu.cn

中图分类号: TV431
计量
- 文章访问数: 0942
- HTML全文浏览量: 0477
- PDF下载量: 063
出版历程
- 收稿日期: 2021-10-14
- 修回日期: 2021-12-09
- 录用日期: 2021-12-12
- 网络出版日期: 2021-12-21
- 刊出日期: 2022-10-31

Experiment on dynamic mechanical properties of steel and macro-polypropylene hybrid fibers reinforced recycled aggregate concrete under uniaxial compression

1.
School of Science, Chang’an University, Xi’an 710064, China
2.
Shaanxi Tietou Engineering Testing Technology CO., LTD., Xi’an 710304, China
3.
School of Civil Engineering and Architecture, Zhengzhou University of Science and Technology, Zhengzhou 450064, China

摘要

摘要: 为探究钢-塑钢混杂纤维再生混凝土的压缩动态力学性能，设计了A、B和C 3个系列混杂纤维再生混凝土包含3种再生粗骨料取代率和5种体积分数1.5vol%的钢纤维和塑钢混掺纤维组合，采用了4种加载应变率。试验表明：随应变率增加，混杂纤维再生混凝土峰值应力、弹性模量和压缩韧性增大，峰值应变减小。相较于基准组，在相同应变率下3个系列中的含纤维组峰值应力最大增幅分别为23%、16%和16%；峰值应变最大增幅分别为19%、12%和13%；弹性模量最大增幅分别为15%、14%和35%；压缩韧性最大增幅分别为46%、32%和37%。在试验应变率范围内，再生粗骨料显著提高峰值应力、弹性模量和压缩韧性的应变率敏感性，对峰值应变的应变率敏感性并无明显影响；掺入纤维降低混凝土峰值应变和弹性模量的应变率敏感性，提高普通混凝土峰值应力和压缩韧性的应变率敏感性，降低再生混凝土峰值应力和压缩韧性的应变率敏感性。提出的动态损伤本构模型考虑了纤维增强系数、再生粗骨料取代率和应变率，计算结果与试验结果吻合较好。
- 混杂纤维再生混凝土 /
- 单轴压缩 /
- 动态力学性能 /
- 动态增长因子 /
- 应变率敏感性 /
- 动态损伤本构模型
Abstract: The dynamic compressive behavior of hooked-end steel (HES) and macro-polypropylene (MPP) hybrid fibers reinforced recycled aggregate concrete (HyF/RAC) was studied. Three series (A, B and C) of HyF/RAC specimens were designed, which include three different recycled coarse aggregates (RCA) replacement ratios and five combinations of hybrid fibers at the total volume fraction of 1.5vol%, and four different strain rates were conducted. The results show that with the increase of strain rate, the peak stress, elastic modulus and compressive toughness increase, while the peak strain decreases. Compared with control groups in three series under the same strain rate, the largest increases of peak stress for specimens with fibers are 23%, 16% and 16%, respectively. The largest increases of peak strain are 19%, 12% and 13%, respectively. The largest increases of elastics modulus are 15%, 14% and 35%, respectively. The largest increases of compressive toughness are 46%, 32% and 37%, respectively. In the strain rate range, the strain rate sensitivity of peak stress, elastic modulus and compressive toughness increase with the RCA, and the RCA replacement ratio does not affect the strain rate sensitivity of peak strain. The strain rate sensitivity of peak strain and elastics modulus decrease with the addition of fiber. The addition of fibers enhances the strain rate sensitivity of peak stress and compressive toughness for natural aggregate concrete (NAC). While the strain rate sensitivity of peak stress and compressive toughness decrease for recycled aggregate concrete (RAC). The dynamic constitutive damage model was proposed considering the reinforcing index of fibers, RCA replacement ratio and strain rates. And all the models agree well with the experimental curves.
- hybrid fibers reinforced recycled aggregate concrete /
- uniaxial compression /
- dynamic mechanical properties /
- dynamic increase factor /
- strain rate sensitivity /
- dynamic damage constitutive model

HTML全文

近年来随着工业的快速发展，水污染问题受到越来越多的关注。其中的一部分污染是由抗生素引起的，如阿莫西林、青霉素、四环素等^[1-5]。四环素(Tetracycline，TC)作为一种普遍使用的抗生素，因其独特的抗菌作用而被广泛应用于人类疾病的治疗。然而TC长期存在于水环境中难以自然降解，对生态环境和人类健康有很大危害^[6-10]。因此，开发一种有效的解决方案来去除水环境中难降解的抗生素是极其重要的。半导体光催化技术因其具有环境友好、无污染、低能耗等优点引起了广泛的研究，成为当今处理有机污染物最有前景的方法之一^[11-13]。

在各种光催化剂中，BiOX(X=Cl, Br, I)因其特殊的层状结构、适宜的禁带宽度和较高的稳定性，被广泛用于光降解有机污染物和光催化分解水^[14-15]。其中BiOI具有较窄的禁带宽度(1.77~1.92 eV)和较宽的可见光响应范围，但由于光生电子空穴对的高复合率，其光催化性能并不理想。将BiOI与其他半导体材料相结合被认为是增强光催化性能最有前途的策略，2个或2个以上半导体相结合可以形成半导体/半导体异质结，通过提高光生电子空穴对的分离速率从而提高光催化活性。

Bi₂O₃的带隙介于2.1~2.8 eV之间，由于其具有较强的可见光区响应、无毒、电化学稳定性高、热稳定性好和低成本等特性^[16-18]，是一种很有前途的可见光光催化候选材料，可与其他半导体材料形成异质结结构。如CdS/BiOCl/Bi₂O₃^[19]、GO/AgI/Bi₂O₃^[20]、α-Bi₂O₃/g-C₃N₄^[21]、Bi₂O₃/ZnS^[22]等。

Wei等^[23]采用一锅沉淀法在多孔Bi₂O₃纳米棒上成功沉积了BiOI纳米片。结果表明：与原始Bi₂O₃和BiOI相比，50% Bi₂O₃/BiOI复合材料具有更高的光生电子空穴对分离效率和更大的比表面积，在可见光照射下，其光催化还原Cr(VI)的活性显著增强。此外，50% Bi₂O₃/BiOI复合材料还具有优异的光化学稳定性和可回收性。Li等^[24]采用化学刻蚀法制备了BiOI/Bi₂O₃异质结，在降解苯酚和4-氯苯酚(4-CP)方面表现出良好的光催化活性。其光催化性能的提高是由于BiOI/Bi₂O₃异质结的形成促进了电子空穴对的有效分离，并提出了光生电荷转移的过程。

目前所制备的同类光催化剂大多数用于去除水环境中的重金属离子和有机染料等，对降解抗生素类药物的研究较少。本文采用简单的溶剂热法制备了Bi₂O₃/BiOI复合光催化材料，在模拟太阳光照射下通过降解四环素研究了其光催化性能，探究了BiOI与Bi₂O₃不同摩尔比、反应温度、反应时间、pH等条件对光催化性能的影响。并通过活性物种捕捉实验提出了Bi₂O₃/BiOI复合光催化材料降解四环素可能的机制。

1. 实验材料和方法

1.1 原材料

五水硝酸铋(上海麦克林生化有限公司，AR)、碘化钾(天津市大茂化学试剂厂，AR)、乙二醇(天津市北辰方正试剂厂，AR)、四环素(上海麦克林生化有限公司，AR)。

1.2 实验仪器

EL104型电子天平(梅特勒-托利多有限公司)、HC-3018型高速离心机(安徽中科中佳科学仪器有限公司)、TGL-5A台式离心机(常州润华电器有限公司)、KSW-4D-I2型马弗炉(北京中兴伟业仪器有限公司)、HJ-1型磁力加热搅拌器(红杉实验设备厂)、101-1A型电热鼓风干燥箱(北京中兴伟业仪器有限公司)、721型可见分光光度计(上海仪电分析仪器有限公司)、KQ5200E型超声波清洗器(昆山市超声仪器有限公司)、250 W金卤灯(上海亚明)。

1.3 实验内容

1.3.1 BiOI光催化材料的制备

称取1 mmol五水硝酸铋置于15 mL乙二醇中，超声处理15 min以获得均匀悬浮液。在不断搅拌下向其中逐滴加入10 mL含1 mmol碘化钾的水溶液，继续搅拌2 h。将产物离心，用水和无水乙醇洗涤数次，在80℃下干燥12 h得到红色的BiOI。

1.3.2 Bi₂O₃光催化材料的制备

称取一定量的五水硝酸铋，在600℃的马弗炉里煅烧4 h，冷却至室温后，将产物研磨成粉末状，得到淡黄色的Bi₂O₃。

1.3.3 Bi₂O₃/BiOI复合光催化材料的制备

将1 mmol五水硝酸铋置于15 mL乙二醇中，超声处理15 min以获得均匀悬浮液。在不断搅拌下向其中逐滴加入10 mL含1 mmol碘化钾的水溶液，继续搅拌2 h。在此期间，用1 mol/L的H₂SO₄溶液将混合液的pH调至5。然后向上述溶液中加入0.8 mmol已制备好的Bi₂O₃，继续搅拌1 h。将得到的混合溶液转移至50 mL聚四氟乙烯内衬的不锈钢高压反应釜中，在180℃下反应20 h。自然冷却至室温后，将产物离心，用水和无水乙醇洗涤数次，在80℃下干燥12 h，得到Bi₂O₃/BiOI复合光催化材料。

1.3.4 光催化性能测试

使用250 W金卤灯模拟太阳光照射，通过降解四环素来评价所制备样品的光催化性能。取50 mg制得的光催化材料放入装有100 mL 25 mg/L TC溶液的烧杯中，黑暗搅拌30 min达到吸附-脱附平衡。然后将混合液置于光反应器中，光照开始计时，每隔20 min取3 mL样，将样品放入离心机中离心取其上层清液并测定吸光度。计算四环素的残余率：

$\eta = C/{C_0} \times 100\% = A/{A_0} \times 100\%$

式中：C和C₀分别表示t时刻和初始四环素的质量浓度(mg·L⁻¹)；A和A₀分别表示t时刻和初始四环素的吸光度。

2. 结果与讨论

2.1 Bi₂O₃/BiOI复合光催化材料的晶相结构

BiOI、Bi₂O₃和Bi₂O₃/BiOI的XRD图谱如图1所示。BiOI曲线在9.658°、29.645°、31.657°、37.392°、45.666°、51.345°、55.15°、66.344°和74.09°处出现的衍射峰分别对应BiOI(JCPDS 10-0445)的(001)、(102)、(110)、(112)、(104)、(114)、(212)、(214)和(302)晶面。Bi₂O₃在21.722°、25.757°、27.377°、33.241°、35.406°、37.595°、42.353°、46.305°、52.373°和58.563°处出现的衍射峰分别对应Bi₂O₃(JCPDS 41-1449)的(020)、(002)、(120)、(200)、(031)、(112)、(122)、(041)、(−321)和(−331)晶面。Bi₂O₃/BiOI同时出现了Bi₂O₃和BiOI的主要衍射峰，说明本实验成功制备了Bi₂O₃/BiOI复合光催化材料。

图 1 不同光催化材料的XRD图谱

Figure 1. XRD patterns of different photocatalytic materials

下载: 全尺寸图片幻灯片

2.2 Bi₂O₃/BiOI复合光催化材料的微观形貌

通过SEM分析了所制备光催化材料的微观形貌，结果如图2所示。可以看出，所制备的BiOI是由纳米片自组装形成的花状微球；单一Bi₂O₃呈现出不同尺寸、不规则的块状结构。从图2(c)可以看出，当BiOI与Bi₂O₃复合后，块状Bi₂O₃均匀分散在花状微球的BiOI表面。

图 2 不同光催化材料的SEM图像

Figure 2. SEM images of different photocatalytic materials

下载: 全尺寸图片幻灯片

2.3 Bi₂O₃/BiOI复合光催化材料的结构

样品的FTIR图谱如图3所示。499 cm⁻¹和760 cm⁻¹处是BiOI的特征吸收峰，1617 cm⁻¹处的吸收峰对应Bi₂O₃中Bi—O键的弯曲振动，再次表明BiOI和Bi₂O₃成功复合在一起。

图 3 Bi₂O₃/BiOI复合光催化材料的FTIR图谱

Figure 3. FTIR spectra of Bi₂O₃/BiOI composite photocatalytic material

下载: 全尺寸图片幻灯片

2.4 Bi₂O₃/BiOI复合光催化材料的光学性能

利用UV-Vis DRS分析了所制备样品的光学吸收性能，如图4所示。可以看出，纯BiOI的吸收边缘位于681 nm处，纯Bi₂O₃的吸收边缘位于477 nm，Bi₂O₃/BiOI复合光催化材料的光吸收边缘位于617 nm。与纯BiOI相比，Bi₂O₃/BiOI复合光催化材料的光吸收边缘有轻微的蓝移，这是由于与Bi₂O₃耦合造成的，但其光吸收范围仍然很宽。

图 4 不同光催化材料的紫外漫反射图谱

Figure 4. UV-Vis DRS of different photocatalytic materials

下载: 全尺寸图片幻灯片

不同光催化材料的紫外漫反射(αhv)^1/2-hv转换图如图5所示。根据Kubelka-Munk公式，纯BiOI、Bi₂O₃和Bi₂O₃/BiOI对应的禁带宽度E_g值分别为1.82 eV、2.60 eV和2.01 eV。

图 5 不同光催化材料的禁带宽度

Figure 5. Band gaps of different photocatalytic materials

下载: 全尺寸图片幻灯片

2.5 Bi₂O₃/BiOI复合光催化材料光生电子空穴对的分离

利用荧光强度来分析光生电子空穴对的复合速率，荧光强度越小，则光生电子复合速率越低，图6为不同光催化材料的荧光光谱。可以看出，在520 nm处，Bi₂O₃/BiOI的荧光强度低于单一BiOI和Bi₂O₃，表明复合光催化材料的光生电子空穴对复合速率最低，光催化活性最高。

图 6 不同光催化材料的荧光光谱图

Figure 6. Fluorescence spectroscopy of different photocatalytic materials

下载: 全尺寸图片幻灯片

通过电化学阻抗法研究了不同光催化材料的电荷转移效率，结果如图7所示。Bi₂O₃/BiOI的圆弧半径小于单一BiOI和Bi₂O₃，说明其电荷转移电阻较低，电导率增强。电化学阻抗图表明Bi₂O₃/BiOI能增强光生电子空穴对的电荷转移能力，提高其分离效率，这与荧光分析的结果一致。

图 7 不同光催化材料的阻抗图

Figure 7. Impedance diagrams of different photocatalytic materials

下载: 全尺寸图片幻灯片

2.6 Bi₂O₃/BiOI复合光催化材料的性能

2.6.1 不同制备条件对光催化性能的影响

通过探究反应物的不同摩尔比、反应温度、反应时间及pH对所制备材料的光催化性能的影响。从图8(a)~8(d)可以看出：当Bi₂O₃与BiOI的摩尔比为0.8∶1时，在pH=5、180℃下反应20 h得到的Bi₂O₃/BiOI复合光催化材料对四环素的降解效果最佳，在3 h内对四环素的降解率可达75%。

图 8 不同摩尔比 (a)、反应温度 (b)、反应时间 (c) 及pH (d) 对Bi₂O₃/BiOI光催化材料性能的影响

Figure 8. Effects of different molar ratios (a), reaction temperature (b), reaction time (c) and pH (d) on the properties of Bi₂O₃/BiOI photocatalytic material

下载: 全尺寸图片幻灯片

2.6.2 光催化性能

通过在模拟太阳光照射下降解四环素来评价所制备样品的光催化性能，图9(a)为模拟太阳光照射下降解四环素的曲线图。在3 h内，BiOI、Bi₂O₃、Bi₂O₃/BiOI对四环素的降解率分别为55%、57%、75%。图9(b)为模拟太阳光照射下降解四环素的动力学曲线，Bi₂O₃/BiOI的动力学速率常数(0.007 min⁻¹)分别是BiOI(0.004 min⁻¹)、Bi₂O₃(0.0045 min⁻¹)的1.75倍、1.56倍。因此，所制备出的Bi₂O₃/BiOI具有较高的光催化活性。

图 9 模拟太阳光照射下不同光催化材料的降解曲线 (a) 及动力学曲线 (b)

Figure 9. Degradation curves (a) and kinetic curves (b) of different photocatalytic materials under simulated sunlight irradiation

下载: 全尺寸图片幻灯片

2.7 Bi₂O₃/BiOI复合光催化材料降解四环素的机制

使用对苯醌(BQ)、乙二胺四乙酸二钠盐(EDTA-2Na)、异丙醇(IPA)作为·O₂⁻、h⁺、·OH的捕捉剂，实验结果如图10所示。BiOI对四环素的降解率分别为50%、31%、53%、，由此可以得出h⁺是BiOI降解四环素的主要活性物质。Bi₂O₃对四环素的降解率分别为55%、52%、35%，由此可以得出·OH是Bi₂O₃降解四环素的主要活性物质。

图 10 捕捉BiOI (a)、Bi₂O₃(b)、Bi₂O₃/BiOI (c) 中活性物种的柱状图

Figure 10. Histogram of captured active species in BiOI (a), Bi₂O₃ (b), and Bi₂O₃/ BiOI (c)

下载: 全尺寸图片幻灯片

当Bi₂O₃和BiOI复合后形成Z型异质结时，Bi₂O₃/BiOI光催化材料对四环素的降解率分别为35%、66%、66%，由此可以得出·O₂⁻是光催化材料降解四环素的主要活性物质。

Bi₂O₃/BiOI异质结的形成可以提高光生电子空穴对的分离速率，从而提高光催化活性。BiOI 、Bi₂O₃的导带和价带可以通过下式计算：

${E_{{\rm{CB}}}} = X-{E^{\rm{e}}}-0.5{E_{\rm{g}}}$

${E_{\rm{g}}} = {E_{{\rm{VB}}}}-{E_{{\rm{CB}}}}$

式中：X为半导体的电负性，BiOI和Bi₂O₃的X值分别为5.94 eV 和6.23 eV；E^e为自由电子在氢标上的能量(约为4.50 eV)；E_g为对应的带隙能量，由图3(b)可以得出BiOI和Bi₂O₃的E_g值分别为1.82 eV和2.60 eV。因此，BiOI和Bi₂O₃的导带(CB)边缘分别位于0.53 eV和0.43 eV，BiOI和Bi₂O₃的价带(VB)边缘分别位于2.35 eV和3.03 eV。在可见光照射下所制备的Bi₂O₃/BiOI异质结被激发并生成光生载流子且BiOI比Bi₂O₃的CB更正。事实上，在Bi₂O₃/BiOI异质结中，光子能量会激发BiOI CB上的电子到更高的电位位置(−0.68 eV)，因此BiOI CB上的光生电子会转移到Bi₂O₃的CB上。同时，Bi₂O₃ VB上的空穴将转移到BiOI的VB上。而Bi₂O₃ CB上的电子不能与O₂反应生成·O₂⁻(O₂/·O₂⁻=−0.33 eV)，·O₂⁻是降解四环素的主要活性物质，这与捕获实验的结果不一致。结合以上结果，提出了一种更可能的光催化机制，如图11所示。BiOI和Bi₂O₃在可见光照射下都能产生光生电子空穴对，Bi₂O₃ CB上的光生电子和BiOI VB上的空穴在库仑力的作用下会重新组合。此外，BiOI的CB上的光生电子可以与O₂反应生成·O₂⁻，然后·O₂⁻与TC反应，有效地实现了Bi₂O₃/BiOI异质结的光催化降解过程。综上所述，Bi₂O₃/BiOI异质结能够有效提高光生电子空穴对的分离效率，从而显著提高光催化性能。

图 11 Bi₂O₃/BiOI复合光催化材料的降解机制

Figure 11. Degradation mechanism of Bi₂O₃/BiOI composite photocatalytic material

TC—Tetracycline; E_g—Band gap

下载: 全尺寸图片幻灯片

3. 结论

(1) 以五水硝酸铋为原料，采用溶剂热法制备了Bi₂O₃/BiOI复合光催化材料，在制备过程中加入Bi₂O₃可以提高单一BiOI的光催化性能，在3 h内对四环素的降解率为75%，是单一BiOI降解速率的1.75倍。

(2) BiOI、Bi₂O₃成功复合在一起并形成了异质结结构，Bi₂O₃/BiOI复合光催化材料通过提高光生电子空穴对的分离速率从而提高光催化活性。

(3) 降解机制研究表明，·O₂⁻在降解四环素中起主要作用，且所制得的复合材料可应用于对四环素的降解，并有望进一步用于对其他抗生素的降解处理以解决实际问题。

图 1 压缩试验加载装置(单位：mm)

Figure 1. Loading setup for compressive test (Unit: mm)

下载: 全尺寸图片幻灯片

图 2 不同应变率下HyF/RAC(C0和C3组)试件破坏形态

Figure 2. Failure modes of C0 and C3 specimens for HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 3 不同应变率下HyF/RAC(C0和C3组)试件应力-应变曲线

Figure 3. Stress-strain curve of C0 and C3 specimens for HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 4 不同应变率下HyF/RAC峰值应力 $\sigma^{\rm{p}}$

Figure 4. Peak stress $\sigma^{\rm{p}}$ of HyF/RAC at different strain rates

$\dot \varepsilon$ —Strain rate; ${\dot \varepsilon _{\text{s}}}$ —Quasi-static strain rate

下载: 全尺寸图片幻灯片

图 5 不同应变率下HyF/RAC峰值应力动态增长因子 $F^{{\sigma}^{\rm{p}}}_{\rm{D}}$

Figure 5. Dynamic increase factor $F^{{\sigma}^{\rm{p}}}_{\rm{D}}$ of peak stress of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 6 不同应变率下HyF/RAC峰值应变 $\varepsilon^{\rm{p}}$

Figure 6. Peak strain $\varepsilon^{\rm{p}}$ of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 7 不同应变率下HyF/RAC峰值应变动态增长因子 $F^{{\varepsilon}^{\rm{p}}}_{\rm{D}}$

Figure 7. Dynamic increase factor $F^{{\varepsilon}^{\rm{p}}}_{\rm{D}}$ of peak strain of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 8 不同应变率下HyF/RAC弹性模量 E

Figure 8. Elastic modulus E of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 9 不同应变率下HyF/RAC弹性模量动态增长因子 $F^E_{\rm{D}}$

Figure 9. Dynamic increase factor $F^E_{\rm{D}}$ of elastic modulus of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 10 不同应变率下HyF/RAC压缩韧性T

Figure 10. Compressive toughness T of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 11 不同应变率下HyF/RAC压缩韧性动态增长因子 $F^T_{\rm{D}}$

Figure 11. Dynamic increase factor $F^T_{\rm{D}}$ of compressive toughness of HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 12 HyF/RAC应力-应变曲线特征参数预测模型性能

SD—Standard deviation; Err—Mean relative error

Figure 12. Performance of prediction models for characteristic indices of HyF/RAC stress-strain curves

下载: 全尺寸图片幻灯片

图 13 不同应变率下HyF/RAC(C0组)试验曲线与各模型曲线对比

Figure 13. Comparison of experimental and theoretical stress-strain curves of C0 for HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 14 不同应变率下HyF/RAC(C3组)试验曲线与各模型曲线对比

Figure 14. Comparison of experimental and theoretical stress-strain curves of C3 for HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

图 15 不同应变率下HyF/RAC(C0和C3组)损伤演化

Figure 15. Damage evolution curves of C0 and C3 for HyF/RAC at different strain rates

下载: 全尺寸图片幻灯片

表 1 端钩钢纤维(HES)和塑钢纤维(MPP)属性

Table 1 Properties of hooked-end steel fiber (HES) and macro-polypropylene fiber (MPP)

Fiber type	Equivalent diameter/mm	Length/mm	Aspect ratio	Density/(kg·m⁻³)	Tensile strength/MPa	Young’s modulus/GPa
HES	0.75	35	47	7800	1120	200.0
MPP	0.94	28	30	910	580	5.5

下载: 导出CSV

表 2 钢-塑钢混杂纤维再生混凝土(HyF/RAC)配合比设计

Table 2 Designed mix proportions of hybrid fiber reinforced recycled aggregate concrete (HyF/RAC) kg/m³

Mix	Notation	Water	Cement	Sand	RCA	NCA	HES	MPP	AW
A0	NAC	251	467	639	0	1044	0	0.00	0
A1	1.5%HES/NAC	251	467	639	0	1044	117	0.00	0
A2	1.25%HES-0.25%MPP/NAC	251	467	639	0	1044	98	2.28	0
A3	1.0%HES-0.5%MPP/NAC	251	467	639	0	1044	78	4.55	0
A4	0.75%HES-0.75%MPP/NAC	251	467	639	0	1044	59	6.83	0
A5	0.5%HES-1.0%MPP/NAC	251	467	639	0	1044	39	9.10	0
B0	RAC(50%)	251	467	639	522	522	0	0.00	20
B1	1.5%HES/RAC(50%)	251	467	639	522	522	117	0.00	20
B2	1.25%HES-0.25%MPP/RAC(50%)	251	467	639	522	522	98	2.28	20
B3	1.0%HES-0.5%MPP/RAC(50%)	251	467	639	522	522	78	4.55	20
B4	0.75%HES-0.75%MPP/RAC(50%)	251	467	639	522	522	59	6.83	20
B5	0.5%HES-1.0%MPP/RAC(50%)	251	467	639	522	522	39	9.10	20
C0	RAC(100%)	251	467	639	1044	0	0	0.00	40
C1	1.5%HES/RAC(100%)	251	467	639	1044	0	117	0.00	40
C2	1.25%HES-0.25%MPP/RAC(100%)	251	467	639	1044	0	98	2.28	40
C3	1.0%HES-0.5%MPP/RAC(100%)	251	467	639	1044	0	78	4.55	40
C4	0.75%HES-0.75%MPP/RAC(100%)	251	467	639	1044	0	59	6.83	40
C5	0.5%HES-1.0%MPP/RAC(100%)	251	467	639	1044	0	39	9.10	40
Notes: NAC—Natural aggregate concrete; RAC—Recycled aggregate concrete; RCA—Recycled coarse aggregate; NCA—Natural coarse aggregate; AW—Absorbed water; In iHES-jMPP/RAC(k), i—Volume fraction of HES, j—Volume fraction of MPP, k—Replacement ratio by mass of RCA.

下载: 导出CSV

表 3 不同应变率下HyF/RAC峰值应力 ${\sigma ^{\text{p}}}$

Table 3 Results of peak stress ${\sigma ^{\text{p}}}$ of HyF/RAC at different strain rates

Mix	10⁻⁵ s⁻¹		10⁻⁴ s⁻¹		10⁻³ s⁻¹		5×10⁻³ s⁻¹
Mix	${\sigma ^{\text{p}}}$ /MPa	C_V/%	${\sigma ^{\text{p}}}$ /MPa	C_V/%	${\sigma ^{\text{p}}}$ /MPa	C_V/%	${\sigma ^{\text{p}}}$ /MPa	C_V/%
A0	31.3	1.58	32.4	2.84	33.7	3.15	34.7	0.00
A1	32.4	2.53	34.0	2.72	38.8	4.01	39.3	1.03
A2	32.9	4.31	36.3	0.98	39.1	1.27	40.1	5.14
A3	34.9	0.17	39.0	2.90	41.3	0.34	41.9	0.84
A4	31.5	3.59	32.8	5.40	35.2	4.22	36.9	4.41
A5	32.7	5.19	34.4	3.29	36.6	2.61	37.3	5.13
B0	28.3	1.00	29.1	3.87	32.4	1.46	34.0	2.29
B1	29.6	2.15	30.8	1.15	34.6	4.71	35.7	4.56
B2	31.9	1.30	33.6	5.27	34.2	3.93	36.1	3.73
B3	31.2	0.23	32.4	1.97	35.7	1.98	37.2	6.84
B4	30.4	1.51	32.3	1.99	35.3	3.13	36.1	0.78
B5	31.6	1.59	33.7	1.70	37.3	0.57	38.3	2.22
C0	24.6	8.57	26.9	2.74	30.6	4.48	32.5	0.22
C1	26.2	4.04	27.8	3.89	31.6	1.14	32.4	3.45
C2	26.8	2.24	28.8	0.72	32.2	2.64	32.8	1.72
C3	28.4	2.69	31.1	0.68	33.0	2.69	34.4	3.63
C4	27.8	0.95	30.0	6.21	32.7	2.60	33.1	5.32
C5	26.3	0.79	27.3	2.23	30.6	5.46	32.7	0.43
Note: C_V—Coefficients of variation.

下载: 导出CSV

表 4 不同应变率下HyF/RAC峰值应变 ${\varepsilon ^{\text{p}}}$

Table 4 Results of peak strain ${\varepsilon ^{\text{p}}}$ of HyF/RAC at different strain rates

Mix	10⁻⁵ s⁻¹		10⁻⁴ s⁻¹		10⁻³ s⁻¹		5×10⁻³ s⁻¹
Mix	${\varepsilon ^{\text{p}}}$ /10⁻³	C_V/%	${\varepsilon ^{\text{p}}}$ /10⁻³	C_V/%	${\varepsilon ^{\text{p}}}$ /10⁻³	C_V/%	${\varepsilon ^{\text{p}}}$ /10⁻³	C_V/%
A0	2.376	4.73	2.330	8.37	2.224	1.67	2.101	9.02
A1	2.410	2.87	2.340	7.71	2.256	10.77	2.199	11.43
A2	2.413	1.55	2.390	0.74	2.378	11.52	2.321	6.02
A3	2.599	8.68	2.555	3.18	2.528	3.98	2.500	3.42
A4	2.419	2.70	2.425	6.95	2.413	10.11	2.312	11.72
A5	2.443	6.27	2.432	8.62	2.330	6.22	2.254	1.68
B0	2.593	3.67	2.469	0.79	2.370	3.18	2.325	6.08
B1	2.651	9.27	2.631	6.65	2.620	6.75	2.510	6.20
B2	2.673	3.61	2.645	9.62	2.592	5.28	2.481	9.76
B3	2.760	5.68	2.708	7.48	2.631	7.32	2.610	5.55
B4	2.583	0.39	2.544	2.43	2.544	7.28	2.533	8.45
B5	2.666	2.41	2.658	6.79	2.630	4.84	2.591	2.11
C0	2.814	4.46	2.726	3.44	2.621	2.51	2.524	2.73
C1	2.933	1.81	2.815	11.43	2.708	5.28	2.694	0.33
C2	2.950	1.47	2.813	1.33	2.769	2.75	2.733	2.20
C3	2.941	1.62	2.853	0.99	2.845	6.83	2.648	3.47
C4	3.041	3.67	2.996	4.01	2.891	0.79	2.861	9.33
C5	2.981	3.50	2.859	1.67	2.754	7.66	2.701	0.46

下载: 导出CSV

表 5 不同应变率下HyF/RAC弹性模量E

Table 5 Results of elastic modulus E of HyF/RAC at different strain rates

Mix	10⁻⁵s⁻¹		10⁻⁴s⁻¹		10⁻³s⁻¹		5×10⁻³s⁻¹
Mix	E/GPa	C_V/%	E/GPa	C_V/%	E/GPa	C_V/%	E/GPa	C_V/%
A0	29.5	3.86	33.2	9.20	37.6	9.87	41.2	2.37
A1	31.8	8.13	35.3	1.34	38.6	3.95	42.0	9.60
A2	32.1	7.05	34.3	1.09	38.3	4.35	41.4	4.92
A3	34.1	7.30	34.1	2.88	34.7	0.61	38.1	10.65
A4	32.5	7.19	33.7	5.58	35.7	4.14	37.4	11.49
A5	33.9	4.75	34.0	5.06	35.0	3.23	38.2	2.85
B0	24.8	7.61	26.2	8.55	28.6	3.24	30.8	2.69
B1	25.6	9.08	26.2	0.91	28.6	5.58	30.8	9.23
B2	27.1	0.22	28.1	11.70	29.4	8.73	33.9	8.52
B3	27.3	0.70	28.7	9.85	31.0	6.90	31.7	1.92
B4	28.2	1.65	29.9	3.60	33.2	0.66	33.6	6.38
B5	27.2	4.70	27.8	11.33	28.9	9.67	32.9	11.19
C0	18.7	3.06	21.9	11.63	24.9	6.18	26.7	9.24
C1	20.7	8.05	22.8	11.44	26.3	11.54	27.8	7.55
C2	23.2	7.56	24.3	2.31	26.1	1.54	29.5	10.99
C3	25.1	6.06	26.3	4.08	28.0	11.09	28.1	2.47
C4	22.9	0.56	23.3	2.43	25.2	4.69	28.3	9.75
C5	22.7	0.56	24.4	9.26	27.9	3.17	29.2	9.11

下载: 导出CSV

表 6 不同应变率下HyF/RAC压缩韧性T

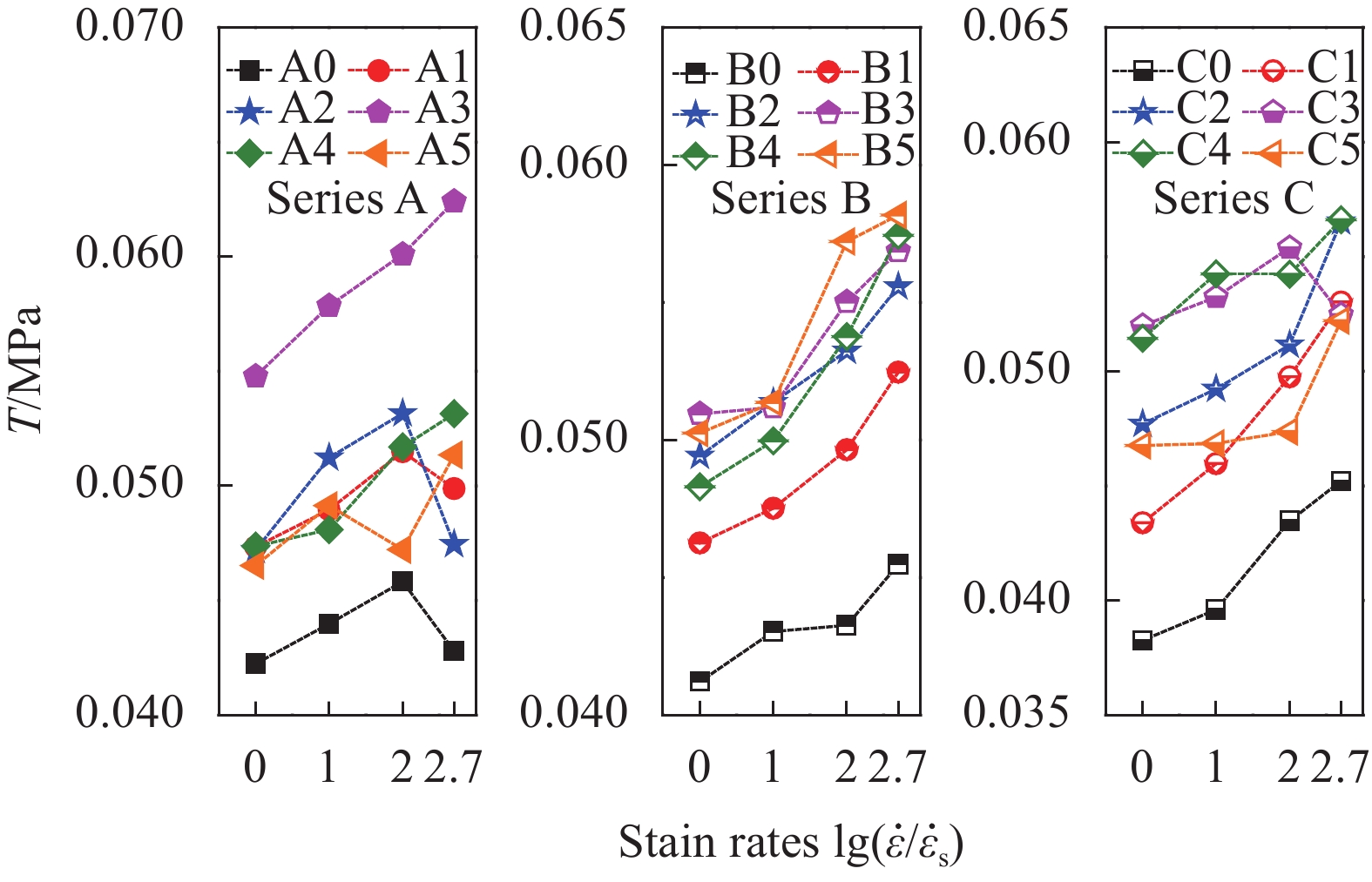
Table 6 Results of compressive toughness T of HyF/RAC at different strain rates

Mix	10⁻⁵ s⁻¹	10⁻⁴ s⁻¹	10⁻³ s⁻¹	5×10⁻³ s⁻¹
Mix	T/MPa	T/MPa	T/MPa	T/MPa
A0	0.042	0.044	0.046	0.043
A1	0.047	0.049	0.051	0.050
A2	0.047	0.051	0.053	0.047
A3	0.055	0.058	0.060	0.062
A4	0.047	0.048	0.052	0.053
A5	0.047	0.049	0.047	0.051
B0	0.041	0.043	0.043	0.045
B1	0.046	0.048	0.050	0.052
B2	0.049	0.051	0.053	0.056
B3	0.051	0.051	0.055	0.057
B4	0.048	0.050	0.054	0.057
B5	0.050	0.051	0.057	0.058
C0	0.038	0.040	0.043	0.045
C1	0.043	0.046	0.050	0.053
C2	0.048	0.049	0.051	0.057
C3	0.052	0.053	0.055	0.052
C4	0.051	0.054	0.054	0.057
C5	0.047	0.047	0.047	0.052

下载: 导出CSV

表 7 现有压缩动态本构模型

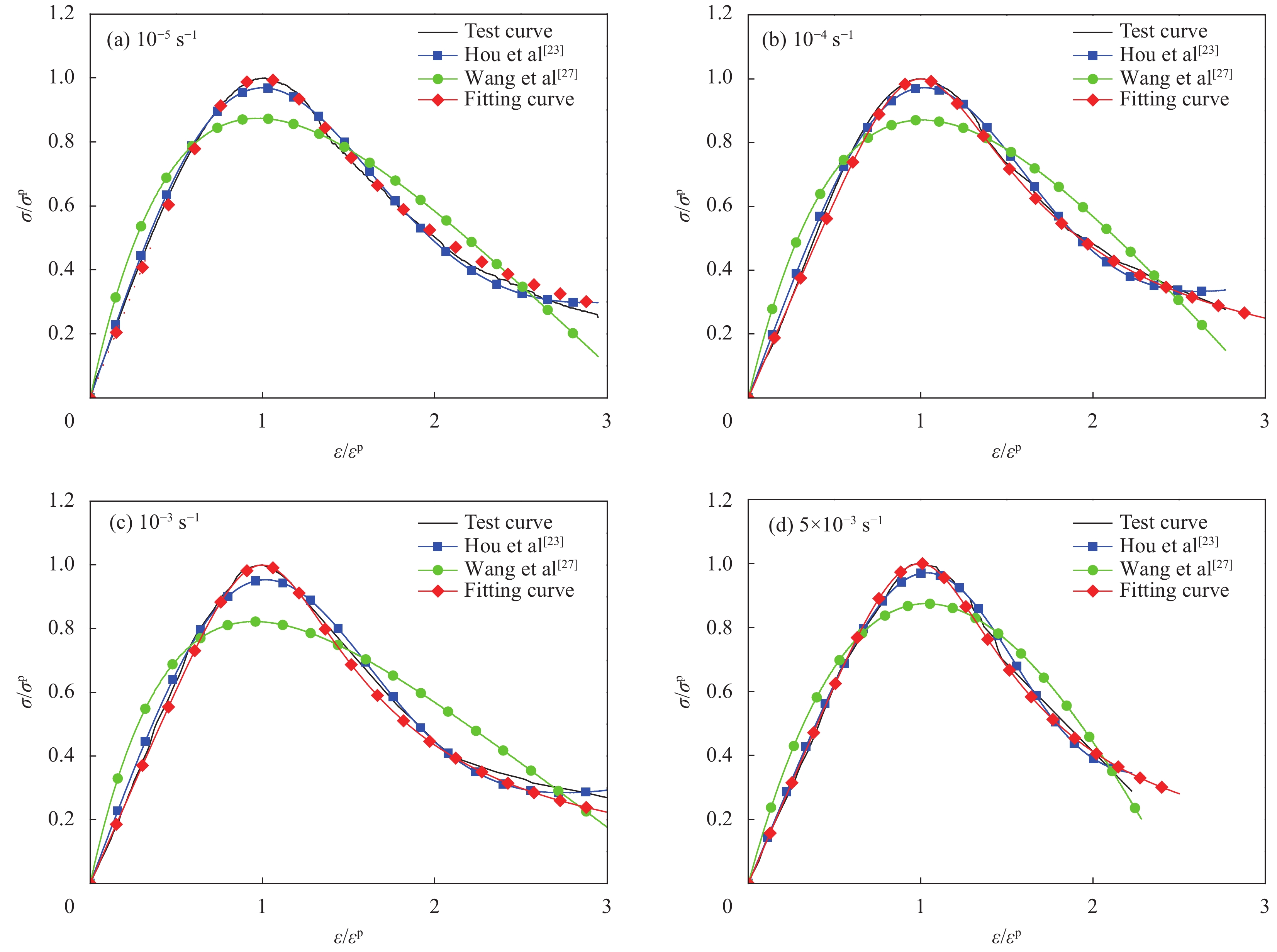
Table 7 Review of dynamic constitutive models under compression

Reference	Model	Parameter	Application range
Ibrahim et al^[21]	$\begin{gathered} y = \frac{{Ax + \left( {B - 1} \right){x^2}}}{{1 + \left( {A - 2} \right)x + B{x^2}}} \\ A\left( {A - 2} \right) - B + 1 \geqslant 0 \\ A + B > 1 \\ \end{gathered}$	$\begin{gathered} A = 3.6\exp \left( {9.0 \times {{10}^{ - 8}}\left( {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{\text{s}}}}}} \right)\left( {1 + 0.01R_V^{0.82}} \right)} \right) \\ B = 0.22\exp \left( {3.8 \times {{10}^{ - 7}}\left( {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_{\text{s}}}}}} \right)\left( {1 + 0.002R_V^{0.82}} \right)} \right) \\ \end{gathered}$	$\begin{gathered} 25{\text{ }}{{\text{s}}^{ - 1}} \leqslant \dot \varepsilon \leqslant 125{\text{ }}{{\text{s}}^{ - 1}} \\ 1.2{\text{% }} \leqslant V \leqslant 1.4\% \\ \end{gathered}$
Zhou et al^[22]	$\begin{gathered} \sigma = {\sigma _{\text{m}}}\left( {1 - D} \right) = E\varepsilon \left( {1 - D} \right) \\ D = 1 - \exp \left[ { - {{\left( {\frac{\varepsilon }{{{F_0}}}} \right)}^m}} \right] \\ \end{gathered}$	$\begin{gathered} {F_0} = 3.3578\ln \dot \varepsilon - 10.6562 \\ m = 1.2804\ln \dot \varepsilon - 1.8711 \\ \end{gathered}$	$19.8{\text{ }}{{\text{s}}^{ - 1}} \leqslant \dot \varepsilon \leqslant 281{\text{ }}{{\text{s}}^{ - 1}}$
Hou et al^[23]	$\begin{gathered} \sigma = {\sigma _{\text{m}}}\left( {1 - {C_{\text{n}}}D} \right) = E\varepsilon \left( {1 - {C_{\text{n}}}D} \right) \\ D = 1 - \exp \left[ { - {{\left( {\frac{\varepsilon }{{{F_0}}}} \right)}^m}} \right] \\ \end{gathered}$	$\begin{gathered} {F_0} = 0.0062 + 0.31{V^{1.7}} - 0.00167\left( {0.1 + V} \right)\ln \dot \varepsilon \\ m = - 0.56 + 3V + \left( {0.35 - 2V} \right)\ln \dot \varepsilon \\ {C_{\text{n}}} = 0.977 - 1.4V + \left( {0.004 + 0.25V} \right)\ln \dot \varepsilon \\ \end{gathered}$	$\begin{gathered} \dot \varepsilon \leqslant 294{\text{ }}{{\text{s}}^{ - 1}} \\ V \leqslant 5\% \\ \end{gathered}$
Sun et al^[25]	$\begin{gathered} \sigma = {\sigma _{\text{m}}}\left( {1 - D} \right) = E\varepsilon \left( {1 - D} \right) \\ \dot D = AD\left( {1 - D} \right) \\ \end{gathered}$	$\begin{gathered} {D} = 0.35 - 8.2 \times {10^{ - 9} }\left( {\frac{ {\dot \varepsilon } }{ { { {\dot \varepsilon }_{\text{s} } } } } } \right) - \\ \qquad 4.4V + 1.3 \times {10^{ - 7} }\left( {\frac{ {\dot \varepsilon } }{ { { {\dot \varepsilon }_{\text{s} } } } } } \right)V \\ A = 234 + 1.3 \times {10^{ - 7} }\left( {\frac{ {\dot \varepsilon } }{ { { {\dot \varepsilon }_{\text{s} } } } } } \right) + \\ \qquad 1718V - 8.6 \times {10^{ - 5} }\left( {\frac{ {\dot \varepsilon } }{ { { {\dot \varepsilon }_{\text{s} } } } } } \right)V \\ \end{gathered}$	$\begin{gathered} 53{\text{ }}{{\text{s}}^{ - 1}} \leqslant \dot \varepsilon \leqslant 152{{\text{s}}^{ - 1}} \\ V \leqslant 6.0\% \\ \end{gathered}$
Zhang et al^[26]	$\begin{gathered} \sigma = \left( {1 - D} \right){\sigma _{\text{m}}} \\ {\sigma _{\text{m}}} = {\sigma _{\text{e}}}\left( \varepsilon \right) + {E_1}\int_0^t {\dot \varepsilon \exp \left( { - \frac{{t - \tau }}{{{\varphi _1}}}} \right){\rm{d}}\tau } + \\ \qquad {E_2}\int_0^t {\dot \varepsilon \exp \left( { - \frac{{t - \tau }}{{{\varphi _2}}}} \right){\rm{d}}\tau } \\ {\sigma _{\text{e}}}\left( \varepsilon \right) = E\varepsilon + \alpha {\varepsilon ^2} + \beta {\varepsilon ^3} \\ D = \left\{ \begin{gathered} 0{\text{ }}\qquad(\varepsilon \leqslant {\varepsilon ^{{\text{th}}}}) \\ 1 - \exp \left[ { - {{\left( {\frac{{\varepsilon - {\varepsilon ^{{\text{th}}}}}}{{{F_0}}}} \right)}^m}} \right]{\text{ }}\qquad(\varepsilon > {\varepsilon ^{{\text{th}}}}) \\ \end{gathered} \right. \\ \end{gathered}$	No fitting equation	$\begin{gathered} 27{\text{ }}{{\text{s}}^{ - 1}} \leqslant \dot \varepsilon \leqslant 94{\text{ }}{{\text{s}}^{ - 1}} \\ V \leqslant 0.2\% \\ \end{gathered}$
Wang et al^[27]	$\begin{gathered} \sigma = \left( {1 - D} \right)\sigma \\ {\sigma _{\text{m}}} = {\sigma _{\text{e}}}\left( \varepsilon \right) + {E_1}\int_0^t {\dot \varepsilon \exp \left( { - \frac{{t - \tau }}{{{\varphi _1}}}} \right){\rm{d}}\tau } + \\ \qquad {E_2}\int_0^t {\dot \varepsilon \exp \left( { - \frac{{t - \tau }}{{{\varphi _2}}}} \right){\rm{d}}\tau } \\ D = \left\{ \begin{gathered} 0{\text{ }}\qquad(\varepsilon \leqslant {\varepsilon ^{{\text{th}}}} ) \\ {K_D}{{\dot \varepsilon }^{\lambda - 1}}{\left( {\varepsilon - {\varepsilon ^{{\text{th}}}}} \right)^\kappa }{\text{ }}\qquad(\varepsilon > {\varepsilon ^{{\text{th}}}} ) \\ \end{gathered} \right. \\ \end{gathered}$	No fitting equation	${10^{ - 4}}{\text{ }}{{\text{s}}^{ - 1}} \leqslant \dot \varepsilon \leqslant {10^3}{\text{ }}{{\text{s}}^{ - 1}}$
Notes: $y = {\sigma \mathord{\left/ {\vphantom {\sigma { {\sigma ^{\text{p} } } } } } \right. } { {\sigma ^{\text{p} } } }}, x = {\varepsilon \mathord{\left/ {\vphantom {\varepsilon { {\varepsilon ^{\text{p} } } } } } \right. } { {\varepsilon ^{\text{p} } } }}$ , $\sigma$ —Stress, ${\sigma ^{\text{p}}}$ —Peak stress, $\varepsilon$ —Strain, ${\varepsilon ^{\text{p}}}$ —Peak strain; R_V—Reinforcing index of hybrid fibers; D—Damage parameter; t—Loading time; τ—Delay time of stress; E₁, ${\varphi _1}$ —Elastic modulus and relaxation time at a low strain rate and frequency; E₂, ${\varphi _2}$ —Elastic modulus and relaxation time at a high strain rate and frequency; α, β—Elastic constant; ${K_D},{\text{ }}\lambda ,{\text{ }}\kappa$ —Material parameter; ${\varepsilon ^{{\text{th}}}}$ —Strain threshold.

下载: 导出CSV

表 8 HyF/RAC修正模型参数 $\alpha$ 拟合值

Table 8 Fitted results of parameter $\alpha$ in modified constitutive models for HyF/RAC

Mix	$\dot \varepsilon$
	10⁻⁵s⁻¹		10⁻⁴s⁻¹		10⁻³s⁻¹		5×10⁻³s⁻¹
	Fitted value	R²	Fitted value	R²	Fitted value	R²	Fitted value	R²
A0	3.434	0.991	3.399	0.946	2.597	0.953	2.285	0.940
A1	1.882	0.978	1.175	0.998	1.699	0.986	1.352	0.973
A2	1.386	0.999	1.401	0.997	1.020	0.981	1.039	0.994
A3	1.442	0.997	1.912	0.992	1.607	0.965	1.650	0.974
A4	2.219	0.994	2.431	0.970	2.057	0.965	1.466	0.984
A5	2.600	0.998	2.633	0.984	2.288	0.971	1.757	0.992
B0	3.524	0.991	3.742	0.994	2.589	0.942	3.053	0.997
B1	1.440	0.976	1.125	0.983	1.225	0.997	1.873	0.996
B2	1.932	0.985	2.124	0.991	2.001	0.996	1.583	0.979
B3	2.026	0.994	1.636	0.999	2.274	0.988	2.297	0.984
B4	1.876	0.990	2.683	0.992	2.305	0.994	2.613	0.935
B5	2.457	0.994	3.036	0.997	2.873	0.940	2.496	0.984
C0	3.173	0.978	2.958	0.978	3.609	0.986	4.137	0.954
C1	1.552	0.993	1.657	0.976	2.280	0.976	2.749	0.993
C2	1.673	0.975	2.013	0.999	2.259	0.999	2.364	0.953
C3	2.059	0.998	2.149	0.999	2.278	0.998	2.732	0.996
C4	1.868	0.976	2.174	0.997	3.339	0.968	2.842	0.934
C5	2.218	0.971	2.859	0.990	3.483	0.964	3.394	0.993

下载: 导出CSV

参考文献(35)

[1]	高光发. 混凝土材料动态压缩强度的应变率强化规律[J]. 高压物理学报, 2017, 31(3):261-270. GAO Guangfa. Effect of strain-rate hardening on dynamic compressive strength of plain concrete[J]. Chinese Jour-nal of High Pressure Physics,2017,31(3):261-270(in Chinese).
[2]	王国盛, 路德春, 杜修力, 等. 混凝土材料真实动态强度及率效应机理研究[J]. 工程力学, 2018, 35(6):58-67. WANG Guosheng, LU Dechun, DU Xiuli, et al. Research on the actual dynamic strength and the rate effect mecha-nisms for concrete materials[J]. Engineering Mechanics,2018,35(6):58-67(in Chinese).
[3]	艾思平, 唐鹏. 考虑地震量级作用下橡胶纤维混凝土受压动力性能试验研究[J]. 建筑材料学报, 2021, 24(5): 1002-1010. AI Siping, TANG Peng. Experimental study on the dynamic behavior of rubber fiber reinforced concrete under the action of earthquake magnitude[J]. Journal of Building Material, 2021, 24(5): 1002-1010(in Chinese).
[4]	白卫峰, 李思蕾, 管俊峰, 等. 再生混凝土单轴压缩动态力学性能试验研究[J]. 建筑材料学报, 2022, 25(5): 498-508. BAI Weifeng, LI Silei, GUAN Junfeng, et al. Study on dynamic mechanical properties of recycled concrete under uniaxial compression[J]. Journal of Building Materials,2022, 25(5): 498-508(in Chinese).
[5]	XIAO J, ZHANG K, ZHANG Q. Strain rate effect on compres-sive stress-strain curves of recycled aggregate concrete with seawater and sea sand[J]. Construction and Building Materials,2021,300:124014. DOI: 10.1016/j.conbuildmat.2021.124014
[6]	董海龙, 彭有开, 骆开静, 等. 粗骨料取代下的高性能再生混凝土率敏性研究[J]. 实验力学, 2019, 34(2):249-257. DONG Hailong, PENG Youkai, LUO Kaijing, et al. Study on rate sensitivity of high performance recycled concrete with different coarse aggregate replacement ratios[J]. Journal of Experimental Mechanics,2019,34(2):249-257(in Chinese).
[7]	TANG Z, LI W, TAM V W Y, et al. Investigation on dynamic mechanical properties of fly ash/slag-based geopolymeric recycled aggregate concrete[J]. Composites Part B: Engi-neering,2020,185:107776. DOI: 10.1016/j.compositesb.2020.107776
[8]	FENG J, YIN G, TUO H, et al. Parameter optimization and regression analysis for multi-index of hybrid fiber-reinforced recycled coarse aggregate concrete using orthogonal experimental design[J]. Construction and Building Materials,2021,267:121013. DOI: 10.1016/j.conbuildmat.2020.121013
[9]	陈宇良, 吉云鹏, 陈宗平, 等. 钢纤维再生混凝土三轴受压力学性能试验[J]. 复合材料学报, 2022, 39(8): 4005-4016. CHEN Yuliang, JI Yunpeng, CHEN Zongping, et al. Experiment on mechanical properties of steel fiber recycled aggregate concrete under triaxial compression[J]. Acta Materiae Compositae Sinica, 2022, 39(8): 4005-4016(in Chinese).
[10]	丁亚红, 郭书奇, 张向冈, 等. 玄武岩纤维对再生混凝土抗碳化性能的影响[J]. 复合材料学报, 2022, 39(3): 1228-1238. DING Yahong, GUO Shuqi, ZHANG Xianggang, et al. Influence of basalt fiber on the anti-carbonation performance of recycled aggregate concrete[J]. Acta Materiae Compositae Sinica, 2022, 39(3): 1228-1238(in Chinese).
[11]	XIE J, KOU S, MA H, et al. Advances on properties of fiber reinforced recycled aggregate concrete: Experiments and models[J]. Construction and Building Materials,2021,277:122345. DOI: 10.1016/j.conbuildmat.2021.122345
[12]	王兴国, 姜茂林, 陈旭, 等. 不同预浸骨料-PVA纤维对再生混凝土力学性能影响[J]. 复合材料学报, 2022, 39(3): 1205-1214. WANG Xingguo, JIANG Maolin, CHEN Xu, et al. Effect of different pre-soaked aggregate-PVA fiber on the mechani-cal properties of recycled aggregate concrete[J]. Acta Materiae Compositae Sinica, 2022, 39(3): 1205-1214(in Chinese).
[13]	孔祥清, 何文昌, 周聪, 等. 混杂掺入钢/聚丙烯纤维再生混凝土力学性能及抗冲击性能试验研究[J]. 建筑科学, 2020, 36(3):94-99. KONG Xiangqing, HE Wenchang, ZHOU Cong, et al. Experimental investigation on the mechanical properties and impact resistance of steel and polypropylene hybrid fiber reinforced recycled aggregates concrete[J]. Building Science,2020,36(3):94-99(in Chinese).
[14]	FENG J, YIN G, TUO H, et al. Uniaxial compressive behavior of hook-end steel and macro-polypropylene hybrid fibers reinforced recycled aggregate concrete[J]. Construction and Building Materials,2021,304:124559. DOI: 10.1016/j.conbuildmat.2021.124559
[15]	周宏宇, 麻全周, 赵晓花, 等. 考虑应变率效应的混凝土材料单轴压缩特性尺寸效应研究[J]. 混凝土, 2021(1):61-65, 69. DOI: 10.3969/j.issn.1002-3550.2021.01.015 ZHOU Hongyu, MA Quanzhou, ZHAO Xiaohua, et al. Experimental study on dynamic rate relevance of concrete size effect[J]. Concrete,2021(1):61-65, 69(in Chinese). DOI: 10.3969/j.issn.1002-3550.2021.01.015
[16]	肖诗云, 张剑. 不同应变率下混凝土受压损伤试验研究[J]. 土木工程学报, 2010, 43(3):40-45. XIAO Shiyun, ZHANG Jian. Compressive damage experiment of concrete at different strain rates[J]. China Civil Engineering Journal,2010,43(3):40-45(in Chinese).
[17]	焦楚杰, 孙伟, 张亚梅, 等. 钢纤维高强混凝土在不同应变率时的单轴受压性能[J]. 建筑结构, 2004, 34(8):65-67. JIAO Chujie, SUN Wei, ZHANG Yamei, et al. Mechanical properties of SFRHSC under uniaxial compression with different strain rates[J]. Building Structure,2004,34(8):65-67(in Chinese).
[18]	梁宁慧, 杨鹏, 刘新荣, 等. 高应变率下多尺寸聚丙烯纤维混凝土动态压缩力学性能研究[J]. 材料导报, 2018, 32(2):288-294. LIANG Ninghui, YANG Peng, LIU Xinrong, et al. A study on dynamic compressive mechanical properties of multi-size polypropylene fiber concrete under high strain rate[J]. Materials Reports,2018,32(2):288-294(in Chinese).
[19]	沈才华, 钱晋, 陈晓峰, 等. 纤维掺量对PVA纤维混凝土力学参数的影响及压缩韧性指标的计算方法[J]. 硅酸盐通报, 2020, 39(10):3152-3160. SHEN Caihua, QIAN Jin, CHEN Xiaofeng, et al. Influence of fiber content on mechanical parameters of PVA fiber concrete and method for calculating compression toughness index[J]. Bulletin of the Chinese Ceramic Society,2020,39(10):3152-3160(in Chinese).
[20]	HE W, KONG X, FU Y, et al. Experimental investigation on the mechanical properties and microstructure of hybrid fiber reinforced recycled aggregate concrete[J]. Construction and Building Materials,2020,261:120488. DOI: 10.1016/j.conbuildmat.2020.120488
[21]	IBRAHIM S M, ALMUSALLAM T H, AL-SALLOUM Y A, et al. Strain rate dependent behavior and modeling for compression response of hybrid fiber reinforced concrete[J]. Latin American Journal of Solids and Structures,2016,13:1695-1715. DOI: 10.1590/1679-78252717
[22]	ZHOU J, CHEN X. Stress-strain behavior and statistical continuous damage model of cement mortar under high strain rates[J]. Journal of Materials in Civil Engineering,2013,25(1):120-130. DOI: 10.1061/(ASCE)MT.1943-5533.0000570
[23]	HOU X, CAO S, RONG Q, et al. Effects of steel fiber and strain rate on the dynamic compressive stress-strain relationship in reactive powder concrete[J]. Construction and Building Materials,2018,170:570-581. DOI: 10.1016/j.conbuildmat.2018.03.101
[24]	CUI T, HE H, YAN W, et al. Compression damage constitutive model of hybrid fiber reinforced concrete and its experimental verification[J]. Construction and Building Materials,2020,264:120026. DOI: 10.1016/j.conbuildmat.2020.120026
[25]	SUN X, ZHAO K, LI Y, et al. A study of strain-rate effect and fiber reinforcement effect on dynamic behavior of steel fiber-reinforced concrete[J]. Construction and Building Materials,2018,158:657-669. DOI: 10.1016/j.conbuildmat.2017.09.093
[26]	ZHANG H, WANG B, XIE A, et al. Experimental study on dynamic mechanical properties and constitutive model of basalt fiber reinforced concrete[J]. Construction and Building Materials,2017,152:154-167. DOI: 10.1016/j.conbuildmat.2017.06.177
[27]	王礼立, 胡时胜, 杨黎明, 等. 聊聊动态强度和损伤演化[J]. 爆炸与冲击, 2017, 37(2):169-179. WANG Lili, HU Shisheng, YANG Liming, et al. Talk about dynamic strength and damage evolution[J]. Explosion and Shock Waves,2017,37(2):169-179(in Chinese).
[28]	CAO S, HOU X, RONG Q. Dynamic compressive properties of reactive powder concrete at high temperature: A review[J]. Cement and Concrete Composites,2020,110:103568. DOI: 10.1016/j.cemconcomp.2020.103568
[29]	中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB/T 50010—2010[S]. 北京: 中国建筑工业出版社, 2015. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of concrete structures: GB/T 50010—2010[J]. Beijing: China Architecture and Building Press, 2015(in Chinese).
[30]	张聪, 余志辉, 韩世诚, 等. 混杂纤维增强应变硬化水泥基复合材料的压缩本构关系[J]. 复合材料学报, 2020, 37(5):1221-1226. ZHANG Cong, YU Zhihui, HAN Shicheng, et al. Compression constitutive relation of hybrid fiber reinforced strain hardening cementitous composites[J]. Acta Materiae Compositae Sinica,2020,37(5):1221-1226(in Chinese).
[31]	SHI X, PARK P, REW Y, et al. Constitutive behaviors of steel fiber reinforced concrete under uniaxial compression and tension[J]. Construction and Building Materials,2020,233:117316. DOI: 10.1016/j.conbuildmat.2019.117316
[32]	ABADEL A, ABBAS H, ALMUSALLAM T, et al. Mechanical properties of hybrid fibre-reinforced concrete-analytical modelling and experimental behaviour[J]. Magazine of Concrete Research,2016,68:823-843. DOI: 10.1680/jmacr.15.00276
[33]	施林林, 宋玉普, 沈璐. 不同应变率下大骨料及湿筛混凝土单轴受压试验研究[J]. 世界地震工程, 2016, 32(2):270-276. SHI Linlin, SONG Yupu, SHEN Lu. Experimental study on uniaxial compression properties of large aggregate and wet-screened concrete at different strain rates[J]. World Earthquake Engineering,2016,32(2):270-276(in Chinese).
[34]	李庆斌, 邓宗才, 张立翔. 考虑初始弹模变化的混凝土动力损伤本构模型[J]. 清华大学学报(自然科学版), 2003(8):1088-1091. DOI: 10.3321/j.issn:1000-0054.2003.08.025 LI Qingbin, DENG Zongcai, ZHANG Lixiang. Dynamic damage constitutive model for concrete accounting for the difference of the initial elastic modulus[J]. Journal of Tsinghua University (Science and Technology),2003(8):1088-1091(in Chinese). DOI: 10.3321/j.issn:1000-0054.2003.08.025
[35]	DONG S, HAN B, YU X, et al. Dynamic impact behaviors and constitutive model of super-fine stainless wire reinforced reactive powder concrete[J]. Construction and Building Materials,2018,184:602-616. DOI: 10.1016/j.conbuildmat.2018.07.027

施引文献(16)

期刊类型引用(8)

1.	谭浩，张文彬，卢文玉，祁志强，蔡红珍，杨科研. 高粱秸秆负载HKUST-1对四环素的吸附行为与机制. 复合材料学报. 2025(01): 514-526 . 本站查看
2.	李碧秋，李希成，熊俊夫，李金韩，贾博雅，汪长征. 铋系光电催化剂降解水中有机污染物的研究进展. 材料工程. 2024(06): 92-108 . 百度学术
3.	黄鹏伟，李静，林博，王宜民，陈仪，谢楠耿. AgI/BiOI异质结光电催化甲醇氧化. 山西化工. 2024(07): 4-6+10 . 百度学术
4.	杜书雅，王旭东，董永浩，吕嘉辰，李洁. MOF-808/AgBr的制备及光催化降解盐酸四环素性能研究. 功能材料. 2024(11): 11137-11146 . 百度学术
5.	严惠儒，林水源，钟祥康，黄学帅，杨玉如，冯梓盈，朱淼，谢伟. Au/BiOI花状微米球的制备及其对抗生素的降解特性. 广州化工. 2023(05): 43-46 . 百度学术
6.	王振宇，刘燕才，陈琨，乔江浩，李晓伟. 等离子喷涂-化学气相沉积制备α/β-Bi_2O_3薄膜的相结构调控和光催化降解性能. 硅酸盐学报. 2023(07): 1800-1810 . 百度学术
7.	刘松林，王仲民，钱熹，王童，冉兆晋，黄志民，吴晨曦，李桂银. 磁性氮掺杂石墨烯改性柿单宁复合材料对四环素的吸附行为. 复合材料学报. 2023(07): 4048-4059 . 本站查看
8.	袁亦雷，谢水波，刘岳林，史艳丹，刘迎九. g-C_3N_4-Bi_2O_3/Al_2O_3复合材料光催化还原水中U(Ⅵ). 化工环保. 2022(05): 609-615 . 百度学术

其他类型引用(8)

资源附件(0)

长摘要

创新点

图(15) / 表(8)

计量

文章访问数:
HTML全文浏览量:
PDF下载量:
被引次数: 16

1. 实验材料和方法
1.1 原材料
1.2 实验仪器
1.3 实验内容
1.3.1 BiOI光催化材料的制备
1.3.2 Bi2O3光催化材料的制备
1.3.3 Bi2O3/BiOI复合光催化材料的制备
1.3.4 光催化性能测试
2. 结果与讨论
2.1 Bi2O3/BiOI复合光催化材料的晶相结构
2.2 Bi2O3/BiOI复合光催化材料的微观形貌
2.3 Bi2O3/BiOI复合光催化材料的结构
2.4 Bi2O3/BiOI复合光催化材料的光学性能
2.5 Bi2O3/BiOI复合光催化材料光生电子空穴对的分离
2.6 Bi2O3/BiOI复合光催化材料的性能
2.6.1 不同制备条件对光催化性能的影响
2.6.2 光催化性能
2.7 Bi2O3/BiOI复合光催化材料降解四环素的机制
3. 结论

1. 实验材料和方法
1.1 原材料
1.2 实验仪器
1.3 实验内容
1.3.1 BiOI光催化材料的制备
1.3.2 Bi₂O₃光催化材料的制备
1.3.3 Bi₂O₃/BiOI复合光催化材料的制备
1.3.4 光催化性能测试
2. 结果与讨论
2.1 Bi₂O₃/BiOI复合光催化材料的晶相结构
2.2 Bi₂O₃/BiOI复合光催化材料的微观形貌
2.3 Bi₂O₃/BiOI复合光催化材料的结构
2.4 Bi₂O₃/BiOI复合光催化材料的光学性能
2.5 Bi₂O₃/BiOI复合光催化材料光生电子空穴对的分离
2.6 Bi₂O₃/BiOI复合光催化材料的性能
2.6.1 不同制备条件对光催化性能的影响
2.6.2 光催化性能
2.7 Bi₂O₃/BiOI复合光催化材料降解四环素的机制
3. 结论

参考文献(35)

施引文献(16)

资源附件(0)

长摘要

创新点

钢-塑钢混杂纤维再生混凝土单轴压缩动态力学性能试验

通讯作者: 尹冠生，博士，教授，博士生导师，研究方向为混凝土结构 E-mail: yings@chd.edu.cn

计量

出版历程

Experiment on dynamic mechanical properties of steel and macro-polypropylene hybrid fibers reinforced recycled aggregate concrete under uniaxial compression

1. 实验材料和方法

1.1 原材料

1.2 实验仪器

1.3 实验内容

1.3.1 BiOI光催化材料的制备

1.3.2 Bi2O3光催化材料的制备

1.3.3 Bi2O3/BiOI复合光催化材料的制备

1.3.4 光催化性能测试

2. 结果与讨论

2.1 Bi2O3/BiOI复合光催化材料的晶相结构

2.2 Bi2O3/BiOI复合光催化材料的微观形貌

2.3 Bi2O3/BiOI复合光催化材料的结构

2.4 Bi2O3/BiOI复合光催化材料的光学性能

2.5 Bi2O3/BiOI复合光催化材料光生电子空穴对的分离

2.6 Bi2O3/BiOI复合光催化材料的性能

2.6.1 不同制备条件对光催化性能的影响

2.6.2 光催化性能

2.7 Bi2O3/BiOI复合光催化材料降解四环素的机制

3. 结 论

期刊类型引用(8)

其他类型引用(8)

计量

出版历程

目录

1. 实验材料和方法

1.1 原材料

1.2 实验仪器

1.3 实验内容

1.3.1 BiOI光催化材料的制备

1.3.2 Bi2O3光催化材料的制备

1.3.3 Bi2O3/BiOI复合光催化材料的制备

1.3.4 光催化性能测试

2. 结果与讨论

2.1 Bi2O3/BiOI复合光催化材料的晶相结构

2.2 Bi2O3/BiOI复合光催化材料的微观形貌

2.3 Bi2O3/BiOI复合光催化材料的结构

2.4 Bi2O3/BiOI复合光催化材料的光学性能

2.5 Bi2O3/BiOI复合光催化材料光生电子空穴对的分离

2.6 Bi2O3/BiOI复合光催化材料的性能

2.6.1 不同制备条件对光催化性能的影响

2.6.2 光催化性能

2.7 Bi2O3/BiOI复合光催化材料降解四环素的机制

3. 结 论

通讯作者:
尹冠生，博士，教授，博士生导师，研究方向为混凝土结构　E-mail: yings@chd.edu.cn

1.3.2 Bi₂O₃光催化材料的制备

1.3.3 Bi₂O₃/BiOI复合光催化材料的制备

2.1 Bi₂O₃/BiOI复合光催化材料的晶相结构

2.2 Bi₂O₃/BiOI复合光催化材料的微观形貌

2.3 Bi₂O₃/BiOI复合光催化材料的结构

2.4 Bi₂O₃/BiOI复合光催化材料的光学性能

2.5 Bi₂O₃/BiOI复合光催化材料光生电子空穴对的分离

2.6 Bi₂O₃/BiOI复合光催化材料的性能

2.7 Bi₂O₃/BiOI复合光催化材料降解四环素的机制

3. 结论

1.3.2 Bi₂O₃光催化材料的制备

1.3.3 Bi₂O₃/BiOI复合光催化材料的制备

2.1 Bi₂O₃/BiOI复合光催化材料的晶相结构

2.2 Bi₂O₃/BiOI复合光催化材料的微观形貌

2.3 Bi₂O₃/BiOI复合光催化材料的结构

2.4 Bi₂O₃/BiOI复合光催化材料的光学性能

2.5 Bi₂O₃/BiOI复合光催化材料光生电子空穴对的分离

2.6 Bi₂O₃/BiOI复合光催化材料的性能

2.7 Bi₂O₃/BiOI复合光催化材料降解四环素的机制

3. 结论