全有机三明治结构PI-ANFm-PI薄膜的制备及其介电性能

段广宇; 胡凤英; 郑雨露; 梁莹浩; 石宜蕊; 胡祖明

doi:10.13801/j.cnki.fhclxb.20240522.002

全有机三明治结构PI-ANFm-PI薄膜的制备及其介电性能

1.
河南工程学院　材料工程学院，郑州 450007
2.
河南省纤维制备与改性工程技术研究中心，郑州 450007
3.
东华大学　纤维材料改性国家重点实验室，上海 201620

基金项目: 国家重点研发项目(2021YFB3700101)；河南工程学院博士培育基金(D2021009)

详细信息

通讯作者:
段广宇，博士，副教授，硕士生导师，研究方向为高性能聚合物电介质材料　E-mail: duanguangyu@dhu.edu.cn

中图分类号: TB332
计量
- 文章访问数: 171
- HTML全文浏览量: 113
- PDF下载量: 21
出版历程
- 收稿日期: 2024-04-10
- 修回日期: 2024-05-06
- 录用日期: 2024-05-12
- 网络出版日期: 2024-06-14
- 发布日期: 2024-05-22
- 刊出日期: 2025-03-14

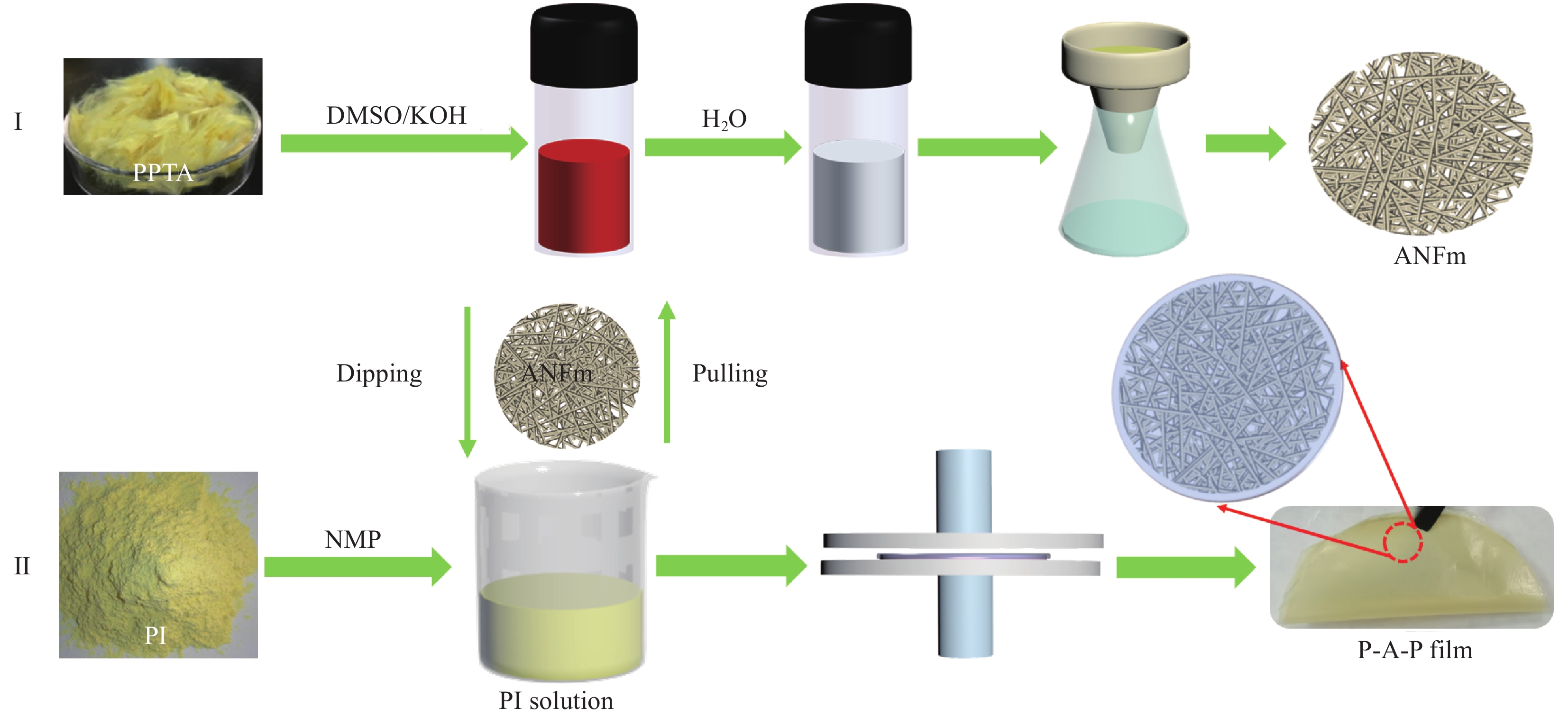
Preparation of all-organic sandwich-structured PI-ANFm-PI films and their dielectric properties

1.
College of Materials Engineering, Henan University of Engineering, Zhengzhou 450007, China
2.
Henan Engineering Technology Research Center for Fiber Preparation and Modification, Zhengzhou 450007, China
3.
State Key Laboratory for Modification of Chemical Fibers and Polymer Materials, Donghua University, Shanghai 201620, China

Funds: National Key R&D Program of China (2021YFB3700101); Foundation for Doctorate Research of Henan University of Engineering (D2021009)

摘要

摘要:
为了打破聚合物电介质材料介电常数和击穿强度间的内禀矛盾关系，优化其在高温、强电场环境中的介电性能和击穿强度。本文采用浸渍提拉法，基于聚酰亚胺(PI)溶液和芳纶纳米纤维薄膜(ANFm)构筑了具有三明治结构的全有机PI-ANFm-PI (P-A-P)复合电介质薄膜。ANFm表面粗糙度的降低以及P-A-P复合薄膜内部电子-空穴对的构建有效抑制了漏电流的形成。当PI溶液浓度为7wt%时，P-A-P复合薄膜在25℃和150℃下的击穿强度分别达411.6 MV/m和350.7 MV/m，较ANFm分别提升了58.4%和44.7%；此外，由于空间电荷极化强度的降低，P-A-P复合薄膜的介电稳定性和绝缘性能明显改善。上述研究结果表明：在ANFm表面形成高绝缘层有助于改善ANFm的击穿强度以及降低其内部漏电流密度，有望为开发新型全有机高温电介质薄膜提供新方法和新思路。
- 聚酰亚胺 /
- 芳纶纳米纤维 /
- 三明治结构 /
- 电介质薄膜 /
- 介电性能
Abstract:
For breaking the endowed paradox between dielectric constant and breakdown strength of polymer dielectric films and optimizing the dielectric properties and breakdown strength at high temperatures under electric field, polyimide (PI) solution and aramid nanofiber film (ANFm) were utilized to construct all-organic sandwich-structured PI-ANF-PI (P-A-P) dielectric films via "dipping and pulling" process. Due to the top and bottom PI layers reduced the surface roughness of ANFm as well as the formation of electron-hole pairs, the leakage current density of the P-A-P film was effectively suppressed. When the concentration of PI solution was 7wt%, the breakdown strength of P-A-P film reached 411.6 MV/m and 350.7 MV/m at 25℃ and 150℃, respectively, which was 58.4% and 44.7% higher than that of single-layer ANFm. Moreover, on account of the reduction of space-charge polarization, the dielectric stability and insulating performance of P-A-P film significantly improved. The obtained results demonstrate that the insulating layers on both surfaces of ANFm contribute to improving the breakdown strength and decreasing the leakage current density. Hence, this work provides a novel approach and a new idea for the development of all-organic high-temperature dielectric films.
- polyimide /
- aramid nanofiber /
- sandwiched-structure /
- dielectric film /
- dielectric property

HTML全文

以连续纤维作为增强相的纤维增强树脂基复合材料(FRP)与金属材料相比具有重量轻，比刚度和比强度高、耐腐蚀、可设计性强等优势，因此广泛应用于建筑、车辆、船舶、航空航天等领域^[1,2]。传统的纤维层合板一般由0°、45°、−45°、90°四种铺层角度组成(Quad)，根据一些半经验的铺层规律和设计方法，通过调整四种角度的比例和排列顺序来设计不同的层合板性能。但Quad层合板存在刚度可设计空间小，铺层设计效率低，减薄设计困难等缺点，这限制了层合板材料的进一步应用^[3]。

为了优化传统的层合板铺层设计思路，Tsai等^[4]提出了一种创新的层合板设计——Double -Double(DD)层合板。DD层合板是两组对称铺层组成的DD铺层单元[±Ф/±Ψ]通过多次重叠构成的层合板结构。DD 层合板可以根据构件的主要载荷方向，通过调整DD单元的两组铺层角度来控制层合板性能，以达到所需刚度。相比与传统的Quad铺层，DD层合板具有同质性和设计性好、生产制造与减薄设计方便等多方面优势^[3]。同时，利用蔡氏模量，DD层合板只需要这一个材料参数便能进行铺层和刚度设计，从而达到类似金属一样的快速设计，有望取代传统的Quad铺层，在各领域得到广泛应用^[5]。

DD层合板在铺层替代与结构减薄设计上的优势近年来得到国内外学者的广泛关注^[6-8]。Erik Kappel^[9]提出了一种根据层压板强度的DD层压板设计优化方案，重点研究了层合板安全识别过程的鲁棒性，提出了一种基于Nettles圆失效包络和DD铺层特征的简单优化方案，用于寻找最优的DD角度与最小重叠次数。Wang等^[10]提出了一种隐式的局部和全局模型，用于优化DD层压板的锥度(变厚度)设计，以在给定的重量约束下最大限度地提高屈曲阻力，或在屈曲约束下减轻重量。杨刚等^[11]比较了不同铺层方式(DD、Woven、Quad 铺层)以及不同基体材料(环氧树脂，聚酰胺6，PA6)层合板的设计流程和力学性能。结果表明，DD 层合板可以保证刚度性能与相同纤维和基体的 Quad 层合板一致，并且 DD 层合板的设计效率要明显高于 Quad 层合板。何靓等^[12]结合DD铺层方法与应变能理论，对复合材料 C 型梁进行了减重优化设计，结果表明DD构件能够有效替代传统铺层构件，在铺层数目一致时 Double-Double 铺层 C 型梁的弯曲刚度和极限载荷分别提高了9.28%和 12.34%。

目前对于DD层合板的研究主要集中在对碳纤维增强树脂基复合材料(CFRP)单一材料的DD层合板设计与性能研究上^[13-15]，CFRP由于其更高的纤维/基体模量比值而具有更小的归一化刚度离散性^[16]，而对于其他纤维以及混杂纤维层合板的蔡氏模量以及DD理论适用性还有待进一步研究。Jia等^[17]推导了两种材料组成的夹层混杂层合板的蔡氏模量和归一化刚度矩阵特性，结果表明混杂层合的蔡氏模量符合混合定律，但没有讨论不同的混杂比例对归一化刚度矩阵的影响，且没有设计相关实验对混杂DD层合板的刚度进行验证。除此之外没有更多的有关混杂DD层合板理论或实验研究。研究混杂DD层合板的刚度等效设计方法以及不同混杂DD层合板构型的同质性性能特点具有重要的探索意义，有望进一步扩展DD理论的应用范围。另一方面，含玻璃纤维增强树脂基复合材料(GFRP)的混杂层合板可以有效改善单纯CFRP材料韧性差的缺陷,并且能够大幅度提高材料的经济性^[18]。因此,开展混杂DD层合板的设计方法研究具有重要的研究价值。

本文根据蔡氏模量不变性与混杂定律，研究了混杂DD层合板的设计方法，讨论了混杂条件下的蔡氏模量以及归一化刚度有效性，提出了混杂DD层合板的铺层等效方法，研究了混杂DD层合板的铺层方式与同质性特点。最后，通过碳纤维/玻璃纤维混杂层合板的拉伸等效实验，验证了混杂DD层合板的铺层等效方法的可行性和在减薄设计上的优势。

1. 混杂DD层合板设计方法

1.1 蔡氏模量与CFRP-DD层合板设计方法

Double-Double层合板的设计理论基础源于Tsai与Melo在2014年提出的不变量理论^[19,20]：层合板刚度矩阵在张量形式下矩阵的迹(对角线元素之和)在任意坐标变换下都保持一致。根据经典层合板理论^[21]，纤维角度θ条件下的单层偏轴刚度矩阵各元素如下式所示：

${\left\{\begin{array}{l}{\bar{Q}}_{11}={Q}_{11}\cos^{4}\theta +2\left({Q}_{12}+2{Q}_{66}\right)\sin^{2}\theta \cos^{2}\theta +{Q}_{22}\sin^{4}\theta \\ {\bar{Q}}_{22}={Q}_{11}\sin^{4}\theta +2\left({Q}_{12}+2{Q}_{66}\right)\sin^{2}\theta \cos^{2}\theta +{Q}_{22}\cos^{4}\theta \\ {\bar{Q}}_{12} = \left({Q}_{11}+{Q}_{22} - 4{Q}_{66}\right)\sin^{2}\theta \cos^{2}\theta +{Q}_{12}\left(\mathrm{s}\mathrm{i}{\mathrm{n}}^{4}\theta +\mathrm{c}\mathrm{o}{\mathrm{s}}^{4}\theta \right)\\ \begin{split} {\bar{Q}}_{66}=&\left({Q}_{11}+{Q}_{22}-2{Q}_{12}-2{Q}_{66}\right)\\&\sin^{2}\theta \cos^{2}\theta +{Q}_{66}\left(\mathrm{s}\mathrm{i}{\mathrm{n}}^{4}\theta +\mathrm{c}\mathrm{o}{\mathrm{s}}^{4}\theta \right) \end{split}\\ \begin{split} {\bar{Q}}_{16}=&\left({Q}_{11}-{Q}_{12}-2{Q}_{66}\right)\sin\theta \cos^{3}\theta +\\&\left({Q}_{12}-{Q}_{22}+2{Q}_{66}\right)\sin^{3}\theta \cos\theta \end{split} \\ \begin{split} {\bar{Q}}_{26}=&\left({Q}_{11}-{Q}_{12}-2{Q}_{66}\right)\sin^{3}\theta \cos\theta +\\& \left({Q}_{12}-{Q}_{22}+2{Q}_{66}\right)\sin\theta \cos^{3}\theta \end{split}\end{array}\right. }$

(1)

其中Q_ij表示单层材料二维刚度矩阵的对应分量， $\stackrel{\mathrm{-}}{\text{Q}}$ _ij表示偏轴条件下二维刚度矩阵的对应分量。张量形式下的刚度矩阵Q通过张量代数运算得到的标量具有不随坐标改变而改变的性质，称为张量的不变量。例如张量形式下的刚度矩阵Q的对角线元素之和(迹，Trace)，与铺层角度与方式无关，由下式可得：

$\begin{split} {\mathrm{Trace}}\left(\bar{Q}\right)=&{\bar{Q}}_{11}+{\bar{Q}}_{22}+2{\bar{Q}}_{66}=\\& {Q}_{11}+{Q}_{22}+2{Q}_{66}={\mathrm{Trace}}\left(Q\right) \end{split}$

(2)

可见Trace(Q)是只与材料有关的参数，其代表了材料刚度性质的总量和上界，对于单向纤维增强的正交各向异性单层，Trace(Q)可由弹性常数估计，如下式所示：

$\begin{split} {\mathrm{Trace}}\left(Q\right)=&{Q}_{11}+{Q}_{22}+2{Q}_{66}=\\& \dfrac{{E}_{1}}{1-{\nu }_{21}^{2}\dfrac{{E}_{2}}{{E}_{1}}}+\dfrac{{E}_{2}}{1-{\nu }_{21}^{2}\dfrac{{E}_{2}}{{E}_{1}}}+2{G}_{12}\approx\\ & {E}_{1}+{E}_{2}+2{G}_{12} \end{split}$

(3)

其中E₁、E₂和G₁₂分别为单层材料纵向拉伸模量、横向拉伸模量、剪切模量。为为了纪念Tsai教授在不变量理论以及复合材料力学领域中的重要贡献，多位学者将层合板刚度矩阵的迹命名为蔡氏模量(Tsai’s modulus)^[22]。蔡氏模量与杨氏模量和剪切模量类似，都是材料本身的属性。对于CFRP材料，刚度设计可以分解为材料和铺层两个独立的参数，如下式所示：

$Q=\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(Q\right)\cdot {Q}^{\mathrm{*}}$

(4)

其中蔡氏模量由所用材料(碳纤维类型及纤维体积分数)自身参数决定，与铺层方式无关；Q^*为刚度矩阵经蔡氏模量标准化之后的归一化刚度矩阵(铺层主刚度，master-ply)，由铺层角度决定，受碳纤维类型的影响不大^[20,23]。

基于蔡氏模量不变理论，Tsai等提出了Double-Double(DD)新型层合板设计理念。DD层合板是由两组对称的角铺层单元(±Φ/±Ψ)经过多次重叠组成的层合板结构，可以在对Quad铺层进行等效替代的同时表现出更多性能优势^[24]。DD层合板的刚度由两组相互独立的角铺层±Φ和±Ψ决定，角度的取值可以连续变化，因此DD层合板的刚度具有连续的可设计区间，提供了微调层合板性能的可能。通过保证刚度矩阵一致，DD层合板可以等效替代现有Quad铺层设计。由式(1)，将θ角度相关的项分离可以得到单层偏轴刚度的另一种矩阵形式^[25]：

$\begin{aligned} \left\{\begin{array}{l} \bar{Q}_{11} \\ \bar{Q}_{22} \\ \bar{Q}_{12} \\ \bar{Q}_{66} \\ \bar{Q}_{16} \\ \bar{Q}_{26} \end{array}\right\}=&\left[\begin{array}{ccccc} U_1 & U_2 & U_3 & 0 & 0 \\ U_1 & -U_2 & U_3 & 0 & 0 \\ U_4 & 0 & -U_3 & 0 & 0 \\ \left(U_1-U_4\right) / 2 & 0 & -U_3 & 0 & 0 \\ 0 & 0 & 0 & U_2 / 2 & U_3 \\ 0 & 0 & 0 & U_2 / 2 & -U_3 \end{array}\right]\\&\left\{\begin{array}{c} 1 \\ \cos 2 \theta \\ \cos 4 \theta \\ \sin 2 \theta \\ \sin 4 \theta \end{array}\right\} \end{aligned}$

(5)

其中，

$\begin{array}{l}{U}_{1}=\dfrac{3}{8}{Q}_{11}+\dfrac{3}{8}{Q}_{22}+\dfrac{1}{4}{Q}_{12}+\dfrac{1}{2}{Q}_{66}\\ {U}_{2}=\dfrac{1}{2}{Q}_{11}-\dfrac{1}{2}{Q}_{22}\\ {U}_{3}=\dfrac{1}{8}{Q}_{11}+\dfrac{1}{8}{Q}_{22}-\dfrac{1}{4}{Q}_{12}-\dfrac{1}{2}{Q}_{66}\\ {U}_{4}=\dfrac{1}{8}{Q}_{11}+\dfrac{1}{8}{Q}_{22}+\dfrac{3}{4}{Q}_{12}-\dfrac{1}{2}{Q}_{66}\end{array}$

(6)

矩阵U为材料参数，由层合板材料决定，与铺层角度无关。对(5)进行蔡氏模量归一化处理后得到：

$\left\{\begin{array}{c} 1 \\ \cos 2 \theta \\ \cos 4 \theta \\ \sin 2 \theta \\ \sin 4 \theta \end{array}\right\}=\operatorname{Trace}(Q) U^*\left\{\begin{array}{c} 1 \\ \cos 2 \theta \\ \cos 4 \theta \\ \sin 2 \theta \\ \sin 4 \theta \end{array}\right\}$

(7)

其中U^*为蔡氏模量归一化后的U，由对应的归一化刚度矩阵元素Q^*代入式(6)中得到。为统一符号，本文中带^*角标的量表示经过蔡氏模量归一化处理后的物理量。进而，对于总层数为n，单层厚度为h，总厚度为H的层合板，拉伸刚度矩阵A的各元素表示为

${ \left\{\begin{array}{l} A_{11} \\ A_{22} \\ A_{12} \\ A_{66} \\ A_{16} \\ A_{26} \end{array}\right\} = \displaystyle\int_{-\tfrac{H}{2}}^{\tfrac{H}{2}}\left[\begin{array}{l} \bar{Q}_{11} \\ \bar{Q}_{22} \\ \bar{Q}_{12} \\ \bar{Q}_{66} \\ \bar{Q}_{16} \\ \bar{Q}_{26} \end{array}\right\} d {\textit{z}} =\operatorname{Trace}(Q) U^*\displaystyle {\sum}_{i=1}^{n} h \left\{\begin{array}{c} 1 \\ \cos 2 \theta_i \\ \cos 4 \theta_i \\ \sin 2 \theta_i \\ \sin 4 \theta_i \end{array}\right\} \\ =\operatorname{Trace}(Q) H \left[\begin{array}{ccccc} U_1^* & U_2^* & U_3^* & 0 & 0 \\ U_1^* & -U_2^* & U_3^* & 0 & 0 \\ U_4^* & 0 & -U_3^* & 0 & 0 \\ \left(U_1^*-U_4^*\right) / 2 & 0 & -U_3^* & 0 & 0 \\ 0 & 0 & 0 & U_2^* / 2 & U_3^* \\ 0 & 0 & 0 & U_2^* / 2 & -U_3^* \end{array}\right]\left\{\begin{array}{c} 1 \\ V_1 \\ V_2 \\ V_3 \\ V_4 \end{array}\right\} }$

(8)

其中V为铺层构型参数，与所用层合板材料无关，表示为

$\begin{array}{c}{V}_{1}=\dfrac{1}{n}\displaystyle\displaystyle{\sum} _{i=1}^{n}\mathrm{c}\mathrm{o}\mathrm{s}2{\theta }_{i},{V}_{2}=\dfrac{1}{n}\displaystyle{\sum} _{i=1}^{n}\mathrm{c}\mathrm{o}\mathrm{s}4{\theta }_{i}\\ {V}_{3}=\dfrac{1}{n}\displaystyle{\sum} _{i=1}^{n}\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{i},{V}_{4}=\dfrac{1}{n}\displaystyle{\sum} _{i=1}^{n}\mathrm{s}\mathrm{i}\mathrm{n}4{\theta }_{i}\end{array}$

(9)

对于Quad层合板，四种角度层的厚度占比分别为 p_0°，p_90°，p_45° ，p_−45° ，则其铺层参数V表示为

$\begin{array}{l}{V}_{1}={p}_{0^\circ}-{p}_{90^\circ}\\ {V}_{2}={p}_{0^\circ}+{p}_{90^\circ}-{p}_{45^\circ}-{p}_{-45^\circ}\\ {V}_{3}={p}_{45^\circ}-{p}_{-45^\circ}\\ {V}_{4}=0\end{array}$

(10)

而对于具有相同材料和单层厚度的DD层合板，其铺层参数V表示为

$\begin{array}{l}{V}_{1}=\left(\mathrm{c}\mathrm{o}\mathrm{s}2\varPhi +\mathrm{c}\mathrm{o}\mathrm{s}2\varPsi \right)/2\\ {V}_{2}=\left(\mathrm{c}\mathrm{o}\mathrm{s}4\varPhi +\mathrm{c}\mathrm{o}\mathrm{s}4\varPsi \right)/2\\ {V}_{3}=0\\ {V}_{4}=0\end{array}$

(11)

当利用相同材料的DD层合板对Quad层合板进行替换时，只需要保证二者V₁、V₂ 的取值对应相同，则根据式(8)，两种层合板的面内刚度A₁₁、A₂₂、A₁₂、A₆₆保持一致。剩余元素A₁₆、A₂₆代表拉伸与剪切的耦合效应，在DD层合板中取值为0，无拉剪耦合。

1.2 混杂条件下的蔡氏模量与归一化刚度

对于碳纤维/玻璃纤维层间混杂的层合板，由于拉伸刚度与铺层顺序无关，因此混杂层合板的蔡氏模量为各自纤维层的蔡氏模量按混杂比例结合，即：

$\begin{split} {\mathrm{Trace}}\left({Q}_{\mathrm{h}\mathrm{y}\mathrm{b}}\right)=& {p}_{\mathrm{c}}{\mathrm{Trace}}\left({Q}_{\mathrm{c}}\right)+{p}_{\mathrm{g}}{\mathrm{Trace}}\left({Q}_{\mathrm{g}}\right)=\\& {p}_{\mathrm{c}}^{\mathrm{*}}{\mathrm{Trace}}\left({Q}_{\mathrm{h}\mathrm{y}\mathrm{b}}\right)+{p}_{\mathrm{g}}^{\mathrm{*}}{\mathrm{Trace}}\left({Q}_{\mathrm{h}\mathrm{y}\mathrm{b}}\right) \end{split}$

(12)

其中p_c、p_g分别表示碳纤维和玻璃纤维各自的混杂比例(厚度比)， ${p}_{\text{c}}^{\text{*}}$ 、 ${\text{p}}_{\text{g}}^{\text{*}}$ 分别定义为碳纤维层和玻璃纤维层对混杂层合板蔡氏模量的贡献比例，即：

$\begin{array}{l}{p}_{\mathrm{c}}^{\mathrm{*}}=\dfrac{{p}_{\mathrm{c}}\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({Q}_{\mathrm{c}}\right)}{{p}_{\mathrm{c}}\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({Q}_{\mathrm{c}}\right)+{p}_{\mathrm{g}}\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({Q}_{\mathrm{g}}\right)}\\ {p}_{\mathrm{g}}^{\mathrm{*}}=\dfrac{{p}_{\mathrm{g}}\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({Q}_{\mathrm{g}}\right)}{{p}_{\mathrm{c}}\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({Q}_{\mathrm{c}}\right)+{p}_{\mathrm{g}}\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({Q}_{\mathrm{g}}\right)}\end{array}$

(13)

引入p^*作为混杂比例是为了简化混杂物理量的表达形式，使其满足关于p^*的混杂定律形式。混杂条件下的归一化刚度满足关于p^*的混杂定律，如下式所示：

$\begin{aligned} {Q}_{\mathrm{h}\mathrm{y}\mathrm{b}}^{\mathrm{*}}=&\dfrac{{Q}_{\mathrm{h}\mathrm{y}\mathrm{b}}}{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({Q}_{\mathrm{h}\mathrm{y}\mathrm{b}}\right)}=\dfrac{{p}_{\mathrm{c}}{Q}_{\mathrm{c}}+{p}_{\mathrm{g}}{Q}_{\mathrm{g}}}{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({Q}_{\mathrm{h}\mathrm{y}\mathrm{b}}\right)}=\\ &\dfrac{{p}_{\mathrm{c}}\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({Q}_{\mathrm{c}}\right){Q}_{\mathrm{c}}^{\mathrm{*}}+{p}_{\mathrm{g}}\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({Q}_{\mathrm{g}}\right){Q}_{\mathrm{g}}^{\mathrm{*}}}{{p}_{\mathrm{c}}\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({Q}_{\mathrm{c}}\right) + {p}_{\mathrm{g}}\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left({Q}_{\mathrm{g}}\right)} = {p}_{\mathrm{c}}^{\mathrm{*}}{Q}_{\mathrm{c}}^{\mathrm{*}}+{p}_{\mathrm{g}}^{\mathrm{*}}{Q}_{\mathrm{g}}^{\mathrm{*}} \end{aligned}$

(14)

其中 ${Q}_{\mathrm{c}}^{\mathrm{*}}$ 与 ${Q}_{\mathrm{g}}^{\mathrm{*}}$ 分布表示单一材料CFRP和GFRP的归一化刚度矩阵。因此混杂DD层合板的拉伸刚度由两种纤维层合板的刚度之和表示，若同种纤维层的厚度相同(碳纤层单层厚h_c，总层数n_c，总厚度H_c；玻纤层单层厚h_g，总层数n_g，总厚度H_g；混杂层合板总厚度为H_hyb)，则式(8)在混杂条件下的表达式为

$\begin{aligned} \left\{\begin{array}{l} A_{11} \\ A_{22} \\ A_{12} \\ A_{66} \\ A_{16} \\ A_{26} \end{array}\right\}=& {{\mathrm{Trace}}}\left(Q_{\mathrm{c}}\right) \cdot H_{\mathrm{c}} U_{\mathrm{c}}^* {\sum}_{i=1}^{n_{\mathrm{c}}} \dfrac{1}{n_{\mathrm{c}}}\left\{\begin{array}{c} 1 \\ \cos 2 \theta_i \\ \cos 4 \theta_i \\ \sin 2 \theta_i \\ \sin 4 \theta_i \end{array}\right\}+\operatorname{Trace}\left(Q_{\mathrm{g}}\right) \cdot H_{\mathrm{g}} U_{\mathrm{g}}^* {\sum}_{i=1}^{n_{\mathrm{g}}} \dfrac{1}{n_{\mathrm{g}}}\left\{\begin{array}{c} 1 \\ \cos 2 \theta_i \\ \cos 4 \theta_i \\ \sin 2 \theta_i \\ \sin 4 \theta_i \end{array}\right\} =\\ & \operatorname{Trace}\left(Q_{\mathrm{hyb}}\right) \cdot H_{\mathrm{hyb}}\left[\begin{array}{ccccc} U_{1_{\mathrm{hyb}}}^* & U_{2_{\mathrm{hyb}}}^* & U_{3_{\mathrm{hyb}}}^* & 0 & 0 \\ U_{1_{\mathrm{hyb}}}^* & -U_{2_{\mathrm{hyb}}}^* & U_{3_{\mathrm{hyb}}}^* & 0 & 0 \\ U_{4_{\mathrm{hyb}}}^* & 0 & -U_{3_{\mathrm{hyb}}}^* & 0 & 0 \\ \dfrac{U_{1_{\mathrm{hb}}}^*-U_{4_{\mathrm{hyb}}}^*}{2} & 0 & -U_{3_{\mathrm{hyb}}}^* & 0 & 0 \\ 0 & 0 & 0 & \dfrac{U_{2_{\mathrm{hyb}}}^*}{2} & U_{3_{\mathrm{hyb}}}^* \\ 0 & 0 & 0 & \dfrac{U_{2_{\mathrm{hyb}}}^*}{2} & -U_{3_{\mathrm{hyb}}}^* \end{array}\right]\left\{\begin{array}{c} 1 \\ V_{1_{\mathrm{hyb}}} \\ V_{2_{\mathrm{hyb}}} \\ V_{3_{\mathrm{hyb}}} \\ V_{4_{\mathrm{hyb}}} \end{array}\right\} \end{aligned}$

(15)

其中，

$\begin{array}{l}{U}_{{i}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}={p}_{\mathrm{c}}^{\mathrm{*}}{U}_{{i}_{\mathrm{c}}}^{\mathrm{*}}+{p}_{\mathrm{g}}^{\mathrm{*}}{U}_{{i}_{\mathrm{g}}}^{\mathrm{*}}\\ {V}_{{1}_{\mathrm{h}\mathrm{y}\mathrm{b}}}={p}_{\mathrm{c}}^{\mathrm{*}}\dfrac{{U}_{{2}_{\mathrm{c}}}^{\mathrm{*}}}{{U}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\displaystyle{\sum} _{i=1}^{{n}_{\mathrm{c}}}\dfrac{\mathrm{c}\mathrm{o}\mathrm{s}2{\theta }_{i}}{{n}_{\mathrm{c}}}+{p}_{\mathrm{g}}^{\mathrm{*}}\dfrac{{U}_{{2}_{\mathrm{g}}}^{\mathrm{*}}}{{U}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\displaystyle{\sum} _{i=1}^{{n}_{\mathrm{g}}}\dfrac{\mathrm{c}\mathrm{o}\mathrm{s}2{\theta }_{i}}{{n}_{\mathrm{g}}}\\ {V}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}={p}_{\mathrm{c}}^{\mathrm{*}}\dfrac{{U}_{{3}_{\mathrm{c}}}^{\mathrm{*}}}{{U}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\displaystyle{\sum} _{i=1}^{{n}_{\mathrm{c}}}\dfrac{\mathrm{c}\mathrm{o}\mathrm{s}4{\theta }_{i}}{{n}_{\mathrm{c}}}+{p}_{\mathrm{g}}^{\mathrm{*}}\dfrac{{U}_{{3}_{\mathrm{g}}}^{\mathrm{*}}}{{U}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\displaystyle{\sum} _{i=1}^{{n}_{\mathrm{g}}}\dfrac{\mathrm{c}\mathrm{o}\mathrm{s}4{\theta }_{i}}{{n}_{\mathrm{g}}}\\ {V}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}={p}_{\mathrm{c}}^{\mathrm{*}}\dfrac{{U}_{{2}_{\mathrm{c}}}^{\mathrm{*}}}{{U}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\displaystyle{\sum} _{i=1}^{{n}_{\mathrm{c}}}\dfrac{\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{i}}{{n}_{\mathrm{c}}}+{p}_{\mathrm{g}}^{\mathrm{*}}\dfrac{{U}_{{2}_{\mathrm{g}}}^{\mathrm{*}}}{{U}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\displaystyle{\sum} _{i=1}^{{n}_{\mathrm{g}}}\dfrac{\mathrm{s}\mathrm{i}\mathrm{n}2{\theta }_{i}}{{n}_{\mathrm{g}}}\\ {V}_{{4}_{\mathrm{h}\mathrm{y}\mathrm{b}}}={p}_{\mathrm{c}}^{\mathrm{*}}\dfrac{{U}_{{3}_{\mathrm{c}}}^{\mathrm{*}}}{{U}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\displaystyle{\sum} _{i=1}^{{n}_{\mathrm{c}}}\dfrac{\mathrm{s}\mathrm{i}\mathrm{n}4{\theta }_{i}}{{n}_{\mathrm{c}}}+{p}_{\mathrm{g}}^{\mathrm{*}}\dfrac{{U}_{{3}_{\mathrm{g}}}^{\mathrm{*}}}{{U}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\displaystyle{\sum} _{i=1}^{{n}_{\mathrm{g}}}\dfrac{\mathrm{s}\mathrm{i}\mathrm{n}4{\theta }_{i}}{{n}_{\mathrm{g}}}\end{array}$

(16)

可以看到混杂层合板的铺层参数V不仅与铺层角度θ有关，还受到混杂比例p^*与归一化刚度矩阵U^*的影响。纤维类型以及纤维体积分数会对Q^*以及U^*产生影响。CFRP纤维模量远远高于基体模量，归一化刚度受纤维类型影响较小，而对于GFRP，归一化刚度受纤维类型影响较大^[16]。对于不同材料或混杂比例的两种层合板的等效，需要考虑替换前后U^*的变化。

混杂DD层合板的铺层单元[±Ф/±Ψ]的各单层可分别由不同的材料组成。若同一角度系列不是同一种材料，例如[+Φ_g/+Ψ_g/−Φ_c/−Ψ_c]_r，其混杂DD单元铺层参数V的表达式为

$\begin{array}{l}{V}_{{1}_{\mathrm{h}\mathrm{y}\mathrm{b}}}=\left(\mathrm{c}\mathrm{o}\mathrm{s}2\varPhi +\mathrm{c}\mathrm{o}\mathrm{s}2\varPsi \right)/2\\ {V}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}=\left(\mathrm{c}\mathrm{o}\mathrm{s}4\varPhi +\mathrm{c}\mathrm{o}\mathrm{s}4\varPsi \right)/2\\ {V}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}=\left(\mathrm{s}\mathrm{i}\mathrm{n}2\varPsi +\mathrm{s}\mathrm{i}\mathrm{n}2\varPhi \right)\dfrac{{p}_{\mathrm{g}}^{\mathrm{*}}{U}_{{2}_{\mathrm{g}}}^{\mathrm{*}}-{p}_{\mathrm{c}}^{\mathrm{*}}{U}_{{2}_{\mathrm{c}}}^{\mathrm{*}}}{2{U}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\\ {V}_{{4}_{\mathrm{h}\mathrm{y}\mathrm{b}}}=\left(\mathrm{s}\mathrm{i}\mathrm{n}4\varPsi +\mathrm{s}\mathrm{i}\mathrm{n}4\varPhi \right)\dfrac{{p}_{\mathrm{g}}^{\mathrm{*}}{U}_{{3}_{\mathrm{g}}}^{\mathrm{*}}-{p}_{\mathrm{c}}^{\mathrm{*}}{U}_{{3}_{\mathrm{c}}}^{\mathrm{*}}}{2{U}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\end{array}$

(17)

可以看到此时铺层参数 V_{1 hyb}、V_{2 hyb}项与单一材料DD的V_{1 hyb}、V_{2 hyb}一致，不受材料类型和混杂比例的影响。但是其V_{3 hyb}、V_{4 hyb}项一般不为0，导致A₁₆、A₂₆不为0，产生拉剪耦合效应，影响层合板性能，并且当DD单元的重复次数增加时， V_{3 hyb}、V_{4 hyb}不会随之减小，因此设计混杂DD层合板应当避免同一角度类型是不同的材料。本文研究对象的混杂DD层合板要求同一角度系列是相同材料，其中±Φ层为玻纤层，±Ψ为碳纤层，同一材料的铺层厚度相同，因此式(16)在[±Φ_g/±Ψ_c]中的表达式为

$\begin{array}{l}{V}_{{1}_{\mathrm{h}\mathrm{y}\mathrm{b}}}={p}_{\mathrm{c}}^{\mathrm{*}}\dfrac{{U}_{{2}_{\mathrm{c}}}^{\mathrm{*}}}{{U}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}cos2{\varPsi }_{\mathrm{c}}+{p}_{\mathrm{g}}^{\mathrm{*}}\dfrac{{U}_{{2}_{\mathrm{g}}}^{\mathrm{*}}}{{U}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}cos2{\varPhi }_{\mathrm{g}}\\ {V}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}={p}_{\mathrm{c}}^{\mathrm{*}}\dfrac{{U}_{{3}_{\mathrm{c}}}^{\mathrm{*}}}{{U}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}cos4{\varPsi }_{\mathrm{c}}+{p}_{\mathrm{g}}^{\mathrm{*}}\dfrac{{U}_{{3}_{\mathrm{g}}}^{\mathrm{*}}}{{U}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}cos4{\varPhi }_{\mathrm{g}}\\ {V}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}=0\\ {V}_{{4}_{\mathrm{h}\mathrm{y}\mathrm{b}}}=0\end{array}$

(18)

与单一材料的DD层合板(式(11))不同，混杂DD层合板的铺层参数V与材料类型以及混杂比例有关。混杂比例会同时影响p^*项与U^*项，需要在铺层等效设计时进行考虑。

1.3 混杂DD层合板的铺层等效方法

与单一材料的DD层合板一样，混杂DD层合板也可以进行层合板的等效替代。混杂DD层合板的等效替代设计流程如图1所示。首先根据替代方案选择合适的材料与混杂比例，对于材料替换，等效替代要求替换前后蔡氏模量一致，根据所用两种纤维层板的蔡氏模量和式(12)，保证替换前后层合板总体蔡氏模量一致以确定混杂比例，此时由于替换前后可能采用不同的材料或混杂比例，求解等效铺层刚度要满足式(15)替换前后对应的U^*·V乘积项一致。对于铺层替代，即当所用的材料与混杂比例不变，层合板总体蔡氏模量与U^*保持不变，只需要铺层参数V的取值保持一致便可进行等效替换。例如替换相同材料和比例的混杂Quad层合板，其中碳纤层和玻纤层0°、90°、+45°、−45°铺层占层合板总厚度的比例分别为p_c0°、p_c90°、p_c45°、p_c−45°与p_g0°、p_g90°、p_g45°、p_g−45°，实现同比例的混杂DD替代需要满足：V_1hybQuad =V_1hybDD，V_2hybQuad =V_2hybDD其中：

图 1 混杂DD层合板铺层等效设计方法

Figure 1. Equivalent design process for hybrid DD laminates

下载: 全尺寸图片幻灯片

$\begin{array}{l}\begin{split} {V}_{{1}_{{\mathrm{h}\mathrm{y}\mathrm{b}}{\mathrm{Q}\mathrm{u}\mathrm{a}\mathrm{d}}}}=&\dfrac{{p}_{\mathrm{c}}^{\mathrm{*}}{U}_{{2}_{\mathrm{c}}}^{\mathrm{*}}}{{p}_{\mathrm{c}}{U}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\left({p}_{{\mathrm{c}}_{0^\circ} }-{p}_{{\mathrm{c}}_{90^\circ} }\right)+\\&\dfrac{{p}_{\mathrm{g}}^{\mathrm{*}}{U}_{{2}_{\mathrm{g}}}^{\mathrm{*}}}{{p}_{\mathrm{g}}{U}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\left({p}_{{\mathrm{g}}_{0^\circ} }-{p}_{{\mathrm{g}}_{90^\circ} }\right) \end{split}\\\begin{split} {V}_{{2}_{{\mathrm{h}\mathrm{y}\mathrm{b}}{\mathrm{Q}\mathrm{u}\mathrm{a}\mathrm{d}}}}=&\dfrac{{p}_{\mathrm{c}}^{\mathrm{*}}{U}_{{3}_{\mathrm{c}}}^{\mathrm{*}}}{{p}_{\mathrm{c}}{U}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\left({p}_{{\mathrm{c}}_{0^\circ} }-{p}_{{\mathrm{c}}{45^\circ }}-{p}_{{\mathrm{c}}_{-45^\circ} }+{p}_{{\mathrm{c}}_{90^\circ} }\right)+\\ & \dfrac{{p}_{\mathrm{g}}^{\mathrm{*}}{U}_{{3}_{\mathrm{g}}}^{\mathrm{*}}}{{p}_{\mathrm{g}}{U}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}}\left({p}_{{\mathrm{g}}_{0^\circ} }-{p}_{{\mathrm{g}}_{45^\circ} }-{p}_{{\mathrm{g}}_{-45^\circ} }+{p}_{{\mathrm{g}}_{90^\circ} }\right) \end{split}\end{array}$

(19)

根据式(18)、(19)可以求解满足等效替代的混杂DD层合板的铺层角度。如果对应方程无解或者蔡氏模量无法保持一致，则混杂DD铺层[±Φ_g/±Ψ_c]无法做到全部分量的等效替代，此时可以需要根据设计要求保证某一方向的刚度分量一致。例如要求替换前后纵向刚度 ${\bar{Q}}_{11}$ 一致，则等效铺层角度需要满足：

${\bar{Q}}_{11}={U}_{1\mathrm{h}\mathrm{y}\mathrm{b}}+{U}_{2\mathrm{h}\mathrm{y}\mathrm{b}}{V}_{1\mathrm{h}\mathrm{y}\mathrm{b}}+{U}_{3\mathrm{h}\mathrm{y}\mathrm{b}}{V}_{2\mathrm{h}\mathrm{y}\mathrm{b}}$

(20)

通过式(18)能得到一系列满足条件的铺层角度，而后根据其他方向的刚度条件或是性能要求进一步确定铺层角度。

混杂比例p^*还会影响DD铺层参数V₁与V₂的取值范围，过大或过小的混杂比例都会缩小V的取值范围，可能使得不存在完全等效的Φ_g与Ψ_c铺层角度。图2显示了保持相同材料进行混杂DD层合板的铺层替代时，不同混杂比例下V₁与V₂取值范围，其中 ${U}_{2\mathrm{c}}^{\mathrm{*}}=0.427,{U}_{2\mathrm{g}}^{\mathrm{*}}=0.227$ , ${U}_{2\mathrm{c}}^{\mathrm{*}}=0.427$ , ${U}_{2\mathrm{g}}^{\mathrm{*}}=0.227$ 。图中绿色曲线代表碳纤维层角度Ψ_c自由变化，玻璃纤维层角度为0°或90°时的V₁、V₂函数关系；图中红色曲线代表玻璃纤维层角度Φ_g自由变化，碳纤维层角度为0°或90°时的V₁、V₂函数关系；图中蓝色曲线代表玻璃纤维层角度Φ_g与碳纤维层角度Ψ_c相等时的V₁、V₂函数关系；图像中各曲线最外侧所围成的区域范围为可能的V₁、V₂取值范围。对于单一材料的情况，即 ${p}_{\mathrm{c}}^{\mathrm{*}}=0$ 或 ${p}_{\mathrm{c}}^{\mathrm{*}}=1$ ，DD层合板简化为角铺层[±θ]_n(single-double)的情况，此时V₁、V₂的取值限制在一条曲线上。随着碳纤层混杂比例 ${p}_{\mathrm{c}}^{\mathrm{*}}$ 的减少，由玻纤角边界的曲线(绿色曲线)向上收缩；当碳纤层混杂比例 ${p}_{\mathrm{c}}^{\mathrm{*}}$ 的增加，由碳纤角边界曲线(红色曲线)向下扩展。当玻纤角边界曲线与碳纤角边界曲线重合时V₂ (V₁=0)取到最大值1.0，此时：

图 2 混杂DD层合板铺层参数V₁、V₂有效设计范围

Figure 2. Effective design range of hybrid DD laminate stacking parameters V₁ and V₂

下载: 全尺寸图片幻灯片

$\begin{aligned} 0=&\frac{{p}_{\mathrm{c}}^{\mathrm{*}}{U}_{{2}_{\mathrm{c}}}^{\mathrm{*}}}{{U}_{2}^{\mathrm{*}}}\cos2\times 90^\circ+\frac{\left(1-{p}_{\mathrm{c}}^{\mathrm{*}}\right){U}_{{2}_{\mathrm{g}}}^{\mathrm{*}}}{{U}_{2}^{\mathrm{*}}}\cos2\times 0^\circ\\& {p}_{\mathrm{c}}^{\mathrm{*}}=\frac{{U}_{{2}_{\mathrm{g}}}^{\mathrm{*}}}{{U}_{{2}_{\mathrm{c}}}^{\mathrm{*}}+{U}_{{2}_{\mathrm{g}}}^{\mathrm{*}}}=0.347 \end{aligned}$

(21)

因此V₁=0时的V₂最大值在 $1\geqslant{p}_{\mathrm{c}}^{\mathrm{*}}\geqslant 0.347$ 随着 ${p}_{\mathrm{c}}^{\mathrm{*}}$ 的增大而增大，在 $0.347 > {p}_{\mathrm{c}}^{\mathrm{*}}\geqslant0$ 随着 ${p}_{\mathrm{c}}^{\mathrm{*}}$ 的增大而减小。对于准各向同性混杂层合板的等效铺层设计( ${p}_{\mathrm{c}0^\circ}= {p}_{\mathrm{c}90^\circ}={p}_{\mathrm{c}45^\circ}={p}_{\mathrm{c}-45^\circ}$ ， ${p}_{\mathrm{g}0^\circ}={p}_{\mathrm{g}90^\circ}={p}_{\mathrm{g}45^\circ}= {p}_{\mathrm{g}-45^\circ}$ )，在不改变材料和混杂比例的条件下进行等效的混杂DD层合板设计，需要满足 ${V}_{1}=0,{V}_{2}=0$ 。当所要求的替代点 (V₁,V₂)=(0,0)包括在曲线所围范围之内时(如图2 (e)~2(i))，则存在Φ_g、Ψ_c角度设计使其能被混杂DD层合板完全替代；当所要求的替代点(V₁,V₂)=(0,0)在曲线所围范围之外时(如图2(a)~2(d))，则不存在能完全等效的混杂DD层合板Φ_g、Ψ_c角度设计，此时需要根据设计要求优先保证某一方向的刚度分量一致进行混杂DD层合板的角度选择。

1.4 混杂DD层合板的同质性

DD层合板的一个重要优势就是其更规则的铺层排列使得层合板优化设计更方便快捷。DD层合板铺层设计只需要对4层的层合板重复单元[±Φ/±Ψ]的叠层方式进行优化，铺层时无需对称，只需要选择合适的角度与铺层顺序，相比传统的Quad层合板优化过程更快捷高效。DD层合板的关键性质是其同质性，要求层合板在沿着厚度方向性能保持一致并且没有拉弯耦合效应，即经过厚度和蔡氏模量标准化后的归一化拉伸刚度A^*与归一化弯曲刚度D^*一致且归一化耦合刚度B^*为0。因此如果层合板满足同质性要求，只需要考虑拉伸刚度就能设计层合板整体刚度性能。对DD层合进行同质性考察时，认为|A^*-D^*|以及|B^*|元素的最大值小于2%时即符合同质性要求^[25][26]，即

$\left\{\begin{array}{l}\text{m}\text{a}\text{x}\left|{A}^{\mathrm{*}}-{D}^{\mathrm{*}}\right| < 0.02\\ \text{m}\text{a}\text{x}\left|{B}^{\mathrm{*}}\right| < 0.02\end{array}\right.$

(22)

其中A^*、B^*、D^*分别表示拉伸刚度A，耦合刚度B，弯曲刚度D对厚度和蔡氏模量标准化之后的归一化拉伸刚度、归一化耦合刚度、归一化弯曲刚度，其表达式为

$\begin{array}{l}{A}^{\mathrm{*}}=\frac{{\displaystyle\int }_{-\frac{H}{2}}^{\frac{H}{2}}\bar{Q}\mathrm{d}{\textit{z}} }{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(Q\right){\displaystyle\int }_{-\frac{h}{2}}^{\frac{h}{2}}\mathrm{d}{\textit{z}} }=\frac{\displaystyle{\sum} _{k=1}^{n}{\bar{Q}}^{k}\left({{\textit{z}} }_{k}-{{\textit{z}} }_{k-1}\right)}{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(Q\right)\cdot H}\\ {B}^{\mathrm{*}}=\frac{{\displaystyle\int }_{-\frac{H}{2}}^{\frac{H}{2}}\bar{Q}{\textit{z}} \mathrm{d}{\textit{z}} }{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(Q\right){\displaystyle\int }_{-\frac{H}{2}}^{\frac{H}{2}}\left|{\textit{z}} \right|\mathrm{d}{\textit{z}} }=\frac{2\displaystyle{\sum} _{k=1}^{n}{\bar{Q}}^{k}\left({{\textit{z}} }_{k}^{2}-{{\textit{z}} }_{k-1}^{2}\right)}{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(Q\right)\cdot {H}^{2}}\\ {D}^{\mathrm{*}}=\frac{{\displaystyle\int }_{-\frac{H}{2}}^{\frac{H}{2}}\bar{Q}{{\textit{z}} }^{2}\mathrm{d}{\textit{z}} }{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(Q\right){\displaystyle\int }_{-\frac{H}{2}}^{\frac{H}{2}}\left|{{\textit{z}} }^{2}\right|\mathrm{d}{\textit{z}} }=\frac{4\displaystyle{\sum} _{k=1}^{n}{\bar{Q}}^{k}\left({{\textit{z}} }_{k}^{3}-{{\textit{z}} }_{k-1}^{3}\right)}{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(Q\right)\cdot {H}^{3}}\end{array}$

(23)

其中n为层合板总层数，z为厚度方向以中性面为原点的坐标。式(22)要求标准化后表达式的最大元素不超过0.02^[26]，随着重复次数的增加，式(22)的值会减小，最优的铺层策略即为达到同质性要求所需的重复叠层次数最少的铺层方式。

对于混杂DD层合板，最优叠层策略会与单一材料CFRP-DD有所不同。混杂的比例以及各层的材料都会影响归一化刚度。研究的混杂DD层合板的偏轴角度Φ_g、Ψ_c角度范围为0~90°，同一材料单层厚度相同，即玻璃纤维+Φ层与−Φ层厚度一致，为h_g；碳纤维+Ψ层与−Ψ层厚度一致，为h_c。混杂DD铺层单元按材料区分存在三种不同的构型：[g/c/c/g]，[g/c/g/c] 和[g/g/c/c]。铺层顺序不影响归一化后的拉伸刚度，对于三种混杂DD材料构型，都有：

$\begin{aligned} {A}^{\mathrm{*}}=&\dfrac{\displaystyle{\sum} _{k=1}^{n}{\bar{Q}}^{k}\left({{\textit{z}} }_{k}-{{\textit{z}} }_{k-1}\right)}{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(Q\right)\cdot H}=\dfrac{{H}_{\mathrm{c}}{\bar{Q}}_{\mathrm{c}}^{\left(\pm {\varPsi }_{\mathrm{c}}\right)}+{H}_{\mathrm{g}}{\bar{Q}}_{\mathrm{g}}^{\left(\pm {\varPhi }_{\mathrm{g}}\right)}}{\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(Q\right)\cdot H}=\\& {p}_{\mathrm{c}}^{\mathrm{*}}{\bar{Q}}_{\mathrm{c}}^{\mathrm{*}\left(\pm {\varPsi }_{\mathrm{c}}\right)}+{p}_{\mathrm{g}}^{\mathrm{*}}{\bar{Q}}_{\mathrm{g}}^{\mathrm{*}\left(\pm {\varPhi }_{\mathrm{g}}\right)} \end{aligned}$

(24)

而不同的铺层顺序会影响厚度和蔡氏模量标准化后的耦合归一化刚度B^*和弯曲归一化刚度D^*。对于[g/c/c/g]单元的混杂DD层合板，铺层角度符合反对称层合板条件，因此B^*元素中 ${B}_{11}^{\mathrm{*}},{B}_{12}^{\mathrm{*}}, {B}_{22}^{\mathrm{*}},{B}_{66}^{\mathrm{*}}$ 为0，D*元素中 ${D}_{16}^{\mathrm{*}},{D}_{26}^{\mathrm{*}}$ 为0。而[g/c/g/c] 和[g/g/c/c]的混杂DD层合板在重复铺设的情况下没有对称性质，上述元素不为0。由式(23)可以推导出DD单元构型对标准化刚度的影响，对耦合刚度有：

$\begin{array}{l}{B}_{\left[\text{g/c/c/g}\right]}^{\mathrm{*}}=\dfrac{{p}_{\mathrm{g}}^{*}{\bar{Q}}_{\mathrm{g}}^{*\varPhi }}{r}\left[\begin{array}{ccc}0& 0& 2-{p}_{\mathrm{g}}\\ 0& 0& 2-{p}_{\mathrm{g}}\\ 2-{p}_{\mathrm{g}}& 2-{p}_{\mathrm{g}}& 0\end{array}\right]+\dfrac{{p}_{\mathrm{c}}^{*}{\bar{Q}}_{\mathrm{c}}^{*\varPsi }}{r}\left[\begin{array}{ccc}0& 0& {p}_{\mathrm{c}}\\ 0& 0& {p}_{\mathrm{c}}\\ {p}_{\mathrm{c}}& {p}_{\mathrm{c}}& 0\end{array}\right]\\ {B}_{\left[\text{g/c/g/c}\right]}^{\mathrm{*}}=\dfrac{{p}_{\mathrm{g}}^{*}{\bar{Q}}_{\mathrm{g}}^{*\varPhi }}{r}\left[\begin{array}{ccc}\dfrac{{p}_{\mathrm{c}}}{2}& \dfrac{{p}_{\mathrm{c}}}{2}& \dfrac{1}{2}\\ \dfrac{{p}_{\mathrm{c}}}{2}& \dfrac{{p}_{\mathrm{c}}}{2}& \dfrac{1}{2}\\ \dfrac{1}{2}& \dfrac{1}{2}& \dfrac{{p}_{\mathrm{c}}}{2}\end{array}\right]+\dfrac{{p}_{\mathrm{c}}^{*}{\bar{Q}}_{\mathrm{c}}^{*\varPsi }}{r}\left[\begin{array}{ccc}\dfrac{{p}_{\mathrm{g}}}{2}& \dfrac{{p}_{\mathrm{g}}}{2}& \dfrac{1}{2}\\ \dfrac{{p}_{\mathrm{g}}}{2}& \dfrac{{p}_{\mathrm{g}}}{2}& \dfrac{1}{2}\\ \dfrac{1}{2}& \dfrac{1}{2}& \dfrac{{p}_{\mathrm{g}}}{2}\end{array}\right]\\ {B}_{\left[\text{g/g/c/c}\right]}^{\mathrm{*}}=\dfrac{{p}_{\mathrm{g}}^{*}{\bar{Q}}_{\mathrm{g}}^{*\varPhi }}{r}\left[\begin{array}{ccc}{p}_{\mathrm{c}}& {p}_{\mathrm{c}}& \dfrac{{p}_{\mathrm{g}}}{2}\\ {p}_{\mathrm{c}}& {p}_{\mathrm{c}}& \dfrac{{p}_{\mathrm{g}}}{2}\\ \dfrac{{p}_{\mathrm{g}}}{2}& \dfrac{{p}_{\mathrm{g}}}{2}& {p}_{\mathrm{c}}\end{array}\right]+\dfrac{{p}_{\mathrm{c}}^{*}{\bar{Q}}_{\mathrm{c}}^{*\varPsi }}{r}\left[\begin{array}{ccc}-{p}_{\mathrm{g}}& -{p}_{\mathrm{g}}& \dfrac{{p}_{\mathrm{c}}}{2}\\ -{p}_{\mathrm{g}}& -{p}_{\mathrm{g}}& \dfrac{{p}_{\mathrm{c}}}{2}\\ \dfrac{{p}_{\mathrm{c}}}{2}& \dfrac{{p}_{\mathrm{c}}}{2}& -{p}_{\mathrm{g}}\end{array}\right]\\ \end{array}$

(25)

其中r表示混杂DD单元的重复次数，达到同质性要求(式(22))所需的重复单元更少时，该构型具有更好的同质性。从三者的表达式可以看出耦合刚度随DD单元数量的增加而减小，下降速率与1/r呈线性关系。 ${B}_{16}^{\mathrm{*}},{B}_{26}^{\mathrm{*}}$ 元素会受到铺层角度正负的影响，因而为了降低耦合刚度，三种构型推荐的角度设计分别为[+Φ_g/−Ψ_c/+Ψ_c/−Φ_g]，[+Φ_g/−Ψ_c/−Φ_g/+Ψ_c],[+Φ_g/−Φ_g/−Ψ_c/+Ψ_c]以减小 ${B}_{16}^{\mathrm{*}}$ , ${B}_{26}^{\mathrm{*}}$ 分量的大小。[g/c/c/g]构型的耦合刚度集中在 ${B}_{16}^{\mathrm{*}},{B}_{26}^{\mathrm{*}}$ 元素上，与[g/c/g/c] 和[g/g/c/c]相比有较大的拉扭耦合效应但不存在拉弯耦合效应。类似地，对于厚度方向上的同质性，由式(23)可以推导出DD单元构型和混杂比例对其的影响：

$\begin{array}{l}{\left|{A}^{\mathrm{*}}-{D}^{\mathrm{*}}\right|}_{\left[\text{g/c/c/g}\right]}=\dfrac{{p}_{\mathrm{g}}^{\mathrm{*}}{\bar{Q}}_{\mathrm{g}}^{\mathrm{*}}}{{r}^{2}}\left(1-{p}_{\mathrm{g}}\right)\left(2-{p}_{\mathrm{g}}\right)-\dfrac{{p}_{\mathrm{c}}^{\mathrm{*}}{\bar{Q}}_{\mathrm{c}}^{\mathrm{*}}}{{r}^{2}}\left(1-{p}_{\mathrm{c}}\right)\left(1+{p}_{\mathrm{c}}\right),\left({\bar{Q}}_{11}^{\mathrm{*}},{\bar{Q}}_{12}^{\mathrm{*}},{\bar{Q}}_{22}^{\mathrm{*}},{\bar{Q}}_{66}^{\mathrm{*}}\right)\\ {\left|{A}^{\mathrm{*}}-{D}^{\mathrm{*}}\right|}_{\left[\text{g/c/g/c}\right]}=\left\{\begin{array}{l}\dfrac{{p}_{\mathrm{g}}^{\mathrm{*}}{\bar{Q}}_{\mathrm{g}}^{\mathrm{*}}}{{r}^{2}}\left(1-{p}_{\mathrm{g}}\right)\dfrac{\left(1-2{p}_{\mathrm{g}}\right)}{2}+\dfrac{{p}_{\mathrm{c}}^{\mathrm{*}}{\bar{Q}}_{\mathrm{c}}^{\mathrm{*}}}{{r}^{2}}\left(1-{p}_{\mathrm{c}}\right)\dfrac{\left(1-2{p}_{\mathrm{c}}\right)}{2},\left({\bar{Q}}_{11}^{\mathrm{*}},{\bar{Q}}_{12}^{\mathrm{*}},{\bar{Q}}_{22}^{\mathrm{*}},{\bar{Q}}_{66}^{\mathrm{*}}\right)\\ \dfrac{{p}_{\mathrm{g}}^{\mathrm{*}}{\bar{Q}}_{\mathrm{g}}^{\mathrm{*}}}{{r}^{2}}\left(1-{p}_{\mathrm{g}}\right)\dfrac{3}{2}-\dfrac{{p}_{\mathrm{c}}^{\mathrm{*}}{\bar{Q}}_{\mathrm{c}}^{\mathrm{*}}}{{r}^{2}}\left(1-{p}_{\mathrm{c}}\right)\dfrac{3}{2},\left({\bar{Q}}_{16}^{\mathrm{*}},{\bar{Q}}_{26}^{\mathrm{*}}\right)\end{array}\right.\\ {\left|{A}^{\mathrm{*}}-{D}^{\mathrm{*}}\right|}_{\left[\text{g/g/c/c}\right]}=\left\{\begin{array}{l}\dfrac{{p}_{\mathrm{g}}^{\mathrm{*}}{\bar{Q}}_{\mathrm{g}}^{\mathrm{*}}}{{r}^{2}}\left(1-{p}_{\mathrm{g}}\right)\left(2-4{p}_{\mathrm{g}}\right)+\dfrac{{p}_{\mathrm{c}}^{\mathrm{*}}{\bar{Q}}_{\mathrm{c}}^{\mathrm{*}}}{{r}^{2}}\left(1-{p}_{\mathrm{c}}\right)\left(2-4{p}_{\mathrm{c}}\right),\left({\bar{Q}}_{11}^{\mathrm{*}},{\bar{Q}}_{12}^{\mathrm{*}},{\bar{Q}}_{22}^{\mathrm{*}},{\bar{Q}}_{66}^{\mathrm{*}}\right)\\ \dfrac{{p}_{\mathrm{g}}^{\mathrm{*}}{\bar{Q}}_{\mathrm{g}}^{\mathrm{*}}}{{r}^{2}}\left(1-{p}_{\mathrm{g}}\right)\left(\dfrac{3}{8}r+\dfrac{9}{2}{p}_{\mathrm{g}}-\dfrac{3}{4}\right)-\dfrac{{p}_{\mathrm{c}}^{\mathrm{*}}{\bar{Q}}_{\mathrm{c}}^{\mathrm{*}}}{{r}^{2}}\left(1-{p}_{\mathrm{c}}\right)\left(\dfrac{3}{8}r+\dfrac{9}{2}{p}_{\mathrm{c}}-\dfrac{3}{4}\right),\left({\bar{Q}}_{16}^{\mathrm{*}},{\bar{Q}}_{26}^{\mathrm{*}}\right)\end{array}\right. \end{array}$

(26)

[g/c/c/g]构型的 $\left|{A}_{16}^{\mathrm{*}}-{D}_{16}^{\mathrm{*}}\right|,\left|{A}_{26}^{\mathrm{*}}-{D}_{26}^{\mathrm{*}}\right|$ 项为0，其余项按1/r²的速率减小。[g/c/g/c]构型的 $\left|{A}^{*}-{D}^{*}\right|$ 收敛速度也为1/r²，但存在 ${D}_{16}^{\mathrm{*}}$ 与 ${D}_{26}^{\mathrm{*}}$ 的耦合系数，与[g/c/c/g]构型相比同质性更差。[g/g/c/c]构型的 ${D}_{16}^{\mathrm{*}}$ 与 ${D}_{26}^{\mathrm{*}}$ 项按1/r的速率减小，收敛速度更慢，同质性不如 [g/c/c/g]构型和[g/c/g/c]构型。

结合式(25)、(26)可以看出，[g/c/c/g]构型具有更少的耦合元素且收敛速度与其他构型一致，因此对于混杂DD铺层，[g/c/c/g]构型具有更好的同质性。由于B*项的收敛速度更慢，其同质性主要由 ${B}_{16}^{\mathrm{*}},{B}_{26}^{\mathrm{*}}$ 元素决定。将正角度碳纤层与正角度玻纤层分离开，可以进一步减小B*项，因此对于重复铺设混杂DD单元的构型，[+Φ_g/−Ψ_c/+Ψ_c/−Φ_g]_r具有更高的同质性。当采用对称的DD构型时，B*项为0，但 $\left|{A}^{\mathrm{*}}-{D}^{\mathrm{*}}\right|$ 项较大，同质性较差但主要体现在归一化拉伸刚度与弯曲刚度不一致上，对于只要求拉伸刚度一致的混杂DD层合板，选用对称构型[±Ф_g/±Ψ_c]_S可以更好地避免耦合效应的影响。

2. 混杂DD层合板铺层等效验证实验

2.1 材料参数与混杂比例

为了验证混杂DD层合板等效替代方法的可行性，测试了混杂准各向同性Quad层合板与等效混杂DD层合板的拉伸性能。本文所用的两种纤维预浸料如表1所示，分别为T300碳纤维增强环氧树脂单向预浸料(威海光威复合材料股份有限公司，USN03000)、S-glass玻璃纤维增强环氧树脂单向预浸料(威海光威复合材料股份有限公司，S15000)。

表 1 两种预浸料的材料参数

Table 1. Material properties of two used prepregs

Material properties	USN03000 (T300/epoxy)	G15000 (S-glass/epoxy)
Ply thickness t	0.030 mm	0.125 mm
Fiber volume fraction V_f/%	40	50
Longitudinal modulus E₁/GPa	95.5	46.4
Transverse modulus E₂/GPa	5.2	14.3
Shear modulus G₁₂/GPa	2.6	4.9
Poisson's ratio μ₂₁	0.3	0.3
Tensile strength X_t/MPa	1538	1494

下载: 导出CSV

| 显示表格

两种预浸料具有不同的单层厚度，本文研究的混杂层合板两种材料各自的层数相同，混杂比例为各自的厚度占比：p_c=0.194, p_g=0.806。两种单层材料的蔡氏模量分别为Tr(Q_c)=106.1 GPa，Tr(Q_g)=70.6 GPa。混杂层合板整体蔡氏模量和两种材料的蔡氏模量混杂比例为：

$\begin{split} Tr\left(Q\right)=&0.194\times 106.1+0.806\times 70.6=77.487\\ &{p}_{\mathrm{c}}^{\mathrm{*}}=\frac{0.194\times 106.1}{77.487}=0.266,{p}_{\mathrm{g}}^{\mathrm{*}}=0.734 \end{split}$

(27)

2.2 等效铺层方案

混杂Quad层合板与等效混杂DD层合板的示意图如图3所示。由于采用相同的混杂比例和材料进行等效替代，根据式(15)，替换前后的蔡氏模量Trace(Q)与材料参数U^*相同，因此只需要保证式(18)的铺层参数V相同即可完成铺层的等效替代。计算铺层参数V时所需的U^*参数可由混杂定律确定，此处有：

$\begin{array}{c}{U}_{{2}_{\mathrm{c}}}^{\mathrm{*}}=0.427,{U}_{{2}_{\mathrm{g}}}^{\mathrm{*}}=0.227,{U}_{{2}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}=0.280\\ {U}_{{3}_{\mathrm{c}}}^{\mathrm{*}}=0.103,{U}_{{3}_{\mathrm{g}}}^{\mathrm{*}}=0.059,{U}_{{3}_{\mathrm{h}\mathrm{y}\mathrm{b}}}^{\mathrm{*}}=0.071 \end{array}$

(28)

图 3 混杂Quad层合板与等效混杂DD层合板

Figure 3. Hybrid Quad laminate and equivalent hybrid DD laminate

下载: 全尺寸图片幻灯片

该混杂比例下可以用混杂DD层合板实现等效铺层替代的铺层参数V取值范围如图4所示。对于混杂准各向同性层合板(V₁=0, V₂=0)，在该混杂比例下，存在混杂DD单元[±Φg/±Ψc]使得替代前后的层合板刚度分布完全一致。根据式(18)，等效铺层角度计算公式为：

${\begin{aligned} {V}_{1}=\dfrac{0.266\times 0.427}{0.280}\cos2\varPsi c+\dfrac{0.734\times 0.227}{0.280}\cos2\varPhi g=0\\ {V}_{2}=\dfrac{0.266\times 0.103}{0.071}\cos4\varPsi c+\dfrac{0.734\times 0.059}{0.071}\cos4\varPhi g=0 \end{aligned}}$

(29)

其中Φ_g与Ψ_c的取值范围在[0°~90°]，求解式(29)可以得到Φ_g=63°，Ψ_c =15°或Φ_g =27°，Ψ_c=75°，即存在[±63°_g/±15°_c]、[±27°_g/ ±75°_c]两种铺层方案的混杂DD层合板实现该铺层条件下的各刚度分量等效替代。

图 4 混杂DD层合板铺层等效范围(

${p}_{\mathrm{c}}^{\mathrm{*}}=0.266$ )

Figure 4. Equivalent range of hybrid DD laminates (

${p}_{\mathrm{c}}^{\mathrm{*}}=0.266$ )

下载: 全尺寸图片幻灯片

本文主要研究混杂DD层合板拉伸性能的等效，弯曲性能沿厚度方向的同质性差异(|A^*−D^*|)不会对其造成影响，为了避免耦合效应对混杂层合板整体同质性的影响，采用对称的混杂DD构型[±Φ_g/±Ψ_c]_{2 S}(|B^*|=0)及其减薄后的构型[±Φ_g/±Ψ_c]_S来比较铺层的等效替代效果。根据式(15)可知，混杂DD对称构型与混杂DD重复构型具有相同的拉伸刚度，不影响拉伸条件下的铺层等效替代效果。具体铺层方案如表2所示，对于混杂各向同性层合板，因为要保持两种纤维层角度均衡对称，不存在更薄的Quad构型使其与混杂各向同性铺层有完全一致的刚度分量，对于混杂DD层合板，可以减少混杂DD单元的铺层重复数目来实现减薄设计，选用了减薄50%的混杂DD层合板来研究减薄后混杂DD层合板的拉伸性能特性。

表 2 对比实验的铺层方案

Table 2. Layup of comparative experiment

Layup	Thickness (mm)	Normalized stiffness [ ${Q}_{11}^{\mathrm{}},{Q}_{22}^{\mathrm{}},{Q}_{66}^{\mathrm{*}}$ ]
[0°_g/90°_g/45°_g/45°_g/ 0°_c/90°_c/45°_c/45°_c]_S ([QI_g/QI_c]_S)	1.24	[0.373,0.373,0.127]
[±27°_g/±75°_c]_2S	1.24	[0.373,0.373,0.127]
[±63°_g/±15°_c]_2S	1.24	[0.373,0.373,0.127]
[±27°_g/±75°_c]_S	0.62	[0.373,0.373,0.127]
[±63°_g/±15°_c]_S	0.62	[0.373,0.373,0.127]

下载: 导出CSV

| 显示表格

2.3 试样测试与制备

混杂层合板采用热压罐成型工艺制备得到，两款预浸料有相同的固化制度：固化压力为4.5 bar，从室温以1~2℃/min的升温速率至120℃，在120℃保温90 min，最后自然降温至60℃以下脱模。准静态拉伸试验根据标准ASTM D3039^[27]进行测试，拉伸试样的总长度为150 mm，宽度为15 mm。拉伸测试在室温下进行，以1 mm/min的速率进行准静态加载。加载力值由试验机测定，试样的应变值由50 mm跨度的引伸计进行测量。为了获得可靠的实验数据，同组别层合板试样不少于 5 个。试样拉伸应力由式计算：

$\sigma =\frac{P}{W\cdot H}$

(30)

其中：P为外加拉伸载荷，由试验机测定；W和H分别为试样宽度和厚度。

3. 实验结果与讨论

3.1 混杂QI层合板与DD层合板拉伸性能对比

图5为混杂准各向同性层合板与等效替代后的混杂DD层合板的代表性拉伸应力应变曲线。结果显示，等效替代前后的混杂层合板具有类似的刚度表现与应力应变响应。表3为混杂QI层合板与等效混杂DD层合板的刚度与拉伸强度，结果显示，混杂准各向同性层合板与等效的混杂DD层合板的刚度误差小于3%，说明DD层合板的等刚度替代在混杂层合板中也能实现。三种构型的最终失效应变和失效应力有所不同(误差−15.3%~+2.1%)，主要是因为不同混杂DD单元的铺层角度影响了层合板的失效模式。[±63°_g/ ±15°_c]_{2 S}与[±27°_g/±75°_c]_{2 S}构型在碳纤层发生断裂之前就发生了层合板整体失效，因此都表现出“一级破坏”的失效模式。[±63°_g/±15°_c]_{2 S}构型由于玻纤层的角度较大，因此加载方向上玻纤层强度较低，发生玻纤层的基体横向破坏，在三种构型中最先失效。并且由于玻纤层的混杂比例较高，玻纤层的基体塑性的影响更大，±63°_g铺层有较大的纤维偏角，因此表现出更多的基体塑性，应力应变曲线略低于其他两种等价铺层。[±27°_g/ ±75°_c]_{2 S}构型的玻纤层角度较小，在加载方向上有更高的强度，表现出最高的失效平均应力，但由于玻纤层单层厚度较大，因此存在较大的自由边缘层间应力，限制了层合板的强度。混杂准各向同性层合板由于在拉伸方向上存在0°纤维，因此具有更小的碳纤层断裂应变。0°碳纤层断裂导致中间层分层，损失部分刚度，应力应变曲线表现出台阶状，表现为“二级破坏”的失效模式。

图 5 混杂QI层合板与等效混杂DD层合板拉伸应力应变代表性曲线

Figure 5. Tensile representative stress-strain response of hybrid QI laminates and equivalent hybrid DD laminates

下载: 全尺寸图片幻灯片

表 3 混杂QI层合板与等效混杂DD层合板的刚度与拉伸强度

Table 3. Stiffness and tensile strength of hybrid QI laminates and equivalent hybrid DD laminates

Layup	Stiffness/GPa	CV/%	Strength/MPa	CV/%
[QI_g/QI_c]_S	28.2	1.3	415.8	3.6
[±27°_g/±75°_c]_{2 S}	29.0	3.0	424.3	2.4
[±63°_g/±15°_c]_{2 S}	27.7	2.6	352.3	5.1

下载: 导出CSV

| 显示表格

图6展示了三种等效构型的试样失效形态。混杂准各向同性铺层[QI_g/QI_c]_S表现出部分纤维断裂和分层过程，由于0°碳纤层比例较小，因此产生的分层区域的面积较少。分层区域的玻纤层承担碳纤层失效后的额外载荷，当玻纤层的0°层发生纤维断裂后层合板整体失效。[±27°_g/±75°_c]_2S构型试样发生自由边缘分层破坏，最外侧的玻纤层表现出边缘部分的翘起与分层，分层区域边缘的角度沿着表面玻纤层的纤维方向。产生翘起与分层的原因是在靠近试样边缘处有较大的层间压力。当从自由边缘引发的分层区域贯穿试样宽度时，整体层合板发生失效。层合板自由边缘应力的大小受到铺层重复次数影响，在层合板整体厚度相同的情况下，使用更小单层厚度的预浸料能增加铺层单元的重复次数，从而减弱自由边上的层间应力集中效应，预计表现出更高的层合板强度。[±63°_g/±15°_c]_2S构型试样表现出基体横向破坏的最终失效模式，层合板整体由于玻纤层的基体横向破坏而失效。中间层碳纤维在层合板整体失效之前没有发生纤维断裂和中间层分层，试样表面没有出现分层损伤。同时能从试样表面观察到玻纤层发生了纤维角度偏转。

图 6 混杂QI层合板与等效混杂DD层合板拉伸试样失效形态

Figure 6. Failure morphology of tensile specimens of hybrid QI laminates and equivalent hybrid DD laminates

下载: 全尺寸图片幻灯片

3.2 减薄后混杂DD层合板拉伸性能对比

为了验证混杂DD层合板在减薄设计方面的优势，对比了减薄厚度对等效混杂层合板的性能影响。实验了[±27°_g/±75°_c]_S构型和[±63°_g/±15°_c]_S构型的拉伸应力应变响应并与减薄前的构型进行比较，实验的代表性拉伸应力应变曲线如图7所示。结果表明，减薄后的构型具有和减薄前基本一致的应力应变响应与刚度变化情况，混杂DD层合板也能做到铺层刚度等效和减薄设计。表4显示了减薄前后构型的失效应力应变，结果显示，减薄后的[±63°_g/±15°_c]_S构型的失效应力应变与减薄前基本一致，这是因为该混杂DD层合板的失效模式主要为玻纤层的基体横向破坏，减薄后对基体的强度影响不大，因此表现出基本一致的失效应力应变。减薄后的 [±27°_g/±75°_c]_S构型在与减薄前相比的强度有所减低，这是因为更薄的试样总厚度使得单层厚度占层合板总厚度的比例更大，自由边缘层间应力的集中作用更大，更容易发生自由边缘分层破坏。

图 7 减薄前后等效混杂DD层合板拉伸应力应变代表性曲线

Figure 7. Tensile representative stress-strain response of thinning equivalent hybrid DD laminates

下载: 全尺寸图片幻灯片

表 4 减薄等效混杂DD层合板的刚度与拉伸强度

Table 4. Stiffness and tensile strength of thinning equivalent hybrid DD laminates

Layup	Stiffness/GPa	CV/%	Strength/MPa	CV/%
[±27°_g/±75°_c]_{2 S}	29.0	3.0	424.3	2.4
[±27°_g/±75°_c]_S	28.7	1.8	367.2	4.2
[±63°_g/±15°_c]_{2 S}	27.7	2.6	352.3	5.1
[±63°_g/±15°_c]_S	27.3	2.2	344.9	4.8

下载: 导出CSV

| 显示表格

图8为减薄构型失效应力应变及模型预测情况与失效试样形态。减薄前后试样表现出相同的失效模式。[±27°_g/±75°_c]_S构型发生自由边缘分层，边缘分层的作用区域相比于减薄前的构型更少，这是由于层合板整体厚度下降，受到自由边缘的层间应力影响的范围更小，但相对的单层厚度占层合板总厚度的比例增大，产生更大的层间应力，导致自由边缘分层提前发生，相比减薄前[±27°_g/±75°_c]_2S构型的失效应力有所下降。 [±63°_g/±15°_c]_S构型发生基体横向破坏，失效应力不受试样厚度以及单层尺寸的影响，与减薄前的±63°_g/±15°_c]_2S构型的拉伸性能基本一致。

图 8 减薄后等效混杂DD层合板拉伸试样失效形态

Figure 8. Failure morphology of thinning equivalent hybrid DD laminates

下载: 全尺寸图片幻灯片

综合理论和实验结果来看，减薄后的混杂DD构型也可以做到刚度等效替代的同时保持相同的失效模式与接近的强度水平，在进行构件的变厚度(锥度设计)以及局部加厚或减薄设计方面具有一定优势。

4. 结论

研究了蔡氏模量和DD层合板设计在混杂条件下的应用，给出了混杂DD层合板的设计方法与铺层等效设计流程。通过铺层替代实验验证了混杂DD层合板刚度等效与减薄设计的可行性。得到的结论如下：

(1)混杂DD层合板的归一化刚度满足关于蔡氏模量混杂比例p*的混杂定律形式。铺层参数V在混杂DD层合板中会受到混杂比例、纤维类型的影响，同时混杂比例会影响能够进行铺层等效设计范围。

(2)混杂DD层合板的同质性受到混杂比例与叠层方式的影响。[g/c/c/g]构型具有更少的刚度矩阵耦合项，|B*|项按1/r的速率收敛，|A*−D*|按1/r²的速率收敛。混杂DD层合板的最优铺层策略为：重复构型[+Φ_g/−Ψ_c/+Ψ_c/−Φ_g]_r(拉弯一致)或对称构型[±Ф_g/±Ψ_c]_S(拉弯无耦合)。

(3)混杂DD层合板也能实现铺层的等效替代，替代后的混杂DD层合板具有与替代前一致的刚度分量，但失效模式和失效强度会受到具体铺层构型的影响。混杂DD层合板也能实现铺层的减薄设计，减薄后的混杂DD层合板也具有相同的刚度分量，但可能因为更大的层间应力而导致提前失效。

图 1 芳纶纳米纤维薄膜 (ANFm)和PI-ANFm-PI (P-A-P)薄膜的制备流程图

Figure 1. Scheme of fabrication procedures for aramid nanofiber film (ANFm) and polyimide-ANFm-polyimide (P-A-P) films

PPTA—Poly-p-phenylene terephthamide; NMP—N-methylpyrrolidone; DMSO—Dimethyl sulphoxide

下载: 全尺寸图片幻灯片

图 2 (a)去质子化过程中ANF/DMSO分散液的光学图片；ANF的TEM图像(b)、PPTA和ANF的红外光谱(c)和XRD谱图(d)

Figure 2. (a) Digital photos of an aramid nanofiber (ANF)/DMSO dispersion during deprotonation process; TEM image of ANF (b), FTIR spectra (c) and XRD patterns (d) of PPTA and ANF

下载: 全尺寸图片幻灯片

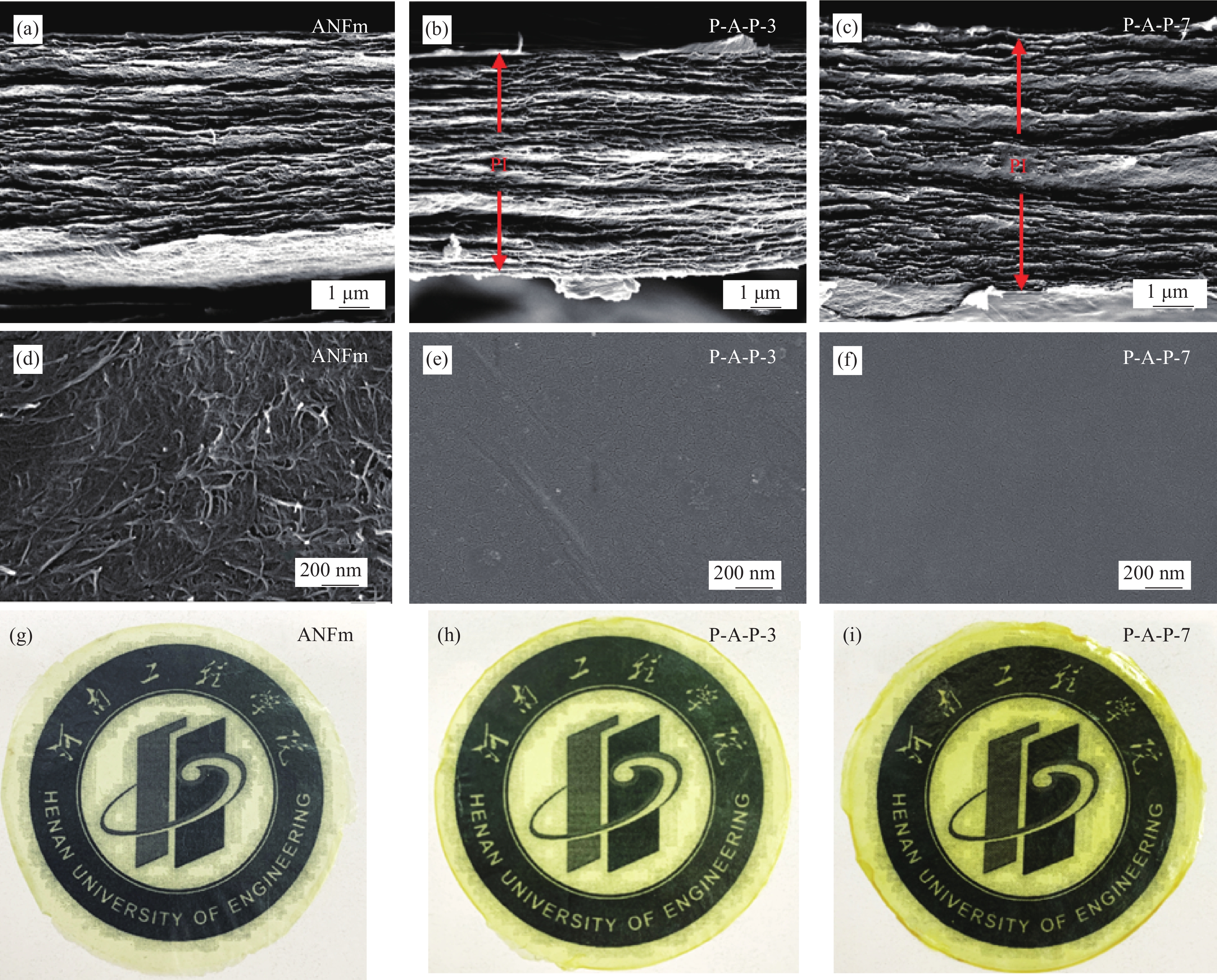
图 3 横截面形貌：ANFm (a)、P-A-P-3 (b)、P-A-P-7 (c)；表面形貌：ANFm (d)、P-A-P-3 (e)、P-A-P-7 (f)；光学图片：ANFm (g)、P-A-P-3 (h)、P-A-P-7 (i)

Figure 3. Cross-sectional morphologies of ANFm (a), P-A-P-3(b), and P-A-P-7 (c); Surface morphologies of ANFm (d), P-A-P-3 (e), and P-A-P-7 (f); Digital photos of ANFm (g), P-A-P-3 (h), and P-A-P-7 (i)

下载: 全尺寸图片幻灯片

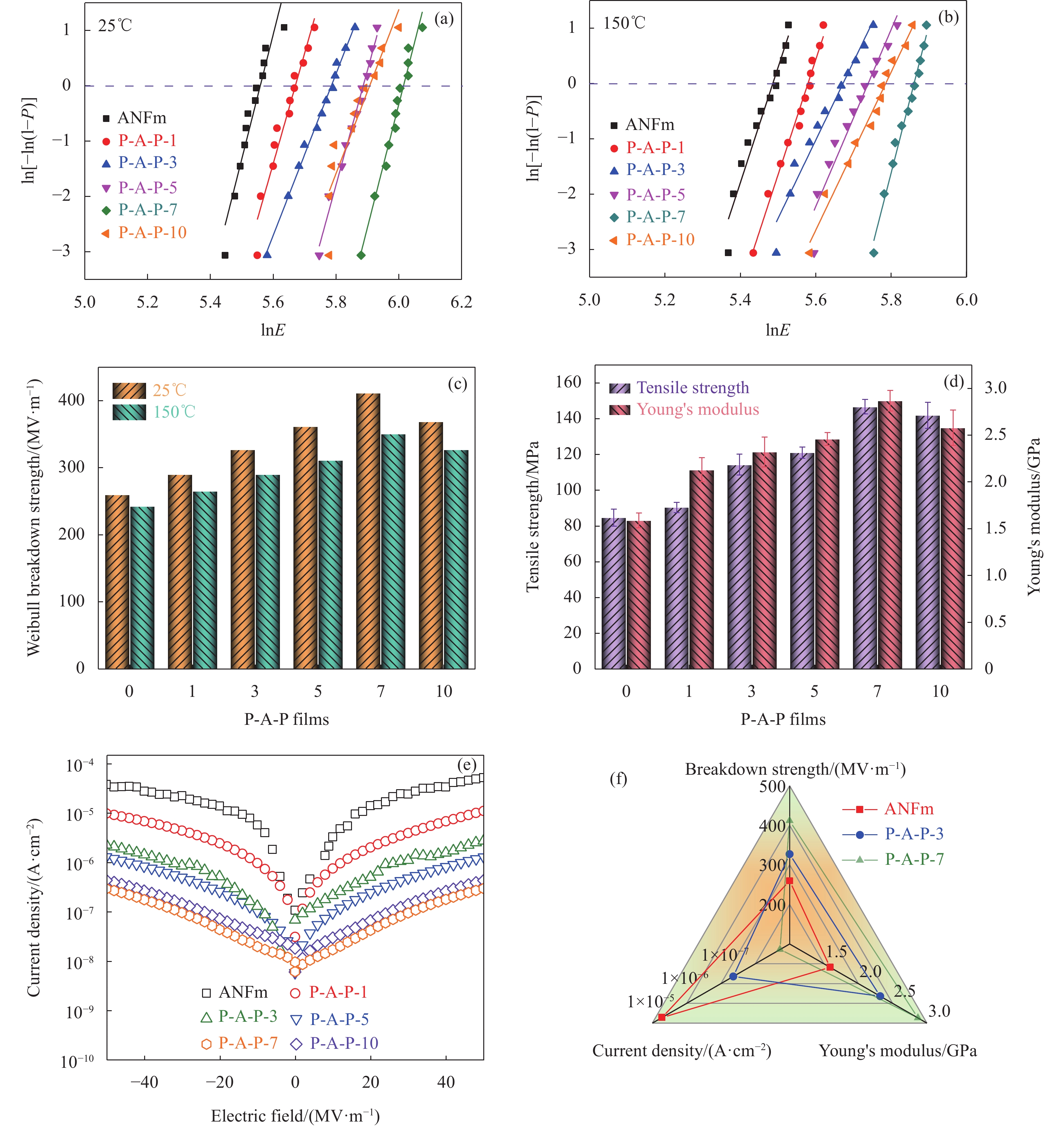
图 4 ANFm和P-A-P复合薄膜25℃ (a)和150℃ (b)的击穿强度威布尔分布、25℃和150℃的击穿强度对比图(c)、力学性能(d)和漏电流密度(e)；(f) ANFm、P-A-P-3和P-A-P-7薄膜击穿强度、漏电流密度和杨氏模量的雷达图

Figure 4. Weibull distribution of breakdown strength at 25℃ (a) and 150℃ (b), comparison of breakdown strength at 25℃ and 150℃ (c), mechanical properties (d), and leakage current density (e) for ANFm and P-A-P composite films; (f) Radar chart of breakdown strength, leakage current density, and Young's modulus for ANFm, P-A-P-3, and P-A-P-7 films

E—Breakdown strength; P—Polarization intensity

下载: 全尺寸图片幻灯片

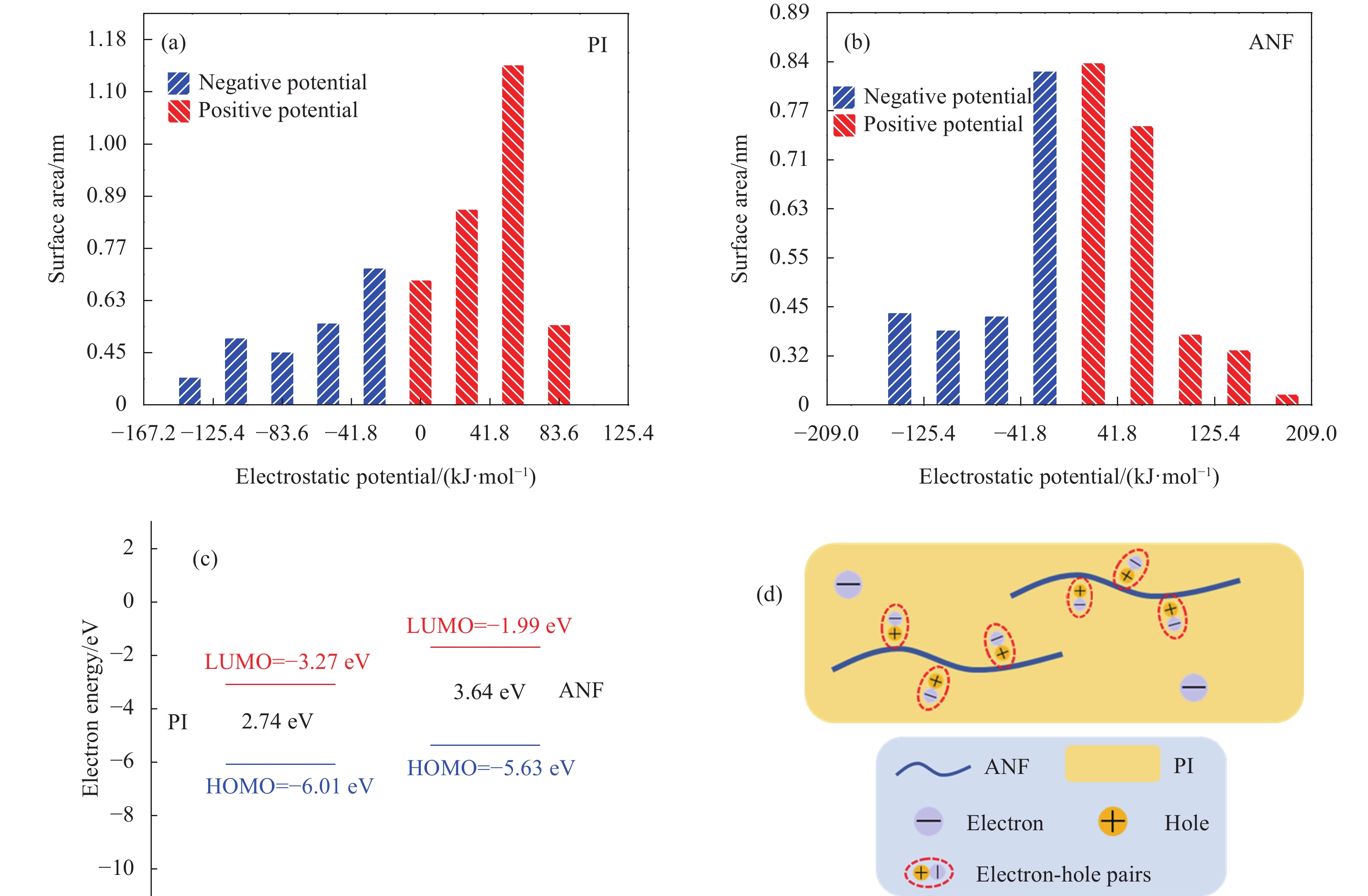
图 5 PI (a)和ANF (b)的静电势分布及各静电势范围内的面积百分比；(c) PI和ANF的分子轨道能级示意图；(d)电子-空穴对的形成与作用机制

Figure 5. Electrostatic potential (ESP) distributions and normalized ESP area distribution statistics of PI (a) and ANF (b); (c) Molecular orbital energy levels of PI and ANF; (d) Formation and mechanism of action of electron-hole pairs

LUMO—Lowest unoccupied molecular orbital; HOMO—Highest occupied molecular orbital

下载: 全尺寸图片幻灯片

图 6 ANFm和P-A-P复合薄膜的介电常数(a)、介电损耗(b)和电导率(c)；P-A-P-7在25℃和150℃下的介电常数(d)、介电损耗(e)和电导率(f)

Figure 6. Dielectric constant (a), dielectric loss (b) and conductivity (c) of ANFm and P-A-P films; Dielectric constant (d), dielectric loss (e) and conductivity (f) of P-A-P-7 at 25℃ and 150℃

下载: 全尺寸图片幻灯片

表 1 材料参数

Table 1 Materials parameters

Samples	outer layer	Middle layer	Thickness of sample/μm	Concentration of PI solution/wt%
P-A-P-1	PI	ANF	14.7	1
P-A-P-3			14.9	3
P-A-P-5			15.2	5
P-A-P-7			15.0	7
P-A-P-10			14.6	10
Notes: PI—Polyimide; ANF—Aramid nanofiber.

下载: 导出CSV

参考文献(35)

[1]	ZHA J W, XIAO M Y, WAN B, et al. Polymer dielectrics for high-temperature energy storage: Constructing carrier traps[J]. Progress in Materials Science, 2023, 140: 101208. DOI: 10.1016/j.pmatsci.2023.101208
[2]	LI H, REN L L, ZHOU Y, et al. Recent progress in polymer dielectrics containing boron nitride nanosheets for high energy density capacitors[J]. High Voltage, 2020, 5(4): 365-376. DOI: 10.1049/hve.2020.0076
[3]	ZHA J W, ZHENG M S, FAN B H, et al. Polymer-based dielectrics with high permittivity for electric energy storage: A review[J]. Nano Energy, 2021, 89: 106438. DOI: 10.1016/j.nanoen.2021.106438
[4]	董久锋, 邓星磊, 牛玉娟, 等. 面向高温介电储能应用的聚合物基电介质材料研究进展[J]. 物理学报, 2020, 69(21): 217701. DOI: 10.7498/aps.69.20201006 DONG Jiufeng, DENG Xinglei, NIU Yujuan, et al. Research progress of polymer-based dielectrics for high-temperature capacitor energy storage[J]. Acta Physica Sinica, 2020, 69(21): 217701(in Chinese). DOI: 10.7498/aps.69.20201006
[5]	李琦, 李曼茜. 高温聚合物薄膜电容器介电材料评述与展望[J]. 高电压技术, 2021, 47(9): 3105-3123. LI Qi, LI Manxi. High-temperature polymer dielectrics for film capacitors: Review and prospect[J]. High Voltage Engineering, 2021, 47(9): 3105-3123(in Chinese).
[6]	LI H, ZHOU Y, LIU Y, et al. Dielectric polymers for high-temperature capacitive energy storage[J]. Chemical Society Reviews, 2021, 50(11): 6369-6400. DOI: 10.1039/D0CS00765J
[7]	LI Q, YAO F Z, LIU Y, et al. High-temperature dielectric materials for electrical energy storage[J]. Annual Review of Materials Research, 2018, 48: 219-243. DOI: 10.1146/annurev-matsci-070317-124435
[8]	DUAN G Y, HU F Y, ZHANG R N, et al. Preparation of a novel cross-linked polyetherimide with enhanced breakdown strength and high-temperature energy storage performance[J]. High Voltage, 2023, 8(3): 630-639. DOI: 10.1049/hve2.12280
[9]	ZHANG Q Y, CHEN X, ZHANG B, et al. High-temperature polymers with record-high breakdown strength enabled by rationally designed chain-packing behavior in blends[J]. Matter, 2021, 4(7): 2448-2459. DOI: 10.1016/j.matt.2021.04.026
[10]	HASSAN Y A, HU H. Current status of polymer nanocomposite dielectrics for high-temperature applications[J]. Composites Part A: Applied Science and Manufacturing, 2020, 138: 106064. DOI: 10.1016/j.compositesa.2020.106064
[11]	WANG Y F, CHEN J, LI Y, et al. Multilayered hierarchical polymer composites for high energy density capacitors[J]. Journal of Materials Chemistry A, 2019, 7(7): 2965-2980. DOI: 10.1039/C8TA11392K
[12]	BAER E, ZHU L. 50th anniversary perspective: Dielectric phenomena in polymers and multilayered dielectric films[J]. Macromolecules, 2017, 50(6): 2239-2256. DOI: 10.1021/acs.macromol.6b02669
[13]	WANG P, PAN Z B, WANG W, et al. Ultrahigh energy storage performance of a polymer-based nanocomposite via interface engineering[J]. Journal of Materials Chemistry A, 2021, 9(6): 3530-3539. DOI: 10.1039/D0TA10044G
[14]	WANG C, HE G H, CHEN S, et al. Enhanced performance of all-organic sandwich structured dielectrics with linear dielectric and ferroelectric polymers[J]. Journal of Materials Chemistry A, 2021, 9(13): 8674-8684. DOI: 10.1039/D1TA00974E
[15]	FENG Q K, ZHONG S L, PEI J Y, et al. Recent progress and future prospects on all-organic polymer dielectrics for energy storage capacitors[J]. Chemical Reviews, 2021, 122(3): 3820-3878.
[16]	SU L Y, MA X Y, ZHOU J L, et al. Large-scale preparation of high-performance boron nitride/aramid nanofiber dielectric composites[J]. Nano Research, 2022, 15: 8648-8655. DOI: 10.1007/s12274-022-4456-6
[17]	VU M C, KANG H, PARK P J, et al. Scalable graphene fluoride sandwiched aramid nanofiber paper with superior high-temperature capacitive energy storage[J]. Chemical Engineering Journal, 2022, 444: 136504. DOI: 10.1016/j.cej.2022.136504
[18]	SANKHLA S, NATH A, NEOGI S. Preparation of aramid-cellulose nanofiber films with improved mechanical and dielectric properties utilizing environmentally friendly hydrothermal treatment for electrical insulation[J]. ACS Sustainable Chemistry & Engineering, 2023, 11(23): 8420-8430.
[19]	MANZETTI S, LU T. The geometry and electronic structure of Aristolochic acid: Possible implications for a frozen resonance[J]. Journal of Physical Organic Chemistry, 2013, 26(6): 473-483. DOI: 10.1002/poc.3111
[20]	LU T, MANZETTI S. Wavefunction and reactivity study of benzo[a]pyrene diol epoxide and its enantiomeric forms[J]. Structural Chemistry, 2014, 25: 1521-1533. DOI: 10.1007/s11224-014-0430-6
[21]	ZHANG J, LU T. Efficient evaluation of electrostatic potential with computerized optimized code[J]. Physical Chemistry Chemical Physics, 2021, 23(36): 20323-20328. DOI: 10.1039/D1CP02805G
[22]	YANG M, CAO K Q, SUI L, et al. Dispersions of aramid nanofibers: A new nanoscale building block[J]. ACS Nano, 2011, 5(9): 6945-6954. DOI: 10.1021/nn2014003
[23]	CHEN H J, BAI Q Y, LIU M C, et al. Ultrafast, cost-effective and scaled-up recycling of aramid products into aramid nanofibers: Mechanism, upcycling, closed-loop recycling[J]. Green Chemistry, 2021, 23(19): 7646-7658. DOI: 10.1039/D1GC01805A
[24]	YANG B, WANG L, ZHANG M Y, et al. Timesaving, high-efficiency approaches to fabricate aramid nanofibers[J]. ACS Nano, 2019, 13(7): 7886-7897. DOI: 10.1021/acsnano.9b02258
[25]	LUO S B, ANSARIT Q, YU J Y, et al. Enhancement of dielectric breakdown strength and energy storage of all-polymer films by surface flattening[J]. Chemical Engineering Journal, 2021, 412: 128476. DOI: 10.1016/j.cej.2021.128476
[26]	FENG M J, FENG Y, ZHANG T D, et al. Recent advances in multilayer-structure dielectrics for energy storage application[J]. Advanced Science, 2021, 8(23): 2102221. DOI: 10.1002/advs.202102221
[27]	LI X, TUNG C H, PEY K L. The nature of dielectric breakdown[J]. Applied Physics Letters, 2008, 93(7): 072903.
[28]	FENG Q K, PING J B, ZHU J, et al. All-organic dielectrics with high breakdown strength and energy storage density for high-power capacitors[J]. Macromolecular Rapid Communications, 2021, 42(12): 2100116. DOI: 10.1002/marc.202100116
[29]	YAN J J, WANG H, ZENG J Y, et al. Carboxylated poly(p-phenylene terephthalamide) reinforced polyetherimide for high-temperature dielectric energy storage[J]. Small, 2023, 19(42): 2304310. DOI: 10.1002/smll.202304310
[30]	YAN C F, WAN Y T, LONG H P, et al. Improved capacitive energy storage at high temperature via constructing physical cross-link and electron-hole pairs based on p-type semiconductive polymer filler[J]. Advanced Functional Materials, 2024, 34(8): 2312238. DOI: 10.1002/adfm.202312238
[31]	XU D, XU W H, SEERY T, et al. Rational design of soluble polyaramid for high-efficiency energy storage dielectric materials at elevated temperatures[J]. Macromolecular Materials and Engineering, 2020, 305(3): 1900820. DOI: 10.1002/mame.201900820
[32]	THAKUR V K, GUPTA R K. Recent progress on ferroelectric polymer-based nanocomposites for high energy density capacitors: Synthesis, dielectric properties, and future aspects[J]. Chemical Reviews, 2016, 116(7): 4260-4317. DOI: 10.1021/acs.chemrev.5b00495
[33]	JIANG Y D, ZHOU M J, SHEN Z H, et al. Ferroelectric polymers and their nanocomposites for dielectric energy storage applications[J]. APL Materials, 2021, 9: 020905. DOI: 10.1063/5.0039126
[34]	WANG T T, WEI C M, YAN L, et al. Thermally conductive, mechanically strong dielectric film made from aramid nanofiber and edge-hydroxylated boron nitride nanosheet for thermal management applications[J]. Composite Interfaces, 2021, 28(11): 1067-1080. DOI: 10.1080/09276440.2020.1855573
[35]	DUAN G Y, CAO Y T, QUAN J Y, et al. Bioinspired construction of BN@polydopamine@Al₂O₃ fillers for preparation of a polyimide dielectric composite with enhanced thermal conductivity and breakdown strength[J]. Journal of Materials Science, 2020, 55: 8170-8184. DOI: 10.1007/s10853-020-04596-5

施引文献

资源附件(1)

其他相关附件
- 本文图文摘要
  10.13801-j.cnki.fhclxb.20240522.002-GA1 点击下载

长摘要

目的
目前，通用聚合物电介质极限使用温度较低(<100 ℃)，无法满足高温环境(>150 ℃)应用要求，急需开发在宽温域中具有良好储能特性的新型聚合物电介质材料。对于聚合物电介质材料，其储能密度(U)与其介电常数(ε)和击穿强度(E)的二次方成正比。但由于击穿强度与介电常数间存在内禀矛盾关系(E~1/ε)，即击穿强度的提升往往伴随着介电常数的下降，进而影响到聚合物电介质薄膜储能特性的改善。为了打破介电常数与击穿强度间的内禀矛盾，基于不同聚合物功能层(极化层、绝缘层、过渡层等)，通过调控空间组装工艺构筑多层聚合物电介质薄膜是目前的主流方法。在多层结构中，特殊的空间电场分布机制赋予绝缘层更高的电场强度，而极化层和多尺度界面结构则通过偶极子极化和Maxwell-Wagner-Sillars(MWS)界面极化提升了介电常数。此外，除了提升聚合物电介质材料的U外，其在高温环境中急剧增加的电导损耗会将储存的电能转化为焦耳热，不但降低了储能特性，同时还会引起热击穿。因此，抑制高温、强电场下聚合物电介质材料内部的电导损耗有助于提升其放电能量密度(U)和充放电效率(η)，优化其高温、强电场环境中的储能特性。
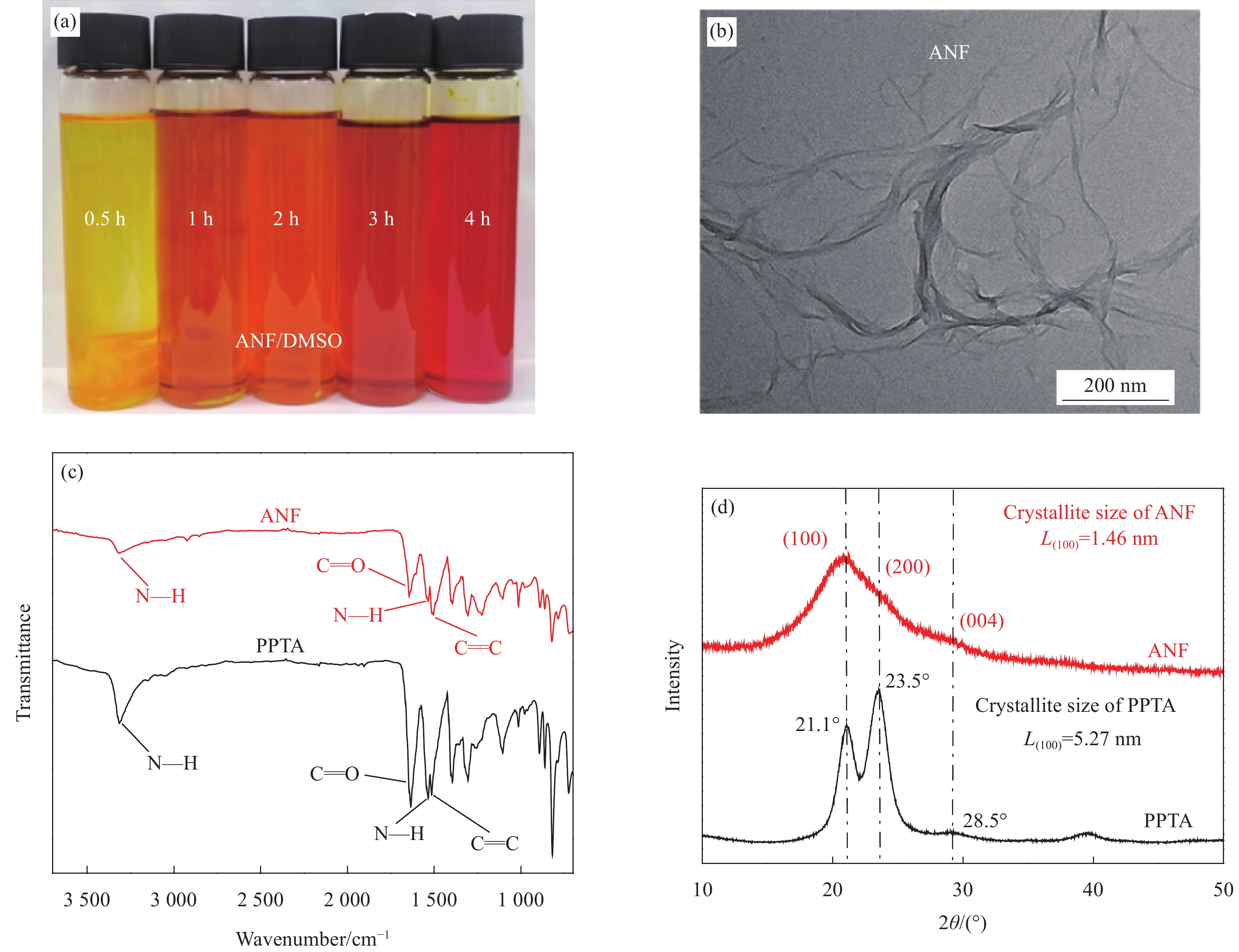
方法
为了制备高温、强电场环境中具有良好储能特性的聚合物电介质材料，首先采用去质子化法制备了芳纶纳米纤维(ANF)，随后真空抽滤制备芳纶纳米纤维薄膜(ANFm)。基于ANFm和可溶性聚酰亚胺(PI，型号P84)，采用浸渍提拉法构筑了具有三明治结构的全有机PI-ANFm-PI(P-A-P)复合薄膜。ANFm具有较高的介电常数以及出众的热学稳定性能；PI具有极高的击穿强度和玻璃化温度，能够满足高温电介质材料的应用需求。研究了三明治结构P-A-P复合薄膜宽在温域内的介电性能、击穿强度、储能特性等。
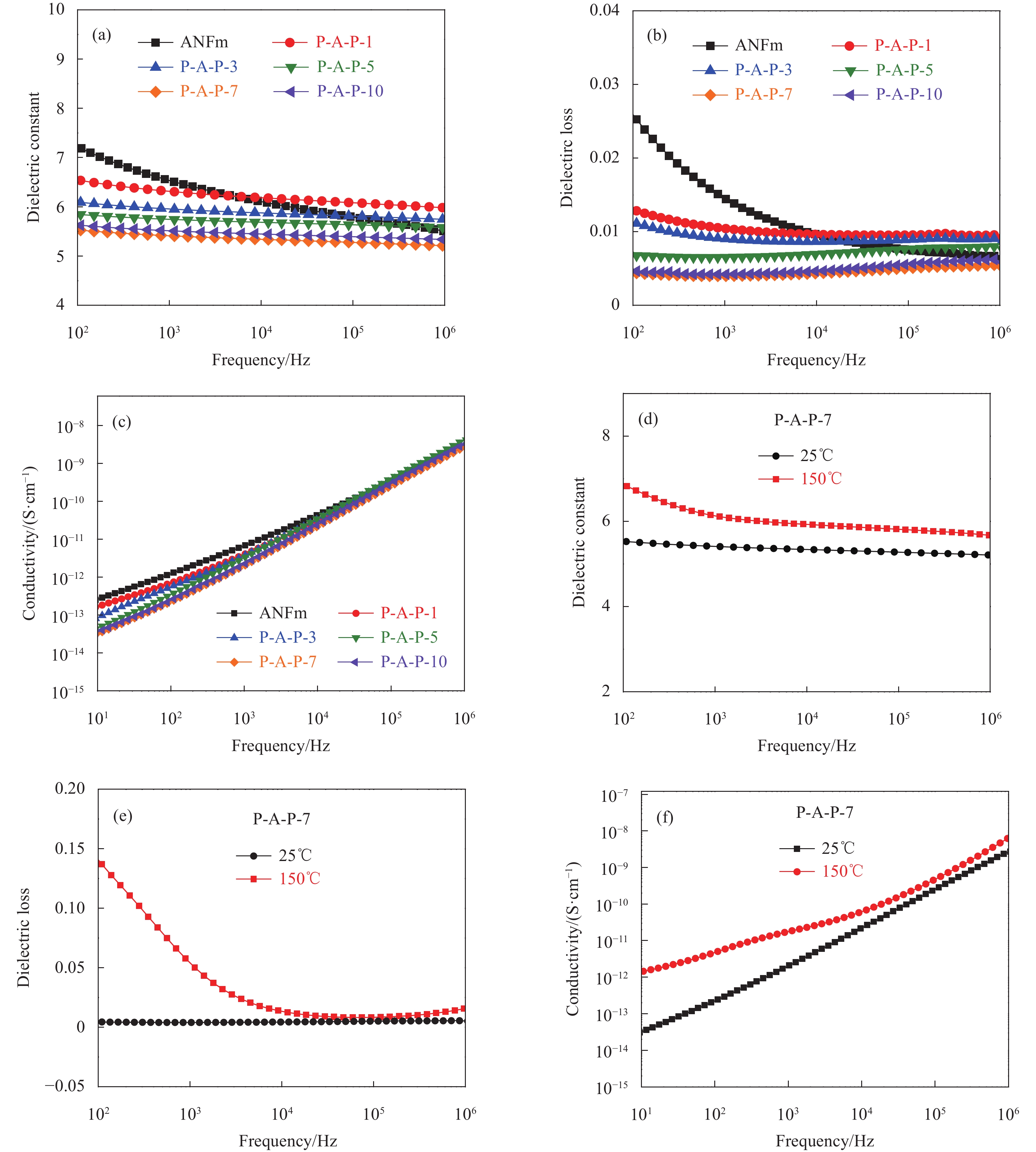
结果
采用浸渍提拉法构筑的P-A-P复合薄膜结构密实。测试结果表明：(1)上下PI层的形成有效降低了ANFm的表面粗糙度，有效避免了电子在电介质薄膜与电极界面处的聚集，抑制了电子的注入；此外，由于PI的LUMO能级与ANF的HOMO能级差别较小(2.36 eV)，PI层的电子与ANF的空穴在库仑力的作用下形成电子-空穴对，作为电子陷阱能够捕获空间载流子，减少P-A-P电介质内部载流子的迁移；(2)随着PI层厚度的增加以及内部漏电流密度的降低，P-A-P复合薄膜的在25 ℃和150 ℃下的击穿强度达411.6 MV/m和350.7 MV/m，较单层ANF薄膜分别提升了58.4%和44.7%；(3)PI层的形成提升了P-A-P复合薄膜的介电稳定性，并且介电损耗随着PI溶液浓度的增加逐渐降低，绝缘性能随着PI溶液浓度的增加逐渐增大。
结论
本文通过在芳纶纳米纤维薄膜(ANFm)两侧形成聚酰亚胺(PI)层构筑了具有三明治结构的全有机PI-ANFm-PI(P-A-P)复合薄膜。PI层不但有效抑制了P-A-P复合薄膜内部漏电流的形成，提升了击穿强度，同时增强了P-A-P复合薄膜的介电稳定性，为开发全有机高温电介质薄膜提供了新方法和新思路。

创新点

随着混合电动汽车、油气勘探技术、航天电力系统的发展及应用环境的复杂化，对聚合物基电介质材料宽温域内的介电性能和击穿强度提出更高要求。目前广泛使用的聚合物电介质薄膜为双向拉伸聚丙烯(BOPP)，但其的热稳定性欠佳，高温下的介电稳定性和击穿强度急剧下降，无法满足高温应用需求。
本文通过采用浸渍提拉法，基于聚酰亚胺(PI)溶液和芳纶纳米纤维薄膜(ANFm)构筑了具有三明治结构的全有机PI-ANFm-PI(P-A-P)复合电介质薄膜。由于PI层的形成的有效降低了ANFm的表面粗糙度，抑制了空间电荷在P-A-P复合薄膜表面的聚集，减少了电极处电子的注入；同时，P-A-P复合薄膜内部电子-空穴对的形成有效抑制了内部载流子的迁移，降低了P-A-P复合薄膜的漏电流密度。因此，P-A-P复合薄膜在25 ℃和150 ℃下的最大击穿强度分别达411.6 MV/m和350.7 MV/m，较ANFm分别提升了58.4%和44.7%，并且PI层的形成提升了P-A-P复合薄膜的介电稳定性，降低了介电损耗。本研究有望为开发新型全有机高温电介质材料提供新方法和新思路。
1
ANFm和P-A-P复合薄膜(a)25 ℃和(b)150 ℃的击穿强度威布尔分布