Static strength reliability and sensitivity analysis of large composite structures based on surrogate models
-
摘要: 基于代理模型的结构可靠性分析方法目前已有多种代理模型和多种失效概率计算方法,参数灵敏度分析也存在多种灵敏度指标,为探讨大尺寸复合材料结构可靠性分析方法,并研究不同代理模型和计算方法对民机复合材料结构静强度预测结果的差异性,以某型飞机碳纤维复合材料升降舵结构为研究对象,考虑单层板力学性能、厚度、密度和不同部位铺层角度等17种输入变量的不确定性,利用Matlab和Optistruct仿真软件,构建Kriging、PC-Kriging和支持向量回归机(SVR)三种代理模型,结合MCS和Subset两种方法求解结构失效概率,根据代理模型验证误差选取最准确的代理模型计算Morris基本效应筛选指标和Sobol指标,从而获得关键设计参数排序,为民机复合材料结构可靠性设计提供参考。Abstract: Multiple surrogate models and multiple calculation methods of structural probability of failure were proposed for the structural reliability analysis based on surrogate model. Multiple sensitivity indices were also proposed for the sensitivity analysis of input variables. For the purpose of studying the reliability analysis methods for large composite structures, and studying the differences among different surrogate models and methods to predict the static strength of composite structures of civil aircrafts, a composite elevator of a certain aircraft was taken as an example. The uncertainty of 17 input variables were considered, including mechanical properties, thickness, density and ply angles. Matlab and Optistruct softwares were used to obtain three surrogate models, including Kriging, PC-Kriging and SVR models. MCS and Subset simulate methods were applied to calculate the structural probability of failure. The best surrogate model can be obtained by comparing validation errors. The critical design parameters can be obtained by the importance ranking based on Morris elementary effects and Sobol indices, which is useful for the design of civil aircraft composite structures.
-
Key words:
- composite structure /
- surrogate modelling /
- Kriging model /
- reliability analysis /
- sensitivity analysis
-
表 1 复合材料升降舵结构随机输入变量正态分布
Table 1. Normal distribution of random input variables of the composite elevator structure
Variable Mean Standard deviation Description E11 /GPa 60 6.0 Elastic modulus in 11 direction E22 /GPa 54 5.4 Elastic modulus in 22 direction G12 /GPa 3.7 0.37 Elastic modulus in 12 direction G13 /GPa 3.0 0.30 Elastic modulus in 13 direction G23 /GPa 3.0 0.30 Elastic modulus in 23 direction ρ /(kg·m−3) 1440 144.0 Density Xt /MPa 830 83.0 Longitudinal tensile strength Xc /MPa 650 65.0 Longitudinal compressive strength Yt /MPa 250 25.0 Transverse tensile strength Yc /MPa 230 23.0 Transverse compressive strength S12 /MPa 100 10.0 In-plane shear strength t /mm 0.216 0.0216 Thickness of a lamina α1/(°) 0 4.5 (0°,90°) ply angle for skin panel α2/(°) 45 4.5 (±45°) ply angle for skin panel α3/(°) 0 4.5 (0°,90°) ply angle for spar α4/(°) 45 4.5 (±45°) ply angle for spar α5/(°) 45 4.5 (±45°) ply angle for ribs 表 2 基于不同代理模型的模型误差和失效概率结果对比
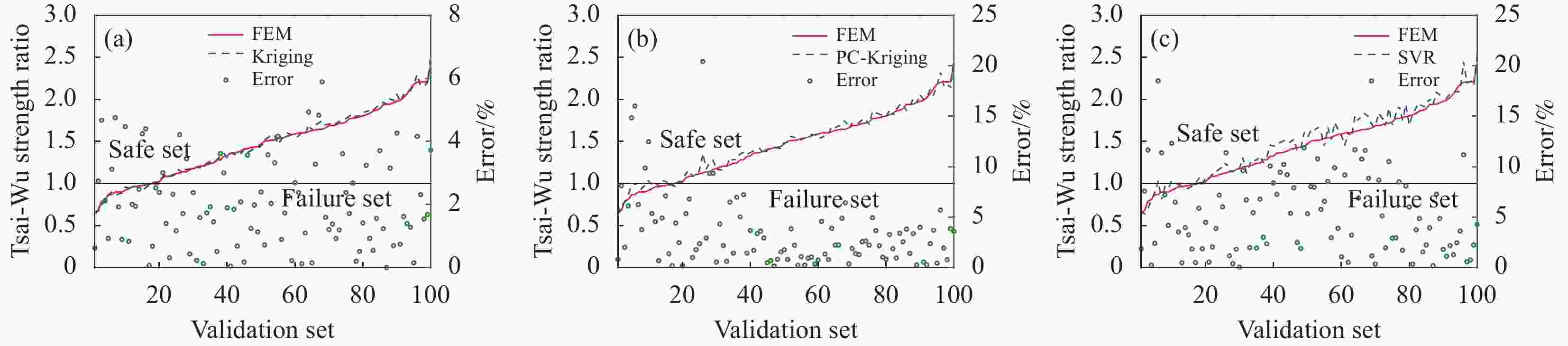
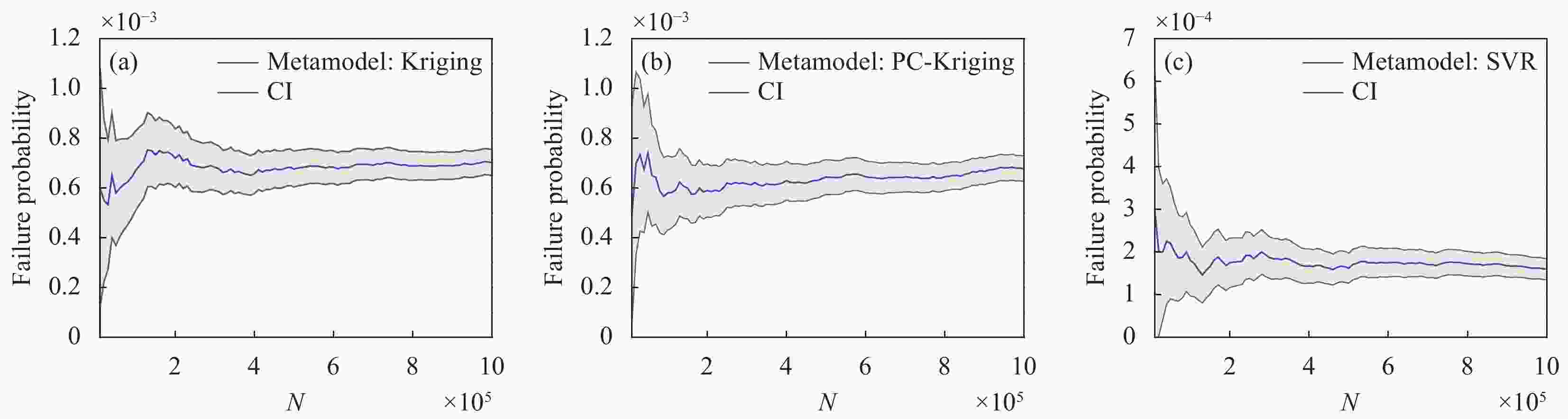
Table 2. Comparison of errors and failure probability results based on different surrogate models
Metamodel $ {e_{{\text{LOO}}}} $ $ {e_{{\text{val }}}} $ $P_{\text{f}}^{{{\mathrm{MCS}}} }$(Evaluations) $P_{\text{f}}^{{\mathrm{Subset}}}$(Evaluations) Kriging 4.56×10−2 8.00×10−3 7.02×10−4 (106) 7.66×10−4 (25900) PC-Kriging 3.61×10−2 2.04×10−2 6.78×10−4 (106) 5.27×10−4 (25900) SVR 1.22×10−1 5.08×10−2 1.60×10−4 (106) 1.18×10−4 (25900) Notes: $ {e_{{\text{LOO}}}} $ and $ {e_{{\text{val }}}} $are leave-one-out cross-validation error and validation error, respectively; $P_{\text{f}}^{{{\mathrm{MCS}}} }$ and $P_{\text{f}}^{{\mathrm{Subset}}}$ are failure probability based on MCS and Subset methods, respectively. -
[1] 李志远, 原崇新. 可靠性分析在航空复合材料结构上的应用及展望[J]. 民用飞机设计与研究, 2023, 2: 145-152.Li Zhiyuan, Yuan Chongxin. Application and future of probabilistic analysis on aeronautical composite structures[J]. Civil Aircraft Design and Research, 2023, 2: 145-152(in Chinese). [2] Moustapha M, Sudret B. Surrogate-assisted reliability-based design optimization: a survey and a unified modular framework[J]. Structural and Multidisciplinary Optimization, 2019, 60: 2157-2176. doi: 10.1007/s00158-019-02290-y [3] 闫海, 邓忠民. 基于深度学习的短纤维增强聚氨酯复合材料性能预测基于深度学习的短纤维增强聚氨酯复合材料性能预测[J]. 复合材料学报, 2019, 36(6): 1413-1420.Yan Hai, Deng Zhongmin. Prediction of properties of short fiber reinforced urethane polymer composites based on deep learning[J]. Acta Materiae Compositae Sinica, 2019, 36(6): 1413-1420(in Chinese). [4] Zhang H, Zhang L, Xu C, et al. Global sensitivity analysis of mechanical properties in hybrid single lap aluminum-CFRP (plain woven) joints based on uncertainty quantification[J]. Composite Structures, 2022, 280: 114841. doi: 10.1016/j.compstruct.2021.114841 [5] Balokas G, Kriegesmann B, Rolfes R. Data-driven inverse uncertainty quantification in the transverse tensile response of carbon fiber reinforced composites[J]. Composites Science and Technology, 2021, 211: 108845. doi: 10.1016/j.compscitech.2021.108845 [6] Reiner J, Linden N, Vaziri R, et al. Bayesian parameter estimation for the inclusion of uncertainty in progressive damage simulation of composites[J]. Composite Structures, 2023, 321: 13. [7] 阮文斌, 吕震宙, 安军, 等. 不确定条件下复合材料结构的全局灵敏度分析[J]. 复合材料学报, 2014, 31(3): 699-706.Ruan Wenbin, Lyu Zhenzhou, An Jun, et al. Global sensitivity analysis for composite structures with uncertainties[J]. Acta Materiae Compositae Sinica, 2014, 31(3): 699-706(in Chinese). [8] Sharma H, Ganguli R. Optimization of a higher-order sandwich composite beam under uncertainties[J]. Composite Structures, 2021, 269: 20. [9] 丁振东, 李洪双, 管晓乐. 基于代理模型的机身蒙皮复合材料夹层结构可靠性分析[J]. 西北工业大学学报, 2022, 40(2): 360-368. doi: 10.3969/j.issn.1000-2758.2022.02.016Ding Zhendong, Li Hongshuang, Guan Xiaole. Reliability analysis of composite sandwich structure for fuselage skin based on surrogate model[J]. Journal of Northwestern Polytechnical University, 2022, 40(2): 360-368(in Chinese). doi: 10.3969/j.issn.1000-2758.2022.02.016 [10] Zhou C, Li C, Zhang H, et al. Reliability and sensitivity analysis of composite structures by an adaptive Kriging based approach[J]. Composite Structures, 2021, 278: 114682. doi: 10.1016/j.compstruct.2021.114682 [11] 周春苹, 刘付超, 周长聪, 等. 石英纤维/环氧树脂复合材料结构静强度的可靠度计算及全局灵敏度分析[J]. 复合材料学报, 2020, 37(7): 1611-1618.Zhou Chunping, Liu Fuchao, Zhou Changcong, et al. Reliability and global sensitivity analysis for static strength of quartz/epoxy composite[J]. Acta Materiae Compositae Sinica, 2020, 37(7): 1611-1618(in Chinese). [12] 龚煜廉, 张建国, 吴志刚, 等. 主动学习基自适应PC-Kriging模型的复材结构可靠度算法[J]. 航空学报, 2023, 45(10): 1-11.Gong Yulian, Zhang Jianguo, Wu Zhigang, et al. Reliability algorithm of composite structure based on active learning basisadaptive PC-Kriging model[J]. Acta Aeronautica et Astronautica Sinica, 2023, 45(10): 1-11(in Chinese). [13] Krige D G. A statistical approach to some mine valuation and allied problems on the Witwatersrand [D]. South Africa; University of the Witwatersrand, 1951. [14] Rasmussen C E, Williams C K I. Gaussian Processes for Machine Learning[M]. MIT Press, 2006. [15] Schöbi R, Sudret B, Wiart J. Polynomial-Chaos-based Kriging[J]. International Journal for Uncertainty Quantification, 2015, 5(2): 171-193. doi: 10.1615/Int.J.UncertaintyQuantification.2015012467 [16] Vapnik V. The Nature of Statistical Learning Theory. [M]. New York: Springer-Verlag, 1995. [17] Au S-K, Beck J L. Estimation of small failure probabilities in high dimensions by subset simulation[J]. Probabilistic Engineering Mechanics, 2001, 16(4): 263-277. doi: 10.1016/S0266-8920(01)00019-4 [18] Morris M D. Factorial Sampling Plans for Preliminary Computational Experiments[J]. Technometrics, 1991, 33(2): 161-174. doi: 10.1080/00401706.1991.10484804 [19] Marelli S, Sudret B, UQLab User Manual – Polynomial Chaos Expansions. Chair of Risk, Safety and Uncertainty Quantification. ETH Zurich, Switzerland. , 2021. [20] Sobol′ I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1-3): 271-280. doi: 10.1016/S0378-4754(00)00270-6 [21] 李宁, 潘慧雨, 李忠献. 一种基于自适应集成学习代理模型的结构可靠性分析方法[J]. 工程力学, 2023, 40(3): 27-35. doi: 10.6052/j.issn.1000-4750.2021.09.0708Li Ning, Pan Huiyu, Li Zhongxian. Structural reliability analysis method based on adaptive ensemble learning-surrogate model[J]. Engineering Mechanics, 2023, 40(3): 27-35(in Chinese). doi: 10.6052/j.issn.1000-4750.2021.09.0708 -

 点击查看大图
点击查看大图
计量
- 文章访问数: 92
- HTML全文浏览量: 71
- 被引次数: 0




 下载:
下载: