Meso-model of 2D woven fabric based on free-form deformation technique
-
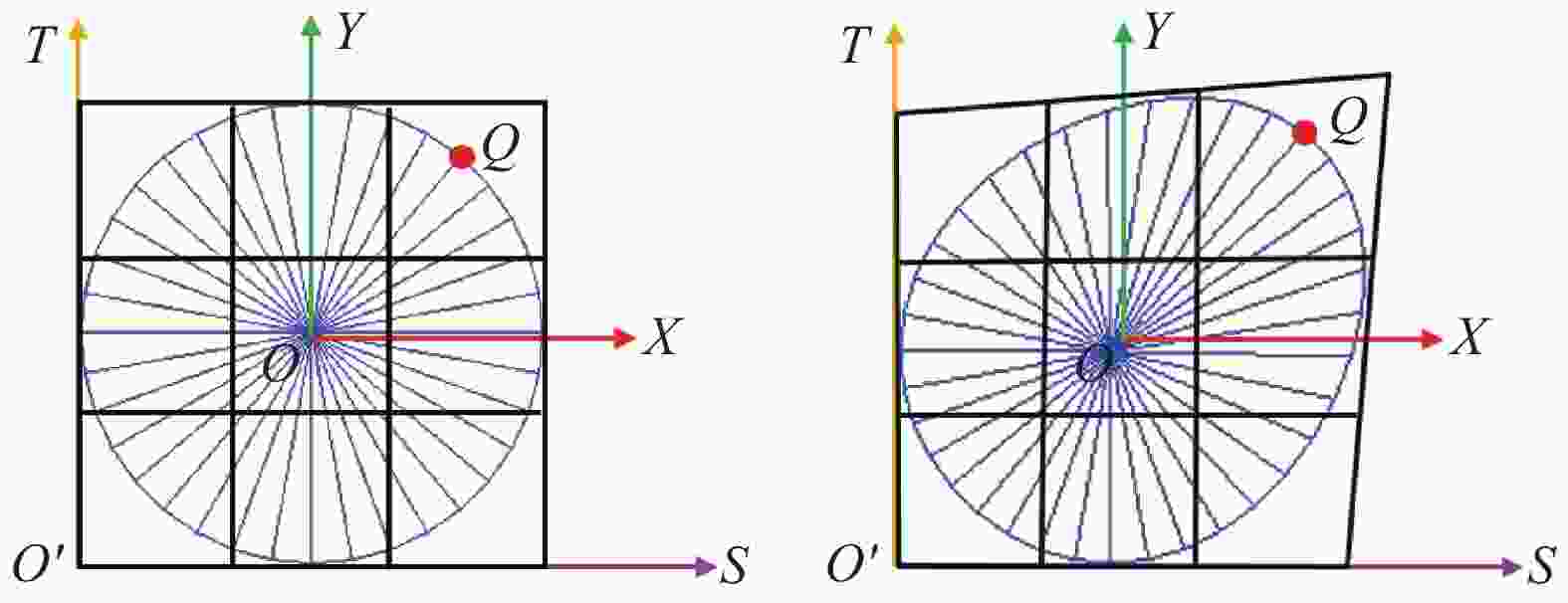
摘要: 为了避免理想化织物模型横截面恒定、纱线间相互渗透的问题,生成具有真实感的二维机织物三维细观模型,提出一种基于自由变形技术的几何变形方法。首先通过理想化的纱线中心线轨迹、横截面建立织物初始几何模型,然后应用自由变形技术对纱线进行变形。在变形过程中,所有纱线横截面在空间位置和参数的约束下进行自由变形,所有横截面变形后的控制网格组成纱线的控制网格,以驱动纱线的整体变形,最终生成具有真实感的织物细观模型。变形过程中纱线间的接触应用基于射线的碰撞检测技术处理。该方法可以扩展并应用于其他织物结构,且可以输出到其他软件中进行模拟计算。Abstract: In order to avoid the problems of constant cross-section and interpenetration between yarns in the idealized fabric model and generate a realistic three-dimensional meso-model of two-dimensional woven fabric, a geometric deformation method based on free deformation technology was proposed. Firstly, the initial geometric model of the fabric was established through the idealized yarn centerline trajectory and cross-section, and then the free-form deformation technology was applied to deform the yarn. In the deformation process, all yarn cross-sections are free-form to deform under the constraints of spatial position and parameters. The control grid of yarn consists of the control grids after all cross sections being deformed to drive the yarn deformation, and finally a realistic fabric meso-model was generated. The contact between yarns in the deformation process was treated by ray based collision detection technique. This method can be extended and applied to other fabric structures, and can be output to other software for simulation.
-
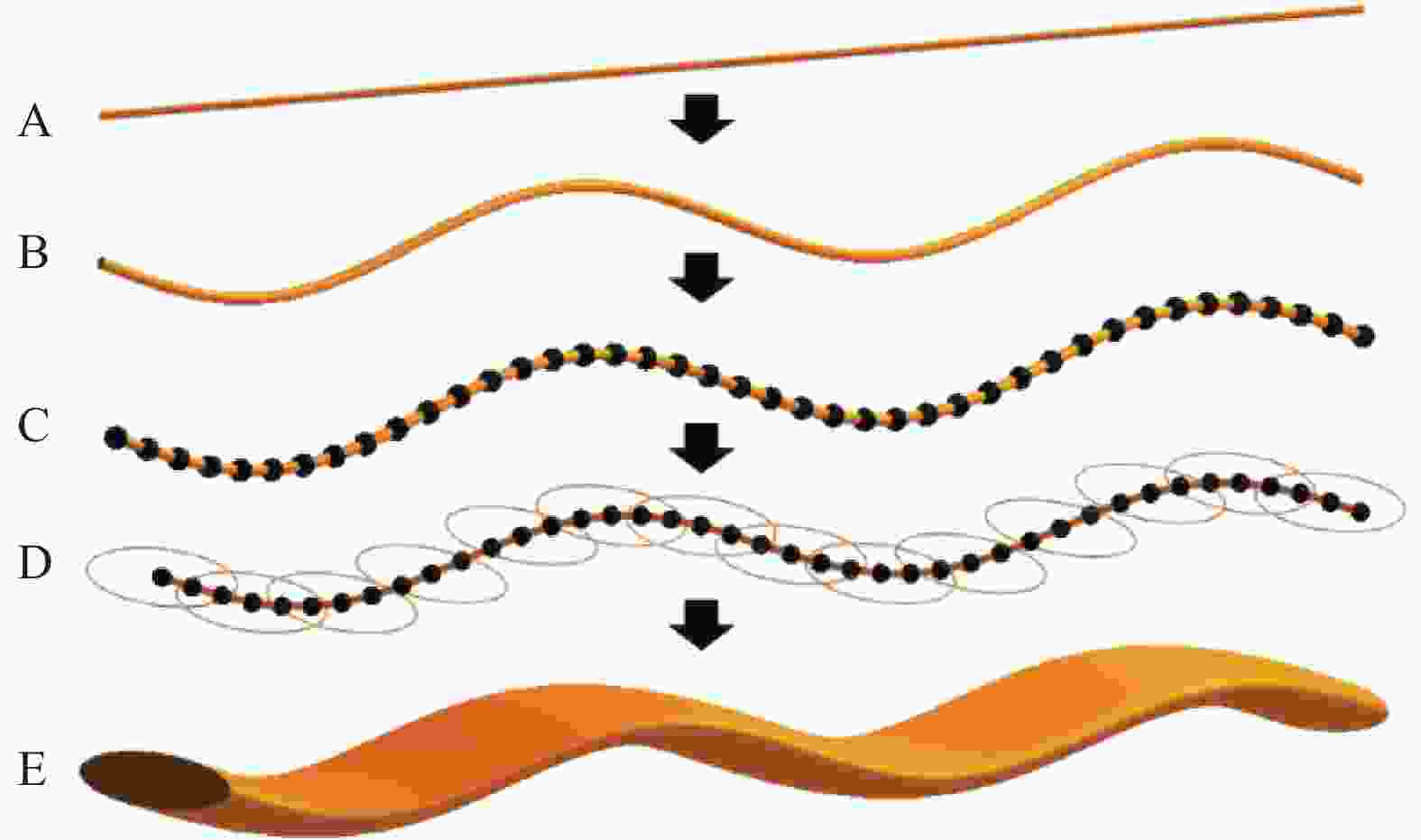
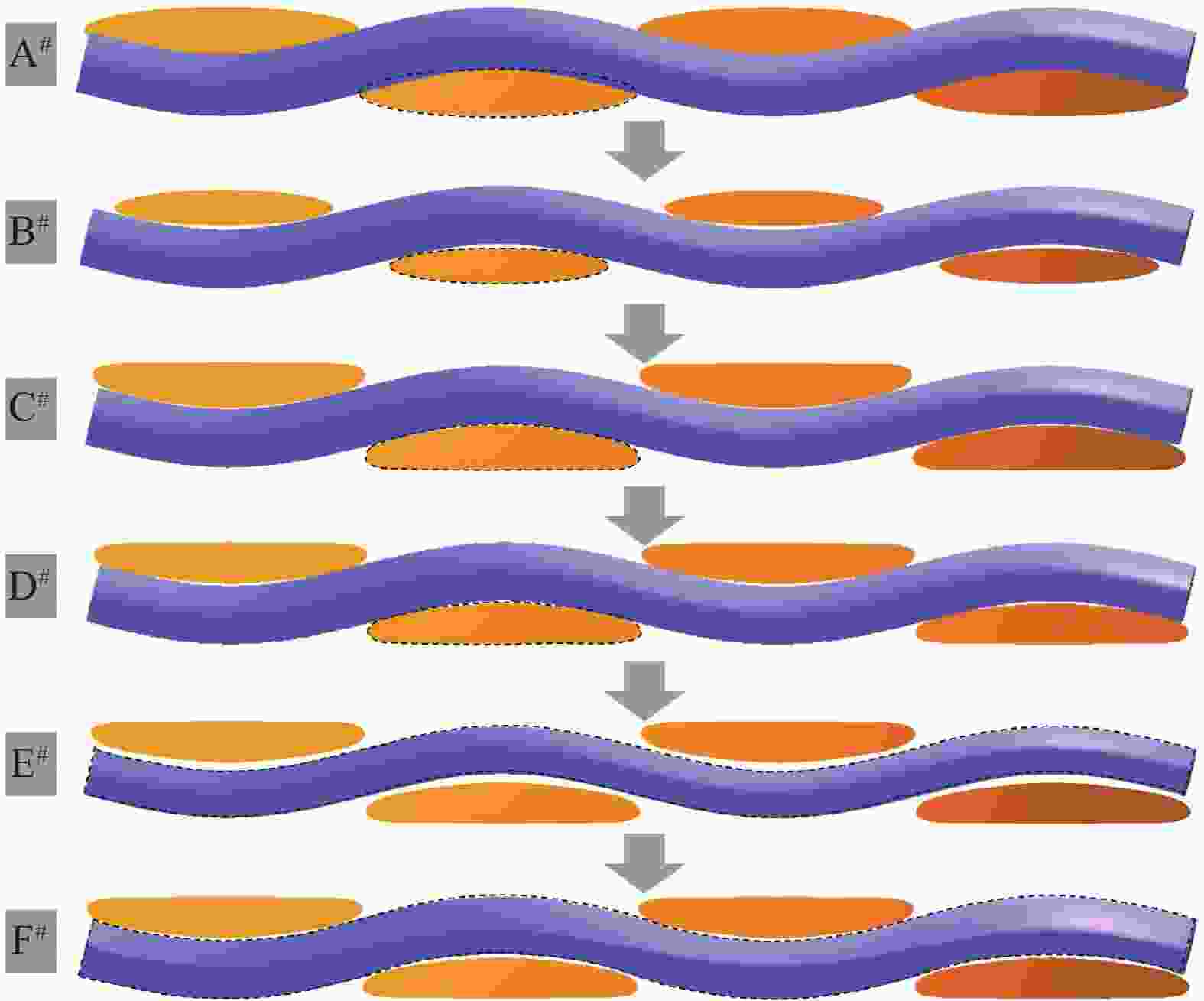
图 10 纬纱横截面视图下纱线变形过程
Figure 10. View of weft yarn cross-section during the process of yarn deformation
A#—Weft yarn cross-section shrinking; B#—Weft yarn cross-section expansion; C#—Weft yarn free form deformation; D#—Warp yarn cross-section shrinking; E#—Warp yarn cross-section expansion; F#—Warp yarn free form deformation
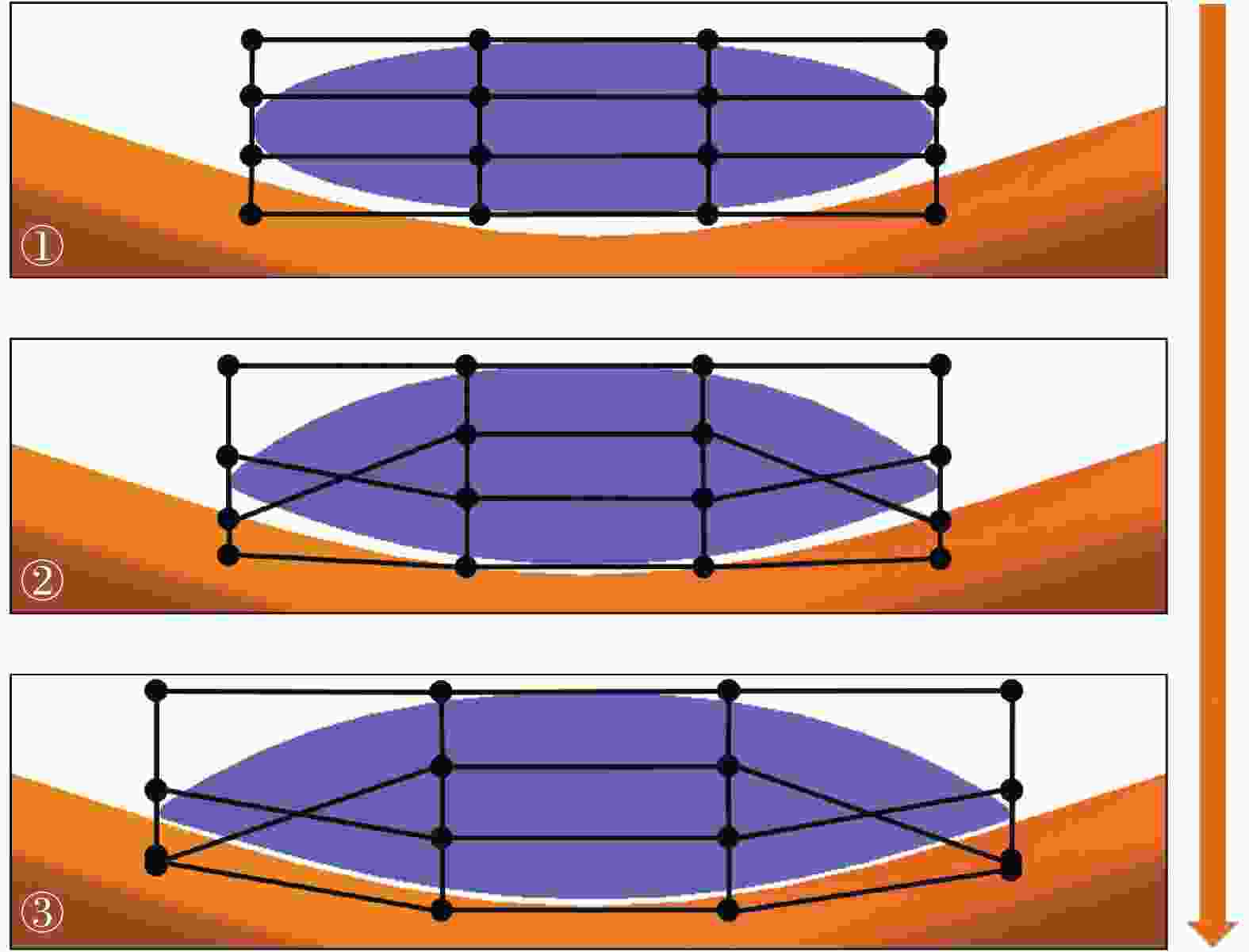
表 1 不同控制网格的纱线截面变形
Table 1. Yarn cross-section deformation of different control meshes
Control
grid typeInitial status Deformed status 1×1 

2×2 

3×3 

表 2 初始织物模型参数
Table 2. Initial fabric model parameters
Parameter Warp Weft Thickness/mm 0.1580 0.1209 Width/mm 0.6172 0.7471 Spacing/mm 0.7471 0.7471 -
[1] 陈利, 焦伟, 王心淼, 等. 三维机织复合材料力学性能研究进展[J]. 材料工程, 2020, 48(8):62-72.CHEN Li, JIAO Wei, WANG Xinmiao, et al. Research progress on mechanical properties of 3D woven composites[J]. Journal of Materials Engineering,2020,48(8):62-72(in Chinese). [2] HIVET G, BOISSE P. Consistent 3D geometrical model of fabric elementary cell. Application to a meshing preprocessor for 3D finite element analysis[J]. Finite Elements in Analysis & Design,2005,42(1):25-49. [3] LOMOV S V, HUYSMANS G, VERPOEST I. Hierarchy of textile structures and architecture of fabric geometric models[J]. Textile Research Journal,2001,71(6):534-543. doi: 10.1177/004051750107100611 [4] HALLAL A, YOUNES R, FARDOUN F. Improved analytical model to predict the effective elastic properties of a 2.5D interlock woven fabric composite[J]. Composite Structures,2012,94(10):3009-3028. doi: 10.1016/j.compstruct.2012.03.019 [5] BUCHANAN S, GRIGORASH A, ARCHER E, et al. Analytical elastic stiffness model for 3D woven orthogonal interlock composites[J]. Composites Science and Technology,2010,70(11):1597-1604. doi: 10.1016/j.compscitech.2010.05.019 [6] LIN H, ZENG X, SHERBURN M, et al. Automated geometric modelling of textile structures[J]. Textile Research Journal,2012,82(16):1689-1702. doi: 10.1177/0040517511418562 [7] GAO Z, CHEN L. A review of multi-scale numerical modeling of three-dimensional woven fabric[J]. Composite Structures,2021,263:113685. doi: 10.1016/j.compstruct.2021.113685 [8] LOMOV S V, PERIE G, IVANOV D S, et al. Modelling 3D fabrics and 3D-reinforced composites: Challenges and solutions[J]. Textile Research Journal,2011,81(1):28-41. doi: 10.1177/0040517510385169 [9] SHERBURN M, LONG A, JONES A, et al. Prediction of textile geometry using an energy minimization approach[J]. Journal of Industrial Textiles,2012,41(4):345-369. doi: 10.1177/1528083711420747 [10] STIG F, HALLSTRM S. Extended framework for geometric modelling of textile architectures[J]. Composite Structures,2020,244:112239. doi: 10.1016/j.compstruct.2020.112239 [11] NILAKANTAN G. Virtual microstructure generation using thermal growth: Case study of a plain-weave Kevlar fabric[J]. Finite Elements in Analysis and Design,2018,147:21-33. doi: 10.1016/j.finel.2018.05.002 [12] 张代雨, 王志东, 凌宏杰, 等. 基于FFD和轴变形方法的翼身融合水下滑翔机外形参数化建模[J]. 舰船科学技术, 2014, 35(3):695-705.ZHANG Daiyu, WANG Zhidong, LING Hongjie, et al. Shape parameterization of blended-wing-body underwater glider based on FFD and axis deformation method[J]. Ship Science and Technology,2014,35(3):695-705(in Chinese). [13] 陈颂, 白俊强, 孙智伟, 等. 基于DFFD技术的翼型气动优化设计[J]. 航空学报, 2014, 35(3):695-705.CHEN Song, BAI Junqiang, SUN Zhiwei, et al. Aerodynamic optimization design of airfoil using DFFD technique[J]. Acla Aeronautica et Astronautica Sinica,2014,35(3):695-705(in Chinese). [14] WANG Y, LIU Z, LIU N, et al. A new geometric modelling approach for 3D braided tubular composites base on free form deformation[J]. Composite Structures,2016,136:75-85. doi: 10.1016/j.compstruct.2015.09.036 [15] LIU J, LONG J, LIANG K, et al. Reverse modeling of complicated folded fabric[J]. Journal of Industrial Textiles,2016,46(2):417-435. doi: 10.1177/1528083715584140 [16] ISART N, MAYUGO J A, BLANCO N, et al. Geometric model for 3D through-thickness orthogonal interlock composites[J]. Composite Structures,2015,119:787-798. doi: 10.1016/j.compstruct.2014.09.044 [17] 李栓, 徐东亮, 周旭东, 等. 基于OpenGL的纤维铺放可视化系统研究[J]. 玻璃钢/复合材料, 2016(12):49-54, 42.LI Shuan, XU Dongliang, ZHOU Xudong, et al. Stidy on the visualization system of fiber placement based on OpenGL[J]. Journal of Fiber Reinforce Plastic/Composite Material,2016(12):49-54, 42(in Chinese). [18] 于广元. 基于自由变形技术的伴随方法优化设计大曲率扩压通道[D]. 南京: 南京航空航天大学, 2014.YU Guangyuan. Aerodynamic design of large curvature diffuser channel by using adjoint method based on FFD technique[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014(in Chinese). [19] 李星, 傅妍芳, 王亮, 等. 基于射线检测的动态碰撞优化算法[J]. 系统仿真学报, 2019, 31(11):2393-2401.LI Xing, FU Yanfang, WANG Liang, et al. Dynamic collision optimization algorithm based on ray detection[J]. Journal of System Simulation,2019,31(11):2393-2401(in Chinese). [20] 李玉虎, 王宗彦. 基于混合层次包围盒碰撞算法的改进[J]. 华东交通大学学报, 2019, 36(6):112-118.LI Yuhu, WANG Zongyan. Improvement of collision algorithm based on mixed level bounding box[J]. Journal of East China Jiaotong University,2019,36(6):112-118(in Chinese). -





 下载:
下载: