Research status of quasi-static stability performance of composite sandwich structures
-
摘要: 复合材料夹芯结构由于其优异的比强度,比刚度及较小的表观密度的优点而广泛应用于航空航天、船舶等各个领域。本文从理论研究、仿真分析、实验研究这三个方面出发,综述了蜂窝、泡沫、点阵、褶皱四种夹芯结构在准静态稳定性研究方面的现状。蜂窝夹芯结构的研究较为成熟,进一步的研究应集中于应用领域;泡沫夹芯结构在面芯问题方面有待增强,可考虑纤维缝合技术;褶皱夹芯结构理论方面有待进一步研究,潜力巨大;点阵夹芯结构较其它结构抗屈曲能力更强,但是依然存在面芯粘接问题。复合材料夹芯结构在准静态稳定性方面的问题主要集中在面芯粘接方面,纤维缝合技术可以有效增强面芯性能,该方面的研究对增强复合材料夹芯结构稳定性有较强的潜力。Abstract: Composite sandwich structures are widely used in aerospace, shipbuilding and other fields due to their excellent strength-and stiffness-to-weight ratio and small apparent density. From the three aspects of theoretical research, simulation analysis and experimental research, this paper summarizes the current situation of quasi-static stability research of honeycomb , foam, lattice and foldcore sandwich structures. The research on honeycomb sandwich structure is relatively mature, and further research should focus on the application field. The foam sandwich structure needs to be strengthened in the panel/core interface, and the fiber stitching technology can be considered. The theory of foldcore sandwich structure needs further study and has great potential. The lattice sandwich structure has stronger anti-buckling ability than other structures, but there is still a problem of face/core bonding. The problem of the quasi-static stability of the composite sandwich structure is mainly focused on the bonding of the face/core. The fiber stitching technology can effectively enhance the performance of the face/core. The research in this area has a strong potential for enhancing the stability of the composite sandwich structure.
-
表 1 四种典型夹芯结构特点
Table 1. Four typical sandwich structure characteristics
Structure Type Strength Carrying capacity Application Manufacture Honey-comb ○ ○ √ × Foam √ × ○ ○ Lattice ○ ○ ○ × Folded ○ √ × √ Notes: ○=very good , √=good , ×=not good. 表 2 金字塔点阵夹芯结构不同边界条件下的屈曲临界载荷理论公式[55]
Table 2. Theoretical formula of buckling critical load of pyramid lattice sandwich structure under different boundary conditions[55]
boundary condition critical buckling load $ {P_{{\text{cr}}}} $/N Simply-supported at both ends $ {P_{{\text{cr}}}} = \dfrac{{2{c^2}\left({A^{\text{t}}}{D^{\text{t}}} - {B^{\text{t}}}{B^{\text{t}}}\right){{\left(n{\text{π}}/L\right)}^4} + 4 S{D^{\text{t}}}{{\left(n{\text{π}}/L\right)}^2}}}{{{C^{\text{2}}}{A^{\text{t}}}{{\left(n{\text{π}}/L\right)}^2} + 2 S}} $ Clamped at one end, and free at the other end $ {P}_{\text{cr}}={\scriptstyle \dfrac{2{c}^{2}\left({A}^{\text{t}}{D}^{\text{t}}-{B}^{\text{t}}{B}^{\text{t}}\right){\left({\left(2n-1\right){\text{π}}/2L}\right)}^{4}+4 S{D}^{\text{t}}{\left(\left(2n-1\right)n{\text{π}}/2L\right)}^{2}}{{C}^{\text{2}}{A}^{\text{t}}{\left(\left(2n-1\right)n{\text{π}}/2L\right)}^{2}+2 S}} $ Clamped at one end, and free to slide in the longitudinal direction at the other end $ {P_{{\text{cr}}}} = \dfrac{{2{c^2}({A^{\text{t}}}{D^{\text{t}}} - {B^{\text{t}}}{B^{\text{t}}}){{\left(2n{\text{π}}/L\right)}^4} + 4 S{D^{\text{t}}}{{\left(2n{\text{π}}/L\right)}^2}}}{{{C^{\text{2}}}{A^{\text{t}}}{{\left(2n{\text{π}}/L\right)}^2} + 2 S}} $ Clamped at one end, and free to slide in oth the longitudinal and transverse directions at the other end $ {P}_{\text{cr}}={\scriptstyle \dfrac{2{c}^{2}\left({A}^{\text{t}}{D}^{\text{t}}-{B}^{\text{t}}{B}^{\text{t}}\right){\left(\left(2n-1\right){\text{π}}/L\right)}^{4}+4 S{D}^{\text{t}}{\left(\left(2n-1\right){\text{π}}/L\right)}^{\text{2}}}{{C}^{\text{2}}{A}^{\text{t}}{\left(\left(2n-1\right){\text{π}}/L\right)}^{2}+2 S}} $ Notes: $n$ represents the buckling mode order ; $S$ represents the shear stiffness of the core ; $c$ represents the thickness of the core ; $A$ represents the tensile stiffness of the face sheet ; $B$ represents the coupling stiffness of the face sheet ; $D$ represents the bending stiffness of the face sheet ; The superscript $t$ represents the upper panel ; The subscript represents the lower panel . 表 3 多层锥体点阵夹芯结构在面内压缩载荷作用下的四种失效模式[57]
Table 3. Four failure modes of multi-layer cone lattice sandwich structure under in-plane compressive load[57]
In-plane compressive failure mode Analytical collapse load expression Macro elastic buckling $ {P_{{\text{cr}}}} = \dfrac{{\dfrac{{2{k^4}{\pi ^4}{D_{\text{f}}}{D_0}}}{{{L^4}}} + \dfrac{{{k^2}{\pi ^2}D}}{{{L^2}}}S}}{{\dfrac{{{k^2}{\pi ^2}{D_0}}}{{{L^2}}} + S}} $,when$ {P_{{\text{cr}}}} < \dfrac{{4 bh{\sigma _y}}}{{\sqrt 3 }} $ Macro inelastic buckling $ {P_{{\text{cr}}}} = \dfrac{{\dfrac{{2{k^4}{\pi ^4}{D_{\text{f}}}{D_0}}}{{{L^4}}} + \dfrac{{{k^2}{\pi ^2}D}}{{{L^2}}}S}}{{\dfrac{{{k^2}{\pi ^2}{D_0}}}{{{L^2}}} + S}} $,when$ {P_{{\text{cr}}}} \geqslant \dfrac{{4 bh{\sigma _y}}}{{\sqrt 3 }} $ Local elastic face buckling $ {P_{{\text{FB}}}} = \dfrac{{{k^{'2}}{\pi ^2}{E_{\text{s}}}b}}{{6(1 - {\nu ^2})}}\dfrac{{{h^3}}}{{{d^2}}} $,when$\dfrac{h}{d} < \sqrt {\dfrac{{24(1 - {v^2}){\sigma _y}}}{{\sqrt 3 {k^{'2}}{\pi ^2}{E_{\text{s}}}}}} $ Local inelastic face buckling $ {P_{{\text{FB}}}} = \dfrac{{{k^{'2}}{\pi ^2}{E_{\text{t}}}b}}{6}\dfrac{{{h^3}}}{{{d^2}}} $,when$\dfrac{h}{d} < \sqrt {\dfrac{{24(1 - {v^2}){\sigma _y}}}{{\sqrt 3 {k^{'2}}{\pi ^2}{E_{\text{s}}}}}} $ Notes: $\nu $ represents the poisson's ratio ; $k$ represents the shear coefficient ; ${k^{'}}$ represents the shear correction factor for face sheet ; ${E_{\text{t}}}$ represents the tangent modulus ; ${E_{\text{s}}}$ represents the solid material modulus ; ${\sigma _y}$ represents the yield strength ; ${D_{\text{f}}}$ represents the face sheet stiffness ; ${D_0}$ represents the core stiffness;$S$ represents the shear stiffness of the core ;$h$ represents the facesheet thickness ; $d$ represents the inter-node spacing ; $b$ represents the width of the core ; $L$ represents the length of the core . 表 4 层级褶皱结构夹层梁压缩载荷作用下失效模式分类
Table 4. Failure modes of the hieratchical structure with second order corrugated under transverse[65]
Destructed sites mode of failure Basic solution of failure criterion First-level hierarchical structure Sandwich plate buckling ${P_x} \geqslant {P_{{\text{cr}}}}$ Euler beam buckling ${P_x} \geqslant {P_{{\text{cr}}}}$ Surface plastic buckling $\sigma \geqslant \left[ \sigma \right]$ Surface plate buckling ${P_x} \geqslant {P_{{\text{cr}}}}$ Surface beam wrinkle ${P_x} \geqslant {P_{{\text{cr}}}}$ Shear failure ${P_x} \geqslant {P_{\text{s}}}$ Second-level hierarchical structure plastic buckling $\sigma \geqslant \left[ \sigma \right]$ buckling of thin plates ${P_x} \geqslant {P_{{\text{cr}}}}$ Euler beam buckling ${P_x} \geqslant {P_{{\text{cr}}}}$ Notes: ${P_{{\text{cr}}}}$ represents the critical buckling load;${P_x}$ represents in-plane compressive load;$\sigma $ represents the stress of the component;$\left[ \sigma \right]$ represents the yield stress of materials 表 5 理论分析总结
Table 5. Theoretical analysis summary
Structure type Theory name Identification number Plate Reissner type theory [24] Hoff type theory [25] Du Qinghua type theory [26] Honeycomb Honeycomb plate theory [30][31] Sandwich theory [32] Hierarchical honeycomb theory [34] Quasi-honeycomb theory [35] Mixed honeycomb core theory [36] Refined Shear Deformation Theory [37] Foam Buckling theory based on rod [41] Fiber reinforcement theory based on Rayleigh-Ritz method [48] Modified buckling theory of columns [49] The formula for calculating the overall stability coefficient [50] Lattice Tetrahedron theoretical formula [55] Pyramid theoretical formula [53][55][56] The theoretical formula of multi-layer cone [57] Folded Zeta fold structure theory [61] Isotropic fold structure theory [63] M-type fold structure theory [64] Hierarchical fold structure theory [65][66] Carbon fiber reinforced wrinkle theory [67] 表 6 混杂蜂窝夹芯板与单层蜂窝夹芯板在不同工况下的临界屈曲载荷比较[69]
Table 6. Comparison of critical buckling loads of hybrid honeycomb sandwich panels and single-layer honeycomb sandwich panels under different working conditions[69]
Type of load Single-layer honeycomb sandwich panel/
(N·mm-1)hybrid honeycombsandwich panel/
(N·mm-1)Critical load growth rate/% Subjected to axial compressive load 895.8 988.2 10.31 Subjected to shear load 2040.7 2212.3 3.34 Under the combined load of shear and compression ratio of 1 : 1 778.3 839.1 7.83 表 7 三种方法下的屈曲载荷与极限承载对比[71]
Table 7. Comparison of buckling load results and limit load results under three methods[71]
Method Buckling load/N Relative accuracy Limit load/N Relative accuracy Eigenvalue method 13.11 13.98 —— —— Arc length method 12.50 17.98 17.95 2.97 Experiment 15.24 0 18.50 0 表 8 屈曲应力计算结果与试验结果的对比[78]
Table 8. Contrast for buckling stress between results of present model and experiments[78]
Failure mode Strength/kN Experiment Sample1 Buckling 20.13 Sample2 Buckling 20.00 Sample3 Buckling 21.96 Sample4 Buckling 19.14 Sample5 Buckling 19.29 Sample6 Buckling 20.74 Mean 20.21 Present mode 18.32 表 9 不同树脂柱弹模下夹层板的屈曲临界载荷[83]
Table 9. Critical buckling loads of sandwich plates for different elastic modulus of resinic columns[83]
Elastic modulus of
resinic columns/MPaCritical buckling load/N 1500 218.98 2000 220.54 2500 221.72 3500 223.43 4500 224.62 表 10 不同树脂柱间距下夹层板的屈曲临界载荷[83]
Table 10. Critical buckling loads of sandwich plates for different cell sizes[83]
Adjacent resinic columns distance/mm Critical buckling load/N 40 223.43 80 209.49 160 199.78 表 11 仿真模型总结
Table 11. Simulation model summary
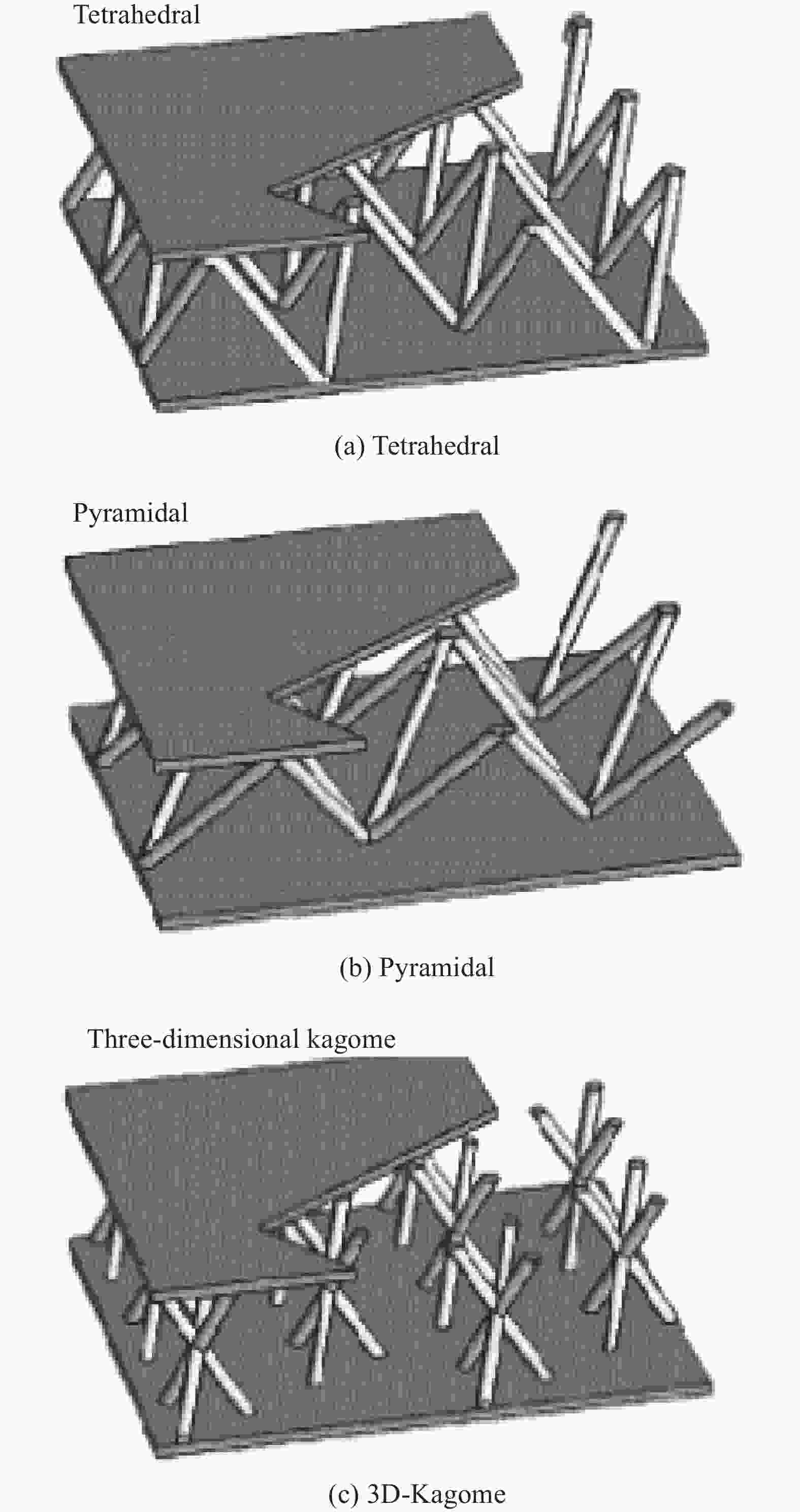
structure type model name identification number Honeycomb Honeycomb sandwich panel with transition zone [68] Hybrid honeycomb sandwich panel [69] Honeycomb cylinder model [70] a novel improved star-shaped honeycomb sand-wich panel [72] Two-Dimensional Dimensional Reduction Model [73] Two-dimensional equivalent plate model [74] Foam Model of grid reinforced foam sandwich webs [76] Foam sandwich plate model simulating sutures [77] Type I sandwich web model filled with aluminum foam [79] Asymmetric Sandwich Panels [80] Lattice Pyramid lattice sandwich plate model [82] 3 D-Kagome lattice sandwich plate model [82] Resin column reinforced lattice sandwich plate model
I-type pyramid lattice sandwich panel model
Double triangular lattice sandwich plate model with reinforcing frame[83]
[87]
[88]Folded Folded core plate model with defects [89] S-shaped fold sandwich plate model [90] Carbon fiber reinforced folded truncated cone shell model [91] 表 12 不同特征角度下试件的刚度与极限承载对比[120]
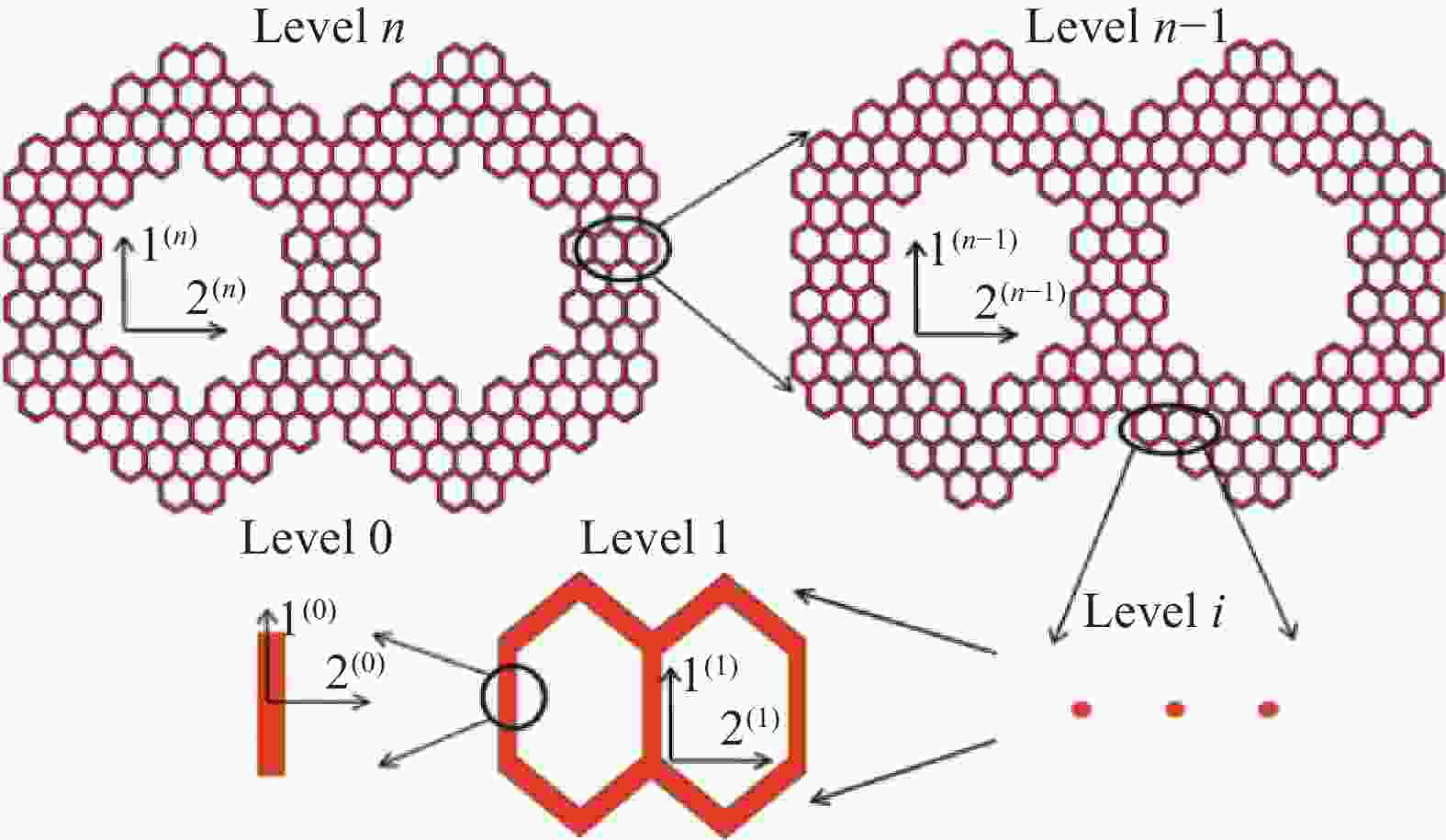
Table 12. Comparison of stiffness and limit load under different characteristic angles
Characteristic angle/(º) Stiffness/(N·mm-1) Limit load/kN 0 8023 25.30 1 7042 20.67 -
[1] 朱子旭, 朱锡, 李永清, 等. 复合材料夹芯结构研究现状及其在船舶工程的应用[J]. 舰船科学技术, 2018, 40(2): 1-7. doi: 10.3404/j.issn.1672-7649.2018.02.001ZHU Zixu, ZHU Xi, LI Yongqing, et al. Present researches about sandwich composite structures and its applies in ship industry[J]. Ship Science and Technology, 2018, 40(2): 1-7(in Chinese). doi: 10.3404/j.issn.1672-7649.2018.02.001 [2] SAYYAD AS, GHUGAL YM. On the free vibration analysis of laminated composite and sandwich plates: a review of recent literature with some numerical results[J]. Composite Structures, 2015, 129: 177-201. doi: 10.1016/j.compstruct.2015.04.007 [3] 钱勤, 李国清, 倪樵. 材料力学[M]. 华中科技大学出版社, 2022.QIAN Qin, LI Guoqing, NI Qiao. Mechanics of materials[M]. Huazhong University of Science and Technology Press, 2022(in Chinese). [4] 韩强, 张善元, 杨桂通. 结构静动力屈曲问题研究进展[J]. 力学进展, 1998, (3): 62-73.HAN Qiang, ZHANG Shanyuan, YANG Guitong. Research progress on static and dynamic buckling of structures[J]. Advances in Mechanics, 1998, (3): 62-73(in Chinese). [5] 徐思萌. 不成熟的潜水器带来悲剧之旅[N]. 中国应急管理报, 2023-06-28(007).XU Simeng. Immature submersible brings a tragic journey[N]. China Emergency Management News, 2023-06-28(007)(in Chinese). [6] 刘涛. 大深度潜水器结构分析与设计研究[D]. 中国船舶科学研究中心, 2001.LIU Tao. Analysis and design of deep-sea submersible structures[D]. China Ship Scientific Research Center, 2001(in Chinese). [7] 张广平, 戴干策. 复合材料蜂窝夹芯板及其应用[J]. 纤维复合材料, 2000, 17(2): 25-27,6. doi: 10.3969/j.issn.1003-6423.2000.02.008ZHANG Guangping, DAI Gance. Composite honeycomb sandwich panel and its application[J]. Fiber Composites, 2000, 17(2): 25-27,6(in Chinese). doi: 10.3969/j.issn.1003-6423.2000.02.008 [8] 吴龙兴. 复合材料泡沫夹芯壁板稳定性及承载能力研究[D]. 南京航空航天大学, 2020.WU Longxing. Research on Stability and Load Carrying Capacity of Foam-core Composite Sandwich Panels[D]. Nanjing University of Aeronautics and Astronautics, 2020(in Chinese). [9] 魏然, 苏震宇, 刘洋. 先进树脂基复合材料在商用航空发动机中的应用[J]. 科技创新与应用, 2024, 14(3): 193-196.WEI Ran, SU Zhenyu, LIU Yang. Application of advanced resin matrix composites in commercial aero-engines[J]. Technology Innovation and Application, 2024, 14(3): 193-196(in Chinese). [10] 叶轶. 复合材料在光伏组件中的应用开发案例[J]. 玻璃纤维, 2023, (5): 46-48. doi: 10.3969/j.issn.1005-6262.2023.05.010YE Yi. Application development case of composite materials in photovoltaic modules[J]. Fiber Glass, 2023, (5): 46-48(in Chinese). doi: 10.3969/j.issn.1005-6262.2023.05.010 [11] 张磊, 许帅康, 陈洁, 等. 列车车体轻量化设计研究进展[J]. 机械工程学报, 1-202024-01-17]. ZHANG Lei, XU Shuaikang, CHEN Jie, et al. Research Progress in Lightweight Design of Train Body[J]. Journal of Mechanical Engineering, 1-20[2024-01-17](in Chinese). [12] 邓锐, 李华丽. 复合材料在轨道交通车体结构中的应用[J]. 机车车辆工艺, 2017, (6): 4-6.DENG Rui, LI Huali. Application of composite materials in the structure of rail transit car body[J]. Locomotive and Rolling Stock Technology, 2017, (6): 4-6(in Chinese). [13] 周文华, 周百能. 夹芯泡沫材料性能及其在风电叶片上的应用[J]. 天津科技, 2023, 50(1): 75-78. doi: 10.3969/j.issn.1006-8945.2023.01.020ZHOU Wenhua, ZHOU Baineng. Applied Research of Sandwich Foam in Wind Turbine Blades[J]. Tianjin Science and Technology, 2023, 50(1): 75-78(in Chinese). doi: 10.3969/j.issn.1006-8945.2023.01.020 [14] 刁明霞, 果春焕, 高华兵, 等. 泡沫金属复合材料的研究进展[J]. 材料工程, 2022, 50(12): 60-70. doi: 10.11868/j.issn.1001-4381.2021.000571DIAO Mingxia, GUO Chunhuan, GAO Huabing, et al. Research progress in metal foam composites[J]. Journal of Materials Engineering, 2022, 50(12): 60-70(in Chinese). doi: 10.11868/j.issn.1001-4381.2021.000571 [15] OSMAN A, GALAL K. Evaluation of Different CFRP Sandwich Deck Cores of Deployable Treadway Bridge Beam[C]//8th International Conference on Advanced Composite Materials in Bridges and Structures: Volume 1. Cham: Springer International Publishing, 2022: 469-479. [16] 鲍瑞雪. 新型四面体点阵夹芯结构汽车材料的隔振特性研究[J]. 科学技术创新, 2023, (17): 1-4. doi: 10.3969/j.issn.1673-1328.2023.17.002BAO Ruixue. Study on Vibration Isolation Characteristics of New Tetrahedral Lattice Sandwich Structure Automotive Materials[J]. Scientific and Technological Innovation, 2023, (17): 1-4(in Chinese). doi: 10.3969/j.issn.1673-1328.2023.17.002 [17] 袁运飞, 廖俊, 宋佳文等. 点阵夹芯主动冷却结构发展现状与展望[J]. 航空工程进展, 2021, 12(6): 13-25.YUAN Yunfei, LIAO Jun, SONG Jiawen et al. Development Status and Prospect of Lattice Sandwich Active Cooling Structure[J]. Advances in Aeronautical Science and Engineering, 2021, 12(6): 13-25(in Chinese). [18] 陈浩. 碳纤维金字塔点阵夹芯假脚结构的力学性能研究[D]. 天津科技大学, 2023.CHEN Hao. Study on Mechanical Properties of Carbon Fiber Pyramid Lattice Sandwich Prosthetic Foot[D]. Tianjin University of Science and Technology, 2023(in Chinese). [19] MIAO X Y, CHEN X. Structural transverse cracking mechanisms of trailing edge regions in composite wind turbine blades[J]. Composite Structures, 2023, 308: 116680. doi: 10.1016/j.compstruct.2023.116680 [20] JOHNSON A. Novel hybrid structural core sandwich materials for aircraft applications[J]. 2008. [21] 李开开. 褶皱夹芯结构的静/动态连接研究[D]. 哈尔滨工业大学, 2021.LI Kaikai. Research on static/dynamic connection of fold sandwich structure[D]. Harbin Institute of Technology, 2021(in Chinese). [22] XU J, FU C, FU Q, et al. Flexible arc-armor inspired by origami[J]. International Journal of Mechanical Sciences, 2021, 201: 106463. doi: 10.1016/j.ijmecsci.2021.106463 [23] DEBNATH S, FEI L J. Origami theory and its applications: a literature review[J]. world academy of science, engineering and technology, 2013: 1131-1135. [24] REISSNER ERIC. On the theory of bending of elastic plates[J]. Journal of Mathematics and Physics, 1947, 23(1-4): 184-191. [25] ERINGEN A C. Bending and buckling of rectangular sandwich plates[J]. Technical Report Archive & Image Library, 1950, 18(2225): 330-330. [26] 杜庆华. 三合板的一般弹性理论[J]. 物理学报, 1954, (4): 395-411. doi: 10.7498/aps.10.395DU Qinghua. General equation of sandwich plates under transverse loads and edgewise shears and compression[J]. Acta Physica Sinica, 1954, (4): 395-411(in Chinese). doi: 10.7498/aps.10.395 [27] 吴文涛, 方耀楚, 倪康. 非连续芯层夹芯结构稳定性研究综述[J]. 工程建设, 2021, 53(4): 1-8.WU Wentao, FANG Yaochu, NI Kang. Research review on stability of sandwich structure of discontinuous core layer[J]. Engineering Construction, 2021, 53(4): 1-8(in Chinese). [28] SHABANI Y, KHORSHIDI K. Buckling Analysis of Sandwich Structures with Metamaterials Core Integrated by Graphene Nanoplatelets Reinforced Polymer Composite[J]. Mechanics Of Advanced Composite Structures, 2023, 10(1): 1-10. [29] ALLEN HG. Analysis and design of structural sandwich panels: the commonwealth and international library: structures and solid body mechanics division[M]. Elsevier, 2013. [30] GIBSON L J, ASHBY M F, SCHAJER G S, et al. The mechanics of two-dimensional cellular materials[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1982, 382(1782), 25-42. [31] 富明慧, 尹久仁. 蜂窝芯层的等效弹性参数[J]. 力学学报, 1999, (1): 113-118. doi: 10.3321/j.issn:0459-1879.1999.01.014FU Minghui, YIN Jiuren. Equivalent elastic parameters of honeycomb core layer[J]. Chinese Journal of Theoretical and Applied Mechanics, 1999, (1): 113-118(in Chinese). doi: 10.3321/j.issn:0459-1879.1999.01.014 [32] 夏利娟, 金咸定, 汪庠宝. 卫星结构蜂窝夹层板的等效计算[J]. 上海交通大学学报, 2003, 37(7): 999-1001. doi: 10.3321/j.issn:1006-2467.2003.07.008XIA Lijuan, JIN Xianding, WANG Xiangbao. Equivalent analysis of honeycomb sandwich plates for satellite structure[J]. Journal of Shanghai Jiaotong University, 2003, 37(7): 999-1001(in Chinese). doi: 10.3321/j.issn:1006-2467.2003.07.008 [33] 张铁亮, 丁运亮, 金海波. 蜂窝夹层板结构等效模型比较分析[J]. 应用力学学报, 2011, 28(3): 275-282.ZHANG Tieliang, DING Yunliang, JIN Haibo. Comparative analysis of equivalent model of honeycomb sandwich plate structure[J]. Chinese Journal of Applied Mechanics, 2011, 28(3): 275-282(in Chinese). [34] CHEN Q, PUGNO NM. In-plane elastic buckling of hierarchical honeycomb materials[J]. European Journal of Mechanics - A/Solids, 2012, 34: 120-129. doi: 10.1016/j.euromechsol.2011.12.003 [35] 李响, 宋小俊, 曹祥斌. 轻质高强类蜂窝夹层结构轴向压缩屈曲失效分析[J]. 塑性工程学报, 2021, 28(9): 137-143. doi: 10.3969/j.issn.1007-2012.2021.09.018LI Xiang, SONG Xiaojun, CAO Xiangbin. Failure analysis of axial compression buckling of lightweight and high strength quasi-honeycomb sandwich structure[J]. Journal of Plasticity Engineering, 2021, 28(9): 137-143(in Chinese). doi: 10.3969/j.issn.1007-2012.2021.09.018 [36] THANG PT, KIM C, JANG H, et al. Buckling behavior analysis of hybrid-honeycomb sandwich cylindrical shells[J]. Ocean Engineering, 2023, 276: 114214. doi: 10.1016/j.oceaneng.2023.114214 [37] LIU S, WANG K, WANG B. Buckling and vibration characteristic of anisotropic sandwich plates with negative Poisson’s ratio based on isogeometric analysis[J]. Mechanics of Advanced Materials and Structures, 2023: 1-16. [38] VAN LIEU P, ZENKOUR A M, LUU G T. Static bending and buckling of FG sandwich nanobeams with auxetic honeycomb core[J]. European Journal of Mechanics-A/Solids, 2024, 103: 105181. doi: 10.1016/j.euromechsol.2023.105181 [39] 胡越. 缝合泡沫夹芯复合材料力学性能的研究[D]. 武汉理工大学, 2021.HU Yue. Study on mechanical properties of sutured foam sandwich composites[D]. Wuhan University of Technology, 2021(in Chinese). [40] MF GLA. Cellular solids: structure and properties, 2nd edn[M]. Cambridge University Press, 1997. [41] 徐诗峰. 泡沫铝夹芯结构抗低速冲击性能研究[D]. 哈尔滨工业大学, 2016.XU Shifeng. Research on the low-velocity impact performance of aluminum foam sandwich structure[D]. Harbin Institute of Technology, 2016(in Chinese). [42] CHEN C, LU TJ. A phenomenological framework of constitutive modelling for incompressible and compressible elasto-plastic solids[J]. International Journal of Solids and Structures, 2000, 37(52): 7769-7786. doi: 10.1016/S0020-7683(00)00003-2 [43] 王二恒, 虞吉林, 王飞, 等. 泡沫铝材料准静态本构关系的理论和实验研究[J]. 力学学报, 2004, 36(6): 673-679. doi: 10.3321/j.issn:0459-1879.2004.06.005WANG Erheng, YU Jilin, WANG Fei, et al. A theoretical and experimental study on the quasi-static constitutive model of aluminum foams[J]. Acta Mechanica Sinica, 2004, 36(6): 673-679(in Chinese). doi: 10.3321/j.issn:0459-1879.2004.06.005 [44] DESHPANDE VS, FLECK NA. Isotropic constitutive models for metallic foams[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(6): 1253-1283. [45] SU B, ZHOU Z, XIAO G, et al. A pressure-dependent phenomenological constitutive model for transversely isotropic foams[J]. International Journal of Mechanical Sciences, 2017, 120: 237-248. doi: 10.1016/j.ijmecsci.2016.12.004 [46] HUANG B, HU X, LIU J. Modelling of inter-laminar toughening from chopped kevlar fibers[J]. Composites Science and Technology, 2004, 64(13-14): 2165-2175. doi: 10.1016/j.compscitech.2004.03.014 [47] DRANSFIELD K, BAILLIE C, MAI Y. Improving the delamination resistance of cfrp by stitching—a review[J]. Composites Science and Technology, 1994, 50(3): 305-317. doi: 10.1016/0266-3538(94)90019-1 [48] 桂良进, 叶宁, 郦正能, 等. 含椭圆分层缝纫复合材料层板的局部屈曲研究[J]. 北京航空航天大学学报, 2000, (6): 701-704.GUI Liangjin, YE Ning, LI Zhengneng, et al. Study on local buckling of composite laminates with elliptical delamination sewing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2000, (6): 701-704(in Chinese). [49] VIDWANS A, TROVALUSCI P, FANTUZZI N, et al. Application of column buckling theory to steel aluminium foam sandwich panels[J]. Structures, 2023, 54: 607-617. doi: 10.1016/j.istruc.2023.04.112 [50] LI CHEN, DARONG PAN, QILIN ZHAO, et al. Overall buckling characteristics of slender FRP-foam sandwich tube under axial compression[J]. Composites Communications, 2021, 24: 100585. doi: 10.1016/j.coco.2020.100585 [51] 郑华勇, 吴林志, 马力, 等. Kagome点阵夹芯板的抗冲击性能研究[J]. 工程力学, 2007, 24(8): 86-92. doi: 10.3969/j.issn.1000-4750.2007.08.016ZHENG Huayong, WU Linzhi, MA Li, et al. Research on impulse-resistant performance of sandwich panels with kagome truss core[J]. Engineering Mechanics, 2007, 24(8): 86-92(in Chinese). doi: 10.3969/j.issn.1000-4750.2007.08.016 [52] WADLEY H. Fabrication and structural performance of periodic cellular metal sandwich structures[J]. Composites Science and Technology, 2003, 63(16): 2331-2343. doi: 10.1016/S0266-3538(03)00266-5 [53] COTE F, BIAGI R, BART-SMITH H, et al. Structural response of pyramidal core sandwich columns[J]. International Journal of Solids and Structures, 2007, 44(10): 3533-3556. doi: 10.1016/j.ijsolstr.2006.10.004 [54] DESHPANDE VS, FLECK NA. Collapse of truss core sandwich beams in 3-point bending[J]. International Journal of Solids and Structures, 2001, 38(36): 6275-6305. [55] 娄佳. 复合材料点阵夹芯结构的弯曲、屈曲和振动特性研究[D]. 哈尔滨工业大学, 2013.LOU Jia. Bending, buckling and vibration properties of composite lattice sandwich structures[D]. Harbin Institute of Technology, 2013(in Chinese). [56] 杨丽红, 韩笑, 吴林志. 应用分解刚度法分析金属点阵夹芯板屈曲问题[J]. 强度与环境, 2017, 44(3): 18-24.YANG Lihong, HAN Xiao, WU Linzhi. Buckling analysis of metal truss-core panels using split rigidity method[J]. Structure & Environment Engineering, 2017, 44(3): 18-24(in Chinese). [57] FENG L, WU L, YU G. The optimum layer number of multi-layer pyramidal core sandwich columns under in-plane compression[J]. Theoretical and Applied Mechanics Letters, 2016, 6(2): 65-68. doi: 10.1016/j.taml.2016.01.002 [58] 丁若晨. 基于激光选区熔化的金属点阵结构力学性能研究[D]. 中国科学院大学(中国科学院工程热物理研究所), 2021.DING Ruochen. Study on mechanical properties of metal lattice structures based on selective laser melting[D]. The Institute of Engineering Thermophysics, Chinese Academy of Sciences, 2021(in Chinese). [59] HEIMBS S. Foldcore sandwich structures and their impact behaviour: an overview[J]. Dynamic Failure of Composite and Sandwich Structures, 2012: 491-544. [60] DOSIKOVA YI. Studies of soundproofing characteristics of sandwich panels with cores of z-crimp type[J]. Russian Aeronautics, 2013, 56(2): 194-198. doi: 10.3103/S1068799813020141 [61] MIURA K. New structural form of sandwich core[J]. Journal of Aircraft, 1975, 12(5): 437-441. doi: 10.2514/3.44468 [62] PAIMUSHIN VN, ZAKIROV II, KARPIKOV YA. Theoretical and experimental technique of determining the mechanical characteristics of folded structure core in the form of z-crimp. Theoretical foundations and core compression in transverse direction[J]. Russian Aeronautics, 2012, 55(3): 233-244. doi: 10.3103/S1068799812030038 [63] LEBEE A, SAB K. Transverse shear stiffness of a chevron folded core used in sandwich construction[J]. International Journal of Solids and Structures, 2010, 47(18-19): 2620-2629. doi: 10.1016/j.ijsolstr.2010.05.024 [64] ZHENG S, YIFENG Z, QINSHAN Y, et al. Applications of vam-based equivalent beam model on effective performance of composite sandwich beam with m-shaped folded core[J]. Composite Structures, 2023, 304: 116395. doi: 10.1016/j.compstruct.2022.116395 [65] 方耀楚, 李刚. 基于板理论的层级褶皱结构失效模式分析[J]. 固体力学学报, 2014, 35(3): 241-248.FANG Yaochu, LI Gang. Failure mode analysis of the structure with hierarchical corrugated truss core by using the theory of plate[J]. Chinese Journal of Solid Mechanics, 2014, 35(3): 241-248(in Chinese). [66] KOOISTRA G W, DESHPANDE V, WADLEY H N G. Hierarchical corrugated core sandwich panel concepts[J]. The American Society of Mechanical Engineers, 2007, 74(2): 259-268(10 pages). [67] 刘彪. 碳纤增强褶皱夹芯板壳的设计制备及力学性能[D]. 哈尔滨工业大学, 2021.LIU Biao. Design, fabrication and mechanical properties of carbon-fiber-reinforced foldcore sandwich panel and shell[D]. Harbin Institute of Technology, 2021(in Chinese). [68] 唐劼尧, 柏敏建. 轴压载荷下复合材料蜂窝夹芯板的稳定性研究[J]. 兵器装备工程学报, 2020, 41(9): 242-246. doi: 10.11809/bqzbgcxb2020.09.045TANG Jieyao, BAI Minjie. Stability evaluation on composite honeycomb sandwich panels subjected to compressive loadings[J]. Journal of Sichuan Ordnance, 2020, 41(9): 242-246(in Chinese). doi: 10.11809/bqzbgcxb2020.09.045 [69] 董国滨. 混杂蜂窝芯的夹芯板稳定性分析[D]. 大连海事大学, 2022.DONG Guobin. Stability analysis of honeycomb sandwich plate with hybrid honeycomb core[D]. Dalian Marine University, 2022. (in Chinese). [70] 魏家睿, 吴琼, 吴伟, 等. 轴压铝合金蜂窝圆筒整体稳定性研究[J]. 北京航空航天大学学报, 2023: 1-16.WEI Jiarui, WU Qiong, WU Wei, et al. Study on global stability of aluminum alloy honeycomb cylinder under axial compression[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023: 1-16(in Chinese). [71] 窦明月, 王显峰, 张冬梅, 等. Nomex蜂窝芯静态压缩屈曲与后屈曲分析[J]. 南京航空航天大学学报, 2019, 51(1): 69-74.DOU Mingyue, WANG Xianfeng, ZHANG Dongmei, et al. Buckling and post-buckling of nomex honeycomb cores under compression[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2019, 51(1): 69-74(in Chinese). [72] XINYI L, YIFENG Z, RONG L, et al. Static and global buckling analysis of sandwich panels with improved star-shaped honeycomb using VAM-based downscaling model[J]. Composite Structures, 2023, 323: 117458. doi: 10.1016/j.compstruct.2023.117458 [73] YANG F, ZHONG Y, LIU R, et al. Effective performance analysis of stiffened honeycomb sandwich panels using VAM-based equivalent model[J]. Thin-Walled Structures, 2023, 185: 110590. doi: 10.1016/j.tws.2023.110590 [74] LIU X, ZHONG Y, LIU R, et al. Buckling and post-buckling analysis of butterfly-shaped auxetic core sandwich plates based on variational asymptotic method[J]. Thin-Walled Structures, 2023, 184: 110464. doi: 10.1016/j.tws.2022.110464 [75] SARAFRAZ M, SEIDI H, KAKAVAND F, et al. Free vibration and buckling analyses of a rectangular sandwich plate with an auxetic honeycomb core and laminated three-phase polymer/GNP/fiber face sheets[J]. Thin-Walled Structures, 2023, 183: 110331. doi: 10.1016/j.tws.2022.110331 [76] 洪俊青, 刘伟庆, 方海. 格构增强型泡沫夹层结构腹板剪切屈曲分析[J]. 工业建筑, 2014, (10): 40-45.HONG Junqing, LIU Weiqing, FANG Hai. Shear buckling analysis of web of lattice enhanced foam sandwich structure[J]. Industrial Construction, 2014, (10): 40-45(in Chinese). [77] YAVUZ AK, PAPOULIA KD, PHOENIX SL, et al. Stability analysis of stitched composite plate system with delamination under hygrothermal pressure[J]. Aiaa Journal, 2006, 44(7): 1579-1585. doi: 10.2514/1.17367 [78] 马元春, 俸翔, 卢子兴, 等. 缝纫泡沫夹芯复合材料板的稳定性分析[J]. 复合材料学报, 2011, 28(2): 201-205.MA Yuanchun, FENG Xiang, LU Zixing, et al. Stability analysis of stitched foam-core composite sandwich plates[J]. Acta Materiae Compositae Sinica, 2011, 28(2): 201-205(in Chinese). [79] 邢鹏程, 陈震, 戴广民. 泡沫铝填充Ⅰ型夹层板尺寸参数对腹板屈曲失效模式的影响分析[J]. 中国舰船研究, 2021, 16(3): 112-119.XING Pengcheng, CHEN Zhen, DAI Guangmin. Analysis of buckling failure modes of composite sandwich panels filled with aluminum foam[J]. Chinese Journal of Ship Research, 2021, 16(3): 112-119(in Chinese). [80] WU D, GU X, PENG A, et al. Post-buckling behavior and failure analysis of asymmetric sandwich panels under uniaxial compression[J]. Journal of Sandwich Structures & Materials, 2024, 26(1): 38-55. [81] MIAO X Y, CHEN X. Structural transverse cracking mechanisms of trailing edge regions in composite wind turbine blades[J]. Composite Structures, 2023, 308: 116680. doi: 10.1016/j.compstruct.2023.116680 [82] HYUN S, KARLSSON AM, TORQUATO S, et al. Simulated properties of kagomé and tetragonal truss core panels[J]. International Journal of Solids and Structures, 2003, 40(25): 6989-6998. doi: 10.1016/S0020-7683(03)00350-0 [83] 朱波, 周叮, 刘伟庆. 树脂柱对复合材料夹层板屈曲及动力学性能的影响分析[J]. 振动与冲击, 2011, 30(4): 8-11. doi: 10.3969/j.issn.1000-3835.2011.04.002ZHU Bo, ZHOU Ding, LIU Qingwei. Effect of resinic columns on buckling and vibration of a composite sandwich plate[J]. Journal of Vibration and Shock, 2011, 30(4): 8-11(in Chinese). doi: 10.3969/j.issn.1000-3835.2011.04.002 [84] 谢闽辉. 碳纤维点阵材料制备及力学行为研究[D]. 长春工业大学, 2023.XIE Minhui. Preparation and mechanical behavior of carbon fiber lattice materials[D]. Changchun University of Technology, 2023(in Chinese). [85] WU Q, VAZIRI A, ASL ME, et al. Lattice materials with pyramidal hierarchy: systematic analysis and three dimensional failure mechanism maps[J]. Journal of the Mechanics and Physics of Solids, 2019, 125: 112-144. doi: 10.1016/j.jmps.2018.12.006 [86] 熊健, 杜昀桐, 杨雯, 等. 轻质复合材料夹芯结构设计及力学性能最新进展[J]. 宇航学报, 2020, 41(6): 749-760. doi: 10.3873/j.issn.1000-1328.2020.06.012XIONG Jian, DU Yuntong, YANG Wen, et al. Research progress on design and mechanical properties of lightweight composite sandwich structures[J]. Journal of Astronautics, 2020, 41(6): 749-760(in Chinese). doi: 10.3873/j.issn.1000-1328.2020.06.012 [87] MOHAMMED AYAZ UDDIN, IMAD BARSOUM, S. KUMAR, et al. Enhancing compressive performance in 3D printed pyramidal lattice structures with geometrically tailored I-shaped struts[J]. Materials and Design, 2024, 237: 112524. doi: 10.1016/j.matdes.2023.112524 [88] ZHONGLIANG C, SIXIN Y. Study on damage failure for a new double-triangular truss core sandwich structure[J]. Heliyon, 2023, 9(9). [89] 周华志, 王志瑾. M-型皱褶芯材夹层板吸能性能研究[J]. 航空学报, 2016, 37(2): 579-587.ZHOU Huazhi, WANG Zhijin. Analysis of energy absorption capability of m-type folded core sandwich structure[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 579-587(in Chinese). [90] DU Y, SONG C, XIONG J, et al. Fabrication and mechanical behaviors of carbon fiber reinforced composite foldcore based on curved-crease origami[J]. Composites Science and Technology, 2019, 174: 94-105. doi: 10.1016/j.compscitech.2019.02.019 [91] 殷乾峰. 碳纤增强褶皱夹芯圆台壳结构设计及力学性能研究[D]. 哈尔滨工业大学, 2021.YIN Qianfeng. Design, fabrication and mechanical properies of carbon-fiber-reinforced foldcore sandwich panel and shell[D]. Harbin Institute of Technology, 2021(in Chinese). [92] 王宝芹, 王沫楠, 刘长喜. 基于多尺度方法的蜂窝夹层复合材料结构轴向压缩稳定性[J]. 复合材料学报, 2020, 37(3): 601-608.WANG Baoqin, WANG Monan, LIU Zhangxi. Stability of honeycomb sandwich composite structure under axial compression based on multi-scale method[J]. Acta Materiae Compositae Sinica, 2020, 37(3): 601-608(in Chinese). [93] 刘玥, 刘伟, 华洲, 等. 复合材料nomex蜂窝夹芯结构的平压试验研究[J]. 航空制造技术, 2020, 63(17): 86-91.LIU Yue, LIU Wei, HUA Zhou, et al. Experimental study on nomex honeycomb sandwich structure subjected to out-of-plane compression load[J]. Aeronautical Manufacturing Technology, 2020, 63(17): 86-91(in Chinese). [94] ZHANG S, MA Y, DENG Z. Analytical solution and experimental verification for the buckling failure of additively manufactured octagonal honeycombs[J]. Composite Structures, 2023, 303: 116306. doi: 10.1016/j.compstruct.2022.116306 [95] LUO Y, HU S P, LIU Y Z, et al. Fabrication and mechanical properties of three-dimensional enhanced TiAl/GH3536 hetero-honeycomb sandwich structure[J]. Journal of Materials Research and Technology, 2023, 26: 7490-7501. doi: 10.1016/j.jmrt.2023.09.064 [96] SUN M, KENDALL P, WOWK D, et al. Out-of-plane compressive response of aluminum honeycomb sandwich panels: Adhesive geometry and bonding effects[J]. Thin-Walled Structures, 2024, 196: 111509. doi: 10.1016/j.tws.2023.111509 [97] WU Z, ZENG J, XIAO J, et al. Flexural performance of integrated 3d composite sandwich structures[J]. Journal of Reinforced Plastics and Composites, 2014, 33(16): 1496-1507. doi: 10.1177/0731684414539026 [98] 欧阳懿桢, 方海, 刘伟庆, 等. 单向纤维腹板格构增强复合材料夹层板侧压试验研究[J]. 水利与建筑工程学报, 2013, 11(4): 24-27.OU Yangyizhen, FANG Hai, LIU Weiqing, et al. Research on lateral compression test for fiber-reinforced composite sandwich plates with one-way web[J]. Journal of Water Resources and Architectural Engineering, 2013, 11(4): 24-27(in Chinese). [99] 陈悦, 朱锡, 李华东, 等. 含分层缺陷复合材料夹芯梁力学特性及失效模式的试验研究[J]. 海军工程大学学报, 2016, 28(6): 65-70.CHEN Yue, ZHU Xi, LI Huadong, et al. Mechanical behavior and failure modes of composite sandwich columns with face/ core debond[J]. Journal of Naval University of Engineering, 2016, 28(6): 65-70(in Chinese). [100] HOSSEINI R, TOOSKI M Y, KHORSHIDVAND A R, et al. Buckling behavior of fiber reinforced Innegra sandwich beams incorporating carbon nanofiber[J]. Functional Composites and Structures, 2023, 5(1): 015003. doi: 10.1088/2631-6331/acb890 [101] MIN-SEOK SOHN, XIAO-ZHI HU. Model II delamination toughness of carbon-fibre/epoxy composites with chopped Kevlar fibre reinforcement[J]. Composites Science and Technology, 1994, 52(3): 439-448. doi: 10.1016/0266-3538(94)90179-1 [102] EYVAZIAN A, TAGHIZADEH S A, HAMOUDA A M, et al. Buckling and crushing behavior of foam-core hybrid composite sandwich columns under quasi-static edgewise compression[J]. Journal of Sandwich Structures and Materials, 2021, 23(7): 2643-2670. doi: 10.1177/1099636219894665 [103] SHARMA SC, KRISHNA M, MURTHY HNN. Buckling response of stitched polyurethane foam composite sandwich structures[J]. Journal of Reinforced Plastics and Composites, 2004, 23(12): 1267-1277. doi: 10.1177/0731684404037042 [104] SONG C, FAN W, LIU T, et al. A review on three-dimensional stitched composites and their research perspectives[J]. Composites Part a:Applied Science and Manufacturing, 2022, 153: 106730. doi: 10.1016/j.compositesa.2021.106730 [105] BILISIK K, ERDOGAN G, SAPANCI E, et al. Three-dimensional nanoprepreg and nanostitched aramid/phenolic multiwall carbon nanotubes composites: experimental determination of in-plane shear[J]. Journal of Composite Materials, 2019, 53(28-30): 4077-4096. doi: 10.1177/0021998319854211 [106] SUN C, ALBUSTANI H, PHADNIS VA, et al. Improving the structural integrity of foam-core sandwich composites using continuous carbon fiber stitching[J]. Composite Structures, 2023, 324: 117509. doi: 10.1016/j.compstruct.2023.117509 [107] LI M, WU L, MA L, et al. Mechanical response of all-composite pyramidal lattice truss core sandwich structures[J]. Journal of Materials Science & Technology, 2011, 27(6): 570-576. [108] LI X, WU L, MA L, et al. Fabrication and mechanical properties of composite pyramidal truss core sandwich panels with novel reinforced frames[J]. Journal of Reinforced Plastics and Composites, 2016, 35(16): 1260-1274. doi: 10.1177/0731684416648229 [109] RACKLIFFE ME, JENSEN DW, LUCAS WK. Local and global buckling of ultra-lightweight isotruss® structures[J]. Composites Science and Technology, 2006, 66(2): 283-288. doi: 10.1016/j.compscitech.2005.04.038 [110] WANG B, WU L, MA L, et al. Fabrication and testing of carbon fiber reinforced truss core sandwich panels[J]. Journal of Materials Science & Technology, 2009, 25(4): 547-550. [111] SCHAEDLER TA, CHAN LJ, CLOUGH EC, et al. Nanocrystalline aluminum truss cores for lightweight sandwich structures[J]. Jom, 2017, 69(12): 2626-2634. doi: 10.1007/s11837-017-2539-8 [112] ZHANG H, SHI H, FAN H. Additively manufactured truss-core sandwich cylinders: Materials, processes and performances[J]. International Journal of Mechanical Sciences, 2024: 108966. [113] KHALEDI H, ROSTAMIYAN Y. Compressive and bending behavior of foam-filled composite sandwich panel with novel M-shaped core reinforced by nano-silica[J]. Journal of Thermoplastic Composite Materials, 2023, 36(6): 2482-2504. doi: 10.1177/08927057221094453 [114] WANG B, LUO B, HU W, et al. Manufacturing and mechanical testing of woven lattice truss C-sandwich radome composites[J]. Composite Structures, 2023, 308: 116675. doi: 10.1016/j.compstruct.2023.116675 [115] FAN M, ZENG T, WU R, et al. Microstructure design and mechanical properties of 3D printed graded lattice sandwich structures with tailored porosity[J]. Composite Structures, 2023, 321: 117323. doi: 10.1016/j.compstruct.2023.117323 [116] HEIMBS S, CICHOSZ J, KLAUS M, et al. Sandwich structures with textile-reinforced composite foldcores under impact loads[J]. Composite Structures, 2010, 92(6): 1485-1497. doi: 10.1016/j.compstruct.2009.11.001 [117] WEAVER PM. Design of laminated composite cylindrical shells under axial compression[J]. Composites. Part B, Engineering, 2000, 31(8): 669-679. doi: 10.1016/S1359-8368(00)00029-9 [118] 易青山. 基于变分渐近法的褶皱夹芯结构等效模型[D]. 重庆大学, 2022.YI Qingshan. Equivalent model of the sandwich structure with folded core based on variational asymptotic method[D]. Chongqing University, 2022(in Chinese). [119] 邓云飞, 曾宪智, 周翔, 等. 复合材料褶皱夹芯结构研究进展[J]. 复合材料学报, 2020, 37(12): 2966-2983.DENG Yunfei, ZENG Xianzhi, ZHOU Xiang, et al. Research progress for the composite sandwich structure with foldcore[J]. Acta Materiae Compositae Sinica, 2020, 37(12): 2966-2983(in Chinese). [120] 田珂. 锥柱一体化褶皱夹芯结构的设计及其力学性能分析[D]. 哈尔滨工业大学, 2022.TIAN Ke. Design and mechanical properties of cone-column integrated fold sanwich structure[D]. Harbin Institute of Technology, 2022(in Chinese). -

 点击查看大图
点击查看大图
计量
- 文章访问数: 169
- HTML全文浏览量: 100
- 被引次数: 0





 下载:
下载: