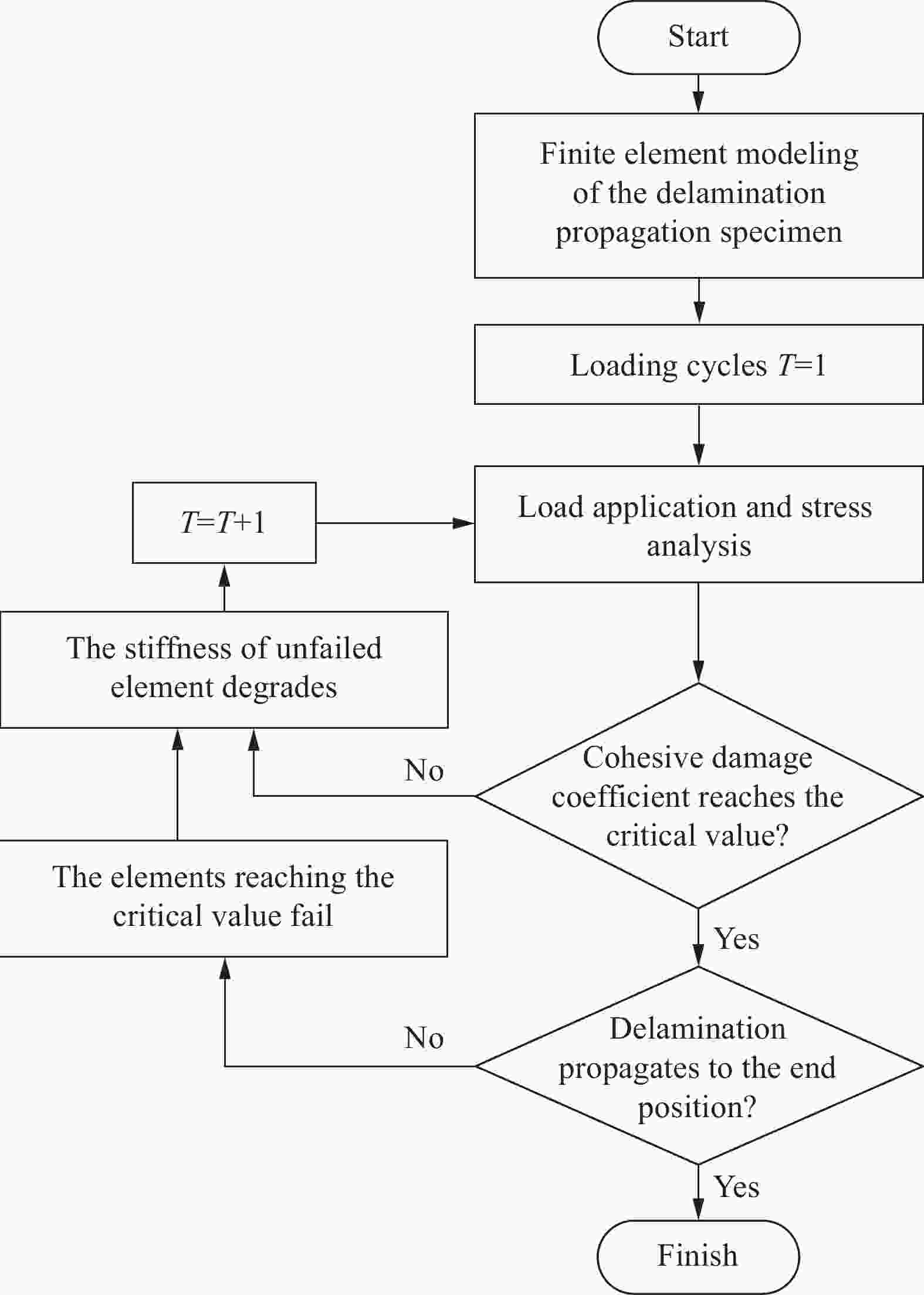
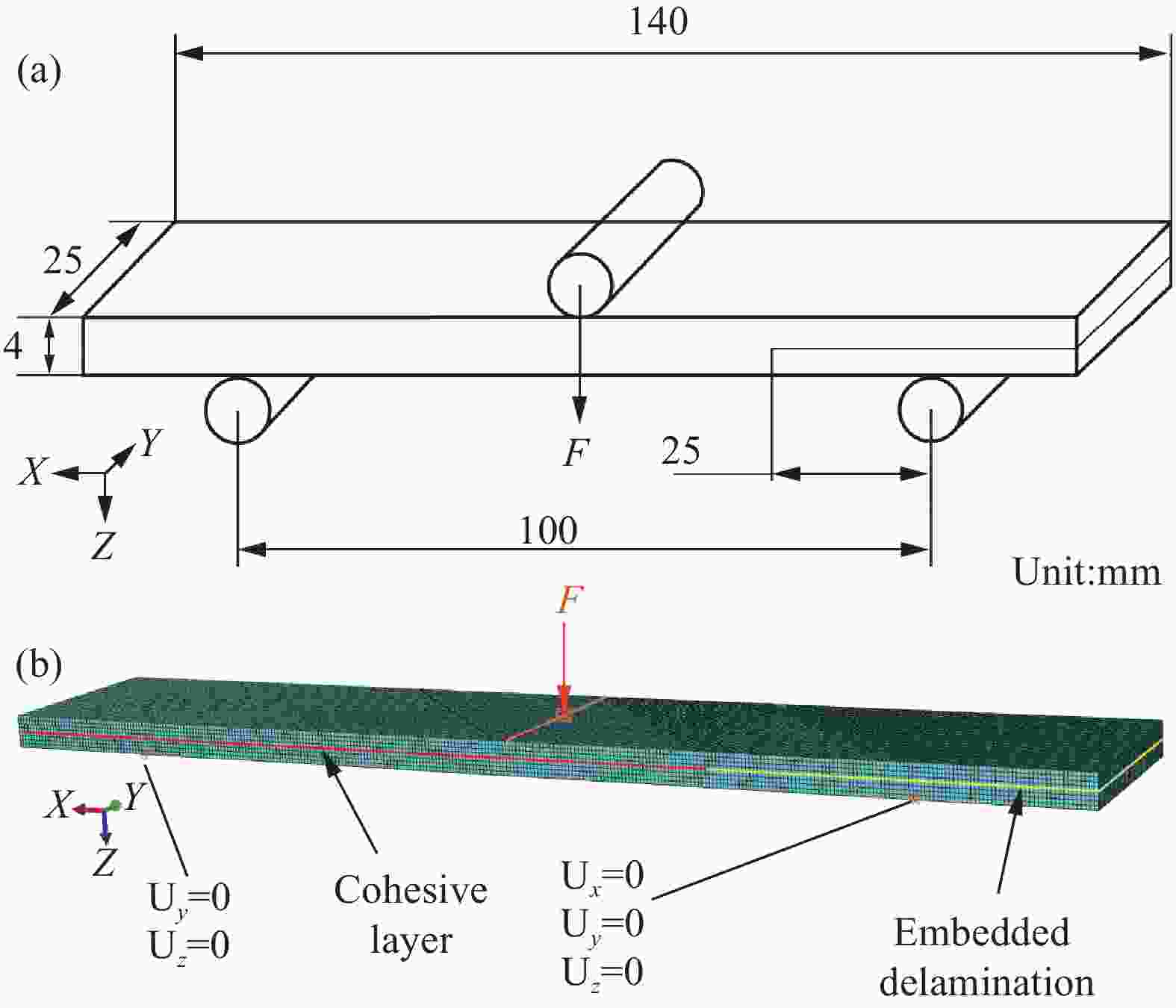
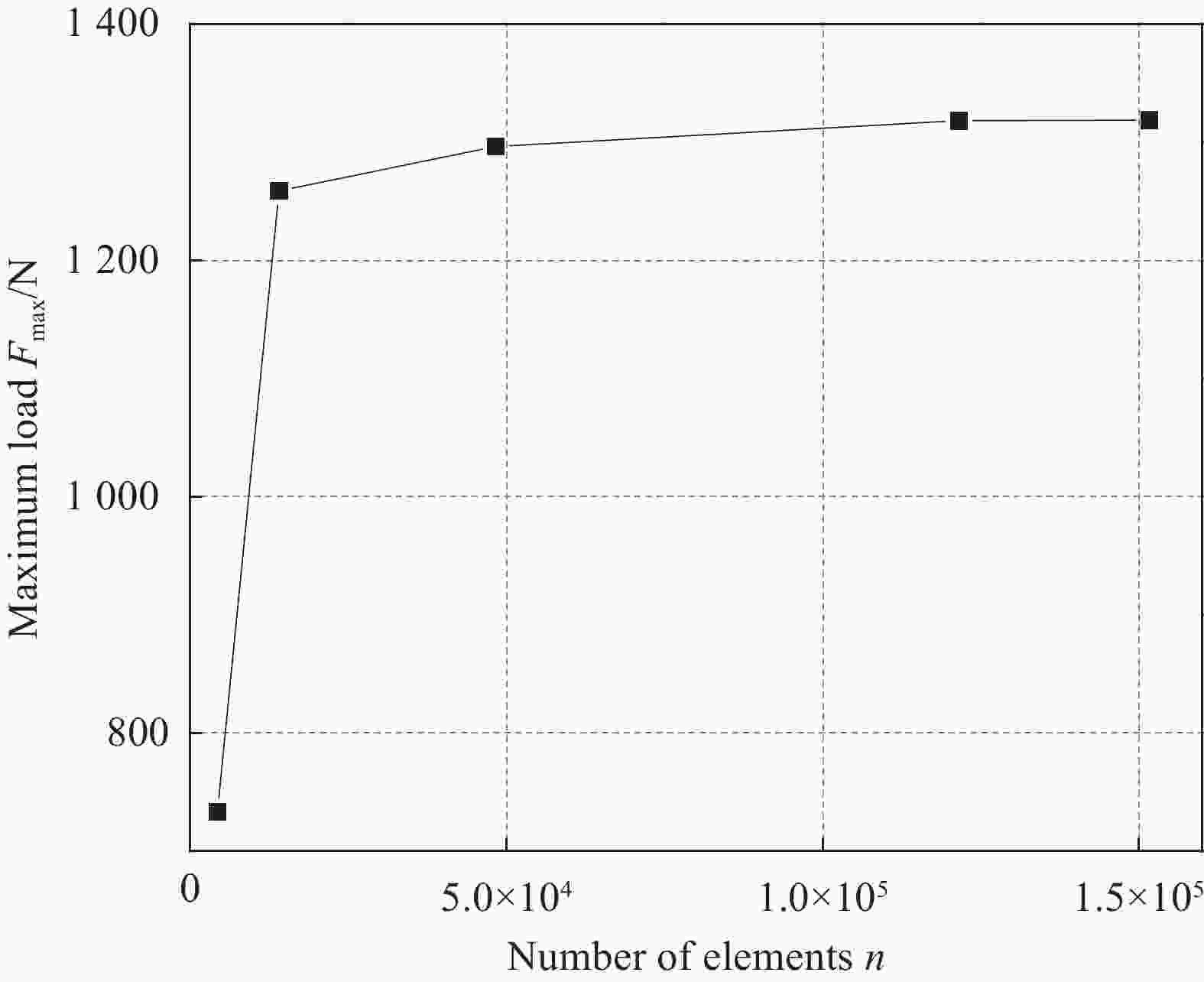
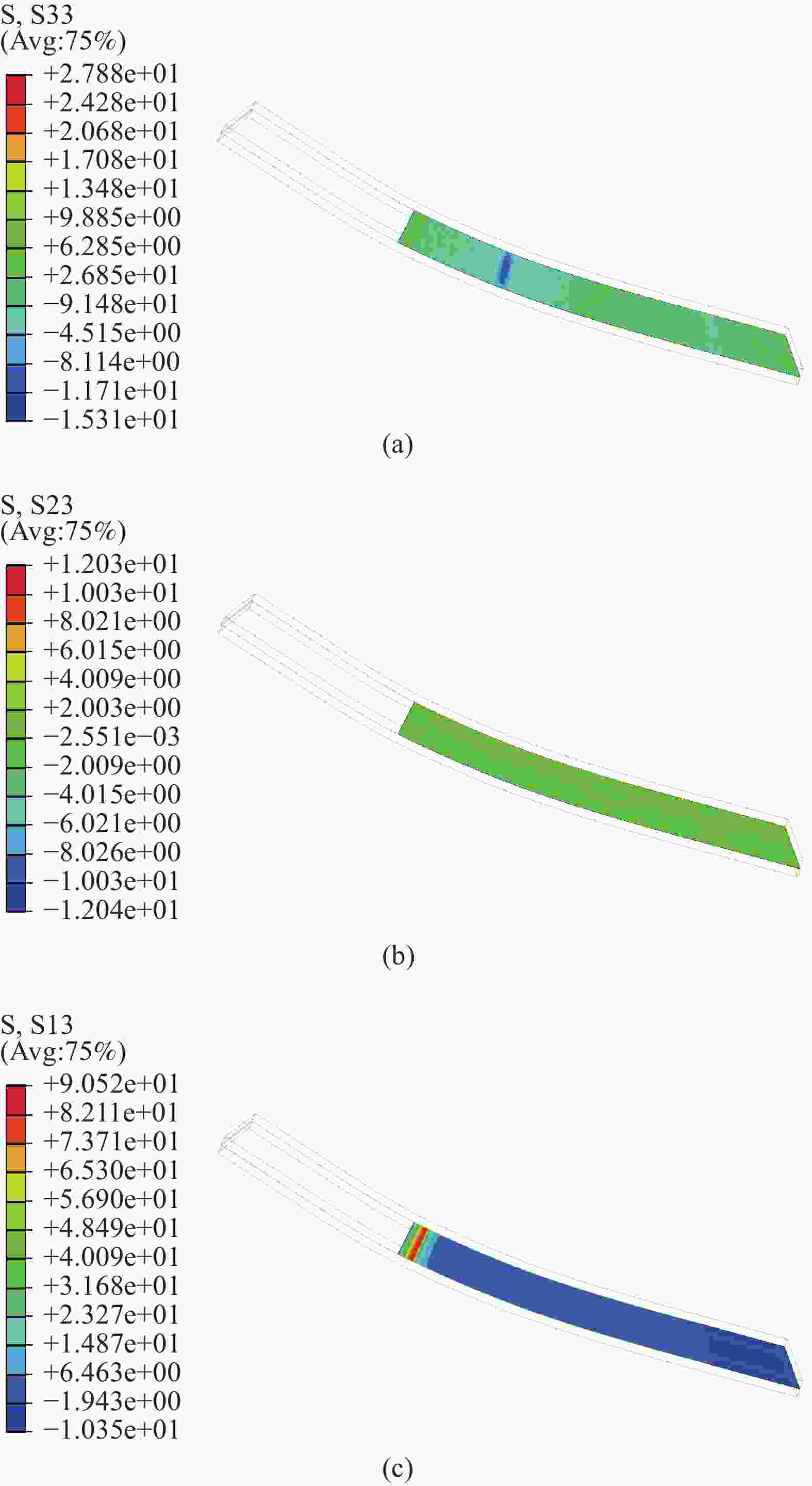
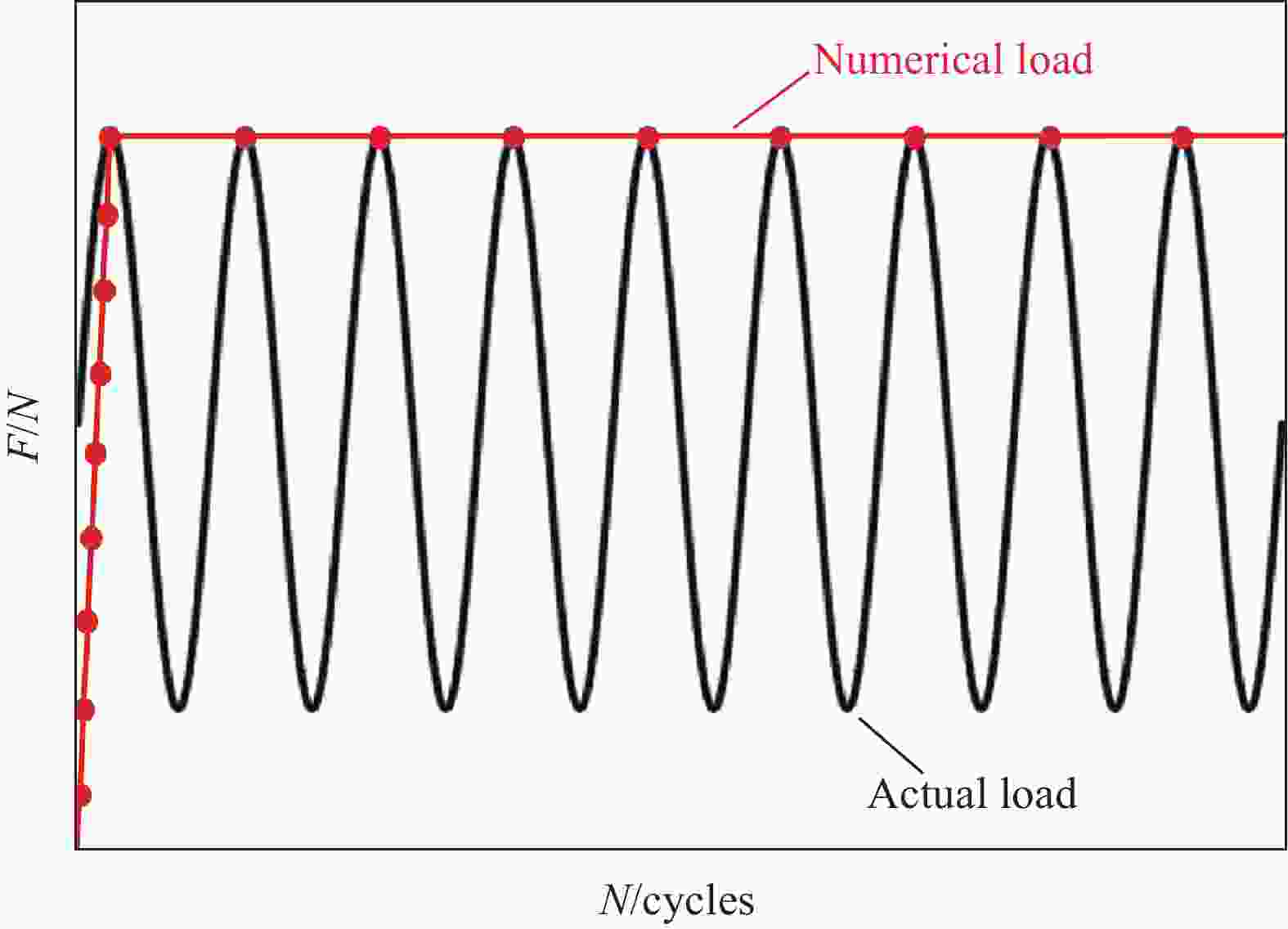
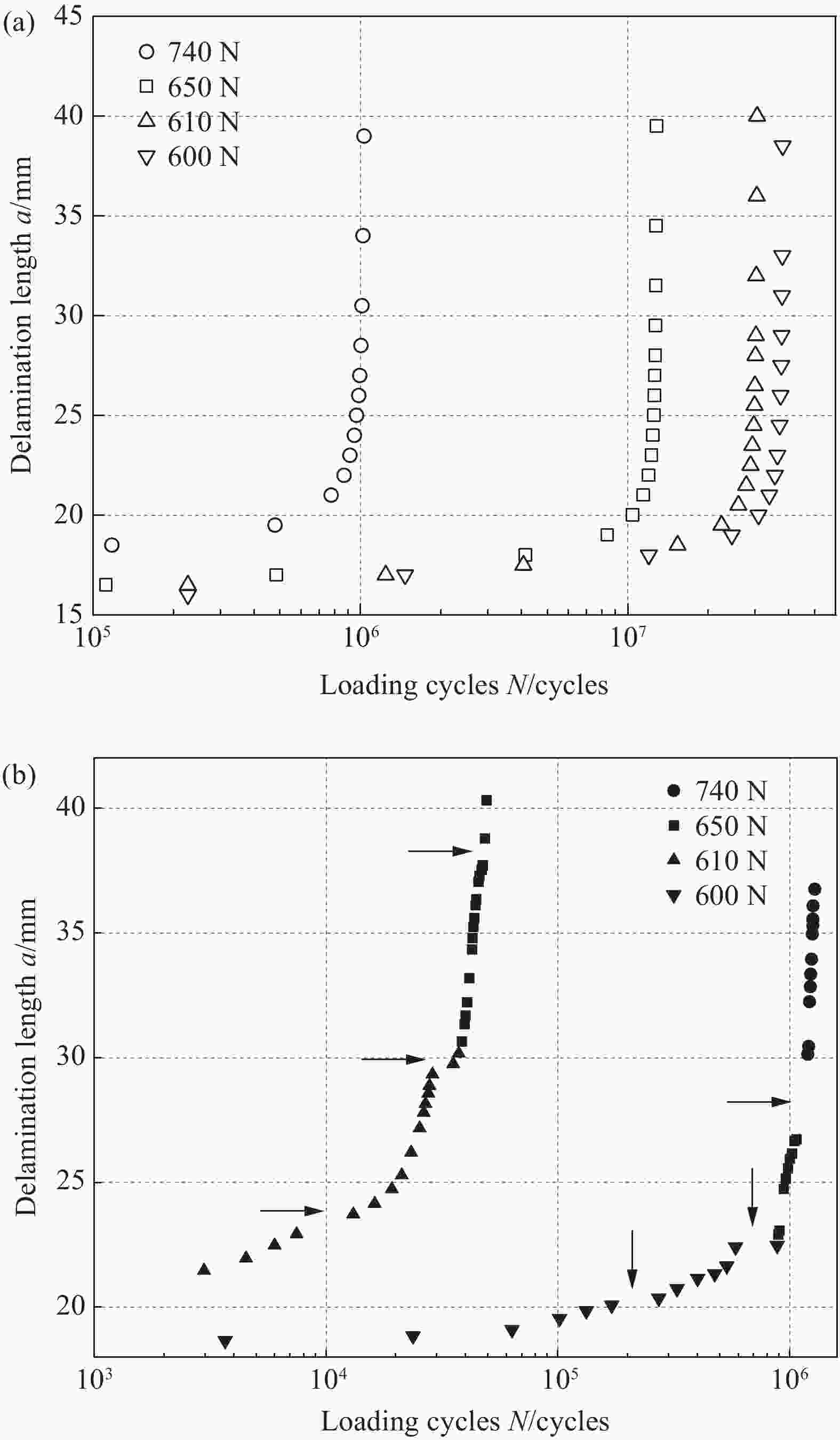
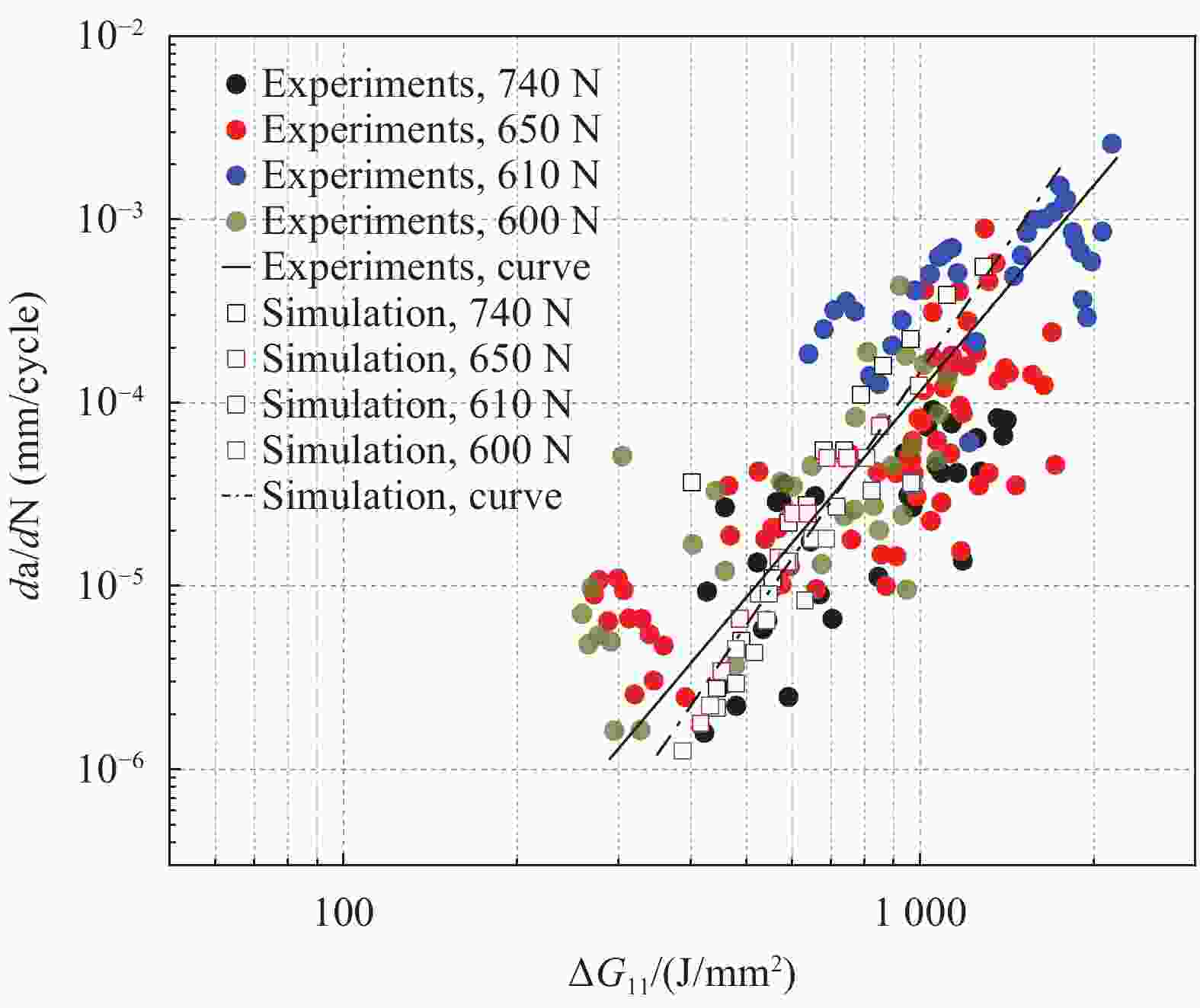
Investigation on numerical analysis method of fatigue delamination damage of plane woven composites
-
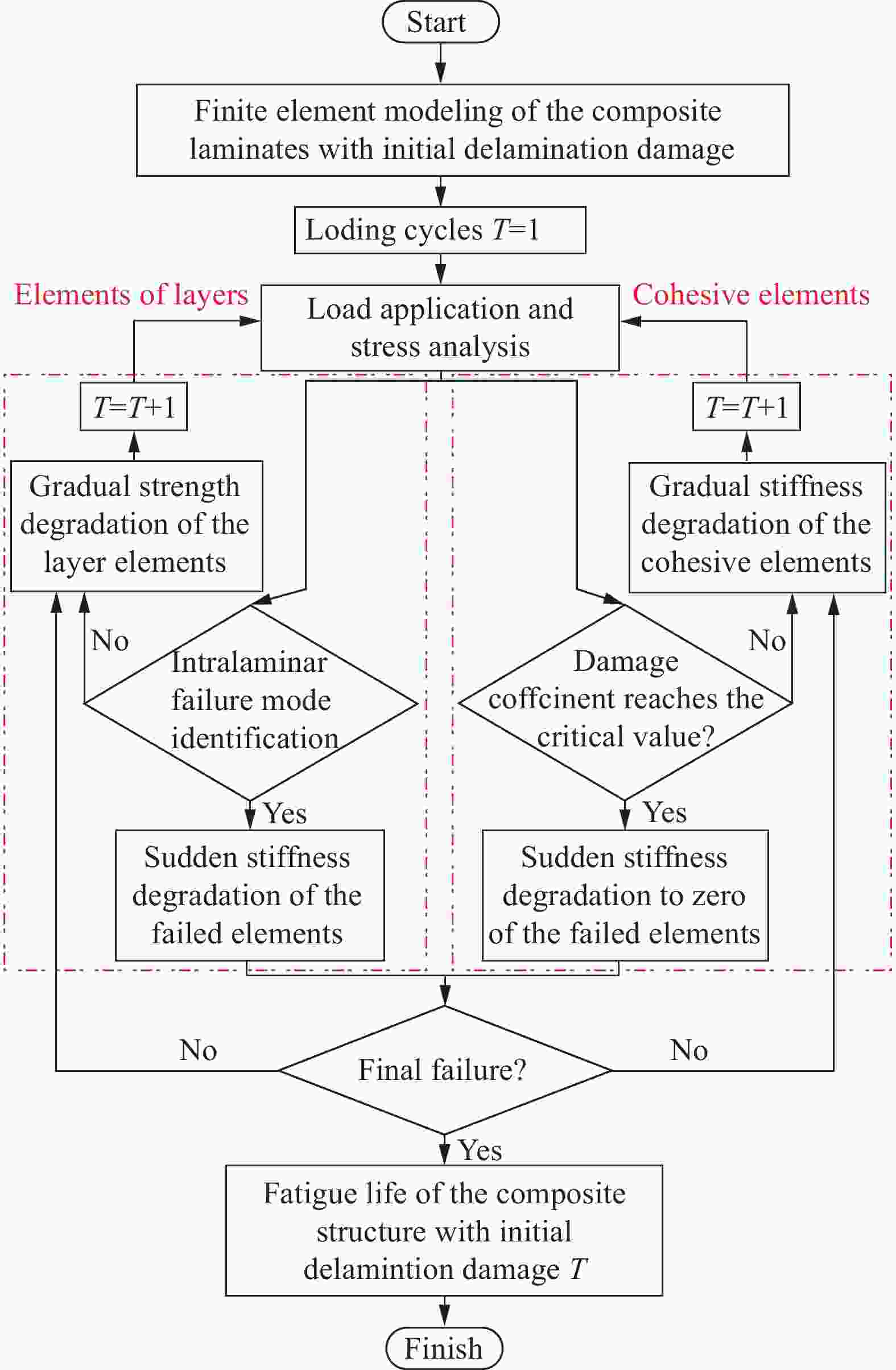
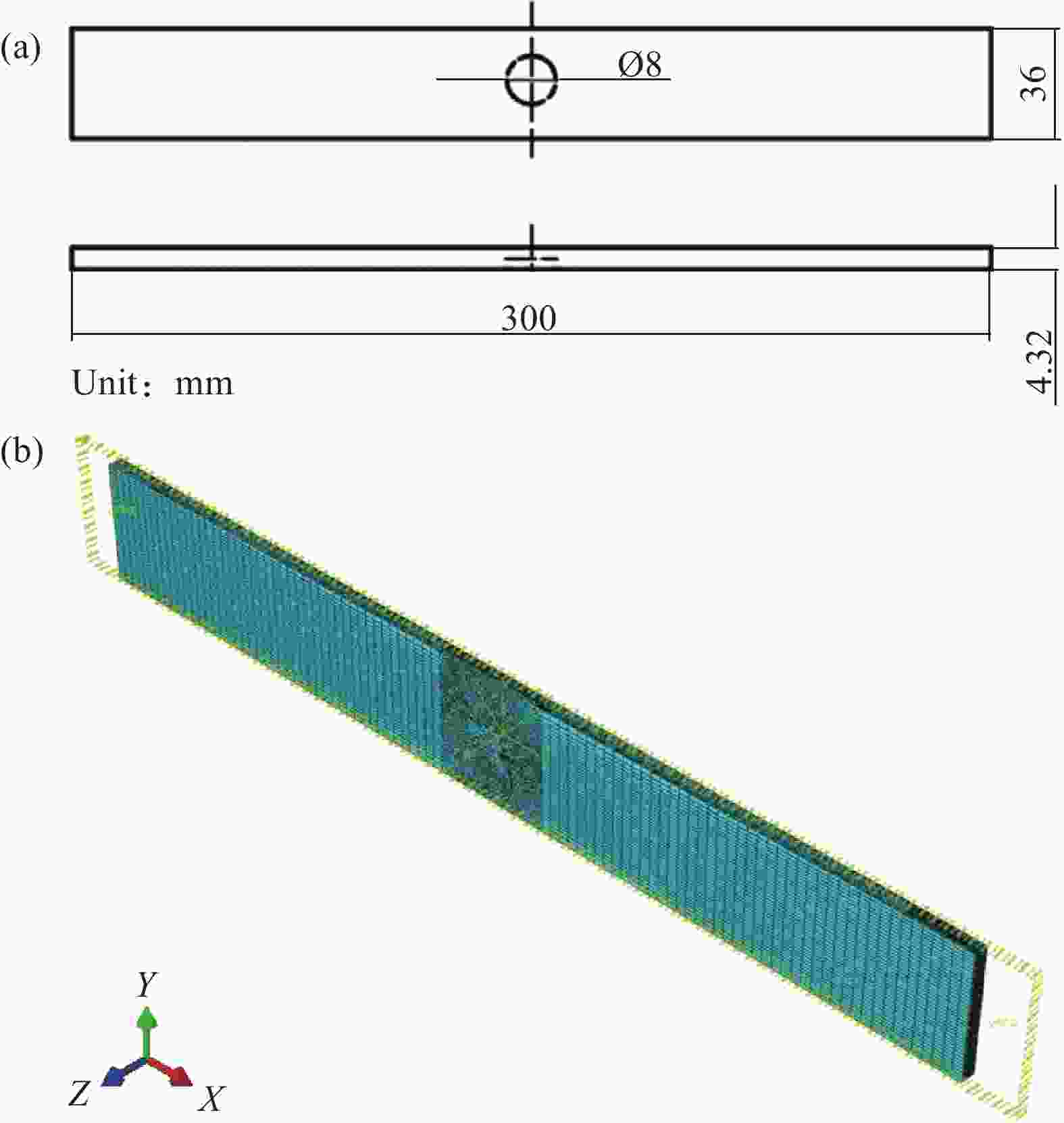
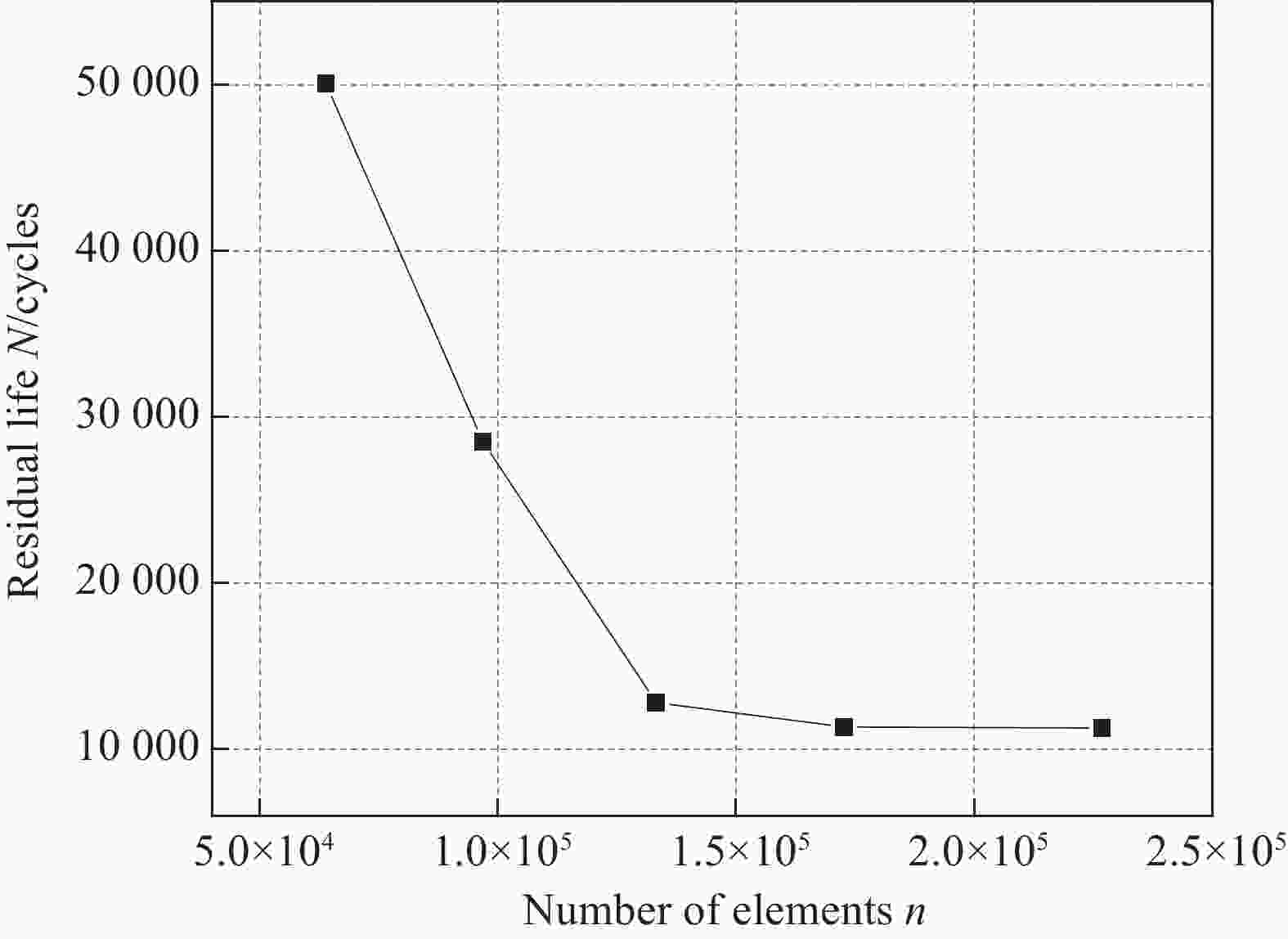
摘要: 本文基于内聚力双线性本构关系，建立考虑疲劳损伤的内聚力模型，结合有限元分析技术，建立复合材料层合板疲劳分层扩展行为数值分析方法，分别对准静态和疲劳加载下平面机织复合材料II型分层扩展行为进行仿真分析，准静态加载下的载荷-位移曲线仿真结果与试验结果吻合良好，疲劳加载下的分层扩展速率-应变能释放率变程曲线仿真结果与试验结果吻合良好，验证了模型和方法的有效性。在此基础上，建立适用于平面机织复合材料的疲劳失效准则，结合层内渐进疲劳损伤分析模型，建立含初始分层损伤平面机织复合材料层合结构剩余寿命预测方法，预测了含初始分层损伤层合板的剩余寿命和渐进损伤过程，剩余寿命仿真结果与试验结果吻合良好，此外，结果表明疲劳损伤从初始分层损伤处起始，并逐渐向边缘扩展，紧邻初始分层损伤的两层0°单层板较早出现层内经向损伤和纬向损伤，单层板中0°层较45°层损伤更多，最后0°层以经向损伤为主导失效模式，45°层则以纬向损伤为主导失效模式，各层间界面均出现大面积损伤。Abstract: Based on bilinear constitutive relationship, a cohesive model considering fatigue damage was established. Integrating with finite element analysis technology, the numerical analysis method of delamination propagation behavior of composite laminates was developed to simulate the mode II delamination propagation behavior of plane woven composite laminates under static and fatigue loading. The simulated load-displacement curve under quasi-static loading has good agreement with the experimental results. The simulated delamination propagation rate-strain energy release rate curve under fatigue loading is also in good agreement with the experimental results. Thus, the cohesive model considering fatigue damage has been validated. On this basis, the fatigue failure criteria for plane woven composites were established. Then the residual life prediction method of plane woven composite laminates with initial delamination damage was developed by integrating with the intralaminar progressive fatigue damage model. Using the developed method, the residual life and fatigue damage propagation of laminates with initial delamination damage were predicted, showing good correlation with the experimental results. In addition, the simulation results indicate that the fatigue damage initiates from the initial delamination damage which then propagates to the edges. The fatigue damage in both warp and weft directions appear early within the two layers of 0° adjacent to the initial delamination damage. And more damage occurs within the 0° layers than the 45° layers in general. Finally, the 0° layers show warp damage dominated failure mode while the 45° layers show weft damage dominated failure mode, and large area of damage appear at all the interlaminar interfaces.
-
Key words:
- plane woven composites /
- fatigue /
- delamination propagation /
- cohesive model /
- residual life
-
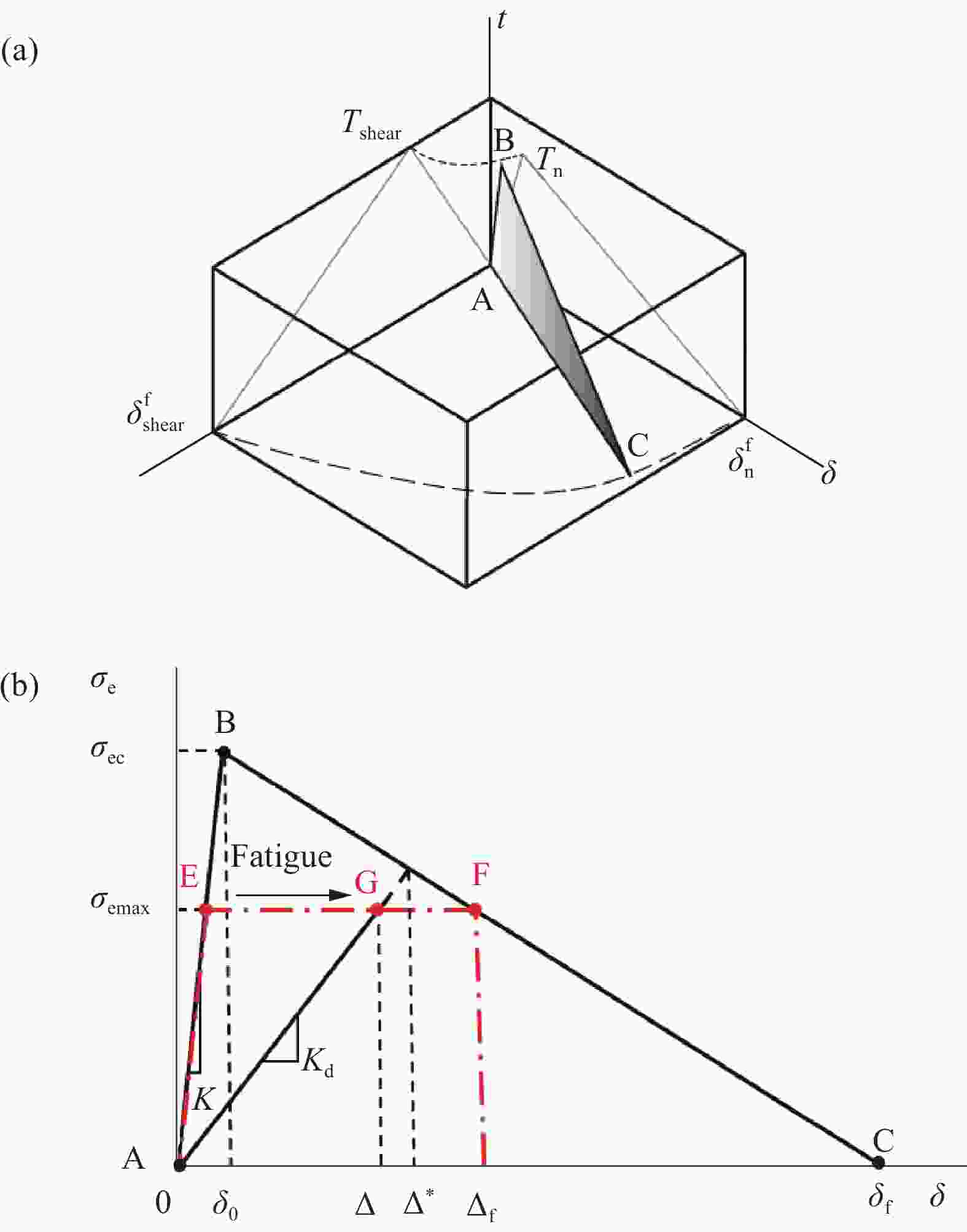
图 1 内聚力损伤本构模型：(a) 混合模式双线性本构模型；(b) 考虑疲劳损伤的双线性本构模型
Figure 1. Cohesive damage constitutive model: (a) Mixed-mode bilinear constitutive model; (b) Bilinear constitutive model considering fatigue damage
${T_{\text{n}}}$ and ${T_{{\text{shear}}}}$ are the normal strength and shear strength of interface, respectively; $\delta _{\text{n}}^{\text{f}}$ and $\delta _{{\text{shear}}}^{\text{f}}$ are the displacements in shear direction and normal direction at complete failure state, respectively; ${\sigma _{{\text{emax}}}}$ and ${\sigma _{{\text{ec}}}}$ are the equivalent stress and its critical value; ${\delta _0}$ and ${\delta _{\text{f}}}$ are the equivalent displacements at damage initiation state and complete failure state under quasi-static loading, respectively; $\Delta $ and ${\Delta ^ * }$are the displacement jump and its critical value; ${\Delta _{\text{f}}}$ is the displacements at complete failure state under fatigue loading; $K$ and ${K_{\text{d}}}$ are the initial stiffness and residual stiffness, respectively
图 2 复合材料疲劳分层扩展数值分析方法流程图
Figure 2. Flow chart of numerical analysis method for fatigue delamination propagation of composite materials
图 3 三点弯曲单端缺口(3-ENF)试样图和有限元模型：(a) 试样图；(b) 有限元模型
Figure 3. Three-point end-notched flexure (3-ENF) specimen diagram and finite element model: (a) Specimen diagram; (b) Finite element model
图 5 平面机织复合材料内聚力层应力云图：(a) S33应力；(b) S23应力；(b) S13应力
Figure 5. Stress contour in cohesive interface of the plane woven composites: (a) S33 Stress; (b) S23 stress; (b) S13 stress
图 6 平面机织复合材料II型分层扩展数值仿真结果：(a) 载荷-位移曲线；(b) 内聚力损伤扩展过程
Figure 6. Numerical simulation results of mode II delamination propagation of plane woven composites: (a) Load-displacement curve; (b) Cohesive damage propagation process
图 8 平面机织复合材料疲劳分层扩展a-N曲线：(a) 仿真结果；(b) 试验结果
Figure 8. Fatigue delamination propagation a-N curve of plane woven composites: (a) Simulation results; (b) Experimental results
图 9 平面机织复合材料疲劳分层扩展da/dN-ΔG曲线
Figure 9. Fatigue delamination propagation da/dN- ΔG curve of plane woven composites
图 10 740 N疲劳载荷作用下平面机织复合材料分层损伤扩展过程
Figure 10. Delamination damage propagation process of plane woven composites under fatigue load of 740 N
图 11 含分层损伤平面机织复合材料结构渐进疲劳损伤分析方法流程图
Figure 11. Flowchart of progressive fatigue damage analysis method for plane woven composite structures with initial delamination damage
图 12 含初始分层损伤层合板试样图和有限元模型：(a) 试样图；(b) 有限元模型
Figure 12. Sample diagram and finite element model of laminates with initial delamination damage: (a) Sample diagram; (b) Finite element model
图 14 平面机织复合材料含初始分层损伤层合板剩余寿命
Figure 14. Residual life of plane woven composite laminates with initial delamination damage
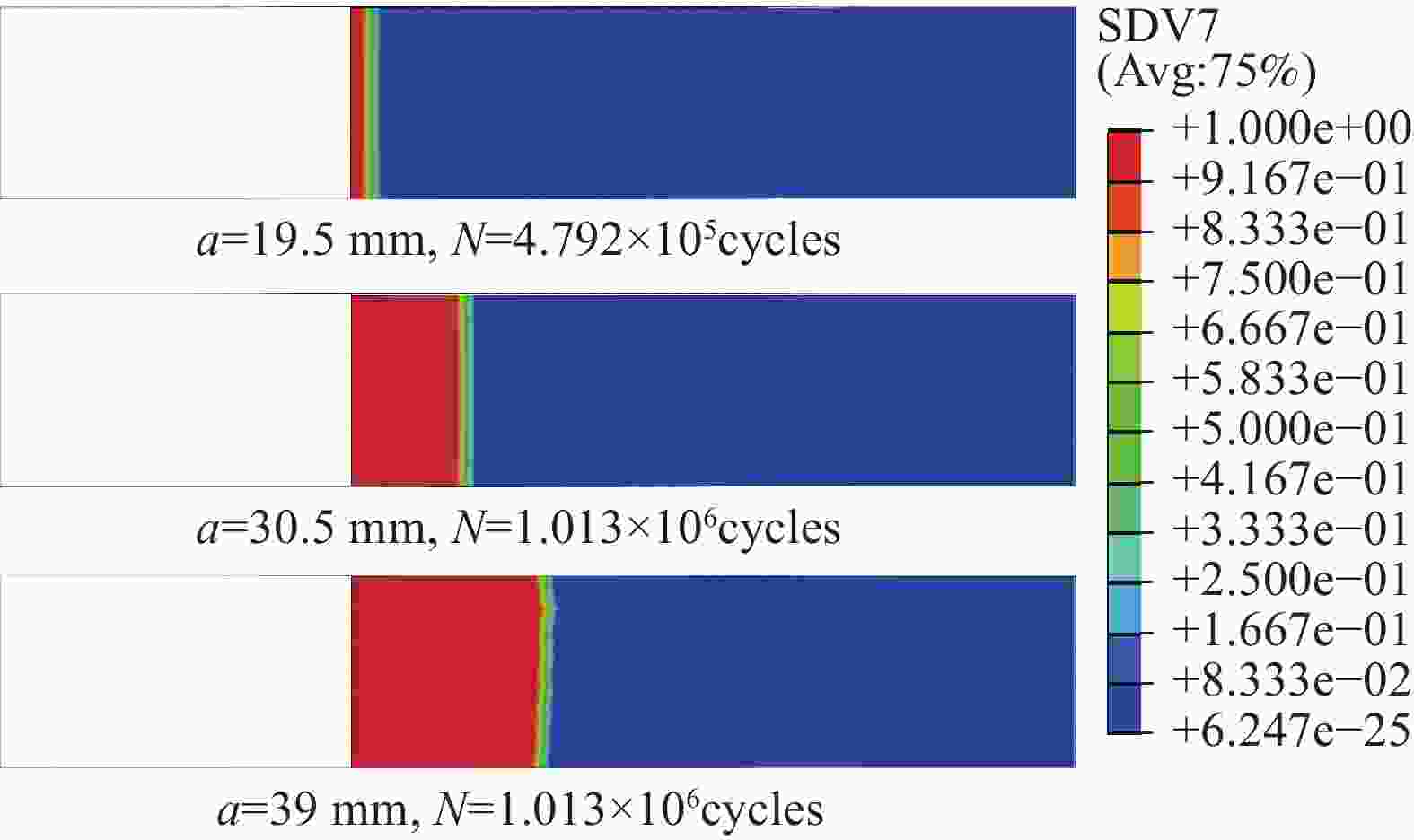
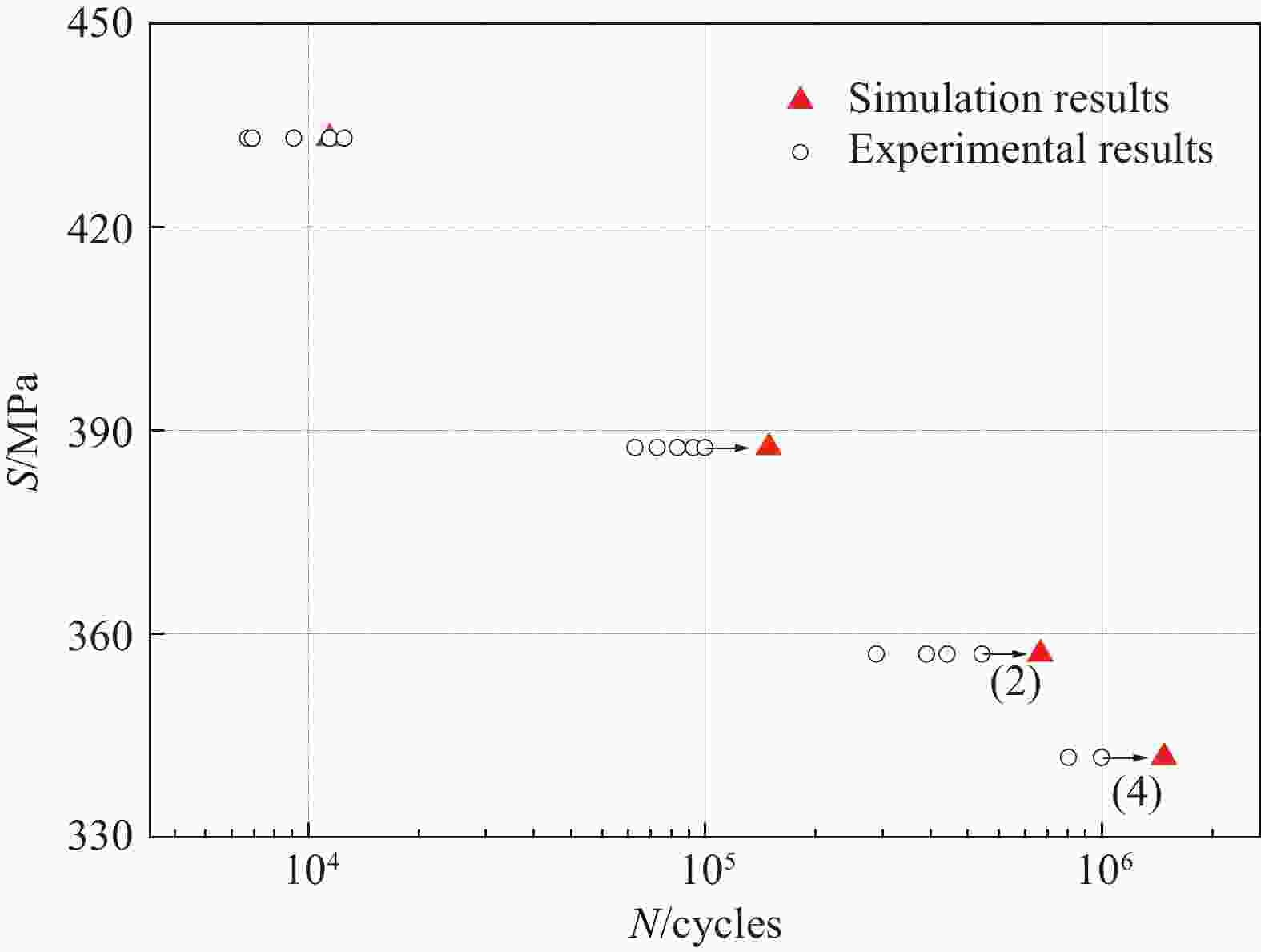
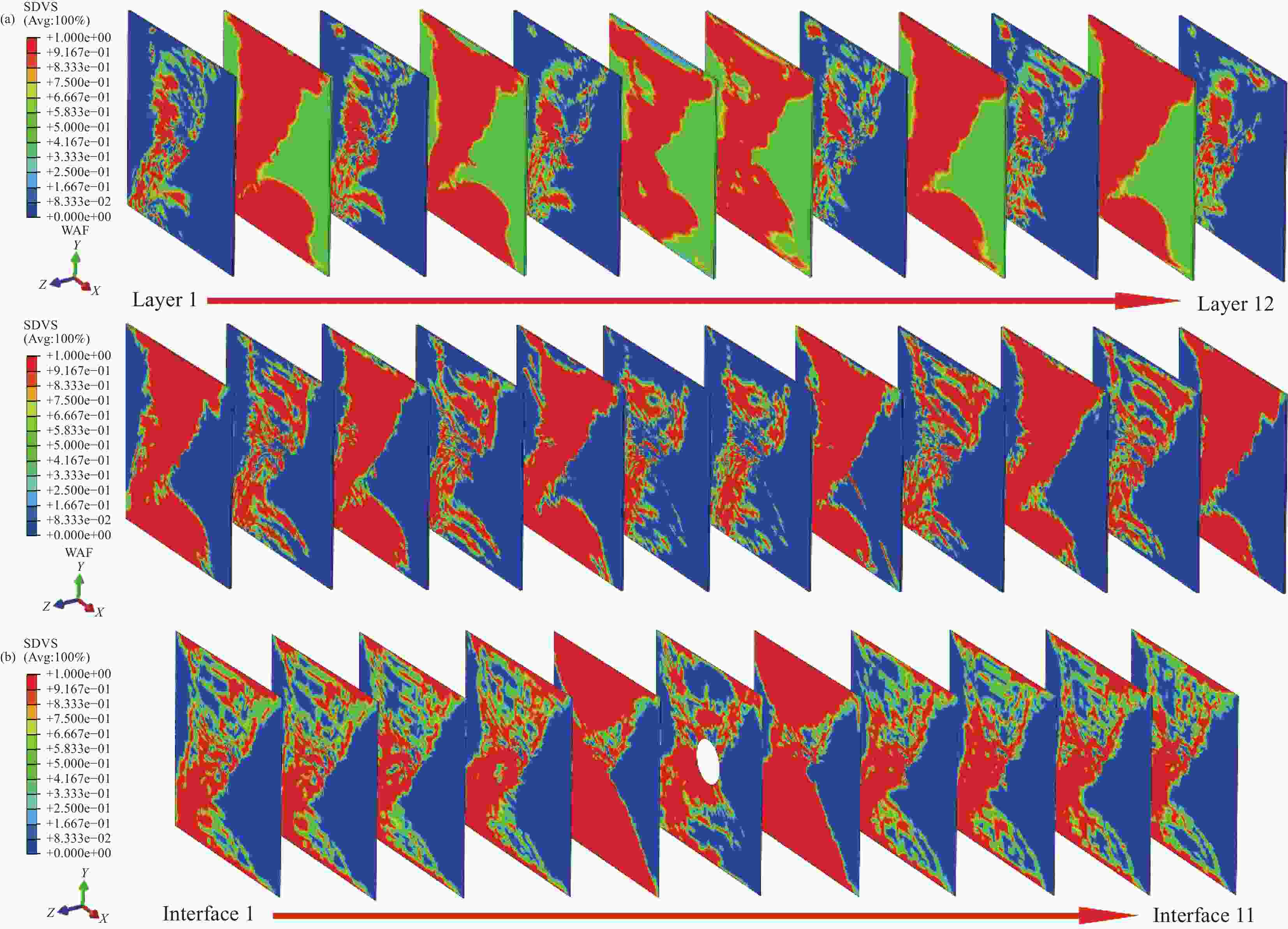
图 15 $ N = 1.417 \times {10^6}{\text{cycles}} $时层合板疲劳损伤仿真结果：(a) 各单层板面内疲劳损伤，WAF表示经向损伤，WEF表示纬向损伤；(b) 各层间界面疲劳损伤
Figure 15. Simulation results of fatigue damage in composite laminates at $ N = 1.417 \times {10^6}{\text{cycles}} $: (a) Intralaminar fatigue damage of each single layer, WAF represents warp damage, WEF represents weft damage; (b) Interlaminar fatigue damage between each two adjacent layers
图 16 层合板失效($ N = 1.435 \times {10^6}{\text{cycles}} $)时疲劳损伤仿真结果：(a) 各单层板面内疲劳损伤；(b) 各层间界面疲劳损伤
Figure 16. Simulation results of fatigue damage in composite laminates at failure of laminates ($ N = 1.417 \times {10^6}{\text{cycles}} $): (a) Intralaminar fatigue damage of each single layer; (b) Interlaminar fatigue damage between each two adjacent layers
表 1 单层板和界面层力学性能参数
Table 1. Mechanical property parameters of single layer and interlaminar interface
Single layer Interlaminar interface $ E_{11}^{} = E_{22}^{} $/GPa 57 $ K_{\text{n}}^{} $/(N·mm−3) 2.5$ \times $105 $ E_{33}^{} $/GPa 8.4 $ K_{\text{s}}^{} $/(N·mm−3) 2.5$ \times $105 $ \mu _{12}^{} $ 0.067 $ K_{\text{t}}^{} $/(N·mm−3) 2.5$ \times $105 $ \mu _{13}^{} = \mu _{23}^{} $ 0.41 $ T_{\text{n}}^{} $/MPa 50 $ G_{12}^{} $/GPa 3.25 $ T_{\text{s}}^{} $/MPa 95 $ G_{13}^{} = G_{23}^{} $/GPa 2.44 $ T_{\text{t}}^{} $/MPa 95 $ X_{\text{T}}^{} = Y_{\text{T}}^{} $/MPa 679 $ G_{\text{n}}^{\text{C}} $/(N·mm−1) 0.65 $ X_{\text{C}}^{} = Y_{\text{C}}^{} $/MPa 557 $ G_{\text{s}}^{\text{C}} $/(N·mm−1) 2.7 $ S_{12}^{} $/MPa 111 $ G_{\text{t}}^{\text{C}} $/(N·mm−1) 2.7 $ S_{13}^{} = S_{23}^{} $/MPa 66.7 $\eta $ 2.09 Notes: $ E_{11}^{} $, $ E_{22}^{} $ and $ {E_{33}} $ are the elastic modulus; $ {\mu _{12}} $, $ \mu _{13}^{} $ and $ \mu _{23}^{} $ are the poisson's ratios; $ {G_{12}} $, $ G_{13}^{} $ and $ G_{23}^{} $ are the shear modulus; $ X_{\text{T}}^{} $ and $ Y_{\text{T}}^{} $ are the tensile strengths in warp direction and weft direction, respectively; $ X_{\text{C}}^{} $ and $ Y_{\text{C}}^{} $ are the compressive strengths in warp direction and weft direction, respectively; $ {S_{12}} $, $ S_{13}^{} $ and $ S_{23}^{} $ are the shear strengths; $ K_{\text{n}}^{} $, $ {K_{\text{s}}} $ and $ {K_{\text{t}}} $ are the stiffness of interface; $ T_{\text{n}}^{} $, $ {T_{\text{s}}} $ and $ {T_{\text{t}}} $ are the strengths of interface; $ G_{\text{n}}^{\text{C}} $, $ G_{\text{s}}^{\text{C}} $ and $ G_{\text{t}}^{\text{C}} $ are the fracture toughness; $\eta $ is the power exponent of BK criterion. 
下载: 导出CSV
表 2 平面机织复合材料等效刚度和峰值载荷结果
Table 2. Results of equivalent stiffness and peak load of plane woven composites
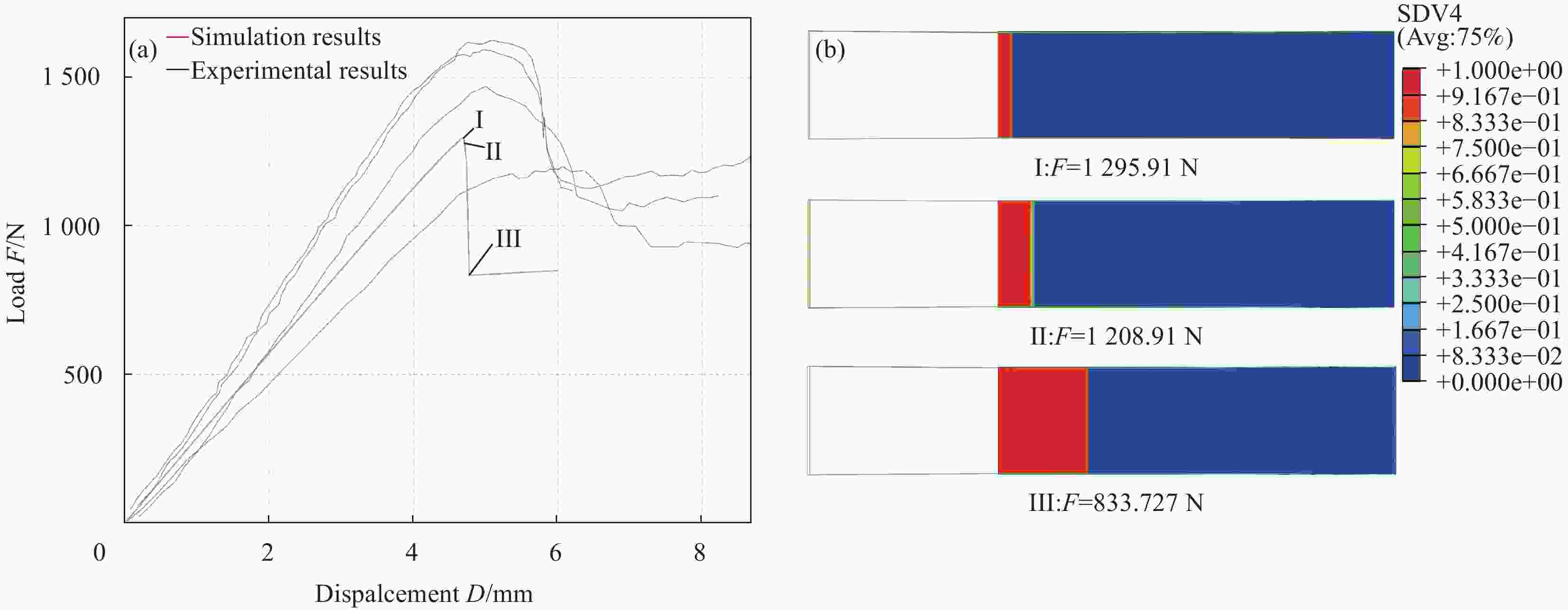
Equivalent stiffness/(N·mm−1) Peak load/N Experimental results Test data 342.9, 323.6,
346.6, 206.51593.9, 1469.0,
1625.5, 1200.2Mean value 304.9 1472.1 Simulation results 284.2 1318.3 Deviations 6.76% 10.45%
下载: 导出CSV
表 3 材料弹性常数退化方案
Table 3. Degradation strategy of material elastic constants
Elastic constants Warp failure Weft failure $ E_{11}^{} $ $ {\gamma _{{\text{wa}}}} $ 1 $ E_{22}^{} $ 1 $ {\gamma _{{\text{we}}}} $ $ E_{33}^{} $ 1 1 $ \mu _{12}^{} $ $ {\gamma _{{\text{wa}}}} $ $ {\gamma _{{\text{we}}}} $ $ \mu _{13}^{} $ $ {\gamma _{{\text{wa}}}} $ 1 $ \mu _{23}^{} $ 1 $ {\gamma _{{\text{we}}}} $ $ G_{12}^{} $ $ {\gamma _{{\text{wa}}}} $ $ {\gamma _{{\text{we}}}} $ $ G_{13}^{} $ $ {\gamma _{{\text{wa}}}} $ 1 $ G_{23}^{} $ 1 $ {\gamma _{{\text{we}}}} $ Notes: $ {\gamma _{{\text{wa}}}} $ and $ {\gamma _{{\text{we}}}} $ are the degradation coefficients at warp failure and weft failure, respectively.
下载: 导出CSV
表 4 平面机织复合材料含初始分层损伤层合板剩余强度模型参数
Table 4. Parameters of residual strength model of plane woven composite laminates with initial delamination damage
Elastic constants $ C $ $ p $ $ q $ $ {S_0} $ $ {R_0} $ Warp tension
(r=0.05)$ 3.72 \times {10^{36}} $ −12.27 1.0 0 679 Warp compression
(r=20)$ 3.28 \times {10^{105}} $ −38.06 1.0 0 557 Weft tension
(r=0.05)$ 3.72 \times {10^{36}} $ −12.27 1.0 0 679 Weft compression
(r=20)$ 3.28 \times {10^{105}} $ −38.06 1.0 0 557 In-plane shear
(r=0.05)$ 3.13 \times {10^{17}} $ −9.71 3.5 0 111 Notes: $ C $, $ p $ and $ q $ are the model parameters, ${S_{\text{0}}}$ is the fatigue limit, ${R_{\text{0}}}$ is the initial static strength.
下载: 导出CSV
-
[1] 杨乃宾, 章怡宁. 复合材料飞机结构设计 [M]. 北京: 航空工业出版社, 2003: 1-9.Yang NB, Zhang YN. Composite aircraft structure design [M]. Beijing: Aviation Industry Press, 2003: 1-9 (in Chinese). [2] Molent L, Haddad A. A critical review of available composite damage growth test data under fatigue loading and implications for aircraft sustainment[J]. Composite Structures, 2020, 232: 111568. doi: 10.1016/j.compstruct.2019.111568 [3] 程小全, 康炘蒙, 邹健, 等. 平面编织复合材料层合板低速冲击后的拉伸性能[J]. 复合材料学报, 2008, 25(5): 163-168. doi: 10.3321/j.issn:1000-3851.2008.05.027Cheng XQ, Kang XM, Zou J et al. Tensile properties of plane woven composite laminates after low velocity impact[J]. Acta Materiae Compositae Sinica, 2008, 25(5): 163-168 (in Chinese). doi: 10.3321/j.issn:1000-3851.2008.05.027 [4] Shao MY, Cai DA, Yu QH, et al. On mechanical properties of double-sided-loop 2D woven laminated composites[J]. Composite Structures, 2023, 312: 116874. doi: 10.1016/j.compstruct.2023.116874 [5] 郑锡涛, 叶天麒. 美国纺织复合材料在航空结构上的应用研究(一)[J]. 航空工程与维修, 2001, (5): 40-42.Zheng XT, Ye TQ. Textile composite applications to airframe structures in USA (I)[J]. Aviation Engineering, 2001, (5): 40-42 (in Chinese). [6] 郑锡涛, 杨胜春, 叶天麒. 美国纺织复合材料在航空结构上的应用研究(二)[J]. 航空工程与维修, 2001, (6): 40-42.Zheng XT, Yang SC, Ye TQ. Textile composite applications to airframe structures in USA (II)[J]. Aviation Engineering, 2001, (6): 40-42 (in Chinese). [7] 果立成, 廖锋, 李志兴, 等. 机织复合材料损伤演化研究进展[J]. 中国科学:技术科学, 2020, 50(7): 876-896. doi: 10.1360/SST-2020-0123Guo LC, Liao F, Li ZX, et al. Research progress in damage evolution of woven composites[J]. SCIENTIA SINICA Technologica, 2020, 50(7): 876-896 (in Chinese). doi: 10.1360/SST-2020-0123 [8] Yao LJ, Alderliesten R, Zhao MY, et al. Bridging effect on mode I fatigue delamination behavior in composite laminates[J]. Composites Part A:Applied Science and Manufacturing, 2014, 63: 103-109. doi: 10.1016/j.compositesa.2014.04.007 [9] Yao LJ, Sun Y, Guo LC, et al. Mode I fatigue delamination growth with fibre bridging in multidirectional composite laminates[J]. Engineering Fracture Mechanics, 2017, 189: 221-231. [10] Yao LJ, Sun Y, Zhao MY, et al. Stress ratio dependence of fibre bridging significance in mode I fatigue delamination growth of composite laminates[J]. Composites Part A:Applied science and manufacturing, 2017, 95: 65-74. doi: 10.1016/j.compositesa.2016.11.030 [11] Gong Y, Zhang B, Hallett SR. Delamination migration in multidirectional composite laminates under mode I quasi-static and fatigue loading[J]. Composite Structures, 2018, 189: 160-176. doi: 10.1016/j.compstruct.2018.01.074 [12] Peng L, Zhang JY, Zhao LB, et al. Mode I delamination growth of multidirectional composite laminates under fatigue loading[J]. Journal of Composite Materials, 2011, 45(10): 1077-1090. doi: 10.1177/0021998310385029 [13] Androuin G, Michel L, Maillet I, et al. Characterization of fatigue delamination growth under mode I and II: Effects of load ratio and load history[J]. Engineering Fracture Mechanics, 2018, 203: 172-185. doi: 10.1016/j.engfracmech.2018.06.030 [14] Khudairi OA, Hadavinia H, Waggott A, et al. Characterising mode I/mode II fatigue delamination growth in unidirectional fibre reinforced polymer laminates – ScienceDirect[J]. Materials and Design, 2015, 66: 93-102. doi: 10.1016/j.matdes.2014.10.038 [15] 云新尧, 梁朝虎, 宋伟科. 斜纹编织碳纤维/环氧树脂复合材料Ⅱ型分层性能及损伤演化表征[J]. 复合材料学报, 2020, 37(10): 2452-2462.Yun XY, Liang CH, Song WK. Mode II delamination property and damage evolution characterization of twill woven carbon fiber/epoxy resin composites[J]. Acta Materiae Compositae Sinica, 2020, 37(10): 2452-2462 (in Chinese). [16] Bienias J, Dadej K. Fatigue delamination growth of carbon and glass reinforced fiber metal laminates in fracture mode II[J]. International Journal of Fatigue, 2020, 130: 105267. doi: 10.1016/j.ijfatigue.2019.105267 [17] Colombo C, Vergani L. Influence of delamination on fatigue properties of a fibreglass composite[J]. Composite Structures, 2014, 107(1): 325-333. [18] Colombo C, Bhujangrao DT, Libonati F, et al. Effect of delamination on the fatigue life of GFRP: A thermographic and numerical study[J]. Composite Structures, 2019, 218: 152-161. [19] 陈群志, 关志东, 王进, 等. 分层缺陷对复合材料结构疲劳寿命影响研究[J]. 机械强度, 2004: 121-123.Chen QZ, Guan ZD, Wang J, Zhu S, Wang YY, Chen XD. Study on influence of delamination flaw on fatigue life of composite structures[J]. Journal of Mechanical Strength, 2004: 121-123 (in Chinese). [20] Reis PNB, Ferreira JAM, Antunes FV, et al. Effect of interlayer delamination on mechanical behavior of Carbon/Epoxy laminates[J]. Journal of Composite Materials, 2009, 43(43): 2609-2621. [21] Wan AS, Xiong JJ, Xu YG. Fatigue life prediction of woven composite laminates with initial delamination[J]. Fatigue & Fracture of Engineering Materials & Structures, 2020, 43: 2130-2146. [22] Pascoe JA, Rans CD, Benedictus R. Characterizing fatigue delamination growth behaviour using specimens with multiple delaminations: The effect of unequal delamination lengths[J]. Engineering Fracture Mechanics, 2013, 109: 150-160. doi: 10.1016/j.engfracmech.2013.05.015 [23] Davila CG, Bisagni C. Fatigue life and damage tolerance of postbuckled composite stiffened structures with initial delamination[J]. Composite Structures, 2017, 161: 73-84. doi: 10.1016/j.compstruct.2016.11.033 [24] Raimondo A, Doesburg SA, Bisagni C. Numerical study of quasi-static and fatigue delamination growth in a post-buckled composite stiffened panel[J]. Composites Part B:Engineering, 2020, 182: 107589. doi: 10.1016/j.compositesb.2019.107589 [25] Pascoe JA, Rans CD, Benedictus R. Characterizing fatigue delamination growth behaviour using specimens with multiple delaminations: The effect of unequal delamination lengths[J]. Engineering Fracture Mechanics, 2013, 109: 150-160. doi: 10.1016/j.engfracmech.2013.05.015 [26] Teimouri F, Rarani MH, Aboutalebi FH. An XFEM-VCCT coupled approach for modeling mode I fatigue delamination in composite laminates under high cycle loading[J]. Engineering Fracture Mechanics, 2021, 249: 107760. doi: 10.1016/j.engfracmech.2021.107760 [27] Raimondo A, Bisagni C. Fatigue analysis of a post-buckled composite single-stringer specimen taking into account the local stress ratio[J]. Composites Part B:Engineering, 2020, 193: 108000. doi: 10.1016/j.compositesb.2020.108000 [28] Hosseini-Toudeshky H, Goodarzi M S, Mohammadi B. Multiple Delaminations Growth in Composite Laminates under Compressive Cyclic Loading in Post-Buckling[J]. Applied Mechanics and Materials, 2012, 225: 195-200. doi: 10.4028/www.scientific.net/AMM.225.195 [29] Tao CC, Qiu JH, Yao WX, et al. A novel method for fatigue delamination simulation in composite laminates[J]. Composites Science and Technology, 2016, 128: 104-115. doi: 10.1016/j.compscitech.2016.03.016 [30] Oliveira LA, Donadon MV. A cohesive zone model to predict fatigue-driven delamination in composites[J]. Engineering Fracture Mechanics, 2020, 235: 107124. doi: 10.1016/j.engfracmech.2020.107124 [31] Peerlings RHJ, Brekelmans WAM, Borst R, et al. Gradient-enhanced damage modelling of high-cycle fatigue[J]. International Journal for Numerical Methods in Engineering, 2000, 49(12): 1547-1569. doi: 10.1002/1097-0207(20001230)49:12<1547::AID-NME16>3.0.CO;2-D [32] Nguyen O, Repetto EA, Radovitzky RA. A cohesive model of fatigue crack growth[J]. International Journal of Fracture, 2001, 110: 351-369. doi: 10.1023/A:1010839522926 [33] Maiti S, Geubelle P H. A cohesive model for fatigue failure of polymers[J]. Engineering Fracture Mechanics, 2005, 72(5): 691-708. doi: 10.1016/j.engfracmech.2004.06.005 [34] Davila CG. From S-N to the Paris law with a new mixed-mode cohesive fatigue model for delamination in composites[J]. Theoretical and Applied Fracture Mechanics, 2020, 106: 102499. doi: 10.1016/j.tafmec.2020.102499 [35] Rad AA, Mashayekhi M, Meer FPVD, et al. A two-scale damage model for high cycle fatigue delamination in laminated composites[J]. Composites Science and Technology, 2015, 120: 32-38. doi: 10.1016/j.compscitech.2015.10.010 [36] Zhu M, Gorbatikh L, Lomov SV. An incremental-onset model for fatigue delamination propagation in composite laminates[J]. Composites Science and Technology, 2020, 200(3): 108394. [37] 李顶河, 李梁轶, 郭巧荣, 等. 基于离散损伤模型的复合材料双悬臂梁分层疲劳扩展分析[J]. 复合材料学报, 2022, 39(7): 3603-3614.Li DH, Li LY, Guo QR, Qian RL. Fatigue delamination analysis of composite double cantilever beams based on discrete damage zone model[J]. Acta Materiae Compositae Sinica, 2022, 39(7): 3603-3614 (in Chinese). [38] Benzeggagh ML, Kenane M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus[J]. Compos Science and Technology, 1996, 56: 439-449. doi: 10.1016/0266-3538(96)00005-X [39] ASTM D7905. Standard test method for determination of the mode II interlaminar fracture toughness of unidirectional fiber-reinforced polymer matrix composites[S]. 2019. [40] 云新尧. 复合材料II型层间开裂强度试验与模型表征技术研究[D]. 北京: 北京航空航天大学, 2015.Yun XY. Mode II delamination resistance tests and characterization models of composites[D]. Beijing: Beihang University, 2015 (in Chinese). [41] Wan AS, Li DH, Lu PC. Three-scale modeling and probabilistic progressive damage analysis of woven composite laminates[J]. Mechanics of Advanced Materials and Structures, 2022: 1-17. [42] Cheng ZQ, Xiong JJ. Progressive damage behaviors of woven composite laminates subjected to LVI, TAI and CAI[J]. Chinese Journal of Aeronautics, 2020, 33(10): 2807-2823. doi: 10.1016/j.cja.2019.12.015 [43] Liu H, Qi G, Renaud G, et al. Application of the effective crack length method to model delamination of unidirectional composite laminates under Mode II shear loadings[J]. Composites Part C:Open Access, 2023, 12: 100401. doi: 10.1016/j.jcomc.2023.100401 [44] Yan XQ, Guo XM, Gao YF, et al. Mode-II fracture toughness and crack propagation of pultruded carbon Fiber-Epoxy composites[J]. Engineering Fracture Mechanics, 2023, 279: 109042. doi: 10.1016/j.engfracmech.2022.109042 [45] Gong Y, Xia KX, Wang YN, et al. A semi-analytical model for the mode II fracture toughness of multidirectional composite laminates[J]. Thin-Walled structures, 2023, 182: 110235. doi: 10.1016/j.tws.2022.110235 [46] Soyugüzel T, Mecitoglu Z, Kaftelen-Odabasi H. Experimental and numerical investigation on the mode I and mode II interlaminar fracture toughness of nitrogen-doped reduced graphene oxide reinforced composites[J]. Theoretical and Applied Fracture Mechanics, 2023, 128: 104103. doi: 10.1016/j.tafmec.2023.104103 [47] Liu CQ, Gong Y, Gong YK, et al. Mode II fatigue delamination behaviour of composite multidirectional laminates and the stress ratio effect[J]. Engineering Fracture Mechanics, 2022, 264: 108321. doi: 10.1016/j.engfracmech.2022.108321 [48] Adamos L, Tsokanas P, Loutas T. An experimental study of the interfacial fracture behavior of Titanium/CFRP adhesive joints under mode I and mode II fatigue[J]. International Journal of Fatigue, 2020, 136: 105586. doi: 10.1016/j.ijfatigue.2020.105586 [49] Hashin Z. A fatigue failure criterion for fiber reinforced materials[J]. Journal of Composite Materials, 1973, 7: 448-464. doi: 10.1177/002199837300700404 [50] Cheng ZQ, Tan W, Xiong JJ. Progressive damage modelling and fatigue life prediction of plain-weave composite laminates with low-velocity impact damage[J]. Composite Structures, 2021, 273(1): 114262. [51] Cheng ZQ, Tan W, Xiong JJ. Modelling pre-fatigue, low-velocity impact and post-impact fatigue behaviours of composite helicopter tail structures under multipoint coordinated loading spectrum[J]. Thin-Walled Structures, 2022, 176: 109349. doi: 10.1016/j.tws.2022.109349 [52] Bienias J, Dadej K, Surowska B. Interlaminar fracture toughness of glass and carbon reinforced multidirectional fiber metal laminates[J]. Engineering Fracture Mechanics, 2017, 175: 127-145. doi: 10.1016/j.engfracmech.2017.02.007 [53] Yang F, Yi FJ, Xie WH. The role of ply angle in interlaminar delamination properties of CFRP laminates[J]. Mechanics of Materials, 2021, 160: 103928. doi: 10.1016/j.mechmat.2021.103928 -
下载:
点击查看大图
计量
- 文章访问数: 100
- HTML全文浏览量: 66
- 被引次数: 0
