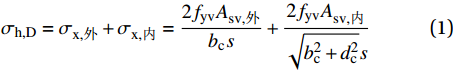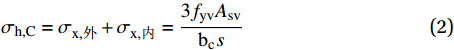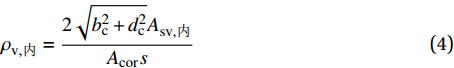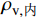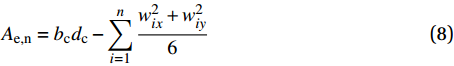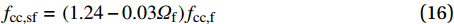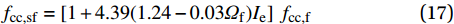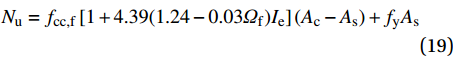箍筋约束超高性能混凝土短柱轴压承载力试验研究

常亚峰; 师俊平; 侯亚鹏; 陆婷婷

doi:10.13801/j.cnki.fhclxb.20210716.006

箍筋约束超高性能混凝土短柱轴压承载力试验研究

常亚峰^{1, 2,},
师俊平^1, ,,
侯亚鹏^1,,
陆婷婷^3,

1.
西安理工大学　土木建筑工程学院，西安 710048
2.
陕西建研结构工程股份有限公司，西安 710082
3.
西京学院　土木工程学院，西安 710199

基金项目: 国家自然科学基金(11872300)；陕西省重点研发计划(2020ZDLSF06-11)；陕西省技术创新引导专项基金(2019CGHJ-02)

详细信息

通讯作者:
师俊平，博士，教授，博士生导师，研究方向为工程力学　E-mail：shijp@xaut.edu.cn

中图分类号: TU375.4
计量
- 文章访问数: 1238
- HTML全文浏览量: 591
- PDF下载量: 65
出版历程
- 收稿日期: 2021-06-03
- 修回日期: 2021-06-30
- 录用日期: 2021-07-04
- 网络出版日期: 2021-07-18
- 刊出日期: 2022-07-29

Experimental study on the axial compression capacity of ultra-high performance concrete stub columns confined with stirrups

1.
School of Civil Engineering and Architecture, Xi’an University of Technology, Xi’an 710048, China
2.
Shaanxi Jianyan Structural Engineering Co., Ltd., Xi’an 710082, China
3.
School of Civil Engineering, Xijing University, Xi’an 710199, China

摘要

摘要: 通过对10组配置菱形、十字形复合箍筋的超高性能混凝土(UHPC)短柱和1组未配置钢筋的UHPC短柱进行轴压承载力试验，研究了其破坏过程和破坏形态，分析了箍筋间距、纤维掺量和箍筋形式对其轴向应变-轴向荷载曲线和应力-应变曲线的影响。结果表明，箍筋形式的闭合环数和纤维掺量对UHPC短柱的变形能力有一定程度的改善作用。箍筋间距和纤维掺量对试件轴压承载力及相应轴向峰值应变有显著的影响，箍筋间距对轴向峰值应变的影响更大。相同箍筋间距的菱形复合箍筋(DC)较十字形复合箍筋(CC)试件的峰值荷载有所提高。随着箍筋间距的减小，各试件归一化应力-应变曲线上升段斜率增大，但其下降段却表现出更大差异。纤维掺量和箍筋类形对UHPC试件的应力-应变归一化曲线影响较小。考虑箍筋约束效应及纤维约束效应，建立了复合箍筋约束UHPC短柱轴心受压承载力计算公式；计算结果与试验结果比较，吻合较好。
- 菱形复合箍筋 /
- 十字形复合箍筋 /
- 约束UHPC /
- 轴压承载力 /
- 纤维掺量
Abstract: The failure process and failure modes of ultra-high performance concrete (UHPC) stub columns were investigated through the axial compression capacity test of ten groups of UHPC stub columns with diamond-shaped and cross-shaped composite stirrups and one group of columns without steel bars. The effects of stirrup spacing, fiber content and stirrup form on their axial strain-axial load curve and stress-strain curve were analyzed. Results show that increasing numbers of closed loops in the form of stirrups and fiber content could improve the deformed capacity of UHPC stub columns. The effects of stirrup spacing and fiber content on the axial compression bearing capacity and corresponding axial peak strain of the UHPC are significant. The impact of stirrup spacing on the axial peak strain is greater. The peak load of diamond-shaped composite stirrups (DC) with the same stirrup spacing is higher than that of cross-shaped composite stirrups (CC) specimens. As the spacing of stirrups decreases, the slope of the ascending section of the UHPC normalized stress-strain curve of each specimen increases, at the same time the differences of descending sections are more significant. The effects of fiber content and different types of stirrups on the stress-strain normalized curve of UHPC specimens are small. Considering the restraint effect of stirrups and fiber restraint, the calculation formula of axial compression capacity of UHPC short columns constrained by composite stirrups was proposed. The calculation results are in good agreement with the experimental results.
- diamond-shaped composite stirrups /
- cross-shaped composite stirrups /
- constrained UHPC /
- axial compression capacity /
- fiber content

HTML全文

超高性能混凝土(UHPC)具有极高的抗压强度^[1,2]，能大幅度提高柱子等受压构件的承载能力，且减小其截面尺寸。近年来，越来越多的学者对UHPC材料受力性能进行了研究，与高强混凝土类似，UHPC材料的延性随着抗压强度增大而减小，因此，研究如何提高UHPC的延性成为亟待解决的问题。目前，主要通过两种方式：一是通过调整纤维掺量及纤维外形来提高UHPC材料层面的延性；二是通过配置箍筋的方法来提高UHPC构件层面的延性。研究表明，通过增加柱内配置钢筋层数(2层或3层)的方式^[3]，并未提高普通混凝土结构柱的延性。与两重螺旋箍筋相比，配置三重螺旋箍筋^[4]导致钢筋用量明显增大，其表现出更大的初始压缩刚度和更好的延性，却未能有效提高柱的极限承载力。配置较密间距的箍筋、较大的体积配箍率时，箍筋约束混凝土的抗压强度比无箍筋约束的混凝土抗压强度有较大幅度的提高^[5]，箍筋形式不同可导致约束效果不同^[6]。当箍筋强度提高时，柱子峰值应力提高不大，但变形能力^[7]可显著提高。包含外围箍筋和内部附加箍筋^[8-9](即复合箍筋)对高强混凝土具有更好的约束效果，但内部附加箍筋的形式对混凝土强度和变形的影响不大。王铁成等^[10]对箍筋约束T形截面柱进行了轴压试验研究，建立了考虑箍筋约束作用的T形截面短柱轴心受压承载力的计算公式。寇佳亮等^[11]通过提高箍筋配箍率、减小箍筋间距、合理选用箍筋形式对约束纤维增强混凝土(FRC)也有很好的约束效果，且采用复合箍筋，其应力-应变曲线下降段更加平缓。李艳等^[12]综合考虑箍筋有效约束指标与聚乙烯醇(PVA)纤维体积掺量的影响，建立了约束工程纤维增强水泥基复合材料(ECC)应力-应变全曲线方程。邓宗才等^[13]对高强箍筋约束UHPC柱轴压性能进行了研究，发现体积配箍率对轴压性能的影响程度大于箍筋强度，影响体积配箍率变化的因素中，箍筋间距对改善约束性能的贡献更大，但其研究的箍筋间距仅涉及60 mm和80 mm两种，箍筋间距变化参量较少。

Wu等^[14]认为轻骨料混凝土的脆性和延展性可通过提高配箍率及合理选择箍筋配置得以显著改善。Lokuge等^[15]发现高强混凝土(HSC)的脆性效应也可通过配置密集箍筋得以改善，使其延性增大。Sharma等^[16]发现圆形、方形箍筋约束HSC短柱的破坏模式为混凝土保护层突然剥落而导致轴向承载力骤降。Mander等^[5,17]通过对螺旋形箍、圆形箍、矩形和复合矩形箍等多种箍筋形式的混凝土柱进行轴压试验研究，提出了箍筋有效约束系数的计算方法。Samani等^[18]考虑了试件高度和长径比的影响，提出了能够预测普通强度混凝土以及HSC的承载能力的模型。Shin等^[19]也发现配箍率较小时，UHPC因保护层突然脱落而脆性破坏。

目前对复合箍筋约束UHPC短柱受压承载力的研究较少，因此本文通过10组箍筋约束UHPC短柱和1组未配置钢筋的UHPC短柱的轴心受压试验，对箍筋及纤维约束UHPC柱的轴压性能进行研究，分析箍筋间距、箍筋形式及纤维掺量对约束UHPC强度的影响，并建立了考虑箍筋约束效应及纤维约束效应的UHPC柱轴心受压承载力的计算公式。本文主要研究配置较密间距箍筋的UHPC短柱的轴心受压承载性能，为其能在工程应用提供理论参考。

1. 试验概况

1.1 试验参数及原材料

本次试验对10组30个配置复合箍筋UHPC短柱和1组未配置钢筋的UHPC短柱进行了轴压承载力的研究，试件编号为UHPC-1~UHPC-11，每组制作3个试件，试件尺寸b×h×l均为200 mm×200 mm×600 mm；每组留置3个100 mm的立方体试块，以测得各组UHPC试件的立方体抗压强度；每组留置6个100 mm×100 mm×300 mm的棱柱体试件，以测得各组UHPC试件的弹性模量和应力-应变曲线。主要研究参数分别为钢纤维掺量、箍筋形式、箍筋间距和配箍率，其中钢纤维体积掺量V_f分为0vol%、1vol%、1.5vol%、2vol% 四种，箍筋类形分为十字形、菱形复合箍两种，箍筋间距s分为40、60、80、100、120 mm 五种，箍筋直径(d₁)为6 mm、配箍率ρ_v为1.02%~3.07%，纵筋采用8根直径(d₂)为10 mm的钢筋，配筋率为1.57%。试件几何尺寸及配筋见图1(a)，箍筋端部设135°弯钩，并插入核心区UHPC内部60 mm，钢筋骨架如图1(b)所示，表1给出了各组试件的详细参数。本试验UHPC原材料质量配合比为：m_水泥∶m_硅灰∶m_砂∶m_减水剂∶m_水=1.00∶0.26∶1.26∶0.03∶0.23，UHPC配制过程中掺入不同掺量的端钩形钢纤维，钢纤维的性能指标见表2。试验前测试了UHPC的立方体抗压强度f_cu、弹性模量E_cc,f和钢筋的屈服强度f_y、抗拉强度f_u、伸长率δ，实测值分别见表1和表3。为保证破坏出现在柱中部位置，在试件上下端均采用180 mm高度的钢管箍，并在其内浇筑100 mm高度的混凝土。

图 1 箍筋约束超高性能混凝土(UHPC)试件几何尺寸和配筋

Figure 1. Dimensions and reinforcement details of ultra-high performance concrete (UHPC) stub column specimen confined with stirrups

CC and DC—Cross- and diamond-shaped stirrups, respectively

下载: 全尺寸图片幻灯片

表 1 箍筋约束UHPC试件参数及UHPC材料性能

Table 1. Parameters of specimens and material properties of UHPC stub column specimen confined with stirrups

Code	Stirrup			V_f/vol%	f_cu/MPa	E_cc,f/GPa	λ_v
Code	s/mm	ρ_v/%	Type	V_f/vol%	f_cu/MPa	E_cc,f/GPa	λ_v
UHPC-1	40	3.07	DC	2	117.5	39.50	0.17
UHPC-2	60	2.05	DC	2	117.5	39.50	0.11
UHPC-3	80	1.54	DC	2	117.5	39.50	0.09
UHPC-4	100	1.23	DC	2	117.5	39.50	0.07
UHPC-5	120	1.02	DC	2	117.5	39.50	0.06
UHPC-6	60	2.05	DC	1.5	114.8	39.04	0.12
UHPC-7	60	2.05	DC	1	110.2	38.72	0.12
UHPC-8	60	2.05	DC	0	92.5	32.52	0.14
UHPC-9	40	2.61	CC	2	117.5	39.50	0.14
UHPC-10	60	1.74	CC	2	117.5	39.50	0.10
UHPC-11	—	—	—	2	117.5	39.50	—
Notes：s—Stirrup spacing; ρ_v—Volume stirrup ratio; CC and DC—Cross- and diamond-shaped stirrups, respectively; V_f—Volume fraction of steel fibers; f_cu—Compressive strength of the fiber UHPC cube; E_cc,f —Elastic modulus of the fiber-constrained UHPC; λ_v—Stirrup characteristic value.

下载: 导出CSV

| 显示表格

表 2 钢纤维性能指标

Table 2. Performance indicators of the steel fibers

Length/mm	Diameter/mm	Aspect ratio	Shape pass rate/%	Mass density/(g·cm⁻³)	Tensile strength/MPa
13	0.2	65	98	7.8	2850

下载: 导出CSV

| 显示表格

表 3 钢筋材料性能

Table 3. Material performance indicators of the steel bars

Rebar grade	d/mm	f_y/MPa	f_u/MPa	δ/%
HRB400	6	444.5	566.5	19.5
HRB400	10	425.8	533.6	17.7
Notes：d—Diameter of steel bars; f_y—Yield strength of steel bars; f_u—Ultimate tensile strength of steel bars; δ—Elongation of steel bars.

下载: 导出CSV

| 显示表格

1.2 试验加载与量测

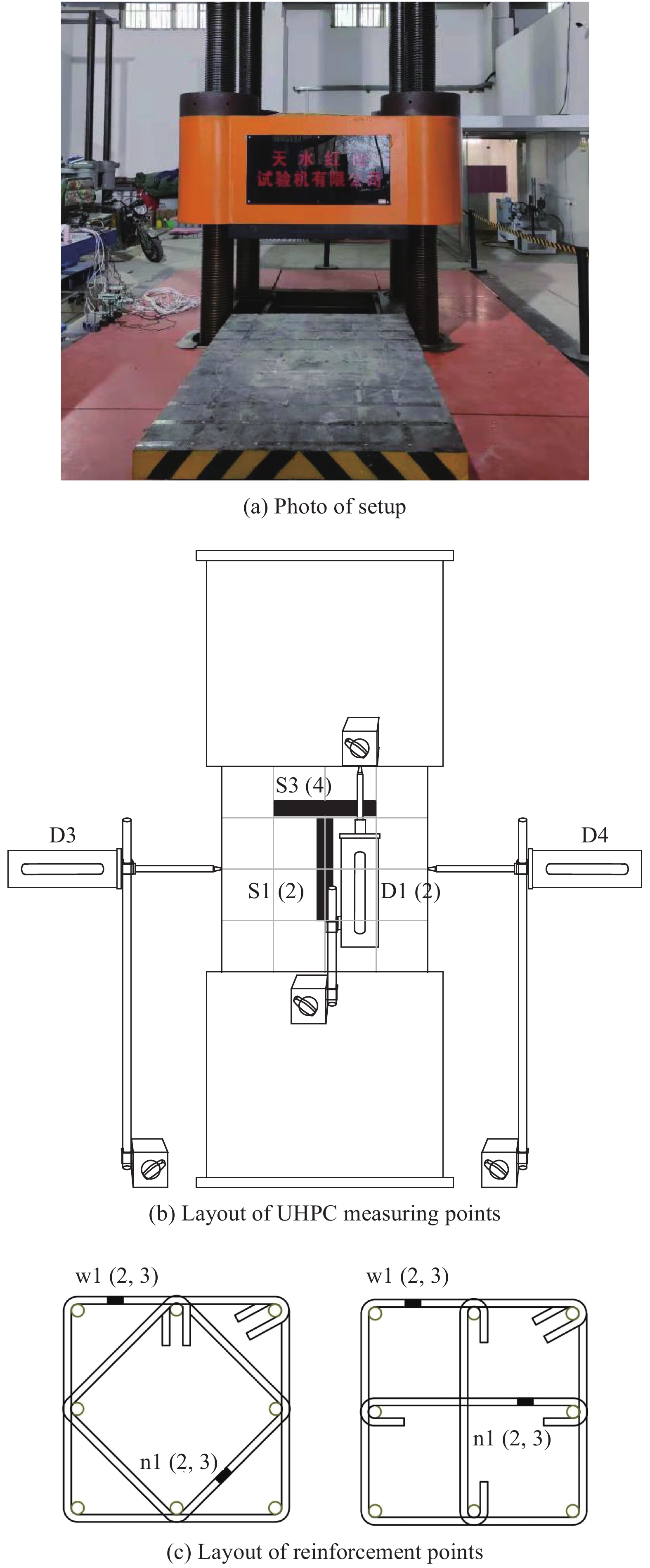
图2给出了试件的加载和量测装置，所有试件均在天水红山-30000 kN的液压试验机上进行加载。试件前后两侧对称布置2个位移传感器(D1、D2)和两个纵向应变片(S1、S2)，以测量试件的轴向变形，并在前后两侧布置横向应变片(S3、S4)；同时在试件左右两侧布置2个位移传感器，以测量试件的横向变形。在试件中部区域3道箍筋上粘贴电阻应变片以测量箍筋应变，菱形复合箍筋分别在每道箍筋的内侧箍筋和外侧箍筋各粘贴1个应变片，十字形复合箍筋分别在矩形箍筋和十字箍筋上粘贴1个应变片。编号从上至下依次排序，测点w1~w3测量外箍筋的应变，n1~n3测量内箍筋的应变。试验中采用等位移连续加载，加载速度为0.3 mm/min，当荷载下降至0.6F_max时，停止加载。

图 2 试验加载装置及测点布置

Figure 2. Test equipment and arrangement of measuring points

下载: 全尺寸图片幻灯片

2. 试验结果及分析

2.1 箍筋约束UHPC破坏现象及破坏形态

当轴压荷载小于极限荷载的60%时，所有UHPC试件均未出现表观裂缝，基本处于弹性阶段。当轴向荷载处于极限荷载的60%~80%时，UHPC试件开始发出钢纤维从基体中滑移的“吱吱”声，但UHPC试件仍未开裂。当轴向荷载超过极限荷载的80%时，UHPC试件中部开始出现裂缝，试件的竖向应变逐渐增大，试件的横向箍筋应变迅速增加。随着荷载的继续增大，裂缝数量逐渐增多，裂缝也逐渐变大变长，同时试件也会发出较大“吱吱”声响。

由图3(a)~3(f)可知，随着菱形复合箍筋间距的逐渐增大，破坏后UHPC柱发生的剪切变形越来越大，但试件中部被压溃外鼓程度减小，产生的主裂纹的条数随之减少，说明UHPC的脆性随着箍筋间距的增密有所改善。由图3(b)、图3(g)~3(i)可知，随着钢纤维掺量的逐渐减小，试件破坏后剪切破坏的特征表现出来的越明显，剪切斜裂缝与试件轴向的夹角逐渐减小，UHPC保护层碎块脱落现象加剧，尤其是未掺钢纤维的试件UHPC保护层直接呈大块脱落(图3(i))，故钢纤维的掺加可以对试件柱保护层起到了很大的保护作用。由图3(a)、3(j)和图3(b)、3(k)可看出，与菱形复合箍筋相比，配置十字形复合箍筋的试件破坏后产生主裂缝数量减少，试件边缘破坏更为严重，说明菱形复合箍筋对核心UHPC的约束更有效，能够更加有效的改善UHPC的破坏模式和整体性。

图 3 箍筋约束UHPC试件破坏形态

Figure 3. Failure patterns of UHPC stub column specimens confined with stirrups

下载: 全尺寸图片幻灯片

2.2 箍筋约束UHPC主要试验结果

约束UHPC试件主要试验结果见表4。表中N_u为受压极限承载力；f_cc,f、ε_cc,f分别为未配置箍筋UHPC棱柱体的峰值应力和相应的峰值应变，由各组3个100 mm×100 mm×300 mm的棱柱体试件测得；f_cc,sf、ε_cc,sf分别为箍筋及纤维共同约束应力状态下UHPC的峰值应力和相应的峰值应变；ε_0.85为试件承载力下降至峰值应力的85%时对应的应变。由表4可知，箍筋形式的闭合环数及纤维掺量的增大，对UHPC的约束效应有一定程度提高作用；箍筋间距的减小，对UHPC的约束效应影响更大。

表 4 箍筋约束UHPC试验结果

Table 4. Test results of UHPC stub columns confined with stirrups

Code	N_u/kN	f_cc,f/MPa	f_cc,sf/MPa	ε_cc,f / 10⁻³	ε_cc,sf / 10⁻³	ε_0.85 / 10⁻³
UHPC-1	5155.3	91.4	122.5	2.63	3.79	6.20
UHPC-2	4644.8	91.4	109.8	2.63	3.46	4.83
UHPC-3	4386.7	91.4	103.3	2.63	3.21	4.10
UHPC-4	4239.4	91.4	99.6	2.63	3.05	3.68
UHPC-5	4092.3	91.4	95.9	2.63	2.92	3.39
UHPC-6	4579.9	89.2	108.1	2.55	3.32	4.50
UHPC-7	4410.7	85.3	103.9	2.45	3.14	4.24
UHPC-8	3810.7	71.7	88.9	2.26	2.85	3.52
UHPC-9	4931.0	91.4	116.9	2.63	3.69	5.64
UHPC-10	4530.7	91.4	106.9	2.63	3.39	4.36
UHPC-11	4031.3	91.4	91.4	2.63	2.63	2.89
Notes：N_u—Maximum load; f_cc,f and ε_cc,f—Peak stress and corresponding strain of UHPC without stirrups, respectively; f_cc,sf and ε_cc,sf—Peak stress and corresponding strain of UHPC under the combined stress of stirrups and fibers, respectively; ε_0.85—Corresponding strain when the bearing capacity of the specimen is reduced to 85% of the peak stress.

下载: 导出CSV

| 显示表格

2.3 箍筋约束UHPC轴向应变-轴向荷载的关系

2.3.1 箍筋间距对轴压荷载-轴向应变曲线的影响

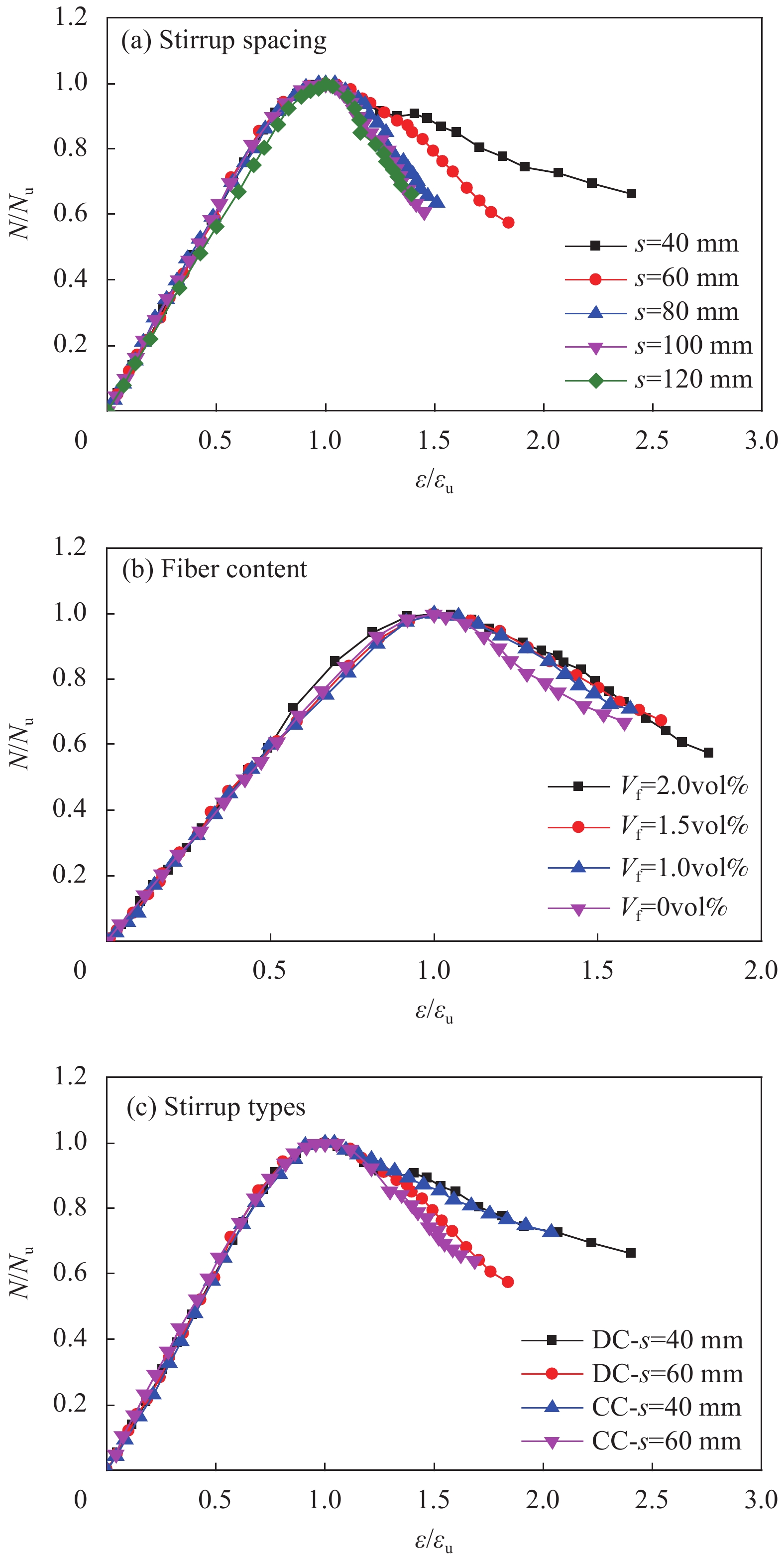
不同箍筋间距对轴压荷载-轴向应变曲线的影响如图4(a)所示，对比可知，各曲线上升段一致性较好；但是随着箍筋间距的减小，各试件峰值荷载逐渐增大且曲线的下降段坡度有所减缓(试件的变形能力增强)。当箍筋间距s分别为120 、100 、80 、60 、40 mm时，箍筋约束UHPC试件的极限承载力分别提高1.5%、5.2%、8.8%、15.2%、27.9%，其轴向峰值应变分别增加11.0%、16.0%、22.1%、31.6%、47.1%，可见箍筋间距对试件轴压承载力及相应轴向峰值应变具有显著的影响。寇佳亮等^[11]也发现箍筋约束纤维混凝土具有类似现象，且对轴向峰值应变的影响更大，说明箍筋间距的增密，可显著改善UHPC的变形能力。

图 4 箍筋约束UHPC轴向应变与轴向压力的关系

Figure 4. Relationship between axial strain and axial force of UHPC stub column specimens confined with stirrups

s—Stirrup spacing; V_f—Volume fraction of steel fibers; N—Axial force of columns; ε—Strain of columns

下载: 全尺寸图片幻灯片

2.3.2 纤维掺量对轴压荷载-轴向应变曲线的影响

不同纤维掺量对轴压荷载-轴向应变曲线的影响如图4(b)所示。可知，与未掺钢纤维试件相比，纤维掺量为1vol%、1.5vol%、2vol%的约束UHPC的峰值荷载均有较大幅度提高；但随着纤维掺量由1vol%增至2vol%时，约束UHPC的峰值荷载提高幅度较小，且各试件的曲线下降段坡度基本一致。与未掺钢纤维试件相比，当纤维掺量V_f分别为1vol%、1.5vol%、2vol%时，箍筋约束UHPC试件的极限承载力分别提高15.7%、20.2%、21.9%，其轴向峰值应变分别增加10.2%、16.5%、21.4%，可见纤维掺量对试件轴压承载力及相应轴向峰值应变具有一定的影响，对轴压承载力的影响更大，说明随着纤维掺量的增加，可一定程度提高箍筋约束UHPC的极限承载力。

2.3.3 箍筋形式对轴压荷载-轴向应变曲线的影响

不同箍筋形式对轴压荷载-轴向应变曲线的影响如图4(c)所示。可知，箍筋形式对其曲线上升段的影响较小，相同箍筋间距的菱形复合箍筋(DC)较十字形复合箍筋(CC)试件的峰值荷载有所提高。当箍筋间距为40 mm时，与CC形箍筋相比，DC形箍筋约束UHPC试件的极限承载力提高4.5%，其轴向峰值应变增加6.6%；当箍筋间距为60 mm时，与CC形箍筋相比，DC形箍筋约束UHPC试件的极限承载力提高2.5%，其轴向峰值应变增加3.0%；可见，箍筋间距越小，DC形复合箍筋较CC形复合箍筋对轴压承载力提高幅度越大。

2.4 箍筋约束UHPC应力-应变曲线

随着UHPC强度的增加及纤维对裂缝的阻碍作用，试件达到峰值荷载时，试件表面仅出现细微裂缝，此时可忽略UHPC保护层的损伤；在试件承载力下降至峰值的0.75倍时，UHPC保护层已严重外鼓及开裂，此时可忽略UHPC保护层的作用，文献[12]采用了类似的方法。本文采用以下两个假定可得出UHPC应力-应变曲线，假定1：试件在达到峰值荷载前，考虑UHPC保护层的受压作用；由峰值荷载下降至其0.75倍的过程中，UHPC保护层的受压作用随轴向应变呈线性变化；下降至0.75倍峰值荷载之后，忽略UHPC保护层的作用。假定2：纵筋应力-应变关系采用理想的弹塑性模型，纵筋屈服前可由其实测应变求得，屈服后可取其屈服强度的实测值。之后通过N/N_u及ε/ε_u进行归一化处理。

2.4.1 箍筋间距对UHPC归一化应力-应变曲线的影响

不同箍筋间距对UHPC应力-应变曲线的影响如图5(a)所示，对比可知，随着箍筋间距的减小，各试件曲线上升段斜率增大，但其下降段却表现出较大差异。当箍筋间距s为80~120 mm时，曲线下降段坡度相当，箍筋间距由80 mm减至60 mm时、由60 mm减至40 mm时，曲线下降段坡度减小很多。箍筋间距分别为120 、100 、80 、60和40 mm时，下降段斜率分别为−1.39、−1.113、−0.846、−0.629和−0.245，说明随着箍筋间距的减小，曲线下降段坡度(斜率的绝对值)也越来越小，对UHPC的约束效应逐渐增强。

图 5 箍筋约束UHPC应力-应变曲线

Figure 5. Stress–strain relationship curves of UHPC stub columns specimens confined with stirrups

N/N_u—Ratio of axial force and the peak load of columns; ε/ε_u—Ratio of strain and the peak strain of columns

下载: 全尺寸图片幻灯片

2.4.2 纤维掺量对UHPC归一化应力-应变曲线的影响

不同纤维掺量对UHPC应力-应变曲线的影响如图5(b)所示，对比可知，随着纤维掺量(V_f)的增大，曲线上升段斜率基本一致，仅在V_f=2vol%时出现上升段软化现象。与未掺纤维试件相比，当纤维掺量V_f为1vol%~2vol%时，曲线下降段坡度基本相当。纤维掺量分别为0vol%、1vol%、1.5vol%、2vol%时，下降段斜率分别为−0.697、−0.59、−0.653和−0.571，说明纤维掺量对配置较密箍筋UHPC试件(s=60 mm)的应力-应变归一化曲线影响较小。

2.4.3 箍筋形式对UHPC归一化应力-应变曲线的影响

不同箍筋形式对UHPC应力-应变曲线的影响如图5(c)所示。可知，当箍筋间距为40 mm时，DC形箍筋和CC形箍筋UHPC试件应力-应变曲线下降段斜率分别为−0.245和−0.236。当箍筋间距为60 mm时，DC形箍筋和CC形箍筋UHPC试件应力-应变曲线下降段斜率分别为−0.629和−0.75。说明DC形箍筋和CC形箍筋对UHPC试件的应力-应变归一化曲线影响大致相当。

3. 复合箍筋约束UHPC抗压强度

3.1 箍筋横向约束应力的计算

3.1.1 横向约束应力同配箍特征值的关系

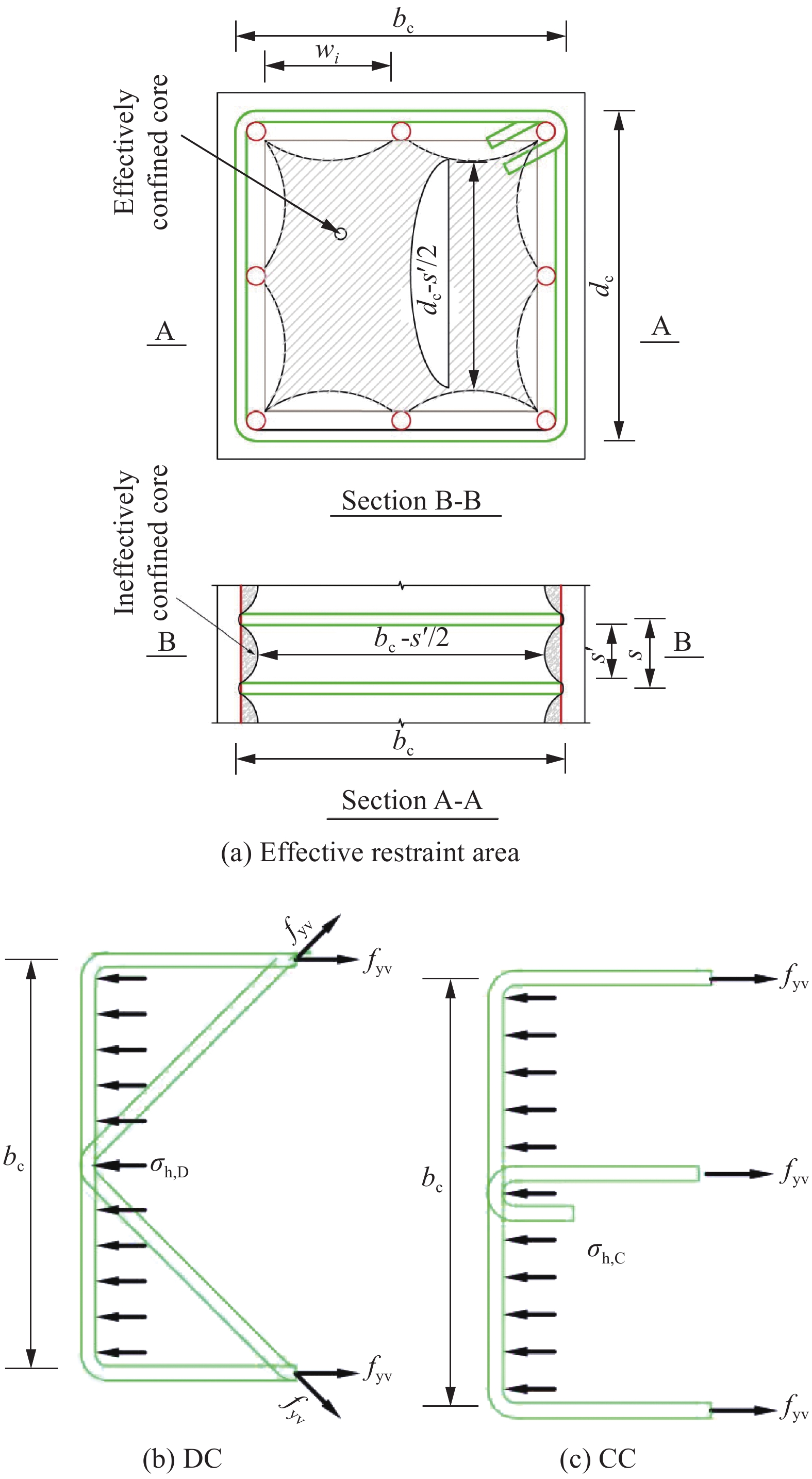
箍筋的配箍特征值越大，其横向约束力也越大，对UHPC短柱核心混凝土的约束作用越强，计算简图如图6所示。假设在轴压作用下，箍筋达到屈服强度时，核心区UHPC所受箍筋的横向约束应力沿箍筋方向均匀分布。对于分别取出外围和内围配置的箍筋组合，由图6可得箍筋的横向约束应力为：

图 6 箍筋及UHPC的应力

Figure 6. Stress of rectangular stirrups and UHPC

w_i—Net distance between adjacent longitudinal bars; f_yv—Yield strength of stirrups; s'—Net distance between stirrups; b_c and d_c—Distances between the axis of the stirrup restraining the short and long sides of the UHPC cross section, respectively

下载: 全尺寸图片幻灯片

${\sigma }_{\rm{h,D}}={\sigma }_{{\rm{x,}}{\text{外}}}+{\sigma }_{{\rm{x,}}{\text{内}}}=\frac{2{f}_{\rm{yv}}{A}_{{\rm{sv,}}{\text{外}}}}{{b}_{\rm{c}}s}+\frac{2{f}_{\rm{yv}}{A}_{{\rm{sv,}}{\text{内}}}}{\sqrt{{b}_{\rm{c}}^{2}+{d}_{\rm{c}}^{2}}s}$

(1)

${\sigma }_{\rm{h,C}}={\sigma }_{{\rm{x,}}{\text{外}}}+{\sigma }_{{\rm{x,}}{\text{内}}}=\frac{3{f}_{\rm{yv}}{A}_{\rm{sv}}}{{\rm{b}}_{\rm{c}}s}$

(2)

式中：σ_h,D为菱形复合箍筋的横向约束力；σ_x,外为外围箍筋的横向约束力；σ_x,内为内围箍筋的横向约束力；f_yv为箍筋屈服应力；A_sv,外为外围箍筋横截面积；A_sv,内为内围箍筋横截面积；b_c为截面宽度方向外围箍筋中心线之间的间距；s为箍筋中心线之间的间距；w_i 为相邻两根纵筋的净间距；σ_h,C为十字形复合箍筋的横向约束力。

菱形复合箍筋的体积配箍率为

${\rho }_{{\rm{v,}}{\text{外}}}=\frac{2({b}_{\rm{c}}+{d}_{\rm{c}}){A}_{{\rm{sv,}}{\text{外}}}}{{A}_{\rm{cor}}s}$

(3)

${\rho }_{{\rm{v,}}{\text{内}}}=\frac{2\sqrt{{b}_{\rm{c}}^{2}+{d}_{\rm{c}}^{2}}{A}_{{\rm{sv,}}{\text{内}}}}{{A}_{\rm{cor}}s}$

(4)

式中： ${\rho }_{{\rm{v,}}{\text{外}}}$ 为菱形复合箍筋的外围箍筋体积配箍率； ${\rho }_{{\rm{v,}}{\text{内}}}$ 为菱形复合箍筋的内围箍筋体积配箍率；d_c为截面长度方向外围箍筋中心线之间的间距(假定d_c≤b_c)；A_cor为外围箍筋围成的面积。

考虑到配箍特征值为

${\lambda _{\rm{v}}} = {\rho _{\rm{v}}}\frac{{{f_{{\rm{yv}}}}}}{{{f_{\rm{c}}}}}$

(5)

式中：λ_v为配箍特征值；f_c为纤维UHPC混凝土的轴心抗压强度。

将式(3)~(5)代入式(1)并考虑d_c=b_c，可得：

${\sigma }_{\rm{h,D}}=\left(\frac{{\lambda }_{{\rm{v,}}{\text{外}}}}{2}+\frac{{\lambda }_{{\rm{v,}}{\text{内}}}}{2}\right){f}_{\rm{c}}$

(6)

式中：λ_v,外为菱形复合箍筋的外围箍筋的配箍特征值；λ_v,内为菱形复合箍筋的内围箍筋的配箍特征值。

同理可得出十字形箍筋横向约束应力：

${\sigma }_{\rm{h,C}}=\left(\frac{{\lambda }_{\rm{v},{\text{外}}}}{2}+\frac{{\lambda }_{\rm{v},{\text{内}}}}{2}\right){f}_{\rm{c}}$

(7)

3.1.2 横向约束应力同箍筋形式的关系

外围箍筋角部及与纵筋相交处约束的效应最强，相邻纵筋的中点处约束作用最弱，可按有效约束面积与核心部分面积的比值，计算外围箍筋形式的约束作用^[5,13]：

${A_{{\rm{e,n}}}} = {b_{\rm{c}}}{d_{\rm{c}}} - \sum\limits_{i = 1}^n {\frac{{w_{ix}^2 + w_{iy}^2}}{6}}$

(8)

式中，A_e,n为外围箍筋的横截面有效约束面积；w_ix为外围箍筋一侧相邻两根纵筋的净间距；w_iy为外围箍筋另一侧相邻两根纵筋的净间距。

则箍筋形式的影响系数α_n^[5,13]为：

${\alpha _{\rm{n}}} = 1 - \sum\limits_{i = 1}^n {\frac{{w_{ix}^2 + w_{iy}^2}}{{6{b_{\rm{c}}}{d_{\rm{c}}}}}}$

(9)

3.1.3 横向约束应力同箍筋间距的关系

沿外围箍筋约束UHPC短柱的纵向有效约束面积是变化的，相邻箍筋的中间截面有效约束面积最小，因此选相邻箍筋中间截面为控制截面。沿柱纵向的有效约束线近似等效成抛物曲线，取抛物线的顶点近似为箍筋净间距的1/4，则A_es为：

${A_{{\rm{es}}}} = \left({b_{\rm{c}}}{\rm{ - }}\frac{{s'}}{2}\right)\left({d_{\rm{c}}}{\rm{ - }}\frac{{s'}}{2}\right)$

(10)

式中：A_es为外围箍筋控制截面的有效约束面积；s´为箍筋间距的净间距。

则箍筋间距的影响系数α_s为：

${\alpha _{\rm{s}}} = \left(1{\rm{ - }}\frac{{s'}}{{2{b_{\rm{c}}}}}\right)\left(1{\rm{ - }}\frac{{s'}}{{2{d_{\rm{c}}}}}\right)$

(11)

综合考虑配箍特征值、外围箍筋形式以及外围箍筋间距对箍筋约束力的影响，由式(5)、(6)、(7)、(9)和(11)可得出箍筋的横向约束应力为：

${\sigma _{\rm{h}}} = {I_{\rm{e}}}{f_{\rm{c}}}$

(12)

${I}_{\rm{e}}=\frac{{\alpha }_{\rm{n}}{\alpha }_{\rm{s}}{\lambda }_{{\rm{v,}}{\text{外}}}}{2}+\frac{{\lambda }_{{\rm{v,}}{\text{内}}}}{2}$

(13)

式中，I_e为复合箍筋有效约束系数。

3.2 纤维有效约束系数

综合考虑了纤维品种、纤维的外形、纤维长径比等参数的影响，纤维约束系数^[20]采用下式进行表述，其具体数值见表5。

${\varOmega _{\rm{f}}} = \sum\limits_{i = 1}^n {{\alpha _{{\rm{c}},i}}} {V_{{\rm{f}},i}}{l_{{\rm{f}},i}}/{d_{{\rm{f}},i}}$

(14)

式中：α_c,i为纤维种类对约束纤维混凝土的影响指数，钢纤维取1.0；V_f,i为纤维体积掺量；l_f,i为纤维长度(mm)；d_f,i为纤维直径(mm)。

表 5 UHPC短柱箍筋及纤维约束系数及其轴压承载力

Table 5. Stirrup and fiber constraint index and compression capacity of UHPC stub columns

Code	σ_l,e/MPa	I_e	Ω_f	N_uc/kN	N_ue/kN	N_ue/N_uc
UHPC-1	5.54	0.061	1.34	5155.3	5026.8	0.98
UHPC-2	3.48	0.038	1.34	4644.8	4598.7	0.99
UHPC-3	2.46	0.027	1.34	4386.7	4387.0	1.00
UHPC-4	1.85	0.020	1.34	4239.4	4261.7	1.01
UHPC-5	1.46	0.016	1.34	4092.3	4179.6	1.02
UHPC-6	3.48	0.039	1.01	4579.9	4518.1	0.99
UHPC-7	3.48	0.041	0.67	4410.7	4370.7	0.99
UHPC-8	3.48	0.048	0.00	3810.7	3847.3	1.01
UHPC-9	4.69	0.051	1.34	4931.0	4850.6	0.98
UHPC-10	2.91	0.032	1.34	4530.7	4481.3	0.99
Notes: σ_l,e—Hoop constraint stress; I_e—Effective constraint indicator; Ω_f—Influence of the fiber constraint coefficient; N_uc—Test value of axial load; N_ue—Calculated value of axial load; N_ue/N_uc—Ratio of the calculated value and test value of axial load.

下载: 导出CSV

| 显示表格

3.3 约束UHPC抗压强度的计算

对于箍筋约束UHPC柱，由于箍筋的侧向约束，核心区UHPC处于三向受压状态，其强度取决于箍筋横向约束应力的大小。依据Richart^[21]提出的线性莫尔强度准则，给出如下破坏准则：

${f_{{\rm{cc,sf}}}} = {f_{{{\rm{cc}}},{\rm{f}}}} + k{\sigma _{l,{\rm{e}}}} = (1 + k{I_{\rm{e}}}){f_{{{\rm{cc}}},{\rm{f}}}}$

(15)

式中，f_cc,f为未配置箍筋UHPC的峰值应力；f_cc,sf为箍筋及纤维共同约束应力状态下UHPC的峰值应力；σ_l,e为峰值应力时箍筋的有效横向约束应力；I_e为复合箍筋有效约束系数；k为待定系数。

为了计算箍筋及纤维共同约束应力状态下UHPC的峰值应力，采用两阶段进行回归分析：(1)考虑钢纤维约束系数Ω_f的影响，由UHPC-2、UHPC-6~UHPC-8的试验数据回归分析，可得到相同箍筋配置下的约束UHPC抗压强度：

${f_{{\rm{cc,sf}}}} = {\kern 1pt} (1.24 - 0.03{\varOmega _{\rm{f}}}){f_{{{\rm{cc}}},{\rm{f}}}}$

(16)

(2)将纤维约束系数代入式(1.24−0.03Ω_f) I_e，其散点图基本满足线性关系(图7)，故采用公式(15)的线性回归分析，得出考虑纤维约束系数和箍筋有效横向约束系数的约束UHPC抗压强度：

${f_{{\rm{cc,sf}}}} = \left[ {1 + 4.39(1.24 - 0.03{\varOmega _{\rm{f}}}){I_{\rm{e}}}} \right]{\kern 1pt} {\kern 1pt} {f_{{{\rm{cc}}},{\rm{f}}}}$

(17)

试验实测值与理论公式计算值比较见图7，可见二者吻合较好。

图 7 箍筋约束UHPC的 f_cc,sf/f_cc,f与(1.24−0.03Ω_f)I_e的关系

Figure 7. Relationship between f_cc,sf/f_cc,f ratio and (1.24−0.03Ω_f)I_e of UHPC stub column specimen confined with stirrups

f_cc,sf/f_cc,f—Ratio of the peak stress of the UHPC under the combined stress of stirrups and without stirrups; Ω_f—Influence of the fiber constraint coefficient; I_e—Effective constraint indicator

下载: 全尺寸图片幻灯片

4. 复合箍筋约束UHPC轴心受压承载力

由于钢纤维的掺入，在复合箍筋约束UHPC短柱达到极限承载力时，UHPC保护层仅出现微小裂缝，因此，承载力计算时可考虑UHPC保护层。由试验结果可知，此时纵筋已经屈服，故约束UHPC短柱轴压承载力由UHPC受压材料和纵向钢筋二者共同承担，则其公式可表示为：

${N}_{\rm{u}}={f}_{{\rm{cc}},{\rm{sf}}}({A}_{\rm{c}}-{A}_{\rm{s}})+{f}_{\rm{y}}{A}_{\rm{s}}$

(18)

将式(17)代入式(18)得：

${N_{\rm{u}}} = {f_{{\rm{cc}},{\rm{f}}}}\left[ {1 + 4.39(1.24 - 0.03{\varOmega _{\rm{f}}}){I_{\rm{e}}}} \right]({A_{\rm{c}}} - {A_{\rm{s}}}) + {f_{\rm{y}}}{A_{\rm{s}}}$

(19)

箍筋约束UHPC短柱的轴心受压承载力的计算结果N_ue、试验结果N_uc及N_ue/N_uc的比值如表5所示。可以看出N_ue/N_uc比值的平均值为0.996，变异系数为0.014，计算结果与试验结果比较，吻合较好。

5. 结论

(1)复合箍筋和钢纤维的掺加对超高性能混凝土(UHPC)柱的破坏起到一定的改善作用，且随着箍筋间距的增密，UHPC的脆性改善的效果越明显。相比十字形复合箍筋，菱形复合箍筋对核心UHPC的约束更有效，能够更加有效地改善UHPC的破坏模式和整体性。

(2)箍筋间距、纤维掺量对试件轴压承载力及相应轴向峰值应变具有显著的影响。箍筋间距对轴向峰值应变的影响更大，说明箍筋间距的增密，可显著改善UHPC的变形能力。但纤维掺量对轴压承载力的影响更大，说明随着纤维掺量的增加，可一定程度提高箍筋约束UHPC的极限承载力。相同箍筋间距的菱形复合箍筋(DC)较十字形复合箍筋(CC)试件的峰值荷载有所提高，且箍筋间距越小，DC形复合箍筋较CC形复合箍筋对轴压承载力提高幅度越大。

(3)随着箍筋间距的减小，各试件UHPC归一化应力-应变曲线上升段斜率增大，但其下降段表现出更大差异。箍筋间距分别为120 、100 、80 、60 和40 mm时，下降段斜率分别为−1.39、−1.113、−0.846、−0.629和−0.245，说明随着箍筋间距的减小，曲线下降段坡度(斜率的绝对值)也越来越小，对UHPC的约束效应逐渐增强。

(4)综合考虑箍筋约束系数及纤维约束系数的影响，建立了约束UHPC的峰值应力计算公式和复合箍筋约束UHPC短柱轴心受压承载力计算公式，计算结果与试验结果比较，吻合较好。

图 1 箍筋约束超高性能混凝土(UHPC)试件几何尺寸和配筋

Figure 1. Dimensions and reinforcement details of ultra-high performance concrete (UHPC) stub column specimen confined with stirrups

CC and DC—Cross- and diamond-shaped stirrups, respectively

下载: 全尺寸图片幻灯片

图 2 试验加载装置及测点布置

Figure 2. Test equipment and arrangement of measuring points

下载: 全尺寸图片幻灯片

图 3 箍筋约束UHPC试件破坏形态

Figure 3. Failure patterns of UHPC stub column specimens confined with stirrups

下载: 全尺寸图片幻灯片

图 4 箍筋约束UHPC轴向应变与轴向压力的关系

Figure 4. Relationship between axial strain and axial force of UHPC stub column specimens confined with stirrups

s—Stirrup spacing; V_f—Volume fraction of steel fibers; N—Axial force of columns; ε—Strain of columns

下载: 全尺寸图片幻灯片

图 5 箍筋约束UHPC应力-应变曲线

Figure 5. Stress–strain relationship curves of UHPC stub columns specimens confined with stirrups

N/N_u—Ratio of axial force and the peak load of columns; ε/ε_u—Ratio of strain and the peak strain of columns

下载: 全尺寸图片幻灯片

图 6 箍筋及UHPC的应力

Figure 6. Stress of rectangular stirrups and UHPC

下载: 全尺寸图片幻灯片

图 7 箍筋约束UHPC的 f_cc,sf/f_cc,f与(1.24−0.03Ω_f)I_e的关系

Figure 7. Relationship between f_cc,sf/f_cc,f ratio and (1.24−0.03Ω_f)I_e of UHPC stub column specimen confined with stirrups

下载: 全尺寸图片幻灯片

表 1 箍筋约束UHPC试件参数及UHPC材料性能

Table 1 Parameters of specimens and material properties of UHPC stub column specimen confined with stirrups

Code	Stirrup			V_f/vol%	f_cu/MPa	E_cc,f/GPa	λ_v
Code	s/mm	ρ_v/%	Type	V_f/vol%	f_cu/MPa	E_cc,f/GPa	λ_v
UHPC-1	40	3.07	DC	2	117.5	39.50	0.17
UHPC-2	60	2.05	DC	2	117.5	39.50	0.11
UHPC-3	80	1.54	DC	2	117.5	39.50	0.09
UHPC-4	100	1.23	DC	2	117.5	39.50	0.07
UHPC-5	120	1.02	DC	2	117.5	39.50	0.06
UHPC-6	60	2.05	DC	1.5	114.8	39.04	0.12
UHPC-7	60	2.05	DC	1	110.2	38.72	0.12
UHPC-8	60	2.05	DC	0	92.5	32.52	0.14
UHPC-9	40	2.61	CC	2	117.5	39.50	0.14
UHPC-10	60	1.74	CC	2	117.5	39.50	0.10
UHPC-11	—	—	—	2	117.5	39.50	—
Notes：s—Stirrup spacing; ρ_v—Volume stirrup ratio; CC and DC—Cross- and diamond-shaped stirrups, respectively; V_f—Volume fraction of steel fibers; f_cu—Compressive strength of the fiber UHPC cube; E_cc,f —Elastic modulus of the fiber-constrained UHPC; λ_v—Stirrup characteristic value.

下载: 导出CSV

表 2 钢纤维性能指标

Table 2 Performance indicators of the steel fibers

Length/mm	Diameter/mm	Aspect ratio	Shape pass rate/%	Mass density/(g·cm⁻³)	Tensile strength/MPa
13	0.2	65	98	7.8	2850

下载: 导出CSV

表 3 钢筋材料性能

Table 3 Material performance indicators of the steel bars

Rebar grade	d/mm	f_y/MPa	f_u/MPa	δ/%
HRB400	6	444.5	566.5	19.5
HRB400	10	425.8	533.6	17.7
Notes：d—Diameter of steel bars; f_y—Yield strength of steel bars; f_u—Ultimate tensile strength of steel bars; δ—Elongation of steel bars.

下载: 导出CSV

表 4 箍筋约束UHPC试验结果

Table 4 Test results of UHPC stub columns confined with stirrups

Code	N_u/kN	f_cc,f/MPa	f_cc,sf/MPa	ε_cc,f / 10⁻³	ε_cc,sf / 10⁻³	ε_0.85 / 10⁻³
UHPC-1	5155.3	91.4	122.5	2.63	3.79	6.20
UHPC-2	4644.8	91.4	109.8	2.63	3.46	4.83
UHPC-3	4386.7	91.4	103.3	2.63	3.21	4.10
UHPC-4	4239.4	91.4	99.6	2.63	3.05	3.68
UHPC-5	4092.3	91.4	95.9	2.63	2.92	3.39
UHPC-6	4579.9	89.2	108.1	2.55	3.32	4.50
UHPC-7	4410.7	85.3	103.9	2.45	3.14	4.24
UHPC-8	3810.7	71.7	88.9	2.26	2.85	3.52
UHPC-9	4931.0	91.4	116.9	2.63	3.69	5.64
UHPC-10	4530.7	91.4	106.9	2.63	3.39	4.36
UHPC-11	4031.3	91.4	91.4	2.63	2.63	2.89
Notes：N_u—Maximum load; f_cc,f and ε_cc,f—Peak stress and corresponding strain of UHPC without stirrups, respectively; f_cc,sf and ε_cc,sf—Peak stress and corresponding strain of UHPC under the combined stress of stirrups and fibers, respectively; ε_0.85—Corresponding strain when the bearing capacity of the specimen is reduced to 85% of the peak stress.

下载: 导出CSV

表 5 UHPC短柱箍筋及纤维约束系数及其轴压承载力

Table 5 Stirrup and fiber constraint index and compression capacity of UHPC stub columns

Code	σ_l,e/MPa	I_e	Ω_f	N_uc/kN	N_ue/kN	N_ue/N_uc
UHPC-1	5.54	0.061	1.34	5155.3	5026.8	0.98
UHPC-2	3.48	0.038	1.34	4644.8	4598.7	0.99
UHPC-3	2.46	0.027	1.34	4386.7	4387.0	1.00
UHPC-4	1.85	0.020	1.34	4239.4	4261.7	1.01
UHPC-5	1.46	0.016	1.34	4092.3	4179.6	1.02
UHPC-6	3.48	0.039	1.01	4579.9	4518.1	0.99
UHPC-7	3.48	0.041	0.67	4410.7	4370.7	0.99
UHPC-8	3.48	0.048	0.00	3810.7	3847.3	1.01
UHPC-9	4.69	0.051	1.34	4931.0	4850.6	0.98
UHPC-10	2.91	0.032	1.34	4530.7	4481.3	0.99
Notes: σ_l,e—Hoop constraint stress; I_e—Effective constraint indicator; Ω_f—Influence of the fiber constraint coefficient; N_uc—Test value of axial load; N_ue—Calculated value of axial load; N_ue/N_uc—Ratio of the calculated value and test value of axial load.

下载: 导出CSV

参考文献(21)

[1]	胡翱翔, 梁兴文, 于婧, 等. 超高性能混凝土轴心受拉力学性能试验研究[J]. 湖南大学学报(自然科学版), 2018, 45(9):30-37. HU Aoxiang, LIANG Xingwen, YU Jing, et al. Experimental study of uniaxial tensile characteristics of ultra-high performance concrete[J]. Journal of Hunan University(Natural Sciences),2018,45(9):30-37(in Chinese).
[2]	胡翱翔, 梁兴文, 李东阳, 等. 超高性能混凝土配合比设计及其受拉性能[J]. 湖南大学学报(自然科学版), 2018, 45(3):39-46. HU Aoxiang, LIANG Xingwen, LI Dongyang, et al. Mix design method and uniaxial tensile characteristics of ultra-high performance concrete[J]. Journal of Hunan University(Natural Sciences),2018,45(3):39-46(in Chinese).
[3]	李立仁, 余瑜, 陈永庆. 不同配箍方式的轴压高强混凝土短柱承载力及延性试验研究[J]. 施工技术, 2005(S2):54-57. LI Liren, YU Yu, CHEN Yongqing. Study on bearing capacity of short column and ductility of high-strength concrete constrained with axial load[J]. Construction Technology,2005(S2):54-57(in Chinese).
[4]	熊海明, 梁厚燃, 梁莹, 等. 多重螺旋筋复合约束钢筋混凝土圆形截面短柱轴压性能试验研究[J]. 工业建筑, 2020, 50(1):84-90. XIONG Haiming, LIANG Houran, LIANG Ying, et al. Experimental research on the performance of composite confined peinforced concrete circular column with multiple spiral stirrups under axial compression[J]. Industrial Construction,2020,50(1):84-90(in Chinese).
[5]	MANDER J B, PRIESTLEY M J N, FELLOW R P. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering,1988,114(8):1804-1826. DOI: 10.1061/(ASCE)0733-9445(1988)114:8(1804)
[6]	钱稼茹, 程丽荣, 周栋梁. 普通箍筋约束混凝土柱的中心受压性能[J]. 清华大学学报(自然科学版), 2002(10):1369-1373. DOI: 10.3321/j.issn:1000-0054.2002.10.026 QIAN Jiaru, CHENG Lirong, ZHOU Dongliang. Central compression performance of concrete columns confined by ordinary stirrups[J]. Journal of Tsinghua University(Science and Technology),2002(10):1369-1373(in Chinese). DOI: 10.3321/j.issn:1000-0054.2002.10.026
[7]	张燕斌, 姬宝霖. 高强箍筋约束混凝土柱轴压试验研究[J]. 结构工程师, 2016, 32(6):123-128. DOI: 10.3969/j.issn.1005-0159.2016.06.018 ZHANG Yanbin, JI Baolin. Studies on the behavior of high-strength concrete columns with high-strength reinforcement under concentric compression[J]. Structural Engineers,2016,32(6):123-128(in Chinese). DOI: 10.3969/j.issn.1005-0159.2016.06.018
[8]	胡海涛, 叶知满. 复合箍筋约束高强混凝土应力应变性能[J]. 工业建筑, 1997(10):24-29. HU Haitao, YE Zhiman. Stress-strain behavior of high-strength concrete confined by overlapping hoops[J]. Industrial Construction,1997(10):24-29(in Chinese).
[9]	胡海涛, 叶知满. 复合方箍约束混凝土轴心受压短柱承载力计算[J]. 建筑结构, 2002(4):12-13. HU Haitao, YE Zhiman. Calculation of bearing capacity of concrete short columns confined by composite square hoop under axial compression[J]. Journal of Building Structures,2002(4):12-13(in Chinese).
[10]	王铁成, 王晓伟. 箍筋约束T形截面短柱轴压承载力试验研究[J]. 地震工程与工程振动, 2009, 29(2):103-109. WANG Tiecheng, WANG Xiaowei. Experimental research on bearing capacity of axially loaded T-shaped short columns confined with stirrups[J]. Journal of Earthquake Engineering and Engineering Vibration,2009,29(2):103-109(in Chinese).
[11]	寇佳亮, 孙方辉, 梁兴文, 等. 箍筋约束纤维增强混凝土轴心受压性能试验研究[J]. 建筑结构学报, 2015, 36(7):124-131. KOU Jialiang, SUN Fanghui, LIANG Xingwen, et al. Experimental investigation on axial compression performance of fiber reinforced concrete confined with stirrups[J]. Journal of Building Structures,2015,36(7):124-131(in Chinese).
[12]	李艳, 刘泽军, 王伟伟, 等. 箍筋约束ECC轴心受压性能试验研究[J]. 建筑结构学报, 2017, 38(7):164-173. LI Yan, LIU Zejun, WANG Weiwei, et al. Experimental study on axial compression performance of ECC confined with stirrups[J]. Journal of Building Structures,2017,38(7):164-173(in Chinese).
[13]	邓宗才, 姚军锁. 高强箍筋约束超高性能混凝土柱轴压性能[J]. 复合材料学报, 2020, 37(10):2590-2601. DENG Zongcai, YAO Junsuo. Axial compression behavior of ultra-high performance concrete columns confined by high-strength stirrups[J]. Acta Materiae Compositae Sinica,2020,37(10):2590-2601(in Chinese).
[14]	WU T, WEI H, ZHANG Y, et al. Axial compressive behavior of lightweight aggregate concrete columns confined with transverse steel reinforcement[J]. Advances in Mechanical Engineering,2018,10(3):1-14.
[15]	LOKUGE W P, SANJAYAN J G, SETUNGE S. Stress-strain model for laterally confined concrete[J]. Journal of Materials in Civil Engineering,2005,17(6):607-616. DOI: 10.1061/(ASCE)0899-1561(2005)17:6(607)
[16]	SHARMA U K, BHARGAVA P, KAUSHIK S K. Behavior of confined high strength concrete columns under axial compression[J]. Journal of Advanced Concrete Technology,2005,3(2):267-281. DOI: 10.3151/jact.3.267
[17]	MANDER J B, PRIESTLEY M J N, FELLOW R P. Observed stress-strain behavior of confined concrete[J]. Journal of Structural Engineering,1988,114(8):1827-1849. DOI: 10.1061/(ASCE)0733-9445(1988)114:8(1827)
[18]	SAMANI A K, ATTARD M M. A stress-strain model for uniaxial and confined concrete under compression[J]. Engineering Structures, 2012, 41: 335-349.
[19]	SHIN H O, YOON Y S, COOK W D, et al. Effect of confinement on the axial load response of ultrahigh-strength concrete columns[J]. Journal of Structural Engineering, 2015, 141(6): 04014151.
[20]	郑州大学. 钢纤维混凝土结构设计标准: JGJ 465—2019[S]. 北京: 中国建筑工业出版社, 2019. Zhengzhou University. Steel fiber concrete structure design standard: JGJ 465—2019[S]. Beijing: China Construction Industry Press, 2019 (in Chinese).
[21]	RICHART F E. Reinforced concrete wall and column footings[J]. ACI Journal Proceedings,1948,45(10):97-127.

施引文献(15)

期刊类型引用(7)

1.	徐龙康，杨勇，张明俊，张扬. 双向螺旋箍筋约束高强蜂窝型钢-UHPC短柱轴压性能研究. 建筑结构学报. 2025(01): 147-159 . 百度学术
2.	路军富，苗志豪，王明胜，汤印. 箍筋间距对型钢混凝土结构轴压性能影响研究. 铁道工程学报. 2025(01): 83-88+100 . 百度学术
3.	唐红元，胡晓维，刘烨. 方形不锈钢管超高性能混凝土(UHPC)短柱轴压性能研究. 工程力学. 2024(12): 116-127 . 百度学术
4.	赵飞，朱鹏飞，李梦瑶，马衍轩，张建，吴磊. 钢筋混凝土的负泊松比设计与抗弯性能研究. 硅酸盐通报. 2023(05): 1640-1649 . 百度学术
5.	章世祥，王序，何迈杰，周权，刘钊. UHPC圆形空心管柱轴压性能试验. 中国公路学报. 2023(09): 134-143 . 百度学术
6.	王勃，周家宇. UHPC加固钢筋混凝土柱轴压承载力研究. 吉林建筑大学学报. 2022(03): 1-8 . 百度学术
7.	纪晟晖，蒋国平，吴能森，郭金龙，刘心勇，卢德辉. 复合箍筋钢筋混凝土柱静力试验与数值模拟分析. 东莞理工学院学报. 2022(05): 111-118 . 百度学术

其他类型引用(8)

资源附件(0)

长摘要

创新点

图(7) / 表(5)

计量

文章访问数: 1238
HTML全文浏览量: 591
PDF下载量: 65
被引次数: 15

1. 试验概况
1.1 试验参数及原材料
1.2 试验加载与量测
2. 试验结果及分析
2.1 箍筋约束UHPC破坏现象及破坏形态
2.2 箍筋约束UHPC主要试验结果
2.3 箍筋约束UHPC轴向应变-轴向荷载的关系
2.3.1 箍筋间距对轴压荷载-轴向应变曲线的影响
2.3.2 纤维掺量对轴压荷载-轴向应变曲线的影响
2.3.3 箍筋形式对轴压荷载-轴向应变曲线的影响
2.4 箍筋约束UHPC应力-应变曲线
2.4.1 箍筋间距对UHPC归一化应力-应变曲线的影响
2.4.2 纤维掺量对UHPC归一化应力-应变曲线的影响
2.4.3 箍筋形式对UHPC归一化应力-应变曲线的影响
3. 复合箍筋约束UHPC抗压强度
3.1 箍筋横向约束应力的计算
3.1.1 横向约束应力同配箍特征值的关系
3.1.2 横向约束应力同箍筋形式的关系
3.1.3 横向约束应力同箍筋间距的关系
3.2 纤维有效约束系数
3.3 约束UHPC抗压强度的计算
4. 复合箍筋约束UHPC轴心受压承载力
5. 结论

1. 试验概况
1.1 试验参数及原材料
1.2 试验加载与量测
2. 试验结果及分析
2.1 箍筋约束UHPC破坏现象及破坏形态
2.2 箍筋约束UHPC主要试验结果
2.3 箍筋约束UHPC轴向应变-轴向荷载的关系
2.3.1 箍筋间距对轴压荷载-轴向应变曲线的影响
2.3.2 纤维掺量对轴压荷载-轴向应变曲线的影响
2.3.3 箍筋形式对轴压荷载-轴向应变曲线的影响
2.4 箍筋约束UHPC应力-应变曲线
2.4.1 箍筋间距对UHPC归一化应力-应变曲线的影响
2.4.2 纤维掺量对UHPC归一化应力-应变曲线的影响
2.4.3 箍筋形式对UHPC归一化应力-应变曲线的影响
3. 复合箍筋约束UHPC抗压强度
3.1 箍筋横向约束应力的计算
3.1.1 横向约束应力同配箍特征值的关系
3.1.2 横向约束应力同箍筋形式的关系
3.1.3 横向约束应力同箍筋间距的关系
3.2 纤维有效约束系数
3.3 约束UHPC抗压强度的计算
4. 复合箍筋约束UHPC轴心受压承载力
5. 结论

参考文献(21)

施引文献(15)

资源附件(0)

长摘要

创新点

箍筋约束超高性能混凝土短柱轴压承载力试验研究

通讯作者: 师俊平，博士，教授，博士生导师，研究方向为工程力学 E-mail：shijp@xaut.edu.cn

计量

出版历程

Experimental study on the axial compression capacity of ultra-high performance concrete stub columns confined with stirrups

1. 试验概况

1.1 试验参数及原材料

1.2 试验加载与量测

2. 试验结果及分析

2.1 箍筋约束UHPC破坏现象及破坏形态

2.2 箍筋约束UHPC主要试验结果

2.3 箍筋约束UHPC轴向应变-轴向荷载的关系

2.3.1 箍筋间距对轴压荷载-轴向应变曲线的影响

2.3.2 纤维掺量对轴压荷载-轴向应变曲线的影响

2.3.3 箍筋形式对轴压荷载-轴向应变曲线的影响

2.4 箍筋约束UHPC应力-应变曲线

2.4.1 箍筋间距对UHPC归一化应力-应变曲线的影响

2.4.2 纤维掺量对UHPC归一化应力-应变曲线的影响

2.4.3 箍筋形式对UHPC归一化应力-应变曲线的影响

3. 复合箍筋约束UHPC抗压强度

3.1 箍筋横向约束应力的计算

3.1.1 横向约束应力同配箍特征值的关系

3.1.2 横向约束应力同箍筋形式的关系

3.1.3 横向约束应力同箍筋间距的关系

3.2 纤维有效约束系数

3.3 约束UHPC抗压强度的计算

4. 复合箍筋约束UHPC轴心受压承载力

5. 结 论

期刊类型引用(7)

其他类型引用(8)

计量

出版历程

目录

1. 试验概况

1.1 试验参数及原材料

1.2 试验加载与量测

2. 试验结果及分析

2.1 箍筋约束UHPC破坏现象及破坏形态

2.2 箍筋约束UHPC主要试验结果

2.3 箍筋约束UHPC轴向应变-轴向荷载的关系

2.3.1 箍筋间距对轴压荷载-轴向应变曲线的影响

2.3.2 纤维掺量对轴压荷载-轴向应变曲线的影响

2.3.3 箍筋形式对轴压荷载-轴向应变曲线的影响

2.4 箍筋约束UHPC应力-应变曲线

2.4.1 箍筋间距对UHPC归一化应力-应变曲线的影响

2.4.2 纤维掺量对UHPC归一化应力-应变曲线的影响

2.4.3 箍筋形式对UHPC归一化应力-应变曲线的影响

3. 复合箍筋约束UHPC抗压强度

3.1 箍筋横向约束应力的计算

3.1.1 横向约束应力同配箍特征值的关系

3.1.2 横向约束应力同箍筋形式的关系

3.1.3 横向约束应力同箍筋间距的关系

3.2 纤维有效约束系数

3.3 约束UHPC抗压强度的计算

4. 复合箍筋约束UHPC轴心受压承载力

5. 结 论

通讯作者:
师俊平，博士，教授，博士生导师，研究方向为工程力学　E-mail：shijp@xaut.edu.cn

5. 结论

5. 结论