基于自洽聚类分析的2D C/SiC压缩性能快速预报

戴新航; 许承海; 王琨杰; 高博

doi:10.13801/j.cnki.fhclxb.20231206.002

基于自洽聚类分析的2D C/SiC压缩性能快速预报

doi: 10.13801/j.cnki.fhclxb.20231206.002

哈尔滨工业大学　特种环境复合材料技术国家级重点实验室，哈尔滨 150001

详细信息

通讯作者:
高博，博士，助理教授，研究方向为复合材料热结构力学行为研究与不确定性量化　E-mail: 20230194@hit.edu.cn

中图分类号: TB332
计量
- 文章访问数: 208
- HTML全文浏览量: 146
- PDF下载量: 1
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-11
- 修回日期: 2023-11-09
- 录用日期: 2023-11-29
- 网络出版日期: 2023-12-07
- 刊出日期: 2024-08-15

Fast prediction of 2D C/SiC compression performance based on self-consistent clustering analysis

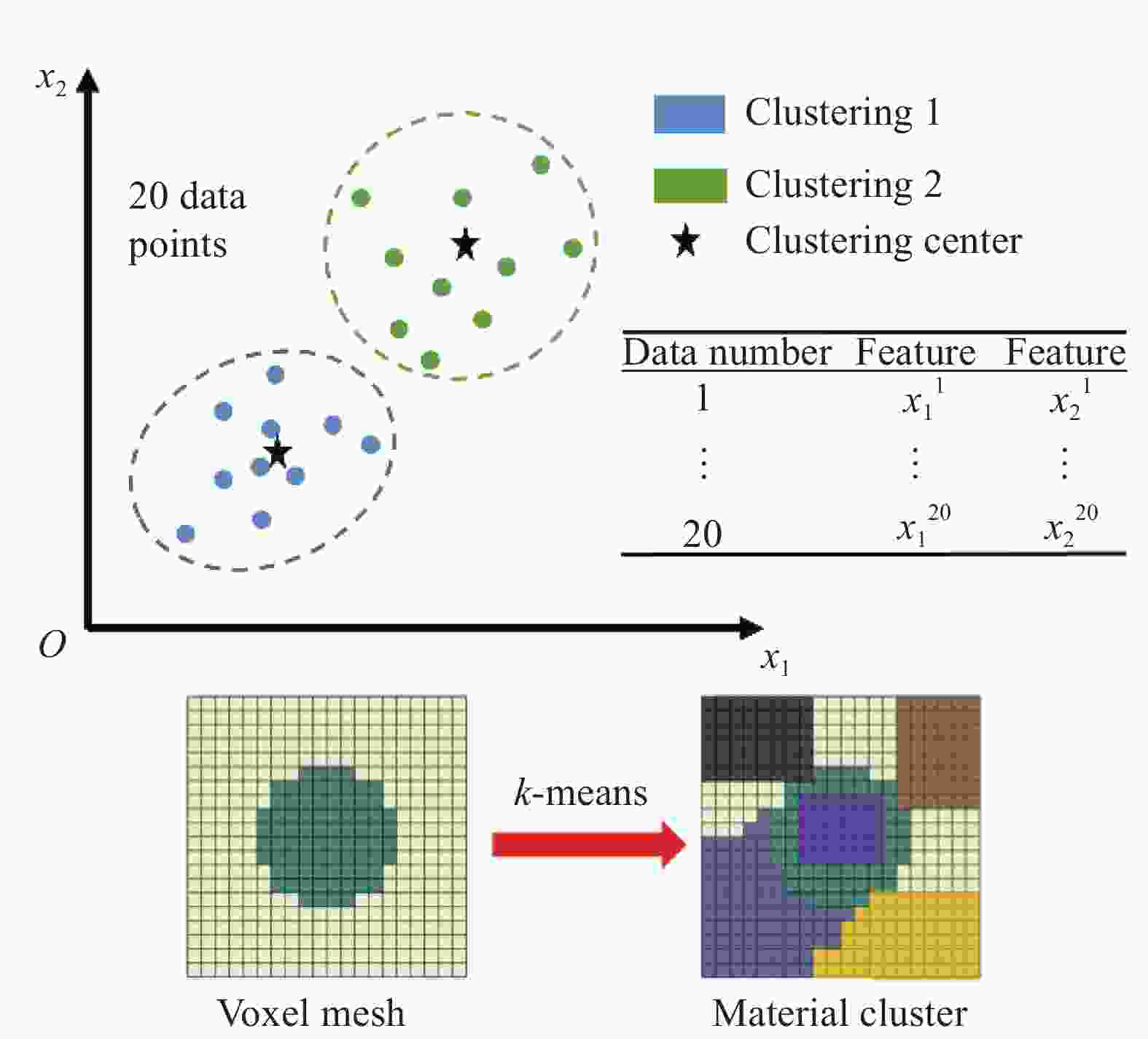
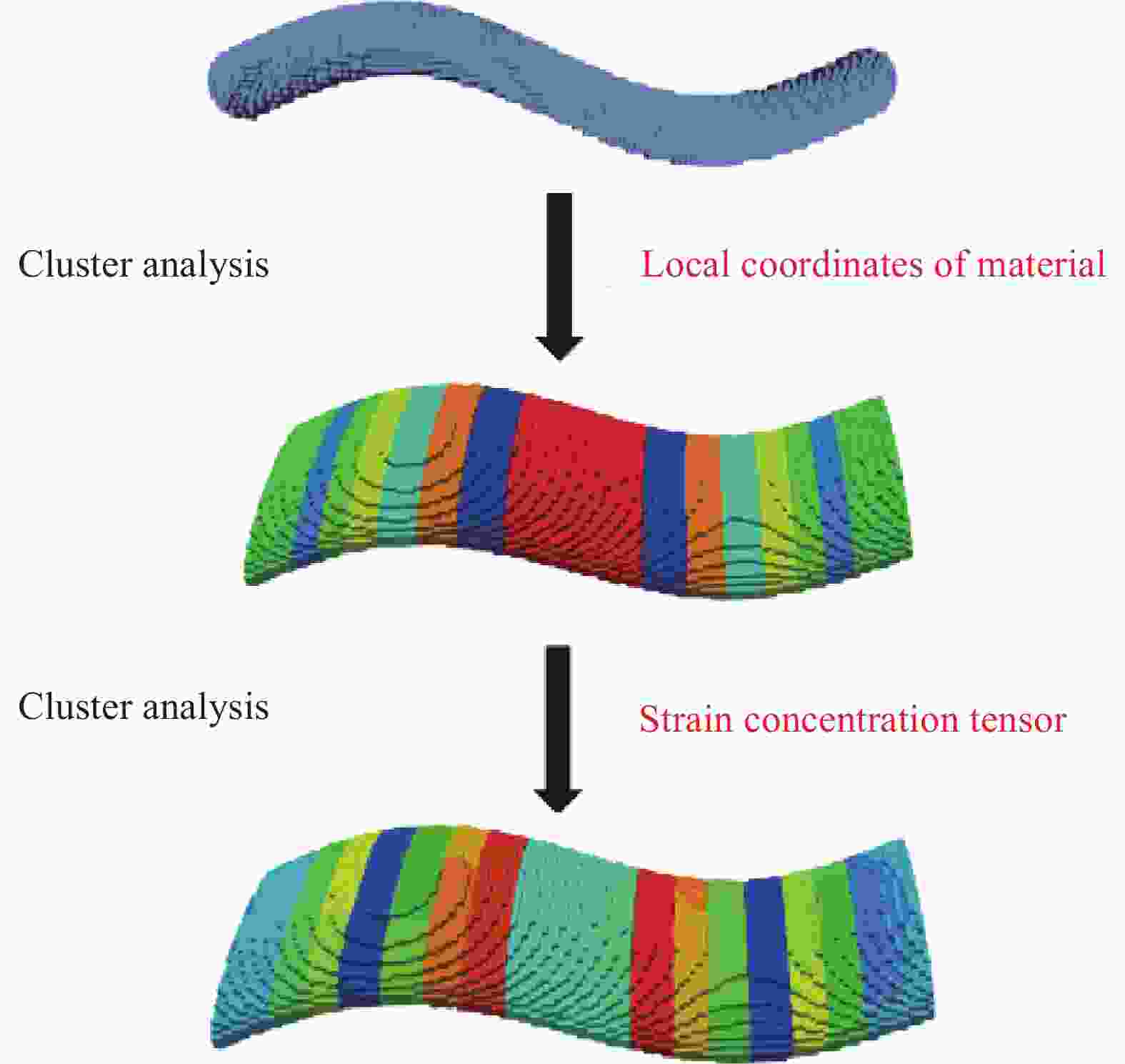
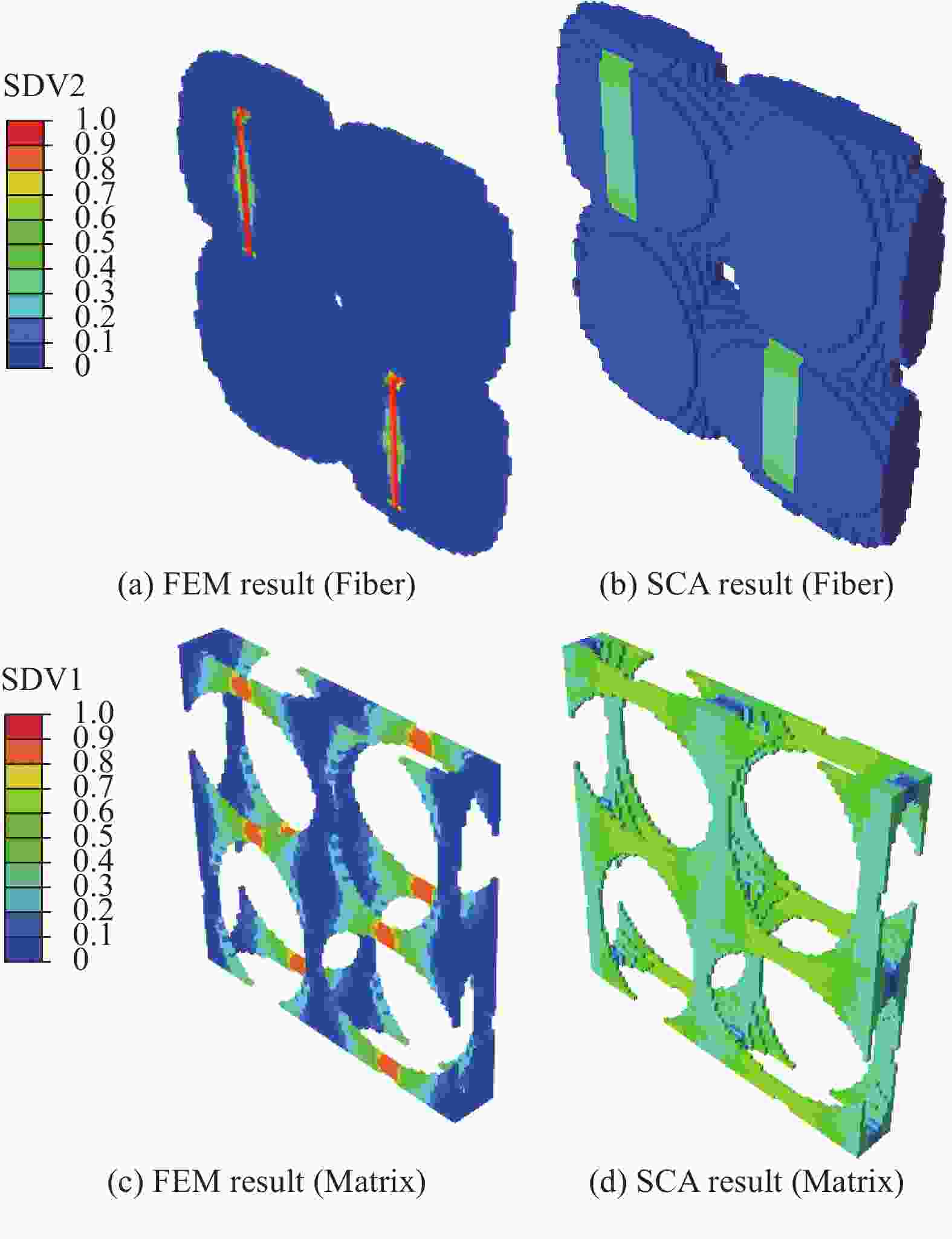
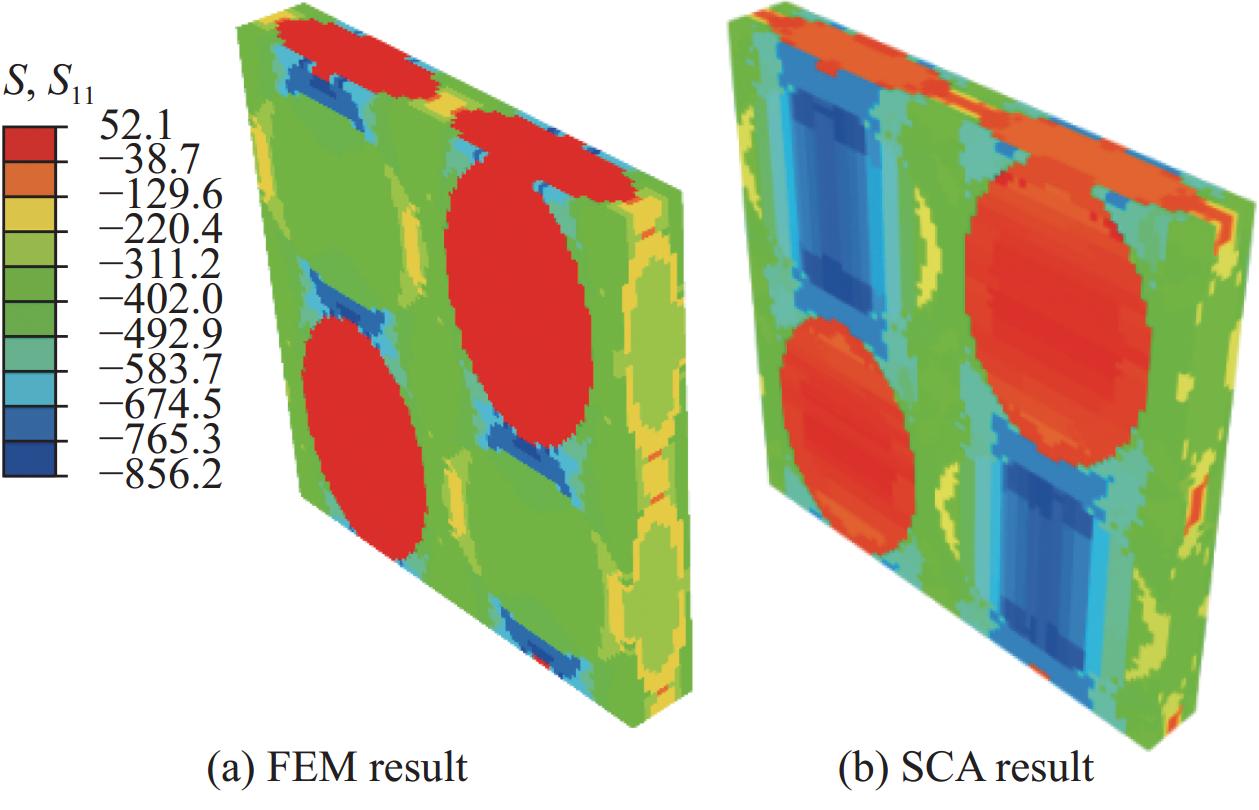
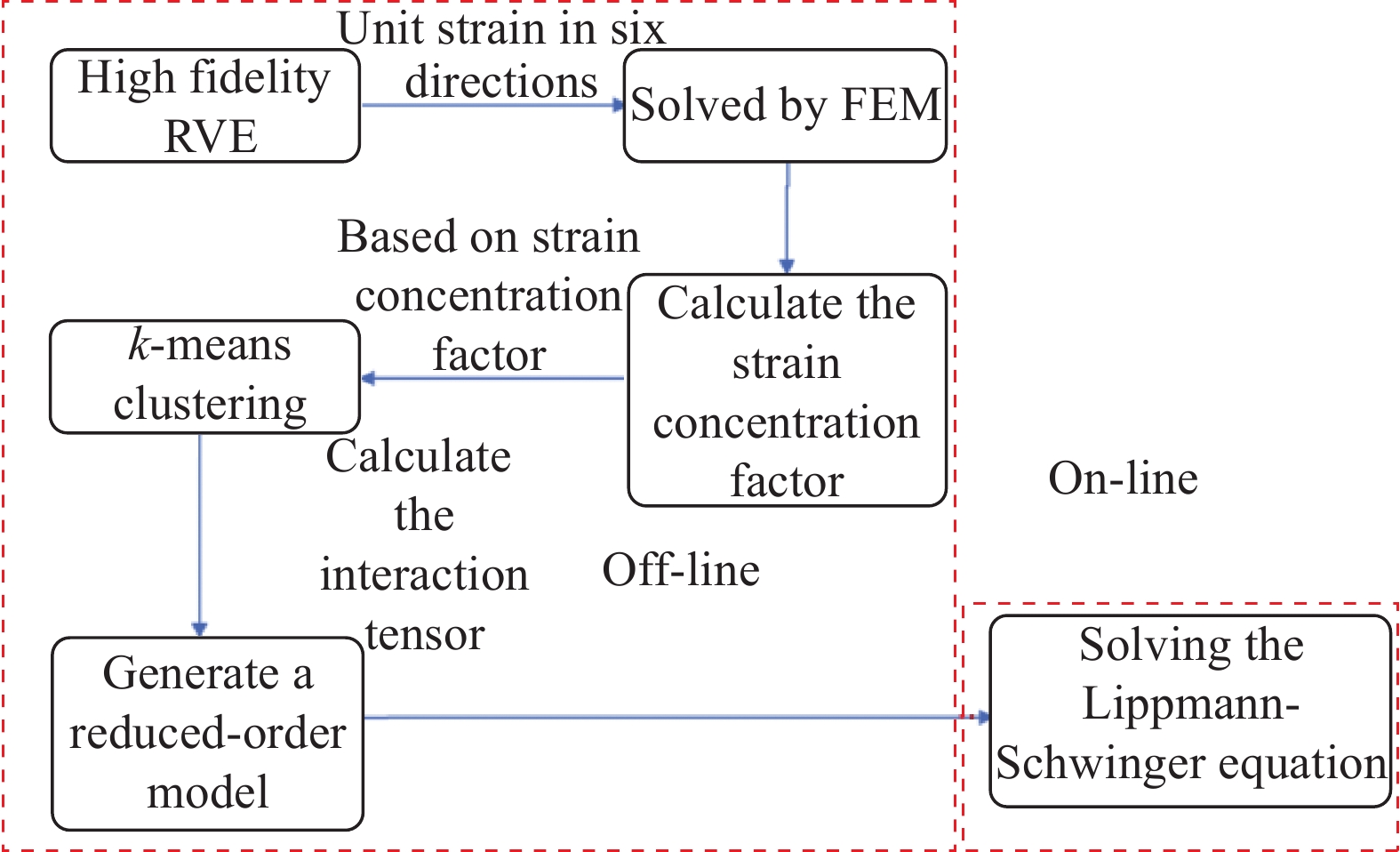
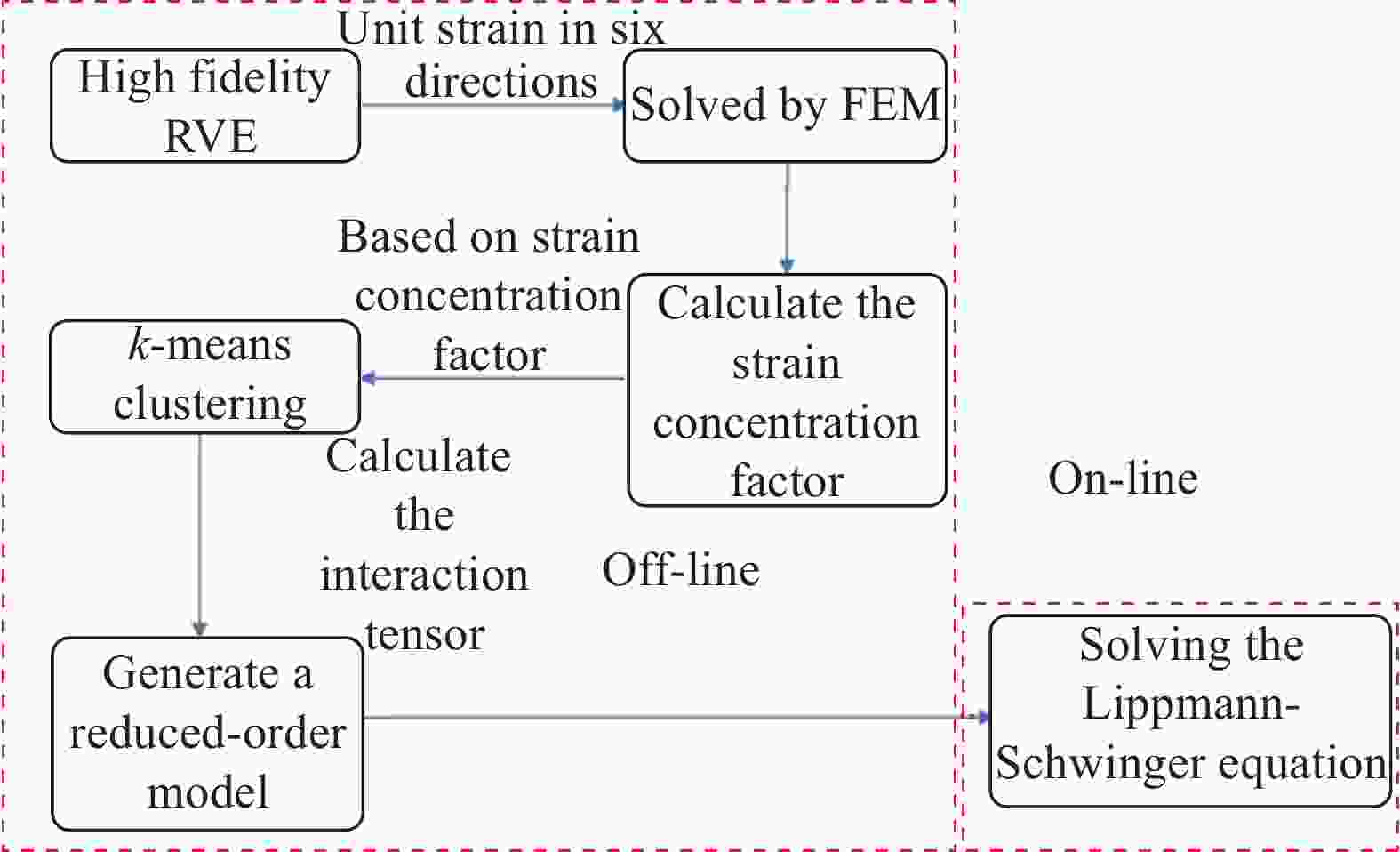
National Key Laboratory of Science and Technology on Advanced Composites in Special Environments, Harbin Institute of Technology, Harbin 150001, China

摘要

摘要: 本文利用自洽聚类分析(Self-consistent clustering analysis，SCA)方法研究了2D C/SiC在单轴压缩载荷下的渐进损伤行为，SCA方法通过应变集中张量对网格单元进行聚类，在不显著降低计算精度的前提下，大幅度降低了模型的自由度，使模型的计算效率得以提高。整个方法由离线和在线两个阶段组成：离线阶段，利用 k-means算法对高保真度的复合材料单胞进行分解、聚类并计算不同聚类间的相互作用张量，最终生成降阶模型；在线阶段，基于降阶模型求解离散的Lippmann-Schwinger方程组获取力学响应。将SCA方法应用于2D C/SiC压缩强度的预报，当聚类总数量为64时，与试验相比，压缩强度求解的计算精度与传统有限元相比降低了1%，但整体计算效率提升了34倍。当不考虑离线阶段花费的聚类时间，即事先已知材料的细观构型对其力学行为进行求解时，其一次在线计算的时间仅为6 s，计算效率比传统有限元提升了10 ⁴倍，在结构性能快速设计、结构状态快速预报等领域，有着广阔的应用前景。
- 2D C/SiC /
- 自洽聚类分析 /
- 渐进损伤 /
- 压缩强度 /
- 细观模型
Abstract: In this paper, the self-consistent clustering analysis (SCA) method was used to investigate the progressive damage behavior of 2D C/SiC under uniaxial compression load. The SCA method clusters the grid elements by strain concentration tensor, which greatly reduces the degree of freedom of the model and improves the computational efficiency of the model without significantly reducing the computational accuracy. The whole method consists of two stages: Offline and online. In the offline stage, the k-means algorithm was used to decompose and cluster the high-fidelity composite unit cells and calculate the interaction tensor between different clusters, and finally the reduced-order model was generated. At the online stage, the mechanical response was obtained by solving the discrete Lippmann-Schwinger equations based on the reduced-order model. The SCA method was applied to predict the compressive strength of 2D C/SiC. When the total number of clusters is 64, compared with the experiment, the calculation accuracy of the compressive strength solution is reduced by 1% compared with the traditional finite element method, but the overall calculation efficiency is improved by 34 times. When the clustering time spent in the offline stage is not considered, that is, the meso-structure of the material is known in advance to solve its mechanical behavior, the time of one-time online calculation is only 6 s, and the calculation efficiency is 10 ⁴ times higher than that of the traditional finite element method. It has broad application prospects in the fields of rapid design of structural performance and rapid prediction of structural state.
- 2D C/SiC /
- self-consistent clustering analysis /
- progressive damage /
- compressive strength /
- mesoscopic model

HTML全文

图 1 自洽聚类分析(SCA)计算流程图

RVE—Representative volume element; FEM—

Figure 1. Self-consistent clustering analysis (SCA) calculation flow chart

下载: 全尺寸图片幻灯片

图 2 聚类算法示意图

Figure 2. Clustering analysis diagram

下载: 全尺寸图片幻灯片

图 3 2D C/SiC复合材料的显微形貌

Figure 3. Microstructure of 2D C/SiC composites

下载: 全尺寸图片幻灯片

图 4 2D C/SiC的RVE

Figure 4. RVE of 2D C/SiC

下载: 全尺寸图片幻灯片

图 5 2D C/SiC纤维束的微观结构

Figure 5. Microstructure of 2D C/SiC fiber bundles

下载: 全尺寸图片幻灯片

图 6 2D C/SiC断裂表面的SEM图像

Figure 6. SEM image of 2D C/SiC fracture surface

下载: 全尺寸图片幻灯片

图 7 2D C/SiC试样的原位变形

Figure 7. In-situ deformation of 2D C/SiC specimen

下载: 全尺寸图片幻灯片

图 8 碳化硅基体聚类可视化结果

Figure 8. Visualization results of silicon carbide matrix clustering

下载: 全尺寸图片幻灯片

图 9 碳纤维束两次聚类示意图

Figure 9. Twice clustering diagram of carbon fiber bundles

下载: 全尺寸图片幻灯片

图 10 碳纤维束聚类可视化结果

Figure 10. Visualization results of carbon fiber bundle clustering

下载: 全尺寸图片幻灯片

图 11 2D C/SiC单轴压缩试验、FEM、SCA应力-应变曲线

Figure 11. Test, FEM, SCA stress-strain curves of 2D C/SiC under uniaxial compression load

下载: 全尺寸图片幻灯片

图 12 碳纤维束和碳化硅基体损伤变量

Figure 12. Damage variables of carbon fiber bundles and silicon carbide matrix

下载: 全尺寸图片幻灯片

图 13 2D C/SiC的应力云图

Figure 13. Stress cloud of 2D C/SiC

下载: 全尺寸图片幻灯片

表 1 代表性体积单元(RVE)几何参数

Table 1. Representative volume element (RVE) geometric parameters

Parameter	Mean value/mm
Long axis of fiber bundle 2 a	0.80
Short axis of fiber bundle 2 b	0.24
Unit cell side length c	1.85
Unit cell height	0.26

下载: 导出CSV

表 2 SiC基体和T300弹性常数

Table 2. SiC matrix and T300 elastic constants

Elastic constant	SiC	T300 carbon fiber
E ₁(compress)/GPa	300.00	130.00
E ₂/GPa	300.00	40.00
G ₁₂/GPa	120.00	24.00
ν ₁₂	0.25	0.26
ν ₂₃	0.25	0.44

下载: 导出CSV

表 3 纤维束弹性常数

Table 3. Elastic constant of fiber bundle

Parameter	E ₁/GPa	E ₂/GPa	G ₁₂/GPa	ν ₁₂	ν ₂₃
Value	173.38	66.80	40.06	0.25	0.43

下载: 导出CSV

表 4 有限元与SCA对2D C/SiC刚度性能的计算结果

Table 4. Results of FEM and SCA calculations for stiffness of 2D C/SiC

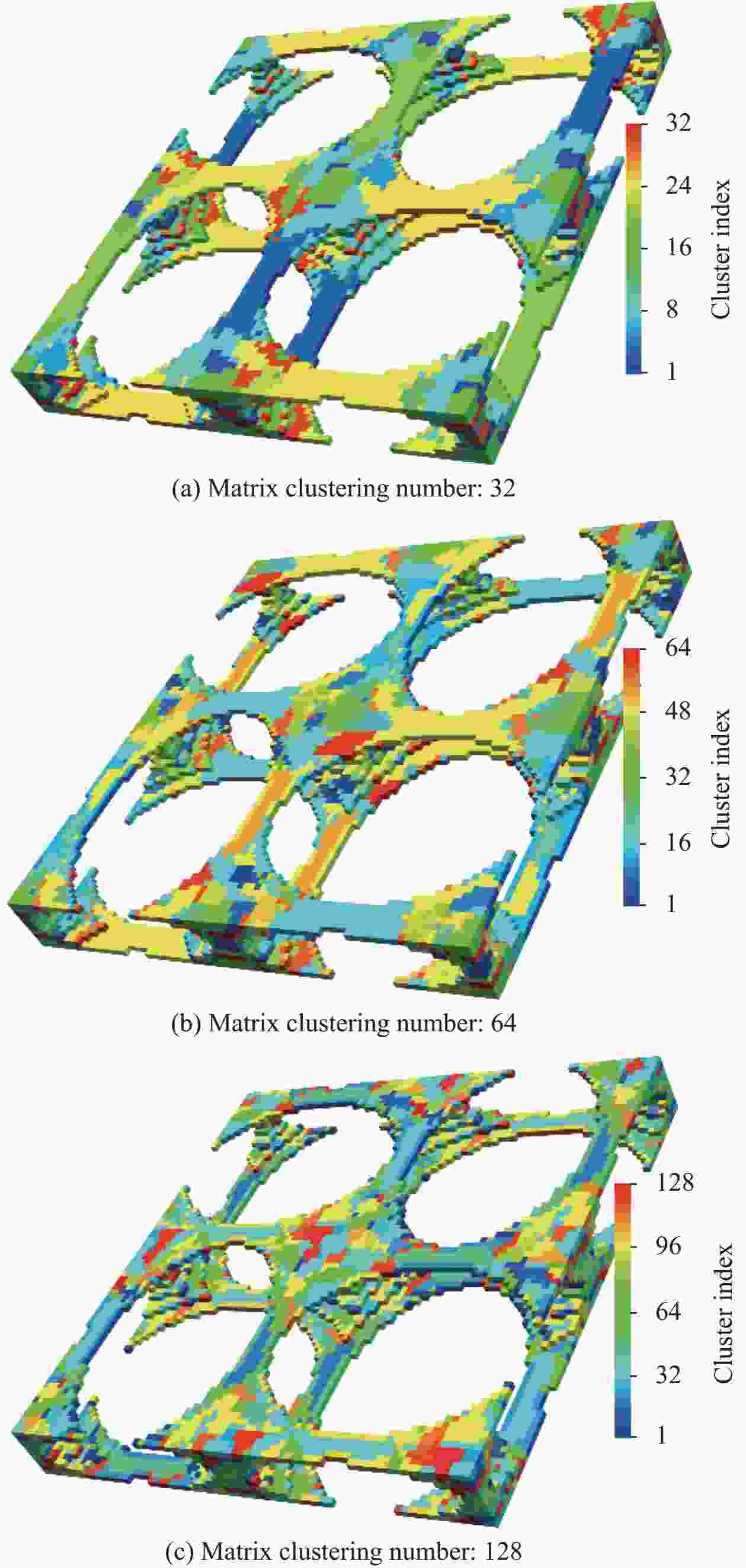
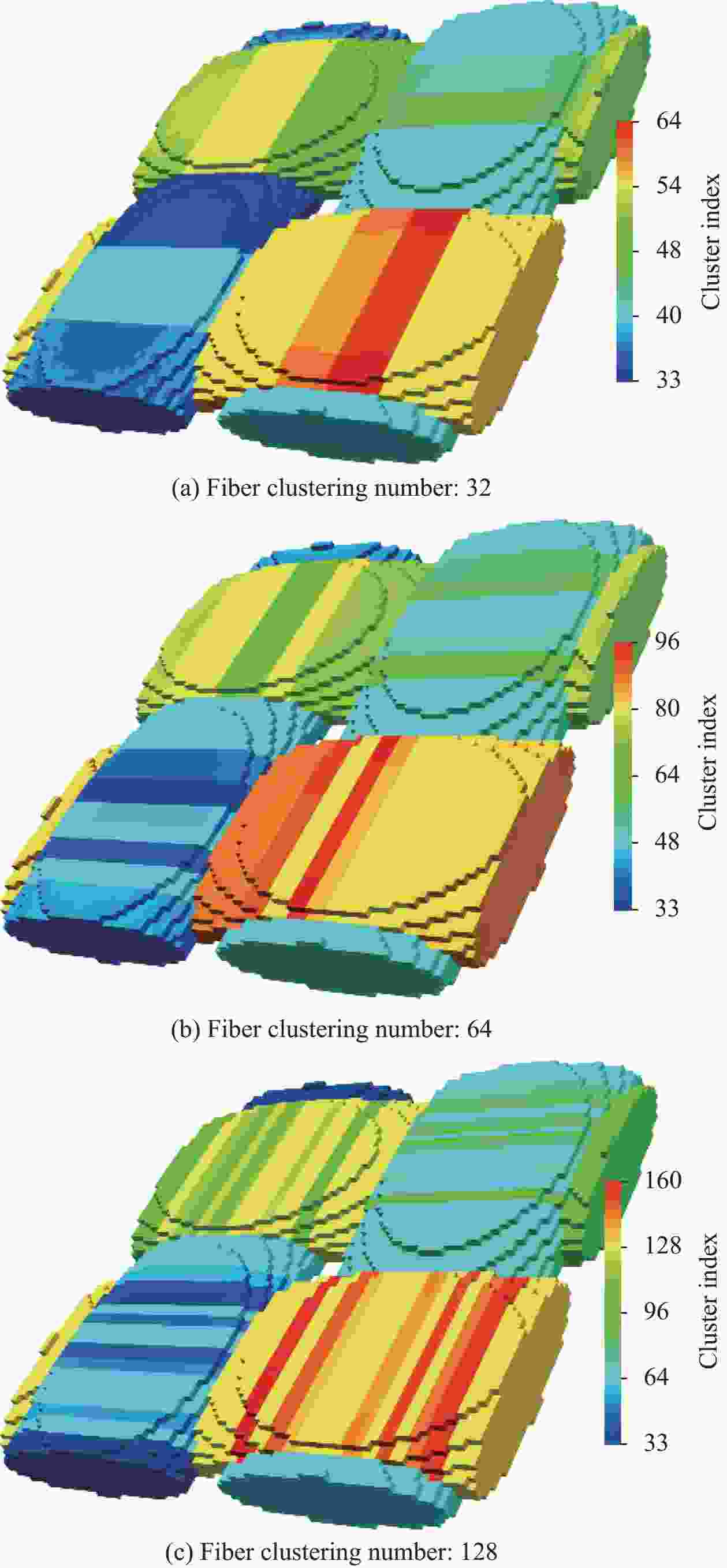
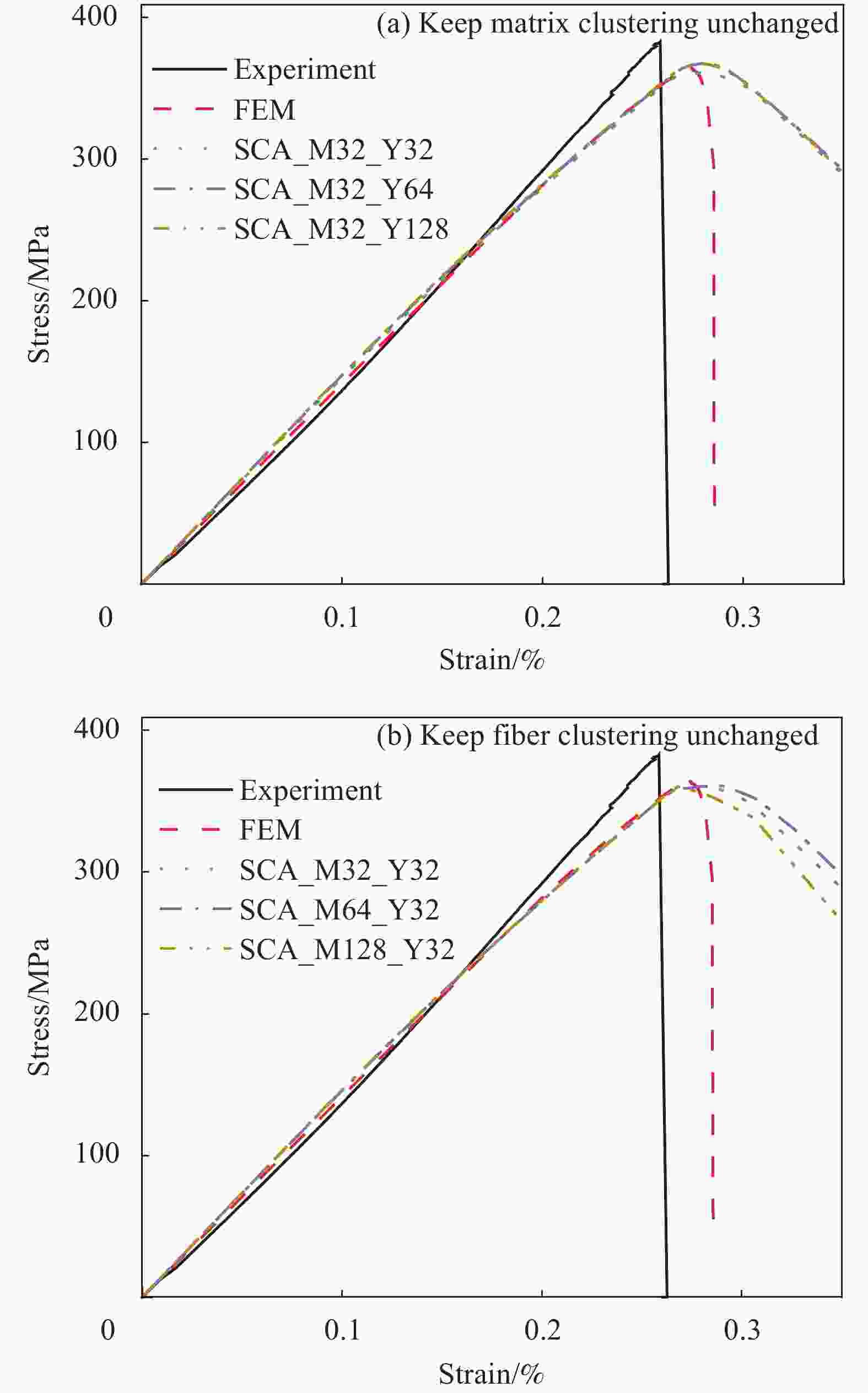
Method	Clustering combination	E ₁₁/GPa	G ₁₂/GPa
FEM	—	130.8	46.2
SCA	Matrix: 32, Yarn: 32	127.6(2.5%)	45.9(0.6%)
	Matrix: 64, Yarn: 32	127.7(2.4%)	46.0(0.4%)
	Matrix: 128, Yarn: 32	128.1(2.1%)	46.0(0.4%)
	Matrix: 32, Yarn: 64	128.6(1.7%)	46.0(0.4%)
	Matrix: 32, Yarn: 128	128.8(1.5%)	46.1(0.2%)

下载: 导出CSV

表 5 2D C/SiC试验、FEM、SCA计算时间与计算结果

Table 5. Calculation time and results of test, FEM and SCA for 2D C/SiC

Method	Clustering combination	Time/s		Strength/MPa	Error
Experiment	—	—		382.7	—
FEM	—	61200		364.4	4.8%
		Offline	Online
SCA	Matrix: 32, Yarn: 32	1800	6	361.0	5.7%
	Matrix: 64, Yarn: 32		11	367.9	3.9%
	Matrix: 128, Yarn: 32		25	367.4	4.0%
	Matrix: 32, Yarn: 64		11	361.3	5.6%
	Matrix: 32, Yarn: 128		29	360.7	5.7%

下载: 导出CSV

参考文献(30)

[1]	冯志海, 李俊宁, 田跃龙, 等. 航天先进复合材料研究进展[J]. 复合材料学报, 2022, 39(9): 4187-4195. FENG Zhihai, LI Junning, TIAN Yuelong, et al. Advances in advanced composites for aerospace[J]. Acta Materiae Compositae Sinica, 2022, 39(9): 4187-4195(in Chinese).
[2]	FAES J C, REZAEI A, VAN PAEPEGEM W, et al. Accuracy of 2D FE models for prediction of crack initiation in nested textile composites with inhomogeneous intra-yarn fiber volume fractions[J]. Composite Structures, 2016, 140: 11-20. doi: 10.1016/j.compstruct.2015.12.024
[3]	GUAN G, JIAO G, HUANG T. Experimental research on failure mechanism of a CVI-fabricated ceramic matrix composite under compression[J]. Key Engineering Materials, 2006, 326-328: 1841-1844. doi: 10.4028/www.scientific.net/KEM.326-328.1841
[4]	程相伟, 张大旭, 杜永龙, 等. 基于X射线CT原位试验的平纹SiC _f/SiC压缩损伤演化机理[J]. 上海交通大学学报, 2020, 54(10): 1074-1083. CHENG Xiangwei, ZHANG Daxu, DU Yonglong, et al. Compression damage evolution mechanism of flat SiC _f/SiC based on X-ray CT in-situ test[J]. Journal of Shanghai Jiao Tong University, 2020, 54(10): 1074-1083(in Chinese).
[5]	王奇志, 林慧星, 许赟泉. 二维编织陶瓷基复合材料偏轴拉伸力学性能预测[J]. 复合材料学报, 2018, 35(12): 3423-3432. WANG Qizhi, LIN Huixing, XU Yunquan. Prediction of off-axis tensile mechanical properties of two-dimensional braided ceramic matrix composites[J]. Acta MateriaeCompositae Sinica, 2018, 35(12): 3423-3432(in Chinese).
[6]	LIU G, ZHANG L, GUO L, et al. Multi-scale progressive failure simulation of 3D woven composites under uniaxial tension[J]. Composite Structures, 2019, 208: 233-243. doi: 10.1016/j.compstruct.2018.09.081
[7]	刘文台, 程坤, 周何乐子, 等. 针刺C/C复合材料面内拉伸强度预测[J]. 复合材料学报, 2023, 40(2): 1142-1153. LIU Wentai, CHENG Kun, ZHOU Helezi, et al. Prediction of in-plane tensile strength of needle-punched C/C composites[J]. Acta Materiae Compositae Sinica, 2023, 40(2): 1142-1153(in Chinese).
[8]	HE C, GAO J, LI H, et al. A data-driven self-consistent clustering analysis for the progressive damage behavior of 3D braided composites[J]. Composite Structures, 2020, 249: 112471. doi: 10.1016/j.compstruct.2020.112471
[9]	DVORAK G J, ZHANG J. Transformation field analysis of damage evolution in composite materials[J]. Journal of the Mechanics and Physics of Solids, 2001, 49(11): 2517-2541. doi: 10.1016/S0022-5096(01)00066-7
[10]	MICHEL J C, SUQUET P. Computational analysis of nonlinear composite structures using the nonuniform transformation field analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(48): 5477-5502.
[11]	DVORAK G J, BAHEI-EL-DIN Y A, WAFA A M. The modeling of inelastic composite materials with the transformation field analysis[J]. Modelling and Simulation in Materials Science and Engineering, 1994, 2(3A): 571. doi: 10.1088/0965-0393/2/3A/011
[12]	LIU Z, BESSA M A, LIU W K. Self-consistent clustering analysis: An efficient multi-scale scheme for inelastic heterogeneous materials[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 306: 319-341. doi: 10.1016/j.cma.2016.04.004
[13]	SCHNEIDER M. On the mathematical foundations of the self-consistent clustering analysis for non-linear materials at small strains[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 354: 783-801. doi: 10.1016/j.cma.2019.06.003
[14]	MOJUMDER S, GAO J, LIU W K. Self-consistent clustering analysis for modeling of theromelastic heterogeneous materials[J]. AIP Conference Proceedings, 2021, 2324(1): 030029.
[15]	BAI X, BESSA M A, MELRO A R, et al. High-fidelity micro-scale modeling of the thermo-visco-plastic behavior of carbon fiber polymer matrix composites[J]. Composite Structures, 2015, 134: 132-141. doi: 10.1016/j.compstruct.2015.08.047
[16]	MACQUEEN J. Some methods for classification and analysis of multivariate observations [C] //Proc. Fifth Berkeley Symposium on Mathematical Statistics and Probability. 1967: 281-297.
[17]	韩新星. 基于聚类分析的编织复合材料多尺度计算方法研究 [D]. 哈尔滨: 哈尔滨工业大学, 2020. HAN Xinxing. Study on multi-scale calculation method of braided composites based on cluster analysis [D]. Harbin: Harbin Institute of Technology, 2020(in Chinese).
[18]	LIU Z, KAFKA O L, YU C, et al. Data-driven self-consistent clustering analysis of heterogeneous materials with crystal plasticity [M]//OATE E, PERIC D, DE SOUZA NETO E, et al. Advances in computational plasticity: A book in honour of D Roger J Owen. Cham: Springer International Publishing, 2018: 221-242.
[19]	HASHIN Z. Failure criteria for unidirectional fiber composites[J]. Journal of Applied Mechanics, 1980, 47(2): 329-334. doi: 10.1115/1.3153664
[20]	LAPCZYK I, HURTADO J A. Progressive damage modeling in fiber-reinforced materials[J]. Composites Part A:Applied Science and Manufacturing, 2007, 38(11): 2333-2341. doi: 10.1016/j.compositesa.2007.01.017
[21]	徐凯. 2D C/C复合材料的力学性能研究 [D]. 哈尔滨: 哈尔滨工业大学, 2014. XU Kai. Study on the mechanical properties of 2D C/C composites [D]. Harbin: Harbin Institute of Technology, 2014(in Chinese).
[22]	ZHOU L, CHEN M, LIU C, et al. A multi-scale stochastic fracture model for characterizing the tensile behavior of 2D woven composites[J]. Composite Structures, 2018, 204: 536-547. doi: 10.1016/j.compstruct.2018.07.128
[23]	RAMAKRISHNAN N R, ARUNACHALAM V S. Effective elastic moduli of porous ceramic materials[J]. Journal of the American Ceramic Society, 1993, 76: 2745-2752. doi: 10.1111/j.1151-2916.1993.tb04011.x
[24]	梁仕飞, 矫桂琼. 2.5维自愈合C/SiC复合材料弹性性能预测[J]. 固体力学学报, 2013, 34(2): 181-187. doi: 10.19636/j.cnki.cjsm42-1250/o3.2013.02.010 LIANG Shifei, YOU Guiqiong. Prediction of elastic properties of 2.5D self-healing C/SiC composites[J]. Chinese Journal of Solid Mechanics, 2013, 34(2): 181-187(in Chinese). doi: 10.19636/j.cnki.cjsm42-1250/o3.2013.02.010
[25]	董士博. 碳/碳化硅复合材料的高温力学性能研究 [D]. 哈尔滨: 哈尔滨工业大学, 2021. DONG Shibo. Research on high temperature mechanical properties of carbon/silicon carbide composites [D]. Harbin: Harbin Institute of Technology, 2021(in Chinese).
[26]	WANG L, WU J, CHEN C, et al. Progressive failure analysis of 2D woven composites at the meso-micro scale[J]. Composite Structures, 2017, 178: 395-405. doi: 10.1016/j.compstruct.2017.07.023
[27]	BUDIANSKY B, FLECK N A. Compressive failure of fibre composites[J]. Journal of the Mechanics and Physics of Solids, 1993, 41(1): 183-211. doi: 10.1016/0022-5096(93)90068-Q
[28]	GUO-DONG F, JUN L, YU W, et al. The effect of yarn distortion on the mechanical properties of 3D four-directional braided composites[J]. Composites Part A: Applied Science and Manufacturing, 2009, 40(4): 343-350. doi: 10.1016/j.compositesa.2008.12.007
[29]	American Society of Testing Materials. Standard test method for monotonic compressive strength testing of continuous fiber-reinforced advanced ceramics with solid rectangular cross-section test specimens at ambient temperatures: ASTM C1358—2018 [S]. West Conshohocken: ASTM International, 2018.
[30]	纤维增强塑料压缩性能试验方法: GB/T 1448—2005 [S]. 北京: 中国标准出版社, 2005. Test method for compression performance of fiber reinforced plastics: GB/T 1448—2005 [S]. Beijing: China Standard Press, 2005(in Chinese).