Preparation and properties of silicone polymer-graphene oxide reinforced glass fiber/epoxy resin composites
-
摘要:
本文将不同比例的硅聚物-氧化石墨烯(Silicon polymer-graphene oxide，PSOL-GO)作为纳米填料来改性玻璃纤维/环氧树脂(Glass fiber/epoxy resin，GF/EP)复合材料，制备得到不同PSOL-GO含量的复合材料，采用观察形貌、测量接触角、红外分析、力学性能、动态力学分析(DMA)等测试方法分析了环氧复合材料的微观结构和增强机制。实验结果表明：PSOL-GO质量比为1∶0.1时PSOL-GO@GF/EP复合材料力学性能最佳：改性后的GF/EP复合材料与纯GF/EP复合材料相比其层间剪切强度提升了13.19%；其弯曲强度提升了33.12%；其拉伸强度提升了35.32%；其冲击强度提升了16.95%。添加质量比为1∶0.1的PSOL-GO可使GF/EP复合材料的玻璃化转变温度(Tg)提高7.1℃，使其耐热性有所提高。引入PSOL-GO纳米填料后的环氧树脂对玻璃纤维的润湿性更佳，同时可以填补纯的GF/EP复合材料自身空隙，增强复合材料的性能。
Abstract:In this study, different proportions of silicon polymer-graphene oxide (PSOL-GO) were used as nano-fillers to modify glass fiber/epoxy resin (GF/EP) composites, the composites with different PSOL-GO contents were prepared. The microstructure and strengthening mechanism of epoxy composites were analyzed by observing morphology, measuring contact angle, infrared analysis, mechanical properties and dynamic mechanical analysis (DMA). The experimental results show that the mechanical properties of PSOL-GO@GF/EP composites are the best when the mass ratio of PSOL-GO is 1∶0.1: The interlayer shear strength of modified GF/EP composites is 13.19% higher than that of pure GF/EP composites; Its bending strength increased by 33.12%; Its tensile strength increased by 35.32%; Its impact strength increased by 16.95%. The glass transition temperature (Tg) of GF/EP composites was increased by 7.1℃ by adding PSOL-GO at 1∶0.1 mass ratio, and the heat resistance of GF/EP composites was improved. The epoxy resin with the introduction of PSOL-GO nano-filler has better wettability to glass fibers, and can fill the gap of pure GF/EP composite itself to enhance the performance of the composite materials.
-
Keywords:
- graphene oxide /
- epoxy resin /
- glass fibers /
- composite materials /
- fillers /
- mechanical properties
-
纤维复合材料具有低密度、高比强度和高比刚度等特点，使其在工业和工程材料中具有广阔的应用前景[1-8]。迄今为止，表现出优异力学性能的纤维复合材料很多是由环氧树脂为基体制成的[9-12]。玻璃纤维/环氧树脂(Glass fiber/epoxy resin，GF/EP)复合材料因其质轻、高比强度、高比模量、耐腐蚀等优点而被广泛应用于飞机、空间飞行器、汽车等领域[13-16]。随着科技的进步，对于纤维增强性能有更高和更创新的应用要求[17-21]。玻璃纤维/环氧树脂复合材料制备工艺简单，其开发目前处于相对成熟的阶段。但其垂直于纤维平面的力学性能较弱，复合材料的分层抵抗能力是目前需要改进的方向[22-25]。优化界面微观结构是有效的改善措施，该方案在纤维表面或树脂基体上引入纳米级增强材料，从而提高复合材料的性能[26-27]。氧化石墨烯(Graphene oxide，GO)因其表面含有羟基、羧基等官能团，能与环氧树脂形成稳定的醚键和酯键。而硅聚物(Silicon polymer，PSOL)表面含有丰富的羟基，与环氧树脂上的环氧基团发生开环反应形成醚键。将硅聚物负载到氧化石墨烯表面，可以提高其在环氧树脂中的分散性，解决无机纳米粒子的团聚问题[28-29]。
本文采用硅聚物-氧化石墨烯(PSOL-GO)作为纳米填料来改性GF/EP复合材料，通过调整PSOL-GO的比例制备得到不同含量的复合材料，探究了不同比例的PSOL-GO对环氧复合材料层间剪切性能、弯曲性能、拉伸性能、冲击性能及动态力学性能的影响，研究分析了环氧复合材料的微观结构和增强机制。本文采用PSOL-GO纳米填料有效提高了GF/EP复合材料强度的同时，还提高了其韧性，同时复合材料的耐热性也不降低。
1. 实验方法
1.1 原材料
氢氧化钠(分析纯)，国药集团化学试剂有限公司。二氧化硅，63~210 μm，日本关东化学KANTO公司。四氢呋喃(分析纯)、氯化钠(分析纯)，上海联化试剂有限公司。无水硫酸镁(分析纯)，西陇科学股份有限公司。石墨，5 μm，青岛金石莱石墨厂。高锰酸钾(分析纯)、硝酸钠(分析纯)，嘉兴永宏化工有限公司。浓硫酸(98%，分析纯)，杭州萧山化学试剂厂。双氧水(30%)，无锡市佳妮化工有限公司。玻璃纤维(Glass fiber，GF，200 g/cm3)，嘉兴隆鑫有限公司。双酚A型环氧树脂(E-51，环氧值0.51)，海宁海龙化工有限公司。固化剂为593固化剂，购于天津威马科技有限公司。脱模剂(922 T)，东莞市麦克斯复合材料有限公司。
1.2 PSOL及GO的制备
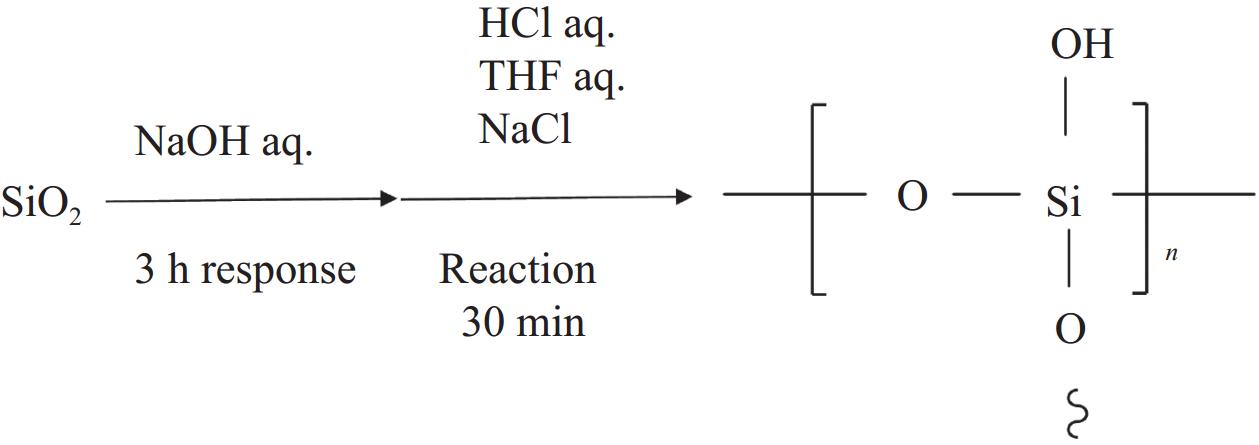
准备固体氢氧化钠1.0 g、去离子水60 mL放入500 mL塑料杯中，超声振荡待溶液充分溶解后加入二氧化硅3.0 g，反应3 h后加入60 mL盐酸、180 mL四氢呋喃(THF)、36 g NaCl，反应30 min，将反应溶液移入分液漏斗中，静置分层，将上层有机溶剂移入烧杯，加入无水硫酸镁，进行脱水处理，抽滤、蒸馏后制得硅聚物。PSOL的制备机制可以解释为二氧化硅分子转变成硅聚物的过程，PSOL具体制备机制见图1。氧化石墨烯的制备采用的是改进后的Hummers法，具体参考之前的工作[30]。
![]()
图 1 硅聚物(PSOL)的制备机制THF—TetrahydrofuranFigure 1. Preparation mechanism of silicon polymer (PSOL)1.3 PSOL-GO的制备
称取一定量的氧化石墨烯加入四氢呋喃，配制得0.2 mg/mL的氧化石墨烯溶液，超声30 min，移入250 mL的三颈烧瓶中，加入磁子，放入水浴锅中低速搅拌同时滴加PSOL溶液，将水浴锅升温至60℃反应4 h，制得PSOL-GO溶液。
1.4 PSOL-GO@GF/EP复合材料的制备
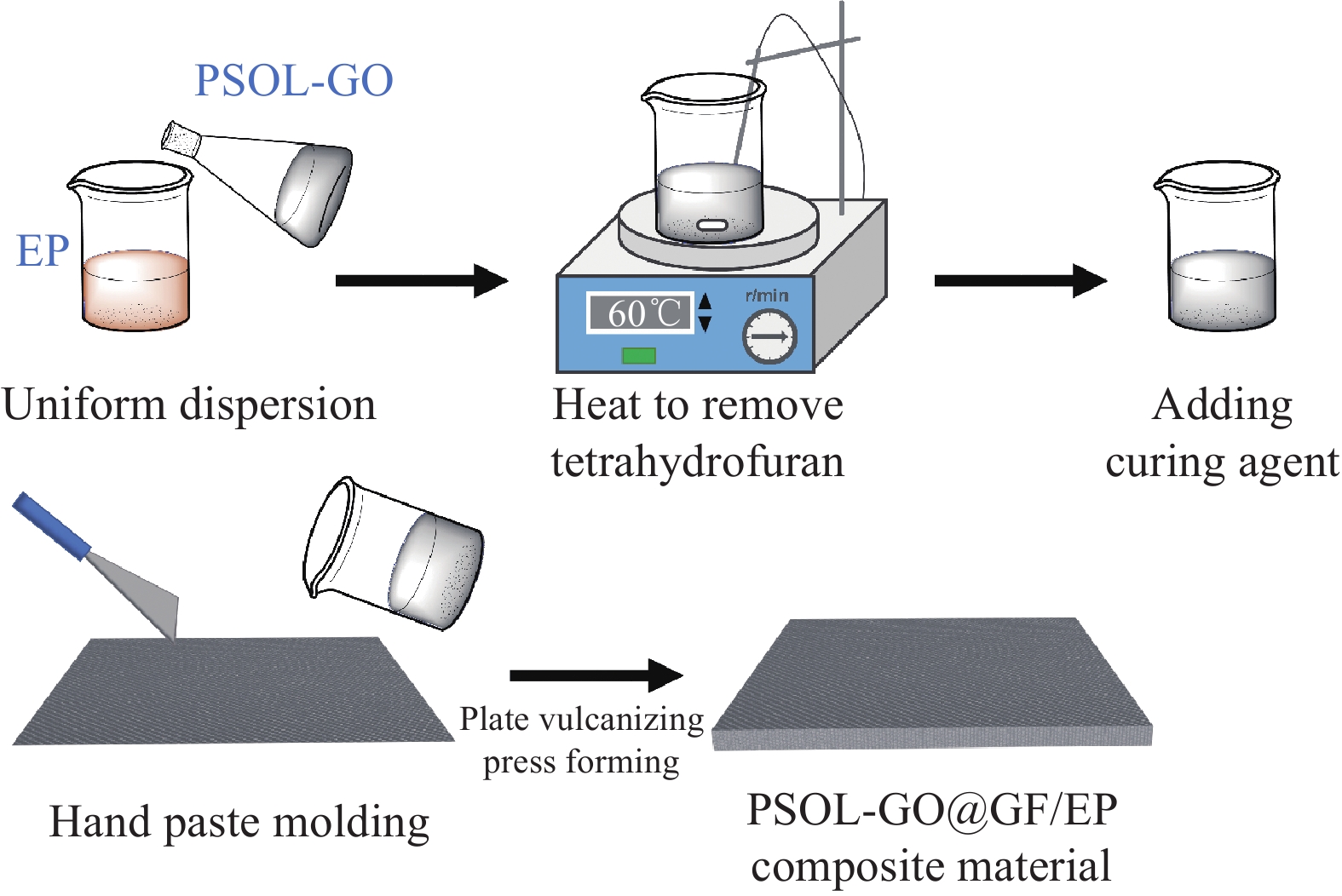
将裁切好的GF织物置于烘箱(XMTD-8222，上海精宏实验设备有限公司)中，80℃，烘干2 h。用磁力搅拌器(DF-101S，杭州明远有限公司)将不同比例的PSOL-GO均匀分散在环氧基体中，加热体系除去体系中的四氢呋喃溶剂，加入固化剂，充分搅拌，用手糊成型技术将树脂混合物均匀涂敷在玻璃纤维织物层中，平板硫化机(XLB-D，湖州顺力橡胶机械有限公司)压实，5 MPa，压制24 h。制得PSOL-GO@GF/EP复合材料，具体流程见图2。
![]()
图 2 PSOL-氧化石墨烯(GO)@玻璃纤维/环氧树脂(GF/EP)复合材料的制备流程图Figure 2. Flowchart of preparation of PSOL-graphene oxide (GO)@glass fiber/epoxy resin (GF/EP) composites1.5 测试与表征
傅里叶红外光谱(FTIR)由德国布鲁克公司的V70红外光谱仪测得，扫描范围为500~
4000 cm−1，分辨率为4 cm−1。采用日本日立公司S-4800场发射扫描电子显微镜(FE-SEM)观察GO、PSOL及PSOL-GO复合材料的表面形貌及试样的层间剥离面微观形貌。按照ASTM D2344[31]采用日本岛津AG-X Plus万能材料试验机对试样进行层间剪切测试。按照GB/T 1449—2005[32]采用日本岛津AG-X Plus万能材料试验机对PSOL-GO@GF/EP层压复合材料进行弯曲测试。按照GB/T 2567—2021[33]采用日本岛津AG-X Plus万能材料试验机对试样进行拉伸测试。按照GB/T 2567—2021[33]对复合材料的冲击性能进行测试。采用深圳三思纵横科技PTM7000-B摆锤式冲击试验机对试样进行冲击测。采用美国TA公司Q850动态热机械分析仪分析试样的动态热力学行为，频率为1 Hz，温度区间为35~135℃，升温速率为2℃/min，试样尺寸为30 mm×6 mm×2 mm。采用德国Kruss DSA30接触角测量分析仪测试PSOL-GO不同添加含量的环氧树脂和玻璃纤维表面的接触角。GF/EP复合材料中复合材料密度及纤维体积分数采用以下方式计算：记录12片玻璃纤维织物的质量(m1)与面积(S1)，单位面积中玻璃纤维质量m的计算公式为m=m1S1 (1) 将GF/EP复合材料切割成矩形，称量该矩形的质量(m2)，根据阿基米德原理计算得到样条的体积(V)，复合材料的密度的计算公式为
ρ=m2V (2) 量取矩形的长和宽，计算得到纤维的面积(S2)，已知玻璃纤维密度ρGF为2.4 g/cm3， GF/EP复合材料中玻璃纤维的体积v计算公式为
v=S2mρGF (3) GF/EP复合材料中GF的体积分数w计算公式为
w=vV×100% (4) 2. 结果与讨论
2.1 PSOL-GO的形貌和结构特征
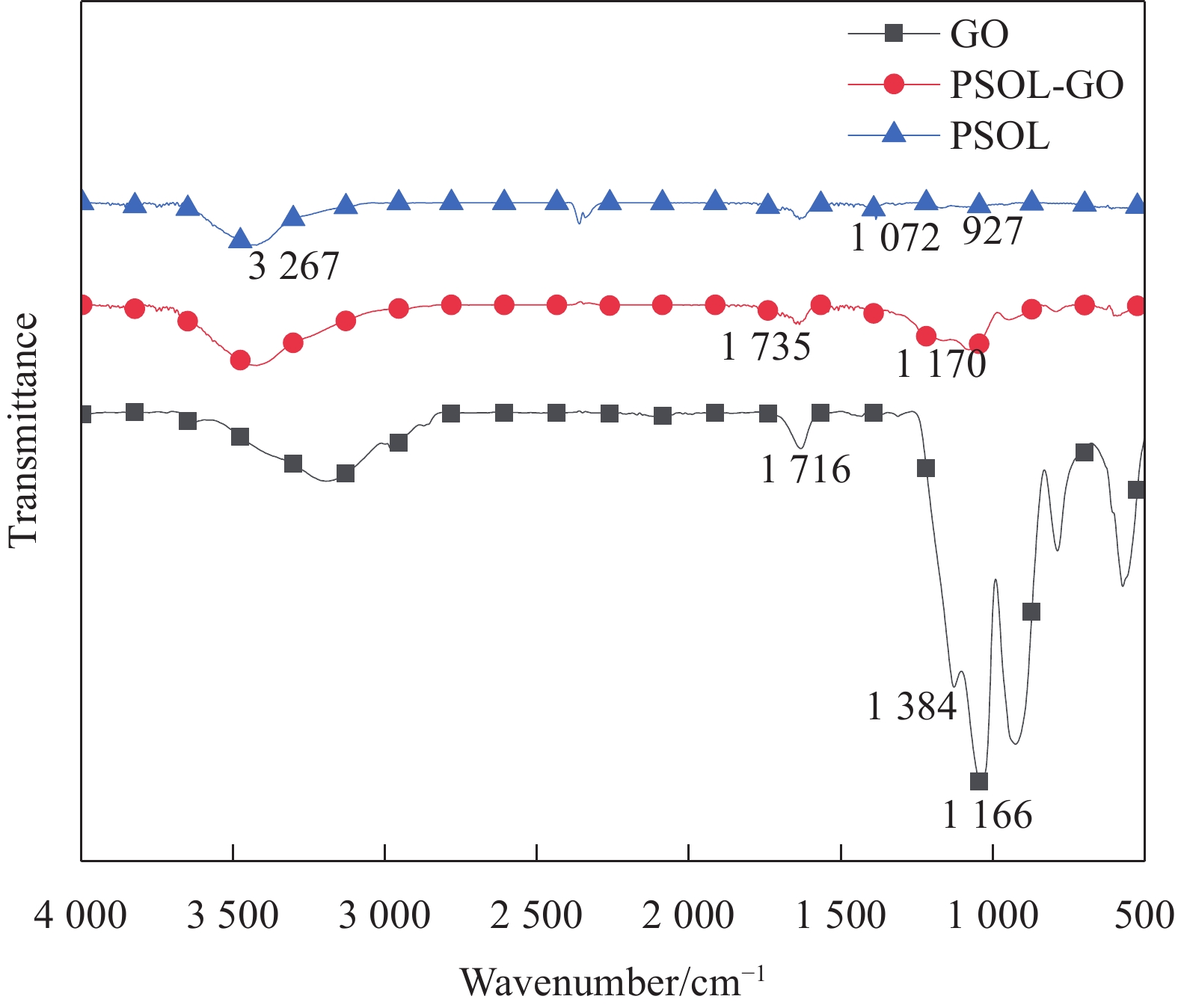
采用场发射扫描电子显微镜(FE-SEM)观察GO、PSOL及PSOL-GO试样的表面形貌。图3(a)为PSOL的SEM图像，PSOL是均相体系。图3(b)为GO的SEM图像，GO呈褶皱形态。图3(c)为PSOL-GO的SEM图像，可以看出有细小褶皱。采用FTIR表征GO、PSOL及PSOL-GO试样内部的成键方式。硅聚物在
3267 cm−1、927 cm−1处为Si—OH的振动峰，在1072 cm−1处为分子链中的Si—O的伸缩振动峰，如图4所示。GO在1716 cm−1、1624 cm−1为—COOH的C=O振动峰，1384 cm−1、1166 cm−1为C—O伸缩振动峰。PSOL-GO的红外谱图具备GO及PSOL的吸收峰趋势，在1735 cm−1为酯键的C=O的伸缩振动峰，在1170 cm−1处为酯键中的C—O伸缩振动峰。![]()
图 3 PSOL (a)、氧化石墨烯(GO) (b)、硅聚物-氧化石墨烯(PSOL-GO) (c)的FE-SEM图像Figure 3. FE-SEM images of PSOL (a), graphene oxide (GO) (b) and silicon polymer-graphene oxide (PSOL-GO) (c)2.2 复合材料的密度
PSOL-GO@GF/EP复合材料中纤维的体积分数和复合材料的密度通过1.5节中计算可得。PSOL-GO@GF/EP复合材料体积分数为63.4vol%。纤维体积含量的变化主要是由其织造的结构致使多余的树脂基体外延造成的。同样计算可知，PSOL-GO@GF/EP复合材料的密度为1.77 g/cm3。
2.3 PSOL-GO@GF/EP复合材料静态力学性能
2.3.1 PSOL-GO@GF/EP复合材料的层间剪切性能
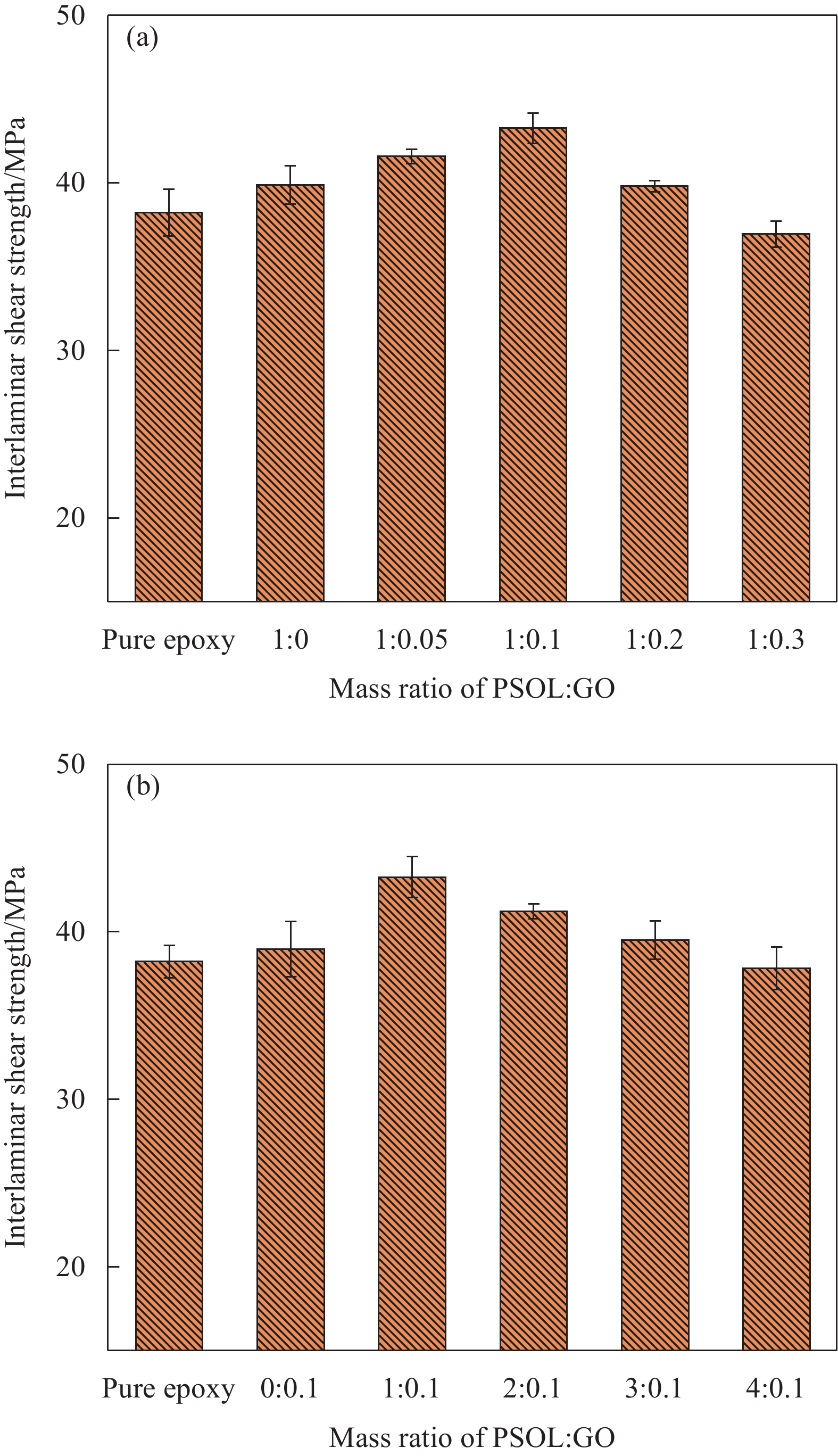
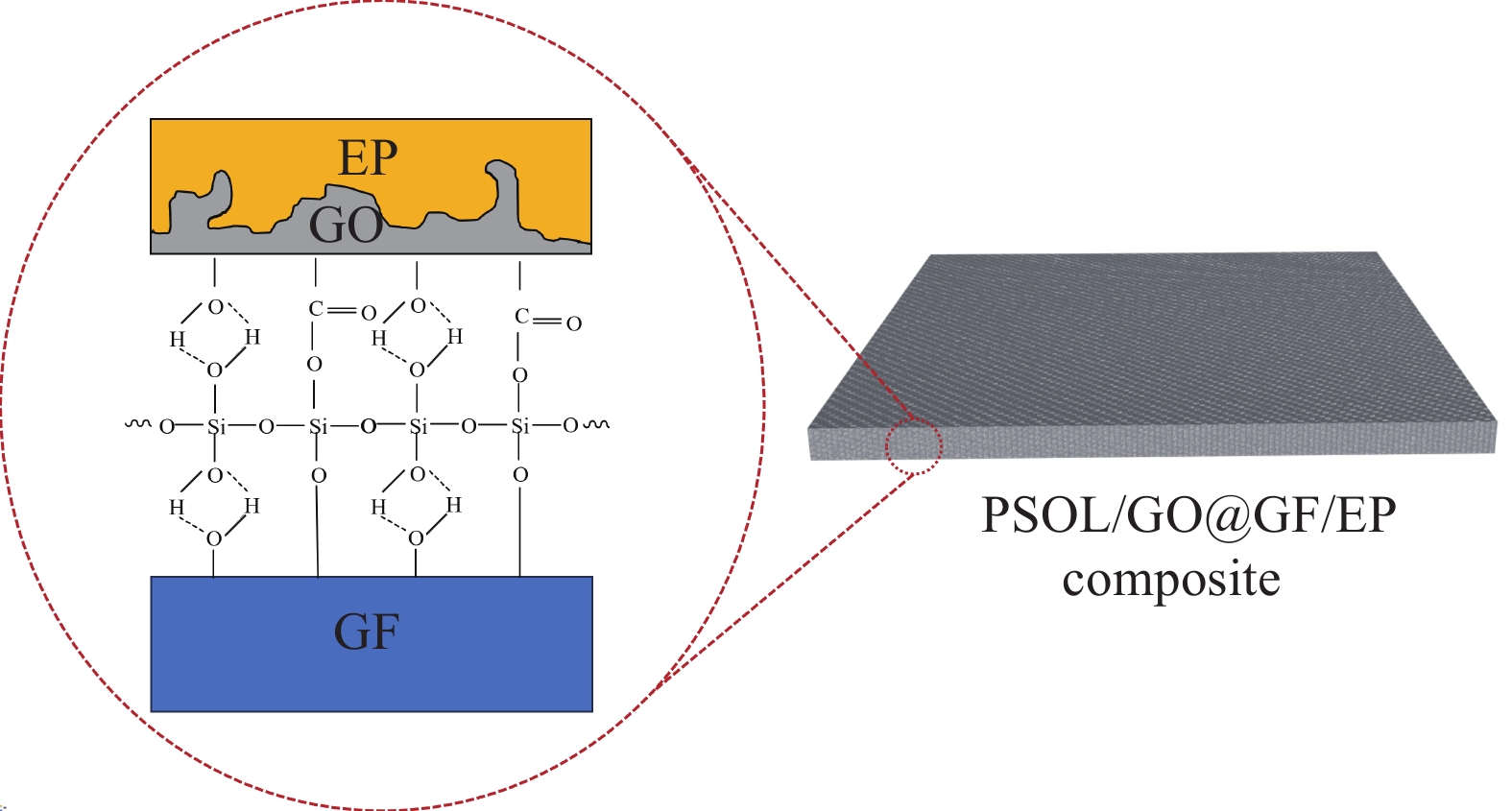
GO可以增强GF/EP复合材料的层间剪切强度[30]，将其按适当的比例加入复合材料中，可能会进一步改善PSOL-GO@GF/EP复合材料的层间剪切强度，不同比例的GO对复合材料的层间剪切性能的影响见图5(a)。PSOL可以增强GF/EP复合材料的层间剪切强度[34]，将其按恰当的比例加入复合材料中，可能会进一步增强PSOL-GO@GF/EP复合材料的层间剪切效果，不同比例的PSOL对复合材料的层间剪切性能的影响见图5(b)。当PSOL与GO质量比为1∶0.1时，PSOL-GO@GF/EP复合材料层间剪切效果最佳，此时的层间剪切强度为43.26 MPa，与纯GF/EP复合材料相比，有13.19%的提高。PSOL-GO@GF/EP复合材料增强机制见图6。PSOL上的羟基与环氧树脂上的环氧基团发生开环反应形成醚键；GO上的羟基和羧基与环氧树脂形成醚键和酯键，同时，GO的褶皱形貌能与环氧树脂形成机械互锁；PSOL上的羟基与GO上的羧基和羟基形成酯键和氢键；PSOL上的羟基与GF表面的羟基产生醚键和氢键，从而改善GF与EP的界面，提升复合材料的力学性能。
![]()
图 5 不同质量比的PSOL与GO对PSOL-GO@GF/EP复合材料层间剪切性能的影响Figure 5. Effects of different mass ratios PSOL and GO on the interlaminar shear properties of PSOL-GO@GF/EP composites![]()
图 6 PSOL-GO@GF/EP复合材料增强机制Figure 6. Strengthening mechanism of PSOL-GO@GF/EP composites复合材料层间剪切性能的主要影响因素有以下3点：纤维/环氧的界面结合情况、环氧树脂的性能和纳米填料的分散效果。图7为不同比例的PSOL-GO的复合材料的断面SEM图像。图7(a)为纯的GF/EP复合材料的层间剥离面，从图中可以看出，纯的GF/EP复合材料的剥离面光滑且表面几乎没有环氧碎屑的残留，同时观察到玻璃纤维与环氧树脂的结合不紧密，部分界面上出现了很大的空隙，这表明玻璃纤维与环氧树脂的界面存在着一定的缺陷。但随着PSOL-GO含量的增加，与纯的GF/EP复合材料相比，发现在GF/EP复合材料的剥离面上玻璃纤维表面粘附有环氧树脂，玻璃纤维和环氧树脂的粘接相对紧密，几乎没有空隙，GF与EP界面处也存在PSOL-GO，见图7(b)。这表明，PSOL-GO可以提高玻璃纤维和环氧树脂的界面强度，从而提高复合材料的力学性能。随着GO含量的提高，玻璃纤维和环氧树脂之间的界面出现空隙，二者界面结合性变差见图7(c)。从图7(d)中得知随着PSOL含量的增加，玻纤/环氧复合材料的界面相容性变差，环氧树脂中存在许多空隙，同时纤维表面有大面积的环氧树脂。这说明在GF/EP中，PSOL-GO超过一定比例，PSOL-GO分散程度逐渐变得不均匀，会产生一些聚集，导致GF/EP复合材料界面结合破坏，使其层间剪切性能下降。
![]()
图 7 PSOL-GO@GF/EP复合材料剥离表面的SEM图像：(a)纯的玻璃纤维/环氧树脂(GF/EP)复合材料；(b) PSOL∶GO=1∶0.1；(c) PSOL∶GO=1∶0.3；(d) PSOL∶GO=4∶0.1Figure 7. SEM images of the peeling surface of PSOL-GO@GF/EP composites: (a) Pure glass fiber/epoxy resin (GF/EP) composites; (b) PSOL∶GO=1∶0.1; (c) PSOL∶GO=1∶0.3; (d) PSOL∶GO=4∶0.1PSOL-GO具有良好的分散性，在固化过程中，它们倾向于随着树脂的流向迁移到GF/EP界面区。在这里，PSOL-GO也参与了与环氧树脂的交联反应，PSOL中的羟基、GO中的羧基与环氧树脂中的环氧基团发生反应，分别形成醚键和酯键。PSOL-GO分散良好，有效地阻碍了平行或垂直于纤维/基体界面的应力集中和裂纹扩展。这反过来又提高了对基体开裂的抵抗能力，有助于提高层间剪切性能。
实验准备了纯环氧材料和力学性能相对最佳的PSOL/GO质量比为1∶0.1的PSOL-GO@GF/EP复合材料。测试了这两种材料与EP树脂胶液的接触角，对比分析浸润性，如图8所示，EP胶液在纯环氧树脂上的接触角为109.3°，在复合材料上的接触角为83.5°，接触角越小润湿性越好，这说明PSOL-GO的加入有效改善了环氧树脂对玻璃纤维的润湿性。
![]()
图 8 PSOL-GO对玻璃纤维润湿性的影：(a)纯环氧；(b) PSOL∶GO=1∶0.1Figure 8. Influence of PSOL-GO on wettability of glass fiber: (a) Pure epoxy; (b) PSOL∶GO=1∶0.12.3.2 PSOL-GO@GF/EP复合材料的弯曲性能
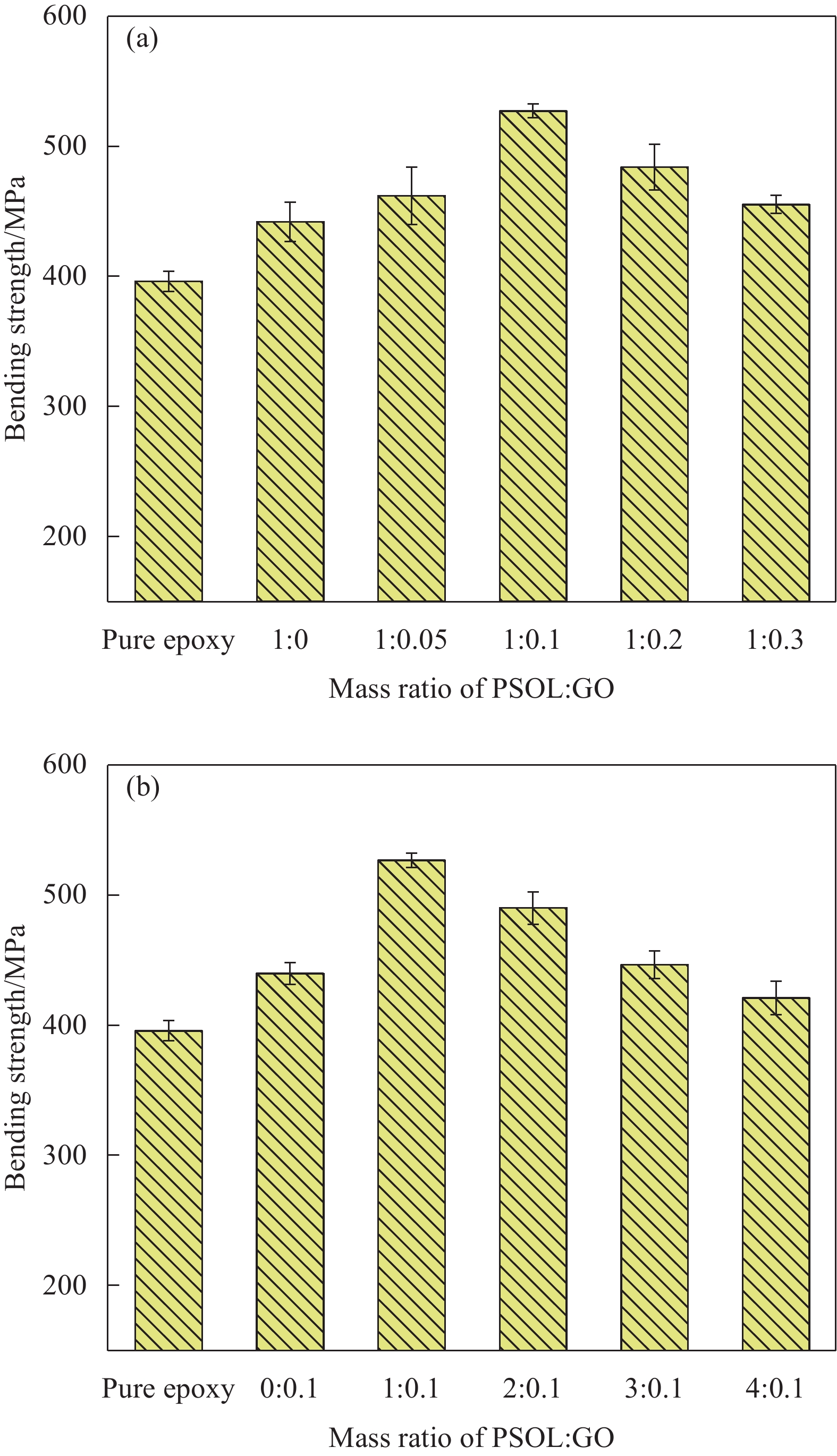
图9为不同比例的PSOL-GO对GF/EP复合材料弯曲强度的影响。从图9(a)中可以看出，随着GO含量的增加，PSOL-GO@GF/EP复合材料的弯曲强度逐渐增强，在GO含量为0.1wt%时，弯曲强度达到最佳。然而，随着GO的继续加入复合材料的弯曲强度逐渐减弱。图9(b)可以看出随着PSOL含量的增加，复合材料的弯曲强度逐渐增加，当硅聚物含量为1wt%时，其弯曲强度达到峰值，但是随着PSOL含量的继续提高，复合材料的弯曲强度逐渐减小。从图9可知，当PSOL与GO质量比为1∶0.1，此时的PSOL-GO@GF/EP复合材料的弯曲强度最佳为526.22 MPa，而纯的GF/EP复合材料的弯曲强度为395.3 MPa，改性后的GF/EP复合材料的弯曲强度提升了33.12%。这说明一定比例的PSOL-GO的加入有效改善了复合材料的弯曲性能。
![]()
图 9 不同质量比的PSOL与GO对PSOL-GO@GF/EP复合材料弯曲性能的影响Figure 9. Influence of different mass ratios of PSOL and GO on the bending properties of PSOL-GO@GF/EP composites2.3.3 PSOL-GO@GF/EP复合材料的拉伸性能
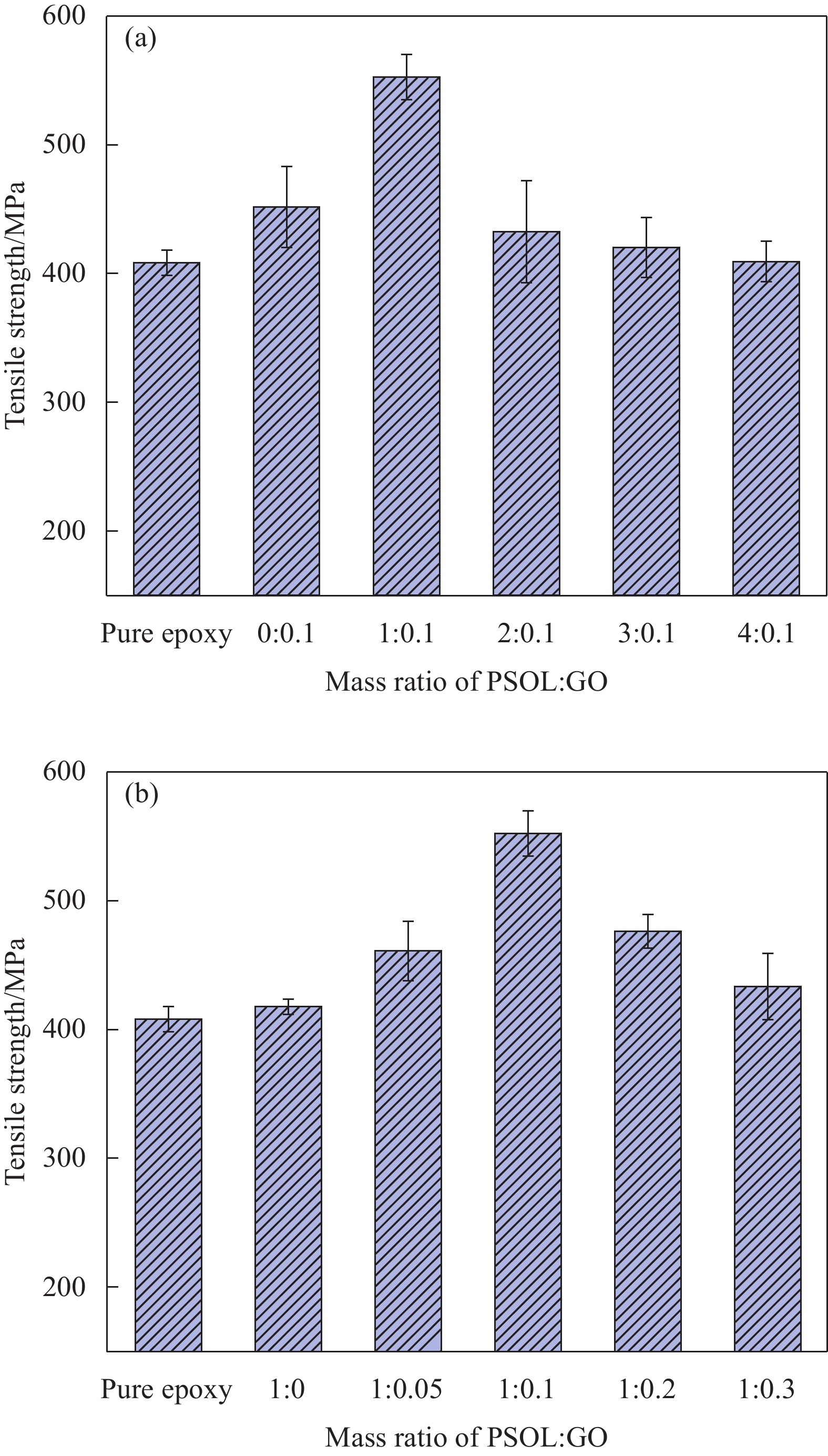
不同比例的PSOL-GO对GF/EP复合材料拉伸强度的影响见图10。从图10(a)中可知，纯的GF/EP复合材料的拉伸强度为418.5 MPa，较纯GF/EP复合材料有小幅度提高，随着GO含量的提高，PSOL-GO@GF/EP复合材料的拉伸强度呈现先增强后减弱的趋势。从图10(b)中可知，随着PSOL含量的增加，复合材料的拉伸性能有所提高。当硅聚物与氧化石墨烯质量比为1∶0.1时，复合材料的拉伸强度达到峰值为552.48 MPa，与纯的GF/EP复合材料相比，其拉伸强度有35.32%的提高。这说明一定比例的PSOL-GO的加入有效改善了复合材料的拉伸性能。
![]()
图 10 不同质量比的PSOL与GO对PSOL-GO@GF/EP复合材料拉伸性能的影响Figure 10. Influence of different mass ratios PSOL to GO on the tensile properties of PSOL-GO@GF/EP composites2.3.4 PSOL-GO@GF/EP复合材料的冲击性能
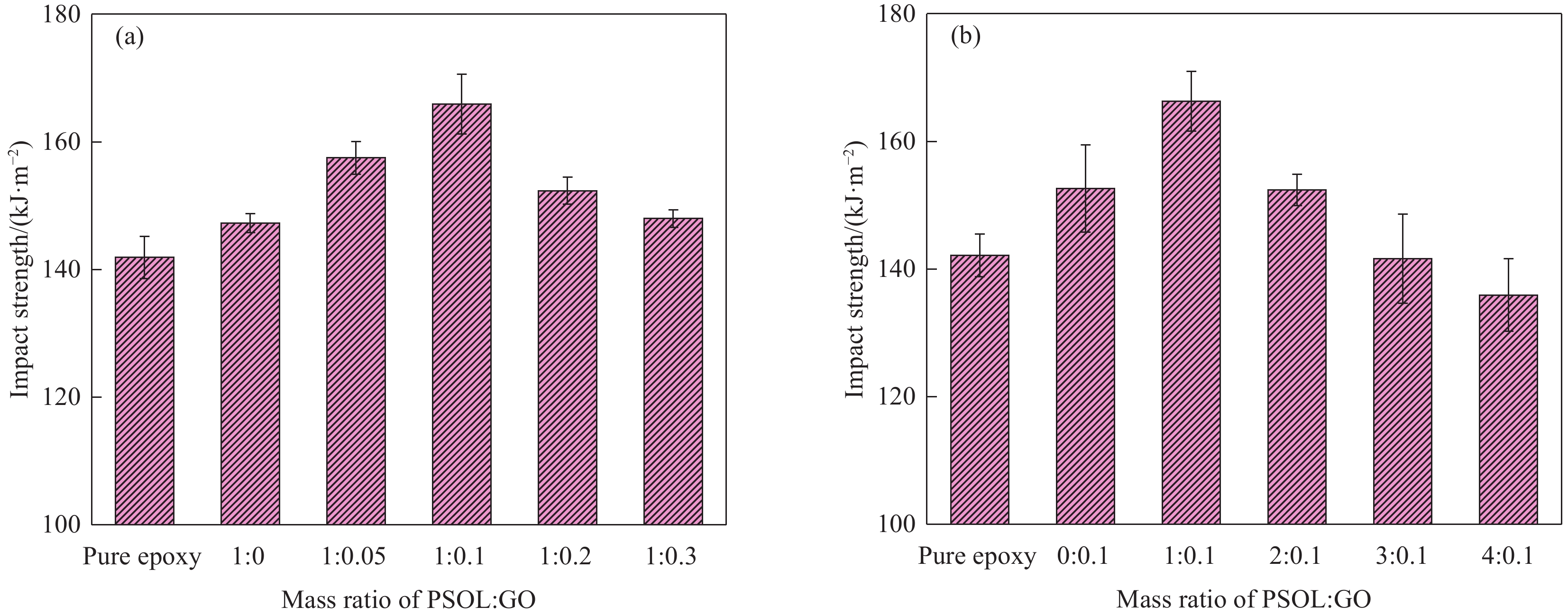
图11为不同比例的PSOL-GO对GF/EP复合材料冲击性能的影响。从图11(a)中可知，PSOL-GO@GF/EP复合材料的冲击强度随GO含量的增加呈现先增大后降低的趋势。从图11(b)中可知，随着PSOL含量的增加，复合材料的冲击性能有所提高。纯GF/EP的冲击强度为141.87 kJ/m2，添加1wt%PSOL的GF/EP复合材料韧性较纯EP有所提高，当硅聚物与氧化石墨烯质量比为1∶0.1时，复合材料的冲击强度可达165.92 kJ/m2，提升了16.95%。但随着PSOL含量的继续增加，其冲击性能开始下降。这说明一定比例的PSOL-GO的加入有效改善了复合材料的冲击性能。
![]()
图 11 不同质量比的PSOL与GO比例对PSOL-GO@GF/EP复合材料冲击性能的影响Figure 11. Influence of different mass ratios PSOL and GO on impact performance of PSOL-GO@GF/EP composites2.4. PSOL-GO@GF/EP复合材料的动态力学性能
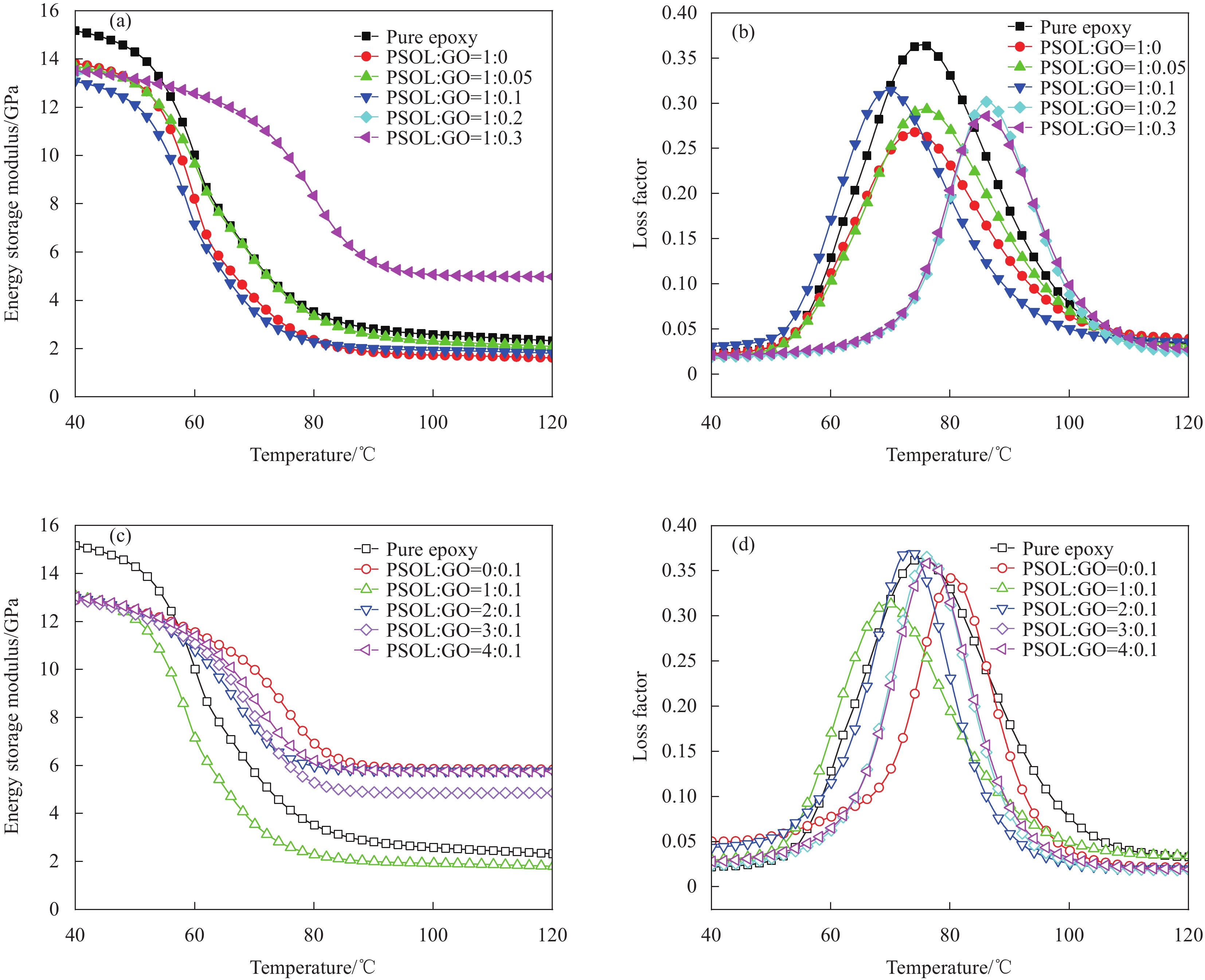
在35℃至135℃的温度区间内，不同质量比PSOL-GO对GF/EP复合材料的储能模量和损耗因子随温度的变化见图12。从图12(a)和图12(c)可以看出，PSOL-GO改性GF/EP复合材料的储能模量会随着温度的升高而不断降低，由于聚合物链会随温度升高而协同运动增加，从而导致能量耗损。在温度为35℃时，改性后的GF/EP复合材料的储能模量低于纯的GF/EP复合材料。由于硅聚物作为柔性链，其模量处于环氧树脂与碳纤维之间。随着硅聚物的加入，GF/EP复合材料的储能模量会有一定程度的下降。图12(b)和图12(d)为损耗因子随温度变化曲线。玻璃化转变温度(Tg)对应损耗因子的峰值温度，说明GF/EP复合材料形成了均匀的交联结构。从图中看出，纯的GF/EP复合材料的玻璃化转变温度为82.90℃。而随着PSOL-GO的添加，各个含量的PSOL-GO@GF/EP复合材料的Tg有着不同的趋势，添加质量比为1∶0.1的PSOL-GO可使GF/EP复合材料的Tg提高7.1℃，适宜含量的PSOL-GO的添加可使GF/EP复合材料的Tg有所提高。
![]()
图 12 PSOL-GO@GF/EP复合材料动态力学性能的影响：((a), (c))储能模量；((b), (d))损耗因子Figure 12. Influence of dynamic mechanical properties of PSOL-GO@GF/EP composites: ((a), (c)) Energy storage modulus; ((b), (d)) Loss factors3. 结 论
本文通过将硅聚物-氧化石墨烯(PSOL-GO)作为填料添加到玻璃纤维/环氧树脂(GF/EP)复合材料中，成功制备了PSOL-GO@GF/EP复合材料，同时探究了PSOL-GO对GF/EP复合材料的力学性能的影响，详细观察了PSOL-GO@GF/EP复合材料的断面形貌结构。得出以下主要结论：
(1)在PSOL-GO@GF/EP复合材料制备过程中将PSOL-GO作为纳米填料引入到GF/EP中，采用手工涂覆及模压成型的方法成功制备出性能优异的PSOL-GO@GF/EP复合材料；
(2)通过接触角试验证明添加PSOL-GO后的环氧树脂对玻璃纤维的润湿效果更好，更加有利于改善PSOL-GO@GF/EP复合材料的界面相容性。通过SEM可知纯的GF/EP复合材料剥离表面较光滑，且界面之间存在很大的空隙。但当加入PSOL-GO后，GF/EP复合材料的剥离面上存在环氧碎片及PSOL-GO填料，玻璃纤维和环氧树脂的粘接较紧密。通过力学性能测试得出PSOL-GO质量比为1∶0.1时PSOL-GO@GF/EP复合材料力学性能最佳：改性后的GF/EP复合材料与纯GF/EP复合材料相比层间剪切强度升高至43.26 MPa，提高了13.19%；弯曲强度为526.22 MPa，提高了33.12%；拉伸强度为552.48 MPa，提高了35.32%；冲击强度为165.92 MPa，提高了16.95%。这说明一定比例的PSOL-GO的加入能有效改善复合材料的力学性能；
(3)通过动态力学性能测试得出添加适宜比例的PSOL-GO可使GF/EP复合材料的玻璃化转变温度(Tg)提高，使其耐热性有所提高。
-
![]()
图 1 硅聚物(PSOL)的制备机制
THF—Tetrahydrofuran
Figure 1. Preparation mechanism of silicon polymer (PSOL)
![]()
图 2 PSOL-氧化石墨烯(GO)@玻璃纤维/环氧树脂(GF/EP)复合材料的制备流程图
Figure 2. Flowchart of preparation of PSOL-graphene oxide (GO)@glass fiber/epoxy resin (GF/EP) composites
![]()
图 3 PSOL (a)、氧化石墨烯(GO) (b)、硅聚物-氧化石墨烯(PSOL-GO) (c)的FE-SEM图像
Figure 3. FE-SEM images of PSOL (a), graphene oxide (GO) (b) and silicon polymer-graphene oxide (PSOL-GO) (c)
![]()
图 5 不同质量比的PSOL与GO对PSOL-GO@GF/EP复合材料层间剪切性能的影响
Figure 5. Effects of different mass ratios PSOL and GO on the interlaminar shear properties of PSOL-GO@GF/EP composites
![]()
图 6 PSOL-GO@GF/EP复合材料增强机制
Figure 6. Strengthening mechanism of PSOL-GO@GF/EP composites
![]()
图 7 PSOL-GO@GF/EP复合材料剥离表面的SEM图像：(a)纯的玻璃纤维/环氧树脂(GF/EP)复合材料；(b) PSOL∶GO=1∶0.1；(c) PSOL∶GO=1∶0.3；(d) PSOL∶GO=4∶0.1
Figure 7. SEM images of the peeling surface of PSOL-GO@GF/EP composites: (a) Pure glass fiber/epoxy resin (GF/EP) composites; (b) PSOL∶GO=1∶0.1; (c) PSOL∶GO=1∶0.3; (d) PSOL∶GO=4∶0.1
![]()
图 8 PSOL-GO对玻璃纤维润湿性的影：(a)纯环氧；(b) PSOL∶GO=1∶0.1
Figure 8. Influence of PSOL-GO on wettability of glass fiber: (a) Pure epoxy; (b) PSOL∶GO=1∶0.1
![]()
图 9 不同质量比的PSOL与GO对PSOL-GO@GF/EP复合材料弯曲性能的影响
Figure 9. Influence of different mass ratios of PSOL and GO on the bending properties of PSOL-GO@GF/EP composites
![]()
图 10 不同质量比的PSOL与GO对PSOL-GO@GF/EP复合材料拉伸性能的影响
Figure 10. Influence of different mass ratios PSOL to GO on the tensile properties of PSOL-GO@GF/EP composites
![]()
图 11 不同质量比的PSOL与GO比例对PSOL-GO@GF/EP复合材料冲击性能的影响
Figure 11. Influence of different mass ratios PSOL and GO on impact performance of PSOL-GO@GF/EP composites
-
[1] SHARMA A K, BHANDARI R, SHARMA C, et al. Polymer matrix composites: A state of art review[J]. Materials Today: Proceedings, 2022, 57: 2330-2333. DOI: 10.1016/j.matpr.2021.12.592
[2] HU L H, TSAI Y T. Carbon fiber surface-modified by polymer derived ceramic incorporated with graphene to strengthen the mechanical and electrochemical properties of ceramic-carbon fiber composite[J]. Composites Science and Technology, 2022, 221: 109294. DOI: 10.1016/j.compscitech.2022.109294
[3] MALALLI C S, RAMJI B R. Characterization of natural fiber reinforced polymer composites and their application in prosthesis: A review[J]. Materials Today: Proceedings, 2022, 62: 3435-3443. DOI: 10.1016/j.matpr.2022.04.276
[4] KARIMAH A, RIDHO M R, MUNAWAR S S, et al. A review on natural fibers for development of eco-friendly bio-composite: Characteristics, and utilizations[J]. Journal of Materials Research and Technology, 2021, 13: 2442-2458.
[5] 韩振宇, 张鹏, 郑天宇, 等. 纤维增强树脂复合材料网格结构成型工艺研究进展[J]. 复合材料学报, 2020, 37(4): 845-858. HAN Zhenyu, ZHANG Peng, ZHENG Tianyu, et al. Research progress of grid structure forming process of fiber-reinforced resin composites[J]. Acta Materiae Compositae Sinica, 2020, 37(4): 845-858(in Chinese).
[6] YANG Y, LI J, SHAN L, et al. All-natural bioinspired nanolignocellulose-derived bulk engineering materials with excellent mechanical properties and environmental stability[J]. Cellulose, 2023, 30(2): 871-884. DOI: 10.1007/s10570-022-04922-x
[7] APPADURAI M, RAJ E F I. Epoxy/silicon carbide (SiC) nanocomposites based small scale wind turbines for urban applications[J]. International Journal of Energy and Environmental Engineering, 2022, 13(1): 191-206. DOI: 10.1007/s40095-021-00417-w
[8] 王刚, 金智康, 宋俊杰, 等. 复合涂层对玻璃纤维增强尼龙6复合材料界面性能的影响[J]. 复合材料学报, 2023, 40(12): 6668-6680. WANG Gang, JIN Zhikang, SONG Junjie, et al. Effect of composite coating on interfacial properties of glass fiber reinforced nylon 6 composites[J]. Acta Materiae Compositae Sinica, 2023, 40(12): 6668-6680(in Chinese).
[9] DEHROOYEH S, VASEGHI M, SOHRABIAN M, et al. Glass fiber/carbon nanotube/epoxy hybrid composites: Achieving superior mechanical properties[J]. Mechanics of Materials, 2021, 161: 104025. DOI: 10.1016/j.mechmat.2021.104025
[10] TIAN X, TODOROKI A, LIU T, et al. 3D printing of continuous fiber reinforced polymer composites: Development, application, and prospective[J]. Chinese Journal of Mechanical Engineering: Additive Manufacturing Frontiers, 2022, 1(1): 100016.
[11] KHURSHID M F. Innovative unidirectional recycled carbon fiber tape structure for high performance thermoplastic composites: Technological developments, technology-structure-property relationship and modeling of composite tensile properties[D]. Dresden: Technische Universität Dresden, 2022.
[12] SHUKLA N, DEVNANI G L. A review on mechanical properties of hybrid natural fiber polymer composites[J]. Materials Today: Proceedings, 2021, 45: 4702-4705. DOI: 10.1016/j.matpr.2021.01.122
[13] SIENGCHIN S. A review on lightweight materials for defence applications: A present and future developments[J]. Defence Technology, 2023, 24: 1-17. DOI: 10.1016/j.dt.2023.02.025
[14] PARVEEZ B, KITTUR M I, BADRUDDIN I A, et al. Scientific advancements in composite materials for aircraft applications: A review[J]. Polymers, 2022, 14(22): 5007. DOI: 10.3390/polym14225007
[15] EL-WAZERY M S, EL-ELAMY M I, ZOALFAKAR S H. Mechanical properties of glass fiber reinforced polyester composites[J]. International Journal of Applied Science and Engineering, 2017, 14(3): 121-131.
[16] Al-FURJAN M S H, SHAN L, SHEN X, et al. A review on fabrication techniques and tensile properties of glass, carbon, and Kevlar fiber reinforced polymer composites[J]. Journal of Materials Research and Technology, 2022, 19: 2930-2959. DOI: 10.1016/j.jmrt.2022.06.008
[17] KEYA K N, KONA N A, KOLY F A, et al. Natural fiber reinforced polymer composites: History, types, advantages and applications[J]. Materials Engineering Research, 2019, 1(2): 69-85.
[18] AMANTAYEVA A, SHEHAB E, MEIIRBEKOV A, et al. Challenges and opportunities of implementing industry 4.0 in recycling carbon fiber reinforced composites[J]. Advances in Science and Technology, 2022, 116: 67-73.
[19] ISLAM M H, AFROJ S, UDDIN M A, et al. Graphene and CNT-based smart fiber-reinforced composites: A review[J]. Advanced Functional Materials, 2022, 32(40): 2205723. DOI: 10.1002/adfm.202205723
[20] GONCALVES R M, MARTINHO A, OLIVEIRA J P. Recycling of reinforced glass fibers waste: Current status[J]. Materials, 2022, 15(4): 1596. DOI: 10.3390/ma15041596
[21] MAJEWSKI P, FLORIN N, JIT J, et al. End-of-life policy considerations for wind turbine blades[J]. Renewable and Sustainable Energy Reviews, 2022, 164: 112538. DOI: 10.1016/j.rser.2022.112538
[22] HUANG X, SU S, XU Z, et al. Advanced composite materials for structure strengthening and resilience improvement[J]. Buildings, 2023, 13(10): 2406.
[23] DASARI S, LOHANI S, PRUSTY R K. An assessment of mechanical behavior of glass fiber/epoxy composites with secondary short carbon fiber reinforcements[J]. Journal of Applied Polymer Science, 2022, 139(12): 51841. DOI: 10.1002/app.51841
[24] RODRIGUEZ-GONZALEZ J A, RUBIO-GONZALEZ C. Influence of graphene nanoplatelet concentration on the electrical, mechanical, and piezoresistive properties of glass fiber/epoxy composites[J]. Polymer Composites, 2022, 43(5): 3276-3289. DOI: 10.1002/pc.26616
[25] AZHARY T, WILDAN M W. Mechanical, morphological, and thermal characteristics of epoxy/glass fiber/cellulose nanofiber hybrid composites[J]. Polymer Testing, 2022, 110: 107560. DOI: 10.1016/j.polymertesting.2022.107560
[26] OU Y, WU L, MAO D. Hierarchical mode I interlaminar toughening of unidirectional CFRP laminates by the synergistic effects of CNT powders and veils[J]. Composites Part A: Applied Science and Manufacturing, 2023, 168: 107464. DOI: 10.1016/j.compositesa.2023.107464
[27] HAN W, ZHOU J, SHI Q. Research progress on enhancement mechanism and mechanical properties of FRP composites reinforced with graphene and carbon nanotubes[J]. Alexandria Engineering Journal, 2022, 64: 541-579.
[28] YANG W J, WEI C X, YUEN A C Y, et al. Fire-retarded nanocomposite aerogels for multifunctional applications: A review[J]. Composites Part B: Engineering, 2022, 237: 109866.
[29] KARNA N, JOSHI G M, MHASKE S T. Structure-property relationship of silane-modified polyurethane: A review[J]. Progress in Organic Coatings, 2023, 176: 107377. DOI: 10.1016/j.porgcoat.2022.107377
[30] DANG C Y, TANG B L, ZENG X L, et al. Improved interlaminar shear strength of glass fiber/epoxy composites by graphene oxide modified short glass fiber[J]. Materials Research Express, 2019, 6(8): 085324. DOI: 10.1088/2053-1591/ab2254
[31] American Society for Testing and Materials. Standard test method for short-beam strength of polymer matrix composite materials and their laminates: ASTM D2344[S]. West Coshoshocken: ASTM International, 2006.
[32] 中国国家标准化管理委员会. 纤维增强塑料弯曲性能试验方法: GB/T 1449—2005 [S]. 北京: 中国标准出版社, 2005. Standardization Administration of the People's Republic of China. Test method for flexure properties of fiber reinforced plastics: GB/T 1449—2005 [S]. Beijing: Standards Press of China, 2005(in Chinese).
[33] 中国国家标准化管理委员会. 树脂浇铸体性能试验方法: GB/T 2567—2021 [S]. 北京: 中国标准出版社, 2021. Standardization Administration of the People's Republic of China. Test method for resin casting performance: GB/T 2567—2021 [S]. Beijing: Standards Press of China, 2021(in Chinese).
[34] LU J J, SHI Y C, GUAN J P, et al. Enhanced mechanical properties of ramie fabric/epoxy composite laminates by silicon polymer[J]. Industrial Crops and Products, 2023, 199: 116778. DOI: 10.1016/j.indcrop.2023.116778
-
期刊类型引用(1)
1. 王立汉，陈子睿，王良清，陈垠锟，钟声，欧华韶. 真空等离子体对改性玻璃纤维及环氧树脂复材的影响. 粘接. 2025(03): 104-107 . 
百度学术
其他类型引用(2)
-
目的
随着玻璃纤维/环氧树脂(GF/EP)复合材料被广泛应用于飞机、空间飞行器、汽车等领域，因此对于玻璃纤维/环氧树脂(GF/EP)复合材料的性能有更高的应用要求。针对玻璃纤维/环氧树脂(GF/EP)复合材料界面性能较弱的问题，提出采用硅聚物-氧化石墨烯(PSOL-GO)作为纳米填料来改性玻璃纤维/环氧树脂(GF/EP)复合材料，优化其界面微观结构进而提高其力学性能。
方法通过调整PSOL-GO的比例，采用手工涂覆及模压成型的方法制备得到不同含量的PSOL-GO@GF/EP复合材料。利用日本日立公司S-4800场发射扫描电子显微镜(FE-SEM)观察GO、PSOL及PSOL-GO复合材料的表面形貌以及试样的层间剥离面微观形貌。采用德国Kruss DSA30接触角测量分析仪测试PSOL-GO不同添加含量的环氧树脂和玻璃纤维表面的接触角。利用FT-IR表征GO、PSOL及PSOL-GO试样内部的成键方式。采用日本岛津AG-X Plus万能材料试验机分别按照ASTMD2344、GB/T1449-2005、GB2567-2021标准对试样进行层间剪切测试、弯曲测试、拉伸测试。利用深圳三思纵横科技PTM7000-B摆锤式冲击试验机对试样进行冲击测试，测试标准参考GB2567-2021。采用美国TA公司Q850动态热机械分析仪分析试样的动态热力学行为。
结果通过扫描电镜图得出：纯的GF/EP复合材料剥离表面较为光滑，且界面之间存在很大的空隙。但加入PSOL-GO后，GF/EP复合材料的剥离面上存在环氧碎片及PSOL-GO填料，玻璃纤维和环氧树脂的粘接较为紧密。通过接触角试验得出：添加PSOL-GO后的环氧树脂对玻璃纤维的润湿效果更好，更加有利于改善PSOL-GO@GF/EP复合材料的界面相容性。通过力学性能测试得出PSOL-GO比例为1:0.1时PSOL-GO@GF/EP复合材料力学性能最佳：改性后的GF/EP复合材料与纯GF/EP复合材料相比层间剪切强度升高至43.26 MPa，提高了13.19%；弯曲强度为526.22 MPa，提高了33.12%；拉伸强度为552.48 MPa，提高了35.32%；冲击强度为165.92 MPa，提高了16.95%，这说明一定比例的PSOL-GO的加入能有效改善复合材料的力学性能。通过动态力学性能测试得出：添加适宜比例的PSOL-GO可使GF/EP复合材料的玻璃化转变温度(Tg)提高了7.1℃，使其耐热性有所提高。
结论在PSOL-GO@GF/EP复合材料制备过程中将PSOL-GO作为纳米填料引入到GF/EP中，采用手工涂覆及模压成型的方法可以成功制备出性能优异的PSOL-GO@GF/EP复合材料。引入PSOL-GO纳米填料后的环氧树脂对玻璃纤维的润湿性更佳，因此环氧树脂与玻璃纤维的界面性能得到改善。PSOL上的羟基与环氧树脂上的环氧基团发生开环反应形成醚键；GO上的羟基和羧基与环氧树脂形成醚键和酯键，同时，GO的褶皱形貌能与环氧树脂形成机械互锁；PSOL上的羟基与GO上的羧基和羟基形成酯键和氢键；PSOL上的羟基与GF表面的羟基产生醚键和氢键，从而改善GF与EP的界面，提升复合材料的力学性能。
下载:
计量
- 文章访问数: 337
- HTML全文浏览量: 146
- PDF下载量: 44
- 被引次数: 3
