Air coupled ultrasonic probabilistic damage imaging of composite laminates based on wavelet packet energy relative variation deviation
-
摘要: 传统椭圆概率损伤成像使用信号幅值差或能量差作为特征参量,对损伤识别不够敏感且抗噪性能较差。为提高损伤识别的敏感程度,提出采用小波包能量比变化率偏差(Energy relative variation deviation,ERVD)作为损伤因子。选取合适的探头入射倾斜角度,使用空气耦合超声探头在复合材料层板中激励单一的Lamb波模态,对采集的扫查信号进行小波包分解,根据结构损伤前后的信号特征变化选取特征频带,计算损伤指数进行椭圆概率损伤成像,并模拟不同噪声环境对比不同损伤因子的成像效果差异。实验结果表明,选取小波包能量比变化率偏差作为损伤因子,具有较强的损伤识别敏感性和抗噪性能。使用此损伤因子进行空气耦合超声概率损伤成像,可提高复合材料损伤的定位和成像效果。Abstract: Traditional elliptical probabilistic damage imaging uses signal amplitude difference or energy difference as characteristic parameters, which is not sensitive enough to damage identification and has poor noise resistance. In order to improve the sensitivity of damage recognition, it was proposed to use the energy relative variation deviation (ERVD) of wavelet packet as the damage factor. A single Lamb wave mode was excited by an air coupled ultrasonic probe in the composite laminate with an appropriate incidence angle of the probe. Wavelet packet decomposition was used to decompose the collected scanning signal. According to the change of signal characteristics before and after structural damage, a specific frequency band was selected. The calculated damage index was used for elliptical probability damage imaging, and the imaging effects of different damage factors were compared by simulating different environmental noise environments. The experimental results show that the wavelet packet energy ratio deviation as the damage factor has strong sensitivity to damage recognition sensitivity and noise resistance. Using this damage factor for air coupled ultrasound probabilistic damage imaging can improve the location and imaging effect of composite material damage.
-
碳纤维增强树脂复合材料(Carbon fiber reinforced polymer, CFRP)因具有轻质高强、耐腐蚀、可设计性好等优异性能,在航空航天、高速铁路、风电机组等大型结构中得到广泛应用[1-3],其结构的健康与否也直接关系到系统的完整性和安全性。在现行的多种无损检测技术中,传统的基于分布式稀疏换能器阵列的Lamb波检测方法通常依据阵列之间的渡越时间实现损伤的定位,其中邱雷等[4]基于换能器阵列和主动Lamb波的结构损伤成像方法,提出了一种基于Shannon复数小波和时间反转聚焦的信号合成成像方法,有效地对复合材料板多个损伤进行定位成像。刘国强等[5]在复合材料加筋壁板上构建压电换能器网络,利用改进的损伤概率成像方法准确地对损伤进行定位成像。Qiang W等[6]基于压电换能器阵列和时间窗函数,开发了一种无需基准信号的时间反转检测方法,所提方法有效地表征出准各向同性板中的损伤。Milad Saeedifar等[7]利用压电传感器网络和声发射传感器对低速冲击下的碳纤维复合材料板进行主动和被动的在线监测,冲击损伤定位误差仅为3.6%。上述方法均利用换能器阵列进行信号的接收,有效地识别复合材料板中的损伤。
然而在实际应用中,接触式换能器阵列仍存在以下不足:(1) 受限于空间分辨率难以针对损伤的尺度、取向等特征作精确评估;(2) 接触式传感器本身安装费力,且容易受到破坏;(3) 阵列排布形式固定,需要大量导线连接;(4) 传感器和被测结构之间需要添加耦合剂,其耦合效果对导波信号的接收和质量影响很大。相比于分布式稀疏阵列换能器,使用非接触扫描式激光多普勒测振(Scanning laser doppler vibration, SLDV)检测方法能够获得复合材料被测区域内高空间分辨率导波场,并据此得到损伤导致的波场特征变化,依据海量数据可达到对损伤精确评估的目的[8-10]。然而导波场需依照奈奎斯特(Nyquist)采样定律进行数据采集,空间采样点间隔至少需达到最小波长的一半,且每个采样点需多次测量求平均以提高信噪比,导致采集过程严重耗时,此外大量的采点数据给数据存储、传输和计算信号分析带来极大挑战。近年来发展的基于压缩传感方法的采样理论可在远小于Nyquist采样频率的条件下,通过非线性算法快速实现信号的重构。Harley J B等[11-12]利用导波中的波数特性在频域空间中的稀疏性,结合压缩感知算法实现频散曲线的重构,随后根据频散关系重构全波场。Ross M. Levine等[13-14]结合压缩感知技术与导波传播模型提出了块状稀疏重构方法,通过假定每个像素都具有相应的多维线性散射模型,据此来定位损伤。Byeongjin Park等[15]将压缩感知与超分辨率算法结合,开发了一种激光超声波场重构技术,首先使用SLDV选取固定的测量点,然后使用超分辨率算法重构高空间分辨率超声波图像。所提方法使超声波场成像所需的测量点数量减少了90%以上,并在含单孔损伤的铝板上进行了实验验证。Tommaso Di Ianni等[16]讨论了不同基函数下的波场稀疏表示,采用压缩感知方法以低于奈奎斯特采样的点数实现了波场的重构。Esfandabadi等[17]将波场在不同基下进行稀疏表示,通过各种基下重构波场的差异实现了对损伤的表征。Mesnil等[18]挖掘了损伤在空间分布上的稀疏性,结合压缩感知算法现了稀疏测点下的全波场数据恢复。骆英等[19]基于压缩感知算法提出了一种均匀稀疏采样的波场重构方法,并在铝板上进行验证,有效地实现波场重构与损伤成像。
综合上述文献调研可总结:压缩感知在导波场中的应用可有效地实现波场的重构和损伤成像。然而上述的应用对象主要为各向同性板或者准各向同性板,受限于导波在复合材料中复杂的各向异性传播特性,压缩感知方法在复合材料板中的应用成为难题。为了解决此问题,本文深入研究了Lamb波在复合材料板中的传播规律,通过考虑各个方向上的波数特性,构建了Lamb波在复合材料板中不同传播方向的波数库,结合压缩感知算法以远低于Nyquist采样的点数重构全波场。在损伤分析阶段,提出了无需基准信号的复合材料散射波场分离技术,完善了基于压缩感知的各向异性复合材料板损伤检测的定位和分析技术。相关成果可为复合材料板损伤检测的实际运用提供理论和方法基础。
1. 波场中的压缩感知方程构造
1.1 压缩感知理论
压缩感知是结合信号稀疏表示理论提出的信号采集理论[20],数学上描述如下:考虑
N 维P -稀疏信号{\mathit{\boldsymbol{x}}} (即{\mathit{\boldsymbol{x}}} 中含有个非零数),将其投影到测量矩阵{{\mathit{\boldsymbol{\varPhi}}} } 上,从而得到采样信号{\mathit{\boldsymbol{y}}} ,矩阵表示为[20]{\mathit{\boldsymbol{y}}} = {{\mathit{\boldsymbol{\varPhi}}} } {\mathit{\boldsymbol{x}}} (1) 其中:
{\mathit{\boldsymbol{x}}} \in {{\rm{R}}^{N \times {\rm{1}}}} 是N 维原始信号;{\mathit{\boldsymbol{y}}} \in {{\rm{R}}^{M \times {\rm{1}}}} 是M 维测量信号,M \ll N ;{{\mathit{\boldsymbol{\varPhi}}} } \in {{\rm{R}}^{M \times N}} 是测量矩阵。当信号{\mathit{\boldsymbol{x}}} 本身不稀疏时,可将信号{\mathit{\boldsymbol{x}}} 通过某种变换(如傅里叶变换、小波变换等)进行稀疏表示,具体为{\mathit{\boldsymbol{x}}} = {\mathit{\boldsymbol{B\alpha}}} (2) 假定
{\mathit{\boldsymbol{\alpha}}} \in {{\rm{R}}^{Q \times {\rm{1}}}} 为{\mathit{\boldsymbol{x}}} 在稀疏基{\mathit{\boldsymbol{B}}} 下的稀疏表示,从而有{\mathit{\boldsymbol{y}}} = {{\mathit{\boldsymbol{\varPhi}}} } {\mathit{\boldsymbol{x}}} = {{\mathit{\boldsymbol{\varPhi}}} } {\mathit{\boldsymbol{B\alpha }}} (3) 式中,
{\mathit{\boldsymbol{H}}} = {\mathit{\boldsymbol{B\alpha}}} ,{\mathit{\boldsymbol{H}}} \in {{\rm{R}}^{M \times Q}} 称为感知矩阵。1.2 压缩感知方程构造
首先对导波场进行如下假设:测量区域空间布满了源,即潜在源,其中只有主动或被动的产生导波的结构(如激励源、损伤、边界等)视为真实源。因此在测量区域中,真实源是有限的,且在大量分布的潜在源下是稀疏的。为简化后续计算,此处假定所有的潜在源均匀散射。
将Lamb波在测量点
m 处接收到的信号视为所有潜在源的贡献,其频域中的传播式为[21]{y_m}\left( f \right) = \sum\limits_{j = {\rm{1}}}^S {\frac{{\rm{1}}}{{\sqrt {{d_{m,j}}} }}} \left( {{v_j}\left( f \right){{\rm{e}}^{ - i{k_{m,j}}\left( f \right){d_{m,j}}}}} \right) (4) 其中:
j 表示潜在源;m 表示测量点;S 为潜在源的总个数;{v_j} 是潜在源函数,包含潜在源处的相位和幅值信息;{d_{m,j}} 是潜在源j 和测量点m 之间的距离;{k_{m,j}}\left( f \right) 是频率f 下潜在源j 到测量点m 方向上的波数。为使式(4)便于后续计算,对其简化为{y_m}\left( f \right) = \sum\limits_{j = {\rm{1}}}^S {{a_j}{v_j}} \left( f \right) (5) 其中,
{a_j} = \dfrac{{{{\rm{e}}^{ - i{k_{m,j}}(f){d_{m,j}}}}}}{{\sqrt {{d_{m,j}}} }} ,式(5)的矩阵形式表达为{\mathit{\boldsymbol{Y}}}\left( f \right) = {\mathit{\boldsymbol{A}}}\left( f \right){\mathit{\boldsymbol{V}}}\left( f \right) (6) 式(6)可通过基于l1最小化算法的SPGL1程序包进行求解[22]
\min {\left\| {{\mathit{\boldsymbol{V}}}(f)} \right\|_1},s.t.\left\| {{\mathit{\boldsymbol{Y}}}(f) - {\mathit{\boldsymbol{A}}}(f){\mathit{\boldsymbol{V}}}(f)} \right\|_{\rm{2}}^{\rm{2}} \leqslant \frac{{\left\| {{\mathit{\boldsymbol{Y}}}(f)} \right\|_{\rm{2}}^{}}}{N} (7) 式中,N与噪音参数有关,文献[23]中给出N的最佳取值为2。本节所构造方程适合于(各向异性或各向同性)板状结构,且结构中损伤有限的情况,形状更加复杂的工程结构需要寻求新的波场稀疏表示方法。
1.3 复合材料波数库的构建
在1.2节波场的压缩感知方程构造中,式(4)中
{k_{m,j}}\left( f \right) 是潜在源j 到测量点m 方向上的波数,因导波在复合材料中传播的各向异性特征,{k_{m,j}}\left( f \right) 为频率和角度的函数。为确保后续压缩感知方程求解的精准性,本节的目的是构建压缩感知框架下的波数库。首先建立潜在源与测量点之间的角度库,图1为构建的测量点与潜在源间的角度模型,实心点表示测量点,空心点表示潜在源,测量点与潜在源之间的夹角{\theta _{m,j}} 表示为{\theta _{m,j}}{\rm{ = }}\arctan \left| {\frac{{\left( {{y_j} - {y_m}} \right)}}{{\left( {{x_j} - {x_m}} \right)}}} \right| (8) 角度矩阵
\left[ {\mathit{\boldsymbol{\theta}}} \right] 的维度为M×S,M为测量点的总个数,S为潜在源的总个数,其展开为\left[ {\mathit{\boldsymbol{\theta}}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{\theta _{1,1}}}&{}& \cdots &{}&{{\theta _{{\rm{1}},S}}} \\ {}& \ddots &{}&{}&{} \\ \vdots &{}&{{\theta _{m,j}}}&{}& \vdots \\ {}&{}&{}& \ddots &{} \\ {{\theta _{M,{\rm{1}}}}}&{}& \cdots &{}&{{\theta _{M,S}}} \end{array}} \right] 已知材料参数情况下,波数常用半解析有限元法求得[24],通过求解计算频带内不同频率下0°~360°的波数,结合角度库将每个角度所在位置替换为对应的波数信息,据此构建所需压缩感知框架下的波数库。为便于理解,将波数库
\left[ {\mathit{\boldsymbol{K}}} \right] 矩阵展开得\left[ {\mathit{\boldsymbol{K}}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{k_{{\rm{1,1}}}}}&{}& \cdots &{}&{{k_{{\rm{1}},S}}} \\ {}& \ddots &{}&{}&{} \\ \vdots &{}&{{k_{m,j}}}&{}& \vdots \\ {}&{}&{}& \ddots &{} \\ {{k_{M,{\rm{1}}}}}&{}& \cdots &{}&{{k_{M,S}}} \end{array}} \right] 矩阵中
{k_{m,j}} 为对应测量点与潜在源之间角度{\theta _{m,j}} 方向上的波数信息,每一个{k_{m,j}} 都为F×1的列向量,F为计算频率个数。1.4 损伤定位与重构质量评价
损伤定位通过源函数
v\left( f \right) 来确定,矢量v\left( f \right) 包含源的位置信息及每个模态和频率的振幅和相位信息。因此,v\left( f \right) 可用于检测和定位损伤。为确保求解的稳定性,对每个频率段求得的源函数进行叠加可得\left| {{v_s}} \right| = \frac{{\rm{1}}}{{\Delta f}}\int\limits_f {{{\hat v}_s}\left( f \right)} {\rm{d}}f (9) 其中,
\Delta f 为频率带宽。\left| v \right| = \left[ {\left| {{v_1}} \right|, \cdots ,\left| {{v_S}} \right|} \right] 在整个重构区域上,提供了包含损伤的位置信息,向量v >0的点表示真实源(包括激励源、损伤)。重建波场的采样压缩率
{\gamma _\text{Scr}} 定义为{\gamma _\text{Scr}}\left( \% \right) = 100\% \times \left( {1 - \frac{M}{{{M_{{\rm{Nyq}}}}}}} \right) (10) 式中,
{M_{{\rm{Nyq}}}} 是Nyquist定理要求的原则上获取测量波场所需要的点数。重建的质量通过波场的相干系数
{G_{\operatorname{cc} }} 表示,定义为{G_{\operatorname{cc} }}(r,f) = \frac{{\left| {{S_\text{Ms,Rc}}(r,f)} \right|}}{{{S_\text{Ms}}(r,f){S_\text{Rc}}(r,f)}} (11) 式中:
{S_\text{Ms}} 、{S_\text{Rc}} 为原始波场和重构波场的自功率谱密度函数;{S_\text{Ms,Rc}} 表示两个波场的互功率谱密度函数。2. 复合材料板波场重构数值模拟
2.1 激励信号选择及模型建立
图2为运用有限元仿真软件COMSOL构建的含穿透损伤的CFRP板模型图。图中建立了测量区域的局部坐标,激励源中心坐标为(20, 40),直径为7 mm,损伤中心坐标为(40, 80),损伤直径为10 mm,重构区域同测量区域为100 mm×100 mm。具体复合材料板参数如表1所示。
表 1 碳纤维增强树脂复合材料(CFRP)板参数设置Table 1. Carbon fiber reinforced polymer (CFRP) plate parameter settingC11=C22/GPa C33/GPa C12/GPa C13=C23/GPa 197.67 8.76 60.75 4.25 C44=C55/GPa C66/GPa ρ/(kg·m−3) Thinckness/mm 5.2 2.0 1580 1 Notes: C—Stiffness coefficients; ρ—Density. 为使激励信号频率集中、能量高,便于损伤信号的识别。本文采用汉宁窗调制的五周期正弦信号作为激励信号,其表达式为[25]
a\left( t \right) = A\left[ {H\left( t \right) - H\left( {t - \frac{n}{{{f_{\rm{c}}}}}} \right)} \right] \times \left( {{\rm{1}} - \cos \frac{{{\rm{2{\text{π}} }}{f_{\rm{c}}}t}}{n}} \right)\sin \left( {{\rm{2{\text{π}} }}{f_{\rm{c}}}t} \right) (12) 式中:A为幅值;H(t)为Heaviside阶跃函数;
n 为波峰数量,取n = 5 ;{f_{\rm{c}}} 为信号的中心频率,取100 kHz。激励信号的时域和频域图如图3所示。图3(b)为归一化频谱图,虚线表示频率计算频带范围,即{f_{\min }} =60 kHz和{f_{\max }} =140 kHz。假设该激励信号频带外的频率含量可以忽略不计,后续仅在该范围内进行讨论。因实验中采用压电陶瓷换能器进行激励产生Lamb波,为更好地与后续实验相验证,故在仿真中采用等效圆形力线对其建模处理[26]。此外,为消除边界反射对损伤散射信号辨识的干扰,在模型四周加入宽度为20 mm的瑞利阻尼吸收层。在建模过程中,数值模型的计算时间步长\Delta t 与网格尺寸\Delta l 在求解结果的稳定性、收敛性及求解精度等方面起着决定性作用。原则上网格尺寸\Delta l 与Lamb波的波长需满足以下关系式[27]:\Delta l \leqslant \frac{{{\lambda _{\min }}}}{{10}} (13) 式中,
{\lambda _{\min }} 为Lamb波在计算频带中的最小波长。由激励信号选取可知最小波长在140 kHz时取得。由半解析有限元法计算可得最小波长为8.9 mm,因此\Delta l \leqslant 0.89 mm,实际取\Delta l = 0.5 mm,单元类型为四面体单元。与此同时,为确保动力学瞬态分析的收敛性与稳定性,有限元计算模型的计算时间步长需满足“Newmark时间增量方案”,其表达为[27]\Delta t \leqslant \frac{1}{{20{f_{\max }}}} (14) 式中,
{f_{\max }} 为计算频带上限值。将{f_{\max }} =140 kHz代入式(14),故\Delta t \leqslant 0.357 µs,为了得到更高的时间分辨率,在实际仿真计算时取\Delta t =0.1 µs,总时长t =150 µs。因仿真信号提取的为离面振动信号,A0模态占主导,故后续结果仅对A0模态进行分析。在给定计算的频谱带宽下,按照Nyquist采样定律(空间间隔满足最小波长8.9 mm的一半),重构区域的所需点数应为529,此处为验证本文所提重构方法的优越性,仅抖动选取48个测量点数据,采样压缩率为90.93%。在具体采样设置中,将重构区域所需的点数均看成潜在源,按照最小波长间隔的一半均匀分布,采样间隔为4.45 mm。测量点通过随机抖动方法选取,在空间间隔14 mm下随机选取48个随机点。采样点示意图如图4所示。图中实心点为规则分布的潜在源,空心点为随机选取的测量点。2.2 波场重构及损伤成像
通过对压缩感知方程求解,得如图5所示的三维A0源函数成像。从图中可直接看出在激励源中心处幅值最大为1,在损伤处幅值因激励源处幅值过高不易直接看出,在其他位置上幅值基本为0。图5中还存在除损伤和激励源外少部分非声源处幅值不为0的情况,此处定义此类值不为0但本身不属于真实源的点为“伪源”。针对上述源成像结果分析如下,压缩感知方程本质上为欠定方程,其求解为优化过程,得出的为符合约束条件下的最优解。受算法本身和模型匹配的影响,求解的源函数中存在一定的伪源。然而伪源成像能量数值较低,其具体原因为:压缩感知方程求解得出的源函数包含真实源的幅值信息,在本文构建的稀疏性假设下,结构中表面安装的传感器、边界、结构特征(如孔、接口、缺陷)等能够主动或者被动引起散射波的视为真实源,导波由激励源处激发并向外扩散,故在激励源中心位置附近其幅值最强;损伤作为次级波源,其散射波场是由激励源产生的入射波与损伤相互作用而形成,因此损伤处源函数值远低于激励源处。非真实源处不存在散射源,理想情况下除激励源和损伤位置处,其他位置都应为0。伪源是受压缩感知方程本身算法和模型的误差所产生,不属于结构改变处,故而其值远低于激励源和损伤处。当移除激励源后,对只含损伤的源函数进行归一化成像,观察可得此时损伤处的幅值为1,其他非0的伪源处幅值远远低于最高处。根据其源成像值量级可总结出伪源的存在不会影响真实源(激励源、损伤)的识别。
在求得源函数后,将源函数代入导波传播方程,结合构建的波数库,即可求得潜在源数据组成的波场图。图6为具有代表性的60 µs时刻重构和原始波场图。图6(a)为60 µs时刻原始波场图,图6(b)为60 µs时刻重构波场图。对比图6(a)和图6(b)可看出重构波场与原始波场整体上相识度很高,具体细节上,重构波场在损伤和激励源位置处存在一定的不连续,原因为受算法本身和模型匹配的影响,求解的源函数中存在一定的伪源,在将含伪源的源函数代入导波传播方程中进行波场重构时,伪源的存在使重构波场出现不连续。利用相干系数
{G_\text{cc}} 对波场重构精度进行定量评价,图7为{G_\text{cc}}{\rm{ - }}f 曲线。可看出,在计算频带60~140 kHz内相干性可达0.96,在计算频带外相干性不足0.7,因计算频带外的频率不在后续分析中,故可忽略不计。2.3 损伤散射波场分离和损伤定位
图8为移除激励源后的A0模态源函数成像,排除激励源干扰后损伤得以凸显。可看出损伤位置附近存在多个幅值高的点。对此结果分析如下:损伤类型为通孔,其位置在激励源上方,故直达波先到达损伤下沿,随后绕过损伤下沿与上沿相互作用,这种非均匀性散射与建模时真实源的均匀散射假设不一致,导致压缩感知方程模型不匹配,出现了损伤处附近幅值高点不唯一的现象。从图8还可看出最高处坐标为(39, 79),与真实损伤中心坐标(40, 80)基本吻合,具体定位信息见表2,损伤评估绝对误差为1.4 mm,低于计算频带内最小波长的一半。图9为分离出的60 µs时刻损伤散射波场图。可直接看出损伤中心附近存在许多波场不连续的点,这与源函数损伤成像中损伤处附近幅值高点不唯一的原因相同。此外可得出损伤散射波场沿着各个方向不均匀散射,其中沿实际激励源中心坐标(20, 40)方向,散射效果明显,波场连续性较好。在其他方向均出现波场不连续的现象。上述现象说明波场重构效果受到激励源和损伤相对位置的影响,在损伤沿着激励源方向,重构效果较好,其他方向重构效果有待改进。
表 2 数值模拟的CFRP板损伤定位信息Table 2. Damage location information of numerical simulation of CFRP plateReal location/
mmEstimated location/
mmAbsolute error/
mm(40, 80) (39, 79) 1.4 3. 复合材料板波场重构实验
3.1 实验平台搭建
搭建PZT激励-SLDV接收实验平台,其中实验仪器主要包括:PSV-500扫描式激光多普勒测振仪(SLDV)、圆形压电片(PZT,APC851,直径为10 mm,厚度为0.2 mm)、功率放大器(KH7602M)、信号发生器(Agilent 33220A)、碳纤维复合材料板(T300/QY8911,尺寸为800 mm×800 mm×1 mm,铺设方式[0/90]4s),具体参数见表1。为加强信号接受的强度以此提高信噪比,在被测量区域粘贴反射纸,其连接示意图如图10所示。将实验仪器依次连接,构造的PZT激励-SLDV接收实验平台实物图如图11所示。
3.2 损伤和测量区域设置
在无损复合材料板上粘贴一直径为10 mm的磁铁作为损伤,损伤设置如图12所示。为验证所提方法对于不同位置损伤定位的有效性,此处损伤位置并未与上节仿真中设置相同。在复合材料板背面粘贴反射纸以加强信号的接收,具体测量区域信息见图13。构建测量区域内的局部坐标,其中激励源中心坐标为(58, 58),损伤中心位置为(28, 88),测量区域为116 mm×116 mm,重构区域同测量区域。按照Nyquist采样定律,理论上需要729个采样点采集全波场,此处选取66个测量点,采样压缩率
{\gamma _\text{Scr}} =90.95%。3.3 含单损伤的波场重构和源成像
通过求解压缩感知方程,对其得出的源函数进行成像,即可得如图14所示的A0源成像图。可看出,激励源处的源函数值最高,损伤位置处可见微弱的源函数值。通过将源函数代入导波传播方程,结合构建的波数库即可重构出波场。具体重构波场和原始波场对比如图15所示,图15为具有代表性的62.3 µs时刻两者的波场图。比较图15(a)、图15(b)可知,整体上重构波场能够基本还原原始波场,两幅图中都可直接看出损伤位置产生的微弱散射波。具体细节上,在激励源中心和损伤中心处两者波场存在轻微的差别,推断原因为激励源定位的误差使重构波场信号存在偏差,致使重构的波场较原始波场出现偏差。通过相干系数定量评估重构精度,相干性
{G_\text{cc}}{\rm{ - }}f 曲线见图16。可看出,{G_\text{cc}}{\rm{ - }}f 曲线呈“几字形”分布,在计算频带60~140 kHz内,相干性为0.92,论证了本文所提出的波场重构方法的精准性。3.4 含单损伤的散射波场分离和损伤定位
在求解压缩感知方程后,将得到的源函数中激励源位置处的值进行归零,即得到只包含损伤信息的源函数,图17为处理后的A0模态源函数成像。可看出损伤位置处源函数值呈现带状分布,方向指向激励源位置。真实损伤周边出现许多幅值较低的伪源,主要原因为潜在源的均匀散射假设与真实损伤散射不均匀之间的差异导致计算模型不匹配,致使压缩感知方程得出的源函数解出现偏差。但是伪源幅值远低于损伤成像幅值,因此对于损伤的识别和定位不会产生太大影响。图中最高点位置为(24, 84),较损伤真实位置(28, 88)有所偏差,具体定位信息见表3,绝对误差为5.66,低于最小传播波长的2/3。定位误差原因分析为:因损伤采用直径为10 mm的圆形磁铁,入射波传到损伤位置时先与损伤外壁进行相互作用,随后部分导波绕过损伤向前传播。因此源函数成像中,损伤位置处最高点更靠近激励源。将只含损伤信息的源函数代入导波传播方程进行计算,由此得出损伤散射波场,此法能够在无需基准信号的情况下精准实现入射波场的去除。图18为具有代表性的62.3 µs时刻的损伤散射波场图,整体上损伤散射波场基本连续。具体细节上,受到源函数误差的影响损伤散射波场中出现许多波场不连续点。
表 3 单损伤实验的CFRP板损伤定位信息Table 3. Damage location information of single damage experiment of CFRP plateReal location/mm Estimated location/mm Absolute error/mm (28, 88) (24, 84) 5.66 3.5 含双损伤的散射波场分离和损伤定位
为验证所提方法对于多损伤定位的优越性,本节在复合材料板中粘贴两个直径10 mm的磁铁模拟双损伤,损伤设置示意图如图19所示。在复合材料板背面粘贴反射纸以加强信号的接收,具体测量区域信息见图20。构建测量区域内的局部坐标,其中激励源中心坐标为(58, 58),两个损伤中心坐标为(48, 98)和(28, 78),测量区域为116 mm×116 mm,重构区域同测量区域。测量点通过抖动方法选取100个点,采样压缩率
{\gamma _\text{Scr}} =86%。图21为通过求解压缩感知方程得出的A0源成像图。可直观看出激励源的位置,损伤处幅值因激励源幅值过强被覆盖。图22为移除激励源后的三维及二维源成像图。依据三维源成像图据此对双损伤进行定位,具体定位信息见表4。两个损伤的评估位置为(49, 94)和(27, 76),绝对误差为4.12mm和2.24mm,均低于计算频带内最小波长的2/3,验证了本文所提方法对于多损伤定位的精准性。图23为50 µs时刻的损伤散射波场,受到源函数误差的影响损伤散射波场中出现波场不连续点。
表 4 CFRP板的双损伤实验损伤定位信息Table 4. Damage location information of double damages experiment of CFRP plateDamage Real location/
mmEstimated location/
mmAbsolute error/
mmNo. 1 (48, 98) (49, 94) 4.12 No. 2 (28, 78) (27, 76) 2.24 4. 结 论
通过构建指定CFRP复合材料板参数的波数库,结合压缩感知算法实现了复合材料板中的波场重构和损伤成像。主要结论如下:
(1) 挖掘导波场在空间中的稀疏特性,将Lamb波在复合材料中的传播方程构造成系列源的叠加,结合压缩感知算法有效获取包含真实源(激励源、损伤)信息的源函数。
(2) 在源函数成像中,激励源函数值能量过强,致使损伤不可见,采用将激励源函数值去除的方法来有效得出损伤位置。针对单损伤的结果表明,以90%的采样压缩率进行数据采集仿真结果误差仅为1.4mm,实验结果误差为5.66 mm,低于最小波长的2/3。针对多损伤的实验结果表明,以86%的采样压缩率进行数据采集,双定位误差为4.12 mm和2.24 mm,均低于最小波长的2/3,验证了本方法可有效地检测双损伤。未来会深入研究复杂损伤及复合材料分层损伤的定位。
(3) 将去除激励源函数值后的源函数代入导波传播方程进行计算,可得损伤散射波场,该法可在无需基准信号的情况下精准实现入射波场的去除。
(4) 仿真和实验证明所提方法可在低于Nyquist采样点的情况下实现波场的重构,重构波场与原始波场相干性均在0.9以上,极大提高波场获取的效率,相关成果可为波场技术在实际应用提供理论和方法基础。
-
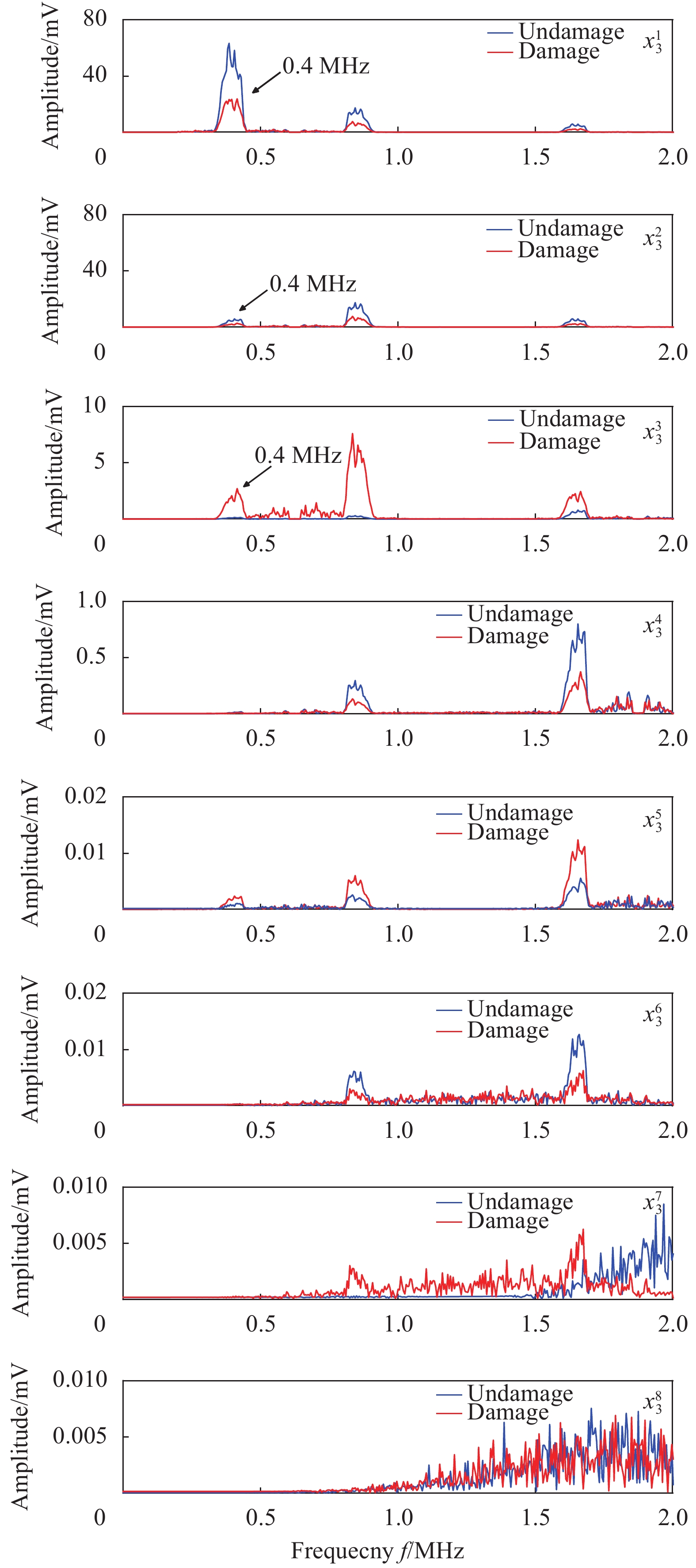
表 1 CFRP层板损伤前后各频段信号能量
Table 1 Signal energy of each frequency band before and after damage of CFRP composite laminate
Sub
bandEnergy before
damage/{{\rm{V}}^2}Energy after
damage/{{\rm{V}}^2}Energy ratio
change/%x_3^1 39.0691 6.9306 0.2203 x_3^2 3.5042 0.6390 0.2091 x_3^3 0.0809 0.0149 0.0065 x_3^4 0.0080 0.0017 0.0036 x_3^5 0.0014 2.832×10−4 0.0003 x_3^6 1.640×10−4 5.287×10−5 3.123×10−4 x_3^7 2.311×10−5 2.352×10−5 2.559×10−4 x_3^8 2.333×10−5 2.366×10−5 2.572×10−4 表 2 CFRP层板不同损伤因子定位结果对比
Table 2 Comparison of imaging localization results of different damage factors of CFRP composite laminate
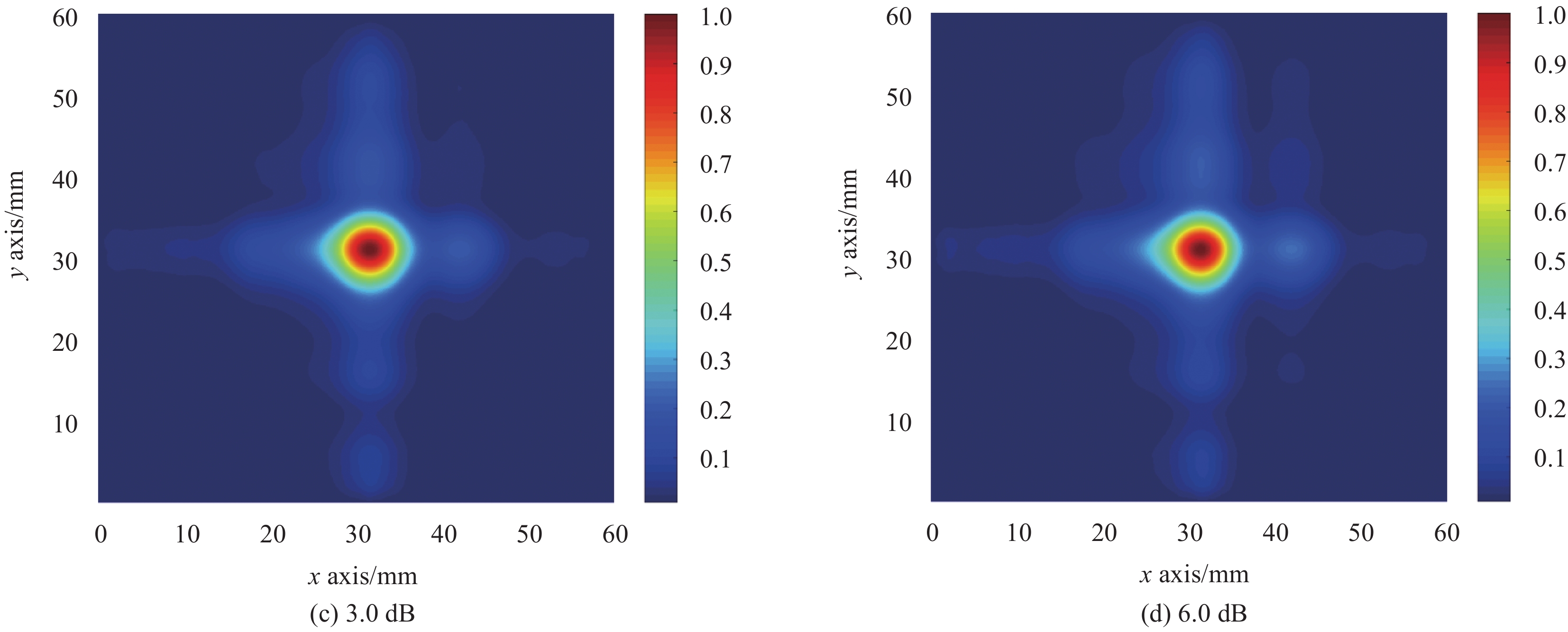
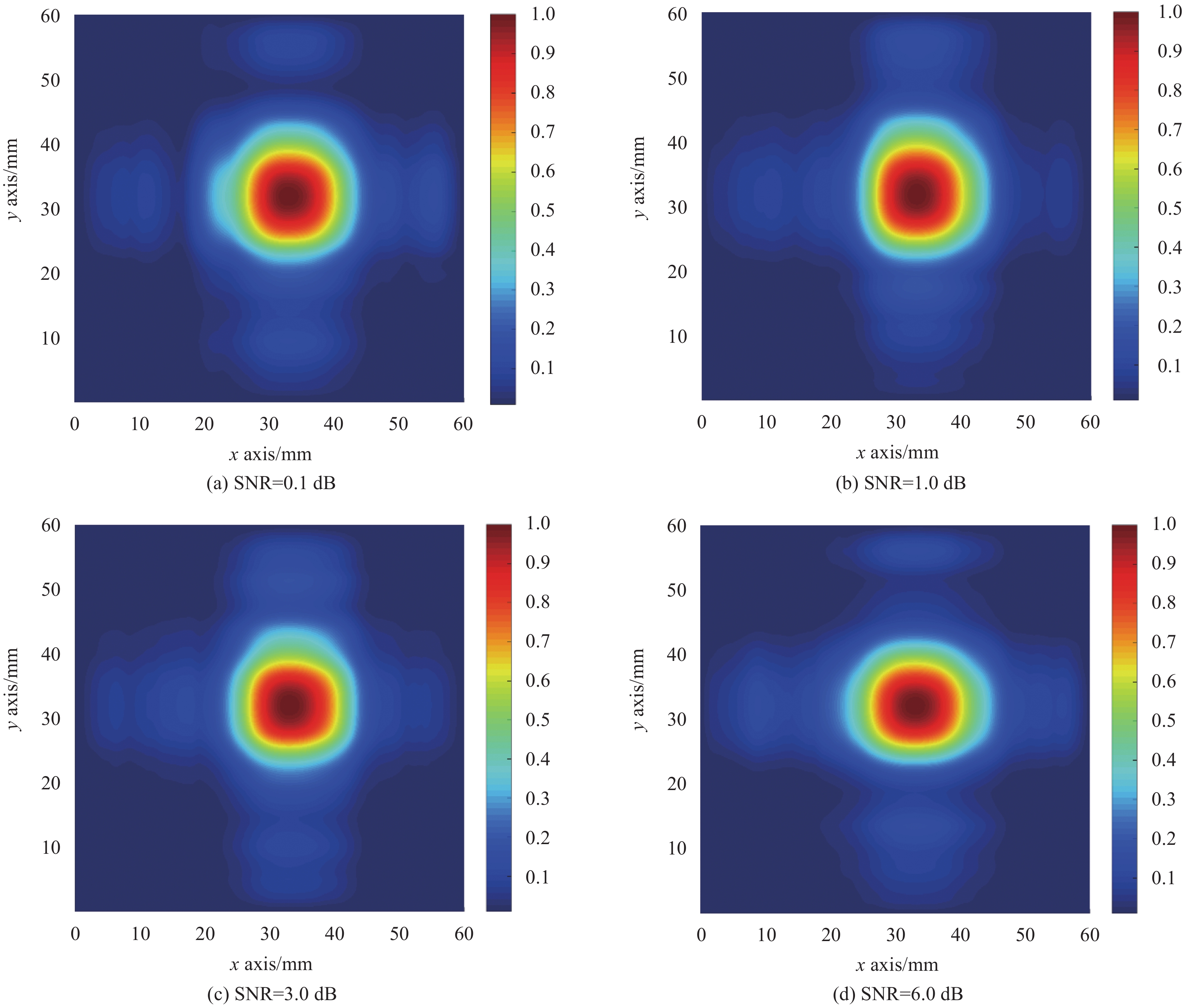
Noise level Actual position ERVDI position Absolute error/mm IEDI position Absolute error/mm (x,y) (x,y) (x,y) No noise (32,32) (31.5,32) 0.5 (33,32) 1 6 dB (32,32) (31.5,32) 0.5 (33,32) 1 3 dB (32,32) (32,31.5) 0.5 (32.5,32) 0.5 1 dB (32,32) (32,31.5) 0.5 (33.5,32) 1.5 0.1 dB (32,32) (32.5,31.5) 0.7 (33,32) 1 表 3 CFRP层板不同损伤因子定量结果对比
Table 3 Comparison of quantitative results of different damage factors of CFRP composite laminate
Noise level Actual size ERVDI size Error/mm IEDI position Error/mm x/mm y/mm x/mm y/mm x/mm y/mm x/mm y/mm x/mm y/mm No noise 10 10 10.6 10.1 0.6 0.1 15 16 5 6 6 dB 10 10 10.6 10.1 0.6 0.1 15 15.5 5 5.5 3 dB 10 10 10.6 10.1 0.6 0.1 15.5 15.5 5.5 5.5 1 dB 10 10 10.6 10.1 0.6 0.1 15 16.5 5 6.5 0.1 dB 10 10 10.6 10.6 0.6 0.6 15.5 16.5 5.5 6.5 -
[1] 刘松平, 刘菲菲, 史俊伟, 等. 复合材料冲击损伤高分辨率超声成像检测与损伤行为分析[J]. 机械工程学报, 2013, 49(22):16-23. LIU Songping, LIU Feifei, SHI Junwei, et al. High resolution ultrasonic imaging evaluation and behavior analysis of impact damages in composites[J]. Journalof Mechanical Engineering,2013,49(22):16-23(in Chinese).
[2] LAU Kintak, YUAN Libo, ZHOU Limin, et al. Strain monitoring in FRP laminates and concrete beams using FBG sensor[J]. Composites Structures, 2001, 51(1): 9-20.
[3] HUA Jiadong, LIN Jing, ZENG Liang. High-resolution damage detection based on local signal difference co-efficient model[J]. Structural Health Monitoring,2015,14(1):20-34.
[4] SURIANI M J, ALI A, SAPUAN S M, et al. Non-destructive techniques (NDT) in composite materials[J]. Key Engineering Materials,2011,462-463:918-924. DOI: 10.4028/www.scientific.net/KEM.462-463.918
[5] GUO Weichao, ZHAO Huaishan, GAO Xinqin, et al. An efficient representative for object recognition in structural health monitoring[J]. The International Journal of Advanced Manufacturing Technology,2018,94:3239-3250. DOI: 10.1007/s00170-016-9309-6
[6] LIU Zenghua, YU Hongtao, FAN Junwei, et al. Baseline-free delamination inspection in composite plates by synthesizing non-contact air-coupled Lamb wave scan method and virtual time reversal algorithm[J]. Smart Materials and Structures. 2015, 24(4): 045014.
[7] 李骥, 李力, 邓勇刚, 等. 空气耦合超声换能器的频域声场研究[J]. 机械工程学报, 2019, 55(10):10-16. DOI: 10.3901/JME.2019.10.010 LI Ji, LI Li, DENG Yonggang, et al. Study on acoustic field of air-coupled ultrasonic transducer in frequency domain[J]. Journal of Mechanical Engineering,2019,55(10):10-16(in Chinese). DOI: 10.3901/JME.2019.10.010
[8] 饶璐雅, 陈果, 卢超, 等. 碳纤维复合材料层板冲击损伤的空气耦合兰姆波成像检测[J]. 宇航材料工艺, 2017, 47(5):69-74. RAO Luya, CHEN Guo, LU Chao, et al. Imaging of CFRP plate impact damage using air-coupled lamb waves[J]. Aerospace Materials and Technology,2017,47(5):69-74(in Chinese).
[9] KAZYS R, MAZEIKA L, ZUKAUSKAS E. Investigation of accurate imaging of the defects in composite materials using ultrasonic air-coupled technique[J]. International Journal of Materials and Product Technology,2011,41(1-3):105-116.
[10] 常俊杰, 卢超, 川嶋紘一郎. 非接触空气耦合超声波的材料无损评价与检测[J]. 浙江理工大学学报, 2015, 33(7):532-536, 542. CHANG Junjie, LU Chao, KAWASHIMA Kouitirou. Nondestructive material evaluation and testing based on noncont-act air-coupled ultrasonics[J]. Journal of Zhejiang Sci-Tech University,2015,33(7):532-536, 542(in Chinese).
[11] 刘增华, 樊军伟, 何存富, 等. 基于概率损伤算法的复合材料板空气耦合Lamb波扫描成像[J]. 复合材料学报, 2015, 32(1):227-235. LIU Zenghua, FAN Junwei, HE Cunfu, et al. Scanning imaging of composite plate using air-coupled Lamb waves based on probabilistic damage algorithm[J]. Acta Materiae Composite Sinica,2015,32(1):227-235(in Chinese).
[12] KABBAN C M S, GREENWELL B M, DESIMIO M P, et al. The probability of detection for structural health monitoring systems: Repeated measures data[J]. Structural Health Monitoring,2015,14(3):252-264. DOI: 10.1177/1475921714566530
[13] WU Zhanjun, LIU Kehai, WANG Yishou, et al. Valiation and evaluation of damage identification using probability-based diagnostic imaging on a stiffened composite panel[J]. Journal of Intelligent Material Systems and Structures,2015,26(16):2181-2195. DOI: 10.1177/1045389X14549873
[14] 张海燕, 刘镇清, 吕东辉. 全局矩阵法及其在层状各向异性复合板中Lamb波传播特性研究中的应用[J]. 复合材料学报, 2004, 21(2):111-116. DOI: 10.3321/j.issn:1000-3851.2004.02.020 ZHANG Haiyan, LIU Zhenqing, LV Donghui. Global matrix and its application to study on Lamb wave propagation in layered anisotropic composite plates[J]. Acta Materiae Composite Sinica,2004,21(2):111-116(in Chinese). DOI: 10.3321/j.issn:1000-3851.2004.02.020
[15] 刘镇清, 他得安. 用二维傅里叶变换识别兰姆波模式的研究[J]. 声学技术, 2000, 19(4):212-214, 219. DOI: 10.3969/j.issn.1000-3630.2000.04.019 LIU Zhenqing, TA Dean. Mode identify of Lamb wave by means of 2D-FFT[J]. Technical Acoustics,2000,19(4):212-214, 219(in Chinese). DOI: 10.3969/j.issn.1000-3630.2000.04.019
[16] 严宏, 周丽. 基于损伤存在概率成像方法的复合材料结构损伤识别[J]. 振动与冲击, 2012, 31(13):76-80. DOI: 10.3969/j.issn.1000-3835.2012.13.016 YAN Hong, ZHOU Li. Damage identification of composite structures based on reconstruction algorithm for probabilistic inspection of damage[J]. Journal of Vibration and Shock,2012,31(13):76-80(in Chinese). DOI: 10.3969/j.issn.1000-3835.2012.13.016
[17] 张倩昀, 张华, 赵银燕. 复合材料冲击损伤监测的概率成像方法[J]. 应用声学, 2016, 35(5):426-430. ZHANG Qianyun, ZHANG Hua, ZHAO Yinyan. A probability imaging method of composite impact damage monitoring[J]. Applied Acoustics,2016,35(5):426-430(in Chinese).
[18] 苏晨辉, 姜明顺, 梁建英, 等. 强噪声下碳纤维增强树脂复合材料结构Lamb波层析损伤成像方法[J]. 复合材料学报, 2020, 37(4):886-895. SU Chenhui, JIANG Mingshun, LIANG Jianying, et al. Lamb wave tomography damage imaging of composite structures in strong noise environment[J]. Acta Materiae Compositae Sinica,2020,37(4):886-895(in Chinese).
[19] 万陶磊, 常俊杰, 曾雪峰, 等. 基于经验模态分 解和相关系数对玻璃纤维增强聚合物复合材料板的损伤识别及扫查成像[J]. 复合材料学报, 2020, 37(8): 1921-1931. WAN Taolei, CHANG Junjie, ZENG Xuefeng, et al. Damage identification and scanning imaging of glass fiber reinforced polymer composite plates based on empirical mode decomposition and correlateion coefficient[J]. Acta Materiae Composite Sinica, 2020, 37(8): 1921-1931(in Chinese).
[20] 任宜春, 张杰峰, 刘哲峰. 钢筋混凝土梁损伤的小波包识别方法[J]. 振动. 测试与诊断, 2011, 31(5):605-609, 665. REN Yichun, ZHANG Jiefeng, LIU Zhefeng. Damage identification of reinforced concrete beam based on wavelet packet[J]. Journal of Vibration, Measurement & Diagnosis,2011,31(5):605-609, 665(in Chinese).
[21] 丁幼亮, 李爱群. 基于振动测试与小波包分析的结构损伤预警[J]. 力学学报, 2006(5):639-644. DOI: 10.3321/j.issn:0459-1879.2006.05.010 DING Youliang, LI Aiqun. Structural damage early warning based on vibration testing and wavelet packet analysis[J]. Chinese Journal of Theoretical and Applied Mechanics,2006(5):639-644(in Chinese). DOI: 10.3321/j.issn:0459-1879.2006.05.010
[22] 张凯南, 张立茂, 吴贤国, 等. 基于小波包能量谱的地铁隧道健康监测预警[J]. 铁道标准设计, 2018, 62(12):130-135. ZHANG Kainan, ZHANG Limao, WU Xianguo, et al. Subway tunnel health alarming and warning method based on wavelet packet energy spectrum[J]. Railway Standard Design,2018,62(12):130-135(in Chinese).
[23] HU Keting, LIU Zhigang, LIN Shuangshuang. Wavelet entropy-based traction inverter open switch fault diagnosis in high-speed railways[J]. Entropy,2016,18(3):78. DOI: 10.3390/e18030078
[24] 王鑫, 孟昭博, 梁志闯. 基于小波包能量谱的西安钟楼木结构的损伤识别[J]. 应用力学学报, 2020, 37(3):1245-1252, 1403-1404. WANG Xin, MENG Zhaobo, LIANG Zhichuang. Damaged identification of Xi’an bell tower wood structures based on wavelet packet energy spectrum[J]. Chinese Journal of Applied Mechanics,2020,37(3):1245-1252, 1403-1404(in Chinese).
-
期刊类型引用(3)
1. 程涛,杨明,吴小龙. 基于压缩感知的兰姆波下采样和损伤定位. 机械设计与制造. 2024(04): 77-80 .  百度学术
百度学术
2. 冯继启,叶波,邹杨坤,朱之贞,杨常春. 基于MVDR加权稀疏重建的CFRP损伤成像. 复合材料学报. 2024(10): 5673-5686 .  本站查看
本站查看
3. 马骁阳,肖文,沙刚刚,左洪福. 复合材料板冲击损伤的Lamb波场成像算法研究. 航空计算技术. 2022(04): 51-55 .  百度学术
百度学术
其他类型引用(2)
-

















































 下载:
下载: