Calculation method of thermal deformation and residual stress of arbitrarily laminated FRP tube based on three-dimensional elastic theory
-
摘要: 为了解决纤维增强树脂复合材料(FRP)圆管在工程中热变形和热残余应力的问题，提出了一种针对任意铺层FRP圆管等效热膨胀系数和热残余应力的计算方法，该方法是综合考虑了层合效应、各向异性材料三维本构关系的三维弹性理论。通过与本文试验和ANSYS数值模型的多组数据进行对比分析，验证了理论的正确性。并以此理论模型为基础，首先对多种铺层FRP圆管等效热膨胀系数进行研究，其次结合Hashin失效准则的强度比方程，对由热残余应力引起FRP圆管强度失效进行分析。结果表明：FRP圆管铺层角度对等效热膨胀系数的影响在热缩阶段、热胀阶段表现不同，且存在等效热膨胀系数为0的铺层方式；径厚比仅对等效径向热膨胀系数影响较大，对等效轴向热膨胀系数无影响；温差大小及温差方向影响FRP圆管的破坏模式及破坏位置，热残余应力引起的FRP圆管的强度破坏均为基体破坏。Abstract: In order to solve the problems of thermal deformation and thermal residual stress of fiber reinforced polymer (FRP) circular pipe in engineering, a calculation method of equivalent thermal expansion coefficient and thermal residual stress of FRP tube with arbitrary ply was proposed. This method is a three-dimensional elastic theory considering lamination effect and three-dimensional constitutive relationship of anisotropic material. The correctness of the theory was verified by comparing and analyzing with multiple groups of data of the test and ANSYS numerical model in this paper. Based on this theoretical model, firstly, the equivalent thermal expansion coefficients of many kinds of laminated FRP circular pipes were studied. Secondly, combined with the strength ratio equation of Hashin failure criterion, the strength failure of FRP tube caused by thermal residual stress was analyzed. The results show that the influence of FRP tube ply angle on the equivalent thermal expansion coefficient is different in the thermal shrinkage stage and thermal expansion stage, and there is a laminated mode with zero equivalent thermal expansion coefficient; The diameter thickness ratio only has a great influence on the equivalent radial thermal expansion coefficient, but has no influence on the equivalent axial thermal expansion coefficient; Temperature difference and direction affect the failure mode and location of FRP tubes. The strength failure of FRP tubes caused by thermal residual stress is matrix failure.
-
图 1 纤维增强树脂复合材料(FRP)层合管坐标系、铺层角度和铺层参数
Figure 1. Coordinate system, layer angle and layer parameters of fiber reinforced polymer (FRP) laminated tube
rn—Inner radius of the n layer
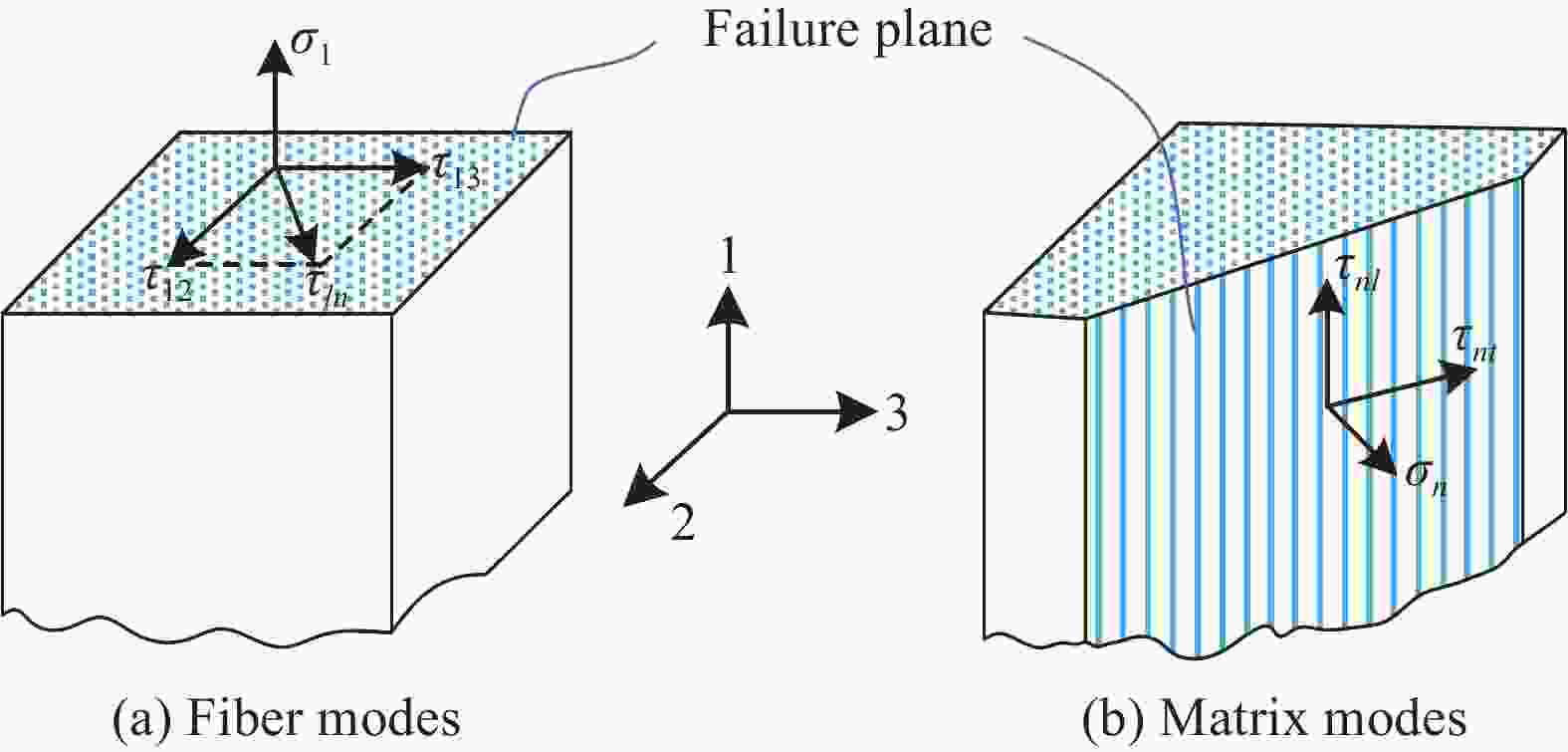
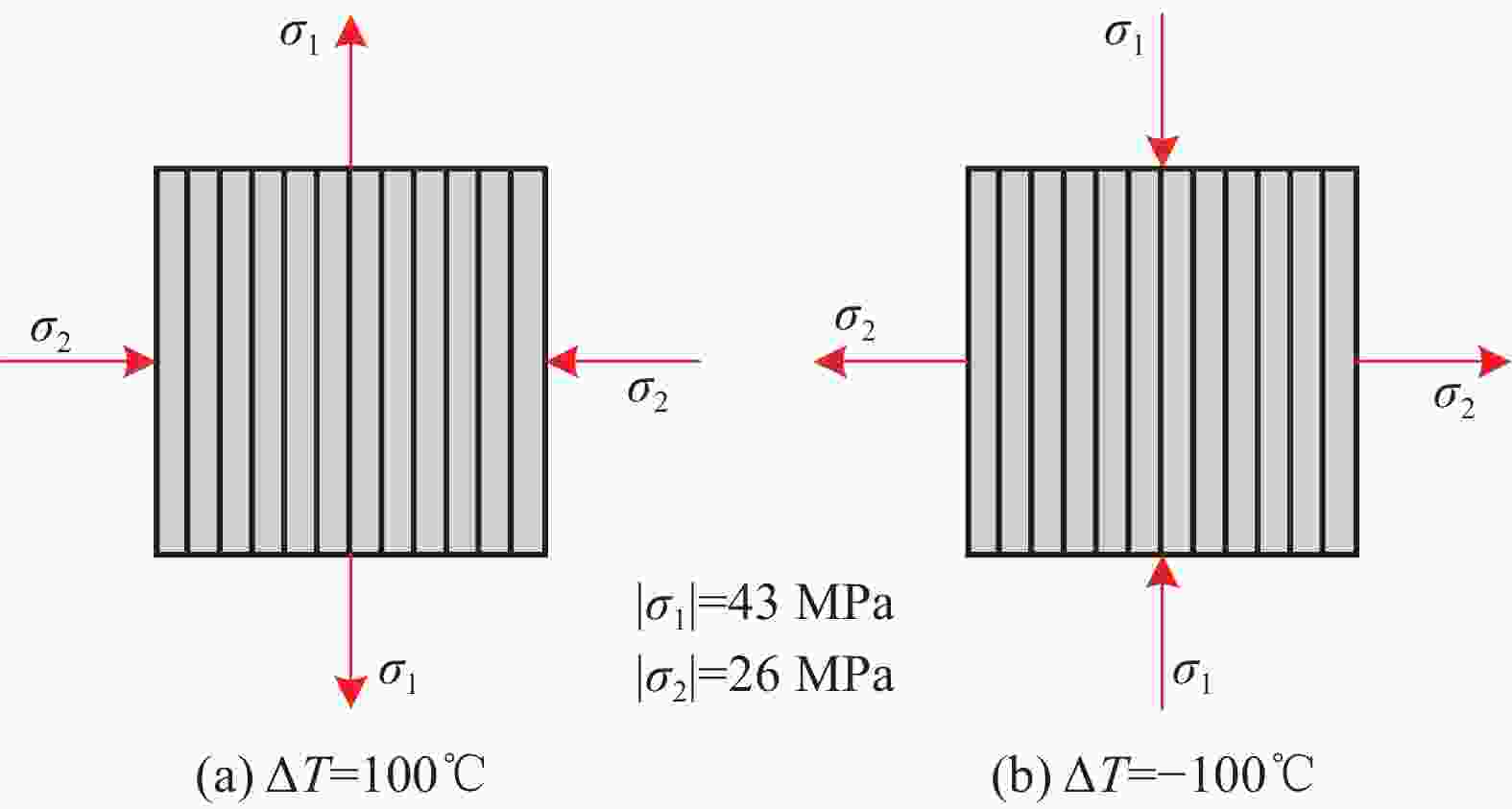
图 4 纤维和基体失效模式与失效界面
Figure 4. Failure modes and failure planes of fiber and matrix
σ1—Fiber direction normal stress; τ—Shear stress, subscripts 1, 2 and 3 indicate the axial, radial and circumferential directions of the fiber, respectively; σn—Normal stress in normal direction; τnt—Transverse shear stress; τln—Axial shear stress
图 9 FRP层合管试件Tube B变形协调机制示意图
Figure 9. Schematic diagram of deformation coordination of FRP laminated tube specimen Tube B
图 10 ANSYS定义材料参数、铺层参数
Figure 10. ANSYS defines material parameters and layering parameters
图 11 FRP圆管的铺层信息和模型的端部约束方式
Figure 11. Layup information of FRP circular tube and the end constraint mode of the model
图 12 ANSYS数值模型计算结果的查看方法
Figure 12. View method of ANSYS numerical model calculation results
图 13 FRP层合管ANSYS数值模型应变计算结果
Figure 13. ANSYS numerical model strain calculation results of FRP laminated tubes
图 15 约束铺层位于不同位置时FRP层合管等效热膨胀系数随约束铺层θ的变化关系(ΔT=100℃)
Figure 15. Relation of the equivalent thermal expansion coefficient with θ of FRP laminated tubes when the constraint layer is located at different positions (ΔT=100℃)
图 14 FRP层合管试件Tube B应力应变沿壁厚分布图
Figure 14. Distribution diagram of stress and strain along wall thickness of FRP laminated tube specimen Tube B
图 16 FRP层合管等效热膨胀系数
$\bar \alpha $ 随环向约束铺层层数n增加的变化曲线Figure 16. Curve of equivalent thermal expansion coefficient
$\bar \alpha $ with the increase of the constraint layer n of FRP laminated tube
图 17 圆形变形的几何关系
Figure 17. Geometric relation of circular deformation
R—Radius before deformation; Rf—Radius after free temperature deformation
图 18 不同径厚比λ时FRP圆管等效热膨胀系数与铺层角度θ的关系
Figure 18. Relationship between equivalent thermal expansion coefficient of FRP tubes with different diameter-thickness ratios λ and layer angle θ
图 19 FRP层合管等效热膨胀系数与径厚比λ的关系
Figure 19. Relationship between equivalent thermal expansion coefficient and diameter-thickness ratio λ of FRP laminated tube
图 20 FRP层合管强度比和极限温差的计算方法流程图
Figure 20. Flow chart of calculation method of strength ratio and limit temperature difference of FRP laminated tube
图 21 FRP层合管试件Tube B应力沿壁厚分布
Figure 21. Stress distribution along wall thickness of FRP laminated tube specimen Tube B
$\sigma _{2}^{\max } $—Maximum normal stress in 2 direction
图 22 FRP层合管试件Tube B节点的坐标位置
Figure 22. Coordinates of node point of FRP laminated tube specimen Tube B
图 23 FRP层合管试件Tube B破坏点处的应力单元体
Figure 23. Stress element at failure point of FRP laminated tube specimen Tube B
图 24 FRP圆管强度比R与铺层角度θ的关系
Figure 24. Relationship between the strength ratio R of FRP laminated tubes and ply angles θ
图 25 FRP圆管垂直纤维方向的变形协调
Figure 25. Deformation coordination of FRP laminated tubes in vertical fiber direction
图 26 FRP圆管纤维方向的变形协调
Figure 26. Deformation coordination of FRP laminated tubes in fiber direction
表 1 T700SC-12K-50C碳纤维/YPH-307环氧树脂预浸料基本力学性能参数
Table 1. Basic mechanical property parameters of T700SC-12K-50C carbon fber/YPH-307 epoxy prepreg
Engineering
constantsValue Strength
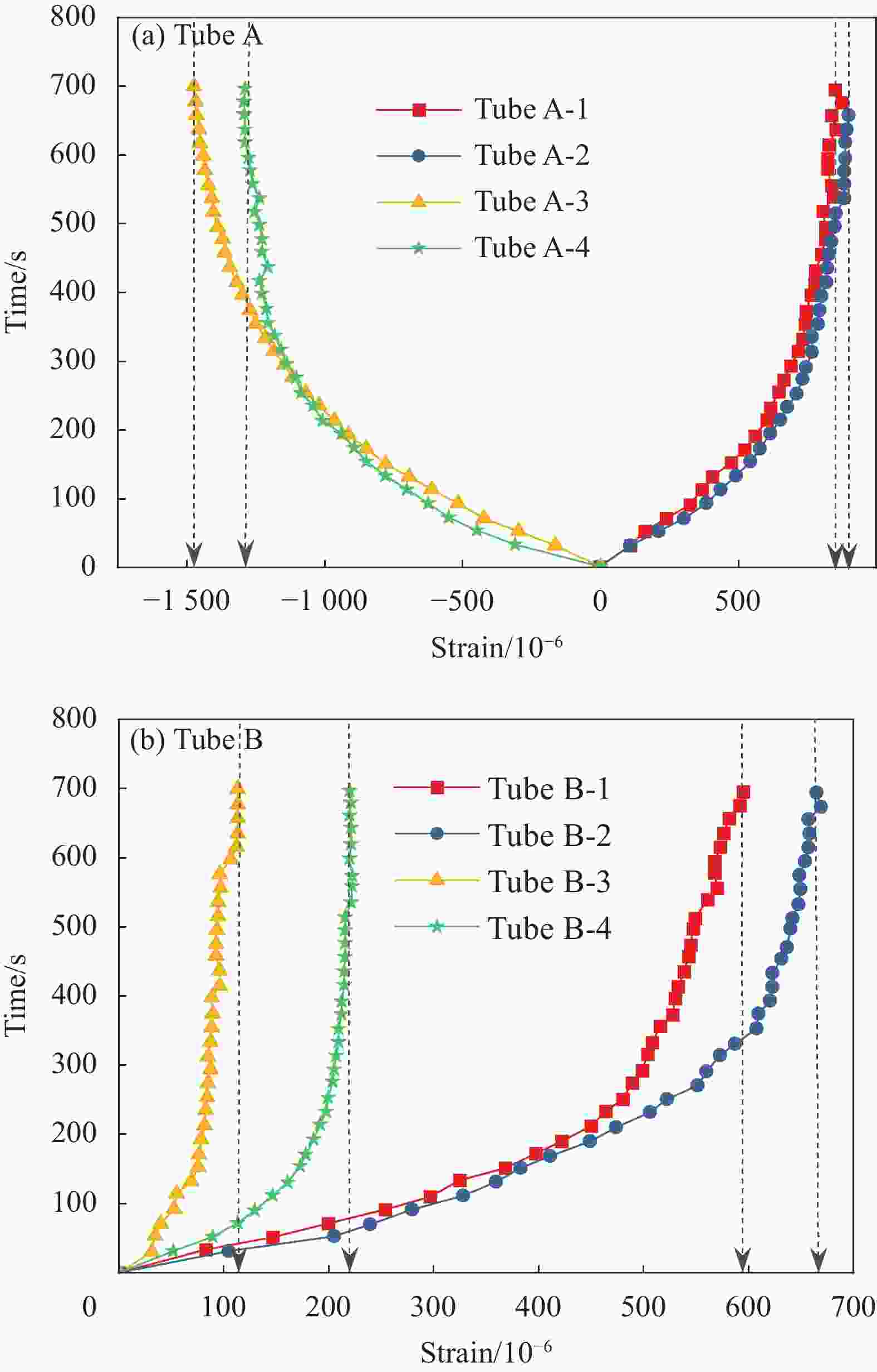
parametersValue E1/GPa 95.0 Xt/MPa 2448 E2/GPa 7.4 Xc/MPa 835 G12/GPa 3.60 Yt/MPa 31.0 G23/GPa 2.74 Yc/MPa 103.9 v12 0.30 Q/MPa 45.0 v23 0.35 S/MPa 53.2 αL/(10−6 ℃−1) −15 αT/(10−6 ℃−1) 23 Notes: E, G, and ν—Elastic modulus, shear modulus and Poisson's ratio; Subscripts 1, 2 and 3—Axial, radial and circumferential directions of the fiber respectively; αL—Axial thermal expansion coefficient; αT —Transverse thermal expansion coefficient; Xt—Tensile failure stress in fiber direction; Xc—Compressive failure stress in fiber direction (absolute value); Yt—Tensile failure stress transverse to fiber direction; Yc—Compressive failure stress transverse to fiber direction (absolute value); Q—Transverse failure shear, τnt in Fig. 4(b); S—Axial failure shear, τln in Fig. 4(a). 
下载: 导出CSV
表 2 FRP层合管试件表观应变值
Table 2. Apparent strain of FRP laminated tube specimens
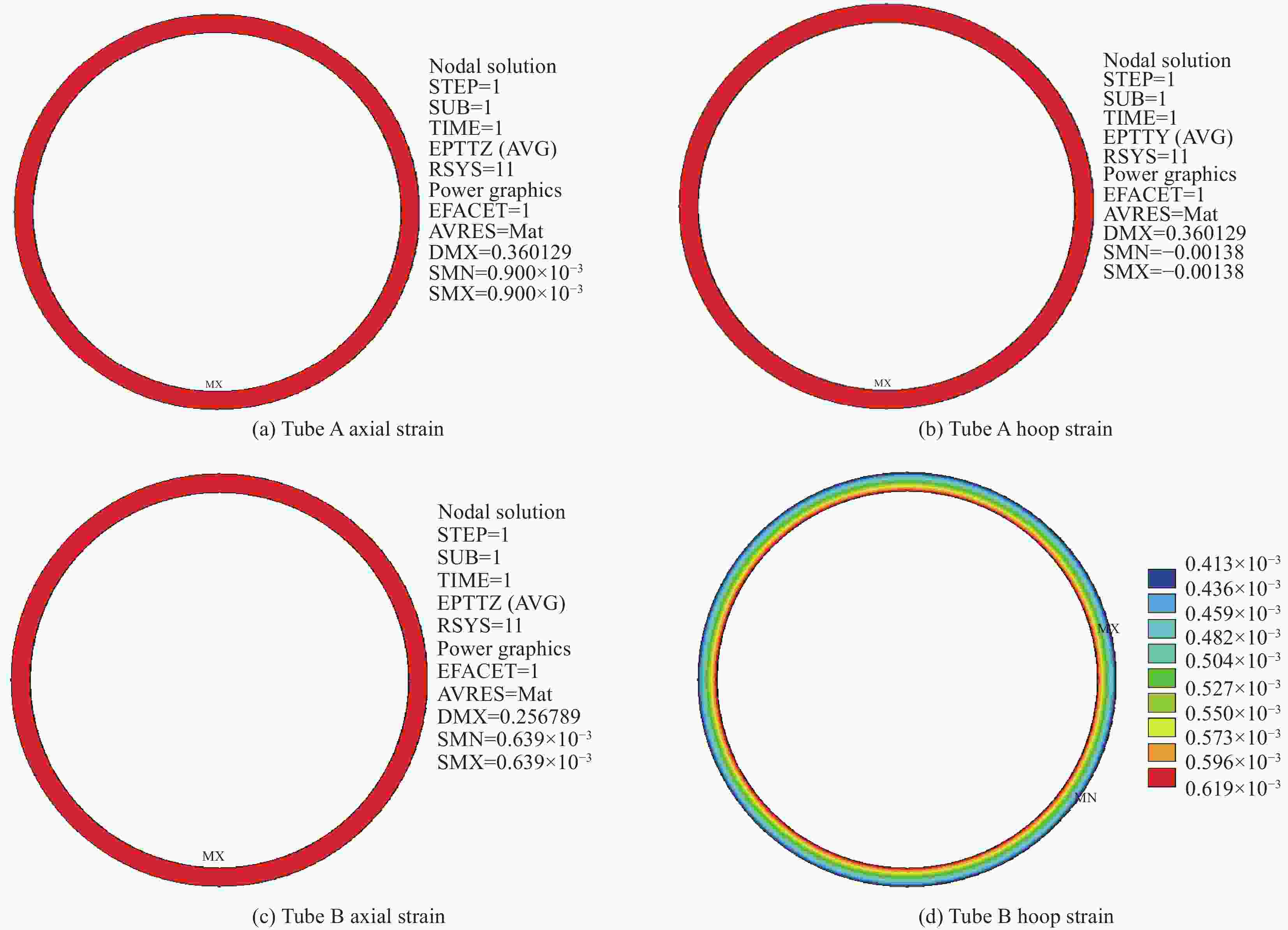
10−6 Specimen Measuring points Measured strain Mean strain Tube A 1 850 875 2 900 3 −1474 −1381 4 −1288 Tube B 1 594 629 2 664 3 114 167 4 220
下载: 导出CSV
表 3 FRP层合管试验、理论、ANSYS结果对比
Table 3. Comparison of experimental, theoretical and ANSYS results of FRP laminated tubes
10−6 Specimen Test
resultsANSYS
resultsTheoretical
resultsRelative error/% Tube A Axial strain 875 900 900 2.9 Hoop strain −1381 −1380 −1380 0.1 Tube B Axial strain 629 639 639 1.4 Hoop strain 167 413 413 146.0
下载: 导出CSV
表 4 FRP圆管破坏位置及破坏模式
Table 4. Location and mode of failure of FRP laminated tubes
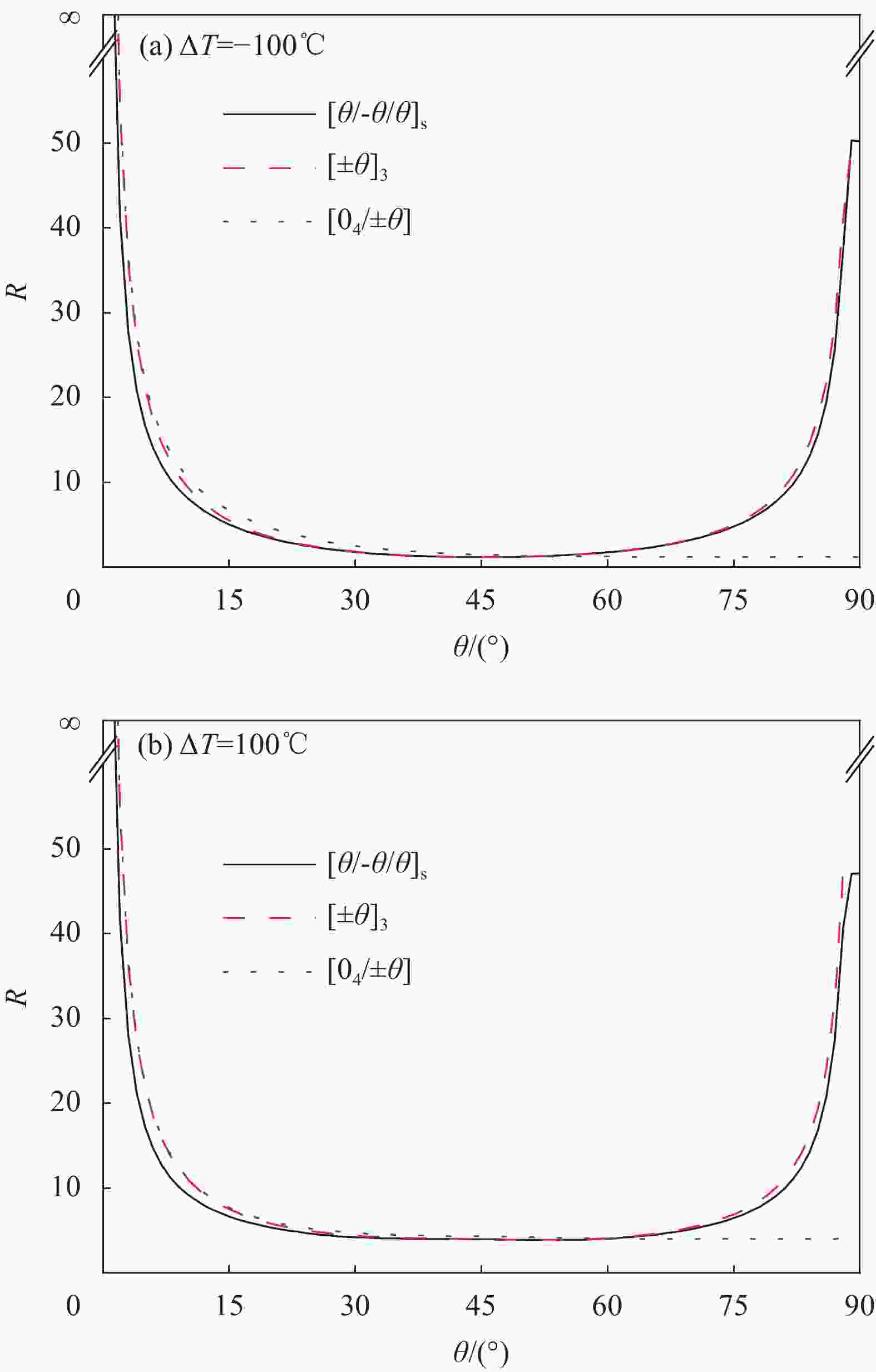
Laminated θ Failure layer Failure mode Temperature difference [04/±θ] 0°-90°
(exclude 0°)Fifth layer Transverse tensile failure of matrix −100℃ Transverse compression failure of matrix 100℃ [±θ]3 0°-90°
(exclude 0°, 90°)First layer Transverse tensile failure of matrix −100℃ Transverse compression failure of matrix 100℃ [±θ/θ]s 0°-10°
(exclude 0°)Fifth layer Transverse tensile failure of matrix −100℃ Transverse compression failure of matrix 100℃ 11°-90°
(exclude 90°)Second layer Transverse tensile failure of matrix −100℃ Transverse compression failure of matrix 100℃
下载: 导出CSV
-
[1] ZHANG D, YUAN J, LI F, et al. Experimental characterization of static behavior of a new GFRP-metal space truss deployable bridge: Comparative case study[J]. Journal of Bridge Engineering,2021,26:5020011. doi: 10.1061/(ASCE)BE.1943-5592.0001650 [2] ZHANG D. Static performance of a new GFRP-metal string truss bridge subjected to unsymmetrical loads[J]. Steel and Composite Structures,2020,35:641-657. [3] ZHANG D, LV Y, ZHAO Q, et al. Development of lightweight emergency bridge using GFRP-metal composite plate-truss girder[J]. Engineering Structures,2019,196:109291. doi: 10.1016/j.engstruct.2019.109291 [4] ZHANG D, LI F, SHAO F, et al. Evaluation of equivalent bending stiffness by simplified theoretical solution for an FRP-aluminum deck-truss structure[J]. KSCE Journal of Civil Engineering,2018,23:367-375. [5] GAO J, ZHAO Q, LI F, et al. Fatigue failure investigation of pultruded GFRP pre-tightened single-tooth connector (PTSTC)[J]. Engineering Failure Analysis,2019,106:104191. doi: 10.1016/j.engfailanal.2019.104191 [6] ZHU R, LI F, CHEN Y, et al. The effect of tube-in-tube buckling-restrained device on performance of hybrid PFRP-aluminium space truss structure[J]. Composite Structures,2021,260:113260. doi: 10.1016/j.compstruct.2020.113260 [7] ZHU R, LI F, CHEN Y, et al. A hybrid beam-column element for direct second-order nonlinear analysis of PFRP frame structures[J]. Composite Structures,2021,271:114171. doi: 10.1016/j.compstruct.2021.114171 [8] ZHU R, LI F, SHAO F, et al. Static and dynamic behaviour of a hybrid PFRP-aluminium space truss girder: Experimental and numerical study[J]. Composite Structures,2020,243:112226. doi: 10.1016/j.compstruct.2020.112226 [9] 吴杰, 肖正航. 碳纤维复合材料残余应力消除方法探讨[J]. 航天制造技术, 2012(4):38-40.WU Jie, XIAO Zhenghang. Discussion on carbon fiber composite residual stress relief[J]. Aerospace Maunfacturing Technology,2012(4):38-40(in Chinese). [10] 赵启林, 高一峰, 李飞. 复合材料预紧力齿连接技术研究现状与进展[J]. 玻璃钢/复合材料, 2014(12):52-56.ZHAO Qilin, GAO Yifeng, LI Fei. Current reseach and development of the application of the pre-tightened tooth connection[J]. Fiber Reinforced Plastics/Composites,2014(12):52-56(in Chinese). [11] 左扬, 李飞, 赵启林, 等. 基于挤压法的复合材料预紧力齿连接预紧力计算方法研究[J]. 复合材料科学与工程, 2020(5):32-39. doi: 10.3969/j.issn.1003-0999.2020.05.005ZUO Yang, LI Fei, ZHAO Qilin, et al. Study on the calculation method of preload for composite pre-tightened tooth connections based on extrusion method[J]. Composites Science and Engineering,2020(5):32-39(in Chinese). doi: 10.3969/j.issn.1003-0999.2020.05.005 [12] 孙宝玉. 轻型大视场光学遥感器结构动态特性研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2004.SUN Baoyu. Research on dynamic characteristic of the light-duty great visual field optical remote sensor[D]. Changchun: Chinese Academy of Sciences (Changchun Institute of Optics, Fine Mechanics and Physics), 2014(in Chinese). [13] 王建花. 复合材料身管残余应力研究[D]. 南京: 南京理工大学, 2007.WANG Jianhua. Study on residual stress of the composite materials barrel[D]. Nanjing : Nanjing University of Science & Technology, 2007(in Chinese). [14] MAIER G, HOFMANN F. Performance enhancements of polymer-matrix composites by changing of residual stresses[J]. Composites Science and Technology,2008,68(9):2056-2065. doi: 10.1016/j.compscitech.2008.03.001 [15] SHOKRIEH M M, AKBARI S, DANESHVAR A. A comparison between the slitting method and the classical lamination theory in determination of macro-residual stresses in laminated composites[J]. Composite Structures,2013,96:708-715. doi: 10.1016/j.compstruct.2012.10.001 [16] 梁群, 冯喜平. 复合材料壳体固化成型过程残余应力和形变分析[J]. 固体火箭技术, 2019, 42(5):628-634.LIANG Qun, FENG Xiping. Residual stress and structural distortion analysis for the curing process of srm composite case[J]. Journal of Solid Rocket Technology,2019,42(5):628-634(in Chinese). [17] 刘加顺, 李峰, 张恒铭. 树脂基碳纤维卷铺管件热残余应力分析[J]. 玻璃钢/复合材料, 2016(2):18-23.LIU Jiashun, LI Feng, ZHANG Hengming. Thermal residual stress analysis of polymer matrix carbon fiber reinforced composite winding tubes[J]. Fiber Reinforced Plastics/Composites,2016(2):18-23(in Chinese). [18] 娄菊红, 杨延清. 基体性能对复合材料热残余应力的影响[J]. 材料研究学报, 2016, 30(7):503-508.LOU Juhong, YANG Yanqing. Effect of matrix properties on thermal residual stress of fiber reinforced ti-matrix composities[J]. Chinese Journal of Materials Research,2016,30(7):503-508(in Chinese). [19] 杨雷, 武湛君. 热残余应力对纤维增强树脂基复合材料横向力学性能的影响[C]. 上海: 中国力学大会, 2015.YANG Lei, WU Zhanjun. Effect of thermal residual stress on transverse mechanical properties of fiber reinforced resin matrix composites[C]. Shanghai: Chinese Conference on Mechanics, 2015(in Chinese). [20] PETRUSHIN S I. Calculation of thermal residual stresses in multilayer composite materials[J]. Applied Mechanics and Materials,2013,379:95-100. doi: 10.4028/www.scientific.net/AMM.379.95 [21] 徐亮工. 缠绕玻璃钢管道的残余热应力[J]. 玻璃钢/复合材料, 1997(1):11-12.XU Lianggong. Thermal residual stress in filament winding FRP pipe[J]. Fiber Reinforced Plastics/Composites,1997(1):11-12(in Chinese). [22] 王建花, 钱林方, 袁人枢. 复合材料身管的热残余应力[J]. 弹道学报, 2007(1):82-85. doi: 10.3969/j.issn.1004-499X.2007.01.023WANG Jianhua, QIAN Linfang, YUAN Renshu. Thermal residual stresses in composite material barrel[J]. Journal of Ballistics,2007(1):82-85(in Chinese). doi: 10.3969/j.issn.1004-499X.2007.01.023 [23] WANG J, QIAN L, YUAN R. The Residual stresses and strains in the composite material barrel[C]. Proceedings of the International Conference on Mechanical Engineering and Mechanics, Nanjing, 2005. [24] 徐芝纶. 弹性力学简明教程[M]. 第五版. 北京: 高等教育出版社, 2018: 167-172.XU Zhilun. Concise course of elasticity[M]. Fifth Edition. Beijing: Higher Education Press, 2018: 167-172(in Chinese). [25] 李峰, 李若愚. 复合材料力学与圆管计算方法[M]. 北京: 科学出版社, 2021: 170-172.LI Feng, LI Ruoyu. Mechanics of composite materials and calculation methods for circular tubes[M]. Beijing: Science Press, 2021: 170-172(in Chinese). [26] 国家质量技术监督局. 定向纤维增强塑料拉伸性能试验方法: GB/T 3354—1999[S]. 北京: 中国标准出版社, 1999.State Bureau of Quality and Technical Supervision. Test method for tensile properties of oriented fiber reinforced plastics: GB/T 3354—1999[S]. Beijing: China Standards Press, 1999(in Chinese). [27] 中华人民共和国国家质量监督检验检疫总局. 单向纤维增强塑料平板压缩性能试验方法: GB/T 3856—2005[S]. 北京: 中国标准出版社, 2005.General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. Test method for compression properties of unidirectional fiber reinforced plastics: GB/T 3856—2005[S]. Beijing: China Standards Press, 2005(in Chinese). [28] ASTM International. Standard test method for shear pro-perties of composite materials by V-notched rail shear method: ASTM D7078/D7078M-12[S]. West Conshohocken: ASTM International, 2012. [29] 张恒铭, 李峰, 潘大荣. 基于三维梁理论的复合材料层合管等效抗弯刚度[J]. 复合材料学报, 2016, 33(8):1694-1701.ZHANG Hengming, LI Feng, PANG Darong. Equivalent bending stiffness of composite laminated tube based on 3D beam theory[J]. Acta Materiae Compositae Sinica,2016,33(8):1694-1701(in Chinese). [30] 姜海林. 基于等效位移法的低速冲击载荷下复合材料层合板损伤力学模型[D]. 大连: 大连理工大学, 2020.JIANG Hailin. Damage mechanics model of composite laminates under low speed impact loading based on equivalent displacement method[D]. Dalian: Dalian University of Technology, 2020(in Chinese). [31] 沈观林, 胡更开, 刘彬. 复合材料力学[M]. 第二版. 北京: 清华大学出版社, 2013: 129-133.SHEN Guanlin, HU Gengkai, LIU Bin. Mechanics of composite materials[M]. Second Edition. Beijing: Tsinghua University Press, 2013: 129-133(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 1020
- HTML全文浏览量: 491
- PDF下载量: 52
- 被引次数: 0
