Crack initiation and propagation mechanism during uniaxial compression of SiC/AZ91D magnesium matrix composites
-
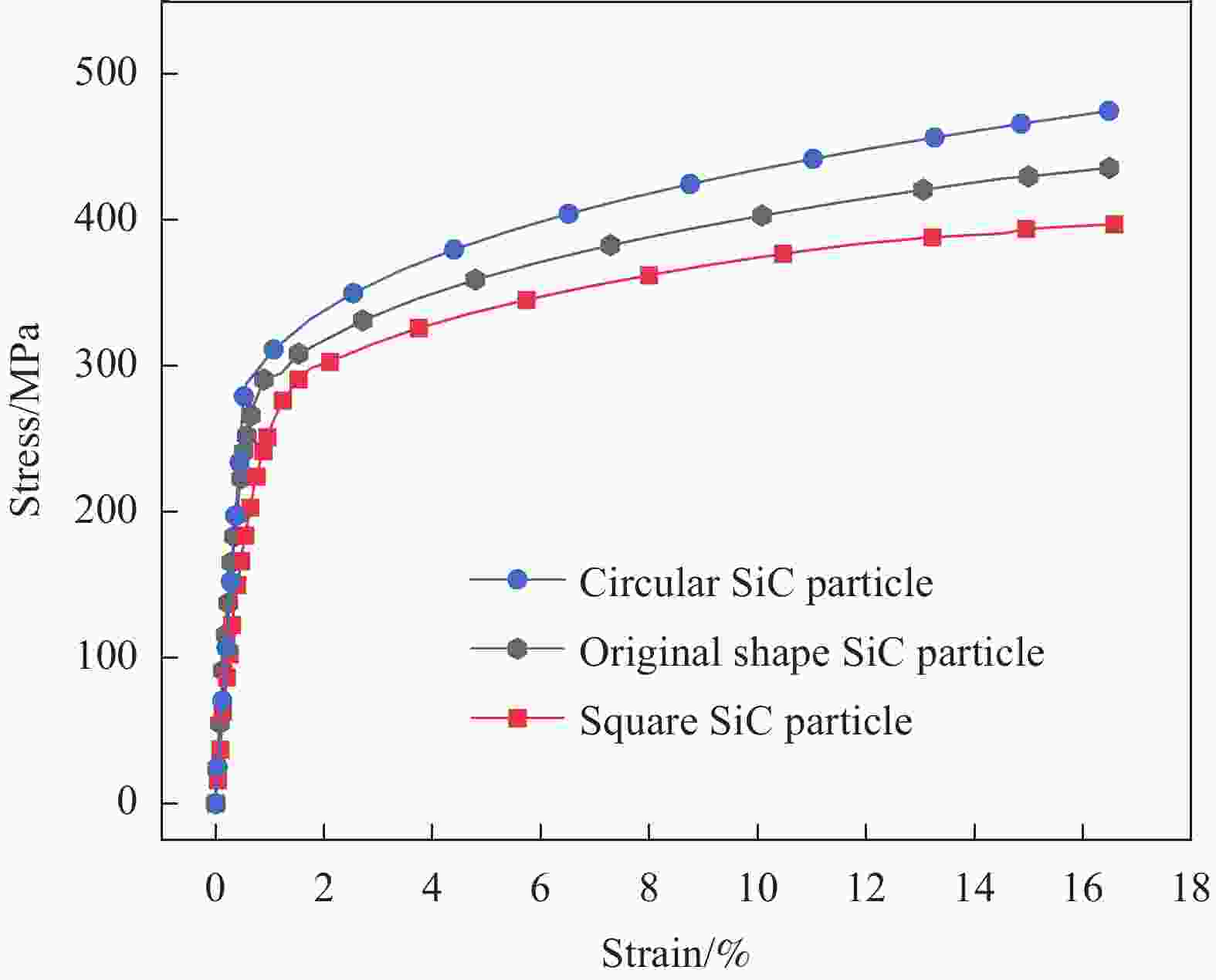
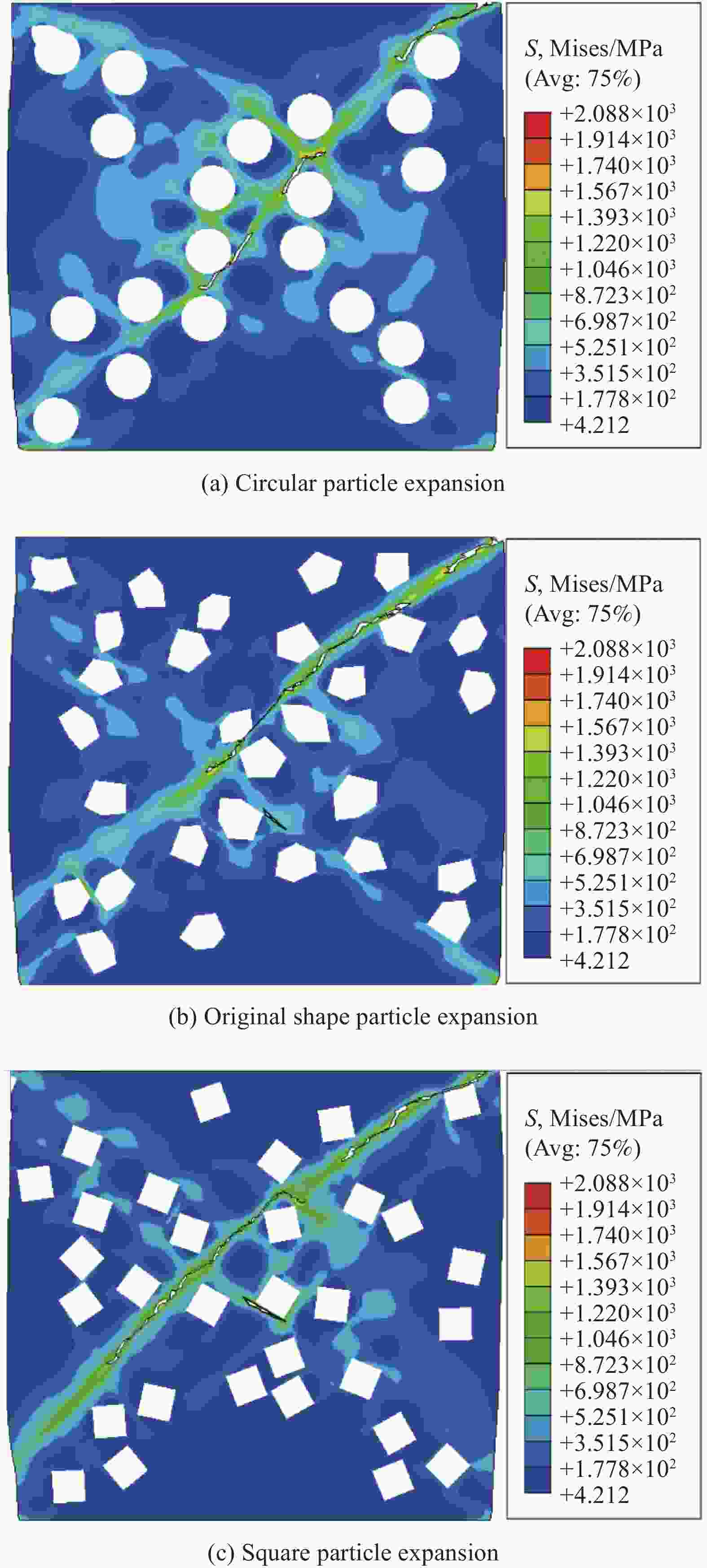
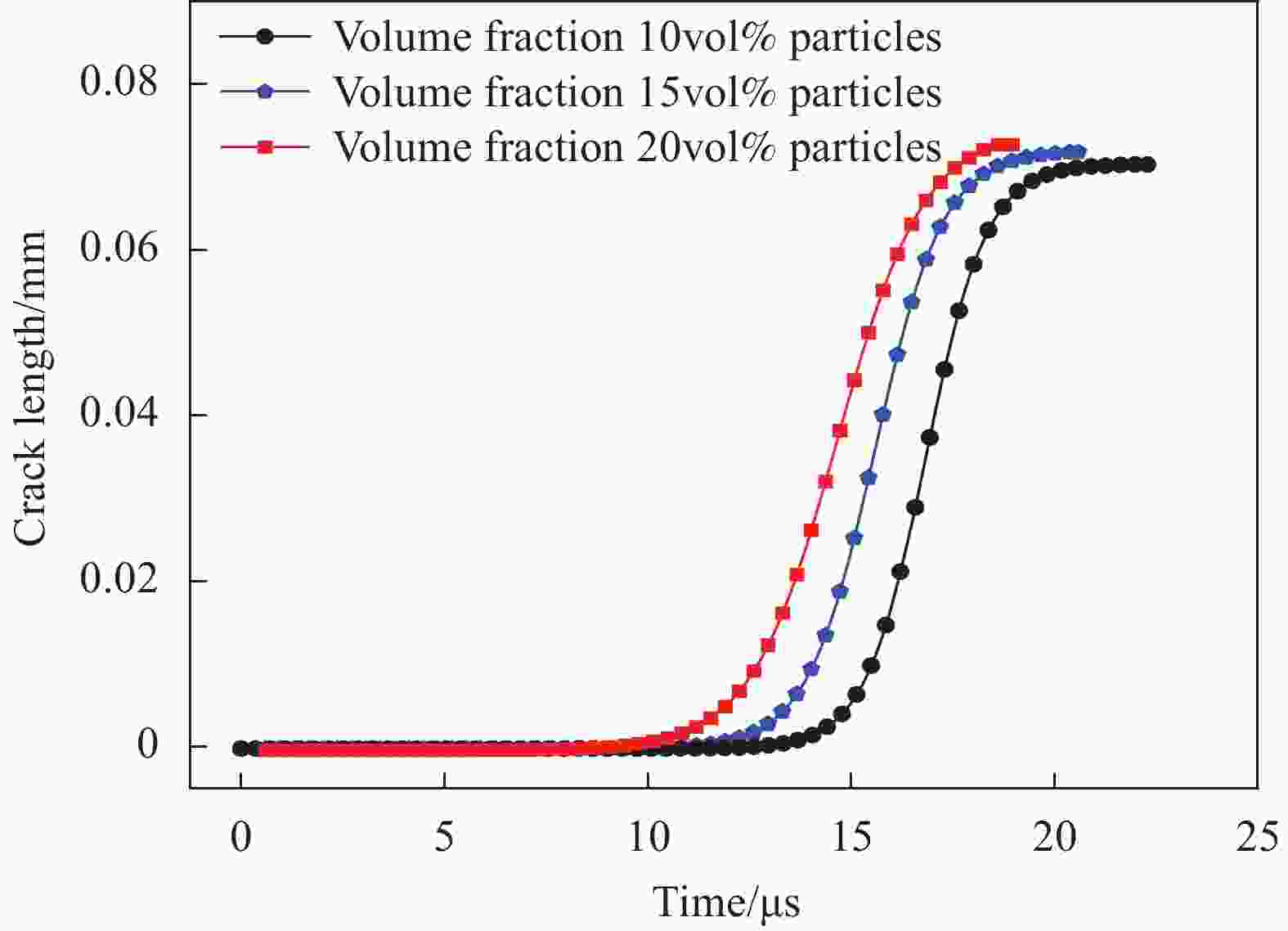
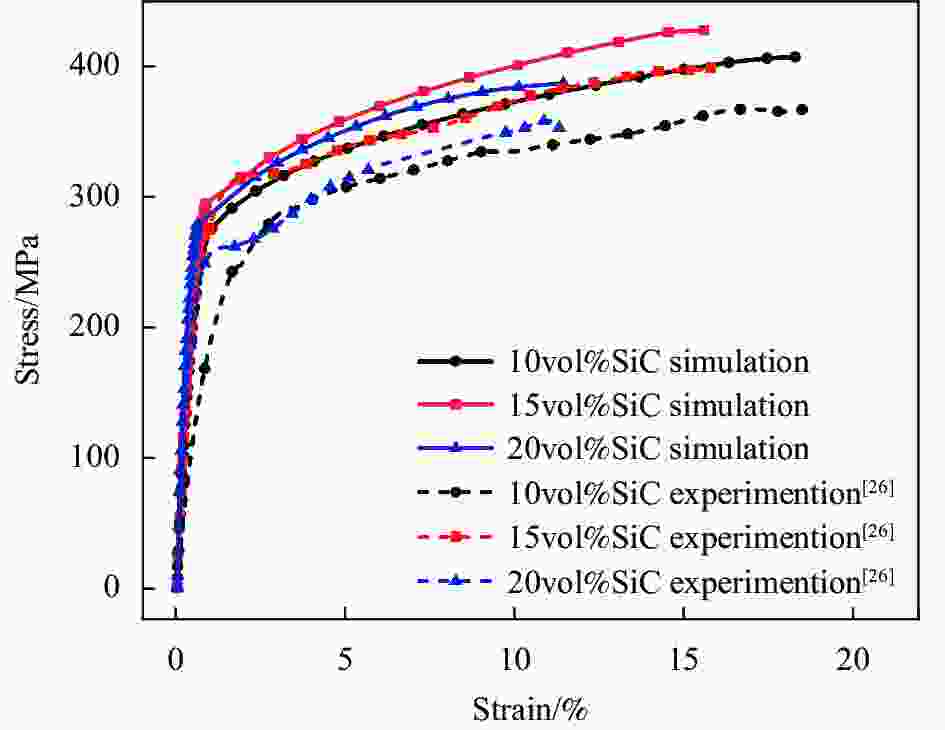
摘要: 利用有限元分析软件Abaqus在有限元模型颗粒界面引入内聚力单元, 研究了不同形状和不同体积分数SiC颗粒的SiC/AZ91D镁基复合材料在单轴压缩情况下裂纹萌生扩展机制。内聚力单元的引入避免了线弹性力学需要在试件中预制裂纹和裂纹尖端存在奇异性的弊端，提供了一种解决裂纹扩展问题的新手段。结果表明：圆形、原始形状和正方形颗粒SiC/AZ91D镁基复合材料抗压强度分别为474.853 MPa、435.783 MPa和397.211 MPa；其裂纹萌芽和断裂时间分别为施载后第15.6 μs、第14.4 μs、第12.6 μs和第22.2 μs、第20.4 μs、第18 μs；圆形颗粒复合材料裂纹扩展机制是基体损伤萌生的裂纹扩张导致材料断裂，而正方形和原始形状颗粒复合材料裂纹扩展机制是颗粒与基体交界处萌生裂纹，主裂纹和次生裂纹相互贯通，致使材料断裂；体积分数10%、15%和20%原始形状颗粒的SiC/AZ91D镁基复合材料裂纹萌芽和断裂时间分别在施载后第15.6 μs、第14.4 μs、第11.4 μs和第22.2 μs、第20.4 μs和第18 μs；颗粒体积分数的增加会加速SiC/AZ91D镁基复合材料的裂纹扩展过程。Abstract: The crack initiation and propagation mechanism of SiC/AZ91D magnesium matrix composites with different shapes and volume fractions of SiC particles under uniaxial compression was investigated by using the finite element analysis software Abaqus to introduce a cohesive force element into the interface of the finite element model. The introduction of cohesive force element avoids the defects of prefabrication crack and singularity of crack tip in linear elasticity, and provides a new method to solve the problem of crack propagation. The results show that the compressive strengths of round, original shape and square SiC/AZ91D magnesium matrix composites are 474.853 MPa, 435.783 MPa and 397.211 MPa, respectively. The time of crack initiation and fracture are 15.6 μs, 14.4 μs, 12.6 μs, 22.2 μs, 20.4 μs, 18 μs after loading, respectively. The crack propagation mechanism of circular particle composites is the crack propagation initiated by matrix damage, which leads to material fracture, while the crack propagation mechanism of square and original shape particle composites is the crack initiation at the junction of particle and matrix, and the primary crack and secondary crack are connected with each other, which leads to material fracture. The crack initiation and fracture time of SiC/AZ91D magnesium matrix composites with 10%, 15% and 20% original shape particles are 15.6 μs, 14.4 μs, 11.4 μs, 22.2 μs, 20.4 μs and 18μs after loading, respectively. The crack propagation process of SiC/AZ91D magnesium matrix composites is accelerated with the increase of particle volume fraction.
-
Key words:
- SiC/AZ91D /
- finite element analysis /
- cohesion model /
- uniaxial compression /
- crack propagation
-
图 2 SiCp/AZ91D镁基复合材料颗粒模型建立及网格划分和载荷施加
Figure 2. Establishment of particle model, meshing and load application of SiCp/AZ91D magnesium matrix composites
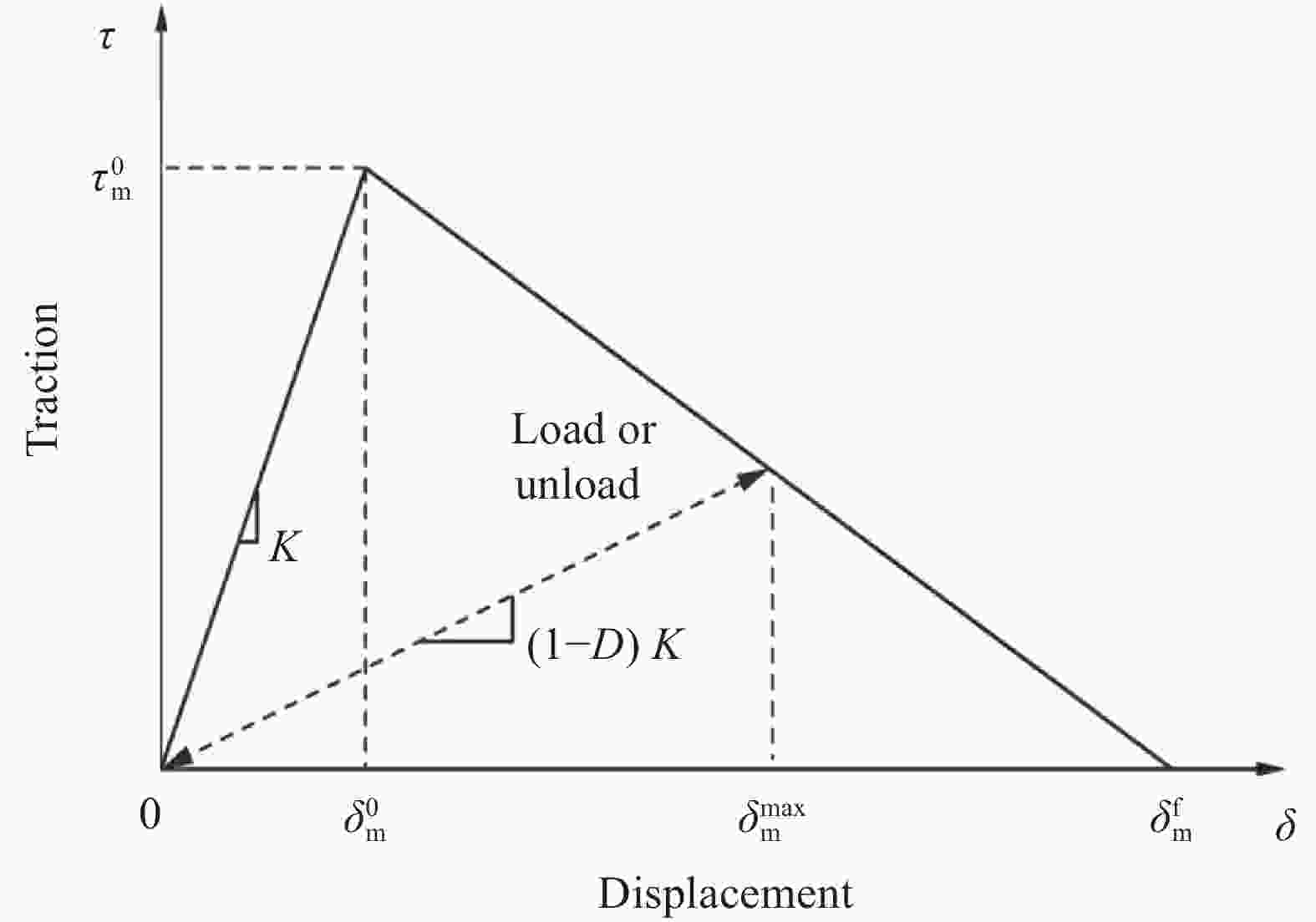
图 3 双线性内聚力模型
Figure 3. Bilinear cohesive zone model
$ {\delta }_{\mathrm{m}}^{\text{max}} $ is the maximum value of the effective displacement; $ {\delta }_{\mathrm{m}}^{\mathrm{f}} $ is the effective displacement at complete failure; $ {\delta }_{\mathrm{m}}^{0} $ is the effective displacement at the initiation of damage; $ {\tau }_{\mathrm{m}}^{0} $ is the maximum separation stress.
图 4 不同颗粒形状的SiC/AZ91D镁基复合材料模型图
Figure 4. Model diagrams of SiC/AZ91D magnesium matrix composites with different particle shapes
图 5 压缩过程中不同形状颗粒SiC/AZ91D镁基复合材料应力应变曲线
Figure 5. Stress-strain curves of SiC/AZ91D magnesium matrix composites with different shapes of particles during compression
图 6 压缩过程中不同形状颗粒SiC/AZ91D镁基复合材料屈服强度和抗压强度柱状图
Figure 6. Histogram of yield strength and compressive strength of SiC/AZ91D magnesium matrix composites with different shapes of particles during compression
图 7 不同颗粒形状的SiC/AZ91D镁基复合材料裂纹长度随时间变化曲线
Figure 7. Curves of crack length of SiC/AZ91D magnesium matrix composites with different particle shapes over time
图 8 不同形状颗粒的SiC/AZ91D镁基复合材料在载荷施加后裂纹萌芽情况
Figure 8. Crack germination of SiC/AZ91D magnesium matrix composites with particles of different shapes after loading
图 9 不同形状颗粒的SiC/AZ91D镁基复合材料在载荷施加后裂纹扩展情况
Figure 9. Crack growth of SiC/AZ91D magnesium matrix composites with particles of different shapes after loading
图 10 颗粒体积分数不同的SiC/AZ91D镁基复合材料模型图
Figure 10. Model diagram of SiC/AZ91D magnesium matrix composites with different particle volume fractions
图 11 不同体积分数颗粒的SiC/AZ91D镁基复合材料压缩应力-应变曲线
Figure 11. Compression stress-strain curves of SiC/AZ91D composites with different particle volume fractions
图 12 不同颗粒体积分数的SiC/AZ91D镁基复合材料抗压强度和压缩率
Figure 12. Compressive strength and compressibilility after fracture of SiC/AZ91D magnesium matrix composites with different particle volume fractions
图 13 不同体积分数颗粒的SiC/AZ91D镁基复合材料裂纹长度随时间变化的曲线
Figure 13. Curves of crack length versus time for SiC/AZ91D magnesium matrix composites with different volume fractions of particles
图 14 颗粒体积分数不同的SiC/AZ91D镁基复合材料在载荷施加后裂纹萌芽情况
Figure 14. Crack germination of SiC/AZ91D magnesium matrix composites with different volume fractions after loading
图 15 颗粒体积分数不同的SiC/AZ91D镁基复合材料在载荷施加后第17.4 μs裂纹扩展情况
Figure 15. Crack propagation of SiC/AZ91D magnesium matrix composites with different particle volume fraction at 17.4 μs after loading
图 17 不同体积分数SiC颗粒增强AZ91D镁合金的模拟与实验压缩应力-应变曲线对比
Figure 17. Comparison of simulated and experimental compressive stress-strain curves of AZ91D magnesium alloy reinforced by SiC particles with different volume fractions
表 1 AZ91D镁合金和SiC颗粒的基本参数
Table 1. Basic parameters of AZ91D magnesium alloy and SiC particles
Material $ \rho $/(kg/m3) E/GPa $ \mu $ ${\sigma }_{\rm{b}}$/MPa AZ91D 1800 45 0.33 164 SIC 3215 450 0.17 2000 Notes: $ \rho $ is the material density; E is the modulus of elasticity; $ \mu $ is Poisson’s ratio; $ {\sigma }_{\rm{b}} $ is the tensile strength. 
下载: 导出CSV
表 2 SiCp/AZ91D颗粒界面的本构模型参数
Table 2. Constitutive model parameters of SiCp/AZ91D particle interface
$ {t}_{\mathrm{n}}/\mathrm{M}\mathrm{P}\mathrm{a} $ $ {t}_{\mathrm{t}}/\mathrm{M}\mathrm{P}\mathrm{a} $ $ {\delta }_{\mathrm{m}\mathrm{a}\mathrm{x}}/\mathrm{m}\mathrm{m} $ $ {\delta }_{\mathrm{f}}/\mathrm{m}\mathrm{m} $ 400 400 0.00015 0.00005 Notes: $ {t}_{\mathrm{n}} $ is the interface normal nominal stress; $ {t}_{\mathrm{t}} $ is the interfacial tangential nominal stress; $ {\delta }_{\mathrm{m}\mathrm{a}\mathrm{x}} $ is the destruction displacement; $ {\delta }_{\mathrm{f}} $ is the material complete failure separation.
下载: 导出CSV
表 3 AZ91D镁合金的Johnson-Cook(J-C)本构参数
Table 3. Johnson-Cook (J-C) constittive model parameters for AZ9ID magnesium alloy
A/MPa $ B/\mathrm{M}\mathrm{P}\mathrm{a} $ n C $ {u}_{\mathrm{f}}^{\mathrm{p}\mathrm{l}} $/mm 164 600 0.283 0.021 0.00015 Notes: A is the yield strength of AZ91D matrix under static load; $ B $ is the hardening constant;$ n $ is the hardening exponent; $ C $ is the strain rate constant; $ {u}_{\mathrm{f}}^{\mathrm{p}\mathrm{l}} $ is the failure displacement.
下载: 导出CSV
表 4 SiC颗粒的本构参数
Table 4. Constitutive parameters of SiC particles
$ {\sigma }_{\mathrm{f}}^{\mathrm{p}} $/MPa $ {e}_{\mathrm{f}}^{\mathrm{p}}/\mathrm{m}\mathrm{m} $ $ {e}_{\text{max}}^{\text{ck}} $/mm p 2000 0.2 0.2 2 Notes: $ {\sigma }_{f}^{\mathrm{p}} $ is the tensile strength; $ {e}_{f}^{\mathrm{p}} $ is the fracture strain; p and $ {e}_{\text{max}}^{\text{ck}} $ are material parameters used to control the shear retention.
下载: 导出CSV
-
[1] AKINWEKOMIAD, LAWWC, TANGCY, CHENL, TSUICP. Rapidmicrowave sintering of carbon nanotube-filled AZ61 magnesium alloy composites[J]. Composites Part B,2016,93:302-309. doi: 10.1016/j.compositesb.2016.03.041 [2] 赵明明. 颗粒增强镁基复合材料力学性能的有限元数值分析[D]. 沈阳工业大学, 2014.ZHAO Mingming. Finite element numerical analysis of mechanical properties of particle reinforced magnesium matrix composites [D]. Shenyang University of Technology, 2014. (in Chinese) [3] 秦丽媛, 孟松鹤, 李金平, 等. 基于微观图像及内聚力模型的复合材料裂纹扩展模拟[J]. 固体火箭技术, 2017, 40(4):501-505. doi: 10.7673/j.issn.1006-2793.2017.04.018QIN Liyuan, MENG Songhe, Li Jinping, et al. Simulation of Crack Propagation in Composite Materials Based on Microscopic Image and Cohesion Model[J]. Solid Rocket Technology,2017,40(4):501-505(in Chinese). doi: 10.7673/j.issn.1006-2793.2017.04.018 [4] 何振鹏, 邓殿凯, 刘国峰, 等. 基于内聚力模型的复合材料裂纹扩展研究[J]. 复合材料科学与工程, 2022(1):5-12. doi: 10.19936/j.cnki.2096-8000.20220128.001HE Zhenpeng, DENG Diankai, LIU Guofeng, et al. Research on crack propagation of composite materials based on cohesive force model[J]. Composite Materials Science and Engineering,2022(1):5-12(in Chinese). doi: 10.19936/j.cnki.2096-8000.20220128.001 [5] 翁琳. 基于微观结构的颗粒增强复合材料力学性能数值分析[D]. 上海交通大学, 2015.WENG Lin. Numerical analysis of mechanical properties of particle-reinforced composites based on microstructure [D]. Shanghai Jiaotong University, 2015. (in Chinese) [6] ARSENAULT R J, FISHMAN S, TAYA M. Deformation and fracture behavior of metal-ceramic matrix composite materials[J]. Progress in Materials Science,1994,38:1-157. doi: 10.1016/0079-6425(94)90002-7 [7] 彭鹏. B4Cp/6061Al复合材料力学性能与三维有限元力学模拟[D]. 大连理工大学, 2021.PENG Peng. Mechanical properties and 3D finite element mechanical simulation of B4Cp/6061Al composites [D]. Dalian University of Technology, 2021. (in Chinese) [8] RAHIMIAN M, EHSANI N, PARVIN N, et al. The effect of particle size, sinteringtemperature and sintering time on the properties of Al-A12O3 composites, made by powder metallurgy[J]. Journal of Materials Processing Technology,2009,209:5387-5393. doi: 10.1016/j.jmatprotec.2009.04.007 [9] 崔岩, 倪浩晨, 曹雷刚, 杨越, 王一鸣. SiC颗粒整形对高体分铝基复合材料力学性能的影响及有限元模拟[J]. 材料导报, 2019, 33(24):4126-4130. doi: 10.11896/cldb.18120123CUI Yan, NI Haochen, CAO Leigang, YANG Yue, WANG Yiming. Effect of SiC particle shaping on mechanical properties of high-volume aluminum matrix composites and finite element simulation[J]. Materials Review,2019,33(24):4126-4130(in Chinese). doi: 10.11896/cldb.18120123 [10] 李昆, 金晓东, 颜本达, 李鹏兴. SiC颗粒体积分数对SiCp/Al复合材料疲劳裂纹扩展的影响[J]. 复合材料学报, 1992(2):83-88. doi: 10.13801/j.cnki.fhclxb.1992.02.013LI Kun, JIN Xiaodong, YAN Benda, LI Pengxing. Effect of SiC particle volume fraction on fatigue crack growth of SiCp/Al composites[J]. Journal of Composite Materials,1992(2):83-88(in Chinese). doi: 10.13801/j.cnki.fhclxb.1992.02.013 [11] 魏俊磊. 颗粒增强镁基复合材料力学行为的研究[D]. 太原理工大学, 2018.WEI Junlei. Research on mechanical behavior of particle-reinforced magnesium matrix composites [D]. Taiyuan University of Technology, 2018. (in Chinese) [12] SUGIMURA Y, SURESH S. Effects of SiC content on fatigue crack growth in aluminum alloys reinfor- ced with SiC partic les[J]. Metallurgical and Materials Transactions A,1992,23(8):2231-2242. doi: 10.1007/BF02646016 [13] SU Yishi, LI Zan, YU Yang, et al. Structural modeling and tensile simulation of graphene-reinforced metal matrix composites[J]. Science China Materials,2018,61(1):112-124. doi: 10.1007/s40843-017-9142-2 [14] 邱鑫. 挤压铸造SiCp/AZ91镁基复合材料的显微结构与性能[D]. 哈尔滨工业大学, 2006.QIU Xin. Microstructure and properties of squeeze cast SiCp/AZ91 magnesium matrix composites [D]. Harbin Institute of Technology, 2006. (in Chinese) [15] Jie ZHANG, Qiubao OUYANG, Qiang GUO, et al. 3D Microstructure-based finite element modeling of deformation and fracture of SiCp/Al composites[J]. Composites Science and Technology,2016,123:1-9. doi: 10.1016/j.compscitech.2015.11.014 [16] 张成. 基于内聚力模型的双相TiAl合金裂纹扩展的多尺度模拟[D]. 兰州理工大学, 2021.ZHANG Cheng. Multi-scale simulation of crack propagation in dual-phase TiAl alloys based on cohesion model [D]. Lanzhou University of Technology, 2021. (in Chinese) [17] 翁琳. 基于微观结构的颗粒增强复合材料力学性能数值分析[D]. 上海交通大学, 2015.WENG Lin. Numerical analysis of mechanical properties of particle-reinforced composites based on microstructure [D]. Shanghai Jiaotong University, 2015. (in Chinese) [18] 张炯, 屈展, 黄其青, 等. 基于内聚力模型的圆形夹杂与基体界面渐进脱粘分析[J]. 西安石油大学学报(自然科学版), 2014, 29(3):106-110+12.ZHANG Jiong, QU Zhan, HUANG Qiqing, et al. Progressive debonding analysis of circular inclusion and matrix interface based on cohesion model[J]. Journal of Xi'an Shiyou University (Natural Science Edition),2014,29(3):106-110+12(in Chinese). [19] ZHANG Jie, OUYANG Qiubao, GUO Qiang, et al. 3D Microstructure-based finite element modeling of deformation and fracture of SiCp/Al composites[J]. Composites Science and Technology,2016,123:1-9. doi: 10.1016/j.compscitech.2015.11.014 [20] 耿昆. SiCp/Al复合材料基于微细观的有限元建模拟实[D]. 上海交通大学, 2017.GENG Kun. Simulation of SiCp/Al composites based on microscopic finite element construction [D]. Shanghai Jiaotong University, 2017. [21] 周圣杰. B4C/2024Al复合材料变形断裂行为研究[D]. 哈尔滨工业大学, 2020.ZHOU Shengjie. Research on deformation and fracture behavior of B4C/2024Al composites [D]. Harbin Institute of Technology, 2020. (in Chinese) [22] 周爽. 纳米增强体镁基复合材料力学性能数值模拟[D]. 沈阳工业大学, 2017.ZHOU Shuang. Numerical simulation of mechanical properties of nano-reinforced magnesium matrix composites [D]. Shenyang University of Technology, 2017. (in Chinese) [23] 云龙. 基于多尺度内聚力模型的PRMMCs动态力学行为研究[D]. 武汉理工大学, 2015.YUN Long. Research on dynamic mechanical behavior of PRMMCs based on multi-scale cohesion model [D]. Wuhan University of Technology, 2015. (in Chinese) [24] SU Yishi, LI Zan, YU Yang, et al. Composite structural modeling and tensile mechanical behavior of graphene rein-forced metal matrix composites[J]. Science China Materials,2018,61(1):112-124. doi: 10.1007/s40843-017-9142-2 [25] 马英纯. 软相尺寸对SiC/Mg纳米复合材料压缩性能及破坏机理的影响[D]. 西南交通大学, 2021.Ma Yingchun. Effect of soft phase size on compressive properties and failure mechanism of SiC/Mg nanocomposites[D]. Southwest Jiaotong University, 2021. (in Chinese) [26] 杨柳. SiCp/B4Cp增强AZ9ID镁基复合材料的制备及性能研究[D]. 南昌航空大学, 2020.YANG Liu. Preparation and properties of SiCp/B4Cp reinforced AZ9ID magnesium matrix composites[D]. Nanchang Aviation University, 2020. (in Chinese) [27] 张世强. 曲线回归的拟合优度指标的探讨[J]. 中国卫生统计, 2002, 19(1):9-11. doi: 10.3969/j.issn.1002-3674.2002.01.003ZHANG Shiqiang. Study on the goodness-of-fit in dex of curve regression[J]. China health statistics,2002,19(1):9-11(in Chinese). doi: 10.3969/j.issn.1002-3674.2002.01.003 -
下载:
点击查看大图
计量
- 文章访问数: 247
- HTML全文浏览量: 218
- PDF下载量: 2
- 被引次数: 0
