基于增量微分求积单元法的功能梯度材料夹层板非线性瞬态传热分析

张忠; 许家婧; 曹小建; 王艳超; 朱军; 姚潞

基于增量微分求积单元法的功能梯度材料夹层板非线性瞬态传热分析

张忠¹,
许家婧¹,
曹小建¹,
王艳超^{1, 2, 3},
朱军⁴,
姚潞^{1, 4, ,}

1.
南通大学　交通与土木工程学院, 南通 226019
2.
博众精工科技股份有限公司, 苏州 215200
3.
中国矿业大学　力学与土木工程学院, 徐州 221116
4.
南通泰胜蓝岛海洋工程有限公司, 启东 226259

基金项目: 国家自然科学基金(11802145；52308260)；江苏省高等学校基础科学(自然科学)研究项目(23KJB560021)；南通市科技项目(JC12022058)；南通市社会民生科技计划面上研究项目(MS22022103)

详细信息

通讯作者:
姚潞，博士，讲师，研究方向为复合材料结构　E-mail: yaolu@ntu.edu.cn

中图分类号: TK124
计量
- 文章访问数: 46
- HTML全文浏览量: 33
- 被引次数: 0
出版历程
- 收稿日期: 2023-12-26
- 修回日期: 2024-01-23
- 录用日期: 2024-02-07
- 网络出版日期: 2024-03-13

Nonlinear transient heat transfer analysis of functionally graded material sandwich slabs by incremental differential quadrature element method

ZHANG Zhong¹,
XU Jiajing¹,
CAO Xiaojian¹,
WANG Yanchao^{1, 2, 3},
ZHU Jun⁴,
YAO Lu^{1, 4
, ,}

1.
School of Transportation and Civil Engineering, Nantong University, Nantong 226019, China
2.
BOZHON Precision Industry Technology Co., Ltd., Suzhou 215200, China
3.
School of Mechanics and Civil Engineering, China University of Mining and Technology, Xuzhou 221116, China
4.
Nantong Taisheng Blue Island Offshore Co., Ltd.,Qidong 226259, China

Funds: National Natural Science Foundation of China (11802145; 52308260); Natural Science Foundation of the Jiangsu Higher Education Institutions of China (23KJB560021); Science and Technology Project of Nantong City (JC12022058); Nantong City Social Livelihood Science and Technology Project (MS22022103)

摘要

摘要: 作为首次尝试，采用增量微分求积单元法(IDQEM)开展了功能梯度材料(FGM)夹层板的一维非线性瞬态传热分析。夹层板组分材料的热工参数随空间位置变化，且具有温度依赖性。基于IDQEM，沿层界面将夹层板划分为三个空间子域，同时将整个受热过程划分为若干时间子域。采用微分求积技术对任一时间子域内的控制方程、初始条件、界面条件以及边界条件进行离散处理。由于所获得的离散方程建立在不同区域的节点上，因此对方程进行修改并将其表示为矩阵形式，以便它们可以建立在同一区域中。采用Kronecker积将联立的矩阵方程转化为一系列代数方程组，并采用Newton-Raphson迭代法近似求解，即可获得单个时间子域内的温度解。由于每个时间子域的初始条件可由上一个时间子域最终时刻的温度分布决定，因此从第一个时间子域逐渐递推到最后一个子域，即可获得整个受热过程的温度分布。数值算例验证了本方法的快速收敛性，与已有文献的解析和数值结果的对比验证了本方法的正确性。最后，讨论了热工参数温度依赖性、体积分数指数以及热边界条件对FGM夹层板温度分布的影响。
- 功能梯度材料夹层板 /
- 温度依赖性 /
- 瞬态传热 /
- 增量微分求积单元法 /
- Newton-Raphson迭代法
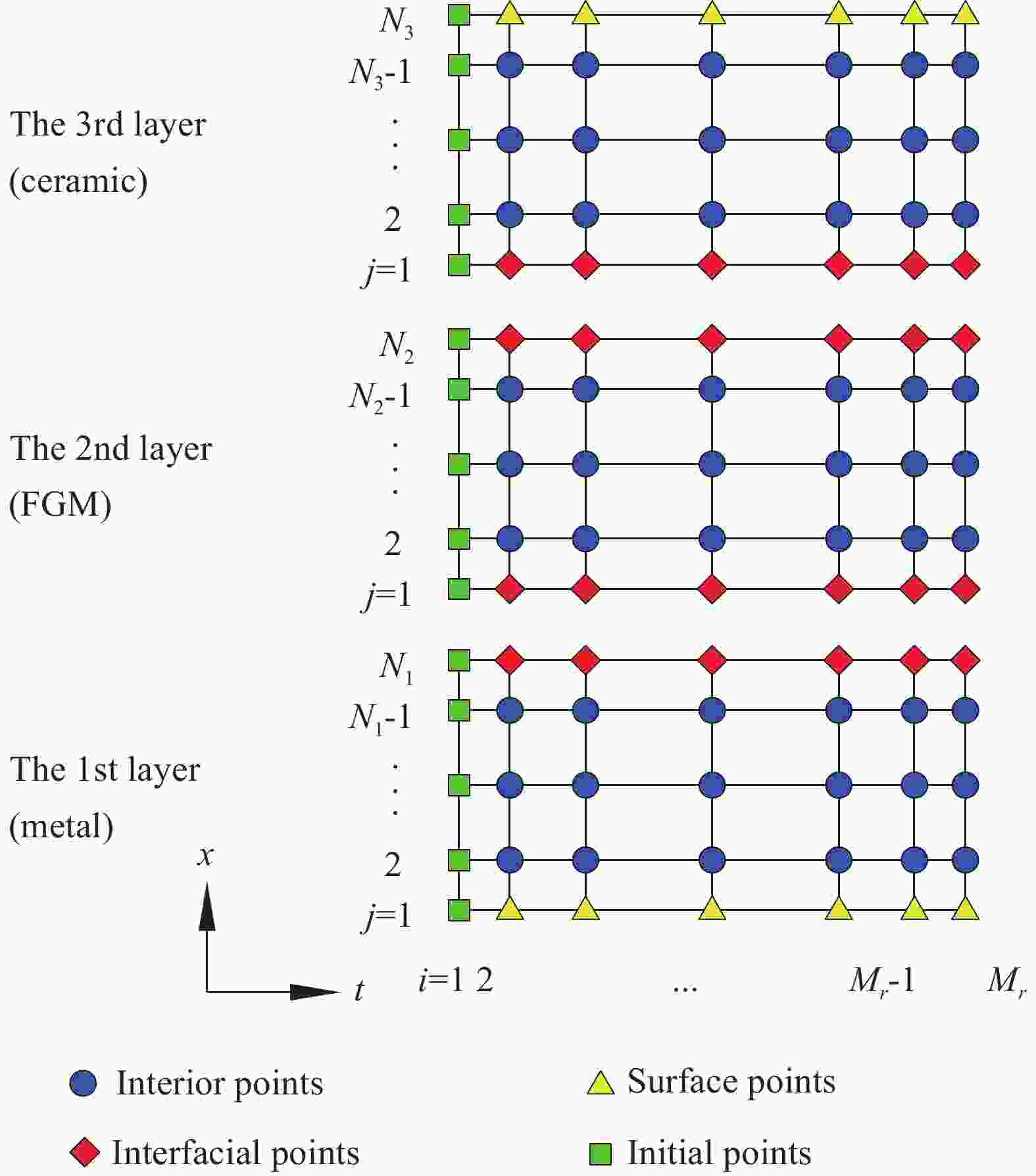
Abstract: As a first attempt, the incremental differential quadrature element method (IDQEM) was adopted to perform the one-dimensional nonlinear transient heat transfer analysis of functionally graded material (FGM) sandwich slabs. The thermophysical properties of the slab were considered to be position- and temperature-dependent. To implement the IDQEM, the sandwich slab was divided into three spatial sub-domains along the layer interfaces, and the entire heating process was also divided into several temporal sub-domains. For each temporal sub-domain, the governing equations as well as the initial condition, interfacial condition, and boundary condition were discretized by the differential quadrature technique. Because the obtained discrete equations were built in different regions of grid points, a modification of the equations was proposed which were then expressed in the matrix forms so that they can be built in the same regions. Using the Kronecker product, the simultaneous matrix equations were transformed into a set of nonlinear algebraic equations, which were then solved by the Newton-Raphson iteration method to obtain the temperature profile for each temporal sub-domain. Because the initial condition of each temporal sub-domain was defined by the temperature results at the end of the previous sub-domain, the temperature profile of the slab during the entire heating process can be obtained by repeating the calculation procedure from the first temporal sub-domain to the last one. Numerical examples were carried out to verify the fast convergence of the present method. The correctness of the present method was verified through comparison with the analytical and numerical results reported in previous works. The effects of temperature-dependent thermophysical properties, volume fraction index, and thermal boundary on the temperature profile of the slab were discussed.
- functionally graded material sandwich slab /
- temperature dependence /
- transient heat transfer /
- incremental differential quadrature element method /
- Newton-Raphson iteration method

HTML全文

图 1 功能梯度材料(FGM)夹层板示意图

Figure 1. Schematic view of the functionally graded material (FGM) sandwich slab

x – Global coordinate for the sandwich slab; x^(s) (s = 1, 2, 3) – Local coordinate for the sth layer; H – Total thickness of the sandwich slab;H_s – Thickness of the sth layer

下载: 全尺寸图片幻灯片

图 2 第r个时间子域下的节点分布

Figure 2. Grid point distribution in the rth temporal sub-domain

M_r and N_s – Grid point numbers in the rth temporal sub-domain and the sth spatial sub-domain, respectively; t – Time variable

下载: 全尺寸图片幻灯片

图 3 η = 0.2和2两种情况下SUS304/Si₃N₄夹层板x = 0.5H处温度变化

Figure 3. Temperature variations at x = 0.5H for the SUS304/Si₃N₄ sandwich slab with η = 0.2 and 2

T – Temperature; η – volume fraction index

下载: 全尺寸图片幻灯片

图 4 η = 2时SUS304/Si₃N₄夹层板x = 0.5H处温度变化

Figure 4. Temperature variations at x = 0.5H for the SUS304/Si₃N₄ sandwich slab with η = 2

TI – Temperature independent; TD – Temperature dependent

下载: 全尺寸图片幻灯片

图 5 不同时刻SUS304/Si₃N₄夹层板的温度分布

Figure 5. Temperature profiles at different times for the SUS304/Si₃N₄ sandwich slab

下载: 全尺寸图片幻灯片

图 6 不同上表面温度T_c作用下SUS304/Si₃N₄夹层板的温度分布

Figure 6. Temperature profiles of the SUS304/Si₃N₄ sandwich slab under different top surface temperatures T_c

下载: 全尺寸图片幻灯片

图 7 T_c = 600 K时SUS304/Si₃N₄夹层板的热扩散率α时空分布

Figure 7. Thermal diffusivity α contour of the SUS304/Si₃N₄ sandwich slab under the surface temperature T_c = 600 K

下载: 全尺寸图片幻灯片

图 8 SUS304/Si₃N₄夹层板x = 0.5H处的温度与T_c的关系

Figure 8. Temperature at x = 0.5H versus T_c for the SUS304/Si₃N₄ sandwich slab

下载: 全尺寸图片幻灯片

图 9 η = 0.2, 1, 5三种情况下Ti−6Al−4V/ZrO₂夹层板的温度变化

Figure 9. Temperature variations of the Ti−6Al−4V/ZrO₂ sandwich slab for η=0.2, 1, 5

(a) x = 0 (b) x = H

下载: 全尺寸图片幻灯片

图 10 Ti−6Al−4V/ZrO₂夹层板的热扩散率时空分布

Figure 10. Thermal diffusivity contour of the Ti−6Al−4V/ZrO₂ sandwich slab

(a) η = 0.2 (b) η = 5

下载: 全尺寸图片幻灯片

图 11 Ti−6Al−4V/ZrO₂夹层板上表面的热流

Figure 11. Heat flux on the top surface of the Ti−6Al−4V/ZrO₂ sandwich slab

q_top – Heat flux generated on the top surface

下载: 全尺寸图片幻灯片

图 12 Ti−6Al−4V/ZrO₂夹层板的温度时空分布

Figure 12. Temperature contour of the Ti−6Al−4V/ZrO₂ sandwich slab

下载: 全尺寸图片幻灯片

表 1 组分材料热工参数的温度系数^[23–26]

Table 1. Temperature coefficients of thermophysical properties for the component materials^[23–26]

Material	Property	P₀	P₋₁	P₁	P₂	P₃
SUS304	λ/(W∙(m∙K)⁻¹)	15.379	0	−1.264 × 10⁻³	2.092×10⁻⁶	−7.223×10⁻¹⁰
	c/(J∙(kg∙K)⁻¹)	496.56	0	−1.151×10⁻³	1.636×10⁻⁶	−5.863×10⁻¹⁰
	ρ/(kg∙m⁻³)	8166.0	0	0	0	0
Si₃N₄	λ/(W∙(m∙K)⁻¹)	13.723	0	−1.032× 10⁻³	5.466 × 10⁻⁷	−7.876×10⁻¹¹
	c/(J∙(kg∙K)⁻¹)	555.11	0	1.016×10^-3	2.920×10⁻⁷	−1.670×10⁻¹⁰
	ρ/(kg∙m⁻³)	2370.0	0	0	0	0
Ti−6Al−4V	λ/(W∙(m∙K)⁻¹)	1.0000	0	1.704×10⁻²	0	0
	c/(J∙(kg∙K)⁻¹)	625.30	0	−4.224×10⁻⁴	7.179×10⁻⁷	0
	ρ/(kg∙m⁻³)	4420.0	0	0	0	0
ZrO₂	λ/(W∙(m∙K)⁻¹)	1.7000	0	1.276×10⁻⁴	6.648×10⁻⁸	0
	c/(J∙(kg∙K)⁻¹)	487.34	0	3.049×10⁻⁴	−6.037×10⁻⁸	0
	ρ/(kg∙m⁻³)	5700.0	0	0	0	0
Notes: λ, c, and ρ−Thermal conductivity, specific heat, and density, respectively; P_k (k = −1, 0, 1, 2, 3) − Temperature coefficients; SUS304, Si₃N₄, Ti−6Al−4V, and ZrO₂ denote stainless steel, silicon nitride, titanium alloy, and zirconia, respectively.

下载: 导出CSV

表 2 η = 0.2时SUS304/Si₃N₄夹层板x = 0.75H处的温度结果(单位：K)

Table 2. Temperature results at x = 0.75H for the SUS304/Si₃N₄ sandwich slab with η = 0.2 (Unit: K)

Time	Temporal grid point number	Spatial grid point number
Time	Temporal grid point number	N = 12	N = 20	N = 28	N = 36
t = 0.01 s	M = 4	342.16 (0.0312 s)	342.96 (0.0625 s)	342.98 (0.0938 s)	342.99 (0.1154 s)
	M = 12	342.16 (0.1406 s)	343.01 (0.1719 s)	343.00 (0.2193 s)	343.01 (0.4688 s)
	M = 20	342.16 (0.1875 s)	343.01 (0.3281 s)	343.01 (0.5806 s)	343.01 (1.0312 s)
	M = 28	342.16 (0.2031 s)	343.01 (0.5156 s)	343.01 (1.1562 s)	343.01 (2.1094 s)
t = 0.03 s	M = 4	362.95 (0.0469 s)	362.80 (0.0712 s)	362.81 (0.1024 s)	362.80 (0.1193 s)
	M = 12	362.87 (0.1562 s)	362.69 (0.1736 s)	362.68 (0.2056 s)	362.68 (0.5021 s)
	M = 20	362.87 (0.1719 s)	362.70 (0.3598 s)	362.69 (0.6006 s)	362.69 (1.0156 s)
	M = 28	362.87 (0.2031 s)	362.70 (0.5469 s)	362.69 (1.0625 s)	362.69 (2.2188 s)
Notes: M and N – Total numbers of grid points in the temporal and spatial domains, respectively. The content in parentheses represents the CPU-time.

下载: 导出CSV

表 3 两种情况下数值结果和CPU计算时间的对比

Table 3. Comparison of numerical results and CPU-time in the two cases

Position	Time/s	Case 1/K	Case 2/K	Error	CPU-time of case 1/s	CPU-time of case 2/s
x = 0.25H	0.01	302.43	301.40	0.34%	0.6094	0.6310
	0.03	314.28	312.23	0.66%	0.5938	0.5781
x = 0.75H	0.01	349.05	343.01	1.76%	0.6094	0.6310
	0.03	365.93	362.69	0.89%	0.5938	0.5781
Notes: In Case 1, only the thermal conductivity is considered to be TD; in Case 2, all the thermophysical properties are considered to be TD.

下载: 导出CSV

表 4 时变热流的多项式拟合

Table 4. Polynomial fits for the time-dependent heat flux

Time/s	a₀	a₁	a₂/10⁻³	a₃/10⁻⁶
0-431.1	0	0.003196	1.021	−1.383
431.1-660.2	−228.7	1.595	−2.670	1.471
660.2-1561	253.4	−0.5961	−0.6477	−0.2043
1561-2200	−1257	2.307	−1.212	0.1929
Notes: a_k (k = 0, 1, 2, 3) – Fitting coefficients.

下载: 导出CSV

[1]	刘浩洋, 吕超雨, 石姗姗, 等. 芳纶纤维增韧碳纤维增强环氧树脂复合材料-铝蜂窝夹芯结构界面性能和增韧机制[J]. 复合材料学报, 2022, 39(2): 559-567. LIU Haoyang, LV Chaoyu, SHI Shanshan, et al. Interfacial toughening and toughening mechanism of aramid staple fiber to carbon fiber reinforced epoxy resin composite-aluminum honeycomb sandwich structure[J]. Acta Materiae Compositae Sinica, 2022, 39(2): 559-567 (in Chinese).
[2]	李华冠, 丁颖, 章月, 等. 玻璃纤维立体织物增强环氧树脂泡沫夹层复合材料的制备及力学性能[J]. 复合材料学报, 2023, 40(1): 601-612. LI Huaguan, DING Ying, ZHANG Yue, et al. Preparation and mechanical properties of glass fiber reinforced 3D fabric reinforced epoxy foam sandwich composites[J]. Acta Materiae Compositae Sinica, 2023, 40(1): 601-612 (in Chinese).
[3]	Xie H, Li W, Fang H, et al. Flexural behavior evaluation of a foam core curved sandwich beam[J]. Composite Structures, 2024, 328: 117729. doi: 10.1016/j.compstruct.2023.117729
[4]	Wang X, Wang Z, Zeng T, et al. Exact analytical solution for steady-state heat transfer in functionally graded sandwich slabs with convective-radiative boundary conditions[J]. Composite Structures, 2018, 192: 379-386. doi: 10.1016/j.compstruct.2018.03.006
[5]	Daikh A A, Megueni A. Thermal buckling analysis of functionally graded sandwich plates[J]. Journal of Thermal Stresses, 2018, 41(2): 139-159. doi: 10.1080/01495739.2017.1393644
[6]	Daikh A A, Drai A, Bensaid I, et al. On vibration of functionally graded sandwich nanoplates in the thermal environment[J]. Journal of Sandwich Structures & Materials, 2021, 23(6): 2217-2244.
[7]	Shen H-S, Li S-R. Postbuckling of sandwich plates with FGM face sheets and temperature-dependent properties[J]. Composites Part B:Engineering, 2008, 39(2): 332-344. doi: 10.1016/j.compositesb.2007.01.004
[8]	Pandey S, Pradyumna S. A finite element formulation for thermally induced vibrations of functionally graded material sandwich plates and shell panels[J]. Composite Structures, 2017, 160: 877-886. doi: 10.1016/j.compstruct.2016.10.040
[9]	Pandey S, Pradyumna S. Transient stress analysis of sandwich plate and shell panels with functionally graded material core under thermal shock[J]. Journal of Thermal Stresses, 2018, 41(5): 543-567. doi: 10.1080/01495739.2017.1422999
[10]	Malekzadeh P, Rahideh H. IDQ two-dimensional nonlinear transient heat transfer analysis of variable section annular fins[J]. Energy Conversion and Management, 2007, 48(1): 269-276. doi: 10.1016/j.enconman.2006.04.005
[11]	Chen Y, Zhang L, He C, et al. Thermal insulation performance and heat transfer mechanism of C/SiC corrugated lattice core sandwich panel[J]. Aerospace Science and Technology, 2021, 111: 106539. doi: 10.1016/j.ast.2021.106539
[12]	Striz A, Chen W, Bert C. Static analysis of structures by the quadrature element method[C]//35th Structures, Structural Dynamics, and Materials Conference. Reston, Virigina: American Institute of Aeronautics and Astronautics, 1994, 3(94): 1567–1574.
[13]	沈景凤, 张翠, 刘方. 基于热弹性耦合理论的功能梯度材料薄壁旋转碟片力学性能[J]. 复合材料学报, 2019, 36(4): 1017-1028. SHEN Jingfeng, ZHANG Cui, LIU Fang. Thermally coupled analysis of thermoelastic field in a thin-walled rotating FGM circular disk[J]. Acta Materiae Compositae Sinica, 2019, 36(4): 1017-1028 (in Chinese).
[14]	金晶, 邢誉峰, 廖选平, 等. 瞬态传热问题的微分求积和精细积分求解方法[J]. 北京航空航天大学学报, 2015, 41(8): 1526-1531. JIN Jing, XING Yufeng, LIAO Xuanping, et al. Application of differential quadrature and precise integration methods in analysis of transient heat transfer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8): 1526-1531 (in Chinese).
[15]	林鹏程, 滕兆春. 热冲击下轴向运动FGM梁的自由振动分析[J]. 振动与冲击, 2020, 39(12): 249-256. LIN Pengcheng, TENG Zhaochun. Free vibration analysis of axially moving FGM beams under thermal shock[J]. Journal of Vibration and Shock, 2020, 39(12): 249-256 (in Chinese).
[16]	Wang X, Gu H. Static analysis of frame structures by the differential quadrature element method[J]. International Journal for Numerical Methods in Engineering, 1997, 40(4): 759-772. doi: 10.1002/(SICI)1097-0207(19970228)40:4<759::AID-NME87>3.0.CO;2-9
[17]	Chen W, Striz A G, Bert C W. A new approach to the differential quadrature method for fourth-order equations[J]. International Journal for Numerical Methods in Engineering, 1997, 40(11): 1941-1956. doi: 10.1002/(SICI)1097-0207(19970615)40:11<1941::AID-NME145>3.0.CO;2-V
[18]	Malekzadeh P, Heydarpour Y, Haghighi M R G, et al. Transient response of rotating laminated functionally graded cylindrical shells in thermal environment[J]. International Journal of Pressure Vessels and Piping, 2012, 98: 43-56. doi: 10.1016/j.ijpvp.2012.07.003
[19]	Dai T, Li B, Tao C, et al. Thermo-mechanical analysis of a multilayer hollow cylindrical thermal protection structure with functionally graded ultrahigh-temperature ceramic to be heat resistant layer[J]. Aerospace Science and Technology, 2022, 124: 107532. doi: 10.1016/j.ast.2022.107532
[20]	Shen H-S, Xiang Y, Reddy J N. Assessment of the effect of negative Poisson’s ratio on the thermal postbuckling of temperature dependent FG-GRMMC laminated cylindrical shells[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 376: 113664. doi: 10.1016/j.cma.2020.113664
[21]	Wang Y, Feng C, Yang J, et al. Nonlinear vibration of FG-GPLRC dielectric plate with active tuning using differential quadrature method[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 379: 113761. doi: 10.1016/j.cma.2021.113761
[22]	Wang X, Yuan Z. Accurate stress analysis of sandwich panels by the differential quadrature method[J]. Applied Mathematical Modelling, 2017, 43: 548-565. doi: 10.1016/j.apm.2016.11.034
[23]	Hao Y X, Cao Z, Zhang W, et al. Stability analysis for geometric nonlinear functionally graded sandwich shallow shell using a new developed displacement field[J]. Composite Structures, 2019, 210: 202-216. doi: 10.1016/j.compstruct.2018.11.027
[24]	Zenkour A M, Sobhy M. Dynamic bending response of thermoelastic functionally graded plates resting on elastic foundations[J]. Aerospace Science and Technology, 2013, 29(1): 7-17. doi: 10.1016/j.ast.2013.01.003
[25]	Reddy J N, Chin C D. Thermomechanical analysis of functionally graded cylinders and plates[J]. Journal of Thermal Stresses, 1998, 21(6): 593-626. doi: 10.1080/01495739808956165
[26]	Wang B L, Tian Z H. Application of finite element-finite difference method to the determination of transient temperature field in functionally graded materials[J]. Finite Elements in Analysis and Design, 2005, 41(4): 335-349. doi: 10.1016/j.finel.2004.07.001
[27]	Zhang Z, Zhou D, Zhang J, et al. Transient analysis of layered beams subjected to steady heat supply and mechanical load[J]. Steel and Composite Structures, 2021, 40(1): 87-100.
[28]	Uyanna O, Najafi H, Rajendra B. An inverse method for real-time estimation of aerothermal heating for thermal protection systems of space vehicles[J]. International Journal of Heat and Mass Transfer, 2021, 177: 121482. doi: 10.1016/j.ijheatmasstransfer.2021.121482