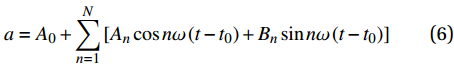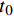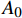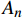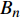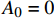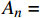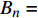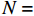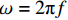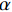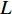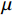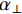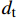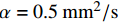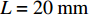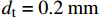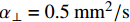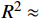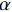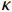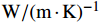Simulation study on thermal diffusion of woven carbon fiber/epoxy resin composite
-
摘要: 对编织碳纤维/环氧树脂(CF/EP)复合材料的三维热扩散性能进行有限元仿真研究。通过TexGen软件创建20层编织CF/EP复合材料三维仿真模型，计算了不同孔隙率样品的有效体积比热和热导率来设置材料属性，并使用幅值曲线模拟周期性点光源进行仿真。首先以孔隙率为0%的样品为例，采用非线性拟合求解热扩散系数，选出最优的调制频率范围为0.1~2 Hz。在此基础上研究了孔隙率对复合材料热扩散性能的影响。结果表明，编织CF/EP复合材料在平面内的热扩散系数随着孔隙率的增大而减小，孔隙率小于1.55%时，孔隙率每增加1%，热扩散系数下降5.4%。孔隙率大于1.55%时，下降速度变慢，仅为2.4%。在平面内沿着经纱和纬纱方向的热扩散较快，经(纬)纱45°方向的热扩散较慢，而在垂直方向上，由于点光源的穿透性使法向的热扩散最快，体现了热扩散的各向异性。Abstract: The finite element method was used to simulate the three dimensional thermal diffusion properties of woven carbon fiber/epoxy resin (CF/EP) composite. TexGen was used to create a 3D simulation model of 20-layer woven CF/EP composite. The effective volumetric specific heat and thermal conductivity of the porous matrix in samples with different thicknesses were calculated to set the material properties. The amplitude curve was used to simulate periodic laser point light source for finite element simulation. Taking a sample with a porosity of 0% as an example, non-linear fitting was used to solve the thermal diffusivity, and the optimal modulation frequency range was selected as 0.1-2 Hz. On this basis, samples with different thicknesses were studied to analyze the influence of porosity on the thermal properties and the anisotropy of thermal diffusion. The results show that the in-plane thermal diffusivity of the woven CF/EP composites decreases with the increase of porosity. When the porosity is less than 1.55%, the thermal diffusivity decreases by 5.4% as the porosity increases by 1%. When the porosity is greater than 1.55%, the rate of decline slows down, just as 2.4%. In the plane, the thermal diffusion rate along the weft yarn and warp yarn is faster, but along the 45° direction of the warp (weft) yarn is slower. While in the vertical direction, the thermal diffusion along the normal is the fastest due to the penetration of the point light source, which reflects the anisotropy of the thermal diffusion.
-
Keywords:
- carbon fiber /
- composites /
- finite element method /
- thermal diffusivity /
- thermal conductivity /
- porosity
-
碳纤维/环氧树脂(Carbon fiber/epoxy resin，CF/EP)复合材料因其卓越的高强度、低密度、耐高温等性能广泛地应用于航空航天、汽车工业和高速列车等领域[1-3]。针对不同应用环境，CF/EP复合材料需要经历复杂而又苛刻的力学和热性能测试，准确预测复合材料的热性能对于实际工程领域的可靠性设计极为重要[4-6]。国内外学者对于CF/EP复合材料的热性能的关注度越来越高。周雅斌等[7]针对CF/EP复合材料圆筒结构，利用布拉格光栅水热平衡法和傅里叶热传导方程，建立了圆柱坐标系下的热扩散系数理论求解模型。WOJCIECH等[8]将热源和红外探测器位于试样的同一侧，利用反求法将空间内温度场分布拟合到测量数据上来确定CF/EP复合材料的热导率。RYOHEI等[9]利用热扩散的角分布与纤维导向的相关性，来测量片状CF/EP复合材料在纤维导向上的热扩散系数。
在CF/EP复合材料的热压罐固化过程中，由于气体的机械夹杂及内部成核作用，会在纤维束内部和层间产生孔隙，孔隙的存在会影响CF/EP复合材料的热扩散性能[10-12]。吴恩启等[13-14]利用锁相红外热成像技术获取了编织CF/EP复合材料表面的相位和幅值信号，来计算热扩散系数，并发现低频率的相位信号随着孔隙率的增加呈现递减趋势。wróbel G等[15]成功将瞬态热成像法—闪光法应用到CF/EP复合材料上，测量了不同孔隙率样品的热扩散系数，发现不同孔隙率样品的热扩散系数与碳含量呈线性关系。
随着CAE技术的不断发展，逐渐开始采用有限元仿真模拟和实验验证相结合的方式进行研究[16-17]。Dong等[18]利用有限元法研究了2.5D机织复合材料的孔隙缺陷和界面热阻对导热系数的影响并进行了实验验证。RÜDIGE等[19]利用有限元法模拟发现CF/EP复合材料中大部分传热是由高温下碳层之间的热辐射引起的。T. Ishizaki等[20-21]利用锁相热像仪测量三维热扩散系数，利用AutoCAD建模进行瞬态热分析来验证实验。但是，由于CF/EP复合材料构造的复杂性，建模过程都相对简化，不能很好地反应内部纤维束排布结构。
本文通过TexGen软件建立了20层编织CF/EP复合材料结构模型，设置纱线的数量、宽度、间距和编织排布方式还原了真实的平纹结构，模拟了周期性点光源加载下的编织CF/EP复合材料的温度场分布情况，分析了点光源的调制频率对热扩散系数计算结果的影响。将含孔隙基体的有效体积比热和热导率作为材料属性进行设置，用来分析孔隙率对热扩散性能的影响。计算了编织CF/EP复合材料在平面内和垂直方向上的热扩散参数来分析热扩散的各向异性。通过与实验结果的对比，来验证仿真结果的准确性。
1. 热扩散参数计算原理
一束波长为
$\lambda $ ，调制频率为f的激光投射到样品表面，其调制光强表达式：$$I = \frac{{{I_0}}}{2}\left[ {1 + \cos (\omega t)} \right] $$ (1) 其中：
${I_0}$ 为入射光源强度；$\omega $ 为入射光源调制激光角频率，且$\omega = 2{\text{π}}f$ 。结合仿真软件中的周期性幅值曲线，可以设置不同调制频率下的加载情况，来接近实际加载效果。不同厚度大小的CF/EP复合材料样品在时域上的温度分布表达式[22]：
$$T\left( {d,t} \right) = {T_0} + \frac{{{I_0}}}{{\rho c\sqrt {{\text{π}} \alpha t} }}\exp \left( { - \frac{{{d^2}}}{{4 \alpha t}}} \right)$$ (2) 其中：
${T_0}$ 为初始温度；d为样品厚度；$\alpha $ 是热扩散系数；$\rho $ 和c分别是样品的密度和比热容。利用式(2)结合有限元仿真所得温度场分布即可求出热扩散系数，具体步骤如下：
(1)对式(2)进行线性化处理， 计算
${1\!/\!t}$ 和$\ln \left[\! {T\!\left( \!{d,t} \right) }\right.\!\!- \! $ $ \left. {{T_0}} \right] + {1/{2\ln \left( t \right)}}$ 的值并作散点图；(2)通过最小二乘法求得拟合直线的斜率k，根据下式求出热扩散系数
$\alpha $ ：$$\alpha = - \frac{{{d^2}}}{{4k}}$$ (3) 由于CF/EP复合材料的基体含有较多孔隙，使其热性能在空间上并不连续，引入有效体积比热的概念能使含孔隙的基体达到匀质材料的效果[23-24]。CF/EP复合材料整体的有效体积比热及含孔隙EP基体的有效体积比热和热导率公式如下：
$$\begin{split} &{S_{{\rm{eff}}}} = \left( {1 - {V_{\rm{M}}}} \right) \cdot {S_{\rm{M}}} + {V_{\rm{F}}} \cdot {S_{\rm{F}}} \\& {S_{\rm{M}}} = \dfrac{{{V_{\rm{P}}}}}{{{V_{\rm{R}}} + {V_{\rm{P}}}}} \cdot {S_{\rm{P}}} + \left( {1 + \dfrac{{{V_{\rm{P}}}}}{{{V_{\rm{R}}} + {V_{\rm{P}}}}}} \right) \cdot {S_{\rm{R}}} \\& {\kappa _{\rm{M}}} = {\kappa _{\rm{R}}}\left( {\dfrac{{{\kappa _{\rm{R}}}\left( {1 - \dfrac{{{V_{\rm{P}}}}}{{{V_{\rm{R}}} + {V_{\rm{P}}}}}} \right) + {\kappa _{\rm{F}}}\left( {1 + \dfrac{{{V_{\rm{P}}}}}{{{V_{\rm{R}}} + {V_{\rm{P}}}}}} \right)}}{{{\kappa _{\rm{R}}}\left( {1 + \dfrac{{{V_{\rm{P}}}}}{{{V_{\rm{R}}} + {V_{\rm{P}}}}}} \right) + {\kappa _{\rm{F}}}\left( {1 - \dfrac{{{V_{\rm{P}}}}}{{{V_{\rm{R}}} + {V_{\rm{P}}}}}} \right)}}} \right) \end{split} $$ (4) 其中：下标P、F、R和M分别表示孔隙、CF、EP和含有孔隙的EP基体；下标eff表示有效值；V、S和
$\kappa $ 分别表示体积分数、体积比热和热导率。通过编织CF/EP复合整体的有效体积比热，得到热扩散系数$\alpha $ 与热导率$\kappa $ 的关系式为$$\kappa = \alpha \cdot {S_{{\rm{eff}}}}$$ (5) 2. 仿真分析
2.1 仿真模型与材料属性
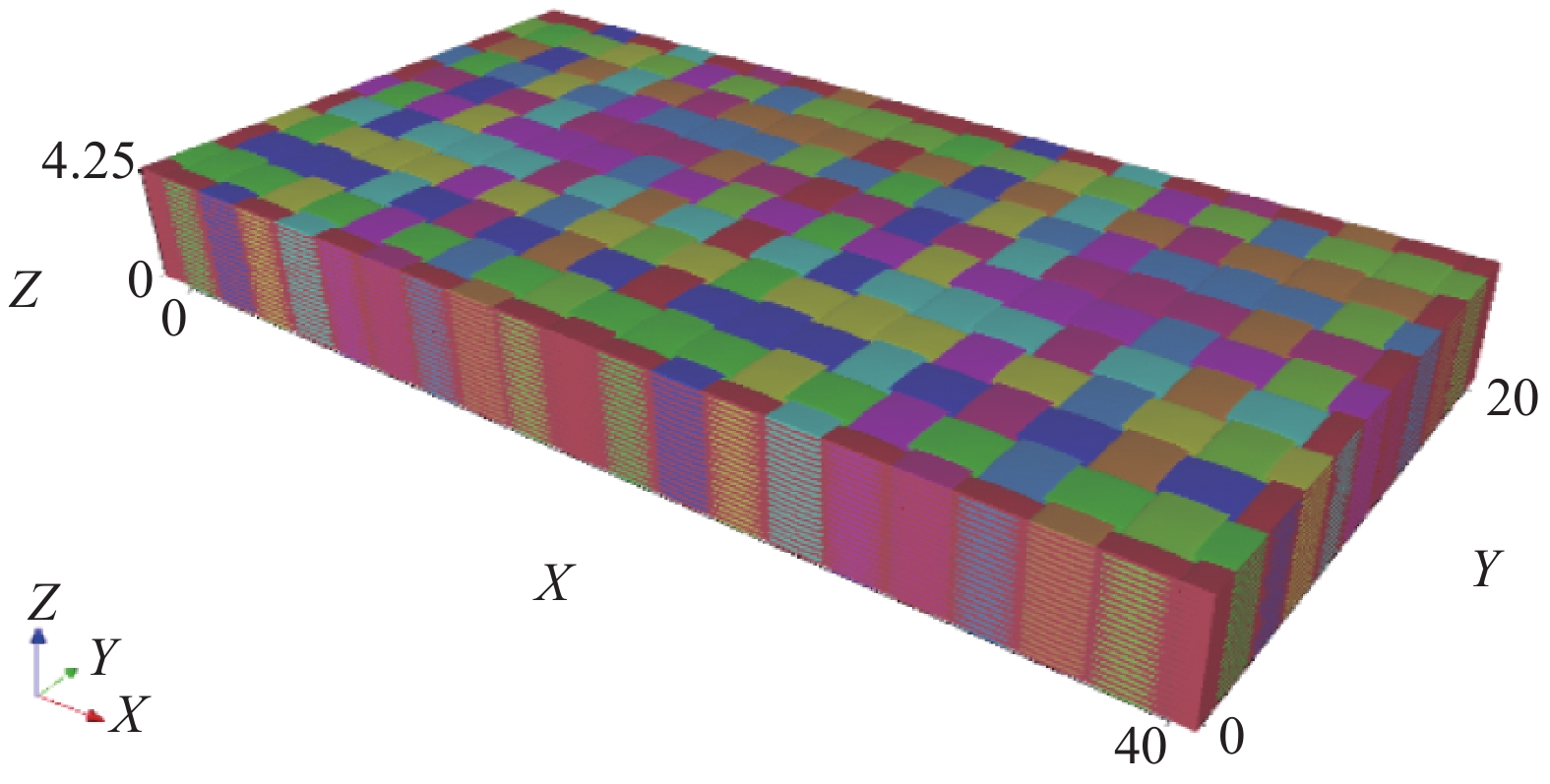
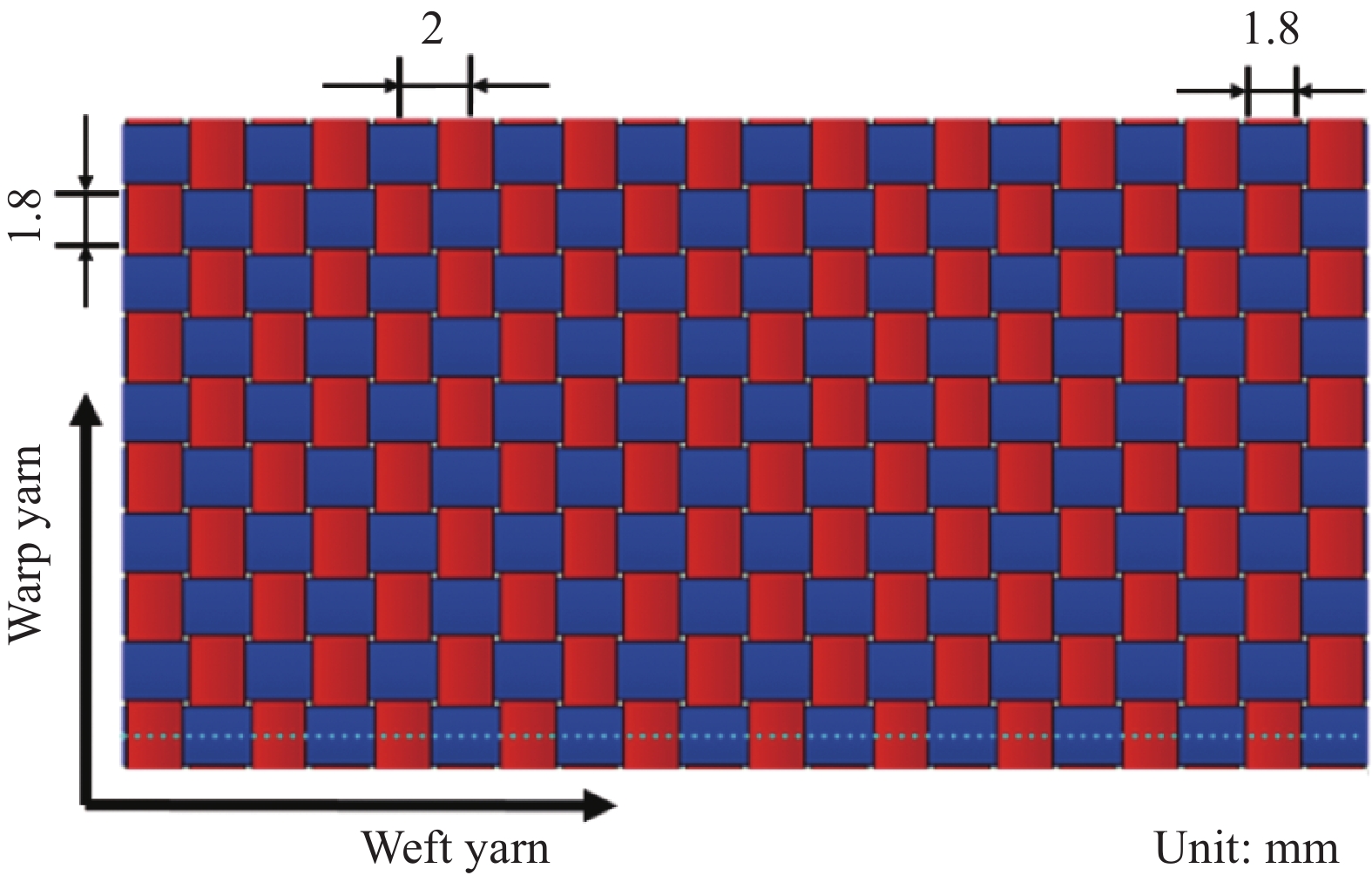
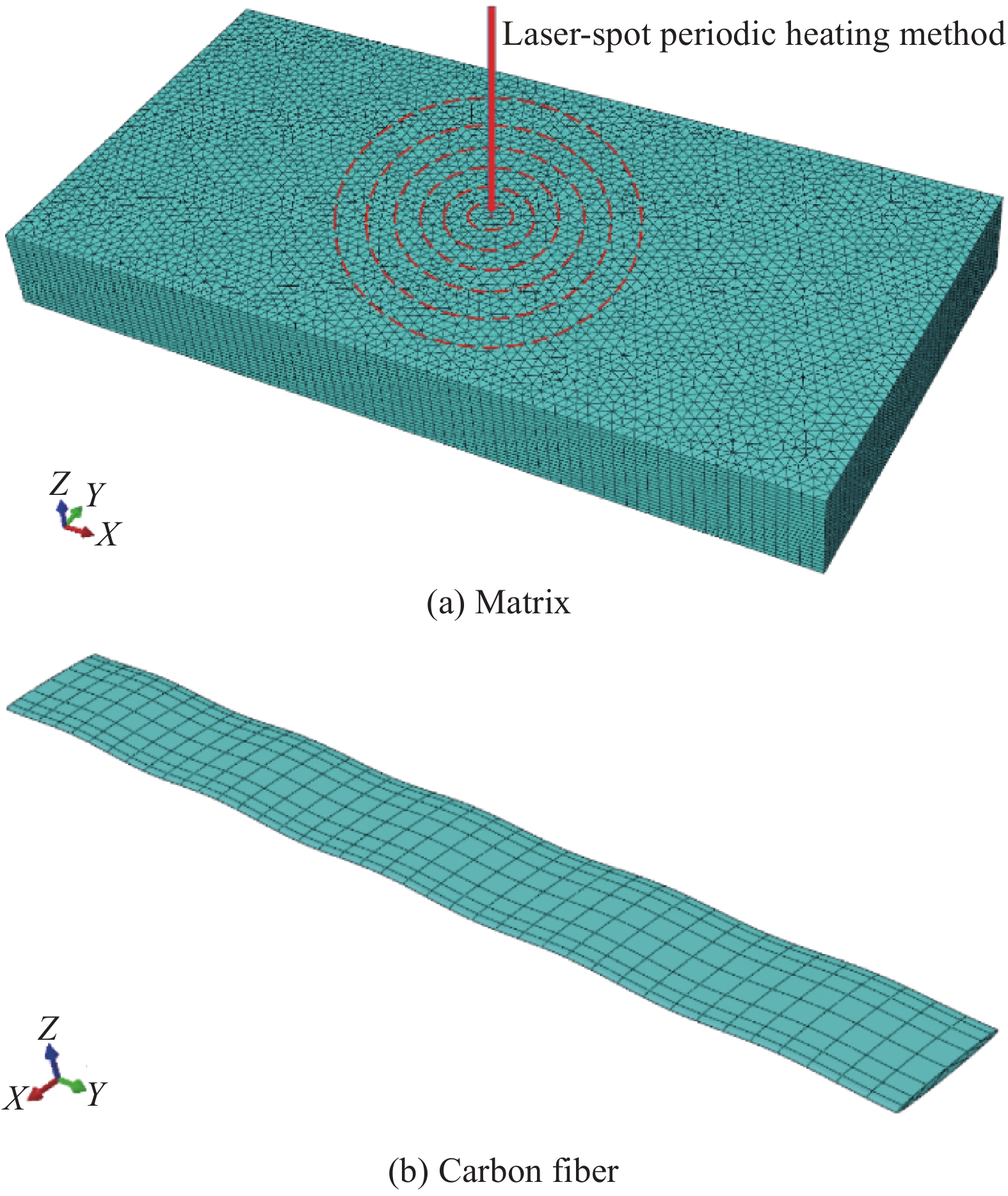
根据CF/EP复合材料的使用要求[25-26]，选择孔隙率为0%~5.3%范围内6组样品进行研究，其具体孔隙率和对应的厚度，如表1所示。样品的基体为EP，其体积分数均为40vol%，因此厚度方向尺寸随孔隙率的增大而增大。图1为通过TexGen软件建立的20层编织CF/EP复合材料仿真模型，平面尺寸取40 mm×20 mm。在平纹结构中，设置经纱和纬纱的数量分别为10和20，经纱和纬纱的宽度均为1.8 mm，纱线间距为2 mm，具体单层纱线的数量、宽度、间距和排布方式，如图2所示。
表 1 编织碳纤维/环氧树脂(CF/EP)复合材料样品的孔隙率与厚度Table 1. Porosity and thickness of woven carbon fiber/epoxy resin (CF/EP) compositesSample 1 2 3 4 5 6 $\varphi $/% 0 0.32 0.45 1.55 3.64 5.3 d/mm 4.25 4.32 4.36 4.42 4.56 4.66 Notes: $\varphi $—Porosity; d—Thickness. ![]()
图 1 编织CF/EP复合材料结构仿真模型Figure 1. Simulation model of woven carbon fiber/epoxy resin composites![]()
图 2 编织CF/EP复合材料单层纱线的数量、间距、宽度及排布方式Figure 2. Number, spacing, width and arrangement of single layer yarns of woven carbon fiber/epoxy resin composites在有限元仿真软件中，需要设定CF与含孔隙EP基体的有效体积比热和热导率，来完成编织CF/EP复合材料的材料属性创建。
已知该材料样品中CF、EP和孔隙的体积比热和热导率如表2所示。
表 2 编织CF/EP复合材料组成成分的热性能参数Table 2. Thermal property parameters of woven CF/EP compositesProperty Carbon fiber Epoxy resin Pore S/(J·m−3·K−1) 1.63×106 2.21×106 1.21×103 $\kappa $/(W(m·K)−1) 8.4 0.2 0.06 Notes: S—specific heat;$\kappa $—Thermal conductivity. 将表2的编织CF/EP复合材料各组成成分的热性能参数代入式(4)求得含孔隙基体的有效体积比热和热导率及该材料整体的有效体积比热，如表3所示。
表 3 编织CF/EP复合材料不同孔隙率样品的有效体积比热与热导率Table 3. Effective volume specific heat and thermal conductivity of woven CF/EP composites with different porositiesSample 1 2 3 4 5 6 SM/(106J·m−3·K−1) 2.210 2.198 2.193 2.154 2.067 1.996 ${\kappa _{\rm{M}}}$/(W(m·K)−1) 0.200 0.199 0.198 0.194 0.186 0.180 Seff/(106J·m−3·K−1) 1.862 1.859 1.857 1.846 1.82 1.796 Notes: SM—Effective volume specific heat of matrix with porosity; ${\kappa _{\rm{M}}}$—Thermal conductivity of matrix with porosity; Seff—Effective volume specific heat of woven CF/EP composite. 2.2 周期性载荷与网格划分
当采用光强周期性变化的激光入射到样品表面时，表面先会迅速将这部分能量吸收，然后转化为热能来形成周期性热源，最后在材料的内部产生热扩散，具体示意如图3(a)所示。由于加载的方式为周期性点光源，故选择Periodic幅值曲线，其傅里叶级数表达式：
$$a = {A_0} + \sum\limits_{n = 1}^N {\left[ {{A_n}\cos n\omega \left( {t - {t_0}} \right) + {B_n}\sin n\omega \left( {t - {t_0}} \right)} \right]} $$ (6) 其中：
${t_0}$ 为初始时间；${A_0}$ 为初始幅值；${A_n}$ 为cos项的系数；${B_n}$ 为sin项的系数。比较式(1)得到幅值曲线需要设置的参数为：${A_0} = 0$ ，${A_n} = $ 0.5，${B_n} = $ 0，$N = $ 1，$\omega = 2{\text{π}}f$ 需要根据加载点光源的频率而定。![]()
图 3 编织CF/EP复合材料有限元仿真模型与周期性点光源加载示意图Figure 3. Finite element model of woven CF/EP composites and the diagram of laser-spot periodic heating method由于三维编织复合材料内部纤维束之间的挤压变形，使纤维束的截面形状呈近似六边形[27-28]。为了接近真实纤维束的细观模型，对纤维束截面形状做类椭圆化处理，在TexGen软件中选择纤维束的截面形状为Power Ellipse，并设定power值为1.2，具体纤维束截面形状如图3(b)所示。在网格划分时，对纤维束两侧较薄处进行局部网格加密处理，并用二次热传导楔形单元DC3D15对基体和纤维束进行网格划分。图3为编织CF/EP复合材料基体和纤维束有限元仿真模型的网格划分图。
3. 编织CF/EP复合材料热扩散参数的计算与分析
3.1 激光频率对计算结果的影响
激光调制频率受样品长度和宽度的限制，如果点光源和边界之间的距离比实际热扩散长度长得多，会导致热流的衰减产生变化[29]。该条件可表示为
$$f \geqslant \frac{{7.57\alpha }}{{{\text{π}}{L^2}}} $$ (7) 其中：
$\alpha $ 是平面内热扩散系数；$L$ 为点光源到样品边界的距离。在点光源加载过程中，热扩散长度必须大于样品的单层预浸料叠层厚度，不然会降低点光源的穿透性，从而影响对样品热扩散性能的分析。该条件可表示为
$$\mu = \sqrt {\frac{{{\alpha _ \bot }}}{{{\text{π}}f}}} \geqslant {d_{\rm{t}}}$$ (8) 其中：
$\mu $ 为热扩散长度；${\alpha _ \bot }$ 为垂直方向上的热扩散系数；${d_{\rm{t}}}$ 为单层预浸料叠层厚度。综上，根据式(7)和式(8)得到调制频率所受的条件为
$$\frac{{7.57\alpha }}{{{\text{π}}{L^2}}} \leqslant f \leqslant \frac{{{\alpha _ \bot }}}{{{\text{π}}{d_{\rm{t}}}^2}}$$ (9) 初步取
$\alpha = 0.5\;{\rm{m}}{{\rm{m}}^{\rm{2}}}{\rm{/}} {\rm{s}}$ ,$L = 20\;{\rm{mm}}$ ,${d_{\rm{t}}} = 0.2\;{\rm{mm}}$ ,${\alpha _ \bot } = 0.{\rm{5}}\;{\rm{m}}{{\rm{m}}^{\rm{2}}}{\rm{/}} {\rm{s}}$ ，得到激光频率的取值范围约为0.003~4 Hz。为了方便对样品的热扩散方向进行描述，以点光源加载中心为原点，定义平面内纬纱方向为横向(θ=0°)，经纱方向为纵向(θ=90°)，垂直平面方向为法向(γ=90°)，建立不同热扩散方向的角度坐标示意，如图4所示。
![]()
图 4 编织CF/EP复合材料平面内和垂直方向上热扩散角度坐标Figure 4. Coordinates of heat diffusion angles in the plane and the vertical direction of woven CF/EP composites当激光频率为1 Hz时，样品1在平面内和垂直方向上的温度分布云图，如图5所示。选取平面内0°方向上距离激光入射点分别为2 mm、4 mm和6 mm的3个节点，具体示意如图5(b)所示，并将在点光源加载过程中3个节点的节点温度值代入式(2)，得到线性化后的拟合效果，如图6所示。
![]()
图 5 编织CF/EP复合材料样品S1的三维温度分布云图Figure 5. Three-dimensional temperature distribution cloud diagram of woven CF/EF composites for S1 sample![]()
图 6 编织CF/EP复合材料0°方向上3个节点温度值线性化后的拟合效果图Figure 6. Fitting graph of the temperature distribution values of 3 nodes in the 0° direction after linearization of woven CF/EP composites可以看出，0°方向上距离不同的3个节点所对应拟合直线的斜率近似相等，说明沿同一方向上热扩散系数相对稳定，与节点到激光入射点的距离无关。因此取3个节点拟合直线的平均斜率来计算热扩散系数，以确保计算准确性。通过计算得到3个节点的平均斜率k=−7.964，相关系数
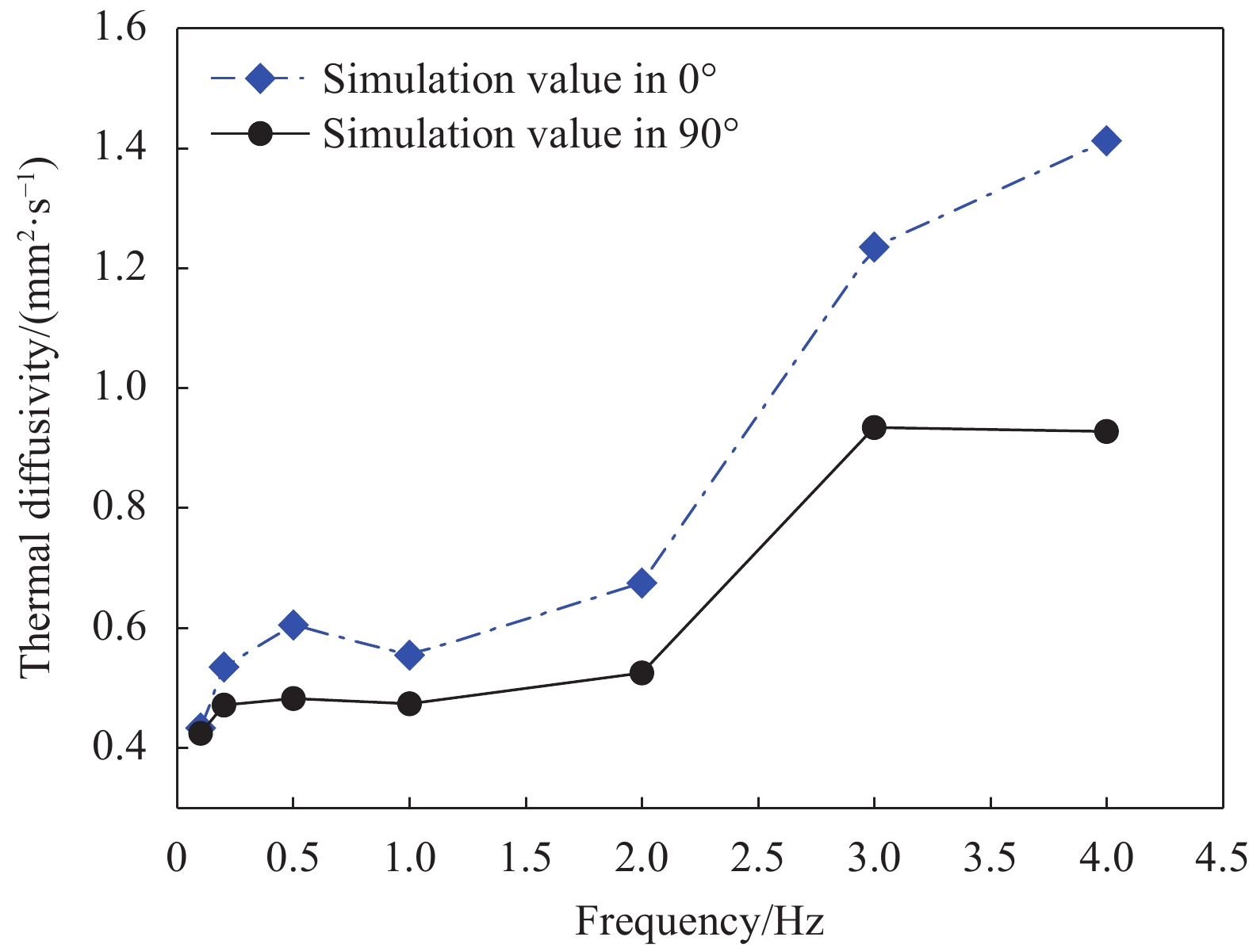
${R^2} \approx$ 0.985，代入式(3)和式(5)求得热扩散系数$\alpha$ =0.567 mm2/s，热导率$\kappa $ =1.054$ {\rm{W}}/ {({\rm{m}} \cdot {\rm{K}})^{{\rm{ - 1}}}}$ 。选取激光频率0.003~4 Hz内的几组频率值，计算样品1在平面内0°与90°方向的热扩散系数，如图7所示。可以看出，调制频率在0.1~2 Hz时，计算得到的热扩散系数保持稳定，而当调制频率大于2 Hz时，热扩散系数随着调制频率的增加会发生较大的变化。因此在仿真分析时，选取调制频率范围为0.1~2 Hz。
![]()
图 7 编织CF/EP复合材料样品1的热扩散系数-频率曲线Figure 7. Thermal diffusivity-frequency curves of woven CF/EF composites for sample NO.13.2 孔隙率对编织CF/EP复合材料热扩散性能的影响
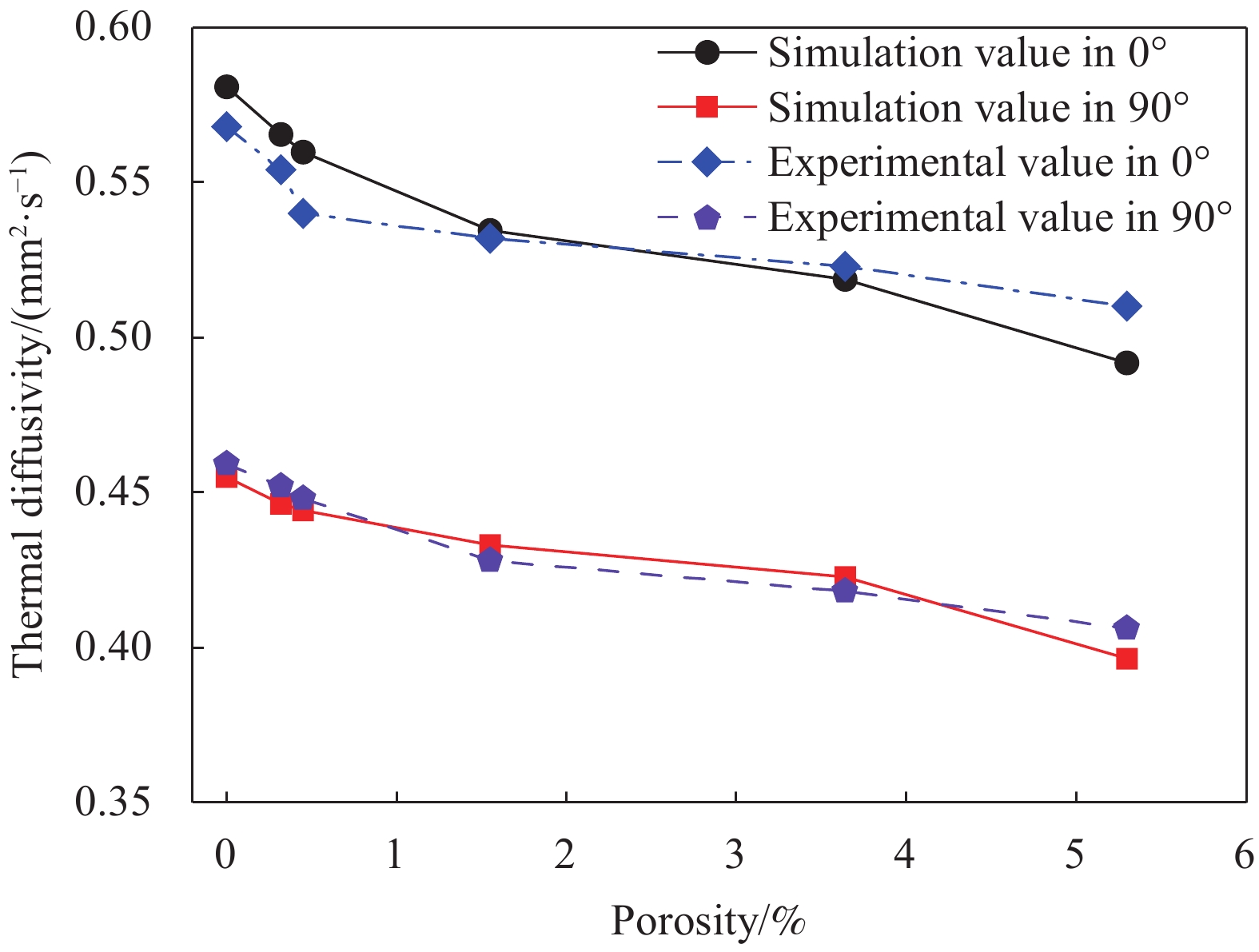
通过TexGen软件建立不同厚度的样品模型，导入有限元分析软件中设置不同孔隙率样品的材料属性来模拟温度场分布。在调制频率为1 Hz时，计算孔隙率为0%~5.3%样品在平面内0°与90°方向上的热扩散系数和热导率分别如图8和9所示。
![]()
图 8 不同厚度编织CF/EP复合材料的热扩散系数-孔隙率曲线Figure 8. Thermal diffusivity-frequency curves for woven CF/EP composites with different thicknesses![]()
图 9 不同厚度编织CF/EP复合材料的热导率-孔隙率曲线Figure 9. Thermal conductivity-frequency curves for woven CF/EP composites with different thicknesses可以得到，编织CF/EP复合材料在平面内的热扩散系数和热导率都随着孔隙率的增加而降低。孔隙率小于1.55%时，孔隙率每增加1%，热扩散系数和热导率分别下降5.4%和6%。当孔隙率大于1.55%时，下降速度变慢，孔隙率每增加1%，热扩散系数和热导率分别下降2.4%和3%。同文献[14]的实验值相比，平均相对误差率为2%，吻合度较好。
3.3 编织CF/EP复合材料热扩散的各向异性分析
由图5(a)的温度分布云图可以看出，编织CF/EP复合材料的热扩散并不呈现同心圆分布，而沿着纤维束横向和轴向的热扩散较快，呈现各向异性的特点。取调制频率为1 Hz，通过计算样品1在平面内和垂直方向上的热扩散系数和热导率，来研究热扩散的各向异性。图10和图11分别为平面内和垂直方向上不同热扩散角度的热扩散系数与热导率极坐标图。
![]()
图 10 编织CF/EP复合材料平面内不同角度热扩散系数和热导率极坐标图Figure 10. Polar coordinate diagram of in-plane thermal diffusivity and thermal conductivity with different angles for woven CF/EP composites![]()
图 11 编织CF/EP复合材料垂直方向上不同角度热扩散系数和热导率极坐标图Figure 11. Polar coordinate diagram of thermal diffusivity and thermal conductivity in the vertical direction with different angles for woven CF/EP composites可以得到，编织CF/EP复合材料在平面内的热扩散系数和热导率随着θ的不同而变化，沿着经纱和纬纱方向的热扩散最快，热扩散系数和热导率的最大值分别为0.56 mm2/s和1.05 W(m·K)−1。在经(纬)纱45°方向的热扩散最慢，热扩散系数和热导率最小值分别为0.25 mm2/s和0.46 W(m·K)−1。沿着纬纱方向的热扩散系数和热导率略高于经纱方向，这是由于周期性点光源加载中心处，横向纤维束位于纵向纤维束上方，导致周期性点光源产生的热波先接触横向的纤维束，再沿纵向纤维束进行热扩散。与参考文献[14]的实验值进行比较，热扩散系数与热导率的实验值和仿真值吻合度较好，平均相对误差率为9.5%。在垂直方向上，热扩散系数与热导率的平均变化量为0.016 mm2/s和0.29 W(m·K)−1，相比平面内变化较小。在90°方向上的热扩散系数与热导率数值最大，分别为0.37 mm2/s和0.69 W(m·K)−1，并向两侧递减，这可能由于点光源的穿透性造成的。
4. 结 论
模拟了编织碳纤维/环氧树脂(CF/EP)复合材料在周期性点光源加载下的温度场分布，并分析了孔隙率对热扩散性能的影响及热扩散的各向异性。
(1) 编织CF/EP复合材料在平面内的热扩散系数和热导率都随着孔隙率的增加而降低。孔隙率小于1.55%时，孔隙率每增加1%，热扩散系数和热导率分别下降5.4%和6%。当孔隙率大于1.55%时，孔隙率每增加1%，热扩散系数和热导率分别下降2.4%和3%。
(2) 编织CF/EP复合材料在平面内沿着经纱和纬纱方向的热扩散最快，热扩散系数和热导率最大值分别为0.56 mm2/s和1.05 W(m·K)−1。在经(纬)纱45°方向的热扩散最慢，热扩散系数和热导率最小值分别为0.25 mm2/s和0.46 W(m·K)−1。在垂直方向上，由于点光源的穿透性使90°方向上的热扩散系数与热导率数值最大，分别为0.37 mm2/s和0.69 W(m·K)−1，并向两侧递减。
(3) 通过热扩散仿真分析得到热扩散系数和热导率与实验结果吻合，验证了论文所提出的研究方法。
-
![]()
图 1 编织CF/EP复合材料结构仿真模型
Figure 1. Simulation model of woven carbon fiber/epoxy resin composites
![]()
图 2 编织CF/EP复合材料单层纱线的数量、间距、宽度及排布方式
Figure 2. Number, spacing, width and arrangement of single layer yarns of woven carbon fiber/epoxy resin composites
![]()
图 3 编织CF/EP复合材料有限元仿真模型与周期性点光源加载示意图
Figure 3. Finite element model of woven CF/EP composites and the diagram of laser-spot periodic heating method
![]()
图 4 编织CF/EP复合材料平面内和垂直方向上热扩散角度坐标
Figure 4. Coordinates of heat diffusion angles in the plane and the vertical direction of woven CF/EP composites
![]()
图 5 编织CF/EP复合材料样品S1的三维温度分布云图
Figure 5. Three-dimensional temperature distribution cloud diagram of woven CF/EF composites for S1 sample
![]()
图 6 编织CF/EP复合材料0°方向上3个节点温度值线性化后的拟合效果图
Figure 6. Fitting graph of the temperature distribution values of 3 nodes in the 0° direction after linearization of woven CF/EP composites
![]()
图 7 编织CF/EP复合材料样品1的热扩散系数-频率曲线
Figure 7. Thermal diffusivity-frequency curves of woven CF/EF composites for sample NO.1
![]()
图 8 不同厚度编织CF/EP复合材料的热扩散系数-孔隙率曲线
Figure 8. Thermal diffusivity-frequency curves for woven CF/EP composites with different thicknesses
![]()
图 9 不同厚度编织CF/EP复合材料的热导率-孔隙率曲线
Figure 9. Thermal conductivity-frequency curves for woven CF/EP composites with different thicknesses
![]()
图 10 编织CF/EP复合材料平面内不同角度热扩散系数和热导率极坐标图
Figure 10. Polar coordinate diagram of in-plane thermal diffusivity and thermal conductivity with different angles for woven CF/EP composites
![]()
图 11 编织CF/EP复合材料垂直方向上不同角度热扩散系数和热导率极坐标图
Figure 11. Polar coordinate diagram of thermal diffusivity and thermal conductivity in the vertical direction with different angles for woven CF/EP composites
表 1 编织碳纤维/环氧树脂(CF/EP)复合材料样品的孔隙率与厚度
Table 1 Porosity and thickness of woven carbon fiber/epoxy resin (CF/EP) composites
Sample 1 2 3 4 5 6 $\varphi $/% 0 0.32 0.45 1.55 3.64 5.3 d/mm 4.25 4.32 4.36 4.42 4.56 4.66 Notes: $\varphi $—Porosity; d—Thickness. 
下载: 导出CSV
表 2 编织CF/EP复合材料组成成分的热性能参数
Table 2 Thermal property parameters of woven CF/EP composites
Property Carbon fiber Epoxy resin Pore S/(J·m−3·K−1) 1.63×106 2.21×106 1.21×103 $\kappa $/(W(m·K)−1) 8.4 0.2 0.06 Notes: S—specific heat;$\kappa $—Thermal conductivity.
下载: 导出CSV
表 3 编织CF/EP复合材料不同孔隙率样品的有效体积比热与热导率
Table 3 Effective volume specific heat and thermal conductivity of woven CF/EP composites with different porosities
Sample 1 2 3 4 5 6 SM/(106J·m−3·K−1) 2.210 2.198 2.193 2.154 2.067 1.996 ${\kappa _{\rm{M}}}$/(W(m·K)−1) 0.200 0.199 0.198 0.194 0.186 0.180 Seff/(106J·m−3·K−1) 1.862 1.859 1.857 1.846 1.82 1.796 Notes: SM—Effective volume specific heat of matrix with porosity; ${\kappa _{\rm{M}}}$—Thermal conductivity of matrix with porosity; Seff—Effective volume specific heat of woven CF/EP composite.
下载: 导出CSV
-
[1] 包建文, 蒋诗才, 张代军. 航空碳纤维树脂基复合材料的发展现状和趋势[J]. 科技导报, 2018, 36(19):52-63. BAO J W, JIANG S C, ZHANG D J. Current status and trends of aeronautical resin matrix composites reinforced by carbon fiber[J]. Science & Technology Review,2018,36(19):52-63(in Chinese).
[2] 邢丽英, 蒋诗才, 周正刚. 先进树脂基复合材料制造技术进展[J]. 复合材料学报, 2013, 30(1):107-111. XING L Y, JIANG S C, ZHOU Z G. Progress of manufacturing technology development of advanced polymer matrix composites[J]. Acta Materiea Compositae Sinica,2013,30(1):107-111(in Chinese).
[3] 龙巍, 郑学林, 臧建彬. 基于碳纤维复合材料热性能的研究进展综述[J]. 应用化工, 2019, 48(9):2251-2255. DOI: 10.3969/j.issn.1671-3206.2019.09.052 LONG W, ZHENG X L, ZANG J B. Review of research of progress based on thermal properties of carbon fiber composites[J]. Applied Chemical Industry,2019,48(9):2251-2255(in Chinese). DOI: 10.3969/j.issn.1671-3206.2019.09.052
[4] LI H Z, LI S, WANG Y C. Prediction of effective thermal conductivities of woven fabric composites using unit cells at multiple length scales[J]. Journal of Materials Research, 2011, 26 (3): 384-394.
[5] ZHANG L L, LI H J, LI K Z, et al. Double-layer TC4/Sr substituted hydroxyapatite bioactive coating for carbon composites[J]. Ceramics International, 2015, 41: 427-435.
[6] 姜黎黎, 吴日娜, 徐美玲, 等. 三维四向编织碳纤维/环氧树脂复合材料在热环境中的拉压力学性能实验[J]. 复合材料学报, 2020, 37(2):309-317. JIANG L L, WU R N, XU M L, et al. Experimental investigation on the tensile and compressive properties of 3D 4-directional braided carbon fiber/epoxy resin composites in thermal environment[J]. Acta Materiea Compositae Sinica,2020,37(2):309-317(in Chinese).
[7] 周雅斌, 曾捷, 张倩昀, 等. 基于光纤传感水热平衡法测量碳纤维圆筒结构的热扩散系数[J]. 中国激光, 2013, 11:200-205. ZHOU Y B, ZENG J, ZHANG Q Y, et al. Measurement of the thermal diffusivity of carbon composite by water-heat balance method[J]. Chinese Journal of Lasers,2013,11:200-205(in Chinese).
[8] WOJCIECH P. A, SEBASTIAN P, ZIEMOWIT O. Determination of thermal conductivity of CFRP composite materials using unconventional laser flash technique[J]. Measurement,2018,124:147-155. DOI: 10.1016/j.measurement.2018.04.022
[9] RYOHEI F, HOSEI N. Novel fiber orientation evaluation method for CFRP/CFRTP based on measurement of anisotropic in-plane thermal diffusivity distribution[J]. Composites Science and Technology,2017,140:116-122. DOI: 10.1016/j.compscitech.2016.12.006
[10] 刘玲, 张博明, 王殿富. 碳/环氧复合材料孔隙问题研究进展[J]. 宇航材料工艺, 2004(6):6-10. DOI: 10.3969/j.issn.1007-2330.2004.06.002 LIU L, ZHANG B M, WANG D F. Development of void problem for carbon/epoxy composite materials[J]. Aerospace Materials & Technology,2004(6):6-10(in Chinese). DOI: 10.3969/j.issn.1007-2330.2004.06.002
[11] 益小苏, 杜善义, 张立同. 复合材料手册[M]. 北京: 化学工业出版社, 2009: 7-12. YI X S, DU S Y, ZHANG L T. Composites materrials handbook[M]. Beijing: Chemical industry press, 2009: 7-12 (in Chinese).
[12] DONG C S. Effects of process-induced voids on the properties of fiber reinforced composites[J]. Journal of Materials Science & Technology,2016,32:596-604.
[13] 吴恩启, 徐紫红, 郭新欣, 等. 孔隙率对碳纤维增强复合材料光热辐射信号的影响[J]. 中国激光, 2015, 42 (7):185-189. WU E Q, XU Z H, GUO X X et al. Influence of porosity on photothermal radiometry of carbon fiber reinforced polymers[J]. Chinese Journal of Lasers,2015,42 (7):185-189(in Chinese).
[14] WU E Q, GAO Q, LI M H, et al. Study on in-plane thermal conduction of woven carbon fiber reinforced polymer by infrared thermography[J]. NDT & E International,2018,94:56-61.
[15] WROBEL G, RDZAWSKI Z, MUZIA G, et al. Determination of thermal diffusivity of carbon/epoxy composites with different fiber content using transient thermography[J]. Journal of Achievements in Materials & Manufacturing Engineering,2009,37 (2):518-525.
[16] GOU J J, DAI Y J, LI S G, et al. Numerical study of effective thermal conductivities of plain woven composites by unit cells of different sizes[J]. International Journal of Heat and Mass Transfer,2015,91:829-840. DOI: 10.1016/j.ijheatmasstransfer.2015.07.074
[17] 赵玉芬, 宋磊磊, 李嘉禄, 等. 三维机织碳纤维/环氧树脂复合材料在两种测量方法下的热响应机制对比[J]. 复合材料学报, 2018, 35 (1):103-109. ZHAO Y F, SONG L L, LI J L, et al. Comparison of thermal response mechanisms for three dimensional woven carbon fiber/epoxy resin composites under two measurement methods[J]. Acta Materiea Compositae Sinica,2018,35 (1):103-109(in Chinese).
[18] DONG K, LIU K, PAN L J, et al. Experimental and numerical investigation on the thermal conduction properties of 2.5D angle-interlock woven composites[J]. Composite Structures,2016,154:319-333. DOI: 10.1016/j.compstruct.2016.07.071
[19] RÜDIGER S, VADIM A. Modelling the heating process of CFRP by cw-laser radiation with special focus on the heat transfer by thermal radiation between the carbon fibers[J]. Procedia CIRP, 2018, 74: 562-567.
[20] TAKUYA I, HOSEI N. Measurement of three-dimensional anisotropic thermal diffusivities for carbon fiber-reinforced plastics using lock-in thermography[J]. International Journal of Thermophysics,2015,36:2577-2589. DOI: 10.1007/s10765-014-1755-5
[21] TAKUYA I, HOSEI N. Measurement of 3D thermal diffusivity distribution with lock-in thermography and application for high thermal conductivity CFRPs[J]. Infrared Physics & Technology,2019,99:248-256.
[22] MAYR G, PLANK B, SEKELJA J, et al. Active thermography as a quantitative method for non-destructive evaluation of porous carbon fiber reinforced polymers[J]. NDT & E International,2011,44:537-543.
[23] ZALAMEDA J. Measured through-the-thickness thermal diffusivity of carbon fiber reinforced composite materials[J]. Journal of Composites Technology and Research, 1999; 21 (2): 98–102.
[24] KULKARNI M, BRADY R. A model of global thermal conductivity in laminated carbon/carbon composites[J]. Composites Science and Technology, 1997; 57 (3): 277–85.
[25] 朱洪艳, 李地红, 张东兴, 等. 孔隙率对碳纤维/环氧树脂复合材料层合板湿热性能的影响[J]. 复合材料学报, 2010, 27(2):24-30. ZHU H Y, LI D H, ZHANG D X, et al. Effect of porosity on the hygrothermal behaviour of carbon fiber reinforced epoxy composite laminates[J]. Acta Material Composite Silica,2010,27(2):24-30(in Chinese).
[26] 李波, 赵美英, 万小朋. 孔隙微观特征对碳纤维/环氧树脂复合材料横向拉伸强度的影响[J]. 复合材料学报, 2018, 35(7):1864-1868. LI B, ZHAO M Y, WAN X P. Influence of void micro-characteristics on transverse tensile strength of unidirectional carbon fiber/epoxy resin composites[J]. Acta Materiae Compositae Sinica,2018,35(7):1864-1868(in Chinese).
[27] 朱元林, 崔海涛, 温卫东, 等. 含纤维束截面形状变化的三维编织复合材料细观模型及刚度预报[J]. 复合材料学报, 2012, 29(6):187-196. ZHU Y L, CUI H T, WEN W D, et al. Microstructure model and stiffness prediction of 3D braided composites considering yarn′cross-section variation[J]. Acta Materiae Compositae Sinica,2012,29(6):187-196(in Chinese).
[28] 卢子兴, 杨振宇, 刘振国. 三维四向编织复合材料结构模型的几何特性[J]. 北京航空航天大学学报, 2006(1):92-96. DOI: 10.3969/j.issn.1001-5965.2006.01.022 LU Z X, YANG Z Y, LIU Z G. Geometrical characteristics of structural model for 3D braided composites[J]. Journal of Beijing University of Aeronautics and Astronautics,2006(1):92-96(in Chinese). DOI: 10.3969/j.issn.1001-5965.2006.01.022
[29] MASAYA K, HOSEI N. Anisotropic thermal diffusivity measurements in high-thermal-conductive carbon fiber reinforced plastic composites[J]. Journal of Electronics Cooling and Thermal Control,2015,5 (1):15-25. DOI: 10.4236/jectc.2015.51002
-
期刊类型引用(1)
1. 赵昌方，周志坛，张克斌，仲健林，任杰，乐贵高. 碳纤维复合材料燃气射流热冲击研究:冲蚀形貌及热力分析. 湘潭大学学报(自然科学版). 2022(03): 37-45+71 . 
百度学术
其他类型引用(8)
-
计量
- 文章访问数: 1202
- HTML全文浏览量: 618
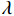
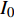
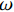
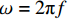
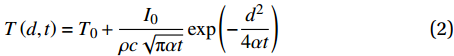
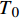
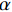
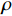
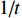
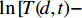
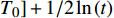
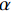
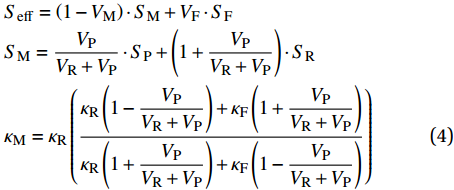
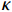
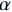
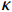
- PDF下载量: 126
- 被引次数: 9
