复合材料II型疲劳分层扩展预测：从应变能释放率-寿命(<i>G</i>-<i>N</i>)曲线到Paris' law

祝曼; 王阳; 刘强; 易敏

doi:10.13801/j.cnki.fhclxb.20221213.001

复合材料II型疲劳分层扩展预测：从应变能释放率-寿命(G-N)曲线到Paris' law

doi: 10.13801/j.cnki.fhclxb.20221213.001

祝曼^{1, 2,},
王阳³,
刘强^2, ,,
易敏^2, ,

1.
南京工业大学　土木工程学院，南京 211800
2.
南京航空航天大学　航空学院，航空航天结构力学及控制全国重点实验室，南京 210016
3.
北京宇航系统工程研究所，北京 100076

基金项目: 国家自然科学基金 (12102179；12272174)；江苏省自然科学基金(BK20200409)；中央高校基本科研业务费专项资金(3082021 NS2021001)；江苏省“双创博士”计划(JSSCBS20210618)

详细信息

通讯作者:
刘强，博士，副教授，博士生导师，研究方向为复合材料极端环境性能评价及工艺力学　E-mail: liuqiang2015@nuaa.edu.cn

易敏，博士，教授，博士生导师，研究方向为先进材料结构和先进制造的多尺度多场耦合力学　E-mail: yimin@nuaa.edu.cn

中图分类号: TB332
计量
- 文章访问数: 652
- HTML全文浏览量: 474
- PDF下载量: 83
- 被引次数: 0
出版历程
- 收稿日期: 2022-10-04
- 修回日期: 2022-11-12
- 录用日期: 2022-11-25
- 网络出版日期: 2022-12-15
- 刊出日期: 2023-09-15

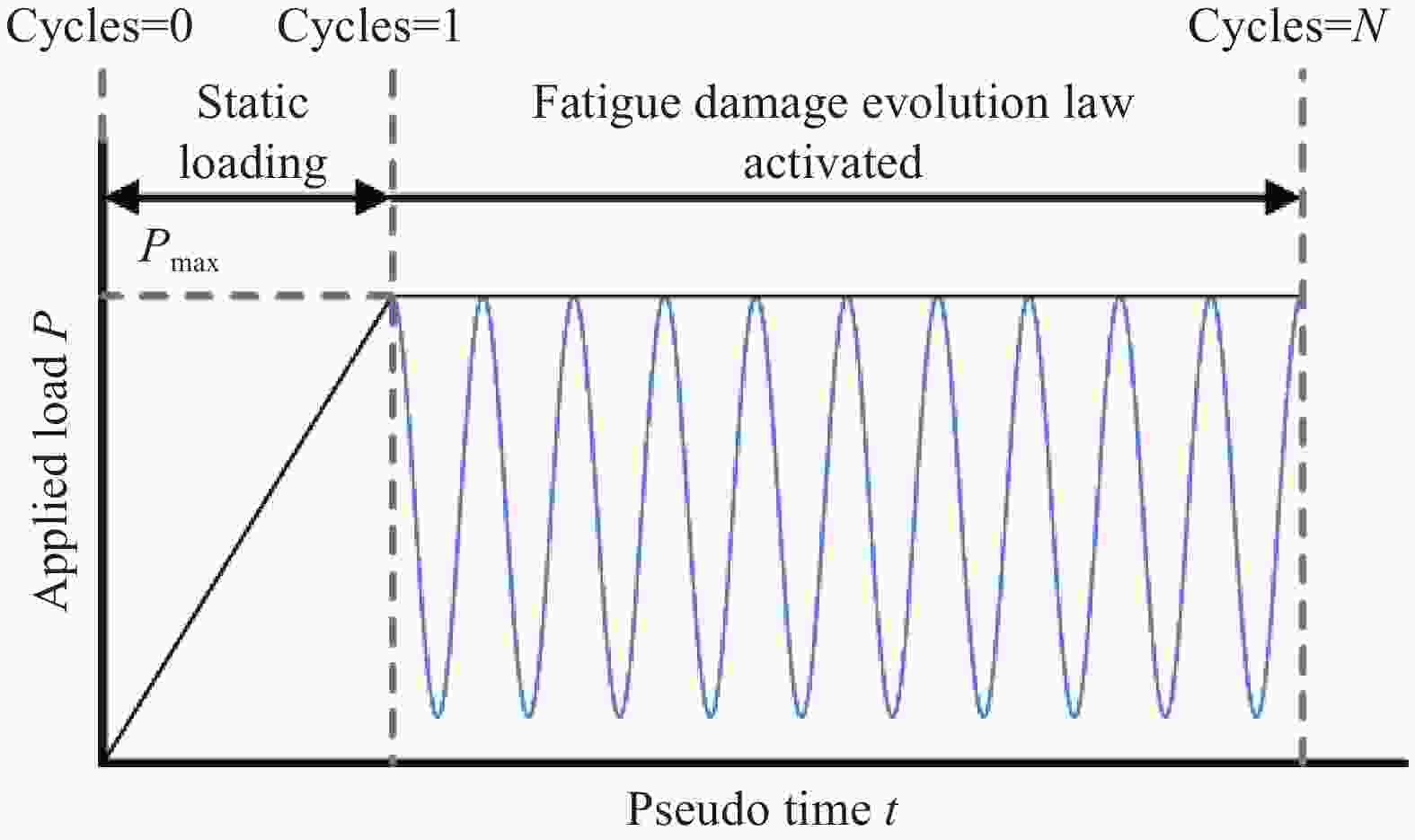
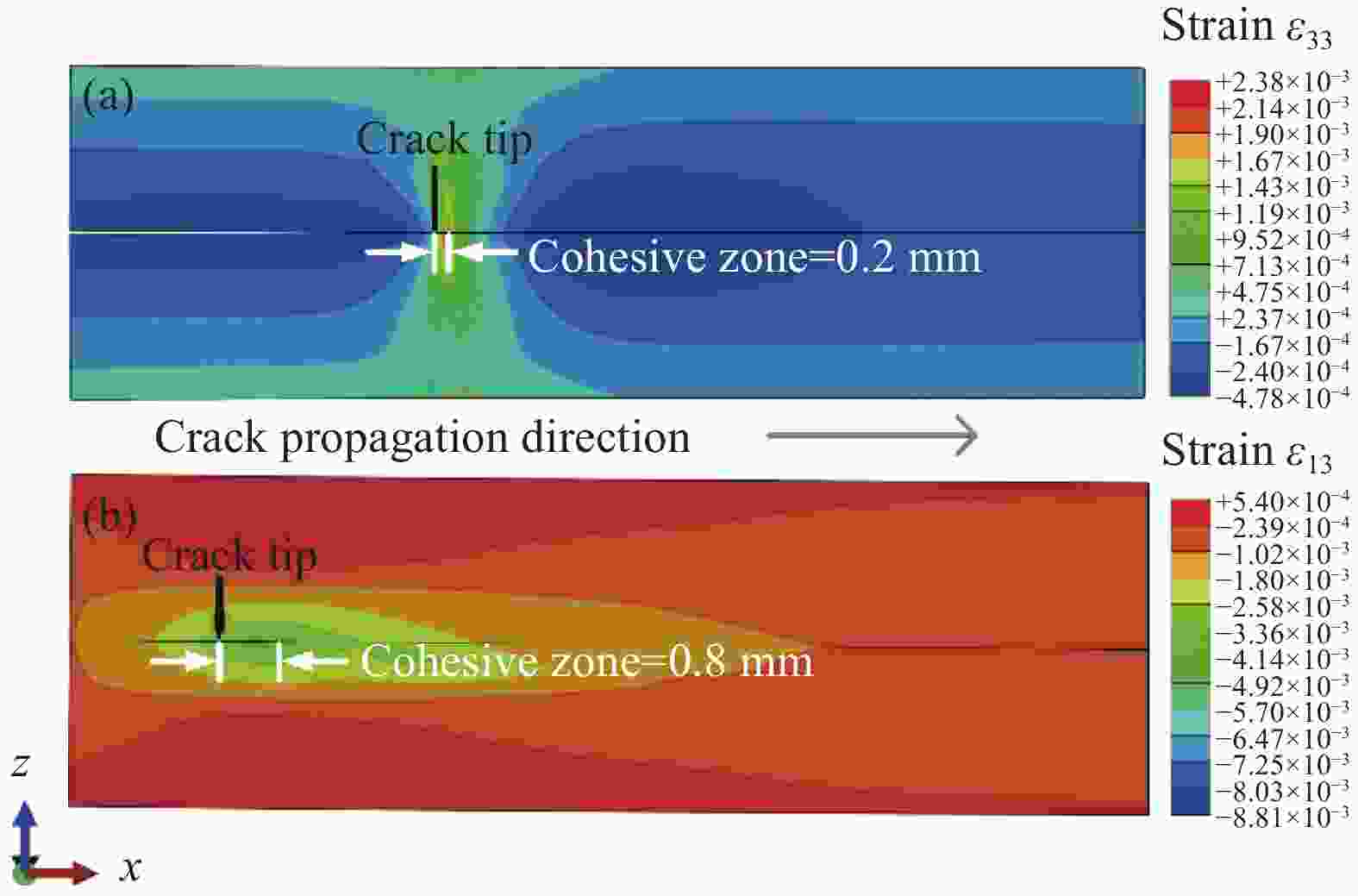
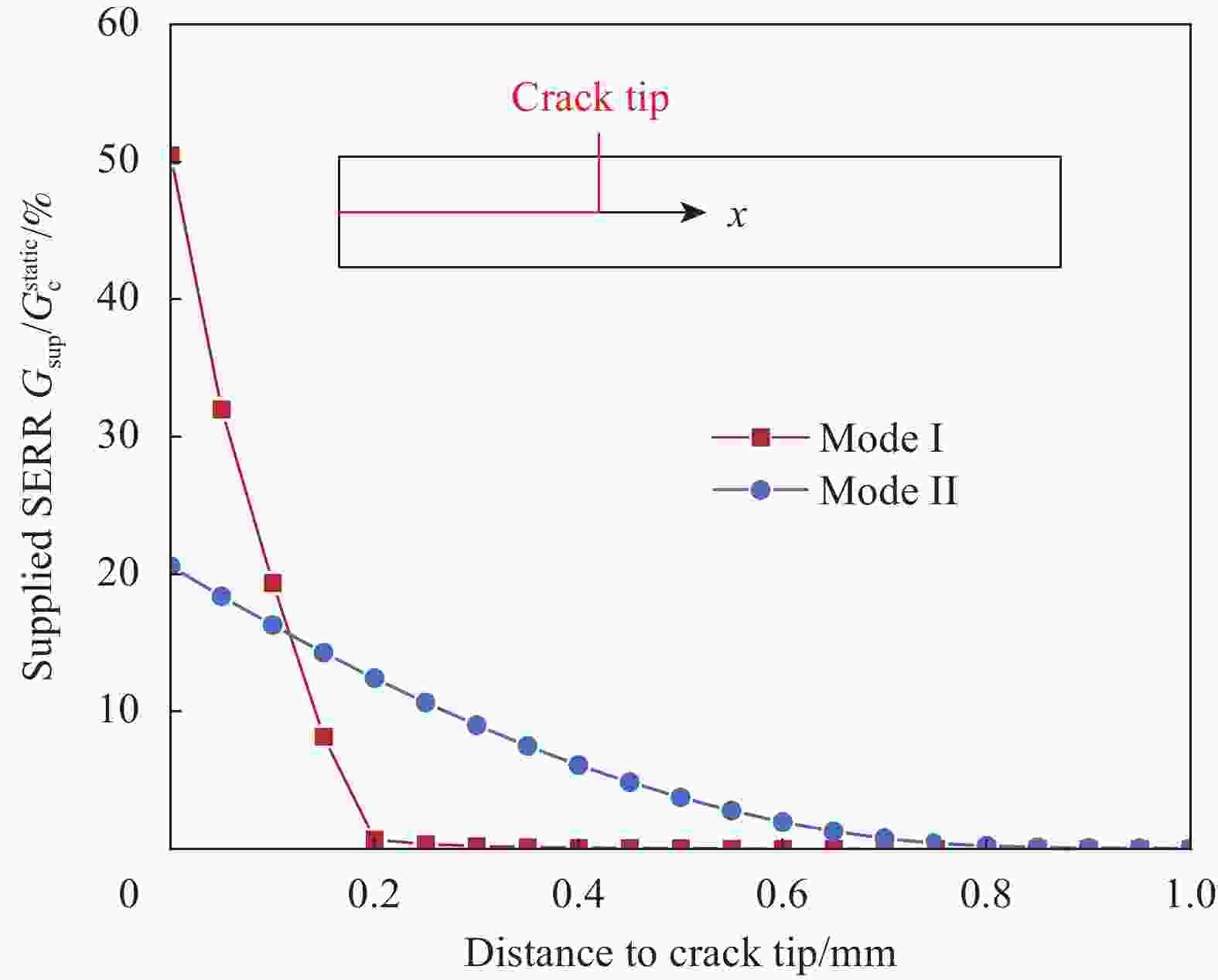
Prediction of mode II fatigue delamination propagation in fibre reinforced composites: From strain energy release rate-life (G-N) curve to Paris' law

ZHU Man^{1, 2
,},
WANG Yang³,
LIU Qiang^{2
, ,},
YI Min^{2
, ,}

1.
College of Civil Engineering, Nanjing Tech University, Nanjing 211800, China
2.
State Key Laboratory of Mechanics and Control for Aerospace Structures, College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
3.
Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China

Funds: National Natural Science Foundation of China (12102179; 12272174); Natural Science Foundation of Jiangsu Province (BK20200409); the Fundamental Research Funds for the Central Universities (3082021 NS2021001); Jiangsu Provincial Double-Innovation Doctor Program (JSSCBS20210618)

摘要

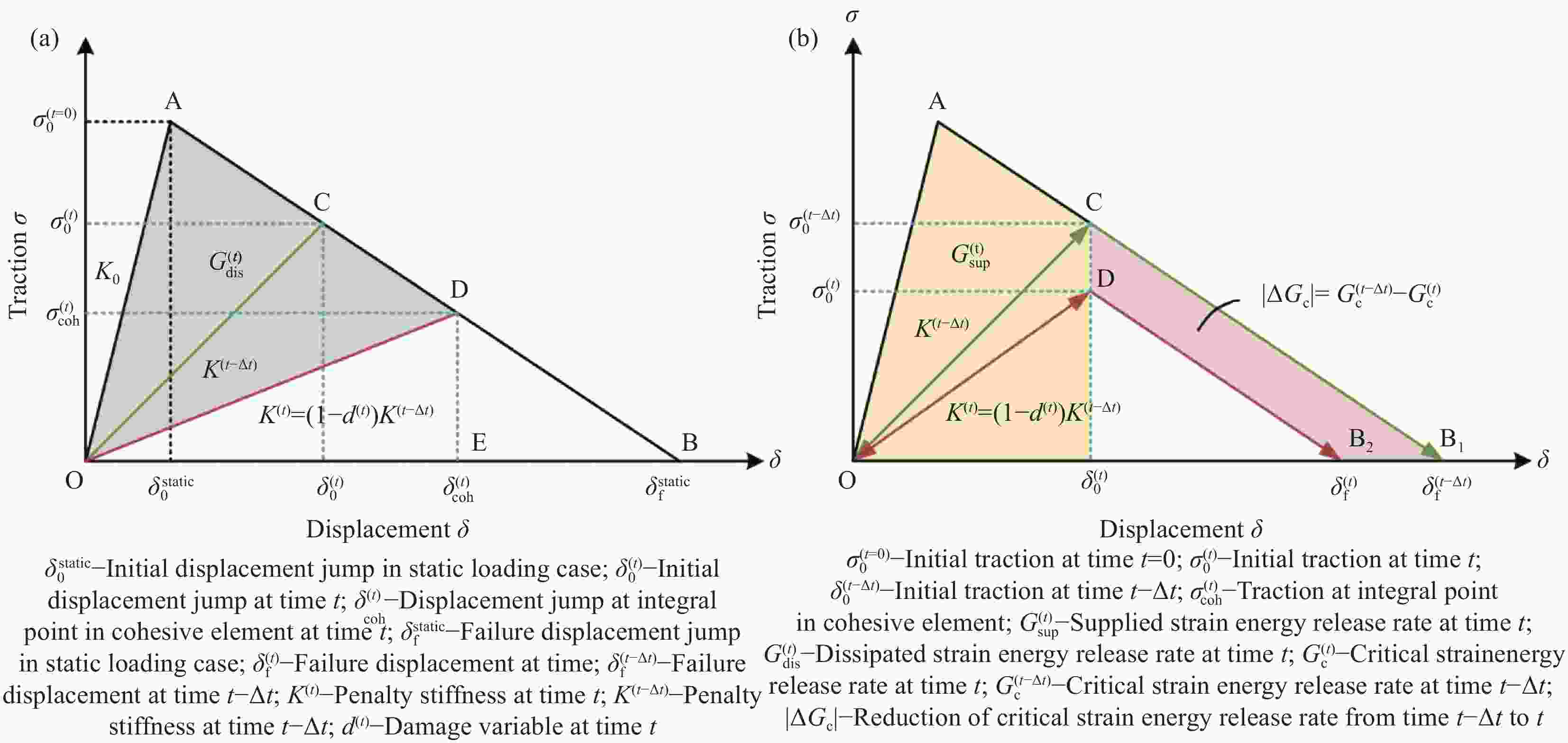
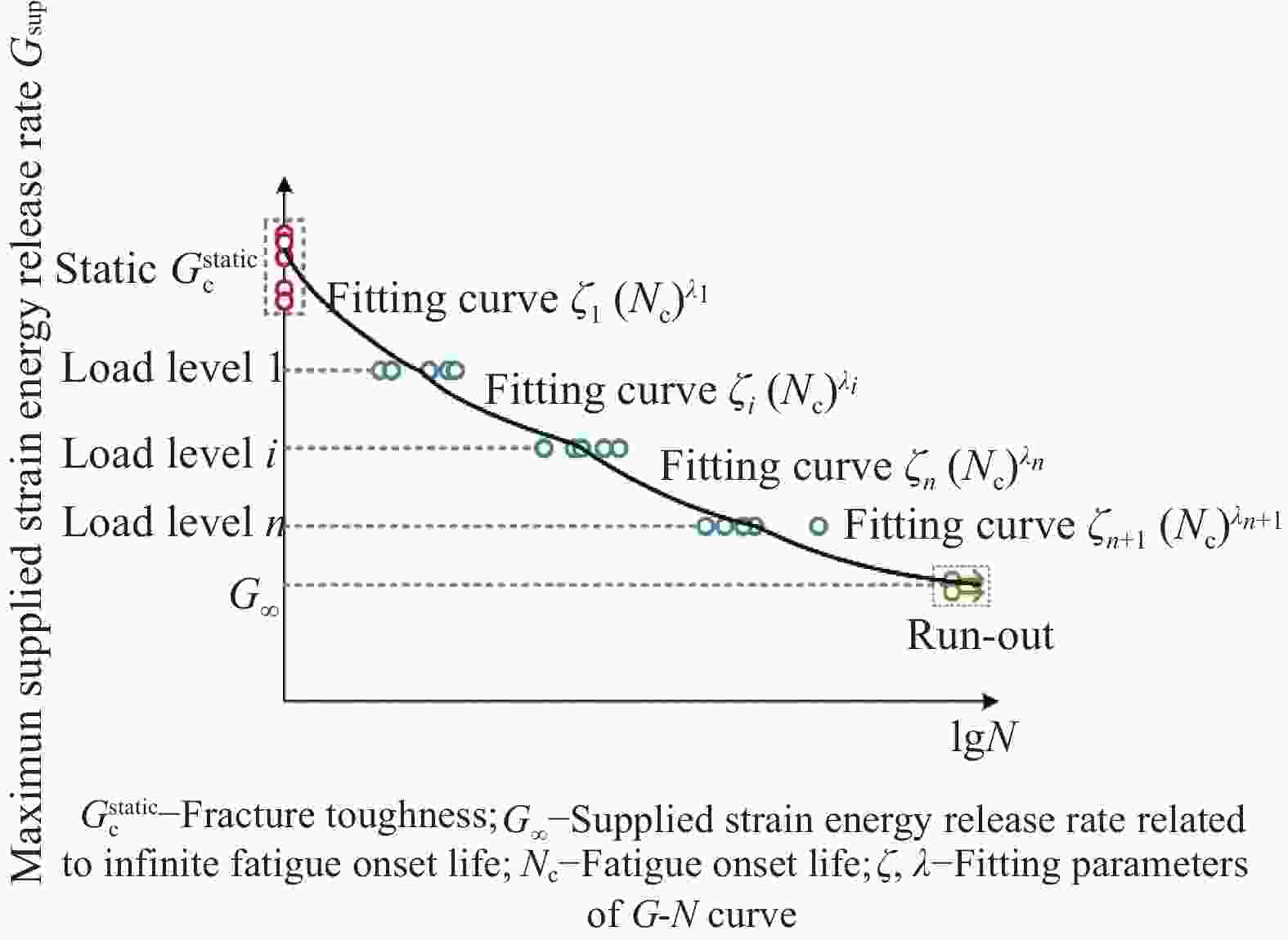
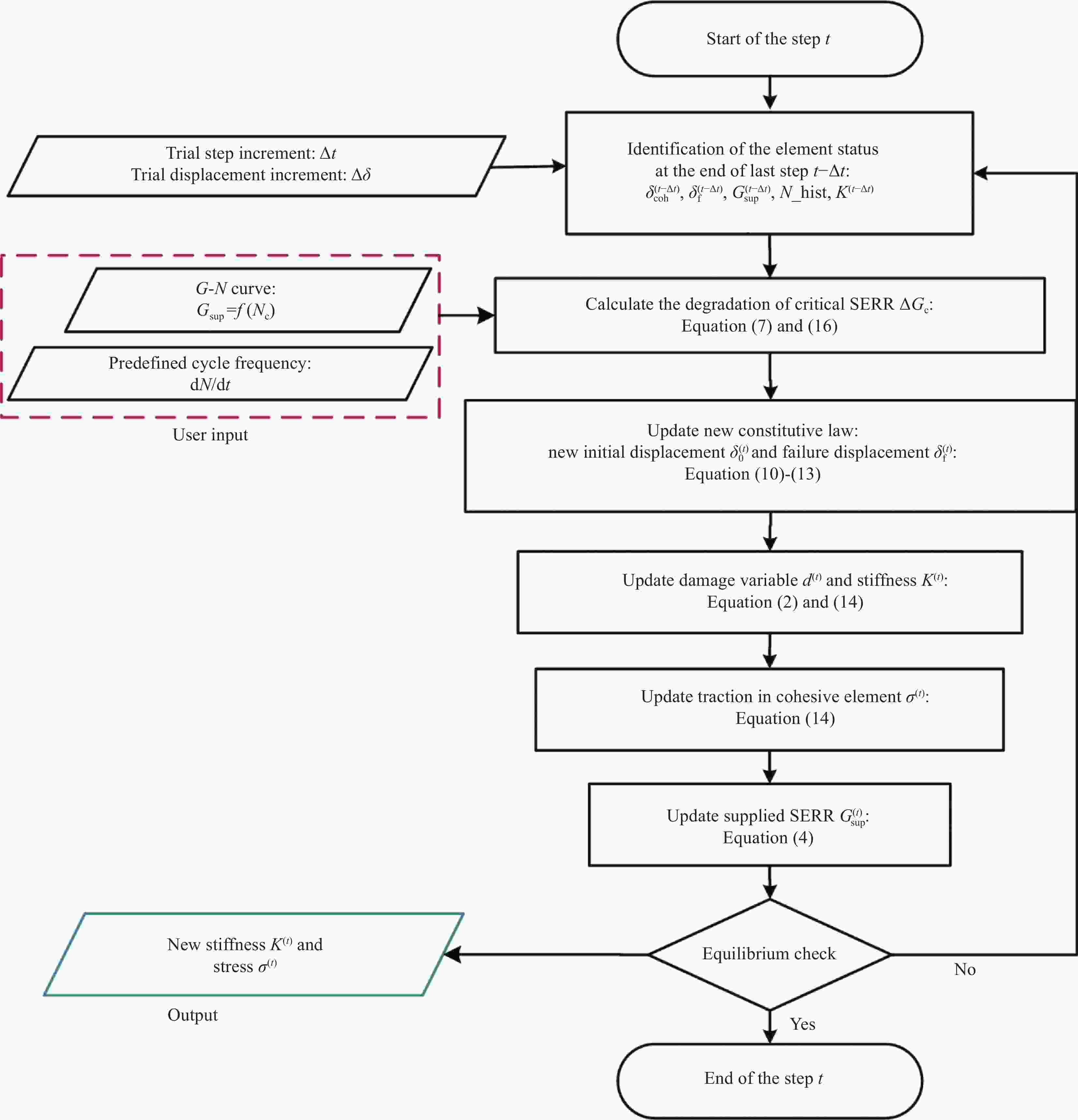
摘要: 疲劳分层是复合材料最常见、最危险的失效模式之一。本文建立了II型加载条件下复合材料疲劳分层扩展的模拟方法。基于对疲劳分层扩展提出的新的物理解释：疲劳分层扩展为一系列连续发生的疲劳分层起始扩展，将疲劳损伤累积描述为层间界面断裂韧性衰减，构建了新的疲劳内聚力单元模型。针对II型加载条件下的材料层间开裂变形场的特殊性，提出了用以描述II型加载条件的层间界面疲劳损伤累积的衰减法则，确立了依据应变能释放率-寿命(G-N)曲线的材料本构参数标定方法。引入疲劳内聚力单元模型，预测了复合材料II型疲劳分层扩展行为，与疲劳分层扩展实验所得Pairs' law能够很好地吻合。本文新提出的疲劳分层模拟方法相较于已有模型的优势在于：无需追踪裂纹扩展路径，降低了模型的应用难度，提高了计算效率；模型所需材料参数标定仅依赖于实验G-N曲线，无需实验Paris' law，参数标定所需的疲劳实验数量及时间大幅减少。
- 疲劳 /
- 分层 /
- 内聚力单元模型 /
- 纤维增强树脂基复合材料 /
- 有限元模拟
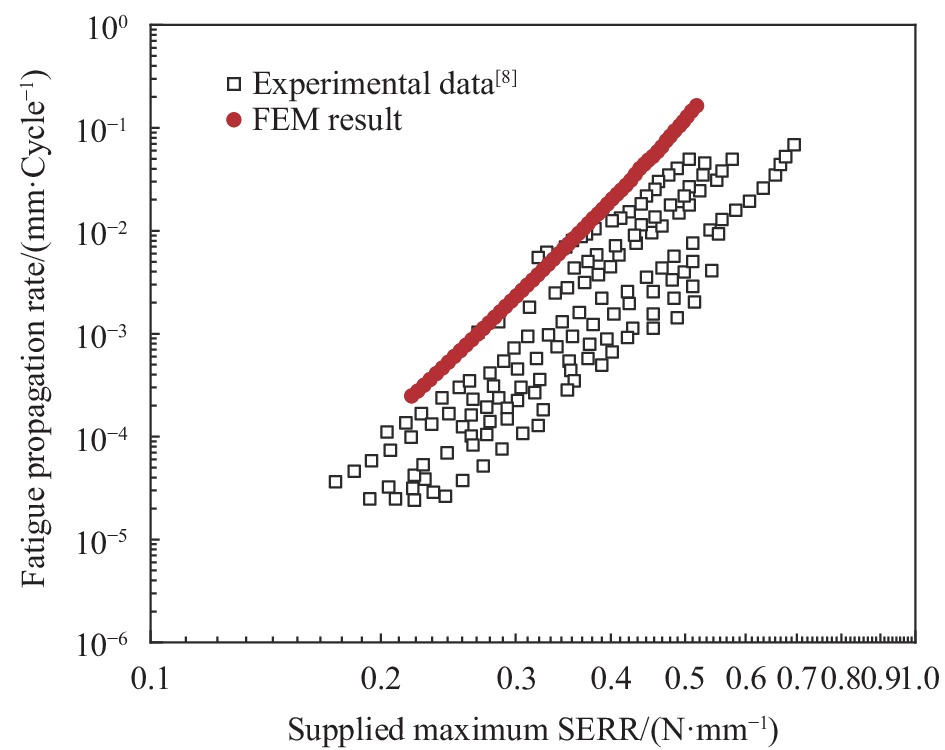
Abstract: Fatigue delamination is one of the most severe damage mode for laminated composites. A new cohesive zone model was adopted in this article for modeling fatigue delamination propagation in laminated composites, in which the strain energy release rate-lifetime (G-N) curve and Paris' law were linked. This model was developed based on a new interpretation of fatigue delamination propagation: Fatigue delamination propagation is a result of multiple onsets. A new fatigue cohesive constitutive law was constructed for describing fatigue damage accumulation in the inter-laminar interface of composites. All the parameters used in the constitutive law are with clear physical meaning and can be calibrated from the experimental G-N curve. Compared to the existing models for fatigue delamination in composites, the constitutive law developed in this model works independently in each element, without algorithms for getting the global crack information or tracking crack tip position. Considering the different deformation fields around the crack tip under mode II loading conditions, a new fatigue damage accumulation law was developed for mode II fatigue delamination propagation, and the predicted Paris' law for mode II was compared well with the experimental results.
- fatigue /
- delamination /
- cohesive zone model /
- fibre reinforced polymer composites /
- finite element modelling

HTML全文

图 1 分层增量起始扩展假设示意图

Figure 1. Sketch of incremental-onset hypothesis

Δa—Delamination length; FDO—Fatigue delamination onset; FDP—Fatigue delamination propagation

下载: 全尺寸图片幻灯片

图 2 内聚力本构关系：(a) 静力学双线性本构关系；(b) 疲劳本构关系

Figure 2. Cohesive constitutive law: (a) Static bi-linear constitutive law; (b) Fatigue constitutive law

下载: 全尺寸图片幻灯片

图 3 应变能释放率-寿命(G-N)曲线示意图

Figure 3. Sketch of strain energy release rate-life (G-N) curve

下载: 全尺寸图片幻灯片

图 4 疲劳损伤算法的有限元分析流程图

Figure 4. Flow chart describing implementation of fatigue damage algorithm in FEM analysis

SERR—Strain energy release rate; N_hist—Historcial cycle number

下载: 全尺寸图片幻灯片

图 5 三点弯端部切口弯曲(ENF)实验的有限元模型：(a) 几何模型示意图；(b) 网格尺寸

Figure 5. FEM model of 3-point bending end-notched flexure (ENF) test: (a) Sketch of geometric model; (b) Mesh size

b—; a₀—Initial crack length; P_max—Maximum applied load

下载: 全尺寸图片幻灯片

图 6 疲劳模拟中的包络加载策略

Figure 6. Envelop loading strategy in fatigue delamination

P_max—Maximum applied load

下载: 全尺寸图片幻灯片

图 7 标定得到的IM7/8552碳纤维/环氧树脂复合材料II型本征G-N曲线

Figure 7. Intrinsic G-N curve calibrated from mode II FDO test of IM7/8552 carbon/epoxy composites

α—Material parameter; SERR—Strain energy release rate

下载: 全尺寸图片幻灯片

图 8 有限元(FEM)复现的IM7/8552碳纤维/环氧树脂复合材料II型疲劳分层起始扩展(FDO)实验

Figure 8. Representing mode II fatigue delamination onset (FDO) test of IM7/8552 carbon/epoxy composites by finite element (FEM)

下载: 全尺寸图片幻灯片

图 9 FEM预测的IM7/8552碳纤维/环氧树脂复合材料II型Paris法则

Figure 9. Prediction of mode II Paris' law of IM7/8552 carbon/epoxy composites from FEM

下载: 全尺寸图片幻灯片

图 10 直接通过实验G-N曲线作为输入参数预测得到的IM7/8552碳纤维/环氧树脂复合材料II型Paris法则

Figure 10. Predicted mode II Paris' law of IM7/8552 carbon/epoxy composites with input direct from experimental G-N curve

下载: 全尺寸图片幻灯片

图 11 直接通过实验G-N曲线作为输入参数模拟得到的IM7/8552碳纤维/环氧树脂复合材料 I型(a)和II型(b)实验G-N曲线

Figure 11. Represented experimental G-N curves of IM7/8552 carbon/epoxy composites for mode I (a) and mode II (b) by using input from experimental G-N curve

下载: 全尺寸图片幻灯片

图 12 I型 (a) 和II型 (b) 加载模式下IM7/8552碳纤维/环氧树脂复合材料层间裂纹尖端附近应变场

Figure 12. Strain field around inter-laminar crack tip under mode I (a) and mode II (b) load condition in IM7/8552 carbon/epoxy composites

下载: 全尺寸图片幻灯片

图 13 IM7/8552碳纤维/环氧树脂复合材料裂纹尖端附近界面材料点输入应变能分布

Figure 13. Distribution of supplied strain energy release rate on the material points around the crack tip in IM7/8552 carbon/epoxy composites

下载: 全尺寸图片幻灯片

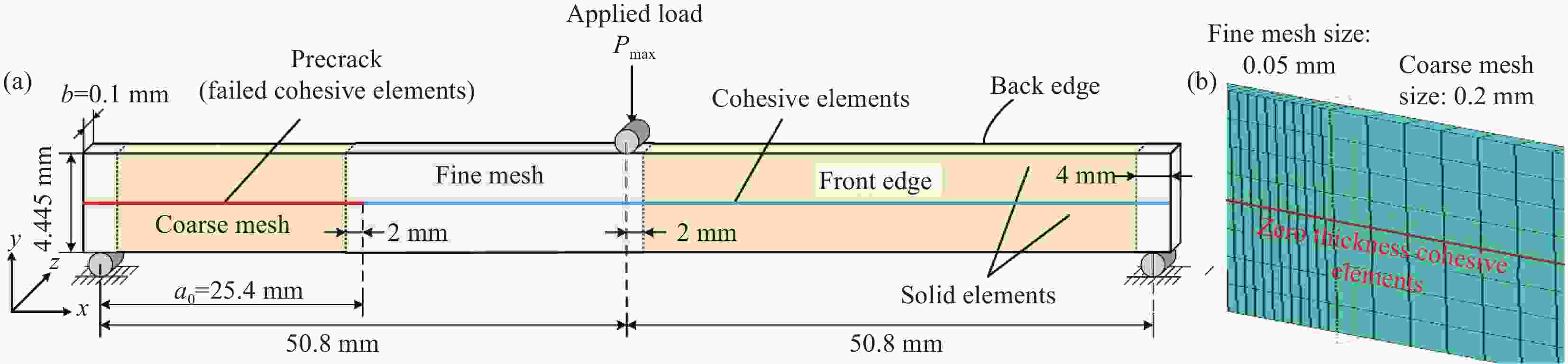
表 1 IM7/8552碳纤维/环氧树脂单向纤维复合材料层合板的相关材料参数^[8]

Table 1. Material properties of IM7/8552 carbon fiber/epoxy unidirectional laminates^[8]

Intra-ply properties	E₁₁/GPa	E₂₂=E₃₃/GPa	ν₁₂=ν₁₃	ν₂₃	G₁₂=G₁₃/GPa	G₂₃/GPa	$G_{\text{c}}^{{\text{static}}}$/ (N·mm⁻¹)	$\sigma _0^{{\text{static}}}$/MPa	K₀/ (N·mm⁻³)
Intra-ply properties	161	11.38	0.32	0.436	5.17	3.98	0.739	90	10⁶

下载: 导出CSV

表 2 ENF实验测试IM7/8552碳纤维/环氧树脂复合材料起始扩展(FDO)寿命N_test及柔度增加百分比^[8]

Table 2. List of experimental fatigue delamination onset (FDO) life N_test and percentage of compliance increase in ENF test of IM7/8552 carbon/epoxy composites^[8]

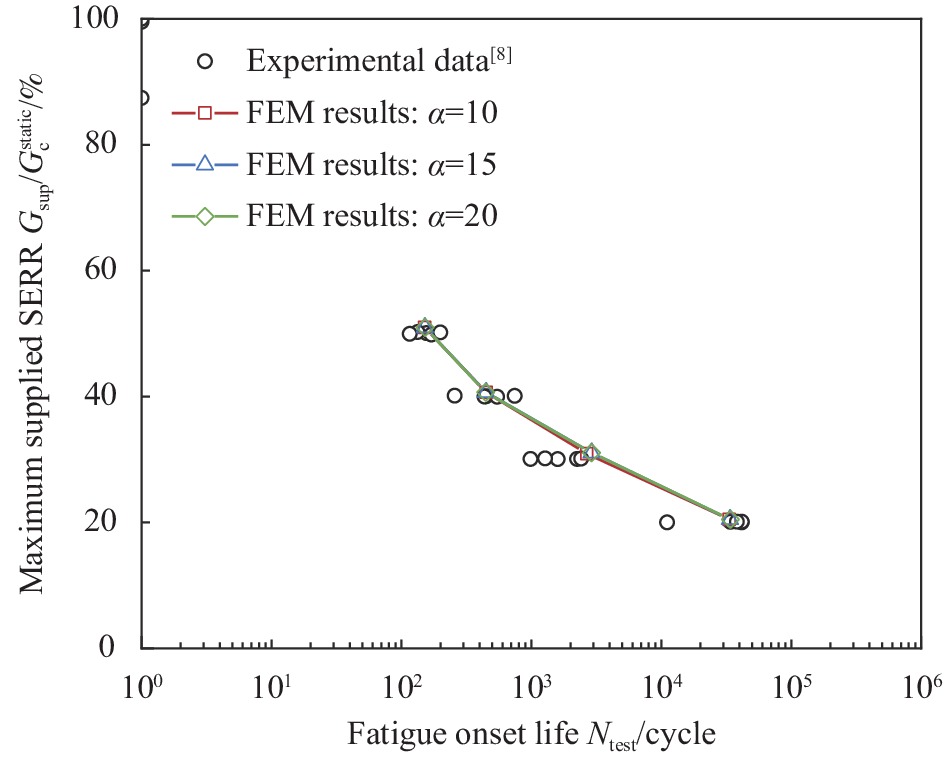
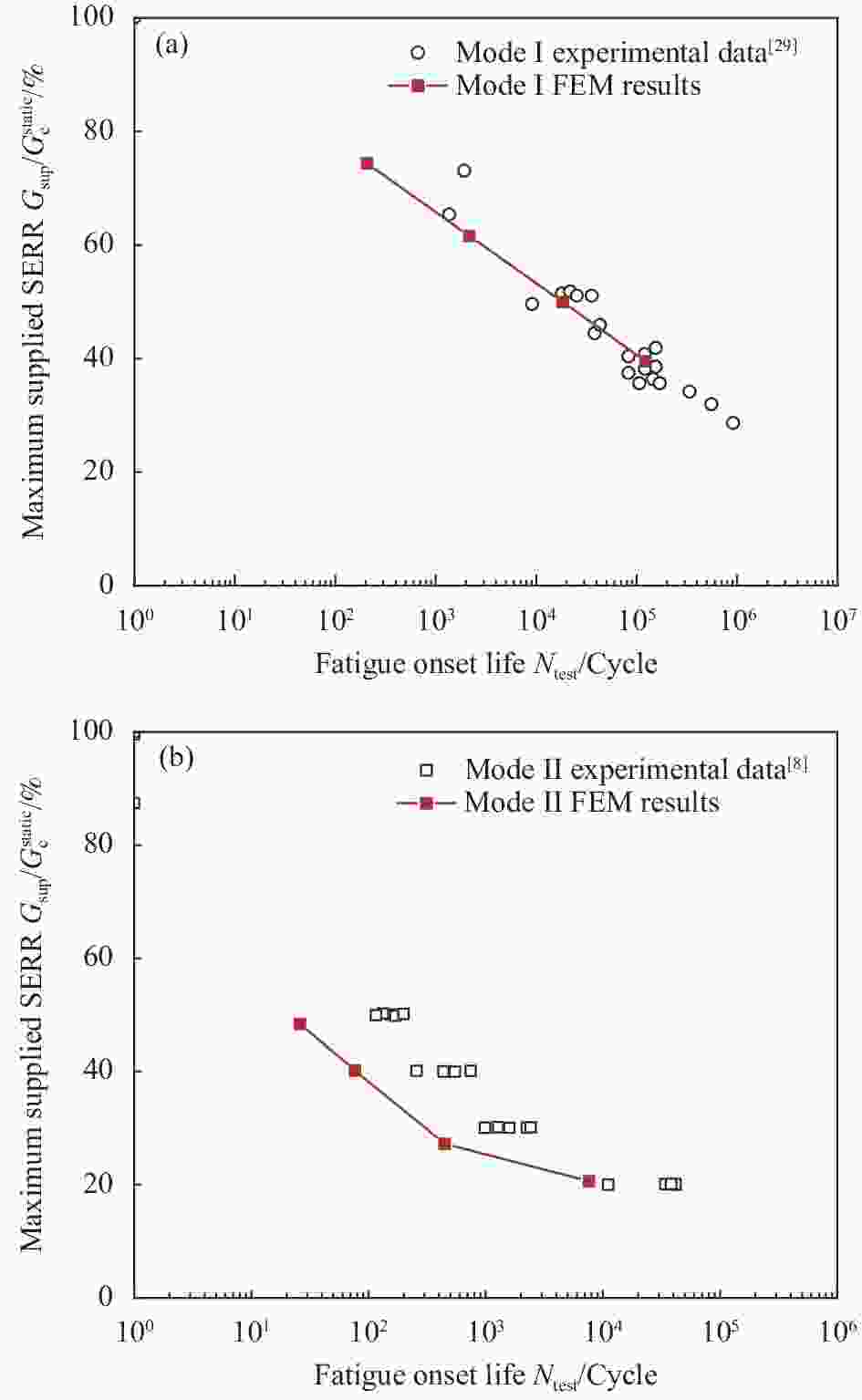
$ {G_{\sup }}/G_{\text{c}}^{{\text{static}}} $	50%	40%	30%	20%
FDO life N_test	156	257	1597	41642
	133	449	987	11080
	170	746	1275	34114
	116	545	2246	41643
	199	436	2420	38271
Average N_test	155	487	1705	33350
Compliance increase/%	1.06	0.77	0.95	0.73

下载: 导出CSV

表 3 IM7/8552碳纤维/环氧树脂复合材料G-N曲线的拟合参数

Table 3. Fitting parameters of G-N curves for IM7/8552 carbon/epoxy composites

α	10	15	20
ξ₁	0.739	0.739	0.739
λ₁	−0.146	−0.148	−0.149
ξ₂	1.048	1.042	1.040
λ₂	−0.219	−0.221	−0.222
ξ₃	0.371	0.361	0.355
λ₃	−0.103	−0.101	−0.100

下载: 导出CSV

参考文献(29)

[1]	TAKEDA N, OGIHARA S. Initiation and growth of delamination from the tips of transverse cracks in CFRP cross-ply laminates[J]. Composites Science and Technology,1994,52(3):309-318. doi: 10.1016/0266-3538(94)90166-X
[2]	OGIHARA S, TAKEDA N. Interaction between transverse cracks and delamination during damage progress in CFRP cross-ply laminates[J]. Composites Science and Technology,1995,54(4):395-404. doi: 10.1016/0266-3538(95)00084-4
[3]	KASHTALYAN M, SOUTIS C. The effect of delaminations induced by transverse cracks and splits on stiffness properties of composite laminates[J]. Composites Part A: Applied Science and Manufacturing,2000,31(2):107-119. doi: 10.1016/S1359-835X(99)00066-4
[4]	ASTM. Standard test method for determination of the mode II interlaminar fracture toughness of unidirectional fiber-reinforced polymer matrix composites: ASTM D7905/D7905M-19e1[S]. West Conshohocken: ASTM International, 2019.
[5]	ISO. Fibre reinforced plastic composites—Determination of the mode II fracture resistance for unidirectionally reinforced materials using the calibrated end-loaded split (C-ELS) test and an effective crack length approach: ISO Standard 15114—2014[S]. Geneva: International Standards Organsiation, 2014.
[6]	ALLEGRI G, JONES M I, WISNOM M R, et al. A new semi-empirical model for stress ratio effect on mode II fatigue delamination growth[J]. Composites Part A: Applied Science and Manufacturing,2011,42(7):733-740. doi: 10.1016/j.compositesa.2011.02.013
[7]	BRUNNER A J, STELZER S, PINTER G, et al. Mode II fatigue delamination resistance of advanced fiber-reinforced polymer-matrix laminates: Towards the development of a standardized test procedure[J]. International Journal of Fatigue,2013,50:57-62. doi: 10.1016/j.ijfatigue.2012.02.021
[8]	O'BRIEN T K, JOHNSTON W M, TOLAND G J. Mode II interlaminar fracture toughness and fatigue characterization of a graphite epoxy composite material: NASA/TM-2010-216838[R]. Hampton: NASA Langley Research Center, 2010.
[9]	LIU C Q, GONG Y, GONG Y K, et al. Mode II fatigue delamination behaviour of composite multidirectional laminates and the stress ratio effect[J]. Engineering Fracture Mechanics,2022,264:108321. doi: 10.1016/j.engfracmech.2022.108321
[10]	CHOWDHURY N M, HEALEY R, WANG J, et al. Using a residual strength model to predict mode II delamination failure of composite materials under block fatigue loading[J]. International Journal of Fatigue,2020,135:105563. doi: 10.1016/j.ijfatigue.2020.105563
[11]	HEALEY R, WANG J, WALLBRINK C, et al. Predicting mode II delamination growth of composite materials to assist simplification of fatigue spectra by truncating non-damaging cycles validated with experiment[J]. International Journal of Fatigue,2021,145:106117. doi: 10.1016/j.ijfatigue.2020.106117
[12]	BORG R, NILSSON L, SIMONSSON K. Simulating DCB, ENF and MMB experiments using shell elements and a cohesive zone model[J]. Composites Science and Technology,2004,64(2):269-278. doi: 10.1016/S0266-3538(03)00255-0
[13]	TURON A, CAMANHO P P, COSTA J, et al. A damage model for the simulation of delamination in advanced composites under variable-mode loading[J]. Mechanics of Materials,2006,38(11):1072-1089. doi: 10.1016/j.mechmat.2005.10.003
[14]	SØRENSEN B F, JACOBSEN T K. Characterizing delamination of fibre composites by mixed mode cohesive laws[J]. Composites Science and Technology,2009,69(3):445-456.
[15]	TURON A, COSTA J, CAMANHO P P, et al. Simulation of delamination in composites under high-cycle fatigue[J]. Composites Part A: Applied Science and Manufacturing,2007,38(11):2270-2282. doi: 10.1016/j.compositesa.2006.11.009
[16]	HARPER P W, HALLETT S R. A fatigue degradation law for cohesive interface elements-development and application to composite materials[J]. International Journal of Fatigue,2010,32(11):1774-1787. doi: 10.1016/j.ijfatigue.2010.04.006
[17]	BAK B L V, TURON A, LINDGAARD E, et al. A simulation method for high-cycle fatigue-driven delamination using a cohesive zone model[J]. International Journal for Numerical Methods in Engineering,2016,106(3):163-191. doi: 10.1002/nme.5117
[18]	KAWASHITA L F, HALLETT S R. A crack tip tracking algorithm for cohesive interface element analysis of fatigue delamination propagation in composite materials[J]. International Journal of Solids and Structures,2012,49(21):2898-2913. doi: 10.1016/j.ijsolstr.2012.03.034
[19]	TAO C C, QIU J H, YAO W X, et al. A novel method for fatigue delamination simulation in composite laminates[J]. Composites Science and Technology,2016,128:104-115. doi: 10.1016/j.compscitech.2016.03.016
[20]	PIRONDI A, MORONI F. A progressive damage model for the prediction of fatigue crack growth in bonded joints[J]. The Journal of Adhesion,2010,86(5-6):501-521. doi: 10.1080/00218464.2010.484305
[21]	MORONI F, PIRONDI A. A procedure for the simulation of fatigue crack growth in adhesively bonded joints based on the cohesive zone model and different mixed-mode propagation criteria[J]. Engineering Fracture Mechanics,2011,78(8):1808-1816. doi: 10.1016/j.engfracmech.2011.02.004
[22]	NOJAVAN S, SCHESSER D, YANG Q D. A two-dimensional in situ fatigue cohesive zone model for crack propagation in composites under cyclic loading[J]. International Journal of Fatigue,2016,82:449-461. doi: 10.1016/j.ijfatigue.2015.08.029
[23]	NOJAVAN S, SCHESSER D, YANG Q D. An in situ fatigue-CZM for unified crack initiation and propagation in composites under cyclic loading[J]. Composite Structures,2016,146:34-49. doi: 10.1016/j.compstruct.2016.02.060
[24]	DAVILA C G. From SN to the Paris' law with a new mixed-mode cohesive fatigue model: NASA/TP-2018-219838[R]. Hampton: NASA Langley Research Center, 2018.
[25]	ZHU M, GORBATIKH L, LOMOV S V. An incremental-onset model for fatigue delamination propagation in composite laminates[J]. Composites Science and Technology,2020,200:108394. doi: 10.1016/j.compscitech.2020.108394
[26]	ASTM. Standard test method for mode I fatigue delamination growth onset of unidirectional fiber-reinforced polymer matrix composites: ASTM D6115-97(2019)[S]. West Conshohocken: ASTM International, 2019.
[27]	BAK B L V, SARRADO C, TURON A, et al. Delamination under fatigue loads in composite laminates: a review on the observed phenomenology and computational methods[J]. Applied Mechanics Reviews,2014,66(6):060803. doi: 10.1115/1.4027647
[28]	ZHU M, GORBATIKH L, LOMOV S V. An incremental cohesive law for delamination under a mixed mode loading[J]. Frontiers in Materials,2020,7:572995.
[29]	MURRI G B. Evaluation of delamination onset and growth characterization methods under mode I fatigue loading: NASA/TM-2013-217966[R]. Hampton: NASA Langley Research Center, 2013.