Ballistic limit velocities of carbon fiber material target plate against fragment penetration
-
摘要:
碳纤维复合材料(CFRPs)在国防科技中广泛应用,已经成为主承力构件及部分结构的防护材料,研究其抗破片侵彻性能为科研人员提高碳纤维复合材料性能、进行防护结构设计提供依据。为研究碳纤维复合材料靶板受破片侵彻的毁伤机制及弹道极限速度,进行8 g立方体钢破片分别侵彻厚5 mm、10 mm、15 mm碳纤维复合材料靶板数值仿真与试验,得到破片侵彻碳纤维复合材料靶板的数值仿真弹道极限与六射弹弹道极限速度,数值仿真弹道极限与六射弹弹道极限最大误差为6.21%。利用数值仿真方法得到大量不同着靶速度与对应的剩余速度,基于THOR公式建立破片侵彻碳纤维复合材料靶板剩余速度模型与弹道极限计算公式。对弹道极限公式进行试验验证,选取不同工况下的六射弹弹道极限,与理论计算值进行对比,结果表明,同一工况下,试验结果与计算结果最大误差为4.54%。
-
关键词:
- 碳纤维复合材料(CFRPs) /
- 数值仿真 /
- 弹道侵彻试验 /
- 毁伤模式 /
- 弹道极限
Abstract:Carbon fiber reinforced plastics (CFRPs) are widely used in national defense science and technology and have become the protective materials for main load-bearing components and some structures. Research on their fragment penetration resistance provides a basis for scientific researchers to improve the performance of CFRPs and design protective structures. To study the damage mechanism and ballistic limit velocity of CFRPs target plates penetrated by fragments, numerical simulations and tests were conducted on 8 g cubic steel fragments penetrating CFRPs target plates with thicknesses of 5 mm, 10 mm and 15 mm, respectively. The numerical simulation of the ballistic limit velocities of the fragments penetrating CFRPs target plates and the six-projectile ballistic limit velocities were obtained, and the maximum error between the numerical simulation of the ballistic limit velocity and the six-projectile ballistic limit velocity was 6.21%. A large number of different impact velocities and corresponding residual velocities were obtained by numerical simulations. Based on the THOR formula, the residual velocity model of the fragments penetrating CFRPs target plates and the ballistic limit calculation formula were established. The ballistic limit formula was verified experimentally, and the six-projectile ballistic limits under different working conditions were selected and compared with the theoretical calculated values. The results show that under the same working condition, the maximum error between the test and calculated results is 4.54%.
-
碳纤维复合材料由碳纤维和树脂基体组成[1]。碳纤维是一种高强度、轻质的纤维,而树脂则用于固定和保护纤维。常见的树脂包括环氧树脂、聚酰亚胺等。传统材料可以是金属、塑料、玻璃等,其成分和结构比较单一[2]。碳纤维复合材料属于各向异性材料,具有密度小,比强度、比模量高,抗疲劳、抗振性能好等优点[3],碳纤维复合材料已经被广泛应用在国防科技中,应用于飞机、巡飞弹、舰船和车辆的防护[4],纤维增强复合材料在冲击载荷作用下的动态力学行为和抗弹性能的研究引起了国内外学者的广泛关注[5-6]。Zhu等[7-8]、李春昀等[9]、Hosur等[10]都通过使用霍普金森压杆试验获取到了碳纤维复合材料在动态载荷下的失效机制,依据他们的研究成果可以得知:在动态压缩载荷下,碳纤维复合材料的失效机制与应变率及加载方向相关,沿厚度方向的载荷会使碳纤维复合材料发生剪切破坏,面内方向的载荷会使碳纤维复合材料发生分层破坏,在应变率增大时纤维的开裂失效会转变成分层屈曲失效。Xiao等[11]利用落锤冲击试验,对碳纤维材料层合板在低速冲击载荷下的粘弹性行为与能量吸收特性进行了研究,研究结果表明:层合板主要吸收冲击能量的方式是通过碳纤维的可逆变形、不可逆损伤及材料本身的粘弹性行为,并且通过试验测得碳纤维层合板在受到冲击时的损伤阈值为9 J,最大允许变形为复合材料板厚度的一半左右。Kim等[12]采用弹道枪发射冰弹的加载方式,研究了高速冲击载荷下环氧树脂为基体、机织碳纤维为增强材料的复合材料的响应,研究结果表明:高速冲击载荷下复合材料层合板在局部区域发生响应,边界条件对层合板失效模式的影响较小。赵九州[13]将一级轻气炮装置作为加载装置进行了弹道冲击试验,主要试验对象为编织复合材料层合板,并通过观察加载后靶板的损伤形态,分析了编织复合材料层合板的失效机制,结果表明靶板主要以纤维材料断裂、基体材料压碎、纤维层界面破坏的形式产生损伤。马小敏等[14]利用轻气炮发射不同冲量的平头弹,进行凯夫拉复合材料层合板的弹道实验,发现纤维增强层合板的失效模式主要有板表面嵌入失效、板背面的分层失效、层合板的弹性变形与塑性大变形及纤维拉伸断裂。Zhou 等[15]自行设计了对碳纤维增强复合材料层合板的低速冲击试验,从弹体的外形尺寸、弹体侵彻着角、纤维的铺层角度及铺层顺序的角度,探讨了各个参量对层合板冲击响应的影响,并获取了材料的残余抗拉强度,对层合板在经过冲击加载后的拉伸响应进行了研究。研究表明,高速冲击载荷与低速冲击载荷对复合材料层合板的影响不同,高速冲击的响应区域存在局部化特点,并且复合材料的组分与力学性能及弹体本身等的参数都会影响层合板的吸能机制与失效模式。
对于纤维增强复合材料弹道冲击方面的研究较广泛[16-17],影响复合材料冲击响应的主要因素包括弹体形状、弹体速度、弹体质量、弹体冲击角度、纤维种类、靶板厚度及树脂含量等。赵云等[18]对纤维增强树脂基复合材料在冲击下的吸能机制和损伤模式进行综述表明:复合材料的主要吸能方式是拉伸变形,主要损伤模式是分层破坏。俞鸣明等[19]开展低速多次冲击下复合材料的失效机制,并开展压缩试验对材料剩余强度进行评估,结果表明:同一冲击能量下,损伤面积随着冲击次数的增加而增大。同一冲击次数下,损伤面积随冲击能级的增加而不断增大,冲击能的增加对多次冲击的损伤面积增幅有所影响;层合板的表面损伤以基体破坏为主,损伤由中心层向上下两边扩展。多次冲击后的压缩破坏损伤过程包括层面鼓起阶段、界面分层扩展阶段和裂纹扩展阶段、断裂失效阶段。王东哲[20]通过对碳纤维复合材料微观与宏观的研究确定最佳防弹性能下的碳纤维与树脂之间的界面结合性能。许明明[21]针对洲际导弹和航天器的外部壳体在高速冲击下的防护,设计碳纤维增强金属层合板,并通过弹道试验和数值仿真研究了金属层合板在高速冲击下的失效机制和弹道防护能力。秦溶蔓等[22]将碳纤维复合材料应用在陶瓷、超高分子量聚乙烯纤维复合材料中间夹层构成复合防弹板,结果表明,复合防弹板可有效防御弹丸侵彻,对弹丸动能吸收和弹速衰减作用明显。
弹道极限是指弹丸以规定着角贯穿给定类型和厚度的靶板所需的着速[23]。对于弹道极限的研究,最早是弹丸侵彻金属靶板[24],后出现了新材料弹道极限的研究,如泡沫铝[25]、陶瓷/铝复合靶[26]等。姜春兰等[27]采用一维平面应变加载实验技术及拉氏分析方法,研究了二维碳纤维织物增强复合材料在高速冲击载荷作用下的宏观动态响应特性,结果表明,该材料具有明显的剥离背部特征。罗锡林等[28]利用Lambert-Jonas公式拟合了柱状弹侵彻层合板弹道极限曲线,得到弹道极限速度及碳纤维复合材料靶板的损伤形貌。李明等[29]建立了钨球贯穿陶瓷复合靶的弹道极限分析模型,并利用该模型对钨球贯穿陶瓷/铝复合靶进行了数值计算,提高了计算精度。
俄乌战争中,无人机、巡飞弹广泛应用,碳纤维复合材料作为其主要构件,了解其抗冲击载荷性能可以指导研发设计人员调整战斗部结构或防护结构,实现更有效率的杀伤或防护。针对以上,本文开展钢破片侵彻不同厚度碳纤维复合材料靶板数值模拟、试验研究,总结了碳纤维复合靶板受破片侵彻的破坏机制与着靶速度的关系,并基于THOR公式建立具有一定普适性的破片侵彻碳纤维复合材料层合板的剩余速度模型与弹道极限计算公式。加强对碳纤维复合材料这一新型材料抗侵彻性能的了解,为后续碳纤维复合材料在各个领域的应用提供理论依据。
1. 数值仿真
1.1 数值仿真模型
本文使用TrueGrid软件建立数值仿真模型,TrueGrid软件采用命令流的形式来完成整个建模过程。通过Block或Cylinder命令创建基本块体,然后使用TrueGrid强大的投影功能完成各种复杂的建模,保证模型的精度、整体性,考虑到模型对称性与计算时间,建立1/2模型。
破片为立方体钢破片,质量为8 g,尺寸为9.5 mm×10 mm×10.8 mm。破片材料参数见表1。
表 1 钢破片材料参数Table 1. Material parameters of the steel fragmentρ/(g·cm−3) G/GPa σ/MPa B/MPa n 7.83 0.77 792 510 0.26 c M TM/K TR/K 0.014 1.03 1793 294 Notes: ρ—Density; G—Shear modulus; σ—Yield stress; B—Hardening coefficient; n—Hardening index; c—Strain rate coefficient; M—Temperature coefficient; TM—Melting temperature; TR—Ambient temperature. 为了避免靶板边界效应对破片侵彻结果产生影响,选用靶板尺寸大于破片尺寸的10倍,靶板尺寸为150 mm×150 mm。为了实现对不同厚度的碳纤维复合材料弹道极限的研究,选取3种厚度的板材进行研究,板材的厚度分别为5、10、15 mm。分层建立有限元模型,两个Part来表征不同的铺层方向。每层纤维层厚度为1 mm,建立3层网格。进行网格收敛分析[30],设置破片网格0.04、0.05、0.06 mm,靶板选择中间与破片接触范围网格加密、周围稀疏的划分形式,设置中间网格0.05、0.1、0.15 mm,周围网格0.45 mm。与试验结果进行对比,平衡计算效率和可靠性,靶板中间网格尺寸为0.1 mm,周围网格尺寸为0.45 mm;破片网格尺寸为0.05 mm,靶板与破片接触区域网格加密。
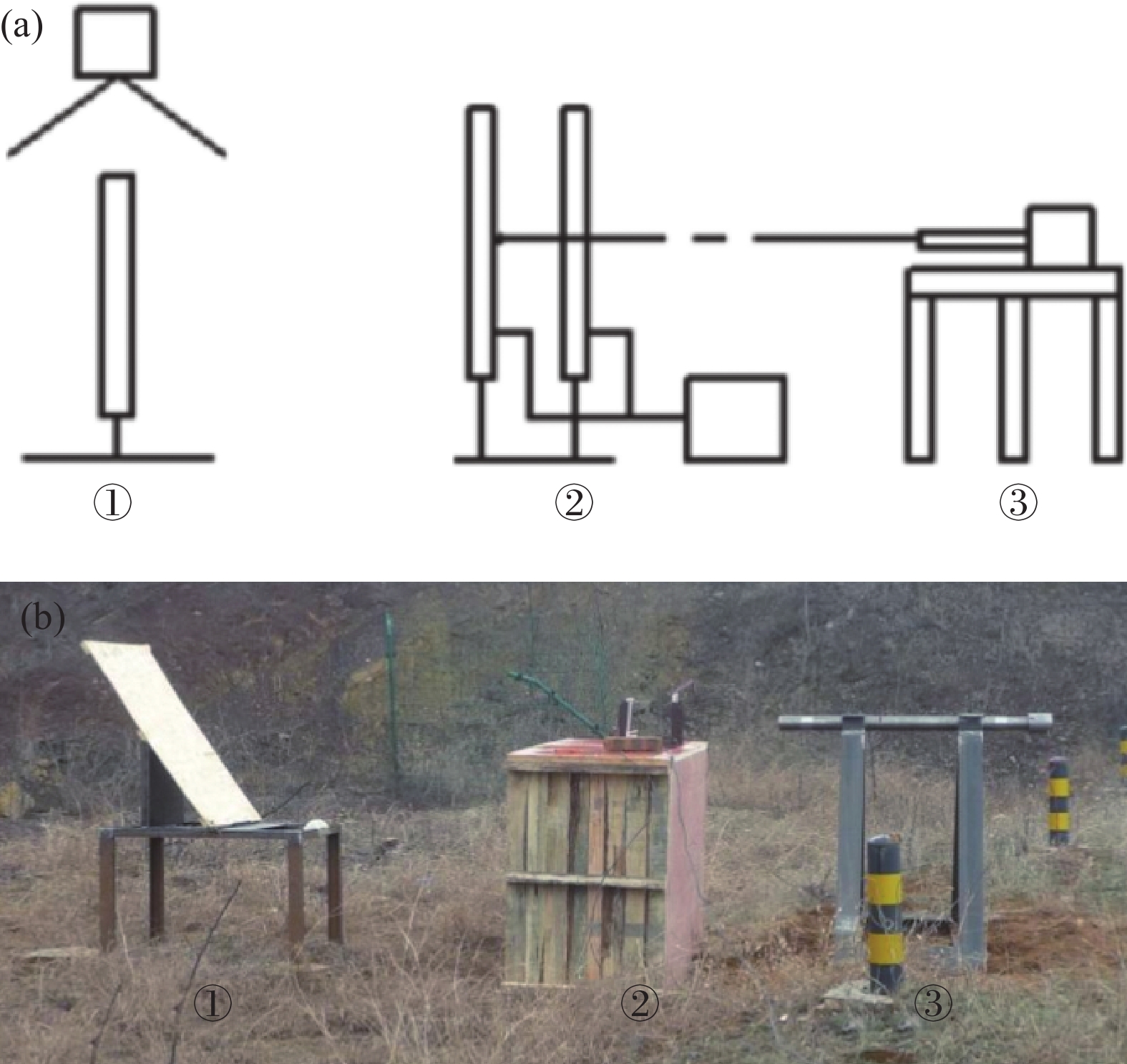
进行图1所示3种典型着靶姿态仿真分析,与试验对应工况下靶板的穿透效果基本相同,破片侵彻碳纤维复合材料靶板初始状态如图1所示。
1.2 数值仿真算法与材料模型
碳纤维复合材料为纤维增强材料,本身具有各向异性与不均匀性,在破片侵彻过程中的能量转化与材料的失效准则判定也十分复杂。采用LS-DYNA软件中的纤维增强复合材料渐进损伤模型(Mat Enhanced Composite Damage,MAT54)[31]。该模型是专门设计用于处理正交各向异性材料的一种渐进损伤力学模型。采用 Chang-Chang失效准则,并使用层合板铺层强度折减法来减低材料性能。当载荷超过铺层强度时,该铺层的力学性能立即下降为0,材料刚度退化,直到所有铺层全部失效时,材料结构破坏。由于该模型简单的退化准则被广泛应用于碳纤维复合材料母材试样的轴向拉压、零部件压溃和汽车碰撞仿真中。本构方程:
{σ11σ22τ12}={E111−v12v21v21E111−v12v210v21E221−v12v21E221−v12v21000G12}{ε11ε22γ12} (1) 式中:σ11、ε11、E11为纤维方向正应力、正应变、弹性模量;σ22、ε22、E22为基体方向正应力、正应变、弹性模量;τ12、γ12、G12为切应力、切应变、弹性模量;v12、v21为主泊松比、次泊松比。
1.3 数值仿真结果
1.3.1 数值仿真与试验结果对比分析
破片侵彻不同厚度碳纤维复合材料靶板数值仿真与试验结果对比如图2~图4所示。数值仿真在模拟破片的穿孔隧道时基本能复现试验所产生的穿孔隧道,破片穿孔出入口剪切破坏所形成的界面清晰,穿孔大小与形状基本与试验结果一致,由于仿真计算时设置材料失效后网格被删除及网格密度的原因,数值仿真在模拟破片的碳纤维层撕裂与分层效果与试验结果存在一定差异,但结合层合板厚度方向的剖面来看,碳纤维复合材料产生的微裂纹、分层与翘曲均有所体现,符合碳纤维复合材料靶板几种破坏形式叠加的失效机制。下面就破片面接触侵彻靶板进行分析。
1.3.2 数值仿真结果
8 g立方体钢破片侵彻不同厚度碳纤维复合材料靶板的弹道极限数值仿真结果如表2所示。
表 2 数值仿真弹道极限Table 2. Numerical simulation of ballistic limitTarget thickness/mm Simulation of ballistic limit velocity/(m·s−1) 5 307.76 10 394.78 15 437.55 由表2可知:8 g立方体破片侵彻5、10、15 mm厚的碳纤维复合材料靶板的数值仿真弹道极限分别为307.76、394.78、437.55 m/s。破片侵彻碳纤维复合材料的过程可大致分为3个阶段:第一个阶段为破片与靶板接触,靶板产生形变,应力波开始传播;第二个阶段应力波传播到达靶板背面,层合板开始失效;第三个阶段为破片逐步侵彻碳纤维复合材料层合板,最终完成侵彻过程。碳纤维复合材料在高于极限速度的冲击载荷下,应力波会以破片撞击区域为中心向周围扩散,层合板的响应随着离冲击位置的距离增大而减弱;碳纤维复合材料层合板在受到冲击后,以多种形式吸收破片的动能,主要的吸能形式有动能转化为变形区动能与应变能,碳纤维复合材料层合板纤维层失效所需的纤维束断裂能及分层损伤和基体开裂所吸收的能量。根据数值仿真过程观测,靶板破坏在应力波传播之前,因此对靶板的破坏作用主要是破片动能的作用,应力波传播过程对损伤有加剧作用,但不会产生新的破坏形式。
2. 试验系统与方法
2.1 试验设备
破片侵彻碳纤维复合材料靶板的弹道侵彻试验,试验系统包括滑膛弹道枪、钢破片及与之匹配的弹托、不同厚度的碳纤维复合材料靶板、测速靶及测速仪与高速摄影仪。破片侵彻碳纤维复合材料靶板试验系统如图5所示。
2.2 弹靶材料
选用8 g立方体预制钢破片,如图6所示。弹道枪通过火药气体燃烧产生的压力将放置于弹托内部的破片发射,由于受到空气阻力的作用,在飞行过程中破片与弹托分离,破片继续运动,以一定速度贯穿靶板前设置的测速靶后侵彻安装于靶架上的碳纤维复合材料靶板。通过调整发射药量控制破片速度进而获取不同着靶速度。破片与弹托装配图如图7所示,破片与发射药筒装配图如图8所示。发射药量与破片速度对应关系如表3所示。
表 3 发射药量与破片着靶速度Table 3. Amount of propellant and the velocity of fragment hitting the targetTarget
thickness/mmDosage of
propellant/gRange of speed/
(m·s−1)5 2.5-3 290-340 10 3.5-4 370-420 15 4.5-5 425-460 本文试验目的是为了探索预制破片侵彻无人机、巡飞弹等关键部件处碳纤维复合材料的弹道极限,因此选用的碳纤维复合材料为由日本东丽公司生产的T300级预浸料与环氧树脂在高温下压制所成的板材,板材间碳纤维的铺层堆叠方式为0°与90°交互铺层[32]。靶板尺寸为150 mm×150 mm,厚度为5 mm、10 mm、15 mm,靶板如图9所示。试验所用碳纤维复合材料板材的材料参数如表4所示。
2.3 试验结果
2.3.1 靶板损伤情况
数值仿真模拟获取的为特定着靶面情况下速度数据,但破片在着靶时的姿态是完全随机的。因此进行验证试验,试验后选取速度差值在30 m/s范围内的三发完全贯穿和三发局部侵彻数据,基于弹道极限试验方法计算钢破片侵彻不同厚度靶板的六射弹弹道极限[33]。破片侵彻碳纤维复合材料靶板局部侵彻与完全贯穿情况如图10所示。
表 4 碳纤维复合材料力学性能Table 4. Mechanical properties of CFRPsMechanical property Parameter Longitudinal tensile strength σxt/MPa 1755 Longitudinal tensile modulus E1t/GPa 138 Main Poisson's ratio v12 0.27 Transverse tensile strength σyt/MPa 48 Transverse tensile modulus E2t/GPa 8.36 Longitudinal compressive strength σxc/MPa 1248 Longitudinal compression modulus E1c/GPa 128 Transverse compressive strength σyc/MPa 214 Transverse compression modulus E2c/GPa 8.48 Longitudinal and transverse shear strength τ12/MPa 113 Longitudinal and transverse shear modulus G12/GPa 4.51 Shear strength of bonded structure τJ/MPa 21.5 2.3.2 弹道极限
8 g立方体钢破片侵彻不同厚度碳纤维复合材料靶板的六射弹弹道极限结果如表5所示。
由表5可知:8 g立方体破片侵彻5、10、15 mm厚的碳纤维复合材料靶板的弹道极限分别为328.17、394.67、436.50 m/s。
表 5 六射弹弹道极限Table 5. Six-shot limit velocityTarget thickness/mm Experimental data/(m·s−1) Six-shot limit velocity/(m·s−1) Local penetration Complete penetration 5 312 335 328.17 318 340 318 342 10 379 404 394.67 384 406 386 409 15 423 439 436.50 429 447 432 449 由表6可见,8 g立方体破片侵彻5、10、15 mm厚的碳纤维复合材料靶板的数值仿真与试验结果弹道极限误差分别为6.21%、0%、0.23%。
表 6 碳纤维复合材料靶板数值仿真与试验误差分析Table 6. Error analysis between numerical simulation and test results for carbon fiber composite target plateTarget
thickness/mmBallistic limit
velocity/(m·s−1)Six-shot limit
velocity/(m·s−1)Deviation/% 5 307.76 328.17 6.21 10 394.78 394.67 0 15 437.55 436.50 0.23 由数值仿真获取的靶板破坏状态与试验靶板的图像对照图来看,数值仿真获取的靶板穿孔的大小、形状都与试验碳纤维层合板的穿孔大小、形状比较接近。由层合板厚度方向的剖面可观察到,靶板的纤维层之间有分层现象,靶板背面的纤维层变形更大,同时碳纤维复合材料产生的微裂纹、分层与翘曲也有所体现。由表6中数据可知,六射弹弹道极限与数值仿真得到的弹道极限偏差最大值为6.21%。说明本文中的数值仿真模型能够用来观测破片侵彻碳纤维复合材料的侵彻过程。
2.4 碳纤维复合材料破坏机制分析
结合数值仿真靶板破坏过程与试验回收靶板的破坏形态,对碳纤维复合材料层合靶板破坏机制进行分析。可以将碳纤维复合材料在受到破片冲击时的破坏形式分为以下几种:纤维层的剪切破坏、纤维的拉伸破坏、基体破裂与纤维层分层。
碳纤维复合材料在受到破片冲击时,迎弹面表面的纤维层最开始受到破片的冲击,破片速度较高,加载在复合材料上的载荷较大,复合材料中的纤维束在没有发生大的拉伸形变时便由于破片接触位置的剪切应变发生失效,形成剪切破坏。此种破坏形式也就形成了靶板上破片穿孔入口与破片形状尺寸十分接近的现象,同时材料的剪切破坏也会形成冲塞,只是相较于钢等金属靶板所形成的冲塞,碳纤维复合材料所形成的冲塞是以表层的纤维层为主,并且由于层合板的分层特性,纤维层之间并非一个完全的整体,纤维所形成的冲塞会在后续的侵彻中发挥作用。
破片着靶速度远大于弹道极限时,整个侵彻过程破片都保持着较高的速度,一直对靶板施加较大的载荷,靶板的所有纤维层都以剪切破坏为主,且由于先接触破片纤维层所形成的冲塞会对破片的后续侵彻产生影响,破片的穿孔隧道会有逐渐扩大呈现锥形的现象。
在破片速度逐渐降低时,层合板上的纤维层会产生变形,从而会在层合板内部产生拉伸应变,在应变累积超过纤维层的极限时,纤维层发生拉伸破坏。
在层合板发生变形的同时,纤维束与基体的弹性模量不同,在两者产生相同应变的情况下内部的应力不同,此时纤维复合材料会存在基体开裂的破坏形式,表现为在破片穿孔出口周围会有纤维分离的现象。碳纤维复合材料层合板是在一定的工艺下压制而成,纤维层界面之间的结合力要小于纤维层内部的结合力,在破片侵彻过程中后层靶板的变形逐渐变大,会使层与层之间分离产生分层破坏,在靶板上的表现形式为靶板背弹面产生大面积鼓包,厚度方向的剖面可以看出靶板纤维层的分离。
综上所述,破片侵彻碳纤维复合材料靶板是一个十分复杂的过程,在工况发生改变时,靶板的失效模式也会随之变化。破片速度高时,靶板以纤维的剪切破坏为主,在破片速度较低时,多种破坏形式所占比例随着速度的变化而变化。不同速度对应的破片侵彻碳纤维破坏形式如表7所示。
表 7 不同速度碳纤维复合靶板破坏形式Table 7. Failure modes of CFRPs with different velocitiesVelocity Damage pattern Shear failure Fiber tensile failure Matrix damage Delamination damage (bulging) >Limit velocity √ =Limit velocity √ √ <Limit velocity √ √ Multiple minor collisions √ 3. 剩余速度模型
3.1 弹道极限
通过破片侵彻碳纤维复合材料靶板的数值仿真研究,可以获取破片以不同着靶速度侵彻碳纤维复合材料靶板的对应剩余速度数据。根据获得的速度数据可以利用经验公式建立破片侵彻碳纤维复合材料靶板的剩余速度模型。
依据侵彻力学相关理论,破片侵彻的剩余速度与破片的着靶面积A、破片质量Mp、破片的着靶速度v0、破片侵彻的着角θ、目标类型及其厚度h有关,建立的普适性经验公式也应该包含这些参量。由弹道研究实验室(Ballistic Research Laboratory,BRL)基于多种破片材料与形状的大量试验数据的统计拟合获得的THOR方程,因其参量全面,试验数据能够较精确预估破片不同工况下的剩余速度[34]。THOR方程的表达形式为
v=v0−0.3048×10C1(61023.75hA)C2(15432.1Mp)C3(secθ)C4(3.2808v0)C5 (2) 式中:h为靶板厚度(m);A为破片的着靶面积(m²);Mp为破片的质量(kg);θ为破片侵彻着角(rad);v0为破片的着靶速度(m/s);C1~ C5为待拟合的靶板系数。
由于THOR方程为依据试验数据拟合而获得的,在与其试验工况接近时的结果更精确,因此方程有一定的限制:破片不能太长,破片在侵彻过程中不能破碎,侵彻着角小于70°。本文模拟及试验工况满足上述要求。
采用非线性最小二乘法进行拟合,选取残差平方和最小的一组参数作为结果。建立具有一定普适性的破片侵彻碳纤维复合材料层合板的剩余速度模型。拟合获得的模型参数如表8所示。
代入式中获得破片侵彻碳纤维复合材料层合板的剩余速度计算公式:
v=v0−1377.70(hA)C2(Mp)C3(secθ)C4(ν0)C5 (3) 式中,依据工况代入对应的着靶面积A、破片质量Mp、破片侵彻的着角θ、靶板厚度h,在剩余速度v=0时的着靶速度v0即可视为破片在该工况下侵彻碳纤维复合材料的弹道极限,由此弹道极限的计算公式:
ν50=253.30(hA)0.231(Mp)−0.741(secθ)0.960 (4) 表 8 拟合系数C1~C5Table 8. Fit coefficient C1-C5C1 C2 C3 C4 C5 6.422 0.302 −0.968 1.254 −0.306 3.2 理论计算结果
由表9可知:8 g立方体破片侵彻5、10、15 mm厚的碳纤维复合材料靶板的理论计算弹道极限分别为323.32、379.46、416.72 m/s。
表 9 碳纤维复合靶板弹道极限理论计算值Table 9. Ballistic limit velocity calculation values of CFRPs target plateTarget thickness/mm Theoretical calculation of ballistic
limit velocity/(m·s−1)5 323.32 10 379.46 15 416.72 3.3 结果分析
将理论计算结果、数值仿真结果与试验结果进行对比,计算相对误差,考察建立的数值仿真模型与理论计算公式的可靠性。
由表10可知:同一工况下,8 g立方体破片侵彻5、10、15 mm厚的碳纤维复合材料靶板的理论计算与试验结果弹道极限误差分别为1.47%、3.88%、4.54%。
表 10 碳纤维复合材料靶板理论计算与试验结果误差Table 10. Errors between theoretical calculation and test results of carbon fiber composite target plateTarget
thickness/mmTheoretical
velocity/(m·s−1)Six-shot limit
velocity/(m·s−1)Deviation/% 5 323.32 328.17 1.47 10 379.46 394.67 3.88 15 416.72 436.50 4.54 4. 结 论
(1)利用LS-DYNA进行破片侵彻碳纤维复合材料的数值仿真,通过模型选取和调整参数,仿真结果与试验结果有较好的一致性且六射弹弹道极限与数值仿真弹道极限最大误差为6.21%,可以通过数值仿真观测破片侵彻碳纤维复合材料靶板的过程。
(2)利用数值仿真方法,得到破片以不同着靶速度侵彻靶板对应剩余速度数据,基于THOR方程建立具有一定普适性的弹道极限计算公式。将理论计算结果与试验结果进行对比,弹道极限计算公式计算出的弹道极限与试验值最大误差为4.54%。
(3)随着靶板厚度的增加,弹道极限增速变慢。
(4)根据仿真与实验结果分析,破片侵彻碳纤维复合材料靶板,靶板的损伤机制与破片着靶速度有关。
-
表 1 钢破片材料参数
Table 1 Material parameters of the steel fragment
ρ/(g·cm−3) G/GPa σ/MPa B/MPa n 7.83 0.77 792 510 0.26 c M TM/K TR/K 0.014 1.03 1793 294 Notes: ρ—Density; G—Shear modulus; σ—Yield stress; B—Hardening coefficient; n—Hardening index; c—Strain rate coefficient; M—Temperature coefficient; TM—Melting temperature; TR—Ambient temperature. 表 2 数值仿真弹道极限
Table 2 Numerical simulation of ballistic limit
Target thickness/mm Simulation of ballistic limit velocity/(m·s−1) 5 307.76 10 394.78 15 437.55 表 3 发射药量与破片着靶速度
Table 3 Amount of propellant and the velocity of fragment hitting the target
Target
thickness/mmDosage of
propellant/gRange of speed/
(m·s−1)5 2.5-3 290-340 10 3.5-4 370-420 15 4.5-5 425-460 表 4 碳纤维复合材料力学性能
Table 4 Mechanical properties of CFRPs
Mechanical property Parameter Longitudinal tensile strength σxt/MPa 1755 Longitudinal tensile modulus E1t/GPa 138 Main Poisson's ratio v12 0.27 Transverse tensile strength σyt/MPa 48 Transverse tensile modulus E2t/GPa 8.36 Longitudinal compressive strength σxc/MPa 1248 Longitudinal compression modulus E1c/GPa 128 Transverse compressive strength σyc/MPa 214 Transverse compression modulus E2c/GPa 8.48 Longitudinal and transverse shear strength τ12/MPa 113 Longitudinal and transverse shear modulus G12/GPa 4.51 Shear strength of bonded structure τJ/MPa 21.5 表 5 六射弹弹道极限
Table 5 Six-shot limit velocity
Target thickness/mm Experimental data/(m·s−1) Six-shot limit velocity/(m·s−1) Local penetration Complete penetration 5 312 335 328.17 318 340 318 342 10 379 404 394.67 384 406 386 409 15 423 439 436.50 429 447 432 449 表 6 碳纤维复合材料靶板数值仿真与试验误差分析
Table 6 Error analysis between numerical simulation and test results for carbon fiber composite target plate
Target
thickness/mmBallistic limit
velocity/(m·s−1)Six-shot limit
velocity/(m·s−1)Deviation/% 5 307.76 328.17 6.21 10 394.78 394.67 0 15 437.55 436.50 0.23 表 7 不同速度碳纤维复合靶板破坏形式
Table 7 Failure modes of CFRPs with different velocities
Velocity Damage pattern Shear failure Fiber tensile failure Matrix damage Delamination damage (bulging) >Limit velocity √ =Limit velocity √ √ <Limit velocity √ √ Multiple minor collisions √ 表 8 拟合系数C1~C5
Table 8 Fit coefficient C1-C5
C1 C2 C3 C4 C5 6.422 0.302 −0.968 1.254 −0.306 表 9 碳纤维复合靶板弹道极限理论计算值
Table 9 Ballistic limit velocity calculation values of CFRPs target plate
Target thickness/mm Theoretical calculation of ballistic
limit velocity/(m·s−1)5 323.32 10 379.46 15 416.72 表 10 碳纤维复合材料靶板理论计算与试验结果误差
Table 10 Errors between theoretical calculation and test results of carbon fiber composite target plate
Target
thickness/mmTheoretical
velocity/(m·s−1)Six-shot limit
velocity/(m·s−1)Deviation/% 5 323.32 328.17 1.47 10 379.46 394.67 3.88 15 416.72 436.50 4.54 -
[1] 周锦地. 基于多尺度方法的碳纤维复合材料温度环境下力学行为研究[D]. 哈尔滨: 哈尔滨工业大学, 2022. ZHOU Jindi. Study of mechanical behavior of carbon fiber composites under temperature environment based on multiscale approach[D]. Harbin: Harbin Institute of Technology, 2022(in Chinese).
[2] ANUSE V S, SHANKAR K, VELMURUGAN R, et al. LVI and CAI analysis of woven carbon fiber reinforced composite laminates with different stacking sequence[J]. Key Engineering Materials, 2023, 969: 93-100. DOI: 10.4028/p-n2McuG
[3] 常新龙, 孙超凡, 齐重阳, 等. 集成于碳纤维复合材料的fsFBG响应特性研究[J]. 兵器装备工程学报, 2023, 45(1): 1-9. CHANG Xinlong, SUN Chaofan, QI Chongyang, et al. Response characteristics of fsFBG sensor based on carbon fiber composite laminate[J]. Journal of Ordnance Equipment Engineering, 2023, 45(1): 1-9(in Chinese).
[4] 贾宝华, 刘翔, 顾永强, 等. 复合材料层合板的抗弹性能模拟分析[J]. 兵器装备工程学报, 2017, 37(8): 147-152. DOI: 10.11809/scbgxb2017.08.031 JIA Baohua, LIU Xiang, GU Yongqiang, et al. Numerical simulation of the anti-bullet property for composite laminated plates[J]. Journal of Ordnance Equipment Engineering, 2017, 37(8): 147-152(in Chinese). DOI: 10.11809/scbgxb2017.08.031
[5] ABRATE S. Impact on laminated composites—Recent advances[J]. Applied Mechanics Reviews, 1994, 47(11): 517-544.
[6] 金子明, 隋金玲, 张菡英, 等. 纤维增强复合防弹板研究进展及抗弹性能研究[J]. 玻璃钢, 2001(1): 1-6. JIN Ziming, SUI Jinling, ZHANG Hanying, et al. Research progress and anti-elastic properties of fiber reinforced composite bulletproof panels[J]. Fiber Reinforced Plastics, 2001(1): 1-6(in Chinese).
[7] ZHU G Q, GOLDSMITH W, DHARAN C H. Penetration of laminated Kevlar by projectiles—I. Experimental investigation[J]. International Journal of Solids and Structures, 1992, 29(4): 399-420. DOI: 10.1016/0020-7683(92)90207-A
[8] ZHU G Q, GOLDSMITH W, DHARAN C K H. Penetration of laminated Kevlar by projectiles—II. Analytical model[J]. International Journal of Solids and Structures, 1992, 29(4): 421-436. DOI: 10.1016/0020-7683(92)90208-B
[9] 李春昀, 孙颖, 张典堂, 等. 缝合铺层碳/环氧复合材料动态压缩性能实验研究[J]. 天津工业大学学报, 2013, 32(1): 1-4. DOI: 10.3969/j.issn.1671-024X.2013.01.001 LI Chunyun, SUN Ying, ZHANG Diantang, et al. Study on dynamic compressive behavior of stitched carbon/epoxy composite laminates[J]. Journal of Tiangong University, 2013, 32(1): 1-4(in Chinese). DOI: 10.3969/j.issn.1671-024X.2013.01.001
[10] HOSUR M V, ALEXANDER J, JEELANI S, et al. High strain compression response of affordable woven carbon/epoxy composites[J]. Journal of Reinforced Plastics and Composites, 2003, 22(3): 271-296. DOI: 10.1177/0731684403022003844
[11] XIAO L, WANG G, QIU S, et al. Exploration of energy absorption and viscoelastic behavior of CFRPs subjected to low velocity impact[J]. Composites Part B: Engineering, 2019, 165: 247-254. DOI: 10.1016/j.compositesb.2018.11.126
[12] KIM H, WELCH D A, KEDWARD K T. Experimental investigation of high velocity ice impacts on woven carbon/epoxy composite panels[J]. Composites Part A: Applied Science and Manufacturing, 2003, 34(1): 25-41. DOI: 10.1016/S1359-835X(02)00258-0
[13] 赵九州. 三维编织复合材料冲击行为与动态强度研究[D]. 哈尔滨: 哈尔滨工业大学, 2016. ZHAO Jiuzhou. Research on the impact behavior and dynamic strength of 3D woven composite [D]. Harbin: Harbin Institute of Technology, 2016(in Chinese).
[14] 马小敏, 李世强, 李鑫, 等. 编织Kevlar/Epoxy复合材料层合板在冲击荷载下的动态响应[J]. 爆炸与冲击, 2016, 36(2): 170-176. DOI: 10.11883/1001-1455(2016)02-0170-07 MA Xiaomin, LI Shiqiang, LI Xin, et al. Dynamic response of woven Kevlar/epoxy composite laminates under impact loadino[J]. Explosion and Shock Waves, 2016, 36(2): 170-176(in Chinese). DOI: 10.11883/1001-1455(2016)02-0170-07
[15] ZHOU J, LIAO B, SHI Y, et al. Low-velocity impact behavior and residual tensile strength of CFRP laminates[J]. Composites Part B: Engineering, 2019, 161: 300-313. DOI: 10.1016/j.compositesb.2018.10.090
[16] MORYE S S, HINE P J, DUCKETT R A, et al. Modelling of the energy absorption by polymer composites upon ballistic impact[J]. Composites Science and Technology, 2000, 60(14): 2631-2642.
[17] LIU P F, ZHENG J Y. Recent developments on damage modeling and finite element analysis for composite laminates: A review[J]. Materials & Design, 2010, 31(8): 3825-3834.
[18] 赵云, 杨波, 陶子伟, 等. 纤维增强树脂基防弹复合材料吸能机制及损伤模式研究进展[J]. 复合材料学报, 2024, 41(9): 4606-4627. ZHAO Yun, YANG Bo, TAO Ziwei, et al. Research progress on energy absorption mechanism and damage mode of fiber reinforced resinbased bulletproof composites[J]. Acta Materiae Compositae Sinica, 2024, 41(9): 4606-4627(in Chinese).
[19] 俞鸣明, 朱雪莉, 刘雪强, 等. 低速多次冲击下碳纤维/环氧树脂基复合材料层合板失效机制及剩余强度评估[J]. 复合材料学报, 2023, 40(9): 5359-5370. YU Mingming, ZHU Xueli, LIU Xueqiang, et al. Failure mechanism and assessment of residual strength of carbon fiber/epoxy resin matrix composite laminates under multiple impacts at low velocities[J]. Acta Materiae Compositae Sinica, 2023, 40(9): 5359-5370(in Chinese).
[20] 王东哲. 纤维增强复合材料抗弹丸侵彻性能的多尺度数值模拟研究[D]. 济南: 山东大学, 2021. WANG Dongzhe. Multi-scale numerical simulation of anti-penetration performance of fiber reinforced composites [D]. Jinan: Shandong University, 2021(in Chinese).
[21] 许明明. 碳纤维增强金属层合板抗高速冲击特性研究[D]. 北京: 北京理工大学, 2018. XU Mingming. High velocity impact resistance of carbonfiber-reinforced metal laminates[D]. Beijing: Beijing Institute of Technology, 2018(in Chinese).
[22] 秦溶蔓, 朱波, 乔琨, 等. 复合结构碳纤维防弹板的防弹性能仿真[J]. 工程科学学报, 2021, 43(10): 1346-1354. QIN Rongman, ZHU Bo, QIAO Kun, et al. Simulation study of the protective performance of composite structure carbon fiber bulletproof board[J]. Chinese Journal of Engineering, 2021, 43(10): 1346-1354(in Chinese).
[23] 徐豫新, 任杰, 王树山. 钨球正撞击下低碳钢板的极限贯穿厚度研究[J]. 北京理工大学学报, 2017, 37(6): 551-556. XU Yuxin, REN Jie, WANG Shushan. Research on perforation limit thickness of low carbon steel plates impacted normally by tungsten spheres[J]. Transactions of Beijing Institute of Technology, 2017, 37(6): 551-556(in Chinese).
[24] 蒋志刚, 曾首义, 周建平. 分析金属靶板弹道极限的延性扩孔模型[J]. 弹道学报, 2004(1): 54-59. DOI: 10.3969/j.issn.1004-499X.2004.01.011 JIANG Zhigang, ZENG Shouyi, ZHOU Jianping. A model for ballistic limit of thick metallic targets struck by projectiles with conical or ogival nose[J]. Journal of Ballistics, 2004(1): 54-59(in Chinese). DOI: 10.3969/j.issn.1004-499X.2004.01.011
[25] 周冰, 李良春, 宋桂飞. 仿真预测泡沫铝弹道极限和弹丸侵彻冲击力[J]. 兵工自动化, 2018, 37(6): 10-13. ZHOU Bing, LI Liangchun, SONG Guifei. Numerical stimulation for predicting ballistic limit and impact force in penetration of aluminum foam by blunt-nosed projectile[J]. Ordnance Industry Automation, 2018, 37(6): 10-13(in Chinese).
[26] 武一丁, 高光发, 王晓东. 不同速度下B4C陶瓷/铝合金轻型复合靶板抗侵彻行为研究[J]. 南京理工大学学报, 2023, 47(4): 503-513. WU Yiding, GAO Guangfa, WANG Xiaodong. Research on the penetration resistance behavior of B, C ceramic/aluminum alloy light weight composite target at different speeds[J]. Journal of Nanjing University of Science and Technology, 2023, 47(4): 503-513(in Chinese).
[27] 姜春兰, 李明, 张庆明, 等. 碳纤维织物增强复合材料的冲击响应特性[J]. 北京理工大学学报, 2000(3): 225-230. JIANG Chunlan, LI Ming, ZHANG Qingming, et al. Impact responses of the carbon fiber fabric reinforced composites[J]. Journal of Beijing Institute of Technology, 2000(3): 225-230(in Chinese).
[28] 罗锡林, 魏建辉, 李飘, 等. 碳纤维编织复合材料层合板抗侵彻性能研究[J]. 材料开发与应用, 2023, 38(4): 61-68. DOI: 10.19515/j.cnki.1003-1545.2023.04.004 LUO Xilin, WEI Jianhui, LI Piao, et al. Study on penetration resistance of carbon fiber braided composite laminates[J]. Development and Application of Materials, 2023, 38(4): 61-68(in Chinese). DOI: 10.19515/j.cnki.1003-1545.2023.04.004
[29] 李明, 姜春兰, 王在成. 钨球贯穿陶瓷 /铝复合靶的弹道极限分析模型[J]. 北京理工大学学报, 2002(4): 389-392. LI Ming, JIANG Chunlan, WANG Zaicheng. A ballistic limit analytical model of tungsten ball perforating ceramic/aluminum composite target[J]. Journal of Beijing Institute of Technology, 2002(4): 389-392(in Chinese).
[30] QI S, HUANG G, ZHI X, et al. External blast flow field evolution and response mechanism of single-layer reticulated dome structure[J]. Defence Technology, 2023, 24(6): 241-253.
[31] 钟正. 碳纤维复合材料力学行为及断裂失效模式仿真[D]. 大连: 大连理工大学, 2021. ZHONG Zheng. CFRP mechanical behavior and fracture failure mode simulation of CFRP[D]. Dalian: Dalian University of Technology, 2021(in Chinese).
[32] SHIRVANIMOGHADDAM K, HAMIM S U, KARBALAEI AKBARI M, et al. Carbon fiber reinforced metal matrix composites: Fabrication processes and properties[J]. Composites Part A: Applied Science and Manufacturing, 2017, 92: 70-96. DOI: 10.1016/j.compositesa.2016.10.032
[33] 隋树元, 王树山. 终点效应学[M]. 北京: 国防工业出版社, 2000: 122-123. SUI Shuyuan, WANG Shushan. Terminal effect[M]. Beijing: National Defence Industry Press, 2000: 122-123(in Chinese).
[34] 赵国志. 穿甲工程力学[M]. 北京: 兵器工业出版社, 1992: 63-69. ZHAO Guozhi. Armor-piercing engineering mechanics[M]. Beijing: Weapons Industry Press, 1992: 63-69(in Chinese).
-
目的
在航空航天领域,碳纤维复合材料已经成为主承力构件及部分结构的防护材料,其他国防科技领域中,碳纤维也广泛使用。研究碳纤维复合材料毁伤特性为科研人员提高碳纤维复合材料性能、进行防护结构设计提供依据。本文开展不同厚度碳纤维复合材料受破片侵彻时的毁伤机理及弹道极限研究。
方法首先,开展8 g立方体钢破片分别侵彻厚5 mm、10 mm、15 mm碳纤维复合材料靶板数值仿真研究,使用TrueGrid软件建立数值仿真模型,利用LS-dyna进行仿真计算,在仿真过程中,考虑模型的可靠性,对网格进行收敛性分析,考虑计算效率,建立1/2模型。破片为立方体钢破片,质量为8 g,尺寸为9.5 mm×10 mm×10.8 mm。为了避免靶板边界效应对破片侵彻结果产生影响,选用靶板尺寸大于破片尺寸的10倍,靶板尺寸为150 mm×150 mm。碳纤维复合材料为纤维增强材料,本身具有各向异性与不均匀性,在破片侵彻过程中的能量转化与材料的失效准则判定也十分复杂。采用Ls-DYNA软件中的纤维增强复合材料渐进损伤模型纤维增强复合材659渐进损伤模型(MAT ENHANCED COMPOSITE DAMAE简称为 MAT54)。其次,基于仿真模型,开展8 g立方体钢破片分别侵彻厚5 mm、10 mm、15 mm碳纤维复合材料靶板弹道枪试验,选用的碳纤维复合材料为由日本东丽公司生产的T300级预浸料与环氧树脂在高温下压制所成的板材。通过火药气体燃烧产生的压力将放置于弹托内部的破片发射,由于受到空气阻力的作用,在飞行过程中破片与弹托分离,破片继续运动,以一定速度贯穿靶板前设置的测速靶后侵彻安装于靶架上的碳纤维复合材料靶板。通过调整发射药量控制破片速度进而获取不同着靶速度。最后,利用数值仿真方法得到大量不同着靶速度与对应的剩余速度,考虑破片侵彻的剩余速度与破片的着靶面积A、破片质量Mp、破片的着靶速度、破片侵彻的着角θ、目标类型及其厚度h有关,建立的普适性经验公式也应该包含这些参量。基于THOR公式建立破片侵彻碳纤维复合材料靶板剩余速度模型与弹道极限计算公式。
结果通过数值仿真,观察破片侵彻碳纤维复合靶板过程,8 g立方体破片侵彻5 mm、10 mm、15 mm厚的碳纤维复合材料靶板的数值仿真弹道极限分别为:307.76 m/s,394.78 m/s,437.55 m/s;通过试验,获取破片着靶速度,回收破片、靶板,观测靶板破坏情况,8 g立方体破片侵彻5 mm、10 mm、15 mm厚的碳纤维复合材料靶板的弹道极限分别为:328.17 m/s,394.67 m/s,436.50 m/s;利用公式计算弹道极限:8 g立方体破片侵彻5 mm、10 mm、15 mm厚的碳纤维复合材料靶板的理论计算弹道极限分别为:323.32 m/s,379.46 m/s,416.72 m/s。
结论结合数值仿真与试验结果综合分析,结果表明:靶板破坏形式与破片速度的关系为:破片速度大于弹道极限时,靶板以纤维的剪切破坏为主;破片速度逐渐降低时,纤维的拉伸破坏,基体破裂与纤维层分层多种破坏形式所占比重随着速度的变化而变化。数值仿真弹道极限与六射弹弹道极限最大误差为6.21%。对弹道极限公式进行试验验证,选取不同工况下的六射弹弹道极限,与理论计算值进行对比,结果表明,同一工况下,试验结果与计算结果最大误差为4.54%。随着靶板厚度的增加,弹道极限增速变慢。其他:针对碳纤维复合材料这一新材料,结合其在无人机、巡飞弹作为主要材料的应用,通过试验的方式了解其性能,并通过数值仿真进行碳纤维材料抗破片侵彻过程研究,为以后的研究应用提供理论依据;通过建立破片侵彻不同厚度碳纤维复合材料靶板剩余速度模型与弹道极限公式,为后续碳纤维作为防护材料设计奠定基础,节约研究成本。
-
碳纤维复合材料属于各向异性材料,因其具有密度小,比强度、比模量高,抗疲劳、抗振性能好等优点,被广泛应用于航空航天主承力构件及部分结构的防护材料。巡飞弹、无人机已在现代战争中广泛使用,“柳叶刀”巡飞弹在俄乌战争中使用,以其成本低廉、自杀式特点能消灭坦克、大炮甚至飞机;我国已有实名登记无人机126.7万架;碳纤维作为巡飞弹机翼、机身重要构件,研究碳纤维复合材料抗破片侵彻性能为科研人员提高碳纤维复合材料性能、进行防护结构设计提供依据。
本文重点关注不同厚度碳纤维复合靶板抗破片侵彻的弹道极限,开展数值模拟与弹道枪试验,主要工作包括:
开展数值仿真与弹道枪试验,探究不同厚度碳纤维复合材料靶板受8g立方体钢破片侵彻的毁伤机理及弹道极限速度,模拟无人机、巡飞弹机翼、机身等重要部位碳纤维材料受侵彻状态。数值仿真过程中,考虑模型与实际情况的一致性,选择8 g立方体钢破片,尺寸为9.5 mm×10 mm×10.8 mm;为了避免靶板边界效应对破片侵彻结果产生影响,选用靶板尺寸大于破片尺寸的10倍,靶板尺寸为150 mm×150 mm;选择符合碳纤维复合材料的仿真模型,MAT ENHANCED COMPOSITE DAMAE简称为MAT54。得到8 g立方体破片侵彻5 mm、10 mm、15 mm厚的碳纤维复合材料靶板的数值仿真弹道极限分别为:307.76 m/s,394.78 m/s,437.55 m/s。弹道枪试验,通过控制火药质量控制破片速度,试验后获取破片着靶速度,回收破片、靶板,观测靶板破坏情况,8 g立方体破片侵彻5 mm、10 mm、15 mm厚的碳纤维复合材料靶板的弹道极限分别为:328.17 m/s,394.67 m/s,436.50 m/s。建立建立破片侵彻碳纤维复合材料靶板剩余速度模型与弹道极限计算公式并验证,8 g立方体破片侵彻5 mm、10 mm、15 mm厚的碳纤维复合材料靶板的理论计算弹道极限分别为:323.32 m/s,379.46 m/s,416.72 m/s。数值仿真弹道极限与六射弹弹道极限最大误差为6.21%。对弹道极限公式进行试验验证,选取不同工况下的六射弹弹道极限,与理论计算值进行对比,结果表明,同一工况下,试验结果与计算结果最大误差为4.54%。结合数值仿真与试验结果综合分析靶板主要的破坏形式以及破坏形式与破片速度的关系。
创新性说明:
针对碳纤维复合材料这一新材料,结合其在无人机、巡飞弹作为主要材料的应用,通过试验的方式了解其抗侵彻性能,并通过数值仿真进行碳纤维材料抗破片侵彻过程研究,得到碳纤维复合材料主要的破坏形式为:纤维层的剪切破坏,纤维的拉伸破坏,基体破裂与纤维层分层,破坏形式与破片速度有关。
建立破片侵彻不同厚度碳纤维复合材料靶板剩余速度模型与弹道极限公式,用以后续进行碳纤维复合材料性能与碳纤维防护研究,针对不同应用场景预测材料所需厚度,进行结构设计。




 下载:
下载: