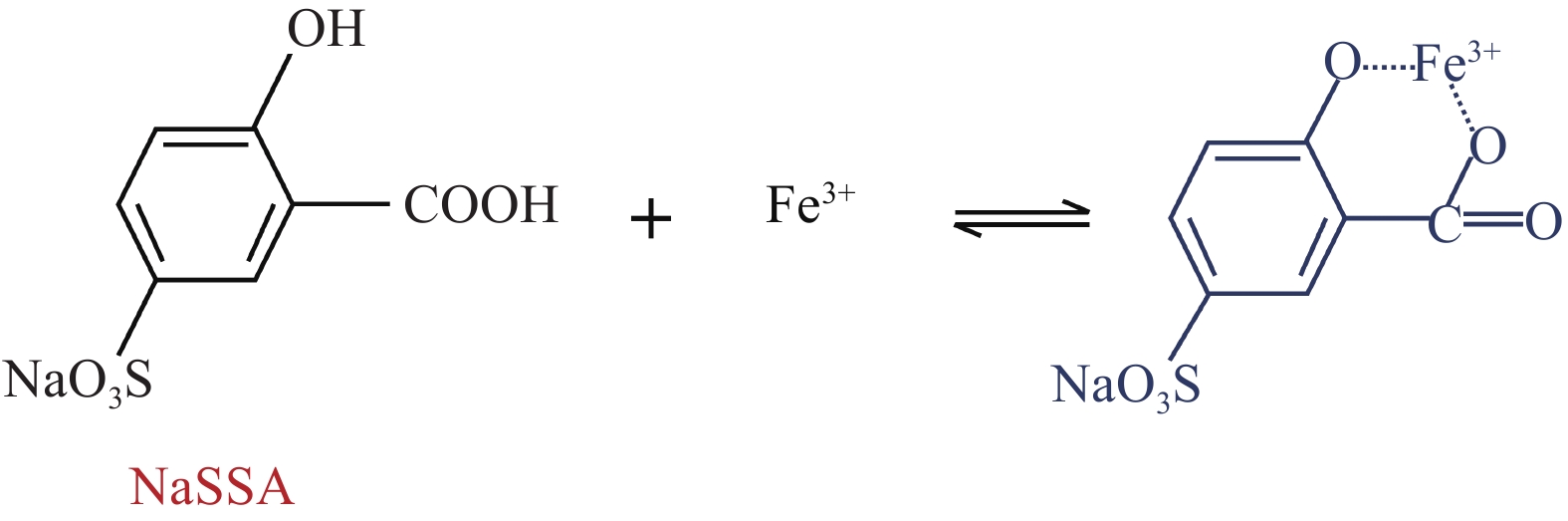Study on the complex band gap characteristic of controllable metastructure
-
摘要:
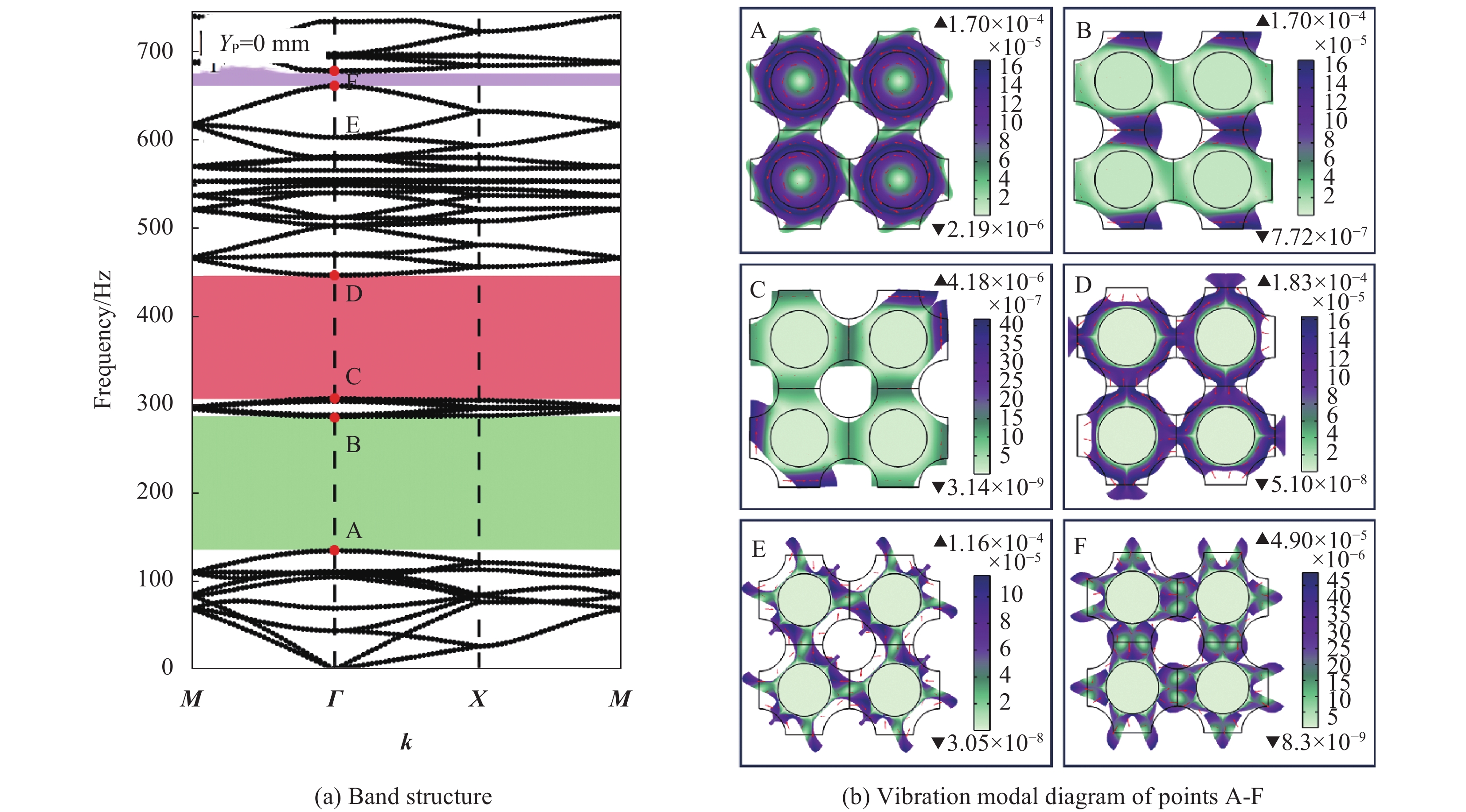
可控超结构可根据目标需求调节结构的带隙特性,实现对不同工况下结构减振的可控调节,在航空航天、轨道交通等工程领域具有广泛的应用前景。本文提出一种新型可控超结构构型,可同时产生局域共振和布拉格散射两种带隙,通过施加位移可实现对带隙的有效调控。应用COMSOL软件建立了该结构的有限元模型,研究了4种可控超结构构型的能带分布及其在外加位移激励作用下的带隙特性调控规律,开展了该结构的振动传输特性实验,并与数值结果进行对比验证。研究结果表明:四振子复合带隙可控超结构在0~800 Hz范围内共有3条完全带隙,第一阶带隙范围低至134.48~287.53 Hz,第二阶带隙范围为307.26~447.81 Hz,第三阶带隙范围为662.44~679.43 Hz。对比分析4种元胞构型带隙特性,在一定频率范围内,随着振子数量增加,带隙数量减少,带宽增加,带隙位置逐渐上移;施加结构位移可有效调控结构带隙,随着位移值增加,结构中低频局域共振带隙变化较小,布拉格带隙中心频率逐渐上移,并出现新带隙。本文的研究表明该结构在带隙范围内具有良好的减振特性,所设计的复合带隙可控超结构可实现对复合带隙的调控,为超结构减振设计研究提供有益的参考。
Abstract:The controllable metastructure can adjust the band gap characteristic of the structure according to the target requirements, and realize the controllable adjustment of structural vibration reduction under different working conditions. It has a wide application prospect in aerospace, rail transit and other engineering fields. A new controllable metastructure configuration was proposed, which can simultaneously generate two kinds of band gaps, local resonance and Bragg scattering. The band gap can be effectively controlled by applying displacement. The finite element model of the structure was established by COMSOL software. The energy band distribution of four controllable metastructure configurations and the regulation of band gap characteristics under external displacement excitation were studied. The vibration transmission characteristics of the structure were tested and compared with the numerical results. The results show that the four-oscillator composite band gap controllable metastructure has three complete band gaps in the range of 0-800 Hz. The first-order band gap range is as low as 134.48-287.53 Hz, the second-order band gap range is 307.26-447.81 Hz, and the third-order band gap range is 662.44-679.43 Hz. The band gap characteristics of four cell configurations were compared and analyzed. In a certain frequency range, as the number of oscillators increases, the number of band gaps decreases, the bandwidth increases, and the band gap position gradually moves up. The application of structural displacement can effectively control the structural band gap. As the displacement value increases, the low-frequency local resonance band gap in the structure changes little, and the center frequency of the Bragg band gap gradually moves up, and a new band gap appears. This study shows that the structure has good vibration reduction characteristics in the band gap range. The results show that the designed composite band gap controllable metastructure can realize the regulation of the composite band gap, which provides a useful reference for the research of metastructure vibration reduction design.
-
玄武岩纤维是以玄武岩矿石为原材料,将矿石破碎后,加入熔窑中,在
1450 ~1700 ℃下进行熔融,生成玻璃状熔融液体,通过铂铑合金拉丝漏板拉制而成的连续纤维[1-4]。玄武岩纤维在整个生产过程中,不会析出任何有毒有害物质,不会释放任何有害气体,因此,玄武岩纤维的生产制造不会造成环境污染,被誉为“21世纪的新型环保纤维” [5]。另一方面,随着纤维增强复合材料在土木工程、交通运输、航空航天等领域中的广泛应用,纤维的可回收性逐渐引起了重视。相比于回收困难的碳纤维,玄武岩纤维原材料本身是天然的玄武岩石,因此,废弃的玄武岩纤维可以直接进行回炉再生,具有较高的回收利用率,这有助于材料的可持续发展。此外,玄武岩纤维拥有许多优异的性能,例如,优异的拉伸性能(拉伸强度可达到4840 MPa)、较强的耐腐蚀性能和化学稳定性、良好的热稳定性能等[6-8]。玄武岩纤维增强复合材料已经广泛地运用在航空航天、汽车船舶、建筑、石油化工、体育器材等领域。随着能源电子、空间技术等尖端科学领域的快速发展,材料的电磁性能愈发重要[9]。然而,玄武岩纤维是一种绝缘材料,其电阻率达到1011 Ω·cm,限制了玄武岩纤维在电磁屏蔽、静电防护等领域的运用,因此实现玄武岩纤维的导电性能够扩宽玄武岩纤维的应用领域,提高材料的附加值。另一方面,多功能复合材料成为目前研究热点。碳纤维增强复合材料(CFRP)由于碳纤维的导电性使CFRP在作为承载构件的同时,也能够实现自感知。而玄武岩纤维增强复合材料(BFRP)由于玄武岩纤维和数值的绝缘性,无法实现自感知。因此,导电玄武岩纤维有望能开发BFRP的自感知性能。目前,开发实现玄武岩纤维导电性的研究较少。谭文军等[10]以过硫酸铵(APS)作为氧化剂,酸性条件下在玄武岩纤维布表面原位生长聚苯胺(PANI),所制的导电玄武岩纤维的电导率可达4 S/cm,但实验过程使用浓硝酸、高氯酸等具有强腐蚀性的强酸,制备方法不够友好。冯倩倩等[11]采用金属沉积法在玄武岩纤维表面镀镍金属层制备导电玄武岩纤维,纤维的平均电阻值为14.2 Ω/cm,电阻率为1.9×10−3 Ω·cm,具有良好的导电性,但制备方法采用重金属,价格昂贵,成本高。马鹏程等[12]提出通过化学气相沉积法,在玄武岩纤维表面沉积碳纳米材料,从而实现玄武岩纤维的导电性。该方法可获得均匀沉积在纤维表面的碳纳米层,但气相沉积法在500~
1000 ℃温度下进行,对玄武岩纤维结构可能会造成一定破坏,从而降低玄武岩纤维的力学性能,有必要提供一种在不损伤玄武岩纤维机械性能的前提下高效、友好的实现玄武岩纤维导电性的改性方法。聚吡咯是由共轭单双键结构排列而成的导电高分子聚合物,具有易于合成、成本低、无毒、导电性和氧化还原性好等优点[13-16]。目前,合成聚吡咯的方法主要有化学氧化剂的化学聚合法和阳极氧化的电聚合法。然而,聚吡咯一般以颗粒状存在,不溶也不融,这限制了聚吡咯的进一步应用。如果将聚吡咯通过原位聚合法沉积在玄武岩纤维上,制备出导电玄武岩纤维,一方面能够赋予玄武岩纤维良好的导电性,且避免高温、酸碱刻蚀等会对纤维造成伤害的工艺,保护纤维的机械性能[17-19],另一方面,也能解决聚吡咯应用难的问题。通过研究[13]发现,无缺陷共轭结构的聚吡咯的导电性较差,因此,需要通过加入合适的掺杂剂来构建具有缺陷的共轭结构,来提高聚吡咯的导电性。掺杂剂在吡咯发生氧化还原反应过程中,在聚吡咯共轭长分子链嵌入/移出电子,形成电荷载体,电荷载体能够沿着聚吡咯长链运动,提高聚吡咯的导电性[20]。Varesano等[21]发现在吡咯聚合过程中,当加入芳香族磺酸盐类的化合物作为掺杂剂时,聚吡咯的导电性明显提升。彭章[22]对比了不同氧化剂和不同掺杂剂对聚吡咯导电性的影响。当分别使用过硫酸铵(APS)、氯化铁(FeCl3)、过氧化氢(H2O2)作为氧化剂,使用FeCl3制备的聚吡咯的电导率具有明显优势,是APS和H2O2的800多倍;当分别用十二烷基苯磺酸钠(SDBS)、5-磺基水杨酸钠(NaSSA)作为掺杂剂对聚吡咯导电性的影响,发现NaSSA的掺杂效果优于SDBS。何青青[23]对比了相同浓度下甲基苯磺酸(PTS)、5-磺基水杨酸钠、蒽醌-2-磺酸钠盐(NaAQSA)作为掺杂剂对聚吡咯导电性影响,发现NaSSA作为掺杂剂时,导电性能最为优异,掺杂效果最好。因此,基于已有研究结论,本文中使用FeCl3作为吡咯单体聚合的氧化剂,NaSSA作为合成聚吡咯的掺杂剂。
本文开发了一种实现玄武岩纤维导电性的改性方法。该方法在实现玄武岩纤维高导电性的同时,提高了玄武岩纤维的拉伸强度。该方法成本低,制备过程简单、高效、友好,是一种适合于大量生产的改性方法。本文以吡咯单体、氧化剂氯化铁和掺杂剂5-磺基水杨酸钠为原料,通过原位聚合法在玄武岩纤维表面沉积导电聚合物聚吡咯,通过调整吡咯单体、氧化剂和掺杂剂的浓度来调控和研究玄武岩纤维上导电聚合物的结构、颗粒大小、涂层厚度及玄武岩纤维的导电性。此外,本文通过纤维单丝拉伸强度来研究改性过程对纤维自身结构造成的影响。该研究实现了在不损伤纤维结构的基础上显著降低玄武岩纤维电阻率,扩宽了玄武岩纤维的应用领域,为玄武岩纤维复合材料实现结构-功能一体化提供了新的方案,具有广阔的运用前景。
1. 试验材料与方法
1.1 原材料
玄武岩纤维布(直径d 约为 13 μm),购自江苏绿材谷新材料科技发展有限公司;无水乙醇、吡咯(Py,AR)、无水三氯化铁(FeCl3,AR)、5-磺基水杨酸钠(NaSSA,AR)均购自上海麦克林生化科技有限公司,所有化学试剂均未做进一步处理。对吡咯单体进行冷藏保存,并在使用前观察吡咯单体颜色,确保使用时吡咯单体为白色而非黄色,从而避免由于保存时间过久和保存条件不当使吡咯自身发生氧化形成二聚体。
1.2 聚吡咯改性玄武岩纤维制备方法
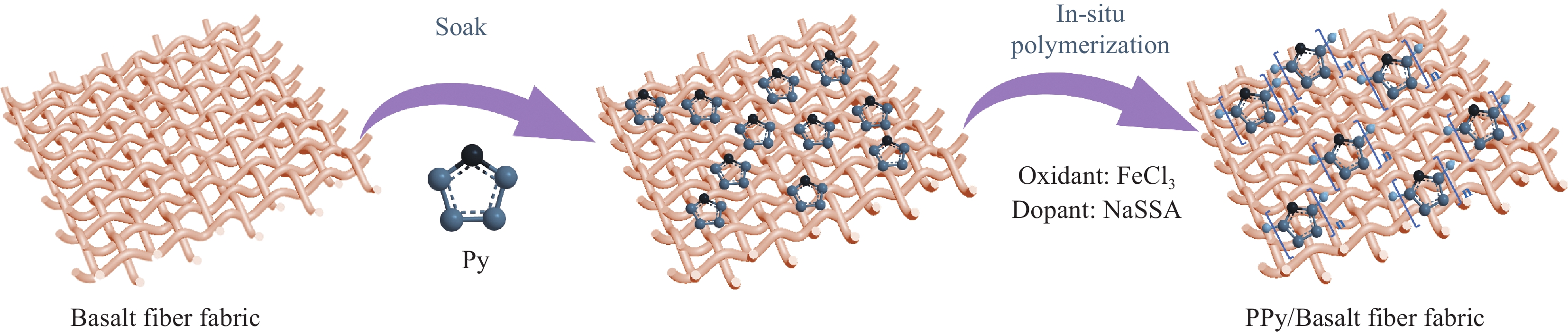
将2 cm×2 cm的玄武岩纤维布用无水乙醇和去离子水洗涤3~5次,去除表面杂质。将其浸泡于一定浓度的吡咯单体溶液中进行吸附30 min,控制温度为0~2℃。配制一定量的氧化剂FeCl3和掺杂剂NaSSA的混合液,将混合液缓慢加入到浸泡玄武岩纤维的吡咯单体溶液中,进行聚合反应5 h,控制聚合反应体系温度为0~2℃。取出玄武岩纤维,用无水乙醇和去离子水洗涤3~5次,洗去未附着的聚吡咯颗粒。最后,将改性后的玄武岩纤维在60℃下烘干至恒重,得到聚吡咯改性的导电玄武岩纤维,记为PPy/BF。主要的制备流程如图1所示。
为了研究吡咯单体浓度对玄武岩纤维导电性和聚吡咯结构的影响,设计了4种浓度的吡咯单体溶液,吡咯单体与氧化剂FeCl3的摩尔比分别为0.5、1、2、3。其中FeCl3的浓度固定为1 mol/L。将4种摩尔比下原位聚合得到的PPy/BF分别记为PPy/BF-0.5、PPy/BF-1、PPy/BF-2、PPy/BF-3。为了研究掺杂剂NaSSA的浓度对玄武岩纤维导电性和聚吡咯结构的影响,在上述导电性最优的PPy/BF的吡咯单体浓度的基础上,选取了5种NaSSA溶液的浓度。其分别与吡咯单体的摩尔比为0、0.05、0.1、0.5、1,将不同NaSSA浓度下原位聚合得到的PPy/BF分别记为PPy/BF(0)、PPy/BF(0.05)、PPy/BF(0.1)、PPy/BF(0.5)、PPy/BF(1) (表1)。
表 1 不同聚吡咯/玄武岩纤维复合材料的合成条件Table 1. Synthesis conditions of different polypyrrole/basalt fiber compositesSample Py/
(mol·L−1)FeCl3/
(mol·L−1)NaSSA/
(mol·L−1)Temperature/
℃Polymerization
time/hPPy/BF-0.5 0.5 1 0 0-2 5 PPy/BF-1 1 1 0 0-2 5 PPy/BF-2 2 1 0 0-2 5 PPy/BF-3 3 1 0 0-2 5 PPy/BF(0) 3 1 0 0-2 5 PPy/BF(0.05) 3 1 0.15 0-2 5 PPy/BF(0.1) 3 1 0.3 0-2 5 PPy/BF(0.5) 3 1 1.5 0-2 5 PPy/BF(1) 3 1 3 0-2 5 Notes: Py—Concentration of pyrrole monomer solution; FeCl3—Concentration of ferric chloride solution; NaSSA—Concentration of sodium 5-sulfosalicylate; BF—Basalt fibers. 1.3 材料表征与性能测试
1.3.1 材料表征
使用场发射扫描电子显微镜(FESEM,JSM-7610 F Plus)来表征聚吡咯改性前后玄武岩纤维的表面形态和微观结构;使用X射线光电子能谱(XPS,Thermo Scientific Escalab 250 Xi)以单色Al Kα射线源测试改性前后玄武岩纤维表面的元素种类和相对含量及各成分的化学状态,分析图谱前将N1s峰位校准至400 eV;使用拉曼光谱(Raman spectra,Thermo Fisher DXRxi)来分析聚吡咯涂层的化学结构,测试光源的激发波长为532 nm。
活性物质聚吡咯的负载量通过以下方式表征。使用聚吡咯改性前的玄武岩纤维布的质量为m0,使用聚吡咯改性后的玄武岩纤维布的质量为m1,因此,活性物质聚吡咯的负载量λ通过下式计算:
λ=m1−m0m0×100% (1) 1.3.2 导电性能测试
采用四探针法(HPS2662,精密四探针电阻率测试仪,常州海尔帕电子科技有限公司)测量玄武岩纤维布表面的方阻值,如图2所示,探针间距为1 mm,对玄武岩纤维布正反面分别测量5次,取平均值,得到表面方阻(R);使用游标卡尺测量玄武岩纤维布的厚度,分别测量5次,取平均值,得到玄武岩纤维布的厚度(d,cm),通过公式(2)计算得到玄武岩纤维布的电阻率(ρ,Ω·cm),并通过公式(3)计算电阻率的标准差(Standard deviation,s)来反映纤维布上负载聚吡咯的均匀性。
ρ=Rd (2) s=√N∑i=1(Xi−μ)2N (3) 其中:N为测试的纤维单丝的总数;Xi为第i根纤维的拉伸强度;μ为纤维单丝拉伸强度的平均值。
1.3.3 纤维单丝拉伸性能测试
采用XQ-2型纤维强伸度仪(上海新纤仪器公司)测量改性前后玄武岩纤维的拉伸强度和模量来表征纤维机械性能,如图3所示。将纤维单丝粘贴于U形纸片上。将U形纸片放置在仪器上,剪断纸框,设置参数为预张力0 cN、加持距离20 mm、拉伸速度10 mm/min,测试得到纤维的单丝强力(P, cN)。选取纤维单丝位于中部断裂的作为有效数据样本,舍弃在根部断裂的样本。采用XY-MRT反式金相显微镜(中国舜宇)测试相应纤维单丝的直径(d,μm),根据公式(4),计算得到纤维的单丝拉伸强度(σ,MPa)。根据GB/T 31290—2022[24],利用公式(5)计算纤维的弹性模量(E,MPa)。通过公式(6)计算离散系数(Cv)来反映拉伸强度和弹性模量的离散性。
σ=Pπ(d/2)2×10000 (4) E=σ1−σ2ε1−ε2 (5) 式中:根据规范,应变ε1=0.1%,ε2=0.3%;σ1为应变为ε1对应的应力,σ2为应变为ε2对应的应力。
Cv=sμ (6) 式中,s和μ分别为拉伸强度和模量的标准差和平均值。
2. 结果与讨论
本文通过原位聚合法使用PPy对玄武岩纤维进行改性,在不牺牲机械性能的基础上实现了玄武岩纤维的高导电性,也为PPy提供了新的应用方向。PPy作为导电聚合物的一种,具有优异的导电性。玄武岩纤维通过吸附Py单体,在氧化剂和掺杂剂的作用下,在表面原位生长PPy,形成厚实稳定的PPy涂层。如图4所示,玄武岩纤维表面的颜色由褐色逐渐变成黑色。通过研究吡咯单体和氧化剂的比例及掺杂剂NaSSA与吡咯单体的比例,得到了导电性能较好的PPy/BF。PPy在玄武岩纤维表面形成了连续有效的导电网络,使玄武岩纤维的电阻大幅度下降,实现了玄武岩纤维的高导电性。在制备过程中,通过原位生长的方法,避免了对纤维造成伤害的高温、酸碱处理等工艺,很好地保护了玄武岩纤维的结构,保护了玄武岩纤维优异的拉伸性能。
2.1 PPy/BF微观形貌和结构组成
图5(a)为未改性的玄武岩纤维的扫描电镜图,玄武岩纤维呈现圆柱状,表面平整光滑,含有少量的杂质。当使用浓度较低的吡咯单体溶液对玄武岩纤维进行改性时(PPy/BF-0.5),从图5(b)中可以看出,聚吡咯颗粒成功负载在玄武岩纤维表面,纤维表面变得粗糙,但由于聚吡咯的负载量较小,聚吡咯颗粒分布不均匀,离散性较大。因此,当吡咯浓度较小时,在玄武岩纤维表面拥有较少的连续导电网络,导致玄武岩纤维的导电性较差。当吡咯浓度较大且引入掺杂剂NaSSA后,聚吡咯在玄武岩纤维上的负载量较大。图5(c)为PPy/BF(1) 的FESEM图,从图中可以看出,玄武岩纤维表面附着上了较厚的聚吡咯涂层,很大地提升了玄武岩纤维表面的粗糙度,有利于玄武岩纤维与树脂基体之间的粘结,可能能够在一定程度上提升了玄武岩纤维增强复合材料的界面性能。相比于PPy/BF-0.5 (图5(b)),聚吡咯涂层均匀稳定地附着在玄武岩纤维表面,在玄武岩纤维表面构建了连续有效的导电网络,因此具有更良好的导电性能。对比PPy/BF-0.5和PPy/BF(1)上的PPy颗粒(图5(d)~图5(f)),可以看出二者所生长的PPy颗粒均呈现“花菜状” [25],PPy/BF(1)上生长的PPy颗粒具有更小的直径,分布更加均一。结合图5(b)和图5(c),PPy的团聚程度也进一步减小,说明掺杂剂NaSSA能够有效地控制PPy分子链有序缓慢地增长,聚吡咯具有更优异的颗粒形貌,进一步实现了PPy颗粒纳米化。
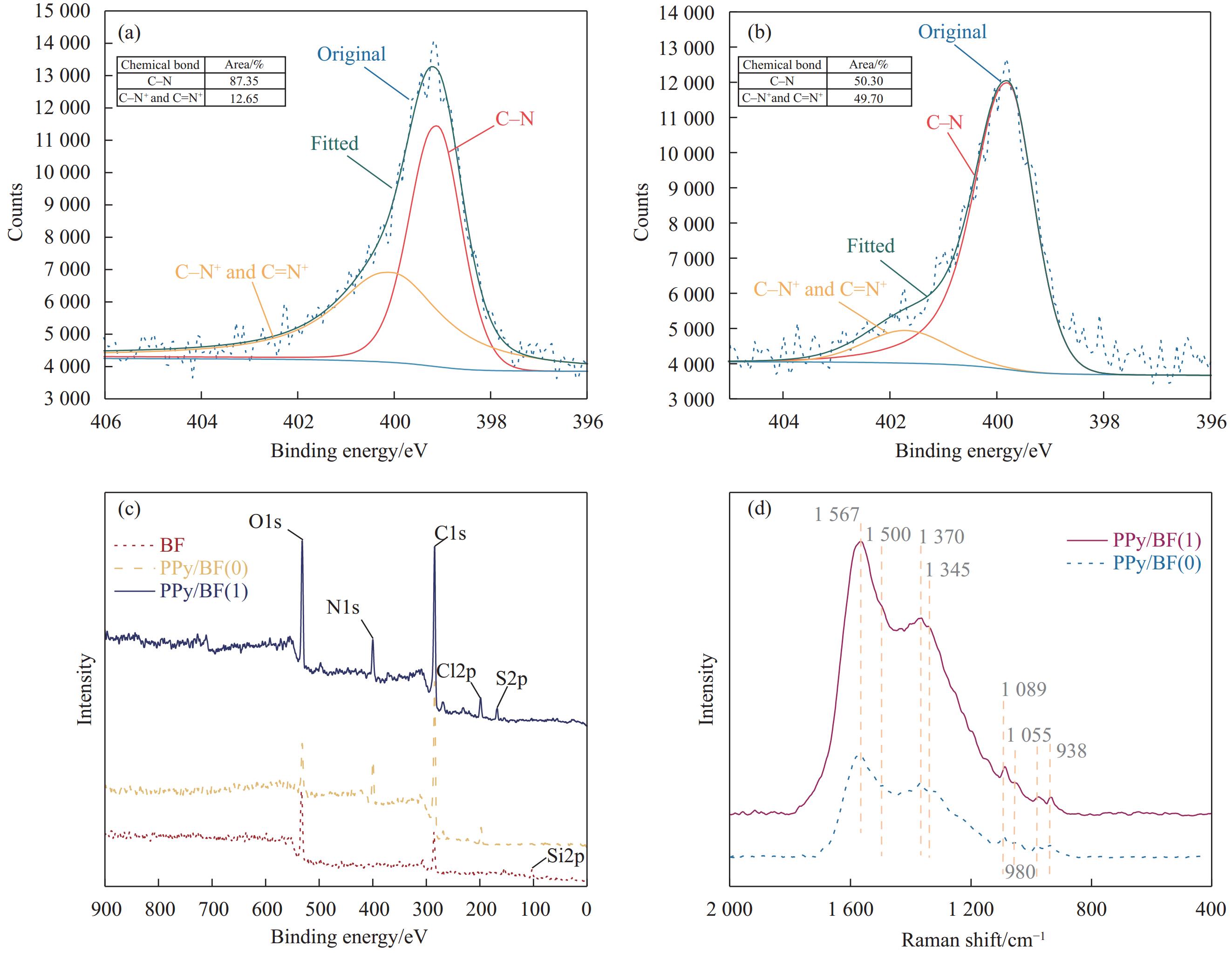
采用XPS对改性前后的玄武岩纤维表面元素变化及元素相对含量进行表征和分析。图6(c)为采用聚吡咯改性玄武岩纤维前后的BF、PPy/BF(0)、PPy/BF(1)的XPS全谱图。通过XPS全谱图中可以看出,玄武岩纤维表面主要含有C、O、Si元素,其中O1s的谱峰位于531.95 eV,C1s的谱峰位于284.80 eV,Si2p的谱峰位于102.35 eV[26]。PPy/BF相比于BF多了N1s、Cl2p和S2p谱峰,其中,N1s、Cl2p和S2p谱峰分别位于400 eV、199 eV和169 eV位置。其中,N元素主要来源于PPy,Cl元素主要来源于氧化剂FeCl3,S元素主要来源于掺杂剂NaSSA。结合XPS全谱图和表2,未改性的玄武岩纤维表面C元素含量最高,O元素和Si元素次之。玄武岩纤维表面含有大量的Si—OH活性官能团,有利于提高玄武岩纤维的表面活性,从而提高涂敷上浆剂的均匀性和复合材料的界面性能。聚吡咯涂层形成过程一般含有C、O、N、Cl、S等元素,通过聚吡咯改性玄武岩纤维后,XPS全谱图中出现了N1s峰,说明聚吡咯成功附着在了玄武岩纤维表面。PPy/BF(1)相比于PPy/BF(0)表面增加了S元素,这是由于在改性过程中,加入了掺杂剂NaSSA。
表 2 XPS全谱图中BF、PPy/BF(0)和PPy/BF(1)表面元素及其原子分数(at%)Table 2. Surface elements and atomic fractions (at%) of BF, PPy/BF(0) and PPy/BF(1) by the XPS spectraSample C O N Cl S Si (Cl+S)/N BF 48.81 39.61 – – – 11.58 – PPy/BF(0) 71.16 11.76 12.72 2.89 – 1.47 0.23 PPy/BF(1) 63.51 20.36 9.50 3.09 2.34 1.21 0.57 对PPy/BF(0)和PPy/BF(1)的N1s图谱进行分峰拟合,结果如图6(a)、图6(b)所示。聚吡咯的N元素可以分出3种波峰,其相应的结合能分别位于402.3 eV、401.0 eV和399.8 eV,对应于质子化醌类亚胺(—N+=)、质子化亚胺(—N+H—)和亚胺(—NH—)。含有质子化氮说明聚吡咯是掺杂态的,可以用质子化氮和氮的比值来反映聚吡咯的掺杂程度([N+]/[N])[27-28],该比值可通过N1s分峰拟合图中曲线的面积来计算。通过计算,得到PPy/BF(0)的[N+]/[N]=12.65%,而PPy/BF(1)的[N+]/[N]=49.70%,因此,PPy/BF(1)具有更高的质子化程度,其纤维表面的聚吡咯也就拥有更高的掺杂水平,这归因于PPy/BF(1)加入了掺杂剂 NaSSA。此外,也可以通过XPS全谱图来反映聚吡咯的掺杂水平。Cl和S元素分别来自于氧化剂FeCl3 和掺杂剂NaSSA,氯离子和磺酸根阴离子都可以作为反离子起到对聚吡咯的掺杂作用,基于此,可以使用(Cl+S)/N 来表征聚吡咯的掺杂程度[29]。根据计算,如表2所示,PPy/BF(0)的(Cl+S)/N= 0.23,而PPy/BF(1)的(Cl+S)/N=0.57,这也说明了PPy/BF(1)表面的聚吡咯拥有更高的掺杂水平。而掺杂水平影响着聚吡咯的导电性、氧化还原性、柔韧性及微观结构等。由于掺杂剂的加入会显著增加聚吡咯链上电荷的载体数量,因此,更高的掺杂水平意味着聚吡咯具有更优异的导电性能。通过PPy/BF(0)和PPy/BF(1)的Raman图谱来对比其上负载的聚吡咯分子的结构差异。如图6(d)所示,PPy/BF(0)和PPy/BF(1)展现出一致的Raman光谱特征峰。其中,
1567 cm−1处为PPy骨架中C=C键的伸缩振动,1500 cm−1处为骨架光带,1370 cm−1处是C—N键的反对称伸缩,1345 cm−1处为吡咯环中C—C键的伸缩振动,1089 cm−1处代表双极化子C—H的对称面内弯曲振动,1055 cm−1处代表极化子C—H的对称面内弯曲振动,980 cm−1处为形成极化子时吡咯环的变形振动,938 cm−1处为形成双极化子时吡咯环的变形振动[30-31]。其中,聚吡咯共轭分子链中产生的可移动的自由基阳离子,称为极化子;当失去两个电子,产生的是双阳离子,称为双极化子。双极化子和极化子在电流作用下移动,为聚吡咯提供导电性,双极化子比极化子对于提高聚吡咯导电性更有利。Dauginet-De Pra等[32]提出可以通过Raman光谱中R1=I(938cm−1)I(980cm−1)、R2=I(1089cm−1)I(1055cm−1)、R3=I(938cm−1)+I(1089cm−1)I(980cm−1)+I(1055cm−1)3个值的大小来反映聚吡咯分子中双极化子和极化子的比例(I表示特征峰强度),其结果如表3,通过对比可以看出,PPy/BF(1)的R1、R2、R3值均大于PPy/BF(0),说明PPy/BF(1)具有更高的双极化子比例,说明形成的聚吡咯结构更优异,导电性能更好。此外,Dauginet-De Pra等[32]还提出可以使用L=I(1568cm−1)I(1500cm−1)来表征聚吡咯共轭链的长度,通过表3可以看出,PPy/BF(1)具有比PPy/BF(0)更大的L值。共轭链长度影响着聚吡咯的导电性。由于聚吡咯是一种含有大π键的共轭高分子,其电导率主要受到载流子迁移率的影响,而载流子迁移率主要取决于聚吡咯分子链的链距和载流子在聚吡咯分子链上跃迁的频率。聚吡咯分子链有效共轭长度和取向影响着跃迁频率。因此,由于PPy/BF(1)的有效共轭链长度大于PPy/BF(0),共轭体系更完善,其电导率也更高。
表 3 Raman光谱中不同特征峰强度比Table 3. Intensity ratios of different characteristic peaks in Raman spectraSample R1 R2 R3 L PPy/BF(0) 0.93 1.07 1.02 1.39 PPy/BF(1) 1.17 1.23 1.21 1.64 Notes: R1 =I(938cm−1)I(980cm−1), R2 =I(1089cm−1)I(1055cm−1), R3 = I(938cm−1)+I(1089cm−1)I(980cm−1)+I(1055cm−1), L = I(1568cm−1)I(1500cm−1); I—Intensity of a characteristic peak at a specific position in the Raman spectrum. 2.2 PPy/BF导电性能研究
基于SEM、XPS和Raman光谱的结果,PPy/BF(1)上的聚吡咯具有最优异的结构,因此也具有最好的导电性。以下使用PPy的负载量及电阻率的平均值和方差来量化不同参数下PPy/BF的电阻率,并具体分析机制。
2.2.1 吡咯单体浓度对PPy/BF导电性影响
图7(a)展示了吡咯单体浓度对PPy/BF电阻率的影响。从图中可以看出,随着吡咯单体浓度的增大,聚吡咯的负载量逐渐增加,PPy/BF的电阻率逐渐下降而趋于稳定。当吡咯单体浓度为0.5、1、2、3 mol/L时(即C(Py)C(FeCl3)= 0.5、1、2、3),聚吡咯的负载量分别为12.93wt%、14.24wt%、17.43wt%、21.19wt%,PPy/BF的电导率分别为0.254、0.205、0.148、0.125 Ω·cm。在不添加掺杂剂的条件下,PPy/BF上聚吡咯的负载量能达到20wt%,电阻率能达到0.125 Ω·cm,具有良好的导电性。
![]() 图 7 不同制备参数下PPy/BF的电阻率:(a) Py与FeCl3不同摩尔比(C(Py) : C(FeCl3))的影响;(b) NaSSA与Py不同摩尔比(C(NaSSA) : C(Py))的影响Figure 7. Resistivity of PPy/BF under different preparation parameters: (a) Effect of different molar ratios (C(Py) : C(FeCl3)) of Py to FeCl3; (b) Effect of different molar ratios (C(NaSSA) : C(Py)) of NaSSA to Py
图 7 不同制备参数下PPy/BF的电阻率:(a) Py与FeCl3不同摩尔比(C(Py) : C(FeCl3))的影响;(b) NaSSA与Py不同摩尔比(C(NaSSA) : C(Py))的影响Figure 7. Resistivity of PPy/BF under different preparation parameters: (a) Effect of different molar ratios (C(Py) : C(FeCl3)) of Py to FeCl3; (b) Effect of different molar ratios (C(NaSSA) : C(Py)) of NaSSA to Py当吡咯浓度较低时,合成的聚吡咯较少,聚吡咯在玄武岩纤维布上无法形成较多连续有效的导电通路,且聚吡咯共轭链长度较短,加上玄武岩纤维自身的电绝缘性,导致PPy/BF-0.5的电阻率较高。当吡咯浓度较大时,聚吡咯的负载量提升,玄武岩纤维布上拥有了较多聚吡咯颗粒,聚吡咯共轭链长度增大,此时PPy/BF的电阻率下降。但由于氧化剂的量是固定的,随着聚合反应的进行,氧化剂的量逐渐减少,聚合反应速度逐渐减缓,聚吡咯的负载量和PPy/BF的电导率均逐渐趋于稳定。对所测试的10个不同位置的电阻率进行标准差分析,从图7(a)中可以看出,由于吡咯浓度较小,在玄武岩纤维表面聚合生长的离散性较大,聚合生长均一性差,因此在不同位置的电阻率差异也较大。随着吡咯浓度的增加,聚吡咯在玄武岩纤维表面稳定且均一地生长,因此标准差逐渐减小且趋于稳定。
2.2.2 掺杂剂NaSSA浓度对PPy/BF导电性影响
图7(b)展示了掺杂剂NaSSA的浓度对PPy/BF电阻率的影响。曲线的变化趋势可以看出,随着NaSSA浓度的增大,聚吡咯的负载量逐渐增加,PPy/BF的电阻率逐渐下降而趋于稳定。当掺杂剂NaSSA与吡咯单体的摩尔比为0、0.05、0.1、0.5、1时,相应地,聚吡咯的负载量分别为21.19wt%、24.02wt%、27.47wt%、30.45wt%、31.92wt%,PPy/BF的电导率分别为0.125、
0.0878 、0.0278 、0.0106 、0.00785 Ω·cm。因此,在加入掺杂剂NaSSA之后,PPy/BF的电阻率有了很明显的下降,能达到8×10−3 Ω·cm,聚吡咯的负载量能达到32wt%。相比于未加入掺杂剂的PPy/BF(0),PPy/BF(1)的电阻率下降了94%,负载量提升了51%。氧化剂FeCl3和掺杂剂NaSSA会发生络合反应,Fe3+和SSA−上的羧基和羟基形成紫红色的络合物,隐藏了部分Fe3+,如图8所示。使吡咯单体不容易接近Fe3+,吡咯被氧化的速率得到了减缓,相当于得到了一种温和的氧化剂,防止吡咯被过氧化,控制聚吡咯共轭链缓慢有序地生长,形成有效连通的导电网络。另一方面,在聚合反应的过程中,由于Cl−和SSA−阴离子的存在,聚吡咯的分子链产生正电荷后,Cl−和SSA−阴离子在正电荷附近沉积,并形成掺杂态的聚吡咯,具有较高的导电性[33]。
2.3 纤维单丝拉伸性能
2.3.1 纤维单丝拉伸强度分析
图9和表4展示了玄武岩纤维在改性前后的拉伸性能。玄武岩纤维在改性前强度为
2203 MPa,改性之后玄武岩纤维强度为2657 MPa,相比于未改性前提升了20.6%,改性前后弹性模量几乎保持不变。分析单丝强度的提升原因在于:(1) 改性过程中没有使用到会对玄武岩纤维结构造成伤害的例如高温、酸碱腐蚀等技术方法,因此不会造成纤维结构的破坏和力学强度的下降;(2) 聚吡咯颗粒粒径较小,能够对玄武岩纤维制造过程所产生的表面缺陷和孔洞具有一定的填充和桥接作用,因此提升了玄武岩纤维的单丝拉伸强度。此外,复合材料的破坏很大一部分是由于纤维与基体的界面所引起的。从FESEM图中可以看出,经过聚吡咯改性后,玄武岩纤维表面的粗糙度明显增大,可能能够在一定程度上提升纤维与基体的粘结性能,从而进一步提升复合材料的力学性能。表 4 PPy改性前后玄武岩纤维单丝拉伸强度Table 4. Monofilament tensile strength of basalt fiber before and after PPy modificationSample Monofilament tensile strength/
MPaDispersion coefficient/% Elastic modulus/GPa Dispersion coefficient/% BF 2203 6.5 72.91 4.9 PPy/BF(1) 2657 7.1 74.85 5.2 2.3.2 纤维单丝拉伸强度差异性分析
利用统计学方法对单丝拉伸的试验结果进行检验,使用独立样本T检验得到PPy改性后玄武岩纤维拉伸强度的变化情况。首先,对BF和PPy/BF的拉伸强度进行正态性检验。若BF和PPy/BF的拉伸强度符合正态性分布,则对BF和PPy/BF的拉伸强度进行方差齐次性检验,若能通过方差齐次性检验,则可采用独立样本T检验来对比BF和PPy/BF的拉伸强度是否存在显著性差异,验证PPy改性是否保护了纤维结构和一定程度上提升了纤维的单丝拉伸强度。
BF和PPy/BF的正态性检验采用夏皮洛-威尔克(Shapiro-Wilk,S-W)检验方法,这是由于S-W检验方法适合于对小样本数据进行正态性检验,具体如下式所示:
w=(l∑i=1αixi)2n∑i=1(xi−¯x)2 (7) 式中:αi为权重系数;xi表示第i个排列后的数据;¯x为平均值。
根据α=0.05,查表可得w的临界值为w'= 0.927。如果w > w',则接受原假设,即纤维拉伸强度分布呈现正态分布,通过计算,得到BF和PPy/BF(1)的w统计量和P值,其结果如表5所示。从表中可以看出,BF和PPy/BF(1)的w值均大于临界值0.927,P值均大于0.05,水平不呈现显著性,接受原假设,因此符合正态性检验,满足独立同分布的条件。
表 5 BF和PPy/BF单丝拉伸强度Shapiro-Wilk检验Table 5. Shapiro-Wilk test of BF and PPy/BF monofilament tensile strengthSample w statistical indicator P value BF 0.943 0.213 PPy/BF(1) 0.969 0.672 在进行独立样本T检验之前,需要对BF和PPy/BF进行方差齐次性检验,这是使用独立样本T检验需满足的前提。方差齐次性检验采用F检验的方法,采用P值对结果进行表征,如果P值大于显著性水平0.05,则接受原假设,BF和PPy/BF的单丝拉伸强度满足方差齐次性。方差齐次性检验结果如表6所示,从表中可以看出,F统计量为2.63,P值大小为0.112,水平上呈现不显著,因此,BF和PPy/BF的单丝拉伸强度满足方差齐次性。
表 6 BF和PPy/BF单丝拉伸强度方差齐次性检验Table 6. F-test of BF and PPy/BF monofilament tensile strengthSample F statistical indicator P value BF and PPy/BF(1) 2.63 0.112 因此,基于BF和PPy/BF满足正态性检验和方差齐次性检验,采用独立样本T检验的方法来判断BF和PPy/BF的单丝拉伸强度是否存在显著性差异,结果如表7所示。从表中可以看出,独立样本T检验的P值为0.001,统计结果显著,拒绝原假设,说明BF和PPy/BF的单丝拉伸强度存在明显差异,这证明PPy能够在一定程度上提升玄武岩纤维的单丝拉伸强度。此外,采用Cohen's d效应值来反映差异性程度。Cohen's d效应值为0.2、0.5和0.8分别是显著性差异小、中、大的临界值。从表中可以看出,Cohen's d效应值为1.053,说明BF和PPy/BF(1)的单丝拉伸强度显著性差异明显。这不仅证明了独立样本T检验的结果,也证明了PPy在保护纤维强度、弥补纤维缺陷、提升纤维单丝拉伸强度上的作用。
表 7 BF和PPy/BF单丝拉伸强度独立样本T检验Table 7. Independent samples T-test of BF and PPy/BF monofilament tensile strengthSample T statistical indicator P value Cohen's d value BF and PPy/BF(1) −3.571 0.001 1.053 2.3.3 纤维单丝拉伸强度Weibull分布模型
纤维本身是一种脆性材料,纤维表面的缺陷会对纤维的单丝拉伸强度产生影响。因此,仅使用离散系数来反映离散性不够全面和客观。基于以上的实验结果和差异性分析,下面使用Weibull分布来对BF和PPy/BF的离散性进行分析。
Weibull分布以“最弱链”理论为基础[34-36],认为纤维束长度方向的缺陷是随机分布的,当其中最大的缺陷发生破坏时,整个结构发生失效。Weibull统计模型的密度函数f(σ,β,η)和累积分布函数F(σ,β,η)如公式(8)和公式(9)所示:
f(σ,β,η)=βηβσβ−1exp[−(ση)β] (8) F(σ,β,η)=1−exp[−(ση)β] (9) 式中:F(σ,β,η)表示在应力≤σ时的破坏概率;β为形状参数;η为位置参数。移项后,对两边取对数,得到下式:
lnln11−F=βlnσ−βlnη (10) 通过lnln11−F对lnσ作图后进行线性拟合,如果线性拟合效果好,即相关系数R2接近于1,则证明纤维拉伸强度数据符合Weibull分布,根据线性拟合方程y=wx+b的w和b来求解形状系数和位置系数。公式中F根据下式计算:
F=n1+N (11) 式中:N为纤维单丝总数;n为强度低于σ的纤维单丝的数量。
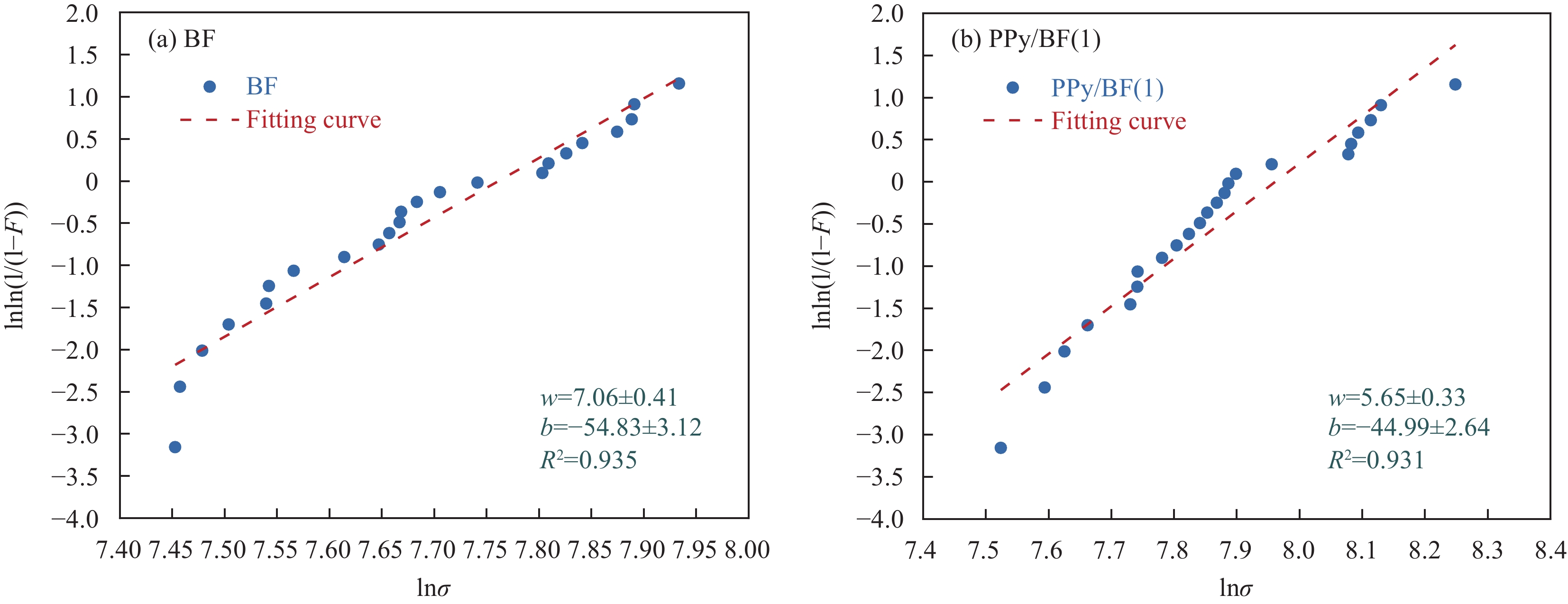
图10为基于公式(10)的BF和PPy/BF(1)单丝拉伸强度的Weibull分布双对数图,图中w、b和R2分别代表拟合直线的斜率,截距和决定系数。表8为Weibull分布线性拟合的相关系数、形状参数和位置参数。从图中可以看出,线性拟合的结果很好,相关系数R分别为0.967、0.965,均大于0.95,说明BF和PPy/BF(1)的纤维单丝拉伸强度分布均符合Weibull分布。
![]() 图 10 BF (a)和PPy/BF(1) (b)纤维单丝拉伸强度Weibull双对数图σ—Tensile strength of a single fiber; F—Failure probability when the stress is less than or equal to σ; w, b—Slope and intercept of the fitted line, respectively; R2—Coefficient of determinationFigure 10. Weibull double logarithmic plot of monofilament fiber tensile strength of BF (a) and PPy/BF(1) (b)
图 10 BF (a)和PPy/BF(1) (b)纤维单丝拉伸强度Weibull双对数图σ—Tensile strength of a single fiber; F—Failure probability when the stress is less than or equal to σ; w, b—Slope and intercept of the fitted line, respectively; R2—Coefficient of determinationFigure 10. Weibull double logarithmic plot of monofilament fiber tensile strength of BF (a) and PPy/BF(1) (b)根据“最弱链“理论,形状参数β与材料缺陷分布的均匀性有关,形状参数越大,意味着纤维的缺陷分布越均匀,纤维单丝拉伸强度的离散性越小。因此,从表8中可以看出,BF和PPy/BF(1)的形状系数分别为7.06和5.65,说明了PPy/BF(1)的离散性较大,这与表4的离散系数结果一致。PPy/BF(1)相比于BF的离散性较大可能是由于PPy在BF上是随机分布的。从离散系数和形状参数的结果来看,PPy/BF(1)相比于BF离散性虽然增大,但在可接受的范围内。位置参数η用来表示纤维强度的统计值大小。根据lnln(1/(1−F(σ,β,η))=0,求得η表示破坏概率为63.21%的纤维单丝拉伸强度。根据表8,BF和PPy/BF(1)的η分别为
2359.70 和2872.20 ,说明PPy/BF(1)的拉伸强度比BF高,这与表4的结果一致。表 8 Weibull分布线性拟合结果Table 8. Linear fitting results for the Weibull distributionSample Correlation
coefficient (R)Shape
parameter (β)Position
parameter (η)BF 0.967 7.06 2359.70 PPy/BF 0.965 5.65 2872.20 3. 结 论
本文开发了一种具有高导电性且同时保护纤维机械性能的低成本、高效、友好的导电玄武岩纤维制备方法。研究了吡咯单体和掺杂剂5-磺基水杨酸钠(NaSSA)浓度的不同对玄武岩纤维导电性的影响及改性前后玄武岩纤维单丝拉伸强度的变化,并通过FESEM、XPS、Raman光谱等方法探究了不同参数对聚吡咯/玄武岩纤维(PPy/BF)导电性能影响的机制,得出以下结论:
(1) 通过对比聚吡咯改性玄武岩纤维前后的FESEM,得到聚吡咯均匀稳定且厚实地附着在玄武岩纤维上,增大了玄武岩纤维表面的粗糙度。对比XPS全谱图和N1s分峰拟合图,PPy/BF(1)的 [N+]/[N]和(Cl+S)/N值均大于PPy/BF(0),说明PPy/BF(1)上的聚吡咯具有更高的掺杂水平。通过Raman光谱分析了PPy/BF上的化学结构,得出PPy/BF(1)上的聚吡咯具有比PPy/BF(0)更高的双极化子比例和共轭链长度;
(2) 吡咯单体浓度和掺杂剂NaSSA的浓度均对PPy/BF的导电性和PPy的负载量有很大的影响。随着浓度的增大,PPy的负载量不断增大,PPy/BF的电阻率均表现出先下降而后趋于稳定。特别地,掺杂剂NaSSA对于降低PPy/BF电阻率具有显著作用,相比于未加入掺杂剂的PPy/BF,其电阻率下降了94%,负载量提升了51%。所制备的导电玄武岩纤维(PPy/BF)电阻率可下降至8×10−3 Ω·cm,导电性能良好。这为玄武岩纤维及其复合材料作为优异结构材料的同时,发展成为具有电磁屏蔽、静电防护或自感知等功能的结构-功能一体化复合材料提供了可能;
(3) PPy/BF单丝拉伸强度比BF提升了20.6%。独立样本T检验结果证明PPy/BF(1) 提升玄武岩纤维单丝拉伸强度具有显著性和可靠性。并且,纤维单丝拉伸强度符合Weibull分布。这证明了本文采用的改性方法不破坏玄武岩纤维自身结构,保留了玄武岩纤维作为结构材料优异的机械性能。由于聚吡咯对于玄武岩制造过程表面产生的孔洞和缺陷具有填充和桥接作用,一定程度上提升了玄武岩纤维的单丝拉伸强度。
-
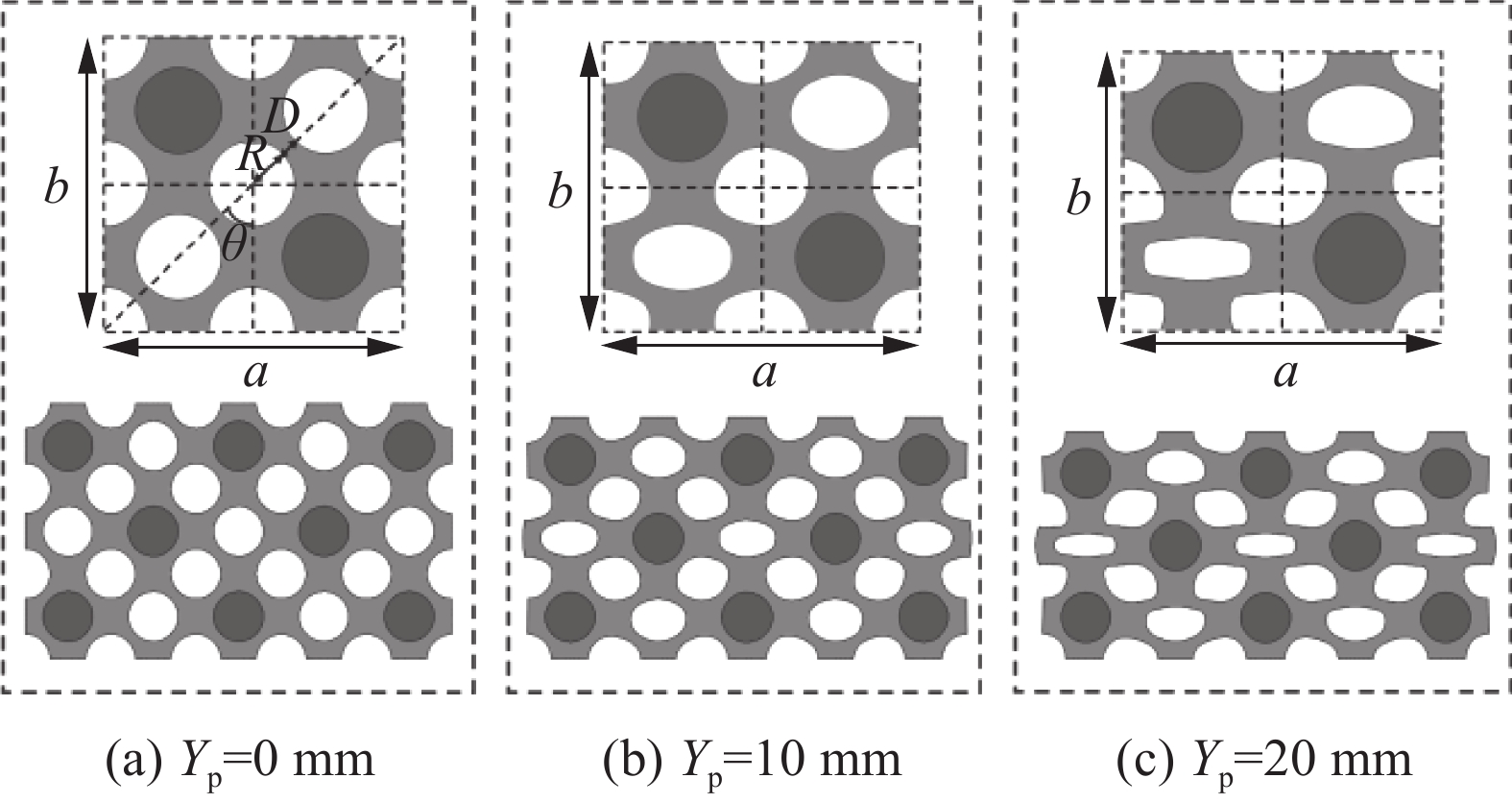
图 2 不同轴向压缩下二振子构型超结构元胞及试件示意图
Figure 2. Schematic diagram of the metastructure cells and specimens of two-oscillator configurations under different axial compressions
Yp—Axial compression of the structure; a, b—Lattice constant; R—Radius of the hole; θ—Angle of the diagonal of the cell; D—Distance between the holes
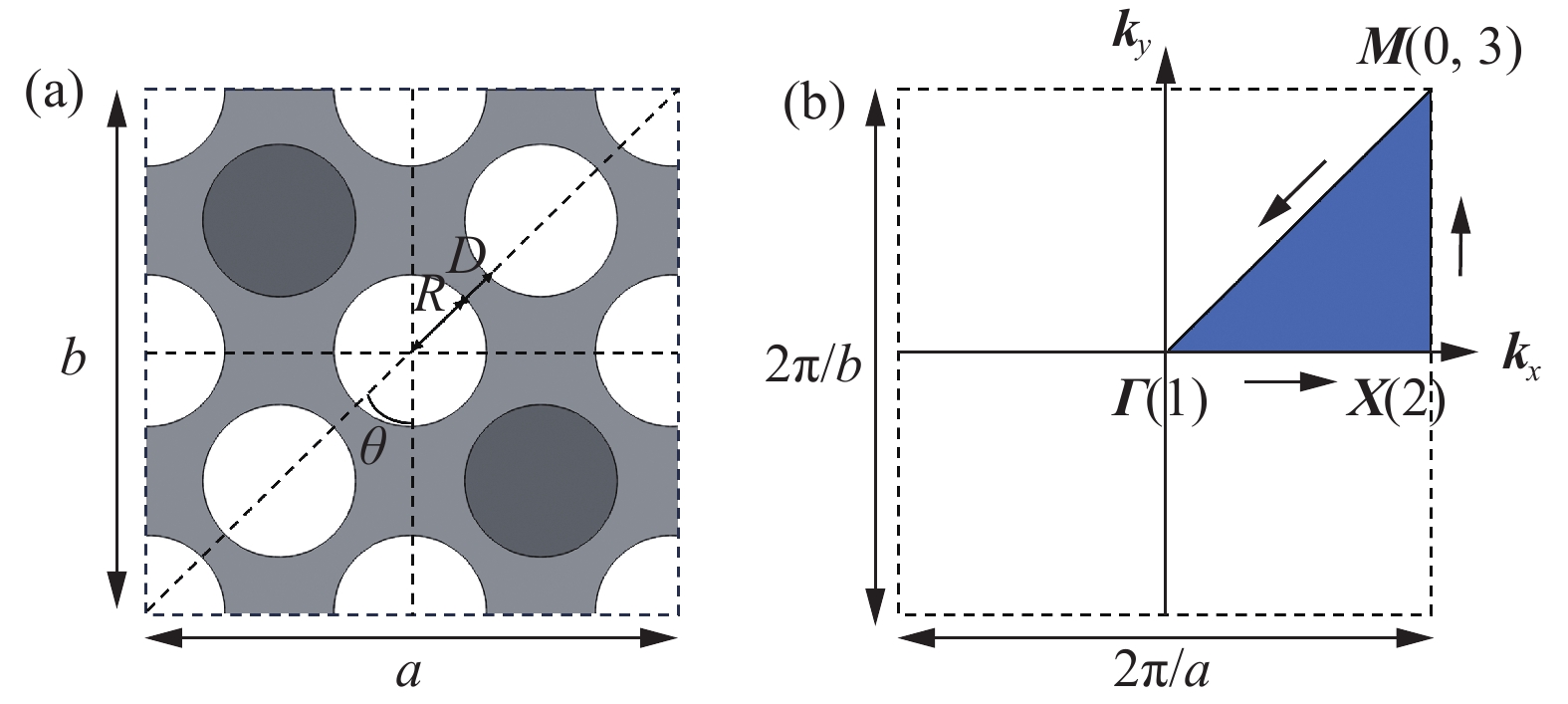
图 3 Yp=0mm时二振子构型超结构元胞(a)及其第一不可约布里渊区(阴影区域) (b)
M, Γ and X are the high symmetry points of the first irreducible Brillouin zone, respectively; kx and ky are the components of wave vector k in x and y directions, respectively
Figure 3. Two-oscillator configuration metastructure cell (a) and its first irreducible Brillouin zone (Shaded region) (b) in Yp=0mm
表 1 几何参数和材料参数
Table 1 Geometric parameters and material parameters
Geometric parameters Value Material Material parameters Value R/mm 17.5 Silicon rubber E/MPa 0.870 ρ/(kg·m−3) 1230 D/mm 7.426 ν 0.499 Lead E/MPa 40.8 θ/(°) 45 ρ/(kg·m−3) 11340 ν 0.37 Notes:E—Elastic modulus;ρ—Density;ν—Poisson's ratio. -
[1] 肖勇, 王洋, 赵宏刚, 等. 面向减振降噪应用的声学超构材料研究进展[J]. 机械工程学报, 2023, 59(19): 277-298. DOI: 10.3901/JME.2023.19.277 XIAO Yong, WANG Yang, ZHAO Honggang, et al. Research progress of acoustic metamaterials for vibration and noise reduction applications[J]. Journal of Mechanical Engineering, 2023, 59(19): 277-298(in Chinese). DOI: 10.3901/JME.2023.19.277
[2] 代洪庆. 基于声学超材料的声场调控及微粒操控研究[D]. 长沙: 湖南大学, 2022. DAI Hongqing. Research on sound field control and particle manipulation based on acoustic metamaterials [D]. Changsha: Hunan University, 2022(in Chinese).
[3] LIU Z Y, ZHANG X X, MAO Y W, et al. Locally resonant sonic materials[J]. Science, 2000, 289(5485): 1734-1736. DOI: 10.1126/science.289.5485.1734
[4] AMER Y A, EL-SAYED A T, AHMED E E. Vibration reduction of a non-linear ship model using positive position feedback controllers[J]. International Journal of Dynamics and Control, 2022, 10(2): 409-426. DOI: 10.1007/s40435-021-00801-8
[5] RUI J F, WANG L, LU P. Summary of research on supporting facilities and structure vibration and noise reduction of high-rise buildings[C]//IOP Conference Series: Earth and Environmental Science. Bristol: IOP Publishing, 2021, 791(1): 012023.
[6] DESAI R, GUHA A, SESHU P. Modelling and simulation of active and passive seat suspensions for vibration attenuation of vehicle occupants[J]. International Journal of Dynamics and Control, 2021, 9(4): 1423-1443.
[7] 郁殿龙. 基于声子晶体理论的梁板类周期结构振动带隙特性研究[D]. 长沙: 国防科学技术大学, 2007. YU Dianlong. Research on the vibration band gap characteristics of beam-plate periodic structures based on phononic crystal theory [D]. Changsha: National University of Defense Science and Technology, 2007(in Chinese).
[8] 王刚. 声子晶体局域共振带隙机理及减振特性研究[D]. 长沙: 国防科学技术大学, 2007. WANG Gang. Study on the local resonance band gap mechanism and vibration reduction characteristics of phononic crystals [D]. Changsha: University of Defense Science and Technology, 2007(in Chinese).
[9] LEE T, IIZUKA H. Bragg scattering based acoustic topological transition controlled by local resonance[J]. Physical Review B, 2019, 99(6): 064305. DOI: 10.1103/PhysRevB.99.064305
[10] ZHOU X, WANG L. Opening complete band gaps in two dimensional locally resonant phononic crystals[J]. Journal of Physics and Chemistry of Solids, 2018, 116: 174-179. DOI: 10.1016/j.jpcs.2018.01.025
[11] 肖鹏, 缪林昌, 郑海忠, 等. 一种新型二维三组元水泥基拟声子晶体复合材料的低频带隙特性与应用[J]. 复合材料学报, 2024, 41(10): 5607-5621. XIAO Peng, MIAO Linchang, ZHENG Haizhong, et al. Low-frequency band gap properties and applications of a new two-dimensional three-component cement-based phononic crystal composite [J]. Acta Materiae Compositae Sinica, 2024, 41(10): 5607-5621(in Chinese).
[12] GAO N, HOU H, WU J H, et al. Low frequency band gaps below 10 Hz in radial flexible elastic metamaterial plate[J]. Journal of Physics D: Applied Physics, 2016, 49(43): 435501. DOI: 10.1088/0022-3727/49/43/435501
[13] ZHOU X, XU Y, LIU Y, et al. Extending and lowering band gaps by multilayered locally resonant phononic crystals[J]. Applied Acoustics, 2018, 133: 97-106. DOI: 10.1016/j.apacoust.2017.12.012
[14] 张思文, 吴九汇. 局域共振复合单元声子晶体结构的低频带隙特性研究[J]. 物理学报, 2013, 62(13): 134302. DOI: 10.7498/aps.62.134302 ZHANG Siwen, WU Jiuhui. Low-frequency band gap characteristics of phononic crystal structure of locally resonant composite unit[J]. Physical Journal, 2013, 62(13): 134302(in Chinese). DOI: 10.7498/aps.62.134302
[15] LI X F, CHENG S L, YANG H Y, et al. Optimization of vibration characteristics and directional propagation of plane waves in branching ligament structures of wind models[J]. Results in Physics, 2023, 47: 106345. DOI: 10.1016/j.rinp.2023.106345
[16] COFFY E, LAVERGNE T, ADDOUCHE M, et al. Ultra-wide acoustic band gaps in pillar-based phononic crystal strips[J]. Journal of Applied Physics, 2015, 118(21): 214902. DOI: 10.1063/1.4936836
[17] 李孟昶, 郭少杰, 张红艳. 管道超结构轴向带隙特性分析及实验研究[J]. 人工晶体学报, 2023, 52(1): 65-72. DOI: 10.3969/j.issn.1000-985X.2023.01.009 LI Mengchang, GUO Shaojie, ZHANG Hongyan. Analysis and experimental study on axial band gap characteristics of pipe metastructure[J]. Journal of Artificial Crystallography, 2023, 52(1): 65-72(in Chinese). DOI: 10.3969/j.issn.1000-985X.2023.01.009
[18] 李潘玉, 游世辉, 李维, 等. 磁流变弹性体基拓扑声子晶体弹性波传输可调性研究[J]. 功能材料, 2021, 52(5): 5151-5158. DOI: 10.3969/j.issn.1001-9731.2021.05.023 LI Panyu, YOU Shihui, LI Wei, et al. Study on the tunability of elastic wave transmission in magnetorheological elastomer-based topological phononic crystals[J]. Functional Materials, 2021, 52(5): 5151-5158(in Chinese). DOI: 10.3969/j.issn.1001-9731.2021.05.023
[19] 王婷英, 柴怡君, 耿谦, 等. 力-压电混合弹性超材料梁的带隙调节特性[J]. 固体力学学报, 2022, 43(4): 406-418. WANG Tingying, CHAI Yijun, GENG Qian, et al. Band gap tuning properties of force-piezoelectric hybrid elastic metamaterial beams[J]. Journal of Solid Mechanics, 2022, 43(4): 406-418(in Chinese).
[20] WU Y, YU K P, YANG L Y, et al. Effect of thermal stresses on frequency band structures of elastic metamaterial plates[J]. Journal of Sound and Vibration, 2018, 413: 101-119. DOI: 10.1016/j.jsv.2017.10.014
[21] YAO Y W, WU F G, ZHANG X, et al. Thermal tuning of lamb wave band structure in a two-dimensional phononic crystal plate[J]. Journal of Applied Physics, 2011, 110(12): 123503. DOI: 10.1063/1.3669391
[22] GENG Q, CAI T, LI Y. Flexural wave manipulation and energy harvesting characteristics of a defect phononic crystal beam with thermal effects[J]. Journal of Applied Physics, 2019, 125(3): 035103. DOI: 10.1063/1.5063949
[23] DAI H, XIA B, YU D. Temperature-controlled tunable underwater acoustic topological insulators[J]. Journal of Applied Physics, 2019, 125(23): 235105. DOI: 10.1063/1.5090789
[24] LI X F, CHENG S L, YANG H Y, et al. Integrated analysis of bandgap optimization regulation and wave propagation mechanism of hexagonal multi-ligament derived structures[J]. European Journal of Mechanics-A/Solids, 2023, 99: 104952. DOI: 10.1016/j.euromechsol.2023.104952
[25] LI X F, CHENG S L, YANG H Y, et al. Bandgap tuning and in-plane wave propagation of chiral and anti-chiral hybrid metamaterials with assembled six oscillators[J]. Physica A: Statistical Mechanics and Its Applications, 2023, 615: 128600. DOI: 10.1016/j.physa.2023.128600
[26] BERTOLDI K, BOYCE M C. Wave propagation and instabilities in monolithic and periodically structured elastomeric materials undergoing large deformations[J]. Physical Review B, 2008, 78(18): 184107. DOI: 10.1103/PhysRevB.78.184107
[27] SHAN S, KANG S H, WANG P, et al. Harnessing multiple folding mechanisms in soft periodic structures for tunable control of elastic waves[J]. Advanced Functional Materials, 2014, 24(31): 4935-4942. DOI: 10.1002/adfm.201400665
[28] LI J, WANG Y S, CHEN W Q, et al. Harnessing inclusions to tune post-buckling deformation and bandgaps of soft porous periodic structures[J]. Journal of Sound and Vibration, 2019, 459: 114848. DOI: 10.1016/j.jsv.2019.114848
[29] GEI M. Wave propagation in quasiperiodic structures: Stop/pass band distribution and prestress effects[J]. International Journal of Solids and Structures, 2010, 47(22): 3067-3075.
[30] 黄屹澜. 软材料周期结构中波传播行为主动调控[D]. 杭州: 浙江大学, 2020. HUANG Yilan . Active control of wave propagation behavior in periodic structures of soft materials [D]. Hangzhou: Zhejiang University, 2020(in Chinese).
[31] HUANG Y, LI J, CHEN W Q, et al. Tunable bandgaps in soft phononic plates with spring-mass-like resonators[J]. International Journal of Mechanical Sciences, 2019, 151: 300-313. DOI: 10.1016/j.ijmecsci.2018.11.029
[32] HUANG Y, GAO N, CHEN W Q, et al. Extension/compression-controlled complete band gaps in 2D chiral square-lattice-like structures[J]. Acta Mechanica Solida Sinica, 2018, 31(1): 51-65.
[33] 付强, 姚飞, 张红艳. 局域共振夹芯超结构梁带隙特性及实验研究[J]. 人工晶体学报, 2024, 53(1): 65-72. DOI: 10.3969/j.issn.1000-985X.2024.01.007 FU Qiang, YAO Fei, ZHANG Hongyan. Band gap characteristics and experimental study of locally resonant sandwich metastructure beams[J]. Journal of Artificial Crystallography, 2024, 53(1): 65-72(in Chinese). DOI: 10.3969/j.issn.1000-985X.2024.01.007
-
目的
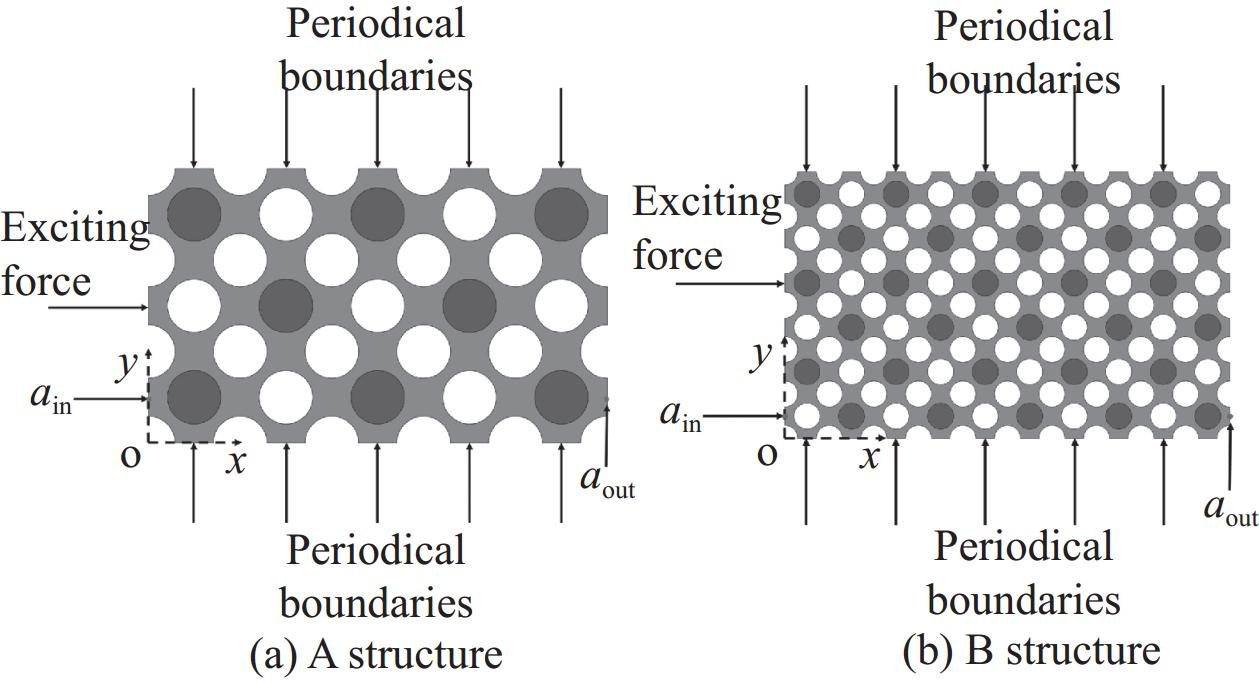
传统超结构设计方法无法实现参数连续控制,实际工程中结构随不同工况动态特性相应发生变化,可控超结构可根据目标需求调节结构的带隙特性,实现对不同工况下结构减振的可控调节。通过在超结构中引入外部激励(例如机械载荷、电场、磁场和温度场等外部条件)可以改变结构的能带结构从而达到实时调控带隙的目的。本文提出一种新型可控超结构构型,该结构由多孔软材料和局域共振振子组成,可同时产生局域共振和布拉格散射两种带隙,通过施加位移可实现对带隙的有效调控。该结构可以实现结构在不同工况下的带隙调控,在航空航天、轨道交通等领域有广阔的应用前景。
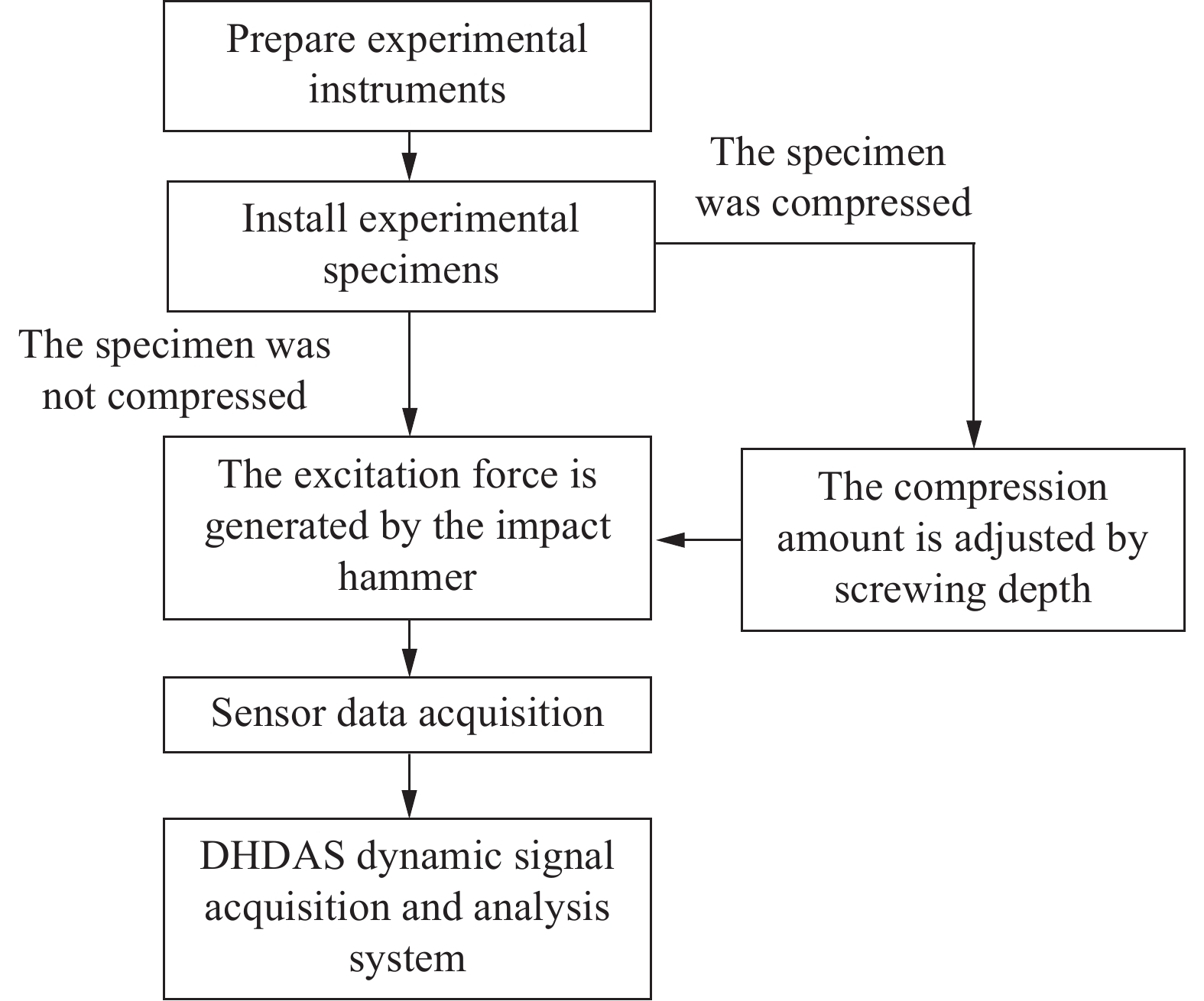
方法应用COMSOL软件建立了4种可控超结构的有限元模型,施加周期性边界条件。令波矢扫略第一不可约布里渊区的边界、、,计算得到结构的前50阶特征频率,进而可得到波矢与频率的色散曲线。研究了4种可控超结构构型的能带分布及其在外加位移激励作用下的带隙特性调控规律。制作了二振子元胞结构试件,搭建了有限周期结构的振动传输特性实验平台,使用力锤沿水平方向冲击产生激励,采集输入、输出端的加速度响应,得到该结构的振动传输特性曲线,并与数值结果进行对比验证。
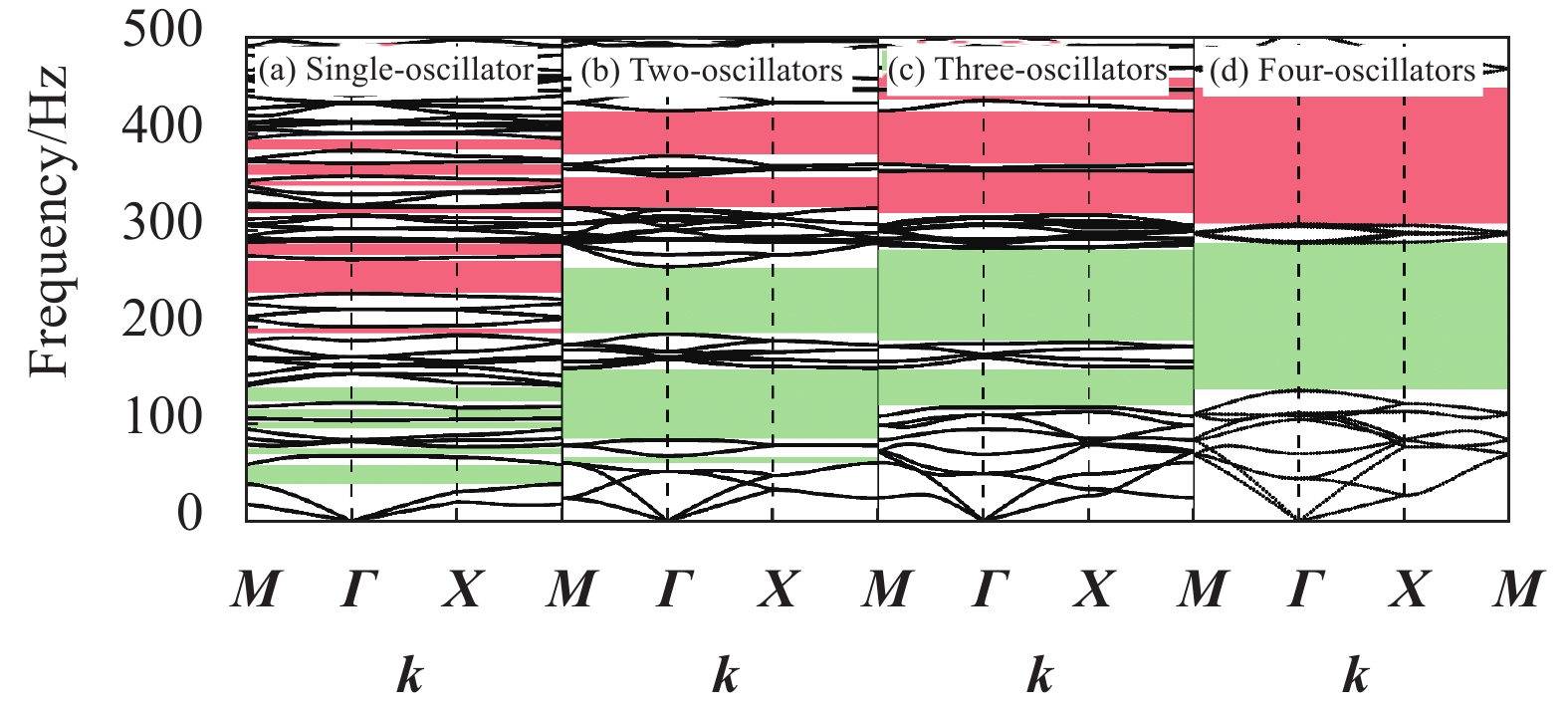
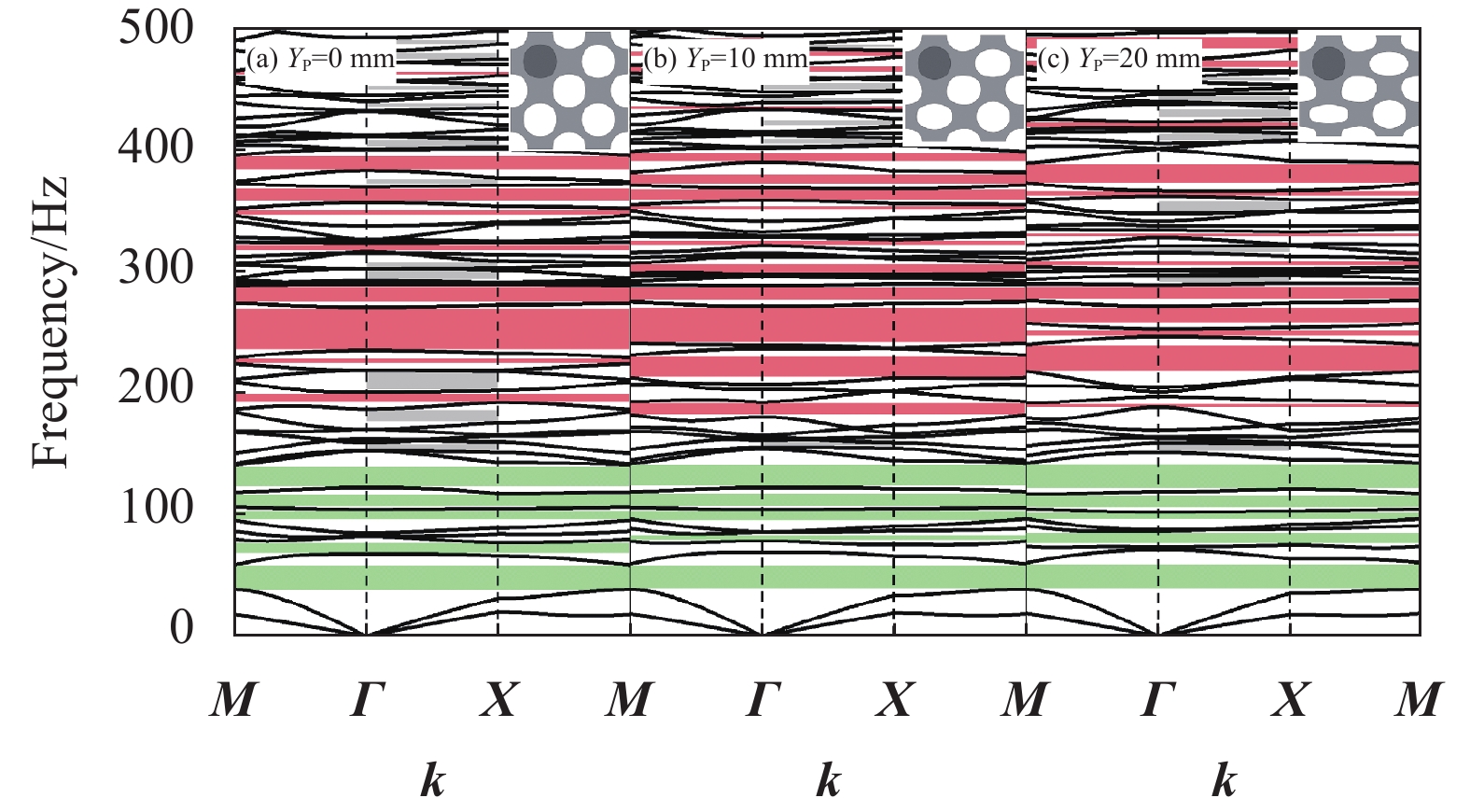
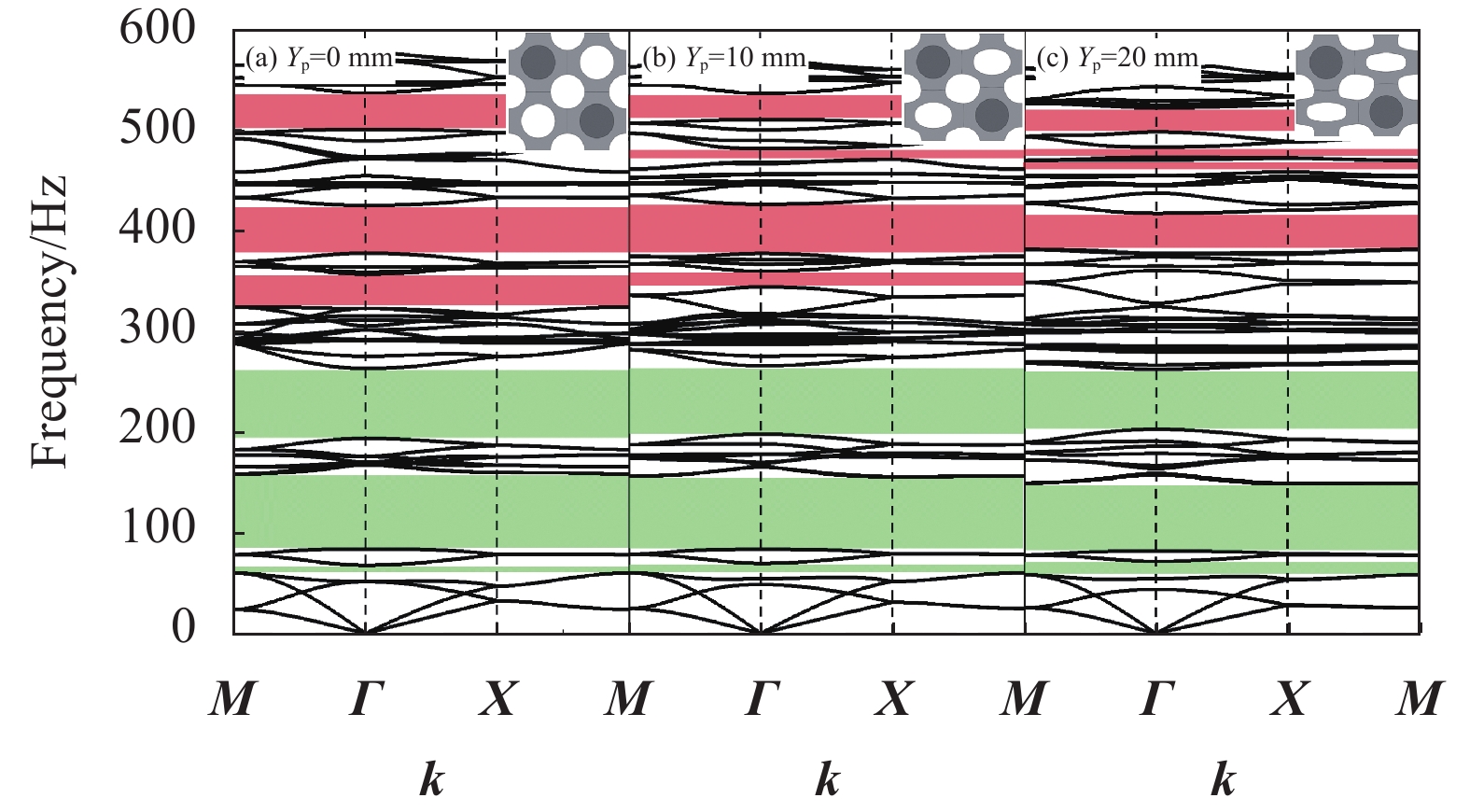
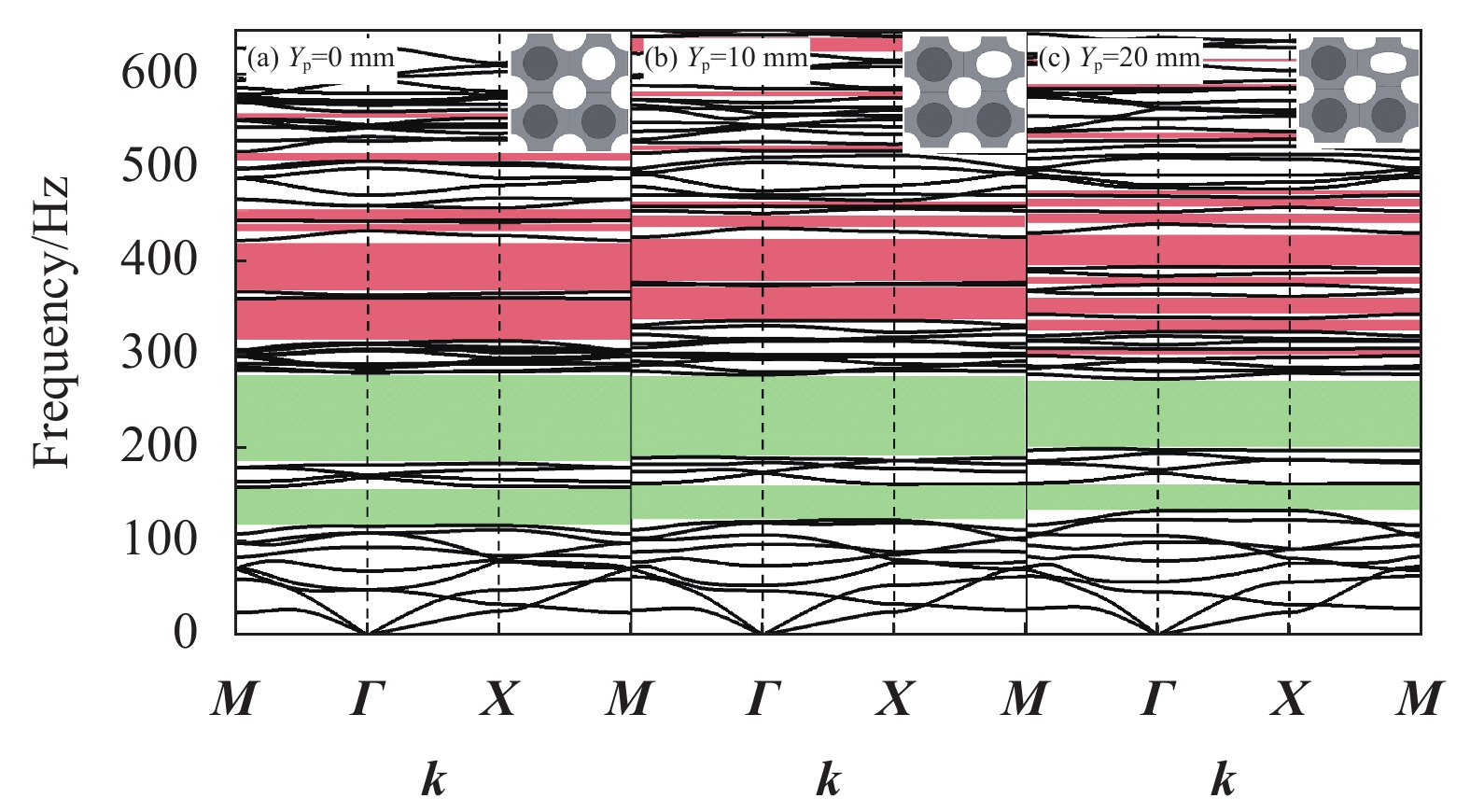
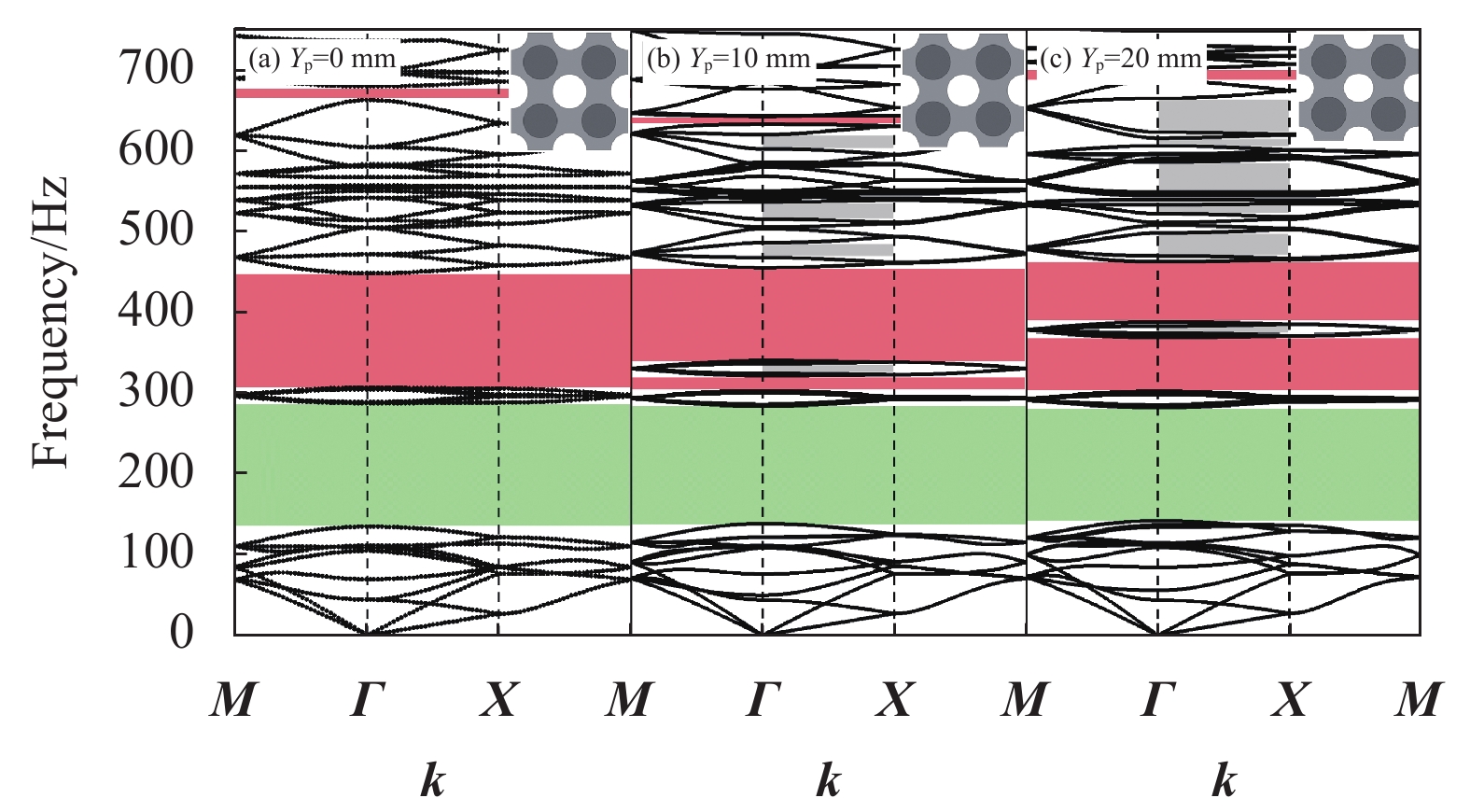
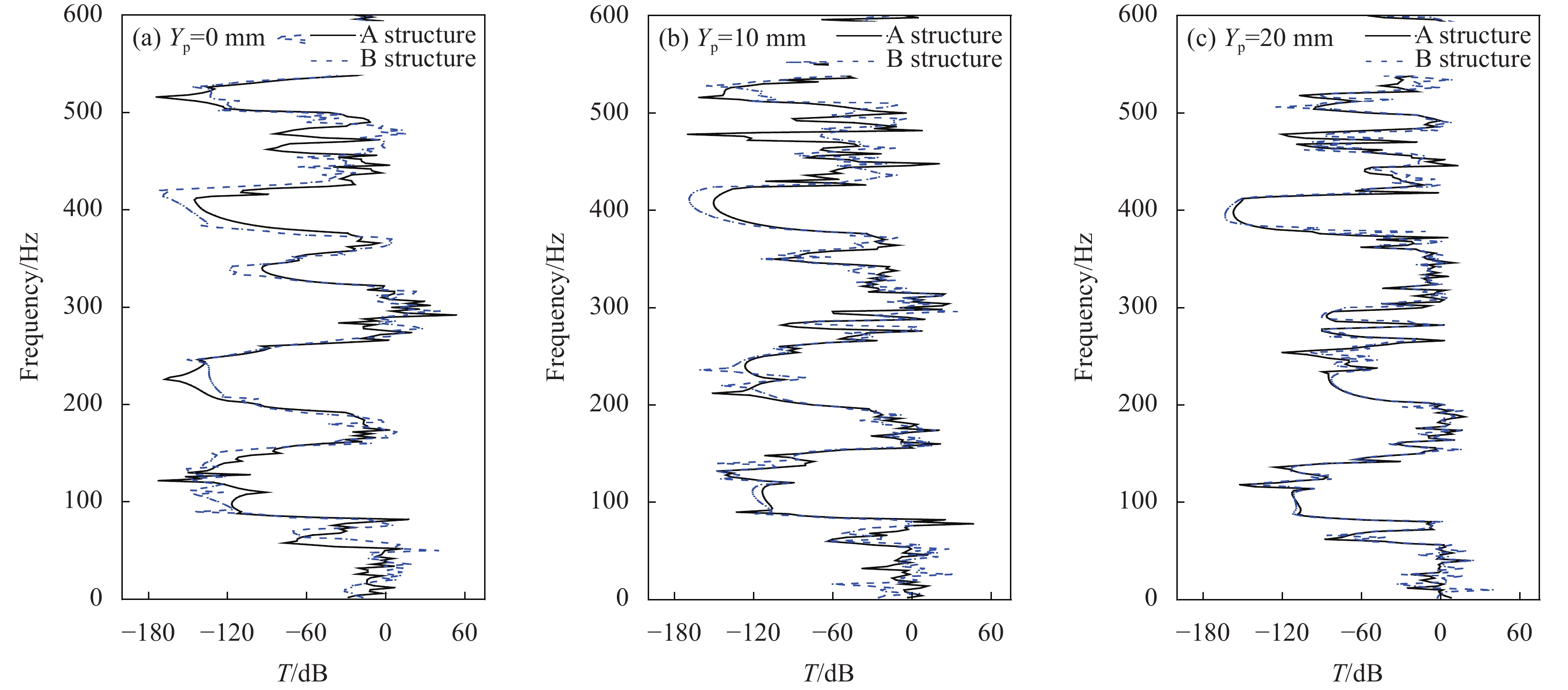
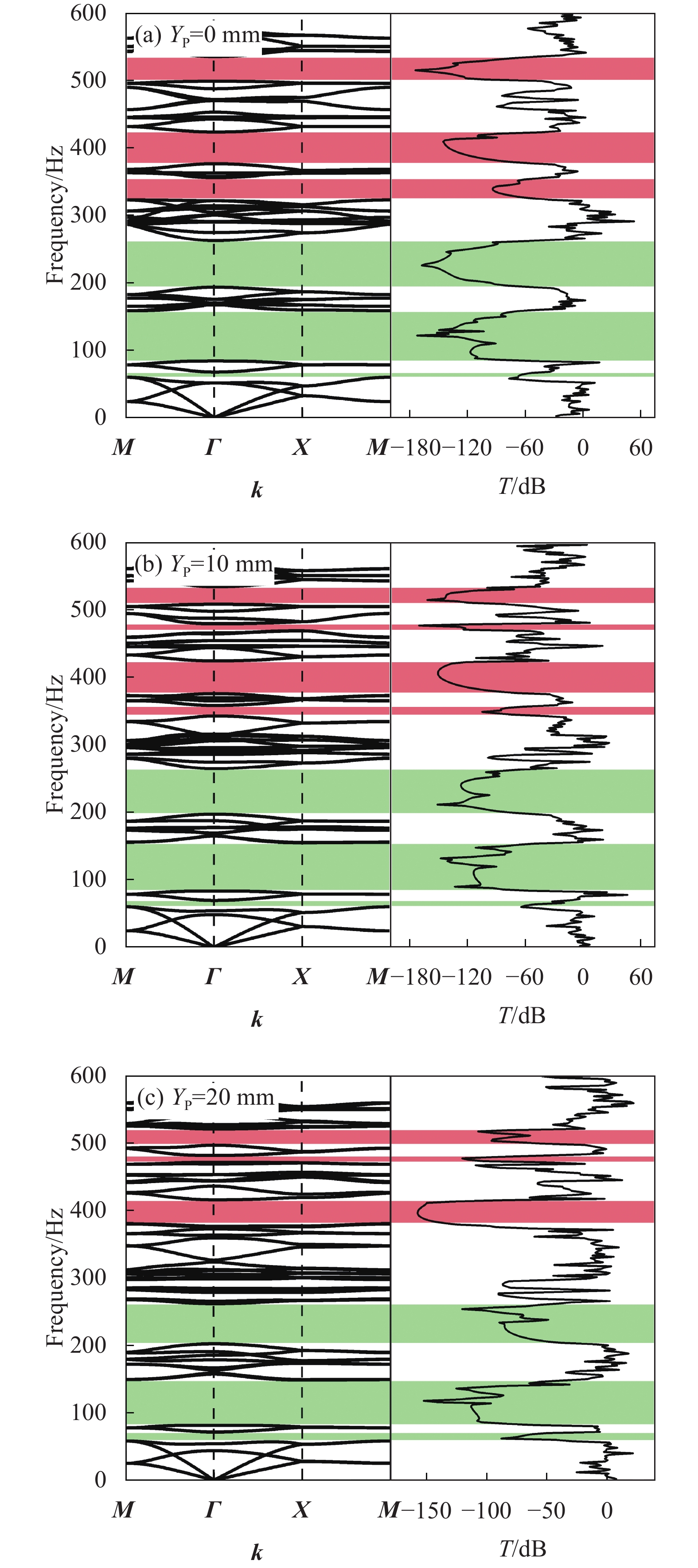
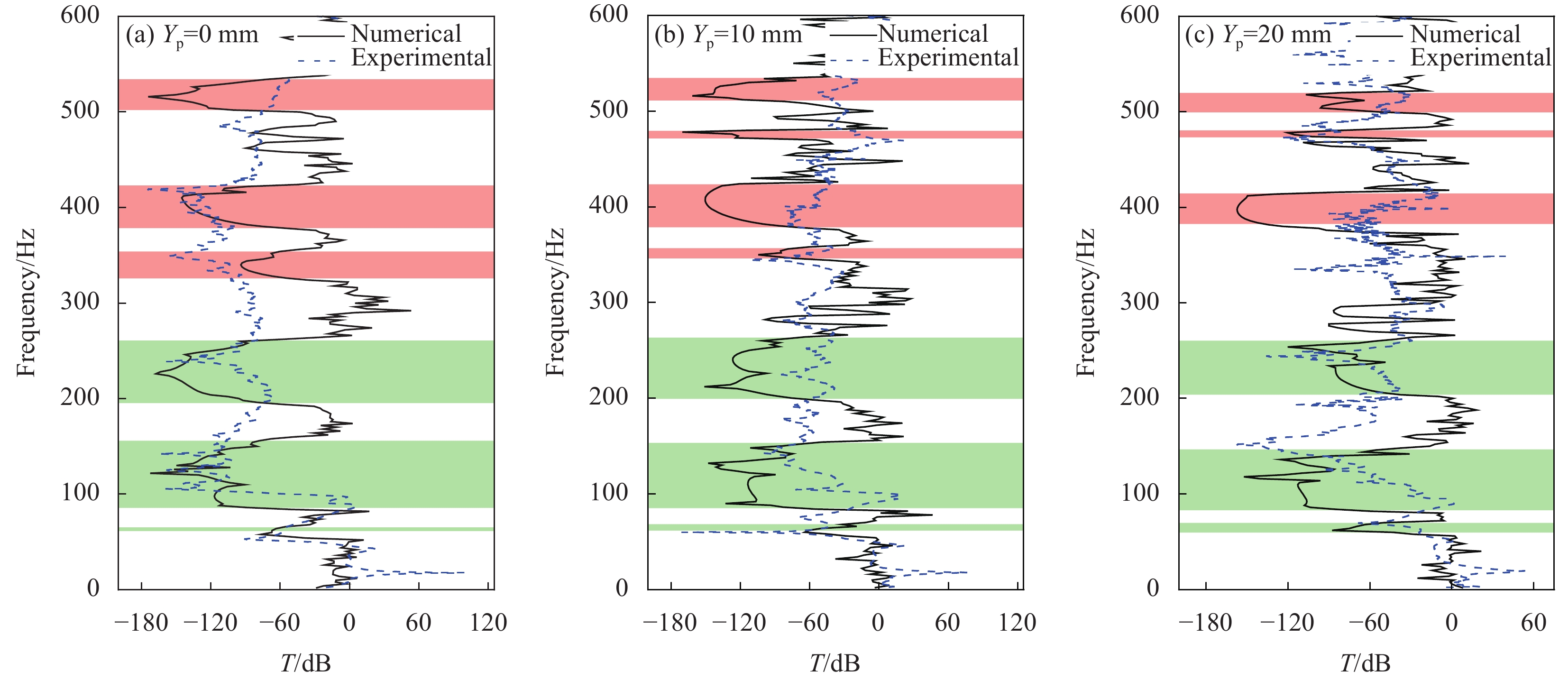
结果复合带隙可控超结构的4种构型均可产生局域共振型和布拉格散射型两种带隙。四振子构型在0~800Hz范围内共有3条完全带隙,第一阶带隙范围低至134.48~287.53Hz,第二阶带隙范围为307.26~447.81Hz,第三阶带隙范围为662.44~679.43Hz。对比分析4种构型的带隙特性,随着元胞中局域共振振子数量增加,300Hz内的低阶带隙宽度增加,结构中带隙数量逐渐减少,且振子数量的增加使结构刚度逐渐增大进而导致了带隙中心频率增加,带隙位置逐渐上移。轴向压缩对该结构带隙分布具有一定的调控作用,随着竖向位移量的增大,局域共振带隙变化较小,布拉格散射带隙中心频率逐渐向上移动,并在较高频率范围内出现了新的完全带隙和方向带隙,且轴向压缩对4种复合带隙可控超结构具有相同的带隙调控规律。计算了二振子复合带隙可控超结构传输特性,数值结果表明其在带隙范围内具有较好的减振效果,未压缩结构与轴向压缩结构的最大衰减均可达到150dB,且振动传输特性曲线实验结果与数值结果中衰减部分基本吻合,因此,弹性波在带隙频率范围内会出现明显的衰减。
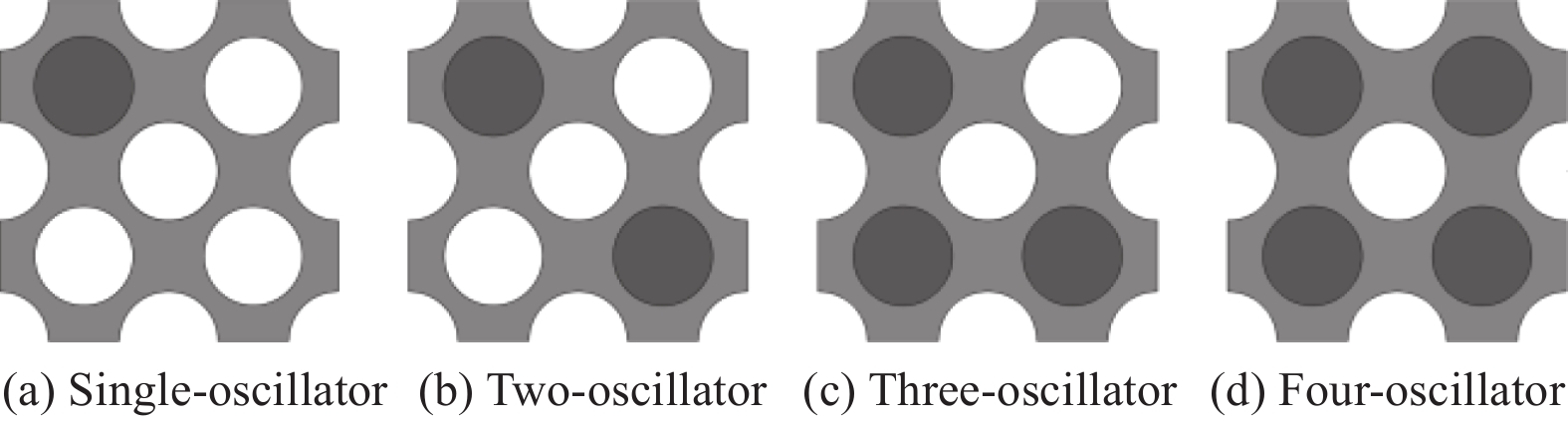
结论本文提出的复合带隙可控超结构,由多孔软材料及内部嵌入的局域共振振子构成,根据振子分布位置不同,分别有单振子、二振子、三振子及四振子四种构型。该结构均可同时产生低频的局域共振型带隙和较高频的布拉格散射型带隙。通过调节振子位置可以实现对低频局域共振带隙的调控,施加可控位移可调节较高频的布拉格散射带隙。该结构在带隙范围内具有良好的减振特性。复合带隙可控超结构可实现对复合带隙的调控,为超结构减振设计研究提供有益的参考,在航空航天、轨道交通等领域有广阔的应用前景。




 下载:
下载: