A novel approach to construct a thickness-independent bridging law for large scale bridging in type I delamination of composites
-
摘要: 大范围纤维桥接是复合材料分层扩展中的一种重要的增韧机制，通常用R曲线和桥接牵引-分离定律表征。然而R曲线和桥接牵引-分离定律都与结构厚度有关，需用不同厚度试件分别进行实验测量。近期的研究指出：桥接现象的厚度相关性实质上是由于不同厚度结构弯曲刚度不同所造成的；将裂纹张开的转角引入，构建的桥接牵引-分离转角关系与厚度无关。但是，现有的构造方法需要试件预埋光纤测量应变，试验过程复杂。本文通过弹性约束梁模型解析推导双悬臂梁预制裂纹尖端张开位移和转角，并结合J-积分法构建桥接牵引-分离转角关系，通过实验验证该关系是厚度无关的。进一步基于这种厚度无关的桥接律，提出了一种根据单一厚度试验数据逆推其他任意厚度R曲线与桥接牵引-分离定律的方法。通过不同厚度的碳纤维/环氧树脂、芳纶纤维/环氧树脂复合材料层合板双悬臂梁试验，证明逆推出来的R曲线和桥接牵引-分离关系曲线与用试验直接测量的曲线吻合很好。本文方法基于解析模型，仅需测量载荷-位移曲线即可，避免了裂纹长度的测量以及不同厚度的多次试验，简化了试验流程，为复合材料结构性能表征提供了有力工具。
-
关键词:
- 复合材料结构I型分层 /
- DCB试验 /
- 纤维桥接 /
- R曲线 /
- J-积分法
Abstract: Large-scale fiber bridging plays a crucial role in enhancing the toughness of composite structures during delamination, typically analyzed through the R-curve and the bridging traction-separation law. These metrics, however, are influenced by the specimen's thickness, necessitating separate experimental evaluations for each thickness variation. Recent research indicates that this thickness-dependency originates from the varying bending stiffness across structures of different thicknesses. By incorporating the crack opening angle, a thickness-independent traction-separation and angle relationship was developed. Existing methods for establishing this relationship require embedding optical fibers to gauge the internal strain, complicating the experimental procedure. This study introduced an elastic restraint beam model to get analytical solution of the double cantilever beam (DCB) test, based on which the pre-crack tip opening displacement and deflection angle were derived. These equations, combined with the J-integral method, formed a thickness-independent bridging traction-separation and angle relationship. Experimental validation confirmed the thickness-independence of the derived bridging law. Furthermore, an iterative method was proposed to inversely calculate the R-curves and bridging traction-separation laws for any thickness based on data from a single thickness DCB experiment. Experiments on carbon fiber/epoxy resin and aramid fiber/epoxy resin composite laminates of varying thicknesses demonstrated the accuracy of the inversely deduced curves compared to direct measurements. The present method is based on an analytical model and requires only the measurement of load-displacement curves, avoiding the need to measure crack length and conduct multiple experiments with different thicknesses. This simplifies the experimental process and provides a powerful tool for characterizing the performance of composite material structures.-
Key words:
- type I delamination of composite structures /
- DCB test /
- fiber bridging /
- R curve /
- J-integral method
-
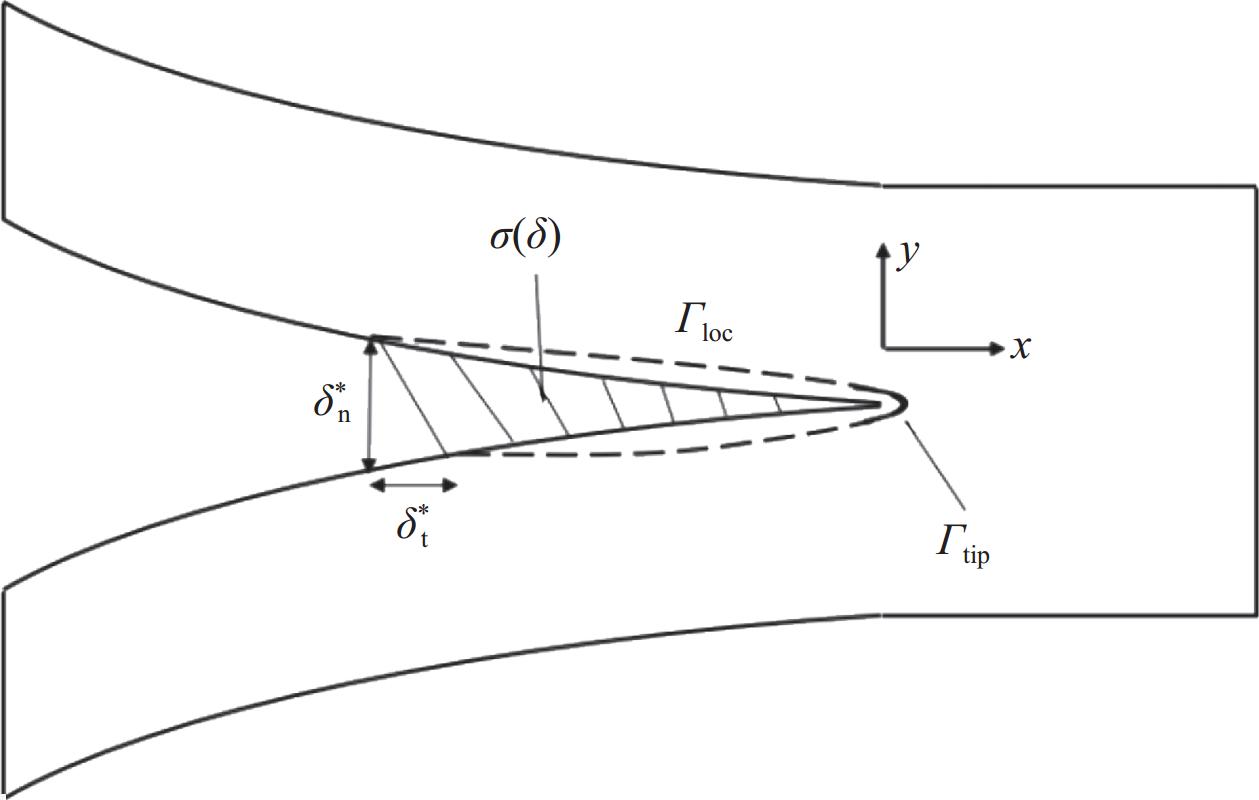
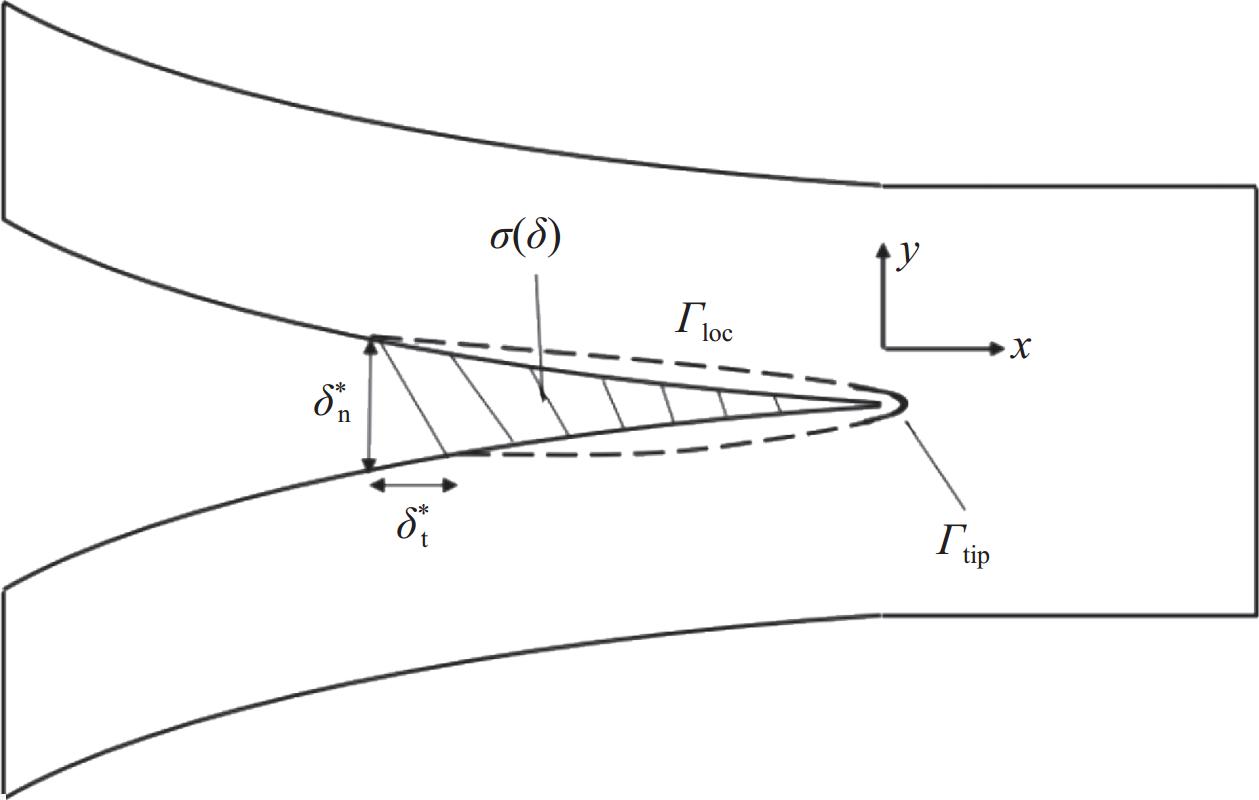
图 1 J-积分法的积分路径
Figure 1. Integral path of J-integral method
$ \delta _{\text{n}}^ * $—Opening displacement of pre-crack tip; $ \delta _{\text{t}}^ * $—Sliding displacement of pre-crack tip; $ {\varGamma _{{\text{loc}}}} $—Integral path locally round the bridging zone; $ {\varGamma _{{\text{tip}}}} $—Integral path of crack tip; $ \sigma \left( \delta \right) $—Relationship between bridging stress and crack opening displacement
图 2 双悬臂梁(DCB)试件的几何形状
Figure 2. Geometric shape of double cantilever beam (DCB) specimen
a0—Initial crack length; a—Crack length; b—Width of DCB specimen; 2h—Thickness of DCB specimen
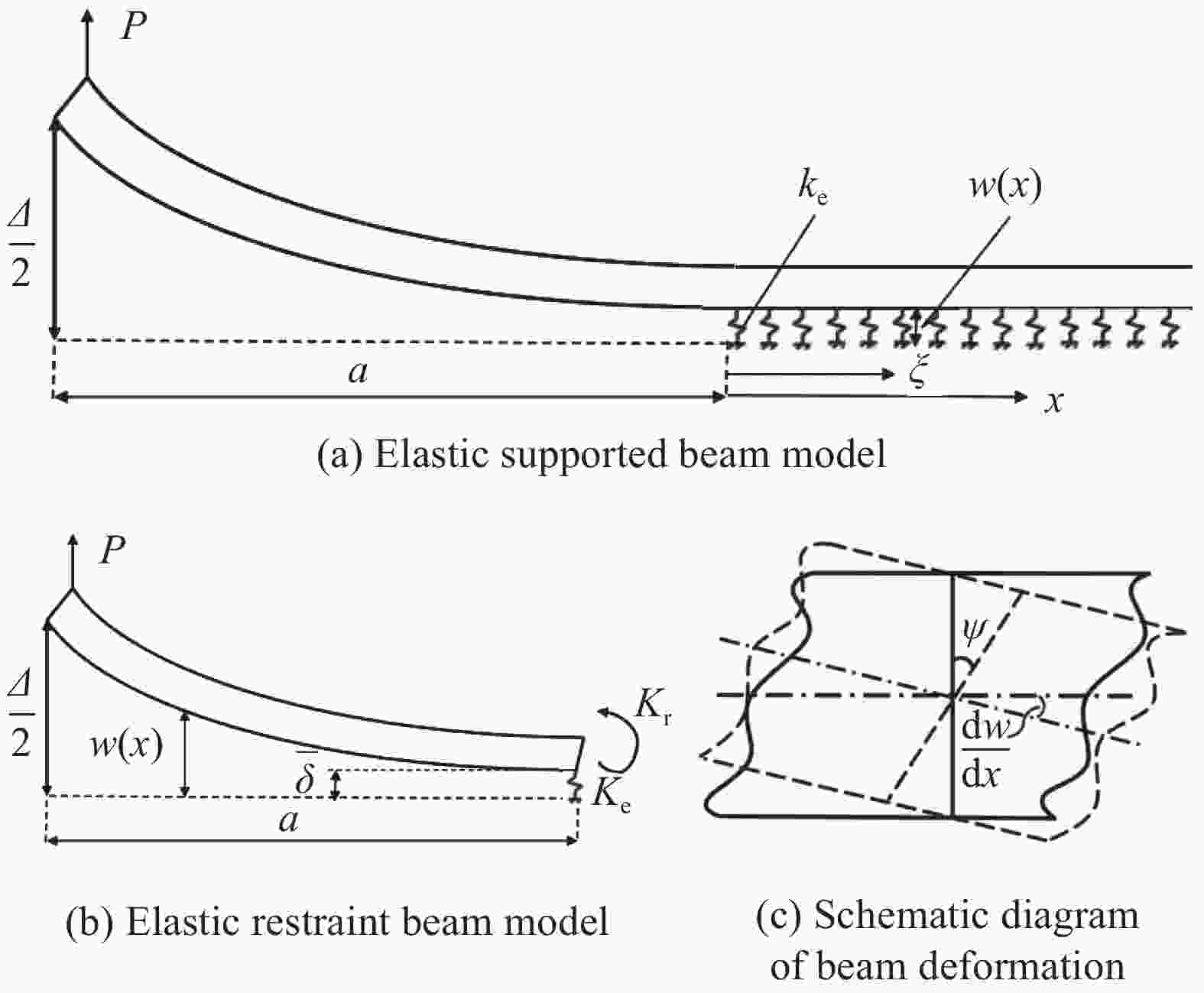
图 3 弹性梁模型及变形示意图
Figure 3. Elastic beam model and its deformation
$ P $—Load of loading point; $ \varDelta $—Displacement of loading point; $ {k_{\text{e}}} $—Spring restraint stiffness; $ a $—Crack length; $ w $—Beam deflection; $ \xi $—Opening displacement of crack tip in elastic supported beam model; $ \overline \delta $—Opening displacement of crack tip in elastic restraint beam model; $ {K_{\text{e}}} $—Spring stiffness; $ {K_{\text{r}}} $—Torsion spring stiffness; $ \psi $—Corner of beam section
图 4 (a)实际裂纹拓展；(b)等效裂纹拓展
Figure 4. (a) Actual crack growth; (b) Equivalent crack growth
Δa—Extended crack displacement
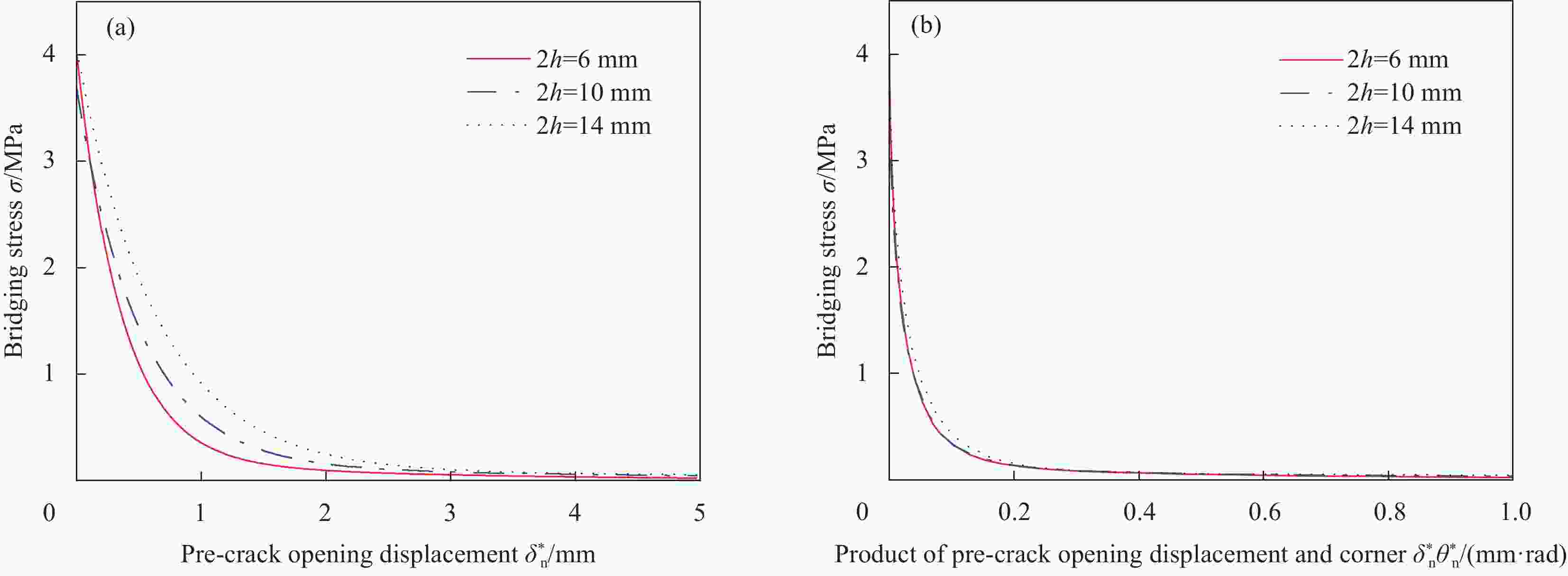
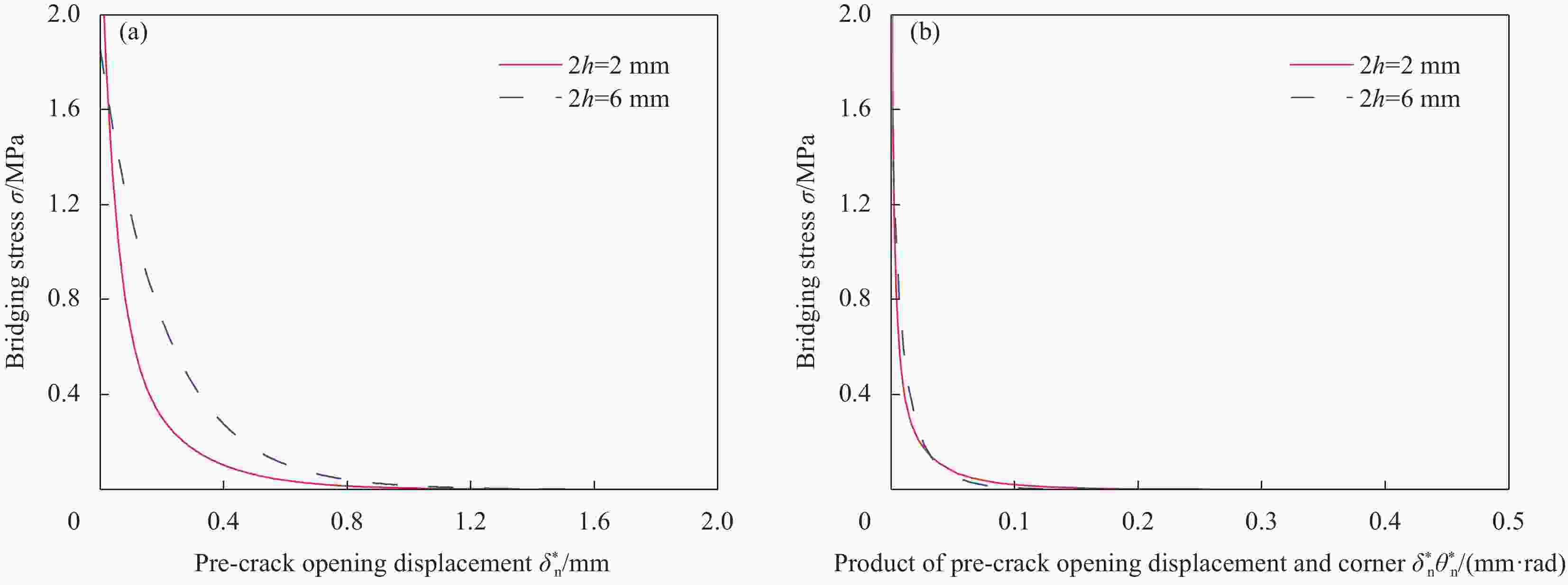
图 5 不同厚度(2h)碳/环氧树脂复合材料DCB试验的桥接律：(a) $ \sigma {\text{-}} \delta _{\text{n}}^ * $曲线；(b)$ \sigma {\text{-}} \delta _{\text{n}}^ * \theta _{\text{n}}^ * $曲线
Figure 5. Bridging law for DCB test of carbon/epoxy composites with different thicknesses (2h): (a) $ \sigma {\text{-}} \delta _{\text{n}}^ * $ curves; (b) $ \sigma{\text{-}} \delta _{\text{n}}^ * \theta _{\text{n}}^ * $ curves
$\theta _{\text{n}}^ * $—Pre-crack opening corner
图 6 $ \sigma {\text{-}}\delta _{\text{n}}^ * \theta _{\text{n}}^ * $曲线构建方法流程图
Figure 6. Flow chart of $ \sigma {\text{-}}\delta _{\text{n}}^ * \theta _{\text{n}}^ * $ curve construction
图 7 逆推法流程图
Figure 7. Flow chart of inverse method
The tilde over the symbol represents the iterative estimate value.
图 8 碳/环氧树脂复合材料DCB试验的GI与裂纹拓展长度的关系对比
Figure 8. Comparison of the relationship between GI and extended crack displacement of carbon/epoxy composites in DCB test
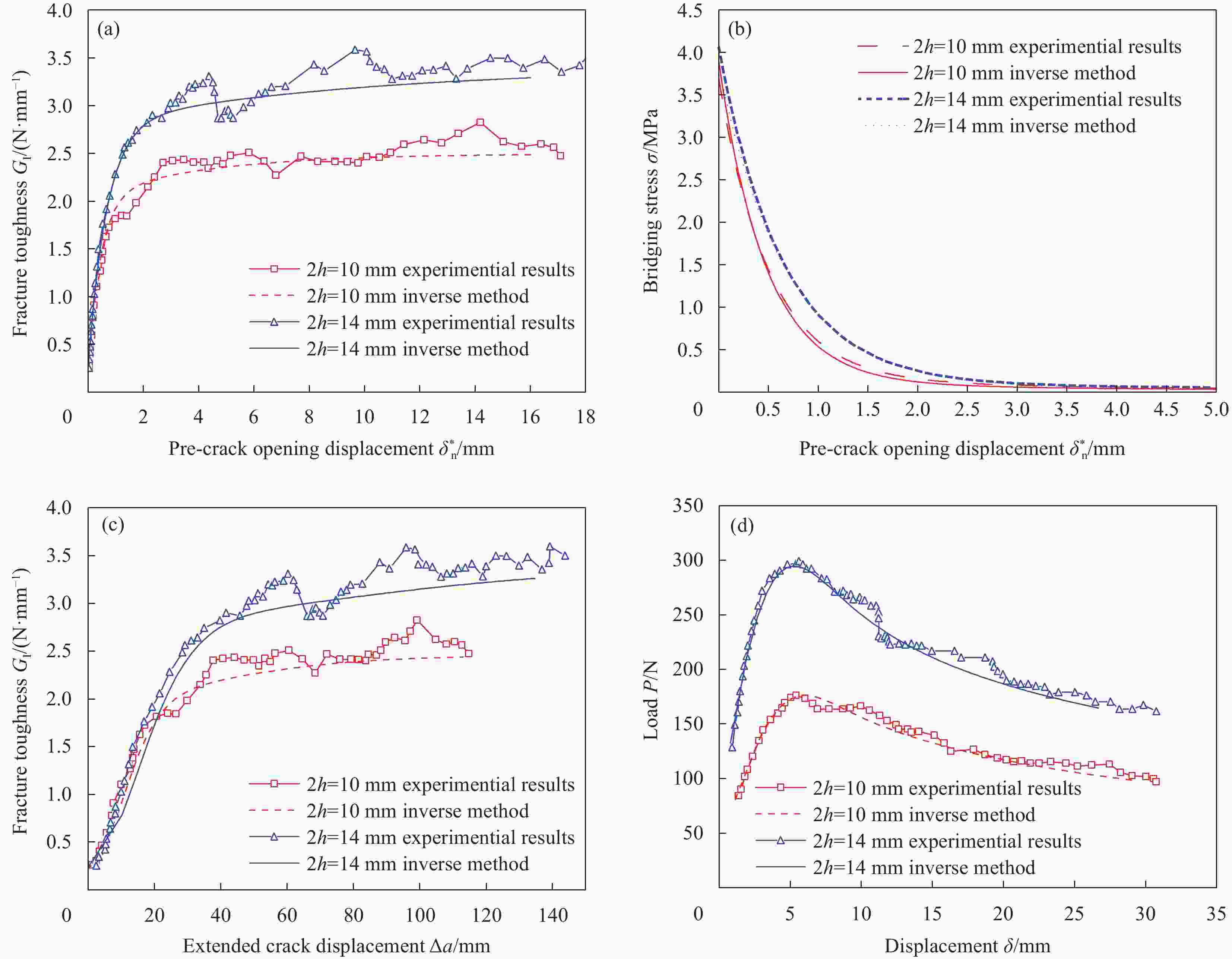
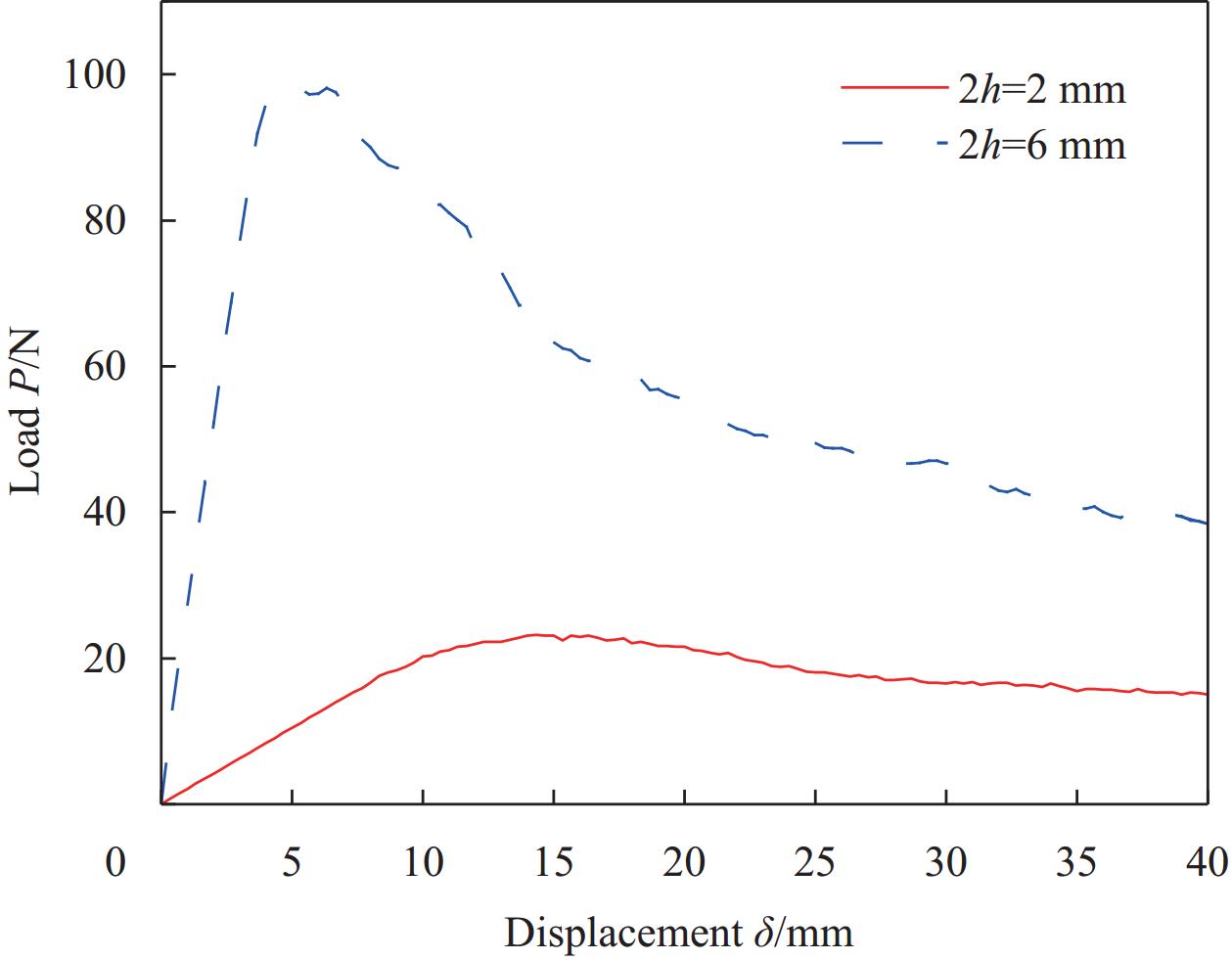
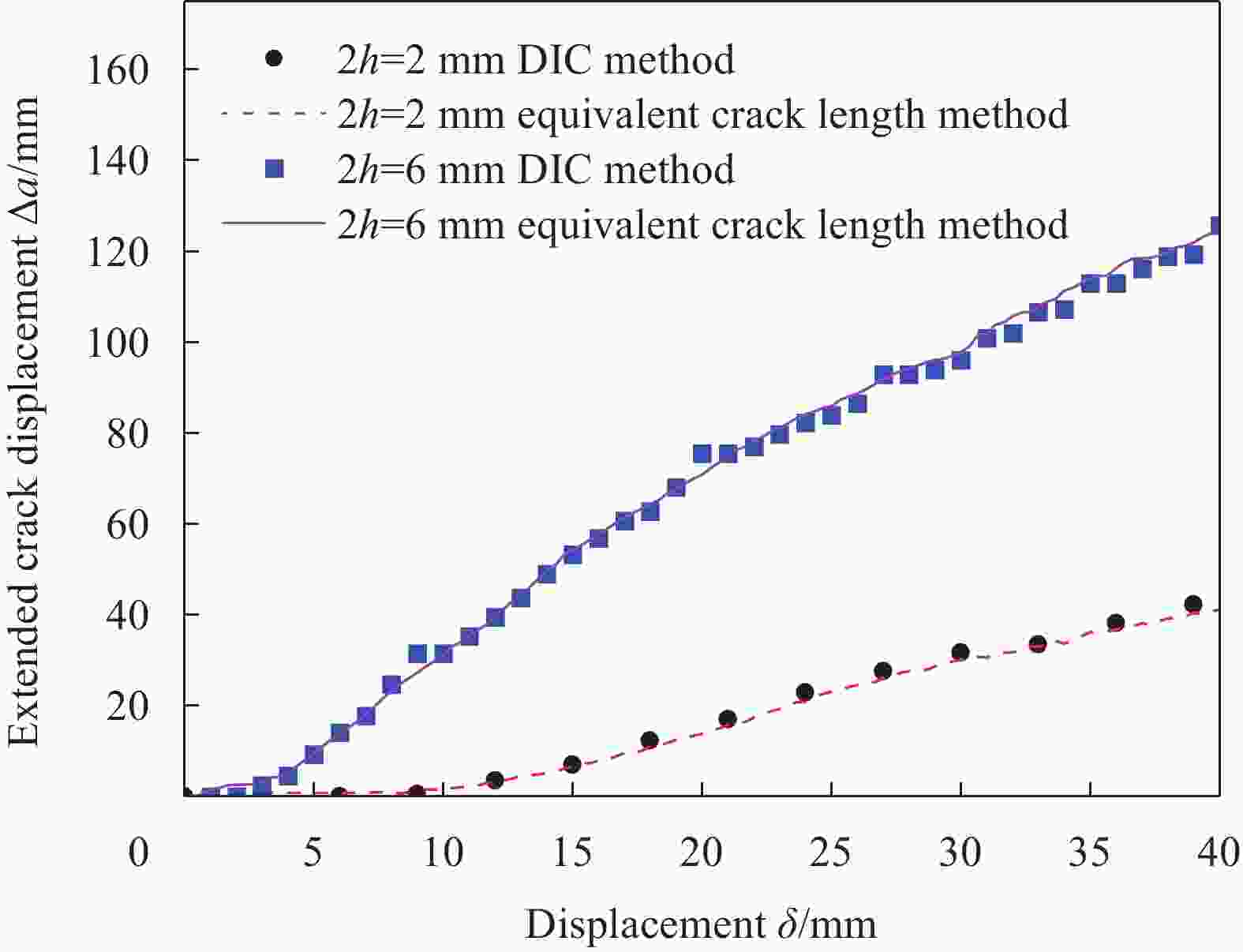
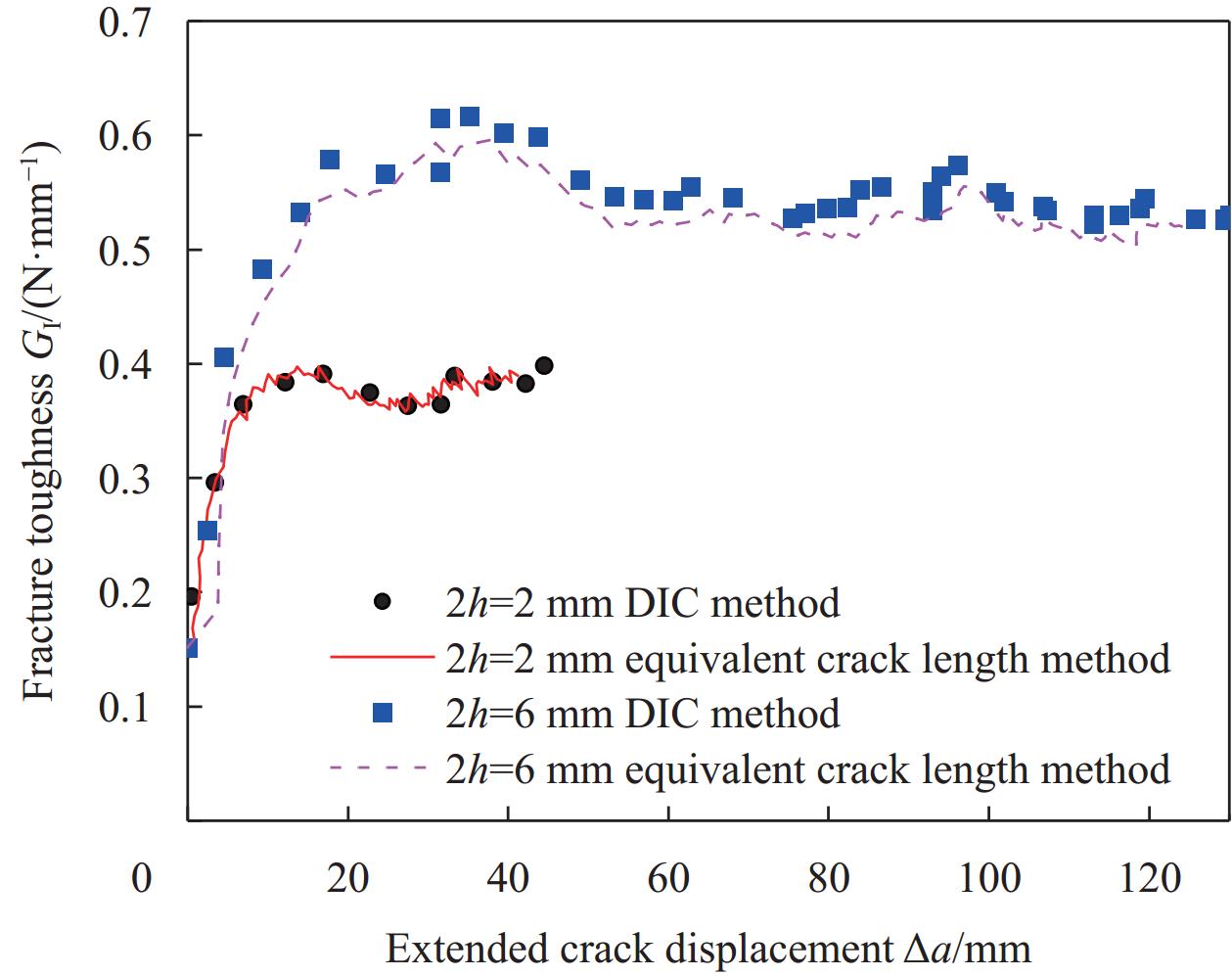
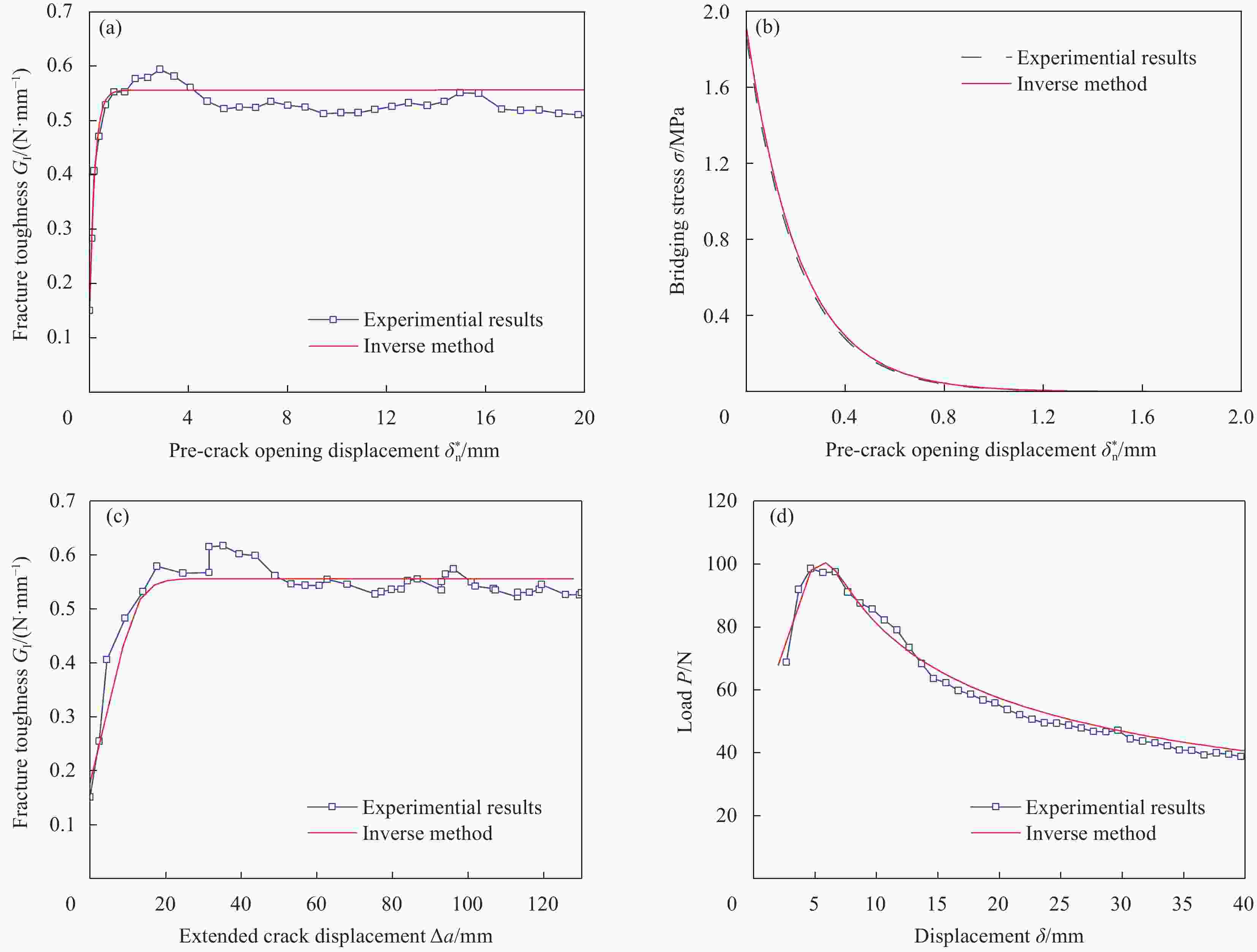
图 9 碳/环氧树脂复合材料逆推方法结果与试验结果对比图：(a) I型断裂韧性与预制裂纹尖端张开位移的关系；(b)桥接应力与预制裂纹张开位移的关系；(c) I型断裂韧性与裂纹拓展长度的关系；(d)载荷-位移曲线
Figure 9. Comparison between the results of the inverse method and the experimental results of carbon/epoxy composites: (a) Relationship between mode I fracture toughness and pre-crack opening displacement; (b) Relationship between bridging stress and pre-crack opening displacement; (c) Relationship between mode I fracture toughness and extended crack displacement; (d) Load-displacement curves
图 11 芳纶/环氧树脂复合材料DCB试验的载荷-位移曲线
Figure 11. Load-displacement curves of aramid/epoxy composites in DCB tests
图 12 芳纶/环氧树脂复合材料DCB试验的裂纹拓展长度-加载点位移曲线
Figure 12. Extended crack displacement-loading point displacement curves of aramid/epoxy composites in DCB test
DIC—Digital image correlation
图 13 芳纶/环氧树脂复合材料DCB试验的I型断裂韧性R曲线
Figure 13. R curves of mode I fracture toughness of aramid/epoxy composites in DCB test
图 14 不同厚度芳纶/环氧树脂复合材料DCB试验的桥接律：(a) $ \sigma {\text{-}} \delta _{\text{n}}^ * $曲线；(b) $ \sigma {\text{-}} \delta _{\text{n}}^ * \theta _{\text{n}}^ * $曲线
Figure 14. Bridging law for DCB test of aramid/epoxy composites with different thicknesses: (a) $ \sigma {\text{-}} \delta _{\text{n}}^ * $ curves; (b) $ \sigma {\text{-}} \delta _{\text{n}}^ * \theta _{\text{n}}^ * $ curves
图 15 芳纶/环氧树脂复合材料逆推法结果与试验结果对比图：(a) I型断裂韧性与预制裂纹尖端张开位移的关系；(b)桥接应力与预制裂纹张开位移的关系；(c) I型断裂韧性与裂纹拓展长度的关系；(d)载荷-位移曲线
Figure 15. Comparison between the results of the inverse method and the experimental results of aramid/epoxy composites: (a) Relationship between mode I fracture toughness and pre-crack opening displacement; (b) Relationship between bridging stress and pre-crack opening displacement; (c) Relationship between mode I fracture toughness and extended crack displacement; (d) Load-displacement curves
表 1 碳/环氧树脂复合材料DCB试验$ {G_{\text{I}}} {\text{-}}\delta _{\text{n}}^ * $曲线的拟合参数
Table 1. Fitting parameters for $ {G_{\text{I}}} {\text{-}} \delta _{\text{n}}^ * $ curves of carbon/epoxy composites in DCB test
Thickness/mm $ {B_1} $ $ {B_2} $ $ {B_3} $ $ {B_4} $ 6 0.4529 2.392 1.364 0.3562 10 0.6238 4.389 1.782 0.5032 14 0.8462 9.091 2.532 0.6392 Notes: GI—Mode I fracture toughness; $ {B_1} $-$ {B_4} $—Fitting parameters. 
下载: 导出CSV
表 2 碳/环氧树脂复合材料DCB试件的几何尺寸
Table 2. Geometric dimensions of carbon/epoxy composite DCB specimens
Test piece number Length/mm Width/mm Thickness/mm 01 340 10 6 02 340 10 10 03 340 10 14
下载: 导出CSV
表 3 芳纶/环氧树脂复合材料参数
Table 3. Aramid/epoxy composite material parameters
$ {E_{\text{f}}} $/$ {\text{GPa}} $ $ {E_{22}} $/$ {\text{MPa}} $ $ {G_{12}} $/$ {\text{MPa}} $ 70.01 6042 5102 Notes：$ {E_{\text{f}}} $—Flexural modulu in direction 1; $ {E_{22}} $—Elastic modulu in direction 2; $ {G_{12}} $—Shear modulu in direction 12.
下载: 导出CSV
表 4 芳纶/环氧树脂复合材料DCB试验$ {G_{\text{I}}} {\text{-}} \delta _{\text{n}}^ * $曲线的拟合参数
Table 4. Fitting parameters for $ {G_{\text{I}}} {\text{-}} \delta _{\text{n}}^ * $ curves of aramid/epoxy composites in DCB test
Thickness/mm $ {B_1} $ $ {B_2} $ $ {B_3} $ $ {B_4} $ 2 0.1501 0.2002 0.07974 0.0483 6 1.3230 0.1978 − 0.9344 0.1933
下载: 导出CSV
-
[1] TAY T E. Characterization and analysis of delamination fracture in composites: An overview of developments from 1990 to 2001[J]. Applied Mechanics Reviews, 2003, 56(1): 1-32. doi: 10.1115/1.1504848 [2] PEREIRA A B, DE MORAIS A B, DE MOURA M, et al. Mode I interlaminar fracture of woven glass/epoxy multidirectional laminates[J]. Composites Part A: Applied Science and Manufacturing, 2005, 36(8): 1119-1127. doi: 10.1016/j.compositesa.2005.01.006 [3] GONG Y, ZHANG B, ZHAO L, et al. R-curve behaviour of the mixed-mode I/II delamination in carbon/epoxy laminates with unidirectional and multidirectional interfaces[J]. Composite Structures, 2019, 223: 110949. doi: 10.1016/j.compstruct.2019.110949 [4] FOOTE R, MAI Y W, COTTERELL B. Crack growth resistance curves in strain-softening materials[J]. Journal of the Mechanics & Physics of Solids, 1986, 34(6): 593-607. [5] DÁVILA C G, ROSE C A, CAMANHO P P. A procedure for superposing linear cohesive laws to represent multiple damage mechanisms in the fracture of composites[J]. International Journal of Fracture, 2009, 158(2): 211-223. doi: 10.1007/s10704-009-9366-z [6] HEIDARI-RARANI M, SHOKRIEH M M, CAMANHO P P. Finite element modeling of mode I delamination growth in laminated DCB specimens with R-curve effects[J]. Composites Part B: Engineering, 2013, 45(1): 897-903. doi: 10.1016/j.compositesb.2012.09.051 [7] HOJO M, AOKI T. Thickness effect of double cantilever beam specimen on interlaminar fracture toughness of AS4/PEEK and T800/epoxy laminates[M]//STINCHCOMB W, ASHBAUGH N. Composite Materials: Fatigue and Fracture. West Conshohocken: ASTM International, 1993: 281–298. [8] TAMUZS V, TARASOVS S, VILKS U. Progressive delamination and fiber bridging modeling in double cantilever beam composite specimens[J]. Engineering Fracture Mechanics, 2001, 68(5): 513-525. doi: 10.1016/S0013-7944(00)00131-4 [9] MANSHADI B D, VASSILOPOULOS A P, BOTSIS J. A combined experimental/numerical study of the scaling effects on mode I delamination of GFRP[J]. Composites Science & Technology, 2013, 83: 32-39. [10] FARMAND-ASHTIANI E, CUGNONI J, BOTSIS J. Specimen thickness dependence of large scale fiber bridging in mode I interlaminar fracture of carbon epoxy composite[J]. International Journal of Solids & Structures, 2015, 55: 58-65. [11] PAPPAS G A, BOTSIS J. Variations on R-curves and traction-separation relations in DCB specimens loaded under end opening forces or pure moments[J]. International Journal of Solids & Structures, 2020, 191: 42-55. [12] PAPPAS G A, BOTSIS J. Towards a geometry independent traction-separation and angle relation due to large scale bridging in DCB configuration[J]. Composites Science and Technology, 2020, 197: 108172. doi: 10.1016/j.compscitech.2020.108172 [13] PAPPAS G, CANAL L P, BOTSIS J. Characterization of intralaminar mode I fracture of AS4/PPS composite using inverse identification and micromechanics[J]. Composites Part A: Applied Science and Manufacturing, 2016, 91: 117-126. doi: 10.1016/j.compositesa.2016.09.018 [14] CANAL L P, ALFANO M, BOTSIS J. A multi-scale based cohesive zone model for the analysis of thickness scaling effect in fiber bridging[J]. Composites Science and Technology, 2017, 139: 90-98. doi: 10.1016/j.compscitech.2016.11.027 [15] DE MORAIS A B. A new fibre bridging based analysis of the double cantilever beam (DCB) test[J]. Composites Part A: Applied Science and Manufacturing, 2011, 42(10): 1361-1368. doi: 10.1016/j.compositesa.2011.05.019 [16] FROSSARD G, CUGNONI J, GMÜR T, et al. Mode I interlaminar fracture of carbon epoxy laminates: Effects of ply thickness[J]. Composites Part A: Applied Science and Manufacturing, 2016, 91: 1-8. doi: 10.1016/j.compositesa.2016.09.009 [17] SAKAI M, MIYAJIMA T, INAGAKI M. Fracture toughness and fiber bridging of carbon fiber reinforced carbon composites[J]. Composites Science & Technology, 1991, 40(3): 231-250. [18] 杨露, 校金友, 文立华, 等. PBO纤维增强环氧树脂复合材料层间I型断裂韧性的DIC技术测量[J]. 复合材料学报, 2023, 40(1): 72-82.YANG Lu, XIAO Jinyou, WEN Lihua, et al. Mode I interlaminar fracture toughness measurement of PBO fiber reinforced epoxy composites with DIC technology[J]. Acta Materiae Compositae Sinica, 2023, 40(1): 72-82 (in Chinese). [19] ARRESE A, BOYANO A, DE GRACIA J, et al. A novel procedure to determine the cohesive law in DCB tests[J]. Composites Science and Technology, 2017, 152: 76-84. doi: 10.1016/j.compscitech.2017.09.012 [20] DE GRACIA J, BOYANO A, ARRESE A, et al. A new approach for determining the R-curve in DCB tests without optical measurements[J]. Engineering Fracture Mechanics, 2015, 135: 274-285. doi: 10.1016/j.engfracmech.2015.01.016 [21] LIU W, CHEN P. Determination of the bridging law for mode I delamination via elastic restraint beam model and equivalent crack method[J]. Engineering Fracture Mechanics, 2020, 226: 106867. doi: 10.1016/j.engfracmech.2020.106867 [22] GONG Y, CHEN X, LI W, et al. Delamination in carbon fiber epoxy DCB laminates with different stacking sequences: R-curve behavior and bridging traction-separation relation[J]. Composite Structures, 2021, 262: 113605. doi: 10.1016/j.compstruct.2021.113605 [23] YE J, GONG Y, TAO J, et al. Efficiently determining the R-curve and bridging traction-separation relation of mode I delamination in a simple way[J]. Composite Structures, 2022, 288: 115388. doi: 10.1016/j.compstruct.2022.115388 [24] RICE J R. A path independent integral and the approximate analysis of strain concentration by notches and cracks[J]. Journal of Applied Mechanics, 1968, 35(2): 379-386. doi: 10.1115/1.3601206 [25] LIU W, CHEN P. A novel method for the determination of the interface strength with coarse meshes for laminated composite materials[J]. Engineering Fracture Mechanics, 2021, 242: 107469. doi: 10.1016/j.engfracmech.2020.107469 [26] KANNINEN M F. An augmented double cantilever beam model for studying crack propagation and arrest[J]. International Journal of Fracture, 1973, 9: 83-92. doi: 10.1007/BF00035958 [27] WILLIAMS J G. End corrections for orthotropic DCB specimens[J]. Composites Science & Technology, 1989, 35(4): 367-376. [28] MURTHY M V V. An improved transverse shear deformation theory for laminated anisotropic plates[R]. Virginia: NASA, 1981. [29] DANIEL I M, ISHAI O. Engineering mechanics of composite materials[M]. New York: Oxford University Press, 2006: 142–178. [30] JOKI R K, GRYTTEN F, HAYMAN B, et al. Determination of a cohesive law for delamination modelling—Accounting for variation in crack opening and stress state across the test specimen width[J]. Composites Science and Technology, 2016, 128: 49-57. doi: 10.1016/j.compscitech.2016.01.026 [31] PAPPAS G, BOTSIS J. Intralaminar fracture of unidirectional carbon/epoxy composite: Experimental results and numerical analysis[J]. International Journal of Solids & Structures, 2016, 85: 114-124. [32] ASTM. Standard test method for mode I interlaminar fracture toughness of unidirectional fiber-reinforced polymer matrix composites: ASTM D5528—01[S]. West Conshohocken: ASTM International, 2001. [33] SUN F, BLACKMAN B R K. Using digital image correlation to automate the measurement of crack length and fracture energy in the mode I testing of structural adhesive joints[J]. Engineering Fracture Mechanics, 2021, 255: 107957. doi: 10.1016/j.engfracmech.2021.107957 [34] DE MOURA M, DE MORAIS A B. Equivalent crack based analyses of ENF and ELS tests[J]. Engineering Fracture Mechanics, 2008, 75(9): 2584-2596. doi: 10.1016/j.engfracmech.2007.03.005 -
下载:
点击查看大图
计量
- 文章访问数: 168
- HTML全文浏览量: 95
- PDF下载量: 11
- 被引次数: 0
