Design and performance validation of a zero-stiffness vibroisolating metamaterialbased on machine learning
-
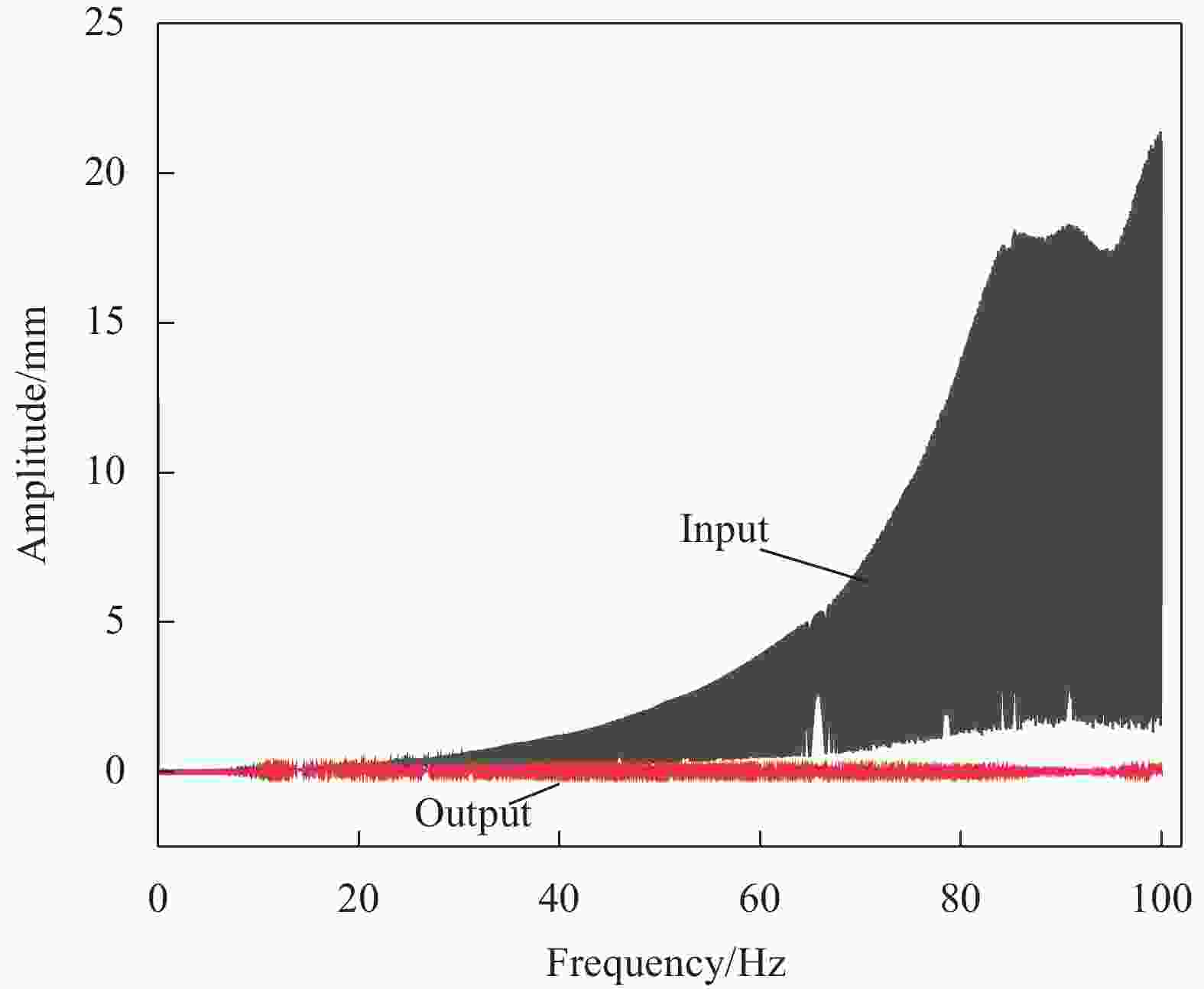
摘要: 准零刚度隔振器作为国内外主流的非线性隔振器,凭借其高静态刚度和低动态刚度力学特性,在机械工程领域应用较多,但近零刚度范围窄、后期组装繁琐等问题限制了其隔振的应用范围,通过结构设计使近零刚度范围增大,且能通过一体化成型技术快速制备方面的研究仍较稀缺。本文基于能量屏蔽理论设计了一种新型零刚度单元结构,通过将外界输入能量循环于超材料内部,从而屏蔽外界对隔振对象的能量输入,达到隔振效果。该研究首先设计出具有优化潜力的初始结构,然后使用机器学习与有限元分析结合的方法对初始结构进行优化,自动搜索出最优的超材料结构参数,且最优结构满足零刚度性能设计要求,之后使用3D打印对最优结构单元及2×2阵列结构进行一体化制造。并对样件进行静态实验验证,实验结果表明:在静态压缩过程中,该结构的等效刚度在大范围内近似于0。又对阵列结构进行动态振动实验,结果得出,阵列结构在23 mm振幅下0.1~100 Hz范围内,9.2 kg载荷隔振性能最优,最小传递率可达−61 dB,载荷越接近9.2 kg隔振性能越好。该结构具有结构简单、一体化成型等优势,可应用于列车座椅、康复医疗设备、精密仪器保护及微重力环境等领域下的隔振。Abstract: The quasi-zero stiffness isolator, as a mainstream nonlinear isolator both domestically and internationally, was widely applied in the field of mechanical engineering due to its high static stiffness and low dynamic stiffness mechanical characteristics. However, limitations such as a narrow range of quasi-zero stiffness, complicated post-assembly procedures, etc., had restricted its application scope in vibration isolation. Through structural design, the range of quasi-zero stiffness could be expanded, and research on rapid preparation through integrated molding technology was still relatively scarce. In that study, a novel zero stiffness unit structure was designed based on the theory of energy shielding. By circulating external input energy within the metamaterial, the energy input from the external environment to the isolated object was shielded, thus achieving the isolation effect. The research first designed an initial structure with optimization potential, then used a combination of machine learning and finite element analysis to optimize the initial structure, automatically searching for the optimal parameters of the metamaterial structure. The optimal structure met the requirements of zero stiffness performance design. Subsequently, 3D printing was employed to manufacture the optimal structural unit and a 2×2 array structure in an integrated manner. Static experiments were conducted on the samples for validation. The experimental results show that the equivalent stiffness of this structure approximates zero over a wide range during static compression. Dynamic vibration experiments were also conducted on the array structure. The results reveal that within the range of 0.1 Hz to 100 Hz and under a 23 mm amplitude, the array structure exhibites its best isolation performance with a 9.2 kg load, achieving a minimum transmissibility of up to −61 dB. The closer the load is to 9.2 kg, the better the isolation performance. This structure offers advantages such as simplicity in design, integrated molding, etc., and can be applied in vibration isolation for fields such as train seats, rehabilitation medical equipment, protection of precision instruments, and microgravity environments.
-
Key words:
- metamaterial /
- machine learning /
- zero-stiffness /
- vibration isolation /
- 3D printing
-
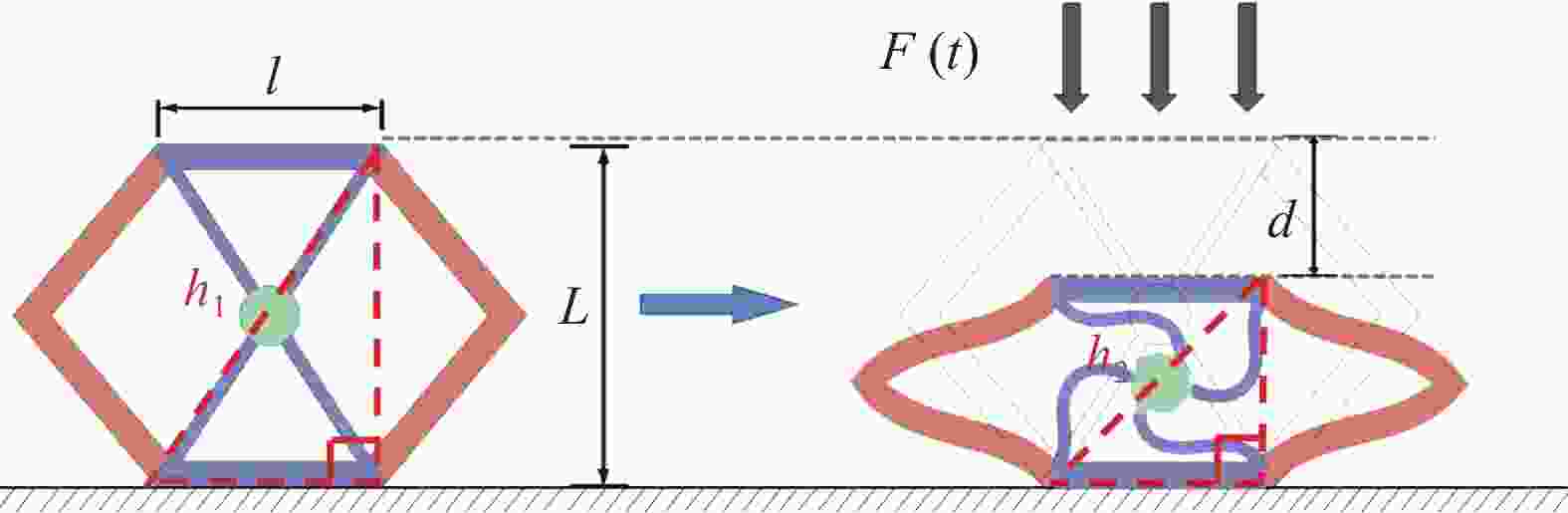
图 4 初始结构压缩位移示意图
h1—Length of the thin plate before buckling; h2—Length of the plate after buckling; L—Height of the vibration isolation unit structure before compression; t—Compression displacement; F(t)—The force applied to the upper surface
Figure 4. Schematic diagram of the initial structure's compression displacement
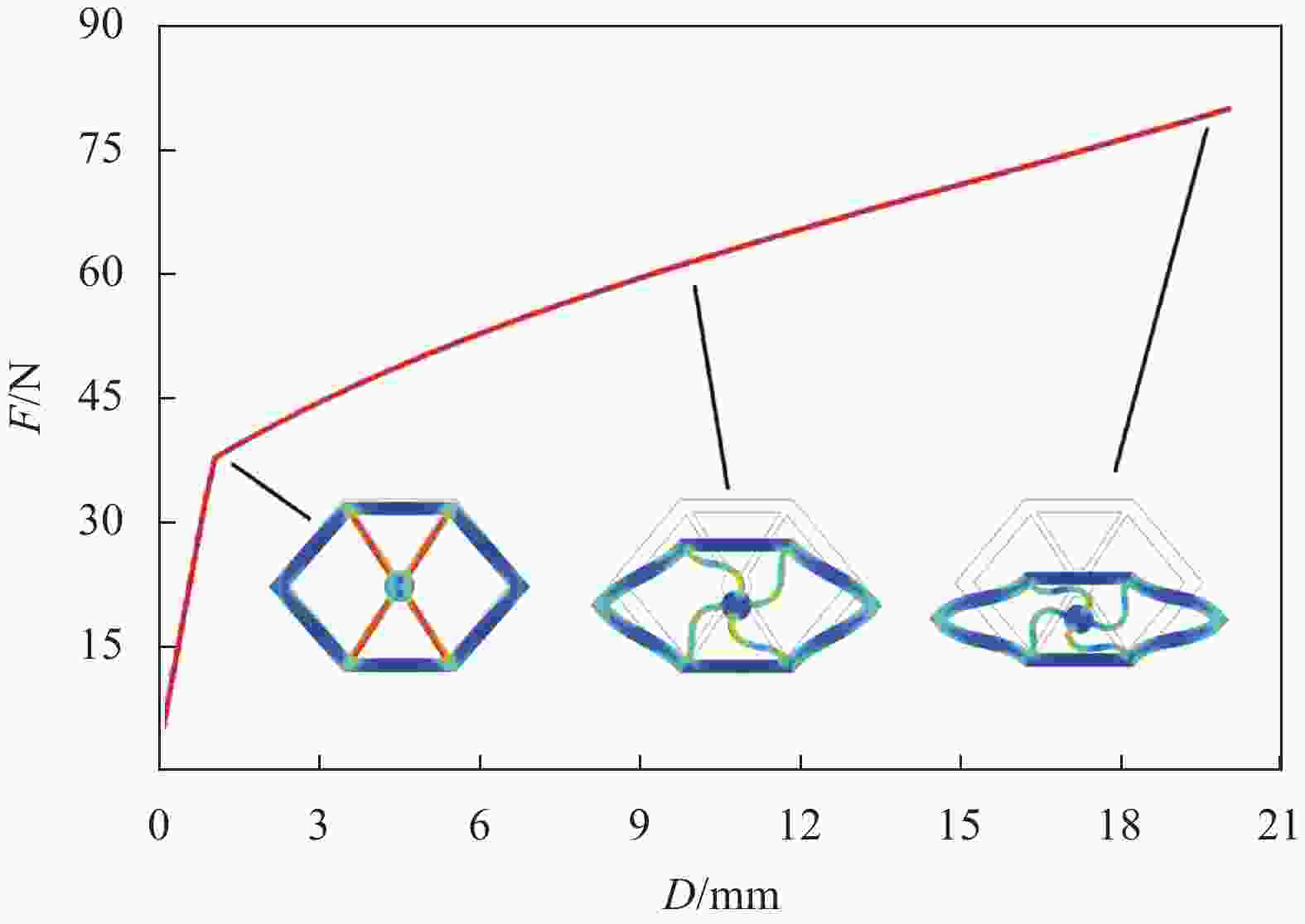
图 9 (a)基于遗传算法(GA)的优化迭代曲线;(b)优化过程中不同代数最优结构的力-位移曲线;((c)~(f))优化过程中不同代数最优结构的形状、参数和适应度值
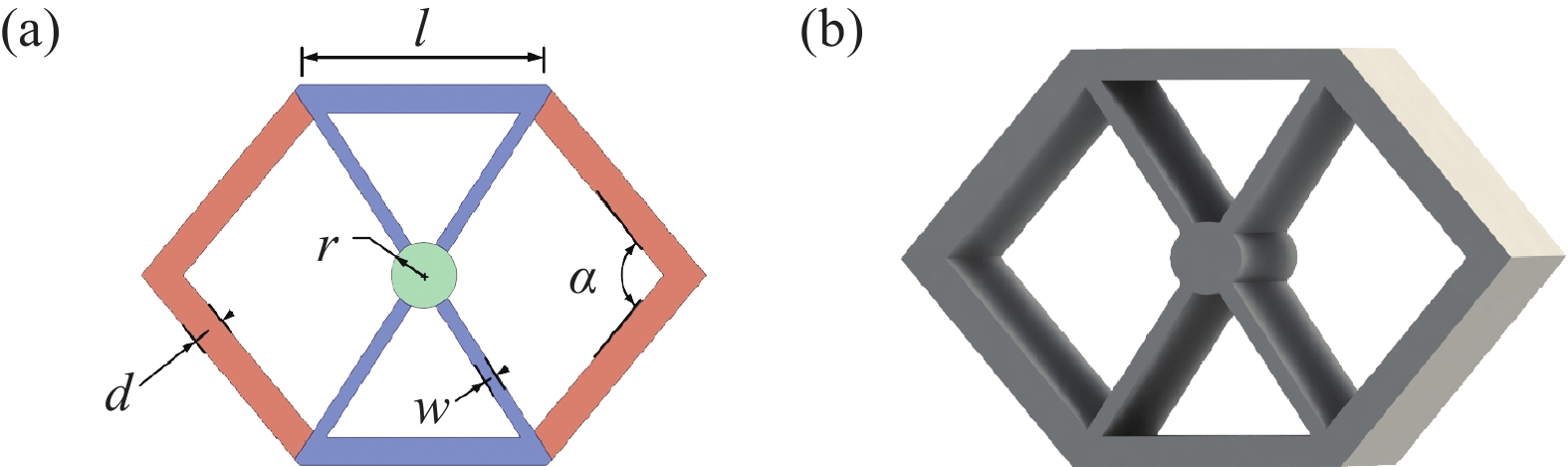
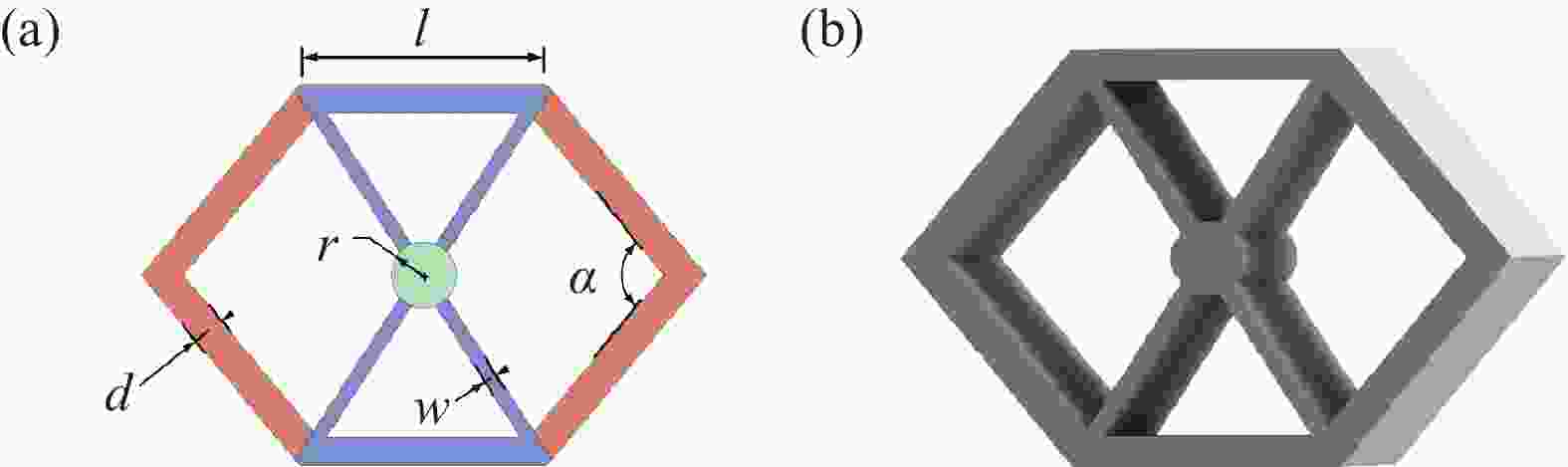
r—Radius of the center circle; α—Inner angle of the hexagon side; d—Side width; ①, ② and ③ show the best configuration of the 3rd, 20th, and 86th generation, respectively; x, y—Different coordinate directions
Figure 9. (a) Optimization iteration history by applying genetic algorithm (GA); (b) Force-displacement curves of optimization process; ((c)-(f)) Structure shape, parameters and fitness value of different algebraic optimal structures in the optimization process
-
[1] 李婷. 工业生产振动的危害及其控防对策研究[J]. 中国个体防护装备, 2017(2): 48-52. doi: 10.16102/j.cnki.cppe.2017.02.011LI Ting. Explore the syrian industrial production vibration harm and control countermeasures[J]. China Personal Protective Equipment, 2017(2): 48-52(in Chinese). doi: 10.16102/j.cnki.cppe.2017.02.011 [2] 黄自武, 何卫. 地铁列车对数据中心精密设备的振动影响评价[J]. 噪声与振动控制, 2023, 43(3): 167-174. doi: 10.3969/j.issn.1006-1355.2023.03.026HUANG Ziwu, HE Wei. Influence of subway trains on precision equipment vibration in a data center[J]. Noise and Vibration Control, 2023, 43(3): 167-174(in Chinese). doi: 10.3969/j.issn.1006-1355.2023.03.026 [3] SOUKOULIS C, KAFESAKI M, ECONOMOU E. Negative-index materials: New frontiers in optics[J]. Advanced Materials, 2006, 18(15): 1941-1952. doi: 10.1002/adma.200600106 [4] BALAJI P S, KARTHIK SELVAKUMAR K. Applications of nonlinearity in passive vibration control: A review[J]. Journal of Vibration Engineering & Technologies, 2021, 9(2): 183-213. [5] MA Z Z, ZHOU R P, YANG Q C. Recent advances in quasi-zero stiffness vibration isolation systems: An overview and future possibilities[J]. Machines, 2022, 10(9): 813. doi: 10.3390/machines10090813 [6] CARRELLA A, BRENNAN M J, WATERS T P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic[J]. Journal of Sound and Vibration, 2007, 301(3-5): 678-689. doi: 10.1016/j.jsv.2006.10.011 [7] XU D L, YU Q P, ZHOU J X, et al. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic[J]. Journal of Sound and Vibration, 2013, 332(14): 3377-3389. doi: 10.1016/j.jsv.2013.01.034 [8] 陈文华, 黄伟稀, 郝夏影, 等. 面向大振幅低频振动的重力倒摆式准零刚度隔振器研究[J]. 振动与冲击, 2022, 41(18): 205-209, 227. doi: 10.13465/j.cnki.jvs.2022.18.026CHEN Wenhua, HUANG Weixi, HAO Xiaying, et al. On the quasi-zero-stiffness isolator with a gravity inverted pendulum applied in large amplitude low frequency vibration isolation[J]. Journal of Vibration and Shock, 2022, 41(18): 205-209, 227(in Chinese). doi: 10.13465/j.cnki.jvs.2022.18.026 [9] JI J C, LUO Q T, YE K. Vibration control based metamaterials and origami structures: A state-of-the-art review[J]. Mechanical Systems and Signal Processing, 2021, 161: 107945. doi: 10.1016/j.ymssp.2021.107945 [10] ZHANG Q, GUO D K, HU G K. Tailored mechanical metamaterials with programmable quasi-zero-stiffness features for full-band vibration isolation[J]. Advanced Functional Materials, 2021, 31(33): 2101428. doi: 10.1002/adfm.202101428 [11] LU Z Q, ZHAO L, DING H, et al. A dual-functional metamaterial for integrated vibration isolation and energy harvesting[J]. Journal of Sound and Vibration, 2021, 509: 116251. doi: 10.1016/j.jsv.2021.116251 [12] TAN X J, CHEN S, WANG B, et al. Real-time tunable negative stiffness mechanical metamaterial[J]. Extreme Mechanics Letters, 2020, 41: 100990. doi: 10.1016/j.eml.2020.100990 [13] FAN H G, YANG L J, TIAN Y C, et al. Design of metastructures with quasi-zero dynamic stiffness for vibration isolation[J]. Composite Structures, 2020, 243: 112244. doi: 10.1016/j.compstruct.2020.112244 [14] WU L L, WANG Y, ZHAI Z R, et al. Mechanical metamaterials for full-band mechanical wave shielding[J]. Applied Materials Today, 2020, 20: 100671. doi: 10.1016/j.apmt.2020.100671 [15] KADIC M, MILTON G W, VAN HECKE M, et al. 3D metamaterials[J]. Nature Reviews Physics, 2019, 1(3): 198-210. doi: 10.1038/s42254-018-0018-y [16] YU X L, ZHOU J, LIANG H Y, et al. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review[J]. Progress in Materials Science, 2018, 94: 114-173. doi: 10.1016/j.pmatsci.2017.12.003 [17] KATOCH S, CHAUHAN S S, KUMAR V. A review on genetic algorithm: Past, present, and future[J]. Multimedia Tools and Applications, 2021, 80(5): 8091-8126. doi: 10.1007/s11042-020-10139-6 [18] CHIN C K, AL-BERMANI F G, KITIPORNCHAI S. Finite element method for buckling analysis of plate structures[J]. Journal of Structural Engineering, 1993, 119(4): 1048-1068. [19] LOU J J, ZHU S J, HE L, et al. Experimental chaos in nonlinear vibration isolation system[J]. Chaos, Solitons & Fractals, 2009, 40(3): 1367-1375. [20] WANG X, JIANG M, ZHOU Z W, et al. 3D printing of polymer matrix composites: A review and prospective[J]. Composites Part B: Engineering, 2017, 110: 442-458. doi: 10.1016/j.compositesb.2016.11.034 [21] CANO-VICENT A, TAMBUWALA M M, HASSAN S S, et al. Fused deposition modelling: Current status, methodology, applications and future prospects[J]. Additive Manufacturing, 2021, 47: 102378. doi: 10.1016/j.addma.2021.102378 -





 下载:
下载: