Failure analysis of composite materials based on phase field method: A review
-
摘要: 预测复合材料的失效行为,对复合材料结构设计具有重要意义。由于其失效模式和失效机制较复杂,传统的计算断裂力学方法和基于损伤力学的数值方法在对其进行失效分析存在一定困难。相场法结合了断裂力学和损伤力学的优点,无需额外的判据便可精确捕捉裂纹的萌生、扩展和扭结行为,近年来被广泛地应用于复合材料的失效分析。本文首先简要介绍相场法的基本理论,给出了基本的断裂能模型和控制方程。然后着重介绍了基于相场法的复合材料失效分析的研究进展,梳理了相场法在复合材料领域的应用范围。最后,对相场法模拟复合材料在疲劳、疲劳湿热环境下和冲击下的损伤进行了展望。Abstract: Predicting the failure behavior of composite materials is of great significance to the design of composite structures. Due to the complexity of its failure mode and failure mechanism, the traditional computational fracture mechanics method and the numerical method based on damage mechanics are difficulty to model modeling its failure behavior. The phase field method combines the advantages of fracture mechanics and damage mechanics. It can accurately capture the crack initiation, propagation and kink behavior without additional criteria. Recently, it has been widely used in the failure analysis of composite materials. In this paper, the basic theory of phase field method was briefly introduced, and the fundamental fracture energy model and governing equations were given. Following that, the review focused on the research progress of composite failure analysis based on phase field method. The application ranges of phase field method on composite material field were reviewed. Finally, the damage simulations of composites under fatigue, hygrothermal environment and impact by using phase field method were discussed.
-
Key words:
- phase field method /
- composite material /
- failure analysis /
- cohesive zone model /
- delamination
-
图 6 纤维桥联模型的机制和桥联区长度[28]
L—Length; h—Height; at—Crack length; ae—Effective crack length; lc—Fracture process zone length; lb—Bridging zone length; ${\delta _{\rm{n}}} $—Opening displacement of the bridging ligament; $\delta _{\rm{n}}^{\rm{f}} $—Opening displacement of the cracked fiber
Figure 6. Sketch of the fibre bridging mechanism and the bridging zone length[28]
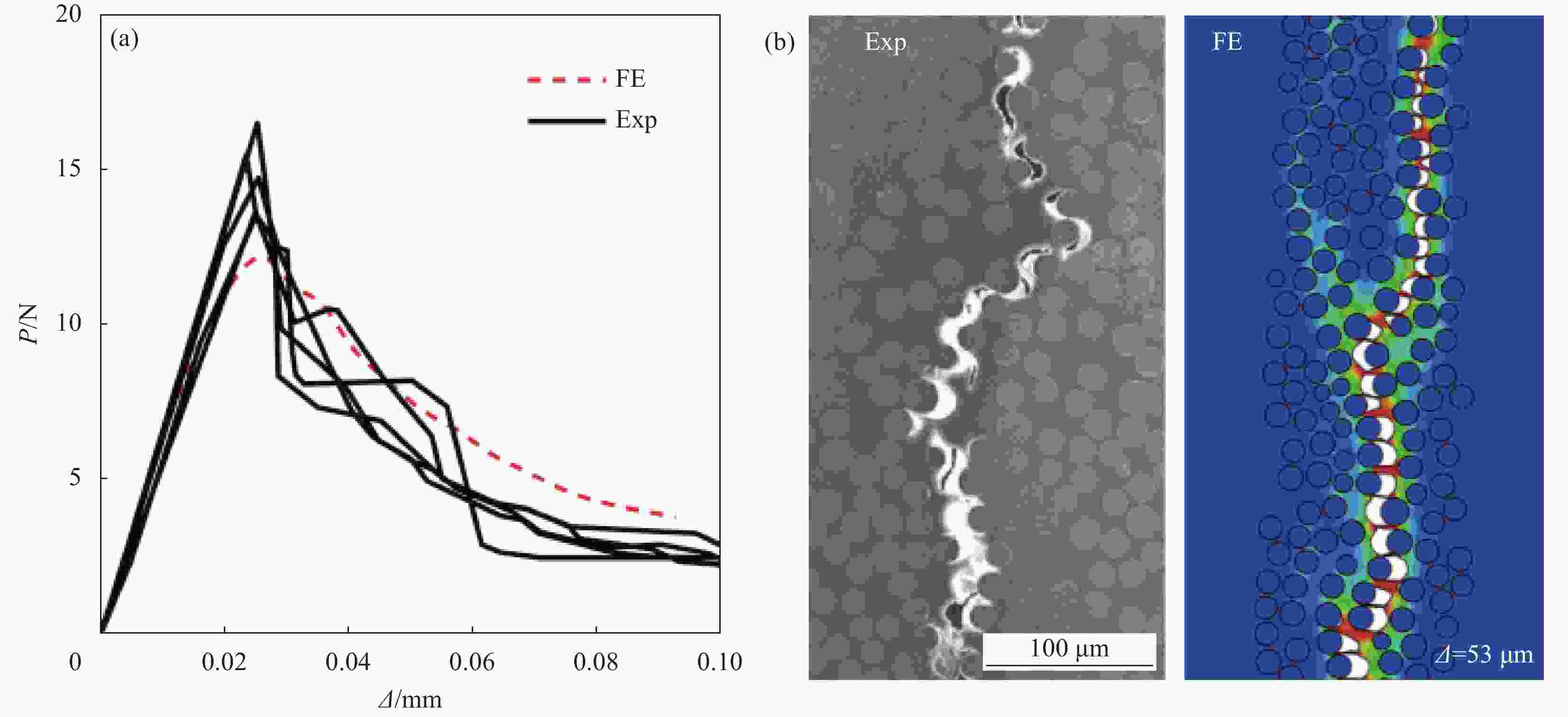
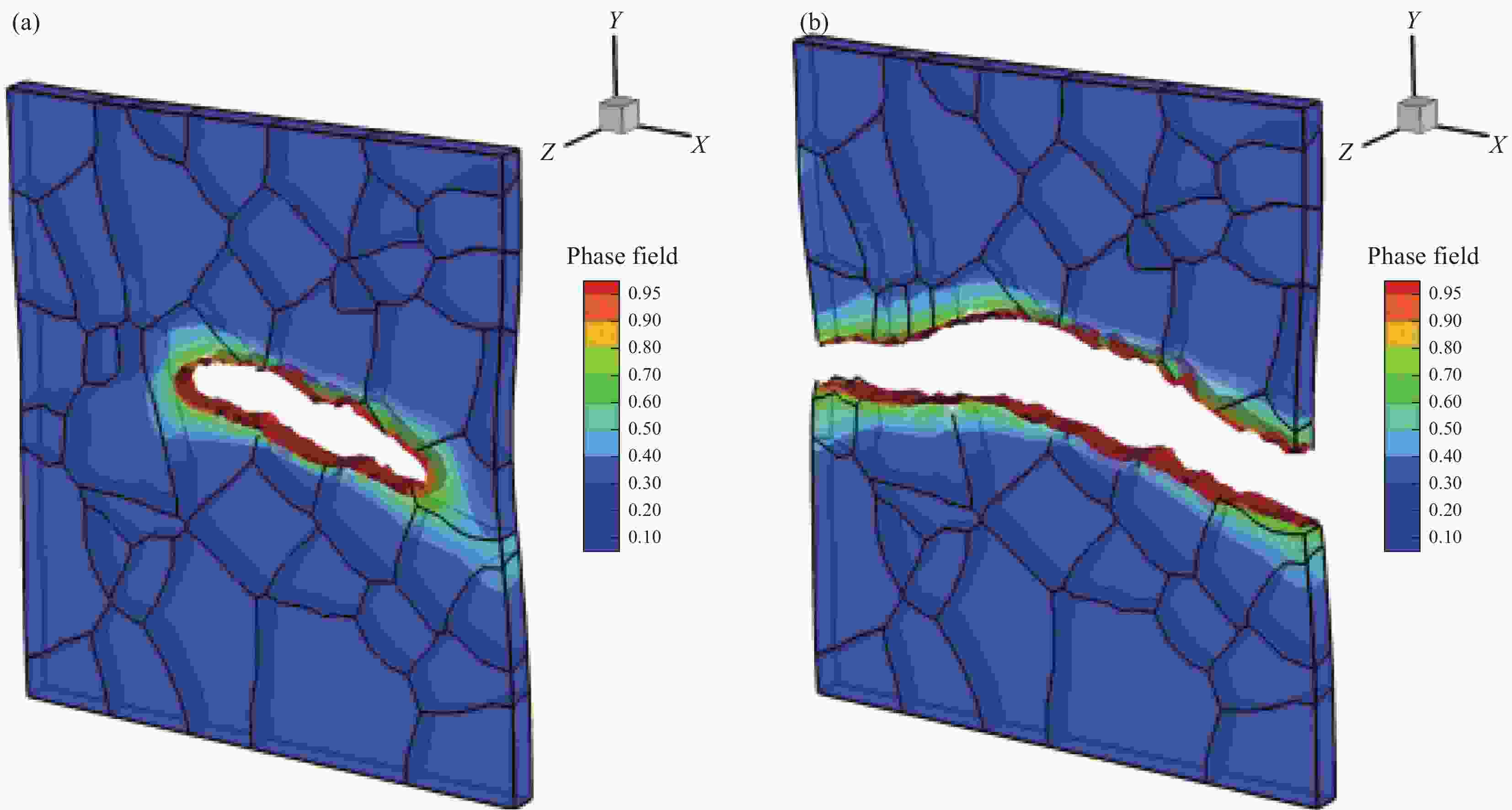
图 9 模拟[39]和测量[40]得到的纤维增强复合材料的载荷-裂纹口张开位移(CMOD)曲线(a)和裂纹扩展路径(b)
FE—Finite element simulation; Exp—Experimental results; P—Loading; Δ—Crack mouth opening displacement
Figure 9. Predicted[39] and measured[40] of load-crack opening displacement (CMOD) curves (a) and crack propagation path (b) for fibre-reinforced composites
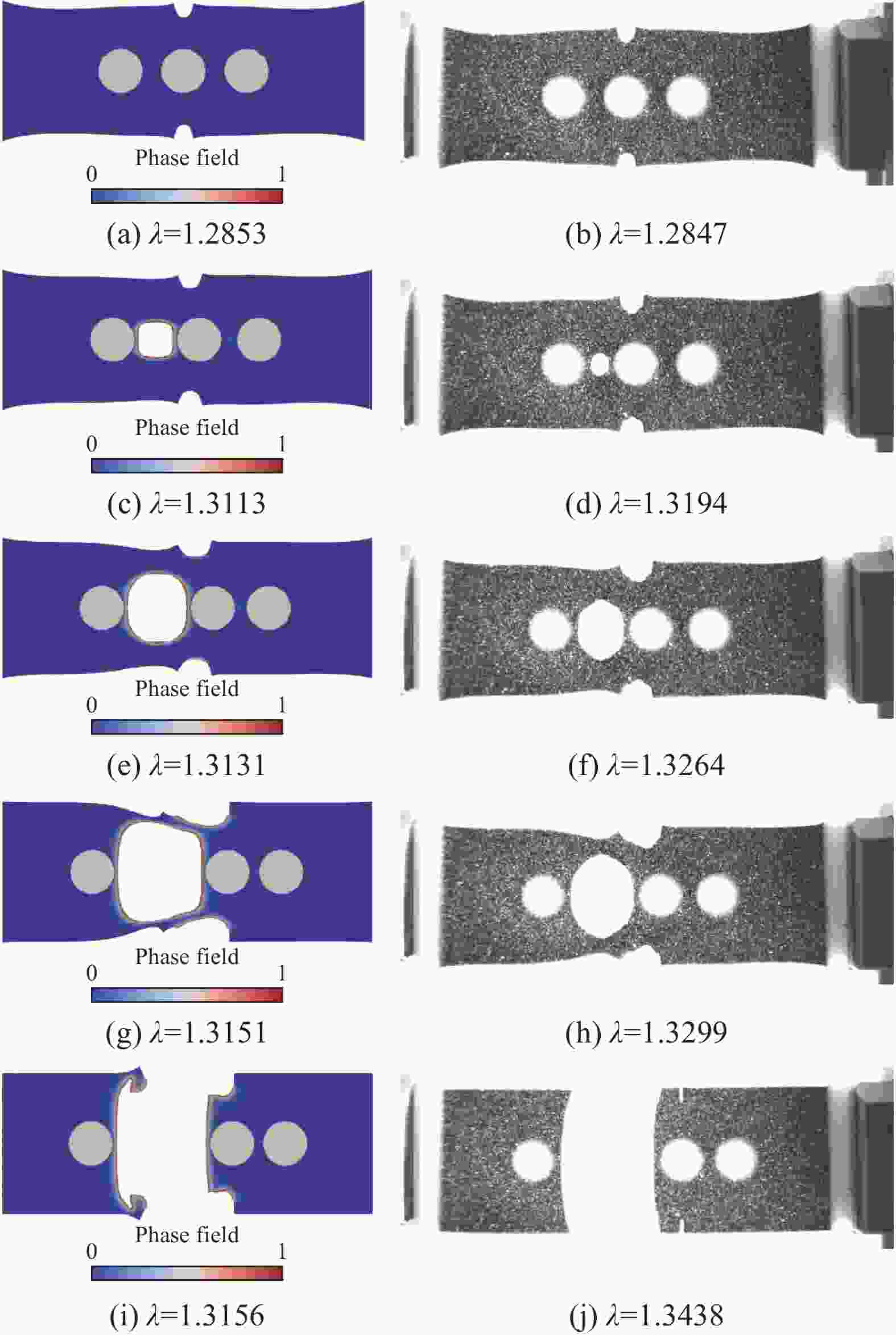
图 12 3D打印聚合物复合材料在不同伸长下的裂纹萌生序列[52]:((a), (c), (e), (g), (i)) 数值结果;((b), (d), (f), (h), (j))实验结果
Figure 12. Crack initiation sequence of 3D-printed hyperelastic composites at different values of global stretch[52]: ((a), (c), (e), (g), (i)) Numerical results; ((b), (d), (f), (h), (j)) Experimental results
表 1 复合材料的相场断裂能模型
Table 1. Phase field fracture energy model of composite material
Model Mathematical model Ref. Second-order anisotropic model $\dfrac{1}{2}\left[ {\dfrac{1}{ { {l_0} } }{\phi ^2} + {l_0}\left( {\nabla \phi {{A} } \nabla \phi } \right)} \right]$ ${A_{ij}} = {\delta _{ij}} + \gamma {M_{ij}}$ ${M_{ij}}{\text{ = }}{N_i}{N_j}$ [13] Double isotropic model for different crack mode $\displaystyle\int_\varOmega {\dfrac{{{G_{{\rm{cI}}}}}}{2}\left[ {\dfrac{1}{{{l_0}}}\phi _1^2 + {l_0}\left( {\nabla {\phi _1} \cdot \nabla {\phi _1}} \right)} \right]} {\rm{d}}V + \displaystyle\int_\varOmega {\dfrac{{{G_{{\rm{cII}}}}}}{2}\left[ {\dfrac{1}{{{l_0}}}\phi _2^2 + {l_0}\left( {\nabla {\phi _2} \cdot \nabla {\phi _2}} \right)} \right]} {\rm{d}}V$ [15] Double isotropic model for different component $\displaystyle\int_\varOmega {\dfrac{{{G_{\rm{f}}}}}{2}\left[ {\dfrac{1}{{{l_0}}}\phi _{\rm{f}}^2 + {l_0}\left( {\nabla {\phi _{\rm{f}}} \cdot \nabla {\phi _{\rm{f}}}} \right)} \right]} {\rm{d}}V + \displaystyle\int_\varOmega {\dfrac{{{G_{\rm{m}}}}}{2}\left[ {\dfrac{1}{{{l_0}}}\phi _{\rm{m}}^2 + {l_0}\left( {\nabla {\phi _{\rm{m}}} \cdot \nabla {\phi _{\rm{m}}}} \right)} \right]} {\rm{d}}V$ [16] Double second-order anisotropic model $ \displaystyle\int_\varOmega {\dfrac{{{G_{{\rm{cI}}}}}}{2}\left[ {\dfrac{1}{{{l_0}}}{\phi ^2} + {l_0}{{{A}}_1}:\left( {\nabla \phi \otimes \nabla \phi } \right)} \right]} {\rm{d}}V + \displaystyle\int_\varOmega {\dfrac{{{G_{{\rm{cII}}}}}}{2}\left[ {\dfrac{1}{{{l_0}}}{\phi ^2} + {l_0}{{{A}}_2}:\left( {\nabla \phi \otimes \nabla \phi } \right)} \right]} {\rm{d}}V $ [17] Fourth-order transverse isotropic model $ \begin{array}{l}{\displaystyle {\int }_{\varOmega }\dfrac{1}{2}\left[\dfrac{1}{{l}_{0}}{\phi }^{2}+\dfrac{{l}_{0}}{2}A:\left(\nabla \phi \otimes \nabla \phi \right)+\dfrac{{l}_{0}^{3}}{16}\left(\nabla \nabla \phi :\mathbb{A}:\nabla \nabla \phi \right)\right]}{\rm{d}}V,{A}_{ij}={\delta }_{ij}+\gamma {M}_{ij},{M}_{ij}\text{= }{N}_{i}{N}_{j}\\ {\mathbb{A}}_{ijkl}={\delta }_{ij}{\delta }_{kl}+{\rm{sym}}\left({\beta }_{1}{M}_{ij}{M}_{kl}+{\beta }_{2}{\delta }_{ij}{M}_{kl}\right)+\dfrac{{\beta }_{3}}{2}\left({\delta }_{ik}{M}_{jl}+{M}_{ik}{\delta }_{jl}+{\delta }_{il}{M}_{jk}+{M}_{il}{\delta }_{jk}\right)\end{array} $ [18] Fourth-order orthotropic model $ \begin{array}{l}{\displaystyle {\int }_{\varOmega }\dfrac{1}{2}\left[\dfrac{1}{{l}_{0}}{\phi }^{2}+\dfrac{{l}_{0}}{2}A:\left(\nabla \phi \otimes \nabla \phi \right)+\dfrac{{l}_{0}^{3}}{16}\left(\nabla \nabla \phi :\mathbb{A}:\nabla \nabla \phi \right)\right]}{\rm{d}}V\\ {A}_{ij}={\delta }_{ij}+{\gamma }_{1}{M}_{ij}^{1}+{\gamma }_{2}{M}_{ij}^{2},{M}_{ij}^{1}\text{= }{N}_{i}^{1}{N}_{j}^{1},{M}_{ij}^{2}\text{= }{N}_{i}^{2}{N}_{j}^{2}\\ {\mathbb{A}}_{ijkl}=\dfrac{1}{2}\left({\delta }_{ij}{\delta }_{kl}+{\delta }_{il}{\delta }_{kj}\right)+{\rm{sym}}[{\displaystyle \sum _{s=1}^{2}\left({\alpha }_{1}^{s}{M}_{ij}^{s}{M}_{kl}^{s}+{\alpha }_{2}^{s}{\delta }_{ij}{M}_{kl}^{s}\right)}+{\alpha }_{7}{M}_{ij}^{1}{M}_{kl}^{2}+\\ \text{ }{\displaystyle \sum _{s=1}^{2}\dfrac{{\alpha }_{3}^{s}}{2}\left({\delta }_{ik}{M}_{jl}^{s}+{M}_{ik}^{s}{\delta }_{jl}+{\delta }_{il}{M}_{jk}^{s}+{M}_{il}^{s}{\delta }_{jk}\right)}]\end{array} $ [18] Fourth-order cubic symmetric model $ \begin{array}{l}{\displaystyle {\int }_{\varOmega }\dfrac{1}{2}\left[\dfrac{1}{{l}_{0}}{\phi }^{2}+\dfrac{{l}_{0}}{2}\left(\nabla \phi \cdot \nabla \phi \right)+\dfrac{{l}_{0}^{3}}{16}\left(\nabla \nabla \phi :\mathbb{A}:\nabla \nabla \phi \right)\right]}{\rm{d}}V\\ {\mathbb{A}}_{ijkl}=\dfrac{1}{2}\left({\delta }_{ij}{\delta }_{kl}+{\delta }_{il}{\delta }_{kj}\right)+{\displaystyle \sum _{m=1}^{2}{\displaystyle \sum _{n=1}^{2}\left[\alpha {\delta }_{mn}+\dfrac{\beta }{2}\left(1-{\delta }_{mn}\right)\right]}}{M}_{ij}^{m}{M}_{kl}^{m}\end{array} $ [18] Notes: A and ${A_{ij}}$—Second-order structure tensor and its component form; ${\delta _{ij}}$—Component of the second-order indentiy tensor; $\gamma $—Penalty parameter;${N_i}$—Component of unit vector along the fiber direction; ${G_{{\rm{cI}}}}$ and ${G_{{\rm{cII}}}}$—Crtical energy release rate for mode I and mode II crack; ${\phi _1}$ and ${\phi _2}$—Phase field variables for mode I and mode II crack ; ${G_{\rm{f}}}$ and ${G_{\rm{m}}}$—Crtical energy release rate of fiber and matrix; ${\phi _{\rm{f}}}$ and ${\phi _{\rm{m}}}$—Phase field variables of fiber and matrix; $ {{{A}}_1} $ and $ {{{A}}_2} $—Second-order structure tensor for mode I and mode II crack ; $ \mathbb{A} $—Fourth-order structure tensor; $ N_i^1 $and $ N_i^2 $—Components of two orthonomal basis;$ {\beta _1} $, $ {\beta _2} $, $ {\beta _3} $, $ {\gamma _1} $, $ {\gamma _2} $, $ \alpha _1^s $, $ \alpha _2^s $, $ \alpha _3^s $, $ {\alpha _7} $, $ \alpha $and $ \beta $—Material parameters. 表 2 复合材料的长度尺度参数模型
Table 2. Length scale parameter model of composite material
Model Mathematical model Ref. Zhang's model $l_0^{{\rm{ani}}}\left( {{\varphi _1}} \right) = l_0^{{\rm{iso}}}\sqrt {1 + \beta {{\cos }^2}{\varphi _1}} $ [13] Transverse isotropic model $l_0^{{\rm{tran}}}\left( {\varphi ,\theta } \right) = {l_0}\left[ {1 + \alpha {{\sin }^2}\left( {\varphi - \theta } \right)} \right]$ [18] Orthotropic model $l_0^{{\rm{orth}}}\left( {\varphi ,\theta } \right) = {l_0}\left[ {1 + {\alpha ^1}{{\sin }^2}\left( {\varphi - \theta } \right) + {\alpha ^2}{{\cos }^2}\left( {\varphi - \theta } \right)} \right]$ [18] Cubic symmetric model $\begin{gathered} l_0^{\rm cubic}\left( {\varphi ,\theta } \right) = \gamma {\left\{ {1 + \eta \cos \left[ {4\left( {\varphi - \theta } \right)} \right]} \right\}^{1/3}} \\ \gamma = {l_0}{\left( {\frac{{8 + 6\alpha + \beta }}{8}} \right)^{1/3}},\quad \eta = \left( {\frac{{8 + 6\alpha + \beta }}{{2\alpha - \beta }}} \right) \\ \end{gathered} $ [18] Notes: ${\varphi _1}$—Angle between the direction of gradient of phase field and the weak failure direction; ${l_0}$—Length scale parameter of isotropic phase field fracture model; $\varphi $—Angle between the horizontal axis and the tangent of the crack at position; $\theta $—Angle between the horizontal axis and the direction of the fiber; $\alpha $, ${\alpha ^1}$, ${\alpha ^2}$, $\gamma $, $\eta $, $\beta $—Material parameter. -
[1] 杜善义, 关志东. 我国大型客机先进复合材料技术应对策略思考[J]. 复合材料学报, 2008, 25(1):1-10. doi: 10.3321/j.issn:1000-3851.2008.01.001DU Shanyi, GUAN Zhidong. Strategic considerations for development of advanced composite technology for large commercial aircraft in China[J]. Acta Materiae Compositae Sinaca,2008,25(1):1-10(in Chinese). doi: 10.3321/j.issn:1000-3851.2008.01.001 [2] 李西宁, 王悦舜, 周新房. 复合材料层合板分层损伤数值模拟方法研究现状[J]. 复合材料学报, 2021, 38(4):1076-1086. doi: 10.13801/j.cnki.fhclxb.20210302.006LI Xi'ning, WANG Yueshun, ZHOU Xinfang. Status of numerical simulation methods for delamination damage of composite laminates[J]. Acta Materiae Compositae Sinica,2021,38(4):1076-1086(in Chinese). doi: 10.13801/j.cnki.fhclxb.20210302.006 [3] ZHANG P, YAO W, HU X, et al. An explicit phase field model for progressive tensile failure of composites[J]. Engineering Fracture Mechanics,2021,241:107371. doi: 10.1016/j.engfracmech.2020.107371 [4] PRANAVI D, RAJAGOPAL A, REDDY J N. Interaction of anisotropic crack phase field with interface cohesive zone model for fiber reinforced composites[J]. Composite Structures,2021,270:114038. doi: 10.1016/j.compstruct.2021.114038 [5] BUI T Q, HU X. A review of phase-field models, fundamentals and their applications to composite laminates[J]. Engineering Fracture Mechanics,2021,248:107705. doi: 10.1016/j.engfracmech.2021.107705 [6] ZHUANG X, ZHOU S, HUYNH G D, et al. Phase field modelling and computer implementation: A review[J]. Engineering Fracture Mechanics,2022 , 262:108234. doi: 10.1016/j.engfracmech.2022.108234 [7] FRANCFORT G A, MARIGO J J. Revisiting brittle fracture as an energy minimization problem[J]. Journal of the Mechanics and Physics of Solids,1998,46(8):1319-1342. doi: 10.1016/S0022-5096(98)00034-9 [8] 吴建营. 固体结构损伤破坏统一相场理论、算法和应用[J]. 力学学报, 2021, 53(2):301-329. doi: 10.6052/0459-1879-20-295WU Jianying. On the theoretical and numerical aspects of the unified phase-field theory for damage and failure in solids and structures[J]. Chinese Journal of Theoretical and Applied Mechanics,2021,53(2):301-329(in Chinese). doi: 10.6052/0459-1879-20-295 [9] WU J Y, NGUYEN V P, NGUYEN C T, et al. Phase-field modeling of fracture[J]. Advances in Applied Mechanics,2020,53:1-183. [10] BOURDIN B, FRANCFORT G A, MARIGO J J. Numerical experiments in revisited brittle fracture[J]. Journal of the Mechanics and Physics of Solids,2000,48(4):797-826. [11] BOURDIN B, FRANCFORT G A, MARIGO J J. The variational approach to fracture[J]. Journal of Elasticity,2008,91(1):5-148. [12] AMOR H, MARIGO J J, MAURINI C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments[J]. Journal of the Mechanics and Physics of Solids,2009,57(8):1209-1229. doi: 10.1016/j.jmps.2009.04.011 [13] ZHANG P, HU X, BUI T Q, et al. Phase field modeling of fracture in fiber reinforced composite laminate[J]. International Journal of Mechanical Sciences,2019,161:105008. [14] CAHILL L M A, NATARAJAN S, BORDAS S P A, et al. An experimental/numerical investigation into the main driving force for crack propagation in uni-directional fibre-reinforced composite laminae[J]. Composite Structures,2014,107:119-130. doi: 10.1016/j.compstruct.2013.05.039 [15] BLEYER J, ALESSI R. Phase-field modeling of anisotropic brittle fracture including several damage mechanisms[J]. Computer Methods in Applied Mechanics and Engineering,2018,336:213-236. doi: 10.1016/j.cma.2018.03.012 [16] NGUYEN T T, RÉTHORÉ J, BAIETTO M C. Phase field modelling of anisotropic crack propagation[J]. European Journal of Mechanics-A/Solids,2017,65:279-288. [17] ZHANG P, TAN S, HU X, et al. A double-phase field model for multiple failures in composites[J]. Composite Structures,2022,293:115730. doi: 10.1016/j.compstruct.2022.115730 [18] TEICHTMEISTER S, KIENLE D, ALDAKHEEL F, et al. Phase field modeling of fracture in anisotropic brittle solids[J]. International Journal of Non-Linear Mechanics,2017,97:1-21. [19] MIEHE C, WELSCHINGER F, HOFACKER M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations[J]. International Journal for Numerical Methods in Engineering,2010,83:1273-1311. doi: 10.1002/nme.2861 [20] ASUR VIJAYA KUMAR P K, DEAN A, REINOSO J, et al. A multi phase-field-cohesive zone model for laminated composites: Application to delamination migration[J]. Composite Structures,2021,276:114471. doi: 10.1016/j.compstruct.2021.114471 [21] PILLAI U, TRIANTAFYLLOU S P, ESSA Y, et al. An anisotropic cohesive phase field model for quasi-brittle fractures in thin fibre-reinforced composites[J]. Composite Structures,2020,252:112635. [22] CAROLLO V, REINOSO J, PAGGI M. A 3D finite strain model for intralayer and interlayer crack simulation coupling the phase field approach and cohesive zone model[J]. Composite Structures,2017,182:636-651. doi: 10.1016/j.compstruct.2017.08.095 [23] ZHANG P, YAO W, HU X, et al. Phase field modelling of progressive failure in composites combined with cohesive element with an explicit scheme[J]. Composite Structures,2021,262:113353. doi: 10.1016/j.compstruct.2020.113353 [24] ZHANG P, FENG Y, BUI T Q, et al. Modelling distinct failure mechanisms in composite materials by a combined phase field method[J]. Composite Structures,2020,232:111551. doi: 10.1016/j.compstruct.2019.111551 [25] RAO S, BUDZIK M K, DIAS M A. On microscopic analysis of fracture in unidirectional composite material using phase field modelling[J]. Composites Science and Technology,2022,220:109242. doi: 10.1016/j.compscitech.2021.109242 [26] GARCÍA-MACÍAS E, D'ALESSANDRO A, CASTRO-TRIGUERO R, et al. Micromechanics modeling of the electrical conductivity of carbon nanotube cement-matrix composites[J]. Composites Part B: Engineering,2017,108:451-469. doi: 10.1016/j.compositesb.2016.10.025 [27] QUINTEROS L, GARCÍA-MACÍAS E, MARTÍNEZ-PAÑEDAE. Micromechanics-based phase field fracture modeling of CNT composites[J]. Composites Part B: Engineering,2022,236:109788. doi: 10.1016/j.compositesb.2022.109788 [28] TAN W, MARTÍNEZ-PAÑEDA E. Phase field fracture predictions of microscopic bridging behaviour of composite materials[J]. Composite Structures,2022,286:115242. doi: 10.1016/j.compstruct.2022.115242 [29] GUILLÉN-HERNÁNDEZ T, QUINTANA-COROMINAS A, GARCIA I G, et al. In-situ strength effects in long fibre reinforced composites: A micro-mechanical analysis using the phase field approach of fracture[J]. Theoretical and Applied Fracture Mechanics,2020,108:102621. doi: 10.1016/j.tafmec.2020.102621 [30] LI X, XU Y. Phase field modeling scheme with mesostructure for crack propagation in concrete composite[J]. International Journal of Solids and Structures,2022,234:111259. [31] XIA Y, WU W, YANG Y, et al. Mesoscopic study of concrete with random aggregate model using phase field method[J]. Construction and Building Materials,2021,310:125199. doi: 10.1016/j.conbuildmat.2021.125199 [32] PAGGI M, CORRADO M, REINOSO J. Fracture of solar-grade anisotropic polycrystalline silicon: A combined phase field-cohesive zone model approach[J]. Computer Methods in Applied Mechanics and Engineering,2018,330:123-148. [33] HEISTER T, WHEELER M F, WICK T. A primal-dual active set method and predictor-corrector mesh adaptivity for computing fracture propagation using a phase-field approach[J]. Computer Methods in Applied Mechanics and Engineering,2015,290:466-495. doi: 10.1016/j.cma.2015.03.009 [34] NGUYEN-THANH N, LI W, HUANG J, et al. Multi phase-field modeling of anisotropic crack propagation in 3D fiber-reinforced composites based on an adaptive isogeometric meshfree collocation method[J]. Computer Methods in Applied Mechanics and Engineering,2022,393:114794. doi: 10.1016/j.cma.2022.114794 [35] SHAO Y, DUAN Q, QIU S. Adaptive analysis for phase-field model of brittle fracture of functionally graded materials[J]. Engineering Fracture Mechanics,2021,251:107783. doi: 10.1016/j.engfracmech.2021.107783 [36] CHEN Y, GÉLÉBART L, MARANO A, et al. FFT phase-field model combined with cohesive composite voxels for fracture of composite materials with interfaces[J]. Computational Mechanics,2021,68(2):433-457. [37] CAO Y J, SHEN W Q, SHAO J F, et al. A novel FFT-based phase field model for damage and cracking behavior of heterogeneous materials[J]. International Journal of Plasticity,2020,133:102786. doi: 10.1016/j.ijplas.2020.102786 [38] ROY P, DEEPU S P, PATHRIKAR A, et al. Phase field based peridynamics damage model for delamination of compo-site structures[J]. Composite Structures,2017,180:972-993. doi: 10.1016/j.compstruct.2017.08.071 [39] TAN W, MARTÍNEZ-PAÑEDA E. Phase field predictions of microscopic fracture and R-curve behaviour of fibre-reinforced composites[J]. Composites Science and Technology,2021,202:108539. doi: 10.1016/j.compscitech.2020.108539 [40] CANAL L P, GONZÁLEZ C, SEGURADO J, et al. Intraply fracture of fiber-reinforced composites: Microscopic mechanisms and modeling[J]. Composites Science and Technology,2012,72:1223-1232. doi: 10.1016/j.compscitech.2012.04.008 [41] ESPADAS-ESCALANTE J J, VAN DIJK N P, ISAKSSON P. A phase-field model for strength and fracture analyses of fiber-reinforced composites[J]. Composites Science and Technology,2019,174:58-67. doi: 10.1016/j.compscitech.2018.10.031 [42] QUINTANAS-COROMINAS A, REINOSO J, CASONI E, et al. A phase field approach to simulate intralaminar and translaminar fracture in long fiber composite materials[J]. Composite Structures,2019,220:899-911. doi: 10.1016/j.compstruct.2019.02.007 [43] SONG K, LI Y, ROSE C. Continuum damage mechanics models for the analysis of progressive failure in open-hole tension laminates[J]. Archives of Biochemistry & Biophysics, 1957, 69: 634-643. [44] LI G, YIN B B, ZHANG L W, et al. Modeling microfracture evolution in heterogeneous composites: A coupled cohesive phase-field model[J]. Journal of the Mechanics and Physics of Solids,2020,142:103968. doi: 10.1016/j.jmps.2020.103968 [45] LI G, YIN B B, ZHANG L W, et al. A framework for phase-field modeling of interfacial debonding and frictional slipping in heterogeneous composites[J]. Computer Methods in Applied Mechanics and Engineering,2021,382:113872. [46] ALESSI R, FREDDI F. Phase-field modelling of failure in hybrid laminates[J]. Composite Structures,2017,181:9-25. doi: 10.1016/j.compstruct.2017.08.073 [47] ALESSI R, FREDDI F. Failure and complex crack patterns in hybrid laminates: A phase-field approach[J]. Composites Part B: Engineering,2019,179:107256. doi: 10.1016/j.compositesb.2019.107256 [48] PAN Z Z, ZHANG L W, LIEW K M. A phase-field framework for failure modeling of variable stiffness composite lami-nate[J]. Computer Methods in Applied Mechanics and Engineering,2022,388:114192. [49] NATARAJAN S, ANNABATTULA R K. Modeling crack propagation in variable stiffness composite laminates using the phase field method[J]. Composite Structures,2019,209:424-433. doi: 10.1016/j.compstruct.2018.10.083 [50] WU J, MCAULIFFE C, WAISMAN H, et al. Stochastic analysis of polymer composites rupture at large deformations modeled by a phase field method[J]. Computer Methods in Applied Mechanics and Engineering,2016,312:596-634. doi: 10.1016/j.cma.2016.06.010 [51] WANG X, JIANG M, ZHOU Z, et al. 3D printing of polymer matrix composites: A review and prospective[J]. Compo-sites Part B: Engineering,2017,110:442-458. doi: 10.1016/j.compositesb.2016.11.034 [52] RUSS J, SLESARENKO V, RUDYKH S, et al. Rupture of 3D-printed hyperelastic composites: Experiments and phase field fracture modeling[J]. Journal of the Mechanics and Physics of Solids,2020,140:103941. doi: 10.1016/j.jmps.2020.103941 [53] MANDAL T K, NGUYEN V P, WU J Y. A length scale insensitive anisotropic phase field fracture model for hyperelastic composites[J]. International Journal of Mechani-cal Sciences,2020,188:105941. [54] BHARDWAJ G, SINGH I, MISHRA B, et al. Numerical simulation of functionally graded cracked plates using NURBS based XIGA under different loads and boundary conditions[J]. Composite Structures,2015,126:347-359. doi: 10.1016/j.compstruct.2015.02.066 [55] DUC H, TINH Q, NGUYEN D, et al. Hybrid phase field simulation of dynamic crack propagation in functionally graded glass-filled epoxy[J]. Composites Part B: Engineering,2016,99:266-276. doi: 10.1016/j.compositesb.2016.06.016 [56] THOM V, DUC H, NGUYEN D, et al. Phase-field thermal buckling analysis for cracked functionally graded compo-site plates considering neutral surface[J]. Composite Structures,2017,182:542-548. doi: 10.1016/j.compstruct.2017.09.059 [57] PHUC P, NGUYEN D. The effect of cracks on the stability of the functionally graded plates with variable-thickness using HSDT and phase-field theory[J]. Composites Part B: Engineering,2019,175:107086. [58] HIRSHIKESH, NATARAJAN S, ANNABATTULA R K, et al. Phase field modelling of crack propagation in functionally graded materials[J]. Composites Part B: Engineering,2019,169:239-248. doi: 10.1016/j.compositesb.2019.04.003 [59] TAN Y, HE Y, LI X. Phase field fracture modeling of transversely isotropic piezoelectric material with anisotropic fracture toughness[J]. International Journal of Solids and Structures,2022,248:111615. doi: 10.1016/j.ijsolstr.2022.111615 [60] DAN S, TARAFDER P, GHOSH S. Adaptive wavelet-enhanced cohesive zone phase-field FE model for crack evolution in piezoelectric composites[J]. Computer Methods in Applied Mechanics and Engineering,2022,392:114636. doi: 10.1016/j.cma.2022.114636 [61] SOUKAINA R, DIDIER B, JULIEN R. Unified phase field model to simulate both intergranular and transgranular failure in polycrystalline aggregates[J]. Finite Elements in Analysis and Design,2021,194:103555. doi: 10.1016/j.finel.2021.103555 [62] CHENG J, TU X, GHOSH S. Wavelet-enriched adaptive hierarchical FE model for coupled crystal plasticity-phase field modeling of crack propagation in polycrystalline microstructures[J]. Computer Methods in Applied Mechanics and Engineering,2020,361:112757. doi: 10.1016/j.cma.2019.112757 [63] EMDADI A, ZAEEM M A. Phase-field modeling of crack propagation in polycrystalline materials[J]. Computational Materials Science,2021,186:110057. doi: 10.1016/j.commatsci.2020.110057 -





 下载:
下载: