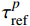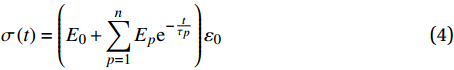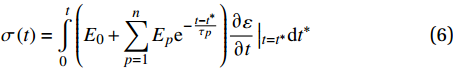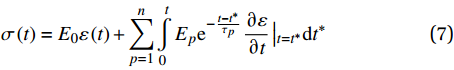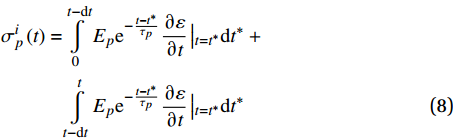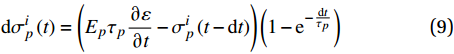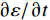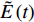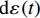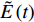连续碳纤维增强聚醚醚酮复合材料泛温度域本构模型

李泽超; 雷鸣; 校金友; 文立华; 侯晓

doi:10.13801/j.cnki.fhclxb.20210806.001

连续碳纤维增强聚醚醚酮复合材料泛温度域本构模型

李泽超¹,
雷鸣^1, ,,
校金友^1, ,,
文立华¹,
侯晓²

1.
西北工业大学　航天学院，西安 710072
2.
中国航天科技集团有限公司，北京 100048

基金项目: 国家自然科学基金重点项目 (52090051)；国家自然科学基金委员会-中国航天科技集团有限公司航天先进制造技术研究联合基金(U1837601)

详细信息

通讯作者:
雷鸣，博士，助理教授，硕士生导师，研究方向为复合材料力学　E-mail: leiming@nwpu.edu.cn

校金友，博士，教授，博士生导师，研究方向为计算结构力学、复合材料结构设计　E-mail：xiaojy@nwpu.edu.cn

中图分类号: TB332
计量
- 文章访问数: 1676
- HTML全文浏览量: 947
- PDF下载量: 242
出版历程
- 收稿日期: 2021-06-17
- 修回日期: 2021-07-15
- 录用日期: 2021-07-27
- 网络出版日期: 2021-08-08
- 刊出日期: 2022-07-29

A constitutive model of continuous carbon fiber reinforced thermoplastic polyether ether ketone composites in a wide temperature range

1.
School of Astronautics, Northwestern Polytechnical University, Xi′an 710072, China
2.
China Aerospace Science and Technology Corporation, Beijing 100048, China

摘要

摘要: 连续碳纤维增强热塑性聚醚醚酮复合材料(CF/PEEK)具有抗冲击、易修复、耐高温等优异特性，是新一代航空航天热端结构的优选材料。PEEK基体的结晶特性使其在高于玻璃化转变温度(143℃左右)时仍具有较强承载能力，因此，CF/PEEK复合材料能够在200℃条件下长期服役。然而，CF/PEEK复合材料的成型温度域宽、服役温度范围广，高温条件下PEEK树脂会逐渐松弛，导致CF/PEEK复合材料呈现出与时间、温度、加载历史相关的各向异性黏弹性，对复合材料结构成型过程与服役历史的精细化设计带来了挑战。现有复合材料高温预测模型主要基于弹塑性本构的刚度折减方法，未充分考虑材料的各向异性松弛行为。发展了一种描述CF/PEEK复合材料力学性能随时间、温度演化的各向异性黏弹本构模型。通过表征热塑性PEEK树脂的松弛模量主曲线，基于广义Maxwell黏弹模型，获取泛温度域(25~200℃)热塑性PEEK的黏弹性本构参数，结合复合材料等效力学性能的半经验解法，给出了三维复合材料各向异性黏弹本构模型。通过与CF/PEEK复合材料的横向高温松弛实验和代表性体积单元(RVE)仿真模拟结果比较，证明了该模型的有效性。这一本构模型可用于CF/PEEK复合材料结构的成型过程仿真和高温力学性能设计。
- 热塑性复合材料 /
- 高温松弛 /
- 黏弹性 /
- 细观均匀化 /
- 代表性体积单元
Abstract: As preferred high-temperature structural materials for the next generation aerospace craft, carbon fiber reinforced thermoplastic polyether ether ketone composite (CF/PEEK) has excellent properties, such as high impact resistance, repairability, high temperature resistance and so forth. Because of the crystallization characteristics, the PEEK matrix still has a high load-carrying capacity above the glass transition temperature (around 143℃), and therefore CF/PEEK composite can be used under long term operation at 200℃. However, due to the wide forming temperature range and service temperature range of CF/PEEK composites, PEEK resin will gradually relax at high temperature. Consequently, CF/PEEK composites will show obvious time-, temperature-, and loading history-dependent anisotropic viscoelasticity, which make it very hard to accurately design the forming history and service history of the composite structures. Currently, the existing high temperature prediction model of composites is usually based on the elastic-plastic constitutive stiffness reduction method, which does not fully consider the anisotropic relaxation behavior of the composites. An anisotropic viscoelastic constitutive model was developed to describe the time- and temperature- dependent properties of composites. The generalized Maxwell viscoelastic parameters of the PEEK resin were obtained by characterizing the relaxation modulus main curve in a wide temperature range (25~200℃). Then, by semi-empirical solution for equivalent mechanical properties of composite materials, a three-dimensional anisotropic constitutive model was developed. Finally, the developed model has been verified by comparing with the high temperature relaxation experiments and the finite element simulation by the representative volume element (RVE) along the transverse direction. Overall, the developed model can be used to simulate the forming process and design the high temperature mechanical properties of CF/PEEK composites.
- thermoplastic composite /
- high temperature relaxation /
- viscoelasticity /
- homogenization /
- representative volume element

HTML全文

聚醚醚酮(PEEK)是一种半结晶热塑性聚合物，相较于传统的热固性环氧树脂，PEEK具有优异的力学性能，如高强度、高模量和高韧性，同时具有优异的热稳定性和化学惰性^[1-2]。因此，连续碳纤维增强聚醚醚酮(CF/PEEK)复合材料具有轻质、高强、易修复、可焊接等优异特性^[3-5]，同时PEEK的结晶特性使其在高于玻璃化转变温度(143℃左右)时仍具有较强承载能力。因此，CF/PEEK复合材料能够在200℃条件下长期服役，是新一代航空航天热端结构的优选材料，对我国航空航天飞行器结构的发展具有重要意义^[6-8]。

在高温使用时，PEEK基体中的非晶区将会经历玻璃化转变，导致其在高于玻璃化转变温度时出现明显的软化和松弛现象，同时会进一步引起CF/PEEK复合材料的各向异性黏弹性^[9-11]。由于CF/PEEK复合材料中，纤维排列的取向，将导致在垂直于纤维方向复合材料变形热衰减显著^[11-12]。考虑到新一代航天器在往复使用中的泛温度域加载条件，CF/PEEK复合材料的各向异性高温力学性能衰减，将对复合材料热结构响应的精确设计带来严峻挑战。

为了准确预测复合材料的高温条件下的各向异性力学性能衰减，国内外研究者针对复合材料提出了一些力学性能预测方法。早在20世纪50年代，力学家Eshelby^[13] 提出了等效夹杂理论，研究了无限大均匀各向同性弹性体中存在相变夹杂的问题，并基于该理论进行了复合材料性能预测，但是该理论是基于线弹性无限域假设得到，对有限域的问题求解困难。随着计算机技术的快速发展，有限元方法的出现为解决有限域问题的求解带来了可能，尤其是复合材料的多尺度有限元方法的发展，通过构建复合材料细观结构有限元模型，实现了复合材料性能的预测^[14-15]。有学者采用材料力学方法构建了复合材料等效性能预测的半经验解法，仅通过复合材料中纤维和基体的材料参数和体积分数，便可以很方便计算出材料的等效弹性常数^[16-18]。研究发现复合材料在高温下的力学响应不再是线弹性响应，其响应呈现出明显的与时间和温度相关的黏弹性响应^[19-20]。梁军等^[21]采用 Eshelby的等效夹杂方法研究了复合材料的黏弹性问题，预报了颗粒增强复合材料的蠕变行为。任超等^[22]基于黏弹性本构结合有限元方法预测了纤维增强复合材料黏弹性响应。Fritzen等^[23]采用代表性体积单元方法、考虑基体黏弹性，建立了颗粒增强复合材料的黏弹性蠕变本构模型，采用有限元均匀化仿真获取了复合材料等效性能参数。

上述已有的复合材料高温预测方法能够简单、满足一定精度地解决结构仿真问题^[24]，但是仍难以依据基体黏弹性以及纤维体积含量直接预测复合材料的各向异性黏弹性。针对这一问题，2020年，Fliegener^[25]提出了各向异性Kelvin-Voigt模型，能够依据基体黏弹性以及纤维体积含量准确预测的复合材料各向异性蠕变行为。Fliegener提出的Kelvin-Voigt形式具有清晰的物理意义同时其参数易于校准，然而 Kelvin-Voigt形式的蠕变模型由于存在多个粘壶串联，相较于并联形式的广义Maxwell形式，Kelvin-Voigt在复杂加载条件下收敛较慢。

本文基于广义Maxwell模型以及复合材料细观力学方法，设计了一种描述CF/PEEK复合材料力学性能随时间、温度演化的各向异性黏弹本构模型。该模型能够依据基体黏弹性和纤维体积分数，准确预测泛温度域(25~200℃)下单向CF/PEEK复合材料的各向异性黏弹性力学响应，通过与试验结果和代表性体积单元(RVE)仿真结果的对比验证，证明了这一各向异性黏弹本构模型的有效性。

1. 热塑性复合材料松弛模型

本研究的目的是构建CF/PEEK复合材料的各向异性黏弹性泛温度域本构模型。基于各向同性广义Maxwell模型，直接描述PEEK基体的响应，并考虑线弹性纤维的作用，基于复合材料细观力学的半经验解法将该模型推广到复合材料的各向异性黏弹性响应。

1.1 树脂基体本构模型

本模型中树脂基体采用广义Maxwell黏弹模型，为一个弹性元件以及多个Maxwell元件并联，如图1所示。

图 1 广义Maxwell松弛模型

Figure 1. Generalized Maxwell relaxation model

E—Elastic modulus of spring; η—Viscosity of dashpot

下载: 全尺寸图片幻灯片

对热塑性树脂基体黏弹性采用广义Maxwell模型进行描述。对PEEK在不同温度下开展松弛试验，基于时温等效原理获取黏弹性基体的松弛模量主曲线^[26]，其松弛模量表达式为

$E = {E_{\rm{0}}} + \sum\limits_{p = 1}^n {{E_p}} {{\rm{e}}^{ - \frac{t}{{{\tau _p}}}}}$

(1)

式中：E₀为模型中平衡分支的模量；E_p为非平衡分支中弹性元件模量；t为时间；τ_p为每个非平衡分支的松弛时间：

${\tau _p} = \tau _{{\rm{ref}}}^p{\alpha _T}$

(2)

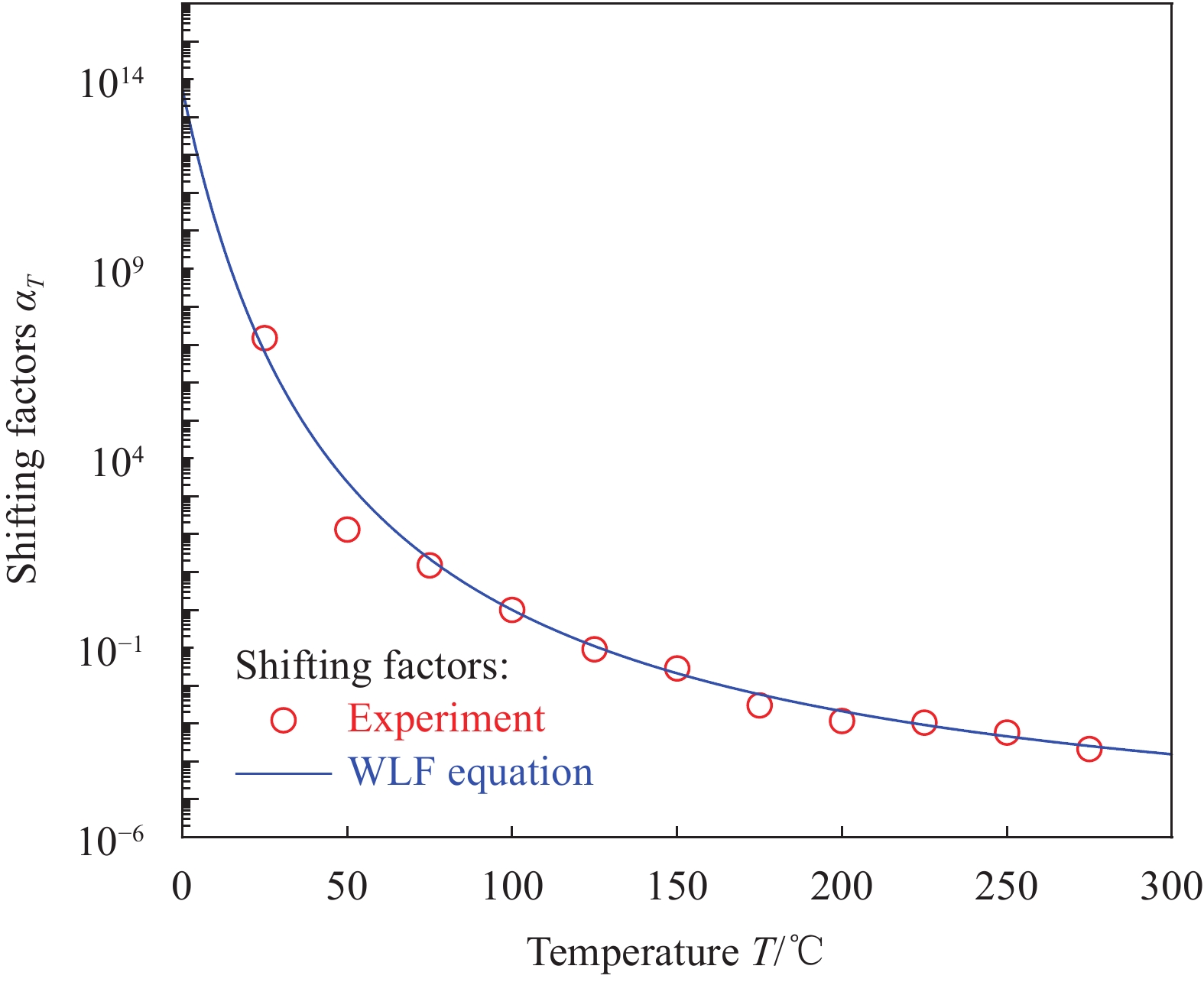
式中： $\tau _{{\rm{ref}}}^p$ 为参考温度下的非平衡分支松弛时间；α_T为时温转换因子，其一般用Williams-Landel-Ferry (WLF)方程描述^[27-29]：

$\lg \left( {{\alpha _T}} \right) = - \frac{{{C_{\rm{1}}}\left( {T - {T_{\rm{R}}}} \right)}}{{{C_{\rm{2}}} + \left( {T - {T_{\rm{R}}}} \right)}}$

(3)

式中：T_R为参考温度；C₁和C₂是与材料有关的常数。

参考Fliegener 等^[25]提出的黏弹性本构推导方法，基于广义Maxwell模型推导PEEK的一维黏弹性本构方程。在恒定应变ε₀作用下，模型的时变应力响应由下式给出：

$\sigma \left( t \right) = \left( {{E_0} + \sum\limits_{p = 1}^n {{E_p}} {{\rm{e}}^{ - \frac{t}{{{\tau _p}}}}}} \right){\varepsilon _0}$

(4)

式中：E_p表示弹性模量；t 表示时间；τ_p表示松弛时间：

${\tau _p} = \frac{{{\eta _p}}}{{{E_p}}}\begin{array}{*{20}{c}} {}&{p = 1,2,3 \cdots n} \end{array}$

(5)

式中：η_p为表征材料黏度的参数。

对于非恒定应变，t时刻的应力σ(t)由标准的卷积公式给出：

$\sigma \left( t \right) = \int\limits_0^t {\left( {{E_0} + \sum\limits_{p = 1}^n {{E_p}} {{\rm{e}}^{ - \frac{{t - {t^*}}}{{{\tau _p}}}}}} \right)} \frac{{\partial \varepsilon }}{{\partial t}}\left| {_{t = {t^*}}{\rm{d}}{t^*}} \right.$

(6)

由玻尔兹曼的叠加原理可知，上式对应变加载历程进行积分，在数值计算方面效率低。为了避免计算效率低下的问题，将式(6)写为增量形式。求解与时间无关项的积分得到：

$\sigma \left( t \right) = {E_0}\varepsilon \left( t \right) + \sum\limits_{p = 1}^n {\int\limits_0^t {{E_p}} {{\rm{e}}^{ - \frac{{t - {t^*}}}{{{\tau _p}}}}}} \frac{{\partial \varepsilon }}{{\partial t}}\left| {_{t = {t^*}}{\rm{d}}{t^*}} \right.$

(7)

其中最后一项定义了广义Maxwell模型中非平衡分支随时间变化的应力之和，体现了黏弹性效应导致的应力松弛现象。

式(7)的每一个非平衡分支的黏弹性应力σⁱ_p(t)采用遗传积分定义：

$\begin{split} \sigma _p^i\left( t \right) = &\int\limits_0^{t - {\rm{d}}t} {{E_p}} {{\rm{e}}^{ - \frac{{t - {t^*}}}{{{\tau _p}}}}}\frac{{\partial \varepsilon }}{{\partial t}}\left| {_{t = {t^*}}{\rm{d}}{t^*}} \right. + \\& \int\limits_{t - {\rm{d}}t}^t {{E_p}} {{\rm{e}}^{ - \frac{{t - {t^*}}}{{{\tau _p}}}}}\frac{{\partial \varepsilon }}{{\partial t}}\left| {_{t = {t^*}}{\rm{d}}{t^*}} \right. \end{split}$

(8)

将时间历史分为从0到t−dt和剩余的时间区间t−dt到t两段。第一段可以认为是在t−dt段内残余的黏弹性应力，第二段积分可以通过积分计算得到，假设应变的变化量为可以忽略的小量，松弛应力的增量为

${\rm{d}}\sigma _p^i\left( t \right) = \left( {{E_p}{\tau _p}\frac{{\partial \varepsilon }}{{\partial t}} - \sigma _p^i\left( {t - {\rm{d}}t} \right)} \right)\left( {1 - {{\rm{e}}^{ - \frac{{{\rm{d}}t}}{{{\tau _p}}}}}} \right)$

(9)

由此给出了黏弹性松弛应力σⁱ_p。由于黏弹性聚合物的松弛是一个缓慢长期的过程，在推导上式时，忽略了dt时间内的应变速率 $\partial \varepsilon /\partial t$ (即应变对时间的二阶导数)的变化。

将一维本构方程写为增量形式：

${\rm{d}}\sigma \left( t \right) = {E_0}{\rm{d}}\varepsilon \left( t \right) + \sum\limits_{p = 1}^n {{\rm{d}}\sigma _p^i\left( t \right)}$

(10)

将式(9)的应力增量代入式(10)中，求得应变增量表达式如下：

${\rm{d}}\varepsilon \left( t \right) = \frac{{{\rm{d}}\sigma \left( t \right) + \displaystyle\sum\limits_{p = 1}^n {\sigma _p^i(t - {\rm{d}}t)(1 - {{\rm{e}}^{ - \frac{{{\rm{d}}t}}{{{\tau _p}}}}})} }}{{\tilde E\left( t \right)}}$

(11)

式中： $\tilde E\left( t \right)$ 为材料随时间变化的等效刚度：

$\tilde E\left( t \right) = {E_0} + \sum\limits_{p = 1}^n {{E_p}\frac{{{\tau _p}}}{{{\rm{d}}t}}(1 - {{\rm{e}}^{ - \frac{{{\rm{d}}t}}{{{\tau _p}}}}})}$

(12)

式(9)定义了每个非平衡分支应力σⁱ_p的增量，从本构方程(11)可以看出，t时刻的应变增量 ${\rm{d}}\varepsilon \left( t \right)$ 是应力增量dσ(t)、式(12)的等效刚度 $\tilde E\left( t \right)$ 、应力σⁱ_p(t−dt)的显示表达式。通过求解方程(11)即可获得黏弹性基体的松弛响应。

1.2 复合材料本构模型

对于连续单向纤维增强复合材料，由于增强相的存在会使材料表现出各向异性。这种情况下的各向异性模型是通过各向同性黏弹性模型(式(11))与横观各向同性胡克定律的叠加得到的。因此，总应变增量由下式给出：

${\rm{d}}{\varepsilon _{ij}} = {\rm{d}}\varepsilon _{ij}^{{\rm{el}}} + {\rm{d}}\varepsilon _{ij}^{{\rm{ve}}}$

(13)

其中黏弹性的应变增量 $d\varepsilon _{ij}^{ve}$ 由方程(11)表示，纤维的弹性应变增量由下式表示：

${\rm{d}}\varepsilon _{ij}^{{\rm{el}}} = {S_{ijkl}}{\rm{d}}\sigma _{ij}^{{\rm{el}}}$

(14)

S_ijkl为横观各向同性线性弹性材料的标准柔度矩阵。

由于纤维的存在，单向连续纤维增强复合材料表现出正交各向异性响应，基于王震鸣等^[24]提出的复合材料等效弹性参数计算方法进行修正，从而获得了复合材料在不同方向弹性模量与温度和时间的关系：

$\begin{split} & {E_{\rm{1}}}\left( {t,T} \right) = {E_{{\rm{f1}}}}{V_{\rm{f}}} + {E_{\rm{m}}}\left( {t,T} \right){V_{\rm{m}}} \\& {E_{\rm{2}}}\left( {t,T} \right) = \frac{{\left( {{V_{\rm{f}}} + {\eta _{\rm{2}}}\left( {t,T} \right){V_{\rm{m}}}} \right){E_{{\rm{f2}}}}{E_m}\left( {t,T} \right)}}{{{V_{\rm{f}}}{E_{\rm{m}}}\left( {t,T} \right) + {\eta _{\rm{2}}}\left( {t,T} \right){V_{\rm{m}}}{E_{{\rm{f2}}}}}} \end{split}$

(15)

式中：E_f1和E_f2分别为纤维的纵向和横向模量；V_f和V_m分别为复合材料中纤维和基体的体积分数；E_m(t,T)为基体随时间和温度变化的模量；η₂(t,T)是与纤维和基体有关的参数，表达式如下：

$\begin{split} {\eta _{\rm{2}}}\left( {t,T} \right) =& \left( {1.1{\rm{ - }}\sqrt {\frac{{{E_{\rm{m}}}\left( {t,T} \right)}}{{{E_{{\rm{f2}}}}}}} {\rm{ + }}\frac{{3.5{E_{\rm{m}}}\left( {t,T} \right)}}{{{E_{{\rm{f2}}}}}}} \right) \\& {\frac{{0.115}}{{1{\rm{ - }}{V_{\rm{m}}}}}\left( {1{\rm{ + }}0.22{V_{\rm{f}}}} \right)} \end{split}$

(16)

复合材料剪切模量与温度和时间关系的表达式如下：

$\begin{split} & {G_{{\rm{12}}}}\left( {t,T} \right) = \frac{{\left( {{V_{\rm{f}}} + {\eta _{{\rm{12}}}}{V_{\rm{m}}}} \right){G_{{\rm{f12}}}}{G_{\rm{m}}}\left( {t,T} \right)}}{{{V_{\rm{f}}}{G_{\rm{m}}}\left( {t,T} \right) + {\eta _{{\rm{12}}}}{V_{\rm{m}}}{G_{{\rm{f12}}}}}} \\& {G_{{\rm{23}}}}\left( {t,T} \right) = \frac{{\left( {{V_{\rm{f}}} + {\eta _{{\rm{23}}}}{V_{\rm{m}}}} \right){G_{{\rm{f23}}}}{G_{\rm{m}}}\left( {t,T} \right)}}{{{V_{\rm{f}}}{G_{\rm{m}}}\left( {t,T} \right) + {\eta _{{\rm{23}}}}{V_{\rm{m}}}{G_{{\rm{f23}}}}}} \end{split}$

(17)

式中：G_f12和G_f23分别为纤维的面内和面外剪切模量；G_m(t,T)为基体随时间和温度变化的剪切模量；η₁₂(t,T)和η₂₃(t,T) 是与纤维和基体有关的参数，表达式如下：

$\begin{split} & {\eta _{{\rm{12}}}}\left( {t,T} \right) = 0.28 + \sqrt {\frac{{{E_{\rm{m}}}\left( {t,T} \right)}}{{0.5{E_{{\rm{f2}}}}{\rm{ + }}0.5{E_{{\rm{f1}}}}}}} \\& {\eta _{{\rm{23}}}}\left( {t,T} \right) = 0.388 - 0.665\sqrt {\frac{{{E_{\rm{m}}}\left( {t,T} \right)}}{{{E_{{\rm{f2}}}}}}} + \frac{{{E_{\rm{m}}}\left( {t,T} \right)}}{{{E_{{\rm{f2}}}}}} \end{split}$

(18)

复合材料的泊松比表达式如下：

$\begin{split} & {\mu _{{\rm{12}}}} = {\mu _{{\rm{f12}}}}{V_{\rm{f}}} + {\mu _{\rm{m}}}{V_{\rm{m}}} \\& {\mu _{{\rm{23}}}} = \frac{{{\mu _{{\rm{12}}}}\left( {1 - {\mu _{{\rm{12}}}}\dfrac{{{E_{\rm{2}}}\left( {t,T} \right)}}{{{E_{\rm{1}}}\left( {t,T} \right)}}} \right)}}{{1 - {\mu _{{\rm{12}}}}}} \end{split}$

(19)

式中：μ_f12和μ_m分别为纤维和基体的泊松比。

将以上公式获取的复合材料的等效弹性参数代入柔度矩阵，通过方程求解可获得复合材料的松弛响应：

${\varepsilon _{ij}} = {S_{ijkl}}\left( {t,T} \right){\sigma _{ij}}$

(20)

式中：S_ijkl(t,T)为单向连续纤维增强复合材料的等效柔度矩阵。

2. 试验验证与数值仿真

为了验证本文建立的CF/PEEK复合材料泛温度域本构模型的合理性与有效性，本节拟通过选取不同温度开展松弛试验，同时结合有限元数值仿真对该本构模型进行验证。

2.1 试验材料

本试验中所用的CF/PEEK热塑性复合材料板由TEIJIN公司生产的TPUD PEEK-HTS45预浸料模压制成，纤维体积分数为59vol%。试验在三思纵横生产的包含高低温环境箱的UTM5000电子万能试验机上开展。试验中所用的PEEK试样为哑铃形，中间部分宽度6.36 mm，厚度5.94 mm，PEEK试样如图2(a)所示，CF/PEEK试样名义尺寸为150 mm×15 mm×3 mm，CF/PEEK试样如图2(b)所示。

图 2 聚醚醚酮(PEEK)及碳纤维/聚醚醚酮(CF/PEEK)松弛试样

Figure 2. Polyether ether ketone (PEEK) and carbon fiber/ polyether ether ketone (CF/PEEK) relaxation samples

下载: 全尺寸图片幻灯片

2.2 松弛试验

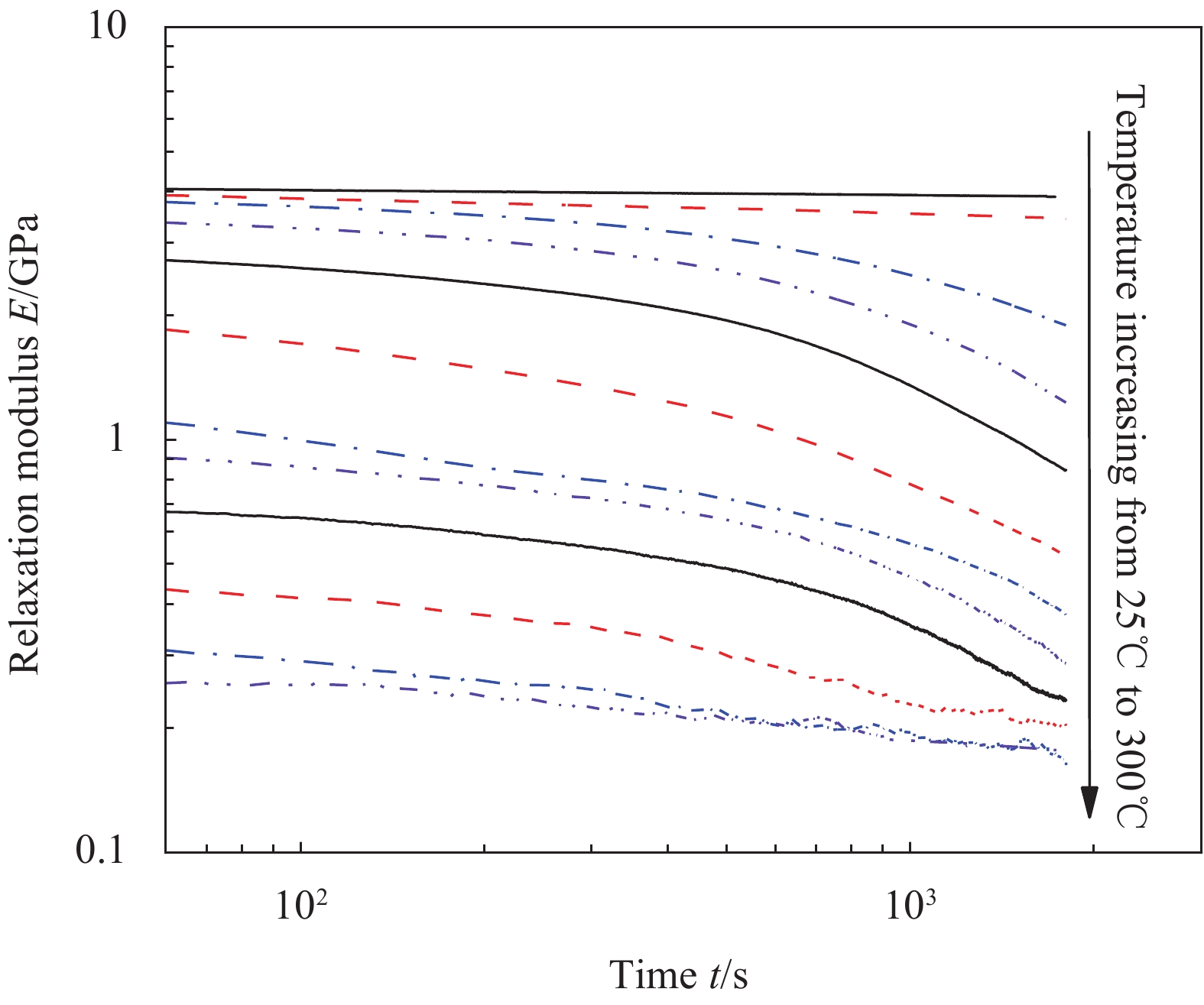
为了获得CF/PEEK复合材料中PEEK的黏弹性本构参数，从25~300℃每隔25℃对PEEK试样开展松弛试验，松弛试验的应变为1%，在每个温度下松弛30 min，获得PEEK在不同温度下的模量松弛曲线，如图3所示。

图 3 温度从25℃到300℃的PEEK松弛试验曲线

Figure 3. PEEK relaxation test curves from 25℃ to 300℃

下载: 全尺寸图片幻灯片

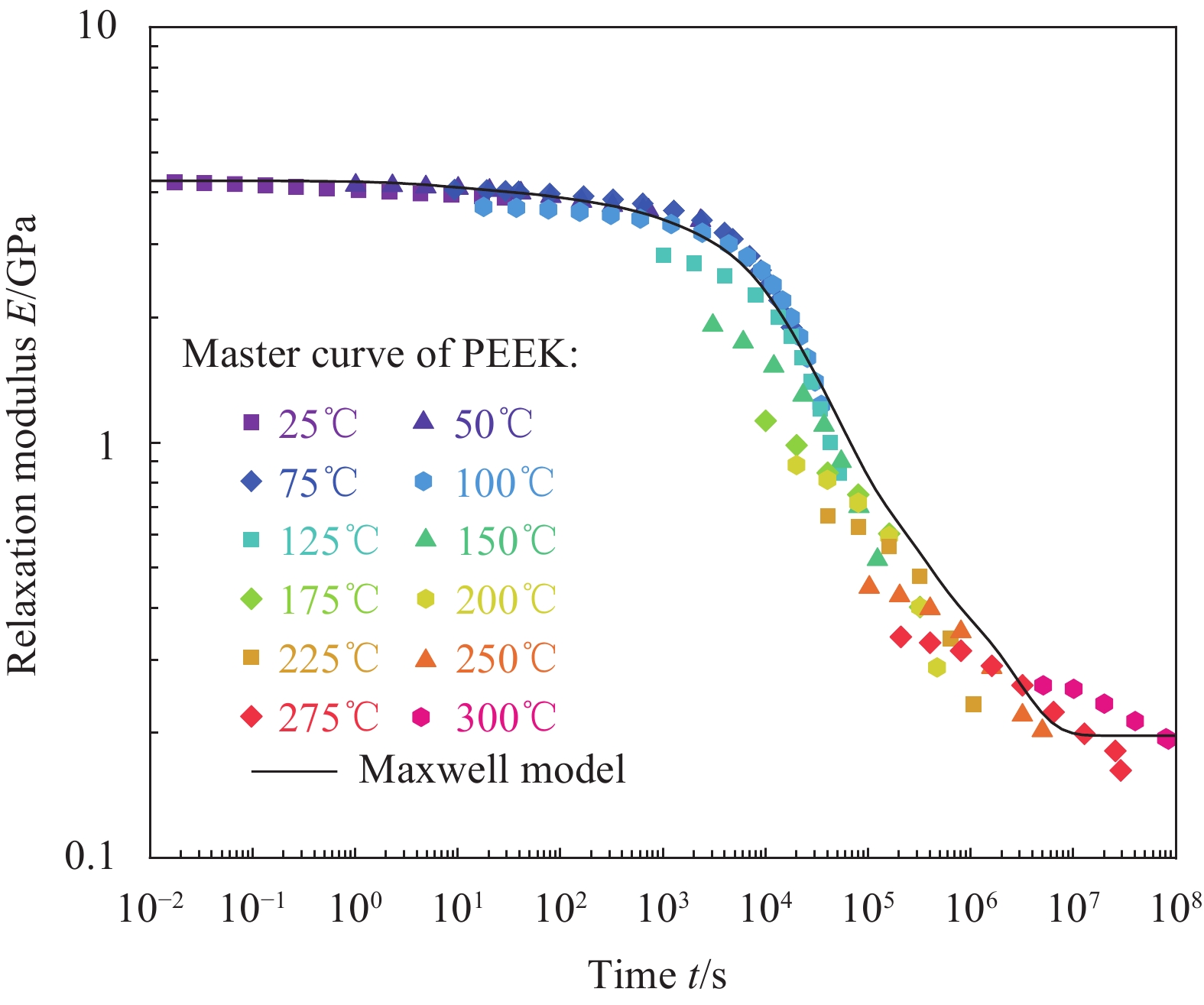
基于时温等效原理获取PEEK的松弛模量主曲线，首先取100℃作为参考温度，然后将其余温度下的松弛曲线通过在半对数坐标系中进行平移，与参考温度下的松弛曲线进行合并组成PEEK的松弛模量主曲线，基于广义Maxwell模型对获得的松弛模量主曲线进行拟合，结果如图4所示，空心圆圈代表试验获得的PEEK松弛模量主曲线，实线为Maxwell模型拟合得到的松弛模量主曲线，模型与试验结果吻合良好。并求出每个温度下对应的时温转换因子，由WLF 方程拟合的时温转换因子曲线如图5所示。

图 4 PEEK松弛模量主曲线

Figure 4. Relaxation master curves of PEEK

下载: 全尺寸图片幻灯片

图 5 PEEK时温转换因子曲线

Figure 5. Time-temperature shifting factors curve of PEEK

下载: 全尺寸图片幻灯片

2.3 数值仿真

细观力学计算模型是通过对材料细观结构选取代表性体积单元，并对其进行应力均匀化从而实现对材料等效性能的预测。针对由纤维和基体两相材料复合而成的单向纤维复合材料，纤维在基体中呈点阵分布，因此单向复合材料的RVE微观结构被理想化为圆形纤维在聚合物基体中平行均匀分布^[30-31]。本文利用有限元软件对复合材料进行松弛仿真计算，构建了如图6所示的长方体代表性体积单元模型，该模型在边界处满足几何周期性边界条件，从而通过施加周期性边界条件，可达到使用较小的计算量准确仿真复合材料力学响应的目的^[32-34]。

图 6 CF/PEEK复合材料代表性体积单元模型

Figure 6. Representative volume element model of CF/PEEK composite

下载: 全尺寸图片幻灯片

有限元仿真计算中细观单胞模型的纤维材料为T300碳纤维，材料参数取自文献[35]，具体参数如表1所示，基体材料为黏弹性的PEEK热塑性树脂，其黏弹性参数由2.2节中的松弛试验获得，具体参数如表2所示。

表 1 碳纤维材料弹性常数^[35]

Table 1. Elastic constants of carbon fiber materials^[35]

E_f1/GPa	E_f2/GPa	μ₁₂	μ₂₃	G₁₂/GPa	G₂₃/GPa
230	15	0.2	0.07	15	7
Notes：E_f1—Longitudinal modulus; E_f2—Transverse modulus; μ₁₂—Poisson ratio in 12 directions; μ₂₃—Poisson ratio in 23 directions; G₁₂—Axial shear modulus; G₂₃—Transverse shear modulus.

下载: 导出CSV

| 显示表格

3. 模型验证与讨论

本部分将结合试验与模型计算结果进行对比，从而说明该本构模型对CF/PEEK复合材料松弛响应预测的有效性。所提出的本构模型需要从三方面进行检验：(1)本模型对单向CF/PEEK复合材料纵向在高温条件下的应力松弛响应预测是否适用；(2)本模型对CF/PEEK复合材料横向在不同温度下的应力松弛响应预测是否可靠；(3)本模型对含有不同纤维体积分数的CF/PEEK复合材料横向应力松弛响应预测是否有效。

3.1 CF/PEEK复合材料纵向松弛响应

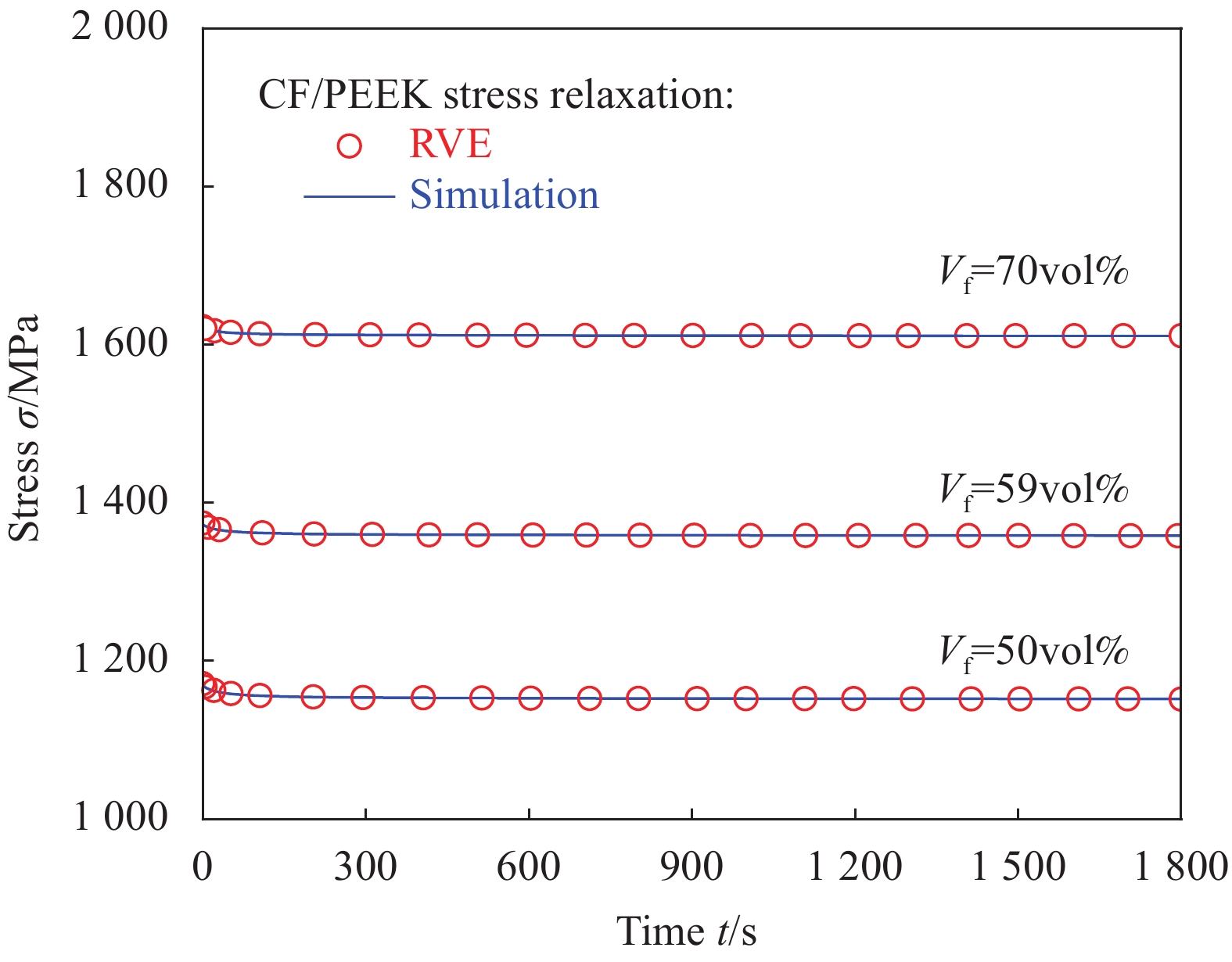
针对复合材料在高温下的纵向响应，在200℃条件下分别对体积分数为50vol%、59vol%和70vol%的CF/PEEK复合材料纵向施加1%应变，进行纵向松弛实验仿真计算，通过将有限元仿真结果与本文的数值模型进行对比，结果如图7所示。

表 2 PEEK广义Maxwell模型参数

Table 2. Generalized Maxwell model parameters of PEEK

Parameter	Nonequilibrium branch							Equilibrium branch
Parameter	1	2	3	4	5	6	7	Equilibrium branch
Modulus E_p/MPa	173.78	198.68	252.92	1431.96	1297.08	442.70	277.30	197.16
τⁱ_ref /s	7.851	78.51	785.1	9159.5	39255	225100	2117000	—
WLF parameters	T_R/K	373.15		C₁	6.63		C₂	148.21
Notes：τⁱ_ref—Relaxation time; T_R—Reference temperature; C₁, C₂—Constants related to materials.

下载: 导出CSV

| 显示表格

图 7 CF/PEEK复合材料纵向松弛曲线

Figure 7. Longitudinal relaxation curves of CF/PEEK composite material

RVE—Representative volume element

下载: 全尺寸图片幻灯片

图中空心圆点为代表性体积单元的仿真计算结果，实线为本文中的黏弹性本构模型的仿真计算结果，两种方法的计算结果在CF/PEEK复合材料纵向非常一致。CF/PEEK复合材料纵向纤维弹性模量远远大于基体的弹性模量，在200℃条件下，纤维的弹性模量几乎不变，基体高温下软化松弛导致弹性模量随时间变小，然而复合材料纵向主要依靠纤维承载，因此，即使在高温条件下复合材料纵向的弹性模量变化也很小，纵向的松弛效应并不明显。根据松弛仿真计算结果发现，CF/PEEK热塑性复合材料纵向应力主要受纤维体积分数的影响较大，温度造成的基体松弛效应对复合材料纵向响应影响很小，这与Fliegener等^[25]的试验研究结果一致。

3.2 温度对CF/PEEK复合材料横向松弛的影响

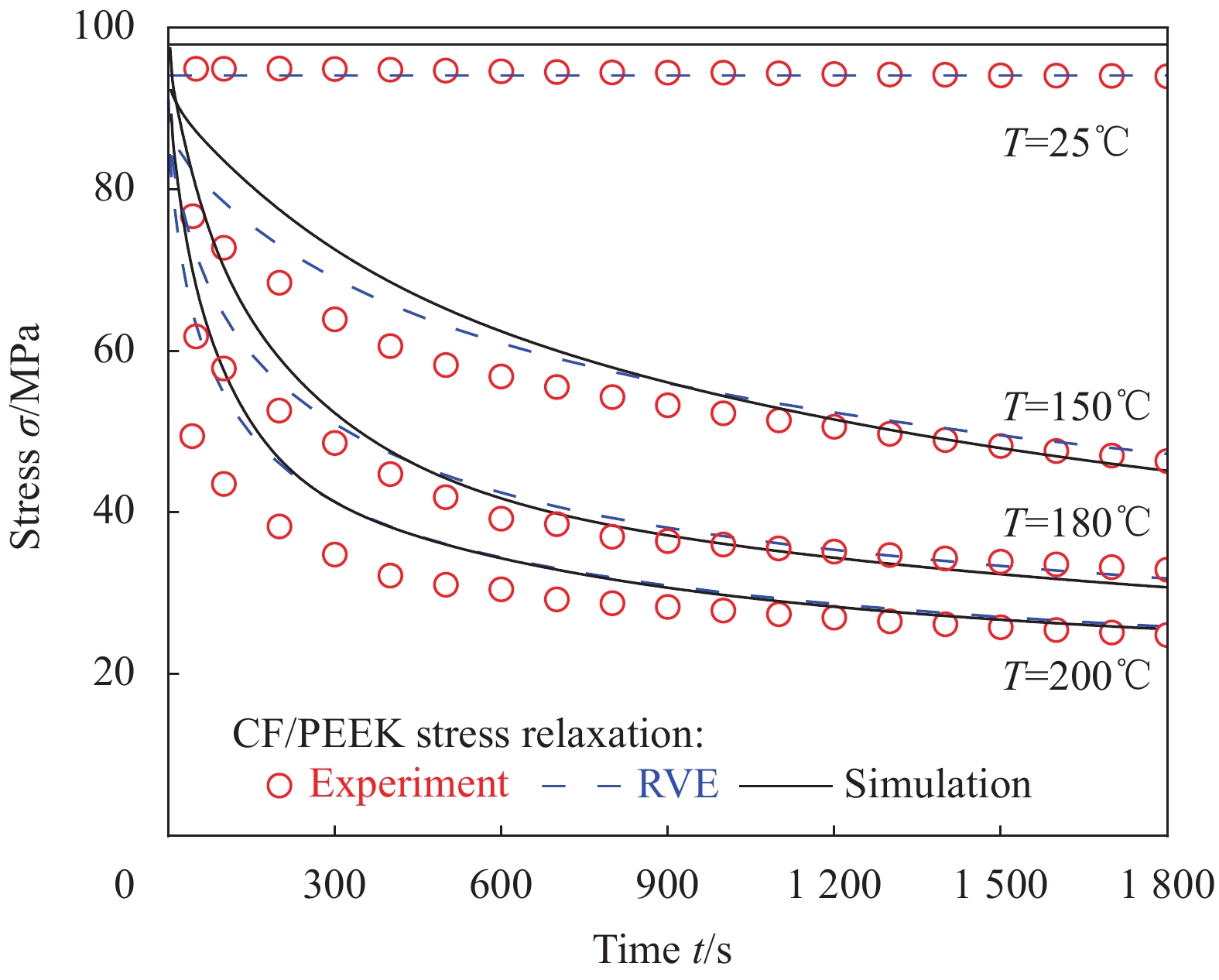
为了研究温度对CF/PEEK复合材料横向松弛的影响，分别在25、150、180和200℃对复合材料施加1%的应变，开展横向松弛试验，将试验获得的松弛曲线与数值方法和代表性体积单元的计算结果进行对比，结果如图8所示。

图 8 CF/PEEK复合材料在不同温度下的横向松弛曲线

Figure 8. Transverse relaxation curves of CF/PEEK composite materials at different temperatures

下载: 全尺寸图片幻灯片

随着温度升高，CF/PEEK复合材料横向松弛效应越来越明显，根据试验和仿真计算结果说明在常温下，横向应力几乎没有松弛，可以解释CF/PEEK复合材料在常温下，其横向近似认为是线弹性响应。在高温下，复合材料的横向松弛效应远不如纯基体材料明显，说明纤维的存在会阻碍基体的松弛。

在不同温度下，复合材料横向松弛试验结果与RVE和本论文中的本构模型仿真结果吻合良好，证明了本文中所采用的各向异性本构模型可以有效预测泛温度域(25~200℃)下CF/PEEK复合材料横向的力学性能。

3.3 体积分数对CF/PEEK复合材料横向松弛的影响

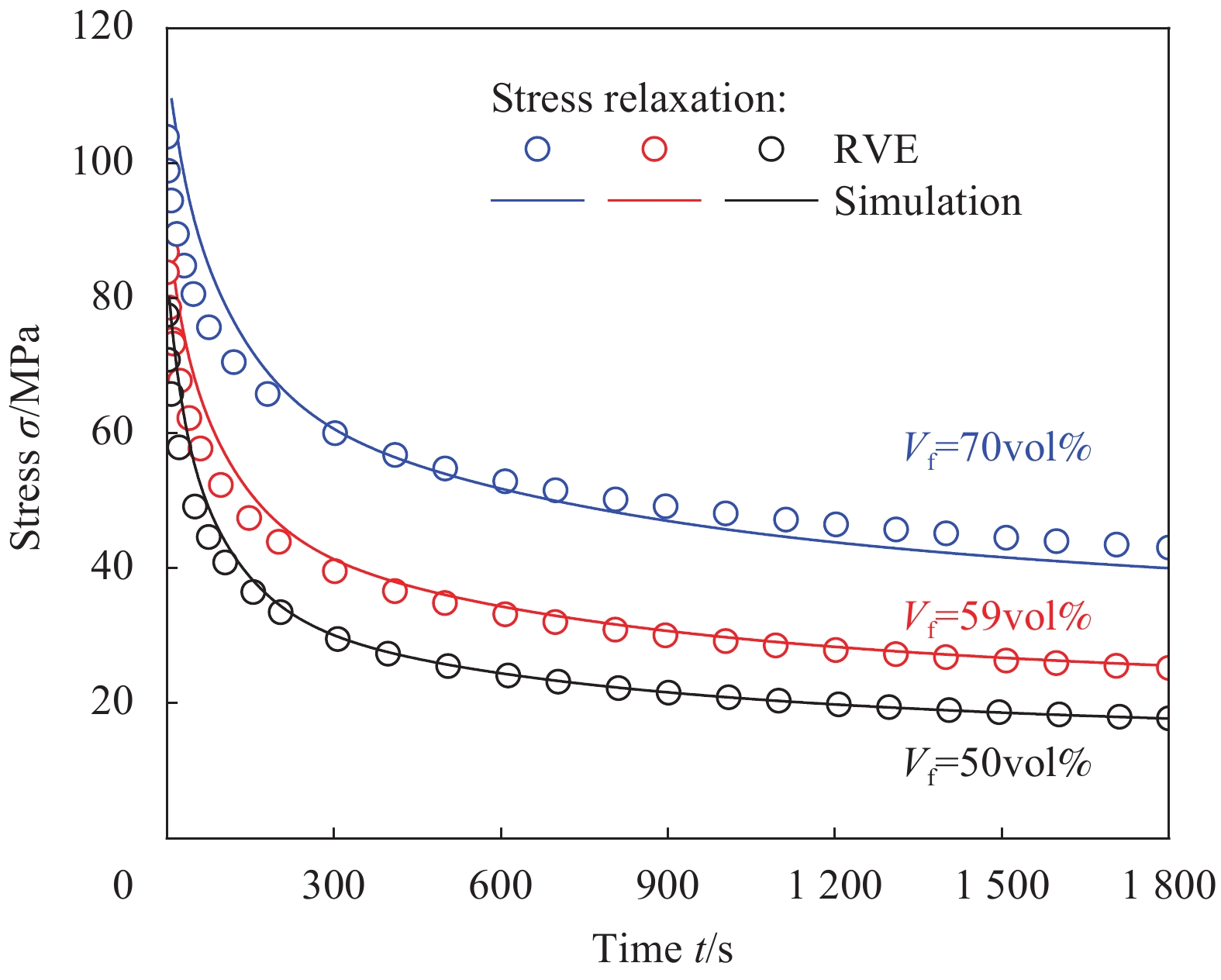
CF/PEEK复合材料中的碳纤维在高温下响应属于线弹性，而且相比黏弹性的基体，其模量较大，为了研究CF/PEEK复合材料中纤维含量对复合材料横向松弛响应的影响规律，200℃条件下，通过构建纤维含量50vol%、59vol%和70vol%的CF/PEEK复合材料细观单胞模型，采用代表性体积单元方法进行有限元仿真计算，将结果与本文中本构模型的计算结果进行对比，如图9所示。

图 9 不同纤维体积分数的CF/PEEK复合材料横向松弛曲线

Figure 9. Transverse relaxation curves of CF/PEEK composites with different fiber volume fractions

下载: 全尺寸图片幻灯片

CF/PEEK复合材料中纤维的体积分数对横向松弛有所影响，随着纤维体积分数增大，横向松弛效应逐渐降低，线弹性纤维的存在对横向松弛具有阻碍效应，适当提高纤维体积分数有利于提高复合材料高温下的横向力学性能。

4. 结论

本文基于广义Maxwell模型以及复合材料细观力学方法，发展了一种描述连续碳纤维增强聚醚醚酮(CF/PEEK)复合材料力学性能随时间、温度演化的各向异性黏弹本构模型。该模型能够依据基体黏弹性和纤维体积分数，准确预测泛温度域(25~200℃)下单向CF/PEEK复合材料的各向异性黏弹性力学响应，结合代表性体积单元的仿真计算，进一步揭示了温度和纤维体积分数对复合材料横向松弛的影响规律，结果表明：

(1) CF/PEEK热塑性复合材料在高温环境下的力学响应受黏弹性基体影响，由于纤维的弹性模量远大于基体的弹性模量，沿纤维纵向应力松弛表现得并不明显，但是在垂直于纤维的方向，复合材料的力学响应受基体影响较大，复合材料的响应呈现出明显的应力松弛效应。

(2) CF/PEEK热塑性复合材料在恒定应变的高温环境下，随着使用温度升高，热塑性PEEK基体的黏弹性效应越显著，横向的应力松弛随温度升高表现得越明显。

(3) CF/PEEK热塑性复合材料中碳纤维的存在会阻碍基体的应力松弛效应，随着纤维体积分数升高，复合材料横向应力松弛效应逐渐下降。

图 1 广义Maxwell松弛模型

Figure 1. Generalized Maxwell relaxation model

E—Elastic modulus of spring; η—Viscosity of dashpot

下载: 全尺寸图片幻灯片

图 2 聚醚醚酮(PEEK)及碳纤维/聚醚醚酮(CF/PEEK)松弛试样

Figure 2. Polyether ether ketone (PEEK) and carbon fiber/ polyether ether ketone (CF/PEEK) relaxation samples

下载: 全尺寸图片幻灯片

图 3 温度从25℃到300℃的PEEK松弛试验曲线

Figure 3. PEEK relaxation test curves from 25℃ to 300℃

下载: 全尺寸图片幻灯片

图 4 PEEK松弛模量主曲线

Figure 4. Relaxation master curves of PEEK

下载: 全尺寸图片幻灯片

图 5 PEEK时温转换因子曲线

Figure 5. Time-temperature shifting factors curve of PEEK

下载: 全尺寸图片幻灯片

图 6 CF/PEEK复合材料代表性体积单元模型

Figure 6. Representative volume element model of CF/PEEK composite

下载: 全尺寸图片幻灯片

图 7 CF/PEEK复合材料纵向松弛曲线

Figure 7. Longitudinal relaxation curves of CF/PEEK composite material

RVE—Representative volume element

下载: 全尺寸图片幻灯片

图 8 CF/PEEK复合材料在不同温度下的横向松弛曲线

Figure 8. Transverse relaxation curves of CF/PEEK composite materials at different temperatures

下载: 全尺寸图片幻灯片

图 9 不同纤维体积分数的CF/PEEK复合材料横向松弛曲线

Figure 9. Transverse relaxation curves of CF/PEEK composites with different fiber volume fractions

下载: 全尺寸图片幻灯片

表 1 碳纤维材料弹性常数^[35]

Table 1 Elastic constants of carbon fiber materials^[35]

E_f1/GPa	E_f2/GPa	μ₁₂	μ₂₃	G₁₂/GPa	G₂₃/GPa
230	15	0.2	0.07	15	7
Notes：E_f1—Longitudinal modulus; E_f2—Transverse modulus; μ₁₂—Poisson ratio in 12 directions; μ₂₃—Poisson ratio in 23 directions; G₁₂—Axial shear modulus; G₂₃—Transverse shear modulus.

下载: 导出CSV

表 2 PEEK广义Maxwell模型参数

Table 2 Generalized Maxwell model parameters of PEEK

Parameter	Nonequilibrium branch							Equilibrium branch
Parameter	1	2	3	4	5	6	7	Equilibrium branch
Modulus E_p/MPa	173.78	198.68	252.92	1431.96	1297.08	442.70	277.30	197.16
τⁱ_ref /s	7.851	78.51	785.1	9159.5	39255	225100	2117000	—
WLF parameters	T_R/K	373.15		C₁	6.63		C₂	148.21
Notes：τⁱ_ref—Relaxation time; T_R—Reference temperature; C₁, C₂—Constants related to materials.

下载: 导出CSV

参考文献(35)

[1]	CEBE P, CHUNG S Y, HONG S. Effect of thermal history on mechanical properties of polyetheretherketone below the glass transition temperature[J]. Journal of Applied Polymer Science,1987,33(2):487-503.
[2]	WANG P, ZOU B, XIAO H, et al. Effects of printing parameters of fused deposition modeling on mechanical properties, surface quality, and microstructure of PEEK[J]. Journal of Materials Processing Technology,2019,271:62-74. DOI: 10.1016/j.jmatprotec.2019.03.016
[3]	孙银宝, 李宏福, 张博明. 连续纤维增强热塑性复合材料研发与应用进展[J]. 航空科学技术, 2016, 27(5):01-07. SUN Yinbao, LI Hongfu, ZHANG Boming. Progress in research and application of continuous fiber reinforced thermoplastic composites[J]. Aeronautical Science & Technology,2016,27(5):01-07(in Chinese).
[4]	ZHU K, TAN H, WANG Y, et al. Crystallization and mechanical properties of continuous carbon fiber reinforced polyether-ether-ketone composites[J]. Fibers and Polymers,2019,20(4):839-846. DOI: 10.1007/s12221-019-8791-5
[5]	DIEZ-PASCUAL A M, NAFFAKH M, GOMEZ M A, et al. Development and characterization of PEEK/carbon nanotube composites[J]. Carbon,2009,47(13):3079-3090. DOI: 10.1016/j.carbon.2009.07.020
[6]	肇研, 刘寒松. 连续纤维增强高性能热塑性树脂基复合材料的制备与应用[J]. 材料工程, 2020(8):49-61. DOI: 10.11868/j.issn.1001-4381.2019.000209 ZHAO Yan, LIU Hansong. Preparation and application of continuous fiber reinforced high-performance thermoplastic resin matrix composites[J]. Materials Engineering,2020(8):49-61(in Chinese). DOI: 10.11868/j.issn.1001-4381.2019.000209
[7]	唐见茂. 航空航天材料发展现状及前景[J]. 航天器环境工程, 2013(2):115-121. DOI: 10.3969/j.issn.1673-1379.2013.02.001 TANG Jianmao. Development status and prospects of aerospace materials[J]. Spacecraft Environmental Engineering,2013(2):115-121(in Chinese). DOI: 10.3969/j.issn.1673-1379.2013.02.001
[8]	邢丽英, 包建文, 礼嵩明, 等. 先进树脂基复合材料发展现状和面临的挑战[J]. 复合材料学报, 2016, 33(7):1327-1338. XING Liying, BAO Jianwen, LI Songming, et al. Development status and challenges of advanced resin matrix composites[J]. Acta Materiae Compositae Sinica,2016,33(7):1327-1338(in Chinese).
[9]	LI W, GAZONAS G, BROWN E N, et al. Thermomechanical model for monotonic and cyclic loading of PEEK[J]. Mechanics of Materials,2019,129(JAN.):113-138.
[10]	LEI M, HAMEL C M, CHEN K, et al. Thermomechanical behaviors of polyether ether ketone (PEEK) with stretch-induced anisotropy[J]. Journal of the Mechanics and Physics of Solids,2020,148:104271.
[11]	GABRION X, PLACET V, TRIVAUDEY F, et al. About the thermomechanical behaviour of a carbon fibre reinforced high-temperature thermoplastic composite[J]. Composites Part B: Engineering,2016,95:386-394. DOI: 10.1016/j.compositesb.2016.03.068
[12]	WANG C, SUN C T. Experimental characterization of constitutive models for PEEK thermoplastic composite at heating stage during forming[J]. Journal of Composite Materials,1997, 31(15):1480-1506.
[13]	ESHELBY J D. The determination of the elastic field of an ellipsoidal inclusion, and related problems[J]. Proceedings of the Royal Society of London,1957,241(1226):376-396.
[14]	SUN C T, VAIDYA R S. Prediction of composite properties from a representative volume element[J]. Composites Science & Technology,1996,56(2):171-179.
[15]	OTERO F, OLLER S, MARTINEZ X, et al. Numerical homogenization for composite materials analysis. Comparison with other micro mechanical formulations[J]. Composite Structures,2015,122:405-416. DOI: 10.1016/j.compstruct.2014.11.041
[16]	CHAMIS C C. Simplified composite micromechanics equations for hygral, thermal and mechanical properties [C]. Houston: The Thirty-eight Annual Conference of the Society of the Plastics Industry, 1983: 1-10.
[17]	AFFDL J, KARDOS J L. The Halpin-Tsai equations: A review[J]. Polymer Engineering & Science,1976,16(5):344-352.
[18]	GENIN G M, BIRMAN V. Micromechanics and structural response of functionally graded, particulate-matrix, fiber-reinforced composites[J]. International Journal of Solids and Structures,2009,46(10):2136-2150. DOI: 10.1016/j.ijsolstr.2008.08.010
[19]	YI Y M, PARK S H, YOUN S K. Asymptotic homogenization of viscoelastic composites with periodic microstructures[J]. International Journal of Solids & Structures,1998,35(17):2039-2055.
[20]	LEI M, HAMEL C M, YUAN C, et al. 3D printed two-dimensional periodic structures with tailored in-plane dynamic responses and fracture behaviors[J]. Composites Science and Technology,2018,159:189-198.
[21]	梁军, 杜善义. 粘弹性复合材料力学性能的细观研究[J]. 复合材料学报, 2001, 18(1):97-100. LIANG Jun, DU Shanyi. Mesoscopic study on the mechanical properties of viscoelastic composite materials[J]. Acta Materiae Compositae Sinica,2001,18(1):97-100(in Chinese).
[22]	任超, 陈建钧, 潘红良. 纤维增强复合材料黏弹性行为的预测模型[J]. 复合材料学报, 2012, 29(1):162-168. REN Chao, CHEN Jianjun, PAN Hongliang. Prediction model for viscoelastic behavior of fiber reinforced composites[J]. Acta Materiae Compositae Sinica,2012,29(1):162-168(in Chinese).
[23]	FRITZEN F, BOHLKE T. Reduced basis homogenization of viscoelastic composites[J]. Composites Science and Technology,2013,76:84-91.
[24]	王震鸣, 游绍建. 单向复合材料弹性常数微观力学分析的探讨[J]. 复合材料学报, 1987, 4(4):72-78+102-103. WANG Zhenming, YOU Shaojian. Discussion on micromechanical analysis of elastic constants of unidirectional composites[J]. Acta Materiae Compositae Sinica,1987,4(4):72-78+102-103(in Chinese).
[25]	FLIEGENER S, HOHE J. An anisotropic creep model for continuously and discontinuously fiber reinforced thermoplastics[J]. Composites Science and Technology,2020,194:108168. DOI: 10.1016/j.compscitech.2020.108168
[26]	KAI Y, QI G, QI H J. Reduced time as a unified parameter determining fixity and free recovery of shape memory polymers[J]. Nature Communications, 2014, 5: 3066.
[27]	WILLIAMS M L, LANDEL R F, FERRY J D. The temperature dependence of relaxation mechanism in amorphous polymers and other glass forming liquid[J]. Journal of the American Chemical Society,1955,77(14):3701-3707.
[28]	KUKI Á, CZIFRAK K, KARGER-KOCSIS J, et al. An approach to predict the shape-memory behavior of amorphous polymers from dynamic mechanical analysis (DMA) data[J]. Mechanics of Time-Dependent Materials,2015,19(1):87-93. DOI: 10.1007/s11043-014-9253-5
[29]	PETTERMANN H E, DESIMONE A. An anisotropic linear thermo-viscoelastic constitutive law[J]. Mechanics of Time-Dependent Materials,2018,22:421-433.
[30]	GONZALEZ C, LLORCA J. Mechanical behavior of unidirectional fiber-reinforced polymers under transverse compression: Microscopic mechanisms and modeling[J]. Composites Science and Technology,2007,67(13):2795-2806. DOI: 10.1016/j.compscitech.2007.02.001
[31]	NAYA F, GONZALEZ C, LOPES C S, et al. Computational micromechanics of the transverse and shear behavior of unidirectional fiber reinforced polymers including environmental effects[J]. Composites Part A Applied Science & Manufacturing,2017,92:146-157.
[32]	GITMAN I M, ASKES H, SLUYS L J. Representative volume: Existence and size determination[J]. Engineering Fracture Mechanics,2007,74(16):2518-2534. DOI: 10.1016/j.engfracmech.2006.12.021
[33]	LI S. Boundary conditions for unit cells from periodic microstructures and their implications[J]. Composites Science and Technology,2008,68(9):1962-1974. DOI: 10.1016/j.compscitech.2007.03.035
[34]	张超, 许希武, 严雪. 纺织复合材料细观力学分析的一般性周期性边界条件及其有限元实现[J]. 航空学报, 2013, 34(7):1636-1645. ZHANG Chao, XU Xiwu, YAN Xue. General periodic boundary conditions for micromechanical analysis of textile composites and their finite element realization[J]. Acta Aeronautica Sinica,2013,34(7):1636-1645(in Chinese).
[35]	PDS A, MJH B, ASK A. Lamina properties, lay-up configurations and loading conditions for a range of fibre-reinforced composite laminates[J]. Composites Science and Technology,1998,58(7):1011-1022. DOI: 10.1016/S0266-3538(98)00078-5

施引文献(6)

期刊类型引用(3)

1.	赵英男，李慧颖，尹高冲，侯帅昌. 高速永磁电机表贴式转子碳纤维护套分析. 轨道交通材料. 2025(01): 21-25 . 百度学术
2.	高亮，贾伟，石峰晖，霍红宇，周典瑞，刘焕君，张宝艳. 反气相色谱法测定聚醚醚酮的表面性质及在提升热塑性复合材料层间性能中的应用. 复合材料学报. 2023(05): 2587-2597 . 本站查看
3.	夏振宝，张鹏飞，李俊儒，李欣琳，张传伟，何田，王晓. PEEK/CF成型用六自由度FDM 3D打印系统设计及仿真. 工程塑料应用. 2022(10): 77-83+89 . 百度学术