Progressive failure analysis of composite materials based on rate-dependent three-dimensional elastoplastic damage model
-
摘要: 建立了一个同时考虑复合材料非线性力学响应、应变率效应和损伤累积导致材料属性退化的弹塑性三维损伤本构模型。采用改进的塑性力学模型表征材料在动态荷载下的非线性力学行为。为准确预测复合材料在动态荷载下的弹塑性力学响应，引入了率相关放大系数对准静态下的塑性强化函数进行修正。采用“断裂带模型”对已开发的本构模型软化段进行规则化，以减轻有限元分析结果的网格敏感性。采用分区反抛物线插值法对基体损伤初始断裂面角度及纤维扭结/劈裂平面角度进行求解。开发包含数值积分算法的用户材料自定义子程序VUMAT，并嵌于有限元程序ABAQUS V6.14中，对力学行为展现显著非线性力学效应和应变率效应的IM7/8552碳纤维/环氧树脂复合材料层合板进行了渐进失效分析，验证本文提出的材料本构模型的有效性。结果显示，预测结果与已报道的试验结果吻合良好，表明已建立的率相关三维弹塑性损伤本构模型能准确预测此类复合材料层合板的在动态荷载下的力学行为，为复合材料构件及其结构设计提供了一种有效的分析方法。Abstract: A three-dimensional elastoplastic damage constitutive model which takes into account the nonlinear mechanical response, strain rate effects of composites, material properties degradation due to damage evolution was proposed. A modified plastic model was used to characterize the nonlinear mechanical response under dynamic load. To accurately describe the elastoplastic mechanical response of composite materials under dynamic load, the rate-dependent amplification factor was introduced to modify the plastic hardening law under static condition. In order to alleviate mesh sensitivity of finite element analysis results, the“Crack Band Theory”was applied to regularize the softening branch of the material constitutive model. The Selective Range Inverse Parabolic Interpolation algorithm was used to calculate the angle of the initial fracture plane of matrix damage and the angle of the fiber kinking/splitting plane. User-defined material subroutine VUMAT containing the numerical integration algorithm was coded and implemented in finite element procedure ABAQUS V6.14. The efficiency of the material constitutive model was demonstrated through progressive failure analysis of IM7/8552 carbon fiber/epoxy composite laminates, the mechanical behavior of which demonstrates significant nonlinear mechanical response. The numerical results agree well with the experimental data reported in the literature. It is shown that the rate-dependent three-dimensional elastoplastic damage constitutive model can predict the mechanical behavior of composites under dynamic loads with sufficient accuracy. The proposed approach provides an efficient method for the design of composite components and structures.
-
复合材料具有比强度和比刚度高、可设计性强、疲劳性能好、重量轻、耐腐蚀等优异性能，被广泛应用于航空航天领域[1]。复合材料薄壁结构承载效率较高，是飞机中常见的结构形式，其中机身侧壁板、梁腹板等结构主要承受剪切载荷的作用。在剪切载荷作用下，机身侧壁板的蒙皮容易局部失稳，已有研究表明，蒙皮失稳后不会立即失效，还能继续承载，表现出较高的承载能力[2-4]。因此，在复合材料薄壁结构设计中应考虑其剪切稳定性，充分发挥后屈曲承载潜力，这对减轻飞机结构重量、提高结构承载效率和确保飞机服役过程中的安全具有重要工程价值。
目前，国内外学者对复合材料薄壁结构的稳定性研究多集中在压缩载荷工况下[5-8]，对剪切稳定性的研究相对较少。谭翔飞等[9]基于蒂尔曼和迪奥模型，进行了加强筋间蒙皮剪切屈曲及后屈曲性能理论分析，得出的理论屈曲载荷与试验屈曲载荷的相对误差为7.2%，后屈曲阶段的理论载荷-应变曲线与试验结果的相对误差在10%以内，并确定了后屈曲角随屈曲比的变化规律。汪厚冰等[10]对复合材料帽形加筋壁板的剪切屈曲性能进行了试验、理论分析和数值模拟，并指出选择合适的几何初始缺陷系数利用几何非线性分析方法可模拟蒙皮在剪切载荷作用下的屈曲过程。李真等[11]通过剪切稳定性试验及张力场分析研究了复合材料机身单曲率壁板的剪切失稳及破坏特性。以上研究工作均未考虑冲击损伤，而复合材料结构在使用和维护过程中受到工具坠落、跑道碎石和冰雹等低速冲击的作用容易产生损伤，导致剩余强度急剧下降[12]，因此冲击损伤的影响不可忽视。
对含冲击损伤复合材料结构的强度预测，一般采用损伤累积法[13]和软化夹杂法[14-16]。损伤累积法需要进行冲击及压缩等外载作用的全过程分析，计算规模庞大，收敛困难，不便于工程使用。基于实际冲击损伤，采用软化夹杂法对冲击损伤进行等效是一种可行且高效的方法。Fardin等[14]将冲击损伤简化为具有不同材料参数的椭圆夹杂物，Debski等[15]通过减少厚度、降低材料属性将冲击损伤等效，两位学者均高效地计算了复合材料结构冲击后的剩余强度。Li等[16]基于软化夹杂模型建立了一种边缘冲击损伤的简化方法，快速而准确地预测了加筋板的后屈曲行为。然而，以上软化夹杂模型更适用于冲击后压缩剩余强度预测，对于本文冲击后剪切强度预测，还应考虑剪切非线性效应的影响。
本文以无损伤及含冲击损伤的复合材料层合板为研究对象，基于数字图像相关方法(Digital image correlation，DIC)[17]对其在剪切载荷作用下的屈曲后屈曲行为进行了实时测量，分析和总结了冲击损伤对屈曲波形和承载能力的影响。随后，采用软化夹杂法将冲击损伤等效简化，将损伤的几何边界信息写入损伤模型中，建立了考虑剪切非线性效应的复合材料渐进损伤模型，并对试验过程进行数值仿真。最后，讨论了数值仿真结果与试验结果的一致性。
1. 试 验
1.1 试件
试件材料为碳纤维增强环氧树脂基复合材料CCF300/BA3202，单层名义厚度为0.155 mm，材料属性见表1，参考ASTM标准[18-22]测得。试件外廓尺寸为370 mm×250 mm(详见图1)，共4件，编号为T1~T4，所有试件铺层顺序为[45/45/0/45/90/0/−45/0]S，名义厚度为2.48 mm。试件四周用玻璃钢加强，加强片与蒙皮之间用J-116 B胶粘接，加强片厚度为2.5 mm。
表 1 CCF300/BA3202碳纤维增强环氧树脂复合材料性能参数Table 1. Material properties of CCF300/BA3202 carbon fiber reinforced epoxy compositeParameter Value E1/GPa 118 E2/GPa 8.98 G12/GPa 4.21 ν12 0.306 XT/MPa 1835 XC/MPa 1296 YT/MPa 82.5 YC/MPa 240 SL/MPa 166 GIC/(N·mm−1) 0.744 GIIC/(N·mm−1) 1.90 Notes：E1—Longitudinal elastic modulus; E2—Ransverse elastic modulus; G12—Shear modulus; ν12—Poisson's ratio; XT—Longitudinal tensile strength; XC—Longitudinal compressive strength; YT—Transverse tensile strength; YC—Transverse compressive strength; SL—Shear strength; GIC—Mode I fracture toughness ; GIIC—Mode II fracture toughness. 1.2 冲击损伤引入
试验前，在T4试件正中心引入了冲击损伤。冲击采用落锤式冲击设备，冲头质量为1.023 kg，端部为半球形，直径为16 mm，冲击能量为8 J。冲击后立即用凹坑深度仪测量，得到的凹坑深度为0.27 mm。随后，采用EPOCH XT超声波探伤仪进行无损检测，并用白色记号笔对损伤进行标识。A扫结果显示：分层损伤尺寸为18 mm×12 mm，如图2所示。
![]()
图 2 T4试件冲击支持方式及分层尺寸Figure 2. Impact support mode and delamination size of T4 specimen1.3 试验方法
正式试验前，在试件一侧表面喷涂白漆，待白漆干后喷涂黑漆，形成随机的散斑图案。在试件的另一侧表面粘贴花片，花片的0°、45°、90°方向的应变片与试件铺层方向一致。T1~T3试件应变片粘贴位置及编号见图3，通过1#~4#花片检验加载对称性，通过中心处的5#花片判断初始屈曲。T4试件的5#花片沿着90°方向移动了10 mm。
![]()
图 3 无损伤试件(T1~T3)应变片分布及编号Figure 3. Strain gauges distributions and numbers of undamaged specimens (T1-T3)试验夹具和试件安装如图4所示，采用对角拉伸的方法进行剪切载荷施加。试验在MTS1000 kN试验机上进行，采用道姆公司制造的ARAMIS 3D数字散斑系统测量面外变形，同时采用中国飞机强度研究所自主研发的ST24数据采集系统测量应变。
![]()
图 4 CCF300/BA3202复合材料层合板剪切试验方法Figure 4. Shear test method for CCF300/BA3202 composite laminates2. 数值仿真模型
2.1 失效准则
2.1.1 纤维失效准则
复合材料主要失效模式包括纤维拉伸/压缩失效和基体的拉伸/压缩失效等。Hashin准则[23]是最常用的失效准则，但Li等[24]从理论上分析了Hashin纤维拉伸失效判据中包含的剪切应力项可以忽略，并给出了预测纤维拉伸/压缩失效的统一表达式：
fFF=(XC−XT)σ1XTXC+σ21XTXC (1) 式中：
fFF 为纤维失效函数，fFF>1 时表征纤维失效；σ1 为纤维方向应力；XT、XC 分别为单向板纤维方向拉伸、压缩强度。2.1.2 纤维间失效准则
对于纤维间失效，Hashin准则难以反映横向压缩对基体剪切失效的抑制作用。Li等[24]从Mohr失效面理论的基本假设出发，建立了一种纤维间失效准则，可有效预测横向压缩的增强效应。而且，不同于Puck等[25]提出的纤维间失效准则，该准则所有系数均可由基本强度及断裂面角度计算给出，准则形式如下：
fIFF={A1σn+A2σ2n+B2τ2nl+C2τ2ntσn⩾ (2) 式中：
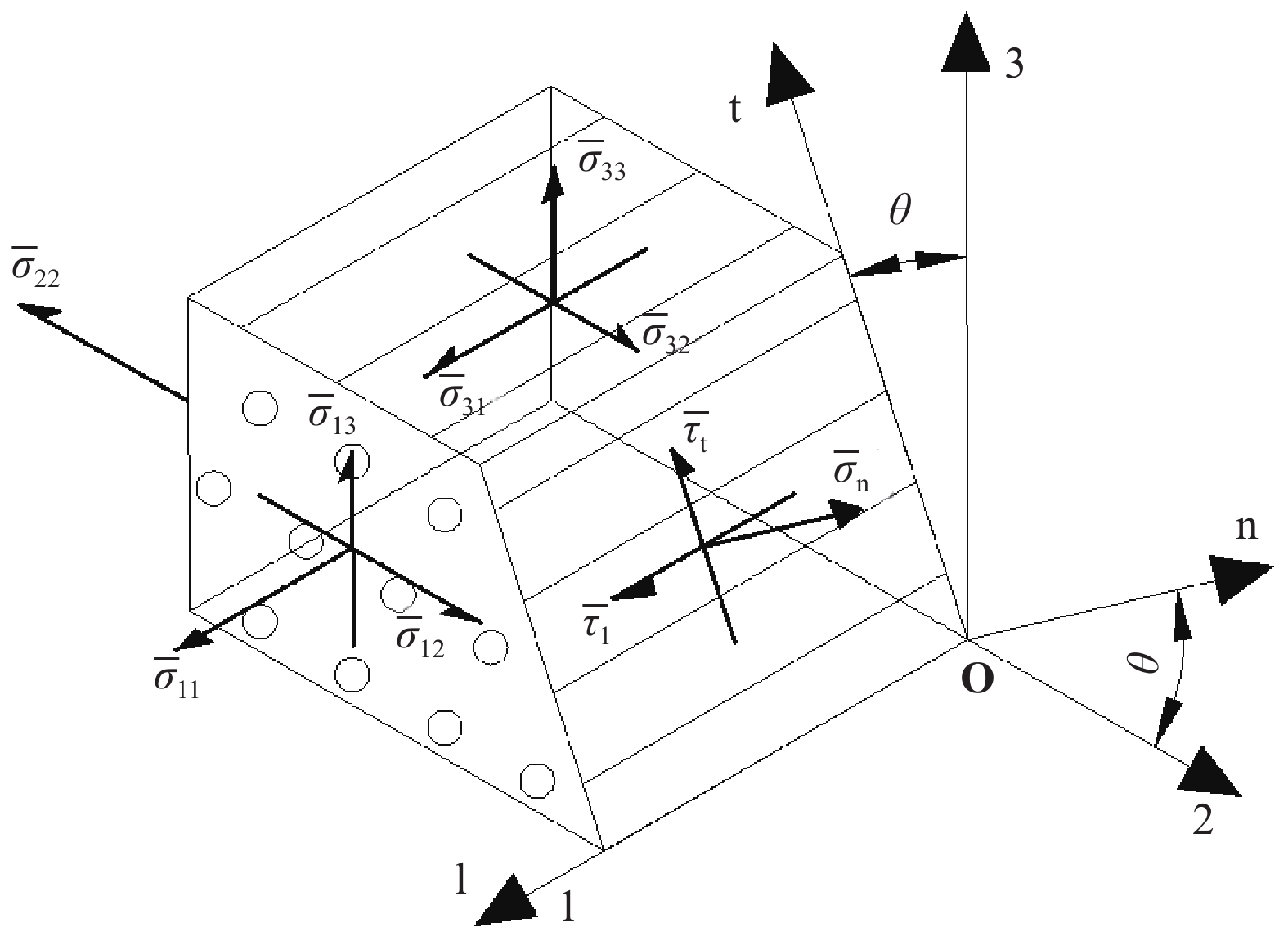
f_{\text {IFF }} 为纤维间失效函数，f_{\mathrm{IFF}}>1 时表征纤维间失效，即基体失效；{\sigma }_{\text{n}}、{\tau }_{\text{nt}}、{\tau }_{\text{nl}} 为潜在断裂面上的应力(如图5所示)；A_{1}、A_{2}、B_{2}、 C_{2} 为系数，计算公式如下：\left\{ \begin{gathered} {\sigma _{\text{n}}} = {\sigma _2}{\cos ^2}{\theta _{{\text{fp}}}} + {\sigma _3}{\sin ^2}{\theta _{{\text{fp}}}} + {\tau _{23}}\sin 2{\theta _{{\text{fp}}}} \\ {\tau _{{\text{nt}}}} = \dfrac{{\left( {{\sigma _3} - {\sigma _2}} \right)\sin 2{\theta _{{\text{fp}}}}}}{2} + {\tau _{23}}\cos 2{\theta _{{\text{fp}}}} \\ {\tau _{{\text{nl}}}} = {\tau _{13}}\sin {\theta _{{\text{fp}}}} + {\tau _{12}}\cos {\theta _{{\text{fp}}}} \\ \end{gathered} \right. (3) \left\{ \begin{gathered} {A_1} = \dfrac{{{{\sin }^2}{\theta _0} - {{\cos }^2}{\theta _0}}}{{{Y_{\text{C}}}{{\cos }^4}{\theta _0}}} \\ {A_2} = \dfrac{1}{{Y_{\text{T}}^2}}\left[ {1 - {Y_{\text{T}}}\left( {\dfrac{{{{\sin }^2}{\theta _0} - {{\cos }^2}{\theta _0}}}{{{Y_{\text{C}}}{{\cos }^4}{\theta _0}}}} \right)} \right] \\ {B_2} = \dfrac{1}{{S_{\text{L}}^2}} \\ {C_2} = \dfrac{1}{{Y_{\text{C}}^2{{\cos }^4}{\theta _0}}} \\ \end{gathered} \right. (4) 式中：
{\sigma }_{2}、{\sigma }_{3}、{\tau }_{12}、{\tau }_{13}、{\tau }_{23} 为材料主轴坐标系下的应力分量；{Y}_{\text{T}}、{Y}_{\text{C}}、{S}_{\text{L}} 分别为横向拉伸强度、横向压缩强度和面内剪切强度；\theta_{0} 为纯横向压缩失效时的断裂角，本文参考文献[25]取为53°；\theta_{\mathrm{fp}} 为潜在断裂面角度。![]()
图 5 基体潜在断裂面上的应力分量[24]Figure 5. Stress components on potential fracture surface of matrix[24]{\sigma _1} , {\sigma _2} , {\sigma _3} , {\tau _{12}} , {\tau _{13}} , {\tau _{23}} , {\tau _{21}} , {\tau _{31}} , {\tau _{32}} —Stress components in the material's principal axis coordinate system; {\theta _{{\text{fp}}}} —Angle of the potential fracture surface of matrix; {\sigma _{\text{n}}} , {\tau _{{\text{nt}}}} , {\tau _{{\text{nl}}}} —Stress components on potential fracture surface of matrix纤维间失效函数
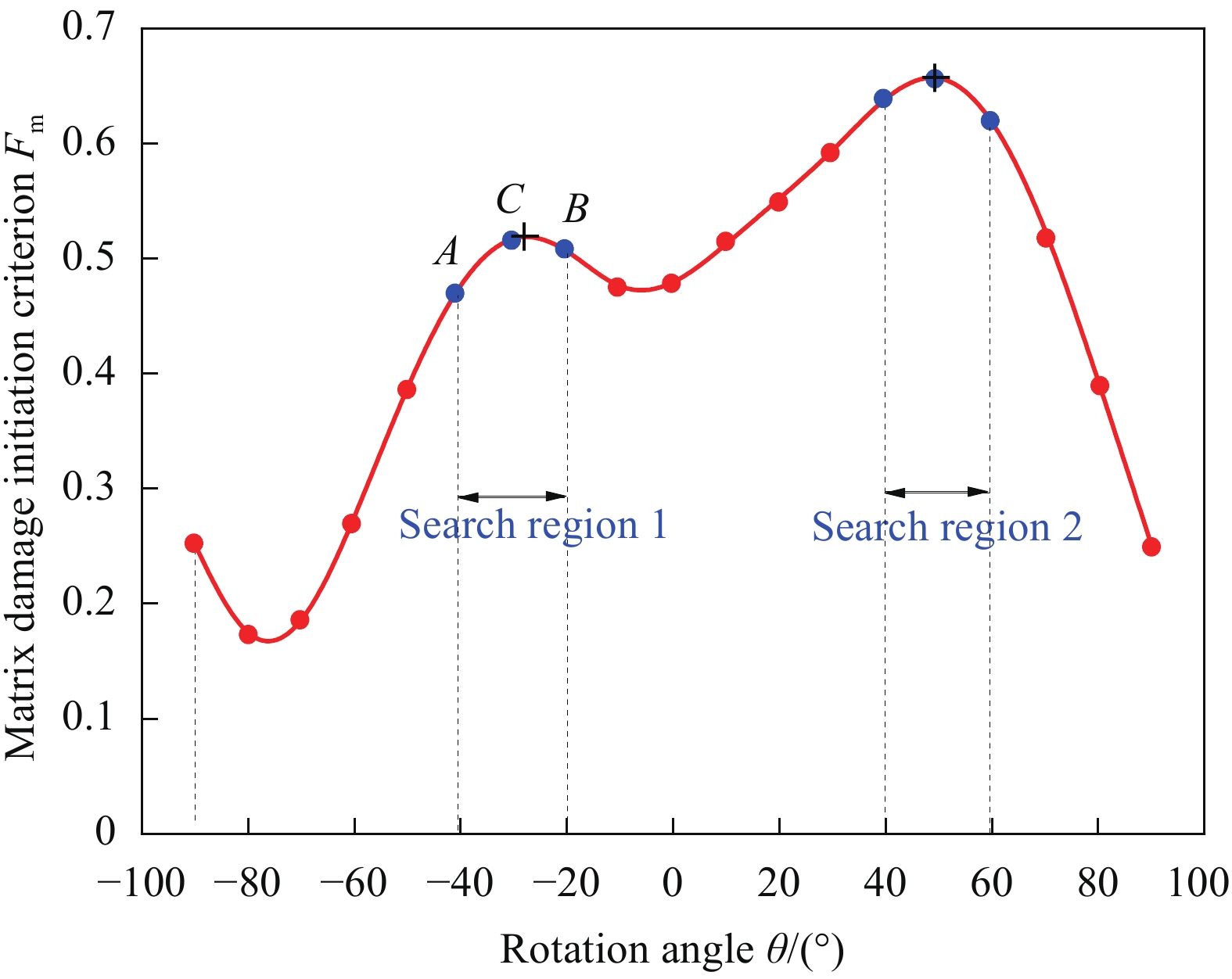
f_{\mathrm{IFF}} 的最大值及相应的潜在断裂面角度\theta_{\mathrm{fp}} 可通过遍历法[25]、分区黄金搜索法[26]、分区抛物线法[27]求解，综合考虑效率和精度本文采用了分区黄金搜索法。2.2 剪切非线性模型
在面内纵横剪切试验中发现，CCF300/BA3202表现出了明显的剪切非线性行为。因此，本文采用多项式函数描述其剪切非线性响应。同时，注意到剪应力是剪应变的奇函数，剪切应力-应变关系如下：
{\tau _{12}} = \left\{ \begin{aligned} &{{G_1}{\gamma _{12}} + {G_2}\gamma _{12}^2 + {G_3}\gamma _{12}^3 + \cdots }+{G_i}\gamma _{12}^i \\ &\qquad {{\gamma _{12}} < 0} \\ & {{G_1}{\gamma _{12}} - {G_2}\gamma _{12}^2 + {G_3}\gamma _{12}^3 - \cdots }+{G_i}\gamma _{12}^i\\ &\qquad{{\gamma _{12}} \geqslant 0} \end{aligned} \right. (5) 式中：
{\tau }_{12}、{\gamma }_{12} 分别为剪切应力和工程剪应变；G_{i}(i=1,2,3 \cdots) 为系数，由试验数据拟合给出。如图6所示，取前4项时已足够精确，各系数分别为：G1=5.02 GPa、G2=1.48×102 GPa、G3=2.16×103 GPa、G4=1.18×104 GPa。由此，等效剪切刚度
G_{12}^{{\text{eq}}} ，计算公式如下：G_{12}^{{\text{eq}}} = \left\{ \begin{aligned} & {{G_1} + {G_2}{\gamma _{12}} + {G_3}\gamma _{12}^2 + {G_4}\gamma _{12}^3}&{{\gamma _{12}} < 0} \\ & {{G_1} - {G_2}{\gamma _{12}} + {G_3}\gamma _{12}^2 - {G_4}\gamma _{12}^3}&{{\gamma _{12}} \geqslant 0} \end{aligned} \right. (6) 2.3 基于软化夹杂法的损伤演化模型
材料失效后的损伤演化行为主要由断裂韧性控制，参考Linde等[28]提出的指数型损伤演化模型，并引入单元特征长度以降低模型对网格的依赖性，纤维损伤状态变量dFF及纤维间损伤状态变量dIFF定义如下：
\begin{gathered} {d_{{\text{FF}}}} = \left\{ {\begin{array}{*{20}{c}} {1 - \dfrac{{\exp (X_{\text{T}}^2{L_{\text{C}}}(1 - {f_{{\text{FF}}}})/({E_1}{G_{{\text{FT}}}}))}}{{{f_{{\text{FF}}}}}}}&{{\sigma _1} \geqslant 0} \\ {1 - \dfrac{{\exp (X_{\text{C}}^2{L_{\text{C}}}(1 - {f_{{\text{FF}}}})/({E_1}{G_{{\text{FC}}}}))}}{{{f_{{\text{FF}}}}}}}&{{\sigma _1} < 0} \end{array}} \right. \\ {d_{{\text{IFF}}}} = \left\{ {\begin{array}{*{20}{c}} {1 - \dfrac{{\exp (Y_{\text{T}}^2{L_{\text{C}}}(1 - {f_{{\text{IFF}}}})/({E_2}{G_{{\text{MT}}}}))}}{{{f_{{\text{IFF}}}}}}}&{{\sigma _{\rm{n}}} \geqslant 0} \\ {1 - \dfrac{{\exp (Y_{\text{C}}^2{L_{\text{C}}}(1 - {f_{{\text{IFF}}}})/({E_2}{G_{{\text{MC}}}}))}}{{{f_{{\text{IFF}}}}}}}&{{\sigma _{\rm{n}}} < 0} \end{array}} \right. \end{gathered} (7) 式中：
L_{\mathrm{C}} 为单元特征长度；G_{\mathrm{FT}} 、G_{\mathrm{FC}} 为纵向拉伸、压缩断裂韧性，目前还没有公认的标准方法进行测试，参考同类材料的性能[29-30]，G_{\mathrm{FT}} 、G_{\mathrm{FC}} 分别取为71.4 N·mm−1、35.6 N·mm−1；G_{\text {MT }} 、G_{\mathrm{MC}} 为横向拉伸、压缩断裂韧性，近似取为层间I型、II型断裂韧性。纤维失效后，纵向模量E1、横向模量E2、泊松比ν12、剪切模量G12折减为无损材料值的(1−dFF)倍。纤维间失效后，横向模量E2、泊松比ν12、剪切模量G12折减为无损材料值的(1−dIFF)倍。
对于冲击损伤区，采用软化夹杂法进行等效。文献[16, 29]根据损伤的严重程度，将冲击损伤区划分为两个区域，并分别采用不同的系数对初始性能进行折减。本文研究的试件冲击能量小，冲击点处检测未发现纤维大量断裂的情况，为简化模型，整个损伤区采用同一系数η进行性能折减。
上述基于软化夹杂法的损伤演化模型材料性能退化方案如表2所示。
表 2 材料性能退化方案Table 2. Material performance degradation schemeFail mode No damage zone Impact damage zone None — \begin{gathered} {E_1} \to \eta {E_1} \\ {E_2} \to \eta {E_2} \\ G_{12}^{{\text{eq}}} \to \eta G_{12}^{{\text{eq}}} \\ \end{gathered} Fiber failure \begin{gathered} {E_1} \to (1 - {d_{{\text{FF}}}}){E_1} \\ {E_2} \to (1 - {d_{{\text{FF}}}}){E_2} \\ G_{12}^{{\text{eq}}} \to (1 - {d_{{\text{FF}}}})G_{12}^{{\text{eq}}} \\ {\nu _{12}} \to (1 - {d_{{\text{FF}}}}){\nu _{12}} \\ \end{gathered} \begin{gathered} {E_1} \to (1 - {d_{{\text{FF}}}})\eta {E_1} \\ {E_2} \to (1 - {d_{{\text{FF}}}})\eta {E_2} \\ G_{12}^{{\text{eq}}} \to (1 - {d_{{\text{FF}}}})\eta G_{12}^{{\text{eq}}} \\ {\nu _{12}} \to (1 - {d_{{\text{FF}}}}){\nu _{12}} \\ \end{gathered} Inter-fiber failure \begin{gathered} {E_2} \to (1 - {d_{{\text{IFF}}}}){E_2} \\ G_{12}^{{\text{eq}}} \to (1 - {d_{{\text{IFF}}}})G_{12}^{{\text{eq}}} \\ {\nu _{12}} \to (1 - {d_{{\text{IFF}}}}){\nu _{12}} \\ \end{gathered} \begin{gathered} {E_2} \to (1 - {d_{{\text{IFF}}}})\eta {E_2} \\ G_{12}^{{\text{eq}}} \to (1 - {d_{{\text{IFF}}}})\eta G_{12}^{{\text{eq}}} \\ {\nu _{12}} \to (1 - {d_{{\text{IFF}}}}){\nu _{12}} \\ \end{gathered} Notes: G_{12}^{{\text{eq}}} —Equivalent shear modulus; η—Stiffness reduction factor; {d_{{\text{FF}}}} —Fiber damage state variable; {d_{{\text{IFF}}}} —Matrix damage state variable. 2.4 考虑冲击损伤的有限元模型
采用商业有限元软件ABAQUS 6.14对含冲击损伤的层合板进行剪切后屈曲失效分析。
有限元模型中，剪切边框和螺栓进行了如下简化：剪切框架简化为S4 R壳单元(厚度10 mm)，并在8个对角点处施加铰接约束；螺栓简化为B31梁单元(直径8 mm)，分别与试件及上下剪切框架绑定在一起；剪切边框和螺栓材料均为低碳钢。低碳钢的弹性模量为200 GPa、泊松比为0.3。
试件也均采用S4 R壳单元模拟，其中加强区上下各增加一层玻璃钢(厚度2.5 mm)。玻璃钢纵向模量为53.48 GPa、横向模量为17.7 GPa、剪切模量为5.83 GPa、泊松比为0.278。复合材料单向板本构模型由自定义场子程序USDFLD实现，其中场变量为F1~F4：F1表征纤维损伤、F2表征纤维间损伤、F3表征剪切非线性行为、F4区分是否为冲击损伤区，F4=0时表示非冲击损伤区，F4=1时表示冲击损伤区。F1~F3定义如下：
\begin{gathered} {F_1} = {d_{{\text{FF}}}} \\ {F_2} = {d_{{\text{IFF}}}} \\ {F_3} = 1 - \frac{{G_{12}^{{\text{eq}}}}}{{{G_{12}}}} \end{gathered} (8) 对于含冲击损伤的试件，采用软化夹杂法对冲击损伤进行模拟，并根据单元中心坐标确定单元是否位于冲击损伤区域。试件T4的冲击损伤边界近似于椭圆，且有限元模型原点在试件中心，由此F4可由下式确定：
{F_4} = \left\{ \begin{aligned} & 1&{\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} < 1} \\ & 0&{\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} \geqslant 1} \end{aligned} \right. (9) 式中：长半轴a=9 mm；短半轴b=6 mm。
有限元模型网格及边界条件如图7所示：剪切框架网格尺寸为10 mm×10 mm，试件网格尺寸为1 mm×1 mm。边界条件设置如下：在对角坐标系(x'Oy')下，约束y'轴方向的4个主节点的面外平动自由度(Uz'=0)，绕x'、y'轴的转动自由度(URx'=URy'=0)；x'轴方向的4个主节点仅放开绕z'轴的转动自由度(Ux'=Uy'=Uz'=0，URx'=URy'=0)。加载时+x'轴方向的2个主节点施加沿x'轴方向4 mm位移(Ux'=4 mm)。
![]()
图 7 CCF300/BA3202复合材料层板剪切试验有限元模型Figure 7. Finite element model for shear test of CCF300/BA3202 composite laminatesMPC—Multi-point constraints通过场变量表征的等效冲击损伤区域如图8所示，本文采用的方法保证了网格的整体质量。
![]()
图 8 T4试件等效冲击损伤区域Figure 8. Equivalent impact damage area of T4 specimenF4—Impact damage field variable3. 结果与讨论
3.1 试验结果分析
通过粘贴的花片可以测得0°、45°、90°方向的正应变
{\varepsilon }_{0}、{\varepsilon }_{45}、{\varepsilon }_{90} ，由此可以确定测量点的工程剪应变{\gamma _{12}} ：{\gamma _{12}} = {\varepsilon _0} + {\varepsilon _{90}} - 2{\varepsilon _{45}} (10) T1试件的载荷-应变曲线如图9所示，其中虚线为拟合的载荷-应变曲线，根据0~40 kN范围内的载荷及应变线性回归得到。加载到64.6 kN以后应变曲线有明显偏转，由此确定试件屈曲载荷约为64.6 kN。其余试件屈曲载荷确定方法与之类似，试验结果统计如表3所示。
表 3 CCF300/BA3202复合材料层板剪切试验结果Table 3. Shear test results of CCF300/BA3202 composite laminatesNumber Buckling load/kN Fracture load/kN Test Average Test Average T1 64.6 64.2 153.5 156.8 T2 65.0 156.2 T3 63.1 160.7 T4 63.0 141.6 不含冲击损伤的试件(T1~T3)屈曲载荷平均值为64.2 kN，破坏载荷平均值为156.8 kN。3个试件的屈曲模态一致，包含3个屈曲半波，沿着垂直于对角拉伸方向分布。破坏模式均为靠近对角拉伸区长边加强片处因应力集中而断裂。无损伤的试件(T1)典型屈曲模态及失效照片如图10所示。
![]()
图 10 无损伤的T1试件屈曲及失效时的面外位移云图Figure 10. Out-of-plane displacement cloud diagram of undamaged T1 specimen during buckling and failureW—Out of plane displacement含冲击损伤的试件(T4)屈曲载荷测试值为63.0 kN，破坏载荷测试值为141.6 kN，分别比无损伤试件平均值低1.92%、9.69%。如图11所示，T4试件屈曲模态与无损伤试件一致，破坏模式为损伤沿着冲击点向4个角点扩展直至完全失去承载能力，与无损伤试件不同。对比分析可知：试件中心引入冲击损伤后，损伤尺寸较小，整体刚度变化不明显，因此屈曲载荷变化不大。冲击点附近因后屈曲变形导致应力集中，承载能力明显降低。
![]()
图 11 含冲击损伤的T4试件屈曲及失效时的面外位移云图Figure 11. Out-of-plane displacement cloud diagram of T4 specimen with impact damage during buckling and failure3.2 仿真结果与试验对比
试件制造过程中的几何缺陷，特别是翘曲对初始屈曲影响较大，因此数值仿真模型需加以考虑。比较常见的做法是引入一阶屈曲模态作为初始几何缺陷[31]，几何缺陷因子ξ定义为缺陷幅值与试件考核区厚度之比。汪厚冰等[10]研究指出几何缺陷因子取值对稳定性影响较大，需进行参数分析确定。
图12为几何缺陷因子和剪切非线性对CCF300/BA3202复合材料层板屈曲载荷、破坏载荷的影响。横坐标表示几何缺陷因子，纵坐标分别表示无损伤试件仿真的屈曲载荷与无损伤试件试验平均屈曲载荷之比、仿真的破坏载荷与无损伤试件试验平均破坏载荷之比。
![]()
图 12 几何缺陷因子和剪切非线性对CCF300/BA3202复合材料层合板屈曲载荷、破坏载荷的影响Figure 12. Effects of geometric defect factor and shear nonlinearity on buckling load and failure load of CCF300/BA3202 composite laminates由图12(a)可以看出，线性剪切响应和非线性剪切响应得到的初始屈曲载荷一致，这是由于初始屈曲时，屈曲应变较小，剪切应力-应变关系接近于线性。随着初始几何缺陷因子增加，分析得到的屈曲载荷随之而减小；初始几何缺陷因子ξ=3%时，与试验结果较接近，相对误差为2.34%。
由图12(b)可以看出，考虑线性剪切响应和非线性剪切响应时的破坏载荷相差较大，采用线性模型误差可达20%以上，而采用非线性模型误差均在5%以内。这是由于临近破坏时，试件剪切应变较高，线性模型已难以反映真实的剪切应力-应变关系。而随着初始几何缺陷因子增加，两种模型分析得到的破坏载荷均无明显变化。
基于以上对无损伤试件的研究结果，对含冲击损伤的试件剪切屈曲后屈曲行为进行分析时，采用非线性剪切响应模型，初始几何缺陷因子取为3%。冲击损伤区刚度折减系数η对承载能力的影响如图13所示，破坏载荷随着η的减小而减小，当η在0.2~0.3之间时与试验结果接近。
![]()
图 13 刚度折减系数对CCF300/BA3202复合材料层板破坏载荷的影响Figure 13. Effects of stiffness reduction factor on failure load of CCF300/BA3202 composite laminatesFEM—Finite element modelingη=0.25时，含冲击损伤的试件屈曲载荷、破坏载荷预测值分别为61 kN、139.8 kN，与试验相比，相对误差分别为−3.17%、−1.27%。仿真的屈曲模态、破坏模式见图14、图15，与图11对比看出，数值仿真的屈曲波形、破坏模式均与试验一致，由此表明了本文考虑剪切非线性效应的软化夹杂模型的有效性。
![]()
图 14 T4试件仿真的屈曲模态Figure 14. Simulated buckling mode of T4 specimenU3—Out of plane displacement![]()
图 15 T4试件仿真的失效模式Figure 15. Simulated failure mode of T4 specimenF1—Fiber damage field variable; F2—Matrix damage field variable含冲击损伤试件从初始损伤到最终破坏的过程十分短暂，DIC设备未能捕捉到，因此通过数值仿真结果对其失效过程进行分析。T4试件预测的载荷-位移曲线和损伤扩展过程如图16、图17所示：试件加载到61 kN以后开始屈曲，冲击点附近开始往外鼓包，导致应力集中。加载至132 kN后，冲击点附近出现新增损伤。随着继续加载，损伤沿着4个角点缓慢扩展，达到最大载荷139.8 kN后，损伤急剧扩展并迅速掉载，直到完全破坏。这清晰地反映了冲击损伤对损伤起始和扩展的影响。
![]()
图 17 T4试件纤维间损伤扩展过程Figure 17. Inter-fiber failure propagation process of T4 specimenP—Load; U—Displacement4. 结 论
以无损伤和含冲击损伤的CCF300/BA3202碳纤维增强环氧树脂复合材料层合板为研究对象，基于数字图像相关方法(DIC)进行了试验测试，并对试验过程进行了仿真分析，主要结论如下：
(1) 无损伤试件的屈曲载荷、破坏载荷平均值分别为64.2 kN、156.8 kN；引入冲击损伤后，试件屈曲载荷降为63.0 kN，变化不大；承载能力下降至141.6 kN，降幅为9.69%。
(2) 几何缺陷对复合材料层合板的初始剪切屈曲影响显著，本文通过引入一阶屈曲模态模拟获得了与试验一致的初始屈曲载荷(相对误差仅为2.34%)；后续可将实际测量的翘曲变形引入模型中以更准确地模拟结构的初始屈曲行为。
(3) 剪切非线性效应对层合板剪切承载能力影响较大，线性模型预测的失效载荷与试验测试值误差超过20%，而考虑了剪切非线性响应的仿真模型预测精度可达5%以内。
(4) 本文采用的考虑剪切非线性效应的软化夹杂法可有效地预测含冲击损伤的复合材料层合板的剪切强度，屈曲载荷、破坏载荷误差分别为−3.17%、−1.27%，得到的屈曲波形、破坏模式均与DIC测量结果一致，可为复合材料结构冲击损伤简化和剪切强度预测提供一种思路。
-
![]()
图 1 复合材料单向板基体断裂面上应力分量
Figure 1. Stress components on matrix fracture surface of unidirectional composite
![]()
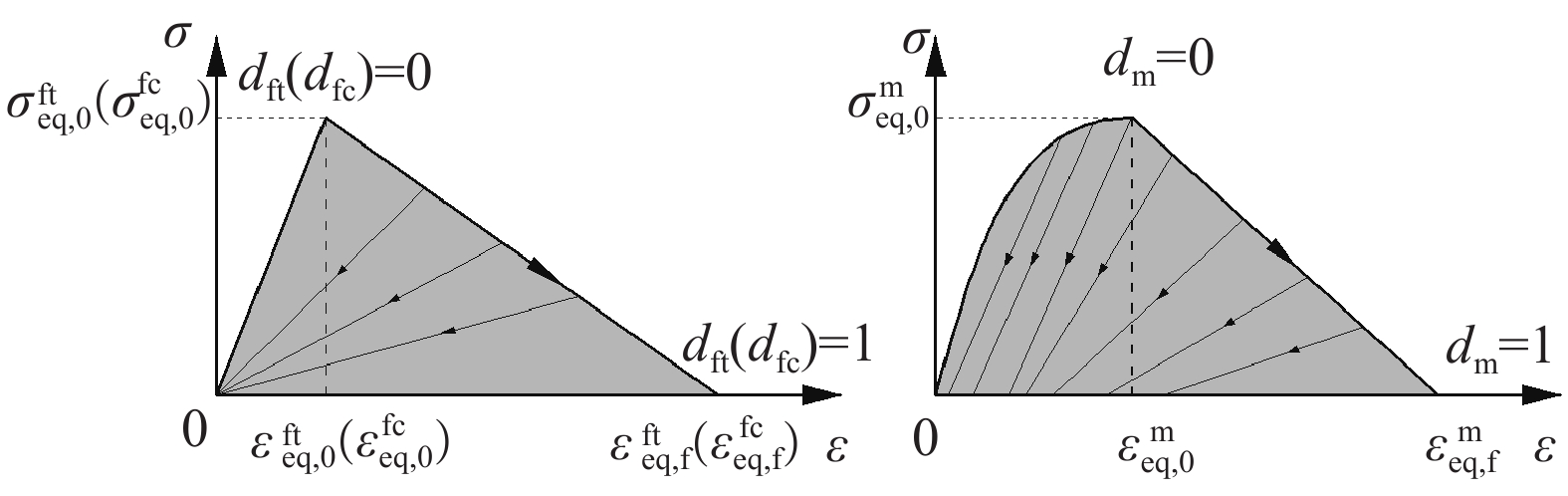
图 3 横向和剪切方向材料损伤本构关系
Figure 3. Material damage constitutive relationships in the transverse and shear directions
dI (I=ft,fc,m)—Damage variables corresponding to tensile and compressive failure in the fiber direction and matrix cracking, respectively; {\sigma }^I_{{\rm{e}}{\rm{q}},0} and {\varepsilon }^I_{{\rm{e}}{\rm{q}},0}(I=ft,fc,m)—Equivalent stresses and equivalent strains when damage initiation criteria corresponding to tensile and compressive failure in the fiber direction and matrix cracking (see Eq. (17)) are met; {\varepsilon }^I_{{\rm{e}}{\rm{q}},{\rm{f}}}(I=ft,fc,m)—Equivalent strains at complete tensile and compressive failure in the fiber direction and complete matrix failure
![]()
图 4 分区反抛物线插值法(SRIPI)示意图
Figure 4. Illustration of selective range inverse parabolic interpolation algorithm (SRIPI)
![]()
图 6 IM7/8552碳纤维/环氧树脂偏轴压缩试件的几何形状及尺寸
Figure 6. Geometry and dimensions of IM7/8552 carbon fiber/epoxy resin off-axial compressive specimens
![]()
图 7 IM7/8552碳纤维/环氧树脂复合材料单向层合板试件有限元模型
Figure 7. Finite element model of IM7/8552 carbon fiber/epoxy unidirectional laminated specimen
![]()
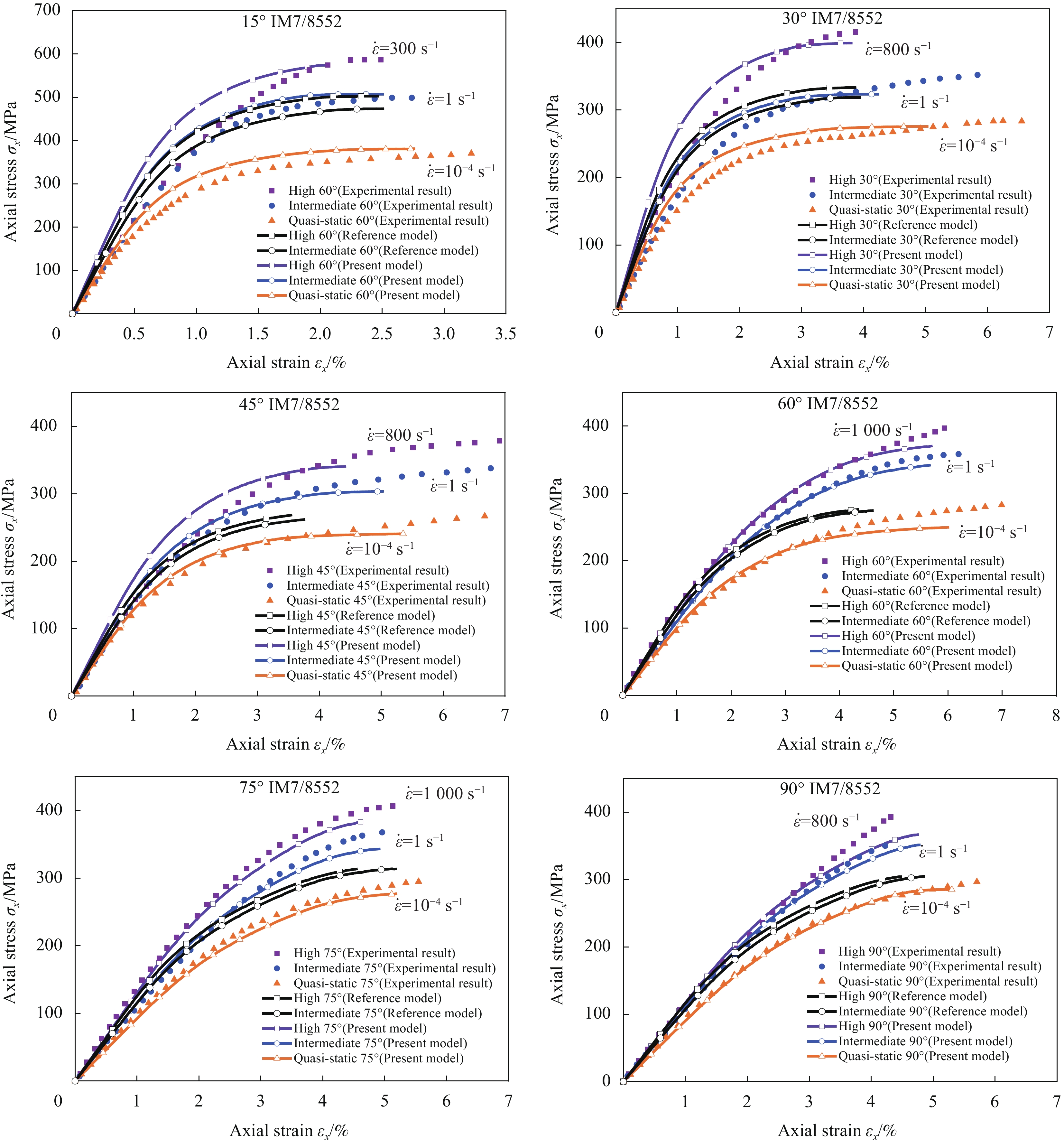
图 8 不同偏轴角度IM7/8552碳纤维/环氧树脂复合材料单向层合板在应变率分别为10−4 s−1(准静态)、1 s−1(中应变率)和高应变率压缩荷载下的试验与预测应力-应变曲线
Figure 8. Experimental and predicted stress-strain curves of off-axis IM7/8552 carbon fiber/epoxy unidirectional laminated specimens subjected to compressive loadings at strain rates of 10−4 s−1 (quasi-static), 1 s−1 (intermediate) and high strain rates
表 1 IM7/8552碳纤维/环氧树脂复合材料单向板属性
Table 1 Material properties of IM7/8552 carbon fiber/epoxy unidirectional composite laminate
{E}_{11} ^0/GPa {E}_{22}^0={E}_{33} ^0/GPa {X}_{\rm{T}} /MPa {X}_{\rm{C}} /MPa {Y}_{\rm{T}} /MPa {Y}_{\rm{C}} /MPa {S}_{12} /MPa 154 9 1725 2650 76.4 288 89 {\nu }_{12}={\nu }_{13} {\nu }_{23} {G}_{12}^0={G}_{13} ^0/GPa {G}_{23} ^0/GPa {G}_{{\rm{I}}{\rm{C}}} /(N·mm−1) {G}_{{\rm{I}}{\rm{I}}{\rm{C}}}={G}_{{\rm{I}}{\rm{I}}{\rm{I}}{\rm{C}}} /(N·mm−1) 0.33 0.43 5.6 3.98 0.26 1.002 {G}_{{\rm{f}}{\rm{t}},{\rm{c}}} /(N·mm−1) {G}_{{\rm{f}}{\rm{c}},{\rm{c}}} /(N·mm−1) {m}_{\rm{e}} {m}_{\rm{s}} {a}_{66} β {n}_{\rm{p}} 80 80 0.035 0.055 2 794.233 0.1973 Notes: {E}_{11} ^0, {E}_{22} ^0, {E}_{33} ^0—Quasi static elastic moduli in the fiber, transverse and through-thickness directions; {X}_{\rm{T}} , {X}_{\rm{C}} —Tensile and compressive strengths in the fiber direction; {Y}_{\rm{T}} , {Y}_{\rm{C}} —Tensile and compressive strengths in the transverse direction; {S}_{12} —Shear strength in 1-2 plane; {\nu }_{ij} , {G}_{ij} ^0 (ij=12,13,23)—Poisson’s ratios and shear moduli in the 1-2,1-3, 2-3 planes; {G}_{{\rm{I}}{\rm{C}}} , {G}_{{\rm{I}}{\rm{I}}{\rm{C}}} , {G}_{{\rm{I}}{\rm{I}}{\rm{I}}{\rm{C}}} —Fracture toughnesses for Mode I, II and III failure in the through-thickness direction, respectively; {G}_{{\rm{f}}{\rm{t}},{\rm{c}}} , {G}_{{\rm{f}}{\rm{c}},{\rm{c}}} —Tensile and compressive fracture toughnesses in the fiber direction; {m}_{\rm{e}} , {m}_{\rm{s}} —Strain-rate parameters related to elastic moduli and failure strengths; {a}_{66} —Material parameter of the plastic model; β, {n}_{\rm{p}} —Coefficients that fit the experimental hardening curve. 
下载: 导出CSV
-
[1] WANG J, CALLUS P J, BANNISTER M K. Experimental and numerical investigation of the tension and compression strength of un-notched and notched quasi-isotropic lami-nates[J]. Composite Structures,2004,64(3/4):297-306.
[2] LAFARIE-FRENOT M C, TOUCHARD F. Comparative in-plane shear behaviour of long-carbon-fibre composites with thermoset or thermoplastic matrix[J]. Composites Science and Technology,1994,52(3):417-425.
[3] VOGLER T J, KYRIAKIDES S. Inelastic behavior of an AS4/PEEK composite under combined transverse compression and shear. Part I: Experiments[J]. International Journal of Plasticity,1999,15(8):783-806. DOI: 10.1016/S0749-6419(99)00011-X
[4] HSU S Y, VOGLER T J, KYRIAKIDES S. Inelastic behavior of an AS4/PEEK composite under combined transverse compression and shear. Part II: Modeling[J]. International Journal of Plasticity,1999,15(8):807-836. DOI: 10.1016/S0749-6419(99)00012-1
[5] SODEN P D, HINTON M J, KADDOUR A S. Lamina properties, lay-up configurations and loading conditions for a range of fibre-reinforced composite laminates[J]. Composites Science and Technology,1998,58(7):1011-1022. DOI: 10.1016/S0266-3538(98)00078-5
[6] HARDING J. Effect of strain rate and specimen geometry on the compressive strength of woven glass-reinforced epoxy laminates[J]. Composites,1993,24(4):323-332. DOI: 10.1016/0010-4361(93)90042-7
[7] El-HABAK A. Compressive resistance of unidirectional GFRP under high rate of loading[J]. Journal of Compo-sites, Technology and Research,1993,15(4):311-317. DOI: 10.1520/CTR10384J
[8] HSIAO H M. Strain rate effects on the transverse compressive and shear behavior of unidirectional composites[J]. Journal of Composite Materials,1999,33(17):1620-1642. DOI: 10.1177/002199839903301703
[9] HOSUR M V, VAIDYA U K, ABRAHAM A, et al. Static and high strain rate compression response of thick section twill weave S-2 glass/vinyl ester composites manufactured by affordable liquid molding processes[J]. Journal of Engineering Materials and Technology,1999,121(4):468-475. DOI: 10.1115/1.2812403
[10] HOSUR M V, ALEXANDER J, VAIDYA U K, et al. High strain rate compression response of carbon/epoxy laminate composites[J]. Composite Structures,2001,52(3):405-417.
[11] GRIMES G C. Composite materials: Testing and design (Tenth volume) || A method for evaluating the high strain rate compressive properties of composite materials[J]. 1992: 54-54-12.
[12] DANIEL I M, WERNER B T, FENNER J S. Strain-rate-dependent failure criteria for composites[J]. Composites Science and Technology,2010,71(3):357-364.
[13] AZZI V D, TSAI S W. Anisotropic strength of composites[J]. Experimental Mechanics,1965,5(9):283-288. DOI: 10.1007/BF02326292
[14] HOFFMAN O. The brittle strength of orthotropic materials[J]. Journal of Composite Materials,1967,1(2):200-206. DOI: 10.1177/002199836700100210
[15] TSAI S. A general theory of strength for anisotropic materials[J]. Journal of Composite Materials,1971,5(1):58-80. DOI: 10.1177/002199837100500106
[16] HASHIN Z. A fatigue failure criterion for fiber reinforced materials[J]. Journal of Composite Materials,1973,7(4):448-464. DOI: 10.1177/002199837300700404
[17] HASHIN Z. Failure criteria for unidirectional fiber composites[J]. Journal of Applied Mechanics,1980,47(2):329-334. DOI: 10.1115/1.3153664
[18] PUCK A, SCHUMANN H. Failure analysis of FRP laminates by means of physically based phenomenological models[J]. Composites Science and Technology,2002,62(12):1633-1662.
[19] PUCK A, SCHUMANN H. Failure analysis of FRP laminates by means of physically based phenomenological models[J]. Composites Science and Technology,1998,58(7):1045-1067. DOI: 10.1016/S0266-3538(96)00140-6
[20] 杨凤祥, 陈静芬, 陈善富, 等. 基于剪切非线性三维损伤本构模型的复合材料层合板失效强度预测[J]. 复合材料学报, 2020, 37(9):2207-2222. YANG F X, CHEN J F, CHEN S F, et al. Failure strength prediction of composite laminates using 3D damage constitutive model with nonlinear shear effects[J]. Acta Materiae Compositae Sinica,2020,37(9):2207-2222(in Chinese).
[21] DAVILA C G. Failure criteria for FRP laminates[J]. Journal of Composite Materials,2003,39(4):404-408.
[22] PINHO S T, DAVILA C G, CAMANHO P P, et al. Failure models and criteria for FRP under in-plane or three-dimensional stress states including shear non-linearity[R]. NASA/TM-2005-213530, 2005.
[23] PINHO S. T. Modelling failure of laminated composites using physically-based failure models[D]. London: Imperial College London, 2005.
[24] PINHO S T, IANNUCCI L, ROBINSON P. Physically-based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking: Part I: Development[J]. Composites Part A: Applied Science and Manufacturing,2005,37(1):63-73.
[25] PINHO S T, IANNUCCI L, ROBINSON P. Physically based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking. Part II: FE implementation[J]. Composites Part A: Applied Science & Manufacturing,2006,37(5):766-777.
[26] PINHO S T, DARVIZEH R, ROBINSON P, et al. Material and structural response of polymer-matrix fibre-reinforced composites[J]. Journal of Composite Materials,2012,46(19-20):2313-2341. DOI: 10.1177/0021998312454478
[27] ARGON A S. Fracture of composites[J]. Treatise on Materials Science and Technology,1972,1:79-114.
[28] GIANNADAKIS K, VARNA J. Analysis of non-linear shear stress-strain response of unidirectional GF/EP composite[J]. Composites Part A: Applied Science and Manufacturing,2014,62(17):67-76.
[29] CHEN J F, MOROZOV E V, SHANKAR K. A combined elastoplastic damage model for progressive failure analysis of composite materials and structures[J]. Composite Structures,2012,94(12):3478-3489.
[30] 陈静芬. 基于弹塑性损伤本构模型的复合材料层合板破坏荷载预测[J]. 复合材料学报, 2017, 34(4):545-557. CHEN J F. Failure loads prediction of composite laminates using a combined elastoplastic damage model[J]. Acta Materiae Compositae Sinica,2017,34(4):545-557(in Chinese).
[31] SUN C T, CHEN J L. A simple flow rule for characterizing nonlinear behavior of fiber composites[J]. Journal of Composite Materials,1989,23(10):1009-1020. DOI: 10.1177/002199838902301004
[32] 薛康, 肖毅, 王杰, 等. 单向纤维增强聚合物复合材料压缩渐进破坏[J]. 复合材料学报, 2019, 36(6):1398-1412. XUE K, XIAO Y, WANG J, et al. Compression progressive failure of unidirectional fiber reinforced polymer composites[J]. Acta Materiae Compositae Sinica,2019,36(6):1398-1412(in Chinese).
[33] CHEN J F, MOROZOV E V. A consistency elasto-viscoplastic damage model for progressive failure analysis of composite laminates subjected to various strain rate loadings[J]. Composite Structures,2016,148:224-235.
[34] THIRUPPUKUZHI S V, SUN C T. Models for the strain-rate-dependent behavior of polymer composites[J]. Composites Science and Technology,2001,61(1):1-12.
[35] BAZANT Z P, OH B H. Crack band theory for fracture of concrete[J]. Matériaux et Construction,1983,16(3):155-177.
[36] WINN V M, SRIDHARAN S. An investigation into the accuracy of a one-parameter nonlinear model for unidirectional composites[J]. Journal of Composite Materials,2001,35(16):1491-1507. DOI: 10.1106/M99D-14RL-NHHF-CHWN
[37] SCHULTHEISZ C R, WAAS A M. Compressive failure of composites, part I: Testing and micromechanical theories[J]. Progress in Aerospace Sciences,1996,32(1):1-42. DOI: 10.1016/0376-0421(94)00002-3
[38] SCHAEFER J D, WERNER B T, DANIEL I M. Strain-rate-dependent failure of a toughened matrix composite[J]. Experimental Mechanics,2014,54(6):1111-1120. DOI: 10.1007/s11340-014-9876-0
[39] MUKHOPADAYAY S, JONES M I, STEPHEN R, et al. Compressive failure of laminates containing an embedded wrinkle: Experimental and numerical study[J]. Composites Part A: Applied Science and Manufacturing,2015,73:132-142.
-
计量
- 文章访问数: 1378
- HTML全文浏览量: 655
- PDF下载量: 173
